Important Questions for CBSE Class 12 Physics Chapter 11 Dual Nature of Radiation and Matter 2024-25

Very Short Question and Answer (1 Mark Questions)

1. Calculate the energy associated in \[\mathbf{eV}\] with a photon of wavelength  \[4000\overset{o}{\mathop{A}}\,\].

Ans: Given the wavelength of given photon is

\[\lambda =4000\overset{o}{\mathop{A}}\,=4\times {{10}^{-7}}m\]

Hence the energy associated is

$E=\frac{hc}{\lambda }=\frac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{4000\times {{10}^{-10}}}$

\[E=4.95\times {{10}^{-19}}J\]

$E=\frac{4.95\times {{10}^{-19}}J}{1.6\times {{10}^{-19}}}eV=3.09eV$

2. Mention one physical process for the release of electrons from the surface of a metal.

Ans: Photoelectric emission. 

The phenomenon in which the electrons from the surface of a metal are given energy in form of electromagnetic waves and they are ejected out, this phenomenon is called the photoelectric emission.

3. The maximum kinetic energy of photoelectron is \[2.8\text{ }eV\]. What is the value of stopping potential?

Ans: Given an electron that is moving with a kinetic energy. For it to be not ejected, it has to be held back using a stopping potential \[{{V}_{0}}\]. The relation between the two is:

$KE=e{{V}_{o}}=2.8eV$

$\Rightarrow {{V}_{o}}=2.8V$

4. Calculate the threshold frequency of photon for photoelectric emission from a metal of work function \[0.1\,eV\].

Ans: Given is the work function \[0.1\,eV\]

${{\phi }_{o}}=h{{\nu }_{0}}$

$\Rightarrow {{\nu }_{0}}=\frac{{{\phi }_{o}}}{h}=\frac{0.1eV}{6.6\times {{10}^{-34}}Js}$

\[\Rightarrow {{\nu }_{0}}=\frac{0.1\times 1.6\times {{10}^{-19}}J}{6.6\times {{10}^{-34}}Js}=2.4\times {{10}^{14}}Hz\]

And hence the threshold frequency is $2.4\times {{10}^{14}}Hz$.

5. Ultraviolet light is incident on two photosensitive materials having work function${{\phi }_{1}}$ and  ${{\phi }_{2}}$ (${{\phi }_{1}}>{{\phi }_{2}}$). In which of the case will K.E. of emitted electrons be greater? Why?

Ans: According to the energy balance equation of the photoelectric effect$hv={{\phi }_{o}}+K.E$

If  ${{\phi }_{1}}>{{\phi }_{2}}$ thus K.E. will be more for second surface whose work function is less.

6. Show graphically how the stopping potential for a given photosensitive surface varies with the frequency of incident radiations.

Ans: Suppose 

${{\nu }_{o}}$ is the threshold of frequency or cut off frequency;

${{V}_{o}}$ is the corresponding stopping potential

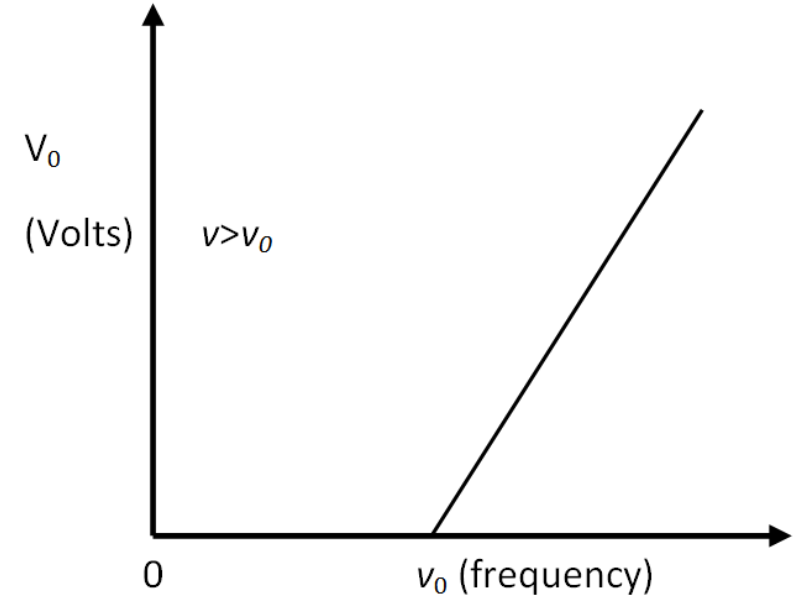
7. How does the stopping potential applied to a photocell change if the distance between the light source and the cathode of the cell is doubled?

Ans: Intensity of light drops quadratically with distance. However, the stopping potential does not depend on the intensity of the light. Hence it is independent of distance as well.

8. On what factor does the retarding potential of a photocell depend? 

Ans: The retarding photocell depends upon the frequency of the incident light.

9. Electron and proton are moving with same speed, which will have more wavelength?

Ans: Since the wavelength is inversely proportional to the square root of the mass of the body, $\lambda \propto \frac{1}{\sqrt{m}}$. So, electrons being lighter will have more wavelengths.

Short Question and Answer (2 Marks Questions)

1. Derive an expression for the de Broglie wavelength of an electron.

Ans: If a beam of electrons traveling through a potential difference of $V$ volt, the electron acquires kinetic energy which can be written as:

$\frac{1}{2}m{{v}^{2}}=eV$

$\Rightarrow mv=\sqrt{2meV}$

The de Broglie wavelength is $\lambda =\frac{h}{mv}\Rightarrow \lambda =\frac{h}{\sqrt{2meV}}\,\,$

Since  $eV=E$

$\Rightarrow \lambda =\frac{h}{\sqrt{2mE}}\text{  }$

Substituting the values of the constants $m,e,h\text{ }$we get:

$\Rightarrow \lambda =\frac{12.27}{\sqrt{V}}\overset{o}{\mathop{A}}\,$

Hence the expression for de Broglie wavelength is derived.

2. Light of wavelength $2000\overset{o}{\mathop{A}}\,$falls on an aluminium surface. In aluminium\[4.2\text{ }eV\]are required to remove an electron. What is the kinetic energy of (a) fastest (b) the slowest photoelectron?

Ans: Given wavelength is $\lambda =2000{{A}^{o}}=22\times {{10}^{-7}}m$and ${{\phi }_{o}}=4.2eV$  

The kinetic energy is $K.{{E}_{\max }}=\frac{1}{2}m{{V}^{2}}_{\max }=hv-{{\phi }_{o}}$

(a) $\frac{1}{2}m{{V}^{2}}_{\max }=\frac{hc}{\lambda }-{{\phi }_{o}}=\frac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{2\times {{10}^{-7}}}-4.2$

$\Rightarrow \frac{1}{2}m{{V}^{2}}_{\max }=2eV$

This is the K.E of the fastest electron is 2eV

(b) The velocity of the slowest electron would be zero, hence the kinetic energy it possesses is also zero.

3. An electromagnetic wave of wavelength $\mathbf{\lambda }$ is incident on a photosensitive surface of negligible work function. If the photoelectrons emitted from this surface have de Broglie wavelength ${{\lambda }_{1}}$. Prove that  $\lambda =\left( \frac{2mc}{h} \right){{\lambda }_{1}}^{2}$.

Ans: According to the energy balance equation of the Photoelectric effect

$hv=\phi +K.E$

For a metal with zero work function

$\frac{hv}{\lambda }=0+K.E$

Using ${{\lambda }_{1}}=\frac{h}{\sqrt{2mK.E}}$

${{\lambda }_{1}}=\frac{h}{\sqrt{2m\frac{hc}{\lambda }}}=\sqrt{\frac{h\lambda }{2mc}}$

Or

$\lambda =\left( \frac{2mc}{n} \right){{\lambda }^{2}}_{1}$

Hence proved.

4. Is it more difficult to remove a free electron from copper than from sodium? Why?

Ans: Since ${{\phi }_{o}}=\frac{hc}{{{\lambda }_{o}}}$

Where ${{\lambda }_{o}}$  is the threshold wavelength

And since  ${{\lambda }_{o}}_{Na}>{{\lambda }_{o}}_{Cu}$;

The work function for copper is greater and it becomes difficult to remove a free electron from copper.

5. Obtain the expression for the maximum kinetic energy of the electrons emitted from a metal surface in terms of the frequency of the incident radiation and the threshold frequency.

Ans: According to the energy balance equation of the Photoelectric effect

$K.{{E}_{\max }}=hv-w$

w is the threshold energy or work function depends upon threshold frequency  ${{v}_{o}}$ and $w=h{{v}_{o}}$

In other words;

$hv=\frac{1}{2}m{{v}_{\max }}^{2}+h{{v}_{o}}$.

6. For a given K.E. which of the following has the smallest de–Broglie wavelength: electron, proton, alpha -particle?

Ans: It is known that,

de Broglie wavelength, $\lambda =\frac{h}{mv}$

And the momentum is $mv=\sqrt{2mE}$

When E is energy$\Rightarrow \lambda =\frac{h}{\sqrt{2mE}}$

Comparing masses, we get mass of $\alpha $-particle is more; hence wavelength of alpha particle is the smallest.

7. Photoelectrons are emitted with a maximum speed of \[7\times {{10}^{5}}m/s\] from a surface when light of frequency \[8\times {{10}^{14}}Hz\] is incident on it. Find the threshold frequency for this surface?

Ans: It is known that

$h\left( v-{{v}_{{}^\circ }} \right)=\frac{1}{2}m{{v}_{\max }}^{2}$

${{v}_{{}^\circ }}=\frac{v-m{{v}^{2}}_{\max }}{2h}$

${{v}_{{}^\circ }}=8\times {{10}^{14}}-\frac{9.1\times {{10}^{-31}}\times {{\left( 7\times {{10}^{5}} \right)}^{2}}}{2\times 6..63\times {{10}^{-34}}}$

${{v}_{{}^\circ }}=4.64\times {{10}^{14}}Hz$, which is the required threshold frequency.

8. Is photoelectric emission possible at all frequencies? Give reason for your answer.

Ans: No, photoelectric emission is not possible at all frequencies because it is possible only if radiation energy is greater than work function $\omega =h{{v}_{{}^\circ }}$   of the emitter.

9. Assume that the frequency of the radiation incident on a metal plate is greater than its threshold frequency. How will the following change, if the incident radiation is doubled? 

(1) Kinetic energy of electrons

(2) Photoelectric current

Ans: (1) If the frequency of the incident radiation is doubled, $hv-h{{v}_{{}^\circ }}$ is increased, hence kinetic energy is increased.

(2) If the frequency of the incident radiation is doubled, there will be no change in the number of photoelectrons i.e., photo electronic current.

10. Why are de Broglie waves associated with a moving football not visible?

Ans: The wavelength of a wave associated with a moving football is extremely small, which cannot be detected.

Since  $\lambda =\frac{h}{mv}$

11. By how much would the stopping potential for a given photosensitive surface go up if the frequency of the incident radiations were to be increased from\[4\times {{10}^{15}}Hz\text{ }to\text{ }8\times {{10}^{15}}Hz\] ? ( $\mathbf{h=6}\mathbf{.4\times 1}{{\mathbf{0}}^{\mathbf{-3}}}\mathbf{4Js,e=1}\mathbf{.6\times 1}{{\mathbf{0}}^{\mathbf{-19}}}\mathbf{C,c=3\times 1}{{\mathbf{0}}^{\mathbf{8}}}\mathbf{m/s}$ )

Ans: Stopping potential,  ${{V}_{0}}\propto v$

$\Rightarrow \frac{{{V}_{02}}}{{{V}_{01}}}=\frac{{{v}_{2}}}{{{v}_{1}}}=\frac{8\times {{10}^{15}}}{4\times {{10}^{15}}}=2$

$\Rightarrow {{V}_{02}}=2{{V}_{01}}$

Hence the stopping potential will go up to twice.

12. Work function of Na is\[2.3eV\]. Does sodium show photoelectric emission for light on the velocity of photoelectrons?

Ans: Since  $\frac{1}{2}m{{v}^{2}}\propto \frac{1}{\lambda }$

Hence, the velocity of photoelectrons increases with the decrease in the wavelength of the incident light.

13. An electron and an alpha particle have the same de Broglie wavelength associated with them? How are their kinetic energies related to each other?

Ans: It is known that de Broglie wavelength is expressed as:

$\lambda =\frac{h}{p}=\frac{h}{\sqrt{2mK}}$

It is provided that \[{{\lambda }_{\alpha }}={{\lambda }_{e}}\];

$\Rightarrow \frac{h}{\sqrt{2{{m}_{\alpha }}{{K}_{\alpha }}}}=\frac{h}{\sqrt{2{{m}_{e}}{{K}_{e}}}}$

$\Rightarrow \sqrt{\frac{{{K}_{\alpha }}}{{{K}_{e}}}}=\sqrt{\frac{{{m}_{e}}}{{{m}_{\alpha }}}}$

Now, the values of ${{m}_{e}}$ and ${{m}_{\alpha }}$ are $9.1\times {{10}^{-31}}kg$ and $6.64\times {{10}^{-27}}kg$ respectively. 

Clearly,

$\Rightarrow \frac{{{K}_{\alpha }}}{{{K}_{e}}}=\frac{{{m}_{e}}}{{{m}_{\alpha }}}=7294$

$\Rightarrow {{K}_{e}}=7294{{K}_{\alpha }}$, which is the required ratio of kinetic energies.

14. An $\alpha $-particle and a proton are accelerated from rest through the same potential difference $V$ . Find the ratio of de–Broglie wavelength associated with them.

Ans: It is provided that

${{V}_{\alpha }}={{V}_{p}}=V$

It is known that momentum is given by

$p=\sqrt{2mE}=\sqrt{2mqV}$

Now, it is known that

\[{{m}_{\alpha }}=4{{m}_{p}};{{q}_{\alpha }}=2{{q}_{p}}\]

\[\Rightarrow {{p}_{\alpha }}=\sqrt{2\times 4{{m}_{p}}}\times 2{{q}_{p}}V\]

Clearly, taking ratio of momenta,

$\frac{{{p}_{\alpha }}}{{{p}_{p}}}=\frac{\sqrt{2\times 4{{m}_{p}}\times 2{{q}_{p}}V}}{\sqrt{2{{m}_{p}}{{q}_{p}}V}}=\frac{\sqrt{8}}{1}$

Now, since $\lambda \propto \frac{1}{p}$

$\Rightarrow \frac{{{\lambda }_{\alpha }}}{{{\lambda }_{p}}}=\frac{1}{\sqrt{8}}=\frac{1}{2\sqrt{2}}$

$\Rightarrow {{\lambda }_{\alpha }}:{{\lambda }_{p}}=1:2\sqrt{2}$

Thus, the wavelength of proton is $2\sqrt{2}$ times the wavelength of alpha particle.

15. The photoelectric cut-off voltage in a certain experiment is\[~1.5\text{ }V\] . What is the maximum kinetic energy of photoelectrons emitted?

Ans: The given photoelectric cut-off voltage,  \[{{V}_{{}^\circ }}=\text{ }1.5\text{ }V~\].

The maximum kinetic energy of the emitted photoelectrons is given as:

$KE=1.5\,e{{V}_{{}^\circ }}$

Where,

\[e=\]Charge on an electron\[~=1.6\times {{10}^{-19}}C~\]

$\Rightarrow KE=1.6\times {{10}^{-19}}\times 1.5=2.4\times {{10}^{-19}}J$

Therefore, the maximum kinetic energy of the photoelectrons emitted in the given experiment is  $2.4\times {{10}^{-19}}$ J.

16. The threshold frequency for a certain metal is $3.3\times {{10}^{14}}$  Hz. If light of frequency $8.2\times {{10}^{14}}$  Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission.

Ans: Given that

Threshold frequency of the metal, ${{v}_{{}^\circ }}=3.3\times {{10}^{14}}$

Frequency of light incident on the metal,$v=8.2\times {{10}^{14}}Hz$

Charge on an electron, \[e=1.6\times {{10}^{-19}}C~\]

Planck's constant, \[h=6.626\times {{10}^{-34}}Js~\]

Cut-off voltage for the photoelectric emission from the metal $={{V}_{{}^\circ }}$

The equation for the cut-off energy is given as:

$e{{V}_{{}^\circ }}=h\left( v-{{v}_{{}^\circ }} \right)$

$\Rightarrow {{V}_{{}^\circ }}=\frac{h\left( v-{{v}_{o}} \right)}{e}=\frac{6.626\times {{10}^{-34}}\mp \left( 8.2\times {{10}^{14}}-3.3\times {{10}^{14}} \right)}{1.6\times {{10}^{-19}}}=2.0292V$

Therefore, the cut-off voltage for the photoelectric emission is \[2.0292\text{ }V~\].

17. The work function for a certain metal is \[\mathbf{4}\mathbf{.2 eV}\]. Will this metal give photoelectric emission for incident radiation of wavelength \[\mathbf{330 nm}\]?

Ans: No.

Work function of the metal,${{\phi }_{o}}=4.2eV$

Charge on an electron\[,e=1.6\times {{10}^{-19}}C~\]

Planck's constant, \[h=6.626\times {{10}^{-34}}Js~\]

Wavelength of the incident radiation,  \[\lambda =330nm=330\times {{10}^{-9}}m~\]

Speed of light, \[c=3\times {{10}^{8}}m/s~\]

The energy of the incident photon is given as:

$E=\frac{hc}{v}=\frac{6.626\times {{10}^{-34}}\times 3\times {{10}^{8}}}{330\times {{10}^{-9}}}=6.0\times {{10}^{-19}}J$

$\Rightarrow E=\frac{6.0\times {{10}^{-19}}}{1.6\times {{10}^{-19}}}=3.76eV$

It can be observed that the energy of the incident radiation is less than the work function of the metal. Hence, no photoelectric emission will take place.

Long Question and Answer (3 Marks Questions)

1. The following table gives the values of work functions for a few sensitive metals.

If each of these metals is exposed to radiations of wavelength \[3300nm,\] which of these will not exit photoelectrons and why?

Ans: It is known that material will not emit photoelectrons whose work function is greater than the energy of the incident radiation.

$E=\frac{hc}{\lambda }=\frac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{33\times {{10}^{-8}}}$

$E=6.20\times {{10}^{-19}}J$

$\Rightarrow E=\frac{6.20\times {{10}^{-19}}}{1.6\times {{10}^{-19}}eV}$

\[\Rightarrow E\text{ }=\text{ }3.76\text{ }eV~\]

Hence work function of ${{M}_{o}}$  is (\[4.17eV\]) which is greater than the energy of the incident radiation (\[=\text{ }3.76\text{ }eV\] ) so ${{M}_{o}}$will not emit photoelectrons.

2. Define threshold wavelength for photoelectric effect? de Broglie wavelength associated with an electron associated through a potential difference $\mathbf{V}$ is $\mathbf{\lambda }$. What will be the new wavelength when the accelerating potential is increased to \[\mathbf{~4V}\]?

Ans: The maximum wavelength of radiation needed to cause photoelectric emission is known as threshold wavelength.

$\lambda =\frac{12.27}{\sqrt{V}}{{A}^{o}}$

$\lambda '=\frac{12.27}{\sqrt{4V}}\overset{o}{\mathop{A}}\,=\frac{12.27}{2\sqrt{V}}\overset{o}{\mathop{A}}\,$

$\frac{\lambda '}{\lambda }=\frac{1}{2}$

Or

$\lambda '=\frac{\lambda }{2}$

Hence the new wavelength is half of the earlier one.

3. An electron has kinetic energy equal to\[\mathbf{100eV}\]. Calculate (1) momentum (2) speed (3) de Broglie wavelength of the electron.

Ans: The given kinetic energy is $\frac{1}{2}m{{v}^{2}}=100eV=100\times 1.6\times {{10}^{-19}}J=1.6\times {{10}^{-17}}J$

Multiply by $m$

$\frac{1}{2}{{m}^{2}}{{v}^{2}}=1.6\times {{10}^{-17}}\times 9.11\times {{10}^{-31}}=14.5\times {{10}^{-48}}$

1) (Momentum) $P=mv=\sqrt{2\times 14.5\times {{10}^{-48}}}$

$P=5.40\times {{10}^{-24}}kgm/s$

2) Speed is equal to $\frac{P}{m}$.

$v=\frac{5.40\times {{10}^{-24}}}{9.1\times {{10}^{-31}}}=5.93\times {{10}^{6}}m/s$

3) de Broglie wavelength $\lambda =\frac{h}{mV}$

$\Rightarrow \lambda =\frac{6.6\times {{10}^{-34}}}{5.40\times {{10}^{-24}}}$

$\Rightarrow \lambda =1.23\overset{{}^\circ }{\mathop{A}}\,$

4. 

a) Define photoelectric work function? What is its unit?

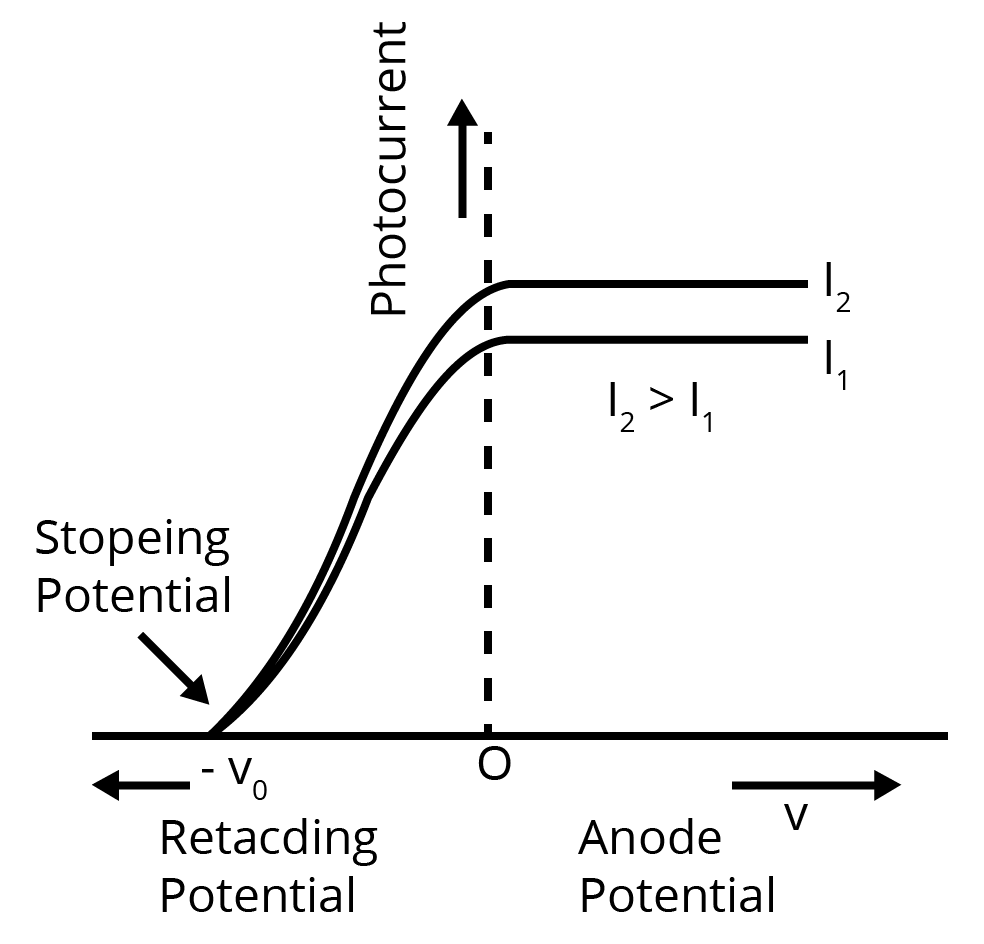
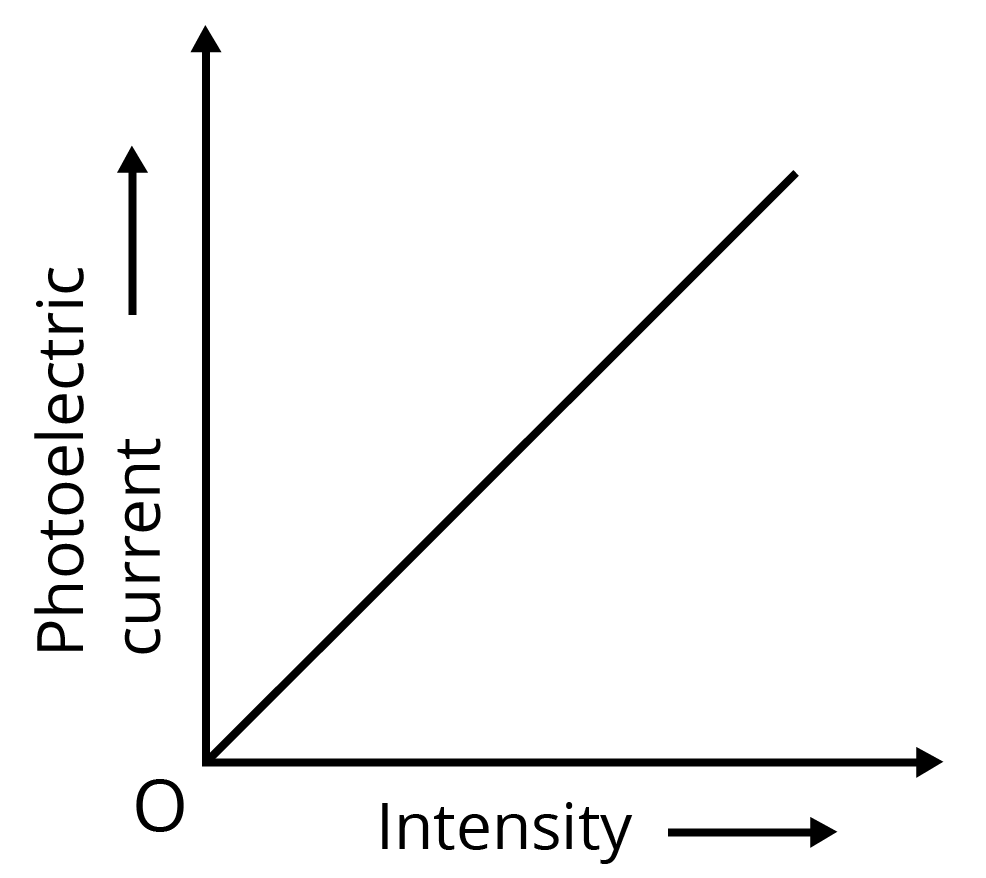
b) In a plot of photoelectric current versus anode potential, how does:

i) Saturation current varies with anode potential for incident radiations of different frequencies but same intensity?

ii) The stopping potential varies for incident radiations of different intensities but same frequency?

iii) Photoelectric current varies for different intensities but same frequency of radiations? Justify your answer in each case.

Ans: The minimum amount of energy required to take out an electron from the surface of metal. It is measured in electron volt (eV).

i) Saturation current depends only on the intensity of incident radiation but is independent of the frequency of incident radiation.

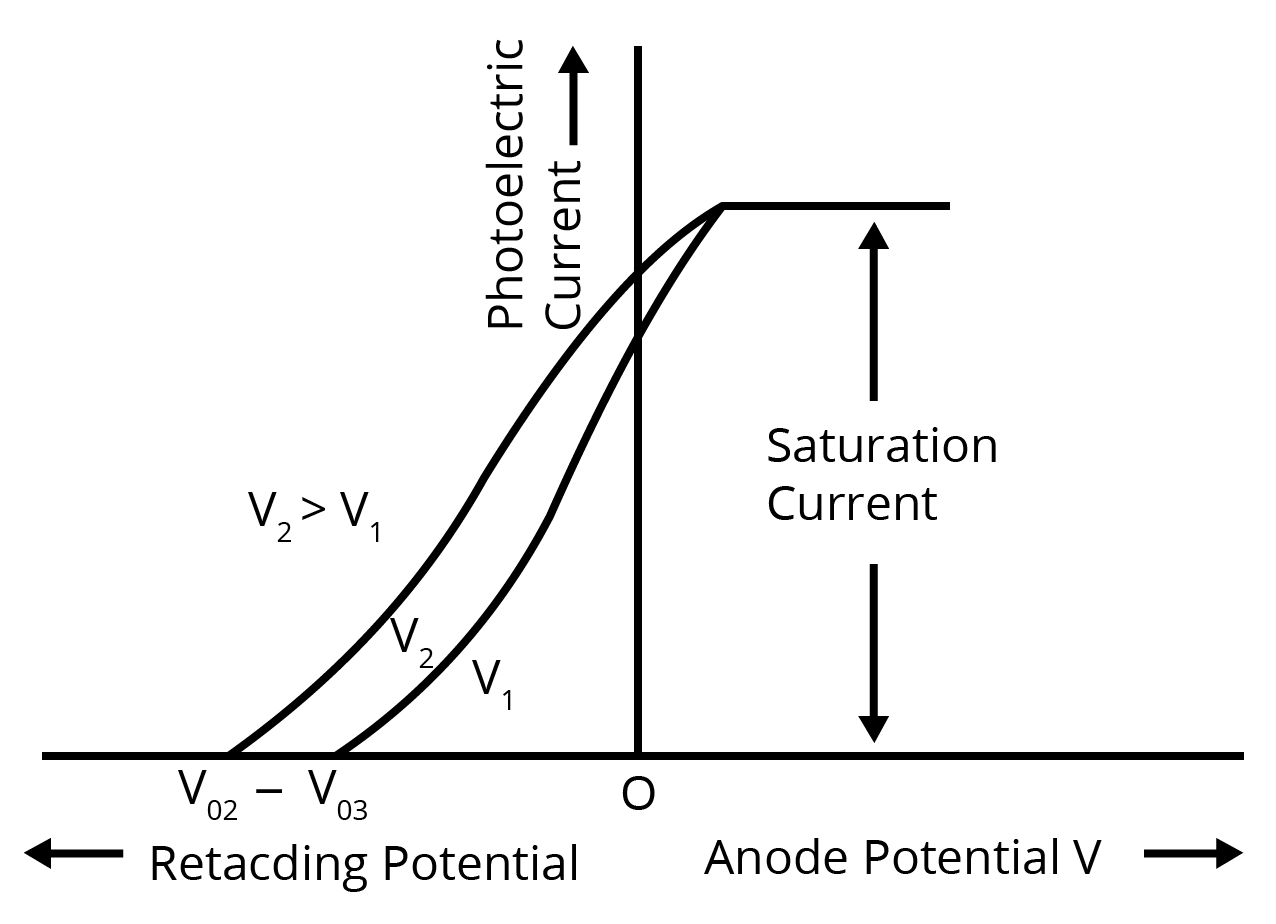
ii) Stopping potential does not depend on the intensity of incident radiations.

iii) Photoelectric current is directly proportional to the intensity of incident radiations, provided the given frequency is greater than the threshold frequency.

5. Photoelectric work function of a metal is\[\mathbf{1eV}\]. Light of wavelength $\mathbf{3000}{{\mathbf{A}}^{\mathbf{o}}}$ falls on it. What is the velocity of the affected photoelectron?

Ans: Given the work function is \[W=1eV\] 

And the wavelength is\[\lambda =3000\overset{o}{\mathop{A}}\,=3\times {{10}^{-7}}(meters)=\frac{h}{mv}\text{ or }mv=\frac{h}{\lambda }\]

According to photoelectric effect:

\[(1/2)m{{v}^{2}}=\frac{hc}{\lambda }-W\]

\[\Rightarrow v=\sqrt{2\frac{\left( \frac{hc}{\lambda }-W \right)}{m}}\approx {{10}^{6}}m/s\]

Hence the photoelectron is ejected with the velocity of \[{{10}^{6}}m/s\].

6. The wavelength  $\mathbf{\lambda }$  of a photon and de Broglie wavelength of an electron have the same value. Show that the energy of the photon is $\frac{\mathbf{2\lambda mc}}{\mathbf{h}}$  times the kinetic energy of electron where m, c, and h have their usual meanings?

Ans: Energy of a photon  \[E=hv=\frac{hc}{\lambda }....(1)\]

Kinetic energy $E'=\frac{1}{2}m{{v}^{2}}=\frac{{{m}^{2}}{{v}^{2}}}{2m}=\frac{{{\left( mv \right)}^{2}}}{2m}$   of an electron

But de-Broglie wavelength of an electron is given by

$\lambda =\frac{h}{mv}\text{ or }mv=\frac{h}{\lambda }$

$\Rightarrow K.E\left( E \right)=\frac{{{h}^{2}}}{2m{{\lambda }^{2}}}....(2)$

Dividing (1) by (2)

$\frac{E}{E'}=\frac{hc}{\lambda }\times \frac{2m{{\lambda }^{2}}}{{{h}^{2}}}=\frac{2m\lambda c}{h}$

$\Rightarrow E=\left( \frac{2m\lambda c}{h}E' \right)$

7. Draw a graph showing the variation of stopping potential with frequency of the incident radiations. What does the slope of the line with the frequency axis indicate? Hence define threshold frequency.

Ans: Slope of the following graph $=\frac{\Delta {{V}_{o}}}{\Delta \nu }$

Einstein photoelectric equation

$e{{V}_{o}}=h\nu -{{\phi }_{o}}$ …..(1)

Differentiating equation (1)

$e\Delta {{V}_{o}}=h\Delta \nu $

$\Rightarrow \frac{\Delta {{V}_{o}}}{\Delta \nu }=\frac{h}{e}$

Thus, slope is equal to the ratio of Planck’s constant to the charge on electron.

Threshold frequency – The minimum values of frequency of the incident light below which photoelectric emission is not possible is called threshold frequency.

8.  Find the

a) maximum frequency of X-rays produced by \[30\,kV\]electrons.

Ans: Given, The potential of the electrons,\[{{V}_{0}}=30kV\], 

The total energy is equal to the sum of the work function and the kinetic energy, 

\[h\upsilon ={{\phi }_{0}}+{{K}_{\max }}\]

\[\Rightarrow e{{V}_{0}}=h\upsilon -{{K}_{\max }}\]

For maximum frequency, it can be assumed that \[KE=0\]

\[\Rightarrow {{\upsilon }_{\max }}=e{{V}_{0}}/h\]

Using \[e=\mathbf{1}.\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{19}}}\mathbf{C}\,,\,\,h=6.63\times {{10}^{-34}}\,J.s\]\

[\Rightarrow {{\upsilon }_{\max }}=7.24\times {{10}^{18}}Hz\]
Hence the maximum frequency is \[=7.24\times {{10}^{18}}Hz\]

b) Minimum wavelength of X-rays produced by \[30\,kV\]electrons.

Ans: It is known that the product of the wavelength of a particle and its frequency is equal to the speed

\[c=\lambda \upsilon \]

This means that to obtain the minimum wavelength, we need the wavelength corresponding to maximum frequency

\[\Rightarrow \lambda =c/{{\upsilon }_{\max }}=(3\times {{10}^{8}})/(7.24\times {{10}^{18}})=0.041nm\]

Thus, the minimum wavelength is obtained as \[=0.041\,nm\].

9. The work function of caesium metal is \[\mathbf{2}.\mathbf{14}\text{ }\mathbf{eV}\]. When light of frequency \[6\times {{10}^{14}}Hz\] is incident on the metal surface, photoemission of electrons occurs. 

a) What is the maximum kinetic energy of the emitted electrons? 

Ans: Given the work function of caesium, \[{{\phi }_{0}}=\mathbf{2}.\mathbf{14}\text{ }\mathbf{eV}=2.14\times (1.6\times {{10}^{19}})J\]

And the frequency of incident light,\[\upsilon =6\times {{10}^{-14}}Hz\]

Maximum kinetic energy is the difference between the photon energy and the work function of the metal. 

The total energy is equal to the sum of the work function and the Kinetic energy of the emitted electron

\[h\upsilon ={{\phi }_{0}}+{{K}_{\max }}\]

\[\Rightarrow {{K}_{\max }}=h\upsilon -{{\phi }_{0}}\]

Hence the kinetic energy is obtained by substituting the values of the frequency, the Planck’s constant and the work function:

\[\Rightarrow {{K}_{\max }}=(6.63\times {{10}^{-34}}\,\times 6\times {{10}^{-14}})-(2.14\times (1.6\times {{10}^{19}})=5.54\times {{10}^{-20}}J\]

\[\Rightarrow {{K}_{\max }}=0.346eV\].

The maximum KE is \[0.346eV\].

b) What is the stopping potential? 

Ans: Stopping potential is the one required to stop the emission, which means that the energy this potential provides should cancel the maximum kinetic energy

\[\Rightarrow e{{V}_{stop}}={{K}_{\max }}\]

\[\Rightarrow e{{V}_{stop}}={{K}_{\max }}/e=0.346V\].

Hence the stopping potential is 0.346V

c) What is the maximum speed of the emitted photoelectrons?

Ans: Maximum KE of the photoelectron is the KE corresponding to the fastest ones, 

\[\Rightarrow {{K}_{\max }}=\frac{m{{v}^{2}}}{2}\] 

It is known that \[{{m}_{e}}=9.11\times {{10}^{-31}}kg\,\]

\[\Rightarrow ~v\text{ }=\text{ }344\text{ }km/\text{ }s\]  

Hence the fastest velocity of the electron is \[344\text{ }km/\text{ }s\].

10.  The energy flux of sunlight reaching the surface of the earth is \[\mathbf{1}.\mathbf{388}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{3}}}\text{ }\mathbf{W}/{{\mathbf{m}}^{\mathbf{2}}}\]. How many photons (nearly) per square meter are incident on the Earth per second? Assume that the photons in the sunlight have an average wavelength of \[550nm\]. 

Ans: The energy flux is the rate of energy being incident on the earth’s surface per unit area. It is equal to the product of the energy of each photon and the number rate of them: 

Energy flux = \[1388\text{ }W/{{m}^{2}}\]

wavelength = \[550nm\]

The energy of each photon \[E=h\frac{c}{\lambda }=3.6\times {{10}^{-19}}J\]

Total energy flux: \[P\text{ }=\text{ }E\times N\]

Here N is the no. of photons per unit area 

\[\Rightarrow N=\text{ }P\text{ }/\text{ }E=4\times {{10}^{21}}{{m}^{-2}}{{s}^{-1}}\]

Hence the number of photons being incident per unit meter square per second is \[4\times {{10}^{21}}\].

11.  In an experiment on photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be \[\mathbf{4}.\mathbf{12}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{15}}}\mathbf{V}s\]. Calculate the value of Planck’s constant. 

Ans: Slope here refers to the ratio of Planck’s constant to the charge of an electron.

Given value of the slope = \[\mathbf{4}.\mathbf{12}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{15}}}\mathbf{V}s\]

\[\Rightarrow h/e=\mathbf{4}.\mathbf{12}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{15}}}\mathbf{V}s\,\]where e is the charge of an electron

\[\Rightarrow h=\mathbf{4}.\mathbf{12}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{15}}}\times 1.6\times {{10}^{-19}}=6.59\times {{10}^{-34}}Js\]

Hence Planck's constant is obtained as \[=6.59\times {{10}^{-34}}Js\,\,\].

12. A \[\mathbf{100W}\] sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is \[589nm\].

a) What is the energy per photon associated with the sodium light? 

Ans: The radiation power is given as \[P\text{ }=\text{ }100\text{ }W\] and the wavelength of the radiation is \[\lambda =589nm\]

The energy of each photon \[E=h\frac{c}{\lambda }=3.37\times {{10}^{-19}}J\,\](c is the speed of light).

b) At what rate are the photons delivered to the sphere?

Ans: The number of photons per second or the rate of photons emitted is the ratio of the total imparted power and the energy of each photon, \[=\text{ }P/E=3\times {{10}^{20}}/s\].

Very Long Question and Answer (5 Mark Questions)

1. Monochromatic light of wavelength \[\mathbf{632}.\mathbf{8}\text{ }\mathbf{nm}\] is produced by a helium-neon laser. The power emitted is \[\mathbf{9}.\mathbf{42}\text{ }\mathbf{mW}\]. 

a) Find the energy and momentum of each photon in the light beam, 

Ans: The wavelength of the given monochromatic light, \[\lambda =\mathbf{632}.\mathbf{8}\text{ }\mathbf{nm}\]

The power of the given He-ne laser, \[P=\mathbf{9}.\mathbf{42}\text{ }\mathbf{mW}\,\]

Energy of a photon is given by 

\[E\text{ }=\text{ }hv=h\frac{c}{\lambda }\]

Substituting the wavelength we get:

\[E\text{ }=\text{ 3}\text{.14}\times \text{1}{{\text{0}}^{-19}}J\] 

Now momentum of a photon 

\[p=h\text{/}\lambda =1.05\times {{10}^{-27}}kg\,m/s\]

Hence the energy and the momentum are \[\text{3}\text{.14}\times \text{1}{{\text{0}}^{-19}}J\]and \[1.05\times {{10}^{-27}}kg\,m/s\] respectively.

b) How many photons per second, on the average, arrive at a target irradiated by this beam? (Assume the beam to have uniform cross-section which is less than the target area), and  

Ans: Power is the rate of energy imparted to the target, which is given as the product of energy per particle and the number rate of particles hitting the target

\[P\text{ }=\text{ }E\times N\] 

Where, 

P = power emitted 

E = energy of photon 

N = number of photons 

Simplifying for N and substituting the values of P and E gives 

\[N=3\times {{10}^{16}}{{s}^{-1}}\] 

\[3\times {{10}^{16}}\]photons per second arrive at the target.

c) How fast does a hydrogen atom have to travel in order to have the same momentum as that of the photon? 

Ans: Given momentum of the photons from He-Ne laser \[p=h\text{/}\lambda =1.05\times {{10}^{-27}}kg\,m/s\]

The momentum of a hydrogen atom is: \[{{p}_{H}}={{m}_{H}}{{v}_{H}}\]

\[\Rightarrow {{v}_{H}}={{p}_{H}}/{{m}_{H}}=1.05\times {{10}^{-27}}/1.6\times {{10}^{-27}}=0.63m/s\]

The required speed for hydrogen atom is 0.63 m / s.

2. Light of frequency \[7.21\times \mathbf{1}{{\mathbf{0}}^{\mathbf{14}}}\mathbf{Hz}\] is incident on a metal surface. Electrons with a maximum speed of \[6.0\times {{10}^{5}}m/s\] are ejected from the surface. What is the threshold frequency for photoemission of electrons?

Ans: Given frequency of the incident light is \[{{\upsilon }_{{}}}=7.21\times {{10}^{14}}Hz\]

And the velocity of the ejected electron is \[v=6\times {{10}^{5}}m/s\]

And hence, the kinetic energy is\[{{K}_{{}}}=\frac{1}{2}m{{v}^{2}}\], here m is the mass of the electron

Also, in the case of photoelectric effect: \[K=h(\upsilon -{{\upsilon }_{0}})\], here h is the Planck’s constant

Solving for the cut-off frequency, we get \[{{\upsilon }_{0}}=4.73\times {{10}^{14}}Hz\].

3. Light of wavelength \[488nm\] is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut-off) potential of photoelectrons is \[0.38V\]. Find the work function of the material from which the emitter is made.

Ans: Given wavelength of the incident light is \[\lambda =\,488nm\,\]

Hence the energy of the incident photons is obtained as \[E=h\frac{c}{\lambda }\]; here h is the Planck’s constant and c is the speed of light.

And the stopping potential/cut-off potential is \[\,{{V}_{0}}=0.38V\]

Hence the corresponding energy is \[e{{V}_{0}}\]

The work function is the obtained as

\[E-e{{V}_{0}}=h\frac{c}{\lambda }-e{{V}_{0}}=3.46\times {{10}^{-10}}J=2.16eV\]

Hence the work function is obtained as \[2.16eV\].

4.  Calculate the

a) Momentum of the electrons accelerated through a potential difference of \[56V\].

Ans: The given potential difference is \[V=56V\]

Momentum of a particle can be expressed as \[p=\sqrt{2meV}\] 

Here The mass of the electron \[{{m}_{e}}=9.1\times {{10}^{-31}}kg\] , e is the charge 

Hence the obtained momentum is \[\Rightarrow p=4.04\times {{10}^{-24}}kg\,m/s\].

b) De Broglie wavelength of the electrons accelerated through a potential difference of \[56V\].

Ans: Corresponding de Broglie wavelength is given as \[\lambda =h/p=0.164nm\], here the h is for the Planck’s constant.

5. What is the

a) Momentum of an electron with kinetic energy of \[120eV\]?

Ans: The given kinetic energy \[K=120eV\]

Momentum can be written as \[p=\sqrt{2mK}\]

\[\Rightarrow p=5.91\times {{10}^{-24}}kg\,m/s\].

b) Speed of an electron with kinetic energy of \[120eV\]?

Ans: The speed of an electron can be written as \[v=\sqrt{\frac{K}{2m}}=6.5\times {{10}^{6}}m/s\]. Here, K is the kinetic energy and m is the mass of the electron.

c) De Broglie wavelength of an electron with kinetic energy of \[120eV\]?

Ans: The de Broglie wavelength is given as \[\,\lambda =h/p=0.112nm\], where h is the Planck’s constant and p is the momentum.

6. The wavelength of light from the spectral emission line of sodium is \[589nm\]. Find the kinetic energy at which, 

a) An electron and

Ans: Given wavelength of the incident light is \[\,\lambda =589nm\,\,\]

For h as Planck’s constant the momentum can be given as \[\,p=h/\lambda =1.12\times {{10}^{-17}}kg\,m/s\]

If the de Broglie wavelength of an electron is same as that of a neutron, then their respective momenta are also equal.

Using this kinetic energy is related to the momentum by: \[K={{p}^{2}}/2{{m}_{e}}=6.9\times {{10}^{-25}}J\]

b) A neutron would have the same de Broglie wavelength.

Ans: The momentum is the same as obtained earlier

Similarly, the kinetic energy for a neutron is

\[{{K}_{n}}={{p}^{2}}/2{{m}_{n}}=3.7\times {{10}^{-28}}J\].

7. What is the de Broglie wavelength of

a) a bullet of mass \[0.040kg\] travelling at the speed of \[1.0km/s\],

Ans: Given mass is \[m=0.040kg\], moving with velocity\[v=1.0km/s=1000m/s\]

De Broglie wavelength is given by \[\lambda =\frac{h}{mv}=1.66\times {{10}^{-35}}m\]

Hence the de Broglie wavelength of the bullet is \[1.66\times {{10}^{-35}}m\].

b) A ball of mass \[0.060kg\] moving at a speed of \[1.0m/s\], and

Ans: Given mass is \[m=0.060kg\]moving with velocity\[v=1.0m/s\]

De Broglie wavelength is given by \[\lambda =\frac{h}{mv}=1.1\times {{10}^{-32}}m\]

Hence the de Broglie wavelength of the bullet is \[1.1\times {{10}^{-32}}m\].

c) A dust particle of mass \[1.0\times {{10}^{-9}}kg\] drifting with a speed of \[\mathbf{2}.\mathbf{2}\text{ }\mathbf{m}/\mathbf{s}\]?

Ans: Given mass of the dust particle is \[m={{10}^{-9}}kg\]moving with velocity\[v=2.2m/s\]

De Broglie wavelength is given by \[\lambda =\frac{h}{mv}=3\times {{10}^{-25}}m\]

Hence the de Broglie wavelength of the bullet is \[3\times {{10}^{-25}}m\].

8. An electron and a photon each have a wavelength of \[\mathbf{1}.\mathbf{00nm}\]. Find

a) Their momenta,

Ans: Given wavelength for photon and electron is \[\lambda =1.00nm\]

The mass of the electron \[{{m}_{e}}=9.1\times {{10}^{-31}}kg\]

The momentum of the electron is given by\[{{p}_{e}}=h/\lambda \]

\[\Rightarrow p=6.63\times {{10}^{-25}}kg\,m/s\]

Momentum of the photon is given by \[{{p}_{p}}=h/\lambda \]

\[\Rightarrow p=6.63\times {{10}^{-25}}kg\,m/s\]

Both the momenta are equal

b) The energy of the photon, and

Ans: Energy of photon: \[E=h\,c/\lambda \]

Here, h is the Planck’s constant and c is the speed of light 

Hence by substituting these values the energy is obtained as \[1.24keV\]

c) The kinetic energy of electron.

Ans: Given wavelength is  \[\lambda =1.00nm\]

Hence the kinetic energy of the electron is \[K={{p}^{2}}/2{{m}_{e}}=1.51eV\].

9. 

a) For what kinetic energy of a neutron will the associated de Broglie wavelength be \[1.40\times {{10}^{-10}}m\]?

Ans: Given de Broglie wavelength is \[\lambda =1.40\times {{10}^{-10}}m\,\]

Hence the associated momentum is \[p=h/\lambda \]

Kinetic energy associated with this neutron is \[K={{p}^{2}}/2{{m}_{e}}=\frac{{{h}^{2}}}{2m{{\lambda }^{2}}}=6.68\times {{10}^{-21}}J\]

Hence the kinetic energy is obtained as \[6.68\times {{10}^{-21}}J\]

b) Also find the de Broglie wavelength of a neutron, in thermal equilibrium with matter having an average kinetic energy of \[\left( \mathbf{3}/\mathbf{2} \right)\mathbf{kT}\] at \[\mathbf{300}\text{ }\mathbf{K}\].

Ans: Given is the kinetic energy as \[K=(3/2)\,k\,T\]with temperature \[T=300K\]

Here k is the Boltzmann constant \[k=1.38\times {{10}^{-23}}J/K\]

\[\Rightarrow K=6.21\times {{10}^{-21}}J\]

Hence the wavelength is obtained as \[\lambda =\frac{h}{\sqrt{2mK}}=0.145nm\]

10. Show that the wavelength of electromagnetic radiation is equal to the de Broglie wavelength of its quantum (photon). 

Ans: The momentum of a photon having energy $\left( hv \right)$ is expressed as: 

$p=\frac{h}{\lambda }$ 

$\Rightarrow \lambda =\frac{h}{p}\to (1)$ 

Where, 

$\lambda $ is the wavelength of the electromagnetic radiation 

h is the Planck's constant 

Now, de Broglie wavelength of the photon is expressed as: 

$\lambda =\frac{h}{mv}$ 

However, it is known that 

\[p=mv~\] 

$\Rightarrow \lambda =\frac{h}{p}\to (2)$ 

Where, 

‘m’ is the mass of the photon 

‘v’ is the velocity of the photon 

Clearly, it can be concluded from equations (1) and (2) that the wavelength of the electromagnetic radiation is the same as the de Broglie wavelength of the photon.

11. What is the de Broglie wavelength of a nitrogen molecule in air at \[\mathbf{300}\text{ }\mathbf{K}\]? Assume that the molecule is moving with the root-mean square speed of molecules at this temperature. (Atomic mass of nitrogen \[=\mathbf{14}.\mathbf{0076}\text{ }\mathbf{u}\])

Ans: Given temperature is 300K.

Mass of the molecule= \[m=14.0076\times {{10}^{-27}}kg\]

The kinetic energy is\[\text{K }=1.5kT\]

And the de Broglie wavelength is \[\lambda =\frac{h}{\sqrt{2mk}}=0.038nm\]

Hence the de Broglie wavelength is obtained as 0.038nm.

12. 

a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of \[500V\] with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be \[\mathbf{1}.\mathbf{76}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{11}}}\mathbf{Ck}{{\mathbf{g}}^{-\mathbf{1}}}\].

Ans: Given potential difference is \[V=5\mathbf{00}\text{ }\mathbf{V}\,\], and charge per mass of electron is \[\,e/m=\mathbf{1}.\mathbf{76}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{11}}}\mathbf{Ck}{{\mathbf{g}}^{-\mathbf{1}}}\]

Kinetic energy can be written as: \[\text{K }=eV=m{{v}^{2}}/2\]

Hence, the speed of each emitted electron is: \[v=\sqrt{2V\frac{e}{m}}=1.366\times {{10}^{7}}m/s\]

b) Use the same formula you employ in (a) to obtain electron speed for a collector potential of 10MV. Do you see what is wrong? In what way is the formula to be modified?

Ans: Collector potential is given as \[V={{10}^{7}}V\]

The velocity is hence obtained as \[v=\sqrt{2V\frac{e}{m}}=1.88\times {{10}^{9}}m/s\]

This velocity is greater than that of the speed of light. This is not possible. We seem to have skipped the relativistic corrections as follows:

\[E=m{{c}^{2}}={{m}_{0}}{{\left( 1-\frac{{{v}^{2}}}{{{c}^{2}}} \right)}^{1/2}}\]; here \[{{m}_{0}}\]is the rest frame mass.

Accordingly, the kinetic energy becomes \[K=m{{c}^{2}}-{{m}_{0}}{{c}^{2}}\].

13. 

a) A mono energetic electron beam with electron speed of \[\mathbf{5}.\mathbf{20}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{6}}}\mathbf{m}/s\] is subject to a magnetic field of \[\mathbf{1}.\mathbf{30}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{4}}}\mathbf{T}\] normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals \[=\mathbf{1}.\mathbf{76}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{11}}}\mathbf{Ck}{{\mathbf{g}}^{-\mathbf{1}}}\].

Ans: The electrons have a speed of \[v=\,5.20\times {{10}^{6}}m/s\]  and the magnetic field is \[B=\,\mathbf{1}.\mathbf{30}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{4}}}\mathbf{T}\,\]

The specific charge i.e., charge to mass \[e/m=\mathbf{1}.\mathbf{76}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{11}}}\mathbf{Ck}{{\mathbf{g}}^{-\mathbf{1}}}\]

The force exerted on electron is:

\[F=e|v\times B|=evB\sin \theta \]

Here, \[\theta \] is the angle between the magnetic field and the beam velocity. The value of the force is maximum if the velocity and the field are perpendicular to each other.

Let’s say that the beam traces a circular path of radius, r. 

This means that the centripetal force needs to be equated to the magnetic force mentioned above

\[\Rightarrow \frac{m{{v}^{2}}}{r}=qvB\]

\[\Rightarrow r=\frac{m{{v}^{{}}}}{qB}=22.7cm\]

Hence the radius of the circular trajectory is 22.7cm

b) Is the formula you employ in (a) valid for calculating the radius of the path of a \[\mathbf{20}\text{ }\mathbf{MeV}\] electron beam? If not, in what way is it modified? {Note: Exercises 11.20(b) and 11.21(b) take you to relativistic mechanics which is beyond the scope of this book. They have been inserted here simply to emphasize the point that the formulas you use in part (a) of the exercises are not valid at very high speeds or energies.}

Ans: Given kinetic energy of an electron beam \[K=\mathbf{20}\text{ }\mathbf{MeV}\,\]. Hence, the corresponding velocity\[v=\sqrt{2k/m}\]. It can be seen that the velocity is higher than that of the speed of light. Hence relativistic corrections should be introduced.

\[m={{m}_{0}}{{\left[ 1-{{\left( \frac{v}{c} \right)}^{2}} \right]}^{-1/2}}\]; here, \[{{m}_{0}}\] is the rest mass, c is the speed of light

Hence the corrected radius of the trajectory would become:

\[r=mv/(e\,B)\]

\[r=\frac{{{m}_{0}}v}{eB}{{\left[ 1-{{\left( \frac{v}{c} \right)}^{2}} \right]}^{-1/2}}\]

Hence, the corrected radius is \[r=\frac{{{m}_{0}}v}{eB}{{\left[ 1-{{\left( \frac{v}{c} \right)}^{2}} \right]}^{-1/2}}\].

14. An electron gun with its an electron gun with its collector at a potential of \[\mathbf{100}\text{ }\mathbf{V}\] fires out electrons in a spherical bulb containing hydrogen gas at low pressure (\[\mathbf{1}{{\mathbf{0}}^{-\mathbf{2}}}\mathbf{mm}\] of Hg). A magnetic field of \[\mathbf{2}.\mathbf{83}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{4}}}\mathbf{T}\] curves the path of the electrons in a circular orbit of radius \[\mathbf{12}.\mathbf{0}\text{ }\mathbf{cm}\]. (The path can be viewed because the gas ions in the path focus the beam by attracting electrons, and emitting light by electron capture; this method is known as the ‘fine beam tube’ method. Determine e/m from the data.

Ans: Given potential of an anode, \[V\text{ }=\text{ }100\text{ }V\]

The magnetic field experienced by the electrons\[B=2.83\times {{10}^{-4\text{ }}}T\]

The radius of the circular orbit \[r=12.0\text{ }cm\text{ }=\text{ }12.0\text{ }\times \text{ }{{10}^{-2}}\text{ }m\]

Mass of each electron = m, Charge on each electron = e, Velocity of each electron = v

The kinetic of each electron is equal to the product of the applied potential and the charge 

\[\frac{1}{2}m{{v}^{2}}=eV\]

Hence the velocity can be obtained. 

Now, we know that for a circular trajectory the centripetal force is equal to the magnetic field:

\[\Rightarrow \frac{m{{v}^{2}}}{r}=qvB\]

Hence the velocity can be obtained

Equating the velocities in the above two equations we get:

\[\frac{e}{m}=\frac{2V}{{{B}^{2}}{{r}^{2}}}=1.73\times \mathbf{1}{{\mathbf{0}}^{\mathbf{11}}}\mathbf{Ck}{{\mathbf{g}}^{-\mathbf{1}}}\,\,\].

15.

a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at \[\mathbf{0}.\mathbf{45{{A}^{0}}}\]. What is the maximum energy of a photon in the radiation?

Ans: Given wavelength of the X-ray beam \[\lambda =0.45\times {{10}^{-10}}m\]

Energy is directly proportional to the frequency which is inversely proportional to wavelength. This means that maximum energy corresponds to the highest frequency which corresponds to the shortest wavelength as given in the question:

\[E=hc/\lambda =27.6keV\]

Hence the maximum energy of the X-ray photon is \[27.6keV\]

b) From your answer to (a), guess what order of accelerating voltage (for electrons) is required in such a tube?

Ans: Accelerating voltage is needed to excite the electrons to the energy of \[27.6keV\]. Thus, the voltage required is \[V=E/q=27.6keV/e=27.6kV\].

16. In an accelerator experiment on high-energy collisions of electrons with positrons, a certain event is interpreted as annihilation of an electron-positron pair of total energy \[\mathbf{10}.\mathbf{2}\text{ }\mathbf{B}\text{ }\mathbf{eV}\] into two γ-rays of equal energy. What is the wavelength associated with each γ-ray? (\[\mathbf{1BeV}=\mathbf{1}{{\mathbf{0}}^{\mathbf{9}}}\mathbf{eV}\])

Ans: Given total energy of the two\[\gamma \]-rays: \[E=10.2BeV=10.2\times {{10}^{9}}eV\].

Therefore, the energy of each of the \[\gamma \]-rays \[E'=\frac{E}{2}=8.16\times {{10}^{-10}}J\]

Wavelength corresponding to this energy is: \[\lambda =hc/E'=2.4\times {{10}^{-16}}m\]

Hence the wavelength of each \[\gamma \]-rays is \[2.4\times {{10}^{-16}}m\].

17. Estimating the following two numbers should be interesting. The first number will tell you why radio engineers do not need to worry much about photons! The second number tells you why our eye can never ‘count photons’, even in barely detectable light.

a) The number of photons emitted per second by a medium wave transmitter of \[\mathbf{10kW}\] power, emitting radio waves of wavelength \[500m\]. 

Ans: The given power of the transmitter, \[P=10\text{ }kW={{10}^{4\text{ }}}W={{10}^{4\text{ }}}J/s\] 

Hence, energy emitted per second, \[E={{10}^{4\text{ }}}J\], 

The wavelength of the radio wave, \[\lambda =500\text{ }m\]

The energy of the wave is given as: \[{{E}_{1}}=hc/\lambda \] 

Where, h = Planck’s constant =\[h=6.63\times {{10}^{-34}}\,J.s\] , c = Speed of light \[=3\times {{10}^{8}}\text{ }m/s\]

\[\Rightarrow E=3.96\times {{10}^{-28}}J\]

The number of photons emitted \[\Rightarrow n\,=E/{{E}_{1}}=2.525\times {{10}^{31}}\]

Hence the number of photons emitted is \[2.525\times {{10}^{31}}\]

b) The number of photons entering the pupil of our eye per second corresponding to the minimum intensity of white light that we humans can perceive (\[\sim \mathbf{1}{{\mathbf{0}}^{-\mathbf{10}}}\text{ }\mathbf{W}{{\mathbf{m}}^{-\mathbf{2}}}\]). Take the area of the pupil to be about \[\mathbf{0}.\mathbf{4}\text{ }\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\], and the average frequency of white light to be about \[\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{14}}}\mathbf{Hz}\].

Ans: Minimum light perceivable by eyes is \[I={{10}^{-10}}W{{m}^{-2}}\]

Area of the pupil, \[A=0.4\times {{10}^{-4}}{{m}^{2}}\]

The average frequency of light is \[\upsilon =\,\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{14}}}\mathbf{Hz}\]

Thus, the energy radiation is obtained as, \[E=h\upsilon =3.96\times {{10}^{-19}}J\]

Total energy for n photons per unit area per second: \[E=n\times 3.96\times {{10}^{-19}}J/s/{{m}^{2}}\]

The energy per unit area per second is the intensity: \[n=\frac{{{10}^{-10}}}{3.96\times {{10}^{-19}}}=2.5\times {{10}^{8}}{{m}^{2}}{{s}^{-1}}\]

Hence the total number of photons entering pupil is given as: \[nA=1.008\times {{10}^{4}}{{s}^{-1}}\]

These are too many photons to count even when they are going in the pupil.

18. Ultraviolet light of wavelength \[\mathbf{2271}\text{ }\mathbf{{{A}^{0}}}\] from a \[\mathbf{100}\text{ }\mathbf{W}\] mercury source irradiates a photocell made of molybdenum metal. If the stopping potential is \[-\mathbf{1}.\mathbf{3}\text{ }\mathbf{V}\], estimate the work function of the metal. How would the photo-cell respond to a high intensity (\[\mathbf{1}{{\mathbf{0}}^{\mathbf{5}}}\mathbf{W}{{\mathbf{m}}^{-\mathbf{2}}}\]) red light of wavelength \[\mathbf{6328}\text{ }\mathbf{{{A}^{0}}}\] produced by a He-Ne laser?

Ans: The given wavelength of UV light is \[2271\mathbf{{{A}^{0}}}\,=2271\times {{10}^{-10}}m\]

The stopping potential for the Molybdenum metal \[{{V}_{0}}=1.3V\]

The charge of an electron, \[e=\mathbf{1}.\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{19}}}\mathbf{C}\]

The Planck’s constant is, \[\,h=6.63\times {{10}^{-34}}\,J.s\]

Work function of the Molybdenum\[={{\phi }_{0}}\], Frequency of the light \[=\upsilon \]

We have the energy equation for photoelectric effect: \[e{{V}_{0}}=h\upsilon -{{\phi }_{0}}\]

Let \[{{\upsilon }_{0}}\] be the threshold frequency of the metal. 

\[{{\upsilon }_{0}}={{\phi }_{0}}/h=10.06\times {{10}^{14}}Hz\]

Wavelength of red light  \[{{\lambda }_{c}}=6328\mathbf{{{A}^{0}}}\]

Frequency of red light  \[{{\upsilon }_{r}}=\frac{c}{{{\lambda }_{c}}}=4.74\times {{10}^{14}}Hz\]

Since \[{{\upsilon }_{0}}>\text{ }{{\upsilon }_{r}}\], the photocell will not respond to the red light generated by the laser.

19. Monochromatic radiation of wavelength\[\mathbf{640}.\mathbf{2nm}\text{ }\left( \mathbf{1nm}=\mathbf{1}{{\mathbf{0}}^{-\mathbf{9}}}\mathbf{m} \right)\]from a neon lamp irradiates photosensitive material made of caesium on tungsten. The stopping voltage is measured to be \[\mathbf{0}.\mathbf{54V}\]. The source is replaced by an iron source and its \[\mathbf{427}.\mathbf{2nm}\]line irradiates the same photo-cell. Predict the new stopping voltage.

Ans: The given wavelength of the monochromatic radiation, \[\lambda =640.2nm=640.2\times {{10}^{-9}}m\]

The Stopping potential of the neon lamp, \[{{V}_{0}}=\text{ }0.54\text{ }V\]

The charge of an electron, \[e=\mathbf{1}.\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{19}}}\mathbf{C}\]

The Planck’s constant is, \[\,h=6.63\times {{10}^{-34}}\,J.s\]

The photo energy relation: \[e{{V}_{0}}=h\upsilon -{{\phi }_{0}}\]

\[\Rightarrow {{\phi }_{0}}=1.39eV\]

Wavelength of radiation from iron, \[\lambda '=427.2nm=427.2\times {{10}^{-9}}m\]

Now let \[{{V}_{0}}'\] be the new stopping potential. And the photo-energy is given as

\[\text{e}{{V}_{0}}'=\text{ hc/}\lambda \text{ }\!\!'\!\!\text{ -}{{\phi }_{0}}=2.401\times {{10}^{-19}}J=1.5eV\]

Therefore, the stopping potential is \[1.5eV\].

20. A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used: \[\mathbf{\lambda 1}\text{ }=\mathbf{3650{angstrom}}\], \[\mathbf{\lambda 2}=\mathbf{4047{angstrom}}\], \[\mathbf{\lambda 3}=\mathbf{4358{angstrom}}\], \[\mathbf{\lambda 4}=\text{ }\mathbf{5461}\text{ }\mathbf{{angstrom}}\], \[\mathbf{\lambda 5}=\mathbf{6907{angstrom}}\], The stopping voltages, respectively, were measured to be: \[\mathbf{V01}=\mathbf{1}.\mathbf{28V}\], \[\mathbf{V02}=\mathbf{0}.\mathbf{95V}\], \[\mathbf{V03}=\mathbf{0}.\mathbf{74V}\] , \[\mathbf{V04}=\mathbf{0}.\mathbf{16V}\], \[\mathbf{V05}=\mathbf{0V}\]. Determine the value of Planck’s constant h, the threshold frequency and work function for the material. (Note: You will notice that to get h from the data, you will need to know e (which you can take to be \[\mathbf{1}.\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{19}}}\mathbf{C}\]). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.)

Ans: The photo-energy equation is given as: \[e{{V}_{0}}=h\upsilon -{{\phi }_{0}}\]

\[\Rightarrow {{V}_{0}}=h\upsilon /e-{{\phi }_{0}}/e\]

Here \[{{V}_{0}}=\]stopping potential, 

The charge of an electron, \[e=\mathbf{1}.\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{19}}}\mathbf{C}\]

The Planck’s constant is, \[\,h=6.63\times {{10}^{-34}}\,J.s\]

\[{{\phi }_{0}}=\]Work function of a material

Hence evidently, stopping potential is proportional to frequency

Now the frequencies corresponding to given wavelengths\[{{\upsilon }_{m}}=c/{{\lambda }_{m}}\], here \[m=1\,to\,5\]. And the corresponding stopping potentials:

\[{{\upsilon }_{1}}=c/{{\lambda }_{1}}=8.219\times {{10}^{14}}Hz\]; \[{{V}_{0,1}}=1.28V\]

\[{{\upsilon }_{2}}=c/{{\lambda }_{2}}=7.412\times {{10}^{14}}Hz\]; \[{{V}_{0,2}}=0.95V\]

\[{{\upsilon }_{3}}=c/{{\lambda }_{3}}=6.882\times {{10}^{14}}Hz\]; \[{{V}_{0,3}}=0.74V\]

\[{{\upsilon }_{4}}=c/{{\lambda }_{4}}=5.492\times {{10}^{14}}Hz\]; \[{{V}_{0,4}}=0.16V\]

\[{{\upsilon }_{5}}=c/{{\lambda }_{5}}=4.343\times {{10}^{14}}Hz\]; \[{{V}_{0,5}}=0V\]

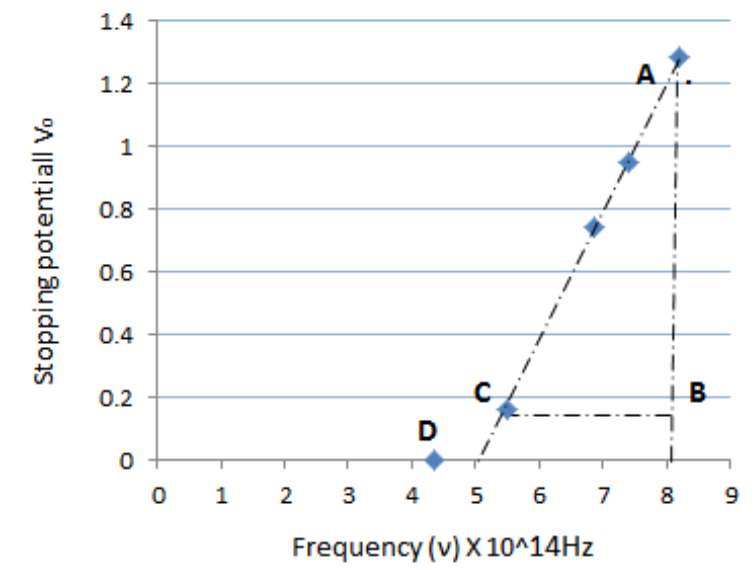
The obtained curve is a straight line. It intersects the \[\upsilon \] -axis at \[5\times {{10}^{14}}Hz\], which is the threshold frequency (\[{{\upsilon }_{0}}\]) of the material. At Point D the frequency is less than the threshold frequency. Hence, there would be no photoelectric emission for the \[{{\lambda }_{5}}\] line, and therefore, no stopping voltage is required to stop the current.

Slope of the straight-line AC: \[=\frac{AB}{CB}=\frac{1.28-0.16}{(8.124-5.493)\times {{10}^{14}}}\]

This slope physically is the ratio of Planck’s constant and charge of an electron: \[\frac{h}{e}=\frac{1.28-0.16}{(8.124-5.493)\times {{10}^{14}}}\]

\[\Rightarrow h=6.57\times {{10}^{-34}}Js\]

For a metal the work function is written as: 

\[{{\phi }_{0}}=h{{\upsilon }_{0}}=3.286\times {{10}^{-19}}J=2.054eV\]

21. The work function for the following metals is given:\[\mathbf{Na: 2}\mathbf{.75 eV; K: 2}\mathbf{.30 eV; Mo: 4}\mathbf{.17 eV; Ni: 5}\mathbf{.15 eV}\] . Which of these metals will not give photoelectric emission for a radiation of wavelength \[\mathbf{3300}\overset{{}^\circ }{\mathop{A}}\,\] from a He-Cd laser placed 1 m away from the photocell? What happens if the laser is brought nearer and placed 50 cm away?

Ans: \[Mo\text{ and }Ni\] will not show photoelectric emission in both the cases.

Wavelength for a radiation\[,~\text{ }\lambda =\text{ }3300~{{A}^{o}}=300\times {{10}^{-10}}m\]

Planck's constant, \[h~=6.626\times {{10}^{-34}}Js~\]

Speed of light, $c=3\times {{10}^{8}}m/s$

The energy of incident radiation is given as:

$E=\frac{hc}{\lambda }=\frac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{3300\times {{10}^{-10}}}=6\times {{10}^{-19}}~\text{J}$

$\Rightarrow E=\frac{6\times {{10}^{-19}}}{1.6\times {{10}^{-19}}}=3.158\text{eV}$

It can be observed that the energy of the incident radiation is greater than the work function of Na and K only. It is less for Mo and Ni. Hence, Mo and Ni will not show photoelectric emission.

If the source of light is brought near the photocells and placed 50 cm away from them, then the intensity of radiation will increase. This does not affect the energy of the radiation. Hence, the result will be the same as before. However, the photoelectrons emitted from Na and K will increase in proportion to intensity.

22. Light of intensity $\mathbf{1}{{\mathbf{0}}^{\mathbf{-5}}}\mathbf{W}{{\mathbf{m}}^{\mathbf{-2}}}$falls on a sodium photo-cell of surface area $\mathbf{2c}{{\mathbf{m}}^{\mathbf{2}}}$ . Assuming that the top 5 layers of sodium absorb the incident energy, estimate time required for photoelectric emission in the wave-picture of radiation. The work function for the metal is given to be about 2 eV. What is the implication of your answer?

Ans: Given that,

Intensity of incident light, \[I={{10}^{-5}}W{{m}^{-2}}\]

Surface area of a sodium photocell,\[~A=~2c{{m}^{2}}~=2\times {{10}^{-4}}{{m}^{2}}~\]

Incident power of the light,$P=I\times A={{10}^{-5}}\times 2\times {{10}^{-4}}=2\times {{10}^{-9}}W~$

Work function of the metal,  \[{{\phi }_{o}}=2\text{ }eV~=2\times 1.6\times {{10}^{-19}}=3.2\times {{10}^{-19}}J\]

Number of layers of sodium that absorbs the incident energy, \[n=\text{ }5\]

We know that the effective atomic area of a sodium atom ${{A}_{e}}$ is ${{10}^{-20}}{{m}^{2}}$

Hence, the number of conduction electrons in n layers is given as:

$n'=n\times \frac{A}{{{A}_{e}}}={{10}^{17}}$

The incident power is uniformly absorbed by all the electrons continuously. Hence, the amount of energy absorbed per second per electron is:

$E=\frac{P}{n'}=\frac{2\times {{10}^{-9}}}{{{10}^{17}}}=2\times {{10}^{-26}}J/s$

Time required for photoelectric emission:

$t=\frac{{{\phi }_{o}}}{E}=\frac{3.2\times {{10}^{-19}}}{2\times {{10}^{-26}}}=1.6\times {{10}^{7}}s\approx 0.507\text{years}$

The time required for the photoelectric emission is nearly half a year, which is not practical. Hence, the wave picture is in disagreement with the given experiment.

23.Crystal diffraction experiments can be performed using X-rays, or electrons accelerated through appropriate voltage. Which probe has greater energy? (For quantitative comparison, take the wavelength of the probe equal to $\mathbf{1}{{\mathbf{A}}^{\mathbf{o}}}$, which is of the order of interatomic spacing in the lattice)$\left( {{\mathbf{m}}_{\mathbf{e}}}\mathbf{=9}\mathbf{.11\times 1}{{\mathbf{0}}^{\mathbf{-31}}}\mathbf{kg} \right)$.

Ans: An X-ray probe has a greater energy than an electron probe for the same wavelength. Wavelength of light emitted from the probe, $\lambda =1{{A}^{o}}={{10}^{-10}}m$

Mass of an electron, ${{m}_{e}}=9.11\times {{10}^{-31}}kg$

Planck's constant, $h=6.6\times {{10}^{-34}}Js$

Charge on an electron, $e=1.6\times {{10}^{-19}}C$

The kinetic energy of the electron is given as:

$E=\frac{1}{2}{{m}_{6}}{{v}^{2}}$

${{m}_{e}}v=\sqrt{2E{{m}_{e}}}~\text{s}$

Where, $v=$ Velocity of the electron

${{m}_{e}}v$ = Momentum ($p$ ) of the electron

According to the de Broglie principle, the de Broglie wavelength is given as:

$\lambda =\frac{h}{P}=\frac{h}{{{m}_{e}}v}=\frac{h}{\sqrt{2E{{m}_{e}}}}$

\[\Rightarrow E=\frac{{{h}^{2}}}{2{{\lambda }^{2}}{{m}_{e}}}\]

\[\Rightarrow E=\frac{{{\left( 6.6\times {{10}^{-34}} \right)}^{2}}}{2\times {{\left( {{10}^{-10}} \right)}^{2}}\times 9.11\times {{10}^{-31}}}=2.39\times {{10}^{-11}}J=149.375\text{eV}\]

Energy of a photon,

${{E}^{\prime }}=\frac{hc}{\lambda e}eV=\frac{6.6\times {{10}^{-34}}\times 3\times {{10}^{8}}}{{{10}^{-10}}\times 1.6\times {{10}^{-19}}}$

$\Rightarrow E'=12.375\times {{10}^{3}}\text{eV}=12.375\text{keV}$

Hence, a photon has a greater energy than an electron for the same wavelength.

24.

a) Obtain the de Broglie wavelength of a neutron of kinetic energy \[\mathbf{150eV}\]. As you have seen in Exercise 11.31, an electron beam of this energy is suitable for crystal diffraction experiments. Would a neutron beam of the same energy be equally suitable? Explain. (\[{{m}_{n}}=1.675\times {{10}^{-27}}kg\])

Ans: Given that,

The charge of an electron, \[e=\mathbf{1}.\mathbf{6}\times \mathbf{1}{{\mathbf{0}}^{-\mathbf{19}}}\mathbf{C}\]

The Planck’s constant is, \[\,h=6.63\times {{10}^{-34}}\,J.s\]

Given the kinetic energy of a neutron \[K=150eV=2.4\times {{10}^{-17}}J\]

Mass of the neutron\[{{m}_{n}}=1.675\times {{10}^{-27}}kg\],

Hence the kinetic energy of the neutron is obtained as \[K=\frac{1}{2}m{}_{n}{{v}^{2}}\] 

\[\Rightarrow {{m}_{n}}v=\sqrt{2{{m}_{n}}E}\]

Here v is the velocity of neutrona and\[{{m}_{n}}\]is the neutron mass. And \[{{m}_{n}}v\] is the momentum.

Hence the de Broglie wavelength is obtained as, \[\lambda =\frac{h}{{{m}_{0}}v}=\frac{h}{\sqrt{2K{{m}_{0}}}}=2.327\times {{10}^{-2}}m\] 

Hence the wavelength drops with increase in mass and vice-versa

In the previous problem, the inter-atomic spacing of a crystal is ~ 1 Å, i.e., \[{{10}^{-10}}m\]. Hence, the interatomic spacing is about a hundred times greater. Hence, a neutron beam of energy 

150 eV is not suitable for diffraction experiments.

b) Obtain the de Broglie wavelength associated with thermal neutrons at room temperature (\[\mathbf{27}{}^\text{o}\mathbf{C}\]). Hence explain why a fast neutron beam needs to be thermalized with the environment before it can be used for neutron diffraction experiments.

Ans: The given de Broglie wavelength = \[1.447\times {{10}^{16}}m\]; Room temperature\[T\text{ }=\text{ }27{}^\circ C\text{ }=\text{ }27\text{ }+\text{ }273\text{ }=\text{ }300K\]

Hence the average kinetic energy of the neutron is given as: \[K=\frac{3}{2}kT\]

Where, Boltzmann constant, \[k=1.38\times {{10}^{-23}}\text{ }J\text{ /}mol\text{ }/K\] .

The wavelength of the neutron under consideration is given as:

\[\lambda =\frac{h}{{{m}_{0}}v}=\frac{h}{\sqrt{2K{{m}_{0}}}}=1.447\times {{10}^{-10}}m\]

This wavelength is comparable to the inter-atomic spacing of a crystal. Hence, before using it for diffraction, the high energy neutron beam should first be thermalized.

25. An electron microscope uses electrons accelerated by a voltage of 50 kV. Determine the de Broglie wavelength associated with the electrons. If other factors (such as numerical aperture, etc.) are taken to be roughly the same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light?

Ans: Given that,

Electrons are accelerated by a voltage, $V=\text{ }50\text{ }kV=1.38\times {{10}^{-23}}Jmo{{l}^{-1}}{{K}^{-1}}$

Charge on an electron,\[e=1.6\times {{10}^{-19}}C\]

Mass of an electron, \[me=~9.11\times {{10}^{-31}}kg\]

Wavelength of yellow light $=5.9\times {{10}^{-7}}m$

The kinetic energy of the electron is given as:

\[E=eV~\Rightarrow E=1.6\times {{10}^{-19}}\times 50\times {{10}^{3}}=8\times {{10}^{-15}}J\]

de Broglie wavelength is given by the relation:

$\lambda =\frac{h}{\sqrt{2{{m}_{n}}E}}=\frac{6.6\times {{10}^{-34}}}{\sqrt{2\times 9.11\times {{10}^{-31}}\times 8\times {{10}^{-15}}}}=5.467\times {{10}^{-12}}m$

This wavelength is 100 thousand times less than the yellow light wavelength. Hence the resolving power will be 100 thousand times higher in case of electron microscope.

26. The wavelength of a probe is roughly a measure of the size of a structure that it can probe in some detail. The quark structure of protons and neutrons appears at the minute length-scale of 10-15m or less. This structure was first probed in the early 1970's using high energy electron beams produced by a linear accelerator at Stanford, USA. Guess what might have been the order of energy of these electron beams. (Rest mass energy of electron =\[\mathbf{0}\mathbf{.511 MeV}\])

Ans: It is known that,

Wavelength of a proton or a neutron, $\lambda \approx {{10}^{-15}}m$

Rest mass energy of an electron:

${{m}_{o}}{{c}^{2}}=0.511MeV=0.511\times {{10}^{5}}\times 1.6\times {{10}^{-19}}$

Planck's constant, \[h=\text{ }6.6\text{ }\times \text{ }10\text{ }-\text{ }34Js\]

Speed of light, $c=3\times {{10}^{8}}m/s$

The momentum of a proton or a neutron is given as:

$P=\frac{h}{\lambda }=\frac{6.6\times {{10}^{-34}}}{{{10}^{-15}}}=6.6\times {{10}^{-19}}kgm/s$

The relativistic relation for energy (E) is given as:

${{E}^{2}}={{p}^{2}}{{c}^{2}}+m_{0}^{2}{{c}^{4}}=\left( 6.6\times {{10}^{-19}}\times 3\times {{10}^{8}} \right)+\left( 0.8176\times {{10}^{-13}} \right)=392.04\times {{10}^{-22}}+0.6685\times {{10}^{-25}}$$\Rightarrow {{E}^{2}}\approx 392.04\times {{10}^{-22}}{{J}^{2}}$

Therefore, the energy is

$\Rightarrow E=1.98\times {{10}^{-10}}J=\frac{1.98\times {{10}^{-10}}}{1.6\times {{10}^{-19}}}=1.24\times {{10}^{9}}\text{eV}=1.24\text{BeV}$

The energy radiation is in the order of \[{{10}^{9}}\]eV.

27. Find the typical de Broglie wavelength associated with a He atom in helium gas at room temperature$\left( \mathbf{2}{{\mathbf{7}}^{\mathbf{o}}}\mathbf{C} \right)$   and 1 atm pressure; and compare it with the mean separation between two atoms under these conditions.

Ans: Given de Broglie wavelength associated with He atom = \[0.7268\text{ }\times {{10}^{-10}}m\]

The room temperature, \[T\text{ }=\text{ }27{}^\circ C\text{ }=\text{ }27\text{ }+\text{ }273\text{ }=\text{ }300\text{ }K\] 

Atmospheric pressure, \[P\text{ }=\text{ }1\text{ }atm\text{ }=\text{ }1.01\text{ }\times \text{ }{{10}^{5}}\text{ }Pa\]

Atomic weight of a He atom = 4 

Avogadro’s number\[{{N}_{A}}\text{ }=\text{ }6.023\text{ }\times \text{ }{{10}^{23}}\]

Boltzmann constant, \[k=1.38\times {{10}^{-23\text{ }}}Jmo{{l}^{-1}}{{K}^{-1}}\] 

The average energy of a gas at temperature T, is:

\[K=\frac{3}{2}kT\]

And the de Broglie wavelength is given by the relation: 

\[\lambda =\frac{h}{\sqrt{2Em}}\]

Where, 

\[m\text{ }=\] Mass of a He atom \[\text{ }=At\,Weight/{{N}_{A}}=6.64\times {{10}^{-27}}kg\]

\[\Rightarrow \lambda =\frac{h}{\sqrt{3mkT}}=0.727\times {{10}^{-10}}m\]

Using the ideal gas equation, it can be said that     \[\frac{V}{N}=\frac{kT}{P}\]

\[\Rightarrow r={{\left( \frac{V}{N} \right)}^{1/3}}={{\left( \frac{kT}{P} \right)}^{1/3}}=3.35\times {{10}^{-9}}m\]

Thus, the mean gap/separation between the atoms, r is much greater than the de Broglie wavelength.

28. Compute the typical de Broglie wavelength of an electron in a metal at  $\mathbf{2}{{\mathbf{7}}^{\mathbf{{}^\circ }}}\mathbf{C}$ and compare it with the mean separation between two electrons in a metal which is given to be about $\mathbf{2\times 1}{{\mathbf{0}}^{\mathbf{-10}}}\mathbf{m}$ .

(Note: Exercises 11.35 and 11.36 reveal that while the wave-packets associated with gaseous molecules under ordinary conditions are non-overlapping, the electron wave packets in a metal strongly overlap with one another. This suggests that whereas molecules in an ordinary gas can be distinguished apart, electrons in a metal cannot be distinguished apart from one another. This distinguishing ability has many fundamental implications which you will explore in more advanced Physics courses.)

Ans: Given temperature,  \[T={{27}^{{}^\circ }}\text{C= }27\text{ }+\text{ }273\text{ }=\text{ }300\text{ }K~\]

Mean separation between two electrons, \[r=~2\times {{10}^{-10}}m\]

De Broglie wavelength of an electron is given as:

$\lambda =\frac{h}{\sqrt{3mkT}}$

Where, h= Planck's constant  \[h=\text{ }6.6\text{ }\times \text{ }{{10}^{-34}}\,Js\]

Mass of an electron = $={{m}_{e}}=9.11\times {{10}^{-31}}kg$

Boltzmann constant =\[k=1.38\times {{10}^{-23}}Jmo{{l}^{-1}}{{K}^{-1}}\]

$\Rightarrow \lambda =\frac{6.6\times {{10}^{-34}}}{\sqrt{3\times 9.11\times {{10}^{-31}}\times 1.38\times {{10}^{-23}}\times 300}}==\mathbf{6}\mathbf{.2\times 1}{{\mathbf{0}}^{\mathbf{-9}}}\mathbf{m}$

Hence, the de Broglie wavelength is much greater than the given inter-electron separation.

29.Answer the following questions:

a) Quarks inside protons and neutrons are thought to carry fractional charges [\[\left( +\mathbf{2}/\mathbf{3} \right)\mathbf{e}\text{ };\text{ }\left( -\mathbf{1}/\mathbf{3} \right)\mathbf{e}\]]. Why do they not show up in Millikan’s oil-drop experiment?

Ans: Quarks are sub-nuclear particles and the attraction forces between them are very strong. In fact, this force increases with even a fractional increase in the separation between two quarks. In Millikan’s Oil drop experiment, the external field might be causing some disturbance in the separation of quarks, but this is opposed but much stronger attractive force, which makes the neutron and protons intact

b) Of e and m separately?

Ans: In terms of the effects of the fundamental fields of electric fields and magnetic fields on the dynamics of electrons, there are contributions only because of e/m instead of e or m individually.

For example, an electron under the influence of potential\[V\] has velocity: \[v=\sqrt{2V\frac{e}{m}}\];

For an electron under the influence of magnetic field, its velocity: \[v=\sqrt{B\,r\frac{e}{m}}\]

c) Why should gases be insulators at ordinary pressures and start conducting at very low pressures?

Ans: At low pressures, the gasses have a chance to ionize and the ions can move to reach their respective electrodes and constitute a current. At ordinary pressures, ionization itself is difficult and the ions have no chance to do so because of collisions with gas molecules and recombination.

d) Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?

Ans: Work function of a metal indicates the minimum energy required to excite an electron in the highest level of the conduction band to get out of the metal. Not all electrons in the metal stay at this level. They occupy a continuous band of energy levels, which means that electrons in different energy levels will need different energies to jump out of their levels. Therefore, for the same incident radiation, electrons knocked off from different levels come out with different energies.

e) The energy and momentum of an electron are related to the frequency and wavelength of the associated matter wave by the relations:

\[\mathbf{E}=\mathbf{h}\upsilon ;\text{ }\mathbf{p}=\frac{h}{\lambda }\]

But while the value of \[\lambda \] is physically significant, the value of ν (and therefore, the value of the phase speed \[\lambda \upsilon \]) has no physical significance. Why?

Ans: In case of any particle, the absolute value of energy i.e., \[h\upsilon \]of a particle is arbitrary within the additive constant and the momentum i.e., \[h/\lambda \] isn’t arbitrary within the additive constant. Hence, wavelength (\[\lambda \]) is significant, but the frequency (\[\upsilon \]) associated with an electron isn’t. 

Similarly, the product of this frequency with the wavelength (\[\upsilon \lambda \]) i.e., phase speed has no physical significance.

Benefits of Important Question of Physics Class 12 Chapter 11

Students who are weak in science benefit greatly from regularly practising the chapter 11 physics class 12 important questions. It serves as a guide for each pupil. So here are some of the advantages of referring to essential questions for class 12 physics chapter 11:

• The questions on this page were chosen with the format and syllabus enforced by the CBSE board in mind, as departures from them might lose pupils a lot of marks.

• These questions are chosen by a group of experts who are specialists in the subject and have worked for many years.

• The questions are chosen with the pupils' intellectual abilities in mind, so that they can answer all of them. The questions are chosen with the pupils' intellectual abilities in mind, so that they can answer all of them.

• The questions on the list are most likely to appear in final exams, therefore they will better prepare pupils.

Important Related Links for CBSE Class 12 Physics