Important Questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism 2024-25

Very Short Answer Questions  1 Mark

1. State two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer.  

Ans: Two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer are:

1. Non-Brittle conductor 

2. Restoring Torque per unit twist should be small. 

2. What will be the path of a charged particle moving along the direction of a uniform magnetic field? 

Ans: The path of a charged particle moving along the direction of a uniform magnetic field would be a straight line path as no force would act on the particle. 

3. Two wires of equal lengths are bent in the form of two loops. One of the loops is square shaped whereas the other loop is circular. These are suspended in a uniform magnetic field and the same current is passed through them. Which loop will experience greater torque? Give reasons.  

Ans: We know the expression for torque as, 

$\tau =\text{NIAB}$

\[\Rightarrow \tau \propto A\]

Since, we know that the area of circular loops is more than that of a square loop, torque which is directly proportional to area would experience greater torque than the square loop.  

Therefore, torque experienced by a circular loop is greater.

4. A cyclotron is not suitable to accelerate electron. Why? 

Ans: A cyclotron is not suitable to accelerate electron as its mass is known to be less due to which they gain speed and step out of the dee immediately.

Short Answer Questions 2 Marks

1. A steady current flows in the network shown in the figure. What will be the magnetic field at the center of the network?

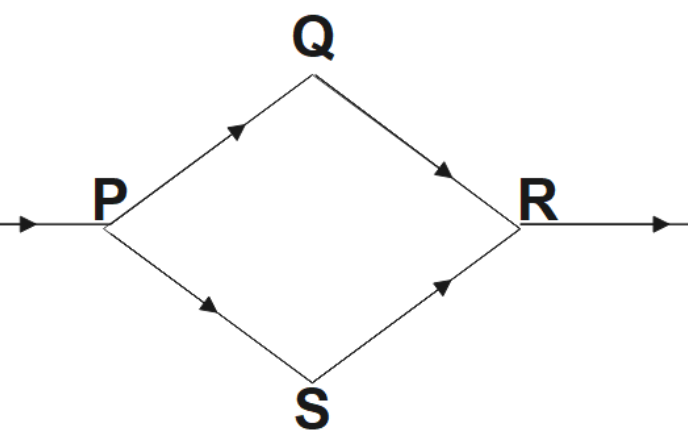
Ans:  The magnetic field at the center of the network is zero. This is because, the magnetic field at the center of the loop would just be equal and opposite i.e., magnetic field due \[\text{PQR}\] is equal and opposite to that due to \[\text{PSR}\].

2. An $\alpha $ - particle and a proton are moving in the plane of paper in a region where there is uniform magnetic field B directed normal to the plane of paper. If two particles have equal linear momenta, what will be the ratio of the radii of their trajectories in the field? 

Ans: We know the radius of the path to be given by, 

 \[R=\frac{mv}{Bq}\]

\[\Rightarrow R\propto \frac{1}{q}\] 

\[\Rightarrow \frac{{{R}_{\alpha }}}{{{R}_{p}}}=\frac{{{q}_{p}}}{{{q}_{\alpha }}}=\frac{e}{2e}=\frac{1}{2}\] 

Where, ${{R}_{\alpha }}\text{ and }{{\text{R}}_{p}}$are radii of $\alpha $-particle and proton respectively and ${{q}_{\alpha }}\text{ and }{{\text{q}}_{p}}$ are their respective charges. 

$\therefore {{R}_{\alpha }}:{{R}_{p}}=1:2$ 

Therefore, we find the required ratio to be 1:2. 

3. Give one difference each between diamagnetic and ferromagnetic substances. Give one example of each. 

Ans: Diamagnetic substances are the ones that are weakly repelled by a magnet. For example, gold. Ferromagnetic materials are the ones that are strongly attracted by a magnet. For example, iron. 

4. Write the expression for the force acting on a charged particle of charge q moving with velocity is in the presence of magnetic field B. Show that in the presence of this force,

1. The K.E. of the particle does not change. 

Ans: We know the expression for magnetic force as, $F=q(\vec{v}\times \vec{B})$

Since direction of force is perpendicular to the plane containing $(\vec{v}\times \vec{B})$, 

$F=qvB\sin 90{}^\circ =qvB$

Here, we find the force and displacement to be perpendicular to each other. So, 

$W=FS\cos \theta $ 

$\Rightarrow W=FS\cos 90{}^\circ =0$ 

$\Rightarrow \text{KE}=0$ 

Therefore, we find the kinetic energy to be constant at the given condition. 

2. Its instantaneous power is zero. 

Ans:  We have the expression for instantaneous power given by,

$p=Fv\cos \theta $ 

When force and velocity are perpendicular to each other, 

$p=Fv\cos 90{}^\circ =0$

Therefore, we find the instantaneous power to be zero.

5. An electron of kinetic energy \[25\mathbf{KeV}\]moves perpendicular to the direction of a uniform magnetic field of \[0.2\mathbf{millitesla}\]. Calculate the time period of rotation of the electron in the magnetic field.  

Ans: We are given the magnetic field to be, $B=0.2T=0.2\times {{10}^{-3}}T$ 

We know the expression for Time Period to be, $T=\frac{2\pi M}{QB}$

Substituting the given values, 

$\Rightarrow T=\frac{2\times 3.14\times 9.1\times {{10}^{-31}}}{1.6\times {{10}^{-17}}\times 0.2\times {{10}^{-3}}}$ 

$\Rightarrow T=1.787\times {{10}^{-7}}\text{ second}$ 

We find the time period of rotation of the electron in the magnetic field to be $T=1.787\times {{10}^{-7}}\text{ second}$. 

6. It is desired to pass only \[10%\] of the current through a galvanometer of resistance $90\Omega $. How much shunt resistance should be connected across the galvanometer?  

Ans: Current through galvanometer, 

${{I}_{G}}=10%\text{ of I}=\frac{10}{100}\times I$  

Galvanometer resistance is given to be, $G=90\Omega $ 

Now, we could find the shunt resistance as, 

S $=\frac{\frac{9I}{10I-I}}{100}$ 

$\Rightarrow S=\frac{90I}{90I}=10$ 

$\Rightarrow S=10\Omega $ 

Therefore, we found the shunt resistance to be $S=10\Omega $. 

Short Answer Question 3 Marks

1. Derive an expression for the force acting on a current carrying conductor placed in a uniform magnetic field. Name the rule which gives the direction of the force. Write the condition for which this force will have (1) maximum (2) minimum value.  

Ans: Let us consider a conductor that is placed in a uniform magnetic field \[\vec{B}\]making an angle $\theta $ with \[\vec{B}\]. Let \[I\] be the current that flows through the conductor.

If $n$ is the number of electrons per unit volume of the conductor, then the total number of electrons in the small current element \[dl,\text{ N}=nAdl\].

We have, 

$\theta =Ne$ 

$\Rightarrow \theta =nAdle$ 

Let $\vec{f}$ be the force experienced by each electron, then, 

$\vec{f}=e({{\vec{v}}_{d}}\times \vec{B})$ 

Now, force experienced by a small current element would be, 

\[d\vec{f}=neAdl({{\vec{v}}_{d}}\times \vec{B})\] 

$d\vec{f}=neAdlB\sin \theta $ 

But we have, $I=neAvd$ 

$\Rightarrow d\vec{f}=IdlB\sin \theta $ 

Now, the total force experienced will be,

\[F=\int_{0}^{1}{df}=\int_{0}^{1}{IdlB\sin \theta }\] 

$\Rightarrow F=IBl\sin \theta $ 

In vector form total force could be given by, $\vec{F}=I(\vec{l}\times \vec{B})$ 

1. Force will be maximum when $\theta =90{}^\circ $ 

2. Force will be minimum when $\theta =0{}^\circ $

2. A straight wire carries a current of \[\mathbf{10}\]A. An electron moving at ${{10}^{7}}\text{ m/s}$is at distance \[\mathbf{2}.\mathbf{0}\] cm from the wire. Find the force acting on the electron if its velocity is directed towards the wire.

Ans: We are given the current through the straight wire to be, \[I\text{ }=\text{ }10A\] 

Speed of the electron, $v={{10}^{7}}\text{ m/s}$ 

Distance of electron from the wire, $R=2.0\text{ cm}=2\times {{10}^{-2}}\text{ m}$ 

Force acting on a moving electron would be,  \[F=qVB\sin \theta \] 

We have the expression for magnetic field as, 

\[B=\frac{{{\mu }_{0}}}{4\pi }\frac{2I}{r}\] 

Substituting the given values, 

$B=\frac{{{10}^{-7}}\times 2\times 10}{2\times {{10}^{-2}}}={{10}^{-4}}T$ and it is given to be $\bot $ to the plane of paper and directed towards.

Now, force acting on the electron could be given by, $\Rightarrow F=1.6\times {{10}^{-19}}\times {{10}^{7}}\times {{10}^{-4}}\sin 90{}^\circ $ 

$\Rightarrow F=1.6\times {{10}^{-16}}N$ 

Therefore, we find the force to be, $F=1.6\times {{10}^{-16}}N$. 

3. State Biot-Savart's law. Derive an expression for the magnetic field at the center of a circular coil of \[\mathbf{n}\] -turns carrying current – I. 

Ans: Biot – Savart law states that the magnetic field $dB$ due to a current element $\overrightarrow{dl}$ at any point would be as following:

$dB\propto I$ 

$dB\propto dl$ 

$dB\propto \sin \theta $ 

$dB\propto \frac{1}{{{r}^{2}}}$ 

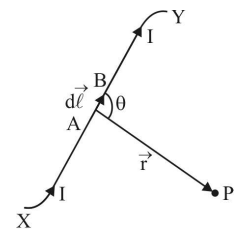
Combining all the above conditions, we get, 

$dB\propto \frac{Idl\sin \theta }{{{r}^{2}}}$ 

\[\Rightarrow dB=\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin \theta }{{{r}^{2}}}\]

Consider a circular loop of radius $r$ that is carrying a current $I$, 

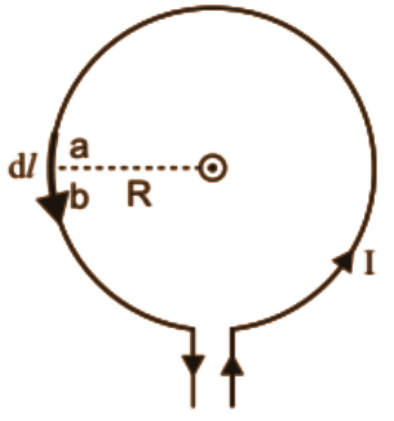
Since $dl\bot \vec{r}$ , 

$\Rightarrow \theta =90{}^\circ $ 

Now, on applying Biot Savart law 

$dB=\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin 90{}^\circ }{{{r}^{2}}}$ 

For entire closed circular loop, 

$B=\int_{0}^{2\pi r}{\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin 90{}^\circ }{{{r}^{2}}}}$ 

$\Rightarrow B=\frac{{{\mu }_{0}}}{4\pi }\frac{I}{{{r}^{2}}}\int_{0}^{2\pi r}{dl}=\frac{{{\mu }_{0}}}{4\pi }\frac{I}{{{r}^{2}}}\times 2\pi r$ 

For $n$ turns of a coil we would get, 

$\Rightarrow B=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nI}{r}$ 

Therefore, we find the expression for magnetic field at the center of a circular coil of n -turns carrying current – I to be, 

$B=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nI}{r}$

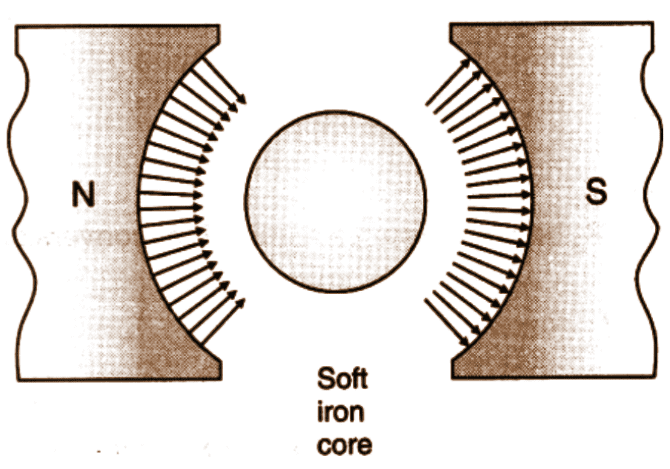
4. What is a radial magnetic field? How is it obtained in a moving coil galvanometer?

Ans: A radial magnetic field is the magnetic field in which the plane of the coil always lies in the direction of the magnetic field. It can be obtained by the following ways:

1. Properly cutting the pole pieces concave in shape. 

2. Placing soft iron cylindrical core between the pole pieces.

5. Two straight parallel current carrying conductors are kept at a distance r from each other in air. The direction for current in both the conductors is the same. Find the magnitude and direction of the force between them. Hence define one ampere. 

Ans: Let us consider two parallel conductors carrying current ${{I}_{1}}\,\text{ and }{{I}_{2}}$ and is separated by a distance \[d\], 

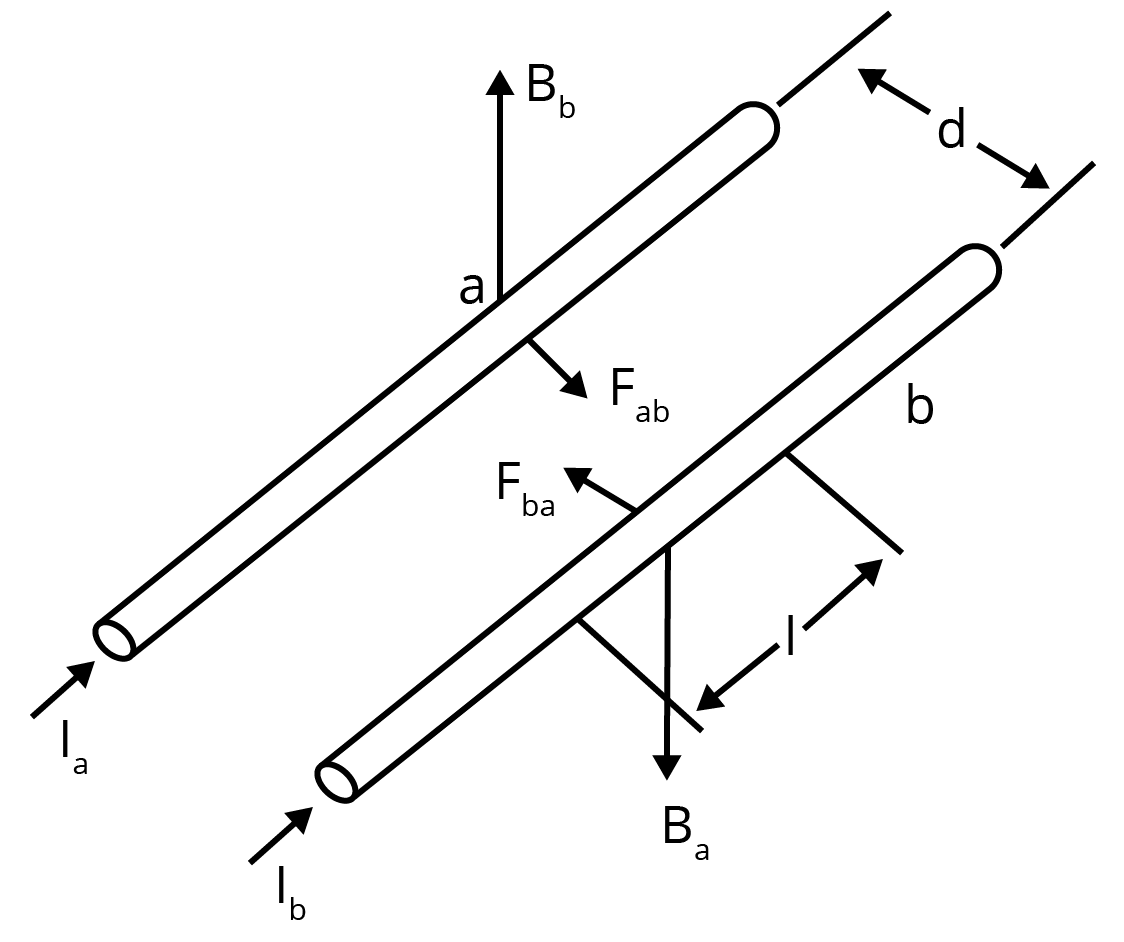
Magnetic field due to current ${{I}_{1}}$ at any point on conductor 2 could be given by, 

\[{{B}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2Il}{d}\,\] ……………………….. (1)

($\bot $ to the plane and downwards $(\times )$)

Since current carrying conductor is placed at right angles with the magnetic field, we get the magnetic force to be, 

$F=BIl\sin 90{}^\circ $ 

$\Rightarrow F=BIl$ ………………………… (2) 

This would be the Force experienced per unit length of conductor. 

Now, we have, 

${{F}_{2}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{I}_{1}}{{I}_{2}}}{d}$…………………………… (3) 

Fleming’s left hand Rule says ${{F}_{2}}$ is directed towards conductor 1.

Similarly, ${{F}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{I}_{1}}{{I}_{2}}}{d}$ (Directed Towards conductor $2$)

Since ${{F}_{1}}\text{ and }{{F}_{2}}$ are equal in magnitude and directed opposite, two parallel current carrying conductors would attract each other.

Since, $F=\frac{{{\mu }_{0}}}{4\pi }\left( \frac{2{{I}_{1}}{{I}_{2}}}{d} \right)$ 

If ${{I}_{1}}={{I}_{2}}=1\text{ A}$  and $d=1\text{m}$ , then, 

$F=2\times {{10}^{-7}}\,\text{m}$ 

Hence, we found that one ampere is that current which is flowing in two infinitely long parallel conductors that are separated by a distance of $1$ meter in vacuum and experiences a force of $F=2\times {{10}^{-2}}\,\text{m}$ on each meter of the other wire.

6. A circular coil of wire consisting of $100$ turns, each of radius $8.0$ cm carries a current of $0.40\,\text{A}$. What is the magnitude of the magnetic field B at the centre of the coil?

Ans: We are given:

Number of turns on the circular coils, $n=100$ 

Radius of each turn, $r=8.0\text{ cm}=0.08\text{ m}$ 

Current flowing in the coil, $I=0.4\,\text{A}$ 

Magnitude of the magnetic field at the centre of the coil could be given by the relation,

$\left| B \right|=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nl}{r}$ 

Where, Permeability of free space, \[{{\mu }_{0}}=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}\] 

$\Rightarrow \left| B \right|=\frac{4\pi \times {{10}^{-7}}}{4\pi }\times \frac{2\pi \times 100\times 0.4}{0.08}$ 

$\Rightarrow \left| B \right|=3.14\times {{10}^{-4}}T$ 

Hence, the magnitude of the magnetic field is found to be $3.14\times {{10}^{-4}}T$.

7. A long straight wire carries a current of $35\,\text{A}$. What is the magnitude of the field B at a point $20$ cm from the wire?

Ans: We are given the following:

Current in the wire, $I=35\text{ A}$ 

Distance of a point from the wire, $r=20\text{ cm}=0.2\,\text{m}$ 

Magnitude of the magnetic field at this point could be given as:

$B=\frac{{{\mu }_{0}}}{4\pi }\frac{2l}{r}$ 

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$ 

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 35}{4\pi \times 0.2}$ 

$\Rightarrow B=3.5\times {{10}^{-5}}\,\text{T}$ 

Hence, the magnitude of the magnetic field at a point $20\,\text{cm}$ from the wire is found to be $3.5\times {{10}^{-5}}\,\text{T}$.

8. A long straight wire in the horizontal plane carries a current of \[50\text{ A}\] in the north to south direction. Give the magnitude and direction of B at a point \[2.5\]m east of the wire. 

Ans: We are given the following:

Current in the wire, \[I\text{ }=\text{ }50\text{ A}\] 

A point is said to be \[2.5\]m away from the East of the wire. 

Magnitude of the distance of the point from the wire is given as, \[r\text{ }=\text{ }2.5\text{ m}\]. 

Magnitude of the magnetic field at that point could be given by the relation, \[B=\frac{{{\mu }_{0}}2I}{4\pi r}\] 

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$ 

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 50}{4\pi \times 2.5}$ 

$\Rightarrow B=4\times {{10}^{-6}}\,\text{T}$

Since, the point is located normal to the wire length at a distance of $2.5\text{ m}$and the direction of the current in the wire is vertically downward, by using Maxwell’s right hand thumb rule we get the direction of the magnetic field at the given point as vertically upward.

9. A horizontal overhead power line carries a current of \[\mathbf{90}\text{ }\mathbf{A}\]in an east to west direction. What is the magnitude and direction of the magnetic field due to the current \[\mathbf{1}.\mathbf{5}\text{ }\mathbf{m}\] below the line? 

Ans: We are given the following: 

Current in the power line, \[I\text{ }=\text{ }90\,\text{A}\] 

A Point is located below the power line that is at distance, \[r\text{ }=\text{ }1.5\text{ m}\] 

Now, the magnetic field at that point could be given by the relation,

\[B=\frac{{{\mu }_{0}}2I}{4\pi r}\]

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$ 

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 50}{4\pi \times 1.5}$ 

$\Rightarrow B=1.2\times {{10}^{-5}}\,\text{T}$

Since, the current is flowing from East to West and the point is given to be below the power line, by using Maxwell’s right hand thumb rule we get the direction of the magnetic field to be towards the South.

10. What is the magnitude of magnetic force per unit length on a wire carrying a current of \[8\text{ A}\] and making an angle of \[30{}^\text{o}\]  with the direction of a uniform magnetic field of \[0.15\text{ T}\] ? 

Ans: We are given the following:

Current in the wire, \[I\text{ }=\text{ }8\text{ A}\] 

Magnitude of the uniform magnetic field, \[B\text{ }=\text{ }0.15\text{ T}\] 

Angle between the wire and magnetic field, $\theta =\text{ }30{}^\circ $ 

Magnetic force per unit length on the wire is given as:

$f=BI\sin \theta $ 

\[\Rightarrow f=0.15\times 8\times 1\times \sin 30{}^\circ \] 

\[\Rightarrow f=0.6\,\text{N }{{\text{m}}^{-1}}\] 

Therefore, the magnetic force per unit length on the wire is found to be $0.6\,\text{N }{{\text{m}}^{-1}}$.

11. A \[\mathbf{3}.\mathbf{0}\] cm wire carrying a current of \[\mathbf{10}\]A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be \[\mathbf{0}.\mathbf{27}\] T. What is the magnetic force on the wire? 

Ans: We are given the following:

Length of the wire, \[l\text{ }=\text{ }3\text{ cm }=\text{ }0.03\text{ m}\] 

Current flowing in the wire, \[I\text{ }=\text{ }10\text{ A}\] 

Magnetic field, \[B\text{ }=\text{ }0.27\text{ T}\] 

Angle between the current and magnetic field, $\theta =\text{ }90{}^\circ $ 

Magnetic force exerted on the wire could be given as:

$F=BIl\sin \theta $ 

Substituting the given values, we get, 

\[\Rightarrow F=0.27\times 10\times 0.03\sin 90{}^\circ \] 

\[\Rightarrow F=8.1\times {{10}^{-2}}\,\text{N}\] 

Therefore, the magnetic force on the wire is found to be \[8.1\times {{10}^{-2}}\,\text{N}\] and the direction of the force can be obtained using Fleming’s left-hand rule.

12. Two long and parallel straight wires A and B carrying currents of \[\mathbf{8}.\mathbf{0}\] A and \[\mathbf{5}.\mathbf{0}\] A in the same direction are separated by a distance of \[\mathbf{4}.\mathbf{0}\] cm. Estimate the force on a \[\mathbf{10}\] cm section of wire A. 

Ans: We are given the following:

Current flowing in wire A, ${{I}_{A}}=8.0\,\text{A}$ 

Current flowing in wire B, ${{I}_{B}}=5.0\text{ A}$ 

Distance between the two wires, \[r\text{ }=\text{ }4.0\text{ cm }=\text{ }0.04\text{ m}\] 

Length of a section of wire A, \[l\text{ }=\text{ }10\text{ cm }=\text{ }0.1\text{ m}\] 

Force exerted on length l due to the magnetic field could be given as:

$B=\frac{{{\mu }_{0}}2{{I}_{A}}{{I}_{B}}l}{4\pi r}$ 

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 8\times 5\times 0.1}{4\pi \times 0.04}$ 

$\Rightarrow B=2\times {{10}^{-5}}\,\text{N}$ 

The magnitude of force is found to be $2\times {{10}^{-5}}\,\text{N}$. This is an attractive force that is normal to A towards B because the direction of the currents in the wires are the same.

13. A closely wound solenoid $80cm$long has $5$ layers of windings of $400$ turns each. The diameter of the solenoid is $1.8cm$. If the current carried is $8.0A$, estimate the magnitude of B inside the solenoid near its centre. 

Ans: We are given the following:

Length of the solenoid, $l=80cm=0.8m$

Since there are five layers of windings of 400 turns each on the solenoid; 

Total number of turns on the solenoid would be, $N=5\times 400=2000$

Diameter of the solenoid, $D=1.8cm=0.018m$

Current carried by the solenoid, $I=8.0A$

We have the magnitude of the magnetic field inside the solenoid near its centre given by the relation, 

$B=\frac{{{\mu }_{0}}NI}{l}$

Where, ${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$is the permeability of free space. 

On substituting the given values we get, 

$B=\frac{4\pi \times {{10}^{-7}}\times 2000\times 8}{0.8}$

$\Rightarrow B=2.512\times {{10}^{-2}}T$

Therefore, the magnitude of the magnetic field inside the solenoid near its centre is found to be $2.512\times {{10}^{-2}}T$.

14. A square coil of side $10cm$consists of 20 turns and carries a current of $12A$. The coil is suspended vertically and the normal to the plane of the coil makes an angle of $30{}^\circ $with the direction of a uniform horizontal magnetic field of magnitude $0.80T$. What is the magnitude of torque experienced by the coil?

Ans: We are given,

Length of a side of the square coil, $l=10cm=0.1m$

Area of the square, $A={{l}^{2}}={{\left( 0.1 \right)}^{2}}=0.01{{m}^{2}}$

Current flowing in the coil, $I=12A$

Number of turns on the coil, $n=20$

Angle made by the plane of the coil with magnetic field, $\theta =30{}^\circ $

Strength of magnetic field, $B=0.80T$

Magnitude of the magnetic torque experienced by the coil in the magnetic field is given by the relation,

$\tau =nIAB\sin \theta $

Substituting the given values, we get,

$\tau =20\times 0.8\times 12\times 0.01\times \sin 30{}^\circ $

$\Rightarrow \tau =0.96Nm$

Therefore, the magnitude of the torque experienced by the coil is 0.96Nm.

15. 

1. A circular coil of \[\mathbf{30}\] turns and radius \[\mathbf{8}.\mathbf{0}cm\] carrying a current of \[\mathbf{6}.\mathbf{0}A\] is suspended vertically in a uniform horizontal magnetic field of magnitude \[\mathbf{1}.\mathbf{0}T\]. The field lines make an angle of with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.

Ans: Given that, number of turns on the circular coil, \[n=30\] 

Radius of the coil, \[r=8.0\text{ cm}=0.08\text{ m}\] 

Area of the coil $=\pi {{r}^{2}}=\pi {{(0.08)}^{2}}=0.0201\text{ }{{\text{m}}^{2}}$ 

Current flowing in the coil, \[I=6.0\text{ A}\] 

Magnetic field strength, \[B=1\text{ T}\] 

Angle between the field lines and normal with the coil surface, $\theta =60{}^\circ $ 

The coil experiences a torque in the magnetic field. So, it turns. The counter torque applied to prevent the coil from turning is given by the relation,

$T=nIBA\sin \theta \,$ ……………………. (1)

$\Rightarrow T=30\times 6\times 1\times 0.0201\times \sin 60{}^\circ $ 

$\Rightarrow T=3.133\text{Nm}$ 

Therefore, counter torque to be applied against coil turning is $3.133\text{Nm}$.

2. Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.) 

Ans: It can be inferred from relation (1) that the magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. Hence, the answer would not change if the circular coil in the above case is replaced by a planar coil of some irregular shape that encloses the same area.

16. A magnetic field of $100G$$\left( where,\text{ }1G={{10}^{-4}}T \right)$ is required which is uniform in a region of linear dimension about $10cm$ and area of cross-section about${{10}^{-3}}{{m}^{2}}$. The maximum current carrying capacity of a given coil of wire is $15A$ and the number of turns per unit length that can be wound a core is at most $1000\text{ turns per m}$. Suggest some appropriate design particulars to a solenoid for the required purpose. Assume the core is not ferromagnetic.

Ans: We are given,

Magnetic field strength,$B=100G=100\times {{10}^{-4}}T$

Number of turns per unit length,$n=1000turns\text{ per m}$

Current flowing in the coil,$I=15A$

Permeability of free space, ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

Magnetic field is given the relation,

$B={{\mu }_{0}}nI$

$\Rightarrow nI=\frac{B}{{{\mu }_{0}}}=\frac{100\times {{10}^{-4}}}{4\pi \times {{10}^{-7}}}$

$\Rightarrow nI\approx 8000A/m$

So, if the length of the coil is taken as 50 cm, radius 4 cm, number of turns 400, and current 10 A, then these values are not unique for the given purpose. There is always a Possibility of some adjustments with limits.

17. A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field 

1. outside the toroid 

Ans: We are given,

Inner radius of the toroid, ${{r}_{1}}=25cm=0.25m$

Outer radius of the toroid, ${{r}_{2}}=26cm=0.26m$

Number of turns on the coil, $N=3500$

Current in the coil, $I=11A$

So, we know, the magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.

2. inside the core of the toroid.

Ans: Magnetic field inside the core of a toroid is given by the relation,

$B=\frac{{{\mu }_{0}}NI}{l}$

Where, Permeability of free space ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

$l$ is the length of toroid

$l=2\pi \left( \frac{{{r}_{1}}+{{r}_{2}}}{2} \right)=\pi \left( 0.25+0.26 \right)=0.51\pi $

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 3500\times 11}{0.51\pi }\approx 3.0\times {{10}^{-2}}T$

Therefore, the magnetic field inside the core of the toroid is approximately $3.0\times {{10}^{-2}}T$.

3. in the empty space surrounded by the toroid.

Ans: Magnetic field in the empty space that is surrounded by the toroid is zero. 

18. Answer the following questions: 

1. A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

Ans: The initial velocity of the particle could either be parallel or be anti-parallel to the magnetic field. So, it travels along a straight path without suffering any deflection in the field.

2. A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment? 

Ans: Yes, the final speed of the charged particle would be equal to its initial speed because the magnetic force can change direction of velocity, but not its magnitude.

3. An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path. 

Ans: An electron travelling from West to East enters a chamber having a uniform electrostatic field along the North-South direction. This moving electron remains undeflected if the electric force acting on it is equal and opposite to the magnetic field. Magnetic force would be directed towards the South. Also, according to Fleming’s left hand rule, the magnetic field should be applied in a vertically downward direction.

19. A straight horizontal conducting rod of length $0.45m$ and mass $60g$is suspended by two vertical wires at its ends. A current of $5.0A$ is set up in the rod through the wires.

1. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

Ans: We are given,

Length of the rod, $l=0.45m$

Mass suspended by the wires, $m=60g=60\times {{10}^{-3}}kg$

Acceleration due to gravity, $g=9.8m{{s}^{-2}}$

Current in the rod flowing through the wire, $I=5A$

We could say that magnetic field (B) is equal and opposite to the weight of the wire i.e.,

$BIl=mg$

$\Rightarrow B=\frac{mg}{Il}=\frac{60\times {{10}^{-3}}\times 9.8}{5\times 0.45}$

$\Rightarrow B=0.26T$

Therefore, a horizontal magnetic field of 0.26 T normal to the length of the conductor should be set up.

2. What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) $g=9.8m{{s}^{-2}}$

Ans: When the direction of the current is reversed, $BIl$ and $mg$ will act downwards. So, the effective tension in the wires is found to be, 

$T=0.26\times 5\times 0.45+\left( 60\times {{10}^{-3}} \right)\times 9.8$

$\Rightarrow T=1.176N$

Therefore, total tension in the wires is $1.176N$. 

20. The wires which connect the battery of an automobile to its starting motor carry a current of $300A$(for a short time). What is the force per unit length between the wires if they are $70cm$long and $1.5cm$ apart? Is the force attractive or repulsive?

Ans: Given that,

Current in both wires, $I=300A$

Distance between the wires, $r=1.5cm=0.015m$

Length of the two wires, $l=70cm=0.7m$

We know that, Force between the two wires is given by the relation,

$F=\frac{{{\mu }_{0}}{{I}^{2}}}{2\pi r}$

Where, Permeability of free space${{\mu }_{0}}=4\pi \times 10Tm{{A}^{-1}}$

Substituting the given values, 

$\Rightarrow F=\frac{4\pi \times {{10}^{-7}}\times {{300}^{2}}}{2\pi \times 0.015}$

$\Rightarrow F=1.2N$

Since the direction of the current in the wires is found to be opposite, a repulsive force exists between them.

21. A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the: (The coil is made of copper wire of cross-sectional area ${{10}^{-5}}{{m}^{2}}$, and the free electron density in copper is given to be about${{10}^{29}}{{m}^{-3}}$).

1. total torque on the coil?

Ans: Given that,

Number of turns on the circular coil, $n=20$

Radius of the coil, $r=10cm=0.1m$

Magnetic field strength, $B=0.10T$

Current in the coil, $I=5.0A$

Since, the angle between force and the normal to the loop, the total torque on the coil is zero. So, $\tau =NIAB\sin \theta $ is zero.

2. total force on the coil, 

Ans: The total force on the coil is zero as the field is uniform.

3. average force on each electron in the coil due to the magnetic field?

Ans: Number of free electrons per cubic meter in copper, $N={{10}^{29}}/{{m}^{3}}$

Charge on the electron would be, $e=1.6\times {{10}^{-19}}C$

Magnetic force, $F=Be{{v}_{d}}$

Where, ${{v}_{d}}$ is Drift velocity of electrons.

${{v}_{d}}=\frac{I}{neA}=\frac{5}{{{10}^{29}}\times 1.6\times {{10}^{-19}}\times {{10}^{-5}}}=3.125\times {{10}^{-5}}m/s$

$\Rightarrow F=0.10\times 1.6\times {{10}^{-19}}\times 3.125\times {{10}^{-5}}$

$\Rightarrow F=5\times {{10}^{-25}}N$

Therefore, the average force on each electron is found to be $5\times {{10}^{-25}}N$.

22. A galvanometer coil has a resistance of $12\Omega $and the metre shows full scale deflection for a current of $3mA$. How will you convert the metre into a voltmeter of range $0$ to $18V$?

Ans: Given that, 

Resistance of the galvanometer coil, $G=12\Omega $

Current for which there is full scale deflection, ${{I}_{g}}=3mA=3\times {{10}^{-3}}A$

Range of the voltmeter needs to be converted to $18V$.

Let a resistor of resistance R be connected in series with the galvanometer to convert it into a voltmeter. This resistance can be given as:

$R=\frac{V}{{{I}_{g}}}-G$

Substituting the given values we get, 

$R=\frac{18}{3\times {{10}^{-3}}}-12=6000-12$

$\Rightarrow R=5988\Omega $

Therefore, we found that a resistor of resistance $5988\Omega $ is to be connected in series with the given galvanometer. 

23. A galvanometer coil has a resistance of $15\Omega $ and the metre shows full scale deflection for a current of $4mA$. How will you convert the metre into an ammeter of range $0$ to $6A$?

Ans: We are given,

Resistance of the galvanometer coil, $G=15\Omega $

Current for which the galvanometer shows full scale deflection, ${{I}_{g}}=4mA=4\times {{10}^{-3}}A$

We said that, Range of the ammeter needs to be $6A$.

In order to convert the given galvanometer into an ammeter, a shunt resistor of resistance S is to be connected in parallel with the galvanometer. 

The value of S could be given as:

$S=\frac{{{I}_{g}}G}{I-{{I}_{g}}}$

Substituting the values, 

$S=\frac{4\times {{10}^{-3}}\times 15}{6-4\times {{10}^{-3}}}=\frac{0.06}{5.996}\approx 0.01\Omega $

$\Rightarrow S=10m\Omega $

Therefore, we found that a $10m\Omega $ shunt resistor is to be connected in parallel with the galvanometer.

Long Answer Questions                                                                                   5 Marks

1. 

1. What is a cyclotron? Explain its working principle.

Ans: Cyclotron is a device used to accelerate charged particles like protons, deuterons, $\alpha $ - particles, etc. 

It works on the basis of the principle that a charged particle can be accelerated to very high energies by making it pass through a moderate electric field a number of times and applying a strong magnetic field at the same time. 

2. A cyclotron’s oscillator frequency is \[10\,\text{MHz}\], what should be the operating magnetic field for accelerating protons? If radius is \[20\,\text{cm}\], what is the K.E. of the proton beam produced by the accelerator? \[\left( e=1.6\times {{10}^{-19}}\text{ c},mp=1.6\times {{10}^{-27}}\text{ kg},1\text{ MeV}=1.602\times {{10}^{-13}}\text{ J} \right)\]

Ans: Given that, \[v=10\,\text{MHz}=10\times {{10}^{6}}\text{ Hz}\] 

\[e=1.6\times {{10}^{-19}}\text{ c}\]

\[mp=1.6\times {{10}^{-27}}\text{ kg}\]

\[r=20\,\text{cm}=20\times {{10}^{-2}}\,\text{m}\] 

We have the expression for kinetic energy, 

KE $=\frac{{{q}^{2}}{{B}^{2}}{{r}^{2}}}{2m}$ 

Using $v=\frac{qB}{2\pi }$ 

$B=\frac{2\pi mV}{q}$ 

$\Rightarrow B=\frac{2\times 3.14\times 1.6\times {{10}^{-27}}\times {{10}^{7}}}{1.6\times {{10}^{-19}}}$ 

$\Rightarrow B=0.628\text{ T}$ 

Therefore, the operating magnetic field for accelerating protons is $0.628\text{ T}$.

KE $=\frac{{{\left( 1.6\times {{10}^{-19}} \right)}^{2}}\times {{\left( 0.66 \right)}^{2}}\times {{\left( 0.2 \right)}^{2}}}{2\times 1.67\times {{10}^{-27}}}$ 

KE $=13.35\times {{10}^{-13}}\text{ J}$ 

But we have, $1.602\times {{10}^{-13}}\text{ Joules}=1\text{ MeV}$ 

Since $12.02\times {{10}^{-13}}\text{ J}$ has $\frac{12.02\times {{10}^{-13}}}{1.602\times {{10}^{-13}}}\text{ MeV}$ 

$\Rightarrow KE=8.3\text{ MeV}$

Therefore, the K.E. of the proton beam produced by the accelerator is $8.3\text{ MeV}$.

2.

1. Draw a labelled diagram of a moving coil galvanometer. Prove that in a radial magnetic field, the deflection of the coil is directly proportional to the current flowing in the coil. 

Ans: When a current $I$ is passed through a coil two equal and opposite forces act on the arms of a coil to form a couple which exerts a Torque on the coil. 

\[\tau =NIAB\sin \theta \] 

If $\theta =90{}^\circ \left( \sin 90{}^\circ =1 \right)$ 

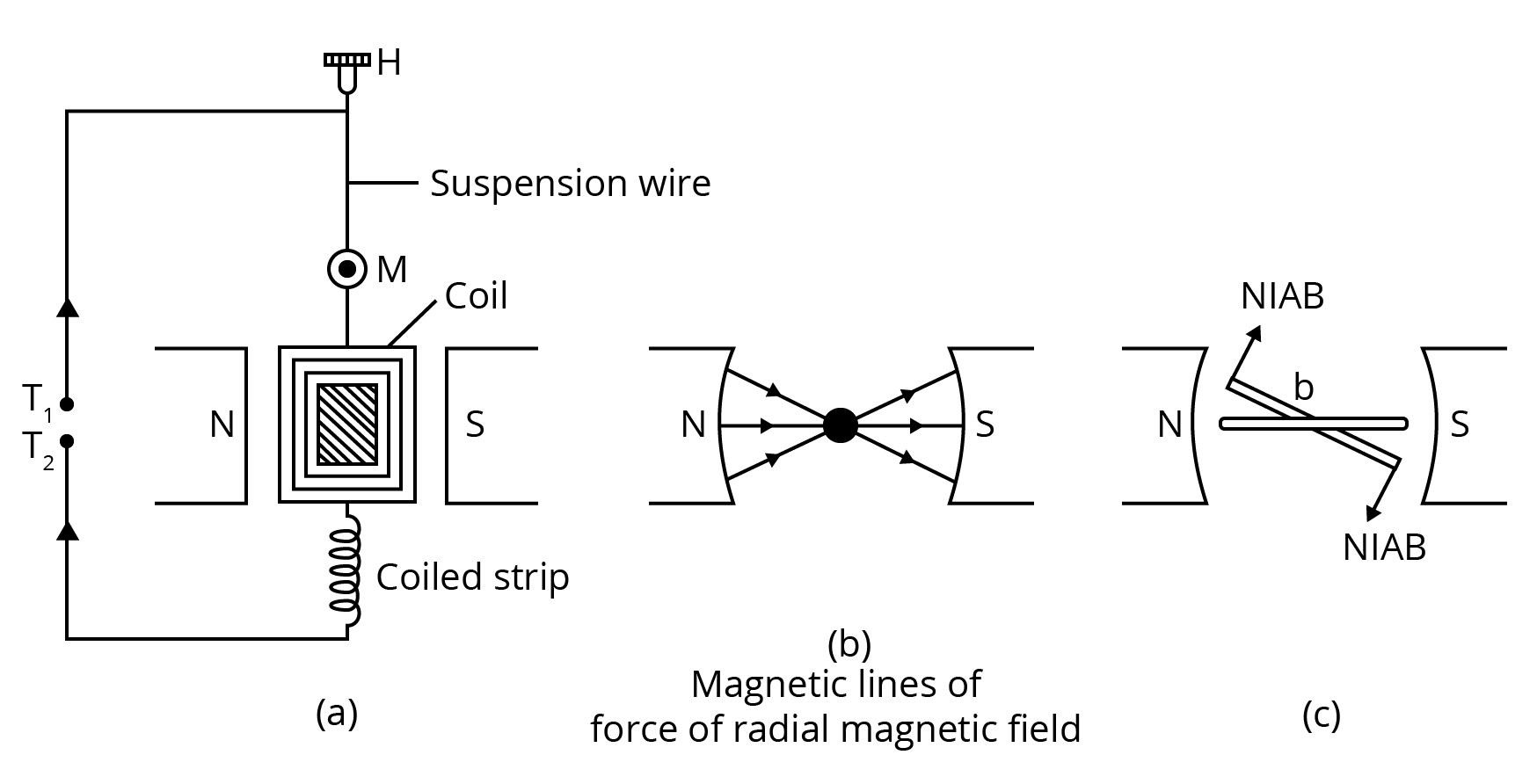
$\theta $ is the angle made by the normal to the plane of coil with B 

$\tau =NIAB\text{ }$ ……………………………….. (1)

This is called as deflecting torque 

As the coil deflected the spring is twisted and a restoring torque per unit twist then the restoring torque for the deflecting & is given by 

${\tau }'=k\phi $ ……………………….. (2)

In equilibrium 

\[\text{Deflecting Torque}=\text{Restoring Torque}\] 

\[NIAB=K\phi \] 

\[I=\frac{K\phi }{NAB}\phi \] 

\[I=G\phi \] where \[G=\frac{K}{NAB}\] (galvanometer constant) 

$\Rightarrow I\propto \phi $ 

Therefore, deflection of the coil is directly proportional to the current flowing in the coil.

2. A galvanometer can be converted into a voltmeter to measure upto 

1. $V$ volt by connecting a resistance ${{R}_{1}}$ series with the coil 

2. \[\frac{V}{2}\] volt by connecting a resistance ${{R}_{2}}$ in series with a coil. Find \[R\] in terms of ${{R}_{1}}\text{ and }{{R}_{2}}$ required to convert – it into a voltmeter that can read up to \['2V'\] volt. 

Ans: We know that, ${{I}_{g}}=\frac{V}{R+{{R}_{G}}}$ 

\[\Rightarrow {{I}_{g}}\text{=}\frac{V}{{{R}_{1}}+{{R}_{G}}}\] …………………………….. (1)

And ${{I}_{g}}=\frac{\frac{V}{2}}{{{R}_{2}}+{{R}_{G}}}$  ……………………………. (2)

Equating \[\left( 1 \right)\text{ }\And \text{ }\left( 2 \right)\] 

$\frac{V}{{{R}_{1}}+{{R}_{G}}}=\frac{\frac{V}{2}}{{{R}_{2}}+{{R}_{G}}}$ 

That is, ${{R}_{1}}+{{R}_{G}}=2\left( {{R}_{2}}+{{R}_{G}} \right)$

${{R}_{G}}=-2{{R}_{2}}+{{R}_{1}}$ 

For conversion ${{I}_{g}}=\frac{2V}{R+{{R}_{G}}}$ 

$\Rightarrow {{I}_{g}}\frac{V}{{{R}_{1}}+{{R}_{G}}}=\frac{2V}{R+{{R}_{G}}}$ 

$\Rightarrow {{I}_{g}}=2{{R}_{1}}+2{{R}_{G}}=R+{{R}_{G}}$ 

$\Rightarrow R=2{{R}_{1}}+{{R}_{G}}$ 

$\Rightarrow R=2{{R}_{1}}+{{R}_{1}}-2{{R}_{2}}$ 

$\Rightarrow R=3{{R}_{1}}-2{{R}_{2}}$ 

Therefore, R in the case can be written as, $R=3{{R}_{1}}-2{{R}_{2}}$.

3. Two moving coil meters, ${{M}_{1}}$ and ${{M}_{2}}$ have the following particulars:

${{R}_{1}}=10\,\Omega ,$ ${{N}_{1}}=30,$${{A}_{1}}=3.6\times {{10}^{-3}}\text{ }{{\text{m}}^{2}},$ ${{B}_{1}}=0.25\text{ T}$

\[{{R}_{2}}=14\,\Omega ,\] \[{{N}_{2}}=42\],${{A}_{2}}=1.8\times {{10}^{-3}}\text{ }{{\text{m}}^{2}},$ ${{B}_{2}}=0.50\text{ T}$

(The spring constants are identical for the two meters). 

Determine the ratio of (a) current sensitivity and (b) Voltage sensitivity of ${{M}_{1}}$ and  ${{M}_{2}}$.

a) current sensitivity of ${{M}_{1}}$ and  ${{M}_{2}}$:

Ans: From given data, moving coil meter ${{M}_{1}}$, 

Resistance, ${{R}_{1}}=10\,\Omega $ 

Number of turns, ${{N}_{1}}=30$ 

Area of cross-section, ${{A}_{1}}=3.6\times {{10}^{-3}}\text{ }{{\text{m}}^{2}}$

Magnetic field strength, ${{B}_{1}}=0.25\text{ T}$

Spring constant ${{K}_{1}}=K$ 

For moving coil meter ${{M}_{2}}$ : 

Resistance, \[{{R}_{2}}=14\,\Omega \]

Number of turns, \[{{N}_{2}}=42\]

Area of cross-section, ${{A}_{2}}=1.8\times {{10}^{-3}}\text{ }{{\text{m}}^{2}}$

Magnetic field strength, ${{B}_{2}}=0.50\text{ T}$

Spring constant, ${{K}_{2}}=K$ 

Current sensitivity of ${{M}_{1}}$ is given as:

${{I}_{s1}}=\frac{{{N}_{1}}{{B}_{1}}{{A}_{1}}}{{{K}_{1}}}$ 

And, the current sensitivity of ${{M}_{2}}$ is given as:

${{I}_{s2}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}}{{{K}_{2}}}$ 

$\therefore $ Ratio $\frac{{{I}_{s2}}}{{{I}_{s1}}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}{{K}_{1}}}{{{N}_{1}}{{B}_{1}}{{A}_{1}}{{K}_{2}}}$ $=\frac{42\times 0.5\times 1.8\times {{10}^{-3}}\times K}{K\times 30\times 0.25\times 3.6\times {{10}^{-3}}}=1.4$

Hence, the ratio of current sensitivity of ${{M}_{2}}\text{ to }{{M}_{1}}$ is $1.4$.

(b) voltage sensitivity of ${{M}_{2}}\text{ and }{{M}_{1}}$ 

Ans: Voltage sensitivity for ${{M}_{2}}$ is given as:

${{V}_{s2}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}}{{{K}_{2}}{{R}_{2}}}$ 

And, voltage sensitivity for ${{M}_{1}}$ is given as:

${{V}_{s1}}=\frac{{{N}_{1}}{{B}_{1}}{{A}_{1}}}{{{K}_{1}}{{R}_{1}}}$

On taking the ratio we get, 

$\frac{{{V}_{S2}}}{{{V}_{S1}}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}{{K}_{1}}{{R}_{1}}}{{{K}_{2}}{{R}_{2}}{{N}_{1}}{{B}_{1}}{{A}_{1}}}$

Substituting the given values, we get, 

$\therefore \frac{{{V}_{S2}}}{{{V}_{S1}}}=\frac{42\times 0.5\times 1.8\times {{10}^{-3}}\times 10\times K}{K\times 14\times 30\times 0.25\times 3.6\times {{10}^{-3}}}=1$

Therefore, the ratio of voltage sensitivity of ${{M}_{2}}\text{ and }{{\text{M}}_{1}}$is 1. 

4. In a chamber, a uniform magnetic field of $6.5G\left( 1G={{10}^{-4}}T \right)$is maintained. An electron is shot into the field with a speed of $4.8\times {{10}^{6}}m{{s}^{-1}}$ normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.$\left( e=1.6\times {{10}^{-19}}C,{{m}_{e}}=9.1\times {{10}^{-31}}kg \right)$

Ans: Given that, magnetic field strength, \[B=6.5\text{ G}=6.5\times {{10}^{-4}}\text{ T}\]

Speed of the electron, \[v=4.8\times {{10}^{6}}\text{ m/s}\]

Charge on the electron, $e=1.6\times {{10}^{-19}}\text{ C}$ 

Mass of the electron, ${{m}_{e}}=9.1\times {{10}^{-31}}\text{ kg}$

Angle between the shot electron and magnetic field, $\theta =90{}^\circ $ 

Magnetic force exerted on the electron in the magnetic field is given as: 

\[F=evB\sin \theta \] 

This force provides centripetal force to the moving electron. Hence, the electron starts moving in a circular path of radius $r$. 

Therefore, centripetal force exerted on the electron, 

${{F}_{c}}=\frac{m{{v}^{2}}}{r}$ 

In equilibrium, the centripetal force exerted on the electron is equal to the magnetic force, 

That is, ${{F}_{c}}=F$ 

$\frac{m{{v}^{2}}}{r}=evB\sin \theta $ 

$\Rightarrow r=\frac{mv}{Be\sin \theta }$ 

$\Rightarrow r=\frac{9.1\times {{10}^{-31}}\times 4.8\times {{10}^{6}}}{6.5\times {{10}^{-4}}\times 1.6\times {{10}^{-19}}\times \sin 90{}^\circ }$ 

$\Rightarrow r=4.2\times {{10}^{-2}}\text{ m}$ 

\[\Rightarrow r=4.2\text{ cm}\] 

Therefore, the radius of the circular orbit of the electron is \[4.2\text{ cm}\].

5. In Exercise \[4.11\] obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain. 

Ans: Given that, magnetic field strength, $B=6.5\times {{10}^{-4}}\text{ T}$ 

Charge of the electron, $e=1.6\times {{10}^{-19}}\text{ C}$ 

Mass of the electron, ${{m}_{e}}=9.1\times {{10}^{-31}}\text{ kg}$ 

Velocity of the electron, \[v=4.8\times {{10}^{6}}\text{ m/s}\] 

Radius of the orbit, \[r=4.2\text{ cm}=0.042\text{ m}\] 

Frequency of revolution of the electron $=\upsilon $ 

Angular frequency of the electron, $\omega =2n\upsilon $  

Velocity of the electron is related to the angular frequency as:

 $v=r\omega $ 

In the circular orbit, the magnetic force on the electron is balanced by the centripetal force. So, 

$evB=\frac{m{{v}^{2}}}{R}$ 

$\Rightarrow eB=\frac{m}{r}\left( r\omega  \right)=\frac{m}{r}\left( r2\pi \upsilon  \right)$ 

$\Rightarrow \upsilon =\frac{Be}{2\pi m}$ 

This expression for frequency is independent of the speed of the electron. 

On substituting, frequency, 

$\Rightarrow \upsilon =\frac{6.5\times {{10}^{-4}}\times 1.6\times {{10}^{-19}}}{2\times 3.14\times 9.1\times {{10}^{-31}}}$ 

$\Rightarrow \upsilon =18.2\times {{10}^{6}}\text{ Hz}$ 

$\Rightarrow \upsilon \approx 18\text{ MHz}$ 

Therefore, the frequency of the electron is around \[18\text{ MHz}\] and is independent of the speed of the electron.

6. Two concentric circular coils X and Y radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

Ans: We are given,

Radius of coil X, ${{r}_{1}}=16cm=0.16m$

Radius of coil Y, ${{r}_{2}}=10cm=0.1m$

Number of turns of on coil X,${{n}_{1}}=20$

Number of turns of on coil Y,${{n}_{2}}=25$

Current in coil X, ${{I}_{1}}=16A$

Current in coil Y,${{I}_{2}}=18A$

Magnetic field due to coil X at their centre is given by the relation,

${{B}_{1}}=\frac{{{\mu }_{0}}{{n}_{1}}{{I}_{1}}}{2{{r}_{1}}}$

Where, Permeability of free space, ${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$

${{B}_{1}}=\frac{4\pi \times {{10}^{-7}}\times 20\times 16}{2\times 0.16}$

$\therefore {{B}_{1}}=4\pi \times {{10}^{-4}}T$(towards East)

Magnetic field due to coil Y at their centre is given by the relation,

${{B}_{2}}=\frac{{{\mu }_{0}}{{n}_{2}}{{I}_{2}}}{2{{r}_{2}}}$

$\Rightarrow {{B}_{2}}=\frac{4\pi \times {{10}^{-7}}\times 25\times 18}{2\times 0.10}$

$\Rightarrow {{B}_{2}}=9\pi \times {{10}^{-4}}T$(towards West)

So, net magnetic field could be obtained as,

$B={{B}_{2}}-{{B}_{1}}=9\pi \times {{10}^{-4}}-4\pi \times {{10}^{-4}}$

$\Rightarrow B=1.57\times {{10}^{-3}}T$(towards West)

Therefore, net magnetic field is $1.57\times {{10}^{-3}}T$ towards west.

7. For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

1. Show that this reduces to the familiar result for the field at the centre of the coil.

Ans: We are given,

Radius of circular coil = R

Number of turns on the coil = N

Current in the coil = I

Magnetic field at a point on its axis at distance x is given by the relation,

Where,${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$Permeability of free space

If the magnetic field at the centre of the coil is considered, then $x=0$

$\therefore B=\frac{{{\mu }_{0}}I{{R}^{2}}N}{2{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\frac{3}{2}}}}$

Therefore, this is the familiar result for the magnetic field at the centre of the coil.

2. Consider two parallel coaxial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the midpoint between the coils is uniform over a distance that is small as compared to R, and is given by, approximately, (Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.)

Ans: Radii of two parallel coaxial circular coils = R

Number of turns on each coil = N

Current in both coils = I

Distance between both the coils = R

Let us consider point Q at distance d from the centre.

Then, one coil is at a distance of $\frac{R}{2}+d$from point Q.

Magnetic field at point Q could be given as:

$B=\frac{{{\mu }_{0}}I{{R}^{2}}N}{2{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\frac{3}{2}}}}$

Also, the other coil is at a distance of  $\frac{R}{2}+d$from point Q.

Magnetic field due to this coil is given as:

${{B}_{2}}=\frac{{{\mu }_{0}}NI{{R}^{2}}}{2{{\left[ {{\left( \frac{R}{2}-d \right)}^{2}}+{{R}^{2}} \right]}^{\frac{3}{2}}}}$

Now we have the total magnetic field as, 

$B={{B}_{1}}+{{B}_{2}}$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. {{\left( \frac{R}{2}-d \right)}^{2}}+{{R}^{2}} \right\} \right.}^{\frac{-3}{2}}}+{{\left. \left\{ {{\left( \frac{R}{2}+d \right)}^{2}}+{{R}^{2}} \right. \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. \frac{5{{R}^{2}}}{4}+{{d}^{2}}-Rd \right\} \right.}^{\frac{-3}{2}}}+{{\left. \left\{ \frac{5{{R}^{2}}}{4}+{{d}^{2}}+Rd \right. \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. 1+\frac{4{{d}^{2}}}{5{{R}^{2}}}-\frac{4d}{5R} \right\} \right.}^{\frac{-3}{2}}}+{{\left\{ 1+\frac{4{{d}^{2}}}{5{{R}^{2}}}+\frac{4d}{5R} \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

Now for $d\ll R$, we could neglect the factor $\frac{{{d}^{2}}}{{{R}^{2}}}$, we get, 

$B\approx \frac{{{\mu }_{0}}I{{R}^{2}}}{2}\times {{\left( \frac{5{{R}^{2}}}{4} \right)}^{\frac{-3}{2}}}\left[ {{\left( 1-\frac{4d}{5R} \right)}^{\frac{-3}{2}}}+{{\left( 1+\frac{4d}{5R} \right)}^{\frac{-3}{2}}} \right]\times N$

$\Rightarrow B\approx \frac{{{\mu }_{0}}I{{R}^{2}}}{2}\times {{\left( \frac{5{{R}^{2}}}{4} \right)}^{\frac{-3}{2}}}\left[ 1-\frac{6d}{5R}+1+\frac{6d}{5R} \right]$

$\Rightarrow B\approx {{\left( \frac{4}{5} \right)}^{\frac{3}{2}}}\frac{{{\mu }_{0}}IN}{R}=0.72\left( \frac{{{\mu }_{0}}IN}{R} \right)$

Therefore, we proved that the field along the axis around the mid-point between the coils is uniform. 

8. An electron emitted by a heated cathode and accelerated through a potential difference of $2.0kV$, enters a region with a uniform magnetic field of $0.15T$. Determine the trajectory of the electron if the field 

1. is transverse to its initial velocity. 

Ans: We are given, 

Magnetic field strength, $B=0.15T$

Charge on the electron, $e=1.6\times {{10}^{-19}}C$

Mass of the electron, $m=9.1\times {{10}^{-31}}kg$

Potential difference, $V=2.0kV=2\times {{10}^{3}}V$

Now we have the kinetic energy of the electron given by, 

$K.E=eV$

Substituting the given values we get, 

$eV=\frac{1}{2}m{{v}^{2}}$

$\Rightarrow v=\sqrt{\frac{2eV}{m}}$…………………….. (1)

Where, $v$is the velocity of the electron

Since the magnetic force on the electron provides the required centripetal force of the electron, the electron traces a circular path of radius $r$.

Now, the magnetic force on the electron is given by the relation, 

$F=Bev$

Centripetal force, 

${{F}_{C}}=\frac{m{{v}^{2}}}{r}$

$\Rightarrow Bev=\frac{m{{v}^{2}}}{r}$

$\Rightarrow r=\frac{mv}{Be}$………………….. (2)

From the equations (1) and (2), we get, 

$r=\frac{m}{Be}{{\left[ \frac{2eV}{m} \right]}^{\frac{1}{2}}}$

Substituting the given values, 

$\Rightarrow r=\frac{9.1\times {{10}^{-31}}}{0.15\times 1.6\times {{10}^{-19}}}{{\left( \frac{2\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{3}}}{9.1\times {{10}^{-31}}} \right)}^{\frac{1}{2}}}$

$\Rightarrow r=100.55\times {{10}^{-5}}$

$\Rightarrow r=1mm$

Therefore, we found that the electron has a circular trajectory of radius 1.0 mm normal to the magnetic field.

2. makes an angle of $30{}^\circ $with the initial velocity.

Ans: When the field makes an angle $\theta $ of $30{}^\circ $with initial velocity, the initial velocity will be,

${{v}_{1}}=v\sin \theta $

From equation (2), we can write the following expression:

${{r}_{1}}=\frac{m{{v}_{1}}}{Be}$

$\Rightarrow {{r}_{1}}=\frac{mv\sin \theta }{Be}$

$\Rightarrow {{r}_{1}}=\frac{9.1\times {{10}^{-31}}}{0.15\times 1.6\times {{10}^{-19}}}\left[ \frac{2\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{3}}}{9\times {{10}^{-31}}} \right]\sin 30{}^\circ $

$\Rightarrow r=0.5\times {{10}^{-3}}m=0.5mm$

Therefore, we found that the electron has a helical trajectory of radius $0.5mm$, with the axis of the solenoid along the magnetic field direction.

9. A magnetic field set up using Helmholtz coils (described in Exercise $4.16$) is uniform in a small region and has a magnitude of $0.75T$. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through $15kV$enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is $9.0\times {{10}^{-5}}V{{m}^{-1}}$ make a simple guess as to what the beam contains. Why is the answer not unique?

Ans: We are given,

Magnetic field, $B=0.75T$

Accelerating voltage, $V=15kV=15\times {{10}^{3}}V$

Electrostatic field, $E=9\times {{10}^{5}}V{{m}^{-1}}$

Mass of the electron$=m$

Charge of the electron $=e$

Velocity of the electron $=v$

Kinetic energy of the electron $=eV$

Thus, 

$\frac{1}{2}m{{v}^{2}}=eV$

$\Rightarrow \frac{e}{m}=\frac{{{v}^{2}}}{2V}$…………………….. (1)

Since the particle remains undeflected by electric and magnetic fields, we could infer that the electric field is balancing the magnetic field.

$eE=evB$

$\Rightarrow v=\frac{E}{B}$……………………….. (2)

Now we could substitute equation (2) in equation (1) to get,

$\Rightarrow \frac{e}{m}=\frac{1}{2}\frac{{{\left( \frac{E}{B} \right)}^{2}}}{V}=\frac{{{E}^{2}}}{2V{{B}^{2}}}$

$\Rightarrow \frac{e}{m}=\frac{{{\left( 9.0\times {{10}^{5}} \right)}^{2}}}{2\times 15000\times {{\left( 0.75 \right)}^{2}}}=4.8\times {{10}^{7}}C/kg$

This value of the specific charge $\left( \frac{e}{m} \right)$ is equal to the value of deuteron or deuterium ions. This is not a unique answer. Other possible answers are $H{{e}^{++}}$, $L{{i}^{+++}}$

10. A uniform magnetic field of $1.5T$ exists in a cylindrical region of radius $10.0cm$, its direction parallel to the axis along east to west. A wire carrying a current of $7.0A$ in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,

1. The wire intersects the axis,

Ans: We are given,

Magnetic field strength, $B=1.5T$

Radius of the cylindrical region, $r=10cm=0.1m$

Current in the wire passing through the cylindrical region, $I=7A$

If the wire intersects the axis, then the length of the wire is the diameter of the cylindrical region. Thus, $l=2r=0.2m$

Angle between magnetic field and current, $\theta =90{}^\circ $

We know that, Magnetic force acting on the wire is given by the relation,

$F=BIl\sin \theta $

$\Rightarrow F=1.5\times 7\times 0.2\times \sin 90{}^\circ $

$\Rightarrow F=2.1N$

Therefore, a force of 2.1 N acts on the wire in a vertically downward direction.

2. The wire is turned from N-S to northeast-northwest direction,

Ans: New length of the wire after turning it to the northeast-northwest direction can be given as:

${{l}_{1}}=\frac{l}{\sin \theta }$

Angle between magnetic field and current, $\theta =45{}^\circ $

Force on the wire,

$F=BI{{l}_{1}}\sin \theta =BIl=1.5\times 7\times 0.2$

$\Rightarrow F=2.1N$

Therefore, a force of 2.1 N acts vertically downward on the wire. This is independent of angle $\theta $ as $l\sin \theta $ is fixed.

3. The wire in the N-S direction is lowered from the axis by a distance of $6.0cm$?

Ans: The wire is lowered from the axis by distance, $d=6.0cm$

Let ${{l}_{2}}$be the new length of the wire, 

${{\left( \frac{{{l}_{2}}}{2} \right)}^{2}}=4\left( d+r \right)=4\left( 10+6 \right)=4\times 16$

$\Rightarrow {{l}_{2}}=8\times 2=16cm=0.16m$

Magnetic force that is exerted on the wire is, 

${{F}_{2}}=BI{{l}_{2}}=1.5\times 7\times 0.16$

$\Rightarrow F=1.68N$

Therefore, a force of $1.68N$acts in a vertically downward direction on the wire.

11. A uniform magnetic field of $3000G$ is established along the positive z-direction. A rectangular loop of sides $10cm$ and $5cm$ carries a current of $12A$. What is the torque on the loop in the different cases shown in Figure? What is the force on each case? Which case corresponds to stable equilibrium?

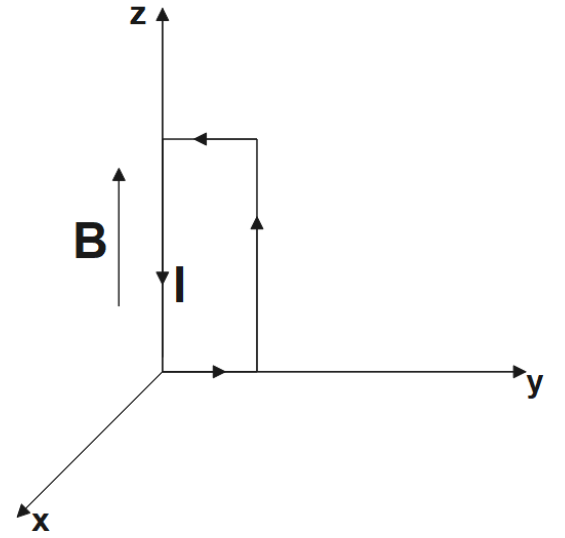
Ans: We are given, 

Magnetic field strength, $B=3000G=3000\times {{10}^{-4}}T=0.3T$

Length of the rectangular loop, $l=10cm$

Width of the rectangular loop, $b=5cm$

Area of the loop, $A=l\times b=\left( 10\times 5 \right)c{{m}^{2}}=50\times {{10}^{-4}}{{m}^{2}}$

Current in the loop, $I=12A$

Now, we could take the anti-clockwise direction of the current as positive and vice-versa, 

We have the expression for torque given as,

\[\vec{\tau }=I\vec{A}\times \vec{B}\]

We could see from the given figure that A is normal to the y-z plane and B is directed along the z-axis. Substituting the given values, 

$\tau =12\times \left( 50\times {{10}^{-4}} \right)\hat{i}\times 0.3\hat{k}$

$\Rightarrow \tau =-1.8\times {{10}^{-2}}\hat{j}Nm$

Now the torque is found to be directed along a negative y-direction. Since the external magnetic field is uniform, the force on the loop would be zero. 

(Image will be uploaded soon)

Ans: This case is very similar to case (a), so, the answer here would be same as (a). 

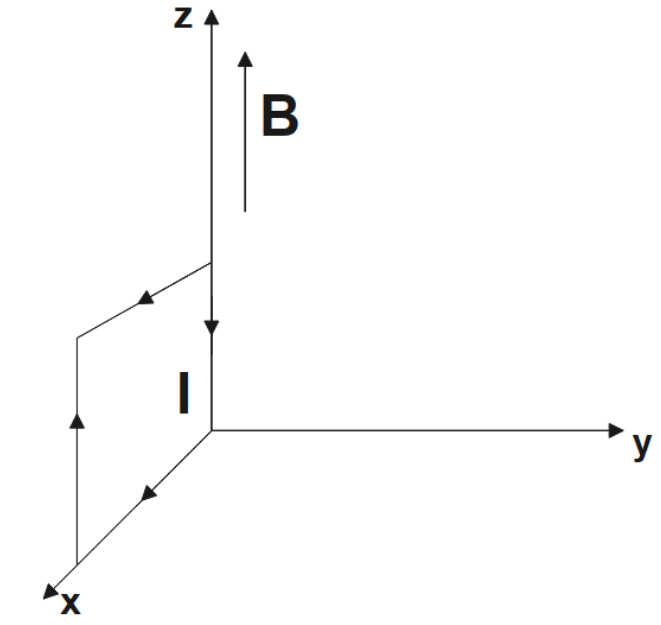
Ans: Torque here would be, 

\[\vec{\tau }=I\vec{A}\times \vec{B}\]

$\Rightarrow \tau =-12\left( 50\times {{10}^{-4}} \right)\hat{j}\times 0.3\hat{k}$

$\Rightarrow \tau =-1.8\times {{10}^{-2}}\hat{i}Nm$

The direction here is along the negative x direction and the force is zero. 

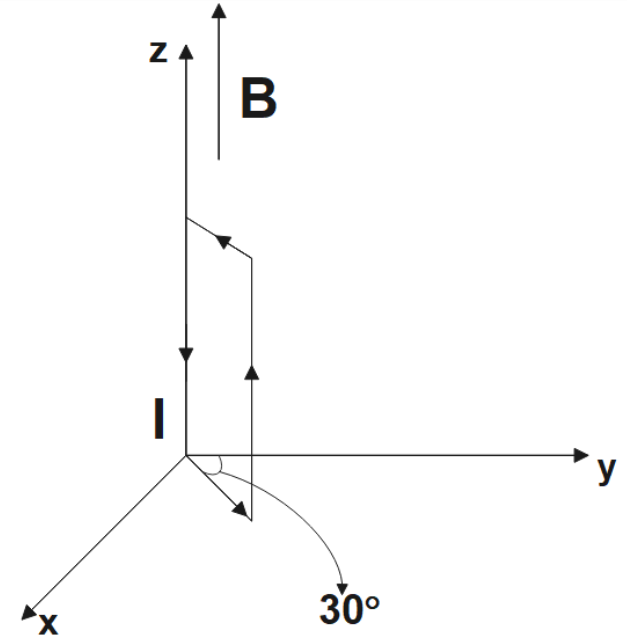
Ans: Torque here would be, 

$\left| \tau  \right|=IAB$

$\Rightarrow \tau =12\times \left( 50\times {{10}^{-4}} \right)\times 0.3$

$\Rightarrow \left| \tau  \right|=1.8\times {{10}^{-2}}Nm$

Here, the direction is found to be at $240{}^\circ $with positive x-direction and the force is zero.

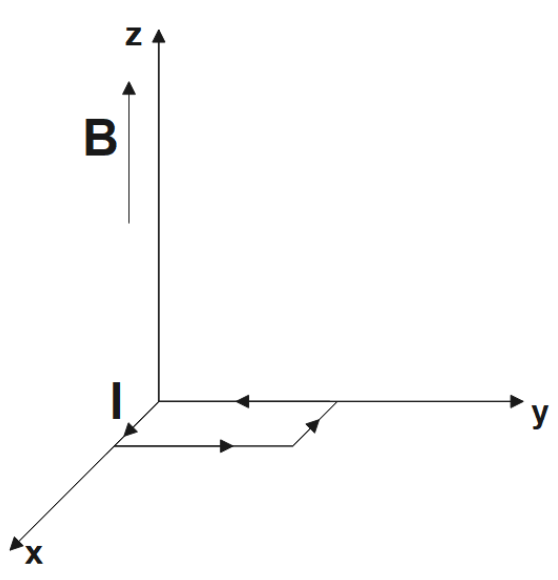
Ans: Torque, 

$\tau =I\vec{A}\times \vec{B}$

$\Rightarrow \tau =\left( 50\times {{10}^{-4}}\times 12 \right)\hat{k}\times 0.3\hat{k}$

$\Rightarrow \tau =0$

Here, both torque and force are found to be zero. For this case, the direction $I\vec{A}$and $\vec{B}$is the same and the angle between them is zero. They would come back to equilibrium on being displaced and so the equilibrium is stable.

(image will be uploaded soon)

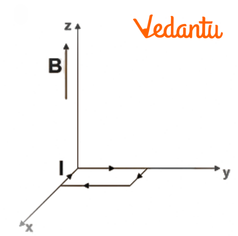
Ans: Torque is given by, 

$\tau =I\vec{A}\times \vec{B}$

$\Rightarrow \tau =\left( 50\times {{10}^{-4}}\times 12 \right)\hat{k}\times 0.3\hat{k}$

$\Rightarrow \tau =0$

Here also both torque and force are found to be zero. 

For this case, the direction of $I\vec{A}$ and $\vec{B}$ are opposite and the angle between them is $180{}^\circ $. Here it doesn’t come back to its original position on being disturbed and hence, the equilibrium is unstable. 

12. A solenoid $60cm$ long and has a radius $4.0cm$ has 3 layers of windings of 300turns each. A $2.0cm$ long wire of mass $2.5g$ lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of $6.0A$ in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? $g=9.8m{{s}^{-2}}$

Ans: We are given:

Length of the solenoid, $L=60cm=0.6m$

Radius of the solenoid, $r=4.0cm=0.04m$

It is given that there are 3 layers of windings of 300 turns each.

Total number of turns, $n=3\times 300=900$

Length of the wire, $l=2cm=0.02m$

Mass of the wire, $m=2.5g=2.5\times {{10}^{-3}}kg$

Current flowing through the wire, $i=6A$

Acceleration due to gravity, $g=9.8m{{s}^{-2}}$

Magnetic field produced inside the solenoid, $B=\frac{{{\mu }_{0}}nI}{L}$

Where, Permeability of free space ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

Current flowing through the windings of the solenoid, $I$

Magnetic force is given by the relation,

$F=Bil=\frac{{{\mu }_{0}}nI}{L}il$

Now, we have the force on the wire equal to the weight of the wire.

$mg=\frac{{{\mu }_{0}}nIil}{L}$

$\Rightarrow I=\frac{mgL}{{{\mu }_{0}}nil}=\frac{2.5\times {{10}^{-3}}\times 9.8\times 0.6}{4\pi \times {{10}^{-7}}\times 900\times 0.02\times 6}$

$\Rightarrow I=108A$

Therefore, the current flowing through the solenoid is 108 A.

Download Important Questions Of Chapter 4 Physics Class 12 PDF

Class 12 Physics Chapter 4 Important Questions

The Class 12 Physics Chapter 4 important questions PDF is highly beneficial for the students who are targeting good grades in competitive exams. The textbook prescribed by NCERT for Class 12 Physics consists of many topics. For elevating the grades and to improve their knowledge in the subject students are suggested to download chapter wise notes available on Vedantu for detailed explanation along with exercise problems. 

For thorough preparation, students should start with Chapter 4 Physics Class 12 important questions. The important questions of Chapter 4 Physics Class 12 are prepared with deep insight into the syllabus according to CBSE board exams, previous year’s questions. The Chapter 4 Physics Class 12 important questions included all the textbook exercises along with many Class 12 Physics Chapter 4 extra questions prepared by experts and the master teachers.

Chapter 4 Moving Charges and Magnetism has good marks allotment in the Board exams. The Moving charges and Magnetism include many interesting topics like magnetic forces, magnetic field, the direction of magnetic force in the current-carrying coil with different cases, etc. These concepts are not only important in the point of board exam but also for students who are aiming for IIT-JEE, NEET exams as well.

Students must start with Class 12 Physics Chapter 4 important questions after revising the chapter. Students must be thoroughly familiar with all the concepts of Chapter 4 for solving Class 12 Physics Chapter 4 extra questions. Let us have a look at some key points of Chapter 4:

• The chapter consists of many direct derivations like ampere circuital law, the force between two parallel current-carrying wires, etc.

• Chapter 4 mainly focused on explaining the idea that electric and magnetic fields are interrelated to one another. Because since the beginning it was assumed that electric fields and magnetic fields are independent of each other.

• We come across the concepts like a magnetic force, Lorentz force which is a piece of evidence about electric and magnetic fields that are related to each other.

• We study the effects of magnetic fields on current. We study a few devices that use the principle of magnetic induction.

• We study cyclotrons, solenoids, moving coil galvanometers, etc.

These are a few key points to be remembered while jumping into the practice of Chapter 4 Physics Class 12 important questions.

Key Features of Vedantu’s CBSE Class 12 Important Questions for Physics Chapter 4 - Moving Charges and Magnetism

The following are the reasons why you should choose Vedantu’s Important Questions for Class 12 CBSE Physics Chapter 4 - Moving Charges and Magnetism:

• Vedantu’s Important Questions for Class 12 CBSE Physics Chapter 4 - Moving Charges and Magnetism are aligned with the CBSE Board guidelines and answering pattern.

• Our questions are prepared in a manner that will serve the purpose of revising the entire chapter to be able to solve any kind of question that is asked in the exam.

• The questions adhere to the strict norms of the CBSE Class 12 Physics syllabus. The answers have also been framed in a straightforward manner using simple language. 

Conclusion

The set of important questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism for the academic year 2024-25 prove to be a valuable tool for students' exam preparation. These questions cover vital concepts such as magnetic fields, Ampere's law, and applications of moving charges in magnetic fields. By practicing these questions, students can strengthen their understanding of the topic and improve problem-solving abilities. The comprehensive nature of these questions ensures thorough coverage of the chapter, enabling students to excel in their examinations. With these resources at their disposal, students can confidently approach the subject and achieve academic success in the upcoming academic year.

Important Related Links for CBSE Class 12 Physics