NCERT Exemplar for Class 12 Physics Chapter-8 (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS - I

1. One requires 11eV of energy to dissociate a carbon monoxide molecule into carbon  and oxygen atoms. The minimum frequency of the appropriate electromagnetic  radiation to achieve the dissociation lies in 

(a) visible region.

(b) infrared region.

(c) ultraviolet region.

(d) microwave region.

Ans: option (c)

$E = {\text{ }}11{\text{ }}eV = 11 \times 1.6 \times {10^{ - 19}}J$

$h = 6.62 \times {10^{ - 34{\text{ }}}}J - S$

$E = hf$

By putting the values in the formula: 

$f = \dfrac{E}{h} = \dfrac{{11 \times 1.6 \times {{10}^{ - 19}}}}{{6.62 \times {{10}^{ - 34}}}} = \dfrac{{8.8 \times {{10}^{ - 19 + 34}}}}{{3.31}}$

$\dfrac{{880}}{{331}} \times {10^{15}}Hz = 2.65 \times {10^{15}}Hz$

Therefore we can see that the above value lies in the range of  UV region

2. A linearly polarized electromagnetic wave given as ${E_i}cos(kz - \omega t)$ is incident  normally on a perfectly reflecting infinite wall at z = a. Assuming that the material of  the wall is optically inactive, the reflected wave will be given as

(a) $E_r{\text{ }}{ = _i}-cos{\text{ }}(kz - \omega t).$

(b) $E_r{\text{ }} = i{E_0}cos{\text{ }}(kz + \omega t)$

(c) $E_r{\text{ }}{ = _i}cos{\text{ }}(kz + \omega t).$

(d) $E_r{\text{ }}{ = _i}cos{\text{ }}(kz - \omega t).$

Ans: Option (b)

As E is along the $ + ve$ X axis so reflected rays will be along the negative X-axis. Its electric component  will also be opposite to earlier, i.e. in -z direction, phase will change by

$E_r = {E_0}\left( { - i} \right){\text{ }}cos[k\left( { - z} \right) - \omega t{\text{ }} + \pi ]$

Since $\cos \theta  = \left( {\pi  - \theta } \right) =  - \cos \theta $

$E_r = -i{E_0}cos[\pi-(kz+ \omega t)]$

$E_r = i{E_0}cos(kz+ \omega t)$

3. Light with an energy flux of $20W/c{m^2}$ falls on a non-reflecting surface at normal  incidence. If the surface has an area of $30c{m^2}$, the total momentum delivered (for  complete absorption) during $30$ minutes is

(a) $36{\text{ }} \times {\text{ }}{10^{ - 5}}{\text{ }}kg{\text{ }}m/s.$

(b) $36{\text{ }} \times {\text{ }}{10^{ - 4}}{\text{ }}kg{\text{ }}m/s.$

(c) ${\text{108 }} \times {\text{ }}{10^4}{\text{ }}kg{\text{ }}m/s.$

(d) ${\text{1}}{\text{.08 }} \times {\text{ }}{10^7}{\text{ }}kg{\text{ }}m/s.$

Ans: Option (b)

Energy flux $ = \phi = 20W/c{m^2}$

Area $A = 30c{m^2}$, time = $t = 30 \times 60$ sec

U= total energy falling t sec= Energy flux $ \times $ Area $ \times $ time =$\phi $

$U = {\text{ }}20 \times 30 \times 30 \times 60{\text{ }}J$

Momentum of the incident light$ = \dfrac{U}{C} = $$\dfrac{{20 \times 30 \times 30 \times 60}}{{3 \times {{10}^8}}}$

$ = 36 \times {10^{ - 4}}kg{\text{ }}m{s^{ - 1}}$

As there is no reflection from the surface and for complete absorption, the momentum of reflected  radiation is zero.
Momentum delivered to surface= Change in momentum

${p_f} = {p_t} = 0 - 36 \times {10^{ - 4}} =  - 36 \times {10^{ - 4}}kg\,m/s$

(-) sign shows the direction of momentum.

4. The electric field intensity produced by the radiations coming from $100W$ bulb at a  $3m$ distance is E. The electric field intensity produced by the radiations coming from $50W$ bulb at the same distance is

(a) $\dfrac{E}{2}$

(b) $2E$

(c) $\dfrac{E}{{\sqrt 2 }}$

(d) $\sqrt 2 E$

Ans: Option (c)

${E_0} \propto \sqrt P $

$\dfrac{{{{({E_0})}_1}}}{{{{({E_0})}_2}}} = \sqrt {\dfrac{{{{(P)}_1}}}{{{{(P)}_1}}}}  = \sqrt {\dfrac{{100W}}{{50W}}}  = \dfrac{{\sqrt 2 }}{1}$

Therefore ${({E_0})_2} = \dfrac{{{{({E_0})}_1}}}{{\sqrt 2 }}$

5. If E and B represent electric and magnetic field vectors of the electromagnetic wave,  the direction of propagation of electromagnetic wave is along

(a) $\overline E $

(b) $\overline B $

(c) $\overline B  \times \overline E $

(d) $\overline E  \times \overline B $

Ans: Option (d) 

The direction of propagation of electromagnetic waves is perpendicular to both $\overline E $  and $\overline B $ by right thumb rule.

$\overline E  \times \overline B $ by the right thumb rule.

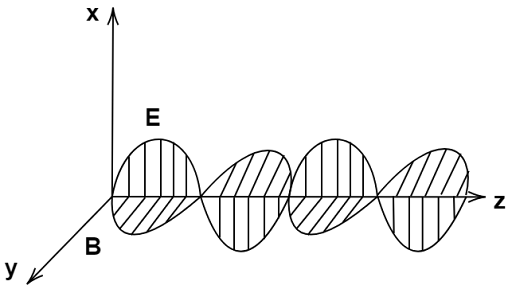
The electric field E is along the $E( + x)$ and $E( - x)$ axis and magnetic field B is along the $B(y)$ and $B( - y)$ axis. So by cross product of E and B, direction is perpendicular to E and B, from and i.e.  $\left( {E \times B} \right)$ in $ + z$.

6. The ratio of contributions made by the electric field and magnetic field components  to the intensity of an EM wave is

(a) $c:1$

(b) ${c^2}:1$

(c) $1:1$

(d) $\sqrt c :1$

Ans: Option (c) 

Average energy by electric field ${E_0}$ is ${U_{av}}$

${U_ \propto } = \dfrac{1}{2}{\varepsilon _0}E_0^2$ 

But ${E_0} = c{B_0}$

${U_{av}}$ , electric field $ = \dfrac{1}{2}{\varepsilon _0}\left( {c{B_0}} \right)_{}^2 = \dfrac{1}{2}{\varepsilon _0}{c^2}B_0^2$

$ = \dfrac{1}{2}{\varepsilon _0}\dfrac{1}{{{\mu _0}{\varepsilon _0}}}{({B_0})^2}$ , here ${c^2} = \dfrac{1}{{{\mu _0}{\varepsilon _0}}}$

${({U_{av}})_{electric\,field}} = \dfrac{1}{{2{\mu _0}}}B_0^2{({U_{av}})_{magnetic\,field}}$

Ratio =$\dfrac{{{U_{{{(av)}_{magnetic\,field}}}}}}{{{U_{{{(av)}_{magnetic\,field}}}}}} = \dfrac{1}{1}$  , i.e.  $1:1$.

7. An EM wave radiates outwards from a dipole antenna, with ${E_0}$ as the amplitude of  its electric field vector. The electric field ${E_0}$ which transports significant energy from  the source falls off as

(a) $\dfrac{1}{{{r^3}}}$

(b) $\dfrac{1}{{{r^2}}}$

(c) $\dfrac{1}{r}$

(d) remains constant.

Ans: Option (c) 

As we know that electromagnetic waves are radiated from dipole antennas and  radiated energy $E \propto \dfrac{1}{r}$.

8. An electromagnetic wave travels in vacuum along $ + z$ direction $E = \left( {{E_1}i + {E_0}J} \right)\cos (kz - \omega t)$

Choose the correct options from the following:
(a) The associated magnetic field is given as $B = \dfrac{1}{C}\left( {{E_1}i - {E_2}j} \right)\cos (kz - \omega t)$

(b) The associated magnetic field is given as $B = \dfrac{1}{C}\left( {{E_1}i - {E_2}j} \right)\cos (kz - \omega t)$

(c) The given electromagnetic field is circularly polarised.
(d) The given electromagnetic wave is plane polarised.

Ans: Options (a) and (d) 

We can see that in the given question we have electromagnetic wave, the electric field vector which is given as  $E = \left( {{E_1}i - {E_2}j} \right)\cos (kz - \omega t)$ . In electromagnetic wave the associated magnetic field Vector $\overline B  = \dfrac{{\overline E }}{{\overline C }} = \dfrac{1}{C}({E_1}i + {E_2}j)\cos (kz - \omega t)$ verify the option (a) and (b) as $\overline E $ and $\overline B $are long X- and Y-axis  respectively so we can say that the direction of propagation is Z-axis and the electromagnetic  wave is plane polarized along the X and Y direction $\overline E $ and $\overline B $ respectively verifies option (d).

9. An electromagnetic wave traveling along z-axis is given as $E{\text{ }}{E_0}{\text{ }}cos{\text{ }}(kz{\text{ }} - \omega t)$ . Choose the correct options from the following: 

(a) The associated magnetic field is given as $B = \dfrac{1}{c}k \times K = \dfrac{1}{\omega }\left( {k \times E} \right)$

(b) The electromagnetic field can be written in terms of the associated magnetic field as $\overline E  = c\left( {\overline B  \times \overline K } \right)$

(c) $\overline K  \times E = 0 \times B \times \overline K  = 0$

(d) $\overline K  \times E = 0 \times \overline B  \times \overline K  = 0$

Ans: Options (a), (b) and ©

In the above question we can see that the electromagnetic wave is traveling in +Z direction. Therefore we can say that its electric field is given by  $E = {\text{ }}{E_0}{\text{ }}cos(kz - \omega t)$ along X direction which is perpendicular to Z-axis i.e., along X direction.  Thus it proves that the associated magnetic field B is also perpendicular to $ + Y$ .

10. A plane electromagnetic wave propagating along x direction can have the following  pairs of E and B

(a) ${E_X},{\text{ }}{B_Y}$

(b) ${E_Y},{\text{ }}{B_{}}$

(c) ${B_x},{\text{ }}{{\text{E}}_y}$

(d) ${E_Z},{\text{ }}{B_Y}$

Ans: Options (b) and (d)

We can see that in the above question  the EM wave is plane polarized and thus its propagation is in +X direction. So we can say that it will be in either Y and Z direction or Z and Y direction. Thus it  verifies the direction of  $\overline E $ and $\overline B$ will be in either Y and Z direction or Z and Y direction. So this verifies answers (b) and (d).

11. A charged particle oscillates about its mean equilibrium position with a frequency of ${10^9}\,Hz$. The electromagnetic waves produced:

(a) will have frequency of ${10^9}\,Hz$

(b) will have frequency of $2 \times {10^9}\,Hz$

(c) will have wavelength of $0.3\,m$

(d) fall in the region of radio waves.

Ans: Options (a) (c) and (d) 

Vibrating particles produce electric and magnetic fields, so will produce  an E.M. wave of same frequency ${10^9}Hz$ verifies answer (a).

$V = {\text{ }}{10^9}{\text{ }}Hz,{\text{ }}c = 3 \times {10^8}m/s$

So $\lambda  = \dfrac{c}{v} = \dfrac{{3 \times {{10}^8}}}{{10 \times {{10}^8}}} = 0.3m$

Therefore it verifies answer (c).

As the range of radio waves is $10Hz$ to ${10^{12}}Hz$ and ${10^9}Hz$ lies between this range. Hence, option (d) is verified.

12. The source of electromagnetic waves can be a charge
(a) moving with a constant velocity.
(b) moving in a circular orbit.
(c) at rest.
(d) falling in an electric field.

Ans: Option (b) 

We know that an electromagnetic wave can be produced either by accelerated or by oscillating charge. Here, we can see that in option (b) charge is moving in a circular orbit. In circular motion, the direction of the motion of charge is changing continuously, thus it proves our explanation that it is an accelerated motion and this option is correct.

13. An E.M. a wave of intensity I falls on a surface kept in vacuum and exerts radiation  pressure p on it. Which of the following are true?

(a) Radiation pressure is $I/c$  if the wave is totally absorbed

(b) Radiation pressure is $I/c$  if the wave is totally reflected

(c) Radiation pressure is $\dfrac{{2I}}{c}$ if the wave is totally reflected.

(d) Radiation pressure is in the range $\dfrac{1}{c} < p < \dfrac{{2I}}{c}$ for real surfaces. 

Ans: Options (a) (c) and (d)

We know that the radiation pressure is the force exerted by particles (dual nature of particle) on unit area, due to the change in momentum of radiated particles  per unit area per $\sec  = \dfrac{1}{c}$

Here we have 

$I$= intensity of radiation 

$C$= velocity of radiation

We know that when the wave is fully absorbed by the surface, then the  momentum of the reflected wave per unit time per unit area is zero. 

Radiations are absorbed, so momentum per unit area per second $ = \dfrac{1}{c}$ thus it verifies the first option i.e.  (a).

When radiation is reflected back, the momentum becomes double as in the earlier case, so  discards the option (b) and it verifies the third option i.e. (c).

So variation of radiation pressure p comes between the range $\dfrac{1}{c} < p < \dfrac{{2I}}{c}$ thus it verifies the option (d) .

14. Why is the orientation of the portable radio with respect to the broadcasting station  important?
Ans: Transmitted carrier wave signals are plane polarized and if the intensity of signal is  poor then the receiving antenna of the radio must be parallel to the component of either electric or  magnetic field. Because energy is only due to amplitudes of electric and magnetic  components in EM waves, magnitude of amplitude is in particular direction perpendicular to  each other and perpendicular to wave propagation.

15. Why does the microwave oven heat up a food item containing water molecules most  efficiently?
Ans: We know that in  Microwave oven, molecules of food items start to vibrate by a driven force due to the frequency of the microwave. But when the natural frequency of water molecules  matches with microwave frequency then it causes resonance (more amplitude) which further causes increase in temperature.

16. The charge on a parallel plate capacitor varies as $q = {\text{ }}{q_0}cos{\text{ }}2\pi \nu t$. The plates are  very large and close together (area $ = A$, separation $ = d$). Neglecting the edge effects, find  the displacement current through the capacitor?

Ans: The displacement current Id in capacitor is

${I_d} = {I_c} = \dfrac{{dq}}{{dt}},$ where $q = {q_0}\cos \left( {2\pi vt} \right)$(Given)

${I_d} = {I_c} = \dfrac{d}{{dt}}{q_0}\cos (2\pi vt)$

${I_d} = {q_0}2\pi v\sin \pi vt$

${I_d} = 2\pi v{q_0}\pi vt$

17. A variable frequency a.c source is connected to a capacitor. How will the
displacement current change with decrease in frequency? 

Ans: As we know that ${X_c} = \dfrac{1}{{2\pi VC}}$ and $I = \dfrac{V}{{{X_c}}}$

So reactance of capacitor increases on decreasing frequency ${X_C} = \dfrac{1}{v}$

So $I = 2\pi v{\text{ }}CV$

As the reactance of the capacitor increases, the current by Ohm’s law will decrease.

$1 \propto \dfrac{1}{{{X_c}}}$

So the displacement current decreases and frequency decreases when the conduction current is  equal to displacement current.

18. The magnetic field of a beam emerging from a filter facing a floodlight is given by $B = {\text{ }}12{\text{ }} \times {\text{ }}{10^{ - 8}}{\text{ }}sin{\text{ }}(1.20{\text{ }} \times {\text{ }}{10^7}z-{\text{ }}3.6{\text{ }} \times {\text{ }}{10^{15}}t){\text{ }}T.$

What is the average intensity of the beam?

Ans: Let the first equation be $B = {\text{ }}12{\text{ }} \times {\text{ }}{10^{ - 8}}{\text{ }}sin{\text{ }}(1.20{\text{ }} \times {\text{ }}{10^7}z-{\text{ }}3.6{\text{ }} \times {\text{ }}{10^{15}}t){\text{ }}T.$

Standard equation $B = {B_0}(kz - \omega t)$

Comparing the different terms in above two (I, II) equations

${B_0} = 12 \times {10^{ - 8}}Tesla$

${I_{av}} = \dfrac{{B_0^2}}{{2{\mu _0}}} = \dfrac{{12 \times {{10}^{ - 8}} \times 12 \times {{10}^{ - 8}} \times 3 \times {{10}^8}}}{{2 \times 4\pi  \times {{10}^{ - 7}}}}$

It gives = $\dfrac{{54}}{{3.14 \times 10}} = 1.72\,W/{m^2}$

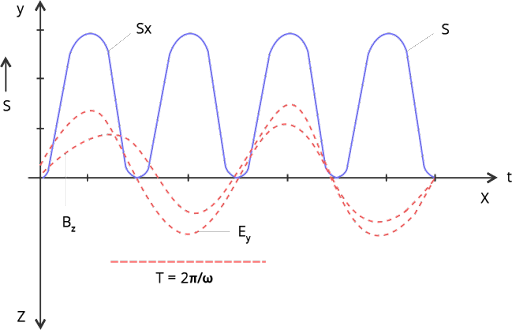
19. Pointing vectors S is defined as a vector whose magnitude is equal to the wave
intensity and whose direction is along the direction of wave propagation.
Mathematically, it is given by $S = \dfrac{1}{{{\mu _0}}}(\overline E  \times \overline B )$ Show the nature of S versus t graph.

Ans: Consider an electromagnetic wave. Let electric field (E) of EM wave varies along Y-axis  the propagation of wave is along X-axis, then $\overline E  \times \overline B $ will give the direction of flow of energy  in electromagnetic wave along X= axis

$\overline E  = {E_0}sin(\omega t - {\text{ }}kx)\hat j$

$\overline B  = {B_0}sin(\omega t - \hat k$

$S = \dfrac{1}{\mu }(\overline E  \times \overline B )$

$S = \dfrac{1}{{{\mu _0}}}{\sin ^2}(wt - kx)\hat i$

Variation of |S| with time will be as given in figure.

20. Professor C.V Raman surprised his students by suspending a tiny light ball in a transparent vacuum chamber by shining a laser beam on it. Which property of EM waves was he exhibiting? Give one more example of this property.

Ans: In this question it is given that Professor C.V Raman once  surprised his students by suspending a tiny light ball freely in a transparent vacuum chamber by shining a laser beam on it. We know that radiation and matter possess dual nature. Also we know the property which states that an EM wave carries energy and  momentum. Due to this change in momentum (by direction or velocity of wave), EM wave exerts pressure on the surface, by reflection and refraction. There this was the property of EM waves that helped  professor CV Raman to surprise his students by suspending a tiny light ball freely in a transparent vacuum chamber by shining a laser beam on it. We should note that the tails of the comets are also  due to radiation pressure. 

Electromagnetic radiation can pass even through vacuum and has particle nature. 

Therefore mobile phones placed in an evacuated transparent chamber can ring up which can be seen  through the transparent chamber, but sound of ring tone cannot be heard, hence it proves the  propagation of electromagnetic waves in vacuum.

21. Show that the magnetic field B at a point in between the plates of a parallel-plate  capacitor during charging is $\dfrac{{{\mu _0}{\varepsilon _0}r}}{2}\dfrac{{dE}}{d}$ (symbols having usual meaning).

Ans: Let Id be the displacement current in the region of magnetic field between two plates of  parallel plate capacitor. The magnetic field induction at a point in a region between two plates of a capacitor at a  perpendicular distance from the axis of plate is

$B = \dfrac{{{\mu _0}I}}{{2\pi r}} = \dfrac{{{\mu _0}}}{{2\pi r}}{I_d}$

$B = \dfrac{{{\mu _0}{\varepsilon _0}}}{{2\pi r}} = \dfrac{d}{{dt}}(E\pi {r^2})$

Therefore it gives the value:

$B = \;$$\dfrac{{{\mu _0}{\varepsilon _0}r}}{2}\dfrac{{dE}}{dt}$

22. Electromagnetic waves with wavelength
(i) ${\lambda _1}$ is used in satellite communication.
(ii) ${\lambda _2}$  is used to kill germs in water purifiers.
(iii) ${\lambda _3}$  is used to detect leakage of oil in underground pipelines.
(iv) ${\lambda _4}$  is used to improve visibility in runways during fog and mist conditions. 

(a) Identify and name the part of the electromagnetic spectrum to which these radiations belong. 

Ans: (i) Microwave is used in satellite communications so , ${\lambda _1}$  is the wavelength of the microwave. It is used in a microwave oven. 

(ii) Ultraviolet rays are used to kill germs in water purifiers so,  ${\lambda _2}$ is the wavelength of  ultraviolet rays.

(iii) X-rays are used to detect leakage of oil in underground pipelines so ${\lambda _3}$ is in the X-ray  region. It is also used to detect cracks in machinery and to detect fractures in bones of the body.

(iv) Infrared rays   ${\lambda _4}$ are used to improve visibility due to larger wavelengths of low  scattering.
Infrared rays are used in optical communication.

(b) Arrange these wavelengths in ascending order of their magnitude. 

Ans: The arrangement of the wavelengths in ascending order are ${\lambda _3},{\lambda _4},{\lambda _2},{\lambda _1}$

(c) Write one more application for each.

Ans: Uses are along with part (a).

23. Show that the average value of radiant flux density ‘S’ over a single period ‘T’ is given by $S = \dfrac{1}{{2c{\mu _0}}}E_0^2$  .

Ans: Radiant flux density $S = \dfrac{1}{{{\mu _0}}}(\overline E  \times \overline B )$

$c = \dfrac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}$

Or, ${c^2} = \dfrac{1}{{{\mu _0}{\varepsilon _0}}}$

$ \Rightarrow \dfrac{1}{{{\mu _0}}} = {\varepsilon _0}{c^2}$

So, the above expression can be written as $S = {\varepsilon _0}{c^2}(\overline E  \times \overline B )$….(i) 

Let electromagnetic waves be propagated along the X-axis so its electric and magnetic field  vectors are along the Y and Z axis.

$\overline E  = {E_0}\cos (kx - \omega t)\hat j$

$ \Rightarrow \overline B  = {B_0}\cos (kx - \omega t)\hat k$

Now by multiplying both the equation: 

$(\overline E  \times \overline B ) = ({E_0}{B_0}){\cos ^2}(kx - \omega t)(\hat j \times \hat k)$

Put E×B in (i)

$ \Rightarrow {S_{av}} = {c^2}{\varepsilon _0}{E_0}{B_0}\left[ {\dfrac{1}{T}} \right]\int\limits_0^T {{{\cos }^2}(kx - \omega t)dt\hat i} $

$ \Rightarrow \dfrac{{{c^2}{\varepsilon _0}{E_0}{B_0}}}{T}\left[ {\dfrac{T}{2}} \right] = \dfrac{{{c^2}}}{2}{\varepsilon _0}{E_0}\left( {\dfrac{{{E_0}}}{c}} \right)$

$ \Rightarrow \dfrac{{c{\varepsilon _0}{E_0}}}{2}$

$ \Rightarrow \dfrac{c}{2} \times \dfrac{1}{{{\mu _0}{c^2}}}E_0^2$

Hence it is proved that ${S_{av}} = \dfrac{{E_0^2}}{{2{\mu _0}c}}$

24. You are given a $2\mu F$ parallel plate capacitor. How would you establish an
instantaneous displacement current of 1mA in the space between its plates?

Ans: $C = 2F = 2 \times {10^{ - 6}}F,{\text{ }}{I_d} = 1{\text{ }}mA = {10^{ - 3}}A$

Therefore $q = CV$

${I_d}dt{\text{ }} = {\text{ }}C.dV$

$ \Rightarrow {I_d} = C\dfrac{{dV}}{{dt}}$

$ \Rightarrow \dfrac{{dV}}{{dt}} = \dfrac{{{I_d}}}{C} = \dfrac{{{{10}^{ - 3}}A}}{{2 \times {{10}^{ - 6}}}}$

$ = \dfrac{{1000}}{2}Volts$

$\therefore \dfrac{{dV}}{{dt}} = 500V/s$

25. Show that the radiation pressure exerted by an EM wave of intensity I on a surface  kept in vacuum is $\dfrac{1}{C}$ .

Ans: Pressure on surface due to particle nature of wave $P = \dfrac{F}{A}$

Force= Rate of change of momentum
If mass (m) of radiant particle for wave of velocity c then

$ \Rightarrow E = m{c^2}$

E= U (let)
$ \Rightarrow U = {\text{ }}mc.c$
$U = {\text{ }}p.c$
Where, momentum $p = mc$

Now differentiating w.r.t. time (t) we get

$ \Rightarrow \dfrac{{dU}}{{dt}} = c \times \dfrac{{d\overline p }}{{dt}}$

By Newton’s second law, 

$\dfrac{1}{c}\dfrac{{dU}}{{dt}} = \dfrac{{dp}}{{dt}}$

Therefore, $F = \dfrac{1}{c}\dfrac{{dU}}{{dt}}$ or, $\dfrac{F}{A} = \dfrac{1}{A} \times \dfrac{1}{c}\dfrac{{dU}}{{dt}}$

Pressure (P) on the surface due to e.m. wave radiation and $P = \dfrac{F}{A}$

$p = \dfrac{1}{c}\left[ {\dfrac{{dU}}{{Adt}}} \right]$

We know that intensity of radiation is equal to the radiant energy (U) falling on the unit surface per second.

$I = \dfrac{1}{A}\dfrac{{dU}}{{dt}}$ or, $P = \dfrac{1}{c}$

Hence it is proved. 

26. What happens to the intensity of light from a bulb if the distance from the bulb is  doubled? As a laser beam travels across the length of a room, its intensity essentially  remains constant. What geometrical characteristic of LASER beam is responsible for the constant intensity which is missing in the case of light from the bulb?

Ans: In this question we have to tell what will  happen to the intensity of light from a bulb if we double the distance from the bulb. We know that the bulb spreads its light in all ground spherically and symmetrically. So if the distance  from the bulb is doubled, then the surface area covered by radiations change from $4\pi {r^2}$ to  $4\pi {\left( {2r} \right)^2}$i.e., ${2^2}$ or four times decreased in straight laser.

But we know that  in a bulb it decreases by $4\left( {4\pi } \right)$ , i.e  $16\pi $  decreases. So the intensity becomes one fourth the initial value in a straight line. Since $I \propto \dfrac{1}{{{r^2}}}$ and for spherical value  $I \propto \dfrac{1}{{4\pi {r^2}}}$ . 

In the case of a laser, it does not spread in all directions. It passes only along a straight line. So its intensity remains almost the same. Also we know that geometrical characteristics of LASER beam which is responsible for the constant intensity
are: 

(i) Monochromatic, (ii) Coherent, (iii) Highly collimated from all around source, (iv)  Unidirectional. 

Therefore these characteristics are missing in the case of light from the bulb.

27.  Even though an electric field E exerts a force $qE$ on a charged particle yet the electric field of an EM wave does not contribute to the radiation pressure (but transfer energy). Explain.

Ans: In electromagnetic waves, the electric field is oscillating, so the resultant electric force on  the particle will be zero, as the direction of electric force changes every half of the time period.  As the electric field vibrates, the radiation of energy will take place only due to vibrating  electric and magnetic fields.

28. An infinitely long thin wire carrying a uniform linear static charge density $\lambda $ is placed along the z-axis . The wire is set into motion along its length with a  uniform velocity $\overline V  = V{K_z}$ . Calculate the poynting vector $S = \dfrac{1}{{{\mu _0}}}(\overline E  \times \overline B )$

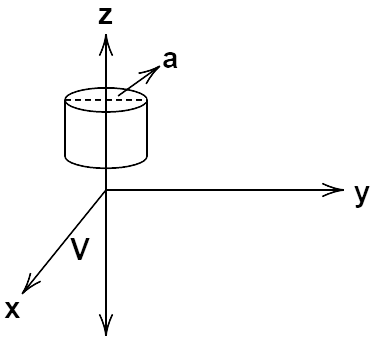
Ans: Consider a cylindrical Gaussian surface in such a way that the axis of the cylinder lies on wire. Electric field intensity due to long straight wire at a distance a and charge density  $\lambda c/m$ .

$\overline E  = \dfrac{\lambda }{{2\pi {\varepsilon _0}a}} = \dfrac{\lambda }{{2\pi {\varepsilon _0}a}}\hat j$

$\overline B  = \dfrac{{{\mu _0}I}}{{2\pi a}}\hat i$

$ \Rightarrow I = \dfrac{q}{t} = \dfrac{{\lambda l}}{t} = \lambda v$

Therefore $\overline B  = \dfrac{{{\mu _0}\lambda v}}{{2\pi a}}\hat i$

$S = \dfrac{1}{{{\mu _0}}}(\overline E  \times \overline B ) = \dfrac{1}{{{\mu _0}}}\left[ {\dfrac{1}{{2\pi {\varepsilon _0}a}}\hat j \times \dfrac{{{\mu _0}\lambda v}}{{2\pi a}}\hat i} \right]$

$S = \dfrac{{ - {\lambda ^2}v}}{{4{\pi ^2}{a^2}{\varepsilon _0}}}\hat k$

29. Sea water at frequency $\nu  = {\text{ }}4{\text{ }} \times {\text{ }}{10^8}{\text{ }}Hz$has permittivity $\varepsilon  = {\text{ }}80{\varepsilon _0}$ , permeability $\mu {\text{ }} \approx {\text{ }}\mu o$and resistivity $\rho {\text{ }} = {\text{ }}0.25{\text{ }}\Omega -m.$Imagine a parallel plate capacitor  immersed in sea water and driven by an alternating voltage source $V(t){\text{ }} = {V_0}sin(2\pi \nu t).$What dfraction of the conduction current density is the displacement current density?

Ans: Suppose distance between the parallel plates of capacitor is ‘d’ and the applied voltage $V(t){\text{ }} = {V_0}sin(2\pi \nu t).$

$E = \dfrac{{V(t)}}{d} = \dfrac{{{V_0}\sin (2\pi vt)}}{d}$

By Ohm’s conduction current density

$\overline {{J_c}}  = \dfrac{1}{\rho }\overline E  = \dfrac{1}{\rho }\dfrac{{{V_0}\sin (2\pi vt)}}{d}$

Let us assume that $J_0^c = \dfrac{{{V_0}}}{{\rho d}}$

The current displacement is given as: 

${J_d} = \varepsilon \dfrac{{dE}}{{dt}} = \varepsilon \dfrac{d}{{dt}}\dfrac{{{V_0}}}{d}\sin (2\pi vt)$

$ \Rightarrow {J_d} = \dfrac{{2\pi v\varepsilon {V_0}}}{d}\cos (2\pi vt)$

Again assume that $J_0^d = \dfrac{{2\pi v\varepsilon {V_0}}}{d}$

Then we have: ${J_d} = J_0^d\cos (2\pi vt)$

$ \Rightarrow \dfrac{{J_0^d}}{{J_0^c}} = 2\pi v{\varepsilon _0}\upsilon $

$ \Rightarrow \dfrac{{J_0^d}}{{J_0^c}} = 2\pi ve\rho  = 2\pi  \times 4 \times {10^9} \times 80{\varepsilon _0} \times 0.25$

$ = 4\pi {\varepsilon _0} \times 2 \times 80 \times 0.25 \times {10^8}$

$ = \dfrac{{160 \times 25}}{{9 \times 10 \times 100}}$

Therefore it gives the answer $\Rightarrow \dfrac{{J_0^d}}{{J_0^c}} = \dfrac{4}{9}$

30. A long straight cable of length l is placed symmetrically along z-axis and has
radius a(<<<l). The cable consists of a thin wire and a coaxial conducting tube. An alternating current $I(t){\text{ }} = {I_0}sin{\text{ }}(2\pi \nu t)$flows down the central thin wire and returns  along the coaxial conducting tube. The induced electric field at a distance s from the wire inside the cable is $\overline E (s,t) = {\mu _0}{I_0}v\cos (2\pi vt){\log _e}\left( {\dfrac{s}{a}} \right)\hat k$

(i) Calculate the displacement current density inside the cable.
Ans: Induced electric field E(s, t) at distance s(s< radius of co- axial cable) is given as $E\left( {s,{\text{ }}t} \right) = {\text{ }}{\varepsilon _0}{I_0}v{\text{ }}cos2vt{\log _e}\left( {\dfrac{s}{a}} \right)k$ ,.

Displacement current density ${J_d}$ is given by

${J_d} = {\varepsilon _0}\dfrac{{dE}}{{dt}} = {\varepsilon _0}{\mu _0}{I_0}v\dfrac{d}{{dt}}\;\left[ {\cos 2\pi vt{{\log }_e}\dfrac{s}{a}} \right]k$

$ \Rightarrow {J_d} =  - {\varepsilon _0}{\mu _0}{I_0}v\cos 2\pi {v^2}\left( {{{\log }_e}\dfrac{s}{a}} \right)\sin (2\pi vt)\hat k$

$ =  - \dfrac{1}{{{c^2}}}{I_0}2\pi {v^2}\left[ { - {{\log }_e}\left( {\dfrac{a}{s}} \right)} \right]\sin (2\pi vt)k$

$ = \dfrac{{2\pi {v^2}}}{{{v^2}{\lambda ^2}}}{I_0}{\log _e}\left( {\dfrac{a}{s}} \right)\sin 2\pi vt\hat k$

Therefore this is the required answer. 

(ii) Integrate the displacement current density across the cross-section of the cable to find the  total displacement current ${I_d}$

Ans: ${I_d} = \int {{J_d}sdsd\theta  = \int\limits_{s = 0}^0 {{J_d}sds\int\limits_0^{2\pi } {d\theta } } }  = \int\limits_{s = 0}^a {{J_d}sds(2\pi )} $

${I_d} = {\left( {\dfrac{{2\pi }}{\lambda }} \right)^2}{I_0}\sin (2\pi vt)\hat k\int\limits_{s = 0}^a {\log \left( {\dfrac{a}{s}} \right)sds} $

Now, we will calculate the integration of $\int\limits_{s = 0}^a {\left( {\log \dfrac{a}{s}} \right)sds} $

$ = \left[ {\log \left( {\dfrac{a}{s}} \right)\int\limits_s^a {ds} } \right]_0^a - \int\limits_{s = 0}^a {\dfrac{d}{{ds}}\left[ {\log \left( {\dfrac{s}{s}} \right)} \right]} \int {sds]ds} $

$ = \left[ {\log \left( {\dfrac{a}{a}} \right)\dfrac{{{a^2}}}{2} - 0} \right] - \dfrac{1}{{2a}}\int\limits_{s = 0}^a {{s^3}ds} $

$ = 0 - \dfrac{1}{{2a}}\left[ {\dfrac{{{s^4}}}{4}} \right]_0^a = \dfrac{{ - {a^3}}}{8}$

Therefore, ${I_d} =  - \dfrac{{{a^3}}}{8}\left( {\dfrac{{2\pi }}{\lambda }} \right)\sin 2\pi vt\hat k$

$ =  - \dfrac{a}{2} \times \dfrac{{{a^4}}}{4}{\left( {\dfrac{{2\pi }}{\lambda }} \right)^2}{I_0}\sin (2\pi vt)\hat k$

The negative sign shows that the displacement current ${I_d}$ is opposite to the conduction current ${I_c}$

${I_d} = \dfrac{a}{2}{\left( {\dfrac{{\pi a}}{\lambda }} \right)^2}{I_0}\sin (2\pi vt)( - k)$

${I_d}$ is in –Z direction as the IC is in +Z direction.

(iii) Compare the conduction current $I_0$ with the displacement current $I_0^d$ .

Ans: ${I_d} = \dfrac{a}{2}{\left( {\dfrac{{\pi a}}{\lambda }} \right)^2}{I_0}\sin (2\pi vt)( - k)$

${I_d} = I_0^d\sin (2\pi vt)$

Where it is given that $I_0^d = \dfrac{a}{2}{\left( {\dfrac{{\pi a}}{\lambda }} \right)^2}{I_0}$

Therefore, the required ratio is $\dfrac{{I_0^d}}{{{I_0}}} = \dfrac{{{\pi ^2}{a^3}}}{{2{\lambda ^2}}}$ .

31. A plane EM wave travelling in vacuum along z-direction is given by $\overline E  = {E_0}sin(kz-\omega t)\,\,and\,\overline B  = {B_0}{\text{ }}sinkz\hat j$

(i) Evaluate $\int {\overline {E.dl} } $ over the rectangular loop 1234 shown 

Ans: As the electromagnetic wave is propagating along the Z-axis then its electric and magnetic field vectors are along the X and Y axis.

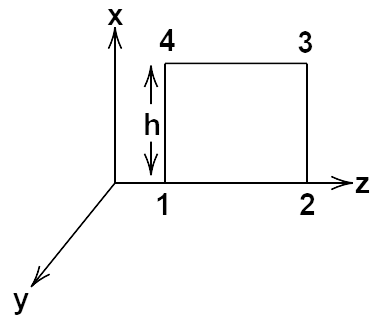
(ii) Evaluate $\int {\overline {B.ds} } $  over the surface bounded by loop 1234.

Ans: $\overline E  = {E_0}\hat i$ and $\overline B  = {B_0}\hat j$ in the figure given below:

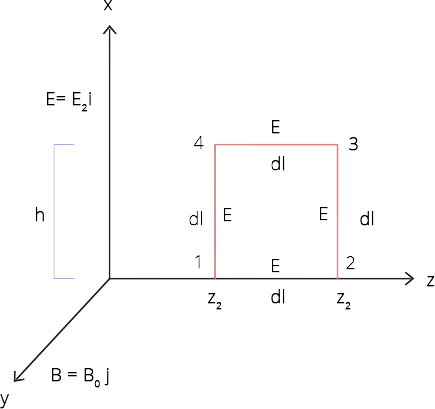
By using the line integral of E over loop 1234,

$\oint {\overline E \overline {dl}  = \int\limits_1^2 {\overline E \overline {dl} } }  + \int\limits_2^3 {\overline E \overline {dl} }  + \int\limits_3^4 {\overline E \overline {dl} }  + \int\limits_4^1 {\overline E \overline {dl} } $

$ = \int\limits_1^2 {E\,dl\cos 90^\circ }  + \int\limits_2^3 {E\,dl\cos 0^\circ }  + \int\limits_5^4 {E\,dl\cos 90^\circ }  + \int\limits_4^1 {E\,dl\cos 180^\circ } $

$ \Rightarrow 0 + {\left[ {Eh} \right]_{z2}} - {\left[ {Eh} \right]_{z1}} = {E_0}h\sin (k{z_2} - \omega t) - {E_0}h\sin (k{z_1} - \omega t)$

$ = h{E_0}\left[ {\sin (k{z_2} - \omega t)} \right] - \sin (k{z_1} - \omega t)$

(iii) Use equation $\;\int {Edl = \dfrac{{ - d{\phi _B}}}{{dt}}} $ to prove $\dfrac{{{E_0}}}{{{B_0}}} = C$

Ans: Consider a strip of area $ds = h.dz$ as in figure. Angle between $\overline {ds} $ and $\overline B $ is zero

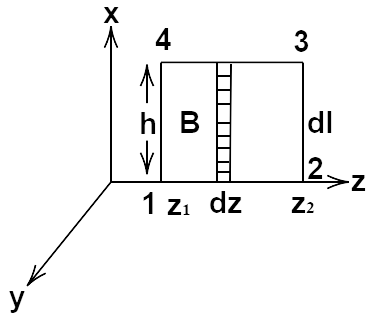
$\int {\overline B \overline {ds} }  = \int {\overline B \overline {ds} \cos 0\hat j} $

$ = \int\limits_{{z_1}}^{{z_2}} {B.ds\hat j} $

$ = \int\limits_{{z_1}}^{{z_2}} {{B_0}\sin (kz - \omega t)h.dz} $

$\int {\overline B \overline {ds}  = \dfrac{{{B_0}h}}{k}(\cos (k{z_1} - \omega t) - \cos (k{z_2} - \omega t)} $

Given $\oint {E\overline {dl}  = \dfrac{{ - d{\phi _B}}}{{dt}} =  - \dfrac{d}{{dt}}\mathop{\int\mkern-20.8mu \circlearrowleft}  {Bds} } $

$ = \dfrac{d}{{dt}}\left[ {\dfrac{{{B_0}h}}{k}\cos (kz - \omega t) - \cos (kz - \omega t)} \right]\hat j$

$ = \dfrac{{{B_0}h}}{k}[ - sin(k{z_1} - \omega t)( - \omega ) + sin(k{z_2} - \omega t)( - \omega )]$

$E = \dfrac{{{B_0}h\omega }}{k}[ - sin(k{z_1} - \omega t) - sin(k{z_2} - \omega t)]$

$E = {E_0}[sin{\text{ }}(k{z_1} - \omega t) - sin(k{z_2} - \omega t)]$

$ \Rightarrow {E_0} = {B_Y}C$

$ \Rightarrow \dfrac{{{E_0}}}{{{B_0}}} = \dfrac{{{E_0}}}{{BY}} = \dfrac{{{B_Y}C}}{{{B_Y}}}$

Therefore it gives the required answer: $\dfrac{{{E_0}}}{{{B_0}}} = C$

(iv) By using similar process and the equation $\oint {B.dl = {\mu _0}I + {\varepsilon _0}\dfrac{{d{\phi _E}}}{{dt}}} $ , prove that $c = \dfrac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}$

Ans: Consider a loop 1.2,3,4 in Y-Z plane as in figure

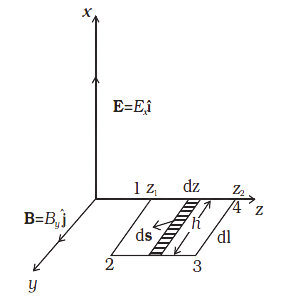
$\oint {B.dl = \int\limits_1^2 {B.dl}  + } \int\limits_2^3 {B.dl}  + \int\limits_3^4 {B.dl}  + \int\limits_4^1 {B.dl} $$ = \int\limits_1^2 {B.dl\cos 0}  + \int\limits_2^3 {B.dl\cos {{90}^ \circ }}  + \int\limits_3^4 {B.dl\cos {{180}^ \circ }}  + \int\limits_4^1 {B.dl\cos {{90}^ \circ }} $${B_0}h[sin{\text{ }}(k{z_1} - \omega t) - sin(k{z_2} - \omega t)]$

Now to evaluate, we will consider the rectangle 1234 to be made of strips of area of hdz each. Therefore we have: 

$ \Rightarrow \int {E.ds = \int {Eds\cos 0 = \int {Eds = \int\limits_z^{{Z_2}} {{E_0}\sin (kz - wt)hdz} } } } $

$ =  - {E_0}h[\cos (k{z_2} - wt) - \cos (k{z_1} - wt)]$

Now we will use the relations that we have obtained in the above equation and it gives us 

$ \Rightarrow {B_0} = {E_0}\dfrac{\omega }{k}\mu {\varepsilon _0}$

$\dfrac{{{E_0}\omega }}{{{B_0}k}} = \dfrac{1}{{{\mu _0}{\varepsilon _0}}}$

But we have $\omega  = c\kappa $

Therefore it gives us the answer $c = \dfrac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}$

32. A plane EM wave travelling along z direction is described by $\overline E  = Esin(kz-\omega t)\hat i$ and $\overline B  = {B_0}sin(kz-\omega t)\hat j$ . Show that
(i) The average energy density of the wave is given by ${U_{av}} = \dfrac{1}{4}{\varepsilon _0}E_0^2 + \dfrac{1}{{4{\mu _0}}}B_0^2$

Ans: The electromagnetic wave carries energy which is due to the electric field vector and  magnetic field vector. In electromagnetic waves, E and B vary with time.  E and B varies with time. The energy density due to electric field $\overline E $ is ${U_E} = \dfrac{1}{2}{\varepsilon _0}{E^2}$

The energy density due to magnetic field B is  ${U_B} = \dfrac{1}{{2{\mu _0}}}{B^2}$

Total average energy density of electromagnetic wave 

${U_E} + {U_B} = \dfrac{1}{{2{\mu _0}}}{B^2} + \dfrac{1}{2}{\varepsilon _0}{E^2}$

$ \Rightarrow E = {E_0}{\text{ }}sin{\text{ }}(kz - \omega t)\hat i$

$ \Rightarrow B = {B_0}{\text{ }}sin{\text{ }}(kz - \omega t)\hat j$

Average value of ${E^2}$  over a cycle $\dfrac{{E_0^2}}{2}$

Therefore it gives the Ans:wer ${U_{av}} = \dfrac{1}{4}\left[ {{\varepsilon _0}E_0^2 + \dfrac{{B_0^2}}{{{\mu _0}}}} \right]$

(ii) The time averaged intensity of the wave is given by ${I_{av}} = \dfrac{1}{2}C{\varepsilon _0}E_0^2$

Ans: We know that ${\text{ }}{E_0} = {\text{ }}C{B_0}$ and $C = \dfrac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}$

$\dfrac{1}{4}\dfrac{{B_0^2}}{{{\mu _0}}} = \dfrac{1}{4}\dfrac{{E_0^2/{C^2}}}{{{\mu _0}}} = \dfrac{{E_0^2}}{{4{\mu _0}}}{\mu _0}{\varepsilon _0} = \dfrac{1}{4}{\varepsilon _0}E_0^2$

${U_B} = {U_E}$

${U_{av}} = \dfrac{1}{4}{\varepsilon _0}E_0^2 + \dfrac{1}{4}\dfrac{{B_0^2}}{{{\mu _0}}}$

Therefore it gives $\dfrac{{{E_0}}}{{{B_0}}} = C$

$ \Rightarrow \dfrac{{E_0^2}}{{B_0^2}} = \dfrac{1}{{{\mu _0}{\varepsilon _0}}} \Rightarrow B_0^2 = {\mu _0}{\varepsilon _0}E_0^2$

$ \Rightarrow {U_{av}} = \dfrac{1}{4}{\varepsilon _0}E_0^2 + \dfrac{1}{4}{\varepsilon _0}E_0^2$

$ \Rightarrow {U_{av}} = \dfrac{1}{4}{\varepsilon _0}E_0^2$

$ \Rightarrow {U_{av}} = \dfrac{1}{4}{\varepsilon _0}\dfrac{{B_0^2}}{{{\varepsilon _0}{\mu _0}}} + \dfrac{1}{4}\dfrac{{B_0^2}}{{{\mu _0}}}$

$ = \dfrac{{B_0^2}}{{4{\mu _0}}} + \dfrac{{B_0^2}}{{4{\mu _0}}}$

Therefore ${U_E} = {U_B}$

Time average intensity of wave 

${I_{av}} = {U_{av}}.C = \dfrac{1}{2}\dfrac{{B_0^2C}}{{{\mu _0}}} = \dfrac{1}{2}{\varepsilon _0}E_0^2C$

NCERT Exemplar for Class 12 Physics - Electromagnetic Waves

Chapter 8 (Electromagnetic Waves) of Class 12 CBSE consists of some important topics that students are expected to learn and get a deeper understanding of. 

This chapter provides information on the origin and application of electromagnetic waves which are used to transfer radio waves of different wavelengths. The application of electromagnetic waves is also present in the regular things in our everyday lives like TV, wireless devices, telephones etc. The transformation of signals and energies is possible with this technology. 

The electromagnetic waves can take the form of microwaves, Ultraviolet rays (UV), Infrared Radiation (IR), X-rays, and Visible light . Considering the all-around usage of this technology in our everyday lives, the CBSE board has given great importance to this chapter from the examination point of view. 

Here are the topics covered in Chapter 8 (Electromagnetic Waves) of Class 12 CBSE

• Displacement Current

• Maxwell’s Equations

• Electromagnetic Waves

• Sources of electromagnetic waves

• Nature of Electromagnetic Waves

• Speed of Electromagnetic Waves

• Electromagnetic Spectrum

Different Types of Electromagnetic Waves

• Radio waves

• Microwaves

• Infrared waves

• Visible rays

• Ultraviolet rays

• X-rays

• Gamma rays

• Microwave Oven

All of these topics hold an important place in the Class 12 Physics examination.

In order to achieve better grades and a high rank in the Class 12 second term board examination, the chapters given in the NCERT Class 12 Physics textbook are extremely Important. And students from Class 12 are advised to learn these chapters using the NCERT exemplar for Class 12 Physics.