Moving Charges And Magnetism Class 12 Questions And Answers - FREE PDF



FAQs on NCERT Solutions For Class 12 Physics Chapter 4 Moving Charges and Magnetism (2025-26)
1. What is the correct stepwise approach to solving exercise questions in NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism?
The stepwise approach includes:
- Carefully reading the question and extracting given data.
- Identifying the relevant physics law or formula, such as the Biot-Savart law or Ampere’s circuital law.
- Substituting known values and performing step-by-step calculations.
- Writing each logical step clearly according to CBSE norms.
- Highlighting the final answer, as practiced in NCERT Solutions for Class 12 Physics Chapter 4.
2. How do NCERT Solutions for Class 12 Physics Chapter 4 help students in understanding concepts like the Lorentz force and its applications?
NCERT Solutions provide stepwise explanations with derivations and examples, making it easier to grasp how the Lorentz force affects the motion of charged particles. They explain the direction and magnitude of the force using right-hand rule applications, and apply the concept in both theoretical and numerical questions, matching the syllabus depth required for CBSE board exams.
3. Are solutions for both intext and end-of-chapter exercises included in the NCERT Solutions for Class 12 Physics Chapter 4?
Yes, the NCERT Solutions for Class 12 Physics Chapter 4 include comprehensive, step-by-step solved answers for all intext and end-of-chapter exercises as per the official NCERT textbook sequence, aligning fully with the CBSE 2025–26 syllabus.
4. Why is using the NCERT stepwise method important for solving derivation and numerical questions in Physics Chapter 4?
The stepwise method ensures clarity in logic, accuracy of calculation, and complete credit in board marking. It breaks down complex derivations and numericals into manageable steps, helps avoid skipping essential reasoning, and matches the CBSE marking scheme for better scores. This method also aids in understanding the physics concepts deeply.
5. What features of the Class 12 Physics Chapter 4 NCERT Solutions support students preparing for both conceptual and application-based questions?
Features include:
- Well-explained stepwise answers for both direct and application-based problems.
- Covers fundamental laws (e.g., Biot-Savart, Ampere’s law), their derivations, and practical applications.
- Answers to conceptual HOTS (Higher Order Thinking Skills) questions as required by CBSE.
6. What should be kept in mind while answering long answer questions from Moving Charges and Magnetism using NCERT Solutions?
For long answer questions, always present a structured, stepwise explanation, include all relevant derivations and labeled diagrams, cover physical principles, and organize the response as shown in the official NCERT pattern to ensure full marks and conceptual clarity.
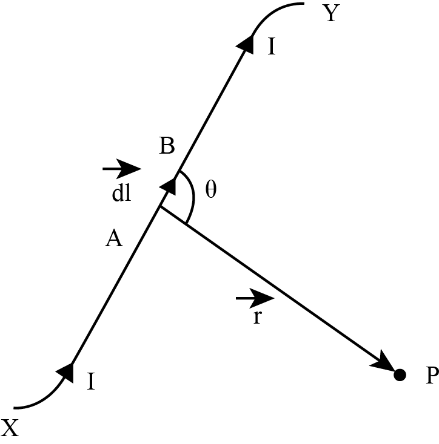
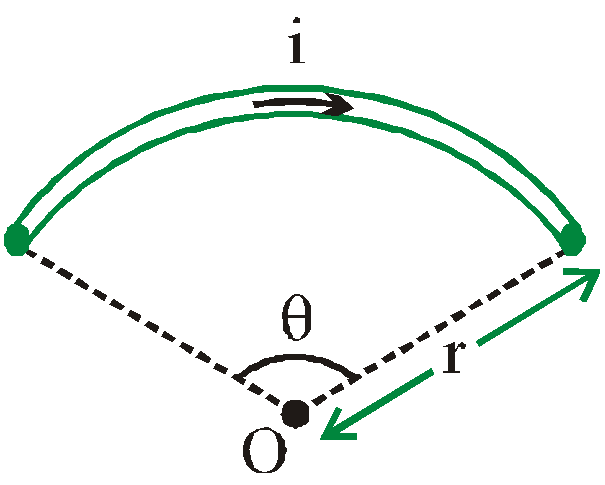
7. How do the NCERT Solutions for Moving Charges and Magnetism handle numericals that use the Biot–Savart law or Ampere’s circuital law?
Such numericals are solved logically:
- Stating the applicable law accurately (e.g., Biot–Savart law or Ampere’s law).
- Substituting all given and standard values with correct units.
- Performing algebraic/vectored steps as needed and showing each intermediate result.
- Presenting the boxed final answer, mirroring CBSE guidelines.
8. In what way do the NCERT Solutions address common misconceptions related to parallel currents and magnetic field direction?
NCERT Solutions clarify that parallel currents attract and anti-parallel currents repel, which is counterintuitive for many students. Stepwise explanations with right-hand rule illustrations are provided, and typical pitfalls, like confusing the direction of magnetic field around wires, are directly resolved through examples and reasoning.
9. Can students use NCERT Solutions for Class 12 Physics Chapter 4 to verify their own methods if their working steps differ slightly from the provided answers?
Minor differences in intermediate steps are acceptable as long as the method follows CBSE guidelines and each logical step is justified. The final result should match the NCERT Solutions, and steps should not be skipped to ensure marks are not lost due to incomplete explanations.
10. How does the stepwise format in NCERT Solutions for this chapter improve a student’s answer-writing skills for board exams?
The stepwise format helps students structure their answers according to CBSE requirements, making the logic and flow clear for examiners. This not only improves presentation but also ensures that students don't miss essential reasoning, leading to maximized marks in the board examination.
11. What is the recommended pattern for writing derivation and formula-based answers as seen in the NCERT Solutions for Moving Charges and Magnetism?
The recommended pattern is to:
- State the principle or law with all initial assumptions.
- Write each derivation step logically and explicitly.
- Define physical quantities used at each stage.
- Clearly highlight the boxed final formula or result, reflecting CBSE answer sheets.
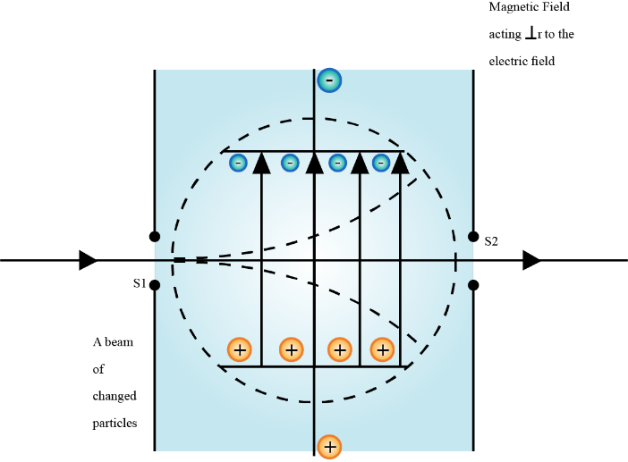
12. How do the NCERT Solutions address practical applications of concepts like solenoids, toroids, and cyclotrons in Chapter 4?
NCERT Solutions include solved numericals and conceptual explanations on how solenoids produce uniform magnetic fields, toroids confine magnetic fields, and cyclotrons accelerate charged particles, along with their limitations and uses in practical devices, meeting the CBSE’s real-life application focus.
13. What strategies can be learned from NCERT Solutions to tackle conceptual HOTS problems from Moving Charges and Magnetism in exams?
Students learn to build clear conceptual frameworks by linking principles (e.g., motion of charges in magnetism, right-hand/left-hand rules), drawing supporting diagrams, applying physical laws methodically, and verifying answers against typical CBSE patterns as illustrated in the NCERT Solutions.