Class 11 Maths Linear Inequalities Solutions with Step-by-Step Explanations
FAQs on NCERT Solutions For Class 11 Maths Chapter 5 Linear Inequalities - 2025-26
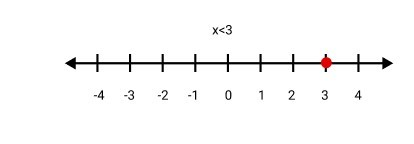
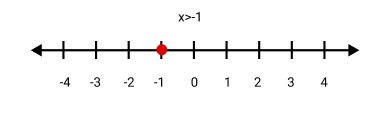
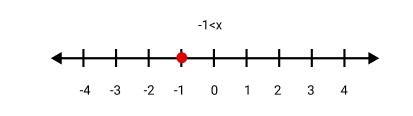
1. What is the step-by-step method to solve a linear inequality in one variable from NCERT Chapter 5?
To solve a linear inequality in one variable, follow these steps as per the NCERT methodology:
1. Collect all terms involving the variable on one side of the inequality and the constant terms on the other.
2. Simplify both sides to get an inequality of the form ax > b, ax < b, ax ≥ b, or ax ≤ b.
3. Divide or multiply both sides by the coefficient of the variable to isolate it. Remember to reverse the inequality sign if you multiply or divide by a negative number. The result is the solution set for the variable.
2. How do you graphically represent the solution of a linear inequality in two variables?
The graphical solution for a linear inequality in two variables involves these key steps:
1. Replace the inequality sign with an equals sign to get a linear equation.
2. Draw the graph of this equation. Use a dotted line for strict inequalities (< or >) and a solid line for slack inequalities (≤ or ≥).
3. This line divides the Cartesian plane into two half-planes.
4. Pick a test point (like (0,0)) not on the line and substitute it into the original inequality.
5. If the test point satisfies the inequality, shade the entire region containing that point. If not, shade the other region. The shaded area is the solution region.
3. What is the main difference between solving a linear equation and a linear inequality?
The primary difference lies in the solution set and one critical rule. A linear equation typically has a single, specific value as its solution. In contrast, a linear inequality's solution is a range of values or an interval. The most important rule unique to inequalities is that the inequality symbol must be reversed whenever you multiply or divide both sides of the inequality by a negative number. This rule does not apply to equations.
4. Why is the inequality sign flipped when multiplying or dividing by a negative number?
Flipping the inequality sign is essential to maintain the mathematical truth of the statement. For example, we know that 4 > 2. If we multiply both sides by -1 without flipping the sign, we would get -4 > -2, which is false. To keep the statement true, we must reverse the inequality sign to get -4 < -2. This rule ensures that the relationship between the two sides of the inequality remains correct after the operation.
5. How are the problems in the Miscellaneous Exercise of Chapter 5 different from those in Exercise 5.1?
The Miscellaneous Exercise in Chapter 5 typically includes more complex and application-based problems, often classified as Higher Order Thinking Skills (HOTS) questions. While Exercise 5.1 focuses on fundamental concepts like solving and graphing basic linear inequalities, the Miscellaneous Exercise combines multiple concepts. You may find problems involving IQ, word problems that require you to formulate the inequality first, and more complex systems of inequalities that test a deeper understanding of the chapter.
6. How do you solve a system of linear inequalities in two variables as per the NCERT curriculum?
To solve a system of linear inequalities, you need to find the common solution region that satisfies all the given inequalities simultaneously. The method is as follows:
- Graph each inequality on the same Cartesian plane.
- For each inequality, determine its solution region by shading the appropriate half-plane.
- The common shaded region, where the shading from all individual inequalities overlaps, represents the final solution set for the system.
7. What is the significance of using a solid line versus a dotted line when graphing an inequality?
The type of line indicates whether the points on the line itself are part of the solution.
- A solid line is used for slack inequalities (≤ or ≥). It signifies that the values on the line are included in the solution set.
- A dotted line is used for strict inequalities (< or >). It signifies that the values on the line are not included in the solution set; they only form the boundary.
8. Where can I find reliable, step-by-step NCERT Solutions for Class 11 Maths Chapter 5 for the 2025-26 session?
For the 2025-26 academic session, you can find detailed and accurate step-by-step NCERT Solutions for Class 11 Maths Chapter 5, Linear Inequalities, on Vedantu. These solutions are prepared by subject matter experts and follow the latest CBSE guidelines, covering all questions from the exercises and the miscellaneous section to help you understand the correct methodology for solving every problem.
9. Can a system of linear inequalities have no solution? How would this be represented graphically?
Yes, a system of linear inequalities can have no solution. This occurs when there is no common region that satisfies all the given inequalities. Graphically, this is represented by a situation where the shaded solution regions of the individual inequalities do not overlap at any point. For instance, the solution regions for the inequalities x > 2 and x < 1 would be two separate, non-intersecting areas on the graph, indicating no common solution.