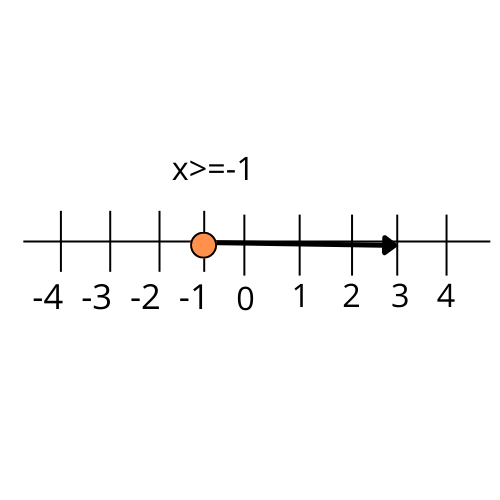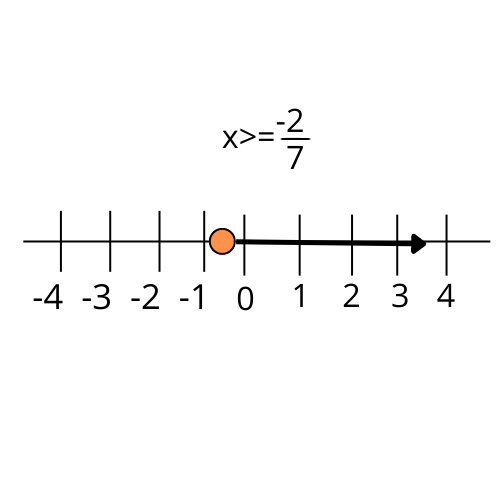Achieve Higher With Class 11 Linear Inequalities Exercise 5.1 Solutions
FAQs on NCERT Solutions for Class 11 Maths Chapter 5 Linear Inequalities
1. Where can I find reliable, step-by-step NCERT Solutions for Class 11 Maths Chapter 5, Linear Inequalities?
You can find detailed and accurate NCERT Solutions for Class 11 Maths Chapter 5 on Vedantu. These solutions are prepared by subject matter experts and provide a step-by-step methodology for solving all problems in the textbook exercises, strictly adhering to the CBSE 2025-26 syllabus and guidelines.
2. What is the correct method for solving a linear inequality in one variable as per the NCERT textbook?
The correct method involves isolating the variable on one side of the inequality. The key steps are:
- Use algebraic operations like addition or subtraction on both sides to group variable terms and constant terms separately.
- Simplify both sides of the inequality.
- If you multiply or divide both sides by a positive number, the inequality symbol remains the same.
- If you multiply or divide both sides by a negative number, the inequality symbol must be reversed (e.g., < becomes >).
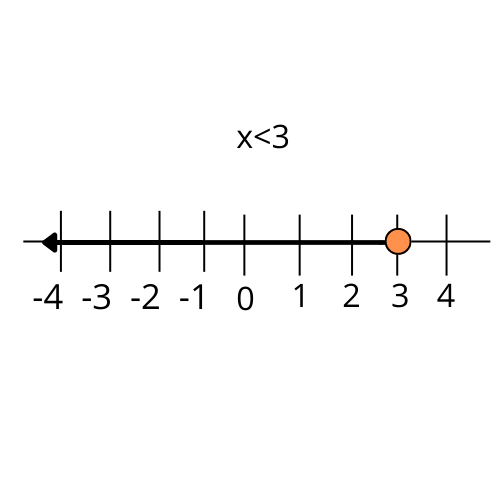
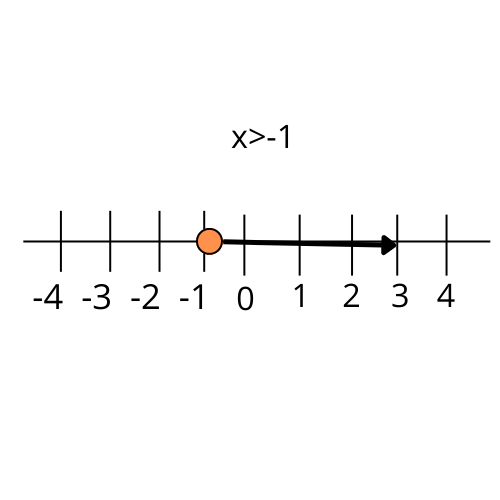
3. How do you represent the solution of a one-variable linear inequality on a number line?
To represent the solution on a number line, first, solve the inequality to find the range of values for the variable. Then, follow these steps:
- Draw a number line and mark the critical point from your solution.
- Use a closed circle (●) on the number if the inequality is strict (≤ or ≥), indicating the value is included in the solution.
- Use an open circle (○) if the inequality is not strict (< or >), indicating the value is not included.
- Shade the portion of the number line that represents all possible values in the solution set.
4. What is the key difference between solving a linear equation and a linear inequality?
The primary difference lies in the solution and the operations. A linear equation (like 2x = 6) typically yields a specific value as a solution (x=3). In contrast, a linear inequality (like 2x > 6) yields a range of values (x > 3). The most critical difference in method is that when multiplying or dividing an inequality by a negative number, you must reverse the inequality symbol, a rule that does not apply to equations.
5. How do you correctly graph the solution for a linear inequality in two variables?
The correct procedure for graphing a two-variable inequality involves these steps:
- First, treat the inequality as an equation to find the boundary line.
- Draw this line on the coordinate plane. Use a solid line for inequalities with ≤ or ≥ and a dashed line for inequalities with < or >.
- Choose a test point (like (0,0)) that is not on the line.
- Substitute this point into the original inequality. If it satisfies the inequality, shade the entire region containing the test point. If not, shade the opposite region.
6. What is the standard method for solving a system of linear inequalities graphically?
To solve a system of linear inequalities, you must find the region that satisfies all inequalities simultaneously. The method is as follows:
- Graph each linear inequality on the same coordinate plane, including its boundary line and shaded region.
- Identify the common region where all the shaded areas overlap.
- This overlapping area is known as the feasible region, which represents the solution set for the entire system.
7. Why is it essential to use a test point when shading the solution for a two-variable inequality?
Using a test point is essential because the boundary line divides the coordinate plane into two half-planes. Only one of these half-planes contains the set of points that satisfy the inequality. By substituting the coordinates of a test point (e.g., the origin (0,0) if it's not on the line) into the inequality, you can determine if that entire half-plane is part of the solution. This provides a definitive way to identify and shade the correct solution region.
8. What are the most common mistakes to avoid when solving problems from NCERT Chapter 5?
When solving linear inequalities, students should be careful to avoid these common errors:
- Forgetting to reverse the inequality sign when multiplying or dividing by a negative number.
- Using a solid line instead of a dashed line for strict inequalities (<, >) or vice versa.
- Choosing a test point that lies on the boundary line, which gives an inconclusive result.
- Incorrectly identifying the common feasible region when solving a system of inequalities.
9. Do Vedantu’s NCERT Solutions for Chapter 5 also provide solutions for the Miscellaneous Exercise?
Yes, Vedantu's NCERT Solutions for Class 11 Maths Chapter 5 are comprehensive and include detailed, step-by-step solutions for all questions from every exercise, including the Miscellaneous Exercise. This ensures students have a complete resource for practice and exam preparation.
10. How does understanding Chapter 5, Linear Inequalities, help in Class 12 Maths?
The concepts from Chapter 5 are foundational for the Linear Programming Problems (LPP) chapter in Class 12 Maths. In LPP, the constraints that define the problem are expressed as a system of linear inequalities. The ability to correctly graph these inequalities and identify the feasible region is a critical first step in finding the optimal solution in any linear programming problem.