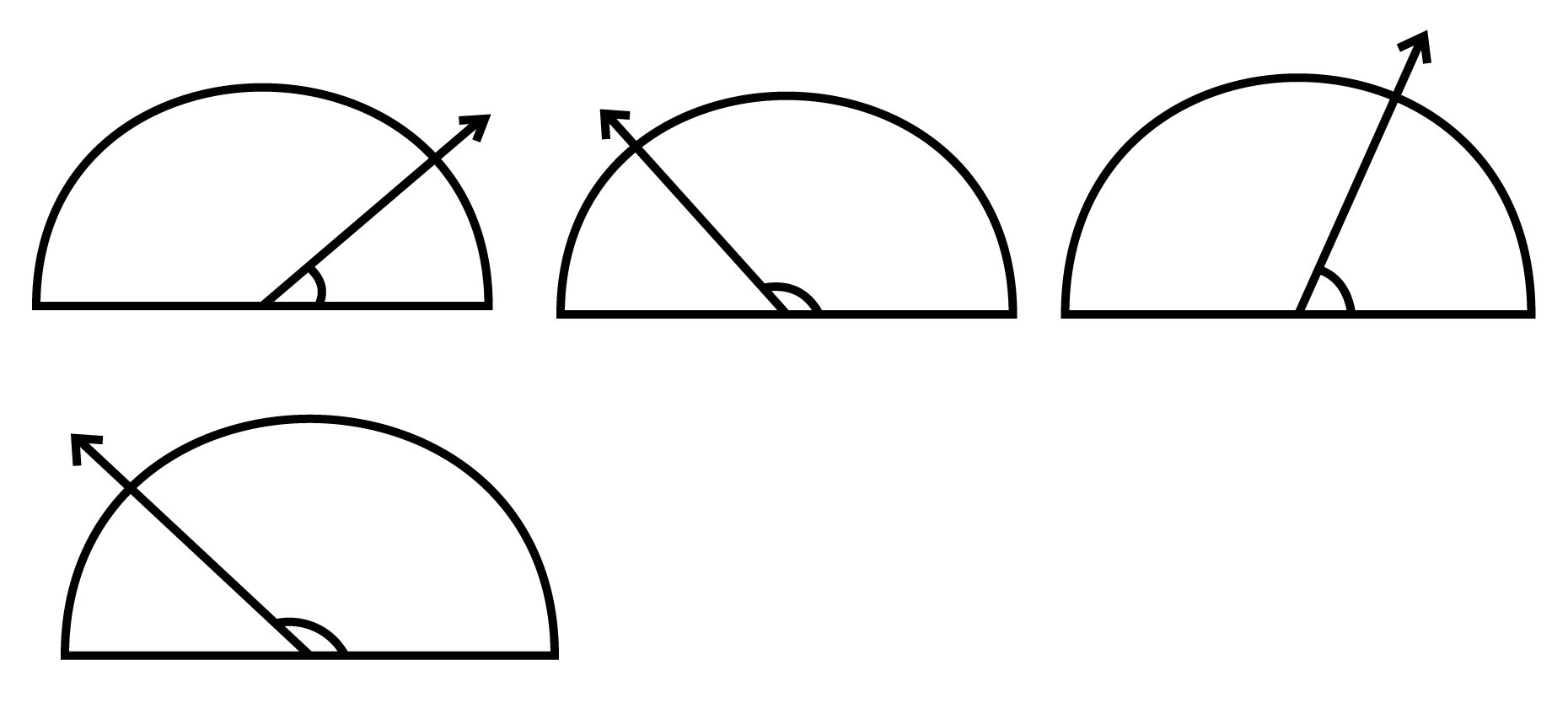Solved NCERT Questions For Class 6 Maths Chapter 5 In Hindi - Free PDF
FAQs on NCERT Solutions For Class 6 Maths In Hindi Chapter 5 Understanding Elementary Shapes - 2025-26
1. Can Hindi Medium students make use of Vedantu’s NCERT Solutions for Class 6 Mathematics?
Vedantu aims at producing high-caliber intellectuals all across India. Vedantu goes the extra mile in preparing its Mathematical solutions for Class 6 in the Hindi language as well. Students from both English and Hindi medium schools have the opportunity to access Vedantu’s NCERT Solutions. The solutions in Hindi are prepared by expert Mathematics teachers who have experience with Hindi medium textbooks. These solutions are available free of cost. Hence the answers are reliable and easy to use for Hindi medium students.
2. Which chapters in NCERT Solutions for Class 6 Maths require more practice?
Mathematics is a subject that requires consistent and regular practice. Students should not take any chapter lightly and practice all chapters with equal diligence. Class 6 Mathematics syllabus lays the foundation of important mathematical concepts for the upcoming academic years. Hence, students should do their best to understand the concepts explained in the NCERT textbook and practice them well. They can always refer to NCERT's solutions and extra reading material.
3. What are the key features of NCERT Solutions for Class 6 Maths?
Vedantu's NCERT Solutions are prepared after keeping in mind the guidelines from the CBSE. They are curated by experienced mathematics teachers who have worked in their field of expertise for several years. The solutions are explained in a pretty straightforward way with the help of relevant figures wherever necessary. An exceptional key feature of Vedantu is that it provides Mathematical solutions for students enrolled in English as well as Hindi medium schools. These solutions can be accessed on Vedantu’s website (vedantu.com). Students can also download the app of Vedantu from Google Playstore and download offline solutions in PDF format.
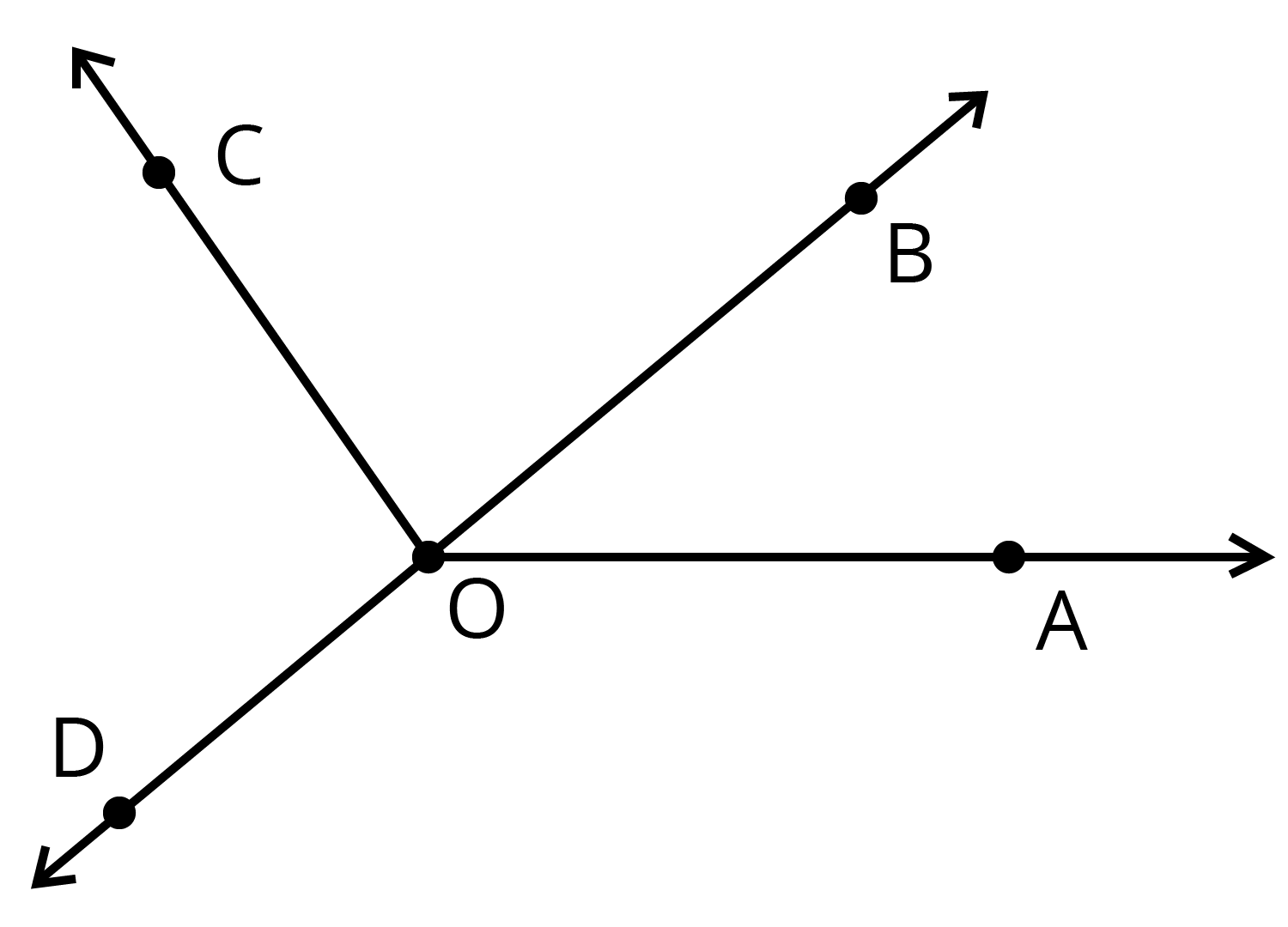
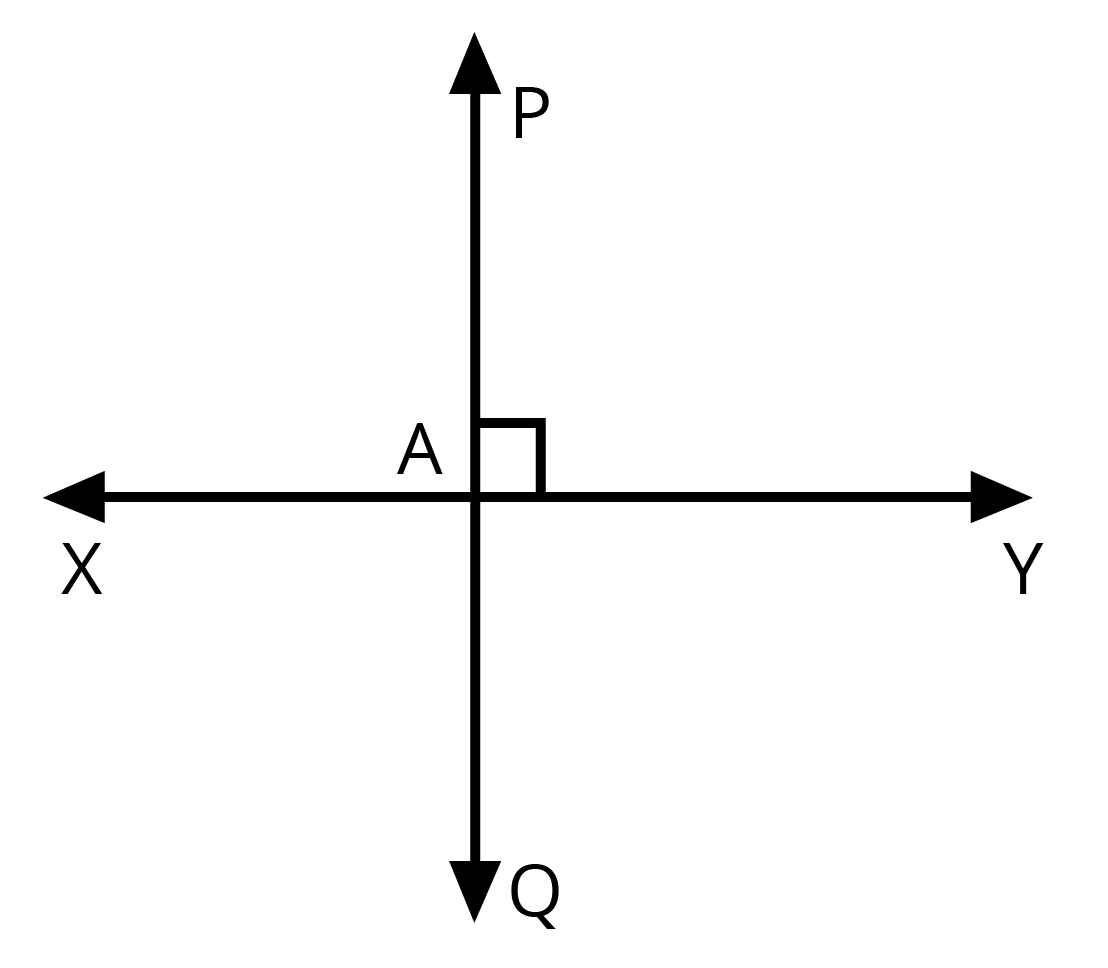
4. Define angles and their types covered under NCERT Solutions for Class 6 Maths Chapter 5?
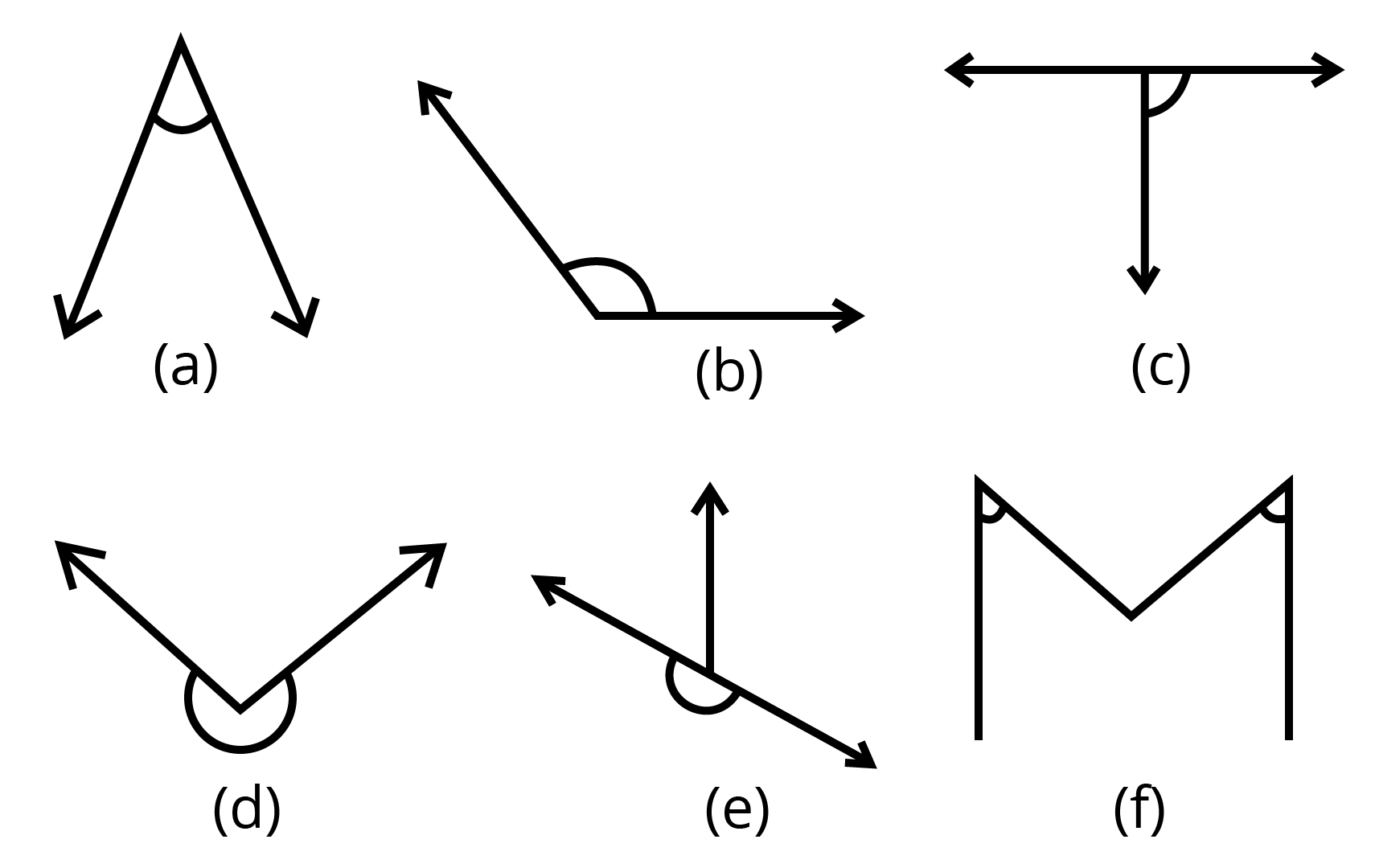
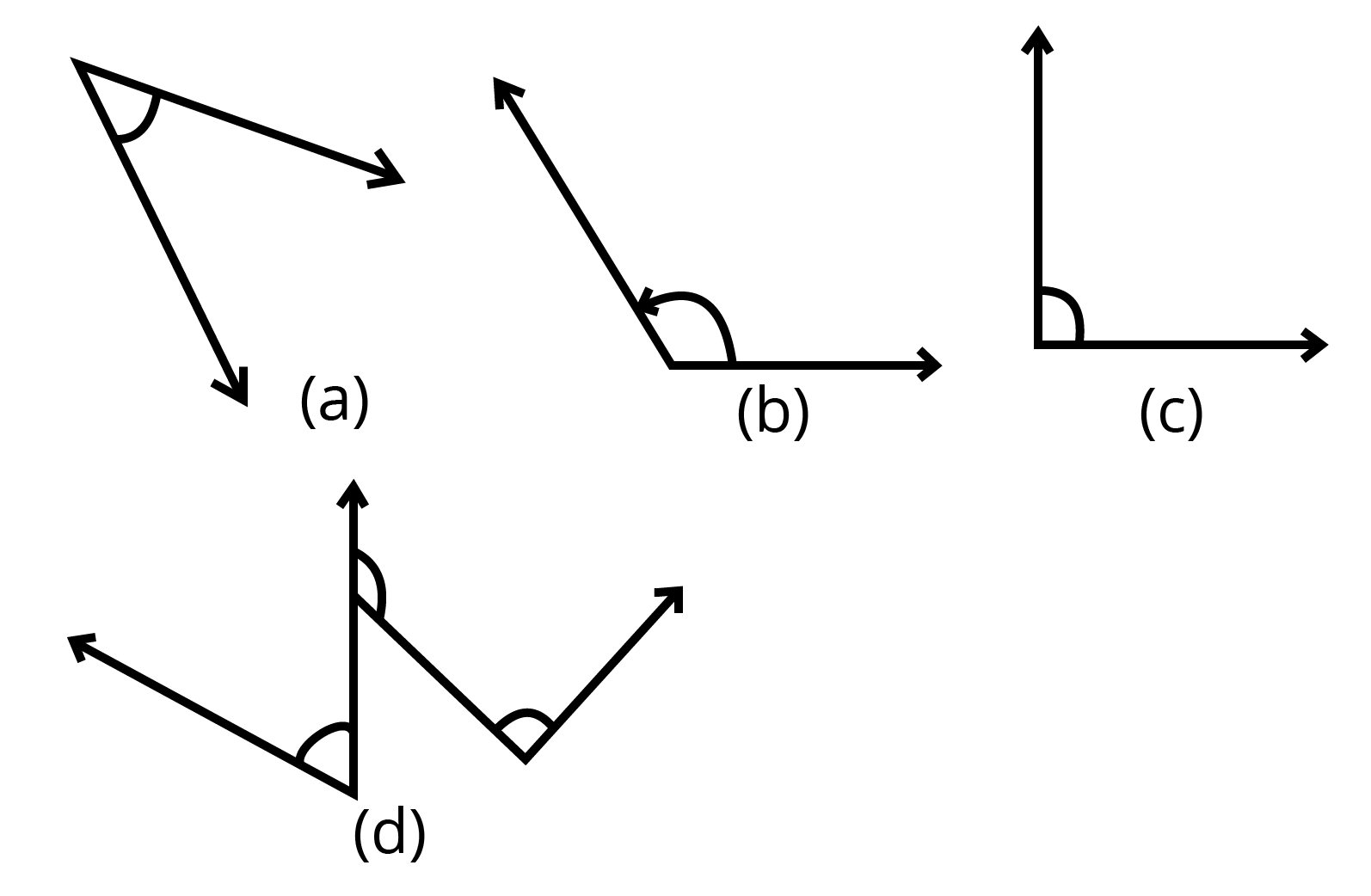
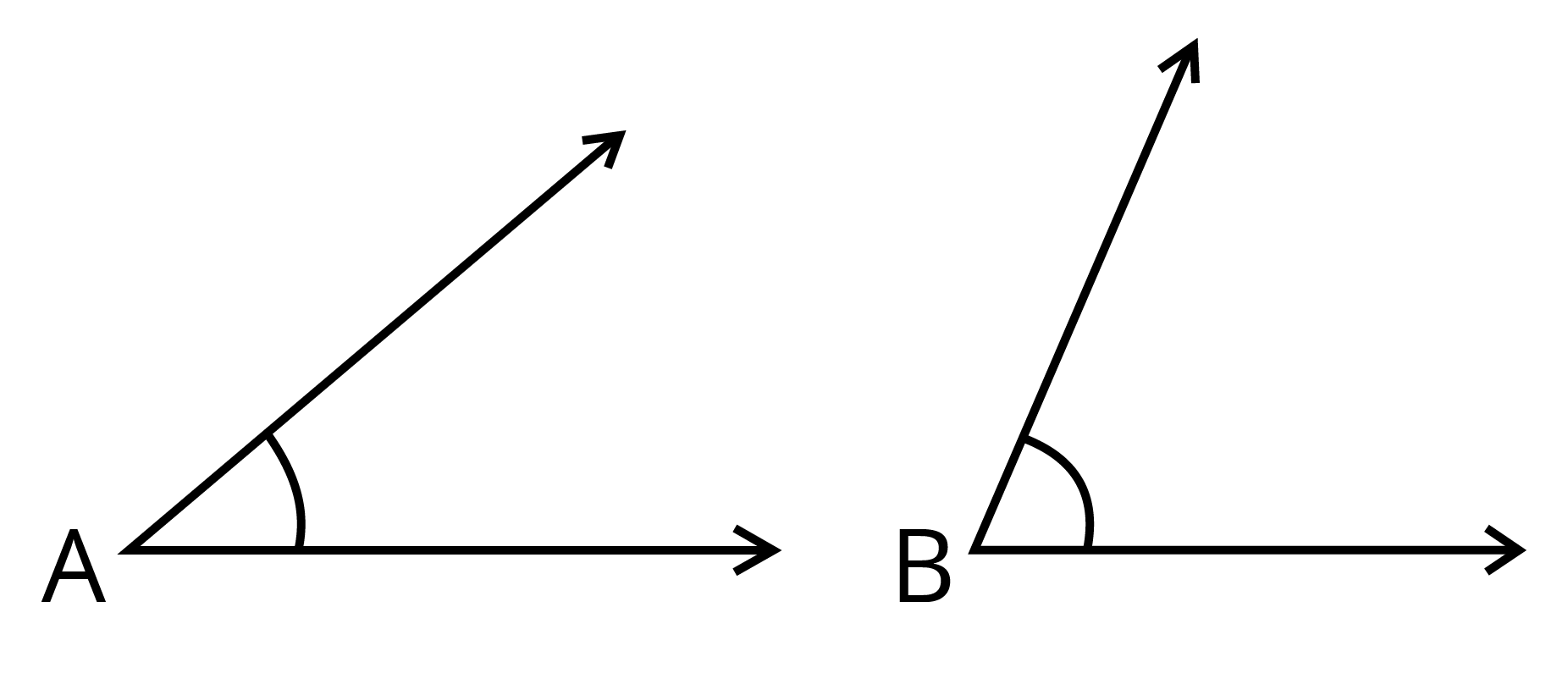
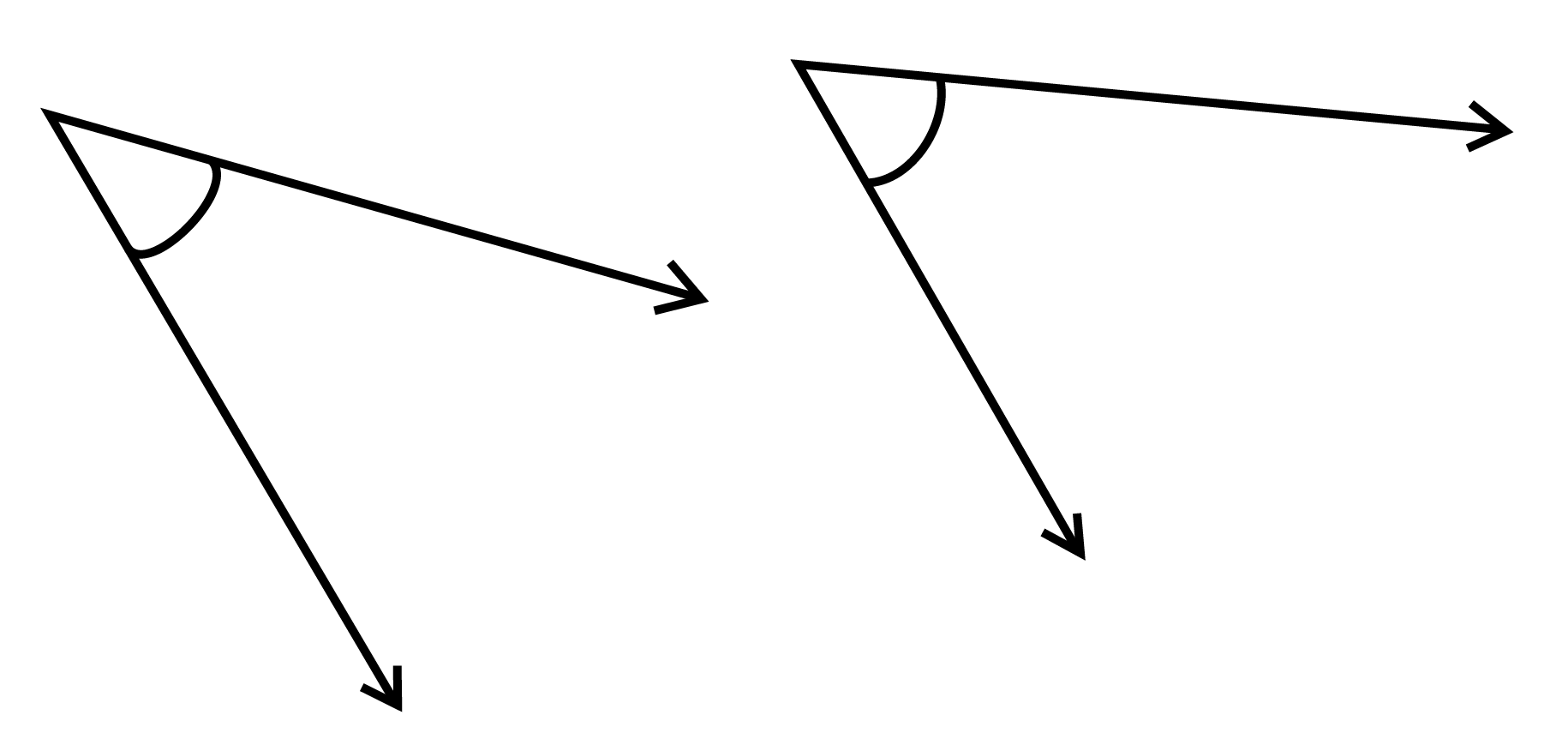
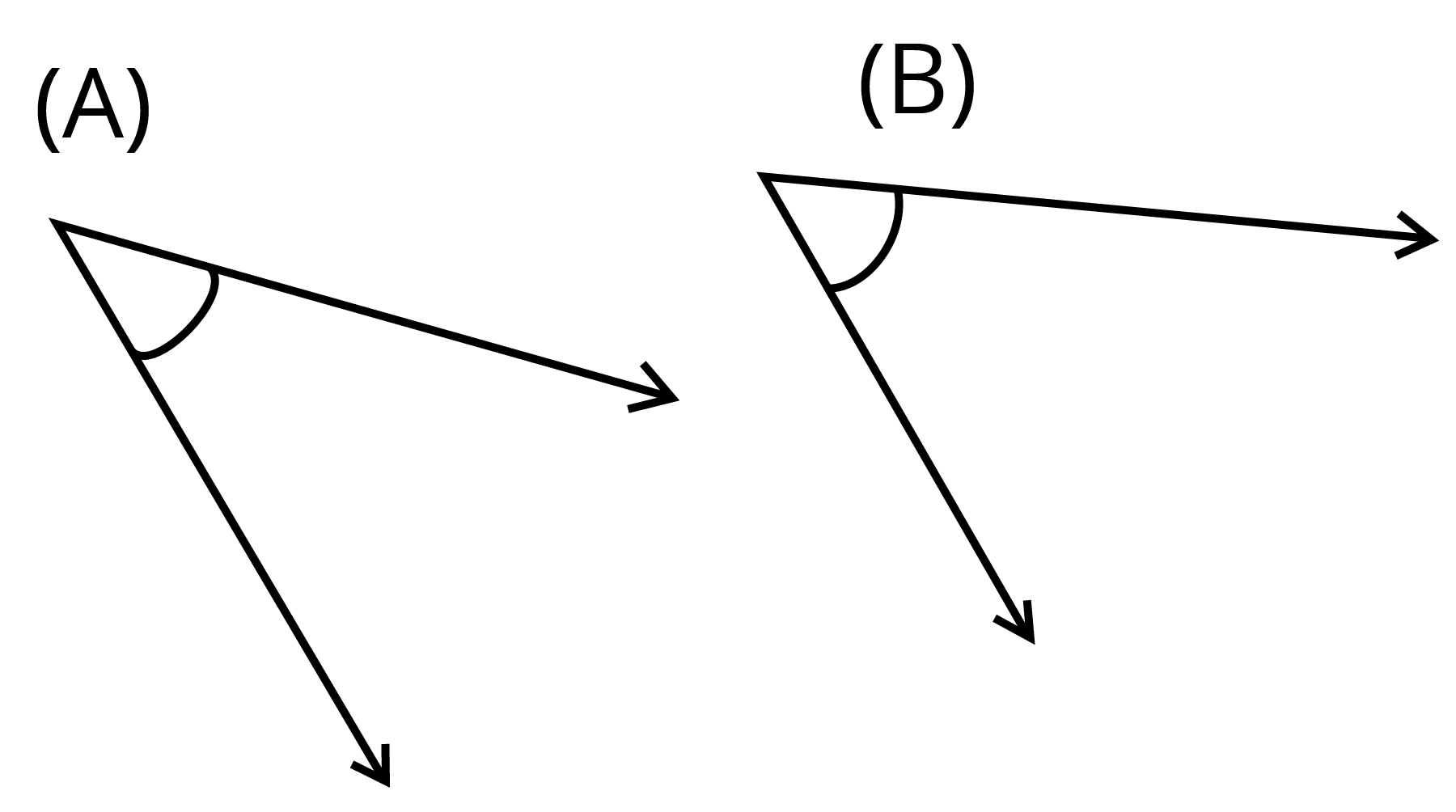
According to Chapter 5 of Class 6 Mathematics, an angle is a figure formed by two rays. Different types of angles are as follows:
Right angle: An angle of exactly 90 degrees.
Straight angle: An angle of exactly 180 degrees.
Acute angle: An angle that measures less than 90 degrees
Obtuse angle: An angle that measures more than 90 degrees and less than 180 degrees.
Reflex angle: An angle more than 180 degrees but less than 360 degrees.
5. Explain solid shapes covered under NCERT Solutions for Class 6 Maths?
Class 6 Chapter 5, "Understanding Elementary Shapes," introduces students to fundamental concepts related to shapes and different kinds of shapes along with their properties. Three-dimensional shapes are also called solid shapes as these shapes are not "flat shapes." Shapes such as cuboid, cube, cone, cylinder, sphere, and pyramid are examples of such shapes. These shapes are characterized by faces, edges, vertices.