NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

• Exercise 9.1: This exercise introduces the concept of a straight line, its slope, and its intercepts. Students will learn to find the slope and intercepts of a line, as well as its equation in various forms.

• Exercise 9.2: In this exercise, students will learn about the point-slope form of the equation of a line, the two-point form of the equation of a line, and the slope-intercept form of the equation of a line. They will practice using these forms to find the equation of a line given certain information.

• Exercise 9.3: This exercise focuses on the distance and midpoint formula. Students will learn how to find the distance between two points and the midpoint of a line segment.

• Miscellaneous Exercise: This exercise includes a mix of questions covering all the concepts taught in the chapter. Students will have to apply their knowledge of straight lines to solve various problems and answer questions. They will also practice finding the equation of a line and calculating its slope, intercepts, distance, and midpoint.

Access NCERT Solutions for Class 11 Maths Chapter 9 – Straight Lines

Exercise 9.1

1. Draw a quadrilateral in the Cartesian plane, whose vertices are $( - 4,5),\,\,(0,7),\,\,(5, - 5)$  and $( - 4, - 2)$. Also, find its area.

Ans.Assume ${\text{PQRS}}$ is the quadrilateral with given vertices ${\text{P}}( - 4,5),\,\,{\text{Q}}(0,7),\,\,{\text{R}}(5, - 5)$, and ${\text{S}}( - 4, - 2).$ 

Plot P, Q, R and S on the Cartesian plane and join ${\text{PQ}},\,\,{\text{QR}},\,\,{\text{RS}}$, and ${\text{SP}}$. Then draw the diagonal \[{\text{PR}}\].

From the figure, area $({\text{PQRS}}) = $ area $(\Delta {\text{PQR}}) + $ area $(\Delta {\text{PRS}})$ 

If the vertices of a triangle are $\left( {{x_1},{y_1}} \right),\,\,\left( {{x_2},{y_2}} \right)$, and $\left( {{x_3},{y_3}} \right)$ , the area is,

$\dfrac{1}{2}\left| {{x_1}\left( {{y_2}\,\, - \,\,{y_3}} \right)\,\, + \,\,{x_2}\left( {{y_3}\,\, - \,\,{y_1}} \right)\,\, + \,\,{x_3}\left( {{y_1}\,\, - \,\,{y_2}} \right)} \right|$

Substitute the values and find the area of each triangle,

Now, area of $\Delta {\text{PQR}}$ $ = \,\,\dfrac{1}{2}\mid  - 4(7\,\, + \,\,5)\,\, + \,\,0(\, - 5\,\, - 5)\,\, + \,\,5(5\,\, - \,\,7)$ unit $^2\mid $

$ = \,\,\dfrac{1}{2}| - 4(7\,\, + \,\,5)\,\, + \,\,0( - 5\,\, - 5)\,\, + \,\,5(5\,\, - \,\,7)|$ unit $^2$

$ = \,\,\dfrac{1}{2}| - 4(12)\,\, + \,\,5( - 2)|$ unit $^2$

$ = \,\,\dfrac{1}{2}| - 48\,\, - \,\,10|$ unit $^2$

$ = \,\,\dfrac{1}{2}| - 58|$ unit $^2$

$ = \,\,\dfrac{1}{2}\,\, \times \,\,58$ unit $^2$

$ = \,\,29$ unit $^2$

Similarly area of $\Delta {\text{PRS}}$is,

$ = \,\,\dfrac{1}{2}| - 4( - 5\,\, + \,\,2)\,\, + \,\,5( - 2\,\, - \,\,5)\,\, + \,\,( - 4)(5\,\, - \,\,5)|$ unit $^2$

$ = \,\,\dfrac{1}{2}| - 4( - 3)\,\, + \,\,5( - 7)\,\, - \,\,4(10)|$ unit $^2$

$ = \,\,\dfrac{1}{2}|12\,\, - \,\,35\,\, - \,\,40|$ unit $^2$

$ = \,\,\dfrac{1}{2}| - 63|$ unit $^2$

$ = \,\,\dfrac{{63}}{2}$ unit $^2$

We have, area $({\text{PQRS}})\,\, = $ area $(\Delta {\text{PQR}}) + $ area $(\Delta {\text{PRS}})$ 

$ = \,\,\left( {29\,\, + \,\,\dfrac{{63}}{2}} \right)$ unit $^2\,\,$

$\, = \,\,\dfrac{{58\,\, + \,\,63}}{2}$ unit $^2\,$

$ = \,\,\dfrac{{121}}{2}$ unit $^2$

Therefore, the area of the quadrilateral is $\,\dfrac{{121}}{2}$ unit $^2$.

2. The base of an equilateral triangle with side $2a$ lies along the $y$-axis such that the midpoint of the base is at the origin. Find vertices of the triangle.

Ans.${\text{PQR}}$ be the given equilateral triangle with side $2a$. 

We know that all the sides of the equilateral triangle will be equal.

That is,

${\text{PQ}}\,\, = \,\,{\text{QR}}\,\, = \,\,{\text{RP}}\,\, = \,\,2a$

Assume that base ${\text{QR}}$ lies along the $y$-axis such that the mid-point of ${\text{QR}}$ is at the origin.

That is, ${\text{QO}}\,\, = \,\,{\text{OR}} = \,\,a$, where ${\text{O}}$ is the origin. 

Now, the coordinates of point ${\text{R}}$ are $(0,a)$, while the coordinates of point ${\text{Q}}\,$are $(0, - a)$.

The line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular. 

Thus, the vertex \[{\text{P}}\]lies on the \[y\]-axis.

Now, plot the figure,

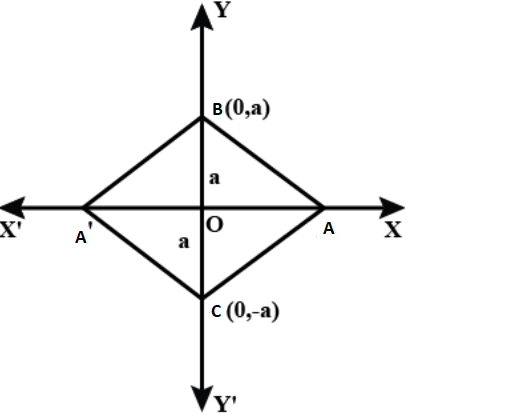
By applying Pythagoras theorem to $\Delta {\text{POR}}$, 

${({\text{PR}})^2}\,\, = \,\,\,{({\text{OP}})^2}\,\, + \,\,{({\text{OR}})^2}$

Substitute the values,

$ \Rightarrow {(2a)^2}\,\, = \,\,{({\text{OP}})^2}\,\, + \,\,{a^2}$

$ \Rightarrow 4{a^2}\,\, - \,\,{a^2}\,\, = \,\,\,{({\text{OP}})^2}$

$ \Rightarrow {({\text{OP}})^2}\,\, = \,\,3{a^2}$

$ \Rightarrow {\text{OP}}\,\, = \,\,\sqrt 3 a$

Thus, Coordinates of point ${\text{P}}\,\, = \,\,( \pm \sqrt 3 a,0)$ 

Therefore, the vertices of the equilateral triangle are $(0,{\text{a}}),\,\,(0, - a)$, and $(\sqrt 3 a,0)\,\,\operatorname{or} \,\,(0,a),\,\,(0, - a)$, and $( - \sqrt 3 a,0)$.

3. Find the distance between ${\text{P}}\left( {{x_1},{y_1}} \right)$ and ${\text{Q}}\left( {{x_2},{y_2}} \right)$ when 

(i) \[{\text{PQ}}\]is parallel to the \[y\]-axis

Ans.Here, the points are ${\text{P}}\left( {{x_1},{y_1}} \right)$ and ${\text{Q}}\left( {{x_2},{y_2}} \right)$.

When PQ is parallel to the ${\text{y}}$-axis, we have ${x_1}\,\, = \,\,{x_2}$. 

The distance between ${\text{P}}$ and ${\text{Q}}$is,

$\sqrt {{{\left( {{x_2}\,\, - \,\,{x_1}} \right)}^2}\,\, + \,\,{{\left( {{y_2}\,\, - \,\,{y_1}} \right)}^2}} $ 

$ = \,\,\sqrt {{{\left( {{y_2}\,\, - \,\,{y_1}} \right)}^2}} $ (since ${x_1}\,\, = \,\,{x_2}$.)

$ = \,\,\left| {{y_2}\,\, - \,\,{y_1}} \right|$

Therefore, the distance between ${\text{P}}\left( {{x_1},{y_1}} \right)$ and ${\text{Q}}\left( {{x_2},{y_2}} \right)$ when \[{\text{PQ}}\]is parallel to the \[y\]-

axis is $\,\left| {{y_2}\,\, - \,\,{y_1}} \right|$.

(ii) ${\text{PQ}}$ is parallel to the $x$-axis.

Ans.The points are ${\text{P}}\left( {{x_1},{y_1}} \right)$ and ${\text{Q}}\left( {{x_2},{y_2}} \right)$.

When ${\text{PQ}}$ is parallel to the $x$-axis, we know \[{y_1}\,\, = \,\,{y_2}\]

Distance between ${\text{P}}$ and ${\text{Q}}$is,

$\sqrt {{{\left( {{x_2}\,\, - \,\,{x_1}} \right)}^2}\,\, + \,\,{{\left( {{y_2}\,\, - \,\,{y_1}} \right)}^2}} $

$ = \,\,\sqrt {{{\left( {{x_2}\,\, - \,\,{x_1}} \right)}^2}} $ (since \[{y_1}\,\, = \,\,{y_2}\])

$ = \,\,\left| {{x_2}\,\, - \,\,{x_1}} \right|$

Therefore, the distance between ${\text{P}}\left( {{x_1},{y_1}} \right)$ and ${\text{Q}}\left( {{x_2},{y_2}} \right)$ when ${\text{PQ}}$ is parallel to the $x$-

axis is $\,\left| {{x_2}\,\, - \,\,{x_1}} \right|$.

4. Find a point on the $x$-axis, which is equidistant from the points $(7,6)$ and $(3,4)$.

Ans.Let ${\text{A}}(7,6)$ and ${\text{B}}(3,4)$be the given points.

Assume ${\text{C}}(a,0)$ as the point on the $X$ - axis that is equidistance from the points $(7,6)$ 

and $(3,4)$.In general, Distance between two points is $\sqrt {{{\left( {{x_2}\,\, - \,\,{x_1}} \right)}^2}\,\, + \,\,{{\left( {{y_2}\,\, - \,\,{y_1}} \right)}^2}} $

Now, Distance between \[{\text{A and C}}\]\[ = \] Distance between \[{\text{B and C}}\].

$\sqrt {{{(7 - a)}^2} + {{(6 - 0)}^2}}  = \sqrt {{{(3 - a)}^2} + {{(4 - 0)}^2}} $

$ \Rightarrow \sqrt {49 + {a^2} - 14a + 36}  = \sqrt {9 + {a^2} - 6a + 16} $  (since \[{(a\,\,\, - \,\,b)^2} = \,\,{a^2}\,\, - \,\,2ab\,\, + \,\,{b^2}\])

$ \Rightarrow \sqrt {{a^2} - 14a + 85}  = \sqrt {{a^2} - 6a + 25} $

Square both sides, 

$ \Rightarrow {a^2} - 14a + 85 = {a^2} - 6a + 25$

$ \Rightarrow  - 14a + 6a = 25 - 85$

$ \Rightarrow  - 8a =  - 60$

$\Rightarrow a = \dfrac{{60}}{8}$

 $= \dfrac{{15}}{2}$

Therefore, the point on the $x$-axis which is equidistant from the points $(7,6)$ and $(3,4)$is 

\[\left( {\dfrac{{15}}{2},0} \right).\]

5. Find the slope of a line, which passes through the origin, and the mid-point of the segment joining the points ${\text{P}}(0, - 4)$ and ${\text{B}}(8,0)$.

Ans.The coordinates of the midpoint of the line segment joining two points are,

\[\left( {\dfrac{{{x_1}\,\, + \,\,{x_2}}}{2},\dfrac{{{y_1}\,\, + \,\,{y_2}}}{2}} \right)\]

Then, the coordinates of the mid-point of the line segment joining the points ${\text{P}}(0, - 4)$ and ${\text{B}}(8,0)$ are,

$\left( {\dfrac{{0\,\, + \,\,8}}{2},\dfrac{{ - 4\,\, + \,\,0}}{2}} \right)\,\, = \,\,(4, - 2)$

We know, the slope \[\left( m \right)\]of a non-vertical line passing through the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2}} \right.,{y_2})$ is,

$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}},\,\,{\text{where }}{x_2} \ne {x_1}$

Thus, the slope of the line passing through $(0,0,$, and $(4, - 2)$ is,

 $\Rightarrow \dfrac{{ - 2 - 0}}{{4 - 0}}$

 $= \dfrac{{ - 2}}{4} $

 $=  - \dfrac{1}{2}$ 

Therefore, the slope of a line, which passes through the origin, and the mid-point of the

segment joining the points ${\text{P}}(0, - 4)$ and ${\text{B}}(8,0)$ is $ - \dfrac{1}{2}$.

6. Without using the Pythagoras theorem, show that the points $(4,4),(3,5)$ and $( - 1, - 1)$ are vertices of a right angled triangle.

Ans.The vertices of the given triangle are ${\text{P}}(4,4),\,\,{\text{Q}}(3,5)$, and ${\text{R}}( - 1, - 1)$.

We know, the slope \[\left( m \right)\]of a non-vertical line passing through the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2}} \right.,{y_2})$ is,

$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}},\,\,{\text{where }}{x_2} \ne {x_1}$

Now calculate the slope of each line,

Slope of ${\text{PQ}} = \dfrac{{5 - 4}}{{3 - 4}} =  - 1$

Slope of \[{\text{QR}} = \dfrac{{ - 1 - 5}}{{ - 1 - 3}} = \dfrac{{ - 6}}{{ - 4}} = \dfrac{3}{2}\]

Slope of ${\text{RP}} = \dfrac{{4 + 1}}{{4 + 1}} = \dfrac{5}{5} = 1$

Here, Slope of ${\text{PQ}} = $ Slope of ${\text{RP}} = 1$

This means that the line segments ${\text{PQ}}$ and ${\text{RP}}$ are perpendicular to each other

That is, the triangle is right-angled at ${\text{P}}(4,4)$. 

Therefore, the points $(4,4),(3,5)$ and $( - 1, - 1)$are vertices of a right angled triangle.

7. Find the slope of the line, which makes an angle of ${30^\circ }$ with the positive direction of $y$-axis measured anticlockwise.

Ans.Given that, the line makes an angle of ${30^\circ }$ with the positive direction of $y$-axis 

measured anticlockwise.

Plot the figure,

From the figure, the angle made by the line with the positive direction of the $x$-axis 

measured anticlockwise is,

 ${90^\circ } + {30^\circ } = {120^\circ }$

Now, the slope of the given line is $\tan {120^\circ }$

${\text{Rewrite}}\tan {120^\circ }\,{\text{as }}\tan \left( {{{180}^\circ } - {{60}^\circ }} \right)$

$=  - \tan {60^\circ } $

$=  - \sqrt 3 $

Therefore, the slope of the line, which makes an angle of ${30^\circ }$ with the positive direction of $y$-axis measured anticlockwise is $ - \sqrt 3 $.

9. Without using distance formula, show that points $( - 2, - 1),(4,0),(3,3)$ and $( - 3,2)$ are vertices of a parallelogram.

Ans.Let points $( - 2, - 1),(4,0),(3,3)$ and $( - 3,2)$ be respectively denoted by ${\text{P,}}\,{\text{Q,}}\,{\text{R and S}}{\text{.}}$

Slopes of ${\text{PQ}} = \dfrac{{0 + 1}}{{4 + 2}} = \dfrac{1}{6}$

Slopes of ${\text{RS}} = \dfrac{{2 - 3}}{{ - 3 - 3}} = \dfrac{{ - 1}}{{ - 6}} = \dfrac{1}{6}$

Here, Slope of ${\text{PQ}} = $ Slope of \[{\text{RS}}\]

This means, \[{\text{PQ and RS}}\] are parallel to each other.

Slope of ${\text{QR}} = \dfrac{{3 - 0}}{{3 - 4}} = \dfrac{3}{{ - 1}} =  - 3$

Slope of ${\text{PS}} = \dfrac{{2 + 1}}{{ - 3 + 2}} = \dfrac{3}{{ - 1}} =  - 3$

Here, Slope of ${\text{QR}} = $ Slope of ${\text{PS}}$ 

This means, \[{\text{QR and PS}}\] are parallel to each other. 

Thus, both pairs of opposite side of the quadrilateral ${\text{PQRS}}$ are parallel and it is a 

parallelogram.

Therefore, $( - 2, - 1),(4,0),(3,3)$ and $( - 3,2)$ are vertices of a parallelogram.

9. Find the angle between the \[x\]-axis and the line joining the point

\[\left( {3,{\text{ }} - 1} \right){\text{ and }}\left( {4,{\text{ }} - 2} \right).\]

Ans.The points are \[\left( {3,{\text{ }} - 1} \right){\text{ and }}\left( {4,{\text{ }} - 2} \right).\]

The slope \[\left( m \right)\]of a non-vertical line passing through the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2}} \right.,{y_2})$ is,

$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}},\,\,{\text{where }}{x_2} \ne {x_1}$

The slope of the line joining the points $(3, - 1)$ and $(4, - 2)$ is,

 $m = \dfrac{{ - 2 - ( - 1)}}{{4 - 3}} $

 $=  - 2 + 1 $

 $=  - 1$ 

The inclination $(\theta )$ of the line joining the points $(3, - 1)$ and $(4, - 2)$ is,

$\tan \theta  = m$

Substitute the value of $m$.

$\tan \theta  =  - 1$ 

$\Rightarrow \theta  = \left( {{{90}^\circ } + {{45}^\circ }} \right)$

$= {135^\circ } $

Therefore, the angle between the $x$-axis and the line joining the points $(3, - 1)$ and 

$(4, - 2)$ is ${135^\circ }$.

10. The slope of a line is double the slope of another line. If the tangent of the angle between them is $\dfrac{1}{3}$, find the slope of the lines.

Ans.Take $m,\,\,{m_1}$ as the slopes of the two lines.

Given that, slope of a line is double of the slope of another line.

That is, ${m_1} = 2\;m$

If $\theta $ is the angle between the lines ${l_1}$ and ${l_2}$ with slopes ${m_1}$ and ${m_2}$ 

We have,

$\tan \theta  = \left| {\dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}} \right|$

It is also given that the tangent of the angle between the two lines is $\dfrac{1}{3}$. 

$\dfrac{1}{3} = \left| {\dfrac{{m - 2m}}{{1 + (2m) \cdot m}}} \right|$

$ \Rightarrow \dfrac{1}{3} = \left| {\dfrac{{ - m}}{{1 + 2{m^2}}}} \right|$

$ \Rightarrow \dfrac{1}{3} = \dfrac{{ - m}}{{1 + 2{m^2}}}$ or

 $\dfrac{1}{3} =  - \left( {\dfrac{{ - m}}{{1 + 2{m^2}}}} \right) = \dfrac{m}{{1 + 2{m^2}}}$

$ \Rightarrow \dfrac{1}{3} = \left| {\dfrac{{ - {\text{m}}}}{{1 + 2{m^2}}}} \right|$

$ \Rightarrow \dfrac{1}{3} = \dfrac{{ - m}}{{1 + 2{m^2}}}$ or 

$\dfrac{1}{3} =  - \left( {\dfrac{{ - m}}{{1 + 2{m^2}}}} \right) = \dfrac{m}{{1 + 2{m^2}}}$

Case 1:

$ \Rightarrow \dfrac{1}{3} = \dfrac{{ - m}}{{1 + 2{m^2}}}$

Cross multiply,

$ \Rightarrow 1 + 2{m^2} =  - 3m$

$ \Rightarrow 2{m^2} + 3m + 1 = 0$

Rewrite the equation,

$ \Rightarrow 2{m^2} + 2m + m + 1 = 0$

Take out the common terms,

$ \Rightarrow 2m(m + 1) + 1(m + 1) = 0$

$ \Rightarrow (m + 1)(2m + 1) = 0$

$ \Rightarrow m =  - 1$ or $m =  - \dfrac{1}{2}$

If $m =  - 1$, then the slopes of the lines are $ - 1$ and $ - 2$. 

Similarly, if $m =  - \dfrac{1}{2}$, then the slopes of the lines are $ - \dfrac{1}{2}$ and $ - 1$. 

Case 2:

$\dfrac{1}{3} = \dfrac{m}{{1 + 2{m^2}}}$

Cross multiply,

$ \Rightarrow 2{m^2} + 1 = 3m$

Equate to zero,

$ \Rightarrow 2{m^2} - 3m + 1 = 0$

$ \Rightarrow 2{m^2} - 2m - m + 1 = 0$

Take out the common terms,

$ \Rightarrow 2m(m - 1) - 1(m - 1) = 0$

$ \Rightarrow (m - 1)(2m - 1) = 0$

$ \Rightarrow m = 1$ or $m = \dfrac{1}{2}$

If $m = 1$, then the slopes of the lines are\[1{\text{ and }}2\]. 

Similarly, if $m = \dfrac{1}{2}$, then the slopes of the lines are $\dfrac{1}{2}$ and 1 . 

Therefore, the slopes of the lines are $ - 1$ and $ - 2$ or $ - \dfrac{1}{2}$ and $ - 1$ or 1 and 2 or $\dfrac{1}{2}$ and 1 .

11. A line passes through $\left( {{x_1},{y_1}} \right)$ and $(h,k).$ It slope of the line is \[m\], show that $k - {y_1} = m\left( {h - {x_1}} \right)$

Ans.Given that, the slope of the line is \[m\].

The slope of the line passing through $\left( {{x_1},{y_1}} \right)$ and $(h,k)$ is $\dfrac{{k - {y_1}}}{{h - {x_1}}}$. 

Now, $\dfrac{{k - {y_1}}}{{h - {x_1}}} = m$

$ \Rightarrow k - {y_1} = m\left( {h - {x_1}} \right)$

Therefore, if the line passes through $\left( {{x_1},{y_1}} \right)$ and $(h,k)$ with a slope of the \[m\], 

$k - {y_1} = m\left( {h - {x_1}} \right)$

Exercise 9.2

1. Write the equation for the $x$ and $y$-axes.

Ans.The equation of $x$-axis is $y = 0$ because, \[y\]-coordinate of every point on the $x$-axis 

is zero.

The equation of the $y$-axis is $y = 0$ because, $x$-coordinate of every point on the $y$-axis 

is zero.

2. Find the equation of the line which passes through the point $( - 4,3)$ with slope $\dfrac{1}{2}$

Ans.Given that, the point $( - 4,3)$ and slope of the line is $\dfrac{1}{2}$.

The equation of the line passing through point $\left( {{x_0},{y_0}} \right)$, whose slope is $m$, is 

$\left( {y - {y_0}} \right) = m\left( {x - {x_0}} \right).$

Thus, the equation of the line passing through point $( - 4,3)$, whose slope is $\dfrac{1}{2}$, is $(y - 3) = \dfrac{1}{2}(x + 4)$

Cross multiply,

$2(y - 3) = x + 4$

$2y - 6 = x + 4$

Move the constants together,

$x - 2y + 10 = 0$

Therefore, the equation of the line which passes through the point $( - 4,3)$ with slope $\dfrac{1}{2}$ is $x - 2y + 10 = 0.$

3. Find the equation of the line which passes through \[\left( {0,0} \right)\] with slope \[m.\]

Ans.Given that, the point is  \[\left( {0,0} \right)\] and slope is \[m.\]

The equation of the line passing through point $\left( {{x_0},{y_0}} \right)$, whose slope is $m$, is 

$\left( {y - {y_0}} \right) = m\left( {x - {x_0}} \right).$

Substitute the values in the equation,

$ \Rightarrow (y - 0) = m(x - 0)$

$ \Rightarrow y\,\, = \,\,mx$

Therefore, the equation of the line which passes through \[\left( {0,0} \right)\] with slope \[m\]is $y = mx.$

4. Find the equation of the line which passes through $(2,2\sqrt 3 )$ and is inclined with the $x$-axis at an angle of ${75^\circ }$

Ans.Given that, the point is  $(2,2\sqrt 3 )$.

The slope of the line that inclines with the $x$-axis at an angle of ${75^\circ }$.

 That is, $m = \tan {75^\circ }$ 

$m = \tan \left( {{{45}^\circ } + {{30}^\circ }} \right) $

$= \dfrac{{\tan {{45}^\circ } + \tan {{30}^\circ }}}{{1 - \tan {{45}^\circ } \cdot \tan {{30}^\circ }}} $

${\text{Substitute the values,}} $

$= \dfrac{{1 + \dfrac{1}{{\sqrt 3 }}}}{{1 - 1 \cdot \dfrac{1}{{\sqrt 3 }}}} $

 $= \dfrac{{\dfrac{{\sqrt 3  + 1}}{{\sqrt 3 }}}}{{\dfrac{{\sqrt 3  - 1}}{{\sqrt 3 }}}} $

 $= \dfrac{{\sqrt 3  + 1}}{{\sqrt 3  - 1}} $ 

The equation of the line passing through point $\left( {{x_0},{y_0}} \right)$, whose slope is $m$, is $\left( {y - {y_0}} \right) = m\left( {x - {x_0}} \right).$

Thus, if a line passes through $(2,2\sqrt 3 )$ and inclines with the $x$-axis at an angle of ${75^\circ }$,then the equation of the line is,

$(y - 2\sqrt 3 ) = \dfrac{{\sqrt 3  + 1}}{{\sqrt 3  - 1}}(x - 2)$

$(y - 2\sqrt 3 )(\sqrt 3  - 1) = (\sqrt 3  + 1)(x - 2)$

$y(\sqrt 3  - 1) - 2\sqrt 3 (\sqrt 3  - 1) = x(\sqrt 3  + 1) - 2(\sqrt 3  + 1)$

$(\sqrt 3  + 1)x - (\sqrt 3  - 1)y = 2\sqrt 3  + 2 - 6 + 2\sqrt 3 $

$(\sqrt 3  + 1)x - (\sqrt 3  - 1)y = 4\sqrt 3  - 4$

That is, $(\sqrt 3  + 1)x - (\sqrt 3  - 1)y = 4(\sqrt 3  - 1)$

Therefore, the equation of the line which passes through $(2,2\sqrt 3 )$ and is inclined with the $x$-axis at an angle of ${75^\circ }$is $(\sqrt 3  + 1)x - (\sqrt 3  - 1)y = 4(\sqrt 3  - 1).$

5. Find the equation of the line which intersects the $x$-axis at a distance of \[3\] units to the left of origin with slope $ - 2$.

Ans.Given that, 

Slope, $m =  - 2$

If a line with slope $m$ makes $x$-intercept $d$, then equation of the line is

$y = m(x - d)$

Also given that, the distance is \[3\]units to the left of origin 

That is, $d =  - 3$

Substitute the values in the equation of line,

$y = ( - 2)(x - ( - 3))$

$y = ( - 2)(x + 3)$

Expand bracket,

$y =  - 2x - 6$

$2x + y + 6 = 0$

Therefore, The equation of the line which intersects the $x$-axis at a distance of \[3\] units to the left of origin with slope $ - 2$ is $2x + y + 6 = 0$.

6. Find the equation of the line which intersects the \[y\]-axis at a distance of \[2\] units above the origin and makes an angle of ${30^\circ }$ with the positive direction of the $x$-axis.

Ans.Given, the line intersects the \[y\]-axis at a distance of \[2\] units above the Origin.

The line makes an angle of ${30^\circ }$ with the positive direction of the $x$-axis.

That is, $c = 2$

$m = \tan {30^\circ } $

$ = \dfrac{1}{{\sqrt 3 }} $

If a line with slope $m$ makes $y$ - intercept $c$, then the equation of the line is,

$y = mx + c$

Substitute the values,

$y = \dfrac{1}{{\sqrt 3 }}x + 2$

$y = \dfrac{{x + 2\sqrt 3 }}{{\sqrt 3 }}$

$\sqrt 3 y = x + 2\sqrt 3 $

$x - \sqrt 3 y + 2\sqrt 3  = 0$

Therefore, the equation of the line which intersects the \[y\]-axis at a distance of \[2\] units above the origin and makes an angle of ${30^\circ }$ with the positive direction of the $x$-axis is $x - \sqrt 3 y + 2\sqrt 3  = 0$.

7.  Find the equation of the line passing through the points (-1,1) and (2,-4)

Ans: We know that the equation passing through the points $({x_1},{y_1})$ and $({x_2},{y_2})$ is $y - {y_1}\, = \,\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$

$\therefore $ The equation of the line that is passing through the points (-1, 1) and (2, -4) is

$(y - 1)\, = \,\frac{{ - 4 - 1}}{{2 + 1}}(x - ( - 1))$

$(y - 1)\, = \,\frac{{ - 5}}{3}(x + 1)$

$3(y - 1)\, = \, - 5(x + 1)$

$3y - 3\, = \, - 5x - 5$

$\therefore \,\,$The equation of line is $5x + 3y + 2 = 0$

8.The vertices of $\Delta {\text{PQR}}$ are ${\text{P}}(2,1),{\text{Q}}( - 2,3)$ and ${\text{R}}(4,5)$. Find equation of the median through the vertex ${\text{R}}$.

Ans.Given that, the vertices of $\Delta {\text{PQR}}$ are ${\text{P}}(2,1),{\text{Q}}( - 2,3)$ and ${\text{R}}(4,5)$. 

Let ${\text{RL}}$ be the median through vertex ${\text{R}}$.

And ${\text{L}}$ be the mid-point of ${\text{PQ}}$. 

By mid-point formula, the coordinates of point $L$ are,

$\left( {\dfrac{{2 - 2}}{2},\dfrac{{1 + 3}}{2}} \right) = (0,2)$

The equation of the line passing through points $\left( {{x_1},{y_1}} \right) = (4,5)$ and $\left( {{x_2},{y_2}} \right) = (0,2)$ is,

$y - 5 = \dfrac{{2 - 5}}{{0 - 4}}(x - 4)$

$ \Rightarrow y - 5 = \dfrac{{ - 3}}{{ - 4}}(x - 4)$

Cross multiply,

$ \Rightarrow 4(y - 5) = 3(x - 4)$

Expand brackets and equate to zero,

$ \Rightarrow 4y - 20 - 3x - 12 = 0$

Rewrite the equation,

$ \Rightarrow 3x - 4y + 8 = 0$

Therefore, equation of the median through the vertex ${\text{R}}$is $3x - 4y + 8 = 0$.

9. Find the equation of the line passing through $( - 3,5)$ and perpendicular to the line through the points $(2,5)$ and $( - 3,6)$.

Ans.The slope of the line joining the points $(2,5)$ and $( - 3,6)$ is,

$m = \dfrac{{6 - 5}}{{ - 3 - 2}} $

$ = \dfrac{1}{{ - 5}} $ 

It is known that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other. 

Thus, slope of the line perpendicular to the line through the points $(2,5)$ and $( - 3,6)$ is,

$ - \dfrac{1}{m} =  - \dfrac{1}{{\left( {\dfrac{{ - 1}}{5}} \right)}} = 5$

The equation of the line passing through point $( - 3,5)$, whose slope is\[5\]is,

 $(y - 5) = 5(x + 3)$

Expand brackets,

$y - 5 = 5x + 15$

That is, $5x - y + 20 = 0$

Therefore, the equation of the line passing through $( - 3,5)$ and perpendicular to the line through the points $(2,5)$ and $( - 3,6)$ is $5x - y + 20 = 0$.

10. A line perpendicular to the line segment joining the points $(1,0)$ and $(2,3)$ divides it in the ratio $1:n$. Find the equation of the line.

Ans.By section formula, the coordinates of the point that divides the line segment joining the points $(1,0)$ and $(2,3)$ in the ration $1:n$ is,

$\left( {\dfrac{{n(1) + 1(2)}}{{1 + n}},\dfrac{{n(0) + 1(3)}}{{1 + n}}} \right) = \left( {\dfrac{{n + 2}}{{n + 1}},\dfrac{3}{{n + 1}}} \right)$

Now, the slope of the line joining the points $(1,0)$ and $(2,3)$ is,

$m = \dfrac{{3 - 0}}{{2 - 1}} $

$  = 3 $

It is known that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other. 

Thus, slope of the line that is perpendicular to the line joining the points $(1,0)$ and $(2,3)$ is,

$ - \dfrac{1}{m} =  - \dfrac{1}{3}$

The equation of the line passing through $\left( {\dfrac{{n + 2}}{{n + 1}},\dfrac{3}{{n + 1}}} \right)$ and whose slope is $ - \dfrac{1}{3}$ is ,

$\left( {y - \dfrac{3}{{n + 1}}} \right) =  - \dfrac{1}{3}\left( {x - \dfrac{{n + 2}}{{n + 1}}} \right)$

Cross multiply,

$ \Rightarrow 3\left( {y - \dfrac{3}{{n + 1}}} \right) =  - \left( {x - \dfrac{{n + 2}}{{n + 1}}} \right)$

Take LCM,

$ \Rightarrow 3[(n + 1)y - 3] =  - [x(n + 1) - (n + 2)]$

$ \Rightarrow 3(n + 1)y - 9 =  - (n + 1)x + n + 2$

$ \Rightarrow (1 + n)x + 3(1 + n)y = n + 11$

Therefore, equation of the line perpendicular to the line segment joining the points $(1,0)$ and $(2,3)$ divides it in the ration $1:n$ is $(1 + n)x + 3(1 + n)y = n + 11$.

11. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the points $(2,3)$.

Ans.The equation of a line in the intercept form is $\dfrac{x}{a} + \dfrac{y}{b} = 1$

Here, \[{\text{ }}a{\text{ and}}\,\,b\]are the intercepts on $x$ and $y$ axes respectively. 

Given that,  the line cuts off equal intercepts on both the axes. 

That is, $a = b$. 

Now, $\dfrac{x}{a} + \dfrac{y}{a} = 1$

$ \Rightarrow x + y = a$

The given line passes through the point $(2,3)$, this equation reduces to

 $2 + 3 = a $

 $\Rightarrow a = 5 $ 

Substitute the value of \[a\] in $x + y = a$

That is, $x + y = 5$

Therefore, the equation of a line that cuts off equal intercepts on the coordinate axes 

and passes through the points $(2,3)$ is $x + y = 5$.

12. Find the equation of the line passing through the points $(2,2)$ and cutting off intercepts on the axes whose sum is \[9\] .

Ans.The equation of the line making intercepts a and $b$ on $x$-and $y$-axis respectively is,

$\dfrac{x}{a} + \dfrac{y}{b} = 1 \ldots ..(1)$

Given that, sum of intercepts $ = 9$

That is, $a + b = 9$

$b = 9 - a$

Substitute value of $b$ in the above equation, 

$\dfrac{x}{a} + \dfrac{y}{{(9 - a)}} = 1$

Also given that, the line passes through the point $(2,2)$

Then, $\dfrac{2}{a} + \dfrac{2}{{(9 - a)}} = 1$

$\dfrac{{2(9 - a) + 2a}}{{a(9 - a)}} = 1$

$\dfrac{{18 - 2a + 2a}}{{a(9 - a)}} = 1$

$\dfrac{{18}}{{a(9 - a)}} = 1$

$18 = a(9 - a)$

$18 = 9a - {a^2}$

${a^2} - 9a + 18 = 0$

Factorize the equation, 

${a^2} - 3a - 6a + 18 = 0$

$a(a - 3) - 6(a - 3) = 0$

$(a - 3)(a - 6) = 0$

$a = 3$ or $a = 6$

Substitute in (1),

Case $1:\,\,(a = 3)$ 

$b = 9 - 3 = 6$

$\dfrac{x}{3} + \dfrac{y}{6} = 1$

$2x + y = 6$

Equate to zero,

$2x + y - 6 = 0$

Case $2:\,\,(a = 6)$ 

$b = 9 - 6 = 3$

$\dfrac{x}{6} + \dfrac{y}{3} = 1$

$x + 2y = 6$

Equate to zero,

$x + 2y - 6 = 0$

Therefore, the equation of the line is $2x + y - 6 = 0$ or $x + 2y - 6 = 0$.

13. Find equation of the line through the points $(0,2)$ making an angle $\dfrac{{2\pi }}{3}$ with the positive $x$ axis. Also, find the equation of the line parallel to it and crossing the \[y\]-axis at a distance of \[2\] units below the origin.

Ans.The slope of the line making an angle $\dfrac{{2\pi }}{3}$ with the positive $x$-axis is,

$m = \tan \left( {\dfrac{{2\pi }}{3}} \right) $

$=  - \sqrt 3 $

The equation of the line passing through points $(0,2)$ and having a slope $ - \sqrt 3 $ is,

$(y - 2) =  - \sqrt 3 (x - 0)$

That is, $\sqrt 3 x + y - 2 = 0$

The slope of line parallel to line $\sqrt 3 x + y - 2 = 0$ is $ - \sqrt 3 $. 

Given that the line parallel to line $\sqrt 3 x + y - 2 = 0$ crosses the \[y\]-axis \[2\] units below the origin.

It passes through point $(0,2)$. 

Thus, the equation of the line passing through points $(0,2)$ and having a slope $ - \sqrt 3 $ is,

$y - ( - 2) =  - \sqrt 3 (x - 0)$

$y + 2 =  - \sqrt 3 x$

$\sqrt 3 x + y + 2 = 0$

Therefore, the equation of the line through the points $(0,2)$ making an angle $\dfrac{{2\pi }}{3}$ with the positive $x$ axis is $\sqrt 3 x + y - 2 = 0$ and the equation of the line parallel to it and crossing the \[y\]-axis at a distance of \[2\] units is $\sqrt 3 x + y + 2 = 0$.

14. The perpendicular from the origin to a line meets it at the point $( - 2,9)$, find the equation of the line.

Ans.Given that, The perpendicular from the origin to a line meets it at the point $( - 2,9)$.

The slope of the line joining the origin $(0,0)$ and point $( - 2,9)$ is,

${m_1} = \dfrac{{9 - 0}}{{ - 2 - 0}} $

$=  - \dfrac{9}{2} $

Then, the slope of the line perpendicular to the line joining the origin and points $( - 2,9)$ is,

${m_2} = \dfrac{1}{{{m_1}}} $

$=  - \dfrac{1}{{\left( { - \dfrac{9}{2}} \right)}} $

$= \dfrac{2}{9} $

Now, the equation of the line passing through point $( - 2,9)$ and having a slope ${m_2}$ is,$(y - 9) = \dfrac{2}{9}(x + 2)$

Cross multiply and expand brackets,

$9y - 81 = 2x + 4$

That is, $2x - 9y + 85 = 0$

Therefore, the equation of the line is $2x - 9y + 85 = 0$.

15. The length ${\text{L}}$ (in centimeter) of a copper rod is a linear function of its Celsius temperature ${\text{C}}$. In an experiment, if ${\text{L}} = 124.942$ when ${\text{C}} = 20$ and ${\text{L}} = 125.134$ when 

${\text{C}} = 110$, express ${\text{L}}$ in terms of ${\text{C}}$.

Ans.It is given that when ${\text{C}} = 20$,  ${\text{L}} = 124.942$ and when ${\text{C}} = 110$,  ${\text{L}} = 125.134$

The points $(20,124.942)$ and $(110,125.134)$ satisfy the linear relation between ${\text{L}}\,{\text{and C}}{\text{.}}$

Assume \[{\text{C}}\]along the \[x\]-axis and L along the \[y\]-axis, we have two points, $(20,124.942)$ 

and $(110,125.134)$ in the ${\text{XY}}$ plane. 

Thus, the linear relation between ${\text{L}}$ and ${\text{C}}$ is the equation of the line passing through 

thepoints $(20,124.342)$ and $(110,125.134)$.

Now, $({\text{L}} - 124.942) = \dfrac{{125.134 - 124.942}}{{110 - 20}}({\text{C}} - 20)$

$({\text{L}} - 124.942) = \dfrac{{0.192}}{{90}}(C - 20)$

${\text{L}} = \dfrac{{0.192}}{{90}}(C - 20) + 124.942$.

16. The owner of a milk store finds that, he can sell \[980\] liters of milk each week at Rs $14/$ liter and\[1220\] liters of milk each week at Rs $16/$ liter. Assuming a linear relationship between selling price and demand, how many liters could he sell weekly at Rs $17/$ liter?

Ans.Given that, the owner can sell \[980\] liters of milk each week at Rs $14/$ liter and \[1220\] liters of milk each week at Rs $16/$ liter. 

The relationship between the selling price and demand is linear. 

Assume selling price per liter along the $x$-axis and demand along the \[y\]-axis, we have two points $(14,980)$ and $(16,1220)$ in the ${\text{XY}}$ plane that satisfy the linear relationship between selling price and demand.

Thus, the line passing through points $(14,980)$ and $(16,1220)$

That is, $y - 980 = \dfrac{{1220 - 980}}{{16 - 14}}(x - 14)$

$y - 980 = \dfrac{{240}}{2}(x - 14)$

$y - 980 = 120(x - 14)$

$y = 120(x - 14) + 980$

If $x = $ Rs $17/$ liter, 

$y = 120(17 - 14) + 980$

$\Rightarrow y = 120 \times 3 + 980 $

 $= 360 + 980 $

 $= 1340 $

Therefore, the owner of the milk store could sell \[1340\] liters of milk weekly at Rs $17/$liter.

17. ${\text{P}}(a,b)$ is the mid-point of a line segment between axes. Show that the equation of the line is $\dfrac{x}{a} + \dfrac{y}{b} = 2$

Ans.Let \[{\text{AB}}\] be a line segment whose midpoint is $P(a,b)$.

Let the coordinates of ${\text{A}}$ and ${\text{B}}$ be $(0,y)$ and $(x,0)$ respectively.

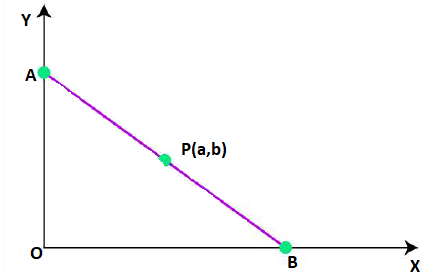
The mid-pint is,

$\left( {\dfrac{{0 + x}}{2},\dfrac{{y + 0}}{2}} \right) = (a,b)$

$ \Rightarrow \left( {\dfrac{x}{2},\dfrac{y}{2}} \right) = (a,b)$

$ \Rightarrow \dfrac{x}{2} = a$ and $\dfrac{y}{2} = b$

$\therefore x = 2a$ and $y = 2b$

Now, the respective coordinates of ${\text{A}}$ and ${\text{B}}$ are $(0,2\;{\text{b}})$ and $(2{\text{a}},0)$.

The equation of the line passing through points $(0,2b)$ and $(2a,0)$ is,

$(y - 2\;b) = \dfrac{{(0 - 2b)}}{{(2a - 0)}}(x - 0)$

$y - 2b = \dfrac{{ - 2b}}{{2a}}(x)$

Cancel \[2\]and cross multiply,

$a(y - 2b) =  - bx$

$ay - 2ab =  - bx$

That is, $bx + ay = 2ab$

Divide both sides by \[ab\], 

$ \Rightarrow \dfrac{{bx}}{{ab}} + \dfrac{{ay}}{{ab}} = \dfrac{{2ab}}{{ab}}$

$ \Rightarrow \dfrac{x}{2} + \dfrac{y}{h} = 2$

Hence, if ${\text{P}}(a,b)$ is the mid-point of a line segment between axes then equation of the line is $\dfrac{x}{a} + \dfrac{y}{b} = 2$.

18.Point ${\text{R}}(h,k)$ divides a line segment between the axes in the ratio\[1:2\]. Find the equation of the line.

Ans.Consider, \[{\text{AB}}\]be the line segment such that $r(h,k)$ divides it in the ratio \[1:2.\]

Then, the coordinates of ${\text{A}}$ and ${\text{B}}$ be $(0,y)$ and $(x,0)$ respectively.

By section formula,

$(h,k) = \left( {\dfrac{{1 \times 0 + 2 \times x}}{{1 + 2}},\dfrac{{1 \times y + 2 \times 0}}{{1 + 2}}} \right)$

$ \Rightarrow (h,k) = \left( {\dfrac{{2x}}{3},\dfrac{y}{3}} \right)$

$ \Rightarrow h = \dfrac{{2x}}{3}$ and $k = \dfrac{y}{3}$

$ \Rightarrow x = \dfrac{{3h}}{2}$ and $y = 3k$

Thus, the respective coordinates of ${\text{A}}$ and ${\text{B}}$ are $\left( {\dfrac{{3h}}{2},0} \right)$ and $(0,3k)$.

Now, the equation of the line AB passing through points $\left( {\dfrac{{3h}}{2},0} \right)$ and $(0,3k)$ is,$(y - 0) = \dfrac{{3k - 0}}{{0 - \dfrac{{3h}}{2}}}\left( {x - \dfrac{{3h}}{2}} \right)$

$y =  - \dfrac{{2k}}{h}\left( {x - \dfrac{{3h}}{2}} \right)$

$hy =  - 2kx + 3hk$

Rewrite the equation,

$2kx + hy = 3hk$

Therefore, the equation of the line is $2kx + hy = 3hk$.

19.By using the concept of equation of a line, prove that the three points $(3,0),\,\,( - 2, - 2)$ and $(8,2)$ are collinear.

Ans.It is necessary to show that the line passing through points $(3,0)$ and $( - 2, - 2)$ also passes through point $(8,2)$in order to show that the points $(3,0),( - 2, - 2)$ and $(8,2)$ are collinear.

The equation of the line passing through points $(3,0)$ and $( - 2, - 2)$ is,

$(y - 0) = \dfrac{{( - 2 - 0)}}{{( - 2 - 3)}}(x - 3)$

$y = \dfrac{{ - 2}}{{ - 5}}(x - 3)$

Cross multiply and expand bracket,

$5y = 2x - 6$

Rewrite the equation,

$2{\text{x}} - 5{\text{y}} = 6$

At $x = 8$ and $y = 2$,

$2 \times 8 - 5 \times 2 = 16 - 10 $

$= 6$

Thus, the line passing through points $(3,0)$ and $( - 2, - 2)$ also passes through point $(8,2)$.

Therefore, the points $(3,0),( - 2, - 2)$, and $(8,2)$ are collinear.

Exercise 9.3

1.Reduce the following equation into slope-intercept form and find their slopes and the \[y\]-intercepts.

(i) $x + 7y = 0$

Ans.Given that, the equation is $x + 7y = 0$

Slope - intercept form is represented as $y = mx + c$, where $m$ is the slope and $c$ is the \[y\] Intercept.

Now, the equation can be expressed as,

$y = \dfrac{{ - 1}}{{7x}} + 0$

Therefore, the above equation is of the form $y = mx + c$, where \[m = \dfrac{{ - 1}}{7}\] and $c = 0$.

(ii) $6x + 3y - 5 = 0$

Ans.Given that, the equation is $6x + 3y - 5 = 0$

Slope - intercept form is represented as $y = mx + c$, where $m$ is the slope and $c$ is the \[y\]intercept.

Now, the equation can be expressed as,

$3y =  - 6x + 5$

$y = \dfrac{{ - 6}}{{3x}} + \dfrac{5}{3}$

$ =  - 2x + \dfrac{5}{3}$

Therefore, the above equation is of the form $y = mx + c$, where $m =  - 2$ and $c = \dfrac{5}{3}$.

(iii) $y = 0$

Ans.Given that, the equation is $y = 0$

Slope - intercept form is given by $y = mx + c$, where $m$ is the slope and $c$ is the y intercept.

Then, $y = 0 \times x + 0$

Therefore, the above equation is of the form $y = mx + c$, where $m = 0$ and $c = 0$.

2.Reduce the following equations into intercept form and find their intercepts on the axes.

(i) $3x + 2y - 12 = 0$

Ans.Given that, the equation is $3x + 2y - 12 = 0$

Rewrite the equation,

$3x + 2y = 12$

Divide both sides by \[12\],

$\dfrac{{3x}}{{12}} + \dfrac{{2y}}{{12}} = 1$

$\dfrac{x}{4} + \dfrac{y}{6} = 1$

This equation is of the form $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where $a = 4$ and $b = 6$. 

Therefore, the equation is in the intercept form, where the intercepts on the $x$ and $y$ axes are \[4\]and \[6\]respectively.

(ii) $4x - 3y = 6$

Ans.Given that, the equation is $4x - 3y = 6$

Divide both sides by \[6\],

$\dfrac{{4x}}{6} - \dfrac{{3y}}{6} = 1$

$\dfrac{{2x}}{3} - \dfrac{y}{2} = 1$

$\dfrac{x}{{\left( {\dfrac{3}{2}} \right)}} + \dfrac{y}{{( - 2)}} = 1$

Therefore, the equation is in the intercept form, where the intercepts on $x$ and \[y\]axes are $\dfrac{3}{2}$ and $ - 2$ respectively.

(iii) $3y + 2 = 0$

Ans.Given that, the equation is $3y + 2 = 0$

Rewrite the equation,

$3y =  - 2$

Divide both sides by $ - 2$,

$ \Rightarrow \dfrac{y}{{\left( { - \dfrac{2}{3}} \right)}} = 1$

Now, equation is in the form $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where $a = 0$ and $b =  - \dfrac{2}{3}$. 

Therefore, the equation is in the intercept form, where the intercept on the \[y\]-axis is $ - \dfrac{2}{3}$ and it has no intercept on the $x$-axis.

3. Find the distance of the points $( - 1,1)$ from the line $12(x + 6) = 5(y - 2)$.

Ans.Given that, the equation of the line is $12(x + 6) = 5(y - 2)$

Expand brackets,

$ \Rightarrow 12x + 72 = 5y - 10$

Rewrite the equation,

$ \Rightarrow 12x - 5y + 82 = 0$

When comparing this equation with general equation of line $Ax + By + C = 0$, we get

$A = 12$, $B =  - 5$, and $C = 82$

We know that the perpendicular distance (\[{\text{d}}\]) of a line$Ax + By + C = 0$ from a point 

$\left( {{x_1},{y_1}} \right)$ is, 

${\text{d}} = \dfrac{{\left| {{\text{A}}{{\text{x}}_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

The given point is $\left( {{x_1},{y_1}} \right) = ( - 1,1)$. 

Thus, the distance of point $( - 1,1)$ from the given line is,

$\dfrac{{|12( - 1) + ( - 5)(1) + 82|}}{{\sqrt {{{(12)}^2} + {{( - 5)}^2}} }}$ units 

$ = \dfrac{{| - 12 - 5 + 82|}}{{\sqrt {169} }}$ units 

$ = \dfrac{{|65|}}{{13}}$ units 

$ = 5$ units

Therefore, the distance of the points $( - 1,1)$ from the line $12(x + 6) = 5(y - 2)$ is $5$ units.

4. Find the points on the ${\text{x}}$-axis whose distance from the line $\dfrac{x}{3} + \dfrac{y}{4} = 1$ are \[4\] units.

Ans.Given that, the equation of line is $\dfrac{x}{3} + \dfrac{y}{4} = 1$

It can be write as $4x + 3y - 12 = 0$

When comparing this equation with general equation of line $Ax + By + C = 0$, we get

$A = 4,\;\,\,B$ $ = 3$, and $C =  - 12$

Let $(a,0)$ be the point on the $x$-axis whose distance from the given line is \[4\] units. 

We know that the perpendicular distance (\[{\text{d}}\]) of a line $Ax + By + C = 0$ from a point 

$\left( {{x_1},{y_1}} \right)$ is ${\text{d}} = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Thus, $4 = \dfrac{{|4a + 3 \times 0 - 12|}}{{\sqrt {{4^2} + {3^2}} }}$

$ \Rightarrow 4 = \dfrac{{|4a - 12|}}{5}$

$ \Rightarrow |4a - 12| = 20$

$ \Rightarrow  \pm (4a - 12) = 20$

$ \Rightarrow (4a - 12) = 20$ or $ - (4a - 12) = 20$

$ \Rightarrow 4a = 20 + 12$ or $4a =  - 20 + 12$

$ \Rightarrow a = 8$ or $ - 2$

Therefore, the required points on $x$-axis are $( - 2,0)$ and $(8,0)$.

5. Find the distance between parallel lines

(i) $15x + 8y - 34 = 0$ and $15x + 8y + 31 = 0$

Ans.We know that the distance(\[{\text{d}}\]) between parallel lines $Ax + By + {C_1} = 0$ and 

$Ax + By + {C_2} = 0$ is,

 $d = \dfrac{{\left| {{C_1} - {C_2}} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

The given parallel lines are $15x + 8y - 34 = 0$ and $15x + 8y + 31 = 0$ 

Here, $A = 15,\;\,B = 8,\,\,{C_1} =  - 34$, and ${C_2} = 31$.

Thus, the distance between the parallel lines is,

$d = \dfrac{{\left| {{C_1} - {C_2}} \right|}}{{\sqrt {{A^2} + {B^2}} }} = \dfrac{{| - 34 - 31|}}{{\sqrt {{{(15)}^2} + {{(8)}^2}} }}$ units 

$ = \dfrac{{| - 65|}}{{\sqrt {289} }}$ units 

$ = \dfrac{{65}}{{17}}$ units

Therefore, the distance between parallel lines $15x + 8y - 34 = 0$ and $15x + 8y + 31 = 0$ is 

$\dfrac{{65}}{{17}}$ units.

(ii) $l(x + y) + p = 0$ and $l(x + y) - r = 0$

Ans.The given parallel lines are $l(x + y) + p = 0$ and $l(x + y) - r = 0$

It can be write as,

$lx + ly + p = 0$ and $lx + ly - r = 0$

Here, $A = l,\;\,B = l,\,\,{C_1} = p$, and ${C_2} =  - r$.

Thus, the distance between the parallel lines is,

$d = \dfrac{{\left| {{C_1} - {C_2}} \right|}}{{\sqrt {{A^2} + {B^2}} }} = \dfrac{{|p + r|}}{{\sqrt {{l^2} + {l^2}} }}$ units 

$ = \dfrac{{|p + r|}}{{\sqrt {2{l^2}} }}$ units 

$ = \dfrac{{|p + r|}}{{l\sqrt 2 }}$ units 

$ = \dfrac{1}{{\sqrt 2 }}\dfrac{{|p + r|}}{l}$ units

Therefore, the distance between parallel lines $l(x + y) + p = 0$ and $l(x + y) - r = 0$

is $\dfrac{1}{{\sqrt 2 }}\dfrac{{|p + r|}}{l}$ units.

6. Find equation of the line parallel to the line $3x - 4y + 2 = 0$ and passing through the point $( - 2,3)$.

Ans.Here, the equation of the given line is $3x - 4y + 2 = 0$

Rewrite as,

$y = \dfrac{{3x}}{4} + \dfrac{2}{4}$

This can be write as,

$y = \dfrac{3}{4}x + \dfrac{1}{2}$ , which is of the form $y = mx + c$

Now, slope of the given line $ = \dfrac{3}{4}$ 

It is known that parallel lines have the same slope.

Thus, slope of the other line ${\text{is }}m = \dfrac{3}{4}$ 

Now, the equation of the line which has a slope of $\dfrac{3}{4}$ and passes through the points 

$( - 2,3)$ is,

$(y - 3) = \dfrac{3}{4}\{ x - ( - 2)\} $

Cross multiply and expand brackets,

$4y - 12 = 3x + 6$

Rewrite as,

$3x - 4y + 18 = 0$

Therefore, the equation of the line parallel to the line $3x - 4y + 2 = 0$ and passing 

through the point $( - 2,3)$ is $3x - 4y + 18 = 0$.

7. Find the equation of the line perpendicular to the line $x - 7y + 5 = 0$ and having $x$ intercept \[3.\]

Ans.The given equation of the line is $x - 7y + 5 = 0$.

It can be write as,

$y = \dfrac{1}{7}x + \dfrac{5}{7}$, which is of the form $y = mx + c$

Now, Slope of the given line $ = \dfrac{1}{7}$ 

The slope of the line perpendicular to the line having a slope of $\dfrac{1}{7}$ is,

$m =  - \dfrac{1}{{\left( {\dfrac{1}{7}} \right)}} =  - 7$

The equation of the line with slope $ - 7$ and $x$-intercept \[3\] is,

$y = m(x - d)$

Substitute the values,

$ \Rightarrow y =  - 7(x - 3)$

Expand bracket,

$ \Rightarrow y =  - 7x + 21$

$ \Rightarrow 7x + y = 21$

Therefore, the equation of the line perpendicular to the line $x - 7y + 5 = 0$ and having $x$

intercept \[3\] is $7x + y = 21$.

8. Find angles between the lines $\sqrt 3 x + y = 1$ and $x + \sqrt 3 y = 1$.

Ans.The given lines are $\sqrt 3 x + y = 1$ and $x + \sqrt 3 y = 1$ 

Consider the first line,

$\sqrt 3 x + y = 1$ can be write as,

$y =  - \sqrt 3 x + 1$ 

The slope of this line is ${m_1} =  - \sqrt 3 $.

Now, consider the second line,

$x + \sqrt 3 y = 1$ can be write as,

$y = \dfrac{1}{{\sqrt 3 }}x + \dfrac{1}{{\sqrt 3 }}$

The slope of this line is ${m_2} =  - \dfrac{1}{{\sqrt 3 }}$. 

The acute angle that is, $\theta $ between the two lines is,

$\tan \theta  = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$

Substitute the values,

$\tan \theta  = \left| {\dfrac{{ - \sqrt 3  + \dfrac{1}{{\sqrt 3 }}}}{{1 + ( - \sqrt 3 )\left( { - \dfrac{1}{{\sqrt 3 }}} \right)}}} \right|$

$\tan \theta  = \left| {\dfrac{{\dfrac{{ - 3 + 1}}{{\sqrt 3 }}}}{{1 + 1}}} \right| $

 $\tan \theta  = \left| {\dfrac{{ - 2}}{{2 \times \sqrt 3 }}} \right|$

$\tan \theta  = \dfrac{1}{{\sqrt 3 }}$

$\theta  = {30^\circ }$

Thus, the angle between the lines $\sqrt 3 x + y = 1$ and $x + \sqrt 3 y = 1$ is either ${30^\circ }$ or 

${180^\circ } - {30^\circ } = {150^\circ }$.

9. The line through the points $(h,3)$ and $(4,1)$ intersects the line $7x - 9y - 19 = 0$At right angle. Find the value of $h$.

Ans.The slope of the line passing through points $(h,3)$ and $(4,1)$ is,

${m_1} = \dfrac{{1 - 3}}{{4 - h}} $

$= \dfrac{{ - 2}}{{4 - h}} $

Given that, the line $7x - 9y - 19 = 0$  

It can be write as,

$y = \dfrac{7}{9}x - \dfrac{{19}}{9}$ 

The slope off this line is,

${m_2} = \dfrac{7}{9}$.

It is given that the two lines are perpendicular. 

Then,  ${m_1} \times {m_2} =  - 1$

Substitute the values,

$ \Rightarrow \dfrac{{ - 14}}{{36 - 9h}} =  - 1$

Cross multiply,

$ \Rightarrow 14 = 36 - 9h$

Rewrite as,

$ \Rightarrow 9h = 36 - 14$

$ \Rightarrow h = \dfrac{{22}}{9}$

Therefore, the value of $h$ is $\dfrac{{22}}{9}$.

10. Prove that the line through the point $\left( {{x_1},{y_1}} \right)$ and parallel to the line $Ax + By + C = 0$ is $A\left( {x - {x_1}} \right) + B\left( {y - {y_1}} \right) = 0$

Ans.One of the line is $Ax + By + C = 0$  

Then, $y = \left( {\dfrac{{ - A}}{B}} \right)x + \left( {\dfrac{{ - C}}{B}} \right)$ 

The slope of this line is,

 $m =  - \dfrac{A}{B}$

We know that parallel lines have the same slope.

Hence, Slope of the other line ${\text{is }}m =  - \dfrac{A}{B}$

The equation of the line passing through point $\left( {{x_1} - {y_1}} \right)$ and having a slope  $m =  - \dfrac{A}{B}$

is,

$y - {y_1} = m\left( {x - {x_1}} \right)$

Substitute the value of \[m\],

$y - {y_1} =  - \dfrac{A}{B}\left( {x - {x_1}} \right)$

Cross multiply,

$B\left( {y - {y_1}} \right) =  - A\left( {x - {x_1}} \right)$

Rewrite as,

$A\left( {x - {x_1}} \right) + B\left( {y - {y_1}} \right) = 0$

Therefore, the line through point $\left( {{x_1} - {y_1}} \right)$ and parallel to line $Ax + By + C = 0$ is 

$A\left( {x - {x_1}} \right) + B\left( {y - {y_1}} \right) = 0$.

11. Two lines passing through the points $(2,3)$ intersects each other at an angle of ${60^\circ }.$ If slope of one line is \[2\] , find equation of the other line.

Ans.Given that the slope of the first line is \[2\]

That is, ${m_1} = 2$. 

Assume that the slope of the other line is ${m_2}$. 

The angle between the two lines is ${60^\circ }$.

We have, $\tan {60^\circ } = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_2}{m_2}}}} \right|$

Substitute the known values,

$ \Rightarrow \sqrt 3  = \left| {\dfrac{{2 - {m_2}}}{{1 + 2{m_2}}}} \right|$

$ \Rightarrow \sqrt 3  =  \pm \left( {\dfrac{{2 - {m_2}}}{{1 + 2{m_2}}}} \right)$

$ \Rightarrow \sqrt 3  = \dfrac{{2 - {m_2}}}{{1 + 2{m_2}}}$  or  $\sqrt 3  =  - \left( {\dfrac{{2 - {m_2}}}{{1 + 2{m_2}}}} \right)$

$ \Rightarrow \sqrt 3 \left( {1 + 2{m_2}} \right) = 2 - {m_2}$  or  $\sqrt 3 \left( {1 + 2{m_2}} \right) =  - \left( {2 - {m_2}} \right)$

$ \Rightarrow \sqrt 3  + 2\sqrt 3 {m_2} + {m_2} = 2$  or  $\sqrt 3  + 2\sqrt 3 {m_2} - {m_2} =  - 2$

$ \Rightarrow \sqrt 3  + (2\sqrt 3  + 1){m_2} = 2$  or  $\sqrt 3  + (2\sqrt 3  - 1){m_2} =  - 2$

$ \Rightarrow {m_2} = \dfrac{{2 - \sqrt 3 }}{{(2\sqrt 3  + 1)}}$  or  ${m_2} = \dfrac{{ - (2 + \sqrt 3 )}}{{(2\sqrt 3  - 1)}}$

Case 1:

${m_2} = \left( {\dfrac{{2 - \sqrt 3 }}{{(2\sqrt 3  + 1)}}} \right)$

The equation of the line passing through point $(2,3)$ and having a slope of $\dfrac{{2 - \sqrt 3 }}{{(2\sqrt 3  + 1)}}$ is,

$(y - 3) = \dfrac{{(2 - \sqrt 3 )}}{{(2\sqrt 3  + 1)}}(x - 2)$

$(2\sqrt 3  + 1)y - 3(2\sqrt 3  + 1) = (2 - \sqrt 3 )x - (2 - \sqrt 3 )2$

$(\sqrt 3  - 2)x + (2\sqrt 3  + 1)y =  - 4 + 2\sqrt 3  + 6\sqrt 3  + 3$

$(\sqrt 3  - 2)x + (2\sqrt 3  + 1)y =  - 1 + 8\sqrt 3 $

Now, the equation of the other line is $(\sqrt 3  - 2)y + (2\sqrt 3  + 1)y =  - 1 + 8\sqrt 3 $.

Case 2:

${m_2} = \dfrac{{ - (2 + \sqrt 3 )}}{{(2\sqrt 3  - 1)}}$

The equation of the line passing through points $(2,3)$ and having a slope of $\dfrac{{ - (2 + \sqrt 3 )}}{{(2\sqrt 3  - 1)}}$ is,

$(y - 3) = \dfrac{{ - (2 + \sqrt 3 )}}{{(2\sqrt 3  - 1)}}(x - 2)$

$(2\sqrt 3  - 1)y - 3(2\sqrt 3  - 1) =  - (2\sqrt 3  - 1)x + 2(2\sqrt 3  - 1)$

$(2\sqrt 3  - 1)y + (2\sqrt 3  - 1)x = 4 + 2\sqrt 3  + 6\sqrt 3  - 3$

$(2 + \sqrt 3 )x + (2\sqrt 3  - 1)y = 1 + 8\sqrt 3 $

Now, the equation of the other line is $(2 + \sqrt 3 )x + (2\sqrt 3  - 1)y = 1 + 8\sqrt 3 $.

Therefore, the required equation of the other line is $(\sqrt 3  - 2)x + (2\sqrt 3  + 1)y =  - 1 + 8\sqrt 3 $ or 

$(2 + \sqrt 3 )x + (2\sqrt 3  - 1)y = 1 + 8\sqrt 3 $.

12. Find the equation of the right bisector of the line segment joining the points $(3,4)$ and $( - 1,2)$.

Ans.The right bisector of a line segment bisects the line segment at an angle ${90^\circ }$. 

The end-points of the line segment are given as ${\text{A}}(3,4)$ and ${\text{B}}( - 1,2)$. 

Now, mid-point of ${\text{AB}} = \left( {\dfrac{{3 - 1}}{2},\dfrac{{4 + 2}}{0}} \right) = (1,3)$

Slope of ${\text{AB}} =  = \dfrac{{2 - 4}}{{ - 1 - 3}} = \dfrac{{ - 2}}{{ - 4}} = \dfrac{1}{2}$

Thus, Slope of the line perpendicular to ${\text{AB}} =  - \dfrac{1}{{\left( {\dfrac{1}{2}} \right)}} =  - 2$ 

The equation of the line passing through $(1,3)$ and having a slope of $ - 2$ is,

$(y - 3) =  - 2(x - 1)$

Expand bracket,

$y - 3 =  - 2x + 2$

$2x + y = 5$

Therefore, the equation of the right bisector of the line segment joining the points $(3,4)$ 

and $( - 1,2)$ is $2x + y = 5$.

13. Find the coordinates of the foot of perpendicular from the points $( - 1,3)$ to the line $3x - 4y - 16 = 0$.

Ans.Let $(a,b)$ be the coordinates of the foot of the perpendicular from the points $( - 1,3)$ 

to the line$3x - 4y - 16 - 0$.

Slope of the line joining $( - 1,3)$ and $(a,b)$ is,

${m_1} = \dfrac{{b - 3}}{{a + 1}}$

$3x - 4y - 16 = 0$ can be write as,

$y = \dfrac{3}{4}x - 4$

Slope of the line is,

${m_2} = \dfrac{3}{4}$

Since these two lines are perpendicular, 

${m_1}{m_2} =  - 1$ $\left( {\dfrac{{b - 3}}{{a + 1}}} \right) \times \left( {\dfrac{3}{4}} \right) =  - 1$

$ \Rightarrow \dfrac{{3b - 9}}{{4a + 4}} =  - 1$

$ \Rightarrow 3b - 9 =  - 4a - 4$

$ \Rightarrow 4a + 3b = 5 \to (1)$

Point $(a,b)$ lies on line $3x - 4y = 16$.

Rewrite as,

$3a - 4\;b = 16 \to (2)$

Solving equations \[\left( 1 \right)\] and \[\left( 2 \right),\] 

We get $a = \dfrac{{68}}{{25}}$ and $b =  - \dfrac{{49}}{{25}}$

Therefore, the required coordinates of the foot of the perpendicular are $\left( {\dfrac{{68}}{{25}}, - \dfrac{{49}}{{25}}} \right)$.

14. The perpendicular from the origin to the line $y = mx + c$ meets it at the point $( - 1,2)$. Find the values of $m$ and $c$.

Ans.The given equation of line is $y = mx + c$. 

It is also given that the perpendicular from the origin meets the given line at $( - 1,2)$. 

Then, the line joining the points $(0,0)$ and $( - 1,2)$ is perpendicular to the given line.

Now, slope of the line joining $(0,0)$ and $( - 1,2) = \dfrac{2}{{ - 1}} =  - 2$ 

The slope of the given line is $m$.

 $\therefore m \times  - 2 =  - 1\quad $ (The two lines are perpendicular )

$ \Rightarrow m = \dfrac{1}{2}$

Since points $( - 1,2)$ lies on the given line, it satisfies the equation $y = mx + c$.

$2 = m( - 1) + c$

$ \Rightarrow 2 = 2 + \dfrac{1}{2}( - 1) + c$

$ \Rightarrow c = 2 + \dfrac{1}{2} = \dfrac{5}{2}$

Therefore, the values of $m$ and $c$ are $\dfrac{1}{2}$ and $\dfrac{5}{2}$ respectively.

15. If $p$ and $q$ are the lengths of perpendicular from the origin to the lines $x\cos \theta  - y\sin \theta  = k$ $\cos 2\theta $ and $x\sec \theta  + y\operatorname{cosec} \theta  = k$, respectively, prove that  ${p^2} + 4{q^2} = {k^2}$

Ans.The equation of given lines are,

$x\cos \theta  - y\sin \theta  = k\cos 2\theta  \to (1)$ 

$x\sec \theta  + y\operatorname{cosec} \theta  = k \to (2)$

The perpendicular distance \[\left( d \right)\]of a line $Ax + By + C = 0$ from a point $\left( {{x_1},{x_2}} \right)$ is,$d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Compare equation \[\left( 1 \right)\] to the general equation of line that is., $Ax + By + C = 0$, 

We get  $A = \cos \theta ,\,\,B =  - \sin \theta $, and $C =  - k\cos 2\theta $

It is given that $p$ is the length of the perpendicular from $(0,0)$ to line \[\left( 1 \right).\]

$\therefore p = \dfrac{{|A(0) + B(0) + C|}}{{\sqrt {{A^2} + {B^2}} }} $

$= \dfrac{{|C|}}{{\sqrt {{A^2} + {B^2}} }} $

$= \dfrac{{| - k\cos 2\theta |}}{{\sqrt {{{\cos }^2}\theta  + {{\sin }^2}\theta } }} $

$= | - k\cos 2\theta | \to (3) $

Compare equation \[\left( 2 \right)\]to the general equation of line that is, $Ax + By + C = 0$, 

We get $A = \sec \theta ,\,\,B = \operatorname{cosec} \theta $, and $C =  - k$.

It is given that ${\text{q}}$ is the length of the perpendicular from $(0,0)$ to line \[\left( 2 \right).\]

$\therefore q = \dfrac{{|A(0) + B(0) + C|}}{{\sqrt {{A^2} + {B^2}} }} $

$= \dfrac{{|C|}}{{\sqrt {{A^2} + {B^2}} }} $

$= \dfrac{{| - k|}}{{\sqrt {{{\sec }^2}\theta  + \cos e{c^2}\theta } }} \to (4) $

From \[\left( 3 \right)\]and\[\left( 4 \right)\], we have

${p^2} + 4{q^2} = {(| - k\cos 2\theta |)^2} + 4{\left( {\dfrac{{| - k|}}{{\sqrt {{{\sec }^2}\theta  + \cos e{c^2}\theta } }}} \right)^2}$

$ = {k^2}{\cos ^2}2\theta  + \dfrac{{4{k^2}}}{{\left( {{{\sec }^2}\theta  + \cos e{c^2}\theta } \right)}}$

$ = {k^2}{\cos ^2}2\theta  + \dfrac{{4{k^2}}}{{\left( {\dfrac{1}{{{{\cos }^2}\theta }} + \dfrac{1}{{{{\sin }^2}\theta }}} \right)}}$

$ = {k^2}{\cos ^2}2\theta  + \dfrac{{4{k^2}}}{{\left( {\dfrac{{{{\sin }^2}\theta  + {{\cos }^2}\theta }}{{{{\sin }^2}\theta {{\cos }^2}\theta }}} \right)}}$

$ = {k^2}{\cos ^2}2\theta  + \dfrac{{4{k^2}}}{{\left( {\dfrac{1}{{{{\sin }^2}\theta {{\cos }^2}\theta }}} \right)}}$

$ = {k^2}{\cos ^2}2\theta  + 4{k^2}{\sin ^2}\theta {\cos ^2}\theta $

$ = {k^2}{\cos ^2}2\theta  + {k^2}{(2\sin \theta \cos \theta )^2}$

$ = {k^2}{\cos ^2}2\theta  + {k^2}{\sin ^2}2\theta $

$ = {k^2}\left( {{{\cos }^2}2\theta  + {{\sin }^2}2\theta } \right)$

$ = {k^2}$

Hence, it is proved that ${p^2} + 4{q^2} = {k^2}$.

16. In the triangle ${\text{ABC}}$ with vertices ${\text{A}}(2,3),\,\,{\text{B}}(4, - 1)$ and ${\text{C}}(1,2)$, find the equation and length of altitude from the vertex ${\text{A}}$.

Ans.Let \[{\text{AD}}\]be the altitude of triangle \[{\text{ABC}}\]from vertex ${\text{A}}$. 

So, \[{\text{AD}} \bot {\text{BC}}\]

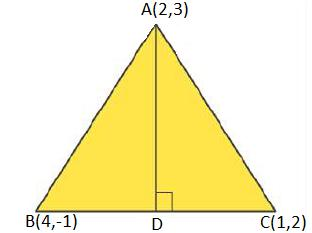
The equation of the line passing through point $(2,3)$ and having a slope of \[1\] is,

$(y - 3) = 1(x - 2)$

$ \Rightarrow x - y + 1 = 0$

$ \Rightarrow y - x = 1$

Thus, equation of the altitude from vertex ${\text{A is }}y - x = 1$.

Length of ${\text{AD}} = $ Length of the perpendicular from ${\text{A}}(2,3)$ to ${\text{BC}}$ 

The equation of ${\text{BC}}$ is,

$(y + 1) = \dfrac{{2 + 1}}{{1 - 4}}(x - 4)$

$ \Rightarrow (y + 1) =  - 1(x - 4)$

Open brackets,

$ \Rightarrow y + 1 =  - x + 4$

$ \Rightarrow x + y - 3 = 0 \to (1)$

The perpendicular distance \[\left( d \right)\] of a line $Ax + By + C = 0$ from a point $\left( {{x_1},{y_1}} \right)$ is,

 $d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Compare equation \[\left( 1 \right)\] to the general equation of line $Ax + By + C = 0$, 

We get, $A = 1$, $B = 1$, and $C =  - 3$.

$\therefore $ Length of ${\text{AD}} = \dfrac{{|1 \times 2 + 1 \times 3 - 3|}}{{\sqrt {{1^2} + {1^2}} }}$ units 

$ = \dfrac{{|2|}}{{\sqrt 2 }}$ units 

$ = \dfrac{2}{{\sqrt 2 }}$ units 

$ = \sqrt 2 $ units

Therefore, the equation and length of the altitude from vertex ${\text{A}}$ are $y - x = 1$ and $\sqrt 2 $ 

units respectively.

17. If $p$ is the length of perpendicular from the origin to the line whose intercepts on the axes are$a$, and $b$, then show that $\dfrac{1}{{{p^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$.

Ans.The equation of a line whose intercepts on the axes are \[a\] and $b$ is,

 $\dfrac{x}{a} + \dfrac{y}{b} = 1$

Or $bx + ay = ab$

Or $bx + ay - ab = 0 \to (1)$

The perpendicular distance \[\left( d \right)\]of a line $Ax + By + C = 0$ from a point $\left( {{x_1},{y_1}} \right)$ is,

$d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Compare equation \[\left( 1 \right)\]to the general equation of line $Ax - By + C = 0$, 

We get, $A = b$, $B = a$, and $C =  - ab$.

Thus, if $p$ is the length of the perpendicular from point $\left( {{x_1},{y_1}} \right) = (0,0)$ to line\[\left( 1 \right)\], 

We get, $p = \dfrac{{|A(0) + B(0) - ab|}}{{\sqrt {{b^2} + {a^2}} }}$

$ \Rightarrow p = \dfrac{{| - ab|}}{{\sqrt {{b^2} + {a^2}} }}$

Square both sides, 

${p^2} = \dfrac{{{{( - ab)}^2}}}{{{a^2} + {b^2}}}$

$ \Rightarrow {p^2}\left( {{a^2} + {b^2}} \right) = {a^2}{b^2}$

$ \Rightarrow \dfrac{{{a^2} + {b^2}}}{{{a^2}{b^2}}} = \dfrac{1}{{{p^2}}}$

$ \Rightarrow \dfrac{1}{{{p^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$

Hence, it is shown that $\dfrac{1}{{{p^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$.

Miscellaneous Exercise

1. Find the value of ${\text{k}}$ for which the line $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$ is

(a) Parallel to $x$-axis

Ans.The given equation of line is $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$

If the line is parallel to $x$-axis,

Slope of the line \[ = \] Slope of the $x$-axis

It can be written as,

$\left( {4 - {k^2}} \right)y = (k - 3)x + {k^2} - 7k + 6 = 0$

We get,

$y = \dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}x + \dfrac{{{k^2} - 7k + 6}}{{\left( {4 - {k^2}} \right)}}$, Which is of the form $y = mx + c$

Here, the slope of the given line$ = \dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}$

Consider the slope of $x$-axis $ = 0$

$\dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}} = 0$

$k - 3 = 0$

$k = 3$

Therefore, if the given line is parallel to the $x$-axis, then the value of $k$ is \[3\] .

(b) Parallel to $y$-axis

Ans.The given equation of line is $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$

Here if the line is parallel to the \[y\]-axis, it is vertical and the slope will be undefined.

So, the slope of the given line$ = \dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}$

Here, $\dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}$ is undefined at ${k^2} = 4$

${k^2} = 4$

$ \Rightarrow k =  \pm 2$

Therefore, if the given line is parallel to the $y$-axis, then the value of $k$ is $ \pm 2$.

(c) Passing through the origin.

Ans.The given equation of line is $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$

Here, if the line is passing through $(0,0)$ which is the origin satisfies the given equation 

of line,

$(k - 3)(0) - \left( {4 - {k^2}} \right)(0) + {k^2} - 7k + 6 = 0$

${k^2} - 7k + 6 = 0$

Separate the terms,

${k^2} - 6k - k + 6 = 0$

$(k - 6)(k - 1) = 0$

$k = 1\,\,{\text{or }}\,{\text{6}}$ 

Therefore, if the given line is passing through the origin, then the value of $k$ is either 

$1\,\,{\text{or }}\,{\text{6}}$.

2. Find the equation of the line, which cut-off intercepts on the axes whose sum and product are \[1\]and $ - 6$, respectively.

Ans.Consider, the intercepts cut by the given lines on the axes are \[a\]and \[b.\]

$a + b = 1 \to (1)$ (1)

$ab =  - 6 \to (2)$

Solve both the equations to get

$a = 3$ and $b =  - 2$ or $a =  - 2$ and $b = 3$

We know that the equation of the line whose intercepts on a and $b$ axes is

$\dfrac{x}{a} + \dfrac{y}{b} = 1$ or $bx + ay - ab = 0$

Case 1: $a = 3$ and $b =  - 2$

Now, the equation of the line is $ - 2x + 3y + 6 = 0$

That is, $2x - 3y = 6$

Case 2: $a =  - 2$ and $b = 3$

Now, the equation of the line is $3x - 2y + 6 = 0$

That is,$ - 3x + 2y = 6$

Therefore, the required equation of the lines are $2x - 3y = 6$ and $ - 3{\text{x}} + 2{\text{y}} = 6$.

3. What are the points on the $y$-axis whose distance from line $\dfrac{x}{3} + \dfrac{y}{4} = 1$ is \[4\] units.

Ans.Consider $(0,b)$ as the point on the $y$-axis whose distance from line $\dfrac{x}{3} + \dfrac{y}{4} = 1$ is  4 units.

It can be written as \[4x + 3y - 12 = 0 \to (1)\]

Compare equation \[\left( 1 \right)\] to the general equation of line $Ax + Bx + C = 0$, we get

$A = 4,\;\,B = 3$ and $C =  - 12$

We know that the perpendicular distance \[\left( d \right)\] of a line $Ax + By + C = 0$ from $\left( {{x_1},{y_1}} \right)$ is,

$d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

If $(0,b)$ is the point on the $y$-axis whose distance from line $\dfrac{x}{3} + \dfrac{y}{4} = 1$  is \[4\] units, then

$4 = \dfrac{{|4(0) + 3(b) - 12|}}{{\sqrt {{4^2} + {3^2}} }}$

$4 = \dfrac{{|3b - 12|}}{5}$

By cross multiplication,

$20 = |3b - 12|$

$20 =  \pm (3b - 12)$

Here, $20 = (3b - 12)$ or $20 =  - (3b - 12)$

It can be written as

$3b = 20 + 12$ or $3b =  - 20 + 12$

Now we get,

$b = \dfrac{{32}}{3}$ or $b = \dfrac{{ - 8}}{3}$

Therefore, the required points are $b = \dfrac{{32}}{3}$ and $b = \dfrac{{ - 8}}{3}$.

4. Find the perpendicular distance from the origin to the line joining the points $(\cos \theta ,\sin \theta )\operatorname{and} (\cos \phi ,\sin \phi )$

Ans.The equation of the line joining the points $(\cos \theta ,\sin \theta )$ and $(\cos \phi ,\sin \phi )$ is,

$(\cos \theta ,\sin \theta )\operatorname{and} (\cos \phi ,\sin \phi )$

$y - \sin \theta  = \dfrac{{\sin \phi  - \sin \theta }}{{\cos \phi  - \cos \theta }}(x - \cos \theta )$

By cross multiplication,

$y(\cos \phi  - \cos \theta ) - \sin \theta (\cos \phi  - \cos \theta ) = x(\sin \phi  - \sin \theta ) - \cos \theta (\sin \phi  - \sin \theta )$

$x(\sin \theta  - \sin \phi ) + y(\cos \phi  - \cos \theta ) + \cos \theta \sin \phi  - \cos \theta \sin \theta  - \sin \theta \cos \phi  + \sin \theta \cos \theta  = 0$

$x(\sin \theta  - \sin \phi ) + y(\cos \phi  - \cos \theta ) + \sin (\phi  - \theta ) = 0$

$Ax + By + C = 0$, where $A = \sin \theta  - \sin \phi ,B = \cos \phi  - \cos \theta $, and $C = \sin (\phi  - \theta )$

It is known that the perpendicular distance \[\left( d \right)\]of a line $Ax + By + C = 0$ from a point 

$\left( {{x_1},{y_1}} \right)$ is,

$d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Thus, the perpendicular distance \[\left( d \right)\] of the given line from point $\left( {{x_1},{y_1}} \right) = (0,0)$ is,

$d = \dfrac{{|(\sin \theta  - \sin \phi )(0) + (\cos \phi  - \cos \theta )(0) + \sin (\phi  - \theta )|}}{{\sqrt {{{(\sin \theta  - \sin \phi )}^2} + {{(\cos \phi  - \cos \theta )}^2}} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {{{\sin }^2}\theta  + {{\sin }^2}\phi  - 2\sin \theta \sin \phi  + {{\cos }^2}\phi  + {{\cos }^2}\theta  - 2\cos \phi \cos \theta } }}$

Group the terms,

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {\left( {{{\sin }^2}\theta  + {{\cos }^2}\theta } \right) + \left( {{{\sin }^2}\phi  + {{\cos }^2}\phi } \right) - 2(\sin \theta \sin \phi  + \cos \phi \cos \theta )} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {1 + 1 - 2(\cos (\phi  - \theta ))} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {2(1 - \cos (\phi  - \theta ))} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {2\left( {2{{\sin }^2}\left( {\dfrac{{\phi  - \theta }}{2}} \right)} \right)} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{2\sin \left( {\dfrac{{\phi  - \theta }}{2}} \right)}}$

Therefore, the perpendicular distance from the origin to the line joining the points 

$(\cos \theta ,\sin \theta )\operatorname{and} (\cos \phi ,\sin \phi )$is $\dfrac{{|\sin (\phi  - \theta )|}}{{2\sin \left( {\dfrac{{\phi  - \theta }}{2}} \right)}}$.

5.Find the equation of the line parallel to $y$-axis and draw through the point of intersection of the lines $x - 7y + 5 = 0$ and $3x + y = 0$.

Ans.The equation of any line parallel to the \[y\]-axis is of the form $x = a \to (1)$

The two given lines are $x - 7y + 5 = 0 \to (2)$

$3x + y = 0 \to (3)$

Solve equation \[\left( 2 \right)\] and \[\left( 3 \right)\], we get $x =  - \dfrac{5}{{22}}$ and $y = \dfrac{{15}}{{22}}$ 

Thus, $\left( { - \dfrac{5}{{22}},\dfrac{{15}}{{22}}} \right)$ is the point of intersection of lines $(2)$ and \[\left( 3 \right).\]

Since line $x = a$ passes through point $\left( { - \dfrac{5}{{22}},\dfrac{{15}}{{22}}} \right),\,\,$

$a =  - \dfrac{5}{{22}}$

Therefore, the required equation of the line is $x =  - \dfrac{5}{{22}}$.

6.Find the equation of a line drawn perpendicular to the line $\dfrac{x}{4} + \dfrac{y}{6} = 1$ through the point, where it meets the $y$-axis.

Ans.Here, the equation of the given line is $\dfrac{x}{4} + \dfrac{y}{6} = 1$ 

This equation can be written as $3x + 2y - 12 = 0$ 

Rewrite as,

$y = \dfrac{{ - 3}}{2}x + 6$, which is of the form $y = mx + c$

Now, Slope of the given line $ = \dfrac{{ - 3}}{2}$

$\therefore $ Slope of line perpendicular to the given line $ =  - \dfrac{1}{{\left( { - \dfrac{3}{2}} \right)}} = \dfrac{2}{3}$ 

Let the given line intersect the \[y\]-axis at $(0,y)$. 

Substitute $x$ with 0 in the equation of the given line, 

$\dfrac{y}{6} = 1 \Rightarrow y = 6$ 

$\therefore $ The given line intersects the \[y\]-axis at $(0,6)$. 

The equation of the line that has a slope of $\dfrac{2}{3}$ and passes through point $(0,6)$ is,$(y - 6) = \dfrac{2}{3}(x - 0)$

Cross multiply and expand brackets,

$3y - 18 = 2x$

$2x - 3y + 18 = 0$

Therefore, the required equation of the line is $2x - 3y + 18 = 0$.

7.Find the area of the triangle formed by the line $y - x = 0,\,\,x + y = 0$ and $x - k = 0$.

Ans.It is given that,

$y - x = 0 \to (1)$ 

$x + y = 0 \to (2)$

$x - k = 0 \to (3)$

Here, the point of intersection of lines \[\left( 1 \right)\]and \[\left( 2 \right)\] is,

$x = 0$ and $y = 0$

The point of intersection of lines $(2)$ and \[\left( 3 \right)\] is,

$x = k$ and $y =  - k$

The point of intersection of lines \[\left( 3 \right)\]and \[\left( 1 \right)\] is,

$x = k$ and $y = k$

Now, the vertices of the triangle formed by the three given lines are $(0,0),\,\,(k, - k)$ and 

$(k,k)$.

Here the area of triangle whose vertices are $\left( {{x_1},{y_1}} \right),\,\,\left( {{x_2},{y_2}} \right)$ and $\left( {{x_3},{y_3}} \right)$ is,

$\dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|$

So the area of triangle formed by the three given lines,

$ = \dfrac{1}{2}|0( - k - k) + k(k - 0) + k(0 + k)|$ square units

$ = \dfrac{1}{2}\left| {{k^2} + {k^2}} \right|$square units

We get,

$ = \dfrac{1}{2}\left| {2{k^2}} \right|$

$ = {k^2}$ square units

Therefore, the area of the triangle formed by the line $y - x = 0,\,\,x + y = 0$ and $x - k = 0$ is 

${k^2}$ square units.

8.Find the value of $p$ so that the three lines $3x + y - 2 = 0,\,\,px + 2y - 3 = 0$ and $2x - y - 3 = 0$ may intersect at one point.

Ans.It is given that,

$3x + y - 2 = 0 \to (1)$

$px + 2y - 3 = 0 \to (2)$

$2x - y - 3 = 0 \to (3)$

Solve equations \[\left( 1 \right)\] and \[\left( 3 \right)\] to get

$x = 1$ and $y =  - 1$

Here, the three lines intersect at one point and the point of intersection of lines \[\left( 1 \right)\] and

\[\left( 3 \right)\]will also satisfy line \[\left( 2 \right)\]

$p(1) + 2( - 1) - 3 = 0$

$ \Rightarrow p - 2 - 3 = 0$

$ \Rightarrow p = 5$

Therefore, the value of $p$ is \[5\].

9.If three lines whose equations are $y = {m_1}x + {c_1},\,\,y = {m_2}x + {c_2}$, and $y = {m_2}x + {c_2}$ are concurrent, then show that ${m_1}\left( {{c_2} - {c_3}} \right) + {m_2}\left( {{c_3} - {c_1}} \right) + {m_3}\left( {{c_1} - {c_2}} \right) = 0$.

Ans.It is given that,

$y = {m_1}x + {c_1} \to (1)$

$y = {m_2}x + {c_2} \to (2)$

$y = {m_3}x + {c_3} \to (3)$

Subtract equation \[\left( 1 \right)\]from \[\left( 2 \right)\],

$0 = \left( {{m_2} - {m_1}} \right)x + \left( {{c_2} - {c_1}} \right)$

$ \Rightarrow \left( {{m_1} - {m_2}} \right)x = {c_2} - {c_1}$

$x = \dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}}$

Substitute this value in equation \[\left( 1 \right)\] 

$y = {m_1}\left( {\dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}}} \right) + {c_1}$

Multiply the terms,

$y = \dfrac{{{m_1}{c_2} - {m_1}{c_1}}}{{{m_1} - {m_2}}} + {c_1}$

Take LCM,

$y = \dfrac{{{m_1}{c_2} - {m_1}{c_1} + {m_1}{c_1} - {m_2}{c_1}}}{{{m_1} - {m_2}}}$

$ \Rightarrow y = \dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}}$

Here,

$\left( {\dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}},\dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}}} \right)$ is the point of intersection of lines $(1)$ and \[\left( 2 \right)\]

Lines \[\left( 1 \right),{\text{ }}\left( 2 \right)\]and \[\left( 3 \right)\] are concurrent. So the point of intersection of lines \[\left( 1 \right)\] and \[\left( 2 \right)\]

 will satisfy equation \[\left( 3 \right)\].

$\dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}} = {m_3}\left( {\dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}}} \right) + {c_3}$

Multiply the terms and take LCM,

$\dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}} = \dfrac{{{m_3}{c_2} - {m_3}{c_1} + {c_3}{m_1} - {c_3}{m_2}}}{{{m_1} - {m_2}}}$

By cross multiplication,

${m_1}{c_2} - {m_2}{c_1} - {m_3}{c_2} + {m_3}{c_1} - {c_3}\;{m_1} + {c_3}\;{m_2} = 0$

Take out the common terms,

${m_1}\left( {{c_2} - {c_3}} \right) + {m_2}\left( {{c_3} - {c_1}} \right) + {m_3}\left( {{c_1} - {c_2}} \right) = 0$

Therefore, If three lines whose equations are $y = {m_1}x + {c_1},\,\,y = {m_2}x + {c_2}$, and $y = {m_2}x + {c_2}$ 

are concurrent, then ${m_1}\left( {{c_2} - {c_3}} \right) + {m_2}\left( {{c_3} - {c_1}} \right) + {m_3}\left( {{c_1} - {c_2}} \right) = 0$.

10.Find the equation of the line through the points $(3,2)$ which make an angle of ${45^\circ }$ with the line $x - 2y = 3$

Ans.Let the slope of the required line be ${m_1}$. 

The given line can be written as,

 $y = \dfrac{1}{2}x - \dfrac{3}{2}$, which is of the form $y = mx + c$

Now, slope of the given line is 

${m_2} = \dfrac{1}{2}$ 

It is given that the angle between the required line and line $x - 2y = 3$ is ${45^\circ }$. 

If $\theta $ is the acute angle between lines ${l_1}$ and ${l_2}$ with slopes ${m_1}$ and ${m_2}$ respectively, then

$\tan \theta  = \left| {\dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}} \right|$

${\text{Now, }}\tan {45^\circ } = \dfrac{{\left| {{m_2} - {m_1}} \right|}}{{1 + {m_1}{m_2}}}$

Substitute the values,

$ \Rightarrow 1 = \left| {\dfrac{{\dfrac{1}{2} - {m_1}}}{{1 + \dfrac{{{m_1}}}{2}}}} \right|$

Take LCM,

$ \Rightarrow 1 = \left| {\dfrac{{\left( {\dfrac{{1 - 2{m_1}}}{2}} \right)}}{{\dfrac{{2 + {m_1}}}{2}}}} \right|$

$ \Rightarrow 1 = \left| {\dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}} \right|$

$ \Rightarrow 1 =  \pm \left( {\dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}} \right)$

$ \Rightarrow 1 = \dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}$ or $1 =  - \left( {\dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}} \right)$

$ \Rightarrow 2 + {m_1} = 1 - 2{m_1}$ or $2 + {m_1} =  - 1 + 2{m_1}$

$ \Rightarrow {m_1} =  - \dfrac{1}{3}$ or ${m_1} = 3$

Case 1: ${m_1} = 3$ 

The equation of the line passing through $(3,2)$ and having a slope of \[3\] is,

$y - 2 = 3(x - 3)$

Expand bracket,

$y - 2 = 3x - 9$

$3x - y = 7$

Case 2: ${m_1} =  - \dfrac{1}{3}$

The equation of the line passing through $(3,2)$ and having a slope of $ - \dfrac{1}{3}$ is

$y - 2 =  - \dfrac{1}{3}(x - 3)$

Cross multiply and expand bracket,

$3y - 6 =  - x + 3$

$x + 3y = 9$

Therefore, the equations of the line are $3x - y = 7$ and $x + 3y = 9$.

11.Find the equation of the line passing through the point of intersection of the line $4x + 7y - 3$ $ = 0$ and $2x - 3y + 1 = 0$ that has equal intercepts on the axes.

Ans.Let the equation of the line having equal intercepts on the axes be $\dfrac{x}{a} + \dfrac{y}{a} = 1$

It can be written as,

$x + y = a \to {\text{(1)}}$

Solve equations $4x + 7y - 3 = 0$ and $2x - 3y + 1 = 0$, we get $x = \dfrac{1}{{13}}$ and $y = \dfrac{5}{{13}}$

$\therefore \left( {\dfrac{1}{{13}},\dfrac{5}{{13}}} \right)$ is the point of the intersection of the two given lines. 

Since equation \[\left( 1 \right)\] passes through point $\left( {\dfrac{1}{{13}},\dfrac{5}{{13}}} \right)$, $\dfrac{1}{{13}} + \dfrac{5}{{13}} = a$

$ \Rightarrow a = \dfrac{6}{{13}}$

Thus, Equation \[\left( 1 \right)\] becomes $x + y = \dfrac{6}{{13}}$ that is, $13x + 13y = 6$

Therefore, the required equation of the line $13x + 13y = 16$.

12.Show that the equation of the line passing through the origin and making an angle $\theta $ with the line $y = mx + c$, is $\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$

Ans.Let the equation of the line passing through the origin be ${\text{y}} = {m_1}x$. 

If this line makes an angle of $\theta $ with line $y = mx + c$, then angle $\theta $ is,

$\tan \theta  = \left| {\dfrac{{{m_1} - m}}{{1 + {m_1}m}}} \right|$

Substitute the values,

$ \Rightarrow \tan \theta  = \left| {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right|$

$ \Rightarrow \tan \theta  =  \pm \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

$ \Rightarrow \tan \theta  = \dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}$ or $\tan \theta  =  - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

Case 1: $\tan \theta  = \dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}$

$ \Rightarrow \tan \theta  + \dfrac{y}{x}m\tan \theta  = \dfrac{y}{x} - m$

$ \Rightarrow m + \tan \theta  = \dfrac{y}{x}(1 - m\tan \theta )$

$ \Rightarrow \dfrac{y}{x} = \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }}$

Case 2: $\tan \theta  =  - \left( {\dfrac{{\dfrac{x}{y} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

$\tan \theta  =  - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

$ \Rightarrow \tan \theta  + \dfrac{y}{x}m\tan \theta  =  - \dfrac{y}{x} + m$

$ \Rightarrow \dfrac{y}{x}(1 + m\tan \theta ) = m - \tan \theta $

Rewrite as,

$ \Rightarrow \dfrac{y}{x} = \dfrac{{m - \tan \theta }}{{1 + m\tan \theta }}$

Hence, it is shown that the equation of the line passing through the origin and making an angle $\theta $with the line $y = mx + c$, is $\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$.

13.In what ratio, the line joining $( - 1,1)$ and $(5,7)$ is divisible by the line $x + y = 4$ ?

Ans.The equation of the line joining the points $( - 1,1)$ and $(5,7)$ is,

$y - 1 = \dfrac{{7 - 1}}{{5 + 1}}(x + 1)$

$y - 1 = \dfrac{6}{6}(x + 1)$

$x - y + 2 = 0 \to (1)$

The equation of the given line is $x + y - 4 = 0 \to (2)$.

The points of intersection of line \[\left( 1 \right)\] and \[\left( 2 \right)\] is $x = 1$ and $y = 3$.

Let point $(1,3)$ divide the line segment joining $( - 1,1)$ and $(5,7)$ in the ratio $1:k$.

Then, by section formula, 

$(1,3) = \left( {\dfrac{{k( - 1) + 1(5)}}{{1 + k}},\dfrac{{k(1) + 1(7)}}{{1 + k}}} \right)$

Simplify,

$ \Rightarrow (1,3) = \left( {\dfrac{{ - k + 5}}{{1 + k}},\dfrac{{k + 7}}{{1 + k}}} \right)$

$ \Rightarrow \dfrac{{ - k + 5}}{{1 + k}} = 1,\,\,\dfrac{{k + 7}}{{1 + k}} = 3$

$\therefore \dfrac{{ - k + 5}}{{1 + k}} = 1$

By cross multiplication,

$ \Rightarrow  - k + 5 = 1 + k$

$ \Rightarrow 2k = 4$

$k=2$
Therefore, the line joining the points $( - 1,1)$ and $(5,7)$ is divided by line $x + y = 4$ in the ratio \[1:2\].

14. Find the distance of the line $4x + 7y + 5 = 0$ from the point $(1,2)$ along the line $2x - y = 0$

Ans.The given lines are $2x - y = 0 \to (1)$

$4x + 7y + 5 = 0 \to (2)$

${\text{P}}(1,2)$ is a point on line\[\left( 1 \right)\]. 

Let ${\text{Q}}$ be the point intersection of line \[\left( 1 \right)\] and \[\left( 2 \right).\]

Solve equations \[\left( 1 \right)\] and \[\left( 2 \right)\] to get $x = \dfrac{{ - 5}}{{18}}$ and $y = \dfrac{{ - 5}}{9}$

Now, Coordinates of point $B$ are $\left( {\dfrac{{ - 5}}{{18}},\dfrac{{ - 5}}{9}} \right)$. 

Use distance formula to obtain the distance between points ${\text{P and Q}}$,

${\text{PQ}} = \sqrt {{{\left( {1 + \dfrac{5}{{18}}} \right)}^2} + {{\left( {2 + \dfrac{5}{9}} \right)}^2}} $ units

Take LCM,

$ = \sqrt {{{\left( {\dfrac{{23}}{{18}}} \right)}^2} + {{\left( {\dfrac{{23}}{9}} \right)}^2}} $ units

Rewrite as,

$ = \sqrt {{{\left( {\dfrac{{23}}{{2 \times 9}}} \right)}^2} + {{\left( {\dfrac{{23}}{9}} \right)}^2}} $ units

$ = \sqrt {{{\left( {\dfrac{{23}}{9}} \right)}^2}{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{{23}}{9}} \right)}^2}} $ units

$ = \sqrt {{{\left( {\dfrac{{23}}{9}} \right)}^2} + \left( {\dfrac{1}{4} + 1} \right)} $ units

$ = \dfrac{{23}}{9}\sqrt {\dfrac{5}{4}} $ units

$ = \dfrac{{23}}{9} \times \dfrac{{\sqrt 5 }}{2}$ units

$ = \dfrac{{23\sqrt 5 }}{{18}}$ units

Therefore, the required distance is $\dfrac{{23\sqrt 5 }}{{18}}$ units,

15. Find the direction in which a straight line must be drawn through the points $( - 1,2)$ so that its point of intersection with line $x + y = 4$ may be at a distance of \[3\] units from this point.

Ans.Consider $y = mx + c$ as the line passing through the point $( - 1,2)$.

Then, 

$2 = m( - 1) + c$

$ \Rightarrow 2 =  - m + c$

$ \Rightarrow c = m + 2$

Substitute the value of $c$,

$y = mx + m + 2 \to (1)$ 

Now, the given line is,

$x + y = 4 \to (2)$

Solve both equations,

$x = \dfrac{{2 - m}}{{m + 1}}$ and $y = \dfrac{{5m + 2}}{{m + 1}}$

$\left( {\dfrac{{2 - m}}{{m + 1}},\,\,\dfrac{{5m + 2}}{{m + 1}}} \right)$ is the point of intersection of lines $(1)$ and \[\left( 2 \right)\].

Given that, the point is at a distance of \[3\] units from $( - 1,2)$

By distance formula,

$\sqrt {{{\left( {\dfrac{{2 - m}}{{m + 1}} + 1} \right)}^2} + {{\left( {\dfrac{{5m + 2}}{{m + 1}} - 2} \right)}^2}}  = 3$

Square both sides,

${\left( {\dfrac{{2 - m + m + 1}}{{m + 1}}} \right)^2} + {\left( {\dfrac{{5m + 2 - 2m - 2}}{{m + 1}}} \right)^2} = {3^2}$

$ \Rightarrow \dfrac{9}{{{{(m + 1)}^2}}} + \dfrac{{9{m^2}}}{{{{(m + 1)}^2}}} = 9$

Divide the equation by \[9\],

$\dfrac{{1 + {m^2}}}{{{{(m + 1)}^2}}} = 1$

By cross multiplication,

$1 + {m^2} = {m^2} + 1 + 2m$

$ \Rightarrow 2\;m = 0$

$ \Rightarrow m = 0$

Therefore, the slope of the required line must be zero that is, the line must be parallel 

to the $x$-axis.

16. The hypotenuse of a right-angled triangle has its ends at the points $(1,3)$ and $( - 4,1)$. Find the equation of the legs (perpendicular sides) of the triangle.

Ans.Consider ${\text{PQR}}$ as the right angles triangle where $\angle {\text{R}} = {90^\circ }$

Here, infinity such lines are present.

$m$ is the slope of ${\text{PR}}$

Then, the slope of ${\text{QR}} = \dfrac{{ - 1}}{m}$

Equation of ${\text{PR}}$is,

$y - 3 = m(x - 1)$

By cross multiplication,

$x - 1 = \dfrac{1}{{m(y - 3)}}$

Equation of ${\text{QR}}$is,

$y - 1 = \dfrac{{ - 1}}{{m(x + 4)}}$

By cross multiplication

$x + 4 =  - m(y - 1)$

If $m = 0$,

$y - 3 = 0,\,\,x + 4 = 0$

If $m = \infty $,

$x - 1 = 0,\,\,y - 1 = 0$ 

That is, $x = 1,\,\,y = 1$

Therefore, the equation of the legs (perpendicular sides) of the triangle is $x = 1,\,\,y = 1$.

17. Find the image of the point $(3,8)$ with respect to the line $x + 3y = 7$ assuming the line to be a plane mirror.

Ans.Given that,

$x + 3y = 7 \to (1)$

Consider \[{\text{B}}\left( {a,{\text{ }}b} \right)\]as the image of point ${\text{A}}(3,8)$

So line \[\left( 1 \right)\]is perpendicular bisector of ${\text{AB}}$.

Slope of ${\text{AB}} = \dfrac{{b - 8}}{{a - 3}}$

Slope of line $(1) =  - \dfrac{1}{3}$

Line \[\left( 1 \right)\] is perpendicular to ${\text{AB}}$

Then,

$\left( {\dfrac{{b - 8}}{{a - 3}}} \right) \times \left( { - \dfrac{1}{3}} \right) =  - 1$

$ \Rightarrow \dfrac{{b - 8}}{{3a - 9}} = 1$

By cross multiplication,

$b - 8 = 3a - 9$

$3a - b = 1 \to (2)$

We know,

Mid-point of ${\text{AB}} = \left( {\dfrac{{a + 3}}{2},\,\,\dfrac{{b + 8}}{2}} \right)$

So the mid-point of line segment ${\text{AB}}$ will satisfy line \[\left( 1 \right)\].

From equation \[\left( 1 \right)\],

$\left( {\dfrac{{a + 3}}{2}} \right) + 3\left( {\dfrac{{b + 8}}{2}} \right) = 7$

By further calculation,

$a + 3 + 3\;b + 24 = 14$

On further simplification,

$a + 3b =  - 13 \to (3)$

Solve equations \[\left( 2 \right)\] and \[\left( 3 \right)\],

$a =  - 1$ and $b =  - 4$

Therefore, the image of the given point with respect to the given line is $( - 1, - 4)$.

19.If the lines $y = 3x + 1$ and $2y = x + 3$ are equally indicated to the line $y = mx + 4$, find the value of $m$.

Ans.The equation of the given lines are ${\text{y}} = 3{\text{x}} + 1$

$2y = x + 3 \to (2)$

\[y = mx + 4 \to (3)\]

Slope of line\[\left( 1 \right)\] is  ${m_1} = 3$

Slope of line $(2)\,\,{\text{is}}\,\,{m_2} = \dfrac{1}{2}$

Slope of line $(3)\,\,{\text{is}}\,\,{m_3} = m$

We know that the lines \[\left( 1 \right)\] and \[\left( 2 \right)\] are equally inclined to line \[\left( 3 \right)\] which means that the angle between lines \[\left( 1 \right)\] and \[\left( 3 \right)\]equals the angle between lines $(2)$ and \[\left( 3 \right)\].

$\left| {\dfrac{{{m_1} - {m_3}}}{{1 + {m_1}{m_3}}}} \right| = \left| {\dfrac{{{m_2} - {m_3}}}{{1 + {m_2}{m_3}}}} \right|$

Substitute the values,

$\left| {\dfrac{{3 - m}}{{1 + 3m}}} \right| = \left| {\dfrac{{\dfrac{1}{2} - m}}{{1 + \dfrac{1}{2}m}}} \right|$

Take LCM

$\left| {\dfrac{{3 - m}}{{1 + 3m}}} \right| = \left| {\dfrac{{1 - 2m}}{{m + 2}}} \right|$

It can be written as,

$\dfrac{{3 - m}}{{1 + 3m}} =  \pm \left( {\dfrac{{1 - 2m}}{{m + 2}}} \right)$

Here,

$\dfrac{{3 - m}}{{1 + 3m}} = \dfrac{{1 - 2m}}{{m + 2}}$ or $\dfrac{{3 - m}}{{1 + 3m}} =  - \left( {\dfrac{{1 - 2m}}{{m + 2}}} \right)$

If $\dfrac{{3 - m}}{{1 + 3m}} = \dfrac{{1 - 2m}}{{m + 2}}$

By cross multiplication,

$(3 - m)(m + 2) = (1 - 2\;m)(1 + 3\;m)$

$ \Rightarrow  - {m^2} + m + 6 = 1 + m - 6{m^2}$

$ \Rightarrow 5{m^2} + 5 = 0$

Divide the equation by $5$

$ \Rightarrow {m^2} + 1 = 0$

$ \Rightarrow m = \sqrt { - 1} $, which is not real.

Therefore, this case is not possible.

If $\dfrac{{3 - m}}{{1 + 3m}} =  - \left( {\dfrac{{1 - 2m}}{{m + 2}}} \right)$

By cross multiplication,

$(3 - m)(m + 2) =  - (1 - 2\;m)(1 + 3\;m)$

$ \Rightarrow  - {m^2} + m + 6 =  - \left( {1 + m - 6\;{m^2}} \right)$

$ \Rightarrow 7{m^2} - 2m - 7 = 0$

Here we get,

$m = \dfrac{{2 \pm \sqrt {4 - 4(7)( - 7)} }}{{2(7)}}$

$m = \dfrac{{2 \pm 2\sqrt {1 + 49} }}{{14}}$

Rewrite as,

$m = \dfrac{{1 \pm 5\sqrt 2 }}{7}$

Thus, the required value of $m$ is $\dfrac{{1 \pm 5\sqrt 2 }}{7}$.

19.If sum of the perpendicular distance of a variable point ${\text{P}}(x,y)$ from the lines $x + y - 5 = 0$ and $3x - 2y + 7 = 0$ is always \[10.\] Show that ${\text{P}}$ must move on a line.

Ans.Given that,

$x + y - 5 = 0 \to (1)$

$3x - 2y + 7 = 0 \to (2)$

Here the perpendicular distances of ${\text{P}}(x,y)$ from lines \[\left( 1 \right){\text{ and }}\left( 2 \right)\]are written as,

${d_1} = \dfrac{{|x + y - 5|}}{{\sqrt {{{(1)}^2} + {{(1)}^2}} }}$ and ${d_2} = \dfrac{{|3x - 2y + 7|}}{{\sqrt {{{(3)}^2} + {{( - 2)}^2}} }}$

Nw, ${d_1} = \dfrac{{|x + y - 5|}}{{\sqrt 2 }}$ and ${d_2} = \dfrac{{|3x - 2y + 7|}}{{\sqrt {13} }}$

We know that ${d_1} + {d_2} = 10$

Substitute the values,

$\dfrac{{|x + y - 5|}}{{\sqrt 2 }} + \dfrac{{|3x - 2y + 7|}}{{\sqrt {13} }} = 10$

$ \Rightarrow \sqrt {13} |x + y - 5| + \sqrt 2 |3x - 2y + 7| - 10\sqrt {26}  = 0$

It can be written as,

$\sqrt {13} (x + y - 5) + \sqrt 2 (3x - 2y + 7) - 10\sqrt {26}  = 0$

Assume $(x + y - 5)$ and $(3x - 2y + 7)$ are positive,

$\sqrt {13} x + \sqrt {13} y - 5\sqrt {13}  + 3\sqrt 2 x - 2\sqrt 2 y + 7\sqrt 2  - 10\sqrt {26}  = 0$

Take out the common terms,

$x(\sqrt {13}  + 3\sqrt 2 ) + y(\sqrt {13}  - 2\sqrt 2 ) + (7\sqrt 2  - 5\sqrt {13}  - 10\sqrt {26} ) = 0$, which is the equation of a line.

Similarly, we can find the equation of line for any signs of $(x + y - 5)$ and 

$(3x - 2y + 7)$.

Therefore, point ${\text{P}}$ must move on a line.

20. Find equation of the line which is equidistant from parallel lines $9x + 6y - 7 = 0$ and $3x + 2{\text{y}} + 6 = 0.$

Ans.The equation of the given lines are $9x + 6y - 7 = 0 \to (1)$

$3x + 2y + 6 = 0 \to (2)$

Consider ${\text{P}}(h,k)$ be the arbitrary point that is equidistant from lines \[\left( 1 \right){\text{ and }}\left( 2 \right)\].

Here, the perpendicular distance of ${\text{P}}(h,k)$ from line $(1)$ is,

${d_1} = \dfrac{{|9h + 6k - 7|}}{{{{(9)}^2} + {{(6)}^2}}} $

$= \dfrac{{|9h + 6k - 7|}}{{\sqrt {117} }} $

$= \dfrac{{|9h + 6k - 7|}}{{3\sqrt {13} }} $

Similarly, the perpendicular distance of ${\text{P}}(h,k)$ from line \[\left( 2 \right)\] is,

${d_2} = \dfrac{{|3h + 2k + 6|}}{{\sqrt {{{(3)}^2} + {{(2)}^2}} }} $

$= \dfrac{{|3h + 2k + 6|}}{{\sqrt {13} }} $

We know that ${\text{P}}(h,k)$ is equidistant from lines \[(1){\text{ and }}\left( 2 \right)\]

That is, ${d_1} = {d_2}$

Substitute the values,

$\dfrac{{|9h + 6k - 7|}}{{3\sqrt {13} }} = \dfrac{{|3h + 2k + 6|}}{{\sqrt {13} }}$

$ \Rightarrow |9h + 6k - 7| = 3|3h + 2k + 6|$

$ \Rightarrow |9h + 6k - 7| =  \pm 3(3h + 2k + 6)$

Now, $9h + 6k - 7 = 3(3h + 2k + 6)$ or $9h + 6k - 7 =  - 3(3h + 2k + 6)$

$ \Rightarrow 9h + 6k - 7 = 3(3h + 2k + 6)$ is not possible as,

$9h + 6k - 7 = 3(3h + 2k + 6)$

$ - 7 = 18$ ,which is wrong

We have,

$9h + 6k - 7 =  - 3(3h + 2k + 6)$

By multiplication

$9h + 6k - 7 =  - 9h - 6k - 18$

$ \Rightarrow 18h + 12k + 11 = 0$

Therefore, the required equation of the line is $18x + 12y + 11 = 0$.

21. A ray of light passing through the point $(1,2)$ reflects on the $x$-axis at point ${\text{A}}$ and the reflected ray passes through the point $(5,3)$. Find the coordinates of ${\text{A}}$.

Ans. 

Consider the coordinates of point ${\text{A}}$ as $(a,0)$

Construct a line \[\left( {{\text{AL}}} \right)\]which is perpendicular to the $x$-axis

Here, the angle of incidence is equal to angle of reflection.

That is,

$\angle {\text{BAL}} = \angle {\text{CAL}} = \emptyset $

$\angle {\text{CAX}}$ $ = \theta $

It can be written as,

$\angle {\text{OAB}} = {180^\circ } - (\theta  + 2\phi ) = {180^\circ } - \left[ {\theta  + 2\left( {{{90}^\circ } - \theta } \right)} \right]$

$ = {180^\circ } - \theta  - {180^\circ } + 2\theta $

$ = \theta $

Now, $\angle {\text{BAX}} = {180^\circ } - \theta $

Slope of line ${\text{AC}} = \dfrac{{3 - 0}}{{5 - a}}$

$\tan \theta  = \dfrac{3}{{5 - a}} \to (1)$

Slope of line ${\text{AB}} = \dfrac{{2 - 0}}{{1 - a}}$

$\tan \left( {{{180}^\circ } - \theta } \right) = \dfrac{2}{{1 - a}}$

$ \Rightarrow  - \tan \theta  = \dfrac{2}{{1 - a}}$

$ \Rightarrow \tan \theta  = \dfrac{2}{{a - 1}}$

From equations \[\left( 1 \right){\text{ and }}\left( 2 \right)\],

$\dfrac{3}{{5 - a}} = \dfrac{2}{{a - 1}}$

By cross multiplication,

$3a - 3 = 10 - 2a$

$ \Rightarrow a = \dfrac{{13}}{5}$

Therefore, the coordinates of point ${\text{A}}$ are $\left( {\dfrac{{13}}{5},0} \right)$.

22. Prove that the product of the lengths of the perpendiculars drawn from the points $\left( {\sqrt {{a^2} - {b^2}} ,0} \right)$ and $\left( { - \sqrt {{a^2} - {b^2}} ,0} \right)$ to the line $\dfrac{x}{a}\cos \theta  + \dfrac{y}{b}\sin \theta  = 1$ is ${b^2}$.

Ans.Given that,

$\dfrac{x}{a}\cos \theta  + \dfrac{y}{b}\sin \theta  = 1$

Rewrite as,

$bx\cos \theta  + ay\sin \theta  - ab = 0 \to (1)$

Here, the length of the perpendicular from point $\left( {\sqrt {{a^2} - {b^2}} ,0} \right)$ to line \[\left( 1 \right)\] is,   

${p_1} = \dfrac{{\left| {b\cos \theta \left( {\sqrt {{a^2} - {b^2}} } \right) + a\sin \theta (0) - ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

$= \dfrac{{\left| {b\cos \theta \sqrt {{a^2} - {b^2}}  - ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

Similarly, the length of the perpendicular from point $\left( { - \sqrt {{a^2} - {b^2}} ,0} \right)$ to line $(2)$ is,

${p_2} = \dfrac{{\left| {b\cos \theta \left( { - \sqrt {{a^2} - {b^2}} } \right) + a\sin \theta (0) - ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

$= \dfrac{{\left| {b\cos \theta \sqrt {{a^2} - {b^2}}  + ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

Multiply equations \[\left( {\text{2}} \right){\text{ and }}\left( {\text{3}} \right),\]

$ = \dfrac{{\left| {\left( {b\cos \theta \sqrt {{a^2} - {b^2}}  - ab} \right)\left( {b\cos \theta \sqrt {{a^2} - {b^2}}  + ab} \right)} \right|}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

From the formula,

$ = \dfrac{{\left| {{{\left( {b\cos \theta \sqrt {{a^2} - {b^2}} } \right)}^2} - {{(ab)}^2}} \right|}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

Square the numerator,

$ = \dfrac{{\left| {{b^2}{{\cos }^2}\theta \left( {{a^2} - {b^2}} \right) - {a^2}{b^2}} \right|}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

Expand using formula,

$ = \dfrac{{\left| {{a^2}{b^2}{{\cos }^2}\theta  - {b^4}{{\cos }^2}\theta  - {a^2}{b^2}} \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

Take out the common terms,

$ = \dfrac{{{b^2}\left| {{a^2}{{\cos }^2}\theta  - {b^2}{{\cos }^2}\theta  - {a^2}} \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

$ = \dfrac{{{b^2}\left| {{a^2}{{\cos }^2}\theta  - {b^2}{{\cos }^2}\theta  - {a^2}{{\sin }^2}\theta  - {a^2}{{\cos }^2}\theta } \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

Here, ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$ (trigonometric identity)

$ = \dfrac{{{b^2}\left| { - \left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)} \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

$ = \dfrac{{{b^2}\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

Cancel common terms,

$ = {b^2}$

Hence, proved that the product of the lengths of the perpendiculars drawn from the points $\left( {\sqrt {{a^2} - {b^2}} ,0} \right)$ and $\left( { - \sqrt {{a^2} - {b^2}} ,0} \right)$ to the line $\dfrac{x}{a}\cos \theta  + \dfrac{y}{b}\sin \theta  = 1$ is ${b^2}$.

23. A person standing at the junction (crossing) of two straight paths represented by the equation $2x - 3y + 4 = 0$ and $3x + 4y - 5 = 0$ wants to reach the path whose equation is $6x - 7y + 8 = 0$in the least time .Find equation of the path that he should follow.

Ans.Given that,

$2x - 3y + 4 = 0 \to (1)$

$3x + 4y - 5 = 0 \to (2)$

$6x - 7y + 8 = 0 \to (3)$ 

Here, the person is standing at the junction of the paths represented by lines 

\[\left( {\text{1}} \right){\text{ and }}\left( {\text{2}} \right){\text{.}}\]

Solve equations \[\left( {\text{1}} \right){\text{ and }}\left( {\text{2}} \right),\]

$x = \dfrac{{ - 1}}{{17}}$ and $y = \dfrac{{22}}{{17}}$

Thus, the person is standing at point $\left( {\dfrac{{ - 1}}{{17}},\dfrac{{22}}{{17}}} \right)$.

It is known that the person can reach path \[\left( 3 \right)\]in the least time if he walks along the perpendicular line to (3) from point $\left( {\dfrac{{ - 1}}{{17}},\dfrac{{22}}{{17}}} \right)$

Here, the slope of the line $(3) = \dfrac{6}{7}$

Now, the slope of the line perpendicular to line $(3) = \dfrac{1}{{\left( {\dfrac{6}{7}} \right)}} = \dfrac{{ - 7}}{6}$

So the equation of line passing through point $\left( {\dfrac{{ - 1}}{{17}},\dfrac{{22}}{{17}}} \right)$and having a slope of $\dfrac{{ - 7}}{6}$ is,

$\left( {y - \dfrac{{22}}{{17}}} \right) =  - \dfrac{7}{6}\left( {x + \dfrac{1}{{17}}} \right)$

$ \Rightarrow 6(17y - 22) =  - 7(17x + 1)$

By multiplication,

$102y - 132 =  - 119x - 7$

$ \Rightarrow 119x + 102y = 125$

Therefore, the path that the person should follow is $119x + 102y = 125$.

NCERT Solutions for Class 11 Maths chapter 9 Sub-Topics

To help you have an initial idea of Ch 10 Maths Class 11, we provide here a brief overview of the concepts discussed in the chapter.

1. Part 1: Introduction

The first subsection introduces students to the concept of straight lines and their different parts and forms. Students will learn about identifying the coordinates of a point and measure the given lines with their help.

In Straight Lines Class 11 NCERT Solutions, you will find solutions to problems that require drawing shapes on a graph with provided coordinates, figuring out coordinates of a given shape’s vertices, and calculating the lengths of sides.

2. Part 2: Slope of a Line

This part is further divided into four sub-parts that delve into the intricacies of calculating the slope of a line. The first sub-topic explains the calculation of slope with given coordinates of two points on a line. Students are then introduced to the conditions for perpendicular and parallelism in terms of slope, calculating angles between two lines, and the conditions for collinearity of three points.

3. Part 3: Various Forms of the Equation of a Line

Here, you will learn about the different types of lines, vertical and horizontal. Additionally, there are 5 subsections dedicated to elaborate on each form of linear equation, namely, normal form, slope-intercept form, point-slope form, two-point form, and intercept-form.

4. Part 4: General Equation of a Line

This section in Straight Lines Class 11 introduces students to the general form of a linear equation and other equations of the same line.

You will find step-by-step answers on conversions of equations from one form to another in NCERT Solutions Class 11 Maths chapter 9.

5. Part 5: Distance of a Point from a Line

The formula to calculate the distance between a point and a straight line and the distance between two parallel lines have been explained in the last section. Straight Lines Class 11 NCERT Solutions PDF download is free on Vedantu. It comes with a comprehensive breakdown of numerical questions based on the application of these formulae that will help students understand the process in detail

Overview of Deleted Syllabus for CBSE Class 11 Maths Straight Lines

Class 11 Maths Chapter 9: Exercises Breakdown

Conclusion

Chapter 9 Class 11 Maths is important for mastering the basics of coordinate geometry. It covers essential concepts such as the slope of a line, various forms of line equations, and the angles between lines. Focus on understanding these concepts deeply, as they form the foundation for more advanced topics in mathematics. From previous year question papers, about 4–6 questions were typically asked, highlighting the importance of this chapter in exams. With Vedantu’s comprehensive solutions, you can confidently solve these problems and excel in your studies.

Other Study Material for CBSE Class 11 Maths Chapter 9

Chapter-Specific NCERT Solutions for Class 11 Maths

Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for CBSE Class 11 Maths