NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

• Exercise 10.1: This exercise introduces the concept of conic sections, including the definitions and standard equations of the circle, parabola, ellipse, and hyperbola. Students will learn how to identify the type of conic section given its equation and solve problems related to it.

• Exercise 10.2: In this exercise, students will learn about the various properties of the circle, such as its equation in different forms, its radius, centre, and diameter, and the equation of a tangent to the circle.

• Miscellaneous Exercise: This exercise includes a mix of questions covering all the concepts taught in the chapter. Students will have to apply their knowledge of conic sections to solve various problems and answer questions. They will also practice finding the equation of a tangent to the circle, parabola, ellipse, and hyperbola.

Access NCERT Solutions for Class 11 Maths Chapter 10 – Conic Sections

Exercise  10.1

1. Find the equation of the circle with centre \[(0,2)\] and radius \[2\]

Ans: The equation of a circle with centre \[(h,k)\] and radius \[r\] is given as

\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

It is given that centre \[(h,k)=(0,2)\] and radius \[(r)=2.\]

Therefore, the equation of the circle is

\[{{(x-0)}^{2}}+{{(y-2)}^{2}}={{2}^{2}}\]

\[\begin{align}   & {{x}^{2}}+{{y}^{2}}+4-4y=4 \\  & {{x}^{2}}+{{y}^{2}}-4y=0 \\ \end{align}\]

2. Find the equation of the circle with centre \[(-2,3)\] and radius \[4\]

Ans: The equation of a circle with centre \[(h,k)\] and radius \[r\] is given as

\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

It is given that centre \[(h,k)=(-2,3)\] and radius \[(r)=4.\]

Therefore, the equation of the circle is

\[{{(x+2)}^{2}}+{{(y-3)}^{2}}={{(4)}^{2}}\]

\[\begin{align}  & {{x}^{2}}+4x+4+{{y}^{2}}-6y+9=16 \\  & {{x}^{2}}+{{y}^{2}}+4x-6y-3=0 \\ \end{align}\]

3. Find the equation of the circle with centre \[\left( \dfrac{1}{2},\dfrac{1}{4} \right)\] and radius \[\left( \dfrac{1}{12} \right)\]

Ans: The equation of a circle with centre \[(h,k)\] and radius \[r\] is given as

\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

It is given that centre \[(h,k)=\left( \dfrac{1}{2},\dfrac{1}{4} \right)\] and radius \[(r)=\left( \dfrac{1}{12} \right).\]

Therefore, the equation of the circle is

\[{{\left( x-\dfrac{1}{2} \right)}^{2}}+{{\left( y-\dfrac{1}{4} \right)}^{2}}={{\left( \dfrac{1}{12} \right)}^{2}}\]

\[{{x}^{2}}-x+\dfrac{1}{4}+{{y}^{2}}-\dfrac{y}{2}+\dfrac{1}{16}=\dfrac{1}{144}\]

\[{{x}^{2}}-x+\dfrac{1}{4}+{{y}^{2}}-\dfrac{y}{2}+\dfrac{1}{16}-\dfrac{1}{144}=0\]

\[144{{x}^{2}}-144x+36+144{{y}^{2}}-72y+9-1=0\] (Solve by taking LCM)

\[144{{x}^{2}}-144x+144{{y}^{2}}-72y+44=0\]

\[36{{x}^{2}}-36x+36{{y}^{2}}-18y+11=0\]

\[36{{x}^{2}}+36{{y}^{2}}-36x-18y+11=0\]

4. Find the equation of the circle with centre \[(1,1)\] and radius \[\sqrt{2}\]

Ans: The equation of a circle with centre \[(h,k)\] and radius \[r\] is given as

\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

It is given that centre \[(h,k)=(1,1)\] and radius \[(r)=\sqrt{2}.\]

Therefore, the equation of the circle is

\[{{(x-1)}^{2}}+{{(y-1)}^{2}}={{(\sqrt{2})}^{2}}\]

\[\begin{align}  & {{x}^{2}}-2x+1+{{y}^{2}}-2y+1=2 \\  & {{x}^{2}}+{{y}^{2}}-2x-2y=0 \\ \end{align}\]

5. Find the equation of the circle with centre \[(-a,-b)\] and radius \[\sqrt{{{a}^{2}}-{{b}^{2}}}\]

Ans: The equation of a circle with centre \[(h,k)\] and radius \[r\] is given as

\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

It is given that centre \[(h,k)=(-a,-b)\] and radius \[(r)=\sqrt{{{a}^{2}}-{{b}^{2}}}.\]

Therefore, the equation of the circle is

\[{{(x+a)}^{2}}+{{(y+b)}^{2}}={{(\sqrt{{{a}^{2}}-{{b}^{2}}})}^{2}}\]

\[\begin{align}   & {{x}^{2}}+2ax+{{a}^{2}}+{{y}^{2}}+2by+{{b}^{2}}={{a}^{2}}-{{b}^{2}} \\  & {{x}^{2}}+{{y}^{2}}+2ax+2by+2{{b}^{2}}=0 \\ \end{align}\]

6. Find the centre and radius of the circle \[{{(x+5)}^{2}}+{{(y-3)}^{2}}=36\]

Ans: The equation of the given circle is \[{{(x+5)}^{2}}+{{(y-3)}^{2}}=36\]

\[{{(x+5)}^{2}}+{{(y-3)}^{2}}=36\]

\[\Rightarrow {{\{x-(-5)\}}^{2}}+{{(y-3)}^{2}}={{(6)}^{2}}\], which is the form of \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\], where \[h=-5,k=3,and\; r=6\].

Thus, the centre of the given circle is \[(-5,3),\] while its radius is 6.

7. Find the centre and radius of the circle \[{{x}^{2}}+{{y}^{2}}-4x-8y-45=0\]

Ans: The equation of the given circle is \[{{x}^{2}}+{{y}^{2}}-4x-8y-45=0\]

\[\Rightarrow {{x}^{2}}+{{y}^{2}}-4x-8y-45=0\]

\[\Rightarrow ({{x}^{2}}-4x)+({{y}^{2}}-8y)=45\]

\[\Rightarrow \{{{x}^{2}}-2(x)(2)+{{(2)}^{2}}\}+\{{{y}^{2}}-2(y)(4)+{{(4)}^{2}}\}-4-16=45\]

\[\Rightarrow {{(x-2)}^{2}}+{{(y-4)}^{2}}=65\]

\[\Rightarrow {{(x-2)}^{2}}+{{(y-4)}^{2}}={{\left( \sqrt{65} \right)}^{2}},\] which is of the form \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\], where \[h=2,k=4,and\; r=\sqrt{65}\]

Thus, the centre of the given circle is \[(2,4),\]while its radius is \[\sqrt{65}\].

8. Find the centre and radius of the circle \[{{x}^{2}}+{{y}^{2}}-8x+10y-12=0\]

Ans: The equation of the given circle is \[{{x}^{2}}+{{y}^{2}}-8x+10y-12=0\]

\[\Rightarrow {{x}^{2}}+{{y}^{2}}-8x+10y-12=0\]
\[\Rightarrow ({{x}^{2}}-8x)+({{y}^{2}}+10y)=12\]

\[\Rightarrow \{{{x}^{2}}-2(x)(4)+{{(4)}^{2}}\}+\{{{y}^{2}}+2(y)(5)+{{(5)}^{2}}-16-25=12\]

\[\Rightarrow {{(x-4)}^{2}}+{{(y+5)}^{2}}=53\]

\[\Rightarrow {{(x-4)}^{2}}+{{\{y-(-5)\}}^{2}}={{\left( \sqrt{53} \right)}^{2}},\] which is of the form \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\], where \[h=4,k=-5,and\; r=\sqrt{53}\]

Thus, the centre of the given circle is \[(4,-5),\] while its radius is \[\sqrt{53}\].

9. Find the centre and radius of the circle \[2{{x}^{2}}+2{{y}^{2}}-x=0\]

Ans: The equation of the given circle is \[2{{x}^{2}}+2{{y}^{2}}-x=0\]

\[\Rightarrow 2{{x}^{2}}+2{{y}^{2}}-x=0\]
\[\Rightarrow (2{{x}^{2}}-x)+2{{y}^{2}}=0\]

\[\Rightarrow 2\left[ \left( {{x}^{2}}-\dfrac{x}{2} \right)+{{y}^{2}} \right]=0\]

\[\Rightarrow \left\{ {{x}^{2}}-2.x\left( \dfrac{1}{4} \right)+{{\left( \dfrac{1}{4} \right)}^{2}} \right\}+{{y}^{2}}-{{\left( \dfrac{1}{4} \right)}^{2}}=0\]

\[\Rightarrow {{\left( x-\dfrac{1}{4} \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \dfrac{1}{4} \right)}^{2}},\] which is of the form \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\], where \[h=\dfrac{1}{4},k=0,\] and \[r = \dfrac{1}{4}\]

Thus, the centre of the given circle is \[\left( \dfrac{1}{4},0 \right),\] while its radius is \[\dfrac{1}{4}\].

10. Find the equation of the circle passing through the points \[(4,1)\] and \[(6,5)\] and whose centre is on the line \[4x+y=16\]

Ans: Let the equation of the required circle be \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

Since the circle passes through points \[(4,1)\] and \[(6,5)\],

\[{{(4-h)}^{2}}+{{(1-k)}^{2}}={{r}^{2}}\] ………(i)

\[{{(6-h)}^{2}}+{{(5-k)}^{2}}={{r}^{2}}\] ………(ii)

Since the centre (h,k) of the circle lies on line \[4x+y=16,\]

\[4h+k=16\] ………(iii)

From equations (i) and (ii), we get

\[\Rightarrow {{(4-h)}^{2}}+{{(1-k)}^{2}}={{(6-h)}^{2}}+{{(5-k)}^{2}}\]

\[\Rightarrow 16-8h+{{h}^{2}}+1-2k+{{k}^{2}}=36-12h+{{h}^{2}}+25-10k+{{k}^{2}}\]

\[\begin{align}   & \Rightarrow 16-8h+1-2k=36-12h+25-10k \\  & \Rightarrow 4h+8k=44 \\ \end{align}\]

\[\Rightarrow h+2k=11\] ………(iv)

On solving equations (iii) and (iv), we obtain \[h=3\] and \[k=4\]

On substituting the values of h and k in equation (i), we obtain

\[{{(4-3)}^{2}}+{{(1-4)}^{2}}={{r}^{2}}\]

\[\Rightarrow {{(1)}^{2}}+{{(-3)}^{2}}={{r}^{2}}\]

\[\Rightarrow 1+9={{r}^{2}}\]

\[\begin{align} & \Rightarrow {{r}^{2}}=10 \\  & \Rightarrow r=\sqrt{10} \\ \end{align}\]

Thus, the equation of the required circle is

\[{{(x-3)}^{2}}+{{(y-4)}^{2}}={{\left( \sqrt{10} \right)}^{2}}\]

\[\begin{align}   & {{x}^{2}}-6x+9+{{y}^{2}}-8y+16=10 \\  & {{x}^{2}}+{{y}^{2}}-6x-8y+15=0 \\ \end{align}\]

11. Find the equation of the circle passing through the points \[(2,3)\] and \[(-1,1)\] and whose centre is on the line \[x-3y-11=0\]

Ans: Let the equation of the required circle be \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

Since the circle passes through points \[(2,3)\] and \[(-1,1)\],

\[{{(2-h)}^{2}}+{{(3-k)}^{2}}={{r}^{2}}\] ………(i)

\[{{(-1-h)}^{2}}+{{(1-k)}^{2}}={{r}^{2}}\] ………(ii)

Since the centre (h,k) of the circle lies on line \[x-3y-11=0\]

\[h-3k=11\] ………(iii)

From equations (i) and (ii), we get

\[\Rightarrow {{(2-h)}^{2}}+{{(3-k)}^{2}}={{(-1-h)}^{2}}+{{(1-k)}^{2}}\]

\[\Rightarrow 4-4h+{{h}^{2}}+9-6k+{{k}^{2}}=1+2h+{{h}^{2}}+1-2k+{{k}^{2}}\]

\[\Rightarrow 4-4h+9-6k=1+2h+1-2k\]

\[\Rightarrow 6h+4k=11\] ………(iv)

On solving equations (iii) and (iv), we obtain \[h=\dfrac{7}{2}\] and \[k=\dfrac{-5}{2}\]

On substituting the values of h and k in equation (i), we obtain

\[\Rightarrow {{\left( 2-\dfrac{7}{2} \right)}^{2}}+{{\left( 3+\dfrac{5}{2} \right)}^{2}}={{r}^{2}}\]

\[\Rightarrow {{\left( \dfrac{4-7}{2} \right)}^{2}}+{{\left( \dfrac{6+5}{2} \right)}^{2}}={{r}^{2}}\]

\[\Rightarrow {{\left( \dfrac{-3}{2} \right)}^{2}}+{{\left( \dfrac{11}{2} \right)}^{2}}={{r}^{2}}\]

\[\begin{align}   & \Rightarrow \dfrac{9}{4}+\dfrac{121}{4}={{r}^{2}} \\  & \Rightarrow \dfrac{130}{4}={{r}^{2}} \\ \end{align}\]

Thus, the equation of the required circle is

\[{{\left( x-\dfrac{7}{2} \right)}^{2}}+{{\left( y+\dfrac{5}{2} \right)}^{2}}=\dfrac{130}{4}\]

\[\begin{align}   & {{\left( \dfrac{2x-7}{2} \right)}^{2}}+{{\left( \dfrac{2y+5}{2} \right)}^{2}}=\dfrac{130}{4} \\ & 4{{x}^{2}}-28x+49+4{{y}^{2}}+20y+25=130 \\ \end{align}\]

\[\begin{align}   & 4{{x}^{2}}+4{{y}^{2}}-28x+20y-56=0 \\  & 4({{x}^{2}}+y{}^{2}-7x+5y-14)=0 \\ \end{align}\]

\[{{x}^{2}}+{{y}^{2}}-7x+5y-14=0\]

12. Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point \[(2,3)\].

Ans: Let the equation of the required circle be \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

Since the radius of the circle  is 5 and its centre lies on the x-axis, \[k=0\] and \[r=5\].

Now, the equation of the circle passes through point \[(2,3).\]

\[\begin{align}   & \therefore {{\left( 2-h \right)}^{2}}+{{3}^{2}}=25 \\  & \Rightarrow {{\left( 2-h \right)}^{2}}=25-9 \\  & \Rightarrow {{\left( 2-h \right)}^{2}}=16 \\ \end{align}\]

\[\begin{align}  & \Rightarrow \left( 2-h \right)=\pm \sqrt{16} \\  & =\pm 4 \\ \end{align}\]

If \[2-h=4,\] then \[h=-2\]

If \[2-h=-4,\] then \[h=6\]

When \[h=-2\], the equation of the circle becomes

\[\begin{align}  & {{\left( x+2 \right)}^{2}}+{{y}^{2}}=25 \\  & {{x}^{2}}+4x+4+{{y}^{2}}=25 \\  & {{x}^{2}}+{{y}^{2}}+4x-21=0 \\ \end{align}\]

When \[h=6\], the equation of the circle becomes

\[\begin{align}   & {{\left( x-6 \right)}^{2}}+{{y}^{2}}=25 \\  & {{x}^{2}}-12x+36+{{y}^{2}}=25 \\  & {{x}^{2}}+{{y}^{2}}-12x+11=0 \\ \end{align}\] So, the equation of the circle can be \[{{x}^{2}}+{{y}^{2}}+4x-21=0 \] or \[{{x}^{2}}+{{y}^{2}}-12x+11=0 \]

13. Find the equation of the circle passing through \[(0,0)\] and making intercepts a and b on the coordinate axes.

Ans: Let the equation of the required circle be \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

Since the circle passes through \[(0,0)\].

\[\begin{align}  & {{(0-h)}^{2}}+{{(0-k)}^{2}}={{r}^{2}} \\  & \Rightarrow {{h}^{2}}+{{k}^{2}}={{r}^{2}} \\ \end{align}\]

The equation of the circle now becomes \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{h}^{2}}+{{k}^{2}}\]

It is given that the circle makes intercepts a and b on the coordinate axes. This means that the circle passes through points \[(a,0)\] and \[(0,b)\]. Therefore,

\[{{(a-h)}^{2}}+{{(0-k)}^{2}}={{h}^{2}}+{{k}^{2}}\] …….(1)

\[{{(0-h)}^{2}}+{{(b-k)}^{2}}={{h}^{2}}+{{k}^{2}}\] …….(2)

From equation (1), we’ll get

\[\begin{align}  & {{a}^{2}}-2ah+{{h}^{2}}+{{k}^{2}}={{h}^{2}}+{{k}^{2}} \\  & \Rightarrow {{a}^{2}}-2ah=0 \\  & \Rightarrow a(a-2h)=0 \\ \end{align}\]

\[\Rightarrow a=0\] or \[(a-2h)=0\]

However, \[a\ne 0;\] hence, \[(a-2h)=0\Rightarrow h=\dfrac{a}{2}\]

From equation (2), we’ll get

\[\begin{align}  & {{h}^{2}}+{{b}^{2}}-2bk+{{k}^{2}}={{h}^{2}}+{{k}^{2}} \\  & \Rightarrow {{b}^{2}}-2bk=0 \\  & \Rightarrow b(b-2k)=0 \\ \end{align}\]

\[\Rightarrow b=0\] or \[(b-2k)=0\]

However, \[b\ne 0;\] hence, \[(b-2k)=0\Rightarrow k=\dfrac{b}{2}\]

Thus, the equation of the required circle is

\[{{\left( x-\dfrac{a}{2} \right)}^{2}}+{{\left( y-\dfrac{b}{2} \right)}^{2}}={{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{b}{2} \right)}^{2}}\]

\[{{\left( \dfrac{2x-a}{2} \right)}^{2}}+{{\left( \dfrac{2y-b}{2} \right)}^{2}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4}\]

\[\begin{align}  & \Rightarrow 4{{x}^{2}}-4ax+{{a}^{2}}+4{{y}^{2}}-4by+{{b}^{2}}={{a}^{2}}+{{b}^{2}} \\  & \Rightarrow 4{{x}^{2}}+4{{y}^{2}}-4ax-4by=0 \\  & \Rightarrow {{x}^{2}}+{{y}^{2}}-ax-by=0 \\ \end{align}\]

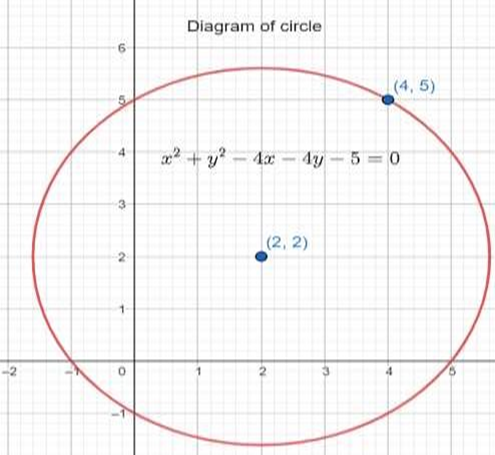
14. Find the equation of a circle with centre \[(2,2)\] and passes through the point \[(4,5)\].

Ans: The centre of the circle is given as \[(h,k)=(2,2)\]

Since the circle passes through point \[(4,5),\] the radius \[(r)\] of the circle is the distance between the points \[(2,2)\] and \[(4,5)\].

\[\begin{align}  & \therefore r=\sqrt{{{(2-4)}^{2}}+{{(2-5)}^{2}}} \\  & =\sqrt{{{(-2)}^{2}}+{{(-3)}^{2}}} \\  & =\sqrt{4+9} \\  & =\sqrt{13} \\ \end{align}\]

Thus, the equation of the circle is 

\[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\]

\[\begin{align}  & {{(x-2)}^{2}}+{{(y-2)}^{2}}={{\left( \sqrt{13} \right)}^{2}} \\  & {{x}^{2}}-4x+4+{{y}^{2}}-4y+4=13 \\  & {{x}^{2}}+{{y}^{2}}-4x-4y-5=0 \\ \end{align}\]

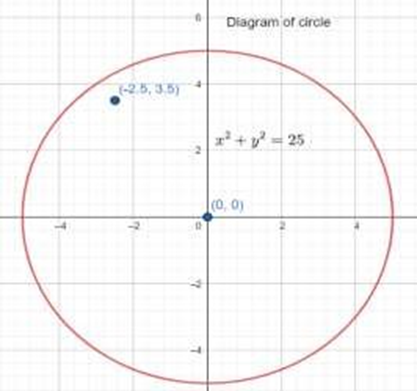
15. Does the point \[(-2.5,3.5)\] lie inside, outside or on the circle \[{{x}^{2}}+{{y}^{2}}=25\]?

Ans: The equation of the given circle is \[{{x}^{2}}+{{y}^{2}}=25\].

\[{{x}^{2}}+{{y}^{2}}=25\]

\[\Rightarrow {{(x-0)}^{2}}+{{(y-0)}^{2}}={{5}^{2}},\] which is of the form of \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\], where \[h = 0, k = 0 \; and\; r=5\]

\[\therefore \] Centre \[=(0,0)\] and radius \[=5\]

Distance between point \[(-2.5,3.5)\] and center \[(0,0)\]

\[=\sqrt{{{(-2.5-0)}^{2}}+{{(3.5-0)}^{2}}}\]

\[\begin{align}  & =\sqrt{6.25+12.25} \\  & =\sqrt{18.25} \\ \end{align}\]

\[=4.3\] (approx.) \[<5\]

Since the distance between point \[(-2.5,3.5)\] and center \[(0,0)\] of the circle is less than the radius of the circle, point \[(-2.5,3.5)\] lies inside the circle.

Exercise 10.2

1. Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for \[{{y}^{2}}=12x\]

Ans: The given equation is \[{{y}^{2}}=12x\].

Here, the coefficient of x is positive. Hence, the parabola opens towards the right. On comparing this equation with \[{{y}^{2}}=4ax,\] we’ll get

\[4a=12\Rightarrow a=3\]

\[\therefore \] Coordinates of the focus = \[=(a,0)=(3,0)\]

Since the given equation involves \[{{y}^{2}}\], the axis of the parabola is the x-axis. Equation of directrix, \[x=-a\text{  }i.e.,\text{  }x=-3\text{  }i.e.,\text{  }x+3=0\] 

Length of latus rectum \[=4a=4\times 3=12\]

2. Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for \[{{x}^{2}}=6y\]

Ans: The given equation is \[{{x}^{2}}=6y\]. 

Here, the coefficient of y is positive. Hence, the parabola opens upwards. 

On comparing this equation with \[{{x}^{2}}=4ay\] we obtain 

\[4a=6\Rightarrow a=\dfrac{3}{2}\]

\[\therefore \]Coordinates of the focus \[=(0,a)=\left( 0,\dfrac{3}{2} \right)\]

Since the given equation involves \[{{x}^{2}}\], the axis of the parabola is the y-axis. Equation of directrix, \[y=-a\]  i.e., \[y=\dfrac{-3}{2}\]

Length of latus rectum \[=4a=6\]

3. Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for \[{{y}^{2}}=-8x\]

Ans: The given equation is \[{{y}^{2}}=-8x\].

Here, the coefficient of \[x\] is negative. Hence, the parabola opens towards the left. On comparing this equation with \[{{y}^{2}}=-4ax,\] we’ll get

\[-4a=-8\Rightarrow a=2\]

\[\therefore \] Coordinates of the focus \[=(-a,0)=(-2,0)\]

Since the given equation involves \[{{y}^{2}}\], the axis of the parabola is the x-axis. Equation of directrix, \[x=a\]  i.e., \[x=2\]

Length of latus rectum \[=4a=8\]

4. Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for \[{{x}^{2}}=-16y\]

Ans: The given equation is \[{{x}^{2}}=-16y.\] 

Here, the coefficient of \[y\] is negative. Hence, the parabola opens downwards. 

On comparing this equation with \[{{x}^{2}}=-4ay\], we’ll get

\[-4a=-16\Rightarrow a=4\]

\[\therefore \] Coordinates of the focus \[=(0,-a)=(0,-4)\]

Since the given equation involves \[{{x}^{2}}\], the axis of the parabola is the y-axis. Equation of directrix, \[y=a\]  i.e., \[y=4\]

Length of latus rectum \[=4a=16\]

5. Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for \[{{y}^{2}}=10x\]

Ans:The given equation is \[{{y}^{2}}=10x\].

Here, the coefficient of \[x\] is positive. Hence, the parabola opens towards the right. On comparing this equation with \[{{y}^{2}}=4ax\], we’ll get

\[4a=10\Rightarrow a=\dfrac{5}{2}\]

\[\therefore \] Coordinates of the focus \[=(a,0)=\left( \dfrac{5}{2},0 \right)\]

Since the given equation involves \[{{y}^{2}}\], the axis of the parabola is the x-axis. Equation of directrix, \[x=-a\]  i.e., \[x=-\dfrac{5}{2}\]

Length of latus rectum \[=4a=10\]

6. Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for \[{{x}^{2}}=-9y\]

Ans: The given equation is \[{{x}^{2}}=-9y\]. 

Here, the coefficient of \[y\] is negative. Hence, the parabola opens downwards. 

On comparing this equation with \[{{x}^{2}}=-4ay\], we’ll get

\[-4a=-9\Rightarrow a=\dfrac{9}{4}\]

\[\therefore \] Coordinates of the focus \[=(0,-a)=\left( 0,-\dfrac{9}{4} \right)\]

Since the given equation involves \[{{x}^{2}}\], the axis of the parabola is the y-axis. Equation of directrix, \[y=a\]  i.e., \[y=\dfrac{9}{4}\]

Length of latus rectum \[=4a=9\]

7. Find the equation of the parabola that satisfies the following conditions: Focus \[(6,0);\] directrix \[x=-6\]

Ans: Focus \[(6,0);\]directrix, \[x=-6\]

Since the focus lies on the x-axis, the x-axis is the axis of the parabola. 

Therefore, the equation of the parabola is either of the form \[{{y}^{2}}=4ax\] or  \[{{y}^{2}}=-4ax\]. 

It is also seen that the directrix, \[x=-6\]is to the left of the y-axis, while the focus \[(6,0)\] is to the right of the y-axis. 

Hence, the parabola is of the form \[{{y}^{2}}=4ax\]. 

Here, \[a=6\]

Thus, the equation of the parabola is \[{{y}^{2}}=24x\].

8. Find the equation of the parabola that satisfies the following conditions: Focus \[(0,-3);\] directrix \[y=3\]

Ans: Focus \[=(0,-3);\] directrix \[y=3\]

Since the focus lies on the y-axis, the y-axis is the axis of the parabola. 

Therefore, the equation of the parabola is either of the form \[{{x}^{2}}=4ay\] or \[{{x}^{2}}=-4ay.\]

It is also seen that the directrix, \[y=3\] is above the x-axis, while the focus \[(0,-3)\] is below the x-axis. 

Hence, the parabola is of the form \[{{x}^{2}}=-4ay.\]

Here, \[a=3\]

Thus, the equation of the parabola is \[{{x}^{2}}=-12y.\] 

9. Find the equation of the parabola that satisfies the following conditions: Vertex \[(0,0);\] focus \[(3,0)\] 

Ans: Vertex \[(0,0);\] focus \[(3,0)\] 

Since the vertex of the parabola is \[(0,0)\] and the focus lies on the positive x-axis, x-axis is the axis of the parabola, while the equation of the parabola is of the form \[{{y}^{2}}=4ax.\] 

Since the focus is \[(3,0)\], \[a=3\]. 

Thus, the equation of the parabola is \[{{y}^{2}}=4\times 3\times x\]  i.e., \[{{y}^{2}}=12x\] 

10. Find the equation of the parabola that satisfies the following conditions: Vertex \[(0,0)\] focus \[(-2,0)\]

Ans: Solution 10: Vertex \[(0,0)\] focus \[(-2,0)\] 

Since the vertex of the parabola is \[(0,0)\] and the focus lies on the negative x-axis, x-axis is the axis of the parabola, while the equation of the parabola is of the form \[{{y}^{2}}=-4ax.\] 

Since the focus is \[(-2,0),\]\[a=2.\] 

Thus, the equation of the parabola is \[{{y}^{2}}=-4\times 2\times x\]  i.e., \[{{y}^{2}}=-8x\]

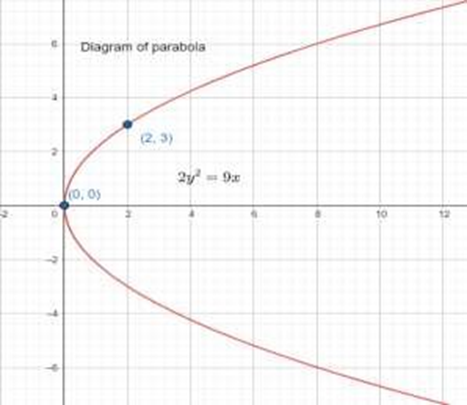
11. Find the equation of the parabola that satisfies the following conditions: Vertex \[(0,0)\]passing through \[(2,3)\]and axis is along x-axis 

Ans: Since the vertex is (0, 0) and the axis of the parabola is the x-axis, the equation of the parabola is either of the form \[{{y}^{2}}=4ax\] or \[{{y}^{2}}=-4ax.\]

The parabola passes through point \[(2,3)\], which lies in the first quadrant. Therefore, the equation of the parabola is of the form \[{{y}^{2}}=4ax\], while point \[(2,3)\] must satisfy the equation \[{{y}^{2}}=4ax\].

\[\therefore {{(3)}^{2}}=4a(2)\Rightarrow a=\dfrac{9}{8}\]

Thus, the equation of the parabola is \[{{y}^{2}}=4\left( \dfrac{9}{8} \right)x\]

\[\begin{align}   & \Rightarrow {{y}^{2}}=\dfrac{9}{2}x \\  & \Rightarrow 2{{y}^{2}}=9x \\ \end{align}\]

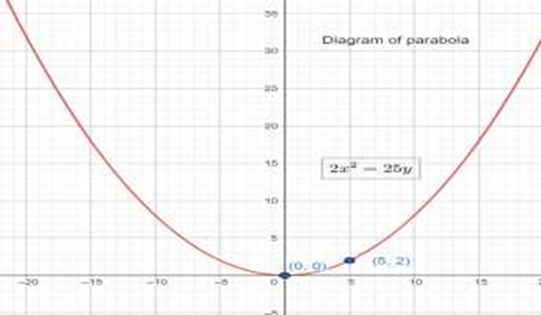
12. Find the equation of the parabola that satisfies the following conditions: Vertex \[(0,0)\], passing through \[(5,2)\] and symmetric with respect to y-axis

Ans: Since the vertex is \[(0,0)\] and the parabola is symmetric about the y-axis, the equation of the parabola is either of the form \[{{x}^{2}}=4ay\] or \[{{x}^{2}}=-4ay.\] 

The parabola passes through point \[(5,2)\], which lies in the first quadrant. Therefore, the equation of the parabola is of the form \[{{x}^{2}}=4ay\], while point \[(5,2)\] must satisfy the equation \[{{x}^{2}}=4ay\]. 

\[\begin{align}   & \therefore {{(5)}^{2}}=4\times a\times 2 \\  & \Rightarrow 25=8a \\  & \Rightarrow a=\dfrac{25}{8} \\ \end{align}\]

Thus, the equation of the parabola is

\[\Rightarrow {{x}^{2}}=4\left( \dfrac{25}{8} \right)y\]

\[\Rightarrow 2{{x}^{2}}=25y\]

Miscellaneous Exercise

1. If a parabolic reflector is \[20\] cm in diameter and \[5\]cm deep, find the focus.

Ans: As we know that the origin of the coordinate plane is taken at the vertex of the parabolic reflector, where the axis of the reflector is along the positive x-axis.

The Diagrammatic representation is represented as follows:

As we know that the equation of the parabola is of the form of \[{{y}^{2}}=4ax\] (as it is opening to the right)

Since, the parabola passes through point \[A \left( 5,10 \right),\]

\[\begin{align}  & \Rightarrow {{y}^{2}}=4ax \\  & \Rightarrow {{10}^{2}}=4\times a\times 5 \\  & \Rightarrow 100=20a \\  & \Rightarrow a=\dfrac{100}{20} \\  & \Rightarrow a=5 \\ \end{align}\]

The focus of the parabola is \[\left( a,0 \right)=\left( 5,0 \right),\] which is the mid–point of the diameter.

Hence, the focus of the reflector is at the midpoint of the diameter.

2. An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?

Ans: As we know that the origin of the coordinate plane is taken at the vertex of the arch in such a way that its axis is along the y-axis.

The diagrammatic representation will be as follows:

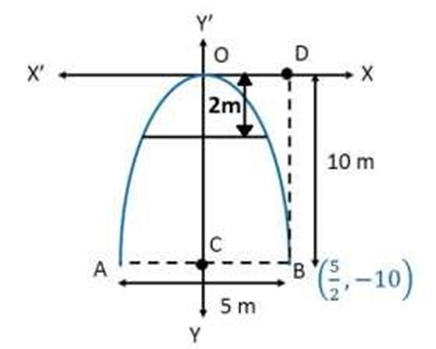
The equation of the parabola is of the form \[{{x}^{2}}=-4ay\] (as it is opening downwards). 

Since the parabola passes through point \[\left( \dfrac{5}{2},-10 \right),\]

\[\begin{align}  & {{\left( \dfrac{5}{2} \right)}^{2}}=-4\times a\times (-10) \\  & \Rightarrow a=\dfrac{25}{4\times 4\times 10}=\dfrac{5}{32} \\ \end{align}\]

Therefore,

The arch is in the form of a parabola whose equation is \[{{x}^{2}}=-\dfrac{5}{8}y\]

When \[y=-2m,{{x}^{2}}=-\dfrac{5}{8}\times (-2)\] because it's 2m away downward from the vertex, so it will be negative.

\[\begin{align}  & \Rightarrow {{x}^{2}}=\dfrac{5}{4} \\  & \Rightarrow x=\sqrt{\dfrac{5}{4}}m \\ \end{align}\]

Width of parabola at 2m away from vertex will be $=2\times \sqrt{\dfrac{5}{4}}m$

$=2\times 1.118m$(approx.) 

$=2.23m$(approx.) 

Hence, when the arch is 2 m from the vertex of the parabola, its width is approximately 2.23m.

3. The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.

Ans: The vertex is at the lowest point of the cable. The origin of the coordinate plane is taken as the vertex of the parabola, while its vertical axis is taken along the positive y-axis. 

This can be diagrammatically represented as

Here, AB and OC are the longest and shortest wires, respectively, attached to the cable.

DF is the supporting wire attached to the roadway, 18m from the middle.

Here, AB\[=30m, OC=6m, and\;  BC=\dfrac{100}{2}=50m\]

The equation of the parabola is of the form \[{{x}^{2}}=4ay\] (as it is opening upwards).

The coordinates of point A are \[(50,30-6)=(50,24)\].

Since A\[(50,24)\] is a point on the parabola,

\[\begin{align}   & {{(50)}^{2}}=4a(24) \\  & \Rightarrow a=\dfrac{50\times 50}{4\times 24}=\dfrac{625}{24} \\ \end{align}\]

\[\therefore \]Equation of the parabola, \[{{x}^{2}}=4\times \dfrac{625}{24}\times y\] or \[6{{x}^{2}}=625y\]

The x-coordinate of point D is 18. 

Hence, at x = 18, 

\[\begin{align}  & 6{{(18)}^{2}}=625y \\  & \Rightarrow y=\dfrac{6\times 18\times 18}{625} \\  & \Rightarrow y=3.11(approx.) \\ \end{align}\]

\[\therefore \]DE = \[3.11\]m 

DF = DE + EF = \[3.11\] m + \[6\] m = \[9.11\] m 

Thus, the length of the supporting wire attached to the roadway 18 m from the middle is approximately \[9.11\] m.

4. An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.

Ans: Since the height and width of the arc from the centre is 2 m and 8 m respectively, it is clear that the length of the major axis is 8 m, while the length of the semi-minor axis is 2 m. 

The origin of the coordinate plane is taken as the centre of the ellipse, while the major axis is taken along the x-axis. 

Hence, the semi-ellipse can be diagrammatically represented as

The equation of the semi-ellipse will be of the form \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1,y\ge 0,\] where a is the semi major axis 

Accordingly,

\[\begin{align}  & 2a=8\Rightarrow a=4 \\  & b=2 \\ \end{align}\]

Therefore, the equation of the semi-ellipse is \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1,y\ge 0,\] ….(1)

Let A be a point on the major axis such that AB = 1.5 m. 

Draw AC ⊥ OB.

OA = (4 – 1.5) m = 2.5 m 

The x-coordinate of point C is 2.5. 

On substituting the value of x with 2.5 in equation (1), we’ll get 

\[\begin{align}  & \dfrac{{{\left( 2.5 \right)}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1 \\  & \Rightarrow \dfrac{6.25}{16}+\dfrac{{{y}^{2}}}{4}=1 \\  & \Rightarrow {{y}^{2}}=4\left( 1-\dfrac{6.25}{16} \right) \\  & \Rightarrow {{y}^{2}}=4\left( \dfrac{9.75}{16} \right) \\  & \Rightarrow {{y}^{2}}=2.4375 \\  & \Rightarrow {y}=1.56(approx.) \\  & \therefore AC=1.56m \\ \end{align}\]

Thus, the height of the arch at a point 1.5 m from one end is approximately 1.56 m.

5. A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.

Ans: Let AB be the rod making an angle θ with OX and P (x, y) be the point on it such that AP = 3 cm. 

Then, PB = AB – AP = (12 – 3) cm = 9 cm [AB = 12 cm] 

From P, draw PQ⊥OY and PR⊥OX.

In ΔPBQ, \[\cos \theta =\dfrac{PQ}{PB}=\dfrac{x}{9}\]

In ΔPRA, \[\sin \theta =\dfrac{PR}{PA}=\dfrac{y}{3}\]

Since, $ {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1,$

$ {{\left( \dfrac{y}{3} \right)}^{2}}+{{\left( \dfrac{x}{9} \right)}^{2}}=1 $

Or,  \[{{\dfrac{x}{81}}^{2}}+{{\dfrac{y}{9}}^{2}}=1\]

Thus, the equation of the locus of point P on the rod is \[{{\dfrac{x}{81}}^{2}}+{{\dfrac{y}{9}}^{2}}=1\]

6. Find the area of the triangle formed by the lines joining the vertex of the parabola \[{{x}^{2}}=12y\] to the ends of its latus rectum.

Ans: The given parabola is \[{{x}^{2}}=12y\]. 

On comparing this equation with \[{{x}^{2}}=4ay\], we’ll get \[4a=12\Rightarrow a=3\]

\[\therefore \]The coordinates of foci are S (0, a) = S (0, 3) 

Let AB be the latus rectum of the given parabola. 

The given parabola can be roughly drawn as

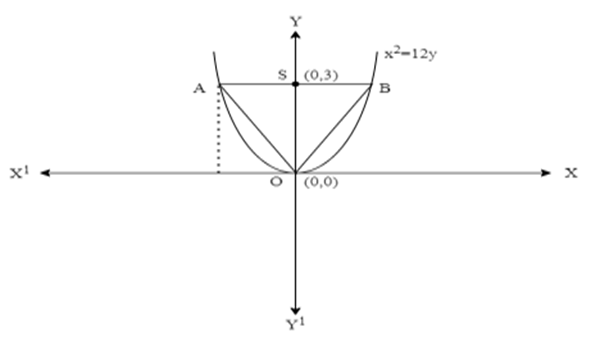
At \[y=3,\] \[{{x}^{2}}=12(3)\Rightarrow {{x}^{2}}=36\Rightarrow x=\pm 6\] 

\[\therefore \]The coordinates of A are (–6, 3), while the coordinates of B are (6, 3). 

Therefore, the vertices of ΔOAB are O (0, 0), A (–6, 3), and B (6, 3). 

Area of ΔOAB \[=\dfrac{1}{2}\left| 0\left( 3-3 \right)+\left( -6 \right)\left( 3-0 \right)+6\left( 0-3 \right) \right|uni{{t}^{2}}\]

$ =\dfrac{1}{2}\left| \left( -6 \right)\left( 3 \right)+6\left( -3 \right) \right|uni{{t}^{2}} $

$  =\dfrac{1}{2}\left| -18-18 \right|uni{{t}^{2}} $

$  =\dfrac{1}{2}\left| -36 \right|uni{{t}^{2}} $

\[=\dfrac{1}{2}\times 36uni{{t}^{2}}\]

\[=18\] \[uni{{t}^{2}}\]

Thus, the required area of the triangle is \[18\] \[uni{{t}^{2}}\].

7. A man running a racecourse notes that the sum of the distances from the two flag posts form him is always 10 m and the distance between the flag posts is 8 m. find the equation of the posts traced by the man.

Ans: Let A and B be the positions of the two flag posts and P(x, y) be the position of the man. Accordingly, PA + PB = 10.

We know that if a point moves in a plane in such a way that the sum of its distances from two fixed points is constant, then the path is an ellipse and this constant value is equal to the length of the major axis of the ellipse.

Therefore, the path described by the man is an ellipse where the length of the major axis is 10 m, while points A and B are the foci.

Taking the origin of the coordinate plane as the centre of the ellipse, while taking the major axis along the x-axis, the ellipse can be diagrammatically represented as

The equation of the ellipse will be of the form of \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1,\] where a is the semi-major axis.

Accordingly, \[2a=10\Rightarrow a=5\]

Distance between the foci \[(2c)=8\Rightarrow c=4\]

On using the relation \[c=\sqrt{{{a}^{2}}-{{b}^{2}}},\] we’ll get

$ 4=\sqrt{25-{{b}^{2}}} $

$ \Rightarrow 16=25-{{b}^{2}} $ 

$  \Rightarrow {{b}^{2}}=25-16 $ 

$  \Rightarrow {{b}^{2}}=9 $

$  \Rightarrow b=3 $

Thus, the equation of the path traced by the man is \[\dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{9}=1\]

8. An equilateral triangle is inscribed in the parabola \[{{y}^{2}}=4ax\], where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.

Ans: Let OAB be the equilateral triangle inscribed in parabola \[{{y}^{2}}=4ax\]

Let AB intersect the x-axis at point C.

Let OC = k 

From the equation of the given parabola, we have \[{{y}^{2}}=4ak\Rightarrow y=\pm 2\sqrt{ak}\]

\[\therefore \]The respective coordinates of points A and B are \[\left( k,-2\sqrt{ak} \right)\] and \[\left( k,-2\sqrt{ak} \right)\]

AB = CA + CB = \[2\sqrt{ak}+2\sqrt{ak}=4\sqrt{ak}\]

Since OAB is an equilateral triangle, \[O{{A}^{2}}=A{{B}^{2}}.\]

$ \therefore {{k}^{2}}+{{\left( 2\sqrt{ak} \right)}^{2}}={{\left( 4\sqrt{ak} \right)}^{2}} $

$  \Rightarrow {{k}^{2}}+4ak=16ak $

$  \Rightarrow {{k}^{2}}=12ak $

$  \Rightarrow k=12a $

$ \therefore AB=4\sqrt{ak}=4\sqrt{a\times 12a} $ 

$ =4\sqrt{12{{a}^{2}}} $

$ =8\sqrt{3}a $ 

Thus, the side of the equilateral triangle inscribed in parabola \[{{y}^{2}}=4ax\] is \[8\sqrt{3}a\]

Summary of Conic Sections

• A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.

• The equation of a circle with centre $(h, k)$ and the radius $r$ is $(x-h)^2+(y-k)^2=r^2$

• A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point in the plane.

• The equation of the parabola with focus at $(a, 0) a>0$ and directrix $x=-a$ is $y^2=4 a x$.

• Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose endpoints lie on the parabola.

• Length of the latus rectum of the parabola $y^2=4 a x$ is $4 a$.

• An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.

• The equation of an ellipse with foci on the $x$-axis is $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.

• Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose endpoints lie on the ellipse.

• Length of the latus rectum of the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $\frac{2 b^2}{a}$.

• The eccentricity of an ellipse is the ratio between the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.

• A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.

• The equation of a hyperbola with foci on the $x$-axis is $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

• Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.

• Length of the latus rectum of the hyperbola: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is $\frac{2 b^2}{a}$.

• The eccentricity of a hyperbola is the ratio of the distances from the centre of the hyperbola to one of the foci and to one of the vertices of the hyperbola.

Overview of Deleted Syllabus for CBSE Class 11 Maths Chapter 10 Conic Sections

Class 11 Maths Chapter 10: Exercises Breakdown

Conclusion

Chapter 10 - Conic Sections is crucial for mastering the fundamentals of ellipses, hyperbolas, and parabolas. It is important to focus on understanding their standard equations and properties. Practising the solved examples and exercises in the NCERT Solutions by Vedantu will help solidify these concepts. In the previous year's question paper, around 3 to 4 questions were asked from this chapter. Paying attention to these solutions will ensure you are well-prepared for your CBSE exams.

Other Study Material for CBSE Class 11 Maths Chapter 10

Chapter-Specific NCERT Solutions for Class 11 Maths

Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for CBSE Class 11 Maths