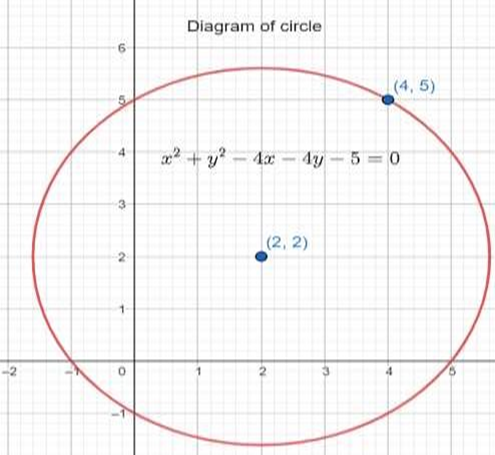
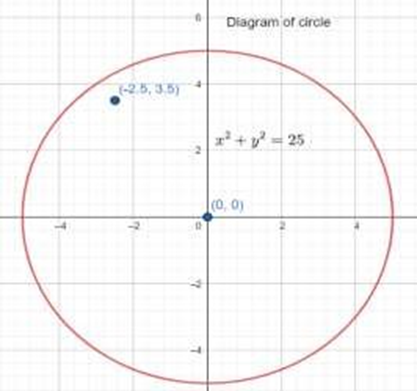
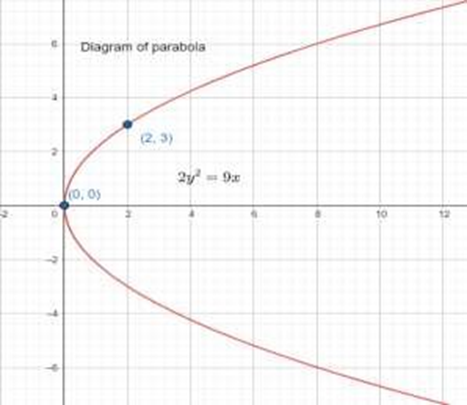
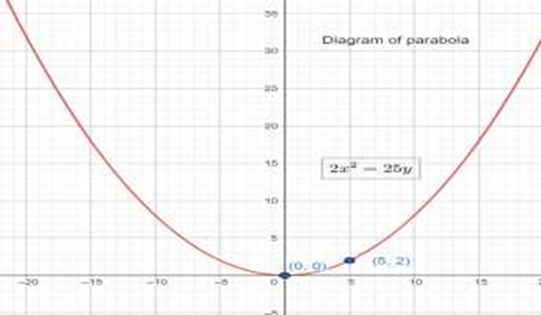
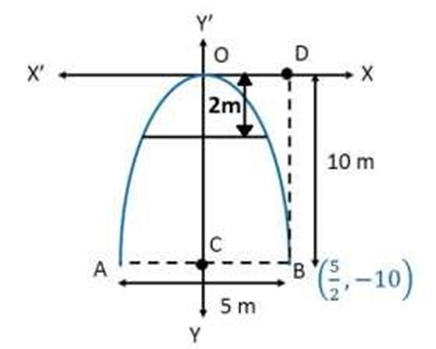
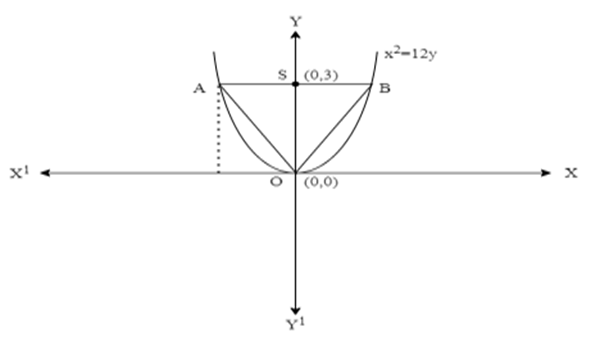
Score Higher With Vedantu's Conic Sections Class 11 Questions And Answers
FAQs on NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections
1. Where can I find NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections in PDF format?
You can download the stepwise NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections in PDF format from reliable educational platforms like Vedantu. The solutions follow the official NCERT answer key structure and align with the CBSE 2025–26 guidelines for all exercises, including Exercise 10.1, 10.2, 10.3, and the miscellaneous exercises.
2. Are the NCERT solutions for Class 11 Maths Chapter 10 Conic Sections and Straight Lines available in Hindi medium?
Yes, you can access NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections in both English and Hindi medium. These solutions are as per the latest CBSE 2025–26 syllabus and follow the official NCERT pattern, providing stepwise explanations for every problem.
3. How can I get the correct, CBSE-approved answers for Miscellaneous Exercise of Class 11 Maths Chapter 10?
The Miscellaneous Exercise solutions for Class 11 Maths Chapter 10 can be found in PDF format on NCERT-aligned educational websites. These answers are given stepwise and checked as per the NCERT answer format, ensuring you get the correct CBSE method for all types of conic section questions.
4. Do NCERT Solutions for Class 11 Maths Chapter 10 cover every exercise like 10.1, 10.2, and 10.3 with stepwise explanations?
Yes, the NCERT Solutions for Class 11 Maths Chapter 10 meticulously solve every exercise (10.1, 10.2, 10.3, and miscellaneous), providing stepwise and detailed answers as per NCERT and CBSE format. Each solution explains the correct approach, matching the latest syllabus requirements.
5. Is the solution for Straight Lines included in NCERT Solutions of Class 11 Maths Chapter 10?
Class 11 Maths Chapter 10 in the official NCERT book is dedicated to Conic Sections. Straight Lines is generally covered in Chapter 9, but if you are searching for Straight Lines solutions, make sure to check the relevant chapter. However, some supplementary materials do include Straight Lines problems for combined practice.
6. How to solve the intext questions of Class 11 Maths Chapter 10 with the NCERT stepwise method?
To solve intext questions in Chapter 10, read the solved examples and follow the stepwise explanation shown in NCERT Solutions. Start by understanding the concept of conic sections (parabola, ellipse, hyperbola), apply the formulas as per the question, and write each calculation in sequence, just like the NCERT answer format recommends.
7. Are the Class 11 Maths Chapter 10 NCERT Solutions provided as per CBSE 2025–26 syllabus?
All solutions available for Class 11 Maths Chapter 10 strictly follow the updated CBSE 2025–26 syllabus. The answers are written in the latest NCERT style and provide complete explanations for textbook and miscellaneous exercise questions, ensuring students score full marks in exams.
8. What is the stepwise approach to solve Exercise 10.2 in Class 11 Maths Chapter 10?
For Exercise 10.2, begin by identifying the conic section and the given equation. Use standard formulas, substitute the provided values, and simplify step-by-step, ensuring your solution matches the NCERT pattern. Each answer should include all calculations and final answers as per CBSE requirements.
9. Can I rely on these NCERT Solutions for scoring full marks in Class 11 Maths Chapter 10 exams?
These NCERT Solutions are CBSE-approved and designed as per NCERT guidelines, making them reliable for exam preparation. They include all intext and exercise questions with official answer formats, enhancing conceptual clarity and improving your chances of scoring full marks.
10. How can I access class 11 maths straight lines miscellaneous exercise solutions?
While the miscellaneous exercise for Straight Lines is part of Chapter 9 in NCERT Class 11 Maths, you can find the solutions compiled in PDF format on educational sites. These answers are structured following the NCERT stepwise and CBSE-approved pattern, ensuring complete understanding.
11. What common mistakes should I avoid while writing answers for conic section questions in the NCERT exam as per CBSE format?
Common mistakes include skipping steps, not highlighting formulas, or using shortcut calculations. Always write each step, include correct NCERT formulas, justify your answer with explanations, and ensure that your solutions are presented in the official CBSE answer format.
12. Are these solutions suitable for CBSE Board and competitive exam preparation?
Yes, since the NCERT Solutions for Class 11 Maths Chapter 10 are prepared according to the latest CBSE 2025–26 syllabus and follow the official NCERT answer style, they are suitable for both board exams and the foundation for competitive exams like JEE (Main) and other entrance tests.
13. Why is it important to follow the NCERT answer format while solving conic section problems?
Using the NCERT answer format is essential as it ensures each step is clearly recorded, matches the evaluation criteria of CBSE, and prevents loss of marks due to skipped methods. This methodical structure also helps in clear conceptual understanding of curves like parabola, ellipse, and hyperbola.
14. Can I find error-free and explained textbook answers for every question in NCERT Solutions for Class 11 Maths Chapter 10?
Yes, these NCERT Solutions are thoroughly checked to be error-free and provide explained, stepwise textbook answers as per CBSE curriculum. Each answer covers all required steps and workings for maximum clarity.