Symmetry Questions and Answers - Free PDF Download
In NCERT Solutions Class 6 Maths Chapter 9 Exercise 9 2, you’ll explore interesting ideas about symmetry and how shapes can look the same in different ways. This part of the chapter explains things like lines of symmetry, angles of rotation, and how to easily spot patterns, making geometry feel like a fun puzzle. If you ever felt confused about rotational symmetry, this exercise will clear up those doubts quickly. For easy chapter-wise study planning, you can check the Class 6 Maths syllabus.
Table of Content
The step-by-step NCERT Solutions from Vedantu are made just for you—they break down tough questions into simple explanations, with lots of examples so you can practise and get it right. Plus, you can download helpful PDFs anytime you want, so revision and homework become stress-free. Don’t forget, you can always access more solutions from the NCERT Solutions for Class 6 Maths collection.
Exercise 9.2
Figure it Out
1. Find the angles of symmetry for 2. Which of the following figures have more than one angle of symmetry? the given figures about the point marked •.
Ans: To determine the angle of symmetry, let’s rotate the figure by 90°.
After a 90° rotation, the figure remains unchanged, indicating that 90° is the angle of symmetry.
A 90° rotation results in a new figure that does not overlap with the original. The figure returns to its original shape only after completing a full 360° rotation, meaning 360° is also an angle of symmetry.
The figure remains unchanged after a 180° rotation, which confirms that 180° is another angle of symmetry.
2. Which of the following figures have more than one angle of symmetry?
Ans: All options except (g) have multiple angles of symmetry. This indicates that those figures possess various ways to rotate and maintain their original appearance.
3. Give the order of rotational symmetry for each figure:
Ans:
(a) 2
(b) 1
(c) 6
(d) 3
(e) 4
(f) 5
Figure it Out
1. Colour the sectors of the circle below so that the figure has
i) 3 angles of symmetry,
ii) 4 angles of symmetry,
iii) what are the possible numbers of angles of symmetry you can obtain by colouring the sectors in different ways?
Ans: (a) It will appear the same after each 120° rotation.
(b) It will look the same after every 90° rotation.
(c) There are four possible ways.
2. Draw two figures other than a circle and a square that have both reflection symmetry and rotational symmetry.
Ans:
3. Draw, wherever possible, a rough sketch of:
a. A triangle with at least two lines of symmetry and at least two angles of symmetry.
Ans:
b. A triangle with only one line of symmetry but not having rotational symmetry.
Ans:
c. A quadrilateral with rotational symmetry but no reflection symmetry.
Ans:
d. A quadrilateral with reflection symmetry but not having rotational symmetry.
Ans:
4. In a figure, 60° is the smallest angle of symmetry. What are the other angles of symmetry of this figure?
Ans: Since 60° is the smallest angle, any angle that is a multiple of 60° up to 360° is also an angle of symmetry. The angles include 120°, 180°, 240°, 300°, and 360°. This means the figure can maintain its symmetry at these specific rotational angles.
5. In a figure, 60° is an angle of symmetry. The figure has two angles of symmetry less than 60°. What is its smallest angle of symmetry?
Ans: The smallest angle of symmetry is calculated as 60° divided by 3, which equals 20°.
6. Can we have a figure with rotational symmetry whose smallest angle of symmetry is:
a. 45°?
Ans: Yes, because 360 is divisible by 45.
b. 17°?
Ans: No, because 360 is not divisible by 17.
7. This is a picture of the new Parliament Building in Delhi.
a. Does the outer boundary of the picture have reflection symmetry? If so, draw the lines of symmetries. How many are they?
Ans: The outer boundary exhibits rotational symmetry around its centre.
The smallest angle of rotation is calculated as 360° ÷ 3 = 120°.
Additional angles of rotation are 240° and 360°.
b. Does it have rotational symmetry around its centre? If so, find the angles of rotational symmetry.
Ans: The outer boundary displays reflection symmetry, featuring 3 lines of symmetry.
8. How many lines of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
Ans:
A 3-sided regular polygon (equilateral triangle) has 3 lines of symmetry.
A 4-sided regular polygon (square) has 4 lines of symmetry.
A 5-sided regular polygon (regular pentagon) has 5 lines of symmetry.
A 6-sided regular polygon (regular hexagon) has 6 lines of symmetry.
We can see a clear pattern: the number of sides in a regular polygon equals the number of lines of symmetry. The number sequence is: 3, 4, 5, 6, 7, …
9. How many angles of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
Ans: The number of angles of symmetry is equal to the number of lines of symmetry. Therefore, we have the following number sequence: 3, 4, 5, 6, 7, …
10. How many lines of symmetry do the shapes in the last shape sequence in Chapter 1, Table 3, the Koch Snowflake sequence, have? How many angles of symmetry?
Ans:
11. How many lines of symmetry and angles of symmetry does Ashoka Chakra have?
Ans: The Ashoka Chakra features 24 spokes that are evenly distributed. These 24 spokes form 12 pairs. A line drawn through each opposite pair represents a line of symmetry, resulting in a total of 12 lines of symmetry. The smallest angle of symmetry is calculated as 360° ÷ 12 = 30°. The other angles of symmetry are multiples of this angle up to 360°. These include 60°, 120°, 150°, and so on, totaling 12 angles.
Benefits of NCERT Solutions for Class 6 Maths Chapter 1 Exercise 9.2 Symmetry
Clear Explanation of Symmetry Concepts: The solutions provide a thorough understanding of symmetry, focusing on lines of symmetry and how to identify them in different shapes.
Step-by-Step Solutions: Each problem in Exercise 9.2 is explained in a detailed, step-by-step manner, making it easier for students to follow and learn.
Aligned with CBSE Syllabus: The solutions are fully aligned with the CBSE Class 6 Maths syllabus, ensuring that students cover all necessary topics.
Improved Problem-Solving Skills: Regular practice with these solutions enhances students' ability to solve symmetry problems confidently and accurately.
Boosts Exam Preparation: These solutions serve as a great tool for revising important concepts and help students prepare effectively for their exams.
FREE PDF Access: Students can easily download the NCERT Solutions for Exercise 9.2 in FREE PDF format, making study material accessible anytime for revision.
Strengthens Foundation: Mastering the concepts of symmetry at this level helps in building a solid foundation for more advanced geometry topics in higher classes.
Practice and Revision: With ample practice questions provided, students can strengthen their understanding of symmetry and ensure they are well-prepared for assessments.
Application of Concepts: The solutions help students apply symmetry concepts to solve real-life problems involving patterns and designs.
Enhances Visualisation Skills: Learning to identify symmetry in different shapes enhances students' spatial and visualisation abilities, essential for geometry.
Class 6 Maths Chapter 9: Exercises Breakdown
Important Study Material Links for Class 6 Maths Chapter 9 - Symmetry
Conclusion
NCERT Solutions for Class 6 Maths Chapter 1 Exercise 9.2 on Symmetry provides a solid foundation for students to grasp essential mathematical concepts. By offering clear, step-by-step explanations, these solutions simplify complex problems and make learning easier. Regular practice with these solutions not only aids in exam preparation but also enhances problem-solving skills and boosts confidence. Using these solutions ensures that students can effectively tackle questions related to Symmetry, helping them succeed in their studies.
Chapter-wise NCERT Solutions Class 6 Maths
The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Related Important Links for Class 6 Maths
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.
FAQs on NCERT Solutions For Class 6 Maths Chapter 9 Symmetry Exercise 9.2 - 2025-26
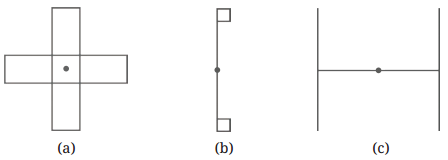
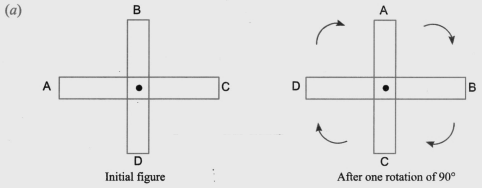
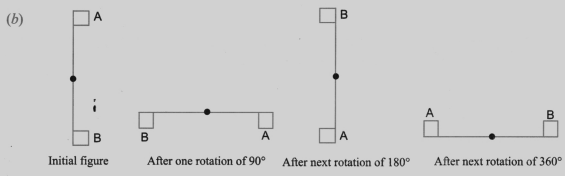
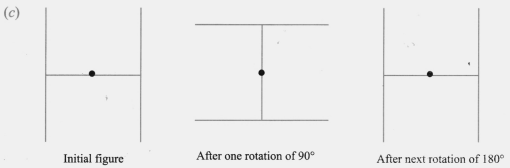
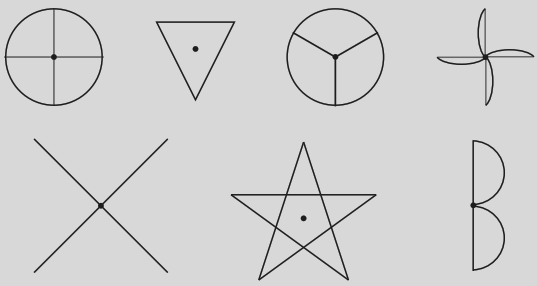
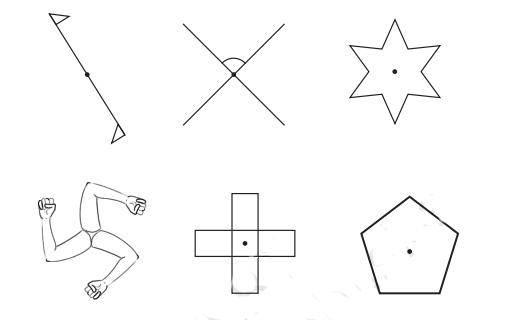
1. How are the lines of symmetry for different shapes correctly identified in the NCERT Solutions for Class 6 Maths Chapter 9?
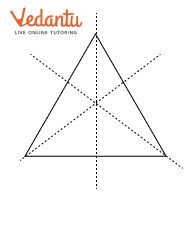
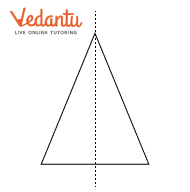
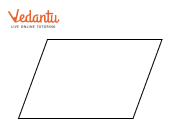
The solutions demonstrate a systematic approach. They guide you to first observe the shape and then imagine a line of reflection. The core method involves folding the shape along a potential line to see if one half perfectly overlaps the other. For each problem, the steps clearly show how to verify if a line is indeed a line of symmetry.
2. What is the correct method to solve problems asking to complete symmetrical figures in Exercise 9.2, as shown in the NCERT solutions?
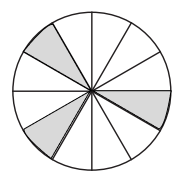
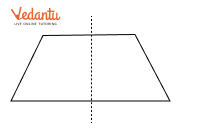
The NCERT solutions teach a methodical way to complete shapes. The key is to treat the given line as a mirror line. For every point on the existing part of the figure, you learn to plot a corresponding point on the other side at the exact same distance from the line. Connecting these new points correctly completes the symmetrical figure as per NCERT guidelines.
3. Are the NCERT Solutions for Class 6 Maths Chapter 9 updated for the 2025-26 academic year?
Yes, the NCERT Solutions for Class 6 Maths Chapter 9 are fully aligned with the latest CBSE syllabus for the 2025-26 academic session. They are designed to help you master the concepts of symmetry exactly as prescribed in the NCERT textbook, ensuring you are preparing with the most current and relevant material.
4. Beyond just finding answers, how do the step-by-step NCERT Solutions for Chapter 9 help in understanding the core concept of symmetry?
The step-by-step solutions do more than provide final answers. They break down the process of identifying symmetry, forcing you to think about balance and reflection. By following each logical step, you move from simple observation to a deeper geometric understanding of why a shape is symmetrical, which is a foundational skill for higher-level geometry.
5. Why is it important to follow the precise steps given in the NCERT Solutions when drawing a line of symmetry, instead of just guessing?
Guessing a line of symmetry can often lead to errors, especially in complex figures. Following the precise steps from the NCERT Solutions is crucial because it reinforces the mathematical definition of symmetry. This methodical approach ensures accuracy, teaches you how to justify your answer, and helps avoid common mistakes like identifying a diagonal as a line of symmetry when it is not.
6. How can using the NCERT Solutions for Class 6 Maths Chapter 9 improve my exam scores?
Using these NCERT solutions can significantly boost exam performance in several ways:
They teach the correct format for presenting answers, which helps in securing full marks.
By practising with verified solutions, you build confidence and reduce errors.
You gain a thorough understanding of the types of questions that can be asked from the Symmetry chapter.
7. What common mistakes do students make when solving symmetry problems, and how do the NCERT Solutions help to prevent them?
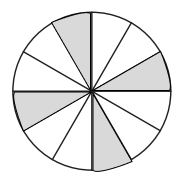
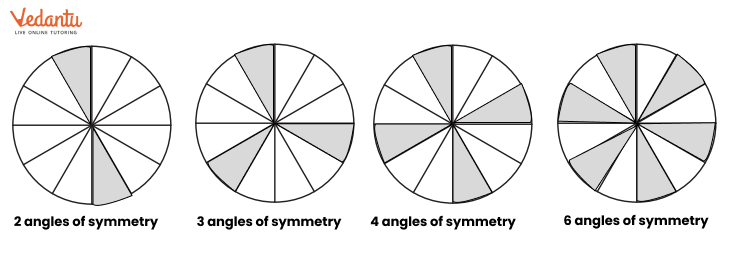
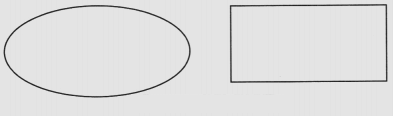
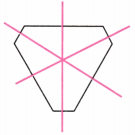
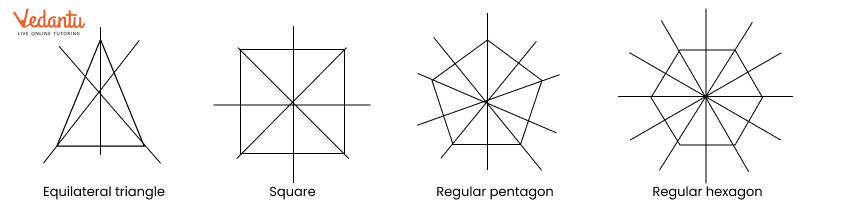
A common mistake is confusing a line that divides a shape into two equal areas with a true line of symmetry (e.g., a diagonal in a rectangle). Another error is miscounting the number of symmetry lines in regular polygons. The NCERT solutions prevent these by providing clear, step-by-step visual explanations for each problem, highlighting the exact criteria for a line of reflection and showing the complete set for each shape.
8. What types of geometrical shapes are covered in the NCERT Solutions for Chapter 9, Exercise 9.2?
The NCERT solutions for Exercise 9.2 cover a wide range of shapes to build a strong foundation. You will find solved problems for:
Different types of triangles (isosceles, equilateral).
Various quadrilaterals (squares, rectangles).
Other polygons and common geometrical figures.
Alphabets and other real-world shapes to test your understanding of lines of symmetry.
