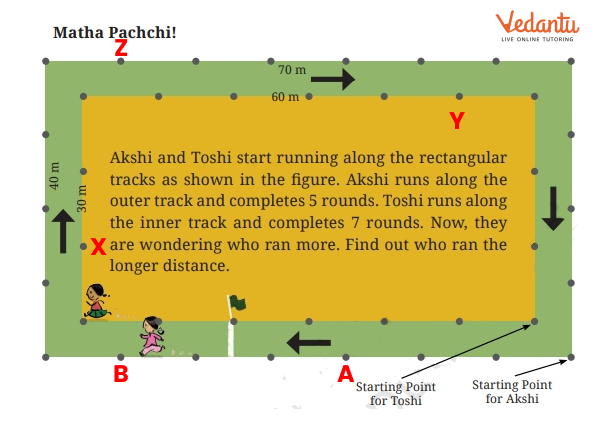
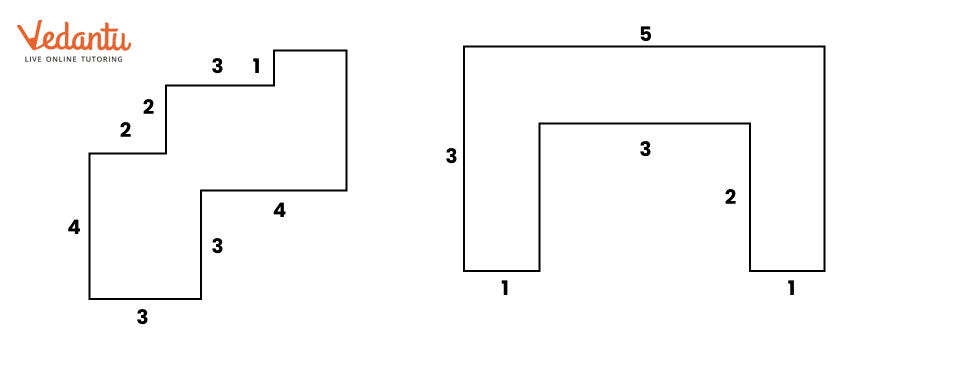
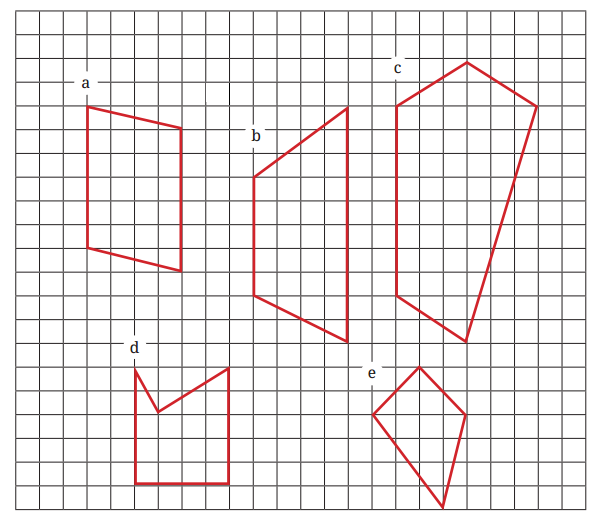
Master Perimeter And Area Class 6 With Vedantu's Expert Guidance
FAQs on NCERT Solutions For Class 6 Maths Chapter 6 Perimeter And Area - 2025-26
1. What are the main topics covered in the NCERT Solutions for Class 6 Maths Chapter 6 Perimeter and Area?
The NCERT Solutions for Class 6 Maths Chapter 6 focus on calculating the perimeter and area of basic shapes including rectangles, squares, triangles, and composite figures. The chapter also covers measurement units, real-life applications, and problem-solving steps as per the CBSE 2025–26 syllabus.
2. How do you calculate the perimeter of a rectangle in NCERT Solutions for Class 6 Maths Chapter 6?
To calculate the perimeter of a rectangle, use the formula:
- Perimeter = 2 × (length + breadth)
3. What formula is used to find the area of a rectangle according to Class 6 Maths Chapter 6?
The area of a rectangle is found by multiplying its length and breadth:
- Area = length × breadth
4. Why is it important to understand both perimeter and area when solving geometry questions in Class 6?
Understanding both perimeter (boundary length) and area (space inside) is crucial for solving geometry questions because they measure different properties of shapes. Knowing both helps students apply mathematics to real-life scenarios, such as fencing a field or laying a carpet, as emphasized in the NCERT solutions.
5. How can you differentiate between perimeter and area in NCERT Class 6 Maths Chapter 6?
- Perimeter is the total length of the sides around a shape (measured in linear units like cm or m).
- Area is the amount of space contained within the shape's boundaries (measured in square units like cm² or m²).
6. What are the different measurement units discussed in Class 6 Maths Chapter 6 for perimeter and area?
For perimeter, common units are centimeters (cm) and meters (m). For area, units include square centimeters (cm²) and square meters (m²). The chapter underlines the importance of using correct units for accurate calculations, in line with CBSE curriculum.
7. How do NCERT Solutions for Class 6 Maths Chapter 6 help in solving real-life word problems involving perimeter and area?
The solutions provide step-by-step examples showing how perimeter and area concepts are used in daily activities, for example:
- Calculating fencing for a garden (perimeter)
- Estimating tiles needed for flooring (area)
8. What are some common mistakes students should avoid when solving perimeter and area questions for Class 6?
Common mistakes include:
- Mixing up perimeter and area formulas
- Forgetting to use appropriate measurement units
- Adding only two sides in perimeter
- Calculating area for irregular shapes without dividing into basic shapes first
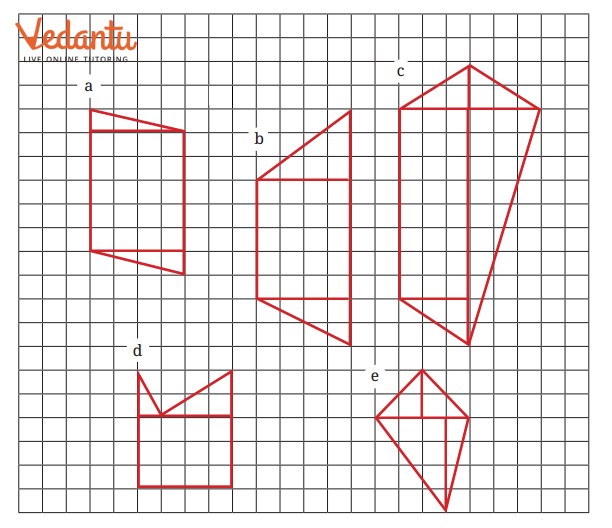
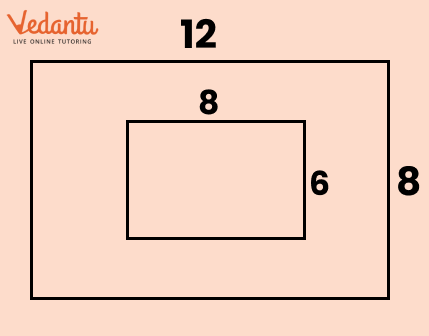
9. How do you solve problems related to composite figures in Class 6 Maths Chapter 6?
To solve composite figure questions:
- Divide the figure into rectangles and/or triangles
- Find the area of each simple shape
- Add the areas to get the total
10. Why is learning perimeter and area considered foundational for advanced geometry as per the CBSE Class 6 Maths syllabus?
Mastering perimeter and area builds the groundwork for advanced topics like volume, surface area, and more complex geometric reasoning. The conceptual clarity developed here is vital for higher mathematics in future classes, as highlighted in NCERT Class 6 Maths Chapter 6 solutions.
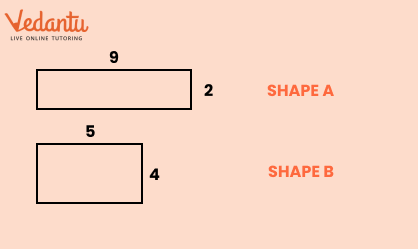
11. Can the same area have different perimeters? Illustrate this concept as discussed in Class 6 Maths Chapter 6.
Yes, shapes can have the same area but different perimeters. For example, a rectangle of 6×4 units and a square of 5×5 units both have areas close to 24–25 units², but their perimeters differ. The solutions in Class 6 Maths perimeter and area use such examples to prevent misconceptions.
12. How does the NCERT Solutions for Class 6 Maths Chapter 6 guide students on using formulas for new shapes or changed dimensions?
The solutions encourage applying perimeter and area formulas to any rectangle, square, or triangle, and even adapting them when the shape changes (e.g., straightening a rectangle into a square, then finding the new side length). This builds flexible problem-solving skills per CBSE guidelines.
13. What is the approach for solving word problems involving cost calculations, such as fencing or tiling, in Class 6 Maths Chapter 6?
The typical approach is:
- Step 1: Calculate the relevant perimeter or area
- Step 2: Multiply by the cost per unit for total cost
14. What steps should you follow if you get stuck on an exercise question in NCERT Solutions for Maths Class 6 Chapter 6?
If stuck, students should:
- Review the related example problems in the solutions
- Break down the question into smaller steps
- Double-check the use of formulas and units