Prime Time - Exercise-wise Questions and Answers For Class 6 Maths - Free PDF Download
Chapter 5 Prime Time focuses on the key concepts of prime numbers, composite numbers, and factorization. Students are introduced to prime numbers and their significance in mathematics. The chapter also covers the identification of factors, multiples, and common divisors. Understanding prime and composite numbers is essential for building a strong foundation in number theory. The NCERT Solutions provide a clear explanation of these topics, making it easier for students to solve problems and develop problem-solving skills.
 Table of Content
Table of ContentOur Class 6 Maths NCERT Solutions PDF breaks the lesson into easy-to-understand explanations, making learning fun and interactive. Students will develop essential language skills with engaging activities and exercises. Check out the revised CBSE Class 6 Maths Syllabus and start practising the Maths Class 6 Chapter 5.
Glance on Class 6 Number Play Chapter 5
Introduction to prime numbers and composite numbers.
Definition and identification of factors and multiples.
Common divisors and common multiples.
Factorization and its applications.
Finding prime factors of a number.
Relationship between HCF (Highest Common Factor) and LCM (Least Common Multiple).
Access NCERT Solutions for Class 6 Maths Chapter 5
5.1 Common Multiples and Common Factors Figure it Out (Page No. 108)
Question 1. At what number is ‘idli-vada’ said for the 10th time?
Solution:
To determine the 10th occurrence of “idli- vada”; we need to identify the numbers that are multiples of both 3 and 5.
The numbers for which “idli-vada” is said are the multiples of 15.
This sequence is: 15,30,45,60, 75,90, 105, 120,135,150,…
Thus, the 10th number for which players should say “idli-vada” is 150.
Question 2.If the game is played for the numbers from 1 till 90, find out:
(a) How many times would the children say ‘idli ’ (including the times they say ‘idli- vada’)?
(b) How many times would the children say ‘vada ’ (including the times they say ‘idli-vada’)?
(c) How many times would the children say ‘idli-vada ’?
Solution:
(a) Idli is said for multiples of 3. Between 1 and 90 the multiples of 3 are 3, 6, 9, 12, 15, 18, …….. 90.
There are 30 such numbers.
Hence the children would say idli 30 times.
(b) Vada is said for multiples of 5. Between 1 and 90 the multiples of 5 are 5, 10,15, 20, 25,…
There are 18 such numbers.
(c) Idli-Vada is said for multiples of both 3 and 5, which is multiple of 15. Between 1 and 90, there are 15, 30,45,60,75,90. There are 6 such numbers.
Question 3. What if the game was played till 900? How would your answers change?
Solution: There are 300 multiples of 3 between 1 and 900 and there are 180 multiples of 5 between 1 and 900. There are 60 multiples of 15 between 1 and 900.
(a) “idli” is said: 300 times (including the times “idli-vada” is said).
(b) “vada” is said: 180 times (including the times “idli-vada” is said).
(c) “idli-vada” is said: 60 times.
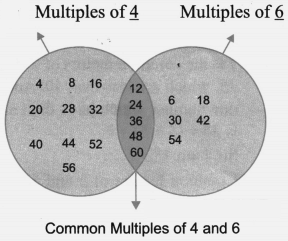
Question 4. Is this figure somehow related to the ‘idli- vada’ game? (Hint: Imagine playing the game till 30. Draw the figure if the game is played till 60.)
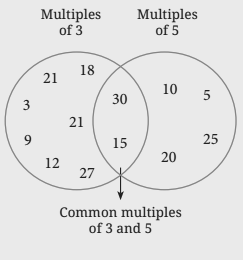
Solution: Yes, this figure is related to the ‘idli-vada’ game. Figure below for game played till 60.
Intext Questions
Question 1. Find out other such numbers that are multiples of both 3 and 5. These numbers are called ___ (Page 107)
Solution: Numbers that are multiples of both 3 and 5 are called common multiples. The smallest common multiple of 3 and 5 is 15, and other such numbers include 30, 45, 60, and so on.
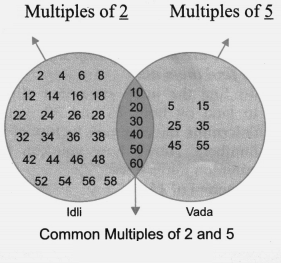
Question 2. Let us now play the ‘idli-vada ’ game with different pairs of numbers: (Page 108)
(a) 2 and 5
Solution:
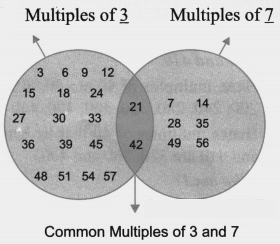
(b) 3 and 7
Solution:
(c) 4 and 6
Solution:
Question 3. Which of the following could be the other number: 2, 3, 5, 8,10? (Page 109)
Answer: 2
Question 4. What jump size can reach both 15 and 30? There are multiple jump sizes possible. Try to find them all. f (Page 110)
Solution: To find the jump sizes that allow Jumpy to land on both 15 and 30, you need to determine the common factors of these two numbers. Here’s how you can find these common jump sizes:
Factors of 15:
15 can be factored into: 15 = 3 × 5
The factors of 15 are: 1, 3, 5, 15
Factors of 30:
30 can be factored into: 30 = 2 × 3 × 5
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
The common factors between these two lists are: 1, 3, 5, 15. So, the jump sizes that will allow Jumpy to land on both 15 and 30 are the common factors of 15 and 30.
Therefore, the jump sizes that will enable Jumpy to land on both 15 and 30 are: 1, 3, 5, 15
Question 5. Which numbers are both shaded and circled? What are these numbers called? (Page 110)
Solution: 36,48,60 are both shaded and circled. These numbers are called common multiples.
5.1 Common Multiples and Common Factors Figure it Out (Page No. 110 – 111)
Question 1. Find all multiples of 40 that lie between 310 and 410.
Solution:
Here, multiples df 40 are 40, 80, 120, 160, 200, 240, 280, 320, 360, 400, 440
Hence multiples of 40 that lie between 310 and 410 are 320, 360 and 400.
Question 2. Who am I?
(a) I am a number less than 40. One of my factors is 7. The sum of my digits is 8.
(b) I am a number less than 100. Two of my factors are 3 and 5. One of my digits is l more than the other.
Solution:
(a) 7 is the common factors of 7, 14, 21,28, 35, which are less than 40. And there is one number which have digit sum of 8, is 35 = (3 + 5) = 8.
So, I am 35.
(b) Common factors of 3 and 5 are 15, 30, 45, 60, 75,90, (which are less than 100). And there is one number which one of digit is 1 more than the other that is 45. So, I am 45.
Question 3. A number for which the sum of all its factors is equal to twice the number is called a perfect number. The number 28 is a perfect number. Its factors are 1, 2, 4, 7, 14 and 28. Their sum is 56 which is twice 28. Find a perfect number between 1 and 10.
Solution:
The only perfect number between 1 and 10 is 6.
Proper divisors are 1, 2, 3, 6
Sum of proper divisors: 1 + 2 + 3 + 6 = 12
12 is twice of 6, hence 6 is a perfect number.
Question 4. Find the common factors of:
(a) 20 and 28
(b) 35 and 50
(0 4, 8 and 12
(d) 5, 15 and 25
Solution:
(a) Factors of 20 are 1, 2, 4, 5, 10, 20 Factors of 28 are 1, 2, 4, 7, 14, 28 Common factors are 1, 2, 4
(b) Factors of 35 are 1, 5, 7, 35 Factors of 50 are 1, 2,’5, 10, 25, 50 Common factors are 1,5
(c) Factors of 4 are 1, 2, 4 Factors of 8 are 1, 2, 4, 8 Factors of 12 are 1, 2, 3, 4, 6, 12 Common factors are 1, 2, 4
(d) Factors of 5 are 1, 5 Factors of 15 are 1, 3, 5, 15 Factors of 25 are 1, 5, 25 Common factors are 1,5.
Question 5. Find any three numbers that are multiples of 25 but not multiples of 50.
Solution:
Numbers that are multiples of 25 are 25, 50, 75, 100, 125, 150, 175, …
Numbers that are multiples of 50 are 50, 100, 150, 200, 250,300,…
Hence, the numbers that are multiples of 25 but not multiples of 50 are 25, 75, 125, 175,…
Question 6. Anshu and his friends play the ‘idli-vada ’ game with two numbers, which are both smaller than 10. The first time anybody says ‘idli-vada’ is after the number 50. What could the two numbers be which are assigned ‘idli’and ‘vada’?
Solution: If ‘idli-vada’ is said after number 50 it means that the least common multiple (LCM) of the two numbers must be slightly greater than 50. The LCM of 6 and 9 is 54,’.which is the first common multiple after 50, making 6 and 9 the possible numbers. Hence the two numbers could be 6 and 9.
Question 7. In the treasure hunting game, Grumpy has kept treasures on 28 and 70. What jump sizes will land on both the numbers?
Solution:
Factors of 28 = 1, 2, 4, 7, 14, 28
Factors of 70 = 1,2, 5, 7, 10, 14, 35, 70
Common factors are 1, 2, 7 and 14
Hence jump sizes which will land at both 28 and 70 are 1, 2, 7 and 14.
Question 8. In the diagram below, Guna has erased all the numbers except the common multiples. Find out what those numbers could be and fill in the missing numbers in the empty regions.
Solution:
Multiples of 6 Multiples of 8
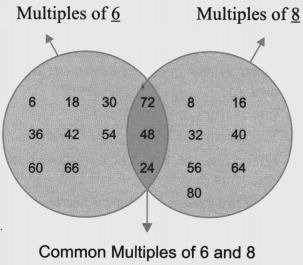
Here 6 could also be replaced by 3.
As 24, 48, 72, are also common multiples of 3 and 8.
Question 9. Find the smallest number that is a multiple of all the numbers from 1 to 10 except for 7.
Solution: To find smallest number that is a multiple of all the numbers between 1 and 10 (both inclusive), let us first find the LCM of all the numbers between 1 and 10 except 7.
Here, 1 = 1
2 = 2
3 = 3
4 = 2 × 2
5 = 5
6 = 2 × 3
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
∴ LCM = Product of the highest power of the prime factors including other factors
= 2 × 2 × 2 × 3 × 3 × 5
= 360
Hence, the smallest number that is a multiple of all the numbers from 1 to 10 except for 7 is 360.
Question 10. Find the smallest number that is a multiple of all the numbers from 1 to 10.
Solution: To find the smallest number that is divisible by all the numbers from 1 to 10 (both inclusive), let us first find the LCM of all the numbers between 1 and 10 (both inclusive)
we have
1 = 1
2 = 2
3 = 3
4 = 2 × 2
5 = 5
6 = 2 × 3
7 = 7
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
∴ LCM = Product of the highest power of the prime factors including other factors = 2 × 2 × 2 × 3 × 3 × 5 × 7
= 8 ×9 × 5 × 7 = 2520
The smallest number that is a multiple of all the numbers from 1 to 10 is 2520
5.2 Prime Numbers Figure it Out (Page No. 114 – 115)
Question 1. We see that 2 is a prime and also an even number. Is there any other even prime?
Solution: No, 2 is the only even prime number. Since 2 is the only even number that meets the criteria of a prime number (its only divisors are 1 and 2), it is the only even prime number. All other even numbers are divisible by 2 and at least one other number, so they are not prime.
Question 2. Look at the list of primes till 106. What is the smallest difference between two successive primes? What is the largest difference?
Solution: To find the smallest difference between two successive prime numbers up to 100, let’s list the prime numbers in that range and calculate the differences between each pair: Prime numbers up to 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Differences between successive primes:
3 – 2 = 1
5 – 3 = 2
7 – 5 = 2
11 – 7 = 4
13 – 11 = 2
17 – 13 = 4
19 – 17 = 2
23 – 19 = 4
29 – 23 = 6
31 – 29 = 2
37 – 31 = 6
41 – 37 = 4
43 – 41 = 2
47 – 43 = 4
53 – 47 = 6
59 – 53 = 6
61 – 59 = 2
67 – 61 = 6
71 – 67 = 4
73 – 71 = 2
79 – 73 = 6
83 – 79 = 4
89 – 83 = 6
97 – 89 = 8
The smallest difference between two successive primes up to 100 is 1 (between the primes 2 and 3).
The largest difference between two successive primes up to 100 is 8, which occurs between the primes 89 and 97.
Question 3. Are there an equal number of primes occurring in every row in the table on the previous page (See NCERT Textbook, Page 113)? Which decades have the least number of primes? Which have the most number of primes?
Solution: There is not an equal number of primes in every row. The number of primes varies between rows. The decade 90-99 has the least number of primes with only 1 prime (97).
The decades 0-9 and 10-19 have the greatest number of primes, each with 4 primes.
Question 4. Which of the following numbers are prime?
23, 51, 37, 26
Solution: 23 and 37 have no divisors other than 1 and themselves, making them prime.
Question 5. Write three pairs of prime numbers less than 20 whose sum is a multiple of 5.
Solution: Three pairs of prime numbers less than 20 whose sum is a multiple of 5 are: (2, 3), (2, 13) and (7, 13).
Question 6. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.
Solution: The valid pairs of prime numbers up to 100 that consist of the same digits are: (13, 31), (17, 71), (37, 73) and (79, 97).
Question 7. Find seven consecutive composite numbers between 1 and 100.
Solution: The seven consecutive composite numbers are: 90,91,92, 93,94, 95,96.
Question 8. Twin primes are pairs of primes having a difference of 2. For example, 3 and 5 are twin primes. So are 17 and 19. Find the other twin primes between l and 100.
Solution: The twin primes between 1 and 100 other than 3 and 5,17 and 19 are as follows: (5, 7), (11, 13), (29, 31), (41, 43), (59, 61), (71, 73).
Question 9. Identify whether each statement is true or false. Explain.
(a) There is no prime number whose units digit is 4.
(b) A product of primes can also be prime.
(c) Prime numbers do not have any factors.
(d) All even numbers are composite numbers.
(e) 2 is a prime and so is the next number, 3. For every other prime, the next number is composite.
Solution:
(a) True.
A prime number must end in 1, 3, 7, or 9 (except for the number 2) because any number ending in 0, 2, 4, 6 or 8 is divisible by 2.
Thus, there is no prime number whose units digit is 4.
(b) False.
A product of prime numbers is only prime if it involves exactly one prime number. When you multiply two or more prime numbers together, the result is always a composite number, not a prime. As this number has 2 factors now.
(c) False.
Prime numbers have exactly two factors 1 and itself.
(d) False.
The number 2 is an even number, but it is not composite. As it is a prime number.
(e) True.
For every prime number greater than 2, the next number is composite.
Question 10. Which of the following numbers is the product of exactly three distinct prime numbers: 45, 60, 91, 105, 330?
Solution: Here, 45 = 3 × 3 × 5 (2 distinct primes)
60 = 2 × 2 × 3 × 5(3 distinct primes)
91 = 7 × 13 (2 distinct primes)
105 = 3 × 5 × 7 (3 distinct primes)
330 = 2 × 3 × 5 × 11 (4 distinct primes)
Number 105 is the product of exactly three distinct prime numbers i.e. 3 × 5 × 7.
Question 11. How many three-digit prime numbers can you make using each of 2, 4 and 5 once?
Solution: 2, 4 and 5 cannot form a single prime number.
Because, when its units digit is 2 or 4 it is divided by 2, and when units digits is 5 it is divided by 5 so that’s why 2, 4 and 5 cannot form a prime number.
Question 12.
Observe that 3 is a prime number, and 2 × 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Solution:
The five prime numbers for which doubling and adding 1 gives another prime are:
2 (since 2 × 2 + 1 = 5)
3 (since 2 × 3 + 1 = 7)
5 (since 2 × 5 + 1 = 11)
11 (since 2 × 11 + 1 = 23)
23 (since 2 × 23 + 1 = 47)
Intext Questions
Question 1. How many prime numbers are there from 21 to 30? (Page 113)
Solution: In total, there are 2 prime numbers between 21 and 30.
They are 23 and 29.
Question 2. How many composite numbers are there from 21 to 30? (Page 113)
Solution: Total number of composite numbers from 21 to 30 is 8.
They are 21,22,24,25, 26, 27, 28, 30.
5.3 Co-prime Numbers for Safekeeping Treasures Figure it Out (Page No. 120)
Question 1. Find the prime factorizations of the following numbers: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Solution:
(a) The prime factorization of 64 is 2 × 2 × 2 × 2 × 2 × 2.
(b) The prime factorization of 104 is 2 × 2 × 2 × 13.
(c ) The prime factorization of 105 is 3 × 5 × 7.
(d) The prime factorization of 243 is 3 × 3 × 3 × 3 × 3.
(e) The prime factorization of 320 is 2 × 2 × 2 × 2 × 2 × 2 × 5.
(j) The prime factorization of 141 is 3 × 47.
(g) The prime factorization of 1728 is 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3.
(h) The prime factorization of 729 is 3 × 3 × 3 × 3 × 3 × 3.
(f) The prime factorization of 1024 is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
(j) The prime factorization of 1331 is 11 × 11 × 11.
(k) The prime factorization of 1000 is 2 × 2 × 2 × 5 × 5 × 5.
Question 2. The prime factorization of a number has one 2, two 3s, and one 11. What is the number?
Solution: To find the number, we multiply these prime factors together:
2 × 3 × 3 × 11 = 198
Thus, the number is 198.
Question 3. Find three prime numbers, all less than 30, whose product is 1955.
Solution: The prime factorization of 1955:
1955 = 5 × 17 × 23
All the factors are prime numbers and are less than 30.
Hence, the three prime numbers whose product is 1955 are 5, 17, and 23.
Question 4. Find the prime factorization of these numbers without multiplying first.
(a) 56 × 25
(b) 108 × 75
(c) 1000 × 81
Solution:
(a) Prime factors of 56 = 2 × 2 × 2 × 7
Prime factors of 25 = 5 × 5
Combined prime factorization of 56 × 25 = 2 × 2 × 2 × 7 × 5 × 5
(b) Prime factors of 108 = 2 × 2× 2 × 3 × 3
Prime factors of 75 = 3 × 5 × 5
Combined prime factorization of
108 × 75 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
(c) Prime factors of 1000 = 2 × 2 × 2 × 5 × 5 × 5
Prime factors of 81 = 3 × 3 × 3 × 3
Combined prime factorization of 1000 × 81 = 2 × 2 × 2 × 5 × 5 × 5 × 3 ×3 × 3 × 3
Question 5. What is the smallest number whose prime factorization has:
(a) three different prime numbers?
(b) four different prime numbers?
Solution:
(a) The smallest prime numbers are 2, 3, and 5. To find the smallest number with these primes as factors, multiply them together:
2 × 3 × 5 = 30
So, the smallest number whose prime factorization has three different prime numbers is 30.
(b) The smallest four prime numbers are 2, 3, 5, and 7. To find the smallest number with these primes as factors, multiply them together:
2 × 3 × 5 × 7 = 210
Thus, the smallest number whose prime factorization has four different prime numbers is 210.
Intext Questions
Question 1. Which of the following pairs of numbers are co-prime? (Page 116)
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
Answer:
(a) Here factors of 18 = 1 × 2 × 3 × 3 and factors of 35 = 1 × 5 × 7
No common factor other than 1.
Hence 18 and 35 are co-prime numbers.
(b) We have factors of 15 = 1 × 3 × 5 and factors of 37 = 1 × 37
No common factor other than 1.
Hence 15 and 37 are co-prime numbers.
(c) Given numbers are 30 and 415 Here factors of 30 = 1 × 2 × 3 × 5 and factors of 415 = 5 × 83
Clearly, 5 is a common factor of 30 and 415.
Hence 30 and 415 are not co-prime numbers.
5.4 Prime Factorisation Figure it Out (Page No. 120)
Question 1. Find the prime factorizations of the following numbers: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Solution:
(a) The prime factorization of 64 is 2 × 2 × 2 × 2 × 2 × 2.
(b) The prime factorization of 104 is 2 × 2 × 2 × 13.
(c ) The prime factorization of 105 is 3 × 5 × 7.
(d) The prime factorization of 243 is 3 × 3 × 3 × 3 ×3.
(e) The prime factorization of 320 is 2 × 2 × 2 × 2 × 2 × 2 ×5.
(f) The prime factorization of 141 is 3 × 47.
(g) The prime factorization of 1728 is 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3.
(h) The prime factorization of 729 is 3 × 3 × 3 × 3 × 3 × 3.
(i) The prime factorization of 1024 is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
(j) The prime factorization of 1331 is 11 × 11 × 11.
(k) The prime factorization of 1000 is 2 × 2 × 2 × 5 × 5 × 5.
Question 2. The prime factorization of a number has one 2, two 3s, and one 11. What is the number?
Solution:
To find the number, we multiply these prime factors together:
2 × 3 × 3 × 11 = 198
Thus, the number is 198.
Question 3. Find three prime numbers, all less than 30, whose product is 1955.
Solution: The prime factorization of 1955:
1955 = 5 × 17 × 23
All the factors are prime numbers and are less than 30.
Hence, the three prime numbers whose product is 1955 are 5, 17, and 23.
Question 4. Find the prime factorization of these numbers without multiplying first.
(a) 56 × 25
(b) 108 × 75
(c) 1000 × 81
Solution:
(a) Prime factors of 56 = 2 × 2 × 2 × 7
Prime factors of 25 = 5 × 5
Combined prime factorization of 56 × 25 = 2 × 2 × 2 × 7 × 5 × 5
(b) Prime factors of 108 = 2 × 2 × 2 × 3 × 3 × 3
Prime factors of 75 = 3 × 5 × 5
Combined prime factorization of
108 75 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
(c) Prime factors of 1000 = 2 × 2 × 2 × 5 × 5 × 5
Prime factors of 81 = 3 × 3 × 3 × 3
Combined prime factorization of 1000 × 81 = 2 × 2 × 2 × 5 × 5 × 5 × 3 × 3 × 3 × 3
Question 5. What is the smallest number whose prime factorization has:
(a) three different prime numbers?
(b) four different prime numbers?
Solution:
(a) The smallest prime numbers are 2, 3, and 5. To find the smallest number with these primes as factors, multiply them together:
2 × 3 × 5 = 30
So, the smallest number whose prime factorization has three different prime numbers is 30.
(b) The smallest four prime numbers are 2, 3, 5, and 7. To find the smallest number with these primes as factors, multiply them together:
2 × 3 × 5 × 7 = 210
Thus, the smallest number whose prime factorization has four different prime numbers is 210.
Intext Questions
Question 1. Which of the following pairs of numbers are co-prime? (Page 116)
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
Solution:
(a) Here factors of 18 = 1 × 2 × 3 × 3 and factors of 35 = 1 × 5 × 7
No common factor other than 1.
Hence 18 and 35 are co-prime numbers.
(b) We have factors of 15 = 1 × 3 × 5 and factors of 37 = 1 × 37
No common factor other than 1.
Hence 15 and 37 are co-prime numbers.
(c) Given numbers are 30 and 415
Here factors of 30 = 1 × 2 × 3 × 5 and factors of 415 = 5 × 83
Clearly, 5 is a common factor of 30 and 415.
Hence 30 and 415 are not co-prime numbers.
5.4 Prime Factorisation Figure it Out (Page No. 122)
Question 1. Are the following pairs of numbers co-prime? Guess first and then use prime factorization to verify your answer.
(a) 30 and 45
(b) 57 and 85
(c) 121 and 1331
(d) 343 and 216
Solution:
(a) Factors of 30 and 45:
30 = 2 × 3 × 5,
45 = 3 × 3 × 5
Common factors: 3 × 5 = 15, hence 30 and 45 are not a pair of co-prime numbers.
(b) Factors of 57 and 85:
57 = 3 × 19,
85 = 5 × 17
No common factors other than 1, hence 57 and 85 are a pair of co-prime numbers.
(c) Factors of 121 and 1331:
121 = 11 × 11,
1331 = 11×11×11
Common factors: 11 × 11 = 121, hence 121 and 1331 are not a pair of co-prime numbers.
(d) Factors of 343 and 216:
343 = 7 × 7 × 7,
216 = 2 × 2 × 2 × 3 × 3 × 3
No common factors other than 1, hence 343 and 216 are a pair of co-prime numbers.
Question 2. Is the first number divisible by the second? Use prime factorization.
(a) 225 and 27
(b) 96 and 24
(c) 343 and 17
(d) 999 and 99
Solution:
(a) Prime Factors of 225 and 27:
225 = 3 × 3 × 5 × 5 and 27 = 3 × 3 × 3
Since 225 contains 3×3 and does not have enough factors of 3 to match 3×3 × 3, 225 does not have sufficient factors to be divisible by 27.
Therefore, 225 is not divisible by 27.
(b) Prime Factors of 96 and 24:
96 = 2 × 2 × 2 × 2 × 2 × 3 and 24 = 2 × 2 × 2 × 3.
Since 96 includes the required factors to match those in 24, it is divisible by 24.
(c) Prime Factors of 343 and 17:
343 = 7 × 7 × 7 and 17 = 1 × 17
Since the prime factorization of 343 contains the prime factor 7 and not 17, 343 is not divisible by 17.
Thus, 343 is not divisible by 17.
(d) Prime Factors of 999 and 99: t
999 = 3 × 3 × 3 × 37 and 99 = 3 × 3 × 11
Since 999 does not include the factor 11 required for 99, 999 is not divisible by 99.
Question 3. The first number has prime factorization 2 × 3 × 7 and the second number has prime factorization 3 × 7 × 11. Are they co-prime? Does one of them divide the other?
Solution: The numbers share the common factors 3 and 7. So they are not co-prime since neither number contains all the factors of the other, neither can divide the other.
Question 4. Guna says, “Any two prime numbers are co-prime”. Is he right?
Solution: Yes, Guna is right. Any two prime numbers are co-prime as they do not have common factor other than 1 which means they are always co-prime. For example, 2 and 3, 5 and 7, 11 and 13.
5.5 Divisibility Tests Figure it Out (Page No. 15-17)
Question 1. 2024 is a leap year (as February has 29 days). Leap years occur in the years that are multiples of 4, e×cept for those years that are evenly divisible by 100 but not 400.
(a) From the year you were born till now, which years were leap years?
(b) From the year 2024 till 2099, how many leap years are there?
Solution:
(a) From the year 2010 till 2024, there are 4 leap years. 2012, 2016, 2020 and 2024.
(b) The leap years from 2024 and 2099 are:
2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076,, 2080, 2084, 2088, 2092, 2096.
Hence, there are 19 leap years from 2024 till 2099.
Question 2. Find the largest and smallest 4-digit numbers that are divisible by 4 and are also palindromes.
Solution:
Largest 4-digit number divisible by 4 and is also palindrome- 8888
Smallest 4-digit number divisible by 4 and is also palindrome- 2112.
Question 3. Explore and find out if each statement is always true, sometimes true or never true. You can give e×amples to support your reasoning.
(a) Sum of two even numbers gives a multiple of 4.
Solution: Sometimes true. Sum of any two even numbers is not always divisible by 4. For e×ample, 6 + 4 = 10 which is not divisible by 4 whereas 2+2 = 4 which is divisible of 4.
(b) Sum of two odd numbers gives a multiple of 4.
Solution: Sometimes true. Sum of two odd numbers can indeed be even but not necessarily a multiple of 4. For e×ample, 1 + 5 = 6 which is not a multiple of 4 whereas 1+3 = 4, which is a multiple of 4. Similarly 7 + 5 = 12, which is a multiple of 4.
Question 4. Find the remainders obtained when each of the following numbers are divided by
(i) 10
(ii) 5
(iii) 2.
78, 99, 173, 572, 980, 1111, 2345
Solution: Here we have to divide 78 by 10, 5 and
2 then

Now do yourself:
99/10: Remainder = 9, 99/5: Remainder = 4, 99/2: Remainder = 1
173/10: Remainder = 3, 173/5: Remainder = 3, 173/2: Remainder = 1
572/10: Remainder = 2, 572/5: Remainder = 2, 572/2: Remainder = 0
980/10: Remainder = 0,980/5: Remainder = 0, 980/2: Remainder = 0
1111/10: Remainder= 1,1111/5: Remainder= 1, 1111/2: Remainder = 1
2345/10: Remainder 5,2345/5: Remainder = 0, 2345/2: Remainder = 1
Question 5. The teacher asked if 14560 is divisible by all of 2, 4, 5, 8 and 10. Guna checked for divisibility of 14560 by only two of these numbers and then declared that it was also divisible by all of them. What could those two numbers be?
Solution:
If a number is divisible by 8, it will automatically be divisible by 4.
If a number is divisible by 10, it is also divisible by 2 and 5. Therefore, checking divisibility by 8 and 10 confirms divisibility by all other numbers (2, 4, 5).
Thus, the pair of numbers that Guna could check to determine that 14560 is divisible by all of 2, 4, 5, 8, and 10 is: 8 and 5.
Question 6. Which of the following numbers are divisible by all of 2, 4, 5, 8 and 10: 572, 2352, 5600, 6000, 77622160?
Solution:
5600, 6000, 77622160
Question 7. Write two numbers whose product is 10000. The two numbers should not have 0 as the units digit.
Solution: We need to write factors of 10000.
10000= 10 × 10 × 10 × 10
= 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5
So, 2 × 2 × 2 × 2 = 16 and 5 × 5 × 5 × 5 = 625.
Hence, 16 and 625 are the two numbers whose product is 10000.
Intext Questions (Page 124)
Question 1. What are all the multiples of 2 between 399 and 411?
Solution:
The multiples of 2 between 399 and 411 are 400, 402, 404, 406, 408,and 410.
Question 2. Find numbers between 330 and 340 that are divisible by 4. Also, find numbers between 1730 and 1740, and 2Q30 and 2040, that are divisible by 4. What do you observe?
Solution:
The numbers between 330 and 340 that are divisible by 4 are 332, 336, and 340. The numbers between 1730 and 1740 that are divisible by 4 are 1732, 1736, and 1740. The numbers between 2030 and 2040 that are divisible by 4 are 2032, 2036, and 2040.
Question 3. Is 8536 divisible by 4?
Solution:
Since the last two digits of 8536 (which is 36) are divisible by 4, the original number 8536 is also divisible by 4.
Question 4. Consider these statements:
(a) Only the last two digits matter when deciding if a given number is divisible by 4.
(b) If the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
(c) If the original number is divisible by 4, then the number formed by the last two digits is divisible by 4.
Do you agree? Why or why not?
Solution:
(a) Yes, that’s correct. When determining if a number is divisible by 4, only the last two digits of the number matter. This is because 100 is divisible by 4, so the divisibility rule for 4 focuses on whether the number formed by the last two digits is divisible by 4.
(b) Yes, that’s correct. If the number formed by the last two digits of a given number is divisible by 4, then the original number is also divisible by 4.
(c) Yes, that’s correct. If the original number is divisible by 4, the last two digits of the number will indeed be divisible by 4.
Benefits of NCERT Solutions for Class 6 Maths Chapter 5 Prime Time
Understand the Difference: Be clear about the difference between prime and composite numbers.
Practice Factorization: Regularly practice prime factorization to strengthen your understanding.
Use Factor Trees: Factor trees can be a helpful visual tool for finding prime factors.
Memorize Prime Numbers: Memorize prime numbers up to at least 50 to quickly identify them in problems.
Work on HCF and LCM: Learn how to calculate the HCF and LCM using both factorization and the division method.
Important Study Material Links for Maths Chapter 5 Class 6
S.No. | Important Study Material Links for Chapter 5 |
1. | Class 6 Prime Time Important Questions |
2. |
Conclusion
Chapter 5: Prime Time introduces students to the essential concepts of prime and composite numbers, which are foundational for many advanced mathematical topics. By practising factorization, understanding HCF and LCM, and identifying prime numbers, students can solidify their understanding of number theory. NCERT Solutions for this chapter is a valuable resource to clarify doubts and practice exercises.
Chapter-wise NCERT Solutions Class 6 Science
After familiarising yourself with the Class 6 Maths Chapters Question Answers, you can access comprehensive NCERT Solutions from all Class 6 Maths textbook chapters.
S. No | NCERT Solutions Class 6 Chapter-wise Maths PDF | |
1. | ||
2. | ||
3. | ||
4. | ||
5. | ||
6. | ||
7. | ||
8. | ||
9. | ||
Related Important Links for Class 6 Maths
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6-
S.No. | Important Links for Class 6 Maths |
1. | |
2. | |
3. | |
4. | |
5. | |
6. | |
7. | |
8. |
FAQs on NCERT Solutions For Class 6 Maths Chapter 5 Prime Time - 2025-26
1. What are prime numbers in Class 6 Maths?
A prime number is a whole number greater than 1 that has exactly two factors: 1 and the number itself. For example, 2, 3, 5, 7, and 11 are prime numbers as they cannot be formed by multiplying other whole numbers.
2. What is the difference between prime and composite numbers?
Prime numbers have only two factors (1 and themselves). Composite numbers have more than two factors. For example, 9 is a composite number because its factors are 1, 3, and 9. The number 1 is neither prime nor composite.
3. Where can I find reliable Prime Time Class 6 NCERT Solutions?
Vedantu offers accurate and easy-to-understand NCERT Solutions for Class 6 Maths. These solutions are prepared by subject experts to help students solve textbook problems, clear doubts, and understand core concepts of prime numbers, factors, and multiples effectively.
4. How do NCERT Solutions help with Prime Time questions and answers for Class 6?
NCERT Solutions provide clear, step-by-step explanations for every problem in the textbook. They help you understand the method for finding prime factors, HCF, and LCM, ensuring you can solve similar questions correctly in exams and build a strong foundation.
5. Is it possible to download the Prime Time Class 6 NCERT PDF for free?
Yes, you can access the chapter solutions easily. The Free PDF download for Class 6 Maths Chapter 5 NCERT Solutions is available on Vedantu, which allows you to study the material offline and revise all the important questions anytime.
6. What is prime factorisation?
Prime factorisation is the method of expressing a number as a product of its prime factors. For example, the prime factorisation of 20 is 2 × 2 × 5. Every composite number has a unique set of prime factors.
7. Why is 1 not considered a prime number?
A prime number must have exactly two distinct factors. The number 1 has only one factor, which is 1 itself. Since it does not meet the two-factor criterion, it is categorised as a unique number—neither prime nor composite.
8. What is the smallest prime number?
The smallest prime number is 2. It is also the only even prime number, as all other even numbers are divisible by 2 and therefore have more than two factors. This is a fundamental concept in the Class 6 Maths chapter.
9. What key topics are covered in the Class 6 Maths Chapter 5 question answers?
The solutions cover all important topics like identifying prime and composite numbers, divisibility tests, finding common factors and multiples, prime factorisation, Highest Common Factor (HCF), and Lowest Common Multiple (LCM). These are crucial for understanding number theory.
10. What are co-prime numbers?
Two numbers are called co-prime (or relatively prime) if their only common factor is 1. The numbers themselves do not have to be prime. For instance, 15 and 16 are co-prime because they share no common factor other than 1.























