Maths Class 6 Chapter 9 Questions and Answers - Free PDF Download
In NCERT Solutions Class 6 Maths Chapter 9 Exercise 9 1, you’ll discover how symmetry works in different shapes all around us. This part of your Class 6 Maths book helps you spot lines of symmetry and understand how some designs or figures can be folded or cut to look the same on both sides. These skills make geometry more fun and easier to grasp!
Table of Content
If you ever get confused about finding lines of symmetry or drawing symmetrical patterns, these step-by-step answers from Vedantu will clear up your doubts. You can also find the full CBSE Class 6 Maths syllabus to plan your study better.
You can easily get all these NCERT Solutions as a downloadable PDF, which is super helpful for quick revisions before exams. Looking for more detailed help? Try the complete set of Class 6 Maths NCERT Solutions anytime you want!
Exercise 9.1
Figure it Out
1. Do you see any line of symmetry in the figures at the start of the chapter? What about in the picture of the cloud?
Ans:
A flower exhibits 6 lines of symmetry. A butterfly has 1 line of symmetry. Rangoli patterns typically have 4 lines of symmetry. A pinwheel does not possess any lines of symmetry. A cloud's shape can vary, so it may or may not have a line of symmetry.
2. For each of the following figures, identify the line(s) of symmetry if it exists
Ans:
Figure is Out
Punching Game:
The fold is a line of symmetry. Punch holes at different locations of a folded square sheet of paper using a punching machine and create different symmetric patterns.
1. In each of the following figures, a hole was punched in a folded square sheet of paper and then the paper was unfolded. Identify the line along which the paper was folded.
Figure (d) was created by punching a single hole. How was the paper folded?
Ans:
2. Given the line(s) of symmetry, find the other hole(s):
Ans:
3. Here are some questions on paper cutting. Consider a vertical fold. We represent it this way:
Similarly, a horizontal fold is represented as follows:
Ans:
4. After each of the following cuts, predict the shape of the hole when the paper is opened. After you have made your prediction, make the cutouts and verify your answer.
Ans:
Ans:
Ans:
Ans:
5. Suppose you have to get each of these shapes with some folds and a single straight cut. How will you do it?
a. The hole in the centre is a square.
Ans:
b. The hole in the centre is a square.
Ans:
Note: For the above two questions, check if the 4-sided figures in the centre satisfy both the properties of a square.
6. How many lines of symmetry do these shapes have?
Ans:
b. A triangle with equal sides and equal angles.
Ans:
c. A hexagon with equal sides and equal angles.
Ans:
7. Trace each figure and draw the lines of symmetry, if any:
Ans:
8. Find the lines of symmetry for the kolam below.
Ans:
9. Draw the following.
a. A triangle with exactly one line of symmetry.
b. A triangle with exactly three lines of symmetry.
c. A triangle with no line of symmetry.
Is it possible to draw a triangle with exactly two lines of symmetry?
Ans:
No, it is not possible to create a triangle that has exactly two lines of symmetry.
10. Draw the following. In each case, the figure should contain at least one curved boundary.
a. A figure with exactly one line of symmetry.
b. A figure with exactly two lines of symmetry.
c. A figure with exactly four lines of symmetry.
Ans:
11. Copy the following on squared paper. Complete them so that the blue line is a line of symmetry. Problem (a) has been done for you.
Hint: For (c) and (f), see if rotating the book helps!
Ans:
12. Copy the following drawing on squared paper. Complete each one of them so that the resulting figure has the two blue lines as lines of symmetry.
Ans:
13. Copy the following on a dot grid. For each figure draw two more lines to make a shape that has a line of symmetry.
Ans:
Benefits of NCERT Solutions for Class 6 Maths Chapter 1 Exercise 9.1 Symmetry
Clear Understanding of Symmetry: The solutions help students easily grasp the concept of symmetry and identify symmetrical patterns in different shapes.
Step-by-Step Guidance: Each problem is solved step-by-step, making it easier for students to follow and learn how to approach similar problems.
Aligned with CBSE Syllabus: The solutions are based on the CBSE Class 6 Maths syllabus, ensuring that all important topics related to symmetry are covered.
Boosts Exam Preparation: These solutions provide ample practice for students to prepare thoroughly for their exams, focusing on key concepts.
Convenient Learning: With the free PDF download available, students can access the solutions anytime, making it a flexible learning tool for quick revision and regular practice.
Class 6 Maths Chapter 9: Exercises Breakdown
Important Study Material Links for Class 6 Maths Chapter 9 - Symmetry
Conclusion
The NCERT Solutions for Class 6 Maths Chapter 9 Exercise 9.1 on Symmetry offer a comprehensive approach to understanding one of the fundamental concepts in geometry. These solutions provide clear, step-by-step explanations, making it easy for students to master symmetry and recognise symmetrical patterns in various figures. Aligned with the CBSE syllabus, the solutions not only aid in exam preparation but also strengthen problem-solving skills. With the added convenience of a free PDF download, students have an accessible resource for effective revision and practice.
Chapter-Specific NCERT Solutions for Class 6 Maths
The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Related Important Links for Maths Class 6
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.
FAQs on NCERT Solutions For Class 6 Maths Chapter 9 Symmetry Exercise 9.1 - 2025-26
1. What are the main concepts explained in the NCERT Solutions for Class 6 Maths Chapter 9, Symmetry?
The NCERT Solutions for Class 6 Maths Chapter 9 provide detailed explanations for key concepts, including:
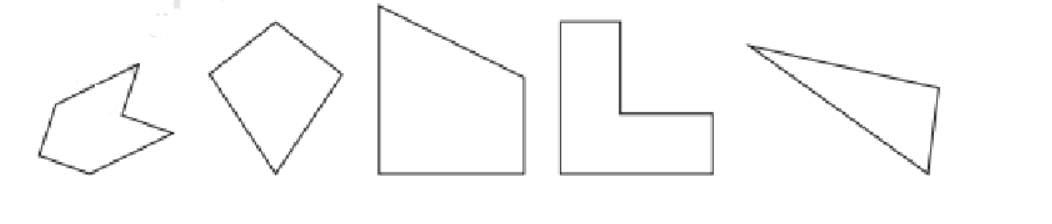
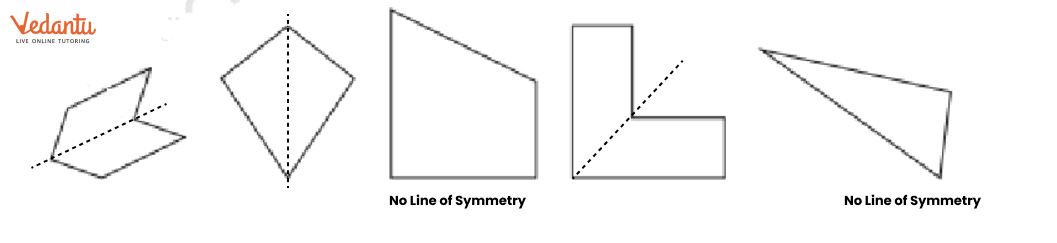
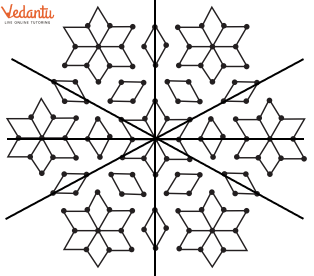
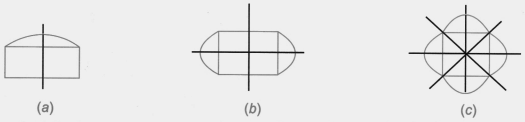
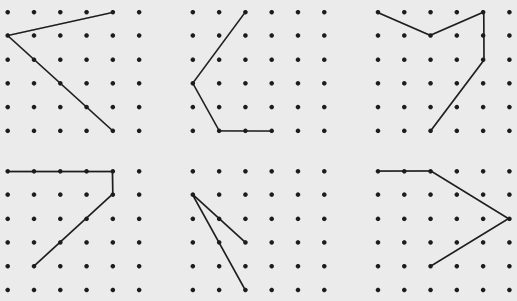
- Identifying a line of symmetry in various figures.
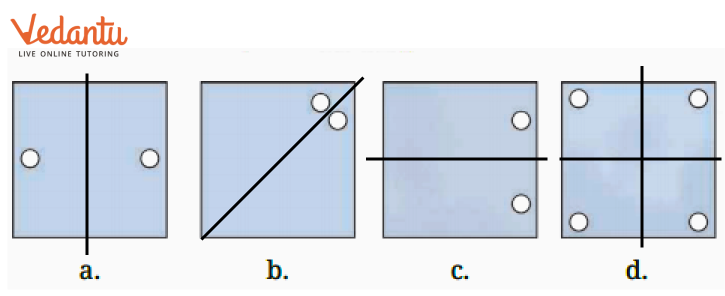
- Understanding the concept of reflection and its relationship to symmetry.
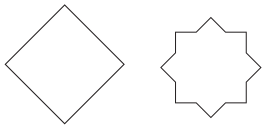
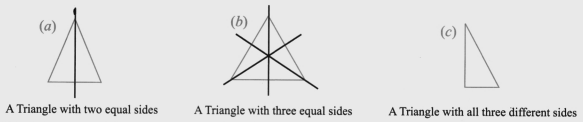
- Finding single and multiple lines of symmetry in regular polygons like squares, rectangles, and triangles.
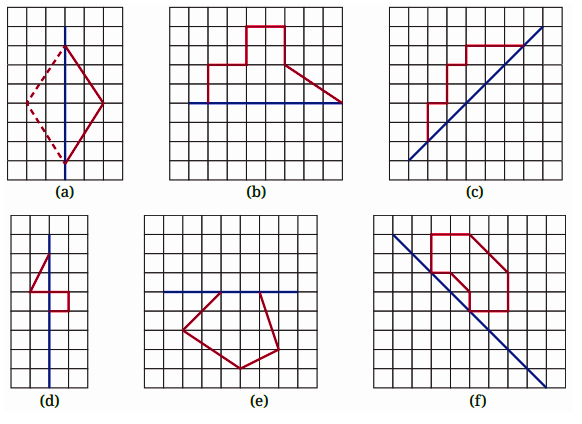
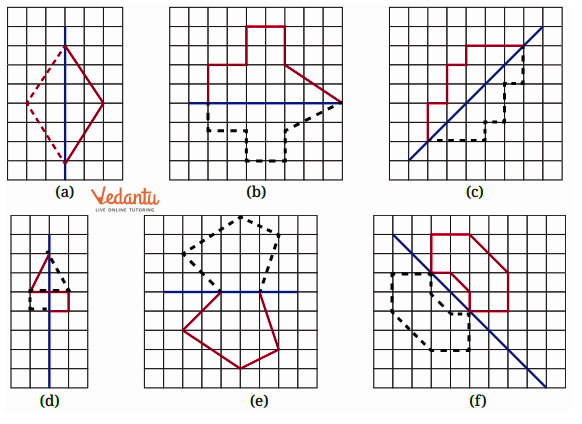
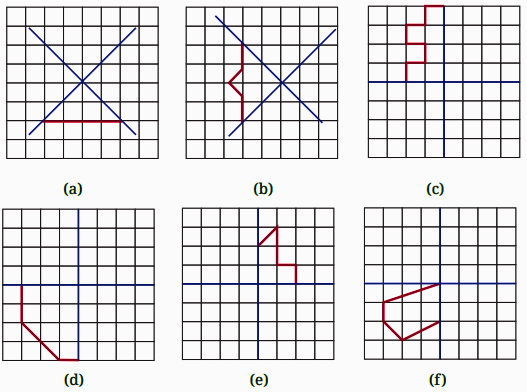
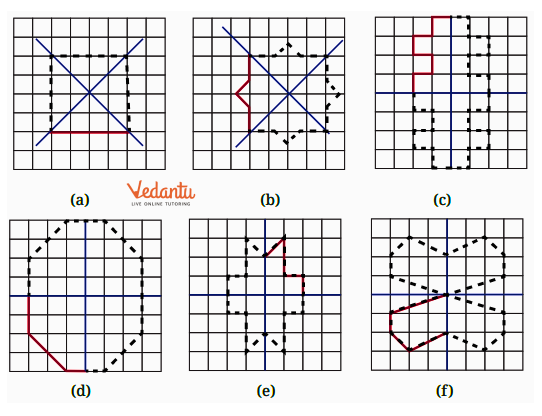
- Techniques for completing a figure to make it symmetrical along a given mirror line.
2. How do the NCERT Solutions for Chapter 9 guide students to solve problems in Exercise 9.1?
The solutions for Exercise 9.1 offer a step-by-step methodology for each problem. They demonstrate the correct approach to identify and draw lines of symmetry for different shapes, ensuring students can replicate the method accurately in their exams and homework.
3. What is the correct method, as per the NCERT Solutions, for checking if a line is a line of symmetry?
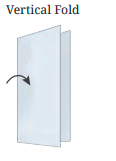
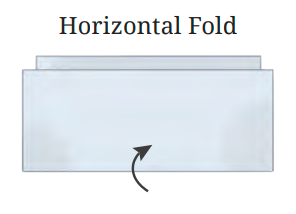
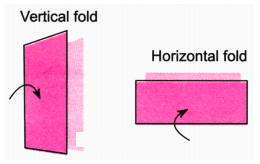
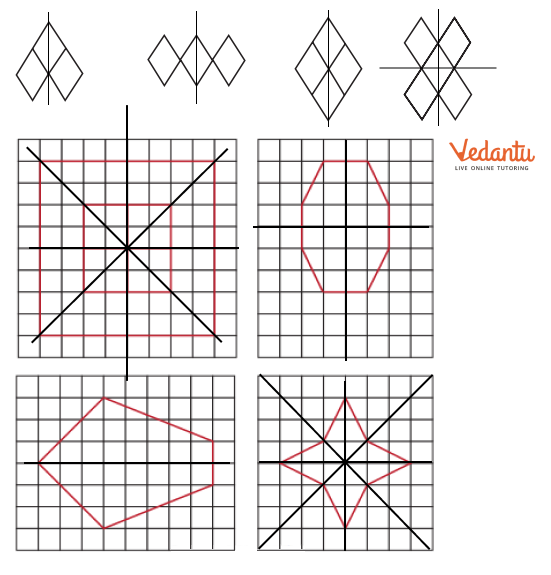
The NCERT Solutions explain the fundamental 'folding method.' A line is considered a line of symmetry if the figure can be folded along that line so that its two parts coincide exactly. The solutions apply this principle to help students verify their answers for any given shape.
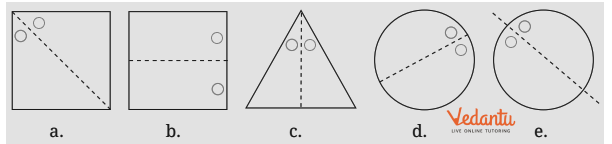
4. How do the solutions for Class 6 Maths Chapter 9 explain finding multiple lines of symmetry in regular polygons?
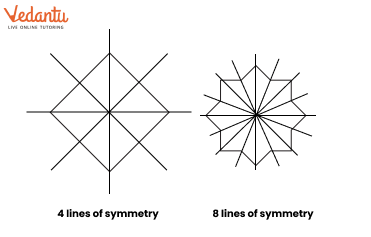
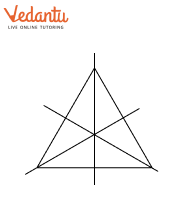
The solutions provide a clear, methodical approach to find all possible lines of symmetry for regular polygons. For example, they illustrate how a square has four lines of symmetry (two diagonals and two lines joining midpoints of opposite sides), while an equilateral triangle has three. This ensures students don't miss any lines.
5. Why is it crucial to follow the step-by-step process from the NCERT Solutions when completing a symmetrical figure?
Following the step-by-step process is crucial because it ensures accuracy. The solutions teach students to plot corresponding points at an equal perpendicular distance from the mirror line. This systematic approach prevents guesswork and errors, resulting in a perfectly symmetrical figure as required by the problem.
6. How do the solved examples in the Chapter 9 solutions help clarify the difference between reflection and symmetry?
The solved examples illustrate that reflection is the transformation that flips a figure across a line to create a mirror image. In contrast, symmetry is a property of a single figure that already possesses two identical halves. By solving problems involving both concepts, students can grasp this important distinction.
7. What problem-solving techniques are taught in the NCERT Solutions for identifying symmetry in the letters of the English alphabet?
The solutions demonstrate how to test each letter for both vertical and horizontal lines of symmetry. For example, they show that the letter 'A' has a vertical line of symmetry, 'H' has both a vertical and a horizontal line of symmetry, and 'R' has none. This builds a practical understanding of applying symmetry rules.
8. Are the NCERT Solutions for Class 6 Maths Chapter 9 aligned with the latest CBSE syllabus for 2025-26?
Yes, the NCERT Solutions for Chapter 9 are fully updated and meticulously aligned with the CBSE syllabus for the 2025-26 academic year. They cover every topic and exercise prescribed in the NCERT textbook, ensuring students are preparing with the most relevant and accurate material.
9. How do the Chapter 9 solutions connect the geometric concept of symmetry to real-world objects?
The solutions help bridge theory and practice by relating symmetry to everyday life. They encourage students to observe symmetry in real-world examples such as butterflies, human faces, architectural designs, and common logos. This application-based approach makes the concept more intuitive and memorable.
