Data Handling And Presentation - Exercise-wise Questions and Answers For Class 6 Maths - Free PDF Download
FAQs on NCERT Solutions For Class 6 Maths Chapter 4 Data Handling And Presentation - 2025-26
1. How do you use tally marks to count data?
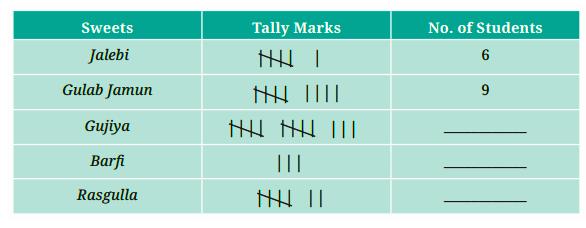
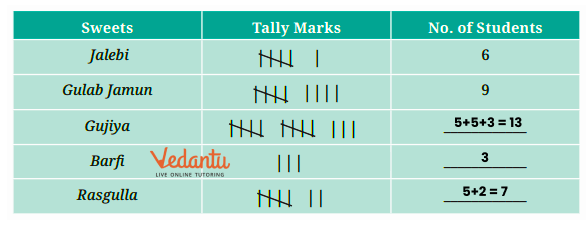
Represent each data point with a single vertical line (|). For every fifth data point, draw a diagonal line across the previous four (||||) to create a group of five. This method makes it easy and fast to count the total frequency for each category in your dataset.
2. How can you organize raw data in a frequency distribution table?
To organize raw data in a frequency distribution table, create a table with three columns to structure your raw data: one for the categories, one for tally marks, and one for the frequency (the numerical count). This is a key skill in data handling and presentation for class 6.
Steps to Follow:
- Make three columns labelled 'Category', 'Tally Marks', and 'Frequency'.
- List all unique items from your data in the first column.
- Go through the raw data one by one, placing a tally mark next to the correct item.
- Count the tally marks for each item and write the total in the frequency column.
3. What is the easiest way to download the Data Handling Class 6 Solutions PDF?
Click the “Download PDF” link available on this page to get the complete NCERT Solutions for Class 6 Maths Chapter 4. You can save this Free PDF file on your phone or computer to study offline, revise formulas, and check answers without needing an internet connection.
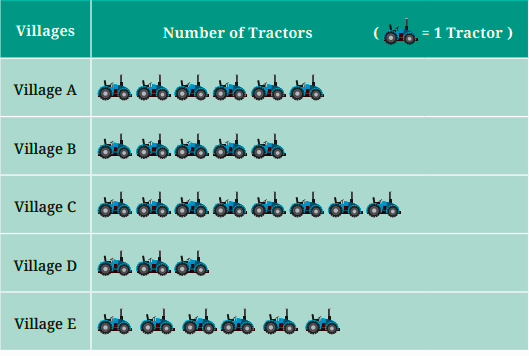
4. What is the process for drawing a pictograph?
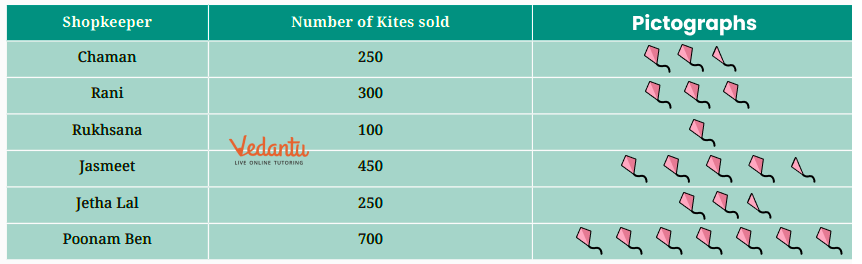
To draw a pictograph, you must represent numerical data using relevant symbols or pictures, where each symbol corresponds to a specific quantity.
Pictographs are visually engaging and make data easy to understand at a glance, especially when comparing different categories.
Steps to Follow:
- Give your pictograph a clear and descriptive title.
- Choose a simple symbol that relates to the data (e.g., a book symbol for library data).
- Define your scale in a key (e.g., 1 symbol = 10 books). This is the most important step.
- Draw the correct number of symbols for each category based on your key.
To draw a pictograph, you must represent numerical data using relevant symbols or pictures, where each symbol corresponds to a specific quantity.
Pictographs are visually engaging and make data easy to understand at a glance, especially when comparing different categories.
Steps to Follow:
Give your pictograph a clear and descriptive title.
Choose a simple symbol that relates to the data (e.g., a book symbol for library data).
Define your scale in a key (e.g., 1 symbol = 10 books). This is the most important step.
Draw the correct number of symbols for each category based on your key.
A good pictograph always includes a title, a symbol, and a key to explain the scale.
5. How should you start analysing a new set of data?
First, arrange the raw data in a systematic way. You can do this by listing the numbers or items in ascending or descending order. This initial step of organising the data makes it much simpler to create tables and graphs later on.
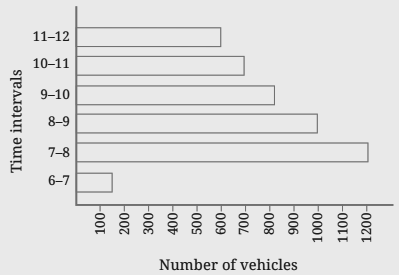
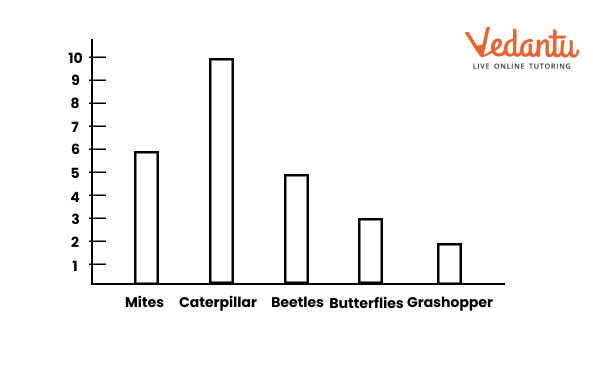
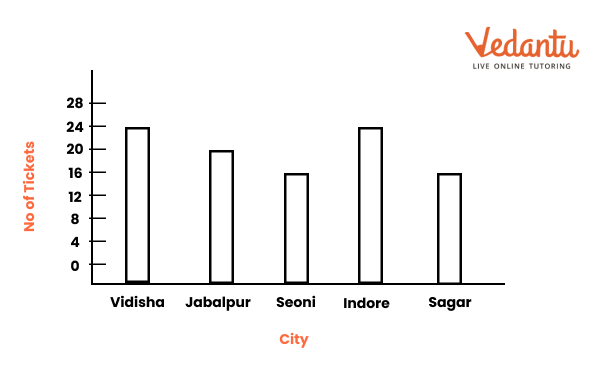
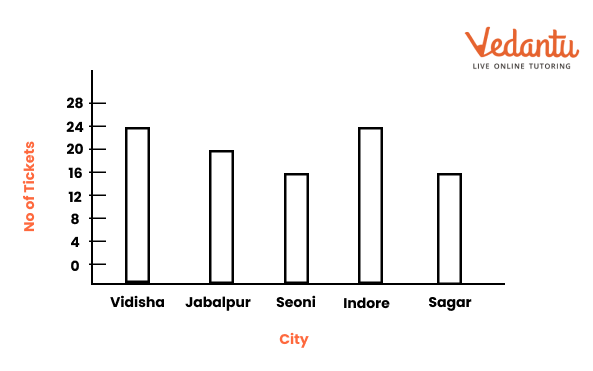
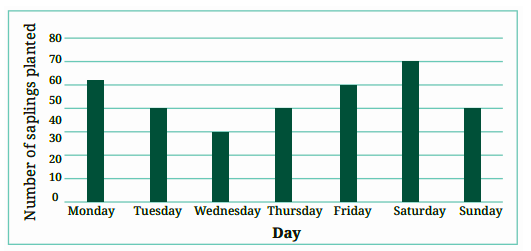
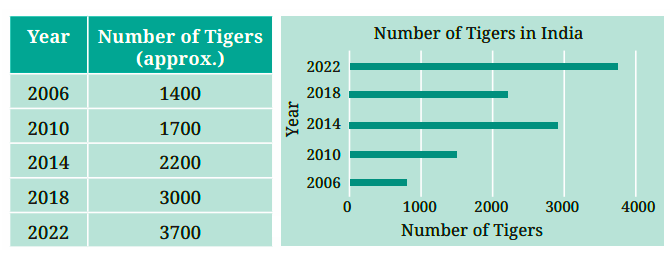
6. How can you interpret information from a bar graph?
Interpret a bar graph by first reading its title and the labels on both the horizontal (x-axis) and vertical (y-axis) axes to understand what is being measured.
This skill helps you quickly compare information across different groups and identify the highest or lowest values without needing to read all the exact numbers.
7. How can you find extra questions for Data Handling Class 6?
Find extra questions by working through the solved examples and in-text questions provided in Vedantu's NCERT solutions. These questions offer more practice on key concepts from class 6 chapter 4 data handling and presentation beyond what is in the main textbook exercises.
8. How can you use NCERT Solutions to revise for an exam?
Use the NCERT Solutions for Data Handling and Presentation Class 6 to revise actively by first solving problems yourself and then using the solutions to analyse your method.
This two-step process helps you identify specific weaknesses in your understanding, rather than just memorising answers. It builds confidence and problem-solving skills for your exam.
9. How do you find the answer to a specific question using the solutions page?
Scroll to the specific exercise number you are working on (e.g., Exercise 4.1, 4.2). Click on the question number to navigate directly to its detailed, step-by-step solution. This allows you to quickly check your work for a single problem without searching the entire document.
10. What is the best way to self-check your homework answers?
Self-check your work by using the data handling and presentation class 6 solutions to verify both your final answer and the accuracy of your method, including tables and graphs.
In data handling, correctly drawing a graph or creating a frequency table is just as important as the final interpretation. A thorough check ensures you have mastered the entire process.