Access NCERT Exemplar Solutions for Class 11 Mathematics

Chapter 11 - CONIC SECTION

(Examples, Easy Methods and Step by Step Solutions)

Solved Questions

Short Answer Type:

Example 1:  Find the center and radius of the circle ${x^2} + {y^2} - 2x + 4y = 8$

Ans: Given ${x^2} + {y^2} - 2x + 4y = 8$

Given equation of the circle is ${x^2} + {y^2} - 2x + 4y = 8$

Adding $1, 4$ on both sides.

$\Rightarrow {x^2} - 2x + 1 + {y^2} + 4y + 4 = 8 + 1 + 4$

$\Rightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} + 4y + 4} \right) = 13$

$\Rightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 13$

$\Rightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = {\left( {\sqrt {13} } \right)^2}$

On comparing with the standard form,

${\left( {h - x} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$

Center and radius of the circle is

$\left( {h,k} \right) = \left( {1, - 2} \right)$

$r = \sqrt {13} $

Hence, the radius of the circle is $\sqrt {13} $.

Example 2:  If the equation of the parabola is ${x^2} = - 8y$, find coordinates of the focus, the equation of the directrix and length of the latus rectum.

Ans: Given${x^2} = - 8y$.

${x^2} = - 8y$

$\Rightarrow {x^2} = -{\text{ 4}} \cdot {\text{2}}y$

On comparing with the standard form,

${x^2} = - 4ay$

We get,

$a = 2$

Coordinates of the focus

$\left( {0, - 2} \right)$

Equation of the directrix

$y = 2$

Length of latus rectum 

$= 4 \times 2 = 8$Units

Example 3: Given the ellipse with equation $9{x^2} + 25{y^2} = 225$, find the major and minor axes, eccentricity, foci and vertices.

Ans: Given $9{x^2} + 25{y^2} = 225$

Dividing $225$ on both sides of $9{x^2} + 25{y^2} = 225$.

$\Rightarrow \dfrac{{9{x^2}}}{{225}} + \dfrac{{25{y^2}}}{{225}} = \dfrac{{225}}{{255}}$

$\Rightarrow \dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1$

$\Rightarrow \dfrac{{{x^2}}}{{{5^2}}} + \dfrac{{{y^2}}}{{{3^2}}} = 1$

On comparing with the standard form.

$\Rightarrow \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

We get,

$a = 5$ and $b = 3$

Since the denominator of ${x^2}$ is larger, the major axis is along $x - $axis, minor axis along $y - $axis,

Now, eccentricity

${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$

$= 1 - \dfrac{{{3^2}}}{{{5^2}}}$

$= 1 - \dfrac{9}{{25}}$

$= \dfrac{{16}}{{25}}$

$e = \dfrac{4}{5}$

And foci $= \left( { \pm ae,0} \right)$

$= \left( { \pm 5 \times \dfrac{4}{5},0} \right)$

$= \left( { \pm 4,0} \right)$

And vertices $= \left( { \pm a,0} \right)$

$= \left( { \pm 5,0} \right)$

Hence, the foci and  vertices of the ellipse is $\left( { - 5,0} \right)\left( { + 5,0} \right)$ and $\left( { + 4,0} \right)\left( { - 4,0} \right)$

Example 4:  Find the equation of the ellipse with foci at $\left( { \pm 5,0} \right)$ and $x = \dfrac{{36}}{5}$ as one of the directrices.

Ans: Given Foci at $\left( { \pm 5,0} \right)$ and $x = \dfrac{{36}}{5}$ as one of the directrices.

$ae = 5$, $\dfrac{a}{e} = \dfrac{{36}}{5}$

$\Rightarrow \dfrac{a}{e} = \dfrac{{36}}{5}$

$\Rightarrow \dfrac{{a \times a}}{5} = \dfrac{{36}}{5}$

$\Rightarrow {a^{^2}} = 36$

$\Rightarrow a = {6^2}$

$\Rightarrow a = 6$

Now, $ae = 5$(given)

$\therefore e = \dfrac{5}{6}$

$\because {b^2} = {a^2}\left( {{e^2} - 1} \right)$

$= {6^2}\left[ {1 - {{\left( {\dfrac{5}{6}} \right)}^2}} \right]$

$= 36\left( {\dfrac{{36 - 25}}{{36}}} \right)$

$= 36\left( {\dfrac{{11}}{{36}}} \right)$

$\Rightarrow b = \sqrt {11} $

Now, putting the value of $a{\text{ and }}b$  in the standard form of ellipse i.e., $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$gives $\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{11}} = 1$.

Example 5: For the hyperbola $9{x^2}-16{y^2} = 144$, find the vertices, foci and eccentricity.

Ans: GivenEquation of the hyperbola $9{x^2}-16{y^2} = 144$.

$9{x^2}-16{y^2} = 144$ (given)

Divide both sides by $144$.

   $\Rightarrow \dfrac{{9{x^2}}}{{144}}-\dfrac{{16{y^2}}}{{144}} = \dfrac{{144}}{{144}}$

   $\Rightarrow \dfrac{{{x^2}}}{{16}}-\dfrac{{{y^2}}}{9} = 1$

   $\Rightarrow \dfrac{{{x^2}}}{{{4^2}}}-\dfrac{{{y^2}}}{{{3^2}}} = 1$ 

Here, ${a^2} = {4^2}{\text{ and }}{b^2} = {3^2}$

$\because e = \sqrt {1 + \dfrac{{{b^2}}}{{{a^2}}}} $

   $= \sqrt {1 + \dfrac{{{3^2}}}{{{4^2}}}} $

   $= \sqrt {1 + \dfrac{9}{{16}}} $

   $= \sqrt {\dfrac{{25}}{{16}}} $

   $= \dfrac{5}{4}$ 

Now, foci  $= \left( { \pm ae,0} \right)$

   $= \left( { \pm \dfrac{5}{4} \times 4,0} \right)$

   $= \left( { \pm 5,0} \right)$ 

Also, vertices $= \left( { \pm a,0} \right)$

$= \left( { \pm 4,0} \right)$

Example 6: Find the equation of the hyperbola with vertices at $\left( {0, \pm 6} \right)$and $e = \dfrac{5}{3}$. Find its focus.

Ans: Given Vertices at $\left( {0, \pm 6} \right)$ ,$e = \dfrac{5}{3}$

Since the vertices are on the $y - $axis (with origin at the mid-point), the equation is of the form $- \dfrac{{{x^2}}}{{{b^2}}} + \dfrac{{{y^2}}}{{{a^2}}} = 1$

vertices$= \left( {0, \pm a} \right)$  [given]

$\therefore a = 6$

$\because {b^2} = {a^2}\left( {{e^2} - 1} \right)$

   $= {6^2}\left( {{{\left( {\dfrac{5}{3}} \right)}^2} - 1} \right)$

   $= 36\left( {\dfrac{{16}}{9}} \right)$

   $\Rightarrow {b^2} = 4\left( {16} \right)$

  $b = 2\left( 4 \right)$

  $b = 8$ 

So, put the value of $a{\text{ and }}b$ in $- \dfrac{{{x^2}}}{{{b^2}}} + \dfrac{{{y^2}}}{{{a^2}}} = 1$

   $\Rightarrow  - \dfrac{{{x^2}}}{{{8^2}}} + \dfrac{{{y^2}}}{{{6^2}}} = 1$

   $\Rightarrow  - \dfrac{{{x^2}}}{{64}} + \dfrac{{{y^2}}}{{36}} = 1$ 

Foci $= (0, \pm ae) = \left( {0, \pm 10} \right).$

Long answer type:

Example 7: Find the equation of the circle which passes through the points $\left( {20,3} \right), \left( {19,8} \right)$and $\left( {2,-9} \right)$ . Find its center and radius.

Ans: Given Coordinate of the points that lies in the circumference of the circle $\left( {20,3} \right), \left( {19,8} \right)$  and $\left( {2,-9} \right)$

Given, circle passes through the point $\left( {20,3} \right), \left( {19,8} \right)$and $\left( {2,-9} \right)$.

The general equation of the circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$.

Substituting the coordinates of these points in the general equation of the circle, we get

  $40g + 6f + c =  - 409$

  $38g + 16 f + c =  - 425$

  $4g - 18f + c =  - 85$ 

From these three equations, we get

$g =  - 7, f =  - 3{\text{ and }}c =  - 111$

Hence, the equation of the circle is 

${x^2} + {y^2} - 14x - 6y - 111 = 0$

Example 8: An equilateral triangle is inscribed in the parabola ${y^2} = 4ax$ whose one vertex is at the vertex of the parabola. Find the length of the side of the triangle. 

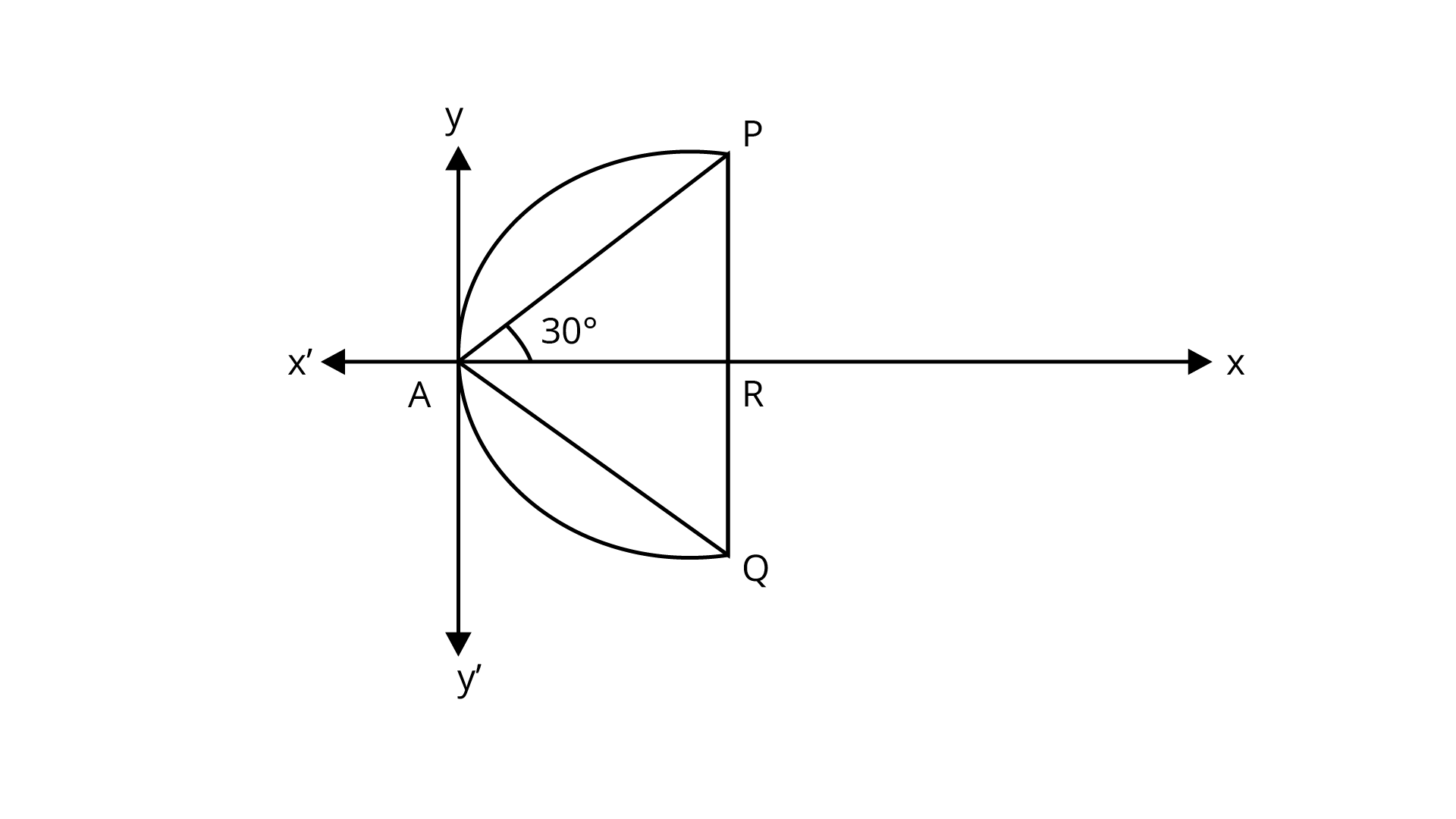
Ans: From the figure $APQ$ denotes the equilateral triangle with its equal side of length $l$.

Here, $AP = l$ so $AR = l\cos 30^\circ $

$AR = l\dfrac{{\sqrt 3 }}{2}$

Also, $PR = l\sin 30^\circ $

$PR = \dfrac{l}{2}$

Thus $l\dfrac{{\sqrt 3 }}{2}, \dfrac{l}{2}$ are the coordinates of the point $P$ lying on the parabola ${y^2} = 4ax$.

Now, put the coordinate of the point in the equation of the parabola

Therefore, $\dfrac{{{l^2}}}{4} = 4a \times \dfrac{{l\sqrt 3 }}{2}$

$\Rightarrow l = 8a\sqrt 3 $

Example 9: Find the equation of the ellipse which passes through the point $\left( {-3,1} \right)$ and has eccentricity $\dfrac{{\sqrt 2 }}{5}$ , with $x - $axis as its major axis and center at the origin.

Ans: Given Coordinate of the point lie on the ellipse is $\left( {-3,1} \right)$, $e = \dfrac{{\sqrt 2 }}{5}$

The standard form of ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

Given that ellipse passes through the point $\left( {-3,1} \right)$

So, $\dfrac{9}{{{a^2}}} + \dfrac{1}{{{b^2}}} = 1$

$\Rightarrow 9{b^2} + {a^2} = {a^2}{b^2}$

$\Rightarrow 9\left[ {{a^2}\left( {1 - {e^2}} \right)} \right] + {a^2} = {a^2}\left[ {{a^2}\left( {1 - {e^2}} \right)} \right]{\text{         }}\left[ {\because {b^2} = {a^2}\left( {1 - {e^2}} \right)} \right]$

$\Rightarrow {a^2} = \dfrac{{32}}{3}$ 

Again, ${b^2} = {a^2}\left( {1 - {e^2}} \right)$

   $= \dfrac{{32}}{3}\left( {1 - {{\left( {\sqrt {\dfrac{2}{5}} } \right)}^2}} \right)$

   $= \dfrac{{32}}{3}\left( {1 - \dfrac{2}{5}} \right)$

   $= \dfrac{{32}}{5}$ 

Hence, the required equation of ellipse is 

   $\Rightarrow \dfrac{{{x^2}}}{{\dfrac{{32}}{3}}} + \dfrac{{{y^2}}}{{\dfrac{{32}}{5}}} = 1$

   $\Rightarrow \dfrac{{3{x^2}}}{{32}} + \dfrac{{5{y^2}}}{{32}} = 1$

   $\Rightarrow 3{x^2} + 5{y^2} = 32$ 

Example 10: Find the equation of the hyperbola whose vertices are $\left( { \pm  6,0} \right)$ and one of the directrices is $x = 4.$

Ans: Given Vertices are $\left( { \pm  6,0} \right)$, Directrices is $x = 4.$

As the vertices are on the $x -$axis and their middle point is the origin, the standard form of equation of hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$

Now, vertices $= \left( { \pm  a,0} \right) = \left( { \pm  6,0} \right)$

Therefore, $a = 6$

And directrices

   $x = 4$

   $\because x =  \pm \dfrac{a}{e}$

   $\Rightarrow 4 = \dfrac{6}{e}$

   $\Rightarrow e = \dfrac{3}{2}$ 

Also, ${b^2} = {a^2}\left( {{e^2} - 1} \right)$

   ${b^2} = 36\left( {\dfrac{9}{4} - 1} \right)$

   ${b^2} = 36\left( {\dfrac{5}{4}} \right)$

   ${b^2} = 45$ 

Hence, the required equation of hyperbola is $\dfrac{{{x^2}}}{{36}} - \dfrac{{{y^2}}}{{45}} = 1$

Sample Question 11: The equation of the circle in the first quadrant touching each coordinate axis at a distance of one unit from the origin is:

(A) ${x^2} + {y^2}-2x-2y + 1 = 0 $       

(B) ${x^2} + {y^2}-2x-2y - 1 = 0 $

(C) ${x^2} + {y^2}-2x-2y = 0$                

(D) ${x^2} + {y^2}-2x + 2y - 1 = 0$

Ans: Given Circle in the first quadrant touching each coordinate axis at a distance of one unit from the origin.

From given conditions it can be observed that the center of the circle will be $(1,1)$ and radius will be $1$ unit.

$\Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = {\left( 1 \right)^2}$

$\Rightarrow {x^2} + {y^2}-2x-2y + 1 = 0 $

Correct Option: a

Sample Question 12: The equation of the circle having center $\left( {1, -2} \right)$and passing through the point of intersection of the lines $3x  +  y  =  14$and $2x  +  5y  =  18$ is:

(a) ${x^2} + {y^2}-2x + 4y-20 = 0$     

(b) ${x^2} + {y^2}-2x - 4y-20 = 0$

(c) ${x^2} + {y^2} + 2x - 4y-20 = 0$

(d) ${x^2} + {y^2} + 2x + 4y-20 = 0$

Ans: Given Circle having center $\left( {1, -2} \right)$and passing through the point of intersection of the lines $3x  +  y  =  14$and $2x  +  5y  =  18$

$3x  +  y  =  14$  ,$2x  +  5y  =  18$

$\Rightarrow 2x + 5\left( {14 - 3x} \right) = 18 \Rightarrow 13x = 52 \Rightarrow x = 4$

$\Rightarrow y = 14 - 3x = 14 - 3(4) = 2$

So, we need a circle with center $\left( {1, -2} \right)$ and passing through $\left( {4, 2} \right)$.

${x^2} + {y^2}-2x + 4y-20 = 0 \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = {\left( 5 \right)^2}$

This circle satisfies the required conditions. So, this will be the required equation. 

Correct Option: a

Sample Question 13: The area of the triangle formed by the lines joining the vertex of the parabola ${x^2} = 12y$ to the ends of its latus rectum is

(a) $12$sq. units      

(b) $16$ sq. units         

(c) $18$ sq. units

(d) $24$ sq. units

Ans: Given Parabola ${x^2} = 12y$

${x^2} = 12y \equiv {x^2} = 4ay \Rightarrow a = 3$

Latus rectum :$y = 3$ which cuts parabola at $\left( { \pm 6,3} \right)$.

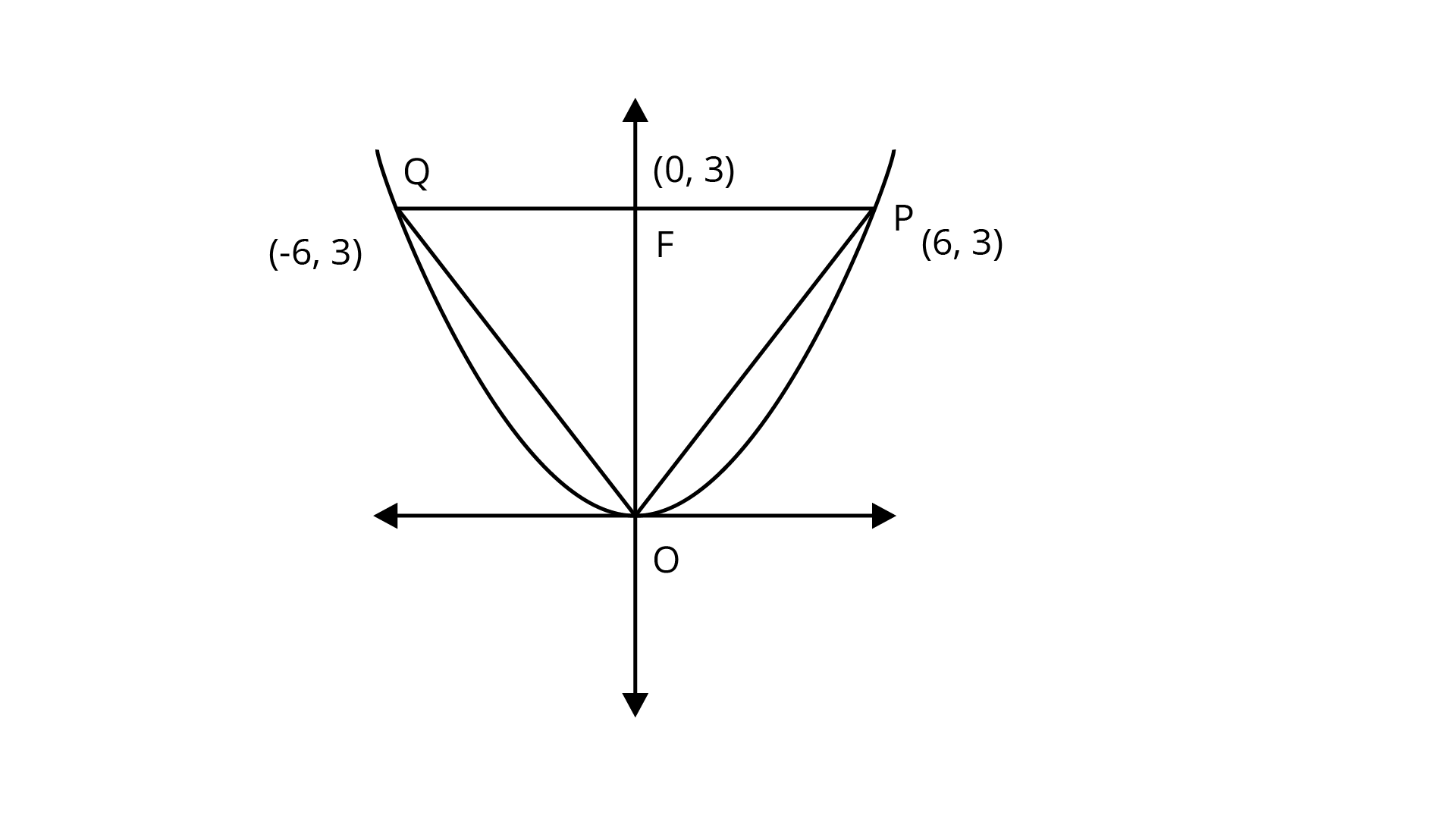
So, area of required triangle = $ar(\Delta OPQ) = \dfrac{1}{2} \times 3 \times 12 = 18$ sq. units

Correct Option: C

Sample Question 14: The equations of the lines joining the vertex of the parabola ${y^2} = 6x$ to the points on it which have abscissa $24$ are:

(a) $y  \pm  2x  =  0 $

(b) $2y  \pm  x  =  0$

(c) $x  \pm  2y  =  0 $

(d) $2x  \pm  y  =  0 $

Ans: Given Parabola ${y^2} = 6x$

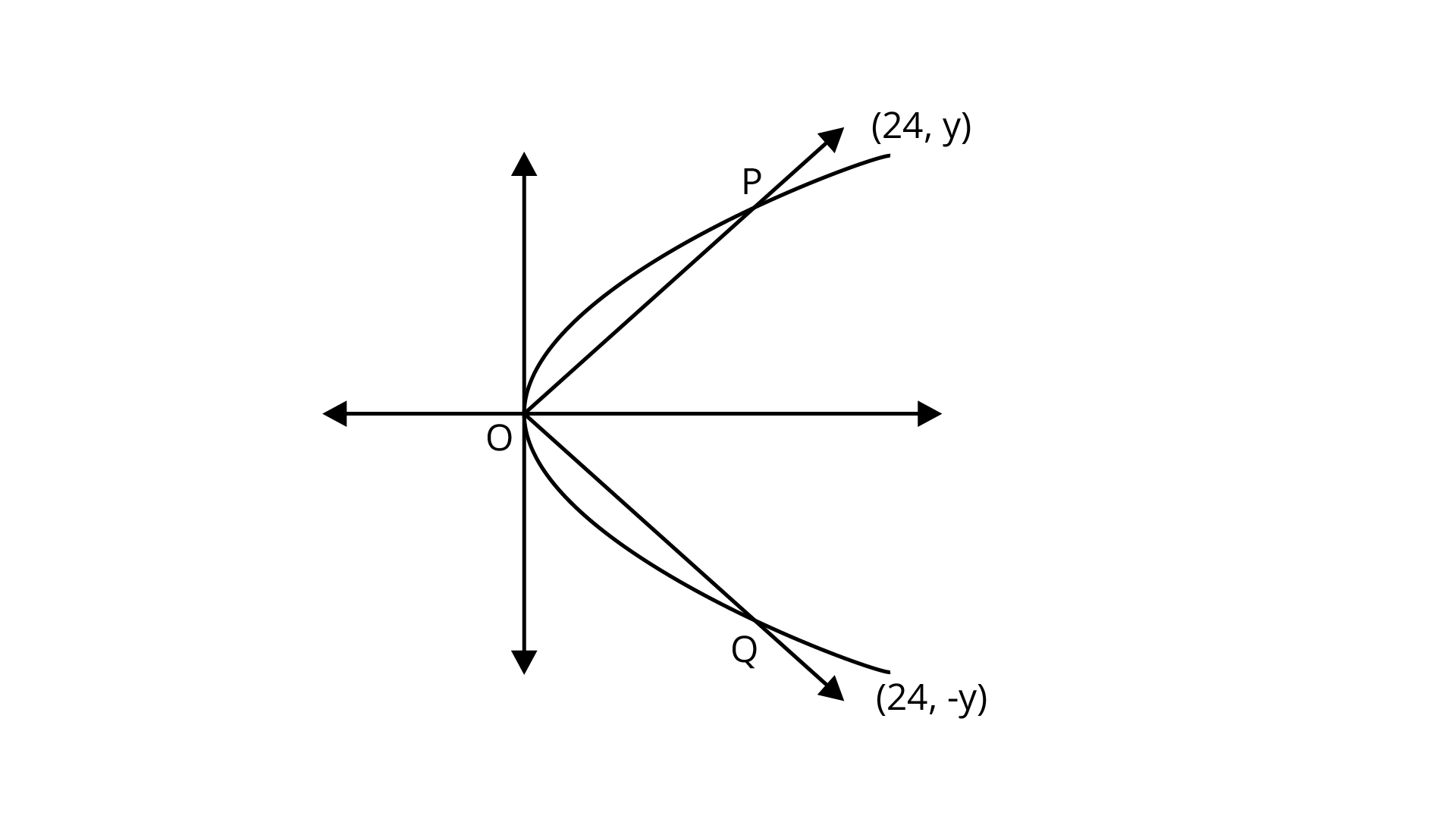
${y^2} = 6x \Rightarrow {y^2} = 6 \times 24 = 144 \Rightarrow y =  \pm 12$

$y - 0 = \left( {\dfrac{{ \pm 12 - 0}}{{24 - 0}}} \right)\left( {x - 0} \right) \Rightarrow y =  \pm \dfrac{x}{2} \Rightarrow 2y \pm x = 0$

Correct Option: B

Sample Question 15: The equation of the ellipse whose center is at the origin and the $x - $ axis, the major axis, which passes through the points $\left( { - 3,1} \right)$ and $\left( {2, - 2} \right)$ is

(A) $5{x^2} + 3{y^2} = 32$

(B) $3{x^2} + 5{y^2} = 32$

(C) $5{x^2} - 3{y^2} = 32$

(D) $3{x^2} + 5{y^2} + 32 = 0$

Ans: Given

The origin is the center of the ellipse.

The major axis is the $x - $ axis.

The ellipse passes through the points $\left( { - 3,1} \right)$and $\left( {2, - 2} \right)$.

The equation of an ellipse whose center is at the origin $\left( {0,0} \right)$ is given by the equation $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$.

Since the ellipse passes through the point $\left( { - 3,1} \right)$ so it will satisfy the equation,

$\Rightarrow \dfrac{9}{{{a^2}}} + \dfrac{1}{{{b^2}}} = 1$                        …… $\left( 1 \right)$

Also, the ellipse passes through the point $\left( {2, - 2} \right)$,

$\Rightarrow \dfrac{4}{{{a^2}}} + \dfrac{4}{{{b^2}}} = 1$                       …… $\left( 2 \right)$

Solving equations $\left( 1 \right)$ and $\left( 2 \right)$ gives $\dfrac{1}{{{a^2}}} = \dfrac{3}{{32}}$and $\dfrac{1}{{{b^2}}} = \dfrac{5}{{32}}$. Therefore, the equation of the ellipse is, $\Rightarrow \dfrac{{3{x^2}}}{{32}} + \dfrac{{5{y^2}}}{{32}} = 1$ $\Rightarrow {x^2} + {y^2} = 32$ 

Correct Option: B

Sample Question 16: The length of the transverse axis along the $x - $ axis with centre at origin of a hyperbola is $7$ and it passes through the point $\left( {5, - 2} \right)$. The equation of the hyperbola is

(A) $\dfrac{4}{{49}}{x^2} - \dfrac{{196}}{{51}}{y^2} = 1$

(B) $\dfrac{{49}}{4}{x^2} - \dfrac{{51}}{{196}}{y^2} = 1$

(C) $\dfrac{4}{{49}}{x^2} - \dfrac{{51}}{{196}}{y^2} = 1$

(D) None of these

Ans: Given The transverse axis of the hyperbola is the $x - $ axis and the centre of the hyperbola is at the origin.

Length of the transverse axis $ = 7{\text{ units}}$.

The hyperbola passes through the point $\left( {5, - 2} \right)$.

The equation of a hyperbola whose centre is at the origin $\left( {0,0} \right)$ and $x - $ axis is the transverse axis is given by the equation $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$.

Since the hyperbola passes through the point $\left( {5, - 2} \right)$ so it will satisfy the equation,

$ \Rightarrow \dfrac{{25}}{{{a^2}}} - \dfrac{4}{{{b^2}}} = 1$                        …… $\left( 1 \right)$

The length of the transverse axis of the hyperbola is $2a$,

$\Rightarrow 2a = 7$

$\Rightarrow {a^2} = \dfrac{{49}}{4}$                             …… $\left( 2 \right)$

Solving equation $\left( 2 \right)$ using $\left( 1 \right)$gives ${b^2} = \dfrac{{196}}{{51}}$. Therefore, the equation of the hyperbola is,

$\Rightarrow \dfrac{4}{{32}}{x^2} - \dfrac{{51}}{{196}}{y^2} = 1$

Correct Option: C

State whether the statements in Sample Questions 17 and 18 are correct or not. Justify:

Sample Question 17: Circle on which the coordinates of any point are $\left( {2 + 4cos\theta ,  - 1 + 4sin\theta } \right)$ where $\theta $ is parameter is given by ${\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 16$.

Ans: Given Coordinates of any point on the circle are $\left( {2 + 4\cos \theta ,  - 1 + 4\sin \theta } \right)$.

Since a point on the circle is given in parametric form as $\left( {2 + 4\cos \theta ,  - 1 + 4\sin \theta } \right)$, assuming a point on the circle in the Cartesian form as $\left( {x,y} \right)$.

$\Rightarrow \left( {x,y} \right) = \left( {2 + 4\cos \theta ,  - 1 + 4\sin \theta } \right)$

On comparing $x$ coordinates,

$\Rightarrow x = 2 + 4\cos \theta $

$\Rightarrow \left( {x - 2} \right) = 4\cos \theta $                        …… $\left( 1 \right)$

On comparing $y$ coordinates,

$\Rightarrow y =  - 1 + 4\cos \theta $

$\Rightarrow \left( {y + 1} \right) = 4\sin \theta $                        …… $\left( 2 \right)$

Squaring and adding equations $\left( 1 \right)$and $\left( 2 \right)$,

$\Rightarrow {\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 16{\cos ^2}\theta  + 16{\sin ^2}\theta $

$\Rightarrow {\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 16\left( {{{\cos }^2}\theta  + {{\sin }^2}\theta } \right)$ 

Using the identity ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$,

$\Rightarrow {\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 16$

Hence, the given statement is correct.

Sample Question 18: A bar of the major given length moves with its extremities on two fixed straight lines at right angles. Any point of the bar describes an ellipse.

Ans: Given Two fixed straight lines at right angles to each other.

A bar with a fixed length has its ends on the two lines and the bar is moving.

In the above diagram $AB$ is the bar and the two perpendicular lines are assumed as $x$ and $y$ axis. Point $P\left( {x,y} \right)$ is any point on the bar. The lengths $AP$ and $BP$ will remain constant as the bar moves. Let us assume $AP = m$and $BP = n$.

In right triangle $BMP$,

$\Rightarrow \sin \theta  = \dfrac{y}{n}$                        …… $\left( 1 \right)$

In right triangle $ANP$,

$\Rightarrow \cos \theta  = \dfrac{x}{m}$                      …… $\left( 2 \right)$

Squaring and adding equations $\left( 1 \right)$and $\left( 2 \right)$,

$\Rightarrow {\sin ^2}\theta  + {\cos ^2}\theta  = {\left( {\dfrac{y}{n}} \right)^2} + {\left( {\dfrac{x}{m}} \right)^2}$

$\Rightarrow \dfrac{{{y^2}}}{{{n^2}}} + \dfrac{{{x^2}}}{{{m^2}}} = {\sin ^2}\theta  + {\cos ^2}\theta $ 

Using the identity ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$,

$\Rightarrow \dfrac{{{y^2}}}{{{n^2}}} + \dfrac{{{x^2}}}{{{m^2}}} = 1$

Clearly the above relation represents an ellipse. Hence, the given statement is true.

Fill in the blanks in Sample Questions 19 and 23:

Sample Question 19: The equation of the circle which passes through the point $\left( {4,5} \right)$ and has its center at $\left( {2,2} \right)$ is _______.

Ans: Given Centre of the circle is at $\left( {2,2} \right)$.

The circle passes through the point $\left( {4,5} \right)$.

The general equation of a circle having its center at $\left( {a,b} \right)$ and radius $r$ is given as ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$.

Given center is $\left( {2,2} \right)$, so the equation of the circle is ${\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = {r^2}$.

Since the point $\left( {4,5} \right)$ lies on the circle that means it will satisfy the equation. Substituting the coordinates,

   $\Rightarrow {\left( {4 - 2} \right)^2} + {\left( {5 - 2} \right)^2} = {r^2}$

   $\Rightarrow 4 + 9 = {r^2}$

   $\Rightarrow 13 = {r^2}$ 

Hence, the equation of the circle is ${\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 13$.

Sample Question 20: A circle has radius $3$ units and its center lies on the line $y = x - 1$. If it passes through the point $\left( {7,3} \right)$, its equation is _______.

Ans: Given Radius of the circle $ = 3{\text{ units}}$

Center of the circle lies on the line $y = x - 1$.

Circle passes through the point $\left( {7,3} \right)$.

The general equation of a circle having its center at $\left( {a,b} \right)$ and radius $r$ is given as ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$.

Given radius is $3{\text{ units}}$, so the equation of the circle is

   $\Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {\left( 3 \right)^2}$

   $\Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = 9$ 

Since the center $\left( {a,b} \right)$ lies on the line $y = x - 1$, so it will satisfy the equation of the line.

$\Rightarrow b = a - 1$                        …… $\left( 1 \right)$

Since the point $\left( {7,3} \right)$ lies on the circle that means it will satisfy the equation of the circle. Substituting the coordinates,

$\Rightarrow {\left( {7 - a} \right)^2} + {\left( {3 - b} \right)^2} = 9$

Using relation $\left( 1 \right)$,

   $\Rightarrow {\left( {7 - a} \right)^2} + {\left( {3 - a + 1} \right)^2} = 9$

   $\Rightarrow {\left( {7 - a} \right)^2} + {\left( {4 - a} \right)^2} = 9$

   $\Rightarrow {a^2} - 11a + 28 = 0$ 

Using the middle term split method,

$\Rightarrow \left( {a - 7} \right)\left( {a - 4} \right) = 0$

$\Rightarrow a = 4$ or $a = 7$

For $a = 4$, $b = 3$ and for $a = 7$, $b = 6$.

Hence, the two possible equations of the circle are ${\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 9$or ${\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} = 9$.

Sample Question 21: If the latus rectum of an ellipse with axis along $x - $ axis and center at origin is $10$, distance between foci $ = $ length of minor axis, then the equation of the ellipse is ______.

Ans: Given Length of the latus rectum of the ellipse $ = 10{\text{ units}}$

Distance between foci $ = $ Length of minor axis

Major axis of the ellipse is along the $x - $ axis.

The general equation of an ellipse which has $x - $ axis as its major axis is given by $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$.

The given length of the latus rectum is $10$ units. The length of the latus rectum of an ellipse is $\dfrac{{2{b^2}}}{a}$.

$\Rightarrow \dfrac{{2{b^2}}}{a} = 10$

$\Rightarrow \dfrac{{{b^2}}}{a} = 5$                        …… $\left( 1 \right)$

It is given that the distance between foci $ = $ length of the minor axis. The length of the minor axis is $2b$ and the distance between the two foci is $2ae$.

$\Rightarrow 2ae = 2b$

$\Rightarrow ae = b$ 

Here $e$ is the eccentricity of the ellipse given as $e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} $.

$\Rightarrow a \times \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}  = b$                        …… $\left( 2 \right)$

Solving equations $\left( 1 \right)$ and $\left( 2 \right)$ gives $a = 10$and $b = 5\sqrt 2 $.

Therefore, the equation of the ellipse is $\dfrac{{{x^2}}}{{100}} + \dfrac{{{y^2}}}{{50}} = 1$.

Sample Question 22: The equation of the parabola whose focus is the point $\left( {2,3} \right)$ and the directrix is the line $x - 4y + 3 = 0$ is ______.

Ans: Given The focus of the parabola is at the point $\left( {2,3} \right)$.

The directrix of the parabola is the line $x - 4y + 3 = 0$.

Let there be a point $P\left( {h,k} \right)$ on the parabola. According to the definition of a parabola: -

Distance between the point $P$ and the focus $ = $ Perpendicular distance between the point and the directrix.

Using the distance formula the distance between $P$ and the focus is $\sqrt {{{\left( {h - 2} \right)}^2} + {{\left( {k - 3} \right)}^2}} $.

The perpendicular distance from the point $P$ to the line $x - 4y + 3 = 0$is $\left| {\dfrac{{\left( {h \times 1} \right) + \left( {\left( { - 4} \right) \times k} \right) + 3}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 4} \right)}^2}} }}} \right|$.

$\Rightarrow \sqrt {{{\left( {h - 2} \right)}^2} + {{\left( {k - 3} \right)}^2}}  = \left| {\dfrac{{\left( {h \times 1} \right) + \left( {\left( { - 4} \right) \times k} \right) + 3}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 4} \right)}^2}} }}} \right|$

$\Rightarrow \sqrt {{{\left( {h - 2} \right)}^2} + {{\left( {k - 3} \right)}^2}}  = \left| {\dfrac{{h - 4k + 3}}{{\sqrt {17} }}} \right|$ 

Squaring both the sides and simplifying,

$\Rightarrow {\left( {h - 2} \right)^2} + {\left( {k - 3} \right)^2} = \dfrac{{{{\left( {h - 4k + 3} \right)}^2}}}{{17}}$

$\Rightarrow 17{h^2} + 68 - 68h + 17{k^2} + 153 - 102k = {h^2} + 16{k^2} + 9 - 8hk - 24k + 6h$

$\Rightarrow 16{h^2} + {k^2} - 74h - 78k + 8hk + 212 = 0$ 

Replacing $h$ with $x$ and $k$ with $y$ gives the equation of the parabola as,

$\Rightarrow 16{x^2} + {y^2} - 74x - 78y + 8xy + 212 = 0$

Sample Question 23: The eccentricity of the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ which passes through the points $\left( {3,0} \right)$ and $\left( {3\sqrt 2 ,2} \right)$ is ______.

Ans: Given The equation of the hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$.

The hyperbola passes through the points $\left( {3,0} \right)$and $\left( {3\sqrt 2 ,2} \right)$.

The equation of the hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$.

Since the point, $\left( {3,0} \right)$ lies on the hyperbola so it will satisfy the equation of the hyperbola.

   $\Rightarrow \dfrac{9}{{{a^2}}} - \dfrac{0}{{{b^2}}} = 1$

   $\Rightarrow \dfrac{9}{{{a^2}}} = 1$

   $\Rightarrow {a^2} = 9$ 

Also, the point $\left( {3\sqrt 2 ,2} \right)$ lies on the hyperbola.

   $\Rightarrow \dfrac{{18}}{{{a^2}}} - \dfrac{4}{{{b^2}}} = 1$

   $\Rightarrow \dfrac{{18}}{9} - \dfrac{4}{{{b^2}}} = 1$

   $\Rightarrow {b^2} = 4$ 

Hence, the eccentricity of the hyperbola is,

   $\Rightarrow e = \sqrt {1 + \dfrac{{{b^2}}}{{{a^2}}}} $

   $\Rightarrow e = \sqrt {1 + \dfrac{4}{9}} $

   $\Rightarrow e = \dfrac{{\sqrt {13} }}{3}$ 

Short Answer Type Question:
1. Find the equation of the circle which touches both axes in the first quadrant and
whose radius is $a$.

Ans:

Given

Center $= \left( {a,a} \right)$

Radius$= r$

Given $r = a$, i.e., $\left( {h,k} \right) = \left( {a,a} \right)$

The standard form of the equation of the circle is

${\left( {x - h} \right)^2} - {\left( {y - k} \right)^2} = {r^2}$

The required equation is,

${\left( {x - a} \right)^2} + {\left( {y - a} \right)^2} = {a^2}$

$\Rightarrow {x^2} + {a^2} - 2ax + {y^2} + {a^2} - 2ay = {a^2}$

$\Rightarrow {x^2} + {y^2} + {a^2} - 2ax - 2ay = 0$

2. Show that the point $\left( {x,y} \right)$ given by $x = \dfrac{{2at}}{{1 + {t^2}}}$ and $y = \dfrac{{a\left( {1 - {t^2}} \right)}}{{1 + {t^2}}}$lies on a circle for all real values of $t$ such that -1 < t < 1 where $a$  is any given real numbers.

Ans: Given

$x = \dfrac{{2at}}{{1 + {t^2}}}$and$y = \dfrac{{a\left( {1 - {t^2}} \right)}}{{1 + {t^2}}}$

$x = \dfrac{{2at}}{{1 + {t^2}}}{\text{          }}...\left( i \right)$and$y = \dfrac{{a\left( {1 - {t^2}} \right)}}{{1 + {t^2}}}{\text{          }}...\left( {ii} \right)$

Squaring and adding equations $\left( i \right){\text{ and }}\left( {ii} \right)$

${x^2} + {y^2} = \dfrac{{4{a^2}{t^2}}}{{{{\left( {1 + {t^2}} \right)}^2}}} + \dfrac{{{a^2}{{\left( {1 - {t^2}} \right)}^2}}}{{{{\left( {1 + {t^2}} \right)}^2}}}$

$\Rightarrow \dfrac{1}{{{a^2}}}\left( {{x^2} + {y^2}} \right) = \dfrac{{4{t^2} + 1 + {t^4} - 2{t^2}}}{{{{\left( {1 + {t^2}} \right)}^2}}}$

$\Rightarrow \dfrac{1}{{{a^2}}}\left( {{x^2} + {y^2}} \right) = \dfrac{{{t^4} + 2{t^2} + 1}}{{{{\left( {1 + {t^2}} \right)}^2}}}$

$\Rightarrow \dfrac{1}{{{a^2}}}\left( {{x^2} + {y^2}} \right) = \dfrac{{{{\left( {1 + {t^2}} \right)}^2}}}{{{{\left( {1 + {t^2}} \right)}^2}}}$

$\Rightarrow \dfrac{1}{{{a^2}}}\left( {{x^2} + {y^2}} \right) = 1$

$\Rightarrow {x^2} + {y^2} = {a^2}$

Hence, the required equation of a circle is ${x^2} + {y^2} = {a^2}$.

3. If a circle passes through the point $\left( {0,0} \right), \left( {a,0} \right) and \left( {0,b} \right)$,  then find the coordinates of its center. 

Ans: Given

Circle passes through the point $\left( {0,0} \right), \left( {a,0} \right){\text{ and }}\left( {0,b} \right)$.

Let the equation is ,

${x^2} + {y^2} + 2gx + 2fy = 0$

According to the Sample Question, this circle pass through the point $\left( {0,0} \right),\left( {a,0} \right){\text{ and }}\left( {0,b} \right)$.

${a^2} + 2ag = 0{\text{          }}...\left( i \right)$and${b^2} + 2bf = 0\,{\text{          }}...\left( {ii} \right)$

From equation $\left( i \right)$

${a^2} + 2ag = 0$

$\Rightarrow 2ag =  - {a^2}$

$\Rightarrow 2g =  - a$

$\Rightarrow g = \dfrac{{ - a}}{2}$

From equation $\left( {ii} \right)$

${b^2} + 2bf = 0$

$\Rightarrow 2bf =  - {b^2}$

$\Rightarrow 2f =  - b$

$\Rightarrow f = \dfrac{{ - b}}{2}$

Thus, coordinate of the center of the circle are 

$= \left( { - f, - g} \right)$

$= \left( {\dfrac{a}{2},\dfrac{b}{2}} \right)$

4. Find the equation of the circle which touches $x - $axis and whose center is $\left( {1,2} \right)$.

Ans: Given                                                        

Center $= \left( {1,2} \right)$                                                        

$r = 2$

$\because r = 2$                                                              

The equation of the circle is,

${\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {2^2}$                                                                              

$\Rightarrow {x^2} + 1 - 2x + {y^2} + 4 - 4y = 4$

$\Rightarrow {x^2} + {y^2} - 2x - 4y + 1 = 0$

5. If the lines $3x - 4y + 4 = 0$ and $6x - 8y - 7 = 0$ are tangents to a circle, then find the radius of the circle.

Ans: Given

$3x - 4y + 4 = 0$

$6x - 8y - 7 = 0$

Distance between given parallel lines gives the diameter of the circle.

For two lines to be parallel ${m_1}$ should be equal to ${m_2}$.

$3x - 4y + 4 = 0{\text{          }}...\left( i \right)$                                                                             

${m_1} = \dfrac{{ - 4}}{3}$                                                                           

$6x - 8y - 7 = 0$or

$3x - 4y - \dfrac{7}{2} = 0{\text{          }}...\left( {ii} \right)$                                                                           

${m_2} = \dfrac{{ - 4}}{3}$

Therefore, ${m_1} = {m_2}$

Now, distance between them.

$d = \left| {\dfrac{{{c_1} - {c_2}}}{{\sqrt {{a^2} + {b^2}} }}} \right|$

$= \left| {\dfrac{{4 - \left( {\dfrac{{ - 7}}{2}} \right)}}{{\sqrt {{3^2} + {4^2}} }}} \right|$

$= \left| {\dfrac{{\dfrac{{8 + 7}}{2}}}{{\sqrt {9 + 16} }}} \right|$

$= \dfrac{3}{2}$

Since, distance between these lines $= $ diameter of the circle.

$d = \dfrac{3}{2}$

$\because r = \dfrac{d}{2}$

$r = \dfrac{3}{4}$

6. Find the equation of a circle which touches both the axis and the line $3x - 4y + 8 = 0$ and lies in the third quadrant.

Ans: Given

Circumference of the circle touches both the axis and the line $3x - 4y + 8 = 0$and lies in the third quadrant.

Let $a$ be the radius of the circle, then $(-a,-a)$ will be the center and the perpendicular distance from the center to the given line gives the radius of the circle.]

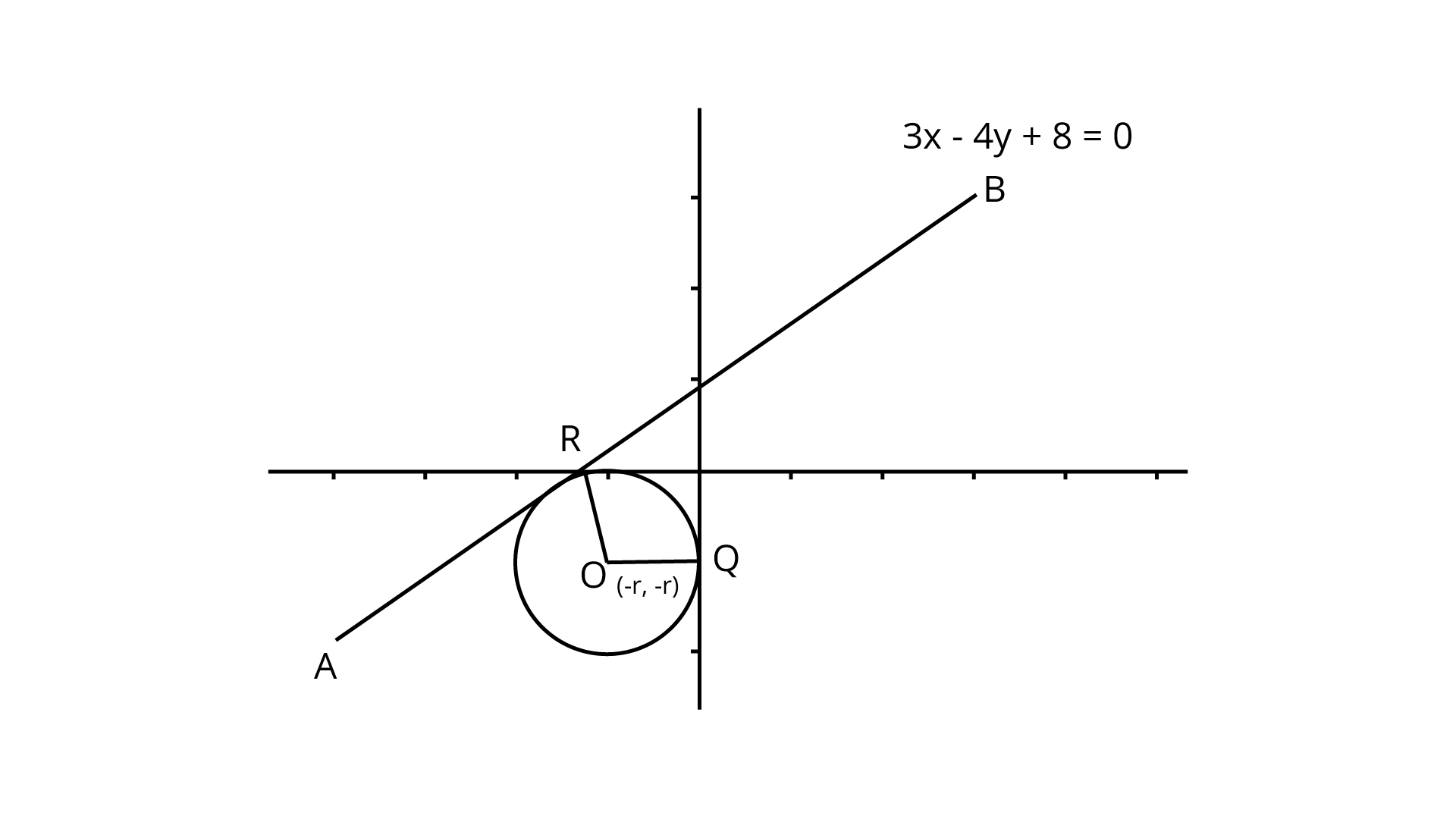
Let $r$ be the radius of the circle.

The coordinates of the center of the circle are  $\left( { - r, - r} \right)$

Now, perpendicular distance from the line $AB = $ radius of the circle.

$d = \left| {\dfrac{{ax + by + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|$

$= \left| {\dfrac{{ - 3r + 4r + 8}}{{\sqrt {{3^2} + {4^2}} }}} \right|$

$= \left| {\dfrac{{ - 3r + 4r + 8}}{{\sqrt {9 + 16} }}} \right|$

$\because r =  \pm \left( {\dfrac{{r + 8}}{5}} \right)$

Taking positive sign.

$r = \dfrac{{r + 8}}{5}$

$\Rightarrow 5r = r + 8$

$\Rightarrow 4r = 8$

$\Rightarrow r = 2$

Now, taking negative sign.

$r = \dfrac{{ - r - 8}}{5}$

$\Rightarrow 5r =  - r - 8$

$\Rightarrow 6r =  - 8$

$\Rightarrow r =  - \dfrac{4}{3}$

But, radius cannot be negative.

So $r \ne  - \dfrac{4}{3}$

$\therefore r = 2$

Now, the equation of circle is.

${\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = {2^2}$

$\Rightarrow {x^2} + 4 + 4x + {y^2} + 4 + 4y = 4$

$\Rightarrow {x^2} + {y^2} + 4x + 4y + 4 = 0$

7. If one end of a diameter of the circle ${x^2} + {y^2}-4x-6y + 11 = 0$is $\left( {3,4} \right)$, then find the coordinate of the other end of the diameter.

Ans: Given

${x^2} + {y^2}-4x-6y + {\text{1}}1 = 0$

Coordinate of one end of a diameter $\left( {3,4} \right)$.

Comparing the standard form of equation of the circle with the given equation of the circle to get the coordinate of the center of the circle i.e., $\left( { - g, - f} \right)$.

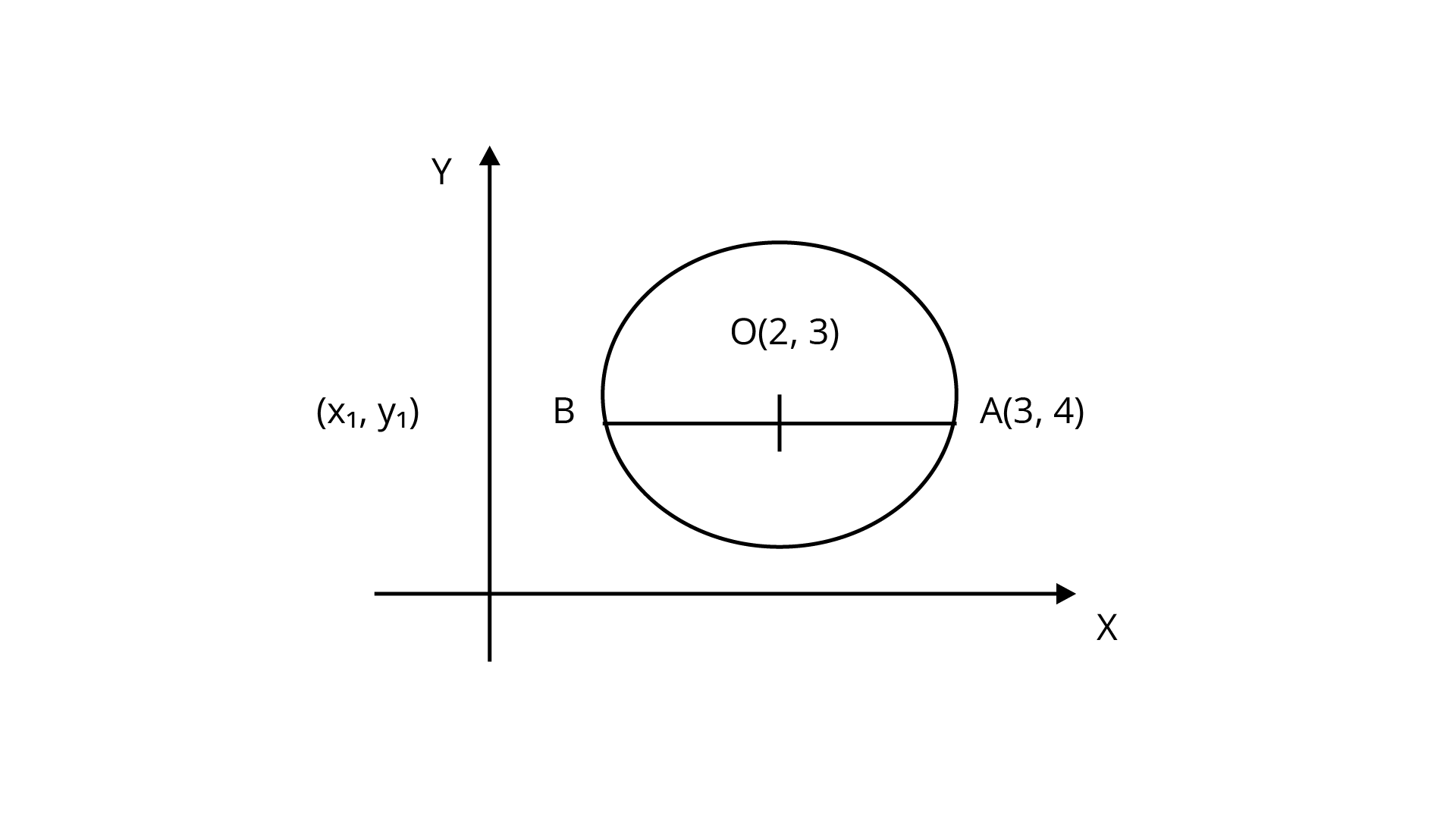
Then, use the midpoint formula to find the required coordinate.

$\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$                                                       

Where,                                                                        

$\left( {x,y} \right)$is the coordinate of midpoint of a line                                                   

$\left( {{x_1},{y_1}} \right)$is the coordinate of one end of a line

$\left( {{x_2},{y_2}} \right)$is the coordinate of other end of a line                                                                 

${x^2} + {y^2}-4x-6y + {\text{1}}1 = 0$

$\therefore $$2g =  - 4$and$2f =  - 6$

So the center of the circle is $\left( { - g, - f} \right)$ i.e, $\left( {2,3} \right)$.

Since, the midpoint of $AB$is $\left( {2,3} \right)$.

$\because \left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$

Then, $2 = \dfrac{{3 + {x_1}}}{2}$

$\Rightarrow 4 = 3 + {x_1}$

$\therefore {x_1} = 1$

And $3 = \dfrac{{4 + {y_1}}}{2}$

$\Rightarrow 6 = 4 + {y_1}$

$\Rightarrow {y_1} = 2$

So, the coordinates of the other end of the diameter will be $\left( {1,2} \right)$.

8. Find the equation of the circle having $\left( {1,-2} \right)$ as its center and passing through

$3x + y = 14, 2x + 5y = 18$ .

Ans: Given

Center $= \left( {1,-2} \right)$

$3x + y = 14$and$2x + 5y = 18$ are the equations of two lines passing through a circle .

Center $ = \left( {1, - 2} \right)$ and the circle passing through the line.

$3x + y = 14{\text{          }}...\left( i \right)$and$2x + 5y = 18{\text{          }}...\left( {ii} \right)$

From equation $\left( i \right)$

$y = 14 - 3x$

Putting the value of $y$ from equation $\left( i \right){\text{ to }}\left( {ii} \right)$

$2x + 70 - 15x = 18$

$\Rightarrow  - 13x =  - 52$

$\Rightarrow x = 4$

Now, put the value of $x$ in equation $\left( i \right)$

$12 + y = 14$

$\Rightarrow y = 2$

Since, point $\left( {4,2} \right)$ lie on these lines also lies on the circle.

Radius of the circle $= \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {2 + 2} \right)}^2}} $

$= \sqrt {9 + 16} $

$= \sqrt {25} $

$= 5$

Now, equation of the circle is 

${\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = {5^2}$

$\Rightarrow {x^2} - 2x + 1 + {y^2} + 4 + 4y = 25$

$\Rightarrow {x^2} + {y^2} - 2x + 4y - 20 = 0$

9. If the line $y = \sqrt 3 x + k$touches the circle ${x^2} + {y^2} = 16$, then find the value of $k$.

Ans: Given

Equation of the circle

${x^2} + {y^2} = 16$

Equate perpendicular distance from the center of the circle to its radius.

Radius $= 4$ and center $= \left( {0,0} \right)$

Now perpendicular distance from $\left( {0,0} \right)$ to the line $y = \sqrt 3 x + k$ is radius of the circle $\left| {\dfrac{{0 - 0 + k}}{{\sqrt {3 + 1} }}} \right| = 4$

Since distance from the point $\left( {m,n} \right)$ to the line  is$d = \left| {\dfrac{{Am + Bn + C}}{{{A^2} + {B^2}}}} \right|$

$\Rightarrow  \pm \dfrac{k}{2} = 4$

$\therefore k =  \pm 8$

10: Find the equation of a circle concentric with the circle ${x^2} + {y^2}-6x + 12y + 15 = 0$and has double of its area.

Ans: Given

Equation of the outer circle:${x^2} + {y^2}-6x + 12y + 15 = 0$

Area of the concentric circle $= $ double the area of the given circle.

Since the concentric circles have the same center.

Both the circles have the same center. So, find the coordinates of the center of the circle using the given equation.

${x^2} + {y^2}-6x + 12y + 15 = 0$ (given)

Comparing the given equation with the standard equation of circle, we get.

$2g =  - 6$

$\Rightarrow g =  - 3$

$2f = 12$

$\Rightarrow f = 6$

And $c = 15$

Therefore, center $= \left( { - g, - f} \right) = \left( {3, - 6} \right)$

So, the center of the required circle is $\left( {3, - 6} \right)$  (since the circle are concentric)

Radius of the given circle $= \sqrt {{g^2} + {f^2} - c} $

$= \sqrt {9 + 36 - 15} $

$= \sqrt {30} $

Let radius of the required circle be ${r_1}$

$\therefore $$2 \times $ Area of the given circle $= $ Area of the required circle

$\Rightarrow 2\left( {\pi {r^2}} \right) = \pi r_1^2$

$\Rightarrow 2\left( {\pi {{\left( {\sqrt {30} } \right)}^2}} \right) = \pi r_1^2$

$\Rightarrow 60\pi  = \pi r_1^2$

$\Rightarrow r_1^2 = 60$

$\Rightarrow {r_1} = \sqrt {60} $

$\therefore \sqrt {{g^2} + {f^2} - c}  = \sqrt {60} $

$\Rightarrow 9 + 36 - c = 60$

$\Rightarrow c =  - 15$

So, the required equation of circle is ${x^2} + {y^2}-6x + 12y - 15 = 0$

11. If the latus rectum of an ellipse is equal to half of minor axis, then find its eccentricity.

Ans: Given

Latus rectum of an ellipse is equal to half of minor axis.

Consider the equation of the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

$\therefore $ Length of major axis $= 2a$

Length of minor axis $= 2b$

And the length of latus rectum $= \dfrac{{2{b^2}}}{a}$

According to the Sample Question, latus rectum of an ellipse is equal to half of minor axis

$\dfrac{{2{b^2}}}{a} = \dfrac{{2b}}{2}$

$\Rightarrow \dfrac{{2b}}{a} = 1$

$\Rightarrow b = \dfrac{a}{2}$

$\because {b^2} = {a^2}\left( {1 - {e^2}} \right)$

$\Rightarrow {\left( {\dfrac{a}{2}} \right)^2} = {a^2}\left( {1 - {e^2}} \right)$

$\Rightarrow \dfrac{{{a^2}}}{4} = {a^2}\left( {1 - {e^2}} \right)$

$\Rightarrow 1 - {e^2} = \dfrac{1}{4}$

$\Rightarrow {e^2} = 1 - \dfrac{1}{4}$

$\therefore e = \dfrac{{\sqrt 3 }}{2}$

12. Given the ellipse with equation $9{x^2} + 25{y^2} = 225$, find the eccentricity and foci

Ans: Given

Equation of ellipse $9{x^2} + 25{y^2} = 225$

$9{x^2} + 25{y^2} = 225$ (given)

$ \Rightarrow \dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1$

$ \Rightarrow a = 5, b = 3$

We know that ${b^2} = {a^2}\left( {1 - {e^2}} \right)$

$ \Rightarrow 9 = 25\left( {1 - {e^2}} \right)$

$ \Rightarrow \dfrac{9}{{25}} = 1 - {e^2}$

$\Rightarrow {e^2} = 1 - 9/25$

therefore $e = \sqrt {1 - 9/25}$

$ = \sqrt {\dfrac{{25 - 9}}{{25}}} $

$ = \sqrt {\dfrac{{16}}{{25}}} $

$ = \dfrac{4}{5}$

13. If the eccentricity of an ellipse is $\dfrac{5}{8}$ and the distance between its foci is $10$, then find the latus rectum of the ellipse.

Ans: Given

Eccentricity $= \dfrac{5}{8}$

Distance between its foci$ = 10$

Eccentricity$ = \dfrac{5}{8}$ i.e.,$e = \dfrac{5}{8}$

Let equation of the ellipse be $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

Since, the foci of the ellipse is $\left( { \pm ae,0} \right)$,

$\therefore $ Distance between foci $ = \sqrt {{{\left( {ae + ae} \right)}^2}} $

$ \Rightarrow 2\sqrt {{a^2}{e^2}}  = 10$ (distance between its foci$ = 10$)

$ \Rightarrow \sqrt {{a^2}{e^2}}  = 5$

$ \Rightarrow {a^2}{e^2} = 25$

$ \Rightarrow {a^2} = \dfrac{{25 \times 64}}{{25}}$

$\therefore a = 8$

$ \Rightarrow {b^2} = {a^2}\left( {1 - {e^2}} \right)$

$ \Rightarrow {b^2} = 64\left( {1 - \dfrac{{25}}{{64}}} \right)$

$ \Rightarrow {b^2} = 64\left( {\dfrac{{64 - 25}}{{64}}} \right)$

${b^2} = 39$

Length of latus rectum of ellipse$ = \dfrac{{2{b^2}}}{a} = 2\left( {\dfrac{{39}}{8}} \right) = \dfrac{{39}}{4}$

14. Find the equation of ellipse whose eccentricity is $\dfrac{2}{3}$, latusrectum is $5$ and the center is$\left( {0,0} \right).$

Ans: Given

$e = \dfrac{2}{3}$

Latusrectum $= 5$.

Center of the circle i.e.,$\left( {h,k} \right) = \left( {0,0} \right)$

$e = \dfrac{2}{3}$and latusrectum $= 5$(given)

i.e.,$\dfrac{{2{b^2}}}{a} = 5$

$ \Rightarrow {b^2} = \dfrac{{5a}}{2}$

$\because {b^2} = {a^2}\left( {1 - {e^2}} \right)$

$ \Rightarrow \dfrac{{5a}}{2} = {a^2}\left( {1 - \dfrac{4}{9}} \right)$

$ \Rightarrow \dfrac{5}{2} = \dfrac{{5a}}{9}$

$ \Rightarrow a = \dfrac{9}{2}$

$ \Rightarrow {a^2} = \dfrac{{81}}{4}$

${b^2} = \dfrac{{5 \times 9}}{{2 \times 2}} = \dfrac{{45}}{4}$

So, the required equation of ellipse is $\dfrac{{4{x^2}}}{{81}} + \dfrac{{4{y^2}}}{{45}} = 1$

15. Find the distance between the directrices of the ellipse $\dfrac{{{x^2}}}{{36}} + \dfrac{{{y^2}}}{{20}} = 1$

Ans: Given

Equation of the ellipse $\dfrac{{{x^2}}}{{36}} + \dfrac{{{y^2}}}{{20}} = 1$

On comparing the equation with $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, we get

$a = 6,b = 2\sqrt 5 $

$\because {b^2} = {a^2}\left( {1 - {e^2}} \right)$

$\Rightarrow 20 = 36\left( {1 - {e^2}} \right)$

$\Rightarrow \dfrac{{20}}{{36}} = 1 - {e^2}$

$\therefore e = \sqrt {1 - \dfrac{{20}}{{36}}} $

$= \sqrt {\dfrac{{16}}{{36}}} $

$= \dfrac{4}{6}$

$= \dfrac{2}{3}$

$\therefore \dfrac{a}{e} = \dfrac{6}{{\dfrac{2}{3}}} = 9$

And $- \dfrac{a}{e} =  - 9$

Therefore, distance between the directrices $= \left| { + \dfrac{a}{e} - \left( { - \dfrac{a}{e}} \right)} \right|$

$= \left| {9 - \left( { - 9} \right)} \right|$

$= 18$

16.  Find the coordinates of a point on the parabola ${y^2} = 8x$whose focal distance is $4$.

Ans: Given

Equation of the parabola ${y^2} = 8x$

Focal distance $= 4$.

${y^2} = 8x$ (given)

On comparing the given equation of parabola with ${y^2} = 4ax$, we get

8x = 4ax

a = 2 

$\therefore $ Focal distance $= \left| {x + a} \right| = 4$

$\Rightarrow \left| {x + 2} \right| = 4$

$\Rightarrow x + 2 =  \pm 4$

$\Rightarrow x = 2, - 6$

But $x \ne  - 6$ (because the given parabola lies in the positive $x - $axis direction).

For $x = 2,$${y^2} = 8 \times 2$

$\therefore {y^2} = 16$

$\Rightarrow y =  \pm 4$

So, the points are $\left( {2,4} \right){\text{ and }}\left( {2, - 4} \right)$

17.Find the length of the line segment joining the vertex of the parabola ${y^2} = 4ax$and a point on the parabola where the line-segment makes an angle $\theta $ to the $x - $axis.

Ans: Given

Equation of the parabola ${y^2} = 4ax$.

${y^2} = 4ax$ (given)

Let the coordinates of any point $P$ on the parabola be $\left( {a{t^2},2at} \right)$

In $\Delta POA$, $\tan \theta  = \dfrac{{2at}}{{a{t^2}}} = \dfrac{2}{t}$

$\tan \theta  = \dfrac{2}{t}$

$\Rightarrow t = 2\cot \theta $

$\therefore $Length of $OP$$ = \sqrt {{{\left( {0 - a{t^2}} \right)}^2} + {{\left( {0 - 2at} \right)}^2}} $

$ = \sqrt {{a^2}{t^4} + 4{a^2}{t^2}} $

$ = at\sqrt {{t^2} + 4} $

$ = 2a\cot \theta \sqrt {4{{\cot }^2}\theta  + 4} $

$ = 4a\cot \theta \sqrt {1 + {{\cot }^2}\theta } $

$ = 4a\cot \theta  \cdot \operatorname{cosec} \theta $

$ = \dfrac{{4a\cos \theta }}{{\sin \theta }} \cdot \dfrac{1}{{\sin \theta }}$

$ = \dfrac{{4a\cos \theta }}{{{{\sin }^2}\theta }}$

18. If the points $\left( {0,4} \right)$ and $\left( {0,2} \right)$ are respectively the vertex and focus of a parabola,then find the equation of the parabola.

Ans: Given

Vertex $= \left( {0,4} \right)$

 Focus $= \left( {0,2} \right)$

By definition of parabola:                    

$\Rightarrow \left| {\dfrac{{0 + y - 6}}{{\sqrt {0 + 1} }}} \right| = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 2} \right)}^2}} $

$\Rightarrow \left| {y - 6} \right| = \sqrt {{x^2} + {y^2} - 4y + 4} $

$\Rightarrow {x^2} + {y^2} - 4y + 4 = {y^2} + 36 - 12y$

$\therefore {x^2} + 8y = 32$

19.If the line $y = mx + 1$ is tangent to the parabola ${y^2} = 4x$ then find the value of $m.$

Ans; Given

Tangent line to the parabola:

$y = mx + 1$

Equation of parabola:

${y^2} = 4x$

Line $y = mx + 1$ is tangent to the parabola ${y^2} = 4x$.

Solving the equation of line and parabola, we obtain a quadratic equation and then apply the tangency condition giving the value of $m$.

Putting the value of $y$ from $y=mx+1$ in $y^2=4x$:

${m^2}{x^2} + 2mx + 1 = 4x$

$\Rightarrow {m^2}{x^2} + 2mx - 4x + 1 = 0$

$\Rightarrow {m^2}{x^2} + x(2m - 4) + 1 = 0$

 As the line touches the parabola, the equation must have equal roots i.e. discriminant$= 0$

$\Rightarrow {(2m - 4)^2} - 4{m^2} \times 1 = 0$

$\Rightarrow 4{m^2} + 16 - 16m - 4{m^2} = 0$

$\Rightarrow 16m - 16 = 0$

$\Rightarrow 16m = 16$

$\therefore m = 1$

20.If the distance between the foci of a hyperbola is $16$ and its eccentricity is $\sqrt 2 $, then obtain the equation of the hyperbola.

Ans: Given

The distance between the foci of a hyperbola is $16$.

$e = \sqrt 2 $

Distance between the foci i.e.,$2ae = 16$

    $\Rightarrow ae = 8$

And $e = \sqrt 2 $

    $\therefore a\sqrt 2  = 8$

    $a = 4\sqrt 2 $ 

We know that, ${b^2} = {a^2}\left( {{e^2} - 1} \right)$

   $\Rightarrow {b^2} = {\left( {4\sqrt 2 } \right)^2}\left[ {{{\left( {\sqrt 2 } \right)}^2} - 1} \right]$

   $= 16 \times 2\left( {2 - 1} \right)$

   $= 32\left( {2 - 1} \right)$ 

So, the equation of hyperbola is

   $\dfrac{{{x^2}}}{{32}} - \dfrac{{{y^2}}}{{32}} = 1$

   $\Rightarrow {x^2} - {y^2} = 32$ 

21. Find the eccentricity of the hyperbola $9{y^2}-4{x^2} = 36$.

Ans: Given

Equation of the hyperbola is$9{y^2}-4{x^2} = 36$

Given the equation of hyperbola

  $9{y^2}-4{x^2} = 36$

  $\Rightarrow \dfrac{{9{y^2}}}{{36}}-\dfrac{{4{x^2}}}{{36}} = \dfrac{{36}}{{36}}$

  $\Rightarrow \dfrac{{{y^2}}}{4} - \dfrac{{{x^2}}}{9} = 1$

  $\Rightarrow  - \dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 1$ 

Since, this equation in form of $- \dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 1$, where $a = 3$ and $b = 2$

  $\therefore e = \sqrt {1 + \dfrac{{{a^2}}}{{{b^2}}}} $

  $= \sqrt {1 + \dfrac{9}{4}} $

  $= \dfrac{{\sqrt {13} }}{2}$ 

22.Find the equation of the hyperbola with eccentricity $\dfrac{3}{2}$ and foci at $\left( { \pm  2,0} \right)$.

Ans: Given

Foci at $\left( { \pm  2,0} \right)$.

$e = \dfrac{3}{2}$

Given that eccentricity i.e., $e = \dfrac{3}{2}$ and $\left( { \pm ae,0} \right) = \left( { \pm  2,0} \right)$

   $\therefore ae = 2$

   $\Rightarrow a \cdot \dfrac{3}{2} = 2$

   $\Rightarrow a = \dfrac{4}{3}$

   $\therefore {b^2} = {a^2}\left( {{e^2} - 1} \right)$

   $= \dfrac{{16}}{9}\left( {\dfrac{9}{4} - 1} \right)$

   $= \dfrac{{16}}{4}\left( {\dfrac{5}{4}} \right)$

   $= \dfrac{{20}}{9}$ 

So, the equation of hyperbola is

  $\dfrac{{{x^2}}}{{\dfrac{{16}}{9}}} - \dfrac{{{y^2}}}{{\dfrac{{20}}{9}}} = 1$

  $\Rightarrow \dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{5} = \dfrac{4}{9}$ 

Long Answer Type Question:

23.If the lines $2x-3y = 5$and $3x-4y = 7$ are the diameters of a circle of area $154$square units, then obtain the equation of the circle.

Ans: Given :

lines are, $2x-3y = 5{\text{          }}...\left( i \right)$

And $3x-4y = 7{\text{         }}... \left( {ii} \right)$

The intersection point of these lines will be coordinate of the center of the circle i.e., coordinate of the center of the circle as $\left( {1, - 1} \right)$.

Let radius of the circle be $r$.

Then, $\pi {r^2} = 154$

$\Rightarrow \dfrac{{22}}{7} \times {r^2} = 154$

$\Rightarrow {r^2} = \dfrac{{154 \times 7}}{{22}}$

$\Rightarrow {r^2} = \dfrac{{14 \times 7}}{2}$

$\Rightarrow {r^2} = 49$

$\Rightarrow r = 7$ 

So the equation of circle is 

$\left( x - 1 \right)^2 + \left( y + 1 \right)^2 = 49$

$\Rightarrow {x^2} - 2x + 1 + {y^2} + 2y + 1 = 49$

$\Rightarrow {x^2} + {y^2} - 2x + 2y = 47$ 

24.Find the equation of the circle which passes through the points $\left( {2, 3} \right) and \left( {4, 5} \right)$and the center lies on the straight line $y-4x + 3 = 0.$

Ans: Let the center of the circle be $C\left( {h,k} \right)$

Since that the circle lies on the line $y-4x + 3 = 0.$

$k - 4h + 3 = 0$or$k = 4h - 3$

So, the center is $C\left( {h,4h - 3} \right)$.

Now, point $\left( {2, 3} \right){\text{ and }}\left( {4, 5} \right)$ lies on the circle.

$\therefore A{C^2} = B{C^2}$

$\Rightarrow {\left( {h - 2} \right)^2} + {\left( {4h - 3 - 3} \right)^2} = {\left( {h - 4} \right)^2} + {\left( {4h - 3 - 5} \right)^2}$

$\Rightarrow {\left( {h - 2} \right)^2} + {\left( {4h - 6} \right)^2} = {\left( {h - 4} \right)^2} + {\left( {4h - 8} \right)^2}$

$\Rightarrow  - 4h + 4 - 48h + 36 =  - 8h + 16 - 64h + 64$

$\Rightarrow 20h = 40$

$\Rightarrow h = 2$ 

So, the center is $C\left( {2,5} \right)$.

And radius $= AC = \sqrt {{{\left( {2 - 2} \right)}^2} + {{\left( {3 - 5} \right)}^2}} $

Radius $= 2$

Therefore, equation of the circle is:

${\left( {x - 2} \right)^2} + {\left( {y - 5} \right)^2} = 4$

$\Rightarrow {x^2} + {y^2} - 4x - 10y + 25 = 0$ 

25.Find the equation of a circle whose center is $\left( {3, - 1} \right)$ and which cuts off a chord of length $6$ units on the line $2x - 5y + 18 = 0$.

Ans: Given

The center of the circle lies at $\left( {3, - 1} \right)$.

The circle cuts off a chord of length $6$ units on the line $2x - 5y + 18 = 0$.

The equation of a circle with center at $\left( {a,b} \right)$ and radius $r$ is given as ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$.

So, for the given circle with center at $\left( {3, - 1} \right)$ and radius $r$ the equation is given as ${\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = {r^2}$.

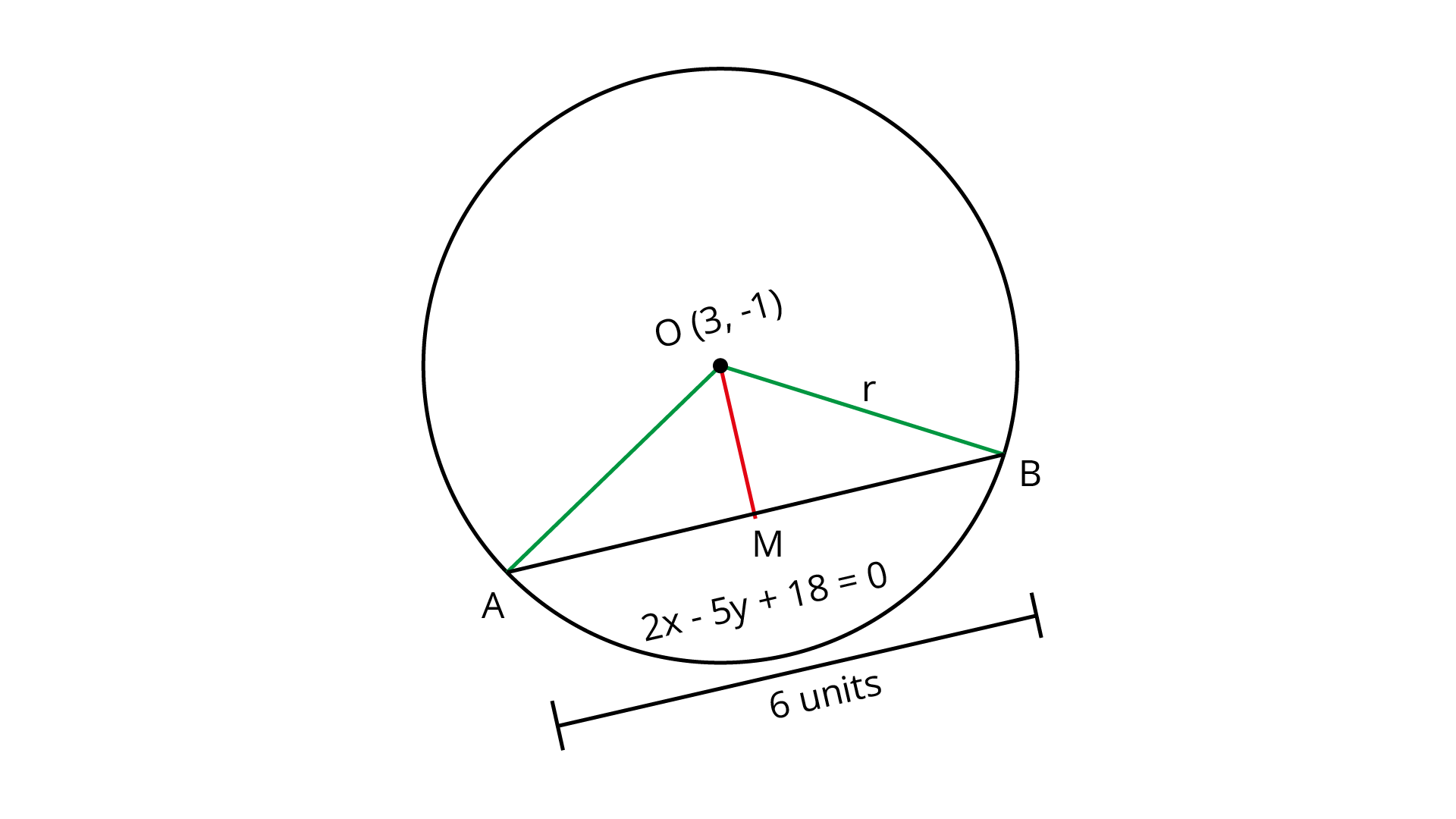
A perpendicular is drawn from the center to the chord $2x - 5y + 18 = 0$. Using the theorem that the perpendicular from the center of the circle bisects the chord, it can be concluded that $MB = 3{\text{ units}}$.

The length of the perpendicular $OM$

$= \left| {\dfrac{{\left( {2 \times 3} \right) + \left( {\left( { - 5} \right) \times \left( { - 1} \right)} \right) + 18}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 5} \right)}^2}} }}} \right|$

$= \left| {\dfrac{{29}}{{\sqrt {29} }}} \right|$

$= \sqrt {29}$ 

In the right triangle $OMB$ using the Pythagoras theorem,

$\Rightarrow {r^2} = {\left( {\sqrt {29} } \right)^2} + {\left( 3 \right)^2}$

$\Rightarrow {r^2} = 38$ 

Hence, the equation of the circle is ${\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 38$.

26.Find the equation of a circle of radius $5$ which is touching another circle ${x^2} + {y^2} - 2x - 4y - 20 = 0$at $\left( {5,5} \right)$.

Ans: Given

The radius of the required circle $ = 5{\text{ units}}$

The required circle is touching another circle having equation ${x^2} + {y^2} - 2x - 4y - 20 = 0$.

Point of contact is at $\left( {5,5} \right)$.

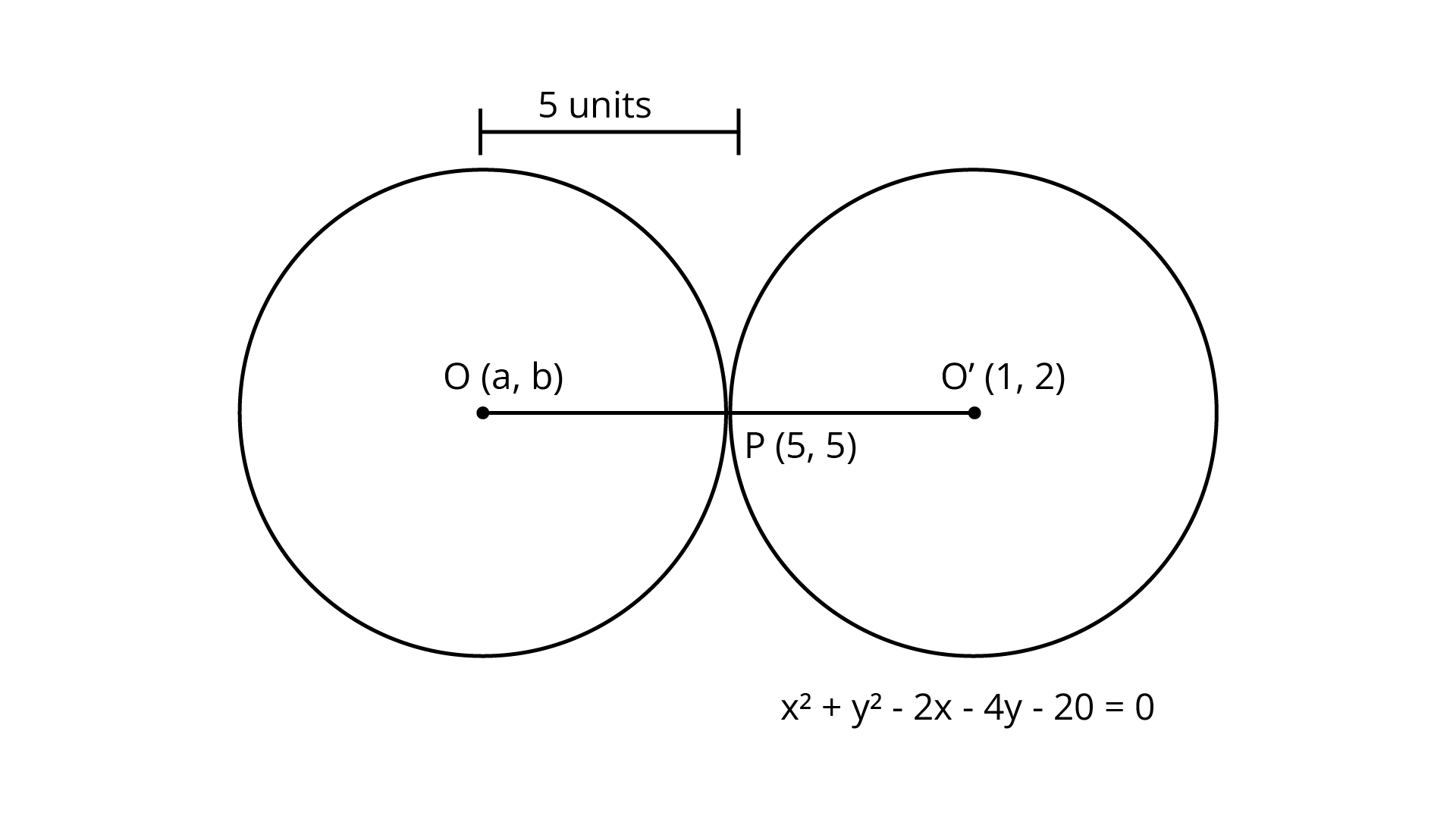
Assuming the center of the required circle as $\left( {a,b} \right)$, its radius is given as $5{\text{ units}}$. So, the equation of the circle can be ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = 25$.

Since, the point $\left( {5,5} \right)$ lies on both the circles, so it will satisfy the above equation also.

$ \Rightarrow {\left( {5 - a} \right)^2} + {\left( {5 - b} \right)^2} = 25$ … (1)

The center of the circle ${x^2} + {y^2} - 2x - 4y - 20 = 0$is $\left( {1,2} \right)$.

Now, the lines $OP$ and $O'P$ will always form a straight line, so their slopes must be equal.

$\Rightarrow \dfrac{{\left( {5 - b} \right)}}{{\left( {5 - a} \right)}} = \dfrac{{\left( {5 - 2} \right)}}{{\left( {5 - 1} \right)}}$

$\Rightarrow \left( {5 - b} \right) = \dfrac{3}{4}\left( {5 - a} \right)$ 

Substituting the value of $\left( {5 - b} \right)$ in equation (1),

$\Rightarrow {\left( {5 - a} \right)^2} + \dfrac{9}{{16}}{\left( {5 - a} \right)^2} = 25$

$\Rightarrow \dfrac{{25}}{{16}}{\left( {5 - a} \right)^2} = 25$

$\Rightarrow {\left( {5 - a} \right)^2} = 16$

$\Rightarrow \left( {5 - a} \right) =  \pm 4$ 

(i) Considering the positive sign,

$\Rightarrow \left( {5 - a} \right) = 4$

$\Rightarrow a = 1$ 

This value of $a$gives $b = 2$. Therefore, the equation of the circle is ${\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 25$.

However this circle is the same as the circle ${x^2} + {y^2} - 2x - 4y - 20 = 0$ if expanded. In this case both the circles will be overlapping.

(ii) Considering the negative sign,

$\Rightarrow \left( {5 - a} \right) =  - 4$

$\Rightarrow a = 9$ 

This value of $a$gives $b = 8$. Therefore, the equation of the circle is ${\left( {x - 9} \right)^2} + {\left( {y - 8} \right)^2} = 25$.

This circle will touch the circle ${x^2} + {y^2} - 2x - 4y - 20 = 0$ at only one point, i.e. $\left( {5,5} \right)$.

27. Find the equation of a circle passing through the point $\left( {7,3} \right)$ having radius $3$ units and whose center lies on the line $y = x - 1$.

Ans: Given

Radius of the circle $ = 3{\text{ units}}$

Center of the circle lies on the line $y = x - 1$.

Circle passes through the point $\left( {7,3} \right)$.

The general equation of a circle having its center at $\left( {a,b} \right)$ and radius $r$ is given as ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$.

Given radius is $3{\text{ units}}$, so the equation of the circle is

   $\Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {\left( 3 \right)^2}$

   $\Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = 9$ 

Since the centre $\left( {a,b} \right)$ lies on the line $y = x - 1$, so it will satisfy the equation of the line.

$\Rightarrow b = a - 1$ … (1)

Since the point $\left( {7,3} \right)$ lies on the circle that means it will satisfy the equation of the circle. Substituting the coordinates,

$\Rightarrow {\left( {7 - a} \right)^2} + {\left( {3 - b} \right)^2} = 9$

Using relation (1),

   $\Rightarrow {\left( {7 - a} \right)^2} + {\left( {3 - a + 1} \right)^2} = 9$

   $\Rightarrow {\left( {7 - a} \right)^2} + {\left( {4 - a} \right)^2} = 9$

   $\Rightarrow {a^2} - 11a + 28 = 0$ 

Using the middle term split method,

$\Rightarrow \left( {a - 7} \right)\left( {a - 4} \right) = 0$

$\Rightarrow a = 4$or$a = 7$

For $a = 4$, $b = 3$ and for $a = 7$, $b = 6$.

Hence, the two possible equations of the circle are ${\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 9$or ${\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} = 9$.

28.Find the equation of each of the following parabolas

(a) Directrix $x = 0$, focus at $\left( {6,0} \right)$

Ans: Let there be a point $P\left( {h,k} \right)$ on the parabola. According to the definition of a parabola: -

Distance between the point $P$ and the focus $ = $ Perpendicular distance between the point and the directrix.

Using the distance formula the distance between $P$ and the focus is $\sqrt {{{\left( {h - 6} \right)}^2} + {{\left( {k - 0} \right)}^2}} $.

The perpendicular distance from the point $P$ to the line $x = 0$is $\left| {\dfrac{{\left( {h \times 1} \right) + \left( {0 \times k} \right) + 0}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2}} }}} \right|$

$\Rightarrow \sqrt {{{\left( {h - 6} \right)}^2} + {{\left( {k - 0} \right)}^2}}  = \left| {\dfrac{{\left( {h \times 1} \right) + \left( {0 \times k} \right) + 0}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2}} }}} \right|$

$\Rightarrow \sqrt {{{\left( {h - 6} \right)}^2} + {k^2}}  = \left| h \right|$ 

Squaring both the sides and simplifying,        

   $\Rightarrow {\left( {h - 6} \right)^2} + {k^2} = {h^2}$

   $\Rightarrow {h^2} + 36 - 12h + {k^2} = {h^2}$

   $\Rightarrow {k^2} = 12\left( {h - 3} \right)$ 

Replacing $h$ with $x$ and $k$ with $y$ gives the equation of the parabola as,

$\Rightarrow {y^2} = 12\left( {x - 3} \right)$

(b) Vertex at $\left( {0,4} \right)$, focus at $\left( {0,2} \right)$

Ans: Here the vertex is at $\left( {0,4} \right)$ and the focus is at $\left( {0,2} \right)$ that means the equation of the parabola is of the form ${\left( {x - h} \right)^2} = 4a\left( {y - k} \right)$ (known as the vertex form), where $\left( {h,k} \right)$ is the vertex and $\left( {h, a + k} \right)$ is the focus. So the equation of the parabola is,

   $\Rightarrow {\left( {x - 0} \right)^2} = 4a\left( {y - 4} \right)$

   $\Rightarrow {x^2} = 4a\left( {y - 4} \right)$ 

Equating the $y$ coordinate of focus,

   $\Rightarrow a + k = 2$

   $\Rightarrow a + 4 = 2$

   $\Rightarrow a =  - 2$ 

Therefore, the equation of the parabola is ${x^2} =  - 8\left( {y - 4} \right)$.

(c) Focus at $\left( { - 1, - 2} \right)$, directrix $x - 2y + 3 = 0$

Ans: Let there be a point $P\left( {h,k} \right)$ on the parabola.

The distance between $P$ and the focus is $\sqrt {{{\left( {h - \left( { - 1} \right)} \right)}^2} + {{\left( {k - \left( { - 2} \right)} \right)}^2}} $.

The perpendicular distance from the point $P$ to the line $x - 2y + 3 = 0$is $\left| {\dfrac{{\left( {h \times 1} \right) + \left( {\left( { - 2} \right) \times k} \right) + 3}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 2} \right)}^2}} }}} \right|$

$\Rightarrow \sqrt {{{\left( {h - \left( { - 1} \right)} \right)}^2} + {{\left( {k - \left( { - 2} \right)} \right)}^2}}  = \left| {\dfrac{{\left( {h \times 1} \right) + \left( {\left( { - 2} \right) \times k} \right) + 3}}{{\sqrt {{{\left( 1 \right)}^2} + {{\left( { - 2} \right)}^2}} }}} \right|$

$\Rightarrow \sqrt {{{\left( {h + 1} \right)}^2} + {{\left( {k + 2} \right)}^2}}  = \left| {\dfrac{{h - 2k + 3}}{{\sqrt 5 }}} \right|$ 

Squaring both the sides and simplifying,

$\Rightarrow {\left( {h + 1} \right)^2} + {\left( {k + 2} \right)^2} = {\dfrac{{\left( {h - 2k + 3} \right)}}{5}^2}$

$\Rightarrow 5{h^2} + 5 + 10h + 5{k^2} + 20 + 20k = {h^2} + 4{k^2} + 9 - 4kh - 12k + 6h$

$\Rightarrow 4{h^2} + {k^2} + 4h + 32k + 4kh + 16 = 0$ 

Replacing $h$ with $x$ and $k$ with $y$ gives the equation of the parabola as,

$\Rightarrow 4{x^2} + {y^2} + 4x + 32y + 4xy + 16 = 0$

29. Find the equation of the set of all points the sum of whose distances from the points $\left( {3,0} \right)$ and $\left( {9,0} \right)$is $12$.

Ans: GivenTwo points $\left( {3,0} \right)$and $\left( {9,0} \right)$.

The sum of distances of a point from the given two points is $12{\text{ units}}$.

Let the required point be $P\left( {x,y} \right)$.

Using the distance formula the distance between $P$ and $\left( {3,0} \right)$ is

   $= \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 0} \right)}^2}} $

   $= \sqrt {{{\left( {x - 3} \right)}^2} + {y^2}} $ 

Similarly, the distance between $P$ and $\left( {9,0} \right)$ is

   $= \sqrt {{{\left( {x - 9} \right)}^2} + {{\left( {y - 0} \right)}^2}} $

   $= \sqrt {{{\left( {x - 9} \right)}^2} + {y^2}} $ 

It is given that the sum of distances is $12{\text{ units}}$, so taking the sum,

$\Rightarrow \sqrt {{{\left( {x - 3} \right)}^2} + {y^2}}  + \sqrt {{{\left( {x - 9} \right)}^2} + {y^2}}  = 12$

$\Rightarrow \sqrt {{{\left( {x - 3} \right)}^2} + {y^2}}  = 12 - \sqrt {{{\left( {x - 9} \right)}^2} + {y^2}} $ 

On squaring both the sides,

$\Rightarrow {\left( {x - 3} \right)^2} + {y^2} = 144 + {\left( {x - 9} \right)^2} + {y^2} - 24\sqrt {{{\left( {x - 9} \right)}^2} + {y^2}} $

$\Rightarrow {x^2} + 9 - 6x + {y^2} = 144 + {x^2} + 81 - 18x + {y^2} - 24\sqrt {{{\left( {x - 9} \right)}^2} + {y^2}} $

$\Rightarrow 2\sqrt {{{\left( {x - 9} \right)}^2} + {y^2}}  = \left( {18 - x} \right)$ 

Again squaring both the sides,

$\Rightarrow 4 \times \left( \left( x - 9 \right)^2 + y^2 \right) = \left( 18 - x \right)^2$

$\Rightarrow 4{x^2} + 324 - 72x + 4{y^2} = 324 + {x^2} - 36x$

$\Rightarrow 3{x^2} - 36x + 4{y^2} = 0$ 

30.Find the equation of the set of all points whose distances from $\left( {0,4} \right)$ are $\dfrac{2}{3}$ of their distance from the line $y = 9$.

Ans: GivenThe point $\left( {0,4} \right)$ and the line $y = 9$.

Let the required point be $P\left( {x,y} \right)$.

Using the distance formula the distance between $P$ and $\left( {0,4} \right)$ is

   $= \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 4} \right)}^2}} $

   $= \sqrt {{x^2} + {{\left( {y - 4} \right)}^2}} $ 

Now, the distance of the point $P$ from the line $y = 9$ is

$= \left| {\dfrac{{\left( {0 \times x} \right) + \left( {1 \times y} \right) - 9}}{{\sqrt {{{\left( 0 \right)}^2} + {{\left( 1 \right)}^2}} }}} \right|$

$= \left| {y - 9} \right|$ 

According to the Sample Question,

$ \Rightarrow \sqrt {{x^2} + {{\left( {y - 4} \right)}^2}}  = \dfrac{2}{3} \times \left| {y - 9} \right|$

On squaring both the sides,

$\Rightarrow {x^2} + {\left( {y - 4} \right)^2} = \dfrac{4}{9} \times {\left( {y - 9} \right)^2}$

$\Rightarrow 9{x^2} + 9{y^2} + 144 - 72y = 4{y^2} + 324 - 72y$

$\Rightarrow 9{x^2} + 5{y^2} - 180 = 0$ 

31.Show that the set of all points such that the difference of their distances from $\left( {4,0} \right)$ and $\left( { - 4,0} \right)$ is always equal to $2$ represents a hyperbola.

Ans: Given Two points $\left( {4,0} \right)$and $\left( { - 4,0} \right)$.

The difference of distances of a point from the given two points is always $2{\text{ units}}$.

Let the required point be $P\left( {x,y} \right)$.

Using the distance formula the distance between $P$ and $\left( {4,0} \right)$ is

   $= \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 0} \right)}^2}} $

   $= \sqrt {{{\left( {x - 4} \right)}^2} + {y^2}} $ 

Similarly, the distance between $P$ and $\left( { - 4,0} \right)$ is

   $= \sqrt {{{\left( {x - \left( { - 4} \right)} \right)}^2} + {{\left( {y - 0} \right)}^2}} $

   $= \sqrt {{{\left( {x + 4} \right)}^2} + {y^2}} $ 

It is given that the difference of the distances is $2{\text{ units}}$, so taking the difference,

$\Rightarrow \sqrt {{{\left( {x - 4} \right)}^2} + {y^2}}  - \sqrt {{{\left( {x + 4} \right)}^2} + {y^2}}  = 2$

$\Rightarrow \sqrt {{{\left( {x - 4} \right)}^2} + {y^2}}  = 2 + \sqrt {{{\left( {x + 4} \right)}^2} + {y^2}} $ 

On squaring both the sides,

$\Rightarrow {\left( {x - 4} \right)^2} + {y^2} = 4 + {\left( {x + 4} \right)^2} + {y^2} + 4\sqrt {{{\left( {x + 4} \right)}^2} + {y^2}} $

$\Rightarrow {x^2} + 16 - 8x + {y^2} = 4 + {x^2} + 16 + 8x + {y^2} + 4\sqrt {{{\left( {x + 4} \right)}^2} + {y^2}} $

$\Rightarrow \sqrt {{{\left( {x + 4} \right)}^2} + {y^2}}  =  - \left( {1 + 4x} \right)$ 

Again squaring both the sides,

$\Rightarrow {\left( {x + 4} \right)^2} + {y^2} = {\left( { - \left( {1 + 4x} \right)} \right)^2}$

$\Rightarrow {x^2} + 16 + 8x + {y^2} = 1 + 16{x^2} + 8x$ 

$\Rightarrow 15{x^2} - {y^2} = 15$

Hence, it can be seen that the above equation represents a hyperbola.

32.Find the equation of the hyperbola with

(a) Vertices $\left( { \pm 5,0} \right)$, foci $\left( { \pm 7,0} \right)$

Ans: The vertices and the foci both lies on the $x - $ axis so the hyperbola is of the form $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$.

The vertex is given as $\left( { \pm a,0} \right)$, so on comparing $a = 5$.

The foci is given as $\left( { \pm ae,0} \right)$, so on comparing $ae = 7$. Here $e = \sqrt {1 + \dfrac{{{b^2}}}{{{a^2}}}} $ is eccentricity. On squaring both the sides,

   $\Rightarrow {a^2}{e^2} = 49$

   $\Rightarrow {a^2} + {b^2} = 49$

   $\Rightarrow 25 + {b^2} = 49$

   $\Rightarrow {b^2} = 24$ 

Therefore, the equation of the hyperbola is $\left( {\dfrac{{{x^2}}}{{25}} - \dfrac{{{y^2}}}{{24}} = 1} \right)$.

(b) Vertex at $\left( {0, \pm 7} \right)$, $e = \dfrac{4}{3}$

Ans: Here the vertex lies on the $y$ axis so the hyperbola is of the form $\dfrac{{{y^2}}}{{{b^2}}} - \dfrac{{{x^2}}}{{{a^2}}} = 1$.

The vertices is given as $\left( {0, \pm b} \right)$, so on comparing $b = 7$.

The eccentricity is given as $e = \sqrt {1 + \dfrac{{{a^2}}}{{{b^2}}}} $. Since $e = \dfrac{4}{3}$, so on squaring both the sides,

   $\Rightarrow {e^2} = \dfrac{{16}}{9}$

   $\Rightarrow 1 + \dfrac{{{a^2}}}{{{b^2}}} = \dfrac{{16}}{9}$

   $\Rightarrow \dfrac{{{a^2}}}{{49}} = \dfrac{7}{9}$

   $\Rightarrow {a^2} = \dfrac{{343}}{9}$ 

Therefore, the equation of the hyperbola is $\left( {\dfrac{{{y^2}}}{{49}} - \dfrac{{9{x^2}}}{{343}} = 1} \right)$.

(c) Foci at $\left( {0, \pm \sqrt {10} } \right)$, passing through $\left( {2,3} \right)$

Ans: Here the foci lies on the $y$ axis so the hyperbola is of the form $\dfrac{{{y^2}}}{{{b^2}}} - \dfrac{{{x^2}}}{{{a^2}}} = 1$.

The foci is given as $\left( {0, \pm be} \right)$, so on comparing $be = \sqrt {10} $.

The eccentricity is given as $e = \sqrt {1 + \dfrac{{{a^2}}}{{{b^2}}}} $. So on squaring both the sides,

$\Rightarrow {b^2}{e^2} = 10$

$\Rightarrow {a^2} + {b^2} = 10$ … (1)

Since, the hyperbola passes through the point $\left( {2,3} \right)$, so this point will satisfy the equation.

$\Rightarrow \dfrac{9}{{{b^2}}} - \dfrac{4}{{{a^2}}} = 1$

$\Rightarrow 9{a^2} - 4{b^2} = {a^2}{b^2}$ … (2)

Solving equations (1) and (2) gives ${a^2} = 5$and ${b^2} = 5$.

Therefore, the equation of the hyperbola is $\left( {\dfrac{{{y^2}}}{5} - \dfrac{{{x^2}}}{5} = 1} \right)$.

State True or False Statements:

33.The line $x + 3y = 0$ is the diameter of the circle ${x^2} + {y^2} + 6x + 2y = 0$.

Ans: Given The line $x + 3y = 0$ is the diameter of the circle ${x^2} + {y^2} + 6x + 2y = 0$. 

The center of the circle ${x^2} + {y^2} + 6x + 2y = 0$is $( - 3, - 1)$.

$( - 3, - 1)$does not lie on $x + 3y = 0$ because $ - 3 + 3( - 1) =  - 6$.

Hence, the given statement is false.

34.The shortest distance from the point $(2, - 7)$ to the circle $x + {y^2} - 14jc - 10y - 151 = 0$ is equal to $5$.

Ans: Given The shortest distance from the point $(2, - 7)$ to the circle $x + {y^2} - 14jc - 10y - 151 = 0$ is equal to $5$.

The center of the circle ${x^2} + {y^2} - 14x - 10y - 151 = 0$is $(7,5)$.

Radius $ = \sqrt {49 + 25 + 151}  = \sqrt {225}  = 15$

The distance between $P(2, - 7)$ and centre$ = \sqrt {{{(2 - 7)}^2} + {{( - 7 - 5)}^2}} $

Distance$ = \sqrt {25 + 144} $

Distance$ = \sqrt {169} $

Distance$ = 13$

So, the shortest distance of point ${\text{P}}$ from the circle $ = |13 - 15| = 2$.

Hence, the given statement is false.

35. If the line $lx + my = 1$ is a tangent to the circle ${x^2} + {y^2} = {a^2}$, then the point $(l,m)$ lies on a circle.

Ans: Given If the line $lx + my = 1$ is a tangent to the circle ${x^2} + {y^2} = {a^2}$, then the point $(l,m)$ lies on a circle.

The center of the circle ${x^2} + {y^2} = {a^2}$ is $(0,0)$ and the radius is $a$.

The line $lx + my - 1 = 0$ is tangent to the circle.

 So, the distance of $(0,0)$ from the line $lx + my - 1 = 0$ is equal to radius $a$.

$\Rightarrow \dfrac{{|0 + 0 - 1|}}{{\sqrt {{l^2} + m} }} = a$

$\Rightarrow {l^2} + {m^2} = \dfrac{1}{{{a^2}}}$

So, the locus of $(l,m)$is ${x^2} + {y^2} = \dfrac{1}{{{a^2}}}$, which is a circle.

Hence, the given statement is true.

36. The point $(1,2)$ lies inside the circle ${x^2} + {y^2} - 2x + 6y + 1 = 0$. 

Ans: Given The point $(1,2)$ lies inside the circle ${x^2} + {y^2} - 2x + 6y + 1 = 0$.

The center of the circle ${x^2} + {y^2} - 2x + 6y + 1 = 0$ is $(1, - 3)$ and the radius is $3$.

The distance of point $P(1,2)$ from the center is $5$.

So, $CP > $ radius.

Thus, point $P$ lies outside the circle.

Hence, the given statement is false.

37.The line $lx + my + n = 0$ will touch the parabola ${y^2} = 4ax$if $ln = a{m^2}$.

Ans: Given The line $lx + my + n = 0$ will touch the parabola ${y^2} = 4ax$if $ln = a{m^2}$.

Solve the line $lx + my + n = 0$ and parabola ${y^2} = 4ax$ to get their point of intersection.

$\Rightarrow \dfrac{l}{{4a}}{y^2} + my + n = 0$

As the line touches the parabola, the above equation must have equal roots i.e. $D = 0$.

$\Rightarrow {m^2} - 4\left( {\dfrac{l}{{4a}}} \right)n = 0$

$\Rightarrow a{m^2} = nl$

Hence, the given statement is true.

38.If $P$ is a point on the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$ whose foci are $S$and $S'$, then $PS + PS' = 8$.

Ans: Given If $P$ is a point on the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$ whose foci are $S$and $S'$, then $PS + PS' = 8$.

For any ellipse, the sum of the distances of any point $P$ on the ellipse from the two foci is equal to the length of the major axis. 

The major axis of the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$is $2b = 2 \times 5 = 10$.

As $S$ and $S'$ are foci,

$\Rightarrow SP + S'P = 10$.

Hence, the given statement is false.

39.The line $2x + 3y = 12$ touches the ellipse $\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 2$ at the point $(3,2)$.

Squaring both sides,

$(2 x)^{2}=(12-3 y)^{2}$

Ans: $4 x^{2}+9 y^{2}=72 \& 2 x+3 y=12$

Solving both the expressions,

$2 x=12-3 y$

$4 x^{2}=(12-3 y)^{2}$

Putting the value of $4 x^{2}$,

$(12-3 y)^{2}+9 y^{2}=72$

$144+9 y^{2}-72 y+9 y^{2}-72=0$

$18 y^{2}-72 y+72=0$

$y^{2}-4 y+4=0$

$(y-2)^{2}=0$

$y=2$

$2 x=12-3 y$

$2 x=12-3(2)$

$2 x=12-6=6$

$x=3$

So, the point of intersection is $(3,2)$.

TRUE

40.The locus of the point of intersection of lines $\sqrt 3 x - y - 4\sqrt 3 k = 0$ and $\sqrt 3 kx + ky - 4\sqrt 3  = 0$ for different value of $k$ is a hyperbola whose eccentricity is $2$.

Ans: Given The locus of the point of intersection of lines $\sqrt 3 x - y - 4\sqrt 3 k = 0$ and $\sqrt 3 kx + ky - 4\sqrt 3  = 0$ for different value of $k$ is a hyperbola whose eccentricity is $2$.

From the line$\sqrt 3 x - y - 4\sqrt 3 k = 0$, $k = \dfrac{{\sqrt 3 x - y}}{{4\sqrt 3 }}$.

And from the line$\sqrt 3 kx + ky - 4\sqrt 3  = 0$, $k = \dfrac{{4\sqrt 3 }}{{\sqrt 3 x + y}}$.

Equate the values of $k$.

$ \Rightarrow \dfrac{{\sqrt 3 x - y}}{{4\sqrt 3 }} = \dfrac{{4\sqrt 3 }}{{\sqrt 3 x + y}}$

$ \Rightarrow 3{x^2} - {y^2} = 48$

$ \Rightarrow \dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{{48}} = 1$which is an equation of a hyperbola.

$ \Rightarrow {a^2} = 16$and${b^2} = 48$

$\Rightarrow {e^2} = 1 + \dfrac{{48}}{{16}}$

$\Rightarrow {e^2} = 1 + 3$

$\Rightarrow {e^2} = 4$

$ \Rightarrow e = 2$

Hence, the given statement is true.

Fill in the Blank in Exercises from 41 to 46:

41. The equation of the circle having center at $\left( {3,-4} \right)$ and touching the line

$5x + 12y-12 = 0$is _______________.

Ans: Perpendicular distance between a point and line is given by:

${\text{D}}$$ = \dfrac{{|a{x_1} + b{y_1} + c|}}{{\sqrt {{a^2} + {b^2}} }}$

Given point $\left( {{x_1},{y_1}} \right)$is $\left( {3,-4} \right)$

The equation is expressed as $ax + by + c = 0$and given equation is $5x + 12y-12 = 0$.

Here,

  ${x_1} = 3$

  ${y_1} =  - 4$ 

  $a = 5$

  $b = 12$

  $c =  - 12$ 

Putting up the values

${\text{D}}\, = \,\dfrac{{|5\left( 3 \right) + 12\left( { - 4} \right) - 12| }}{{\sqrt {{{\left( 5 \right)}^2} + {{\left( {12} \right)}^2}} }}$

$= \,\dfrac{{\{ |15 - 48 - 12|\} }}{{\sqrt {25 + 144} }}$

$= \dfrac{{\{ | - 45|\} }}{{\sqrt {169} }} = \dfrac{{45}}{{13}}$ 

Equation of the circle having center $\left( {h,k} \right)$with $r$units as radius is,

${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$

${\left( {x - 3} \right)^2} + {\left( {y - \left( { - 4} \right)} \right)^2} = {\left( {\dfrac{{45}}{{13}}} \right)^2}$

${x^2} - 6x + 9 + {\left( {y + 4} \right)^2} = \dfrac{{2025}}{{169}}$

${x^2} - 6x + 9 + {y^2} + 8y + 16 = \dfrac{{2025}}{{169}}$

$169{x^2} - 1014x + 1521 + 1352y + 169{y^2} + 2704 - 2025 = 0$

$169{x^2} - 1014x + 1521 + 1352y + 169{y^2} + 679 = 0$

Hence, required equation is $169{x^2} - 1014x + 1521 +  169{y^2} + 1352y + 679 = 0$

42. The equation of the circle circumscribing the triangle whose sides are the lines

$y = x + 2,\,\,3y = 4x,\,\,2y = 3x$is ______________.

Ans: given equations are:

  $y = x + 2$

  $3y = 4x$

  $2y = 3x$ 

On solving the above equations we get points of intersection,

  $x = 6$

  $y = 8$ 

And point of intersection $A\left( {6,8} \right),\,B\left( {4,6} \right),\,C\left( {0,0} \right)$

Equation of the circle:

${x^2} + {y^2} + 2gx + 2fy + c = 0$

Because points lie on the circle then,

  $36 + 64 + 12g + 16f + c = 0$

  $12g + 12f + c =  - 100$

  $16 + 36 + 8g + 12f + c = 0$

  $8g + 12f + c =  - 52$

  $c = 0$

Putting $c = 0,$then we get

  $3g + 4f =  - 25$

  $2g + 3f =  - 13$ 

On solving, we have 

  $g =  - 23$

  $f = 11$ 

Then equation of the circle is:

  ${x^2} + {y^2} - 46x + 22y + 0 = 0$

  ${x^2} + {y^2} - 46x + 22y = 0$ 

43. An ellipse is described by using an endless string which is passed over two pins. If the axes are $6$$cm$and $4\,cm$, the length of the string and distance between the pins are ____________.

Ans: Let's consider equation of ellipse be

$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

As per Sample Question$a = 3,\,b = 2$

Now, ${b^2} = {a^2}\left( {1 - {e^2}} \right)$

Substituting the values,

  ${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$

  ${e^2} = 1 - \dfrac{4}{9}$

  ${e^2} = \dfrac{5}{9}$

  $e = \sqrt {\dfrac{5}{9}}  = \dfrac{{\sqrt 5 }}{3}$

  $\therefore e = \dfrac{{\sqrt 5 }}{3}$ 

For any point $P$on the ellipse, we have $SP + S'P = 2a$

Where $S\,{\text{and }}S'$are the foci of an ellipse.

And length of the endless string is given by

  $SP + S'P + SS'$

   $= 2a + 2ae$

   $= 2\left( 3 \right) + 2\left( 3 \right)\left( {\dfrac{{\sqrt 5 }}{3}} \right)$

   $= 6 + 2\sqrt 5 $ 

Hence, length of the endless string is $6 + 2\sqrt 5 $

44. The equation of the ellipse having foci $\left( {0,1} \right),\,\,\left( {0,-1} \right)$ and minor axis of length $1$ is

________________ .

Ans: Given, foci of the ellipse $\left( {0,1} \right)\,\left( {0. - 1} \right)$

And length of minor axis is $1$

We know that foci of the ellipse is $\left( {0, \pm \,be} \right)$

On comparing given foci$\left( {0,1} \right)\,\left( {0. - 1} \right)$ with $\left( {0, \pm \,be} \right)$we have 

$be = 1$

Length of the minor axis: 

  $2a = 1$

  $a = \dfrac{1}{2}$ 

Now, 

  ${a^2} = {b^2}\left( {1 - {e^2}} \right)$

  $\dfrac{1}{4} = {b^2} - {b^2}{e^2}$

  $\dfrac{1}{4} = {b^2} - 1\,\,\,\,\,\left( {\because be = 1} \right)$

  ${b^2} = \dfrac{5}{4}$

  $b = \sqrt {\dfrac{5}{4}}  = \dfrac{{\sqrt 5 }}{2}$

  $b = \dfrac{{\sqrt 5 }}{2}$ 

Therefore, the equation of ellipse is:

   $\Rightarrow \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

   $\Rightarrow \dfrac{{{x^2}}}{{\dfrac{1}{4}}} + \dfrac{{{y^2}}}{{\dfrac{5}{4}}} = 1$

   $\Rightarrow 4{x^2} + \dfrac{{4{y^2}}}{5} = 1$ 

Hence the required equation is $4{x^2} + \dfrac{{4{y^2}}}{5} = 1$.

45. The equation of the parabola having focus at $\left( {-1,-2} \right)$and the directrix $x-2y + 3 = 0$is ________________.

Ans: Given, focus of parabola at $S$$\left( { - 1, - 2} \right)$ and directrix is $x - 2y + 3 = 0$

Any point on parabola is given by $P\left( {x,y} \right)$

Then the length of the perpendicular from point $S$on the directrix $ = \,SP$

$\Rightarrow \dfrac{{{{\left( {x - 2y + 3} \right)}^2}}}{5} = {\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2}$

$\Rightarrow 5[{x^2} + 2x + 1 + {y^2} + 4y + 4] = {x^2} + 4{y^2} + 9 - 4xy - 12y + 6x$

$\Rightarrow 4{x^2} + {y^2} + 4x + 32y + 16 = 0$ 

Hence, the equation of parabola is $4{x^2} + {y^2} + 4x + 32y + 16 = 0$. 

46. The equation of the hyperbola with vertices at $\left( {0, \pm 6} \right)$and eccentricity $\dfrac{5}{3}$ is ______________ and its foci are ________________.

Ans: Given, vertices are $\left( {0, \pm \,6} \right)$

On comparing it with $\left( {0, \pm \,b} \right)$

Let the equation of hyperbola be:

  $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} =  - 1$ 

Also given $e = \dfrac{5}{3}$

Now, 

  ${a^2} = {b^2}\left( {{e^2} - 1} \right)$

  ${a^2} = {\left( 6 \right)^2}\left( {{{\left( {\dfrac{5}{3}} \right)}^2} - 1} \right) = 64$ 

So, the equation of hyperbola is:

  $\dfrac{{{x^2}}}{{64}} - \dfrac{{{y^2}}}{{36}} =  - 1$ 

Then foci is $ = \,\left( {0,\, \pm \,be} \right) = \left( {0,\, \pm \dfrac{5}{3} \times 6} \right) = \left( {0,\, \pm 10} \right)$

OBJECTIVE TYPE QUESTIONS:

47. The area of the circle centered at $(1,2)$ and passing through $(4,6)$ is

(a)$5\pi $ 

(b)$10\pi $ 

(c)$25\pi $ 

(d)None of these

Ans: Given  The center of the circle is $C(1,2)$ 

The circle passes through the point $P(4,6)$ 

Radius = $CP = \sqrt {{{(4 - 1)}^2} + {{(6 - 2)}^2}} $

$= \sqrt {9 + 16}  = \sqrt {25}  = 5$ 

Area of the circle $\pi {r^2} = \pi  \times {(5)^2} = 25\pi $ sq. units.

Correct Option: C

48. Equation of a circle which passes through $(3,6)$ and touches the axes is

(a) ${x^2}  +  {y^2}  +  6x +  6y +  3  =  0$ 

(b) ${x^2}  +  {y^2} - 6x- 6y- 9  =  0$ 

(c)${x^2} +  {y^2} - 6x- 6y +  9  =  0$  

(d) none of these                                                                                                    

Ans: Let the required circle touch the axes at $\left( {a, 0} \right)$ and $\left( {0, a} \right)$ 

$\therefore $ Centre is $\left( {a, a} \right)$ and $r  =  a$                                            

So, the equation of the circle is                                                                   

${\left( {x - a} \right)^2} +  {\left( {y - a} \right)^2}  =  {a^2}$ 

If passes through a point $P\left( {3, 6} \right)$ then                                                           

${{{\left( {3 - a} \right)}^2}  +  {{\left( {6 - a} \right)}^2}  =  {a^2}}$ 

${ \Rightarrow 9  +  {a^2} - 6a  +  36  +  {a^2} - 12a  =  {a^2}}$

${ \Rightarrow {a^2} - 18a  +  45  =  0}$

${ \Rightarrow {a^2} - 15a - 3a  +  45  =  0}$

${ \Rightarrow a\left( {a - 15} \right) - 3\left( {a - 15} \right)  =  0}$ 

${ \Rightarrow \left( {a - 3} \right) \left( {a - 15} \right)  =  0}$ 

 ⇒ $a  =  3$ and $a  =  15$ which is not possible

 $\therefore a  =  3$ 

So, the required equation of the circle is ${\left( {x - 3} \right)^2}  +  {\left( {y - 3} \right)^2}  =  9$ 

${ \Rightarrow {x^2}  +  9 - 6x  +  {y^2}  +  9 - 6y  =  9}$ 

${ \Rightarrow {x^2}  +  {y^2} - 6x - 6y  +  9  =  0}$ 

Hence, the correct option is (c)

49. Equation of the circle with center on the y-axis and passing through the origin and the point $\left( {{\mathbf{2}}, {\mathbf{3}}} \right)$ is

(a) ${x^2}  +  {y^2}  +  13y  =  0$ 

(b) $3{x^2}  +  3{y^2}  +  13x  +  3  =  0$ 

(c) $6{x^2}  +  6{y^2} - 13x  =  0$ 

(d) ${x^2}  +  {y^2}  +  13x +  3  =  0$ 

Ans: Let the equation of the circle be                              

${\left( {x - h} \right)^2}  +  {\left( {y - k} \right)^2}  =  {r^2}$ 

Let the center be $\left( {0, a} \right)$ 

   $\therefore $  Radius $r  =  a$ 

So, the equation of the circle is 

  ${{{\left( {x - 0} \right)}^2}  +  {{\left( {y - a} \right)}^2}  =  {a^2}}$

  ${ \Rightarrow {x^2}  +  {{\left( {y - a} \right)}^2}  =  {a^2}}$

  ${ \Rightarrow {x^2}  +  {y^2} +  {a^2} - 2ay  =  {a^2}}$ 

  ${ \Rightarrow {x^2}  +  {y^2} - 2ay  =  0  \ldots \left( i \right)}$ 

Now CP = r

   $\Rightarrow \sqrt {{{(2 - 0)}^2} + {{(3 - a)}^2}}  = a$

   $\Rightarrow \sqrt {4 + 9 + {a^2} - 6a}  = a$

   $\Rightarrow \sqrt {13 + {a^2} - 6a}  = a$

   $\Rightarrow 13 + {a^2} - 6a = {a^2}$

   $\Rightarrow 13 - 6a = 0$

   $\therefore a = \dfrac{{13}}{6}$ 

 Putting the value of a in eq. (i) we get

  ${x^2}  +  {y^2} -{\text{ 2}}\left( {\dfrac{{13}}{6}} \right)y  =  0$

  $\Rightarrow 3{x^2}  +  3{y^2} -{\text{ 1}}3y  =  0$ 

Hence, the correct option is (a).

50. The equation of a circle with origin as center and passing through the vertices of an equilateral triangle whose median is of length ${\mathbf{3a}}$ is

(a) ${x^2}  +  {y^2}  =  9{a^2}$ 

(b) ${x^2}  +  {y^2}  =  16{a^2}$ 

(c) ${x^2}  +  {y^2}  =  4{a^2}$ 

(d) ${x^2}  +  {y^2}  =  {a^2}$ 

Ans: Let $ABC$ be an equilateral triangle in which median $AD  =  3a.$ 

 Center of the circle is same as the centroid                                    

 of the triangle i.e., $\left( {0, 0} \right)$ 

$AG : GD  =  2 : 1$                                                                      So, $AG  = \dfrac{2}{3} AD  = \dfrac{2}{3}  \times  3a  =  2a$                              

$\therefore $ The equation of the circle is                                 

${{{\left( {x - 0} \right)}^2}  +  {{\left( {y - 0} \right)}^2}  =  {{\left( {2a} \right)}^2}}$ 

  $ \Rightarrow {x^2}+ {y^2}= 4{a^2}$                                                                          

Hence, the correct option is (c).

51. If the focus of a parabola is $\left( {0, -3} \right)$ and its directrix is $y =  3$ , then its equation is

(A) ${x^2}  =  -12y$ 

(B) ${x^2}  =  12y$ 

(C) ${y^2}  =  -12x$ 

(D) ${y^2}  =  12x$ 

Ans: According to the definition of parabola

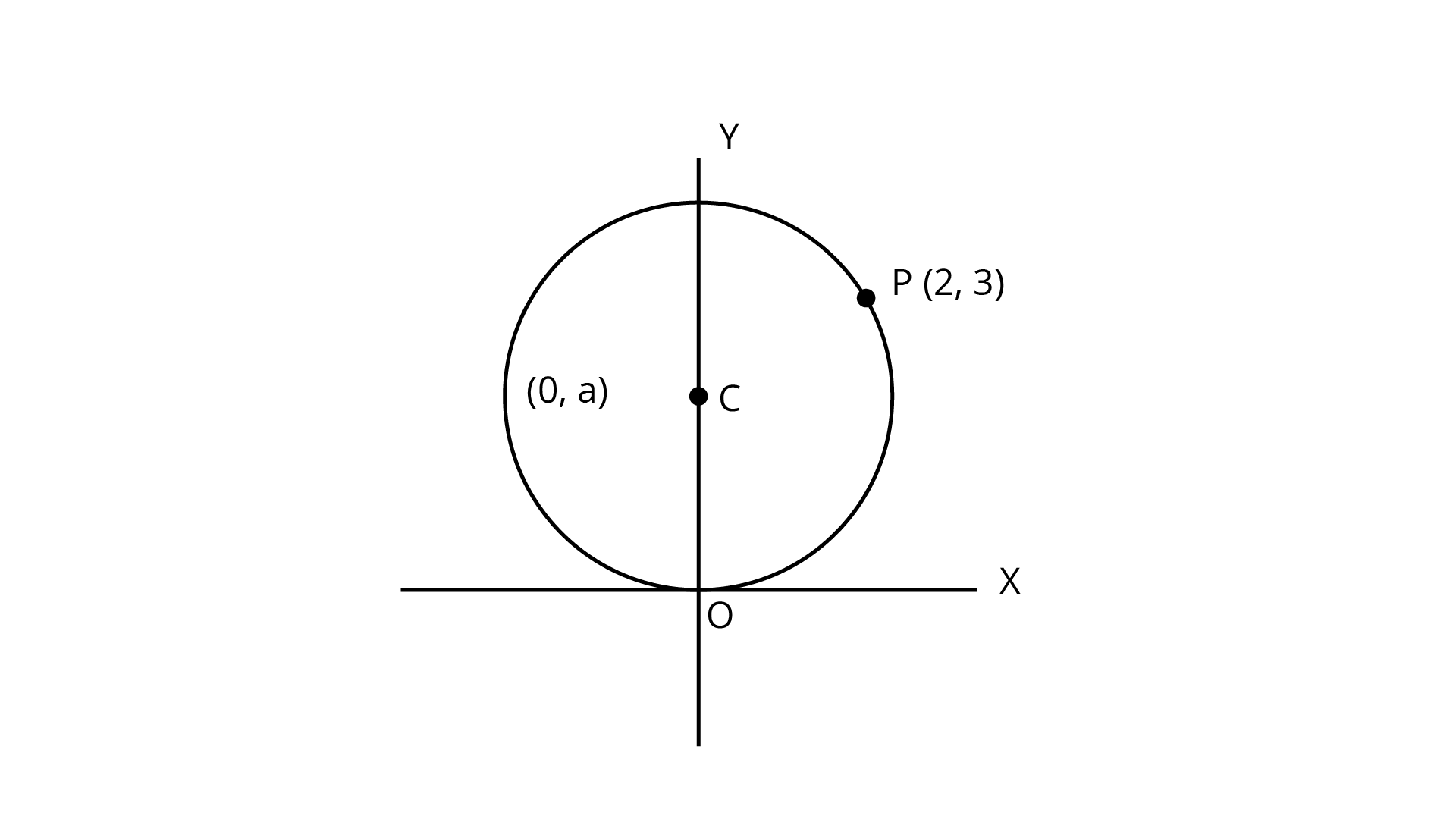
$\sqrt {{{(x - 0)}^2} + {{(y + 3)}^2}}  = \left| {\dfrac{{y - 3}}{{\sqrt {{{(0)}^2} + {{(1)}^2}} }}} \right|$ 

$ \Rightarrow \sqrt {{x^2} + {y^2} + 9 + 6y}  = \left| {y - 3} \right|$ 

Squaring both sides, we have

${{x^2}  +  {y^2}  +  9  +  6y  =  {y^2}  +  9 - 6y}$

${ \Rightarrow {x^2} +  9  +  6y  =  9 - 6y}$ 

${ \Rightarrow {x^2}  =   -  12y}$ 

Hence, the correct option is (a).

52. If the parabola ${y^2}  =  4ax$ passes through the point $\left( {3, 2} \right),$ then the length of its latus rectum is

(A) $\dfrac{2}{3}$   

(B) $\dfrac{4}{3}$ 

(C) $\dfrac{1}{3}$  

(D) $4$ 

Ans: Given parabola is ${y^2}  =  4ax$ 

If the parabola is passing through $\left( {3, 2} \right)$ 

then ${\left( 2 \right)^2}  =  4a  \times  3$ 

$\Rightarrow 4  =  12a \Rightarrow a  = \dfrac{1}{3}$

Now length of the latus rectum $=  4a  =  4  \times \dfrac{1}{3}  = \dfrac{4}{3}$ 

Hence, the correct option is (b).

53. If the vertex of the parabola is the point $\left( {-3, 0} \right)$ and the directrix is the line$x +  5  =  0$ , then its equation is

(a) ${y^2}  =  8 \left( {x +  3} \right)$ 

(b) ${x^2}  =  8 \left( {y  +  3} \right)$ 

(c) ${y^2}  =  - 8 \left( {x +  3} \right)$ 

(d) ${y^2}  =  8 \left( {x +  5} \right)$ 

Ans: Given that vertex $=  \left( { - 3, 0} \right)$ 

$\therefore a  =   -  3$ 

and directrix is $x  +  5  =  0$    

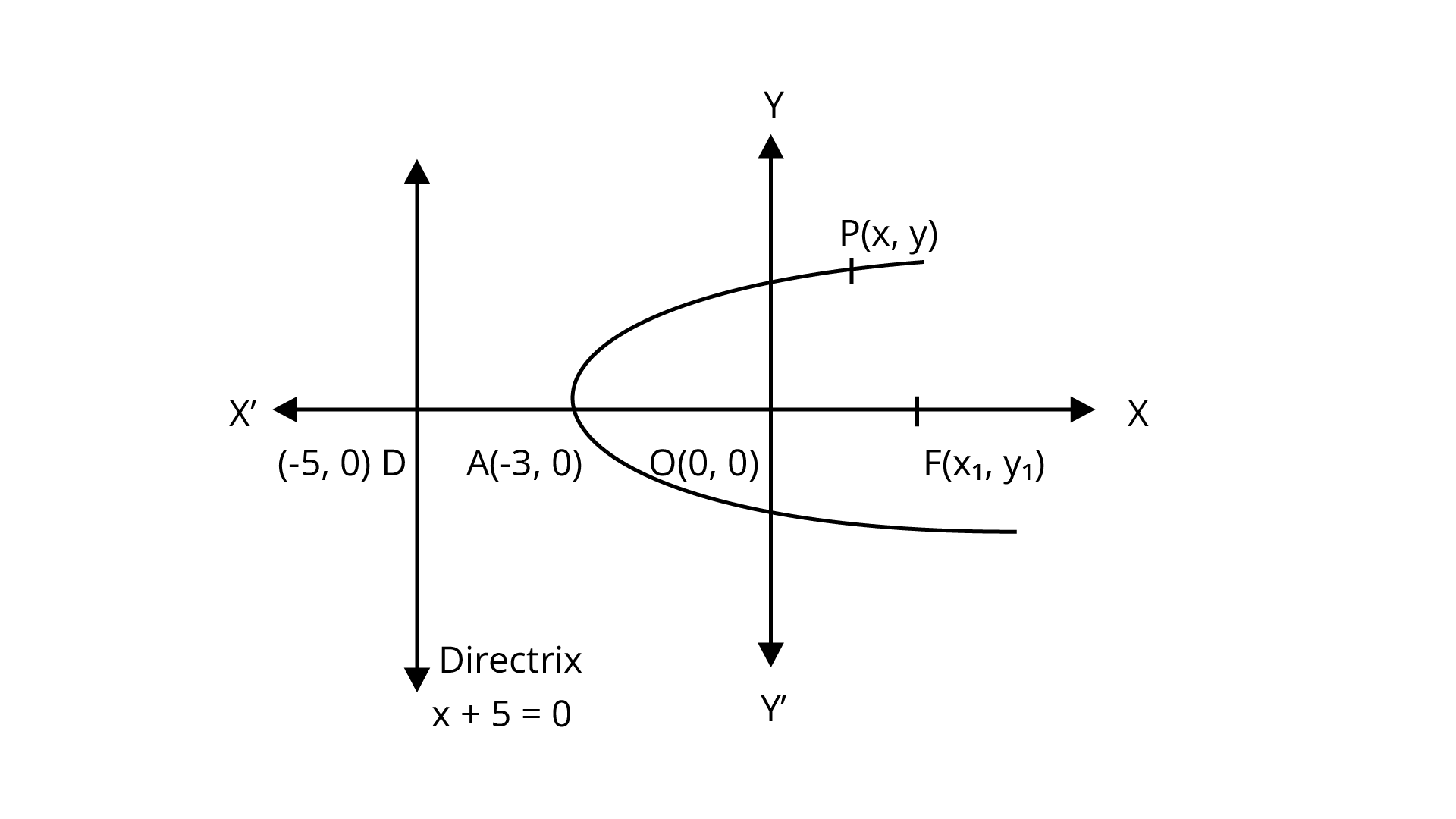
According to the definition of the parabola, we get $AF  =  AD$ i.e., A is the midpoint of $DF$ 

$\therefore  - 3 = \dfrac{{{x_1} - 5}}{2} \Rightarrow {x_1}  =   -  6  +  5  =   -  1$                    

and $0 = \dfrac{{0 + {y_1}}}{2} \Rightarrow {y_1}  =  0$                       

$\therefore Focus F  =  \left( { - 1, 0} \right)$ 

Now $\sqrt {{{(x + 1)}^2} + {{(y - 0)}^2}}  = \left| {\dfrac{{x + 5}}{{\sqrt {{1^2} + {0^2}} }}} \right|$ 

Squaring both sides, we get 

  ${{{\left( {x  +  1} \right)}^2}  +  {y^2}  =  {{\left( {x  +  5} \right)}^2}}$ 

  ${ \Rightarrow {x^2}  +  1  +  2x  +  {y^2}  =  {x^2}  +  25  + 10x}$ 

  ${ \Rightarrow {y^2}  =  10x - 2x  +  24}$  

  ${ \Rightarrow {y^2}  =  8x  +  24}$ 

  ${ \Rightarrow {y^2}  =  8\left( {x  +  3} \right)}$ 

Hence, the correct option is (a)

54. The equation of the ellipse whose focus is $(1, - 1),$ the directrix the line $x - y - 3 = 0$ and eccentricity $\dfrac{1}{2}$  is

(a)$7{x^2}  +  7{y^2}  +  2xy - 10x  +  10y  +  7  =  0$ 

(b) $7{x^2}  +  2xy +  7{y^2}  +  7  =  0$ 

(c) $7{x^2}  +  2xy +  7{y^2}  +  10x- 10y- 7  =  0$ 

(d) None of the above

Ans: Given that focus of the ellipse is $\left( {1,  - 1} \right)$ and the equation of the directrix is $x - y - 3  =  0$ 

and $e = \dfrac{1}{2}$ 

Let $P\left( {x, y} \right)$ by any point on the parabola 

∴  $\dfrac{{PF}}{\text{distance of the point P from the directrix}}= e$ 

$\dfrac{{\sqrt {{{(x - 1)}^2} + {{(y + 1)}^2}} }}{{\left| {\dfrac{{x - y - 3}}{{\sqrt {{{(1)}^2} + {{( - 1)}^2}} }}} \right|}} = \dfrac{1}{2}$

$2\sqrt {{x^2} + 1 - 2x + {y^2} + 1 + 2y}  = \left| {\dfrac{{x - y - 3}}{{\sqrt 2 }}} \right|$ 

Squaring both sides, we have

 ⇒ $4\left( {{x^2}  +  {y^2} - 2x  +  2y  +  2} \right)  = \dfrac{{{x^2} + {y^2} + 9 - 2xy + 6y - 6x}}{2}$ 

$\Rightarrow 8{x^2}  +  8{y^2} - 16x  +  16y  +  16  =  {x^2}  +  {y^2} - 2xy  +  6y - 6x  +  9$ 

$\Rightarrow 7{x^2}  +  7{y^2}  +  2xy - 10x  +  10y  +  7  =  0$ 

Hence, the correct option is (a).

55. The length of the latus rectum of the ellipse $3{x^2}  +  {y^2}  =  12$ is

(a) $4$ 

(b) $3$ 

(c) $8$ 

(d) $\dfrac{4}{{\sqrt 3 }}$ 

Ans: Equation of the ellipse is

$3{x^2}  +  {y^2}  =  12$ 

⇒ $\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{{12}} = 1$ 

Here ${a^2}  =  4 \Rightarrow a  =  2 $  

${b^2}  =  12 \Rightarrow b  =  2\sqrt 3 $

Length of the latus rectum  $ = \dfrac{{2{a^2}}}{b} = \dfrac{{2 \times 4}}{{2\sqrt 3 }} = \dfrac{4}{{\sqrt 3 }}$ 

Hence, the correct option is (d).

56. If e is the eccentricity of the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ (where $a < b$ ) then

(a) ${b^2}  =  {a^2} \left( {1 - {e^2}} \right)$ 

(b) ${a^2}  =  {b^2} \left( {1 - {e^2} } \right)$ 

(c) ${a^2}  =  {b^2} \left( {{e^2} - 1} \right)$ 

(d) ${b^2}  =  {a^2} \left( {{e^2} - 1} \right)$ 

Ans: Give equation is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ (a < b) 

∴ Eccentricity $e  = \sqrt {1 - \dfrac{{{a^2}}}{{{b^2}}}}  \Rightarrow {e^2} = 1 - \dfrac{{{a^2}}}{{{b^2}}}$ 

$\Rightarrow \dfrac{{{a^2}}}{{{b^2}}} = (1 - {e^2}) \Rightarrow {a^2} = {b^2}(1 - {e^2})$ 

Hence, the correct option is (b).

57. The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half of the distance between the foci is

(a) $\dfrac{4}{3}$  

(b)$\dfrac{4}{{\sqrt 3 }}$ 

(c) $\dfrac{2}{{\sqrt 3 }}$

(d) None of these

Ans: Length of the latus rectum of the hyperbola

 $= \dfrac{{2{b^2}}}{a} = 8 \Rightarrow {b^2} = 4a........(i)$ 

Distance between the foci $=  2ae$ 

Transverse axis $=  2a$ 

and Conjugate axis$ =  2b$ 

$\therefore \dfrac{1}{2}\left( {2ae} \right)  =  2b \Rightarrow ae  =  2b \Rightarrow b  =  \dfrac{{ae}}{2} \ldots \left( {ii} \right)$ 

$\Rightarrow {b^2}  = \dfrac{{{a^2}{e^2}}}{4}$ 

$\Rightarrow 4a  = \dfrac{{{a^2}{e^2}}}{4}$  [from eq. (i)] 

$\Rightarrow 16  =  a{e^2}$

$\therefore a = \dfrac{{16}}{{{e^2}}}$ 

∴ Now ${b^2}  =  {a^2} \left( {{e^2} - 1} \right)$ 

$\Rightarrow 4a  =  {a^2} \left( {{e^2} - 1} \right)$ 

$\Rightarrow \dfrac{4}{a} =  {e^2} - 1 \Rightarrow  = \dfrac{4}{{16/e}}{\text{ =  }}{e^2} - 1$ 

$\Rightarrow \dfrac{{{e^2}}}{4} = {e^2} - 1 \Rightarrow {e^2} - \dfrac{{{e^2}}}{4} = 1$

$\Rightarrow \dfrac{{3{e^2}}}{4} = 1 \Rightarrow {e^2} = \dfrac{4}{3}$

$\therefore e = \dfrac{2}{{\sqrt 3 }}$ 

∴ Hence, the correct option is (c).

58. The distance between the foci of a hyperbola is 16 and its eccentricity is $\sqrt 2 $ . Its equation is

(a)${x^2} - {y^2} = 32$ 

(b)$\dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{9} = 1$ 

(c)$2x - 3{y^2} = 7$ 

(d) None of these

Ans: We know that distance between the foci $=  2ae$ 

$\therefore 2ae  =  16 \Rightarrow ae  =  8$ 

Given that $e  = \sqrt 2 $ 

$\therefore \sqrt 2 a  =  8 \Rightarrow a  =  4\sqrt 2 $ 

 Now ${b^2}  =  {a^2} \left( {{e^2} - 1} \right)$ 

 $\Rightarrow {b^2}  =  32\left( {2 - 1} \right) \Rightarrow {b^2}  =  32$ 

So, the equation of the hyperbola is 

$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow \dfrac{{{x^2}}}{{32}} - \dfrac{{{y^2}}}{{32}} = 1$

$\Rightarrow {x^2} - {y^2} = 32$ 

Hence, the correct option is (a).

59. Equation of the hyperbola with eccentricity $\dfrac{3}{2}$ and foci at $( \pm 2,0)$ is

(a) $\dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{5} = \dfrac{4}{9}$ 

(b)$\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{9} = \dfrac{4}{9}$ 

(c)$\dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{9} = 1$ 

(d) None of these

Ans: Given that $e = \dfrac{3}{2}$ 

 and foci $=  \left( { \pm ae, 0} \right)  =  \left( { \pm  2, 0} \right)$ 

$\therefore ae  =  2$ 

$a \times \dfrac{3}{2} = 2 \Rightarrow a = \dfrac{4}{3}$ 

Now we know that ${b^2}  =  {a^2} \left( {{e^2} - 1} \right)$ 

${b^2} = \dfrac{{16}}{9}\left( {\dfrac{9}{4} - 1} \right) \Rightarrow {b^2} = \dfrac{{16}}{9} \times \dfrac{5}{4}$ 

$ \Rightarrow {b^2} = \dfrac{{20}}{9}$ 

So, the equation of the hyperbola is 

$\dfrac{{{x^2}}}{{{{(\dfrac{4}{3})}^2}}} - \dfrac{{{y^2}}}{{\dfrac{20}{9}}} = 1

$\Rightarrow \dfrac{{9{x^2}}}{{16}} - \dfrac{{9{y^2}}}{{20}} = 1 \Rightarrow \dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{{20}} = \dfrac{1}{9}$

$\Rightarrow \dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{5} = \dfrac{4}{9}$ 

Hence, the correct option is (a).

As an important part of Math and Physics, NCERT Exemplar for Class 11 Math, Chapter 11  Conic Sections involve cutting through a cone forming various sections and curves like a parabola, ellipse, hyperbola, etc. Only the circle is considered to be the fourth type but a special case in conic sections. All of these curves are represented through equations and then graphed along a coordinate plane (x and y). Certain features like a focus and a directrix are present in each of the sections- one focus and directrix in a parabola and two each in the ellipse and hyperbola. Some of the important parts of cones and the conic sections have been defined below: 

• Focus- It is the point around which the conic sections are constructed and through which the rays reflected from the curve converge. A parabola has one focus as compared to the ellipse and hyperbola which have two each.

• Directrix- This is a line that is used to construct and define the conic sections. The distance of the directrix from a point on the conic section is of a constant ratio to the distance of the point from the focus. Again, the parabola has one directrix and the ellipse and hyperbola have two each. To explain what a conic section is based on the focus and directrix, it can be stated that a conic section is the locus of point P whose distance to the focus is a constant multiple of the distance from P to the directrix of the conic.  Apart from the above two features, the conic sections are of three types:

• Parabola- It is a set of all points whose distance from the focus/fixed point is equal to the directrix/fixed-line. A point midway between the focus and directrix is the vertex. There are four directions towards which the parabola might open up on the graph: up, down, left and right. 

• Ellipse- It is a set of all points in which the sum of the distances from two fixed points is constant. There are two foci and two directrices in an ellipse.

• Hyperbola- It is a set of all points in which the difference between the distances of two fixed points is constant. Like an ellipse, there are two foci and two directives.