Maths Class 6 Chapter 7 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 6 Maths Chapter 7 Fractions Exercise 7.6 - 2025-26
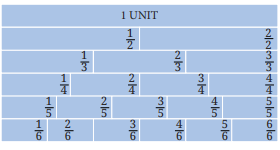
1. What are equivalent fractions in Class 6 Maths?
Equivalent fractions are fractions that represent the same value or proportion, even though they have different numerators and denominators.
2. How can I find equivalent fractions in Class 6 Maths?
To find equivalent fractions, multiply or divide the numerator and denominator of a fraction by the same non-zero number.
3. What does Exercise 7.6 in Class 6 Maths focus on?
Exercise 7.6 focuses on identifying and creating equivalent fractions using various methods.
4. Are the NCERT solutions for Exercise 7.6 in Class 6 Maths available for free?
Yes, NCERT solutions for Exercise 7.6 can be accessed for free online through our Vedantu educational platform.
5. How can I improve my understanding of equivalent fractions using these solutions in Class 6 Maths?
The solutions provide step-by-step explanations and examples that help clarify the concept of equivalent fractions and their calculations.
6. Can I practice more problems on equivalent fractions in Class 6 Maths?
Yes, the NCERT solutions include additional practice problems related to equivalent fractions for further reinforcement of the concept.
7. What grade level is Exercise 7.6 in Class 6 Maths appropriate for?
Exercise 7.6 is designed specifically for Class 6 students as part of the Maths curriculum.
8. Are there any tips for solving problems in Exercise 7.6 of Class 6 Maths?
When solving problems, focus on understanding the relationship between the numerator and denominator, and remember to multiply or divide by the same number.
9. How do the NCERT solutions help in exam preparation for Class 6 Maths?
The solutions provide clear, concise explanations and examples that help students grasp key concepts, making them well-prepared for exams.
10. Can I use these solutions to check my work in Class 6 Maths?
Yes, you can use the NCERT solutions to verify your answers and understand any mistakes in your calculations.
12. How can NCERT Solutions Class 6 Maths Ch 7 Ex 7.6 help overcome these challenges?
The NCERT Solutions Class 6 Maths Ch 7 Ex 7.6, provide clear, detailed steps and examples that guide students through the process, making it easier to understand and apply the concepts.