NCERT Exemplar for Class 6 Maths Solutions Chapter 4 Fractions & Decimals

In examples 1 and 2, write the correct answer from the given four options:

Example 1. Which of the following fractions is the smallest?

(A) $\dfrac{{11}}{9}$

(B) $\dfrac{{11}}{7}$

(C) $\dfrac{{11}}{{10}}$

(D) $\dfrac{{11}}{6}$

Ans: Option (C) is correct

The following fraction of $\dfrac{{11}}{9} = 1.22$

For, $\dfrac{{11}}{7} = 1.57$

For, $\dfrac{{11}}{{10}} = 1.1$

For, $\dfrac{{11}}{6} = 1.83$

In the following fractions $\dfrac{{11}}{{10}}$ have smallest value

So, the option (C) is correct.

Example 2: 0.7625 lies between

(A) $0.7$ and $0.76$

(B) $0.77$ and $0.78$

(C) $0.76$ and $0.761$

(D) $0.76$ and $0.763$

Ans:  Option (D) is correct.

By using the number line the $0.7625$ is lies between $0.76$ and $0.763$

Example 3: Fill in the blanks so that the statement is true:

Decimal $8.125$is equal to the fraction______

Ans:$\dfrac{{65}}{8}$ or $8\dfrac{1}{8}$ 

fraction for the decimal point is $8.125 = \dfrac{{8125}}{{1000}}$

Example 4: Fill in the blanks so that the statement is true:

$6.45 - 3.78 =$_____

Ans: $2.67$

The subtract the numbers get $6.45 - 3.78 = 2.67$

Example 5: State true or false:

The fraction $14\dfrac{2}{5}$ is equal to ${\mathbf{14}}.{\mathbf{2}}.$

Ans: The given statement is false.

For fraction is $14\dfrac{2}{{10}} = 14.2$ 

Example 6: Fill in the blanks using > or <

$\dfrac{8}{{45}}\_\_\dfrac{{16}}{{89}}$

Ans: For the fraction $\dfrac{8}{{45}} = \dfrac{{8 \times 2}}{{45 \times 2}} = \dfrac{{16}}{{90}}$

Now, $\dfrac{{16}}{{90}} < \dfrac{{16}}{{89}},$ 

Therefore,  $\dfrac{8}{{45}} < \dfrac{{16}}{{89}}$

Example 7: Express $\dfrac{{12}}{{25}}$ as a decimal.

Ans: The fraction for $\dfrac{{12}}{{25}} = \dfrac{{12 \times 4}}{{25 \times 4}}$

$= \dfrac{{48}}{{100}} = 0.48$

Decimal for the fraction $\dfrac{{12}}{{25}}$ is $0.48$

Example 8: Convert ${\mathbf{5809g}}$ to kg.

Ans: Since $1000{\text{g}} = 1{\text{kg}},$

${\text{So, }}5809{\text{g}} = \dfrac{{5809}}{{1000}}{\text{kg}}$

$= 5.809{\text{kg}}.$ 

Example 9: Round off ${\mathbf{87}}.{\mathbf{952}}$ to tenths place. 

Ans: For rounding off to tenths place, we look at the hundredths place. 

Here the digit is $5$. So, the digit at the tenths place will be increased by $1$

Hence, rounding off $87.952$ to tenths place, we get $88.0$

Example 10: Add the fractions $5\dfrac{3}{8}$ and $\dfrac{5}{{16}}$

Ans: For the addition of fraction 

Rewrite the mixed fraction

$5\dfrac{3}{8} + \dfrac{5}{{16}}{\text{ }} = \dfrac{{43}}{8} + \dfrac{5}{{16}}$

$= \dfrac{{43 \times 2}}{{8 \times 2}} + \dfrac{5}{{16}} = \dfrac{{86}}{{16}} + \dfrac{5}{{16}}$

$= \dfrac{{86 + 5}}{{16}} = \dfrac{{91}}{{16}} = 5\dfrac{{11}}{{16}}$

Example 11: What should be added to $37.28$ to obtain ${\mathbf{46}}.{\mathbf{8}}$?

Ans:  Let the missing number is $x$

So, $37.28 + x = 46.8$

$x = 46.8 - 37.28$

$= 9.52$

Hence, the required number to be added to $37.28{\text{ }}is{\text{ }}9.52$

Example 12: Arrange the following in ascending order.

$2.2,2.023,2.0226,22.1,20.42$

Ans: To arrange them from the smallest to the greatest number. 

We arrange them as follows 

using the idea of place value and comparing their digits at different places

$2.0226 < 2.023 < 2.2 < 20.42 < 22.1.$

Example 13: Gorang purchased $2kg 280g$ apples, $3kg 375g$ bananas, $225g$ grapes and $5kg 385g$ oranges. Find the total weight of the fruits purchased by Gorang in kg.

Ans: Since $1{\text{kg}} = 1000{\text{g}}$

Weight of apples $= 2{\text{kg}}280{\text{g}} = 2280{\text{g}}$ 

Weight of bananas $= 3{\text{kg}}375{\text{g}} = 3375{\text{g}}$

Weight of grapes $= 225{\text{g}}$

Weight of oranges $= 5{\text{kg}}385{\text{g}} = 5385{\text{g}}$

Total weight $= 2280{\text{g}} + 3375{\text{g}} + 225{\text{g}} + 5385{\text{g}}{\kern 1pt} {\text{ = }}11265g$

Thus, total weight $= 11265{\text{g}} = \dfrac{{11265}}{{1000}}{\text{kg}}$

$= 11.265{\text{kg}}$

Example 14: What is wrong in the following?

$\dfrac{7}{4} + \dfrac{5}{2} = \dfrac{{7 + 5}}{{4 + 2}} = \dfrac{{12}}{6} = 2$

Ans: Writing $\dfrac{7}{4} + \dfrac{5}{2} = \dfrac{{7 + 5}}{{4 + 2}}$ is wrong. It should be as follows:

Converting into like fractions

$\dfrac{7}{4} + \dfrac{5}{2} = \dfrac{7}{4} + \dfrac{{10}}{4}$ 

Only numerators are added

$\dfrac{{7 + 10}}{4} = \dfrac{{17}}{4}$ 

In Questions 1 to 20, out of the four Options, only one Answer is Correct Choose the correct answer

1. The fraction which is not equal to $\dfrac{4}{5}$ is

(A) $\dfrac{{40}}{{50}}$

(B) $\dfrac{{12}}{{15}}$

(C) $\dfrac{{16}}{{20}}$

(D) $\dfrac{9}{{15}}$

Ans: Option D is right

Check option $A \Rightarrow \dfrac{{40 \div 10}}{{50 \div 10}} = \dfrac{4}{5}$

Check option ${\text{B}} \Rightarrow \dfrac{{12}}{{15}} = \dfrac{4}{5}$

Check option ${\text{C}} \Rightarrow \dfrac{{16}}{{20}} = \dfrac{4}{5}$

Check option ${\text{D}} \Rightarrow \dfrac{9}{{15}} = \dfrac{3}{5}$

2. The two consecutive integers between which the fraction $\dfrac{5}{7}$ lies are

(A) ${\mathbf{5}}$ and ${\mathbf{6}}$

(B) ${\mathbf{0}}$ and ${\mathbf{1}}$

(C) ${\mathbf{5}}$ and $7$

(D) ${\mathbf{6}}$ and ${\mathbf{7}}$

Ans: Option B is right

Fundamental from fraction, if the value of a numerator of each fraction implies less than this value of denominator, ever lies between and $0$ and $1$.

Hence, $\dfrac{5}{7}$ are lies between $0$ and $1$.

3. When $\dfrac{1}{4}$ is written with denominator as ${\mathbf{12}}$, its numerator is

(A) ${\mathbf{3}}$

(B) ${\mathbf{8}}$

(C) ${\mathbf{24}}$

(D) ${\mathbf{12}}$

Ans: Option A is right

Since, $\Rightarrow \dfrac{1}{4} \times \dfrac{3}{3} = \dfrac{3}{{12}}$

4. Which of the following is not in the lowest form?

(A) $\dfrac{7}{5}$

(B) $\dfrac{{15}}{{20}}$

(C) $\dfrac{{13}}{{33}}$

(D) $\dfrac{{27}}{{28}}$

Ans: Option B is right

In case of $\dfrac{5}{7}$, the common factor of $7$ and $5$ is $1$.

Hence, already given in the simplest form.

In case of $\dfrac{{15}}{{20}}$, the common factor of $15$ and $20$ is $4.$

In case of $\dfrac{{13}}{{33}}$, the common factor of $13$ and $33$ is $1$.

Hence, already given in the simplest form.

In case of $\dfrac{{27}}{{28}}$, the common factor of $27$ and $28$ is $1$.

Hence, already given in the simplest form.

Hence, $\dfrac{{15}}{{20}}$ not given in the simplest form.

5. If $\dfrac{5}{8} = \dfrac{{20}}{p}$, then value of $p$ is

(A) ${\mathbf{23}}$

(B) ${\mathbf{2}}$

(C) ${\mathbf{32}}$

(D) ${\mathbf{16}}$

Ans: Option ${\text{C}}$ is right

$\dfrac{5}{8} = \dfrac{{20}}{{\text{p}}}$

$\Rightarrow 5 \times {\text{p}} = 20 \times 8$

$\Rightarrow {\text{p}} = \dfrac{{20 \times 8}}{5}$

$\Rightarrow {\text{p}} = 4 \times 8 = 32$

Hence, Value of ${\text{p}}$ is 32

6. Which of the following is not equal to the others?

(A) $\dfrac{6}{8}$

(B) $\dfrac{{12}}{{16}}$

(C) $\dfrac{{15}}{{25}}$

(D) $\dfrac{{18}}{{24}}$

Ans: Option ${\text{C}}$ is right

Check option ${\text{A}} \Rightarrow \dfrac{6}{8} = \dfrac{3}{4}$

Check option ${\text{B}} \Rightarrow \dfrac{{12 \div 4}}{{16 \div 4}} = \dfrac{3}{4}$

Check option ${\text{C}} \Rightarrow \dfrac{{15 \div 5}}{{25 \div 5}} = \dfrac{3}{5}$

Check option D $\Rightarrow \dfrac{{18 \div 6}}{{24 \div 6}} = \dfrac{3}{4}$

Thus, Option ${\text{C}}$ is not equal to the other option.

7. Which of the following fractions is the greatest?

(A) $\dfrac{5}{7}$

(B) $\dfrac{5}{6}$

(C) $\dfrac{5}{9}$

(D) $\dfrac{5}{8}$

Ans: Option B is right

In the above option given that, among the entire fraction with same numerator, the one with smaller denominator will be greatest.

Thus, required fraction is $\dfrac{5}{6}$.

8. Which of the following fractions is the smallest?

(A) $\dfrac{7}{8}$

(B) $\dfrac{9}{8}$

(C) $\dfrac{3}{8}$

(D) $\dfrac{5}{8}$

Ans: Option C is right

In the above option given that, among the entire fraction with same denominator, the one with smaller numerator will be smallest.

Thus, required fraction is $\dfrac{3}{8}$.

9. Sum of $\dfrac{4}{{17}}$ and $\dfrac{{15}}{{17}}$ is

(A) $\dfrac{{19}}{{17}}$

(B) $\dfrac{{11}}{{17}}$

(C) $\dfrac{{19}}{{34}}$

(D) $\dfrac{2}{{17}}$

Ans: Option A is right 

$\dfrac{4}{{17}}$ and $\dfrac{{15}}{{17}}$

Take the LCM of denominators

$\Rightarrow \dfrac{4}{{17}} + \dfrac{{15}}{{17}} = \dfrac{{4 + 15}}{{17}}$

$= \dfrac{{19}}{{17}}$

Thus, required fraction is $\dfrac{{19}}{{17}}$.

10. On subtracting $\dfrac{5}{9}$ from $\dfrac{{19}}{9}$, the result is

(A) $\dfrac{{24}}{9}$

(B) $\dfrac{{14}}{9}$

(C) $\dfrac{{14}}{{18}}$

(D) $\dfrac{{14}}{0}$

Ans: Option B is right 

$\dfrac{5}{9}$ from $\dfrac{{19}}{9}$

Take the LCM of denominators

   $\Rightarrow \dfrac{{19}}{9} - \dfrac{5}{9} = \dfrac{{19 - 5}}{9}$

   $= \dfrac{{14}}{9}$ 

Thus, required fraction is $\dfrac{{14}}{9}$.

11. $0.7499$lies between

(A) $0.7$and $0.74$

(B)$0.75$ and $0.79$

(C) ${\mathbf{0}}.{\mathbf{749}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{0}}.{\mathbf{75}}$

(D) ${\mathbf{0}}.{\mathbf{74992}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{0}}.{\mathbf{75}}$

Ans: Option ${\text{C}}$ is right

$0.7499$ is successor of $0.749$and predecessor of $0.75$

Thus, $0.749$lies between $0.749$and $0.75$

12. ${\mathbf{0}}.{\mathbf{023}}$lies between

(A) $0.2 and 0.3$

(B)${\mathbf{0}}.{\mathbf{02}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{0}}.{\mathbf{03}}$

(C)${\mathbf{0}}.{\mathbf{03}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{0}}.{\mathbf{029}}$

(D)${\mathbf{0}}.{\mathbf{026}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{0}}.{\mathbf{024}}$

Ans: Option B is right

Thus, $0.023$lies between $0.02$and $0.03$

13. $\dfrac{{11}}{7}$ can be expressed in the form

(A) $7\dfrac{1}{4}$

(B) $4\dfrac{1}{7}$

(C) $1\dfrac{4}{7}$

(D) $11\dfrac{1}{7}$

Ans: Option ${\text{C}}$ is right

The mix fraction of $\dfrac{{11}}{7}$ is $1\dfrac{4}{7}$

14. The mixed fraction $5\dfrac{4}{7}$ can be expressed as

(A) $\dfrac{{33}}{7}$

(B) $\dfrac{{39}}{7}$

(C) $\dfrac{{33}}{4}$

(D) $\dfrac{{39}}{4}$

Ans: Option B is right

  $\because 5\dfrac{4}{7} = \dfrac{{(7 \times 5) + 4}}{7}$

   $= \dfrac{{35 + 4}}{7}$

   $= \dfrac{{39}}{5}$ 

15. $0.07 + 0.008$ is equal to

(A) ${\mathbf{0}}.{\mathbf{15}}$

(B)${\mathbf{0}}.{\mathbf{015}}$

(C)${\mathbf{0}}.{\mathbf{078}}$

(D)${\mathbf{0}}.{\mathbf{78}}$

Ans: Option ${\text{C}}$ is right

Sum of $0.07 + 0.008$ is ${\mathbf{0}}.{\mathbf{078}}$

16. Which of the following decimals is the greatest?

(A) ${\mathbf{0}}.{\mathbf{182}}$

(B)${\mathbf{0}}.{\mathbf{0925}}$

(C)${\mathbf{0}}.{\mathbf{29}}$

(D)${\mathbf{0}}.{\mathbf{038}}$

Ans: Option ${\text{C}}$ is right

Convert the above option into like decimal as $0.1820,0.0925,0.2900$and $0.0380.$

Thus, comparing the value of like decimal value, $0.2900$ is the greatest among the given option.

17. Which of the following decimals is the smallest?

(A) ${\mathbf{0}}.{\mathbf{27}}$

(B)${\mathbf{1}}.{\mathbf{5}}$

(C)${\mathbf{0}}.{\mathbf{082}}$

(D)${\mathbf{0}}.{\mathbf{103}}$

Ans: Option ${\text{C}}$ is right

Convert the above option into like decimal as $0.270,1.500,0.082{\text{ and }}0.103.$

Thus, comparing the value of like decimal value, $0.082$is the smallest among the given option.

18. $13.572$correct to the tenths place is

(A) ${\mathbf{10}}$

(B)${\mathbf{13}}.{\mathbf{57}}$

(C)${\mathbf{14}}.{\mathbf{5}}$

(D)${\mathbf{13}}.{\mathbf{6}}$

Ans: Option D is right

Round off the number $13.572$is $13.6$

19. $15.8 - 6.73$ is equal to

(A) ${\mathbf{8}}.{\mathbf{07}}$

(B)${\mathbf{9}}.{\mathbf{07}}$

(C)${\mathbf{9}}.{\mathbf{13}}$

(D)${\mathbf{9}}.{\mathbf{25}}$

Ans: Option B is right

Subtraction of $15.8 - 6.73$is ${\mathbf{9}}.{\mathbf{07}}$

20. The decimal $0.238$ is equal to the fraction

  (A) $\dfrac{{119}}{{500}}$

  (B) $\dfrac{{238}}{{25}}$

  (C) ${\kern 1pt} \,{\kern 1pt} \dfrac{{199}}{{25}}$

  (D) $\dfrac{{119}}{{50}}$ 

Ans: Option A is right

Thus, $0.238$

fraction for $0.238$

   $\Rightarrow \dfrac{{238}}{{1000}} = \dfrac{{238 \div 2}}{{1000 \div 2}}$

   $= \dfrac{{119}}{{500}}$ 

Thus, required option $\dfrac{{119}}{{500}}.$

In Questions 21 to 44, fill in the blanks to make the Statements True

21. A number representing a part of a_____is called a fraction.

Ans: A number representing a part of a whole is called a fraction.

22. A fraction with denominator greater than the numerator is called a ____fraction.

Ans: A fraction with denominator greater than the numerator is called a proper fraction

23. fractions with the same denominator are called ____ fractions.

Ans: fractions with the same denominator are called like fractions.

24. $13\dfrac{5}{{18}}$ Is a ____ fraction.

Ans: $13\dfrac{5}{8}$ Is a mix fraction.

25. $\dfrac{{18}}{8}$ Is a______ fraction.

Ans: $\dfrac{{18}}{5}$ Is a improper fraction

26. $\dfrac{7}{{19}}$ Is a_____ fraction.

Ans: $\dfrac{7}{{19}}$ Is a proper fraction.

27. $\dfrac{5}{8}$ and $\dfrac{3}{8}$ Are _____ proper fractions.

Ans: $\dfrac{5}{8}$ and $\dfrac{3}{8}$ Are like proper fractions.

28. $\dfrac{6}{{11}}$ and $\dfrac{6}{{13}}$ Are____ proper fractions.

Ans: $\dfrac{6}{{11}}$ and $\dfrac{6}{{13}}$ are unlike proper fractions.

29. The fraction $\dfrac{6}{{15}}$ in simplest form is______

Ans: Given fraction is $\dfrac{6}{{15}} = \dfrac{{6 \div 3}}{{15 \div 3}} = \dfrac{2}{5}$

The fraction $\dfrac{6}{{15}}$ in simplest form is $\dfrac{2}{5}$

30. The fraction $\dfrac{{17}}{{34}}$ in simplest forms is_____

Ans: Given fraction is $\dfrac{{17}}{{34}} = \dfrac{{17 \div 17}}{{34 \div 17}} = \dfrac{1}{2}$

The fraction $\dfrac{{17}}{{34}}$ in simplest form is $\dfrac{1}{2}$

31. $\dfrac{{18}}{{135}}$ and $\dfrac{{90}}{{675}}$ Are proper, unlike and _____ fractions.

Ans: $\dfrac{{18}}{{135}}$ and $\dfrac{{90}}{{675}}$ Are proper, unlike and equivalent fractions.

32. $8\dfrac{2}{7}$ Is equal to the improper fraction_____

Ans: Given fraction is 

  $8\dfrac{7}{2} = \dfrac{{(8 \times 7) + 7}}{2}$

  $= \dfrac{{56 + 2}}{7}$

   $= \dfrac{{58}}{7}$ 

$8\dfrac{2}{7}$ Is equal to the improper fraction $\dfrac{{58}}{7}$

33. $\dfrac{{87}}{7}$ Is equal to the mixed fraction _____

Ans: By long division the quotient and reminder will be $12\,\,{\kern 1pt} {\text{and}}{\kern 1pt} \,{\kern 1pt} 3$

 $\dfrac{{87}}{7}$ Is equal to the mixed fraction $12\dfrac{3}{7}$

34. $9 + \dfrac{2}{{10}} + \dfrac{6}{{100}}$ Is equal to the decimal number_____

Ans: The LCM of $10$ and $100$ is$100$.

Hence, $9 + \dfrac{2}{{10}} + \dfrac{6}{{100}}$

$= \dfrac{{9 \times 100 + 2 \times 10 + 6}}{{100}}$

$\Rightarrow \dfrac{{962}}{{100}} = 9.26$

35. Decimal ${\mathbf{16}}.{\mathbf{25}}$are equal to the fraction _____

Ans: Now, $16.25$

$\Rightarrow \dfrac{{1625}}{{100}} = \dfrac{{1625 \div 25}}{{100 \div 25}} = \dfrac{{65}}{4}$

Decimal $16.25$are equal to the fraction $\dfrac{{65}}{4}$.

36. fraction $\dfrac{7}{{25}}$ is equal to the decimal number

Ans: Given fraction is 

  $\dfrac{7}{{25}} = \dfrac{{7 \times 4}}{{25 \times 4}}$

   $= \dfrac{{28}}{{100}}$

   $= 0.28$ 

fraction $\dfrac{7}{{25}}$ is equal to the decimal number $0.28$

37. $\dfrac{{17}}{9} + \dfrac{{41}}{9} =$

Ans: Explanation,

For the fractions denominator is same so add only numerator

$\Rightarrow \dfrac{{17}}{9} + \dfrac{{41}}{9} = \dfrac{{17 + 41}}{9} = \dfrac{{58}}{9}$

So,

$\dfrac{{17}}{9} + \dfrac{{41}}{9} = \dfrac{{58}}{9}$

38. $\dfrac{{67}}{{14}} - \dfrac{{14}}{{14}} =$

Ans: Explanation,

For the fractions denominator is same so subtract only numerator

$\Rightarrow \dfrac{{67}}{{14}} - \dfrac{{24}}{{14}} = \dfrac{{67 - 24}}{{14}} = \dfrac{{43}}{{14}}$

Hence,

$\dfrac{{67}}{{14}} - \dfrac{{24}}{{14}} = \dfrac{{43}}{{14}}$

39. $\dfrac{{17}}{2} + 3\dfrac{1}{2} =$

Ans: Explanation,

Rewrite the mixed fraction and add the numerator

$\Rightarrow \dfrac{{17}}{2} + 3\dfrac{1}{2} = \dfrac{{17}}{2} + \dfrac{7}{2} = \dfrac{{17 + 7}}{2}$

$\Rightarrow \dfrac{{24}}{2} = \dfrac{{24 \div 2}}{{2 \div 2}} = 12$

Hence, $\dfrac{{17}}{2} + 3\dfrac{1}{2} = 12$

40. $9\dfrac{1}{4} - \dfrac{5}{4} =$

Ans: Explanation,

Rewrite the mixed fraction and subtract the numerator

   $\Rightarrow 9\dfrac{1}{4} - \dfrac{5}{4} = \dfrac{{37}}{4} - \dfrac{5}{4}$

   $= \dfrac{{37 - 5}}{4} = \dfrac{{32}}{4}$

   $\Rightarrow \dfrac{{32 \div 4}}{{4 \div 4}} = 8$ 

Therefore, $9\dfrac{1}{4} - \dfrac{5}{4} = 8$

41. $4.55 + 9.73 =$

Ans: Add the numbers

$4.55 + 9.73 = 14.28$

42. $8.76 - 2.68 =$

Ans: Subtract the numbers

$8.76 - 2.68 = 6.08$

43. The value of 50 coins of 50 paisa $=$ Rs____

Ans: $50 \times 50 = 2500$ paisa

   $\Rightarrow {\text{ Rs}}{\text{. }}\dfrac{{2500}}{{100}} = {\text{ Rs}}{\text{.}}\dfrac{{2500 \div 100}}{{100 \div 100}}$

   $= {\text{ Rs}}{\text{. }}25$ 

The value of 50 coins of 50 paisa $=$ Rs. 25

44. 3 Hundredths $ + 3$tenths $=$

Ans: 3 Hundredths $= 0.03$

3 tenths$= 0.3$

3 Hundredths $ + 3$ tenths $= 0.33$

In Each of the Questions 45 to 65, state Whether the Statement is True or False

45. fractions with the same numerator are called like fractions. 

Ans: The given statement is False 

The correct statement is fractions with the same denominator are called like fractions.

46. fraction $\dfrac{{18}}{{39}}$ is in its lowest form.

Ans: The statement is False

Because the fraction is in lowest form is

$\dfrac{{18}}{{39}} \Rightarrow \dfrac{{18 \div 3}}{{39 \div 3}} = \dfrac{6}{{13}}$

47. fractions $\dfrac{{15}}{{39}}$ and $\dfrac{{45}}{{117}}$ are equivalent fractions.

Ans: The statement is True

It is divide by same number

$\dfrac{{45}}{{117}} \Rightarrow \dfrac{{45 \div 3}}{{117 \div 3}} = \dfrac{{15}}{{39}}$

So, Both are equivalent.

48. The sum of two fractions is always a fraction.

Ans: The statement is True

Let, two fraction $\dfrac{{17}}{9}$ and $\dfrac{{41}}{9}$

$\dfrac{{17}}{9} + \dfrac{{41}}{9} = \dfrac{{58}}{9}$

Explanation,

$\Rightarrow \dfrac{{17}}{9} + \dfrac{{41}}{9} = \dfrac{{17 + 41}}{9} = \dfrac{{58}}{9}$, 

This is a fraction.

49. The result obtained by subtracting a fraction from another fraction is necessarily a fraction.

Ans: The statement is False

Let, two fraction $\dfrac{{24}}{{14}}$ and $\dfrac{{67}}{{14}}$

$\dfrac{{24}}{{14}} - \dfrac{{67}}{{14}} =  - \dfrac{{43}}{{14}}$

Explanation, 

$\Rightarrow \dfrac{{24}}{{14}} - \dfrac{{67}}{{14}} = \dfrac{{24 - 67}}{{14}} =  - \dfrac{{43}}{{14}}$, 

which is not a fraction.

50. If a whole or an object is divided into a number of equal parts, then each part represents a fraction.

Ans: The statement is True

51. The place value of a digit at the tenths place is 10 times the same digit at the one's place.

Ans: The given statement is False

The place value of a digit at the tenths place is $\dfrac{1}{{10}}$ times the same digit at the one's place.

$\dfrac{x}{{10}} = 10x$, it is not possible.

52. The place value of a digit at the hundredths place is $\dfrac{1}{{10}}$ times the same digit at the tenths place.

Ans: The given statement is True

53. The decimal $3.725$is equal to $3.72$ correct to two decimal places.

Ans: The given statement is False

Since, $5$are at thousandths place.

$3.725$is written as $3.73,$correct two decimal place.

54. In the decimal form, fraction $\dfrac{{25}}{8} = 3.125$.

Ans: The statement is True

$\dfrac{{25}}{8} = \dfrac{{25 \times 125}}{{8 \times 125}}$

$= \dfrac{{3125}}{{1000}} = 3.125$ 

55. The decimal $23.2 = 23\dfrac{2}{5}$.

Ans: The given statement is False

$23.2 = \dfrac{{232}}{{10}}$

$= \dfrac{{232 \div 2}}{{10 \div 2}} = \dfrac{{116}}{5}$ 

By Long division method the quotient and reminder is $23{\kern 1pt} {\kern 1pt} \,{\text{and}}{\kern 1pt} \,1$.

The correct statement 

The decimal $23.2 = 23\dfrac{1}{5}$.

56. The fraction represented by the shaded portion in the adjoining figure is $\dfrac{3}{8}$.

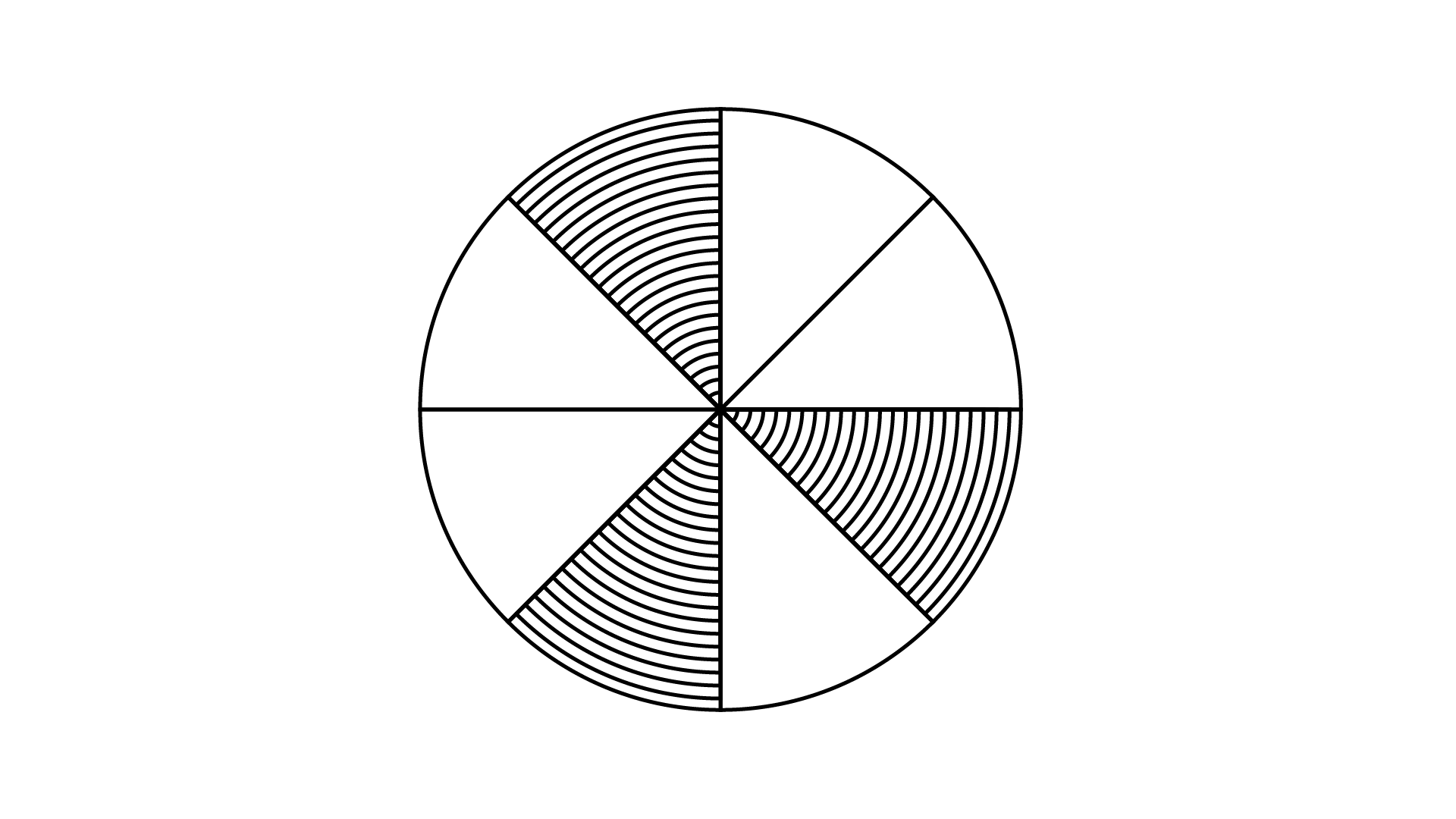
Ans: The given explanation is true.

The figure shows that, number of total part is$8$ and out of these$3$parts is shaded.

The required fraction is $\dfrac{3}{8}$

57. The fraction represented by the un-shaded portion in the adjoining figure is $\dfrac{5}{9}$.

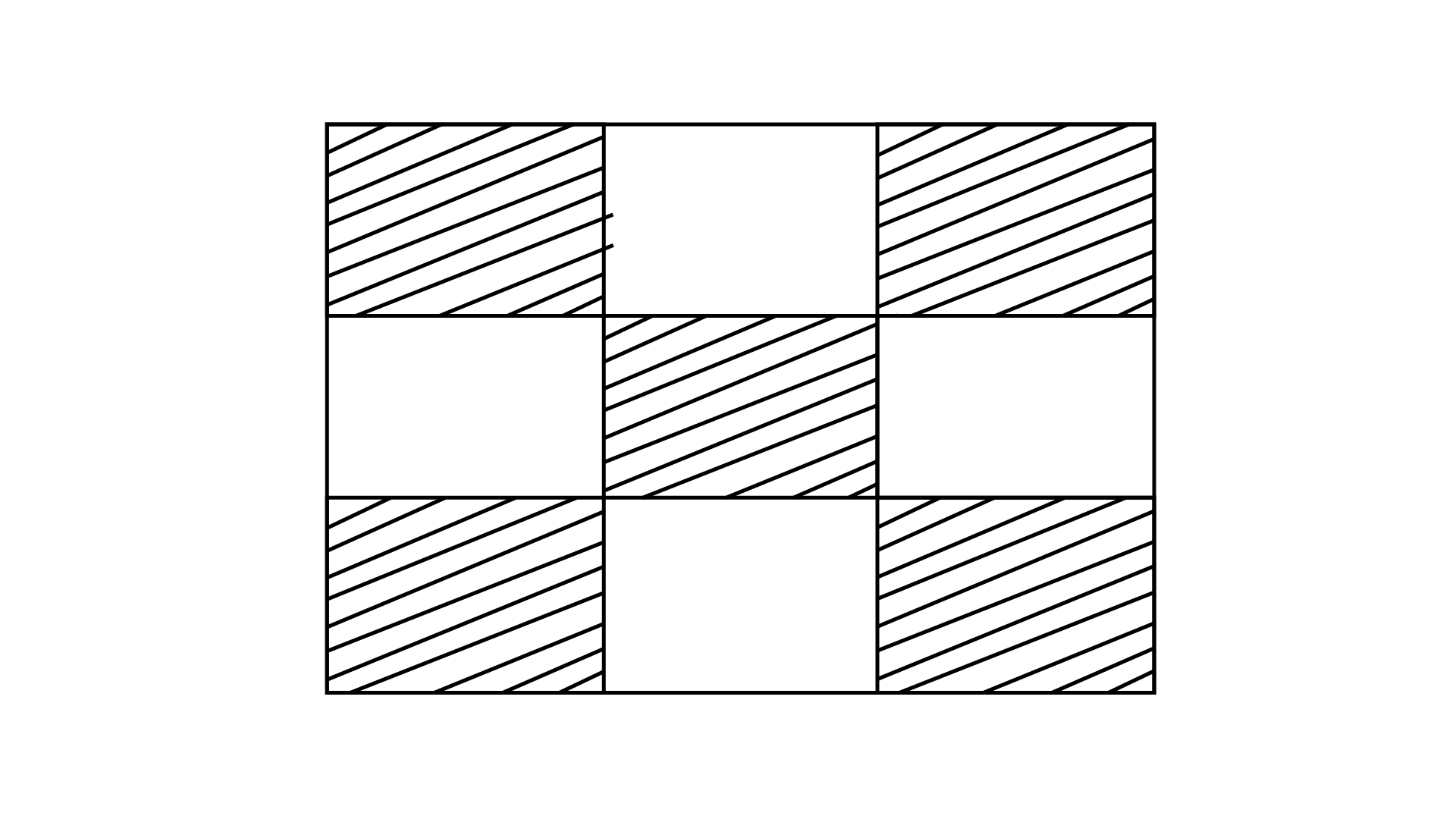
Ans: The given statement for the figure is false.

The figure shows that, number of total part is $9$ and out of these $4$ parts is un-shaded.

The required fraction is $\dfrac{4}{9}$.

58. $\dfrac{{25}}{{19}} + \dfrac{6}{{19}} = \dfrac{{31}}{{38}}$

Ans: The addition of the fraction is False

Denominator is same for the fractions so by adding the numerator 

$\Rightarrow \dfrac{{25}}{{19}} + \dfrac{6}{{19}} = \dfrac{{25 + 6}}{{19}} = \dfrac{{31}}{{19}}$

$\Rightarrow \dfrac{{31}}{{19}} \ne \dfrac{{31}}{{38}}$ 

59. $\dfrac{8}{{18}} - \dfrac{8}{{15}} = \dfrac{8}{3}$

Ans: The subtract of the fraction is False

Cross multiply the both fraction with each other.

$\Rightarrow \dfrac{8}{{18}} - \dfrac{8}{{15}} = \dfrac{{8 \times 15 - 8 \times 18}}{{18 \times 15}}$

$= \dfrac{{120 - 144}}{{270}} = \dfrac{{ - 24}}{{270}}$

$=  - \dfrac{4}{{45}}$ 

$\Rightarrow  - \dfrac{4}{{45}} \ne \dfrac{8}{3}$

60. $\dfrac{7}{{12}} + \dfrac{{11}}{{12}} = \dfrac{3}{2}$

Ans: The addition of the fraction is True

$\Rightarrow \dfrac{7}{{12}} + \dfrac{{11}}{{12}} = \dfrac{{7 + 11}}{{12}}$

$= \dfrac{{18 \div 6}}{{12 \div 6}} = \dfrac{3}{2}$ 

61. $3.03 + 0.016 = 3.019$

Ans: The addition of the numbers is False

$\Rightarrow 3.030 + 0.016 = 3.046$

$\Rightarrow 3.046 \ne 3.019$ 

62. ${\mathbf{42}}.{\mathbf{28}} - {\mathbf{3}}.{\mathbf{19}} = {\mathbf{39}}.{\mathbf{09}}.$

Ans: The subtraction of the two numbers is True

63. $\dfrac{{16}}{{25}} > \dfrac{{13}}{{25}}$

Ans: The statement is True

Given fraction are like fraction. 

Comparing the numerator, we get $\dfrac{{16}}{{25}} > \dfrac{{13}}{{25}}$

64. $19.25 < 19.053$

Ans: The given fraction type is False

Since, convert the $19.25$and $19.053$ in like decimal. It's become $19.250$ and $19.053.$

Compare the place value $19.250 < 19.053$, we get hundred place of $19.250$ is $2$ and the hundred place of $19.053$ is $0$

Hence, the statement is $19.25 > 19.053$

65. $13.730 = 13.73$

Ans: The given number is True

Since, convert the $13.730$ and $13.73$in like decimal. It's become $13.730$ and $13.730$

So,$13.730 = 13.73$

In Each of the Questions 66 to 71, fill in the Blanks Using '>', '<' or '=':

66. $\dfrac{{11}}{{16}} \ldots \dfrac{{14}}{{15}}$

Ans: The L.C.M. of $16$ and $15$ is $2 \times 2 \times 2 \times 2 \times 3 \times 5 = 240$

Make it as like a fraction, multiply in numerator and denominator with the same digit

$\dfrac{{11}}{{16}} \times \dfrac{{15}}{{15}} = \dfrac{{165}}{{240}}$

$\dfrac{{14}}{{15}} \times \dfrac{{16}}{{16}} = \dfrac{{224}}{{240}}$

$\dfrac{{224}}{{240}} > \dfrac{{165}}{{240}}{\text{ So, }}\dfrac{{11}}{{16}} < \dfrac{{14}}{{15}}$

67. $\dfrac{8}{5} \ldots \dfrac{{95}}{{14}}$

Ans: The L.C.M of $15$ and $14$ is $2 \times 3 \times 5 \times 7 = 210$

Make it as like a fraction, multiply in numerator and denominator with the same digit

$\dfrac{8}{{15}} \times \dfrac{{14}}{{14}} = \dfrac{{112}}{{210}}$

$\dfrac{{95}}{{14}} \times \dfrac{{15}}{{15}} = \dfrac{{1425}}{{210}}$

$\dfrac{{1425}}{{210}} > \dfrac{{112}}{{210}}$

Therefore,  $\dfrac{8}{{15}} < \dfrac{{95}}{{14}}$

68. $\dfrac{{12}}{{75}} \ldots \dfrac{{32}}{{200}}$

Ans: The L.C.M of $75$ and $200$is $2 \times 2 \times 2 \times 3 \times 5 \times 5 = 600$

Make it as like a fraction, multiply in numerator and denominator with the same digit

$\dfrac{{12}}{{75}} \times \dfrac{8}{8} = \dfrac{{96}}{{600}}$

$\dfrac{{32}}{{200}} \times \dfrac{3}{3} = \dfrac{{96}}{{600}}$

$\dfrac{{96}}{{600}} = \dfrac{{96}}{{600}}$ 

Hence, $\dfrac{{12}}{{75}} = \dfrac{{32}}{{200}}$

69. $3.25 \ldots 3.4$

Ans: Since, convert the $3.25$and $3.4$in like decimal. It's become $3.25$ and $3.40$

Compare the place value of $3.25$and $3.40,$we get tenth place of $3.25$ is $2$ and the tenth place of $3.40$is $4$

Hence,$3.25 < 3.4$

70. $\dfrac{{18}}{{15}} \ldots 1.3$

Ans: Since, convert $1.3$ into fraction from, we get $\dfrac{{13}}{{10}}$

$\dfrac{{18}}{{15}} \ldots ..\dfrac{{13}}{{10}}$

The L.C.M. of $15$ and $10$ is $2 \times 3 \times 5 = 30$

Make it as like a fraction, multiply in numerator and denominator with the same digit

$\dfrac{{18}}{{15}} \times \dfrac{{10}}{{10}} = \dfrac{{180}}{{150}}{\text{ and }}\dfrac{{13}}{{10}} \times \dfrac{{15}}{{15}} = \dfrac{{195}}{{150}}$

$\dfrac{{180}}{{150}} < \dfrac{{195}}{{150}}{\text{ So, }}\dfrac{{18}}{{15}} < 1.3$

71. $6.25 \ldots \dfrac{{25}}{4}$

Ans: Since, convert $1.3$into fraction from, we get $\dfrac{{625}}{{100}}$

$\Rightarrow \dfrac{{625}}{{100}} = \dfrac{{625 \div 25}}{{100 \div 25}} = \dfrac{{25}}{4}$

$\dfrac{{25}}{4} \ldots .\dfrac{{25}}{4}$

$\dfrac{{25}}{4} = \dfrac{{25}}{4}$

Therefore, $6.25 = \dfrac{{25}}{4}$

72. Write the fraction represented by the shaded portion of the adjoining figure:

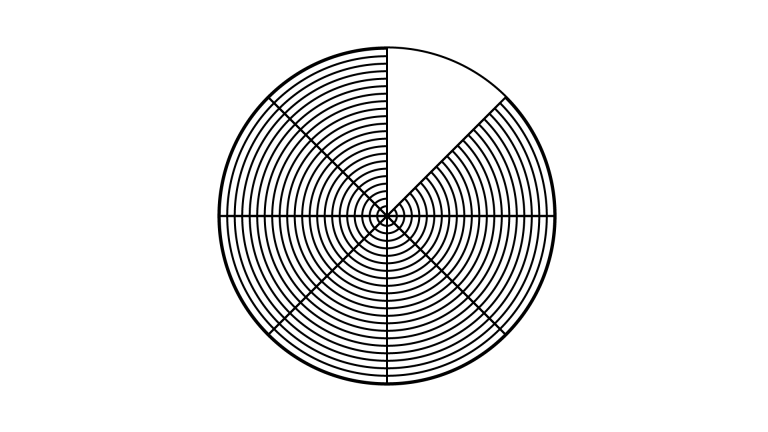
Ans: In the given figure, total parts in the figure is divided into $8$ parts and 7 parts are shaded. 

Total parts $= 8$

Total shaded parts $= 7$

Therefore,

fraction of unshaded portion $= \dfrac{{{\text{ Total shaded parts }}}}{{{\text{ Total parts }}}}$

$= \dfrac{7}{8}$

The required fraction is $\dfrac{7}{8}$.

73. Write the fraction represented by the un-shaded portion of the adjoining figure:

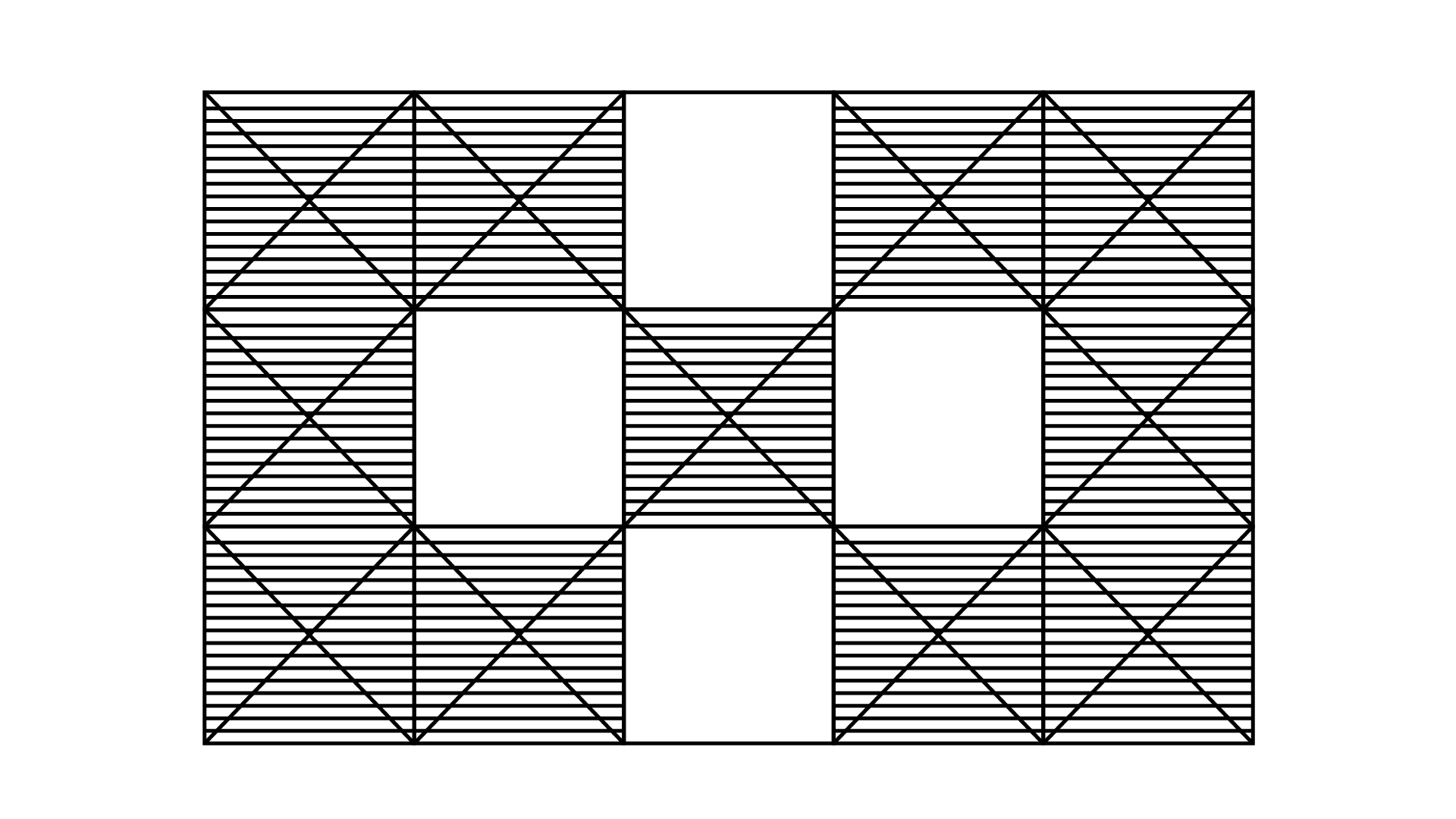
Ans: In the given figure, total parts in which figure has been divided into 15 and out of which 4 parts are unshaded.

Total parts $= 15$

Total unshaded parts $= 4$

Therefore,

fraction of unshaded portion $= \dfrac{{{\text{ Total unshaded parts }}}}{{{\text{ Total parts }}}} = \dfrac{4}{{15}}$

The required fraction is $\dfrac{4}{{15}}$.

74. Ali divided one fruit cake equally among six persons. What part of the cake he gave to each person?

Ans: Given data 

Number of cake $= 1$

Total no. of persons $= 6$

Since,

Ali has to divide one fruit cake among 6 people,

${\text{Each person will get}} = \dfrac{{{\text{ No}}{\text{. of cake }}}}{{{\text{ Total no}}{\text{. of person }}}}$

$= \dfrac{1}{6}{\text{ part}}$

75. Arrange ${\mathbf{12}}.{\mathbf{142}},{\text{ }}{\mathbf{12}}.{\mathbf{124}},{\text{ }}{\mathbf{12}}.{\mathbf{104}},{\text{ }}{\mathbf{12}}.{\mathbf{401}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{12}}.{\mathbf{214}}$in ascending order.

Ans: Given number$12.142,12.124,12.104,12.401{\kern 1pt} \,{\text{and }}12.214$ in like decimal.

So, compare the place value of the digit and arrange them, $12.104 < 12.124 < 12.142 < 12.214 < 12.401$

76. Write the largest four-digit decimal number less than1 using the digits $1,5,3$ and ${\mathbf{8}}$ once.

Ans: Given whole numbers are$1,5,3,{\text{ and }}8$.

Arrange them in descending order to make them large, after arranging the number will be $8531.$

To make it a decimal number we will keep the whole number  8531 in the decimal point.

The required number is 0.8531, which is the largest four  -  digit decimal number less than 1.

77. Using the digits ${\mathbf{2}},{\mathbf{4}},{\mathbf{5}}$ and ${\mathbf{3}}$ once, write the smallest four-digit decimal number. 

Ans: For converting $2,4,5,$and $3$ into smallest four digit decimal number, arrange them in ascending order and then making the numbers decimal, we have to keep the whole numbers in decimal point.

After arranging whole numbers in ascending form it will be $2345.$

To make the number decimal we will keep the numbers in decimal point.

So, the required number is$0.2345$, which is the smallest four digit decimal number.

78. Express $\dfrac{{11}}{{20}}$ as a decimal.

Ans: $\dfrac{{11}}{{20}}$ is an improper fraction.

To get the denominator as whole number we will multiply denominator by$5$,

$\dfrac{{11}}{{20}} = \dfrac{{11 \times 5}}{{20 \times 5}} = \dfrac{{55}}{{100}} = 0.55$

$0.55$ is in decimal form

79. Express $6\dfrac{2}{3}$ as an improper fraction.

Ans: We will convert the mixed fraction $6\dfrac{2}{3}$ into improper fraction. 

We have,

$6\dfrac{2}{3} = \dfrac{{(6 \times 3) + 2}}{3} = \dfrac{{18 + 2}}{3} = \dfrac{{20}}{3}$

Now we got $\dfrac{{20}}{3}$.

$\dfrac{{20}}{3}$ is an improper fraction.

80. Express $3\dfrac{2}{5}$ as a decimal.

Ans: We will convert the mixed fraction $3\dfrac{2}{5}$ into an improper fraction. 

We have, $3\dfrac{2}{5} = \dfrac{{(3 \times 5) + 2}}{5} = \dfrac{{15 + 2}}{5} = \dfrac{{17}}{5}$

Now,

$\dfrac{{17}}{5} = \dfrac{{17 \times 2}}{{5 \times 2}} = \dfrac{{34}}{{10}} = 3.4$

81. Express $0.041$as a fraction. 

Ans: We can write 0.041 as $\dfrac{{0.041}}{1}$.

So, $0.041 = \dfrac{{0.041}}{1}$

Multiply numerator and denominator by ${\mathbf{1000}}$ we have,

$0.041 = \dfrac{{0.041 \times 1000}}{{1 \times 1000}}$

$= \dfrac{{41}}{{1000}}$ 

fraction for the decimal is $\dfrac{{41}}{{1000}}$

82. Express $6.03$as a mixed fraction.

Ans: We have, $6.03$

$6.03 = \dfrac{{603}}{{100}} = 6\dfrac{3}{{100}}$

The fraction for the decimal is $6\dfrac{3}{{100}}$

83. Convert ${\mathbf{5201g}}$ to kg.

Ans: We know that,

$1{\text{Kg}} = 1000{\text{g}}$

$1{\text{g}} = \dfrac{1}{{1000}}{\text{kg}}$

$5201{\text{g}} = \dfrac{1}{{1000}} \times 5201{\text{kg}}$

$\Rightarrow 5201{\text{g}} = \dfrac{{5201}}{{1000}} = 5.201{\text{kg}}$

84. Convert ${\mathbf{2009}}$ paisa to rupees and express the result as a mixed fraction.

Ans: We know that,

1 rupee $= 100$ paisa

1 paisa $= \dfrac{1}{{100}}$ rupees

2009 paisa $= \dfrac{1}{{100}} \times 2009$ rupees

$\Rightarrow 2009$ paisa $= \dfrac{{2009}}{{100}} = 20.09$ rupees

The mixed fraction is Rs. $20\dfrac{9}{{100}}$.

85. Convert $1537cm$ to ${\text{m}}$ and express the result as an improper fraction.

Ans: We know that,

1 meter $= 100$centimeters

1 centimeter $= \dfrac{1}{{100}}$ meter

$1537{\text{cm}} = \dfrac{1}{{100}} \times 1537{\text{m}}$

$\Rightarrow 1537{\text{cm}} = \dfrac{{1537}}{{100}}{\text{m}}$

86. Convert $2435m$ to ${\text{km}}$ and express the result as a mixed fraction.

Ans: We know that

$1{\text{km}} = 1000{\text{m}}$

$1{\text{m}} = \dfrac{1}{{1000}}{\text{km}}$

$2435{\text{m}} = \dfrac{1}{{1000}} \times 2435{\text{km}}$

$2435{\text{m}} = \dfrac{{2435}}{{1000}}{\text{km}} = 2.435{\text{km}}$

Dividing numerator and denominator by $5$ we have,

$\dfrac{{2435 \div 5}}{{1000 \div 5}}{\text{km}} = \dfrac{{487}}{{200}}{\text{km}}$

By long division method quotient and reminder is $2{\kern 1pt} {\kern 1pt} \,{\text{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 87$

The mixed fraction is $2\dfrac{{87}}{{200}}$

87. Arrange the fractions $\dfrac{2}{3},\dfrac{3}{4},\dfrac{1}{2}$ and $\dfrac{5}{6}$ in ascending order.

Ans: Given fraction is $\dfrac{2}{3},\dfrac{3}{4},\dfrac{1}{2}$ and $\dfrac{5}{6}$

Take the LCM of $3,4,2$and $6$

The ${\text{LCM}}$ of $3,4,2$and $6$ is $2 \times 2 \times 3 = 12$

${\text{Now }},\dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}},$

$\dfrac{{3 \times 3}}{{4 \times 3}} = \dfrac{9}{{12}}$

$\dfrac{{1 \times 6}}{{2 \times 6}} = \dfrac{6}{{12}},$

$\dfrac{{5 \times 2}}{{6 \times 2}} = \dfrac{{10}}{{12}}$ 

Now, arrange the following the ascending order

$\dfrac{6}{{12}} < \dfrac{8}{{12}} < \dfrac{9}{{12}} < \dfrac{{10}}{{12}}\quad $

The ascending order of the function is $\dfrac{1}{2} < \dfrac{2}{3} < \dfrac{3}{4} < \dfrac{5}{6}$.

88. Arrange the fractions $\dfrac{6}{7},\dfrac{7}{8},\dfrac{4}{5}$ and $\dfrac{3}{4}$ in descending order

Ans: The given fraction is $\dfrac{6}{7},\dfrac{7}{8},\dfrac{4}{5}$ and $\dfrac{3}{4}$

Take the LCM of $7,8,5$and $4$

The ${\text{LCM}}$ of $7,8,5$and $4 = 2 \times 2 \times 2 \times 5 \times 9 = 280$

${\text{Now, }}\dfrac{6}{7} = \dfrac{{6 \times 40}}{{7 \times 40}} = \dfrac{{240}}{{280}},$

$\dfrac{7}{8} = \dfrac{{7 \times 35}}{{8 \times 35}} = \dfrac{{245}}{{280}}$

$\dfrac{4}{5} = \dfrac{{4 \times 56}}{{5 \times 56}} = \dfrac{{224}}{{280}}{\text{ and }}\dfrac{3}{4} = \dfrac{{3 \times 70}}{{4 \times 70}} = \dfrac{{210}}{{280}}$

Now, arrange the following the descending order

$\dfrac{{245}}{{280}} > \dfrac{{240}}{{280}} > \dfrac{{224}}{{280}} > \dfrac{{210}}{{280}}$

The descending order of the fraction is $\dfrac{7}{8} > \dfrac{6}{7} > \dfrac{4}{5} > \dfrac{3}{4}$.

89. Write $\dfrac{3}{4}$ as a fraction with denominator ${\mathbf{44}}$.

Ans: Given fraction $\dfrac{3}{4}$

If multiply 4 by 11 it become 44

Now,

$\dfrac{3}{4} \times \dfrac{{11}}{{11}} = \dfrac{{3 \times 11}}{{4 \times 11}} = \dfrac{{33}}{{44}}$

$\dfrac{3}{4}$ is equivalent to $\dfrac{{33}}{{44}}$

90. Write $\dfrac{5}{6}$ as a fraction with numerator ${\mathbf{60}}$.

Ans: Given fraction $\dfrac{5}{6}$

If multiply $5$ by $12$ it become $60$

Now,

$\dfrac{5}{6} = \dfrac{{5 \times 12}}{{6 \times 12}}$ 

$\dfrac{5}{6} = \dfrac{{60}}{{72}}$ 

$\dfrac{5}{6}$ is equivalent to $\dfrac{{60}}{{72}}$.

91. Write $\dfrac{{129}}{8}$ as a mixed fraction

Ans: Given fraction is $\dfrac{{129}}{8}$

Now divide the numbers and quotient and reminder of the numbers is $16{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} \,{\kern 1pt} 1$

So, the mixed fraction of the $\dfrac{{129}}{8} = 16\dfrac{1}{8}$

92. Round off $20.83$to nearest tenths

Ans: $20.8$is the nearest round off $20.83$

93. Round off $75.195$ to nearest hundredths.

Ans: $75.20$is the nearest round off $75.195$

94. Round off $27.981$to nearest tenths.

Solution:

$28.0$is the nearest round off $27.981$

95. Add the fractions $\dfrac{3}{8}$ and $\dfrac{2}{3}$.

Ans: Given fraction $\dfrac{3}{8}$ and $\dfrac{2}{3}$

Denominator is different so need to cross multiply

Cross multiply the both fraction with each other.

$\dfrac{3}{8} + \dfrac{2}{3} = \dfrac{{3 \times 3 + 8 \times 2}}{{8 \times 3}}$

$= \dfrac{{9 + 16}}{{24}} = \dfrac{{25}}{{24}}$

The addition of fraction $\dfrac{3}{8}$ and $\dfrac{2}{3}$ is $\dfrac{{25}}{{24}}$.

96. Add the fractions $\dfrac{3}{8}$ and $6\dfrac{3}{4}$.

Ans: Given fraction is $\dfrac{3}{8}$ and $6\dfrac{3}{4}$

Now, rewrite the mixed fraction

$6\dfrac{3}{4} = \dfrac{{(6 \times 4) + 3}}{4} = \dfrac{{24 + 3}}{4} = \dfrac{{27}}{4}$

Add the following fraction $\dfrac{3}{8}$ and $\dfrac{{27}}{4}$

Cross multiply the both fraction with each other.

$\dfrac{{3 \times 4 + 27 \times 8}}{{8 \times 4}} = \dfrac{{12 + 216}}{{32}}$

$= \dfrac{{228}}{{32}} = \dfrac{{228 \div 4}}{{32 \div 4}}$

$= \dfrac{{57}}{8} = 7\dfrac{1}{8}$ 

The addition of fractions $\dfrac{3}{8}$ and $6\dfrac{3}{4}$ is $7\dfrac{1}{8}$

97. Subtract $\dfrac{1}{6}$ from $\dfrac{1}{2}$.

Ans: Given fraction $\dfrac{1}{6}$ and $\dfrac{1}{2}$

Cross multiply the both fraction with each other.

$\dfrac{1}{2} - \dfrac{1}{6} = \dfrac{{1 \times 6 - 1 \times 2}}{{2 \times 6}}$

$= \dfrac{{6 - 2}}{{12}}$

$= \dfrac{4}{{12}} = \dfrac{{4 \div 4}}{{12 \div 4}}$

$= \dfrac{1}{3}$ 

The subtraction of $\dfrac{1}{6}$ and $\dfrac{1}{2}$ is $\dfrac{1}{6}$.

98. Subtract $8\dfrac{1}{3}$ from $\dfrac{{100}}{9}$.

Ans: Given fraction $8\dfrac{1}{3}$ and $\dfrac{{100}}{9}$

Now, rewrite the mixed fraction

$8\dfrac{1}{3} = \dfrac{{(8 \times 3) + 1}}{3} = \dfrac{{24 + 1}}{3} = \dfrac{{25}}{3}$

Subtract the following fraction, $\dfrac{{25}}{3}$ from $\dfrac{{100}}{9}$

Cross multiply the both fraction with each other.

$= \dfrac{{100}}{9} - \dfrac{{25}}{3}$

$= \dfrac{{100}}{9} - \dfrac{{25 \times 3}}{{3 \times 3}}$

$= \dfrac{{100}}{9} - \dfrac{{75}}{9}$

$= \dfrac{{100 - 75}}{9}$

$= \dfrac{{25}}{9} = 2\dfrac{7}{9}$

The subtraction of $\dfrac{{100}}{9} - 8\dfrac{1}{3} = 2\dfrac{7}{9}$.

99. Subtract $1\dfrac{1}{4}$ from $\dfrac{1}{2}$.

Ans: Given fraction $1\dfrac{1}{4}$ and $6\dfrac{1}{2}$

 Now, rewrite the mixed fraction

Now, $1\dfrac{1}{4}$ and $6\dfrac{1}{2}$

$\Rightarrow \dfrac{{(4 \times 1) + 1}}{4} = \dfrac{{4 + 1}}{4}$

$= \dfrac{5}{4}$ 

Now, $6\dfrac{1}{2}$

$\Rightarrow \dfrac{{(6 \times 2) + 1}}{2} = \dfrac{{12 + 1}}{2}$

$= \dfrac{{13}}{2}$

Subtract the following fraction, $\dfrac{5}{4}$ from $\dfrac{{13}}{6}$

$\dfrac{{13}}{2} - \dfrac{5}{4} = \dfrac{{13 \times 2}}{{2 \times 2}} - \dfrac{5}{4}$

$= \dfrac{{26}}{4} - \dfrac{5}{4}$

$= \dfrac{{26 - 5}}{4}$

$= \dfrac{{21}}{4} = 5\dfrac{1}{4}$

The subtraction of the $\dfrac{{13}}{2} - \dfrac{5}{4} = 5\dfrac{1}{4}$.

100. Add $1\dfrac{1}{4}$ and $6\dfrac{1}{2}$

Ans: The given fraction $1\dfrac{1}{2}$ and $6\dfrac{1}{2}$

Now, rewrite the mixed fraction

$1\dfrac{1}{4} = \dfrac{{4 + 1}}{4} = \dfrac{5}{4}$ 

$6\dfrac{1}{2} = \dfrac{{12 + 1}}{2} = \dfrac{{13}}{2}$ 

Now, $\dfrac{5}{4} + \dfrac{{13}}{2} = \dfrac{5}{4} + \dfrac{{13 \times 2}}{{2 \times 2}}$ 

$= \dfrac{5}{4} + \dfrac{{26}}{4}$ 

$= \dfrac{{5 + 26}}{4}$ 

$= \dfrac{{31}}{4} = 7\dfrac{3}{4}$

 The addition of the $\dfrac{5}{4} + \dfrac{{13}}{2} = 7\dfrac{3}{4}$.

101. Katrina rode her bicycle $6\dfrac{1}{2}km$ in the morning and $8\dfrac{3}{4}km$ in the evening. Find the distance traveled by her altogether on that day.

Ans: The distance covers by Katrina in the morning

$= 8\dfrac{3}{4} = \dfrac{{(8 \times 3) + 3}}{4} = \dfrac{{24 + 3}}{4} = \dfrac{{27}}{4}$

The distance covers by Katrina in the evening

$= 8\dfrac{3}{4} = \dfrac{{(8 \times 3) + 3}}{4} = \dfrac{{32 + 3}}{4} = \dfrac{{35}}{4}$

Total distance travelled by her

$= \dfrac{{13}}{2}{\text{km}} + \dfrac{{35}}{4}{\text{km}}$

$= \dfrac{{13 \times 2}}{{2 \times 2}}{\text{km}} + \dfrac{{35}}{4}{\text{km}}$

${\text{L}}{\text{.C}}{\text{.M of }}2{\text{ and }}4 = 4$

$= \dfrac{{26}}{4}{\text{km}} + \dfrac{{35}}{4}{\text{km}} = \dfrac{{(26 + 35){\text{km}}}}{4}$

$= \dfrac{{61}}{4}{\text{km}} = 15\dfrac{1}{4}{\text{km}}$

Distance travelled altogether by Katrina in a day is $15\dfrac{1}{4}{\text{km}}$.

102. A rectangle is divided into a certain number of equal parts. If ${\mathbf{16}}$ of the parts so formed represent the fraction $\dfrac{1}{4}$, find the number of parts in which the rectangle has been divided.

Ans: Let, the number of parts in which the rectangle has been divided be $x$

According to the question, $\dfrac{{16}}{x} = \dfrac{1}{4}$

Cross- multiplication, $16 \times 4 = 1 \times x$

$x = 64$

64 are the parts in which the rectangle has been divided.

103. Grip size of a tennis racquet is $11\dfrac{9}{{80}}cm$. Express the size as an improper fraction.

Ans: Given, Grip size of a tennis racquet is $11\dfrac{9}{{80}}{\text{cm}}$

Now, rewrite the mixed fraction

$\Rightarrow 11\dfrac{9}{{80}} = \dfrac{{(11 \times 80) + 9}}{{80}}$

$= \dfrac{{880 + 9}}{{80}}$

$= \dfrac{{889}}{{80}}$ 

$\dfrac{{889}}{{80}}$ this is a improper fraction.

104. On an average $\dfrac{1}{{10}}$ of the food eaten is turned into organism's own body and is available for the next level of the consumer in a food chain. What fraction of the food eaten is not available for the next level?

Let that total food for the eaten is 1 and out of these, $\dfrac{1}{{10}}$ of the food eaten is turned into organism's own body.

Now, available for the next level of the consumer in a food chain is 

$\Rightarrow 1 - \dfrac{1}{{10}} = \dfrac{{10 - 1}}{{10}} = \dfrac{9}{{10}}$

The fraction of food eaten is not available for next level is $\dfrac{9}{{10}}$

105. Mr. Rajan got a job at the age of 24 years and he got retired from the job at the age of ${\mathbf{60}}$ years. What fraction of his age till retirement was he in the job?

Ans: Given,

Mr. Rajan got a job at the age of 24 years

He got retired from the job at the age of $60$ years

Total working year $= (60 - ( - 24)) = 36$year

The required fraction $\dfrac{{36}}{{60}} = \dfrac{{36 \div 12}}{{60 \div 12}} = \dfrac{3}{5}$

The fraction of his age till retirement was he in the job is $\dfrac{3}{5}$

106. The food we eat remains in the stomach for a maximum of 4 hours. For what fraction of a day, does it remain there?

Ans: Given, 

The food we eat remains in the stomach for a maximum of 4 hours

Total number of hours in a day is $24.$

The required fraction 

$\dfrac{4}{{24}} = \dfrac{{4 \div 4}}{{24 \div 4}} = \dfrac{1}{6}$

The fraction of the day food remains in the stomach is $\dfrac{1}{6}$

107. What should be added to $25.5$to get $50$ ?

Ans: Let ${\mathbf{x}}$ should be added to ${\mathbf{25}}.{\mathbf{5}}$ to get ${\mathbf{50}}$

Now,

$25.5 + x = 50$

$x = 50 - 25.5 = 24.5$ 

The required number is $24.5$

The number that should be added to $25.5$ to get 50 is $24.5$

108. Alok purchased $1kg200g$ potatoes, $250g$ dhania, $5kg300g$ onion, $500g$ palak, and $2kg600g$ tomatoes. Find the total weight of his purchases in kilograms.

Ans: Convert all the data in a signal unit, ${\text{kg}}$

$1{\kern 1pt} {\kern 1pt} kg = \dfrac{1}{{1000}}g$

Given,

Alok purchased $1{\text{kg}}200{\text{g}}$ potatoes, 

$250{\text{g}}$ dhania, 

$5{\text{kg}}300{\text{g}}$ onion, 

$500{\text{g}}$ palak,

$2{\text{kg}}600{\text{g}}$ tomatoes 

$= 1{\text{kg}}200{\text{g}} = 1{\text{kg}} + \dfrac{{200}}{{1000}}{\text{kg}} = 1.200{\text{kg}}$ of potatoes

$= 0{\text{kg}}250{\text{g}} = 0{\text{kg}} + \dfrac{{250}}{{1000}}{\text{kg}} = 0.250{\text{kg}}$ of dhania

$= 5{\text{kg}}300{\text{g}} = 5{\text{kg}} + \dfrac{{300}}{{1000}}{\text{kg}} = 5.300{\text{kg}}$ of onion

$= 0{\text{kg}}500{\text{g}} = 0{\text{kg}} + \dfrac{{500}}{{1000}}{\text{kg}} = 0.500{\text{kg}}$ Of palak

$= 2{\text{kg}}600{\text{g}} = 2{\text{kg}} + \dfrac{{600}}{{1000}}{\text{kg}} = 2.600{\text{kg}}$ Of tomatoes

Total weight is $1.200 + 0.25 + 5.300 + 0.500 + 2.600 = 9.850$

Total weight of the purchase is $9.850{\text{kg}}$

The total weight of purchase of Alok in kilograms is $9.850{\text{kg}}$.

109. Arrange in ascending order: $0.011,1.001,0.101,$ and $0.110$

Ans: Since, all the decimals are already given in like fractions, 

$0.011,1.001,0.101,0.110$

Arranging them in ascending order, we get $0.011,0.101,0.110,1.001$

110. Add the following: $20.02$ and $2.002$

Ans: We have, $20.02$ and $2.002$

To add the above decimals, we must convert them into like decimals first. 

Writing $20.020$ and $2.002$ in a column

So,

$20.020 + 2.002 = 22.022$

Addition of $20.020$ and $2.002$ is $22.022$

111. It was estimated that because of people switching to Metro trains, about ${\mathbf{33000}}$ tonnes of CNG, ${\mathbf{3300}}$tonnes of diesel and ${\mathbf{21000}}$ tonnes of petrol was saved by the end of the year 2007. Find the fraction of:

(i) The quantity of diesel saved to the quantity of petrol saved.

Ans: Given,

By the end of the year 2007 Metro trains was saved

$33000$  tonnes of CNG

$3300$ tonnes of diesel

$21000$ tonnes of petrol

$\dfrac{{{\text{ The quantity of diesel saved }}}}{{{\text{ The quantity of petrol saved }}}} = \dfrac{{3300}}{{21000}}$

$= \dfrac{{3300 \div 300}}{{21000 \div 300}}$

$= \dfrac{{11}}{{70}}$

(ii) The quantity of diesel saved to the quantity of CNG saved.

Ans:  $\dfrac{{{\text{ The quantity of diesel saved }}}}{{{\text{ The quantity of CNG saved }}}} = \dfrac{{3300}}{{33000}}$

$= \dfrac{{3300 \div 3300}}{{33000 \div 3300}}$

$= \dfrac{1}{{10}}$

The quantity of diesel saved to quantity of petrol is $\dfrac{{11}}{{70}}$ 

The quantity of diesel saved to the quantity of CNG is $\dfrac{1}{{10}}$

112. The energy content of different foods are as follows

Which food provides the least energy and which provides the maximum?

Express the least energy as a fraction of the maximum energy

Ans: From the given table it is clear that Milk provides the least energy and Rice provides the maximum

Ratio of the least energy to the maximum energy

$\dfrac{{{\text{ The least energy }}}}{{{\text{ The maximum energy }}}} = \dfrac{3}{{5.3}} = \dfrac{{3 \times 10}}{{5.3 \times 10}} = \dfrac{{30}}{{53}}$

The least energy as a fraction of maximum energy is $\dfrac{{30}}{{53}}$.

113. A cup is $\dfrac{1}{3}$ full of milk. What part of the cup is still to be filled by milk to make it full?

Ans: Total fill required of a cup of milk is 1

Given that Cup is $\dfrac{1}{3}$ full of milk

The remaining part of the cup which is still to be filled by milk 

$= 1 - \dfrac{1}{3} = \dfrac{{3 - 1}}{3}$

$= \dfrac{2}{3}$

The part of cup is still to be filled by milk to make it full is $\dfrac{2}{3}$.

114. Mary bought $3\dfrac{1}{2}m$ of lace. She used $1\dfrac{3}{4}m$ of lace for her new dress. How much lace is left with her?

Ans: Mary bought $3\dfrac{1}{2}{\text{m}}$ of lace

She used $1\dfrac{3}{4}{\text{m}}$ of lace for her new dress

Left lace $=$ bought $3\dfrac{1}{2}{\text{m}}$ of lace $ - $ used $1\dfrac{3}{4}{\text{m}}$ of lace

Rewrite the fraction in same denominator

$= \dfrac{{7 \times 2}}{{2 \times 2}}{\text{m}} - \dfrac{7}{4}{\text{m}} = \dfrac{{14m - 7m}}{4}$

$= \dfrac{7}{4}m = 1\dfrac{3}{4}m$ of lace

The lace left with her is $\dfrac{7}{4}m$.

115. When Sunita weighed herself on Monday, she found that she had gained $1\dfrac{1}{4}kg$. Earlier her weight was $46\dfrac{3}{8}kg.$ What was her weight on Monday?

Ans: Sunita had gained $= 1\dfrac{1}{4}{\text{g}} = \dfrac{5}{4}{\text{kg}}$

Earlier her weight was $46\dfrac{3}{8}{\text{kg}} = \dfrac{{371}}{8}{\text{kg}}$

Her total weight on Monday

$= \dfrac{{371}}{8}{\text{kg}} + \dfrac{5}{4}{\text{kg}}$

$= \dfrac{{371}}{8}{\text{kg}} + \dfrac{{5 \times 2}}{{4 \times 2}}{\text{kg}}$

$= \dfrac{{371}}{8}{\text{kg}} + \dfrac{{10}}{8}{\text{kg}}$

$= \dfrac{{(371 + 10)}}{8}{\text{kg}} = \dfrac{{381}}{8}{\text{kg}}$

$= 47\dfrac{5}{8}{\text{kg}}$

Her weight on Monday was $47\dfrac{5}{8}$

116. Sunil purchased $12\dfrac{1}{2}$ litres of juice on Monday and $14\dfrac{3}{4}$ litres of juice on Tuesday. How many litres of juice did he purchase together in two days?

Ans: Monday Sunil purchased $12\dfrac{1}{2}$ liters of juice $= \dfrac{{25}}{2}$ liters

Tuesday Sunil purchased $14\dfrac{3}{4}$ liters of juice $= \dfrac{{59}}{4}$ liters

Total quantity of juice Sunil purchased in two days $= \left( {\dfrac{{25}}{2} + \dfrac{{59}}{4}} \right)$ litres

$= \left( {\dfrac{{25 \times 2}}{{2 \times 2}} + \dfrac{{59}}{4}} \right)$ litres 

$= \left( {\dfrac{{50}}{4} + \dfrac{{59}}{4}} \right)$ litres

$= \left( {\dfrac{{50 + 59}}{4}} \right)$ litres 

$= \dfrac{{109}}{4}$ litres

$= 27\dfrac{1}{4}$ litres

Litres of juice he purchased in two days is $27\dfrac{1}{4}$

117. Nazima gave $2\dfrac{3}{4}$ litres out of the $5\dfrac{1}{2}$ litres of juice she purchased to her friends. How many litres of juice is left with her?

Ans: Total quantity of juice $= 5\dfrac{1}{2}$ litres $= \dfrac{{11}}{2}$ litres

Nazima gave to her friends $= 2\dfrac{3}{4}$ litres $= \dfrac{{11}}{4}$ litres

The required quantity of juice she is left with 

$= \left( {\dfrac{{11}}{2} - \dfrac{{11}}{4}} \right)$ litres 

$= \left( {\dfrac{{11 \times 2}}{{2 \times 2}} - \dfrac{{11}}{4}} \right)$ litres

$= \left( {\dfrac{{22 - 11}}{4}} \right)$ litres

 $= \dfrac{{11}}{4}$ litres

$= 2\dfrac{3}{4}$ litres

The litre of juice left with her is $2\dfrac{3}{4}$ litres

118. Roma gave a wooden board of length $150\dfrac{1}{4}{\text{cm}}$ to a carpenter for making a shelf. The Carpenter sawed off a piece of $40\dfrac{1}{5}{\text{cm}}$ from it. What is the length of the remaining piece?

Ans: Total length of wood $150\dfrac{1}{4}{\text{cm}} = \dfrac{{601}}{4}{\text{cm}}$

Wood used by carpenter $40\dfrac{1}{5}{\text{cm}} = \dfrac{{201}}{5}{\text{cm}}$

Remaining piece of wood length

$= \left( {\dfrac{{601}}{4} - \dfrac{{201}}{5}} \right){\text{cm}} = \left( {\dfrac{{601 \times 5}}{{4 \times 5}} - \dfrac{{201 \times 4}}{{5 \times 4}}} \right){\text{cm}}$

$= \left( {\dfrac{{3005}}{{20}} - \dfrac{{804}}{{20}}} \right){\text{cm}}$

$= \dfrac{{2201}}{{20}}{\text{cm}}$ or $110\dfrac{1}{{20}}{\text{cm}}$

The length of the remaining piece is $110\dfrac{1}{{20}}{\text{cm}}$

119. Nasir travelled $3\dfrac{1}{2}km$ in a bus and then walked $1\dfrac{1}{8}km$ to reach a town. How much did he travel to reach the town?

Ans: Nasir travel $3\dfrac{1}{2}{\text{km}}$ in a bus $= \dfrac{7}{2}{\text{km}}$

Walked $1\dfrac{1}{8}{\text{km}}$ to reach a town $= \dfrac{9}{8}{\text{km}}$

Total distance covered by Nasir

  $\left( {\dfrac{7}{2} + \dfrac{9}{8}} \right){\text{km}}$

   $= \dfrac{{(7 \times 8) + (9 \times 2)}}{{2 \times 8}}{\text{km}}$

   $= \dfrac{{56 + 18}}{{16}}{\text{km}}$ 

   $= \dfrac{{74}}{{16}}{\text{km}}$

   $= \dfrac{{74 \div 2}}{{16 \div 2}}{\text{km}}$

   $= \dfrac{{37}}{8}{\text{km}}$

   $= 4\dfrac{5}{8}{\text{km}}$ 

The distance he travelled to reach the town is $\dfrac{{37}}{8}{\text{km}}$ or $4\dfrac{5}{8}{\text{km}}$

120. The fish caught by Neetu was of weight $3\dfrac{3}{4}kg$ and the fish caught by Narendra was of weight $2\dfrac{1}{2}kg$. How much more did Neetu's fish weigh than that of Narendra

Ans: The weight of fish caught by Neetu $3\dfrac{3}{4}{\text{kg}} = \dfrac{{15}}{4}{\text{kg}}$

The weight of fish caught by Narendra $2\dfrac{1}{2}{\text{kg}} = \dfrac{5}{2}{\text{kg}}$

Neetus fish weigh more than that of Narendra by

  $\dfrac{{15}}{4}{\text{kg}} - \dfrac{5}{2}{\text{kg}} = \dfrac{{15}}{4}{\text{kg}} - \dfrac{{5 \times 2}}{{2 \times 2}}{\text{kg}}$

   $= \dfrac{{15}}{4}{\text{kg}} - \dfrac{{10}}{4}{\text{kg}}$ 

   $= \dfrac{{(15 - 10)}}{4}{\text{kg}}$

   $= \dfrac{5}{4}{\text{kg or }}1\dfrac{1}{4}{\text{kg}}$ 

Neetu fish weighed $\dfrac{5}{4}{\text{kg}}$ or $1\dfrac{1}{4}{\text{kg}}$ more than Narendra.

121. Neelam's father needs $1\dfrac{3}{4}m$ of cloth for the skirt of Neelam's new dress and $\dfrac{1}{2}{\text{m}}$ for the scarf. How much cloth must he buy in all?

Ans: Neelam's father needs $1\dfrac{3}{4}{\text{m}}\left( {\dfrac{7}{4}{\text{m}}} \right)$ of cloth for the skirt of Neelam's new dress  

$\dfrac{1}{2}{\text{m}}$ for the scarf.

Total cloths buy by her father

 $= \dfrac{7}{4}m + \dfrac{1}{2}m$

   $= \dfrac{7}{4}m + \dfrac{{1 \times 2}}{{2 \times 2}}m$

   $= \dfrac{7}{4}m + \dfrac{2}{4}m$ 

$= \dfrac{{(7 + 2)}}{4}m$

$= \dfrac{9}{4}m$ or $2\dfrac{1}{3}m$

The total cloth Neelam should buy is $\dfrac{9}{4}{\text{m}}$ or $2\dfrac{1}{3}{\text{m}}$

122. What is wrong in the following additions?

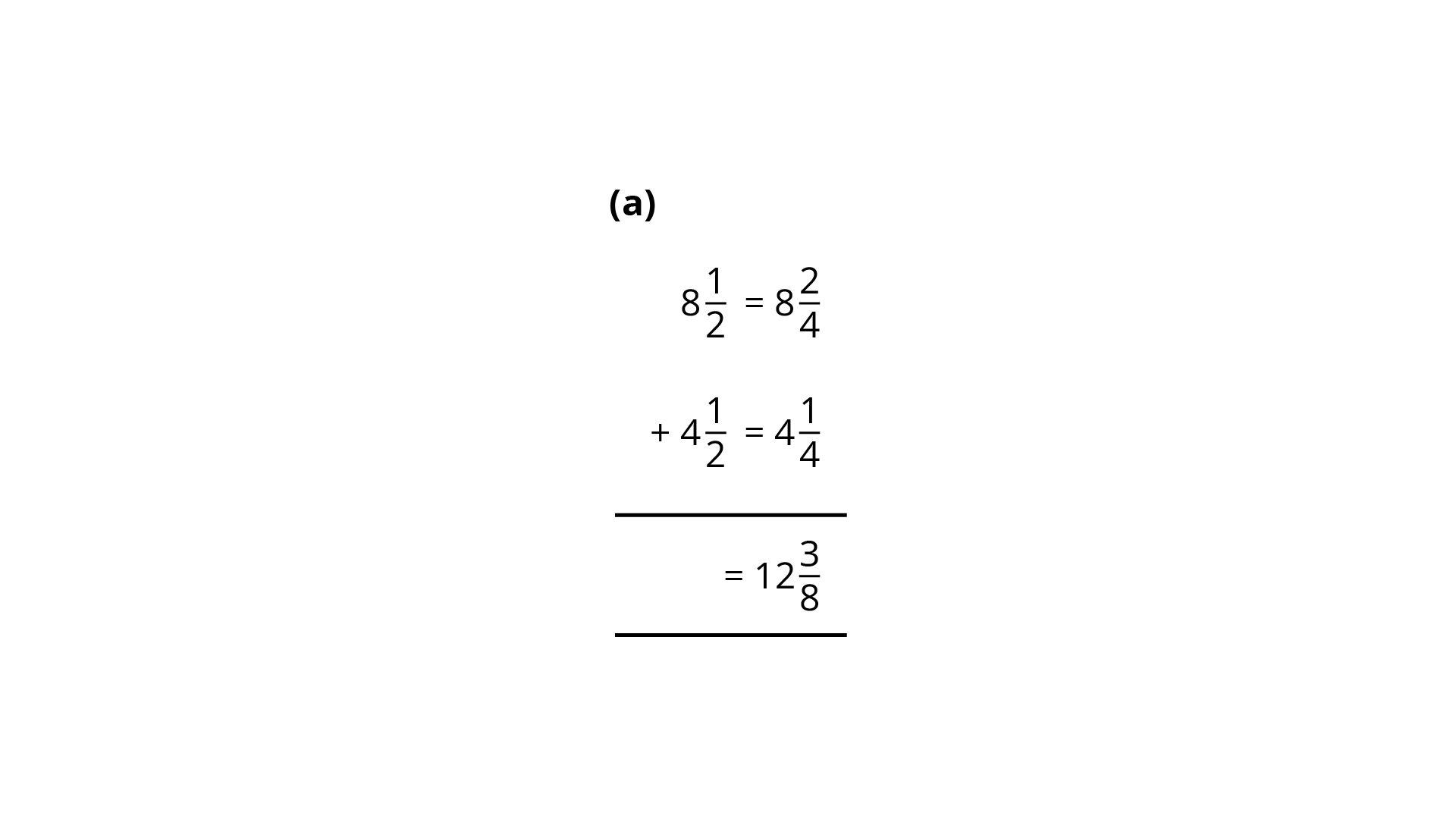
Ans: Equal denominators added.

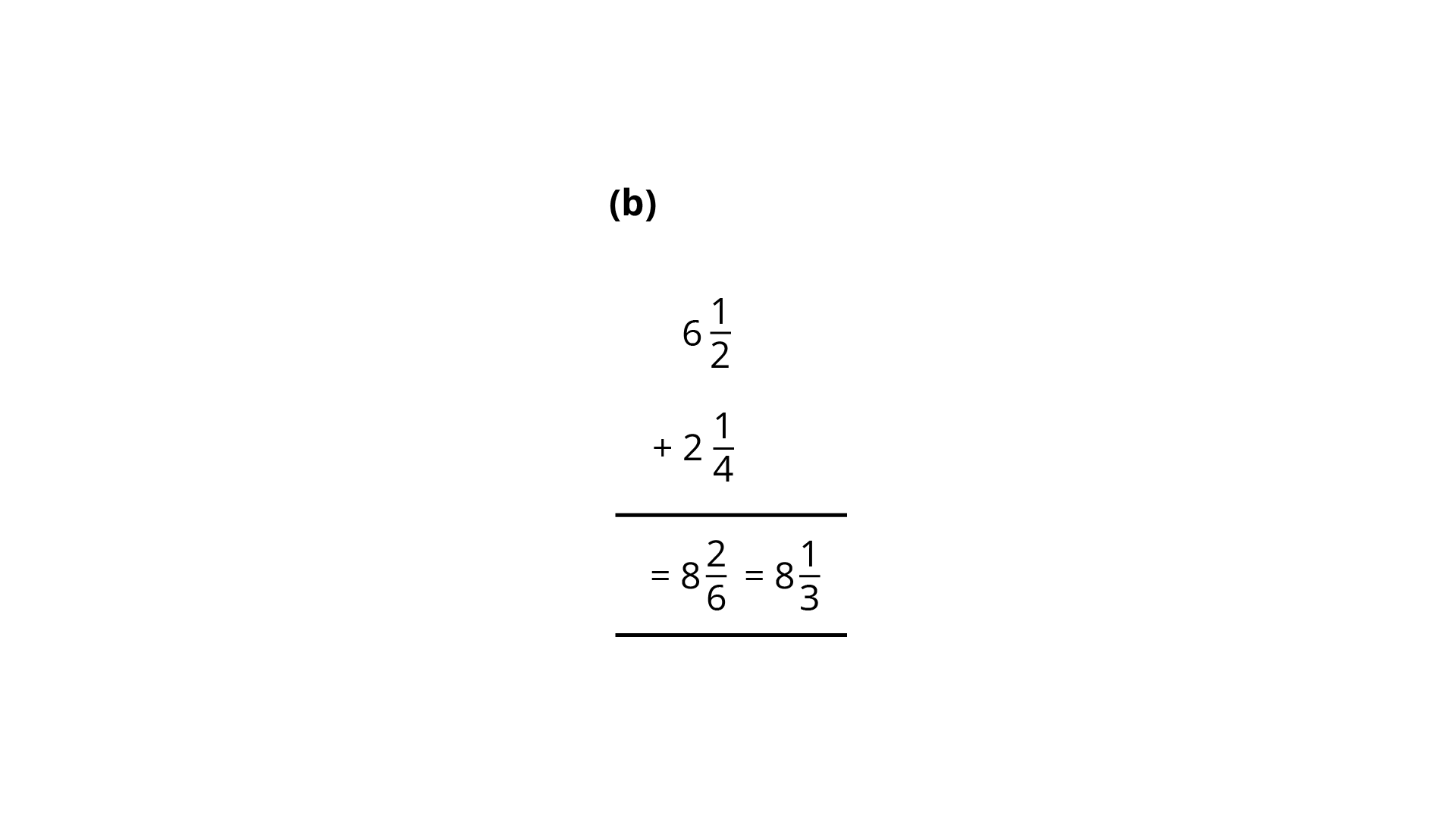
Ans: Numerator and denominator are added.

123. Which one is greater?

${\mathbf{1}}$ meters 40 centimeters $ + 60$ centimeters or $2.6$ meters.

Ans: Know that $1{\text{m}} = 100{\text{cm}}$

$1{\text{cm}} = \dfrac{1}{{100}}{\text{m}}$

Now,

$1$ meters $40$ centimeters $ + 60$ centimeters.

$= 1{\text{m}} + \dfrac{{40}}{{100}}{\text{m}} + \dfrac{{60}}{{100}}{\text{m}}$

$1{\text{m}} + 0.40{\text{m}} + 0.60{\text{m}} = 2.00{\text{m}}$

So, $2.6{\text{m}} > 2.0{\text{m}}$

124. Match the fractions of Column I with the shaded or marked portion of figures of Column II:

Column I	Column II
(i) $\dfrac{6}{4}$	(A)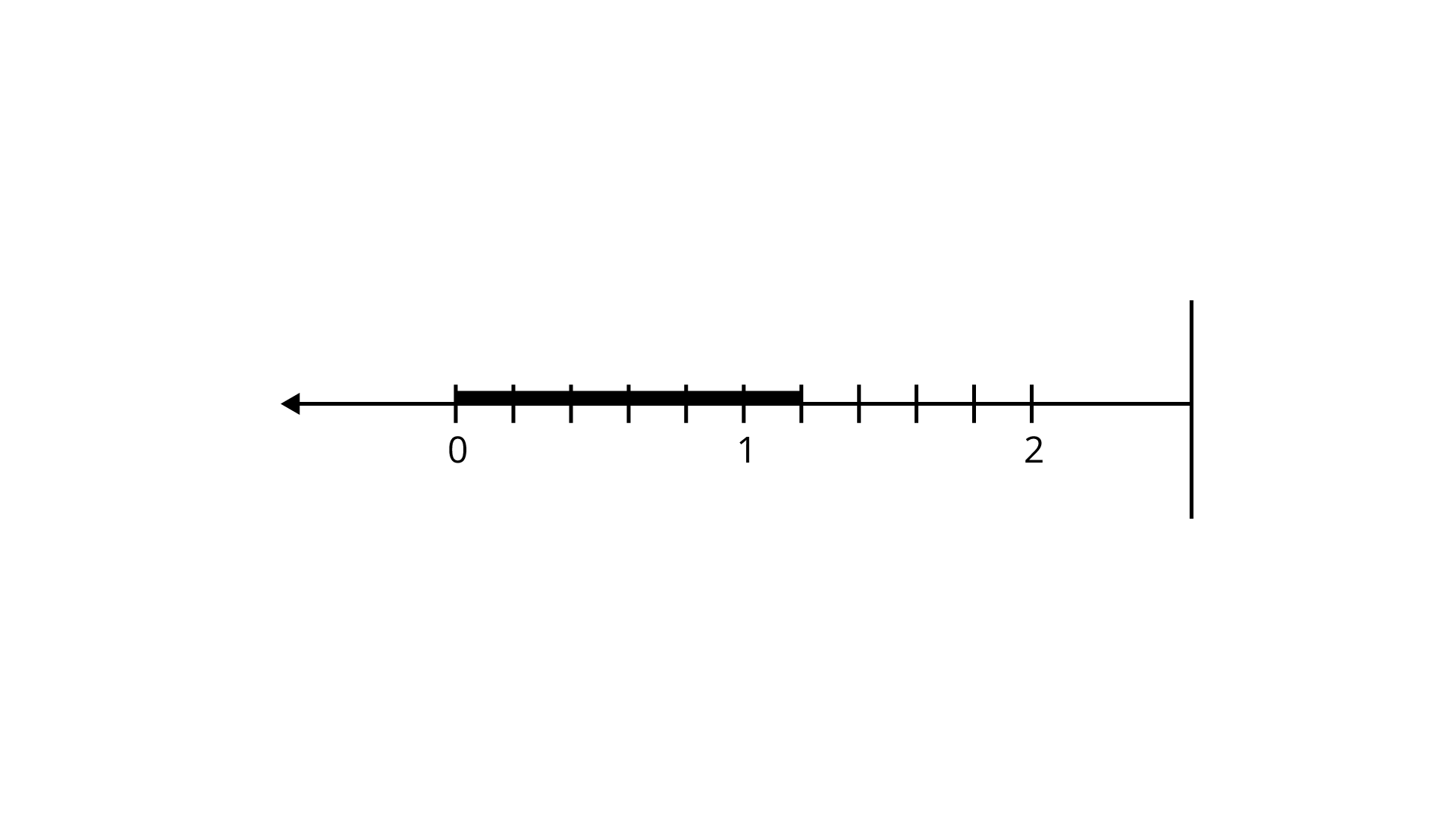
(ii) $\dfrac{6}{{10}}$	(B)
(iii) $\dfrac{6}{6}$	(C)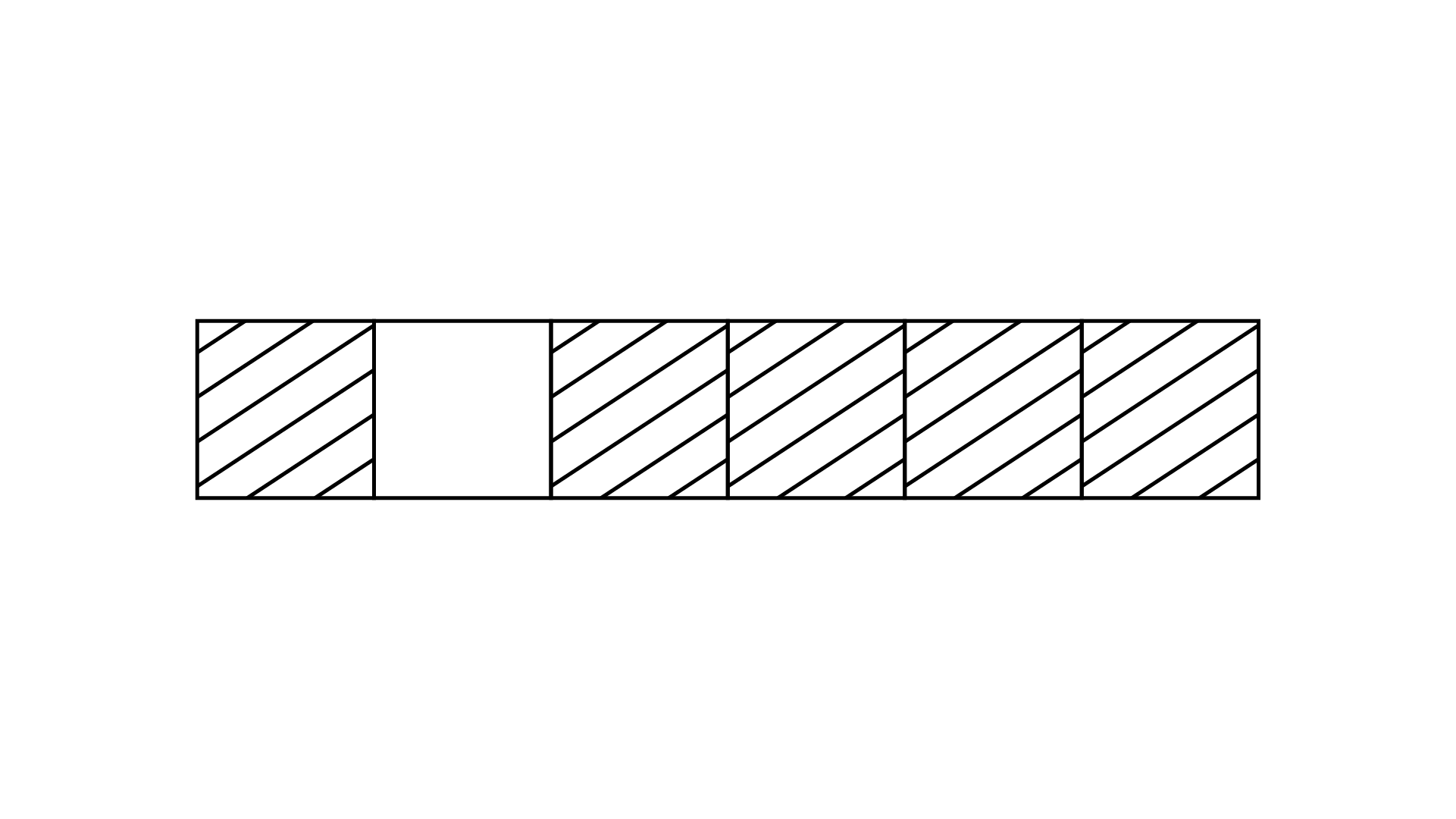
(iv) $\dfrac{6}{{16}}$	(D)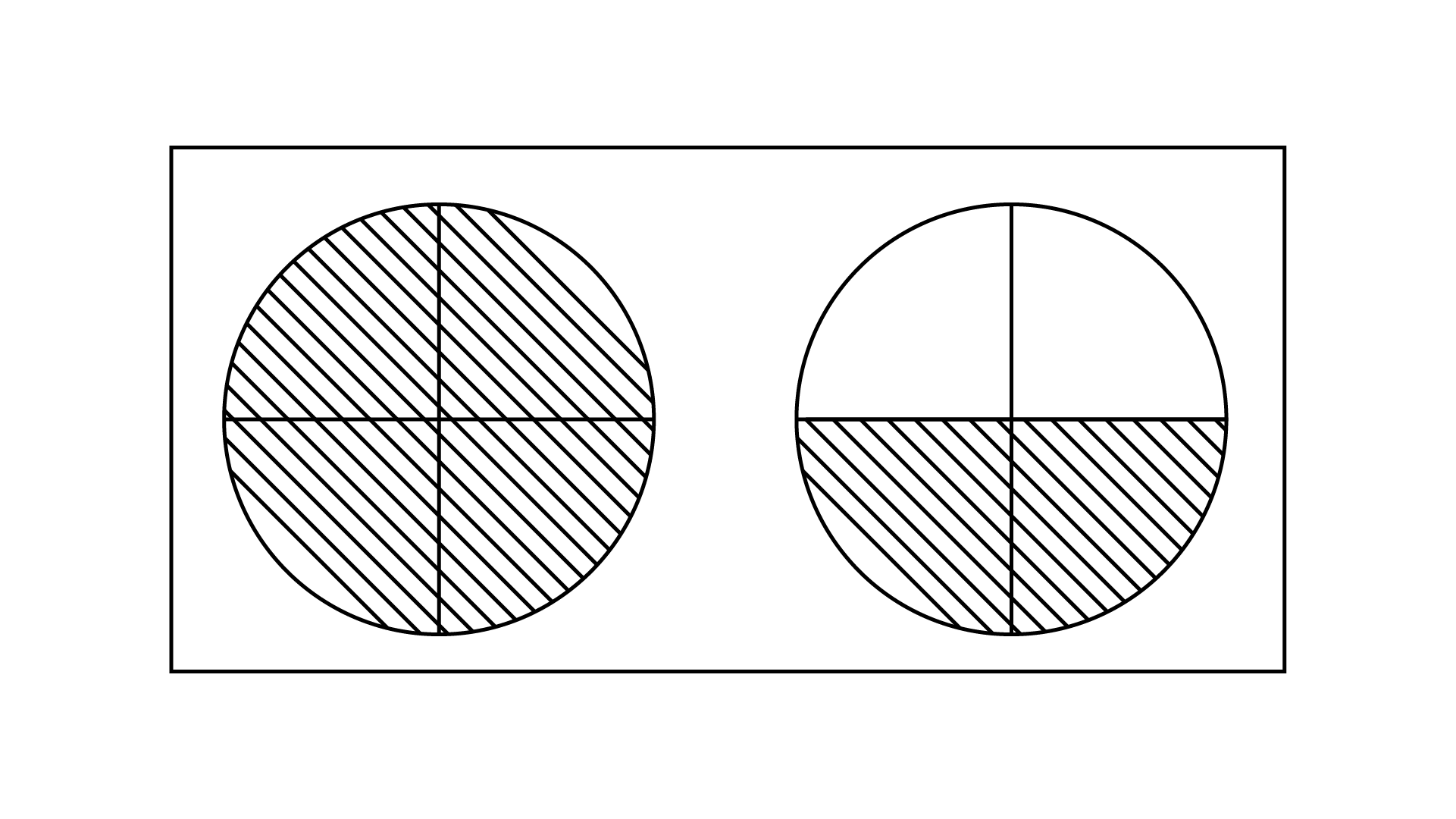
	(E)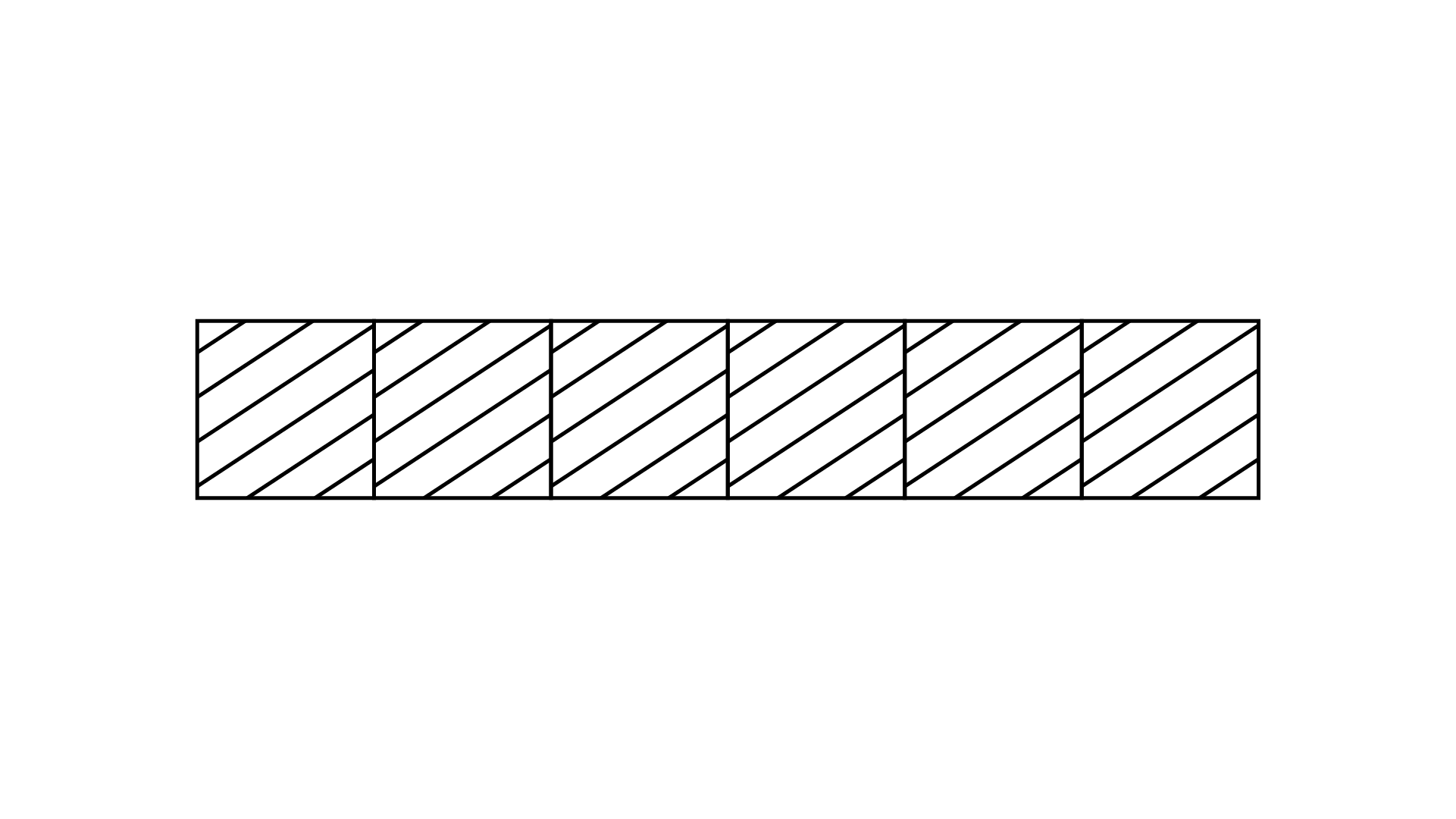

Ans:

Match the correct following

Column I	Column II
(i) $\dfrac{6}{4}$	(D)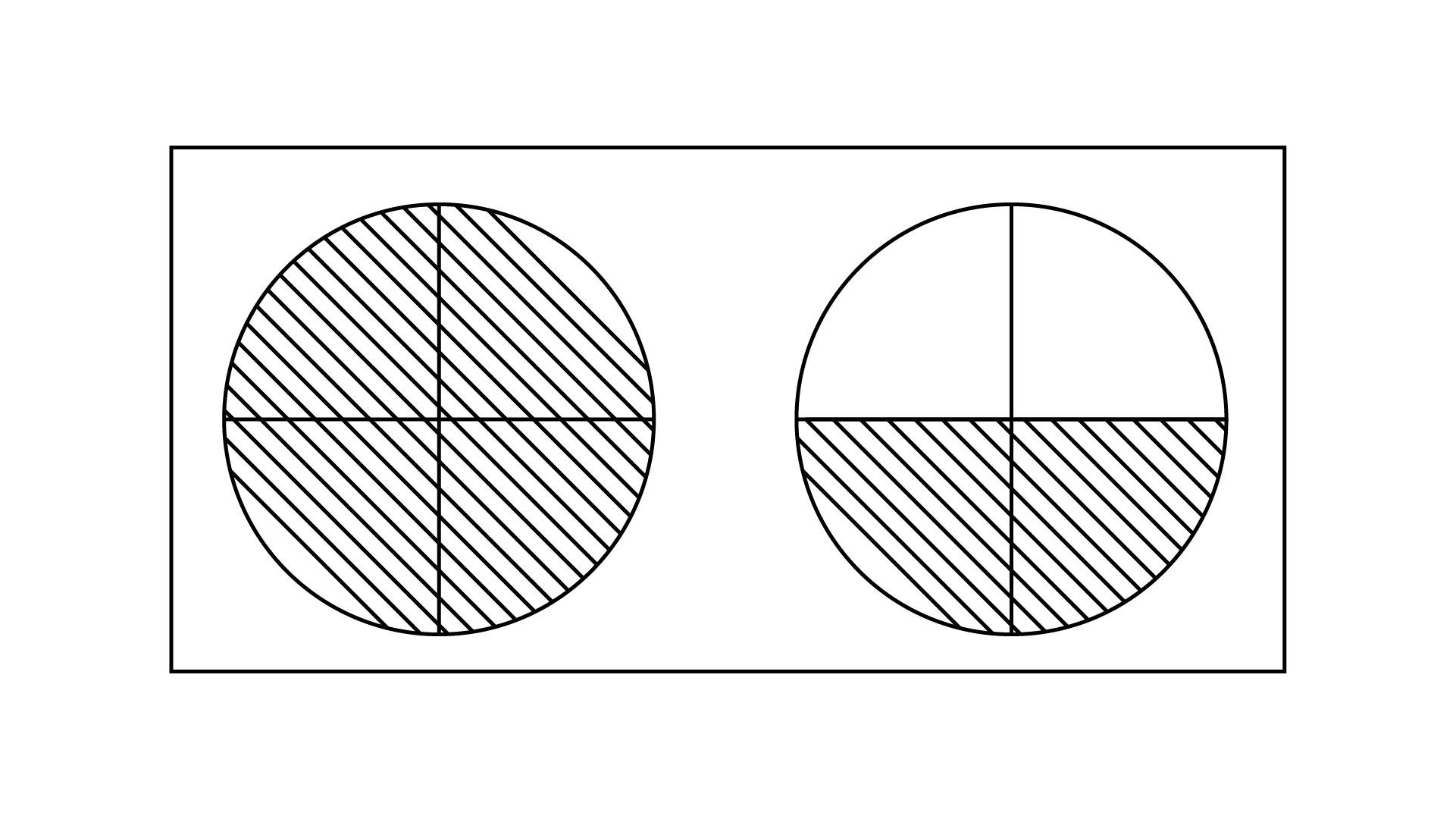
(ii) $\dfrac{6}{{10}}$	(A)
(iii) $\dfrac{6}{6}$	(E)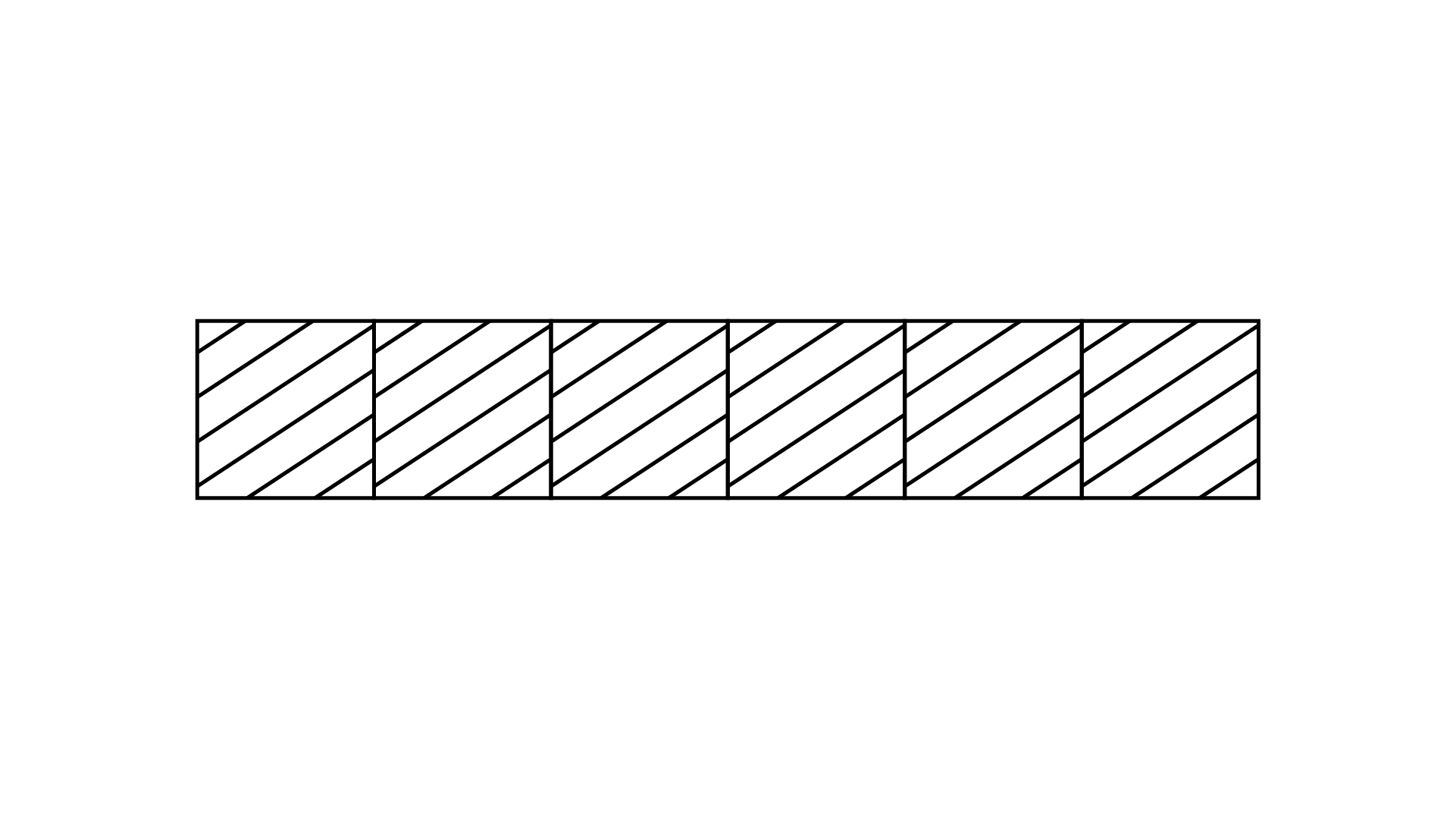
(iv) $\dfrac{6}{{16}}$	(B)

125. Find the fraction that represents the number of natural numbers to total numbers in the collection ${\mathbf{0}},{\mathbf{1}},{\mathbf{2}},{\mathbf{3}},{\mathbf{4}},{\mathbf{5}}$. What fraction will it be for whole numbers?

Ans: From the of collection $0,1,2,3,4,5 \to 1,2,3,4,5$ is natural numbers

The fraction that represents the number of natural numbers to the total numbers $= \dfrac{5}{6}$ 

The whole numbers are $0,1,2,3,4$and $5$.

The fraction that represents the number of whole numbers to the total numbers $= \dfrac{6}{6}$

126. Write the fraction representing the total number of natural numbers in the collection of numbers $- 3, - 2, - 1,0,1,2,3.$  What fraction will it be for whole numbers? What fraction will it be for integers?

Ans: Total collection of numbers $- 3, - 2, - 1, 0, 1, 2, 3$ and out of these $1, 2$ and $3$ is natural number and $0, 1, 2$ and $3$ are whole number and $- 3, - 2, - 1,0,1,2,3$ are integers.

127. Write a pair of fractions whose sum is $\dfrac{7}{{11}}$ and difference is $\dfrac{2}{{11}}$

Ans: Let one fraction be $x$ . 

Another fraction be $\dfrac{7}{{11}} - x$ Now, according to question, 

$x - \left( {\dfrac{7}{{11}} - x} \right) = \dfrac{2}{{11}}$

$x - \dfrac{7}{{11}} + x = \dfrac{2}{{11}}$

$\dfrac{{11x}}{{11}} - \dfrac{7}{{11}} + \dfrac{{11x}}{{11}} = \dfrac{2}{{11}}$

$\dfrac{{11x - 7 + 11x}}{{11}} = \dfrac{2}{{11}}$

$22x - 7 = \dfrac{2}{{11}} \times 11$

$22x - 7 = 2$

$22x = 2 + 7 = 9$

$x = \dfrac{9}{{22}}$

Thus, the fraction is $\dfrac{9}{{22}}$ and another fraction is

$\dfrac{7}{{11}} - \dfrac{9}{{22}} = \dfrac{{7 \times 2}}{{11 \times 2}} - \dfrac{9}{{22}}$

$= \dfrac{{14 - 9}}{{22}}$

$= \dfrac{5}{{22}}$ 

Pair of fractions are $\dfrac{9}{{22}}$ and $\dfrac{5}{{22}}$.

128. What fraction of a straight angle is a right angle?

Ans: Since, we know that the measurement of a straight angle is ${180^\circ }$ and a right angle is ${90^\circ }$. The required fraction is $\dfrac{{{{90}^\circ }}}{{{{180}^\circ }}} = \dfrac{1}{2}$.

The fraction of straight angle is a right angle is $\dfrac{1}{2}$.

129. Put the right card in the right bag

Cards	Bags
(i) $\dfrac{3}{7}$ (ii) $\dfrac{4}{4}$ (iii) $\dfrac{9}{8}$ (iv) $\dfrac{8}{9}$ (v) $\dfrac{5}{6}$ (vi) $\dfrac{6}{{11}}$ (vii) $\dfrac{{18}}{{18}}$ (viii) $\dfrac{{19}}{{25}}$ (ix) $\dfrac{2}{3}$ (x) $\dfrac{{13}}{{17}}$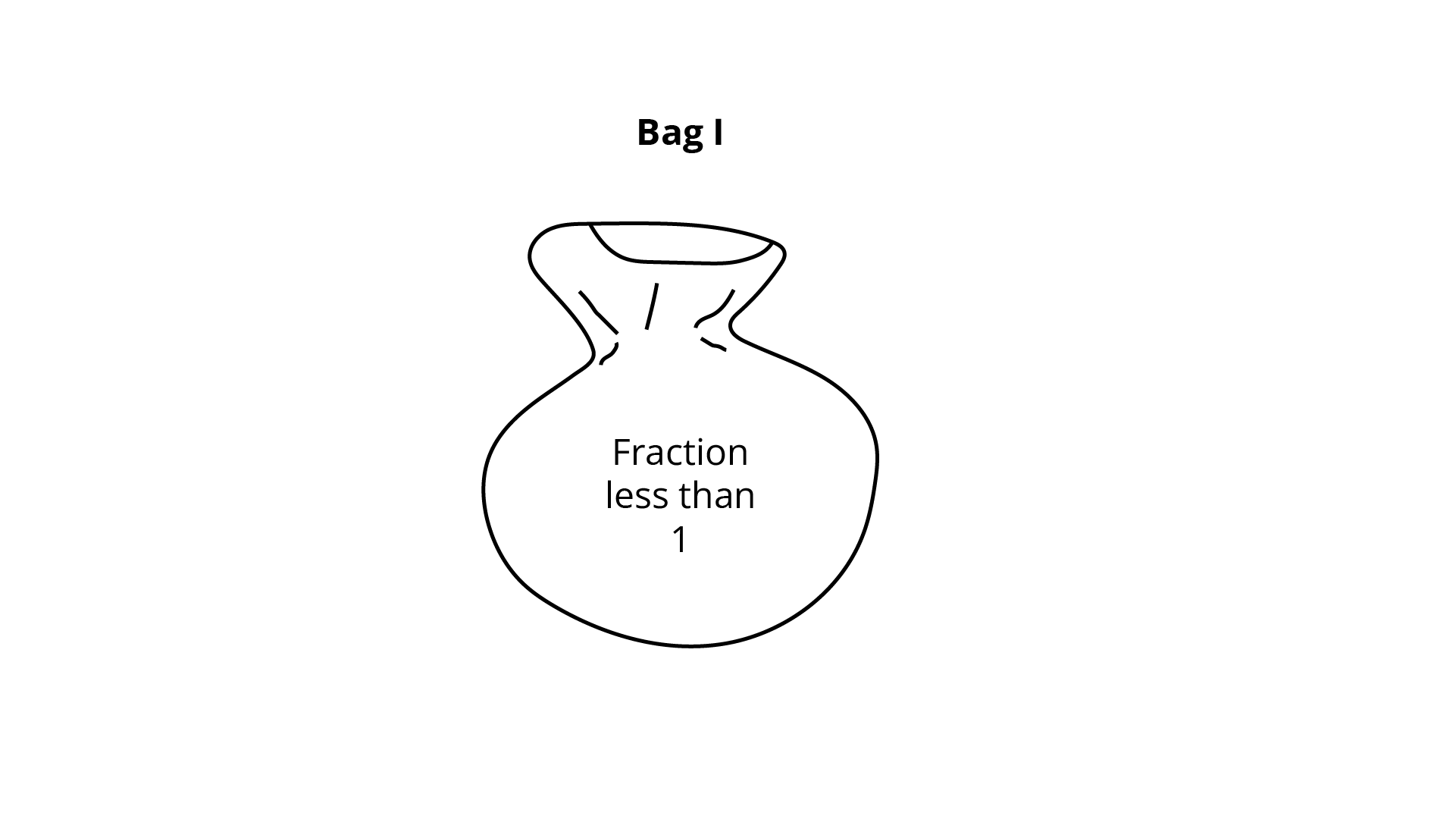

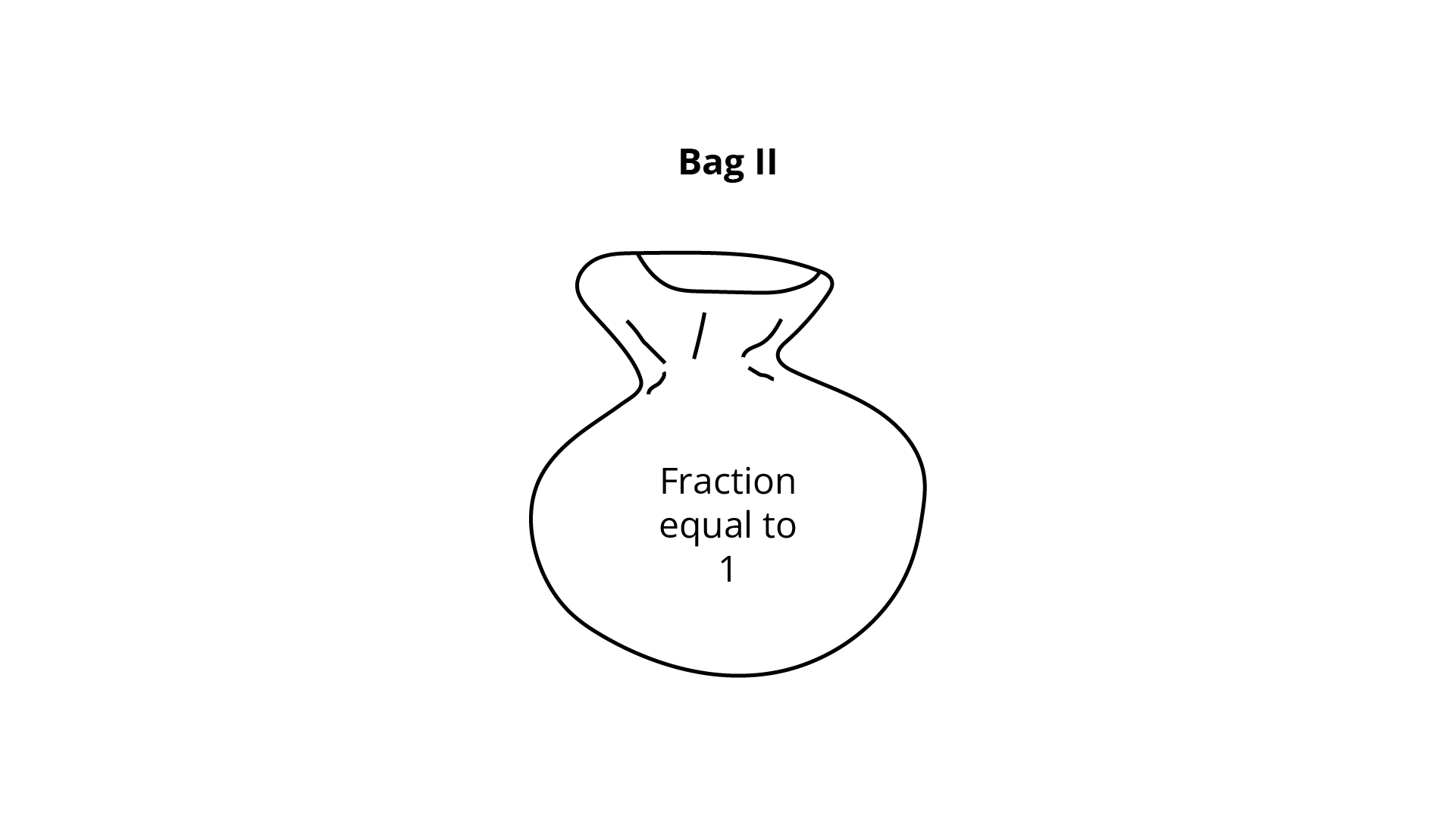
Ans: 

fractions whose numerators are less than the denominators are called proper fractions. (Numerator < denominator) and fraction is less than one.

fractions with the numerator either equal to or greater than the denominator are called improper fractions. (Numerator = denominator or, Numerator > denominator) and the fraction is greater and equal than one.

Now, cards in Bag -I

(i) $\dfrac{3}{7}$

(iv) $\dfrac{8}{9}$

(v) $\dfrac{5}{6}$

(vi) $\dfrac{6}{{11}}$

(viii) $\dfrac{{19}}{{25}}$

(ix) $\dfrac{2}{3}$and (x) $\dfrac{{13}}{{17}}$

Cards in Bag-II

(ii) $\dfrac{4}{4}$ and (vii) $\dfrac{{18}}{{18}}$

Cards in Bag -III

(iii) $\dfrac{9}{8}$

What do we Learn in NCERT Exemplar Solutions for Class 6 Mathematics Chapter 4 Fractions and Decimals?

NCERT Exemplar solutions for Class 6 Mathematics Chapter 4 Fractions and Decimals consists of a fraction which is a number that represents a fraction of a total. This complete may be a single item or a set of items. Fractions with 10, 100 denominators, etc. can be written in the correct order, using a decimal point, called decimal or decimal numbers. Let us now consider some of the concepts discussed in this Chapter.

• Multiplication and division of fractions and other concepts, such as types of fractions.

•  How to change different fractions to like fractions

•  How to compare more than two fractions.

•  How to turn a decimal into a fraction.

•  Converting a fraction into a decimal, adding, and subtracting decimal.

•  Decimal multiplication by 10, 100, 100, etc.

•  Decimal multiplication by a whole number, decimal multiplication by the decimal.

Key Topics for NCERT Exemplar Class 6th Mathematics Solutions Chapter 4: Components and Decimals

Introduction:

A fraction is a number that represents a fraction of a sum. A theme can be a single object or a set of objects. The parts are equal in quantity.

Proper Fraction:

In the right fraction, the number indicates the number of parts considered and the denominator indicates the number of parts in which the total is divided. Therefore, the denominator is always greater than the number in the correct fraction.

Improper Fraction:

Fractions where the number is greater than the denominator, are known as Improper fractions.

Mixed Fraction:

The component numbers that consist of both, part and total, are known as Mixed Fractions. The mixed part can be shown as the wrong part.

Equivalent Fraction:

Equivalent fractions represent the same part of the whole. To find the equal part of a given fraction, you can multiply or divide the number and the denominator of a given fraction by the same number.

Simplest Form of Fraction:

If there are no common features between a number and a denominator, the component should be the simplest.

Like and Unlike Fractions:

Like fractions with the same denominator while different fractions have different denominators. Fractions can be compared by turning them into parallel pieces and arranging them in an ascending or descending order.

Adding and Subtraction:

• Adding and subtracting similar fractions is done by adding their numbers.

• Adding and subtracting different fractions is done by translating them into the same fractions.

Decimals:

• One-tenth of a block is divided into 10 parts and 100 parts can be written as 0.1 and 0.01 by the decimal point, where the dot is the decimal point and reaches the tenth place respectively.

• All decimals can also be represented on a number line.

• All decimals can be written as fractions.

• When decimals are compared, every part is first compared, then tens and so on.

• Addition and subtraction of decimals can be done in the same way as whole numbers by adding/subtracting one hundredth from one hundred and one-tenth out of ten, one in one and so on.

• Decimals have many applications in our daily lives such as representing different units of measurement or representing parts of every business.