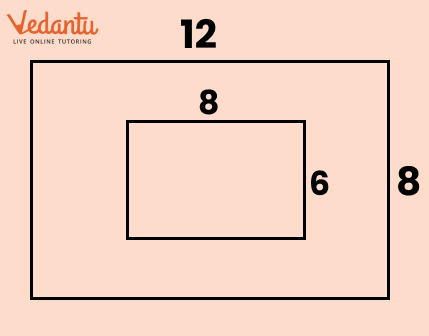
Perimeter And Area Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 6 Maths Chapter 6 Perimeter And Area Exercise 6.3 - 2025-26
1. What does Exercise 6.3 of Class 6 Maths cover?
Exercise 6.3 of Class 6 Maths focuses on the perimeter and area of triangles and composite figures, providing essential practice for students.
2. How can NCERT Solutions for Class 6 Maths Exercise 6.3 help in understanding perimeter and area?
The NCERT Solutions for Exercise 6.3 offer step-by-step explanations, making it easier for students to understand how to calculate the perimeter and area of triangles and composite figures.
3. What is the importance of learning about perimeter and area in Exercise 6.3?
Learning about perimeter and area in Exercise 6.3 is crucial as it forms the basis for solving real-life problems related to measurement and geometry.
4. Are there any shortcuts for solving perimeter and area problems in Exercise 6.3?
NCERT Solutions provides efficient methods and clear steps to solve perimeter and area problems without needing shortcuts, ensuring a thorough understanding.
5. Can I get NCERT Solutions for Class 6 Maths Exercise 6.3 in a free PDF format?
Yes, you can download the free PDF of NCERT Solutions for Class 6 Maths Exercise 6.3 from various educational platforms like Vedantu.
6. How are composite figures explained in NCERT Solutions for Class 6 Maths Exercise 6.3?
In the NCERT Solutions for Exercise 6.3, composite figures are explained by breaking them down into simpler shapes, making it easier to calculate their perimeter and area.
7. Why should I use NCERT Solutions for Class 6 Maths to solve Exercise 6.3?
Using NCERT Solutions for Class 6 Maths Exercise 6.3 ensures that students get accurate answers and understand the correct approach to solving problems on perimeter and area.
8. Can the NCERT Solutions for Exercise 6.3 help with other chapters in Class 6 Maths?
Yes, the methods learned in Exercise 6.3 for calculating perimeter and area can be applied to other chapters involving measurement and geometry.
9. Is it important to memorise formulas for perimeter and area in Exercise 6.3?
Yes, it is important to memorize the basic formulas for perimeter and area, as they are essential for solving the problems in Exercise 6.3 efficiently.
10. Where can I find NCERT Solutions for Class 6 Maths Exercise 6.3 in PDF format?
You can find free PDF versions of NCERT Solutions for Class 6 Maths Exercise 6.3 on platforms like Vedantu, which offer detailed solutions for perimeter and area problems.