
Class 11 Physics Chapter 9 Questions and Answers - Free PDF Download
Mechanical properties of fluids ncert solutions are key for understanding Physics in Class 11. This chapter includes concepts like pressure, buoyancy, and viscosity in fluids. If you need mechanical properties of fluids class 11 ncert solutions in easy steps, you're in the right place.
 Table of Content
Table of ContentVedantu’s expert teachers have solved every problem from Chapter 9, Mechanical Properties Of Fluids, in clear steps. Visit NCERT Solutions Class 11 Physics for guides on all chapters in the subject. These solutions follow the NCERT textbook and syllabus closely.
Our answers help you understand each topic better and solve doubts quickly. You can also get the mechanical properties of fluids ncert pdf for free. Download the NCERT Solutions PDF and start practicing for your Class 11 Physics exams now.
Introduction to Fluids
The liquids and gases together are termed as fluids, in other words, we can say that the substances which can flow are termed as fluids.
Fluid Pressure
Pressure p at any point is defined as the normal force per unit area. The SI unit of pressure is the Pascal and 1 Pascal = 1 N/m2
$P=\frac{dF_{1}}{dA}$
Relative Density and Specific Gravity
Relative density or specific gravity is the ratio of the density (mass of a unit volume) of a substance to the density of a given reference material. If the relative density is exactly 1 then the densities are equal i.e., equal volumes of the two substances have the same mass.
$RD=\frac{\rho_{substance} }{\rho_{reference} }$
Hydrostatic Pressure
Variation of Pressure
Pressure at two points in a horizontal plane or at same level when the fluid is at rest or moving with constant velocity is same.
Pressure at two points which are at a depth separation of h when fluid is at rest or moving with constant velocity is related by the expression
$p_{2}-p_{1}=\rho gh$, where ρ is the density of liquid.
© Pressure at two points in a horizontal plane when fluid container is having some constant horizontal acceleration are related by the expression
$p_{2}-p_{1}=\rho la$
Atmospheric Pressure, Gauge Pressure and Absolute Pressure
Atmospheric Pressure: It is the pressure exerted by earth’s atmosphere. Normal atmospheric pressure at sea level (an average value) is 1 atmosphere (atm) that is equal to 1.013 × 105 Pa.
Gauge Pressure: It is the difference between absolute pressure and atmospheric pressure. If the gauge pressure is above the atmospheric pressure, it is positive. If the gauge pressure is below the atmospheric pressure, it is negative.
Absolute Pressure: Absolute pressure is gauge pressure plus atmospheric pressure. An absolute pressure reading of zero can only be achieved in a perfect vacuum and only naturally occurs in outer space.
Barometer: It is a device used to measure atmospheric pressure while U–tube manometer or simply manometer is a device used to measure the gauge pressure.
Pascal’s Law
A change in the pressure applied to an enclosed fluid is transmitted equally to every portion of the fluid in all direction of the walls of the containing vessel.
Hydraulic lift: Hydraulic lift is a practical applications of Pascal’s law
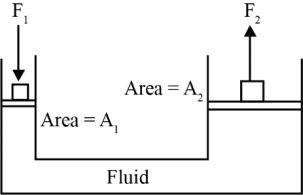
According to principle of hydraulics
$p_{2}=p_{1}\Rightarrow \frac{F_{1}}{A_{1}}=\frac{F_{2}}{A_{2}}\Rightarrow F_{2}=\frac{A_{2}}{A_{1}}F_{1}$
Buoyancy
Buoyancy is the tendency of an object to float in a fluid. All liquids and gases in the presence of gravity exert an upward force known as the buoyant force on any object immersed in them. Buoyancy results from the differences in pressure acting on opposite sides of an object immersed in a static fluid.
Buoyant Force
The buoyant force is the upward force exerted on an object wholly or partly immersed in a fluid. This upward force is also called Upthrust. Due to the buoyant force, a body submerged partially or fully in a fluid appears to lose its weight, i.e.. appears to be lighter.
Following factors affect buoyant force:
(i) the density of the fluid
(ii) the volume of the fluid displaced
(iii) the local acceleration due to gravity
Archimedes’ Principle
Archimedes’ principle states that:
“The upward buoyant force that is exerted on a body immersed in a fluid, whether partially or fully submerged, is equal to the weight of the fluid that the body displaces and acts in the upward direction at the center of mass of the displaced fluid”.
$F_{B}=V\sigma g$
Where, FB=Upthrust of Buoyant force, V = volume of liquid displaced
$\sigma$ = density of liquid.
Apparent decrease in weight of body = Upthrust – weight of liquid displaced by the body
Wapp = FB – W
Types of Fluid Flows
Steady Flow (Streamline Flow): When a body is partially or fully dipped into a fluid, the fluid exerts contact force on the body. The resultant of all these contact forces is called buoyant force (upthrust).
Line of flow: It is the path taken by a particle in flowing liquid. In case of a steady flow, it is called streamline. Two streamlines can never intersect each other.
Urbulent Flow:It is irregular flow in which particles move in zig zag way
Equation of Continuity: In a tube of varying cross section as shown in diagram:
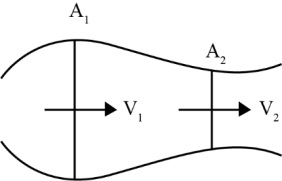
A1 v1 = A2 v2
This equation is known as continuity equation.
Where v1 is velocity of fluid at cross section A1 and v2 is velocity of fluid at cross section A2.
Mass flows rate = ρAv
(Where ρ is the density of the liquid.)
Bernoulli’s Theorem
In a streamline flow of an ideal fluid, the sum of pressure energy per unit volume, potential energy per unit volume and kinetic energy per unit volume is always constant at all cross section of the liquid.
$P+\rho gh+\frac{\rho v^{2}}{2}=Constant$
Viscosity
The property of a fluid by virtue of which it opposes the relative motion between its different layers is known as viscosity and the force that is into play is called the viscous force.
Newton’s Law of Viscosity: According to Newton, the frictional force F (or viscous force) between two layers
$F=\eta A\frac{dv}{dx}$
Where η is a constant depending upon the nature of the liquid and is called the coefficient of viscosity. Its value depends on the nature of the fluid.
The negative sign in the above equation shows that the direction of viscous force F is opposite to the direction of relative velocity of the layer.
S.I. unit of coefficient of viscosity is Pa-s or N-s/m2 or decapoise.
CGS unit of viscosity is poise. (1 decapoise = 10 poise).
Stoke’s Law
When a solid moves through a viscous medium, its motion is opposed by a viscous force depending on the velocity and shape and size of the body.
The viscous drag on a spherical body of radius r, moving with velocity v, in a viscous medium of viscosity η is given by
$F_{viscous}=6\pi r\eta v$
This relation is called Stoke’s law.
Importance of Stoke’s Law
(i) This law is used in the determination of electronic charge with the help of Millikan’s experiment.
(ii) This law accounts the formation of clouds.
(iii) This law accounts why the speed of raindrops is less than that of a body falling freely with a constant velocity from the height of clouds.
(iv) This law helps a man coming down with the help of a parachute.
Terminal Velocity
It is maximum constant velocity acquired by the body while falling freely in a viscous medium.
$v_{r}=\frac{2r^{2}\left ( \rho -\sigma \right )g}{9\eta }$
Where r is radius of body, ρ is density of body, $\sigma$ is density of liquid and η is the coefficient of viscosity.
Poiseuille’s Formula
This law states that the flow of liquid depends on variables such as length of tube (L) radius(r), pressure difference (P) and coefficient of viscosity η.
According to this law volume of liquid coming out of tube per second in given by
$V=\frac{\pi Pr^{4}}{8\eta L}$
Surface Tension
The surface tension of a liquid is defined as the force per unit length in the plane of the liquid surface at right angles to either side of an imaginary line drawn on that surface.
So, $S=\frac{F}{l}$where S = surface tension of liquid
The surface tension can be defined as the property of a liquid at rest by virtue of which its free surface behaves like a stretched membrane under tension and tries to occupy
as small area as possible.
Unit of surface tension in MKS system : N/m, J/m2
CGS system : Dyne/cm, erg/cm
Surface Energy
In order to increase the surface area, the work has to be done over the surface of the liquid. This work done is stored in the liquid surface as its potential energy. Hence the surface energy of a liquid can be defined as the excess potential energy per unit area of the liquid surface.
W = SΔA, where ΔA = increase in surface area.
NOTE:
|
Excess Pressure
Excess pressure in a liquid drop or bubble in a liquid is $P=\frac{2S}{R}$ S is surface tension
Excess pressure in a soap bubble is $P=\frac{4S}{R}$
(Because it has two free surfaces)
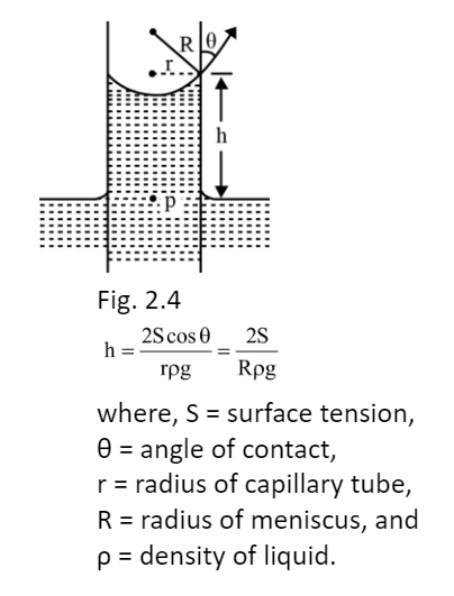
Capillary Tube and Capillarity Action
A very narrow glass tube with fine bore and open at both ends is known as capillary tube. When a capillary tube in dipped in a liquid, then liquid will rise or fall in the tube, this action is termed as capillarity.
Access NCERT Solutions for Class 11 Physics Chapter 9 – Mechanical Properties of Fluids
1. Explain why
(a) The blood pressure in humans is greater at the feet than at the brain
Ans: The pressure of a liquid with density\[\rho \], with the liquid column of \[h\] is given by the relation:
\[P=\text{ }\rho hg\]
here \[g\] is the acceleration due to the gravity
It can be inferred that pressure is directly proportional to height. In the case of humans, the circulatory system can be considered as the liquid (blood)-column.
The height of the column is the least at the head level and the maximum at the feet; hence, the pressure (blood pressure) in human vessels depends on this height. Thus, the blood pressure at the feet is more than what it is at the brain.
(b) Atmospheric pressure at the height of about \[6\,km\] decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than \[100\,km\].
Ans: The density of a fluid depends on how much it has been pressed by the amount of fluid over it. This means that the density of air is the maximum near the sea level.
The density of air increases with a decrease in the height from the sea surface. At the height of about 6 km, the total mass squeezes the layer of air over here to nearly half of the pressure value at sea level.
In the case of just small changes in altitude, the atmospheric pressure is proportional to density. However, when larger height scales are considered, the density itself depends on the height, and the pressure isn't linearly dependent anymore.
Moreover, the pressure increases faster than the linear dependence expected in the case of small changes in altitudes.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Ans: Mathematically, pressure is the perpendicular force per unit area.
So, only the force component that is perpendicular to the surface or along the area vector is used. The direction of this component and the direction of the area vector are the same.
Hence effectively, there is no direction involved anymore.
In other words, when force is applied to a liquid, the pressure in the liquid is transferred in all directions. Thus, the hydrostatic pressure does not have a fixed direction, and it is a scalar physical quantity.
2. Explain why
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
Ans: The angle between the surface inside the liquid and the tangent to the liquid surface at the point of contact is the angle of contact\[(\theta )\], as shown in the following figure
Let \[{{S}_{la}}\] be the interfacial tension at the liquid-air interface, \[{{S}_{sl}}\] be at the solid-liquid interface, and \[{{S}_{sa}}\] be at the solid-air interface. At all the points of contact, the surface forces between the three media must be in equilibrium, i.e.,
\[\cos \theta =\frac{{{S}_{sa}}-{{S}_{sl}}}{{{S}_{la}}}\]
In the case of a mercury drop on glass, \[{{S}_{sl}}>{{S}_{sa}}\], the angle of contact \[(\theta )\] is obtuse.
In the case of water on the glass,\[{{S}_{sl}}<{{S}_{la}}\], the angle of contact\[(\theta )\] is acute.
(b) Water on a clean glass surface tends to spread out, while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Ans: The Mercury molecules have a strong force of attraction between themselves and a weak force of attraction toward solids. Hence, the angle of contact tends to become obtuse, and the molecules come closer and tend to form a drop.
While in the case of water, the ratio of attraction between water molecules and the attraction between water molecules and the glass is lower. Hence the water molecules stay closer to glass molecules as well, keeping the glass surface wet.
(c) The surface tension of a liquid is independent of the area of the surface
Ans: Surface tension can be defined as the force acting per unit length at the interface between the liquid and any other material.
There is no dependency of this force on the area of the surface.
Hence, surface tension is independent of the area of the surface of the liquid.
(d) Water with detergent dissolved in it should have small angles of contact.
Ans: Detergent water has small angles of contact \[(\theta )\] because the detergent molecules are sticky; in other words, they are significantly attracted to the water molecules and the solid which is in contact with the detergent water.
Therefore, the molecules of water can get closer to the solid.
In other words, \[{{S}_{sl}}<{{S}_{la}}\] and the value of \[\cos \theta =\frac{{{S}_{sa}}-{{S}_{sl}}}{{{S}_{la}}}\] increases, leading to a decrease in the value of \[\theta \]making it acute or small.
(e) A drop of liquid under no external forces is always spherical in shape
Ans: Surface tension pulls the surface together as much as possible.
This means that in the absence of any other external force/pressure. The surface tension will try to shrink the area as much as possible.
Beyond a certain extent, the volume cannot be shrunk, and the shape with minimum surface area for the unchanged volume is a sphere.
Hence a droplet will tend to become spherical.
3. Fill in the blanks using the word(s) from the list appended with each statement:
(a) Surface tension of liquids generally ……with temperatures (increases / decreases)
Ans: decreases.
The surface tension of a liquid surface is inversely proportional to the motion of the liquid molecules. An increase in the temperature leads to an increase in the random motion of the molecules, and hence the surface tension drops.
(b) Viscosity of gases…… with temperature, whereas viscosity of liquids …… with temperature (increases / decreases)
Ans: increases; decreases
All fluids experience resistance to their motion when they are made to flow. This resistance is known as viscosity.
The motion of the gas molecules becomes very random, and giving them a direction gets difficult.
The viscosity of gases increases with the increasing random motion of the molecules. The molecules of the liquid are more restricted than and not as free as those of gas. Increasing the temperature of liquids increases the motion of the molecules, making them more mobile and improves their ability to flow.
Hence the viscosity decreases with an increase in temperature.
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to….., while for fluids it is proportional to ……(shear strain / rate of shear strain)
Ans: Shear strain; Rate of shear strain
For elastic solids, shearing force is proportional to the shear strain.
However, the shearing force is proportional to the rate of shear strain in the case of fluids.
(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows……. (conservation of mass / Bernoulli's principle)
Ans: Conservation of mass/Bernoulli’s principle
Bernoulli's principle works in the conservation of mass and energy, which includes the effects of the continuity equation. Hence, Conservation of mass and Bernoulli's Equation is the correct options
(e) For the model of a plane in a wind tunnel, turbulence occurs at a …... speed for turbulence for an actual plane (greater / smaller)
Ans: Greater
As provided in the question, there is a model of a plane in a wind tunnel. Following Bernoulli's Principle and referring to the relevant Reynolds number it can be seen that the turbulence occurs at a greater speed.
4. Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it
Ans: As per Bernoulli's principle, the fluid pressure reduces if the velocity is increased.
The paper falls under gravity, and to make it stay up and horizontal, we need to reduce the pressure on the top of it. For this reason. one should blow on the upper side of the paper.
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
Ans: According to the continuity equation, for a flowing fluid, the rate of volume of fluid crossing any cross-section is constant. This means that the velocity of the flowing fluid is high if the cross-section of the passage is reduced.
Covering the tap opening reduces the cross-section, and hence the water gushes out with a lot of speed.
(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
Ans: The liquid velocity at the needle is much higher than that inside the syringe. And higher velocity means much lower pressure.
Furthermore, the changes in the pressures at the different cross-sections are proportional to the pressures in the regions.
A human thumb cannot constantly provide constant pressure. So the significant change in the pressures is carried to the needle end as well. The pressure over here changes proportionally.
But as mentioned before, the changes in the pressure at the needle end are proportional to the pressure at the needle end, which is very small.
Hence the absolute change in the pressure at the needle end is also minimal. Thus it can be said that the consistency of the pressure is controlled by the cross-section of the needle.
(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel
Ans: As the fluid flows out of a small orifice, its velocity is significantly high according to the continuity equation.
This outgoing liquid generates momentum.
Going by the law of conservation of momentum, a counter momentum is generated on the vessel, making it experience a backward thrust.
(e) A spinning cricket ball in air does not follow a parabolic trajectory
Ans: A thrown spinning cricket ball has two motions – rotational and linear. The falling ball experiences viscosity in the upwards direction.
A rotating ball experiences viscosity due to the relative motion of the surface of the ball and the air in the vicinity. So at any instance, the face that is moving downwards faces an upwards viscosity force while the face going upwards faces a downwards viscosity force.
These viscous forces add up in such a way that the velocity of the air on one side of the ball is much higher than on their side, reducing the pressure on the side which has a higher velocity.
This pressure imbalance causes a force directed towards the low-pressure region. Hence the ball deviates from the expected parabolic trajectory.
5. A \[50\,kg\] girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter \[1.0\,cm\]. What is the pressure exerted by the heel on the horizontal floor?
Ans: As provided, the mass of the girl, \[m\text{ }=\text{ }50\text{ }kg\], the diameter of the heel \[d\text{ }=\text{ }1\text{ }cm\text{ }=\text{ }0.01\text{ }m\] , the radius of the heel, \[r=\frac{d}{2}=0.005m\]
Therefore, the area of the heel, \[A=\pi {{r}^{2}}\]
\[\Rightarrow A=\pi \times {{0.005}^{2}}\]
\[\Rightarrow A=7.85\times {{10}^{-5}}{{m}^{2}}\]
The force exerted by the heel on the floor is:
\[~F\text{ }=\text{ }mg\text{ }=\text{ }50\text{ }\times \text{ }9.8\text{ }=490\text{ }N\]
The pressure exerted on the floor by the heel:
\[P=\frac{F}{A}=\frac{490}{7.85\times {{10}^{-5}}}=6.24\times {{10}^{6}}N{{m}^{-2}}\]
Hence clearly, the pressure exerted by the heel on the horizontal floor is \[6.24\times {{10}^{6}}N{{m}^{-2}}\].
6. Torricelli's barometer used mercury. Pascal duplicated it using French wine of density \[984\,kg/{{m}^{3}}\]. Determine the height of the wine column for normal atmospheric pressure.
Ans: Provided that,
Density of mercury, \[{{\rho }_{1}}=13.6\times {{10}^{3}}kg/{{m}^{3}}\]
The height of the mercury column,
\[{{h}_{1}}=0.76m\]
Provided density of French wine,
\[{{\rho }_{2}}=0.984\times {{10}^{3}}kg/{{m}^{3}}\]
Let the height of the column of wine \[={{h}_{2}}\]
The acceleration due to gravity\[=g=9.8m{{s}^{-2}}\]
The pressure in both the columns (given by\[\rho hg\]) is equal at equal altitudes of the same liquid, which means:
\[{{\rho }_{1}}{{h}_{1}}{{g}_{1}}={{\rho }_{2}}{{h}_{2}}{{g}_{2}}\]
\[\Rightarrow {{h}_{2}}=\frac{{{\rho }_{1}}{{h}_{1}}g}{{{\rho }_{2}}g}=10.5m\]
Thus, the height of the column of wine at normal atmospheric pressure is \[10.5m\].
7. A vertical off-shore structure is built to withstand a maximum stress of \[{{10}^{9}}\,Pa\]. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly \[3\,km\], and ignore ocean currents
Ans: Yes
As provided, the maximum allowable stress for the structure, \[P={{10}^{9}}Pa\]
Depth of the ocean, \[d=3\times {{10}^{3}}m\]
The density of water, \[\rho ={{10}^{3}}kg/{{m}^{3}}\]
The acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
The pressure exerted because of water at depth,
\[P=\rho dg=3\times {{10}^{3}}\times {{10}^{3}}\times 9.8=2.94\times {{10}^{7}}Pa\]
Hence it has been calculated that the maximum allowable stress for the structure is significantly greater than the pressure of the water and hence can be used safely.
8. A hydraulic automobile lift is designed to lift cars with a maximum mass of \[3000\,kg\]. The area of cross-section of the piston carrying the load is \[425\,c{{m}^{2}}\]. What maximum pressure would the smaller piston have to bear?
Ans: As provided, the mass limit on the mass of a car that can be lifted, \[m\text{ }=\text{ }3000\text{ }kg\]
The area of cross-section of the load-carrying piston, \[A=0.0425{{m}^{2}}\]
The maximum force exerted by the load, \[F\text{ }=\text{ }mg\text{ }=\text{ }3000\text{ }\times \text{ }9.8\text{ }=\text{ }29400\text{ }N\]
The maximum pressure experienced by the piston that is carrying the load is, \[P=\frac{F}{A}=\frac{29400}{425\times {{10}^{-4}}}\text{= }6.917\text{ }\times {{10}^{-4}}\text{ }Pa\]
Since the pressure is transferred/transmitted equally in all directions in a liquid, the maximum pressure on the smaller piston would be\[\text{ }6.917\text{ }\times {{10}^{-4}}\text{ }Pa\].
9. A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with \[10.0\,cm\]of water in one arm and \[12.5\,cm\]of spirit in the other. What is the specific gravity of spirit?
Ans: The provided system of water, mercury, and methylated spirit can be shown as follows:
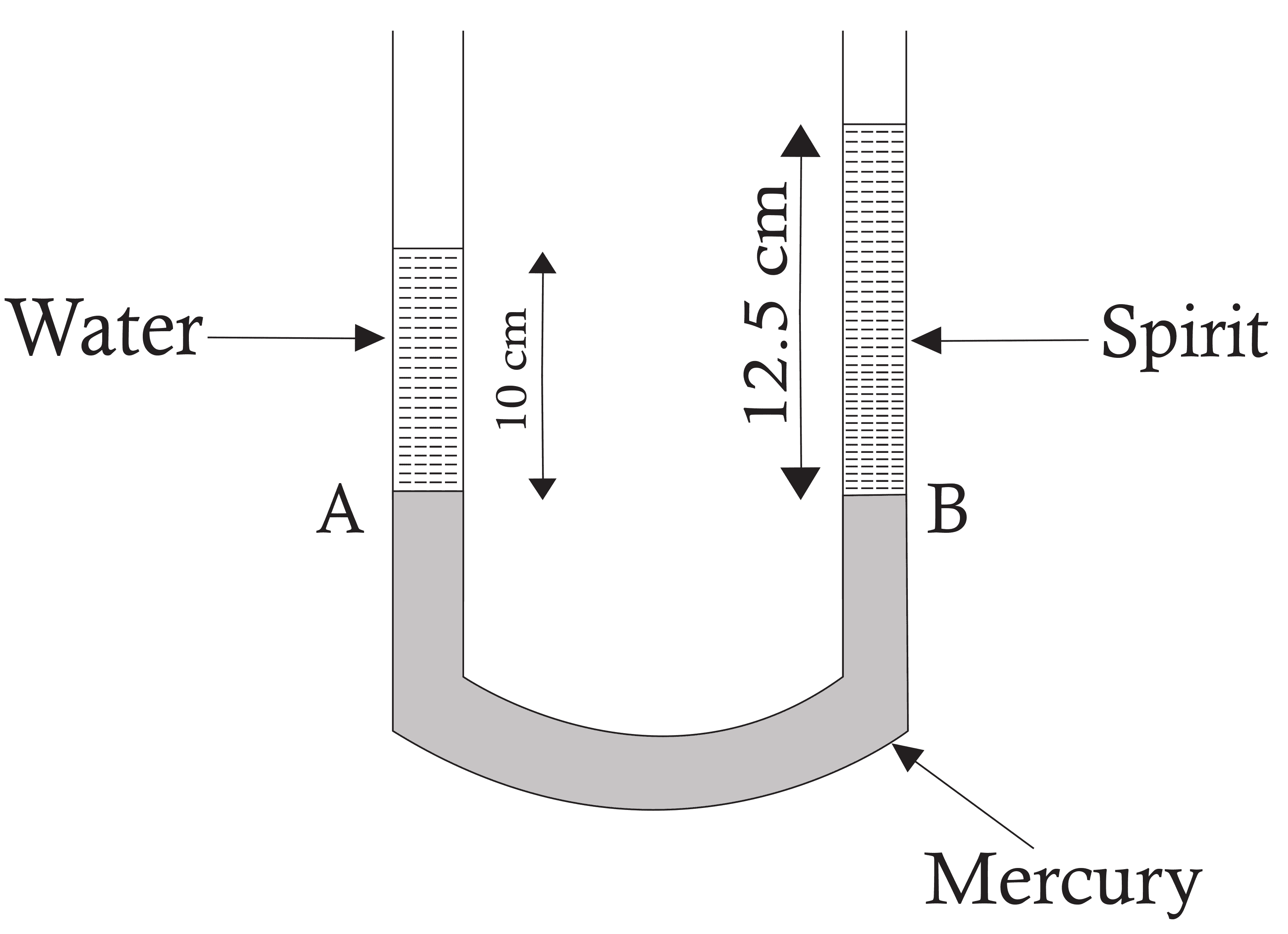
The height of the spirit column, \[{{h}_{1}}=12.5cm=0.125m\]
The height of the water column is: \[{{h}_{2}}=10cm=0.1m\]
\[{{P}_{0}}=\] Atmospheric pressure, \[{{\rho }_{1}}=\] Density of spirit, \[{{\rho }_{2}}=\]Density of water
Pressure at point A, \[{{P}_{0}}+{{\rho }_{1}}{{h}_{1}}g\]
Pressure at point B, \[{{P}_{0}}+{{\rho }_{2}}{{h}_{2}}g\]
The values of pressures at points A and B are equal
\[{{P}_{0}}+{{\rho }_{1}}{{h}_{1}}g={{P}_{0}}+{{\rho }_{2}}{{h}_{2}}g\]
\[\Rightarrow \frac{{{\rho }_{1}}}{{{\rho }_{2}}}=\frac{{{h}_{2}}}{{{h}_{1}}}=0.8\]
Hence, clearly, the specific gravity of spirit is \[0.8\].
10. In problem 10.9, if \[15.0\,cm\]of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = \[13.6\])
Ans: Provided that,
Height of the water column, \[{{h}_{1}}=10+15=25cm\]
Height of the spirit column, \[{{h}_{2}}=12.5+15=27.5cm\]
The density of water, \[{{\rho }_{1}}=1\,g\,c{{m}^{-3}}\] ; that of spirit, \[{{\rho }_{2}}=0.8g\,c{{m}^{-3}}\] and that of mercury is \[13.6\,g\,c{{m}^{-3}}\]
Now, let \[h\] be the difference between the levels of mercury in the two arms. The pressure exerted by the height \[h\] of the mercury column: \[=\rho hg=h\times 13.6\]
The difference between the pressures exerted by water and spirit: \[{{\rho }_{1}}{{h}_{1}}g-{{\rho }_{2}}{{h}_{2}}g=g\left( 25\times 1\text{ }\text{ }27.5\times 0.8 \right)=3g\]
Equating the pressures, we get:
\[13.6\text{ }hg\text{ }=\text{ }3g\text{ }\]
\[\Rightarrow h\text{ }=\text{ }0.220588\text{ }\approx \text{ }0.221\text{ }cm\]
The difference between the levels of mercury in the two arms is \[0.221\text{ }cm\].
11. Can Bernoulli's equation be used to describe the flow of water through a rapid in a river? Explain.
Ans: Bernoulli's equation cannot describe the turbulent flow of fluids like that in a rapid river.
Water flow in a river is chaotic. Bernoulli's equation suggests that an increase in a fluid's velocity occurs concurrently with a decrease in static pressure or simultaneously with a reduction in potential energy throughout the water flow.
This theory is only applicable to isentropic flows, wherein turbulence and other disturbances are ignored.
There are various versions of Bernoulli's equation with respect to various flow kinds. For instance, incompressible flows obey the simple form of Bernoulli's equation whereas compressible flows obey an advanced form of the equation.
Bernoulli's theory is in accordance with the principle of energy conservation. Clearly, at each point on the flowing water in the river, the sum of any and all sources of energy is equal to that as in a steady flow. The sum for kinetic energy, internal energy and potential energy should also maintain stability.
Thus, Bernoulli's equation cannot describe the flow of water through a rapid in a river.
12. Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli's equation? Explain.
Ans: Gauge pressure gives us the pressure difference in the fluid under consideration and some standard pressure. Using gauge pressure will only tell us about the pressure difference.
Bernoulli's principle assumes that the pressures under consideration are linearly proportional to the square of the velocity and the height of the fluid.
However, the difference in pressure cannot be directly shown to have this proportionality. Hence, we need to convert the gauge pressure to absolute pressure before plugging it into Bernoulli's equation.
So yes, it matters if we use gauge instead of absolute pressures in applying Bernoulli's equation.
13. Glycerin flows steadily through a horizontal tube of length \[1.5\,m\]and radius\[1.0\,cm\]. If the amount of glycerin collected per second at one end is\[4.0\times {{10}^{-3}}kg/s\], what is the pressure difference between the two ends of the tube? (Density of glycerin \[1.3\times {{10}^{3}}\,kg/{{m}^{3}}\] and viscosity of glycerin\[=0.83\,Pa\,s\]). (You may also like to check if the assumption of laminar flow in the tube is correct).
Ans: Provided that,
Length of the horizontal tube, \[l=1.5\text{ }m\]
The radius of the tube, \[r=1\,cm=\,0.01m\]
Thus, the diameter of the tube, \[\therefore d=0.02m\]
As given in the question, Glycerine is flowing at a rate of \[M=4.0\times {{10}^{-3}}kg\,{{s}^{-1}}\]
The density of Glycerine, \[\rho =1.3\times {{10}^{3}}kg\,{{m}^{-3}}\]
Viscosity of Glycerine\[\eta =0.83\text{ }Pa\text{ }s\]
The volume of Glycerine flowing per sec:
\[V=M/\rho =\frac{4.0\times {{10}^{-3}}}{1.3\times {{10}^{3}}}=3.08\times {{10}^{-6}}{{m}^{3}}{{s}^{-1}}\]
According to Poiseuille's Law, we have the expression for the rate of flow:
\[V=\frac{\pi P{{r}^{4}}}{8\eta l}\]
here, P is the pressure difference between the two ends of the tube
\[P=\frac{V8\eta l}{\pi {{r}^{4}}}=\text{ }9.8\text{ }\times \text{ }{{10}^{2}}Pa\]
Reynolds' number is given by the following expression:
\[\frac{4\rho V}{\pi d\eta }=\frac{4(1.3\times {{10}^{3}})(3.08\times {{10}^{-6}})}{\pi (0.02)0.83}=0.3\]
Reynolds' number is about \[0.3\]; therefore, the flow is laminar.
14. In a test experiment on a model aero plane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are \[70\,m/s\,\]and \[63\,m/s\] respectively. What is the lift on the wing if its area is\[2.5{{m}^{2}}\]? Take the density of air to be\[1.3\,kg{{m}^{-3}}\].
Ans: The given speed of wind on the wing's upper surface, and the speed of wind relative to the wing's lower surface \[{{v}_{2}}=63m\text{ }{{s}^{-1}}\].
The area of the wing, \[A=2.5{{m}^{2}}\]
The density of air, \[\rho =1.3kg/{{m}^{3}}\]
Now, according to Bernoulli's theorem, we have the relation: \[{{P}_{1}}+\frac{1}{2}\rho {{v}_{1}}^{2}={{P}_{2}}+\frac{1}{2}\rho {{v}_{2}}^{2}\]
In the current case, let \[{{P}_{2}}\] be the pressure on the lower side of the wing and \[{{P}_{1}}\] be the pressure on the upper side, and the v-s are the velocities mentioned initially.
The required lift is the force that comes from the pressure difference in the lower and the upper surface.
This can be obtained as:
\[Lift\,=({{P}_{1}}-{{P}_{2}})A=\left( \frac{1}{2}\rho {{v}_{2}}^{2}-\frac{1}{2}\rho {{v}_{1}}^{2} \right)A\]
\[Lift\,\,=\frac{1}{2}\rho ({{v}_{2}}^{2}-{{v}_{1}}^{2})A=\frac{1}{2}1.3({{70}^{2}}-{{63}^{2}})2.5=1.51\times {{10}^{3}}N\]
Hence, \[1.51\times {{10}^{3}}N\]is the lift on the wing of the airplane.
15. Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?
Ans: Considering the second figure:
Let us say A1 and A2 are the cross-section areas of the pipe and the narrow region, respectively and V1 and V2 are the speeds of the fluid in the normal region of the pipe and at the narrow region, respectively
According to the law of continuity: \[A1\times V1=A2\times V2\]
Hence it can be noted that the velocity of the liquid at the narrow region is higher than that in the normal region.
Now using Bernoulli's theorem, it can be said that the pressure is high in a region where the velocity is low. Hence the pressure at the normally thick (at A1) will be higher than that at A2.
Hence the column connected at this place will also have higher pressure at the point of contact. This is why the liquid column will also rise higher than the column connected at the narrow junction. Therefore, figure (b) is possible.
16. The cylindrical tube of a spray pump has a cross-section of \[8.0c{{m}^{2}}\] one end of which has \[40\] fine holes each of diameter\[1.0mm\]. If the liquid flow inside the tube is\[1.5m\,{{\min }^{-1}}\], what is the speed of ejection of the liquid through the holes?
Ans: Provided that,
Area of the cross-section of the spray pump \[{{A}_{1}}=8\times {{10}^{-4}}{{m}^{2}}\]
Number of holes, \[n\text{ }=\text{ }40\]
Diameter of each hole, \[d={{10}^{-3}}m\]
The radius of each hole, \[r=0.5\times {{10}^{-3}}m\]
Area of the cross-section of each hole, \[a=\pi {{r}^{2}}=\pi {{(0.5\times {{10}^{-3}})}^{2}}\]
The total area of 40 holes, \[A=n\,\,a=n\pi {{r}^{2}}=31.41\times {{10}^{-6}}{{m}^{2}}\]
The speed of flow of liquid inside the tube, \[{{v}_{1}}=1.5m/\min =0.025m/s\]
The liquid is ejected through the holes at the speed of \[{{v}_{2}}\]
According to the continuity equation, we have \[\,{{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}=0.633\text{ }m\text{/}s\]
Therefore, it has been calculated that the speed of ejection of the liquid through the holes is \[0.633\text{ }m/s.\]
17. A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the light slider supports a weight of \[1.5\times {{10}^{-2}}N\]. (Which includes the small weight of the slider). The length of the slider is\[30\,cm\]. What is the surface tension of the film?
Ans: The weight that the soap film supports, \[W=1.5\times \,{{10}^{-2}}N\]
Length of the slider, \[l=0.3m\]
A soap film has two free surfaces.
Therefore, the total length \[=2l=0.6m\]
Hence the surface tension is obtained as
\[S=\frac{Force}{2l}=\frac{1.5\times \,{{10}^{-2}}N}{0.6m}=2.5\times \,{{10}^{-2}}N/m\]
Therefore, the surface tension of the film is obtained as\[2.5\times \,{{10}^{-2}}N/m\].
18. Figure 10.24 (a) shows a thin liquid film supporting a small weight\[4.5\times {{10}^{-2}}N\]. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically
Ans: For case (a):
The length of the liquid film is supported by the weight \[l\text{ }=\text{ }40\text{ }cm\text{ }=\text{ }0.4\text{ }m\].
The weight supported by the film, \[W=4.5\times \,{{10}^{-2}}N\]
Every liquid film has two free surfaces. Hence the surface tension can be calculated as
\[S=\frac{Force}{2l}=\frac{4.5\times \,{{10}^{-2}}N}{2\times \,0.4m}=5.625\times \,{{10}^{-2}}N/m\]
Since the properties of the liquid are the same in all the cases., the surface tension in all three cases is equal. And the weight supported is also the same in all three cases, i.e., \[=5.625\times \,{{10}^{-2}}N/m\].
19. What is the pressure inside the drop of mercury of radius \[3.0mm\]at room temperature? Surface tension of mercury at that temperature \[(20{}^\circ \,C)\] is \[4.65\times {{10}^{-1}}N{{m}^{-1}}\]. The atmospheric pressure \[1.01\times {{10}^{5}}Pa\]. Also give the excess pressure inside the drop.
Ans: As provided, the radius of the mercury drop, \[r=3\times {{10}^{-3}}m\]
The surface tension of mercury, \[S=4.65\times \,{{10}^{-1}}N/m\]
The atmospheric pressure, \[{{P}_{0}}=1.01\times \,{{10}^{5}}Pa\]
Total pressure inside the mercury drop = Excess pressure inside mercury + Atmospheric pressure
Total pressure \[=\frac{2S}{r}+{{P}_{0}}=\frac{2\times 4.65\times \,{{10}^{-1}}}{3\times {{10}^{-3}}}+1.01\times \,{{10}^{5}}=1.013\times \,{{10}^{5}}Pa\]
Hence the excess pressure is obtained as \[=\frac{2S}{r}=310Pa\].
20. What is the excess pressure inside a bubble of soap solution of radius\[5.0mm\], given that the surface tension of soap solution at the temperature \[(20{}^\circ \,C)\] is \[4.65\times {{10}^{-1}}N{{m}^{-1}}\]. If an air bubble of the same dimension were formed at the depth of \[40.0\,cm\]inside a container containing the soap solution (of relative density\[1.20\]), what would be the pressure inside the bubble? (1 atmospheric pressure is \[1.01\times {{10}^{5}}Pa\].
Ans: As provided in the question, the excess pressure inside the soap bubble is \[20\text{ }Pa\];
The pressure inside the air bubble is \[=1.06\times \,{{10}^{5}}Pa\]
A soap bubble is of radius, \[r=5\times {{10}^{-3}}m\]
The surface tension of the soap solution, \[S=2.5\times \,{{10}^{-2}}N/m\]
Also, the relative density of the soap solution \[=\text{ }1.20~\]
Thus, the density of the soap solution, \[\rho =1.2\times {{\rho }_{air}}=1.2\times {{10}^{3}}kg/{{m}^{2}}\]
It is given that the air bubble is formed at a depth, \[h\text{ }=\text{ }40\text{ }cm\text{ }=\text{ }0.4\text{ }m\]
The radius of the air bubble, \[r=5\times {{10}^{-3}}m\]
Acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
Therefore, it can be noted that the excess pressure inside the soap bubble is given by:
\[P=\frac{4S}{r}=20Pa\]
The excess pressure inside the air bubble can be written as:
\[P=\frac{2S}{r}=10Pa\].
The total pressure inside the air bubble under consideration is the sum of the atmospheric pressure, the pressure due to the column of the liquid and the excess pressure:
\[{{P}_{total}}={{P}_{0}}+hg\rho +P=1.057\times \,{{10}^{5}}Pa\]
Hence, the pressure inside the air bubble is \[1.057\times \,{{10}^{5}}Pa\].
21. A tank with a square base of area \[1.0{{m}^{2}}\]is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area \[20.0\,c{{m}^{2}}\] . The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to a height of. compute the force necessary to keep the door closed.\[4.0\,m\]
Ans: Provided that,
Base area of the given tank,\[A=1.0{{m}^{2}}\]
Area of the hinged door, \[a=0.02{{m}^{2}}\]
The density of water, \[{{\rho }_{1}}=1\,{{0}^{3}}kg\,{{m}^{-3}}\]
The density of acid, \[{{\rho }_{2}}=1.7\times 1\,{{0}^{3}}kg\,{{m}^{-3}}\]
Height of the water column, \[{{h}_{1}}=4m\]
Height of the acid column, \[{{h}_{2}}=4m\]
Acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
Now, the pressure due to water is given as: \[{{P}_{1}}={{\rho }_{1}}{{h}_{1}}g=4\times 1\,{{0}^{3}}\times 9.8=3.92\times {{10}^{4}}Pa\]
The pressure due to acid is given as: \[{{P}_{2}}={{\rho }_{2}}{{h}_{2}}g=4\times 1.7\times 1\,{{0}^{3}}\times 9.8=6.662\times {{10}^{4}}Pa\]
The pressure difference between the two columns: \[\Delta P={{P}_{2}}-{{P}_{1}}=2.744\times 1\,{{0}^{4}}Pa\]
Thus, the force exerted on the door \[F=P\times a=54.88N\]
It can be concluded that the force necessary to keep the door closed is \[54.88N\].
22. A manometer reads the pressure of a gas in an enclosure as shown in figure When a pump removes some of the gas, the manometer reads as in figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
Ans: In the first case i.e., fig (a)
Atmospheric pressure, \[{{P}_{0}}=76cm\,Hg\]
The pressure (or height) difference between the levels of mercury in the two limbs denotes the gauge pressure.
Hence, the gauge pressure is 20 cm of Hg.
\[{{P}_{absolute}}\text{ }=\text{ }{{P}_{0}}\text{ }+\text{ }{{P}_{Gauge}}\text{ }=\text{ }76\text{ }+\text{ }20\text{ }=\text{ }96\text{ }cm\text{ }Hg\]
In the second figure (figure (b)), the difference between the levels of mercury in the two limbs \[=\text{ }18\text{ }cm\] Hence, gauge pressure is \[=\text{ }18\text{ }cm\] Hg.
Again, the \[{{P}_{absolute}}\text{ }=\text{ }{{P}_{0}}\text{ }+\text{ }{{P}_{Gauge}}\text{ }=\text{ }76\text{ + (-18) = 58 cm Hg}\]
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).
Ans: Now, \[13.6\,cm\] water is filled into the right limb of figure (b).
The relative density of mercury \[13.6\,cm\]
In other words, a column of \[13.6\,cm\] water is equivalent to \[1\,cm\] mercury.
Consider \[h\] being the difference in the mercury levels in the two limbs.
The pressure experienced in the right limb is given as:
\[{{P}_{right}}\text{ }=\text{ }{{P}_{0}}\text{ }+\text{ }1cm\,Hg\text{ }=\text{ }76\text{ + 1 = 77 cm Hg}\]
The level of the mercury column will go up in the left limb.
Hence, pressure in the left limb, \[{{P}_{L}}=58+h\]
Equating the pressures in both the limbs and simplifying for h, we get:
\[77=58+h\]
$\Rightarrow h=19cm$
It can be hence concluded that the mercury levels differ by \[19cm\].
23. Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill up to a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?
Ans: Yes,
Pressure in a liquid is given as:
\[P=\rho hg\].
The heights up to which the vessels are filled are equal, the densities are equal, and g is the same for both cases. Hence the pressures are also the same
Now, let the force that is experienced at the base of an area \[A\] be \[F=P\times A\]
Therefore, the forces in both cases are equal.
24. During blood transfusion the needle is inserted in a vein where the gauge pressure is \[2000Pa\]. At what height must the blood container be placed so that blood may just enter the vein? (Use the density of whole blood from Table 10.1).
Ans: The given gauge pressure, \[P\text{ }=\text{ }2000\text{ }Pa\]
The density of whole blood, \[\rho =1.06\times 1\,{{0}^{3}}kg\,{{m}^{-3}}\]
Let \[h\] be the height of the blood container
The pressure inside the blood container is \[P=\rho hg\]
Here \[g=9.8m/{{s}^{2}}\] is the acceleration due to gravity,
\[\Rightarrow h=\frac{P}{g\rho }=\frac{2000}{9.8\times 1.06\times 1\,{{0}^{3}}}=0.1925m\]
This means that the blood would enter the vein only if the container is kept at a height of \[0.1925m\]higher than the height at which the needle is inserted.
25. In deriving Bernoulli's equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.
(a) What is the largest average velocity of blood flow in an artery of diameter \[2.0\times {{10}^{-3}}m\] if the flow must remain laminar?
Ans: The diameter of the given artery, \[d=2\times {{10}^{-3}}m\]
The viscosity of blood, \[\eta =2.084\times {{10}^{-3}}Pa\,\,s\]
The density of blood, \[\rho =1.06\times {{10}^{3}}kg/{{m}^{2}}\]
Reynolds' number for laminar flow, \[{{N}_{R}}\text{ }=\text{ }2000\]
The maximum average velocity of blood flowing through the d-diameter orifice is as follows:
\[V=\frac{{{N}_{R}}\eta }{\rho d}=\frac{2000\times 2.084\times {{10}^{-3}}}{(1.06\times {{10}^{3}})(2\times {{10}^{-3}})}=1.966m/s\]
Therefore, the largest average velocity of blood is \[1.966m/s\].
(b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.
Ans: The dissipative forces become more prominent with an increase in the fluid velocity. As the velocity increases, the turbulence also increases. The turbulent nature of the flow causes dissipative loss in a fluid.
26.(a) What is the largest average velocity of blood flow in an artery of radius \[2.0\times {{10}^{-3}}m\]if the flow must remain laminar?
Ans: Provided that,
Radius of the artery, \[r=2\times {{10}^{-3}}m\].
Diameter of the artery, \[d=2(2\times {{10}^{-3}}m)\]
The viscosity of blood, \[\eta =2.084\times {{10}^{-3}}Pa\,\,s\]
The density of blood, \[\rho =1.06\times {{10}^{3}}kg/{{m}^{2}}\]
The Reynolds number of Laminar flow, \[{{N}_{R}}\text{ }=\text{ }2000\]
The largest value of average velocity can be given as:
\[V=\frac{{{N}_{R}}\eta }{\rho d}=\frac{2000\times 2.084\times {{10}^{-3}}}{(1.06\times {{10}^{3}})(4\times {{10}^{-3}})}=0.983m/s\]
Hence the largest average velocity of blood flow in an artery of the radius\[2\times {{10}^{-3}}m~\] is \[0.983m/s\].
(b) What is the corresponding flow rate? (Take viscosity of blood to be \[2.084\times {{10}^{-3}}Pa\,s\]).
Ans: The flow rate is written as the time derivative of the volume that flowed past a cross-section:
\[R=\pi {{r}^{2}}V{}_{Avg}=3.14\,{{(2\times {{10}^{-3}})}^{2}}\,(9.83)=1.235\times {{10}^{-5}}{{m}^{3}}/s\]
Hence the corresponding flow rate is \[1.235\times {{10}^{-5}}{{m}^{3}}/s\].
27. A plane is in level flight at a constant speed and each of its two wings has an area of \[25{{m}^{2}}\]. If the speed of the air is \[180\,km/h\]over the lower wing and \[234\,km/h\]over the upper wing surface, determine the plane's mass. (Take air density to be\[\,1kg/{{m}^{3}}\]).
Ans: As provided in the question, the area of the wings is \[A=2\times 25=50{{m}^{^{2}}}\]
Speed of air over the lower wing, \[{{v}_{1}}=180km/h=50m/s\]
Speed of air over the upper wing, \[{{v}_{2}}=234km/h=65m/s\]
The density of air, \[\rho =1\,kg/{{m}^{3}}\]
The pressure of air over the lower wing\[={{P}_{1}}\]
The pressure of air over the upper wing \[={{P}_{2}}\]
The upward force on the plane can be obtained using Bernoulli's equation as: \[{{P}_{1}}+\frac{1}{2}\rho {{v}_{1}}^{2}={{P}_{2}}+\frac{1}{2}\rho {{v}_{2}}^{2}\]
Thus, the upward force is obtained as:
\[Lift\,=({{P}_{1}}-{{P}_{2}})A=\left( \frac{1}{2}\rho {{v}_{2}}^{2}-\frac{1}{2}\rho {{v}_{1}}^{2} \right)A=43125N\]
The mass of the plane can be obtained as:
\[m=F/g=4400.5kg\]
Hence, the mass of the plane is nearly \[4400.5kg\].
28. In Millikan's oil drop experiment, what is the terminal speed of an uncharged drop of radius \[2.0\times {{10}^{-5}}\,m\]and density\[1.2\times {{10}^{3}}\,kg/{{m}^{3}}\]. Take the viscosity of air at the temperature of the experiment to be \[1.8\times {{10}^{-5}}Pa\,s\]. How much is the viscous force on the drop at that speed? Neglect buoyancy of the drop due to air.
Ans: The given terminal speed \[=5.8cm/s\,\], the viscous force \[\,\,=3.9\times {{10}^{-10}}N\]
The radius of the given uncharged drop, \[r=2.0\times {{10}^{-5}}m\]
The density of the uncharged drop, \[\rho =1.2\times 1\,{{0}^{3}}kg\,{{m}^{-3}}\]
It is known that the viscosity of air, \[\eta =1.8\times {{10}^{-5}}\,Pa\,s\]
In this case, the density of air (\[{{\rho }_{0}}\] ) can be taken as zero to neglect buoyancy of air. Acceleration due to gravity is \[g=9.8m/{{s}^{2}}\]
Terminal velocity (v) is given as:
\[v=\frac{2{{r}^{2}}(\rho -{{\rho }_{0}})g}{9\eta }=\frac{2{{(2.0\times {{10}^{-5}})}^{2}}(1.2\times 1\,{{0}^{3}}-0)9.8}{91.8\times {{10}^{-5}}}=5.8\times {{10}^{-2}}m/s\]
Hence, the terminal velocity of the drop is \[5.8cm/s\]
The viscous force experienced by the drop is given by:
\[F=6\pi \eta rv\]
\[\Rightarrow F=3.9\times {{10}^{-10}}N\]
Hence the viscous force is calculated to be \[3.9\times {{10}^{-10}}N\].
29. Mercury has an angle of contact equal to \[\mathbf{140}{}^\circ \]with soda lime glass. A narrow tube of radius \[\mathbf{1}.\mathbf{00}\text{ }\mathbf{mm}\] made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is \[4.65\times {{10}^{-1}}N{{m}^{-1}}\]. Density of mercury is \[13.6\times {{10}^{3}}\,kg/{{m}^{3}}\]
Ans: As provided in the question, the angle of contact between mercury and soda-lime glass, \[\theta =140{}^\circ \]
The radius of the narrow tube \[r=1.0\times {{10}^{-3}}m\]
The given surface tension of mercury, \[S=0465N/m\]
The density of mercury, \[\rho =13.6\times 1\,{{0}^{3}}kg\,{{m}^{-3}}\]
Dip in the height of the mercury \[=h\]
Acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
The surface tension can be written in terms of the angle of contact and the dip in height:
\[S=\frac{h\rho gr}{2\cos \theta }\]
\[\Rightarrow h=\frac{2\cos \theta }{S\rho gr}=-0.00534m=-5.34mm\]
Notice the negative sign; it shows the dropping level of mercury.
Hence, the mercury level drops by 5.34 mm.
30. Two narrow bores of diameters \[\mathbf{3}.\mathbf{0}\text{ }\mathbf{mm}\] and \[6.\mathbf{0}\text{ }\mathbf{mm}\] are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is \[7.31\times {{10}^{-2}}N{{m}^{-1}}\]. Let the angle of contact to be zero and density of water be \[1.0\times {{10}^{3}}\,kg/{{m}^{3}}\].
Ans: Provided that,
Diameter of the first bore, \[{{d}_{1}}=3.0\times {{10}^{-3}}m\]
Hence the radius of the first bore, \[{{r}_{1}}={{d}_{1}}/2=1.5\times {{10}^{-3}}m\]
Diameter of the second bore, \[{{d}_{2}}=6.0\times {{10}^{-3}}m\]
Hence, the radius of the second bore, \[{{r}_{2}}={{d}_{2}}/2=3.0\times {{10}^{-3}}m\]
The surface tension of water, \[S=7.3\times {{10}^{-2}}N/m\]
The angle of contact between the water surface and the bore surface, \[\theta =0{}^\circ \]
The density of water, \[\rho =1.0\times 1\,{{0}^{3}}kg\,{{m}^{-3}}\]
Acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
Let\[{{h}_{1}}\]and \[{{h}_{2}}\] be the heights to which water rises in the first and second tubes, respectively. These are given as:
\[{{h}_{1}}=\frac{2S\cos \theta }{\rho g{{r}_{1}}}\]and \[{{h}_{2}}=\frac{2S\cos \theta }{\rho g{{r}_{2}}}\]
The difference in the water levels in the two limbs of the tube can be calculated as:
\[\Delta h=\frac{2S\cos \theta }{\rho g{{r}_{1}}}-\frac{2S\cos \theta }{\rho g{{r}_{2}}}=\frac{2\times 7.3\times {{10}^{-2}}\times \cos 0}{1.0\times 1\,{{0}^{3}}\times 9.8}=4.97mm\]
Hence, the difference between the levels is obtained as \[=4.97mm\].
31.(a) It is known that density \[\mathbf{\rho }\] of air decreases with height \[y\] as \[{{\mathbf{\rho }}_{0}}{{e}^{y/{{y}_{0}}}}\]. Where \[{{\mathbf{\rho }}_{0}}=1.25kg\,{{m}^{-3}}\]the density at sea is level, and \[{{y}_{0}}\] is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of the atmosphere remains a constant (isothermal conditions). Also assume that the value of \[g\] remains constant.
Ans: The given volume of the balloon is, \[V\text{ }=\text{ }1425\text{ }{{m}^{3}}\]
Mass of the payload, \[m=400kg\]
And the acceleration due to gravity is, \[g=9.8m/{{s}^{2}}\]
\[{{y}_{0}}=8000m\]
The density of helium is\[{{\rho }_{He}}=0.18kg\,{{m}^{-3}}\] , and that of air at sea level is \[{{\rho }_{0}}=1.25kg\,{{m}^{-3}}\]
Let the density of the balloon be ρ and the height to which the balloon can rise be y.
The air density (\[\rho \]) of decreases with increasing height (\[y\]) as:
\[\rho /{{\rho }_{0}}={{e}^{-y/{{y}_{0}}}}\]
This relation is also called the law of atmospherics.
It can be inferred from the above law-equation that the rate of decrease of density with height is directly proportional to \[\rho \],
\[-\frac{d\rho }{dy}\propto \rho \]
\[\Rightarrow -\frac{d\rho }{dy}=k\rho \]
\[\Rightarrow -\frac{d\rho }{\rho }=kdy\]
Here, k is a proportionality constant.
We set the limits such that the height changes from \[0\] to \[y\], and the density varies from \[{{\rho }_{0}}\]to \[\rho \].
\[\int\limits_{{{\rho }_{0}}}^{\rho }{\frac{d\rho }{\rho }=}\int\limits_{0}^{y}{kdy}\]
Next, integrating the sides between these limits, we obtain:
\[\left[ \ln \,\rho \right]_{{{\rho }_{0}}}^{\rho }=-ky\]
\[\Rightarrow \rho /{{\rho }_{0}}={{e}^{-ky}}\]
Comparing the above equation with the law of atmospherics, we get
\[\Rightarrow k=\frac{1}{{{y}_{0}}}\]
In conclusion, we have been able to derive the expression for the law of atmospherics.
(b) A large He balloon of volume \[1425{{m}^{3}}\] is used to lift a payload of\[\mathbf{400}\text{ }\mathbf{kg}\]. Assume that the balloon maintains a constant radius as it rises. How high does it rise?
(Take \[{{y}_{0}}=8000m\]and \[{{\mathbf{\rho }}_{He}}=0.18kg\,{{m}^{-3}}\] )
Ans: The generic expression for mass density is:
\[\rho =\frac{M}{V}\]
In the current case, it becomes the total mass (including the payload and the helium) per unit volume of the balloon:
\[\rho =\frac{({{M}_{payload}}+{{M}_{He}})}{V}=\frac{m+V{{\rho }_{He}}}{V}\]
\[\Rightarrow \rho =0.46kg/{{m}^{3}}\]
Using the law of atmospherics, we can obtain the value of \[y\]:
\[\rho /{{\rho }_{0}}={{e}^{-y/{{y}_{0}}}}\]
\[\Rightarrow \ln \,\rho /{{\rho }_{0}}=-y/{{y}_{0}}\]
\[\Rightarrow y=-8000\times ln(0.46/1.25)=8000m=8km\]
Therefore, the balloon can rise to a height of 8 km.
NCERT Solutions For Class 11 Physics Chapter 9 Mechanical Properties of Fluids – Free PDF Download
Scoring good marks is imperative in today’s competitive world. It is true that hard work, coupled with smart work, will reward you with your desired grades. Therefore, our team of experts have curated NCERT solutions for class 11 physics chapter 9 to transform your goals into reality.
Chapter 9 class 11 physics NCERT solutions are an excellent tool for reference. It includes all the concepts and topics covered by the NCERT book on the chapter. Your every question is answered in these solutions. The NCERT solutions for class 11 physics chapter mechanical properties of fluids is available for download in a PDF format. You can easily download it for free on the Vedantu app.
Class 11 Physics Mechanical Properties of Fluids – Topics
Class 11 mechanical properties of fluids NCERT solutions discuss the common physical properties of different fluids. Furthermore, it clarifies that fluids refer to both liquids and gases, and not just liquids. It is these properties of fluids that distinguish them from solids.
Chapter 9 Class 11 physics NCERT solutions effectively cover the following topics:
Pressure
Streamline flow
Bernoulli’s Principle
Viscosity
Reynold’s Number
Surface tension
Benefits of NCERT Solution for Class 11 Physics Chapter 9 PDF
Most pupils study reference books alongside their NCERT books as an effort to gain further insight into the subjects. Referring to our Class 11 Physics NCERT solutions chapter 9 will help you in numerous ways, some of which are:
Simplify Learning
CBSE NCERT Solution for Class 11 Physics Chapter 9 was curated with the prime objective of helping you in your studies.
Your Go-to Guide
NCERT solutions for Class 11 physics chapter 9 PDF is created by a team of scholars. Our experts are the masters in their field - teachers, lecturers or PhD holders in the subject.
Problem-Solving Approach
A problem-solving approach to studying by NCERT solutions for Class 11 Physics Chapter 9 PDF is designed to maximise your understanding of the chapter.
Answers all Questions
Chapter 9 Class 11 Physics NCERT solutions answer every question and clarify all your doubts for a better learning experience. Getting your doubts cleared by our solutions make learning a fun activity.
Free Resource
Fluids NCERT solutions Class 11 is available in a PDF format for your convenience.
How does Temperature Affect the Surface Tension of a Liquid?
Class 11 Physics Mechanical Properties of Fluids NCERT solutions offer explanations to various physical properties of fluids. Mechanical Properties of Fluids Class 11 NCERT PDF describe fluids as any substance that continually deforms under external force. Fluids include liquids, gases and plasma.
Class 11 Physics NCERT solutions chapter 1 explains all aspects of surface tension. Surface tension in liquids arises due to the force of attraction between molecules that are on the surface and underneath. Simply put, the molecules on the surface of a liquid experience an inwards pull by the molecules on the interior. As a result, liquids have a tendency to assume a shape that covers the least surface area. The concept is further simplified in the Mechanical Properties of Fluids Class 11 NCERT PDF.
Fluid Mechanics Class 11 NCERT solutions effectively describe the effect of temperature on the surface tension of liquids. With the rise in temperature, the kinetic energy of the molecules increases. As a result, the intermolecular attraction decreases, therefore lowering the surface tension of the liquid.
Similarly, the surface tension of liquids rises with a fall in temperature. You can refer to our Class 11 Physics Ch 9 NCERT solutions for a more elaborate explanation.
NCERT Solution for Class 11 Physics Chapter 9 by Vedantu will help you with your studies today and your future endeavours as well.
Important Study Material Links for Class 11 Physics Chapter 10
S. No | Important Links for Chapter 9 Mechanical Properties of Fluids |
1 | Class 11 Mechanical Properties of Fluids Important Questions |
2 | |
3 | |
4 | Class 11 Mechanical Properties of Fluids NCERT Exemplar Solution |
NCERT Solutions for Class 11 Economics Other Chapter-Wise Links - Download the FREE PDF
S. No | NCERT Solutions Class 11 Physics Chapter-wise List |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | Chapter 6 - Systems of Particles and Rotational Motion Solutions |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 |
CBSE Class 11 Physics Study Materials
S.No. | Study Materials for Class 11 Physics |
|---|---|
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | |
8 |
FAQs on NCERT Solutions For Class 11 Physics Chapter 9 Mechanical Properties Of Fluids - 2025-26
1. What is the correct approach for solving numerical problems in the NCERT solutions for Class 11 Physics Chapter 9?
The correct approach, as per the CBSE 2025-26 pattern, involves a step-by-step method. First, identify the given quantities and the required unknown. Next, state the relevant formula (e.g., Bernoulli's principle, Stokes' law). Then, substitute the values with correct SI units and perform the calculation. Finally, present the result with the appropriate unit. This systematic approach ensures clarity and helps in securing full marks.
2. How do the NCERT Solutions for Chapter 9 align with the latest CBSE 2025-26 syllabus for Mechanical Properties of Fluids?
These NCERT Solutions are fully aligned with the latest CBSE 2025-26 syllabus. They cover every topic and sub-topic prescribed in the NCERT textbook, including pressure, buoyancy, viscosity, surface tension, and their applications. All solutions are structured to meet the curriculum's learning objectives and examination standards.
3. Why is it crucial to follow the step-by-step method shown in NCERT solutions rather than just writing the final answer?
Following the step-by-step method is crucial because it demonstrates your understanding of the underlying concept, not just the calculation. In CBSE evaluations, marks are often allocated for each correct step, including writing the formula, substituting values, and obtaining the final answer. This method also helps in identifying errors and builds a logical problem-solving habit essential for more complex physics problems.
4. Which key topics from Mechanical Properties of Fluids are covered in the Class 11 Physics Chapter 9 NCERT Solutions?
The NCERT Solutions for Chapter 9 provide comprehensive coverage of all key topics, including:
- Pressure and its variation with depth
- Pascal’s Law and its applications like hydraulic lifts
- Archimedes' Principle and buoyancy
- Streamline flow and the equation of continuity
- Bernoulli's principle and its applications
- Viscosity, Stokes’ Law, and terminal velocity
- Surface tension, surface energy, and capillarity
5. How do the solutions for conceptual questions, like those on Pascal's law, help in building a strong understanding of the principles?
The NCERT solutions for conceptual questions on topics like Pascal's law do more than provide an answer; they explain the 'why' behind the phenomenon. By breaking down the logic (e.g., how pressure is transmitted undiminished in a confined fluid), the solutions help you connect the theoretical principle to its practical applications, such as in hydraulic systems, fostering a deeper conceptual understanding beyond simple memorisation.
6. What is the typical structure for solving questions on Bernoulli's principle as per the NCERT pattern?
A typical NCERT-pattern answer for a Bernoulli's principle problem involves these steps:
- State the Bernoulli's equation: P + ½ρv² + ρgh = constant.
- Identify two points in the fluid flow for comparison.
- Write the equation relating the pressure, velocity, and height for these two points.
- Substitute the known values from the problem statement.
- Algebraically solve for the unknown variable, ensuring all units are consistent.
7. If my calculation process seems correct but the final answer doesn't match the NCERT solution, what should I check first?
If your final answer is incorrect despite a correct process, first check for unit conversions. Ensure all quantities are in their standard SI units (e.g., cm to m, g/cm³ to kg/m³). Next, verify the values of constants used, like g (9.8 m/s²) or the density of water. Finally, re-check your algebraic manipulations and rounding off, as minor calculation errors can lead to different results.
8. How are complex problems involving viscosity and terminal velocity broken down in the NCERT solutions?
In NCERT solutions, complex problems on viscosity and terminal velocity are simplified by clearly identifying all forces acting on the object (e.g., gravitational force, buoyant force, viscous drag). The solutions then guide you to apply the condition for terminal velocity, which is when the net force is zero. By setting up the force balance equation (e.g., 6πηrv = (4/3)πr³(ρ-σ)g), the problem becomes a straightforward algebraic calculation.
9. Are the NCERT Solutions for Class 11 Physics Chapter 9 sufficient to build a foundation for competitive exams like JEE or NEET?
Yes, these solutions are an excellent starting point. They help build a strong conceptual foundation by ensuring you master the NCERT textbook inside out, which is the base for competitive exams like JEE and NEET. While these exams require further advanced problem-solving skills, a thorough understanding of the methods and principles in the NCERT solutions is the indispensable first step.
10. Do the provided NCERT solutions cover all in-text and exercise questions from Chapter 9 completely?
Yes, the NCERT Solutions for Class 11 Physics Chapter 9 provide complete, step-by-step answers for every single question from the exercises and in-text examples in the textbook. Each part of a multi-part question is addressed thoroughly to ensure no aspect of the curriculum is missed.
11. How can using these NCERT solutions help identify and avoid common mistakes in problems related to fluid dynamics?
By studying the detailed steps in the NCERT solutions, you can identify common pitfalls. For example, students often forget to account for atmospheric pressure in problems involving absolute and gauge pressure, or mix up the radii and areas in the equation of continuity. The solutions highlight the correct application of these principles, helping you recognise and avoid such errors in your own work.
12. In the NCERT solutions, how is the principle of continuity applied in conjunction with Bernoulli's theorem to solve problems?
The NCERT solutions often demonstrate a two-step approach. First, the principle of continuity (A₁v₁ = A₂v₂) is used to find the fluid velocity at a different point in a pipe of varying cross-section. Second, this calculated velocity is then substituted into the Bernoulli's equation to determine the pressure difference between those two points. This integrated method is key to solving many practical problems involving fluid flow.
























