NCERT Exemplar for Class 11 Physics Chapter 10 - Mechanical Properties of Fluids (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS-I

10.1. A tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. From the plot shown in Figure, indicate the one that represents the velocity $\mathrm{v}$ of the pebble as a function of time (t).

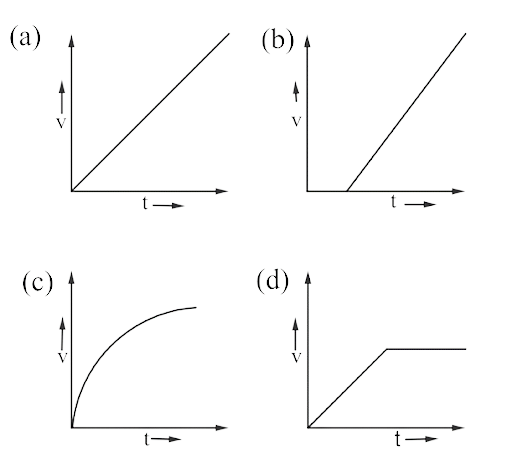
Ans: (c) When the pebble is dropped from the top of the cylinder filled with viscous oil, pebble falls under gravity with constant acceleration, but as it is dropped it enters in oil and dragging force $F=6 \pi \eta r v$ due to viscosity of the oil so acceleration decreases from g to zero velocity increases, but acceleration decreases, when acceleration decreased to zero, velocity becomes constant (terminal velocity). These conditions are verified in option (c).

10.2. Which of the following diagrams (Figure) does not represent a stream line flow?

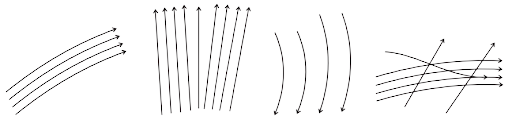
Ans: (d): In streamlined flow, the velocity of the fluid at any given point remains constant (at a particular line) across any cross-sectional area. Hence is streamline flow layers do not cross each other. Hence option (d) is not streamlined.

10.3. Along a streamline

(a) the velocity of a fluid particle remains constant.

(b) the velocity of all fluid particles crossing a given position is constant.

(c) the velocity of all fluid particles at a given instant is constant.

(d) the speed of a fluid particle remains constant

Ans: (b): In stream line flow, the speed at a point in a cross-section is always constant because $A v=$ constant. Hence, verifies the option only (b).

10.4. An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters $2.5 \mathrm{~cm}$ and $3.75 \mathrm{~cm}.$ The ratio of the velocities in the two pipes is

a) $9: 4$

b) $3: 2$

c) $\sqrt{3}: \sqrt{2}$

d) $\sqrt{2}: \sqrt{3}$

Ans: (a): According to continuity equation (Law of Conservation of mass)

$a_{1} v_{1}=a_{2} v_{2}$

$\dfrac{v_{1}}{v_{2}}=\dfrac{a_{2}}{a_{1}}=\dfrac{\pi\left(\dfrac{d_{2}}{2}\right)^{2}}{\pi\left(\dfrac{d_{1}}{2}\right)^{2}}=\dfrac{d_{2}^{2}}{4} \cdot \dfrac{4}{d_{1}^{2}}=\dfrac{d_{2}^{2}}{d_{1}^{2}} \\$

$\dfrac{v_{1}}{v_{2}}=\dfrac{(3.75)^{2}}{(2.50)^{2}}=\left[\dfrac{3}{2}\right]^{2} \\$

$\Rightarrow \dfrac{v_{1}}{v_{2}}=\dfrac{9}{4}$

Or $v_{1}: v_{2}:: 9: 4$

Which verifies the option (a)

10.5. The angle of contact at the interface of water-glass is $0^{\circ}$, Ethyl alcohol-glass is $0^{\circ}$, Mercury-glass is $140^{\circ}$, and Methyliedide glass is $30^{\circ} .$ A glass- capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is:

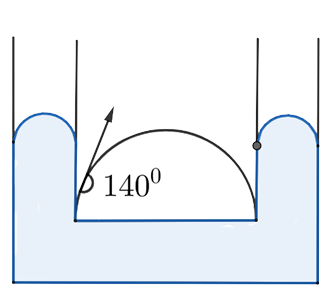
(a) water

(b) ethyl alcohol

(c) mercury

(d) methyl iodide

Ans: (c): Meniscus of liquid is convex so the angle of contact will be the obtuse angle that happens in the case of mercury-glass. Hence, verifies the option only (c).

MULTIPLE CHOICE QUES TIONS - II

10.6. For a surface molecule

(a) the net force on it is zero.

(b) there is a net downward force.

(c) the potential energy is less than that of a molecule inside.

(d) the potential energy is more than that of a molecule inside.

Ans: (b, d): Fig. (b) A molecule viewed from the top to the surface of the fluid. Force exerted on a molecule by all nearby molecules are equal and opposite, so the net horizontal component of force is zero.

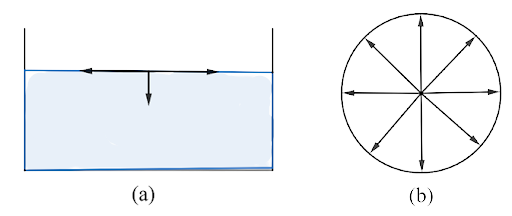
In fig. (a) as a molecule is viewed horizontally to the surface of fluid a vertically downward force acts on the molecule due to which it does not escape from the surface. Hence the right option is (b).

There is a net attractive force on molecules at the surface acting downwards. So the P.E of molecules at the surface is negative to lower ones but in magnitude PE (mgh) is more than that of the lower or inside molecules. This verifies option (d).

10.7. Pressure is a scalar quantity because

(a) it is the ratio of force to the area and both force and area are vectors.

(b) it is the ratio of the magnitude of the force to area.

(c) it is the ratio of the component of the force normal to the area.

(d) it does not depend on the size of the area chosen.

Ans: (c): what makes pressure a scalar quantity is a fact that it is the component of force along the direction of area that is taken into account while defining pressure. Thus the direction of quantities involved remain fixed and pressure becomes a scalar quantity. This verifies (c).

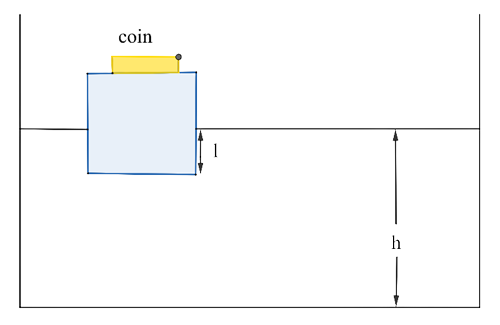
10.8. A wooden block with a coin placed on its top, floats in water as shown in Figure. The distance $l$ and $h$ are shown in the figure. After some time the coin falls into the water. Then

(a) 1 decreases.

(b) $\mathbf{h}$ decreases.

(c) 1 increases.

(d) $\mathbf{h}$ increase.

Ans: (a,b): According to the law of floatation weight of the floating body is equal to the weight of displaced fluid. When a coin falls into the water, the net weight of the floating body is decreased so the floating body will displace less amount of water so the block rises up and I will decrease. But height $h$ of water will decrease as less water is displaced now. So verifies the option $(a, b)$

10.9. With the increase in temperature, the viscosity of

(a) gases decreases.

(b) liquids increases.

(c) gases increases.

(d) liquids decreases.

Ans: (c, d): For coefficient of viscosity of liquid $\eta \propto \dfrac{1}{\sqrt{T}}$. For viscosity of gases $\eta \propto \sqrt{T}$ astemperature increase $\mathrm{KE}$ of gas molecule increases so collisions increases the viscosity.

In the case of liquid on the increasing temperature the KE of fluid increases. So speeds of individual

layers increase but the relative speed of layers remains almost the same. $\underline{\mathrm{S}_{0}}$ option (c) and (d) verifies.

10.10. Streamline flow is more likely for liquids with

(a) high density.

(b) high viscosity.

(c) low density.

(d) low viscosity

Ans: (b, c): Streamline flow is more likely for liquids of low density (or lower gravitational force).

If the viscosity of a liquid is larger it causes more velocity gradient, hence each line of flow can be easily differentiated.

On increasing $\eta$ and decreasing $\mathrm{p}$, Reynold number $R=\dfrac{p v D}{\eta}$ decreases, which makes the flow towards streamline.

Hence verifies the option (c) and (b).

VERY SHORT ANSWER TYPE QUESTIONS

10.11. Is viscosity a vector?

Ans: It is the property of a liquid that is equal to the magnitude of dragging force per unit area between the two layers of liquid whose velocity gradient is unity. So it has no direction (only magnitude of force) so it is not a vector.

10.12. Is surface tension a vector?

Ans: Surface tension $\left[\sigma=\dfrac{W . D}{\text { Change in Surface Area }}\right] .$ So, $\sigma$ is not a vector as it is equal to the work done per unit change in surface area.

10.13. Iceberg floats in water with part of it submerged. What is the fraction of the volume of iceberg submerged if the density of ice is $\rho_{i}=0.917 \mathrm{gm} / \mathrm{cm}^{3} ?$

Ans: As iceberg is floating on surface of sea

Weight of ice berg = Weight of displace liquid

$V \cdot \rho_{2} g=V \cdot \rho_{n} g$

$\mathrm{V}=$ Volume of ice berg

$\mathrm{V}^{\prime}=$ Volume of ice berg inside water or volume of displaced water by iceberg

$\dfrac{\text { Volume of iceberg submerged }}{\text { Volume of iceberg }}=\dfrac{V^{\prime}}{V}=\dfrac{\rho_{i}}{\rho_{\mathrm{w}}}=\dfrac{0.917}{1}$

Hence $0.917$ part of iceberg body is submerged inside water.

10.14. A vessel filled with water is kept on a weighing pan and the scale adjusted to zero. A block of mass $M$ and density $\rho$ is suspended by a massless spring of spring constant $k$. This block is submerged inside into the water in the vessel. What is the reading of the scale?

Ans: Consider the diagram. Beaker filled with water is placed on a weighing pan and then the scale is adjusted to zero.

As the block is submerged in water the Bouxant force (upward) acts on the block by water. This buoyant force acts as a reaction force. $\underline{\mathrm{S}_{0}}$ by Newton's third law block will apply reaction forces downward due to which reading on the scale increases equal to the buoyant force $=V \rho_{n} g$

$\mathrm{V}=\mathrm{V}$ volume of water

displaced By block

$\rho_{w}=$ density of water

Mass of block $=\mathrm{M}=\mathrm{V} \cdot \rho$

or

$V=\dfrac{M}{\rho}$

Reading of weighing scale $=\dfrac{M}{\rho} \cdot \rho_{n} g=\dfrac{\rho_{w}}{\rho} M g$

10.15. A cubical block of density $\rho$ is floating on the surface of the water. Out of its height $L$, fraction $x$ is submerged in water. The vessel is in an elevator accelerating upward with acceleration a. What is the fraction immersed?

Ans: (a) When cubical block is submerged in water, by principle of floatation, $V \rho g=V^{\prime} \rho_{*} g$

$V^{\prime}=V_{\text {olume }}$ of water displaced by

block

$\mathrm{V}=$ Volume of block inside water

$=$ area of base of block $\times$ height $($ inside water $)$

$V^{\prime}=L^{2} x$

$\mathrm{V}=$ Volume of block $L^{3}, \rho_{s}$ Density of block

$\therefore L^{3} \rho_{S}=L^{2} x \rho_{\mathrm{w}}$

Or

$\dfrac{\rho_{S}}{\rho_{W}}=\dfrac{x}{L} \ldots(i) \\$

$x=\dfrac{\rho_{S}}{\rho_{W}} L$

(b) When the immersed block is in lift moving upwards then net acceleration of system $=(\mathrm{g}+\mathrm{a})$

Weight of block $=\mathrm{m}(\mathrm{g}+\mathrm{a})=\mathrm{V} \times \rho_{s}(\mathrm{~g}+\mathrm{a})$

$=L^{3} \rho_{S}(g+a)$

Now let part of block be submerged into water in moving lift (upward) is

Weight of block=Buoyant force

$L^{3} \rho_{s}(g+a)=x_{1} L^{2} \rho_{w}(g+a)$

$\therefore \dfrac{\rho_{S}}{\rho_{w}}=\dfrac{x_{1}}{L}$ $x_{1}=L \cdot \dfrac{\rho_{B}}{\rho_{W}} \ldots(i i i)$

From (i), (ii) we observe that submerged part of cube inside water in both case is $\left(\dfrac{\rho_{s}}{\rho_{W}} L\right)$

which constant or it is independent of acceleration of lift (+ $a,-a$ or zero) i.e. motion of liftupward or downward or at rest.

10.16. The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius $\mathbf{r}=2.5 \times 10^{-5} \mathrm{~m}$. The surface tension of sap is $\mathbf{T}=$ $7.28 \times 10^{-2} \mathrm{Nm}^{-1}$ and the angle of contact is $0^{\circ} .$ Does surface tension alone account for the supply of water to the top of all trees?

Ans: Radius of capillarity $\mathrm{r}=2.5 \times 10^{-5} \mathrm{~m}$

$\mathrm{S}=\mathrm{T}=7.8 \times 10^{-2} \mathrm{Nm}^{-1} \\$

$\mathrm{~g}=9.8 \mathrm{~m} / \mathrm{s}^{2} \\$

$h=\dfrac{25 \cos \theta}{r p g}=\dfrac{2 \times 7.28 \times 10^{-2} \cos 0^{\circ}}{2.5 \times 10^{-5} \times 10^{3} \times 9.8}=\dfrac{2 \times 7.28 \times 10^{-2+5}}{25 \times 10^{3} \times 98} \\$

$h=\dfrac{104 \times 10^{3}}{175 \times 10^{3}}=\dfrac{104}{175}=0.594 \mathrm{~m}=0.6 \mathrm{~m}$

Most of the trees are of more than $0.6 \mathrm{~m}$ height. So capillary action alone cannot account for the rise of water in all other trees.

10.17. The free surface of the oil in a tanker, at rest, is horizontal. If the tanker starts accelerating the free surface will be titled by an angle $\theta$. If the acceleration is $a m s^{-2}$, what will be the slope of the free surface?

Ans: Consider the tanker is pulled by force $F$ which produces acceleration in the truck in forwarding direction.

Consider only a small element of mass om at P. When a tanker is pulled by forwarding acceleration 'a' then this element of mass also experiences it in forwarding direction. But due to inertia of rest, it tries to remain at rest. Due to the same acceleration, it moves in the backward direction as it is free and not rigidly connected to the tanker. Hence force acting on $\mathrm{am}$ are

$\mathrm{F}_{\mathrm{l}}=$ am $a$ in horizontally backward direction due to tanker's acceleration a, vertically downward due to gravity.

The resolution of component off $F_{1}$ and $F_{2}$ along and perpendicular to the inclined

surface of oil are resolved. Normal reaction is balanced by component $\partial m a \sin \theta$ of $F_{1}$ and when surface is inclined at maximum angle then

$m a \cos \theta=\partial mg \sin \theta$

So $\dfrac{\sin \theta}{\cos \theta}=\dfrac{a}{g}$ is required slope

$\tan \theta=\dfrac{a}{g}$ is required slope.

10.18. Two mercury droplets of radii $0.1 \mathrm{~cm}$. and $0.2 \mathrm{~cm}$. collapse into one single drop. What amount of energy is released? The surface tension of mercury $\mathrm{T}=435.5 \times 10^{-3} \mathrm{Nm}^{-1}$.

Ans: Energy due to surface Tension $E=\sigma_{\Delta A}$

By the law of conservation of mass, the volume of drop $V_{1}+V_{2}=V$

$=0.1 \mathrm{~cm}=0.1 \times 10^{-2} \mathrm{~m}=10^{-1} \mathrm{~m} \\$

$=0.2 \mathrm{~cm}=2 \times 10^{-3} \mathrm{~m} \\$

$A=4 \pi r_{1}^{2}+4 \pi r_{2}^{2}-4 \pi R^{2}=4 \pi\left[r_{1}^{2}+r_{2}^{2}-R^{2}\right]$

$R$ is the radius of new drop formed by the combination of two smaller drops.

$\dfrac{4}{3} \pi R^{3}=\dfrac{4}{3} \pi r_{1}^{3}+\dfrac{4}{3} \pi r_{2}^{3} \\$

$\dfrac{4}{3} \pi R^{3}=\dfrac{4}{3} \pi\left[r_{1}^{3}+r_{2}^{3}\right] \Rightarrow R^{3}=r_{1}^{3}+r_{2}^{3} \\$

$R^{3}=\left[\left(1 \times 10^{-1}\right)^{3}+\left(2 \times 10^{-3}\right)^{3}\right]=\left[10^{-3}+8 \times 10^{-3}\right]=9 \times 10^{-3} \\$

$E=2.1 \times 10^{-3} \mathrm{~m} \\$

$E=40=4 \times 3.14\left[\left(10^{-3}\right)^{2}+\left(2.0 \times 10^{-3}\right)^{2}-\left(2.1 \times 10^{-1}\right)^{2}\right] \times 435.5 \times 10^{-3} \\$

$E=4 \times 3.14 \times 435.5 \times 10^{-3}[5-4.41] \\$

$E=1742.0 \times 3.14 \times 10^{-1}[0.59] \\$

$E=5469.88 \times 0.59 \times 10^{-3}$

$E=3227.23 \times 10^{-7} \\$

$E=32.2733 \times 10^{-7} \mathrm{~J} \\$

$E=32.27 \times 10^{-7} \mathrm{~J}$

Energy is released due to formation of bigger drops from smaller drops and finally the area will be smaller.

10.19. If a drop of liquid breaks into smaller droplets, it results in a lowering of the temperature of the droplets. Let a drop of radius $R$, break into $N$ small droplets each of radius r. Estimate the drop in temperature.

Ans: $\Delta \mathrm{E}=\sigma \text { (Final area - initial area) of surface } \\$

$\Delta E=m s \Delta t \\$

$\text { By the law of conservation of mass, final volume initial volume of one drop of } \\$

$\text { radius } \mathrm{R} \text { splitted in } \mathrm{N} \text { drops of radius } \mathrm{r} \\$

$\therefore \dfrac{4}{3} \pi R^{3}=N \cdot \dfrac{4}{3} \pi r^{3} \\$

$\text { Or } \\$

$R^{3}=N r^{3} \\$

$r=\dfrac{R}{(N)^{1 / 3}} \\$

$\Delta E=\sigma \Delta A=\sigma[\text { area of } \mathrm{N} \text { drops of radius } \mathrm{r}-\text { area of big drop }] \\$

$\mathrm{ms} \Delta \mathrm{t}=\sigma\left[N \cdot 4 \pi r^{2}-4 \pi R^{2}\right] \\$

$\mathrm{V} \cdot \rho \mathrm{s} \Delta \mathrm{t}=4 \pi \sigma\left[N r^{2}-R^{2}\right] \\$

$N\left(\dfrac{4}{3} \pi r^{3}\right) \rho s \Delta t=4 \pi \sigma\left[N r^{2}-R^{2}\right] \\$

$\mathrm{M}=\mathrm{mass} \text { of all smaller drops }$

$\rho=$ density of liquid

$s=$ specific heat of

liquid

$\Delta t=$ change in temperature

$\Delta t=\dfrac{4 \pi \sigma \times 3}{N \cdot 4 \pi r^{3} \rho \rho s}\left[N r^{2}-R^{2}\right] \quad\left(\because R^{3}=N r^{3}\right)$

$\Delta t=\dfrac{3 \sigma}{N \rho s}\left[\dfrac{N r^{2}}{r^{3}}-\dfrac{R^{2}}{r^{3}}\right] \quad\left(\therefore r^{3}=\dfrac{R^{3}}{N}\right)$

$\Delta t=\dfrac{3 \sigma}{N \rho s}\left[\dfrac{N}{r}-\dfrac{R^{2} N}{R^{3}}\right]=\dfrac{3 \sigma N}{\rho N s}\left[\dfrac{1}{r}-\dfrac{1}{R}\right]$

$\Delta t=\dfrac{3 \sigma}{\rho s}\left[\dfrac{1}{r}-\dfrac{1}{R}\right]$ as $R>r$

$\therefore \Delta t$ will be positive i.e. $\dfrac{1}{R}<\dfrac{1}{r}$

Hence formation of smaller drops requires the temperature of drops to increase. This energy is taken from surroundings whose temperature decreases.

10.20. The surface tension and vapour pressure of water at $20^{\circ} \mathrm{C}$ is $7.28 \times 10^{-2} \mathrm{Nm}^{-1}$ and $2.33 \times 10^{3} \mathrm{~Pa}$, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at $20^{\circ} \mathrm{C}$ ?

Ans: The drop will evaporate if the water pressure on the liquid, is greater than vapour pressure above the surface of the liquid. Let a water droplet of radius $R$ be formed without evaporation then

Vapour pressure $=$ Excess pressure in a drop

$\rho=\dfrac{2 \sigma}{R}(\underline{\text { only }} \text { one surface in drop }) \\$

$R=\dfrac{2 \times 7.28 \times 10^{-1}}{\text { Vapour pressure }} \\$

$R=\dfrac{2 \times 7.28 \times 10^{-2}}{2.33 \times 10^{3}} \\$

$R=6.25 \times 10^{-5} \mathrm{~m}$

LONG ANSER TYPE QUESTION

10.21 (a) Pressure decreases as one ascends the atmosphere. If the density of air is $\rho$.what is the change in pressure dp over a differential height dh?

(b) Considering the pressure p to be proportional to the density, find the pressure $\mathbf{p}$ at a height $\mathbf{h}$ if the pressure on the surface of the earth is $p_{0}$.

(c) if $p_{0}=1.013 \times 10^{5} N \cdot m^{-2}, p_{0}=1.29 \mathrm{~kg} / \mathrm{m}^{3}$ and $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$, at what height will the pressure drop to $(1 / 10)$ the value at the surface of the earth?

(d) This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.

Ans: Consider a part (packet) of the atmosphere of thickness dh. As the pressure at a point in a fluid is equal in all directions. $\underline{\text { So }}$ the pressure on the upper layer is $\mathrm{p}$ acting downward and on the lower layer is (ptdp) acting upward. Force due to pressure is balanced by Buoyant force by air

$(p+d p) A-p \cdot A=-V p g \\$

$p \cdot A+d p A-p \cdot A=A \cdot d h p g \\$

$d p A=-p p g d h \cdot A \\$

$d p p=-p g d h \ldots(i)$

The negative sign shows that pressure decreases as height increases

(b) Let $p_{0}$ is the density of air on surface of earth

$\because$ pressure $\mathrm{p}$ at a point is directly proportional to density.

$\therefore$ p $\propto \rho$ or $\dfrac{p}{p_{0}}=\dfrac{\rho}{\rho_{0}}$ or $\rho=\left(\dfrac{p}{p_{0}}\right) \rho_{0} \ldots$ (ii)

$d p=\rho g d h$ from (i)

( $\rho$ is density of air in atmosphere)

$d p=-\left(\dfrac{p}{p_{0}}\right) \rho_{0} g d h \\$

$\Rightarrow \dfrac{d p}{p_{0}}=-\dfrac{\rho_{0} g h}{p_{\mathrm{w}}} d h$

Integrating both sides

$\int \log p d p=-\int_{0}^{k} \dfrac{p_{0} g}{p_{0}} \\$

$\log \left(\dfrac{p}{p_{0}}\right)=\dfrac{\rho}{\rho_{0}} g h \ldots(i i i) \\$

$\Rightarrow \dfrac{p}{p_{0}}=e^{-\dfrac{A_{0}}{A}} \\$

$\Rightarrow p=p_{0} e^{-\dfrac{A_{B k}}{A_{0}}}$

(c) From (iii) $\log \dfrac{p}{p_{0}}=-\dfrac{\rho_{0} g h}{p_{0}}$

$\text { put } p=\dfrac{p_{0}}{10} \text { (given) } \\$

$\log \dfrac{p_{0} 110}{p_{a}}=\dfrac{-\rho_{0} g h}{p_{o}} \\$

$\Rightarrow \log \dfrac{1}{10}=\dfrac{-\rho_{0} g h}{p_{a}} \\$

$\Rightarrow \log 10^{-1}=\dfrac{-\rho_{0} g h}{p_{a}} \\$

$\Rightarrow-\log 10=\dfrac{-p_{0} g h}{p_{o}} \\$

$\text { Or } h=\dfrac{-p_{a}}{\rho_{0} g} \log 10 \\$

$h=\dfrac{-p_{0} \log 10 \times 2.303}{\rho_{0} g} \\$

$h=\dfrac{1.013 \times 10^{5} \times 2.303}{1.29 \times 9.8} \\$

$h=0.184 \times 10^{5} m \\$

$h=18.4 / \mathrm{m}$

(d) Temperature (T) remains constant only near the surface of the earth not at a greater height.

10.22. Surface tension is exhibited by liquids due to force of attraction between

molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporization for water

$L_{r}=540 \mathrm{Kcal} \cdot \mathrm{kg}^{-1}$ the mechanical equivalent of heat $J=4.2 \mathrm{Jcal}^{-1}$ density of water $\rho_{w}=10^{3} \mathrm{~kg} / l$. Avogadro's $N_{A}=6.0 \times 10^{26} \mathrm{Kmole}^{-1}$ and the molecular weight of water $M_{A}=18 \mathrm{~kg}$ for $1 \mathrm{Kmol}$.

(a) estimate the energy required for one molecule of water to evaporate.

(b) show that the inter-molecular distance for water is $d=\left[\dfrac{M_{A}}{N_{A}} \cdot \dfrac{1}{\rho_{w}}\right]^{1 / 3}$ and find its value.

(c) $1 \mathrm{~g}$ of water in the vapor state at $1 \mathrm{~atm}$ occupies $1601 \mathrm{~cm}^{3}$. Estimate the intermolecular distance at boiling point, in the vapour state.

(d) During vaporization a molecule overcomes a force $F$, assumed constant, to go from an inter-molecular distance $d$ to $d^{\prime} .$ Estimate the value of $F$, where $\mathrm{d}=3.1 \times 10^{-10} \mathrm{~m}$

(e) Calculate F/d which is a measure of the surface tension.

Ans: $L_{v}=540 \mathrm{Kcal} \cdot \mathrm{kg}^{-1}=540 \times 10^{3} \mathrm{calKgK}^{-1}$

$L_{v}=540 \times 4.2 \times 10^{3} \mathrm{JKg}^{-1}$

Energy required to evaporate $1 \mathrm{~kg}$ water $=L_{v} K c a l$

Energy required to evaporate $M_{A} k g$ of water $=L_{A} M_{A} K c a l$

In $M_{A} k g$ Number of molecule $=N_{A}$

$\therefore$ Energy required to evaporate 1 molecule $=\dfrac{L_{A} M_{A}}{N_{A}} K c a l$

$U=\dfrac{L_{V} M_{A}}{N_{A}} K c a l=\dfrac{L_{V} M_{A} \times 10^{3} \times 4.2 \mathrm{~J}}{N_{A}} \\$

$U=\dfrac{18 \times 540 \times 10^{3} \times 4.2}{6 \times 10^{26}}=12.6 \times 540 \times 10^{3-26} \\$

$U=6840 \times 10^{-23} \mathrm{~J} \\$

$U=6.8 \times 10^{-20} \mathrm{~J}$

(b) Let the water molecules be point sized and separated by distance 'd' from each other.

Volume of $N_{A}$ molecules $=\dfrac{\text { mass of } N_{A} \text { molecule }}{\text { density }}=\dfrac{M_{A}}{\rho_{W}}$

Volume occupied by 1 molecule $=\dfrac{M_{A}}{\rho_{W} N_{A}}$

Volume occupied by 1 molecule $=\mathrm{d}^{3}=\dfrac{M_{A}}{\rho_{W} N_{A}}$

$d=\left[\dfrac{M_{A}}{N_{A} \rho_{w}}\right]^{1 / 3}$

$1 \mathrm{~kg}$ of vapour occupies volume $=1601 \mathrm{~cm}^{3}=1601 \times 10^{-5} \mathrm{~m}^{3}$

(c) $1 \mathrm{~kg}$ of vapour occupies volume $=1601 \mathrm{~cm}^{3}=1601 \times 10^{-3} \mathrm{~m}^{3}$

$18 \mathrm{~kg}$ of vapour occupies volume $=18 \times 1601 \times 10^{-3} \mathrm{~m}^{3}$

$18 \mathrm{~kg}$ of water $=16 \times 10^{25} \mathrm{molecules}$

$\therefore 16 \times 10^{25} \mathrm{molecules}$ occupies volume $=18 \times 1601 \times 10^{-3} \mathrm{~m}^{3}$

1 molecule occupies volume $=\dfrac{18 \times 1601 \times 10^{-3}}{6 \times 10^{26}}$

$\therefore d^{3}=\left[\dfrac{18 \times 1601 \times 10^{-3}}{6 \times 10^{26}}\right]$

$d^{\prime 3}=30 \times 1601 \times 10^{-30}$

$d^{3}=30 \times 1601 \times 10^{-30}$

$d^{\prime}=(30 \times 1601)^{\dfrac{1}{3}} \times 10^{-10} \mathrm{~m}=36.3 \times 10^{-10} \mathrm{~m}$

(d) Work done to change distance between molecules from d to d' or required work done

Required $\mathrm{W}=F\left(d^{\prime}-d\right)$

Energy required to evaporate 1 molecule

$\therefore F\left(d^{\prime}-d\right)=6.8 \times 10^{-20}$

$F\left(36.6 \times 10^{-10}-3.1 \times 10^{-10}\right)=6.8 \times 10^{20}$

$F \times 33.2 \times 10^{-10}=6.8 \times 10^{20}$

$F=\dfrac{6.8 \times 10^{20}}{33.2 \times 10^{-10}}$

$F=2.05 \times 10^{-11}$

(e) Surface Tension $=\dfrac{F}{d}=\dfrac{2.05 \times 10^{-11}}{3.1 \times 10^{-10}}=6.6 \times 10^{-2} \mathrm{~N} / \mathrm{m}$

$\sigma=6.6 \times 10^{-2} \mathrm{~N} / \mathrm{m}$

10.23. A hot air balloon is a sphere of radius $8 \mathrm{~m}$. The air inside is at a temperature of $60^{\circ} \mathrm{C}$. How large a $\mathrm{m}$ ass can the balloon lift when the outside temperature is $20^{\circ} \mathrm{C}$ ? (Assume air is an ideal gas, $\mathrm{R}=8.314 \mathrm{~J} m o l e^{-1} \mathrm{~K}^{-1}, 1 \mathrm{ltm}=1.013 \times 10^{5} \mathrm{~N} . \mathrm{m}^{-2}$ or $\mathrm{Pa}$ the $\mathrm{membranetension~is~} 5 \mathrm{Nm}^{-1}$

Ans: Pressure inside $P_{i}$ balloon is larger than outer pressure $P_{a}$ of atmosphere.

$\therefore P_{c}-P_{a}=\dfrac{2 \sigma}{R}$

$\sigma=$ surface tension in the membrane of balloon $R=$ radius of the balloon.

Gas or air inside is perfect (considered)

$\therefore P V=n_{i} R T_{i}$

$\mathrm{V}=$ volume of balloon

$n_{c}=$ no. of moles of gas in balloon

$R=$ gas constant

$T_{i}=$ temperature of balloon

$n_{i}=\dfrac{P V}{R T_{i}}=\dfrac{\text { mass of balloon(M) }}{\text { molecular mass }\left(\mathrm{M}_{A}\right)} \\$

$n_{i}=\dfrac{\mathrm{M}_{1}}{\mathrm{M}_{A}}=\dfrac{P V}{R T_{i}}$

Similarly, $n_{a}=\dfrac{P_{a} V}{R T_{a}}$

By principal off floatation $W+M, g=M_{\sigma} g$

$W=$ weight lifted by balloon $W=M_{a} g-M_{i} g$

$W=\left(M_{a}-M_{i}\right) g$

Where $n_{\alpha}=$ no. of molecules of air displaced by balloon.

$V=$ volume of air displaced by balloon equal to the volume of balloon If $M_{\alpha}$ mass of air displaced by the balloon

$M_{A}=$ molecular mass inside or outside the balloon

$\therefore n_{\sigma}=\dfrac{M_{a}}{M_{A}} \\$

$n_{o}=\dfrac{M_{a}}{M_{A}}=\dfrac{P_{o} V}{R T_{a}} \\$

$\Rightarrow M_{a}=\dfrac{P_{a} V M_{A}}{R T_{o}}$

From (i), $M_{i}=\dfrac{P_{i} V M_{A}}{R T_{i}}$

W $=\left(\dfrac{P_{0} V M_{A}}{R T_{a}}-\dfrac{P V M_{A}}{R T_{i}}\right) g \\$

W $=\dfrac{V M_{A}}{R}\left(\dfrac{P_{a}}{T_{a}}-\dfrac{P_{c}}{T_{i}}\right) g \\$

$M_{A}=21 \% \text { of } O_{2}+79 \% \text { of } N_{2} \\$

$M_{A}=0.21 \times 32+0.79 \times 28 \\$

$M_{A}=4(0.21 \times 8+0.79 \times 7) \\$

$M_{A}=4(1.68+5.53) \\$

$M_{A}=4(7.21) \\$

$M_{A}=28.84 g \\$

$M_{A}=0.2884 k g \\$

Pi $=P_{\sigma}+\dfrac{2 \sigma}{R} \\$

W $=\dfrac{4}{3} \pi \times 8 \times 8 \times 8 \times 0.2884 \\$

$\left.=\dfrac{1.013 \times 10^{5}}{273+20}-\dfrac{P_{i}}{273+60}\right] g$

$P_{i}=P_{a}+P=P_{a}+\dfrac{2 \sigma}{R} \\$

$P_{i}=\left[1.013 \times 10^{5}+\dfrac{2 \times 5}{8}\right]=101300+1.25 \\$

$P_{i}=101301.25=1.0130125 \times 10^{5}=1.013 \times 10^{5} \\$

$\therefore W=\dfrac{4 \times 3.14 \times 8 \times 8 \times 8 \times 0.02884}{3 \times 8.314}\left[\dfrac{1.013 \times 10^{5}}{293}-\dfrac{1.013 \times 10^{5}}{333}\right] g \\$

$W=\dfrac{4 \times 3.14 \times 8 \times 8 \times 8 \times 0.02884 \times 1.013 \times 10^{5}}{3 \times 8.314}\left[\dfrac{1}{293}-\dfrac{1}{333}\right] g \\$

$W=\dfrac{4 \times 3.14 \times 8 \times 8 \times 8 \times 0.02884 \times 1.013 \times 10^{5} \times 9.8}{3 \times 8.314}\left[\dfrac{1}{293}-\dfrac{1}{333}\right] \\$

$W=\dfrac{4 \times 3.14 \times 8 \times 8 \times 8 \times 0.02884 \times 1.013 \times 10^{5} \times 9.8 \times 40}{3 \times 8.314}=3044.2 N$

Why Should the Students Consult the NCERT Exemplar?

Considering the lack of proper guidance and time the students can have in this pandemic era, to prepare for their Examinations, Vedantu offers all the study materials and course guides for absolutely free on their website. The students can avail themselves of a lot of benefits if they go through the study materials attentively.

• All the concepts associated with the Mechanical properties of Fluids are discussed in detail.

• The books include short Examples and precise explanations and analyses that further elaborate on the basic characteristics and behaviorism of different types of matters.

• The precise explanations will help the students to understand the concepts in detail and in a very short period of time so that they can focus on the other Chapters as well.

• The books include model question papers and mock papers that will help them to revise their courses.

• The questions are solved and explained in proper steps.

• The best part is, the course materials are downloadable so that the students can study the concepts whenever it will be convenient for them.

The other reference books that the students might need in order to understand the concepts are also available on the website of Vedantu. The revision notes are also available on the website that will help the learners to get a fair idea of their performance.