NCERT Solutions for Class 11 Physics Chapter 3 Motion In A Plane

Ans:

Scalar: Mass, volume, density, angular frequency, number of moles, speed.

Vector: Acceleration, angular velocity, velocity, displacement.

A scalar quantity is specified by its magnitude. Mass, volume, density, angular frequency, number of moles, speed are some of the scalar physical quantities.

A vector quantity is specified by its magnitude and the direction associated with it.

Acceleration, angular velocity, velocity, displacement belong to this category.

2. Pick out the two scalar quantities in the following list:

Force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.

Ans:

Work and current are examples of scalar quantities.

Work done is said to be the dot product of force and displacement. As the dot product of two quantities is always a scalar, work is considered as a scalar physical quantity.

Current is described by its magnitude. Its direction is not considered.

Thus, it is a scalar quantity.

3. Pick out the only vector quantity in the following list: Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.

Ans: Impulse

It is given by the product of force and time. As force is a vector quantity, its product with time gives a vector quantity.

4. State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:

(a) adding any two scalars.

(b) adding a scalar to a vector of the same dimension s,

(c) multiplying any vector by any scalar,

(d) multiplying any two scalars,

(e) adding any two vectors,

(f) adding a component of a vector to the same vector.

Ans:

(a) Not Meaningful. 

The addition of two scalar quantities will be meaningful only if they both represent the same physical quantity.

(b) Not Meaningful.

The addition of a vector quantity with a scalar quantity is considered not meaningful.

(c) Meaningful. 

A scalar can be multiplied with a vector. Force is multiplied with time to give impulse.

(d) Meaningful. 

A scalar, respective of the physical quantity, can be multiplied with another scalar having the same or different dimensions.

(e) Not Meaningful. 

The addition of two vector quantities is considered meaningful only if they both represent the same physical quantity.

(f) Meaningful 

A component of a vector can be added to the same vector as both of them have the same dimensions.

5. Read each statement below carefully and state with reasons, if it is true or false:

(a) The magnitude of a vector is always a scalar,

(b) each component of a vector is always a scalar,

(c) the total path length is always equal to the magnitude of the displacement vector of a particle.

(d) the average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time,

(e) Three vectors not lying ${\text{m}}$ a plane can never add up to give a null vector.

Ans:

(a) True. 

The magnitude of a vector is a number. So, it is a scalar.

(b) False. 

Each component of a vector is a vector.

(c) False. 

The total path length is scalar, whereas displacement is a vector quantity.

So, the total path length is greater than the magnitude of displacement. It is equal to the magnitude of displacement only when a particle is moving in a straight line.

(d) True. 

It is because the total path length is always greater than or equal to the magnitude of displacement of a particle.

(e) True. 

Three vectors, which do not lie in a plane, can’t be represented by the sides of a triangle taken in the same order.

6. Establish the following vector inequalities geometrically or otherwise:

(a) $|{\text{a}} + {\text{b}}| \leqslant |{\text{a}}| + |{\text{b}}|$

(b) $|{\text{a}} + {\text{b}}| \geqslant |{\text{a}}| - |{\text{b}}|$

(c) $|{\text{a}} - {\text{b}}| \leqslant |{\text{a}}| - |{\text{b}}|$

(d) $|{\text{a}} - {\text{b}}| \geqslant |{\text{a}}| - |{\text{b}}|$

When does the equality sign above apply?

Ans:

a) Let $\overrightarrow {\text{a}} $ and $\overrightarrow {\text{b}} $ be represented by the adjacent sides of a parallelogram $OMNP$ as shown below:

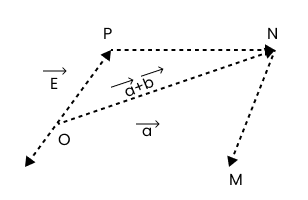
$|\overrightarrow {{\text{OM}}} | = |\overrightarrow a |{\text{         }}...\left( {\text{i}} \right)$

$|\overrightarrow {{\text{MN}}} | = |\overrightarrow {{\text{OP}}} | = |\overrightarrow {\text{b}} |{\text{          }}...\left( {{\text{ii}}} \right)$

$|\overrightarrow {{\text{ON}}} | = |\overrightarrow a  + \overrightarrow b |{\text{            }}...\left( {{\text{iii}}} \right)$

As each side is smaller than the sum of the other two sides in a triangle,

In $\Delta OMN$,

${\text{ON}} < ({\text{OM}} + {\text{MN}})$

\[|\overrightarrow {\text{a}}  + \overrightarrow {\text{b}} | < |\overrightarrow {\text{a}} | + |\overrightarrow {\text{b}} |{\text{         }}...{\text{(iv)}}\]

If $\vec a$ and $\vec b$ act along a straight line in the same direction, then:

$|\overrightarrow {\text{a}}  + \overrightarrow {\text{b}} | = |\overrightarrow {\text{a}} | + |\overrightarrow {\text{b}} |{\text{          }}...{\text{(v)}}$

Combine equations ${\text{(iv)}}$ and ${\text{(v)}}$ 

$|\overrightarrow {\text{a}}  + \overrightarrow {\text{b}} | \leqslant |\overrightarrow {\text{a}} | + |\overrightarrow {\text{b}} |$

b) Let $\vec a$ and $\vec b$ be represented by the adjacent sides of a parallelogram$OMNP$, as shown below:

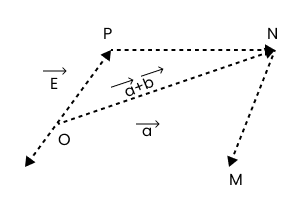
$|\overrightarrow {{\text{OM}}} | = |\overrightarrow a |{\text{         }}...\left( {\text{i}} \right)$

$|\overrightarrow {{\text{MN}}} | = |\overrightarrow {{\text{OP}}} | = |\overrightarrow {\text{b}} |{\text{          }}...\left( {{\text{ii}}} \right)$

$|\overrightarrow {{\text{ON}}} | = |\overrightarrow a  + \overrightarrow b |{\text{            }}...\left( {{\text{iii}}} \right)$

As each side is smaller than the sum of the other two sides in a triangle,

In $\Delta OMN$,

${\text{ON}} + {\text{MN}} > {\text{OM}}$

${\text{ON}} + {\text{OM}} > {\text{MN}}$

$|{\text{ON}}| > |\overrightarrow {{\text{OM}}}  - \overrightarrow {{\text{OM}}} |\quad (\because {\text{OP}} = {\text{MN}})$

If $\vec a$ and $\vec b$ act along a straight line in the same direction, then:

\[|\overrightarrow {\text{a}}  + \overrightarrow {\text{b}} | = ||\overrightarrow {\text{a}} | - |\overrightarrow {\text{b}} ||{\text{          }}...{\text{(v)}}\]

Combine equations ${\text{(iv)}}$ and ${\text{(v)}}$ 

$|\overrightarrow {\text{a}}  + \overrightarrow {\text{b}} | \geqslant ||\overrightarrow {\text{a}} | - |\overrightarrow {\text{b}} ||$

c) Let $\overrightarrow {\text{a}} $ and $\overrightarrow {\text{b}} $ be represented by the adjacent sides of a parallelogram $PQRS$:

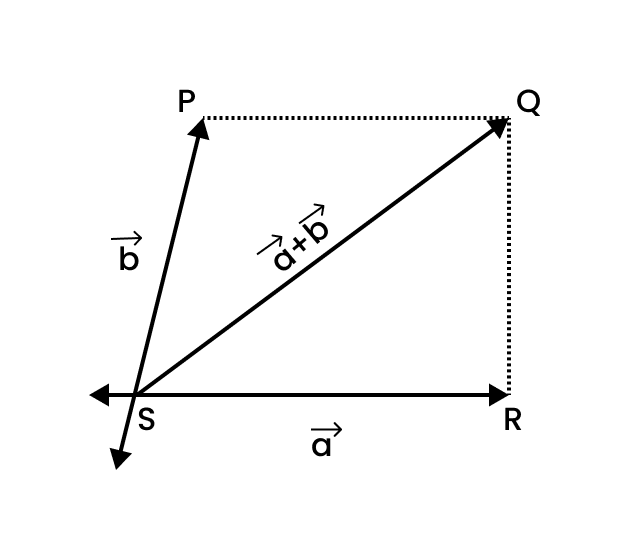
$|\overrightarrow {{\text{OR}}} | = |\overrightarrow {{\text{PS}}} | = |\overrightarrow {\text{b}} |{\text{         }}...{\text{(i)}}$

$|\overline {{\text{OP}}} | = |\overrightarrow {\text{a}} |{\text{       }}...{\text{(ii)}}$

As each side is smaller than the sum of the other two sides in a triangle,

In $\Delta OPS$,

${\text{OS}} < {\text{OP}} + {\text{PS}}$

$|\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} | < |\overrightarrow {\mathbf{a}} | + | - \overrightarrow {\text{b}} |$

$|\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} | < |\overrightarrow {\mathbf{a}} | + |\overrightarrow {\text{b}} |{\text{     }}...{\text{(iii)}}$

If the two vectors act in a straight line but in opposite directions, then:

$|\overrightarrow {\text{a}}  - \overrightarrow {\mathbf{b}} | = |\overrightarrow {\text{a}} | + |\overrightarrow {\text{b}} |$

Combine equations ${\text{(iii)}}$ and ${\text{(iv)}}$

$|\overrightarrow {\text{a}}  - \overrightarrow {\mathbf{b}} | \leqslant |\overrightarrow {\mathbf{a}} | + |\overrightarrow {\mathbf{b}} |$

d) Let $\vec a$ and $\vec b$ be represented by the adjacent sides of a parallelogram $PQRS$:

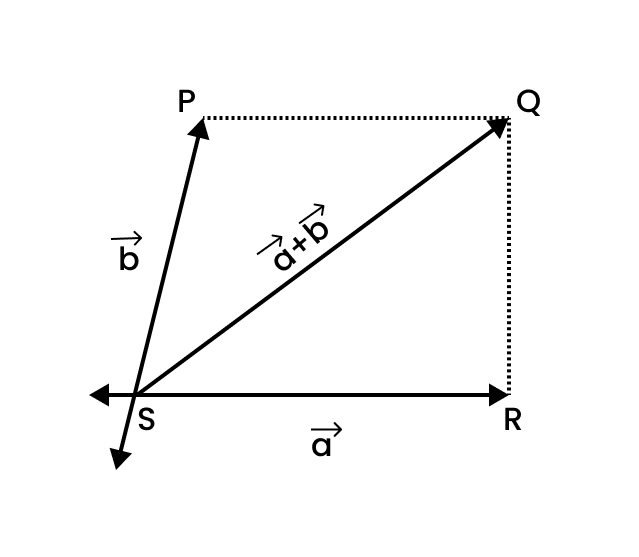
${\text{OS}} + {\text{PS}} > {\text{OP      }}...{\text{(i)}}$

${\text{OS}} > {\text{OP - PS      }}...{\text{(ii)}}$

$|\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} | > |\overrightarrow {\text{a}} | - |\overrightarrow {\text{b}} |{\text{      }}...{\text{(iii)}}$

The L.H.S is always positive and R.H.S can be positive or negative. 

To make both quantities positive, take modulus on both sides.

$\left| {\left| {\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} } \right|} \right| < \left| {\left| {\overrightarrow {\text{a}} } \right| - \left| {\overrightarrow {\text{b}} } \right|} \right|$

\[\left| {\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} } \right| > \left| {\left| {\overrightarrow {\text{a}} } \right| - \left| {\overrightarrow {\text{b}} } \right|} \right|      ...{\text{(iv)}}\]

If the two vectors act in a straight line but in the same direction:

\[\left| {\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} } \right| = \left| {\left| {\overrightarrow {\text{a}} } \right| - \left| {\overrightarrow {\text{b}} } \right|} \right|{\text{          }}...{\text{(v)}}\]

Combine equtaion \[{\text{(iv)}}\] and equation \[{\text{(v)}}\]:

\[\left| {\overrightarrow {\text{a}}  - \overrightarrow {\text{b}} } \right| \geqslant \left| {\left| {\overrightarrow {\text{a}} } \right| - \left| {\overrightarrow {\text{b}} } \right|} \right|\]

7. Given ${\text{a}} + {\text{b}} + {\text{c}} + {\text{d}} = 0$, which of the following statements are correct:

(a) ${\text{a}},{\text{b}},{\text{c}}$, and ${\text{d}}$ must each be a null vector,

(b) The magnitude of $(a + c)$ equals the magnitude of $(b + d)$

(c) The magnitude of a can never be greater than the sum of the magnitudes of ${\text{b}}$, ${\text{c}}$, and ${\text{d}}$,

(d) ${\text{b}} + {\text{c}}$ must lie in the plane of ${\text{a}}$ and ${\text{d}}$ if ${\text{a}}$ and ${\text{d}}$ are not collinear, and in the line of ${\text{a}}$ and ${\text{d}}$.

if they are collinear?

Ans:

(a) Incorrect

To make $\overrightarrow {\text{a}}  + \overrightarrow {\text{b}}  + \overrightarrow {\text{c}}  + \overrightarrow {\text{d}}  = 0$, it is not necessary to have all four vectors as null vectors. There are many other combinations which will give the sum zero.

(b) Correct

$\overrightarrow {\text{a}}  + \overrightarrow {\text{b}}  + \overrightarrow {\text{c}}  + \overrightarrow {\text{d}}  = 0$

$\overrightarrow {\text{a}}  + \overrightarrow {\text{c}}  =  - (\overrightarrow {\text{b}}  + \overrightarrow {\text{d}} )$

Take modulus on both sides:

$|\overrightarrow {\text{a}}  + \overrightarrow {\text{c}} | = | - (\overrightarrow {\text{b}}  + \overrightarrow {\text{d}} )| = |(\overrightarrow {\text{b}}  + \overrightarrow {\text{d}} )|$

So, the magnitude of $(\vec a + \vec c)$ is the same as the magnitude of $(\vec b + \vec d)$

(c) Correct

$\overrightarrow {\text{a}}  + \overrightarrow {\text{b}}  + \overrightarrow {\text{c}}  + \overrightarrow {\text{d}}  = 0$

$\overrightarrow {\text{a}}  =  - (\overrightarrow {\text{b}}  + \overrightarrow {\text{c}}  + \overrightarrow {\text{d}} )$

Take modulus on both sides:

$\vec a = |(\vec b + \vec c + \vec d)|$

$\vec a \leqslant |\vec b| + |\vec c| + |\vec d|{\text{    }}...{\text{(i)}}$

$(\vec b + \vec c + \vec d)$ is the sum of vectors $\vec b$, $\vec c$ and $\vec d$. The magnitude of $(\vec b + \vec c + \vec d)$ is less than, or equal to the sum of the magnitudes of $\vec b$, $\vec c$ and $\vec d.$ So, the magnitude of $\vec a$ cannot be greater than the sum of the magnitudes of $\vec b$, $\vec c$ and $\overrightarrow {\text{d}} .$ Equation ${\text{(i)}}$ shows that the magnitude of $\overrightarrow {\text{a}} $ is equal to or less than the sum of the magnitudes of $\vec b$, $\vec c$ and $\vec d$

(d) Correct

For, $\overrightarrow {\text{a}}  + \overrightarrow {\text{b}}  + \overrightarrow {\text{c}}  + \overrightarrow {\text{d}}  = 0$

$\overrightarrow {\text{a}}  + (\overrightarrow {\text{b}}  + \overrightarrow {\text{c}} ) + \overrightarrow {\text{d}}  = 0$

The resultant sum of the vectors $\vec a,{\text{ }}(\vec b + \vec c)$ and $\vec d$ is zero only if $(\vec b + \vec c)$ lie in the same plane as $\vec a$ and $\vec d$

If $\vec a$ and $\overrightarrow {\text{d}} $ are collinear, then $(\overrightarrow {\text{b}}  + \overrightarrow {\text{c}} )$ is in the line of $\overrightarrow {\text{a}} $ and $\overrightarrow {\text{d}} $. This is true in this case and the vector sum of all the vectors will be zero.

8. Three girls skating on a circular ice ground of radius $200\;{\text{m}}$ start from a point ${\text{P}}$ on the edge of the ground and reach a point ${\text{Q}}$ diametrically opposite to ${\text{P}}$ following different paths as shown in Fig. 4.20 . What is the magnitude of the displacement vector for each? For which girl is this equal to the actual length of the path skated?

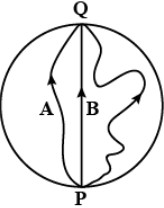
Ans:

The magnitudes of displacements are equal to the diameter of the ground.

Radius of the ground $ = 200\;{\text{m}}$

Diameter of the ground $ = 2 \times 200 = 400\;{\text{m}}$

So, the magnitude of the displacement for each girl is $400\;{\text{m}}$which is equal to the actual length of the path skated by girl ${\text{B}}$.

9. A cyclist starts from the centre ${\text{O}}$ of a circular park of radius $1\;{\text{ km}}$, reaches the edge ${\text{P}}$ of the park, then cycles along the circumference, and returns to the centre along ${\text{QO}}$ as shown in the following figure. If the round trip takes $1\;0$ min, what is the

(a) net displacement,

(b) average velocity, and

(c) average speed of the cyclist?

Ans 9:

(a) The cyclist comes to the starting point after cycling for $1\;0$ minutes. So, his net displacement is zero.

(b) Average velocity $ = \dfrac{{{\text{ Net displacement Total time }}}}{{{\text{ Total time }}}}$

As the net displacement of the cyclist is zero, his average velocity is also zero.

(c) ${\text{Average speed }} = \dfrac{{{\text{ Total path length }}}}{{{\text{ Total time }}}}$

${\text{Total path length }} = {\text{OP}} + {\text{PQ}} + {\text{QO}}$

$ = 1 + \dfrac{1}{4}(2\pi  \times 1) + 1$

$ = 2 + \dfrac{1}{2}\pi 3.570\;{\text{km}}$

Time taken $ = 10\;{\text{min}}$

$ = \dfrac{{10}}{{60}}$

$ = \dfrac{1}{6}\;{\text{h}}$

$\therefore $ Average speed $ = \dfrac{{3.570}}{1} = 21.42\;{\text{km}}/{\text{h}}$

10. On an open ground, a motorist follows a track that turns to his left by an angle of ${{60}^{0}}$ after every $500\;{\text{m}}$. Starting from a given turn, specify the displacement of the total at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.

Ans:

The path is a regular hexagon with side $500\;{\text{m}}$.

Let the motorist start from ${\text{P}}$.

The motorist takes the third turn at $S$.

$\therefore $ Magnitude of displacement $ = {\text{PS}}$

$ = {\text{PV}} + {\text{VS}}$

$ = 500 + 500$

$ = 1000\;{\text{m}}$

Total path length $ = {\text{PQ}} + {\text{QR}} + {\text{RS}}$

$ = 500 + 500 + 500$

$ = 1500\;{\text{m}}$

The motorist takes the sixth turn at $P$, which is the starting point.

$\therefore $ Magnitude of displacement $ = 0$

Total path length $ = {\text{PQ}} + {\text{QR}} + {\text{RS}} + {\text{ST}} + {\text{TU}} + {\text{UP}}$

$ = 500 + 500 + 500 + 500 + 500 + 500$

$ = 3000\;{\text{m}}$

The motorist takes the eight turn at $R$.

$\therefore {\text{ Magnitude of displacement }} = {\text{PR}}$

$ = \sqrt{{PQ^{2}}+{QR^{2}}+(PQ)(QR)cos 60^{0}}$

$ = \sqrt{{500^{2}}+{500^{2}}+(500)(500)cos 60^{0}} $

$ = \sqrt {250000 + 250000 + \left( {500000 \times \dfrac{1}{2}} \right)} $

$ = 866.03\;{\text{m}}$

$\beta  = tan^{-1}\left ( \frac{500\times sin60^{0}}{500+500\times cos 60^{0}} \right )$

$\beta  = {{30}^{0}}$

Thus, the magnitude of displacement is $866.03\;{\text{m}}$ at an angle of ${{30}^{0}}$ with ${\text{PR}}$.

Total path length $ = $ Circumference of the hexagon $ + {\text{PQ}} + $${\text{QR}}$

$ = 6 \times 500 + 500 + 500$

$ = 4000\;{\text{m}}$

11. A passenger arriving in a new town wishes to go from the station to a hotel located $10\;{\text{km}}$ away on a straight road from the station. A dishonest cabman takes him along a circuitous path $23\;{\text{km}}$ long and reaches the hotel in $28\;{\text{min}}$. What is

(a) the average speed of the taxi,

(b) the magnitude of average velocity? Are the two equal?

Ans:

(a) Total distance travelled $ = 23\;{\text{km}}$

Total time taken $ = 28\;{\text{min}} = \dfrac{{28}}{{60}}\;{\text{h}}$

Average speed of the taxi $ = \dfrac{{{\text{ Total distance travelled }}}}{{{\text{ Total time taken }}}}$

(b) Distance between the hotel and the station $ = 10\;{\text{km}} = $ Displacement of the car

$\therefore {\text{ Average velocity }} = \dfrac{{10}}{{\dfrac{{28}}{{60}}}}$

$ = 21.43\;{\text{km}}/{\text{h}}$

12. The ceiling of a long hall is $25\;{\text{m}}$ high. What is the maximum horizontal distance that a ball thrown with a speed of $40\;{\text{m}}{{\text{s}}^{ - 1}}$ can go without hitting the ceiling of the hall?

Ans:

Speed of the ball, $40\;{\text{m}}{{\text{s}}^{ - 1}}$

Maximum height, $h = 25\;{\text{m}}$

In projectile motion, the maximum height reached, by a body projected at an angle $\theta $ is:

$h=\frac{u^{2} sin^{2}\theta}{2g}$

$25=\frac{{{40}^{2}}{sin^{2}\theta}}{{2}\times {9.8}}$

$sin^{2}\theta =0.30625$

$sin \theta = 0.5534$

$\theta =sin^{-1}\left ( 0.5534 \right )$

$\theta = {33.60^ \circ }$

The horizontal range is 

$R=\frac{{u^{2}} sin2\theta }{g}$

${\text{R = }}\dfrac{{{{\left( {40} \right)}^{\text{2}}} \times {\text{sin2}} \times {\text{33}}{\text{.60}}}}{{9.8}}$

${\text{R = }}\dfrac{{1600 \times {\text{sin67}}{\text{.2}}}}{{9.8}}$

${\text{R = }}\dfrac{{1600 \times 0.922}}{{9.8}}$

${\text{R = }}150.53{\text{m}}$

13. A cricketer can throw a ball to a maximum horizontal distance of $100{\text{m}}$.How much high above the ground can the cricketer throw the same ball?

Ans:

Maximum horizontal distance, ${\text{R = }}100{\text{m}}$

The cricketer will throw the ball to the maximum horizontal distance when the angle of projection is ${{45}^{0}}$, i.e., $\theta  = {{45}^{0}}$

The horizontal range for a projection velocity ${\text{v}}$, is:

${\text{R}} = \dfrac{{{{\text{u}}^2}\sin 2\theta }}{{\text{g}}}$

${\text{100}} = \dfrac{{{{\text{u}}^2}\sin {{90}^{0}}}}{{\text{g}}}$

$\dfrac{{{{\text{u}}^2}}}{{\text{g}}} = 100{\text{      }}...{\text{(i)}}$

The ball will reach the maximum height when it is thrown vertically upward. For this type of motion, the final velocity is zero at the maximum height ${\text{H}}$.

Acceleration, ${\text{a}} =  - {\text{g}}$

Use the third equation of motion:

${{\text{v}}^2} - {{\text{u}}^2} =  - 2\;{\text{gH}}$

${\text{H}} = \dfrac{1}{2} \times \dfrac{{{{\text{u}}^2}}}{{\;{\text{g}}}}$

${\text{H}} = \dfrac{1}{2} \times 100$

${\text{H}} = 50\;{\text{m}}$

14. A stone tied to the end of a string $80\;{\text{cm}}$ long is whirled in a horizontal circle with a constant speed. If the stone makes $14$ revolutions in $25\;{\text{s}}$, what is the magnitude and direction of acceleration of the stone?

Ans:

Length of the string, $ = 80\;{\text{cm}} = 0.8\;{\text{m}}$

Number of revolutions $ = 14$

Time taken $ = 25\;{\text{s}}$

Frequency, ${\text{v}} = \dfrac{{{\text{ Number of revolutions }}}}{{{\text{ Time taken }}}} = \dfrac{{14}}{{25}}\;{\text{Hz}}$

Angular frequency, $\omega  = 2\pi {\text{v}}$

$ = 2 \times \dfrac{{22}}{7} \times \dfrac{{14}}{{25}}$

$ = \dfrac{{88}}{{25}}{\text{rad}}{{\text{s}}^{ - 1}}$

Centripetal acceleration, ${{\text{a}}_{\text{e}}} = {\omega ^2}{\text{r}}$

$ = {\left( {\dfrac{{88}}{{25}}} \right)^2} \times 0.8$

$ = 9.91\;{\text{m}}{{\text{s}}^{ - 2}}$

The direction of centripetal acceleration is always along the string, towards the center, at all points.

15. An aircraft executes a horizontal loop of radius $1.00\;{\text{km}}$ with a steady speed of $900\;{\text{km}}/{\text{h}}.$ Compare its centripetal acceleration with the acceleration due to gravity.

Ans:

Radius of the loop, ${\text{r}} = 1\;{\text{km}} = 1000\;{\text{m}}$

Speed of the aircraft, ${\text{v}} = 900\;{\text{km}}{{\text{h}}^{ - 1}}$

$ = 900 \times \dfrac{5}{{18}}$

$ = 250\;{\text{m}}{{\text{s}}^{ - 1}}$

Centripetal acceleration, ${{\text{a}}_{\text{e}}} = \dfrac{{{{\text{v}}^2}}}{{\text{r}}}$

$ = \dfrac{{{{(250)}^2}}}{{1000}}$

$ = 62.5\;{\text{m}}{{\text{s}}^{ - 2}}$

Acceleration due to gravity, ${\text{g}} = 9.8\;{\text{m}}{{\text{s}}^{ - 2}}$

$\dfrac{{{a_c}}}{g} = \dfrac{{6.25}}{{1000}}$

${a_c} = 6.38g$

The Centripetal acceleration is $6.38$ times the acceleration due to gravity.

16. Read each statement below carefully and state, with reasons, if it is true or false:

(a) The net acceleration of a particle m circular motion is always along the radius of the circle towards the centre

(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point

(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector

Ans:

(a) False

In circular motion, the net acceleration of a particle is not always directed along the radius of the circle toward the centre. It happens only in the case of uniform circular motion.

(b) True

At a point on a circular path, a particle appears to move tangentially to the circular path.

Thus, the velocity vector of the particle is always along the tangent at a point.

(c) True

In uniform circular motion, the acceleration vector points towards the centre of the circle. The average of these vectors over one cycle is a null vector.

17. The position of a particle is given by ${\text{r}} = 3.0{\text{t}}\widehat {\text{i}} - 2.0{{\text{t}}^2}\widehat {\text{j}} + 4.0\;{\text{km}}$

Where $t$ is in seconds and the coefficients have the proper units for $r$ to be in metres.

(a) Find the $v$ and $a$ of the particle?

(b) What is the magnitude and direction of velocity of the particle at ${\text{t}} = 2.0\;{\text{s}}?$

Ans:

$\overrightarrow {\text{v}} ({\text{t}}) = (3.0\widehat {\text{i}} - 4.0\widehat {\text{j}}):\overrightarrow {\text{a}}  =  - 4.0\widehat {\text{j}}$

The position of the particle is:

$\overrightarrow {\text{r}}  = 3.0\widehat {\text{i}} - 2.0{{\text{t}}^2}\widehat {\text{j}} + 4.0\widehat {\text{k}}$

Velocity, $\vec v$ of the particle is:

$\overrightarrow {\text{v}}  = \dfrac{{{\text{d}}\overrightarrow {\text{r}} }}{{{\text{dt}}}}$

$\overrightarrow {\text{v}}  = \dfrac{{\text{d}}}{{{\text{dt}}}}\left( {3.0{\text{t}}\widehat {\text{i}} - 2 \cdot {\text{O}}{{\text{t}}^2}\widehat {\text{j}} + 4.0{\text{k}}} \right)$

$\therefore \overrightarrow {\text{v}}  = 3.0\widehat {\text{i}} - 4.0{\text{t}}$

Acceleration of the particle is:

$\overrightarrow {\text{a}}  = \dfrac{{{\text{d}}\overrightarrow {\text{v}} }}{{{\text{dt}}}}$

$\overrightarrow {\text{a}}  = \dfrac{{\text{d}}}{{{\text{dt}}}}(3.0\widehat {\text{i}} - 4.{\text{O}}\widehat {\text{j}})$

$\therefore \overrightarrow {\text{a}}  =  - 4.{\text{O}}\widehat {\text{j}}$

The velocity vector, $\vec v = 3.0\hat i - 4.0t\hat j$

At ${\text{t}} = 2.0\;{\text{s}}$ :

$\overrightarrow {\text{v}}  = 3.0\widehat {\text{i}} - 8.0\widehat {\text{j}}$

The magnitude of velocity is:

$|\overrightarrow {\text{v}} | = \sqrt {{3^2} + {{( - 8)}^2}} $

$|\overrightarrow {\text{v}} | = \sqrt {73} $

$|\overrightarrow {\text{v}} | = 8.54\;{\text{m}}/{\text{s}}$

And $\theta  = {\tan ^{ - 1}}\left( {\dfrac{{{{\text{v}}_{\text{y}}}}}{{{{\text{v}}_{\text{x}}}}}} \right)$

$ = {\tan ^{ - 1}}\left( {\dfrac{{ - 8}}{3}} \right)$

$ =  - {\tan ^{ - 1}}(2.667)$

$ =  - {{69.45}^{0}}$

The negative sign indicates that the direction of velocity is $8.54\;{\text{m}}{{\text{s}}^{ - 1}}$, ${{69.45}^{0}}$ below the $x - $axis.

18. A particle starts from the origin at ${\text{t}} = 0\;{\text{s}}$ with a velocity of $10.07$ and moves in the $x - y$ plane with a constant acceleration of $(8.0\widehat {\text{i}} + 2.0\widehat {\text{j}}){\text{m}}{{\text{s}}^{{\text{ - 2}}}}$

(a) At what time is the $x - $ coordinate of the particle $16{\text{ m}}$? What is the $y - $coordinate of the particle at that time?

(b) What is the speed of the particle at the time?

Ans:

Velocity of the particle, $\overrightarrow {\text{v}}  = 10.0\widehat {\text{j}}{\text{ m}}{{\text{s}}^{ - 1}}$

Acceleration of the particle $\overrightarrow {\text{a}}  = (8.0\widehat {\text{i}} + 2.0\widehat {\text{j}})$

But, $\overrightarrow {\text{a}}  = \dfrac{{{\text{d}}\overrightarrow {\text{v}} }}{{{\text{dt}}}} = 8.0\widehat {\text{i}} + 2.0\widehat {\text{j}}$

${\text{d}}\overrightarrow {\text{v}}  = (8.0\widehat {\text{i}} + 2.0\widehat {\text{j}}){\text{dt}}$

Integrate both sides:

$\overrightarrow {\text{v}} ({\text{t}}) = 8.0\widehat {\text{i}} + 2.0\widehat {\text{j}} + \overrightarrow {\text{u}} $

Where,

$\overrightarrow {\text{u}}  = $ Velocity vector of the particle at ${\text{t}} = 0$

$\overrightarrow {\text{v}}  = $ Velocity vector of the particle at time $\phi $

But $\overrightarrow {\text{v}}  = \dfrac{{{\text{dr}}}}{{{\text{dt}}}}$ 

${\text{d}}\overrightarrow {\text{r}}  = \overrightarrow {\text{v}} {\text{dt}} = (8.0{\text{t}}\widehat {\text{i}} + 2.0{\text{t}}\widehat {\text{j}} + {\text{u}}){\text{dt}}$

Integrate the equations with: at ${\text{t}} = {\text{0}};{\text{ r}} = 0$ and at ${\text{t}} = {\text{t}};{\text{ r}} = {\text{r}}$

$\overrightarrow {\text{r}}  = \overrightarrow {\text{u}} {\text{t}} + \dfrac{1}{2}8.0{{\text{t}}^2}\widehat {\text{i}} + \dfrac{1}{2}2.0{{\text{t}}^2}\widehat {\text{j}}$

$ = \overrightarrow {\text{u}} {\text{t + 4 \times 0}}{{\text{t}}^{\text{2}}}\widehat {\text{i}}{\text{ + }}{{\text{t}}^{\text{2}}}\widehat {\text{j}}$

$ = (10.0{\text{j}}){\text{t}} + 4.0{{\text{t}}^2}\widehat {\text{i}} + {{\text{i}}^2}\widehat {\text{j}}$

${\text{x}}\widehat {\text{i}} + \widehat {\text{y}} = 4.0{{\text{t}}^2}\widehat {\text{i}} + \left( {10{\text{t}} + {{\text{t}}^2}} \right)\widehat {\text{j}}$

Equate the coefficients of $\widehat {\text{i}}$ and $\widehat {\text{j}}$:

$x = 4{t^2}$

$t = {\left( {\dfrac{x}{4}} \right)^{\dfrac{1}{2}}}$

And $y = 10t + {t^2}$

When ${\text{x}} = 16\;{\text{m}}$ :

$t = {\left( {\dfrac{{16}}{4}} \right)^{\dfrac{1}{2}}}$

$t = 2s$

$\therefore y = 10 \times 2 + {(2)^2} = 24m$

Velocity of the particle is:

$\overrightarrow {\text{v}} ({\text{t}}) = 8.0{\text{t}}\widehat {\text{i}} + 2.0\widehat {\text{t}} + \overrightarrow {\text{u}} $

At ${\text{t}} = 2\;{\text{s}}$

$\overrightarrow {\text{v}} ({\text{t}}) = 8.0 \times 2\widehat {\text{i}} + 2.0 \times 2\widehat {\text{j}} + 10\widehat {\text{j}}$

$ = 16\widehat {\text{i}} + 14\widehat {\text{j}}$

$\therefore $ Speed of the particle:

$|\vec v| = \sqrt {{{(16)}^2} + {{(14)}^2}} $

$ = \sqrt {256 + 196} $

$ = \sqrt {452} $

$ = 21.26\;{\text{m}}{{\text{s}}^{ - 1}}$

19. $\widehat {\text{i}}$ and $\widehat {\text{j}}$ are unit vectors along ${\text{x}} - $ and ${\text{y}}$-axis respectively. What is the magnitude and direction of the vectors $\widehat {\text{i}} + \widehat {\text{j}}$ and $\widehat {\text{i}}.\widehat {\text{j}}$? What are the components of a vector ${\text{a}} = 2\widehat {\text{i}} + 3\widehat {\text{j}}$ along the directions of $\widehat {\text{i}} + \widehat {\text{j}}$ and $\widehat {\text{i}} - \widehat {\text{j}}$? 

Ans:

Consider a vector $\overrightarrow {\text{P}} $

\[\overrightarrow {\text{P}}  = \widehat {\text{i}} + \widehat {\text{j}}\]

\[{{\text{P}}_{\text{x}}}\widehat {\text{i}} + {{\text{P}}_{\text{y}}}\widehat {\text{j}} = \widehat {\text{i}} + \widehat {\text{j}}\]

Compare the components on both sides:

\[{{\text{P}}_{\text{x}}}{\text{ = }}{{\text{P}}_{\text{y}}}{\text{ = 1}}\]

\[\left| {\overrightarrow {\text{P}} } \right| = \sqrt {{{\text{P}}_{\text{x}}}^2 + {{\text{P}}_{\text{y}}}^2} \]

\[\left| {\overrightarrow {\text{P}} } \right| = \sqrt {{1^2} + {{\text{1}}^2}} \]

\[\left| {\overrightarrow {\text{P}} } \right| = \sqrt 2 {\text{     }}...{\text{(i)}}\]

So, the magnitude of the vector $\widehat {\text{i}} + \widehat {\text{j}}$ is $\sqrt 2 $

Let $\theta $ be the angle made by $\overrightarrow {\text{P}} $, with the ${\text{x - }}$axis.

So, \[{\text{tan}}\theta {\text{ = }}\left( {\dfrac{{{{\text{P}}_{\text{x}}}}}{{{{\text{P}}_{\text{y}}}}}} \right)\]

\[\theta {\text{ = ta}}{{\text{n}}^{ - 1}}\left( {\dfrac{{\text{1}}}{{\text{1}}}} \right)\]

\[\theta {\text{ = 4}}{{\text{5}}^ \circ }{\text{     }}...{\text{(ii)}}\]

So, the vector $\widehat {\text{i}} + \widehat {\text{j}}$ makes an angle of ${{45}^{0}}$ with the ${\text{x - }}$axis

Let $\theta $ be the angle made by $\overrightarrow {\text{Q}} $, with the ${\text{x - }}$axis.

$\overrightarrow {\text{Q}}  = \widehat {\text{i}} - \widehat {\text{j}}$

${{\text{Q}}_{\text{x}}}\widehat {\text{i}} - {{\text{Q}}_{\text{y}}}\widehat {\text{j}} = \widehat {\text{i}} - \widehat {\text{j}}$

${{\text{Q}}_{\text{x}}} + {{\text{Q}}_{\text{y}}} = 1$

$|\overrightarrow {\text{Q}} | = \sqrt {{\text{Q}}_{\text{x}}^2 + {\text{Q}}_{\text{y}}^2} $

$|\overrightarrow {\text{Q}} | = \sqrt 2 $

So, the magnitude of the vector $\widehat {\text{i}} - \widehat {\text{j}}$ is $\sqrt 2 $.

Let $\theta $ be the angle made by the vector $\overrightarrow {\text{Q}} $, with the ${\text{x - }}$axis.

$\therefore \tan \theta  = \left( {\dfrac{{{{\text{Q}}_y}}}{{{{\text{Q}}_{\text{x}}}}}} \right)$

$\theta  =  - {\tan ^{ - 1}}\left( { - \dfrac{1}{1}} \right)$

$\theta  =  - {{45}^{0}}$

So, the vector $\widehat {\text{i}} - \widehat {\text{j}}$ makes and angle of $ - {{45}^{0}}$ with the axis.

Compare the coefficients of $\widehat {\text{i}}$ and $\widehat {\text{j}}$

$\overrightarrow {\text{A}}  = 2\widehat {\text{i}} + 3\widehat {\text{j}}$

${{\text{A}}_{\text{x}}}\widehat {\text{i}}{\text{ + }}{{\text{A}}_{\text{y}}}\widehat {\text{j}}{\text{ = 2}}\widehat {\text{i}}{\text{ + 3}}\widehat {\text{j}}$

Let $\overline {\text{A}} $ make an angle $\theta $ with the ${\text{x - }}$axis

$\therefore \tan \theta  = \left( {\dfrac{{{A_x}}}{{{A_y}}}} \right)$

$\theta  = {\tan ^{ - 1}}\left( {\dfrac{3}{2}} \right)$

$ = {\tan ^{ - 1}}(1.5)$

$ = {{56.31}^{0}}$

Angle between $(2\hat i + 3\hat j)$ and $(\hat i + \hat j)$

$\theta  = 56.31 - 45 = {{11.31}^{0}}$

$\vec A$, along the direction of $\vec P$ making an angle ${\theta ^\prime }$

$\therefore \tan \theta  = \left( {\dfrac{{{{\text{A}}_{\text{x}}}}}{{{{\text{A}}_{\text{y}}}}}} \right)$

$\tan \theta  = ({\text{A}}\cos \theta ){\text{P}}$

$\tan \theta  = ({\text{A}}\cos 11.31)\dfrac{{(\widehat {\text{i}} + \widehat {\text{j}})}}{{\sqrt 2 }}$

$\tan \theta  = \sqrt {13}  \times \dfrac{{0.9806}}{{\sqrt 2 }}(\widehat {\text{i}} + \widehat {\text{j}})$

$\tan \theta  = 2.5(\widehat {\text{i}} + \widehat {\text{j}})$

$\tan \theta  = \dfrac{{25}}{{10}} \times \sqrt 2 $

$\tan \theta  = \dfrac{5}{{\sqrt 2 }}\quad  \ldots ({\text{v}})$

Let $\theta $ be the angle between $(2\hat i + 3\hat j)$ and $(\hat i + \hat j)$ 

${\theta ^{\prime \prime }} = 45 + 56.31 = {{101.31}^{0}}$

Component of vector ${\text{A}}$, along the direction of ${\text{Q}}$, making an angle $\theta $ 

$ = (A\cos \theta )\vec Q$

$ = (A\cos \theta )\dfrac{{(\hat i - \hat j)}}{{\sqrt 2 }}$

$ = \sqrt {13} \cos \left( {{{901.31}^{0}}} \right)\dfrac{{{\text{(}}\widehat{\text{i}}+{\hat{\text{j}}}})}{{\sqrt {\text{2}}}}$

$ =  - \sqrt {\dfrac{{13}}{2}} \sin {{11.30}^{0}}(\widehat {\text{i}} - \widehat {\text{j}})$

$ =  - 2.550 \times 0.1961(\widehat {\text{i}} - \widehat {\text{j}})$

$ =  - 0.5(\widehat {\text{i}} - {\text{j}})$

$ =  - \dfrac{5}{{10}} \times \sqrt 2 $

$ =  - \dfrac{1}{{\sqrt 2 }}$

20. For any arbitrary motion in space, which of the following relations are true:

(a) ${{\text{v}}_{{\text{average}}}}{\text{ = }}\left( {\dfrac{{\text{1}}}{{\text{2}}}} \right)\left( {{\text{v}}\left( {{{\text{t}}_{\text{1}}}} \right){\text{ + v}}\left( {{{\text{t}}_{\text{2}}}} \right)} \right)$

(b) ${{\text{v}}_{{\text{average}}}}{\text{ = }}\dfrac{{{\text{[r(}}{{\text{t}}_{\text{2}}}{\text{) - r(}}{{\text{t}}_{\text{1}}}{\text{)]}}}}{{{\text{(}}{{\text{t}}_{\text{2}}}{\text{ - }}{{\text{t}}_{\text{1}}}{\text{)}}}}$

(c) ${\text{v(t) = v(0) + at}}$

(d) ${\text{r(t) = r(0) + v(0)t + }}\left( {\dfrac{1}{2}} \right){\text{a}}{{\text{t}}^2}$

(e) ${{\text{a}}_{{\text{average}}}}{\text{ = }}\dfrac{{{\text{[v(}}{{\text{t}}_{\text{2}}}{\text{) - v(}}{{\text{t}}_{\text{1}}}{\text{)]}}}}{{{\text{(}}{{\text{t}}_{\text{2}}}{\text{ - }}{{\text{t}}_{\text{1}}}{\text{)}}}}$

(The ‘average’ stands for average of the quantity over the time interval ${t_1}$ to ${t_2}$)

Ans:

(a) False. As the motion of the particle is arbitrary, the average velocity of the particle cannot be given by this equation.

(b) True. The arbitrary motion of the particle can be represented by the given equation.

(c) False. The motion of the particle is arbitrary. The acceleration of the particle may also be non-uniform. So, this equation cannot represent the motion of the particle in space.

(d) False. The motion of the particle is arbitrary, acceleration of the particle may also be non-uniform. So, this equation cannot represent the motion of particle in space.

(e) True. The arbitrary motion of the particle can be represented by the given equation.

21. Read each statement below carefully and state, with reasons and examples, if it is true or false:

A scalar quantity is one that:

(a) is conserved in a process

(b) can never take negative values

(c) must be dimensionless

(d) does not vary from one point to another in space

(e) has the same value for observers with different orientations of axes

Ans:

(a) False. Energy is not conserved in inelastic collisions.

(b) False. Temperature can take negative values.

(c) False. Total path length is a scalar quantity and has the dimension of length.

(d) False. A scalar quantity like gravitational potential can vary from one point to another in space.

(e) True. The value of a scalar does not change for observers with different orientations of axes.

22. An aircraft is flying at a height of $3400\;{\text{m}}$ above the ground. If the angle subtended at a ground observation point by the aircraft positions $10.0\;{\text{s}}$ apart is ${{30}^{0}}$, what is the speed of the aircraft?

Ans:

The positions of the observer and the aircraft are shown below:

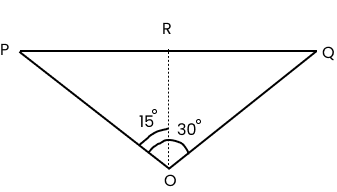
Height of the aircraft from ground, ${\text{OR}} = 3400\;{\text{m}}$

Angle subtended between the positions, $\angle {\text{POQ}} = {{30}^{0}}$

Time $ = 10\;{\text{s}}$

In $\Delta {\text{PRO}}:$

$\tan {{15}^{0}} = \dfrac{{PR}}{{OR}}$

$PR = OR\tan {{15}^{0}}$

$PR = 3400 \times \tan {{15}^{0} }$

$\Delta $PRO is similar to $\Delta RQO$

$\therefore {\text{PR}} = {\text{RQ}}$

${\text{PQ}} = {\text{PR}} + {\text{RQ}}$

${\text{PQ}} = 2{\text{PR}}$

${\text{PQ}} = 2 \times 3400\tan {{15}^{0}}$

${\text{PQ}} = 6800 \times 0.268$

${\text{PQ}} = 1822.4\;{\text{m}}$

$\therefore $ Speed of the aircraft $ = \dfrac{{1822.4}}{{10}} = 182.24\;{\text{m}}/{\text{s}}$

Physics Chapter 3 Motion in a Plane Summary - Class 11 NCERT Solutions

• Scalar quantities are quantities with magnitudes only. Examples are distance, speed, mass and temperature

• Vector quantities are quantities with magnitude and direction both. Examples are displacement, velocity and acceleration. They ob key special rules of vector algebra.

• A vector $ \vec{A}$ multiplied by a real number λ is also a vector, whose magnitude is λ times the magnitude of the vector $ \vec{A}$ and whose direction is the same or opposite depending upon whether λ is positive or negative.

• Two vectors $ \vec{A}$ and $ \vec{B}$ may be added graphically using head to tail method or parallelogram method.

• Vector addition is commutative: $\vec{A}+\vec{B}=\vec{B}+\vec{A}$

• It also obeys the associative law:

$(\vec{A+B)}+\vec{C}=\vec{A}+(\vec{B+C})$

• A null or zero vector is a vector with zero magnitude. Since the magnitude is zero, we don’t have to specify its direction. It has the properties:

$\vec{A}+0=\vec{A}$

$\vec{A}0=0$

$40\vec{A}=0$

• The subtraction of vector $\vec{B}$ from  $\vec{A}$ is defined as the sum of $\vec{A}$ and $\vec{-B}$ :

$\vec{A}-\vec{B}=\vec{A}+(-\vec{B})$

• A vector A can be resolved into component along two given vectors a and b lying in the same plane: 

$\vec{A}=\lambda \vec{A}+\mu \vec{B}$ where λ and µ are real numbers.

• A unit vector associated with a vector $\vec{A}$ has magnitude one and is along the vector $ \vec{A}$ :

$\hat{n}=\dfrac{\vec{A}}{|A|}$

• The unit vectors $ \hat{a},\hat{j}$ and $\hat{k}$ are vectors of unit magnitude and point in the direction of the x-, y-, and z-axes, respectively in a right-handed coordinate system.

• A vector $\vec{A}$ can be expressed as $\vec{A}=A_{x}\hat{i}+A_{y}\hat{j}$ where Ax,Ay are its components along x-, and y-axes. If vector $\vec{A}$ makes an angle θ with the x-axis, then $Ax=\vec{A}cos\theta$ , $Ay=\vec{A}sin\theta$ and $A=\vec{|A|}=\sqrt{A_{x}^{2}+A_{y}^{2}}$ , $tan\theta \dfrac{A_{y}}{A_{x}}$

• Vectors can be conveniently added using analytical method. If sum of two vectors $\vec{A}$ and $\vec{B}$ , that lie in x-y plane, is R, then: $\vec{R}=R_{x}\hat{i}+R_{y}\hat{j}$ . where, Rx=Ax+Bx  and Ry=Ay+By

• The position vector of an object in x-y plane is given by $r=x\hat{i}+y\hat{j}$ and the displacement from position r to position ${r}'$ is given by

$\Delta \hat{r}=\vec{r'}-\vec{r}$

$({x}'-x)\hat{i}+({y}'-y)\hat{j}$

$\Delta x\hat{i}+\Delta y\hat{j}$

• If an object undergoes a displacement $\Delta r$ in time $\Delta t$ , its average velocity is given by $V=\dfrac{\Delta r}{\Delta t}$ . The velocity of an object at time t is the limiting value of the average velocity as  $\Delta t$ tends to zero: $V=\lim_{\Delta t\rightarrow 0}\dfrac{\Delta r}{\Delta t}=\dfrac{dr}{dt}$ . It can be written in unit vector notation as: $V=V_{x}\hat{i}+V_{y}\hat{i}+V_{z}\hat{k}$  where $V_{x}=\dfrac{dx}{dt}$ , $V_{y}=\dfrac{dy}{dt}$ , $V_{z}=\frac{dz}{dt}$ 

• When position of an object is plotted on a coordinate system, $\vec{V}$ is always tangent to the curve representing the path of the object.

• If the velocity of an object changes from $\vec{V}$ to $\vec{V'}$ in time $\Delta t$ , then its average acceleration is given by: $\vec{a}=\dfrac{\vec{v}-\vec{v'}}{\Delta t}=\frac{\Delta \vec{v}}{\Delta t}$

• The acceleration $\vec{a}$ at any time t is the limiting value of $\vec{a}$ as $\Delta t\rightarrow 0$ ,

$\vec{a}=\lim_{\Delta t\rightarrow 0}\dfrac{\Delta \vec{v'}}{\Delta t}=\dfrac{d\vec{v}}{dt}$

• In component form, we have: $\vec{a}=a_{x}\hat{i}+a_{y}\hat{j}+a_{z}\hat{k}$ Where,  $a_{x}=\dfrac{dv_{x}}{dt}$ , $a_{y}=\dfrac{dv_{y}}{dt}$ , $a_{z}=\dfrac{dv_{x}}{dt}$

• Relative motion can be defined as the comparison between the motions of a single object to the motion of another object moving with the same velocity. Relative motion can be easily found out with the help of the concept of relative velocity, relative acceleration or relative speed

• The relative velocity of an object A with respect to object B is the rate of position of the object A with respect of object B.

If VA and VB be the velocities of objects A and B with respect to the ground, then: 

(a) The relative velocity of A with respect to B is 

VAB = VA – VB

(b) The relative velocity of B with respect to A is 

VBA = VA – VB

SI unit: m/s

Dimensional Formula: [LT-1]

• Relative Acceleration: The relative acceleration (also ar) is the acceleration of an object or observer B in the rest frame of another object or observer A.

Acceleration of B relative to A = aB - aA

SI unit: m/s2

Dimensional Formula: [LT-2]

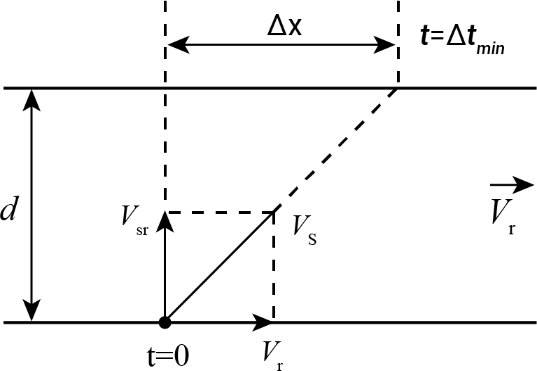
• Time of Crossing: Component (vr + vsr cos 𝜽) will enable the person to drift along the length of river. Hence drift Δx will be 

$\Delta t=\dfrac{d}{v_{sr}sin\theta }$ ….(1)

$\Delta x=(v_{r}+v_{sr}cos\theta )\Delta t$ ....(2)

• Minimum Time of Crossing

$\therefore \Delta t_{min}=\dfrac{d}{v_{sr}}$ And hence

Drift $\Delta x=v_{r}\left ( \dfrac{d}{v_{sr}} \right )$

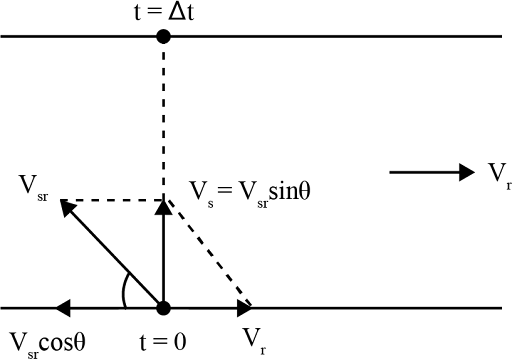
• Shortest Path: The person should try to swim such that the resultant velocity becomes perpendicular to the river flow.

$\therefore \Delta t=\dfrac{d}{\sqrt{v_{sr}^{2}-v_{r}^{2}}}$

• Rain-man Umbrella Problems

A person standing/running in a particular direction would be needed to be protected by properly directing the axis of the umbrella.

Overview of Deleted Syllabus for CBSE Class 11 Physics Motion in a Plane

Conclusion

NCERT Class 11 Physics Chapter 3 Solutions on Motion in a Plane provided by Vedantu equips students with a comprehensive understanding of two-dimensional motion, expanding their analytical skills and preparing them for more advanced topics in physics. Through this chapter, students learn to apply vector algebra to solve problems, analyse the trajectory of projectiles, and understand the dynamics of circular motion. This chapter bridges the gap between basic kinematic concepts and more complex motion analysis. By mastering the concepts in this chapter, students will be well-prepared for future topics in mechanics and other areas of physics. From previous year's question papers, typically around 5–7 questions are asked from this chapter. These questions test students' understanding of theoretical concepts as well as their problem-solving skills.

Other Study Material for CBSE Class 11 Physics Chapter 3

Chapter-Specific NCERT Solutions for Class 11 Physics

Given below are the chapter-wise NCERT Solutions for Class 11 Physics. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

CBSE Class 11 Physics Study Materials