Motion In A Straight Line Class 11 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26
1. What is motion in straight line class 11?
Motion in a straight line refers to the movement of an object along a single dimension where the particle's position can be described by a single coordinate. This type of motion involves concepts like displacement, velocity, acceleration, and equations of motion, forming the foundation of kinematics in physics.
2. How do NCERT Solutions for motion in a straight line help students understand kinematics concepts?
NCERT Solutions provide step-by-step explanations for all textbook problems, breaking down complex kinematic equations and graph interpretations into manageable parts. Students often struggle with connecting mathematical formulas to real-world motion scenarios.
Students can solve similar problems independently after reviewing solutions.
These comprehensive solutions bridge the gap between theoretical concepts and practical problem-solving skills essential for physics mastery.
3. What are the 4 formulas for linear motion?
The four kinematic equations for uniform acceleration are: v = u + at (velocity-time relation), s = ut + ½at² (position-time relation), v² = u² + 2as (velocity-displacement relation), and s = (u + v)t/2 (average velocity relation). These equations connect displacement, initial velocity, final velocity, acceleration, and time.
4. Can students access motion in a straight line class 11 pdf materials for offline study?
Students can download comprehensive study materials including NCERT Solutions, chapter notes, and practice questions in PDF format from Vedantu for convenient offline access.
5. What does uniform acceleration mean in straight line motion?
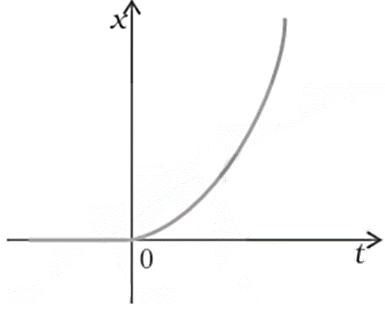
Uniform acceleration occurs when an object's velocity changes by equal amounts in equal time intervals. The acceleration remains constant throughout the motion, making it possible to use kinematic equations. Examples include free fall under gravity and motion of vehicles with constant throttle.
6. How do velocity-time graphs represent different types of motion?
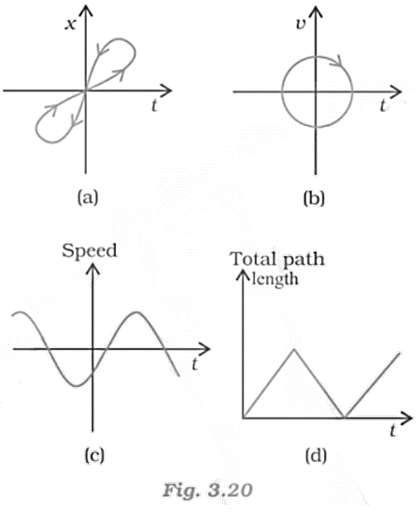
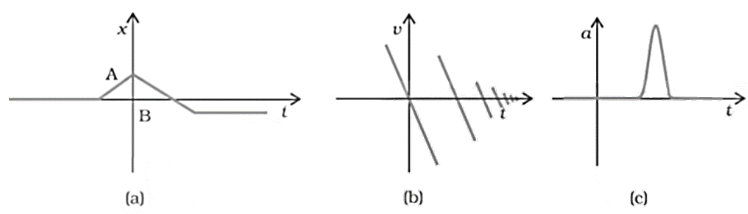
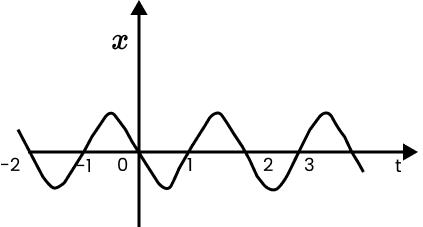
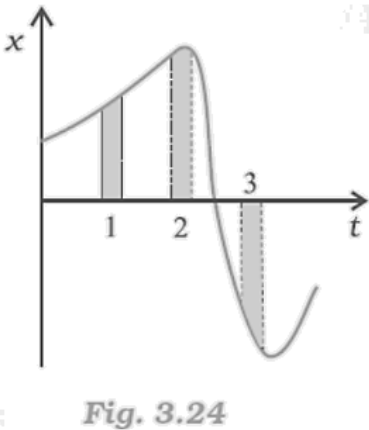
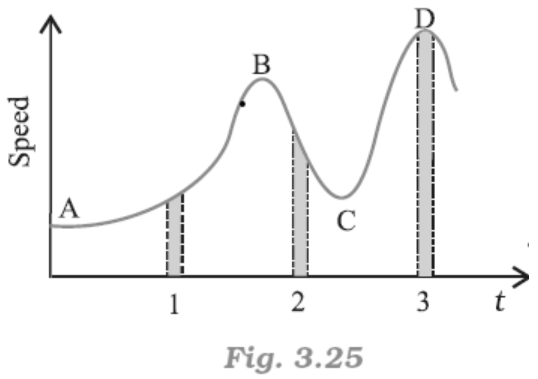
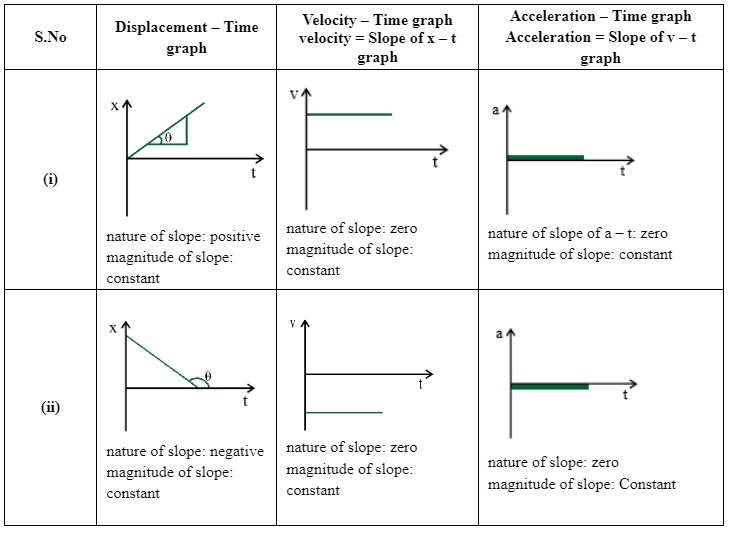
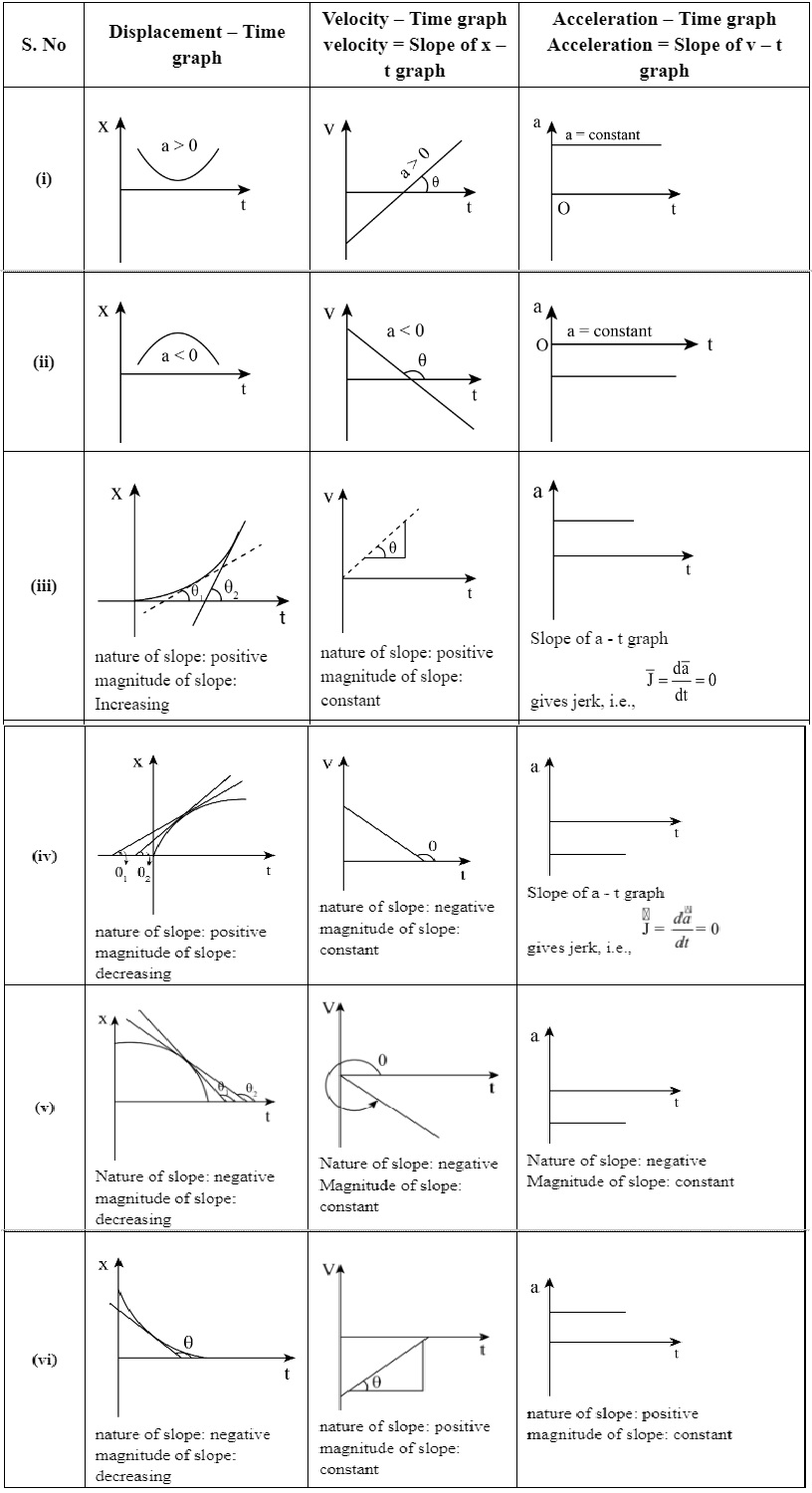
Velocity-time graphs visually represent motion characteristics where the slope indicates acceleration and the area under the curve represents displacement. Graphical interpretation helps students understand motion patterns more intuitively than equations alone.
7. What is relative velocity in one-dimensional motion?
Relative velocity is the velocity of one object as observed from another moving object. In straight line motion, it's calculated as the vector difference of individual velocities. When objects move in the same direction, relative velocity decreases; when opposite, it increases proportionally.
8. Why are sign conventions important in kinematic problems?
Sign conventions establish consistent directional references, typically choosing positive direction as rightward or upward motion and negative for opposite directions. Incorrect sign usage leads to wrong numerical answers and conceptual confusion in physics problems.
9. What are common examples of straight line motion in daily life?
Examples of straight line motion include a car moving on a straight road, a ball thrown vertically upward, an elevator moving between floors, a train on straight tracks, and objects in free fall.
10. How do class 11 Physics motion in a straight line NCERT solutions address numerical problems?
NCERT Solutions provide systematic approaches to numerical problems, showing proper formula selection, unit conversions, and mathematical calculations with clear reasoning. Numerical proficiency builds confidence and prepares students for competitive examinations requiring quick problem-solving skills.