NCERT Exemplar for Class 11 Physics Chapter 3 - Motion in a Straight Line (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS-I

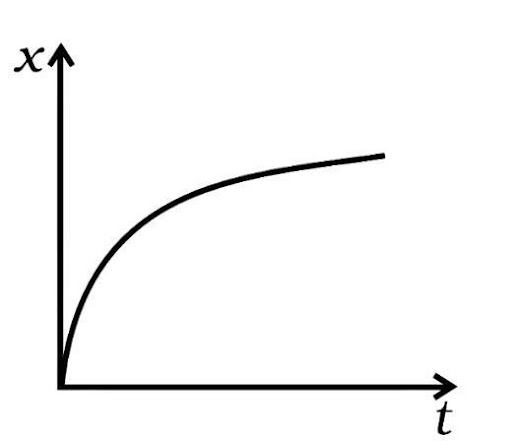
3.1. Among the four graphs given below, there is only one graph for which average velocity over the time interval (0, T) can vanish for a suitably chosen T. Which one is it?

(a) 

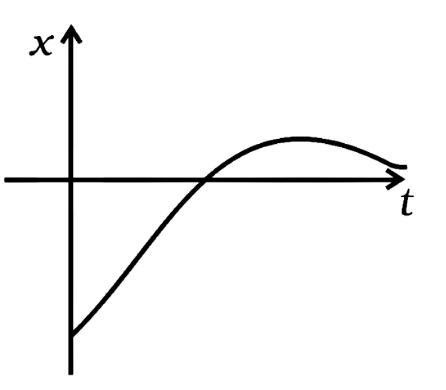
(b) 

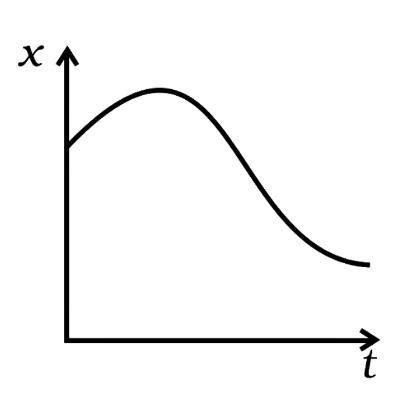
(c) 

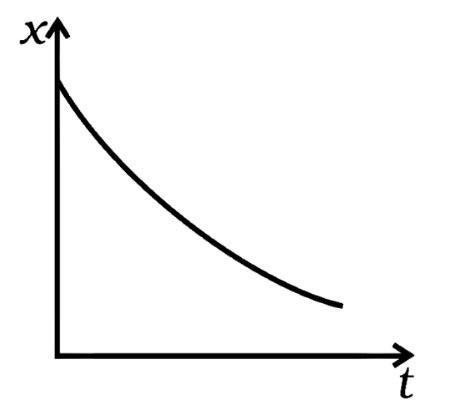
(d) 

Ans: (b)

Main concept used: Average velocity of the body will sum up to be zero (average velocity is total displacement by total time). Here in the above graphs shows displacement for different timings in any time interval-T in the x-t graph.

We must locate the graph in which there is both positive and negative displacement at various timings, implying that these displacements are in opposing directions and that when these opposite displacements are added, net displacement or the average velocity is zero. Only in the graph is this feasible (b).

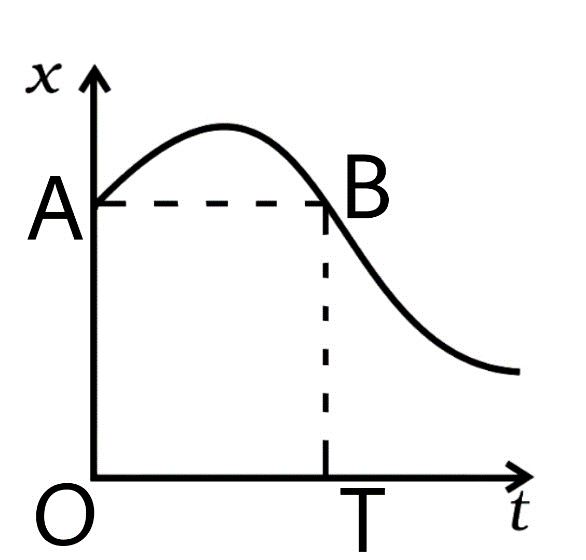
If we draw a line from the point (A) on the graph at t=0 sec which is parallel to the time axis. This line can intersect the graph at B once more. Because the change in displacement (O-T) time is zero at this point, i.e., the displacements at A and B are equal, the average velocity of the body vanishes to zero.

3.2. A lift is coming from the 8th floor and is just about to reach the 4th floor. Taking ground floor as Origin and positive direction upwards for all quantities, which one of the following is correct?

(a) x<0, v<0, a>0

(b) x>o, v<0, a<0

(c) x>o, v<0, a>0

(d) x>o, v>0, a<0

Ans: (a)

As the lift progresses from 8th to 4th, the value of x decreases (becomes negative), i.e., x<0. The speed is decreasing (i.e., negative). So, the velocity v<0. The lift is retarded until it reaches the fourth floor, at which point it accelerates upwards. As a result, a>0

The correct answer is (a).

3.3. In one-dimensional motion, instantaneous speed v satisfies \[{\mathbf{0}} \leqslant {\mathbf{v}} < {{\mathbf{v}}_{\mathbf{0}}}\].

(a) The displacement in time T must always take non-negative values.

(b) The displacement x in time T satisfies -${v_0}$T < x < ${v_0}$T.

(c) The acceleration is always a non-negative number.

(d) The motion has no turning points.

Ans: (b)

We have the magnitude and direction of maximum and minimum velocity and also the value of maximum and minimum displacement.

Maximum velocity in the positive direction is ${v_0}$, 

Maximum velocity in the negative direction is also ${v_0}$, 

As a result, we can claim that the 

Maximum displacement in the positive direction is = ${v_0}$T

and the maximum displacement in the opposite direction is = -${v_0}$T.

As a result, the right statement is - ${v_0}$T < x < ${v_0}$T.

The correct answer is (b).

3.4. A vehicle travels half the distance L with speed v1 and the other half with speed v2, then its average speed is

(a) $\dfrac{{{v_1} + {v_2}}}{2}$

(b) $\dfrac{{2{v_1} + {v_2}}}{{{v_1} + {v_2}}}$

(c) $\dfrac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}$

(d) $\dfrac{{L\left( {{v_1} + {v_2}} \right)}}{{{v_1}{v_2}}}$

Ans: (c) 

The time taken in first half distance ${t_1} = \dfrac{L}{{{v_1}}}$

The time taken in second half distance ${t_2} = \dfrac{L}{{{v_2}}}$

Total time (t) taken in total distance (L+L) is $T = \dfrac{L}{{{v_1}}} + \dfrac{L}{{{v_2}}} = \dfrac{{L\left( {{v_1} + {v_2}} \right)}}{{{v_1}{v_2}}}$

Total distance = L + L = 2L

Average speed of the whole traveling is total distance divided by total time

${S_{avg}} = \dfrac{{2L}}{{\dfrac{{L\left( {{v_1} + {v_2}} \right)}}{{{v_1}{v_2}}}}} = \dfrac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}$

Thus, the correct answer is (c).

3.5. The displacement of a particle is given by $x\left( t \right) = {\left( {t - 2} \right)^2}m$  where x is in meters and t in seconds. The distance covered by the particle in first 4 second is:

(a) 4m

(b) 8m

(c) 12m

(d) 16m

Ans: (b)

Displacement function is $x\left( t \right) = {\left( {t - 2} \right)^2}m$

Velocity $v\left( t \right) = \dfrac{{dx}}{{dt}} = 2\left( {t - 2} \right)m/s$

Acceleration $a\left( t \right) = \dfrac{{dv}}{{dt}} = 2m/{s^2}$

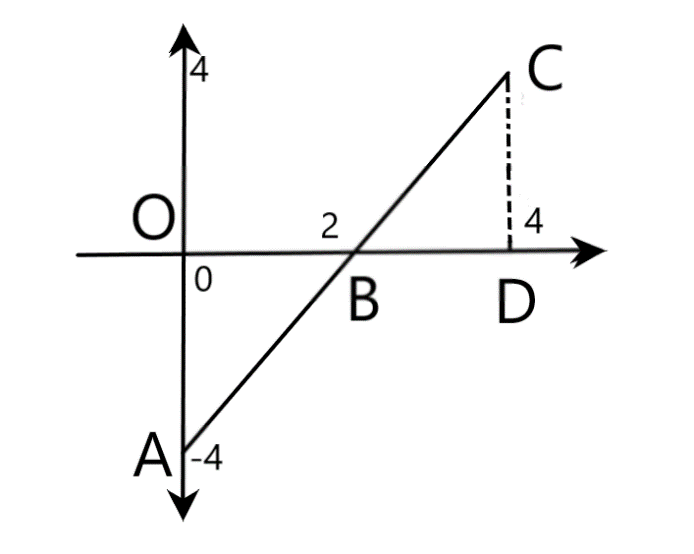
Distance covered = Area between time axis and (v-t) graph

Which is = area of triangle OAB and triangle BCD

Distance $ = \dfrac{1}{2} \times OA \times OB + \dfrac{1}{2} \times BD \times CD = \dfrac{1}{2} \times 2 \times 4 + \dfrac{1}{2} \times 2 \times 4 = 8$ 

Distance travelled is 8 meters.

Correct option is (b).

3.6. At the metro station, a girl walks up a stationary escalator in time ${t_1}$. If she remains stationary on the escalator, then the escalator takes her up in time ${t_2}$. The time taken by her to walk up on the moving escalator will be:

(a) \[\dfrac{{\left( {{t_1} + {t_2}} \right)}}{2}\]

(b) $\dfrac{{\left( {2{t_1}{t_2}} \right)}}{{\left( {{t_1} - {t_2}} \right)}}$

(c) $\dfrac{{\left( {{t_1}{t_2}} \right)}}{{\left( {{t_1} + {t_2}} \right)}}$

(d) \[\left( {{t_1} - {t_2}} \right)\]

Ans: (c) 

Let L be the total length of the escalator.

Velocity of girl with respect to the ground ${v_g} = \dfrac{L}{{{t_1}}}$

Velocity of escalator with respect to the ground ${v_e} = \dfrac{L}{{{t_2}}}$

The effective velocity of the girl on moving escalator with respect to the ground is:

${v_g} + {v_e} = \dfrac{L}{{{t_2}}} + \dfrac{L}{{{t_1}}} = \dfrac{{L\left( {{t_2} + {t_1}} \right)}}{{{t_1}{t_2}}}$

The time taken by the girl on moving escalator in going up the distance L is:

\[t = \dfrac{L}{{\dfrac{{L\left( {{t_2} + {t_1}} \right)}}{{{t_1}{t_2}}}}} = \dfrac{{{t_2}{t_1}}}{{{t_1} + {t_2}}}\]

Thus, the correct option is (c).

MULTIPLE CHOICE QUESTIONS-II

3.7. The variation of quantity A with quantity B, plotted in the figure. Describe the motion of a particle in a straight line.

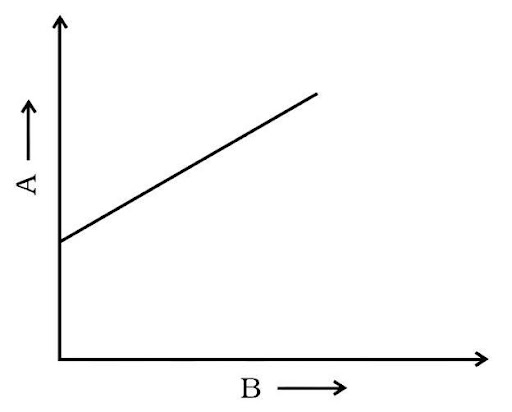
(a) Quantity B may represent time.

(b) Quantity A is velocity if the motion is uniform.

(c) Quantity A is displacement if the motion is uniform.

(d) Quantity A is velocity if the motion is uniformly accelerated.

Ans: (a, c, d,)

If B stands for velocity, the graph becomes the v-t graph is a straight line, indicating evenly accelerated motion; nevertheless, motion is not uniform. Thus, the option (a) and (d) are verified. If B denotes time and A denotes displacement, the graph is known as a (s-t) graph. The option is verified since the s-t graph is a straight line that reflects uniform motion (c).

3.8. A graph of x versus t shown in x figure. Choose correct alternatives from below.

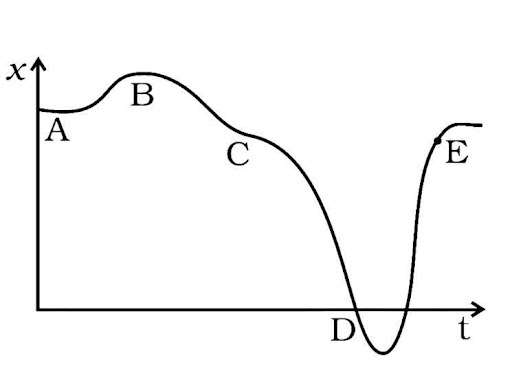
(a) The particle was released from rest at t=0

(b) At B, the acceleration a>0

(c) At C, the velocity and acceleration vanishes.

(d) Average velocity for the motion A and D is positive.

(e) The speed at D exceeds that at E.

Ans: (a, c, e,)

Slope of the graph is $\dfrac{{dx}}{{dt}}$

A graph (x-t) is parallel to the time axis, indicating that $\dfrac{{dx}}{{dt}}$ it is either zero or the particle is at rest. After A, the slope $\dfrac{{dx}}{{dt}}$ rises, and the velocity rises with it. Option is checked (a).

A graph (x-t) that is parallel to the time axis, so the $\dfrac{{dx}}{{dt}} = 0$ or v=0, is tangent at B and C. It implies that a=0 is the acceleration. As a result, option (b) is discarded, and option (a) is verified (c). The slope at D is larger than at E, according to the graph. As a result, the speed at D is greater than the speed at E. Verifies the option (e).

Because x-t is parallel to the time axis, the average velocity at A is zero. The slope or displacement at D is negative. As a result, the fact that the average velocity at D is negative rather than positive eliminates the choice (d). 

3.9. For the one-dimensional motion, described by x=t-sin t

(a) X(t)> 0 for all t>0

(b) V(t)>0 for all t>0

(c) A(t)>0for all t>0

(d) V(t) lies between 0 and 2

Ans: (a, d) 

The displacement function is $x\left( t \right) = t - \sin t$

The velocity function is $v\left( t \right) = \dfrac{{dx}}{{dt}} = 1 - \cos t$

The acceleration function is \[a\left( t \right) = \dfrac{{dv}}{{dt}} = \sin t\]

Now acceleration is a sine function so it will have values between 1 and -1.

Now cosine function has a maximum value of 1 and a minimum value of -1

Now velocity will be maximum when the cosine function is minimum (i.e., -1)

${v_{\max }} = 1 - \left( { - 1} \right) = 2$

Now velocity will be minimum when the cosine function is maximum (i.e., 1)

\[{v_{\max }} = 1 - \left( 1 \right) = 0\]

Since velocity will have a value for time greater than zero so it will discard option (b).

The velocity will be oscillating between 0 and 2.

Now the time value cannot be negative it will start from zero and will go to infinity 

But the sine function will have a range of 1 to -1 only.

Now let’s check the displacement function.

We can see that the displacement function is always greater than zero for any time greater than zero.

Hence the correct option is (a) and (d).

3.10. A spring with one end attached to a mass m and other end to a rigid support is stretched and released.

(a) Magnitude of acceleration, when just released, is maximum.

(b) Magnitude of acceleration, when at equilibrium position is maximum.

(c) Speed is maximum when mass is at equilibrium position.

(d) Magnitude of displacement is always maximum, whenever speed is maximum.

Ans: (a, c) 

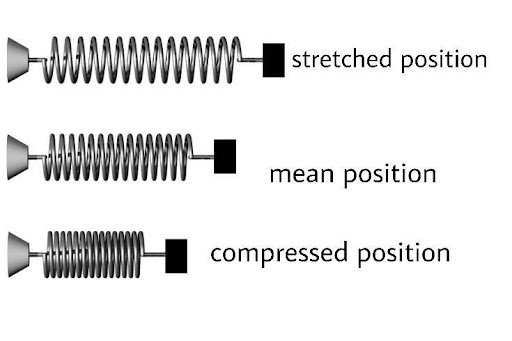
Consider a spring with a spring constant of k that is attached to mass m at one end and fastened at the right support at the other. Spring is resting on a non-stick surface.

When a force F stretches a spring by x displacement, the F=-kx (-) sign indicates that the displacement x is in the opposite direction of the force applied. When a force F acts on a spring, the spring also applies an equal amount of force in the opposite direction.

Now the potential energy of the spring is

P.E $ = \dfrac{1}{2}k{x^2}$

Now acceleration is 

$a = \dfrac{F}{m}$

$a = \dfrac{{ - kx}}{m}$

So, at x = 0 a = 0

At x = x $a = \dfrac{{ - kx}}{m}$

So, Magnitude of a is maximum at x when released. It verifies the option (a).

At the mean position where potential energy is converted into kinetic energy

So, the speed of mass is maximum at x=0.

Hence, It verifies the option (c).

Magnitude of a=0 at x=0;

So (b) is incorrect.

when the mass (m) is at its maximum displacement then it returns at this point

its speed may or may not be zero.

So option (d) incorrect.

3.11. A ball is bouncing elastically with a speed of 1m/s between walls of a railway compartment of size 10m in the direction perpendicular to walls. The train is moving at a constant speed of 10m/s parallel to the direction of motion of the ball. As seen from the ground,

(a) The direction of motion of the ball changes every 10 seconds.

(b)The speed of the ball changes every 10 seconds.

(c) average speed of the ball over any 20 seconds interval is fixed

(d) the acceleration of the ball is the same as from the train.

Ans: (b, c, d)

Main concept used: Motion of ball with respect to observer and relative velocity of body. As seen from the ground, the time to strike the ball with the walls will be every 10 seconds. Because the ball is going at a very slow speed in the moving train, its direction is identical to the train's. As a result, the direction of the ball's motion does not alter in relation to the observer on Earth.

However, because the ball's speed changes following a collision, option (a) is erroneous and option (b) is true.

Because the speed of the ball is constant, the average speed of the train or the ground remains constant at all times, or 1 m/s. As a result, option (c) is right.

When the ball hits the wall, its speed changes. Its starting speed in the direction of the moving train with respect to the ground=${V_{TG}}$=10+1=11 m/s.

Ball speed after contact with train side =${V_{BG}}$(opposite direction of train) =10-1 = 9 m/s

The change in velocity due to the impact will be in the range of 11-9=2m/s. As a result, the magnitude of acceleration on both compartment walls will be the same, but the direction will be opposite.

VERY SHORT ANSWER TYPE QUESTIONS

3.12. Refer to graph of Question 3.1. Match the following.

Graph	Characteristic
(a)	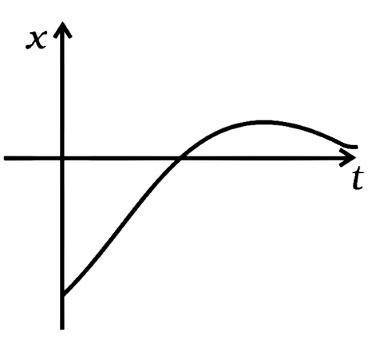(i) has v>0 and a<0 throughout.
(b)	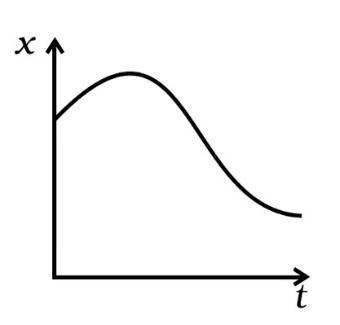(ii) has x>0 throughout and has a point with v=0, and a point a=0.
(c)	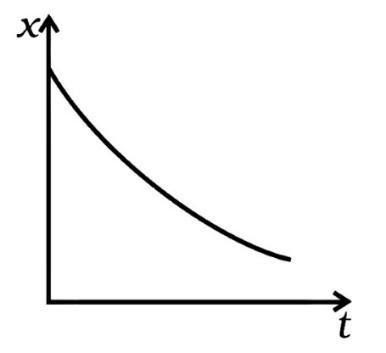(iii) has a point with zero displacement for t>0.
(d)	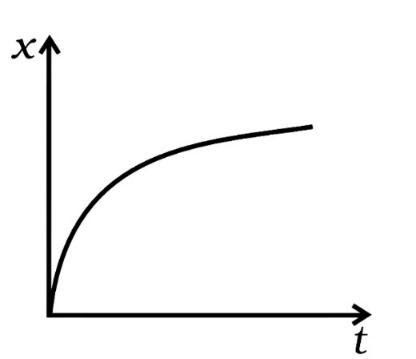(iv) has v<0 and a<0

Ans: (i) v>0 indicates that the slope is always positive, i.e., it matches the graph (d) between 0 degree and 90 degree (tanθ) . As a result, the (i) component corresponds to the graph (d).

(ii) Throughout, x > 0 and v = 0, v = 0 corresponds to the graph (ii). The slope is zero at point A, hence the v=0, a=0 graph always lies in the + x direction, confirming the answer. As a result, the (ii) component corresponds to (b).

(iii) In the graph, y=0 is the only zero displacement (a). As a result, portion (iii) corresponds to the graph (a).

(iv) v<0, i.e., the slope is (-ve) as seen in the graph (c). As a result, portion (iii) corresponds to the graph (c).

3.13. A uniformly moving cricket ball is turned back by hitting it with a bat for a very short time interval. Show the variation of its acceleration with time. (Take acceleration in backward direction as positive).

Ans:

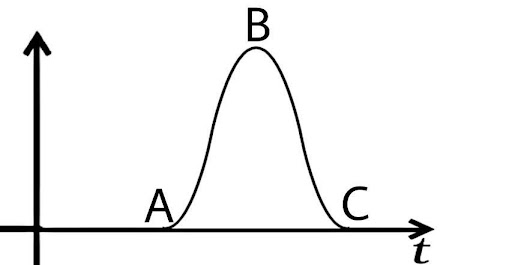
When the bat hits the ball, its acceleration reduces until it reaches zero, indicating that acceleration is in the backward direction, which is positive in this case, as seen in the graph from A to B.

Now that the velocity of the ball has reduced to zero, the velocity of the ball is increasing in the forward direction, resulting in a negative acceleration in the forward direction (as illustrated by section BC in the graph).

3.14. Give examples of a one-dimensional motion where:

(a) The particle moving along positive x-direction comes to rest periodically and moves forward.

Ans: Consider a motion with ω as a positive constant

$x\left( t \right) = \omega t - \sin \omega t$

$v\left( t \right) = \dfrac{{dx}}{{dt}} = \omega  - \omega \cos \omega t$

$a\left( t \right) = \dfrac{{dv}}{{dt}} = {\omega ^2}\sin \omega t$

(b) the particle moving along positive x-direction comes to rest periodically and moves backward.

Ans: Consider a motion with ω and a as a positive constant

$x\left( t \right) =  - a\sin \omega t$and$\omega  = \dfrac{{2\pi }}{T}$

Hence, the particle comes to rest periodically and its displacement is in the negative direction.

Hence, periodic function is $x\left( t \right) =  - a\sin \omega t$

$v\left( t \right) = \dfrac{{dx}}{{dt}} =  - a\omega \cos \omega t$

Hence, the velocity after zero displacement changes periodically.

So required function of motion $x\left( t \right) =  - a\sin \omega t$

Consider a function of motion of time periods and amplitude a, $x\left( t \right) = a\sin \omega t$

$x\left( t \right) = a\sin \omega t$and$\omega  = \dfrac{{2\pi }}{T}$

Hence, the particle is moving with displacement zero periodically and moves in +ive direction i.e., in forward.

Hence, require function is $x\left( t \right) = a\sin \omega t$

3.15 Give an example of a motion where x > 0, v < 0 and a > 0 at a particular instant.

Ans: Let’s take a simple displacement function into consideration

Displacement function $x\left( t \right) = A + B{e^{ - \gamma t}}$

Where A , B , and γ are positive constants 

Since all the constants in the term are positive, the displacement function is positive.

Now velocity function is 

$v\left( t \right) = \dfrac{{dx}}{{dt}} = \dfrac{{d\left( {A + B{e^{ - \gamma t}}} \right)}}{{dt}} =  - \gamma B{e^{ - \gamma t}}$

$v\left( t \right) =  - \gamma B{e^{ - \gamma t}}$

Since all the constants in the term are positive, the velocity function is negative because of the minus sign.

Now acceleration function is 

$a\left( t \right) = \dfrac{{dv}}{{dt}} = \dfrac{{d\left( { - \gamma B{e^{ - \gamma t}}} \right)}}{{dt}} = {\gamma ^2}B{e^{ - \gamma t}}$

$a\left( t \right) = {\gamma ^2}B{e^{ - \gamma t}}$

Since all the constants in the term are positive, the acceleration function is positive.

3.16. An object falling through a fluid is observed to have acceleration given by \[{\mathbf{a}} = {\mathbf{g}}--{\mathbf{bv}}\]; where g = gravitational acceleration and b is a constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?

Ans: After long time of released the velocity of the falling fluid becomes constant:

It means acceleration (differentiation of velocity with respect to time) will be zero.

Now $a = g - bv = 0$

Thus $bv = g$

$v = \dfrac{g}{v}$

Hence, the constant speed after a long time of release will be equal to $v = \dfrac{g}{v}$

SHORT ANSWER TYPE QUESTIONS

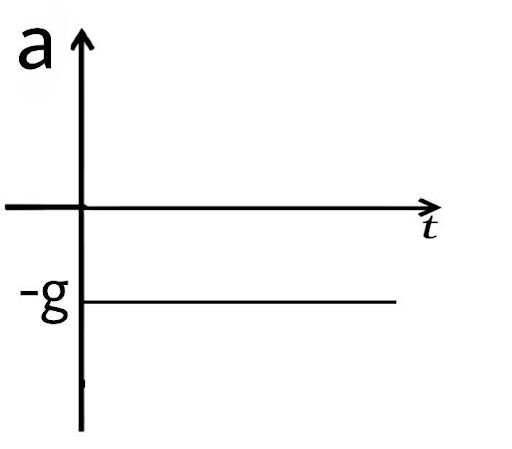
3.17. A ball is dropped and its displacement versus time graph is shown (Displacement x is from ground and all quantities are positive upwards.)

(a) Plot qualitatively velocity versus time graph.

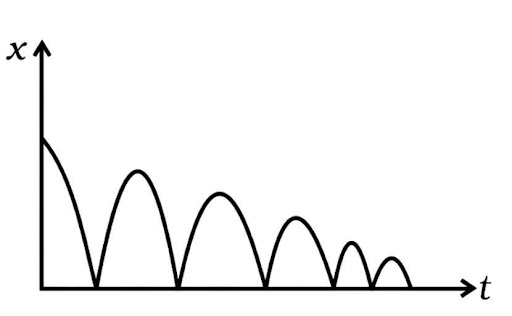
Ans: The graph shows that displacement (x) is always positive. The body's velocity grows until x equals zero, at which point it reverses direction and the velocity (slope of the x-t graph) declines to zero until it achieves a maximum value of x that is smaller than before.

When the body's velocity rises and it approaches x=0, the acceleration is downward. When the body goes higher, i.e., x>0, the velocity drops, and the direction of 'a' reverses. As a result, a= -g is always used.

(a) Plot qualitatively velocity versus time graph.

v=0 at t=0 It grows in the downward direction at a constant 'g' acceleration. As a result, the v-t graph is as follows.

(b) Plot qualitative acceleration versus time graph.

Ans: When x=0, the body bounces upward, but its velocity drops with constant a= g if it returns (downward) with acceleration (-g). As a result, an a-t graph is illustrated below.

3.18. A particle length executes the motion described by $x\left( t \right) = {x_0}\left( {1 - {e^{ - \gamma t}}} \right)$;$t \geqslant 0$,${x_0} > 0$

(a) where does the particle start and with what velocity?

Ans: Main concept: Using the value of x(t), we will calculate the function v(t) and a(t), then determine the maximum and minimum values of x(t), v(t), and a(t). 

Now,

$x\left( t \right) = {x_0}\left( {1 - {e^{ - \gamma t}}} \right)$

$v\left( t \right) = \dfrac{{dx}}{{dt}} = \dfrac{{d\left( {{x_0} - {x_0}{e^{ - \gamma t}}} \right)}}{{dt}} = {x_0}\gamma {e^{ - \gamma t}}$

And $a\left( t \right) = \dfrac{{dv}}{{dt}} = \dfrac{{d\left( {{x_0}\gamma {e^{ - \gamma t}}} \right)}}{{dt}} =  - {x_0}{\gamma ^2}{e^{ - \gamma t}}$

So, now at time t = 0

$x\left( 0 \right) = {x_0}\left( {1 - {e^{ - \gamma 0}}} \right) = {x_0}\left( {1 - 1} \right) = 0$

The particle starts at x = 0

$v\left( 0 \right) = {x_0}\gamma {e^{ - \gamma 0}} = {x_0}\gamma $

The particle starts at x = 0 with a velocity of $v = {x_0}\gamma $

(b) find the maximum and minimum values of x(t), v(t), a(t). Show that x(t) and a(t) increases with time and v(t) decreases with time.

Ans: x(t) is minimum at t=0 

At t=0 ; ${\left[ {x\left( t \right)} \right]_{\min }} = x\left( 0 \right) = 0$,

x(t) is maximum at 

At t =∞ ; ${\left[ {x\left( t \right)} \right]_{\max }} = x\left( \infty  \right) = {x_0}$

v(t) is maximum at t=0 

At t=0 ; ${\left[ {v\left( t \right)} \right]_{\max }} = v\left( 0 \right) = {x_0}\gamma $

v(t) is minimum at

At t =∞ ; ${\left[ {v\left( t \right)} \right]_{\min }} = v\left( \infty  \right) = 0$

a(t) is maximum at 

At t =∞ ; ${\left[ {a\left( t \right)} \right]_{\max }} = a\left( 0 \right) = 0$

a(t) is minimum at t=0 

At t=0 ; ${\left[ {a\left( t \right)} \right]_{\min }} = a\left( \infty  \right) =  - {x_0}{\gamma ^2}$

3.19. A bird is tossing (flying to and fro) between two cars moving towards each other on a straight road. One car has a speed of 18 km/hr while the other has the speed of 27Km/hr. The bird starts moving from the first car towards the order and is moving with the speed of 36Km/hr and when the two cars were separated by 36Km. What is the total distance covered by the bird? What is the total displacement of the bird?

Ans: Main concept: The bird will fly back and forth until both automobiles collide. As a result, the total distance travelled by the bird during the time = the speed at which the bird meets multiplied by the time to meet the cars together.

The relative speed of cars is = 27 + 18 = 45 Km/h

The time taken to meet the two cars together (t) is distance between the cars divided by the relative speed of the cars

$t = \dfrac{{36km}}{{45km/h}} = \dfrac{4}{5}h$

Distance cover by the bird is $\dfrac{4}{5} \times 36km/h = 28.8km$

3.20. A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9m/s, the (horizontal) distance between the two buildings is 10m and the height difference is 9m, will he be able to land on the next building? (take g=10 m/s2)

Ans: Main concept: During the jump the free fall distance is 9m and the horizontal distance covered by man should be at least 10m so that he can cross the building.

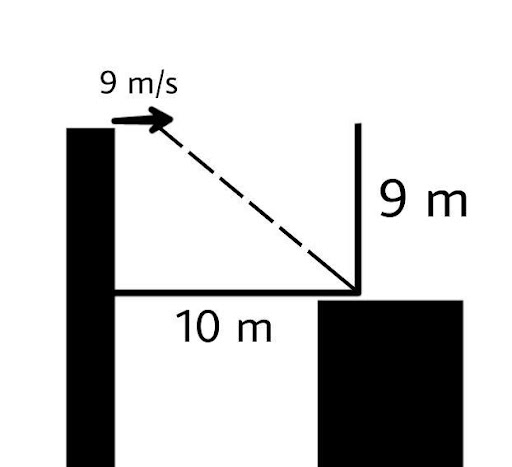
For vertical motion of 9 m

We will use the formula 

$S = ut + \dfrac{1}{2}a{t^2}$to find the time

We have the initial velocity as zero and the distance (height) as 9 m and the acceleration is the acceleration due to gravity.

So, we will put this in the equation

$9 = 0 \times t + \dfrac{1}{2} \times 10{t^2}$

$9 = 5{t^2}$

$t = \dfrac{3}{{\sqrt 5 }}\sec $

The horizontal distance covered by person is

$D = speed \times time$

We have time $t = \dfrac{3}{{\sqrt 5 }}\sec $ and speed as 9 m/s

$D = 9 \times \dfrac{3}{{\sqrt 5 }} = \dfrac{{27}}{{\sqrt 5 }} = 12.07m$

horizontal distance covered = 12.07 m

As 12.07 m covered during the free falling of 9 m due to the jumping of one building to another. 

So, he reaches on the building next farther the first edge by = 12.07-10 = 2.07 m.

3.21. A ball is dropped from a building of height 45m. simultaneously another ball is thrown up with a speed of 40m/s. Calculate the relative speed of the balls as a function of time.

Ans: For the first ball falling from top

${u_1} = 0$, the height is 45 m and the acceleration is acceleration due to gravity.

The equation of motion is:

${v_1} = {u_1} + at$

Now we will substitute the values in the above equation.

${v_1} = 0 + gt = gt$

${v_1} = gt$

Since this ball is moving downwards ${v_1} =  - gt$

For the second ball moving to the top

${u_2} = 45m/s$, and the acceleration is acceleration due to gravity.

The equation of motion is:

${v_2} = {u_2} + at$

Now we will substitute the values in the above equation.

\[{v_2} = 45 - gt\]since it is moving up its velocity will be decreasing so acceleration due to gravity is negative.

Relative velocity of balls is (between the first and the second ball):

${v_{12}} = {v_1} - {v_2}$

Now we will substitute the values

\[{v_{12}} =  - gt - \left( {45 - gt} \right) =  - 45m/s\]

Relative velocity of the first ball with respect to the second ball is 40 m/s downward.

In this problem due to acceleration the speed of one increases and the other decreases with the same rate. So, their relative speed remains as the increase and decrease of speed is compensated equally.

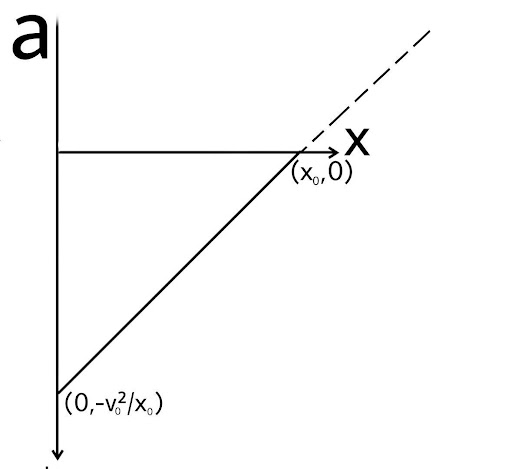
3.22. The velocity-displacement graph of a particle is shown in the figure.

(a) Write the relation between v and x.

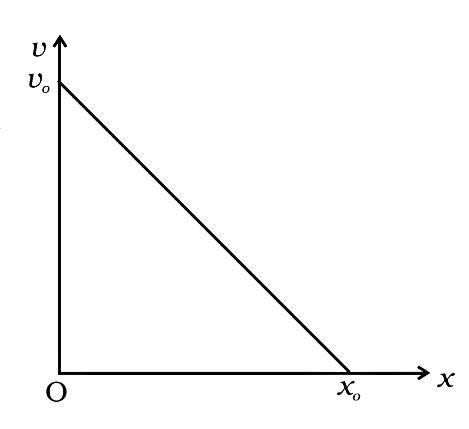
Ans: Let’s consider a point P (x, v) at any time t on the graph.

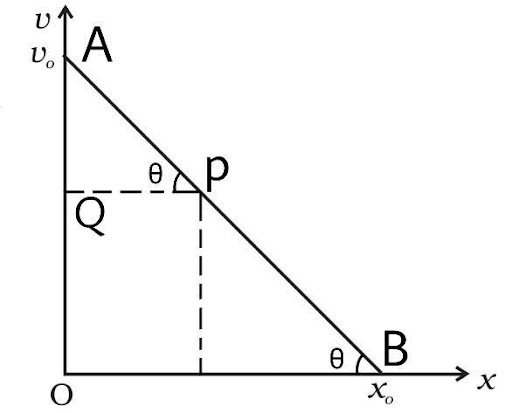
Then in the triangle ABO and triangle AQP

$\tan \theta  = \dfrac{{AQ}}{{QP}} = \dfrac{{{v_0} - v}}{{x - 0}} = \dfrac{{{v_0}}}{{{x_0}}}$

Thus, $\dfrac{{{v_0} - v}}{x} = \dfrac{{{v_0}}}{{{x_0}}}$

$x{v_0} = {x_0}\left( {{v_0} - v} \right)$

$v{x_0} = {x_0}{v_0} - x{v_0}$

$v = {v_0}\left[ {1 - \dfrac{x}{{{x_0}}}} \right]$

The ration between v and x is $v = {v_0}\left[ {1 - \dfrac{x}{{{x_0}}}} \right]$

Since velocity is decreasing as the distance increases it means that the acceleration is negative.

Thus, acceleration can be defined as

$a = \dfrac{{dv}}{{dt}}$ we will multiply this expression by $\dfrac{{dx}}{{dx}}$

$a = \dfrac{{dv}}{{dt}}.\dfrac{{dx}}{{dx}} = \dfrac{{dv}}{{dx}}.\dfrac{{dx}}{{dt}}$

(b) Obtain the relation between acceleration and displacement and plot it.

Ans: Now $\dfrac{{dx}}{{dt}} = v$

So, $a = v\dfrac{{dv}}{{dx}}$

Now $\dfrac{{dv}}{{dx}}$ is the slope of the graph

$a = v\dfrac{{ - {v_0}}}{{{x_0}}}$

Putting the value of v we get

$a = {v_0}\left[ {1 - \dfrac{x}{{{x_0}}}} \right]\dfrac{{ - {v_0}}}{{{x_0}}}$

\[a = \left[ {\dfrac{x}{{{x_0}}} - 1} \right]\dfrac{{{{\left( {{v_0}} \right)}^2}}}{{{x_0}}}\]

Now at x = 0

\[a = \dfrac{{ - {{\left( {{v_0}} \right)}^2}}}{{{x_0}}}\]

And at a = 0

\[0 = \left[ {\dfrac{x}{{{x_0}}} - 1} \right]\dfrac{{{{\left( {{v_0}} \right)}^2}}}{{{x_0}}}\]

\[0 = \left[ {\dfrac{x}{{{x_0}}} - 1} \right]\]

\[x = {x_0}\]

The point required to draw the graph are

$\left( {{x_0},0} \right)$ and $\left( {0, - \dfrac{{{{\left( {{v_0}} \right)}^2}}}{{{x_0}}}} \right)$

The graph is

LONG ANSWER TYPE QUESTIONS

3.23. It is a common observation that rain clouds can be at about a kilometre altitude above the ground.

(a) If a raindrop falls from such a height freely under gravity, what will be its speed? Also, calculate in km/h. (g=10 $m/{s^2}$)

(Assume that the umbrella is circular and has a diameter of 1 m and cloth is not pierced through!!)

Ans:  Main concept:

Force on a particle F = ma

Now, $F = \dfrac{{dp}}{{dt}}$

And $m = \rho V$

Given h=1km=1000m, g=10 $m/{s^2}$

For the raindrop

Initial velocity u=0m/s

Diameter = 4mm

Radius = 2 mm = $2 \times {10^{ - 3}}m$

(a) If a raindrop falls from such a height freely under gravity, what will be its speed? 

Ans: Velocity of rain drop on ground

We will use the formula:

${v^2} = {u^2} - 2aS$to find the final velocity of the rain drop

Here we will take the value of s = h (height which is given 1000m but since displacement covered by raindrop is in downward direction so we will take h as negative)

Here we will take the value of a = g (acceleration due to gravity since acceleration due to gravity acts in downward direction and displacement is also in downward direction, we take g=+ve)

Now the equation becomes,

${v^2} = {u^2} - 2g\left( { - h} \right)$

${v^2} = {u^2} + 2gh$

Since raindrops always have an initial velocity of zero from the start.

\[v = \sqrt {2gh}  = \sqrt {2 \times 10 \times 1000}  = 100\sqrt 2 m/s\]

Now velocity in km/h = $100\sqrt 2  \times \dfrac{{18}}{5} = 360\sqrt 2  = 510km/h$

(b) A typical raindrop is about 4 mm diameter. Momentum is mass speed in magnitude. Estimate its momentum when it hits the ground.

Ans: Mass of the drop = $m = \rho V$

$m = \rho \dfrac{4}{3}\pi {r^3} = 1000 \times \dfrac{4}{3} \times \pi  \times {\left( {2 \times {{10}^{ - 3}}} \right)^3}$

$m = 3.35 \times {10^{ - 5}}kg$

Momentum of the raindrop = $p = mv$

$p = mv = 3.35 \times {10^{ - 5}} \times 100\sqrt 2 $

$p = 4.7 \times {10^{ - 3}}kgm/s$

(c) Estimate the time required to flatten the drop.

Ans: Time required for a drop to be flattened 

Time required for a drop of 4 mm diameter spherical drop to be flattened i.e., to reach the upper part of the spherical drop on ground. We can neglect the gravitational acceleration as the distance is very small it will not have any much effect on the velocity.

distance \[d = 4mm = 4 \times {10^{ - 3}}m\]

time taken = $\dfrac{{distance}}{{speed}}$

$t = \dfrac{{4 \times {{10}^{ - 3}}m}}{{100\sqrt 2 m/s}} = 2\sqrt 2  \times {10^{ - 5}}\sec $

Time  $ = 2.8 \times {10^{ - 5}}\sec $

(d) The rate of change of momentum is a force. Estimate how much force such a drop would exert on you.

Ans: Force exerted$F = \dfrac{{dp}}{{dt}}$

Now the velocity of goes to zero in the time $ = 2.8 \times {10^{ - 5}}\sec $

$F = \dfrac{{dp}}{{dt}} = \dfrac{{mv - 0}}{t} = \dfrac{{4.7 \times {{10}^{ - 3}}}}{{2.8 \times {{10}^{ - 5}}}} = 1.68 \times {10^2} = 168N$

(e) Estimate the order of magnitude force on the umbrella. The typical lateral separation between two raindrops is 5cm.

Ans: Force exerted on the umbrella:

D = 1 m

Area $ = \pi {\left( {\dfrac{d}{2}} \right)^2} = \dfrac{{22}}{7}{\left( {\dfrac{1}{2}} \right)^2} = \dfrac{{11}}{{14}}{m^2}$

Separation between two drops = 5 cm

Square area covered by one drop = $5 \times 5 = 25c{m^2} = 25 \times {10^{ - 4}}{m^2}$

Number of drops falling in the umbrella = $\dfrac{{\dfrac{{11}}{{14}}{m^2}}}{{25 \times {{10}^{ - 4}}{m^2}}} = 0.0314 \times {10^4}$drops

Total drops 314 drops falling.

Total force on the umbrella $ = 314 \times 168 = 52752N$

It is equivalent to 5275.2 kg weight which again is not possible on the umbrella. The velocity of drop decreased to terminal velocity due to retarding force of friction of air molecules.

3.24. A motor car moving at a speed of 72km/h cannot come to a stop in less than 3.0 s while for a truck this time interval is 5.0 s. On a highway the car is behind the truck both moving at 72km/h. The truck gives a signal that it is going to stop in an emergency. At what distance the car should be from the truck so that it does not bump into (collide with) the truck. Human response time is 0.5s.

Ans: Initial velocity of the truck in m/s:

$72km/h = 72 \times \dfrac{5}{{18}}m/s = 20m/s$

Now the conditions of the truck are

v=0, a = unknown, t = 5sec.

Now we will use the formula:

$v = u + at$ to find the acceleration of the truck

$0 = 20 + 5a$

\[a = \dfrac{{ - 20}}{5} =  - 4m{s^{ - 2}}\]

The truck is retarding.

Now for the car the conditions are

v=0, a = ac (unknown), t = 3sec.

initial velocity = 20 m/s

Now we will use the formula:

$v = u + {a_c}t$ to find the acceleration of the car

$0 = 20 + 3{a_c}$

\[{a_c} = \dfrac{{ - 20}}{3}m{s^{ - 2}}\]

The car is at a distance of x metre behind the truck. Car takes time ‘t’ to stop after observing the signal given by the truck to stop.

Time of response for human = 0.5 second

Time t includes the time to stop the car and responding time both. So, time taken by car to stop after applying brakes is (t – 0.5) second.

Now for car

${v_c} = {u_c} + {a_c}t$

$0 = 20 - \dfrac{{20}}{3}\left( {t - 0.5} \right)$     …..(I)

For truck driver, there is no responding time he applies breaks with passing signal to car back side, so

Now for truck

$v = u + at$

$0 = 20 - 4t$        ……..(II)

Now equating equation (I) and (II)

$20 - 4t = 20 - \dfrac{{20}}{3}\left( {t - 0.5} \right)$

$4t = \dfrac{{20}}{3}\left( {t - 0.5} \right)$

\[12t = 20t - 10\]

$8t = 10$

$t = 1.25\sec $

Now,

Distance travel by the truck in 1.25 sec

$S = ut + \dfrac{1}{2}a{t^2}$

$S = 1.25 \times 20 + \dfrac{1}{2}\left( { - 4} \right){\left( {1.25} \right)^2}$

$S = 25 - \dfrac{{25}}{8} = 21.875m$

The Car first travel first 0.5 sec with speed of uniform but after this responding time 0.5 sec brakes are applied and then retarding motion starts for car

${S_c} = \mathop {\left( {{u_c} \times 0.5} \right)}\limits_{uniform}  + \mathop {\left( {{u_c}\left( {t - 0.5} \right) + \dfrac{1}{2}{a_c}{{\left( {t - 0.5} \right)}^2}} \right)}\limits_{retard} $

${S_c} = 20 \times 0.5 + 20 \times 0.75 - \dfrac{1}{2} \times \dfrac{{20}}{3} \times {\left( {0.75} \right)^2}$

${S_c} = 10 + 15 - 1.875 = 23.125m$

The difference between this distance = 23.125 - 21.875 = 1.25 m

So, in order to avoid the bump onto the truck, the car must be behind at least at a distance of 1.25 m.

3.25. A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by \[{\mathbf{v}}\left( {\mathbf{t}} \right) = {\mathbf{2t}}\left( {{\mathbf{3}} - {\mathbf{t}}} \right)\]; 0< t < 3 and \[{\mathbf{v}}\left( {\mathbf{t}} \right) = --\left( {{\mathbf{t}}--{\mathbf{3}}} \right)\left( {{\mathbf{6}}--{\mathbf{t}}} \right)\] for 3 < t < 6 s in m/s. It repeats this cycle till it reaches the height of 20 m.

(a) At what time is its velocity maximum?

Ans: For maximum velocity v(t), its differential will be zero with respect to time.

\[\dfrac{{dV\left( t \right)}}{{dt}} = 0\]

\[\dfrac{{d\left( {2t\left( {3 - t} \right)} \right)}}{{dt}} = \dfrac{{d\left( {6t - 2{t^2}} \right)}}{{dt}} = 0\]

$6 - 4t = 0$

$4t = 6$

$t = 1.5\sec $

(b) At what time is its average velocity maximum?

Ans: We can determine the average velocity by

${V_{avg}} = \dfrac{{{{\left( {Displacement} \right)}_{total}}}}{{{{\left( {time} \right)}_{total}}}}$

$v\left( t \right) = \dfrac{{ds}}{{dt}} = 6t - 2{t^2}$

$ds = \left( {6t - 2{t^2}} \right)dt$

Now we will integrate both the sides

$\int\limits_0^s {ds}  = \int\limits_0^3 {\left( {6t - 2{t^2}} \right)dt} $

\[s = \left[ {\dfrac{{6{t^2}}}{2} - \dfrac{{2{t^3}}}{3}} \right]_0^3 = \left[ {3{t^2} - \dfrac{{2{t^3}}}{3}} \right]_0^3\]

\[s = 3\left( {9 - 0} \right) - \dfrac{2}{3}\left( {27 - 0} \right) = 27 - 18 = 9m\]

Total displacement = 9 m

Total time = 3 sec

${V_{avg}} = \dfrac{{{{\left( {Displacement} \right)}_{total}}}}{{{{\left( {time} \right)}_{total}}}} = \dfrac{9}{3} = 3m/s$

Now,

\[V(t) = 6t - 2{t^2}\]  for (0<t<3)

Maximum average velocity is 3 m/s

Now we need to find this time for which average velocity is maximum (the time at which velocity is 3m/s)

So, we will equate the value of velocity as 3 m/s

\[3 = 6t - 2{t^2}\] 

$2{t^2} - 6t + 3 = 0$

Now, a = 2 , b = -6 , c = 3

Thus, $t = \dfrac{{ - \left( { - 6} \right) \pm \sqrt {36 - 4 \times 3 \times 2} }}{{2 \times 2}}$

$t = \dfrac{{6 \pm \sqrt {36 - 24} }}{4} = \dfrac{{6 \pm \sqrt {12} }}{4} = \dfrac{{6 \pm 2\sqrt 3 }}{4} = 1.5 \pm \dfrac{{\sqrt 3 }}{2}$

Now $t = 1.5 + \dfrac{{1.732}}{2} = 2.36\sec $

And $t = 1.5 - \dfrac{{1.732}}{2} = 0.63\sec $

So, the average velocity is maximum at 2.36 sec and 0.63 sec.

(c) At what time is its acceleration maximum in magnitude?

Ans: Time for maximum acceleration in periodic motion. The acceleration is maximum when body returns at its mean position or changes the direction of motion it at v=0

\[V(t) = 6t - 2{t^2}\]  for (0<t<3)

For maximum acceleration v = 0

\[0 = 6t - 2{t^2}\]

\[2{t^2} - 6t = 0\]

\[2t\left( {t - 3} \right) = 0\]

Since t is greater than zero

$t = 3\sec $

Acceleration is maximum at 3 sec.

(d) How many cycles (counting fractions) are required to reach the top?

Ans: Displacement from 0-3 sec

S =9m [taken from (ii) in (b) part]

For 3 to 6 seconds

\[V\left( t \right) =  - \left( {t - 3} \right)\left( {6 - t} \right)\]

\[V\left( t \right) = \left( {t - 3} \right)\left( {t - 6} \right)\]

\[\dfrac{{ds}}{{dt}} = \left( {{t^2} - 9t + 18} \right)\]

$ds = \left( {{t^2} - 9t + 18} \right)dt$

Now we will integrate both the sides

\[\int\limits_o^s {ds}  = \int\limits_3^6 {\left( {{t^2} - 9t + 18} \right)dt} \]

\[s = \left[ {\dfrac{{{t^3}}}{3} - \dfrac{{9{t^2}}}{2} + 18t} \right]_3^6 = \dfrac{{216 - 27}}{3} - \dfrac{{9\left( {36 - 9} \right)}}{2} + 18\left( {6 - 3} \right) =  - 4.5m\]

So, he climbs 9 m then slips 4.5 meter in the last 3 sec

Total displacement in a cycle = 4.5m

Height climbs in first three cycle = 13.5 m

In the fourth cycle he needs to climb the remaining 20 – 13.5 = 6.5 m

Since, the remaining height to climb by the monkey is 6.5 m but the monkey can climb 9 m up without slip. So, in the 4th cycle, it will slip as it reaches the top of the pole.

3.26. A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between the first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.

Ans: Let the initial speed of the balls be:

Ball 1 = ${u_1}$ = 2u m/s

Ball 2 = ${u_2}$ = u m/s

Let the height covered by balls before coming to rest be:

For ball 1 = ${h_1}$ 

For ball 2 = ${h_2}$ 

Now, we will apply the formula 

${v^2} = {u^2} + 2gh$

Where v is the final velocity which becomes zero at the top 

Since gravity is acting is downward direction it will have a negative value

thus, the equation becomes 

$0 = {u^2} - 2gh$

${u^2} = 2gh$

$\dfrac{{{u^2}}}{{2g}} = h$

Now for ball 1 

\[{h_1} = \dfrac{{{{\left( {{u_1}} \right)}^2}}}{{2g}} = \dfrac{{4{u^2}}}{{2g}}\]

For ball 2 

${h_2} = \dfrac{{{{\left( {{u_2}} \right)}^2}}}{{2g}} = \dfrac{{{u^2}}}{{2g}}$

Now it is given that the difference between these two heights is 15m

${h_1} - {h_2} = \dfrac{{4{u^2}}}{{2g}} - \dfrac{{{u^2}}}{{2g}} = \dfrac{{3{u^2}}}{{2g}} = 15m$

Now, $u = \sqrt {\dfrac{{15 \times 2g}}{3}}  = \sqrt {\dfrac{{15 \times 20}}{3}}  = 10\,m/s$

Value of g taken = $10\,m/{s^2}$

Now,

For ball 1

${u_1} = 20\,m/s$

${v_1} = 0\,m/s$

we will use the formula:

$v = u - gt$ to find the time interval

$0 = {u_1} - g{t_1}$

$10{t_1} = 20$

${t_1} = 2\sec $

For ball 2

${u_2} = 10\,m/s$

${v_2} = 0\,m/s$

we will use the formula:

$v = u - gt$ to find the time interval

$0 = {u_2} - g{t_2}$

$10{t_2} = 10$

${t_2} = 1\sec $

Velocities of ball 1 and ball 2 are 20 m/s and 10 m/s.

Exact time intervals between the two balls = ${t_1}-{t_2}$ = (2 – 1) = 1 second.

Class 11 Physics Chapter 3 - Motion In A Straight Line

This third chapter about the motion of objects along a straight line is also known as rectilinear motion. By studying this chapter we can understand the basic groundwork of dynamic physics or generally call it physics in motion. As the concepts begin with ‘Position,’ ‘Path Length,’ and ‘Displacement’ in section 3.2. Subsequently, the chapter introduces us to the concepts of ‘Average Velocity,’ and ‘Average Speed’ in section 3.3. Then comes the estimation of the instantaneous velocity and speed of the body in motion in section 3.4. In section 3.5 ‘Acceleration,’ we can calculate the rate of increase or decrease in the velocity of an object. Here are also made familiar with the various equations for uniformly accelerated motion, of a body in motion, which are called ‘Kinematic Equations,’ section 3.6. We also get to compare the velocity of two distinct bodies moving at different speeds or even in different directions under section 3.7 ‘Relative Velocity.’ These concepts have been well elaborated and established by NCERT Exemplar for Class 11 Physics in the chapter ‘Motion in a straight line’ for the easy understanding of the students.

The exercise questions at the end of the chapter are also very important to understand the concepts better and practice as well. There are many types of questions related to the subject. These questions have also been solved by experts and have been provided here for your referral.

It is available in pdf format and is free of cost. You can download it immediately and start learning in a very easy way. This will surely help to solve the concepts of this foundational chapter for students as well as teachers.