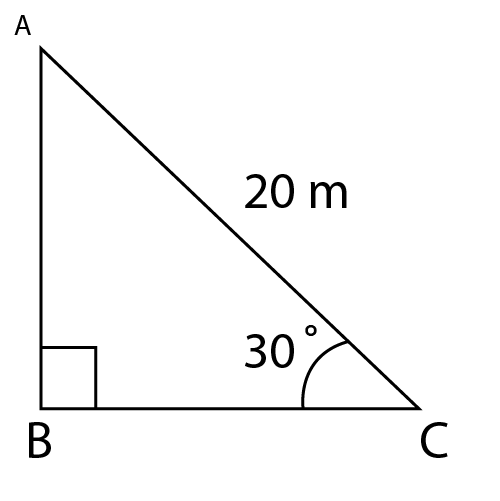
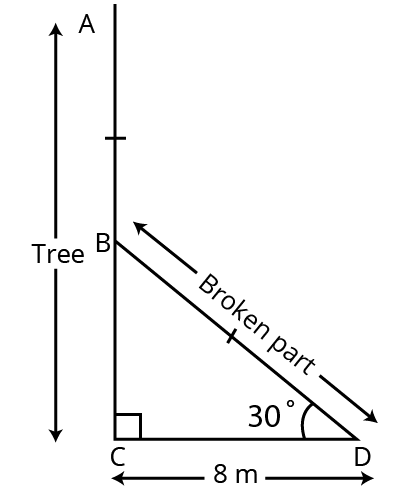
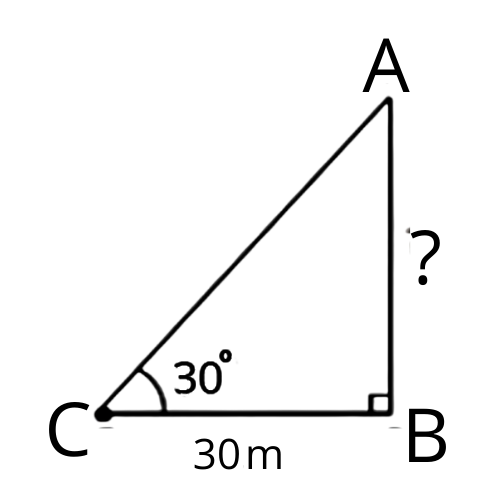
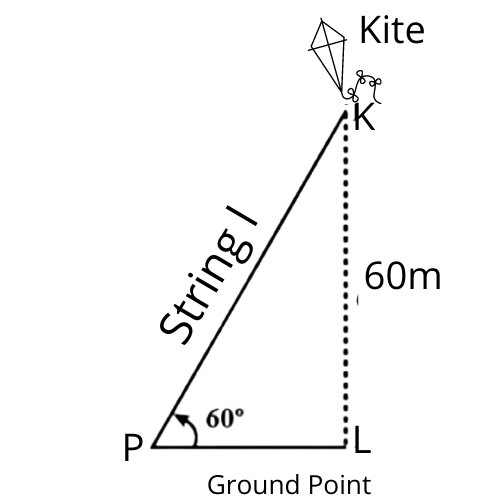
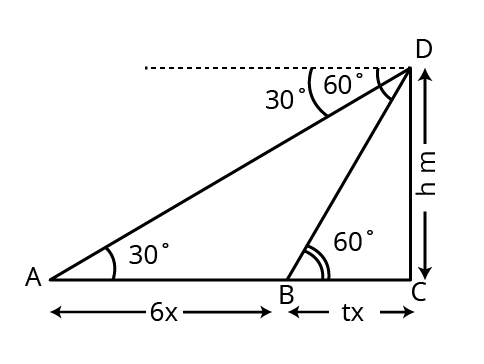
Class 10 Some Applications of Trigonometry Exercise 9.1 Solutions
NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry
FAQs on NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry
1. Where can I get stepwise NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1?
You can find stepwise NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 in the official textbook solution format, fully aligned with the CBSE 2025–26 curriculum. Each question is solved using the correct trigonometric technique as per NCERT guidelines, ensuring you understand every step required for solving heights and distances problems.
2. How do I solve the height and distance questions in Chapter 9 Some Applications of Trigonometry?
To solve height and distance questions in Chapter 9, first make a labelled diagram as per the given scenario, identify the known and unknown values, choose the appropriate trigonometric ratio (sine, cosine, or tangent), and apply the formula as shown in the NCERT solutions for correct stepwise calculation. Ensure you follow the CBSE-approved approach for rationalization and final answer write-up.
3. Is the NCERT Solutions for Class 10 Maths Chapter 9 PDF available for download in Hindi medium?
Yes, NCERT Solutions for Class 10 Maths Chapter 9 PDF are available for download in both English and Hindi medium, following the official CBSE 2025–26 NCERT textbook answer format. These solutions include all stepwise explanations for Exercise 9.1 and intext questions, making them ideal for Hindi medium students seeking clear and accurate answers.
4. What is the CBSE-approved method to solve Example 6 in Chapter 9?
The CBSE-approved method to solve Example 6 in Chapter 9 'Some Applications of Trigonometry' is to draw the situation according to the question, identify which trigonometric ratio applies, set up the equation as per the labelled figure, and solve stepwise, including unit conversions if any, just as shown in the official NCERT answer key.
5. Are these NCERT Solutions for Class 10 Maths Chapter 9 valid for the 2025–26 exam session?
All NCERT Solutions for Class 10 Maths Chapter 9 provided here are specifically designed according to the latest CBSE 2025–26 syllabus. They adhere strictly to the updated NCERT textbook and answer structure, ensuring full validity and reliability for your current academic session and board preparation.
6. Can I access Class 10 Maths Chapter 9 Exercise 9.1 Solutions PDF for free?
Yes, you can access Class 10 Maths Chapter 9 Exercise 9.1 Solutions PDF absolutely free in both English and Hindi languages, following the NCERT answer book format. These solutions deliver detailed explanations as per the latest textbook examples and ensure accuracy for all CBSE-style questions.
7. How to present answers in the NCERT format for Some Applications of Trigonometry?
To present answers in the NCERT format for Some Applications of Trigonometry, always begin with a labelled diagram, clearly mention known/unknown quantities, write the selected trigonometric ratio, substitute the values, and show all calculation steps leading to the final answer. Conclude with the proper unit, as per the CBSE answer key.
8. What is the correct answer format for stepwise solutions in Exercise 9.1 as per CBSE?
The correct answer format for stepwise solutions in Exercise 9.1 includes: 1) Drawing the figure, 2) Writing out the given and required values, 3) Stating the trigonometric ratio used, 4) Showing every calculation step, and 5) Clearly writing the final answer with unit, fully as per CBSE and NCERT solution structure.
9. Are all solved questions in the Class 10 Maths Chapter 9 NCERT Solutions checked as per NCERT answer key?
Yes, all solved questions in the Class 10 Maths Chapter 9 NCERT Solutions strictly follow the official NCERT answer key and CBSE marking scheme. Every explanation, calculation, and diagram is checked for textbook alignment and correct answer sequence, ensuring no step is skipped.
10. How do I avoid common mistakes in height and distance problems in Chapter 9?
To avoid common mistakes in height and distance problems, always draw the figure exactly as per the question, accurately identify angles of elevation or depression, use the correct trigonometric ratio, and double-check your calculations stepwise. Cross-verify unit conversions and ensure final answers are written as shown in the NCERT pattern for maximum accuracy in board exams.
11. Does the solution for Exercise 9.1 include detailed explanations for each trigonometric step as required by CBSE 2025–26?
Every solution for Exercise 9.1 includes detailed explanations for each trigonometric calculation, fully adhering to the CBSE 2025–26 NCERT answer format. All explanation steps, formula applications, and reasoning are shown clearly to help you score full marks in your board exams.
12. What is the best way to learn the application of trigonometric ratios in heights and distances using NCERT solutions?
The best way is to repeatedly practice with solved NCERT solutions, starting from labelled diagrams, choosing correct trigonometric ratios, and moving through all calculation steps as shown in the answer key. This method deepens understanding of textbook application and ensures CBSE-ready answers for every possible scenario in Heights and Distances.




















 Watch Video
Watch Video