
Find Real Numbers Class 10 Questions and Answers With Detailed Solutions
As you go into higher classes, juggling between so many subjects and assignments is not easy for a class 10 student. That is why we at Vedantu have come up with detailed NCERT Solutions for Maths Class 10 Chapter 1 Real Numbers. The solutions follow the updated CBSE curriculum. The subject matter experts at Vedantu have done extensive research to design NCERT Class 10 Maths Chapter 1 so that it is easily understandable by you. By going through these class 10 Maths chapter 1 pdf solutions of NCERT, you can clear your concepts on real numbers at the root level so that you can solve complex problems on your own.
 Table of Content
Table of Content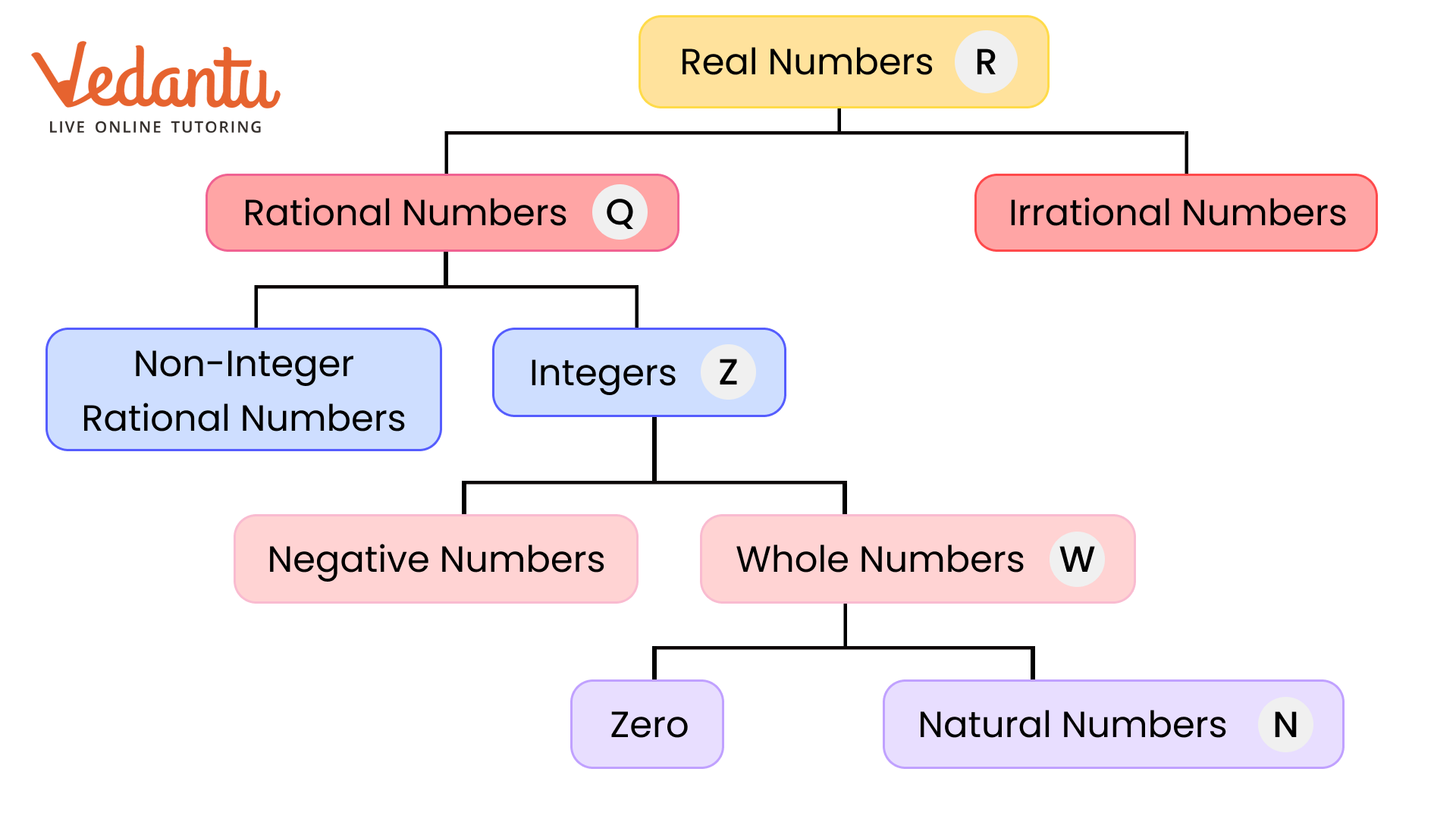
Glance of NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers | Vedantu
If a prime number $p$ divides $a^2$, then p divides a.
The sum or difference of a rational and an irrational number is irrational.
The product and quotient of a non-zero rational and irrational number are irrational.
$\sqrt{p}$ is irrational when 'p' is a prime.
This article contains chapter notes and important questions for Chapter 1 - Real Numbers, which you can download as PDFs.
There are Exercises link provided. It has solutions for each questions from Euclid's division algorithm, finding the highest common factor (HCF), expressing numbers as prime factors, and finding the least common multiple (LCM) and HCF of given pairs of integers.
Access Exercise Wise NCERT Solutions for Chapter 1 Maths Class 10
S. No | Current Syllabus Exercises of Class 10 Maths Chapter 1 | |
1 | ||
2 | ||
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers



Find Real Numbers Class 10 Questions and Answers With Detailed Solutions
NCERT Maths Class 10 Chapter 1 Solutions, "Real Numbers," is based on the concept of real numbers and their properties. The chapter consists of the following exercises:
Exercise 1.2: This exercise covers the concept of irrational numbers and their decimal expansions.
Exercise 1.3: This exercise explains the concept of real numbers and their properties such as closure, commutativity, associativity, distributivity, etc.
Exercise 1.4: This exercise deals with the square roots of positive integers and their properties.
Mastering Class 10 Maths Chapter 1: Real Numbers - Notes, Practice and Exercise Problems
Exercise 1.1 (Not available in the current syllabus)
1. Use Euclid’s division algorithm to find the HCF of:
(i) $135$ and $225$
Ans: We have to find the HCF of $135$ and $225$ by using Euclid’s division algorithm.
According to Euclid’s division algorithm, the HCF of any two positive integers $a$ and $b$, where $a > b$ is found as :
First find the values of $q$ and $r$, where $a=bq+r$, $0\le r < b$.
If $r=0$, the HCF is $b$. If $r\ne 0$, apply Euclid’s lemma to $b$ and $r$.
Continue steps till the remainder is zero. When we get the remainder zero, divisor will be the HCF.
Let $a=225$ and $b=135$.
Since, $a > b$
Using division algorithm, we get
$a=bq+r$
$\Rightarrow 225=135\times 1+90$
Here,
$\Rightarrow b=135$
$\Rightarrow q=1$
$\Rightarrow r=90$
Since $r\ne 0$, we apply the Euclid’s lemma to $b$ (new divisor) and $r$ (new remainder). We get
$\Rightarrow 135=90\times 1+45$
Here,
$\Rightarrow b=90$
$\Rightarrow q=1$
$\Rightarrow r=45$
Since $r\ne 0$, we apply the Euclid’s lemma to $b$ and $r$. We get
$\Rightarrow 90=2\times 45+0$
Now, we get $r=0$, thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $135$ and $225$ is $45$.
(ii) $196$ and $38220$
Ans: We have to find the HCF of $196$ and $38220$ by using Euclid’s division algorithm.
According to Euclid’s division algorithm, the HCF of any two positive integers $a$ and $b$, where $a > b$ is found as :
First find the values of $q$ and $r$, where $a=bq+r$, $0\le r < b$.
If $r=0$, the HCF is $b$. If $r\ne 0$, apply Euclid’s lemma to $b$ and $r$.
Continue steps till the remainder is zero. When we get the remainder zero, divisor will be the HCF.
Let $a=38220$ and $b=196$.
Since, $a > b$
Using division algorithm, we get
$a=bq+r$
$\Rightarrow 38220=196\times 195+0$
Here,
$\Rightarrow b=196$
$\Rightarrow q=195$
$\Rightarrow r=0$
Since, we get $r=0$, thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $196$ and $38220$ is $196$.
(iii) $867$ and $255$
Ans: We have to find the HCF of $867$ and $255$ by using Euclid’s division algorithm.
According to Euclid’s division algorithm, the HCF of any two positive integers $a$ and $b$, where $a > b$ is found as :
First find the values of $q$ and $r$, where $a=bq+r$, $0\le r < b$.
If $r=0$, the HCF is $b$. If $r\ne 0$, apply Euclid’s lemma to $b$ and $r$.
Continue steps till the remainder is zero. When we get the remainder zero, divisor will be the HCF.
Let $a=867$ and $b=255$.
Since, $a > b$
Using division algorithm, we get
$a=bq+r$
\[\Rightarrow 867=255\times 3+102\]
Here,
$\Rightarrow b=255$
$\Rightarrow q=3$
$\Rightarrow r=102$
Since $r\ne 0$, we apply the Euclid’s lemma to $b$ (new divisor) and $r$ (new remainder). We get
$\Rightarrow 255=102\times 2+51$
Here,
$\Rightarrow b=102$
$\Rightarrow q=2$
$\Rightarrow r=51$
Since $r\ne 0$, we apply the Euclid’s lemma to $b$ and $r$. We get
$\Rightarrow 102=51\times 2+0$
Now, we get $r=0$, thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $867$ and $255$ is $51$.
2. Show that any positive odd integer is of the form, $6q+1$ or $6q+3$, or $6q+5$, where $q$ is some integer.
Ans: Let $a$ be any positive integer and $b=6$.
Then, by Euclid’s division algorithm we get $a=bq+r$, where, $0\le r < b$.
Here, $0\le r < 6$.
Substitute the values, we get
$\Rightarrow a=6q+r$
If $r=0$, we get
$\Rightarrow a=6q+0$
$\Rightarrow a=6q$
If $r=1$, we get
$\Rightarrow a=6q+1$
If $r=2$, we get
$\Rightarrow a=6q+2$ and so on
Therefore, $a=6q$ or $6q+1$ or $6q+2$ or $6q+3$ or $6q+4$ or $6q+5$.
We can write the obtained expressions as
\[6q+1=2\times 3q+1\]
$\Rightarrow 6q+1=2{{k}_{1}}+1$
Where, ${{k}_{1}}$ is an integer.
\[6q+3=6q+2+1\]
$\Rightarrow 6q+3=2\left( 3q+1 \right)+1$
$\Rightarrow 6q+3=2{{k}_{2}}+1$
Where, ${{k}_{2}}$ is an integer.
\[6q+5=6q+4+1\]
$\Rightarrow 6q+5=2\left( 3q+2 \right)+1$
$\Rightarrow 6q+5=2{{k}_{3}}+1$
Where, ${{k}_{3}}$ is an integer.
Thus, $6q+1,6q+3,6q+5$ are of the form $2k+1$ and are not exactly divisible by $2$.
Also, all these expressions are of odd numbers.
Therefore, any positive odd integer can be expressed in the form, $6q+1$ or $6q+3$, or $6q+5$, where $q$ is some integer.
3. An army contingent of $616$ members is to march behind an army band of $32$ members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Ans: Given that an army contingent of $616$ members is to march behind an army band of $32$ members in a parade. The two groups are to march in the same number of columns.
We have to find the maximum number of columns in which they can march.
We need to find the HCF of $616$ and $32$ to find the maximum number of columns.
We will use the Euclid’s division algorithm to find the HCF.
Let $a=616$ and $b=32$.
Since, $a > b$
Using division algorithm, we get
$a=bq+r$
\[\Rightarrow 616=32\times 19+8\]
Here,
$\Rightarrow b=32$
$\Rightarrow q=19$
$\Rightarrow r=8$
Since $r\ne 0$, we apply the Euclid’s lemma to $b$ (new divisor) and $r$ (new remainder). We get
$\Rightarrow 32=8\times 4+0$
Since, we get $r=0$, thus we can stop at this stage.
When we get the remainder zero, divisor will be the HCF.
Therefore, the HCF of $616$ and $32$ is $8$.
Therefore, in $8$ columns members can march.
4. Use Euclid’s division lemma to show that the square of any positive integer is either of form $3m$ or $3m+1$ for some integer $m$.
(Hint: Let $x$ be any positive integer than it is of the form $3q,3q+1$ or $3q+2$. Now, square each of these and show that they can be rewritten in the form $3m$ or $3m+1$.)
Ans: Let $a$ be any positive integer and $b=3$.
Then, by Euclid’s division algorithm we get $a=bq+r$, where, $0\le r < b$.
Here, $0\le r < 3$.
Substitute the values, we get
$\Rightarrow a=3q+r$
If $r=0$, we get
$\Rightarrow a=3q+0$
$\Rightarrow a=3q$
If $r=1$, we get
$\Rightarrow a=3q+1$
If $r=2$, we get
$\Rightarrow a=3q+2$
Therefore, $a=3q$ or $3q+1$ or $3q+2$.
Now, squaring each of these, we get
$\Rightarrow {{a}^{2}}={{\left( 3q \right)}^{2}}$ or ${{\left( 3q+1 \right)}^{2}}$ or ${{\left( 3q+2 \right)}^{2}}$
Now, applying the identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$, we get
$\Rightarrow {{a}^{2}}=9{{q}^{2}}$ or $9{{q}^{2}}+6q+1$ or $9{{q}^{2}}+12q+4$
Thus, we get
$\Rightarrow {{a}^{2}}=3\times 3{{q}^{2}}$
$\Rightarrow {{a}^{2}}=3m$, where, $m=3{{q}^{2}}$
And,
${{a}^{2}}=3\times 3{{q}^{2}}+3\times 2q+1$
$\Rightarrow {{a}^{2}}=3\left( 3{{q}^{2}}+2q \right)+1$
$\Rightarrow {{a}^{2}}=3m+1$, where, $m=3{{q}^{2}}+2q$
And,
${{a}^{2}}=3\times 3{{q}^{2}}+6\times 2q+4$
$\Rightarrow {{a}^{2}}=3\times 3{{q}^{2}}+6\times 2q+3+1$
$\Rightarrow {{a}^{2}}=3\left( 3{{q}^{2}}+4q+1 \right)+1$
$\Rightarrow {{a}^{2}}=3m+1$, where, $m=3{{q}^{2}}+4q+1$
Therefore, we can say that the square of any positive integer is either of form $3m$ or $3m+1$ for some integer $m$.
5. Use Euclid’s division lemma to show that the cube of any positive integer is of the form $9m$, $9m+1$ or $9m+8$.
Ans: Let $a$ be any positive integer and $b=3$.
Then, by Euclid’s division algorithm we get $a=bq+r$, where, $0\le r < b$.
Here, $0\le r < 3$.
Substitute the values, we get
$\Rightarrow a=3q+r$
If $r=0$, we get
$\Rightarrow a=3q+0$
$\Rightarrow a=3q$
If $r=1$, we get
$\Rightarrow a=3q+1$
If $r=2$, we get
$\Rightarrow a=3q+2$
Therefore, $a=3q$ or $3q+1$ or $3q+2$.
Now, consider $a=3q$, we get
$\Rightarrow {{a}^{3}}={{\left( 3q \right)}^{3}}$
$\Rightarrow {{a}^{3}}=27{{q}^{3}}$
$\Rightarrow {{a}^{3}}=9\left( 3{{q}^{3}} \right)$
$\Rightarrow {{a}^{3}}=9m$, where, $m=3{{q}^{3}}$
Now, consider $a=3q+1$, we get
$\Rightarrow {{a}^{3}}={{\left( 3q+1 \right)}^{3}}$
Now, applying the identity ${{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}$, we get
$\Rightarrow {{a}^{3}}=27{{q}^{3}}+27{{q}^{2}}+9q+1$
$\Rightarrow {{a}^{3}}=9\left( 3{{q}^{3}}+3{{q}^{2}}+q \right)+1$
$\Rightarrow {{a}^{3}}=9m+1$, where, \[m=3{{q}^{3}}+3{{q}^{2}}+q\]
Now, consider $a=3q+2$, we get
$\Rightarrow {{a}^{3}}={{\left( 3q+2 \right)}^{3}}$
Now, applying the identity ${{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}$, we get
$\Rightarrow {{a}^{3}}=27{{q}^{3}}+54{{q}^{2}}+36q+8$
$\Rightarrow {{a}^{3}}=9\left( 3{{q}^{3}}+6{{q}^{2}}+4q \right)+8$
$\Rightarrow {{a}^{3}}=9m+8$, where, \[m=3{{q}^{3}}+6{{q}^{2}}+4q\]
Therefore, we can say that cube of any positive integer is of the form $9m$, $9m+1$ or $9m+8$.
Exercise 1.2 (Page No. 11)
1. Express each number as product of its prime factors:
(i) $140$
Ans: We know that the procedure of writing a number as the product of prime numbers is known as the prime factorization. Prime numbers that can be multiplied to obtain the original number are known as prime factors.
$\Rightarrow 140=2\times 2\times 5\times 7$
$\therefore 140={{2}^{2}}\times 5\times 7$
Therefore, the prime factors of $140$ are $2,5,7$.
(ii) $156$
Ans: We know that the procedure of writing a number as the product of prime numbers is known as the prime factorization. Prime numbers that can be multiplied to obtain the original number are known as prime factors.
$\Rightarrow 156=2\times 2\times 3\times 13$
$\therefore 156={{2}^{2}}\times 3\times 13$
Therefore, the prime factors of $156$ are $2,3,13$.
(iii) $3825$
Ans: We know that the procedure of writing a number as the product of prime numbers is known as the prime factorization. Prime numbers that can be multiplied to obtain the original number are known as prime factors.
$\Rightarrow 3825=3\times 3\times 5\times 5\times 17$
$\therefore 3825={{3}^{2}}\times {{5}^{2}}\times 17$
Therefore, the prime factors of $3825$ are $3,5,17$.
(iv) $5005$
Ans: We know that the procedure of writing a number as the product of prime numbers is known as the prime factorization. Prime numbers that can be multiplied to obtain the original number are known as prime factors.
$\Rightarrow 5005=5\times 7\times 11\times 13$
$\therefore 5005=5\times 7\times 11\times 13$
Therefore, the prime factors of $5005$ are $5,7,11,13$.
(v) $7429$
Ans: We know that the procedure of writing a number as the product of prime numbers is known as the prime factorization. Prime numbers that can be multiplied to obtain the original number are known as prime factors.
$\Rightarrow 7429=17\times 19\times 23$
$\therefore 7429=17\times 19\times 23$
Therefore, the prime factors of $7429$ are $17,19,23$.
2. Find the LCM and HCF of the following pairs of integers and verify that $LCM\times HCF=\text{Product of two numbers}$.
(i) $26$ and $91$
Ans: First we write the prime factors of $26$ and $91$. We get
$\Rightarrow 26=2\times 13$ and
$\Rightarrow 91=7\times 13$
Now, we know that HCF is the highest factor, among the common factors of two numbers.
Therefore, the HCF of $26$ and $91$ is $13$.
Now, we know that LCM is least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $26$ and $91$ will be
$\Rightarrow 2\times 7\times 13=182$
Therefore, the LCM of $26$ and $91$ is $182$.
Now, the product of two numbers is
$\Rightarrow 26\times 91=2366$
Product of LCM and HCF is
$\Rightarrow 13\times 182=2366$
We get $LCM\times HCF=\text{Product of two numbers}$.
The desired result has been verified.
(ii) $510$ and $92$
Ans: First we write the prime factors of $510$ and $92$. We get
$\Rightarrow 510=2\times 3\times 5\times 17$ and
$\Rightarrow 92=2\times 2\times 23$
Now, we know that HCF is the highest factor, among the common factors of two numbers.
Therefore, the HCF of $510$ and $92$ is $2$.
Now, we know that LCM is least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $510$ and $92$ will be
$\Rightarrow 2\times 2\times 3\times 5\times 17\times 23=23460$
Therefore, the LCM of $510$ and $92$ is $23460$.
Now, the product of two numbers is
$\Rightarrow 510\times 92=46920$
Product of LCM and HCF is
$\Rightarrow 2\times 23460=46920$
We get $LCM\times HCF=\text{Product of two numbers}$.
The desired result has been verified.
(iii) $336$ and $54$
Ans: First we write the prime factors of $336$ and $54$. We get
\[\Rightarrow 336=2\times 2\times 2\times 2\times 3\times 7\]
and
$\Rightarrow 54=2\times 3\times 3\times 3$
Now, we know that HCF is the highest factor, among the common factors of two numbers.
Therefore, the HCF of $336$ and $54$ is $2\times 3=6$.
Now, we know that LCM is least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $336$ and $54$ will be
$\Rightarrow 2\times 2\times 2\times 2\times 3\times 3\times 3\times 7=3024$
Therefore, the LCM of $336$ and $54$ is $3024$.
Now, the product of two numbers is
$\Rightarrow 336\times 54=18144$
Product of LCM and HCF is
$\Rightarrow 6\times 3024=18144$
We get $LCM\times HCF=\text{Product of two numbers}$.
The desired result has been verified.
3. Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) $12,15$ and $21$
Ans: The procedure of writing a number as the product of prime numbers is known as the prime factorization.
The prime factors of $12,15$ and $21$ are as follows:
\[\Rightarrow 12=2\times 2\times 3\]
\[\Rightarrow 15=3\times 5\] and
$\Rightarrow 21=3\times 7$
Now, we know that HCF is the highest factor, among the common factors of two numbers.
Therefore, the HCF of $12,15$ and $21$ is $3$.
Now, we know that LCM is the least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $12,15$ and $21$ will be
$\Rightarrow 2\times 2\times 3\times 5\times 7=420$
Therefore, the LCM of $12,15$ and $21$ is $420$.
(ii) $17,23$ and $29$
Ans: The procedure of writing a number as the product of prime numbers is known as the prime factorization.
The prime factors of $17,23$ and $29$ are as follows:
\[\Rightarrow 17=17\times 1\]
$\Rightarrow 23=23\times 1$ and
$\Rightarrow 29=29\times 1$
Now, we know that HCF is the highest factor, among the common factors of two numbers.
Therefore, the HCF of $17,23$ and $29$ is $1$.
Now, we know that LCM is least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $17,23$ and $29$ will be
$\Rightarrow 17\times 23\times 29=11339$
Therefore, the LCM of $17,23$ and $29$ is $11339$.
(iii) $8,9$ and $25$
Ans: The procedure of writing a number as the product of prime numbers is known as the prime factorization.
The prime factors of $8,9$ and $25$ are as follows:
\[\Rightarrow 8=2\times 2\times 2\]
\[\Rightarrow 9=3\times 3\] and
$\Rightarrow 25=5\times 5$
Now, we know that HCF is the highest factor, among the common factors of two numbers. as there is no common factor.
Therefore, the HCF of $8,9$ and $25$ is $1$.
Now, we know that LCM is least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $8,9$ and $25$ will be
$\Rightarrow 2\times 2\times 2\times 3\times 3\times 5\times 5=1800$
Therefore, the LCM of $8,9$ and $25$ is $1800$.
4. Given that HCF $\left( 306,657 \right)=9$, find LCM $\left( 306,657 \right)$.
Ans: We have been given the HCF of two numbers $\left( 306,657 \right)=9$.
We have to find the LCM of $\left( 306,657 \right)$.
Now, we know that $LCM\times HCF=\text{Product of two numbers}$
Substitute the values, we get
$LCM\times 9=306\times 657$
$\Rightarrow LCM=\dfrac{306\times 657}{9}$
$\therefore LCM=22338$
Therefore, the LCM of $\left( 306,657 \right)=22338$.
5. Check whether ${{6}^{n}}$ can end with the digit $0$ for any natural number $n$.
Ans: We have to check whether ${{6}^{n}}$ can end with the digit $0$ for any natural number $n$.
By divisibility rule we know that if any number ends with the digit $0$, it is divisible by $2$ and $5$.
Thus, the prime factors of ${{6}^{n}}$ is
$\Rightarrow {{6}^{n}}={{\left( 2\times 3 \right)}^{n}}$
Now, we will observe that for any value of $n$, ${{6}^{n}}$ is not divisible by $5$.
Therefore, ${{6}^{n}}$ cannot end with the digit $0$ for any natural number $n$.
6. Explain why $7\times 11\times 13+13$ and $7\times 6\times 5\times 4\times 3\times 2\times 1+5$ are composite numbers.
Ans: The given numbers are $7\times 11\times 13+13$ and $7\times 6\times 5\times 4\times 3\times 2\times 1+5$.
We can rewrite the given numbers as
$\Rightarrow 7\times 11\times 13+13=13\times \left( 7\times 11+1 \right)$
$\Rightarrow 7\times 11\times 13+13=13\times \left( 77+1 \right)$
$\Rightarrow 7\times 11\times 13+13=13\times 78$
$\Rightarrow 7\times 11\times 13+13=13\times 13\times 6$
And,
$\Rightarrow 7\times 6\times 5\times 4\times 3\times 2\times 1+5=5\times \left( 7\times 6\times 4\times 3\times 2\times 1+1 \right)$
$\Rightarrow 7\times 6\times 5\times 4\times 3\times 2\times 1+5=5\times \left( 1008+1 \right)$
$\Rightarrow 7\times 6\times 5\times 4\times 3\times 2\times 1+5=5\times 1009$
Here, we can observe that the given expressions has its factors other than $1$ and the number itself.
A composite number have factors other than $1$ and the number itself.
Therefore, $7\times 11\times 13+13$ and $7\times 6\times 5\times 4\times 3\times 2\times 1+5$ are composite numbers.
7. There is a circular path around a sports field. Sonia takes $18$ minutes to drive one round of the field, while Ravi takes $12$ minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Ans: It can be observed that Ravi takes lesser time than Sonia for completing $1$ round of the circular path. Both are going in the same direction, they will meet again when Ravi will have completed $1$ round of that circular path with respect to Sonia.
The total time taken for completing this $1$ round of circular path will be the LCM of time taken by Sonia and Ravi for ending $1$ round of circular path respectively i.e., LCM of $18$ minutes and $12$ minutes.
The prime factors of $12$ and $18$ are as follows:
\[\Rightarrow 12=2\times 2\times 3\] and
$\Rightarrow 18=2\times 3\times 3$
Now, we know that LCM is least common multiple. To find the LCM multiplies each factor to the number of times it occurs in any number.
Then the LCM of $12$ and $18$ will be
$\Rightarrow 2\times 2\times 3\times 3=36$
Therefore, Ravi and Sonia meet again at the starting point after $36$ minutes.
Exercise 1.2 (Page No. 14)
1. Prove that $\sqrt{5}$ is irrational.
Ans: We have to prove that $\sqrt{5}$ is irrational.
We will use contradiction method to prove it.
Let $\sqrt{5}$ is a rational number of the form $\dfrac{a}{b}$, where $b\ne 0$ and $a$ and $b$ are co-prime i.e. $a$ and $b$ have only $1$ as a common factor.
Let $\sqrt{5}=\dfrac{a}{b}$
Now, squaring both sides, we get
${{\left( \sqrt{5} \right)}^{2}}={{\left( \dfrac{a}{b} \right)}^{2}}$
\[\Rightarrow 5=\dfrac{{{a}^{2}}}{{{b}^{2}}}\]
$\Rightarrow {{a}^{2}}=5{{b}^{2}}$ …….(1)
If ${{a}^{2}}$ is divisible by $5$ than $a$ is also divisible by $5$.
Let $a=5k$, where, $k$ is any integer.
Again squaring both sides, we get
\[\Rightarrow {{a}^{2}}={{\left( 5k \right)}^{2}}\]
Substitute the value in eq. (1), we get
\[\Rightarrow {{\left( 5k \right)}^{2}}=5{{b}^{2}}\]
$\Rightarrow {{b}^{2}}=5{{k}^{2}}$ …..(2)
If ${{b}^{2}}$ is divisible by $5$ than $b$ is also divisible by $5$.
From, eq. (1) and (2), we can conclude that $a$ and $b$ have $5$ as a common factor.
This contradicts our assumption.
Therefore, we can say that $\sqrt{5}$ is irrational.
Hence proved.
2. Prove that $3+2\sqrt{5}$ is irrational.
Ans: We have to prove that $3+2\sqrt{5}$ is irrational.
We will use contradiction method to prove it.
Let $3+2\sqrt{5}$ is a rational number of the form $\dfrac{a}{b}$, where $b\ne 0$ and $a$ and $b$ are co-prime i.e. $a$ and $b$ have only $1$ as a common factor.
Let $3+2\sqrt{5}=\dfrac{a}{b}$
$\Rightarrow 2\sqrt{5}=\dfrac{a}{b}-3$
$\Rightarrow \sqrt{5}=\dfrac{1}{2}\left( \dfrac{a}{b}-3 \right)$ ……..(1)
From eq. (1) we can say that $\dfrac{1}{2}\left( \dfrac{a}{b}-3 \right)$ is rational so $\sqrt{5}$ must be rational.
But this contradicts the fact that $\sqrt{5}$ is irrational. Hence the assumption is false.
Therefore, we can say that $3+2\sqrt{5}$ is irrational.
Hence proved.
3. Prove that following are irrationals:
(i) $\dfrac{1}{\sqrt{2}}$
Ans: We have to prove that $\dfrac{1}{\sqrt{2}}$ is irrational.
We will use contradiction method to prove it.
Let $\dfrac{1}{\sqrt{2}}$ is a rational number of the form $\dfrac{a}{b}$, where $b\ne 0$ and $a$ and $b$ are co-prime i.e. $a$ and $b$ have only $1$ as a common factor.
Let $\dfrac{1}{\sqrt{2}}=\dfrac{a}{b}$
$\Rightarrow \sqrt{2}=\dfrac{b}{a}$ ………..(1)
From eq. (1) we can say that $\dfrac{b}{a}$ is rational so $\sqrt{2}$ must be rational.
But this contradicts the fact that $\sqrt{2}$ is irrational. Hence the assumption is false.
Therefore, we can say that $\dfrac{1}{\sqrt{2}}$ is irrational.
Hence proved.
(ii) $7\sqrt{5}$
Ans: We have to prove that $7\sqrt{5}$ is irrational.
We will use contradiction method to prove it.
Let $7\sqrt{5}$ is a rational number of the form $\dfrac{a}{b}$, where $b\ne 0$ and $a$ and $b$ are co-prime i.e. $a$ and $b$ have only $1$ as a common factor.
Let $7\sqrt{5}=\dfrac{a}{b}$
$\Rightarrow \sqrt{5}=\dfrac{a}{7b}$ ………..(1)
From eq. (1) we can say that $\dfrac{a}{7b}$ is rational so $\sqrt{5}$ must be rational.
But this contradicts the fact that $\sqrt{5}$ is irrational. Hence the assumption is false.
Therefore, we can say that $7\sqrt{5}$ is irrational.
Hence proved.
(iii) $6+\sqrt{2}$
Ans: We have to prove that $6+\sqrt{2}$ is irrational.
We will use contradiction method to prove it.
Let $6+\sqrt{2}$ is a rational number of the form $\dfrac{a}{b}$, where $b\ne 0$ and $a$ and $b$ are co-prime i.e. $a$ and $b$ have only $1$ as a common factor.
Let $6+\sqrt{2}=\dfrac{a}{b}$
$\Rightarrow \sqrt{2}=\dfrac{a}{b}-6$ ………..(1)
From eq. (1) we can say that $\dfrac{a}{b}-6$ is rational so $\sqrt{2}$ must be rational.
But this contradicts the fact that $\sqrt{2}$ is irrational. Hence the assumption is false.
Therefore, we can say that $6+\sqrt{2}$ is irrational.
Hence proved.
Exercise 1.3 (Page No. 17)
1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) $\dfrac{13}{3125}$
Ans: Given a rational number $\dfrac{13}{3125}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $3125$.
Then, factors of $3125$ are
$\Rightarrow 3125=5\times 5\times 5\times 5\times 5$
$\Rightarrow 3125={{5}^{5}}$
Here, the factors of denominator are of the form ${{5}^{m}}$.
Therefore, $\dfrac{13}{3125}$ has terminating decimal expansion.
(ii) $\dfrac{17}{8}$
Ans: Given a rational number $\dfrac{17}{8}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $8$.
Then, factors of $8$ are
$\Rightarrow 8=2\times 2\times 2$
$\Rightarrow 8={{2}^{3}}$
Here, the factors of denominator are of the form ${{2}^{n}}$.
Therefore, $\dfrac{17}{8}$ has terminating decimal expansion.
(iii) $\dfrac{64}{455}$
Ans: Given a rational number $\dfrac{64}{455}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $455$.
Then, factors of $455$ are
$\Rightarrow 455=5\times 7\times 13$
Here, the factors of denominator are not in the form ${{2}^{n}}{{5}^{m}}$. The denominator has factors other than $2$ and $5$.
Therefore, $\dfrac{64}{455}$ has non-terminating repeating decimal expansion.
(iv) $\dfrac{15}{1600}$
Ans: Given a rational number $\dfrac{15}{1600}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $1600$.
Then, factors of $1600$ are
$\Rightarrow 1600=2\times 2\times 2\times 2\times 2\times 2\times 5\times 5$
$\Rightarrow 1600={{2}^{6}}\times {{5}^{5}}$
Here, the factors of denominator are of the form ${{2}^{n}}{{5}^{m}}$.
Therefore, $\dfrac{15}{1600}$ has terminating decimal expansion.
(v) $\dfrac{29}{343}$
Ans: Given a rational number $\dfrac{29}{343}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $343$.
Then, factors of $343$ are
$\Rightarrow 343=7\times 7\times 7$
$\Rightarrow 343={{7}^{3}}$
Here, the factors of denominator are not in the form ${{2}^{n}}{{5}^{m}}$. The denominator has factors other than $2$ and $5$.
Therefore, $\dfrac{29}{343}$ has non-terminating repeating decimal expansion.
(vi) $\dfrac{23}{{{2}^{3}}{{5}^{2}}}$
Ans: Given a rational number $\dfrac{23}{{{2}^{3}}{{5}^{2}}}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is ${{2}^{3}}{{5}^{2}}$.
Here, the denominator is of the form ${{2}^{n}}{{5}^{m}}$.
Therefore, $\dfrac{23}{{{2}^{3}}{{5}^{2}}}$ has terminating decimal expansion.
(vii) $\dfrac{129}{{{2}^{2}}{{5}^{7}}{{7}^{5}}}$
Ans: Given a rational number $\dfrac{129}{{{2}^{2}}{{5}^{7}}{{7}^{5}}}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is ${{2}^{2}}{{5}^{7}}{{7}^{5}}$.
Here, the denominator is of the form ${{2}^{n}}{{5}^{m}}$ but also has factors other than $2$ and $5$.
Therefore, $\dfrac{129}{{{2}^{2}}{{5}^{7}}{{7}^{5}}}$ has non-terminating repeating decimal expansion.
(viii) $\dfrac{6}{15}$
Ans: Given a rational number $\dfrac{6}{15}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $15$.
Then, factors of $3125$ are
$\Rightarrow 15=3\times 5$
But we can write the numerator of the given number as
$\dfrac{6}{15}=\dfrac{2\times 3}{3\times 5}=\dfrac{2}{5}$
Here, the factors of denominator are of the form ${{5}^{m}}$.
Therefore, $\dfrac{6}{15}$ has terminating decimal expansion.
(ix) $\dfrac{35}{50}$
Ans: Given a rational number $\dfrac{35}{50}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $50$.
Then, factors of $50$ are
$\Rightarrow 50=10\times 5$
But we can write the numerator of the given number as
$\dfrac{35}{50}=\dfrac{7\times 5}{10\times 5}=\dfrac{7}{10}$
$\Rightarrow 10=2\times 5$
Here, the factors of denominator are of the form ${{2}^{n}}{{5}^{m}}$.
Therefore, $\dfrac{35}{50}$ has terminating decimal expansion.
(x) $\dfrac{77}{210}$
Ans: Given a rational number $\dfrac{77}{210}$.
If the denominator of a rational number has prime factors of the form ${{2}^{n}}{{5}^{m}}$, where, $m$ and $n$ are positive integers. Then the rational number has terminating decimal expansion. If the denominator has factors other than $2$ and $5$, then it has non-terminating decimal expansion.
The denominator of the given number is $210$.
Then, factors of $210$ are
$\Rightarrow 210=2\times 3\times 5\times 7$
Here, the denominator has factors other than $2$ and $5$.
Therefore, $\dfrac{77}{210}$ has non-terminating repeating decimal expansion.
2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
(i) $\dfrac{13}{3125}$
Ans: To find the decimal expansion of $\dfrac{13}{3125}$, we will divide the numerator of the number by denominator using long division method. We get
$3125\overset{0.00416}{\overline{\left){\begin{align} & 13.00000 \\ & 0 \\ & \overline{130\text{ }} \\ & \text{ 0} \\ & \overline{\text{13000}} \\ & \text{12500} \\ & \overline{\text{ 5000 }} \\ & \text{ 3125} \\ & \overline{\text{ 18750 }} \\ & \underline{\text{ 18750 }} \\ & \text{ 0} \\ \end{align}}\right.}}$
Therefore, the decimal expansion of $\dfrac{13}{3125}$ is $0.00416$.
(ii) $\dfrac{17}{8}$
Ans: To find the decimal expansion of $\dfrac{17}{8}$, we will divide the numerator of the number by denominator using long division method. We get
$8\overset{2.125}{\overline{\left){\begin{align} & 17 \\ & 16 \\ & \overline{\text{ 10 }} \\ & \text{ 8} \\ & \overline{\text{ 20 }} \\ & \text{ 16} \\ & \overline{\text{ 40 }} \\ & \text{ }\underline{\text{40}} \\ & \text{ 0} \\ \end{align}}\right.}}$
Therefore, the decimal expansion of $\dfrac{17}{8}$ is $2.125$.
(iii) $\dfrac{15}{1600}$
Ans: To find the decimal expansion of $\dfrac{15}{1600}$, we will divide the numerator of the number by denominator using long division method. We get
$1600\overset{0.009375}{\overline{\left){\begin{align} & 15.000000 \\ & 0 \\ & \overline{150\text{ }} \\ & \text{ 0} \\ & \overline{\text{1500}} \\ & \text{0} \\ & \overline{\text{15000 }} \\ & \text{14400} \\ & \overline{\text{ 6000 }} \\ & \underline{\text{ 4800 }} \\ & \text{ 12000} \\ & \underline{\text{ 11200}} \\ & \text{ 8000} \\& \text{ }\underline{\text{8000}} \\ & \text{ 0} \\ \end{align}}\right.}}$
Therefore, the decimal expansion of $\dfrac{15}{1600}$ is $0.009375$.
(iv) $\dfrac{23}{{{2}^{3}}{{5}^{2}}}$
Ans: To find the decimal expansion of $\dfrac{23}{{{2}^{3}}{{5}^{2}}}$, we will divide the numerator of the number by denominator using long division method. We get
$\dfrac{23}{{{2}^{3}}{{5}^{2}}}=\dfrac{23}{200}$
$200\overset{00.115}{\overline{\left){\begin{align} & 23.000 \\ & 0 \\ & \overline{23\text{ }} \\ & \text{ 0} \\ & \overline{\text{230 }} \\ & 200 \\ & \overline{\text{ 300 }} \\ & \text{ 200} \\ & \overline{\text{ 1000 }} \\ & \underline{\text{ 1000 }} \\ & \text{ 0} \\ \end{align}}\right.}}$
Therefore, the decimal expansion of $\dfrac{23}{{{2}^{3}}{{5}^{2}}}$ is $0.115$.
(v) $\dfrac{6}{15}$
Ans: To find the decimal expansion of $\dfrac{6}{15}$, we will divide the numerator of the number by denominator using long division method. We get
$\dfrac{6}{15}=\dfrac{2\times 3}{3\times 5}=\dfrac{2}{5}$
$5\overset{0.4}{\overline{\left){\begin{align} & 2.0 \\ & 0 \\ & \overline{20\text{ }} \\ & \underline{20\text{ }} \\ & 0 \\ \end{align}}\right.}}$
Therefore, the decimal expansion of $\dfrac{6}{15}$ is $0.4$.
(vi) $\dfrac{35}{50}$
Ans: To find the decimal expansion of $\dfrac{35}{50}$, we will divide the numerator of the number by denominator using long division method. We get
$50\overset{0.7}{\overline{\left){\begin{align} & 35.0 \\ & 0 \\ & \overline{\text{350 }} \\ & \underline{350\text{ }} \\ & \text{ 0} \\ \end{align}}\right.}}$
Therefore, the decimal expansion of $\dfrac{35}{50}$ is $0.7$.
3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form $\dfrac{p}{q}$, what can you say about the prime factors of $q$?
(i) $43.123456789$
Ans: Given a decimal expansion $43.123456789$.
The given number has terminating expansion, we can write the number as $\dfrac{43123456789}{1000000000}$, which is of the form $\dfrac{p}{q}$.
Therefore, the number $43.123456789$ is a rational number.
Since the number has terminating decimal expansion, the factors of $q$ must be of the form ${{2}^{n}}{{5}^{m}}$.
(ii) $0.120120012000120000......$
Ans: Given a decimal expansion $0.120120012000120000......$.
When we observe the given expansion we can say that the number has non-terminating and non-repeating decimal expansion. Hence we cannot express it in the form of $\dfrac{p}{q}$.
Therefore, the number is irrational.
(iii) $43.\overline{123456789}$
Ans: Given the decimal expansion $43.\overline{123456789}$.
The given number has non-terminating but repeating decimal expansion. So the number will be of the form $\dfrac{p}{q}$.
Therefore, the number $43.\overline{123456789}$ is a rational number.
But the factors of denominator are not of the form ${{2}^{n}}{{5}^{m}}$. Denominator also has factors other than $2$ and $5$.
Important Topics under NCERT Solutions for Class 10 Math Chapter 1 Real Numbers
The first chapter of the class 10 maths syllabus includes Real Numbers, which is an important chapter in maths covered in class 10. The chapter on Real Numbers is divided into 4 major parts. The following is a list of the important topics covered under the chapter Real Numbers. It is recommended that students read through these topics carefully to be able to learn, use, and master this chapter and be able to solve problems based on Real Numbers.
Introduction to Real Numbers
Fundamental Theorem of Arithmetic (H.C.F. and L.C.M.)
Revisiting Irrational Numbers
1.1 Introduction
In the introduction part of ch 1 Maths Class 10 students will be reminded of what they learned in class IX about real numbers and irrational numbers. This section gives a glimpse of what students would learn about positive numbers in the later sections of Chapter 1 Maths Class 10, i.e. Euclid’s division algorithm and the fundamental theorem of arithmetic. The Fundamental Theorem of Arithmetic is based on the fact that a composite number can be expressed as a product of prime numbers, in distinct ways. This theorem has deep and significant applications in mathematics.
1.2 The Fundamental Theorem of Arithmetic
According to this theorem, every composite number can be factorized as a product of some prime numbers. It is a unique prime factorization of natural numbers as the order of the factors does not matter. We will understand this with an example that is based on the following fundamentals:
HCF - The highest common factor of two or more integers is the greatest integer that can exactly divide all the given integers. For example, HCF of 60 and 75 is 15.
LCM - The Least Common Multiple of two or more integers is the smallest integer that is exactly divisible by all the given integers. For example, LCm of 2, 4, and 5 is 20.
For two positive integers a and b; HCF(a,b) * LCM (a, b) = a * b
So, going by this theorem we can express any natural number as a multiplication of prime number, for example, 253 = 11 * 23, 4 = 2 * 2, etc.
1.3 Revisiting Irrational Numbers
In this section of NCERT Solutions for Class 10th Maths Chapter 1, you will remember the definition of Irrational numbers learned in earlier classes and then prove p is an irrational number, where p is a prime number.
If a number “n” can not be written in the form x/y, then it is called an irrational number. Here x and y are integers and n <> 0. Few examples of irrational numbers are 2,3, etc.
The Real Numbers Chapter Discusses:
The Division Algorithm of Euclid: This is a method named after the ancient Greek mathematician Euclid. It's a way to divide numbers and find the quotient and remainder.
The Arithmetic Fundamental Theorem: This is a fancy name for saying we are going to talk about rational and irrational numbers. Rational numbers are those that can be expressed as fractions, like 1/2 or 3/4. Irrational numbers are ones that can't be expressed as fractions, like the square root of 2.
Expansions in Decimals: This is about writing numbers in decimal form. For example, instead of writing 1/2, we can write 0.5. We'll also discuss how to express irrational numbers as decimals, even though they go on forever without repeating.
Class 10 Maths Chapter 1: Exercise Breakdown
Exercise | Number of Questions | |
Exercise 1.1 Solutions | 7 Questions | |
Exercise 1.2 Solutions | 3 Questions | |
Conclusion
NCERT Solutions for Class 10 Math Chapter 1 - Real Numbers provided by Vedantu offer clear explanations and step-by-step solutions for understanding the fundamentals of real numbers. It's important to focus on mastering concepts like irrational numbers, rational numbers, and their properties, as they form the basis for more complex mathematical topics. In the previous year's board exam three questions are typically asked in this chapter on average. The solutions provided by Vedantu ensure a strong foundation in this chapter, which is crucial for tackling higher-level math. By practicing these solutions, students can build confidence and excel in their math studies.
Other Related Links for Chapter 1
Check on the additional study materials provided for Class 10 Maths Chapter 1
Chapter-Specific NCERT Solutions for Class 10 Maths
Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
S.No. | NCERT Solutions Class 10 Chapter-wise Maths PDF |
1 | |
2 | Chapter 3 - Pair Of Linear Equations In Two Variables Solutions |
3 | |
4 | |
5 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 |
NCERT Study Resources for Class 10 Maths
For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.
S.No. | NCERT Study Resources for Class 10 Maths |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | |
8 | |
9 |
FAQs on NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers
1. Is π exactly equal to 22/7?
No, π is an irrational number, and 22/7 is just its rational approximation. The decimal representation of π is non-terminating and non-repeating, while 22/7 is a repeating decimal. This distinction is a key concept in real numbers class 10.
2. Are NCERT Solutions for Real Numbers just for copying homework?
No, these solutions are a learning tool designed to help you verify your method, not just the final answer. Using the real numbers class 10 NCERT solutions helps you understand the correct steps and logic required for solving problems as per the board guidelines.
3. Is the product of two irrational numbers always irrational?
No, the product of two irrational numbers can be rational. The common error is to generalise from examples like √3 × √5 = √15 (irrational). However, a simple counter-example is √3 × √3 = 3, which is a rational number.
4. Do I only need to learn the final formulas in Class 10 Maths Chapter 1?
No, understanding the derivation and logic behind the formulas is crucial. The NCERT Solutions for Class 10 Maths Chapter 1 focus on explaining the 'why' behind concepts like Euclid's Division Lemma and the Fundamental Theorem of Arithmetic, not just the 'what'.
Many students mistakenly believe that memorising the formula HCF × LCM = Product of numbers is enough. However, exams often test your understanding by asking you to apply the underlying prime factorisation method to solve problems or to write formal proofs, such as proving the irrationality of √5.
5. Is Euclid's Division Lemma only used to find HCF?
No, while its most common application in this chapter is finding the HCF, Euclid's Division Lemma is a more fundamental concept. It is also used to prove general properties of integers, such as showing that any positive odd integer is of the form 4q+1 or 4q+3.
6. Are all non-terminating decimal numbers irrational?
No, only decimals that are both non-terminating AND non-repeating are irrational. A decimal that is non-terminating but has a repeating pattern (recurring) is always a rational number. The confusion arises because both types of decimals continue infinitely. The key difference is the pattern.
For instance, the number 1/3 as a decimal is 0.333..., which is non-terminating but clearly repeats. Since it can be written in p/q form, it is rational. In contrast, an irrational number like √2 has a decimal expansion of 1.41421356... that continues forever without any repeating block of digits. This is a crucial distinction in the real numbers class 10 questions and answers. A quick check is to see if a bar can be placed over digits (like 0.12̅); if so, it's rational.
7. Can the HCF and LCM of two numbers be equal?
Yes, the HCF and LCM of two positive integers are equal if and only if the numbers themselves are equal. The misconception that HCF must be smaller than LCM arises from examples involving two *different* numbers.
For example, take the numbers 14 and 14. Their Highest Common Factor (HCF) is 14, and their Least Common Multiple (LCM) is also 14. Here, HCF = LCM. Now consider two different numbers, like 12 and 16.
Their prime factorisations are 2² × 3 and 2⁴. The HCF is 2² = 4, and the LCM is 2⁴ × 3 = 48. In this case, HCF < LCM. Remember the rule: For any two positive integers 'a' and 'b', HCF(a, b) × LCM(a, b) = a × b. This formula works perfectly even when a = b. So, HCF and LCM are identical only when the two numbers are the same.
8. What is included in the free NCERT Solutions PDF for Real Numbers?
The Free PDF of NCERT Solutions from Vedantu contains complete, step-by-step explanations for all in-text and exercise questions, including those from Exercise 1.1 and 1.2. It is not merely a list of final answers for you to check against.
Students often think a real numbers NCERT PDF download will be incomplete or only cover the main exercise problems. However, these resources are created to provide a full learning experience, explaining the application of theorems with the correct statement and logical flow required for exams.
9. Do I need to practice if I have the Class 10 Maths Chapter 1 question answers?
Yes, you must always attempt the problems on your own first. Use the class 10 Maths chapter 1 question answer solutions to verify your work, discover alternative methods, and understand where you went wrong. Passive reading cannot replace active problem-solving for building skills.
10. Does the Fundamental Theorem of Arithmetic just say we can find prime factors?
No, the theorem states something much more specific: every composite number can be expressed as a product of primes, and this prime factorisation is unique, apart from the order of the factors. The 'uniqueness' aspect is the most critical part of the theorem.




















 Watch Video
Watch Video



















