Maths Notes for Chapter 9 Circles Class 9 - FREE PDF Download
Circles Class 9 Maths Chapter 9 CBSE Notes - 2025-26
FAQs on Circles Class 9 Maths Chapter 9 CBSE Notes - 2025-26
1. What are the key concepts covered in the Class 9 Circles revision notes?
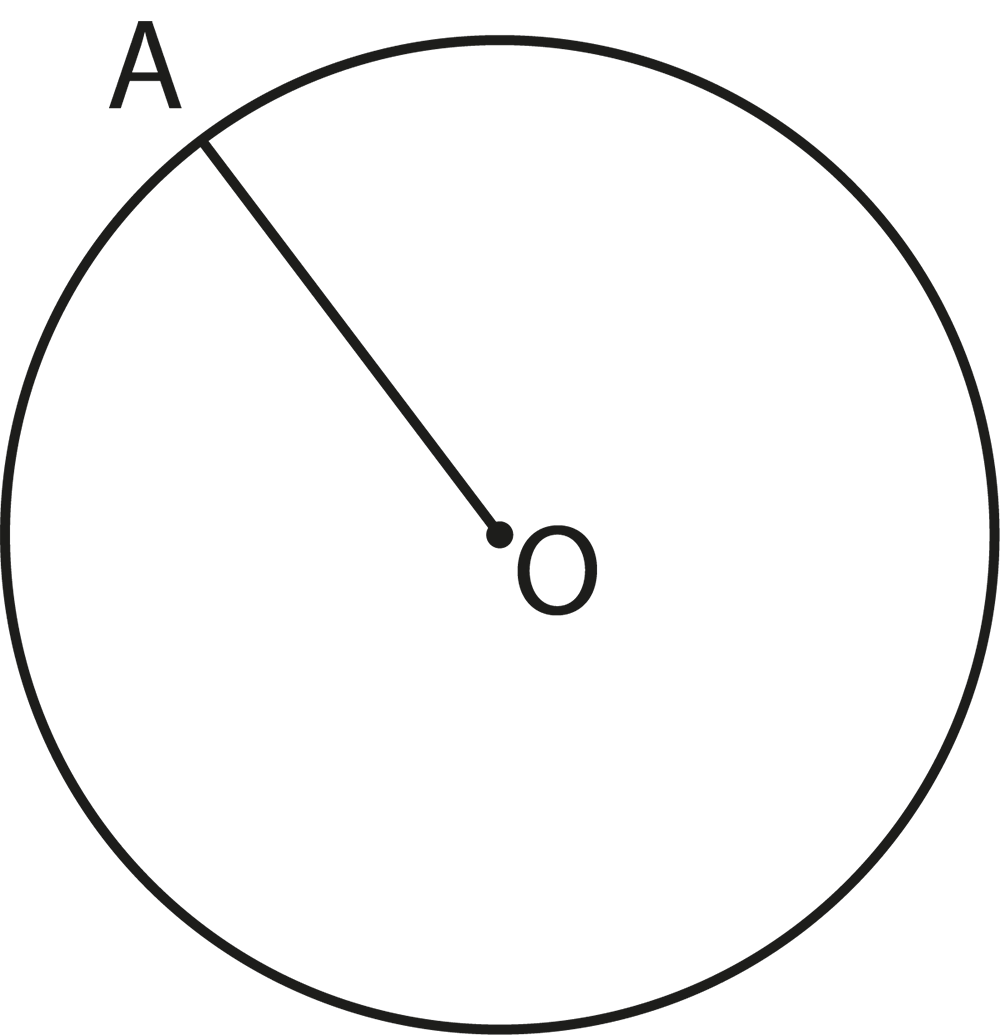
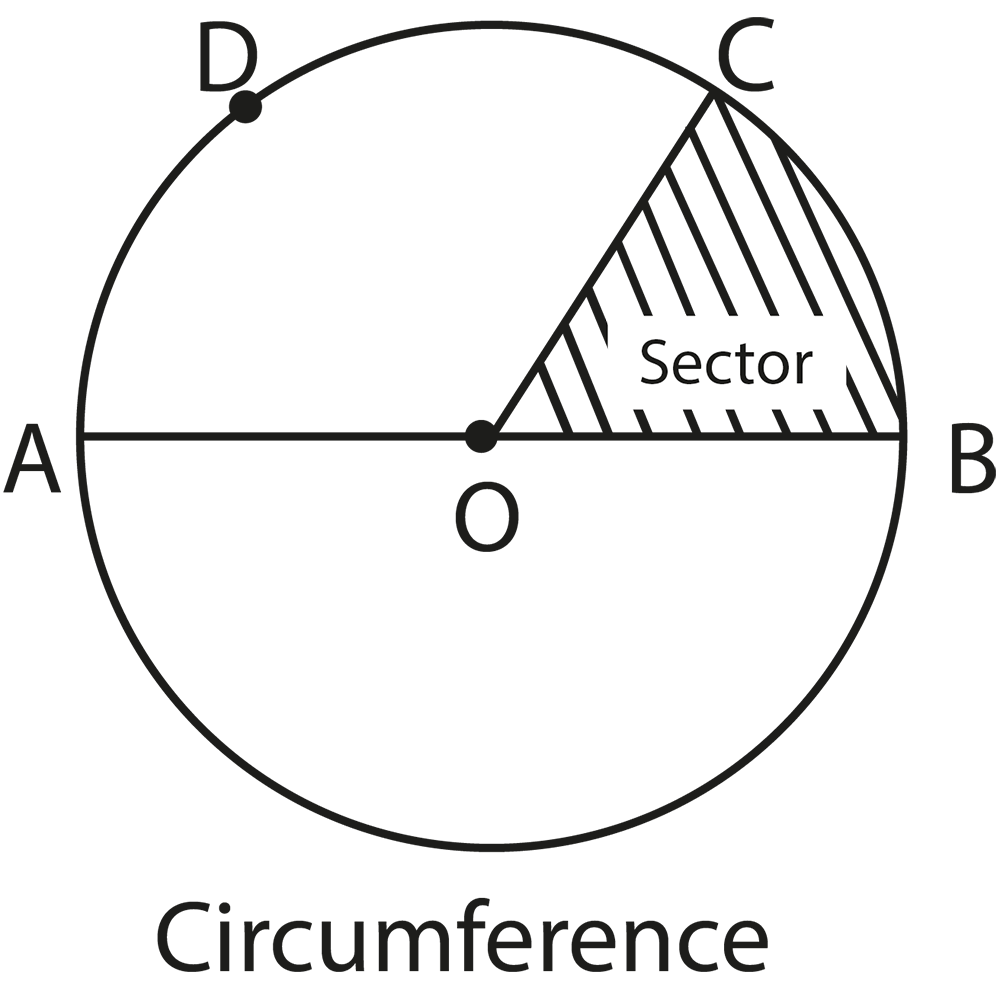
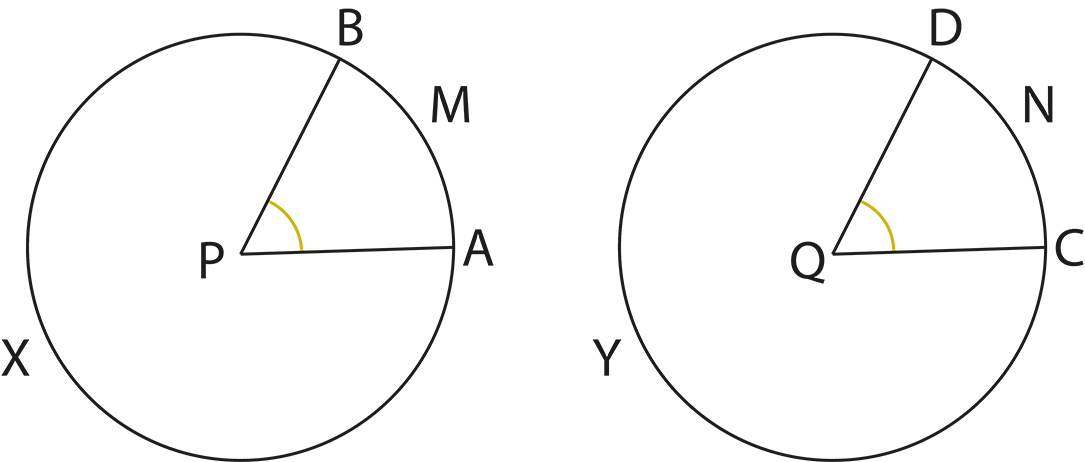
The revision notes for Class 9 Maths Chapter 9 Circles include core concepts like the definition of a circle, properties of chords, diameters, radii, arcs, sectors, and segments, and important theorems such as angles subtended by chords and arcs, properties of cyclic quadrilaterals, and equality of chords and arcs. The notes focus on the relationships between these properties and provide concise summaries for easy revision.
2. How do revision notes help in quick preparation for the Circles chapter in Class 9 Maths?
Revision notes are designed for efficient last-minute review. They consolidate all the main formulas, definitions, and theorems from the Circles chapter into short, organized summaries. This allows students to recap important points quickly before exams and focus on the most test-relevant areas.
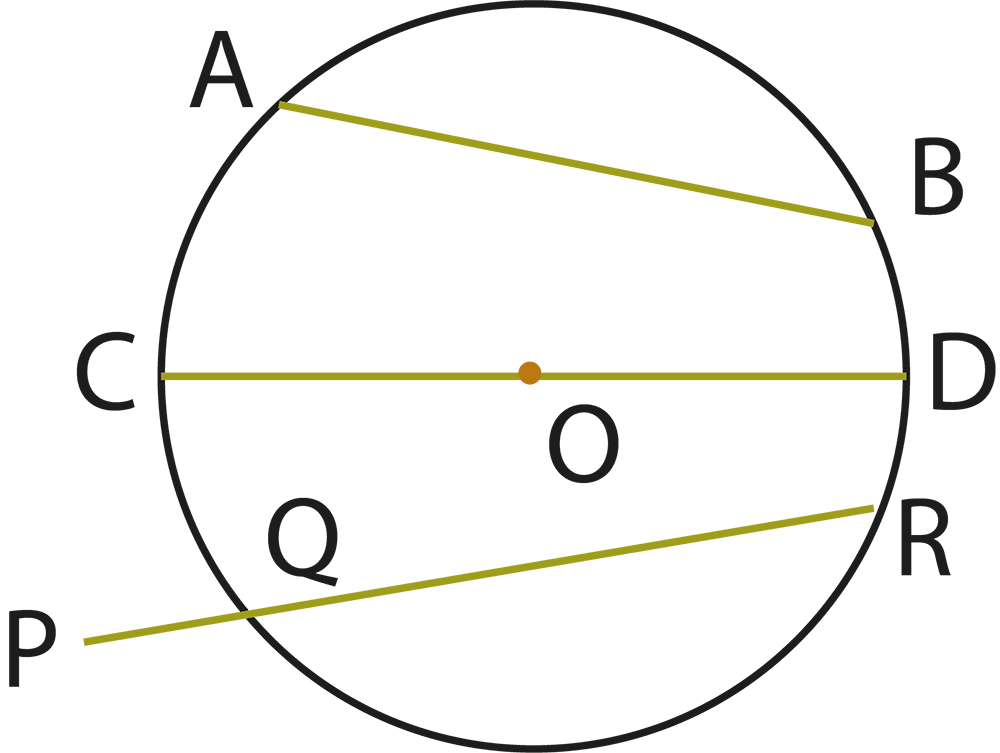
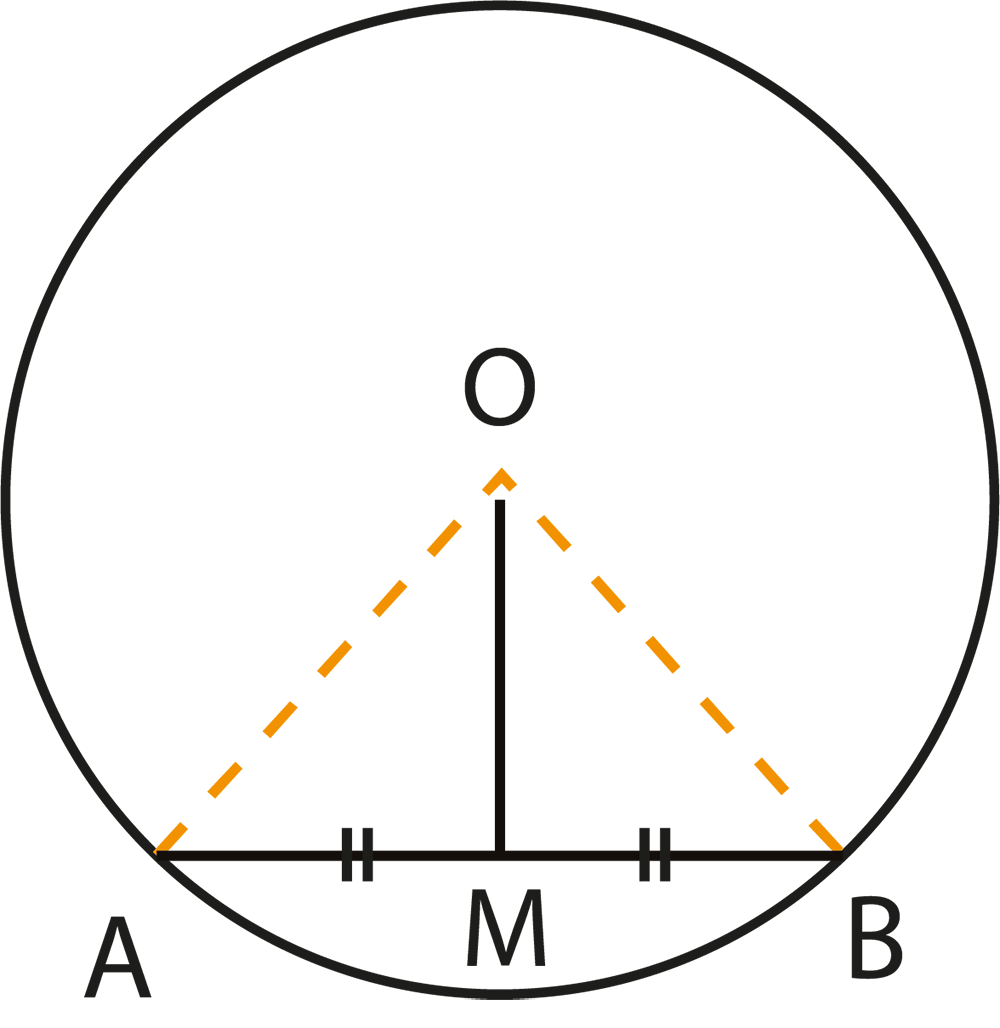
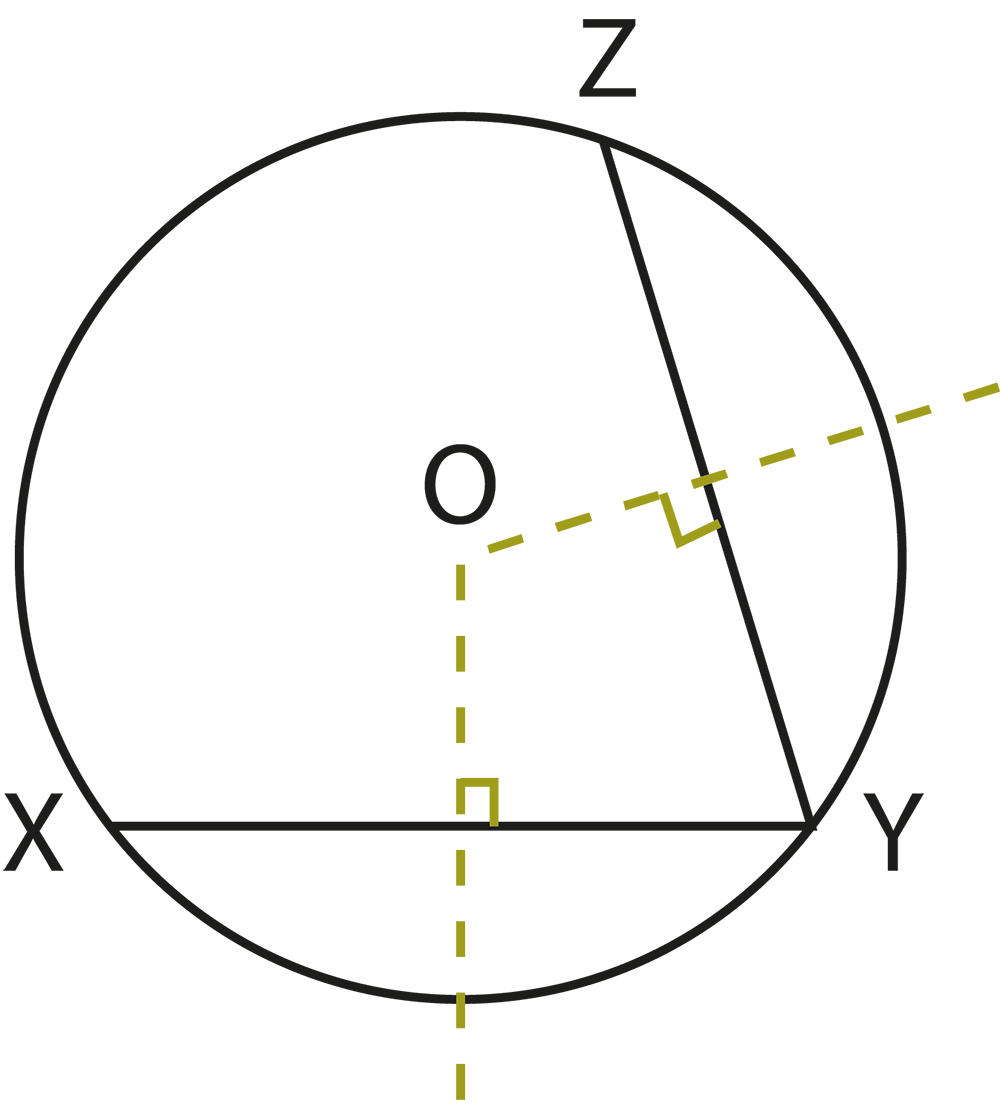
3. What is the relationship between a chord and its distance from the centre of a circle, as highlighted in revision notes?
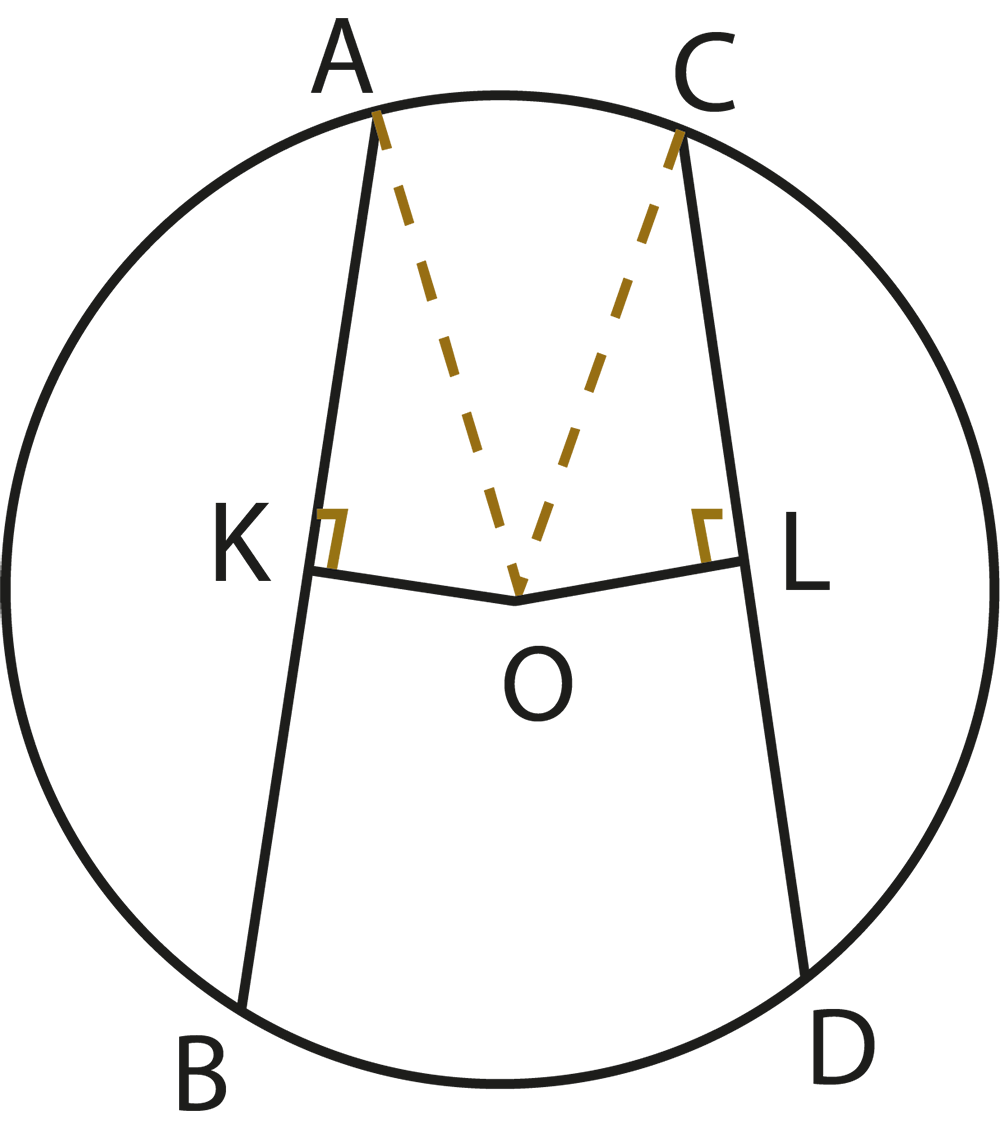
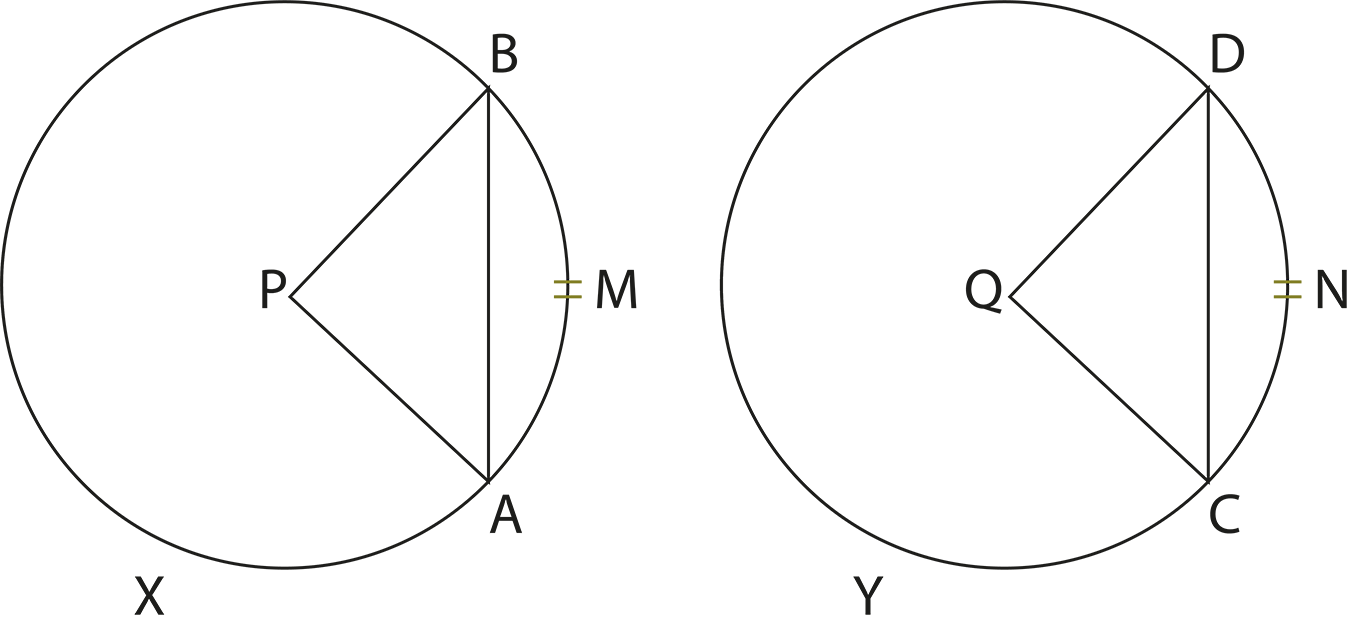
The revision notes explain that equal chords of a circle are equidistant from the centre. Conversely, chords that are equidistant from the centre are equal in length. This relationship helps students solve problems involving chords and their placement within the circle.
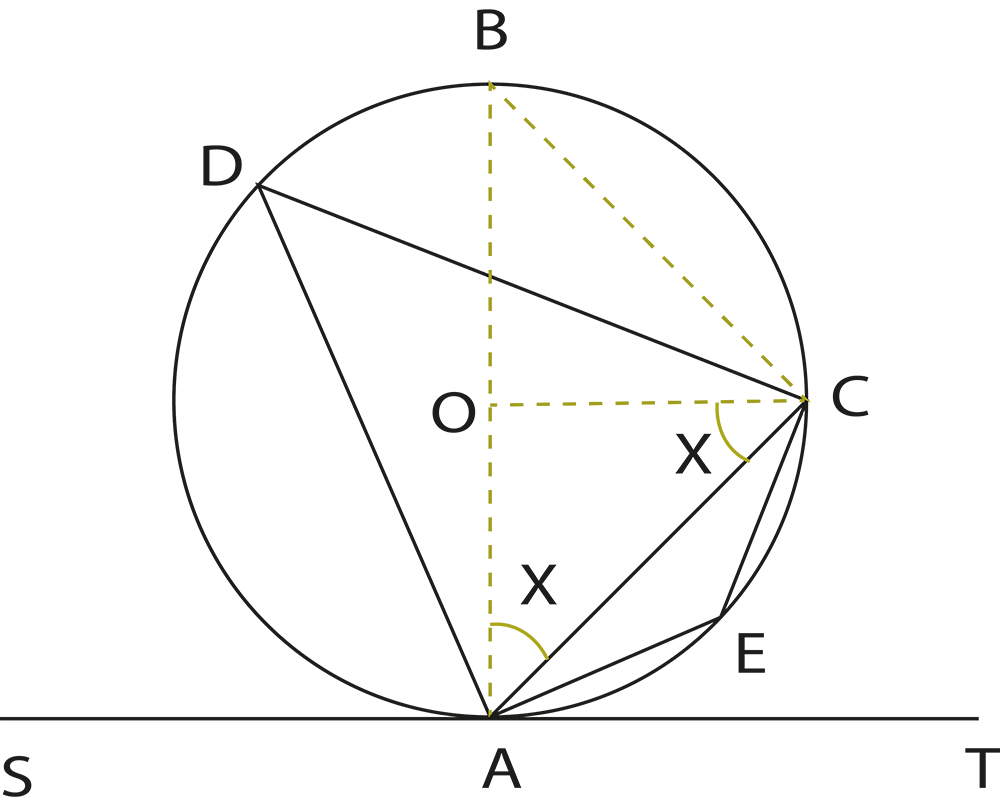
4. How do the theorems about angles in circles support problem-solving in Chapter 9?
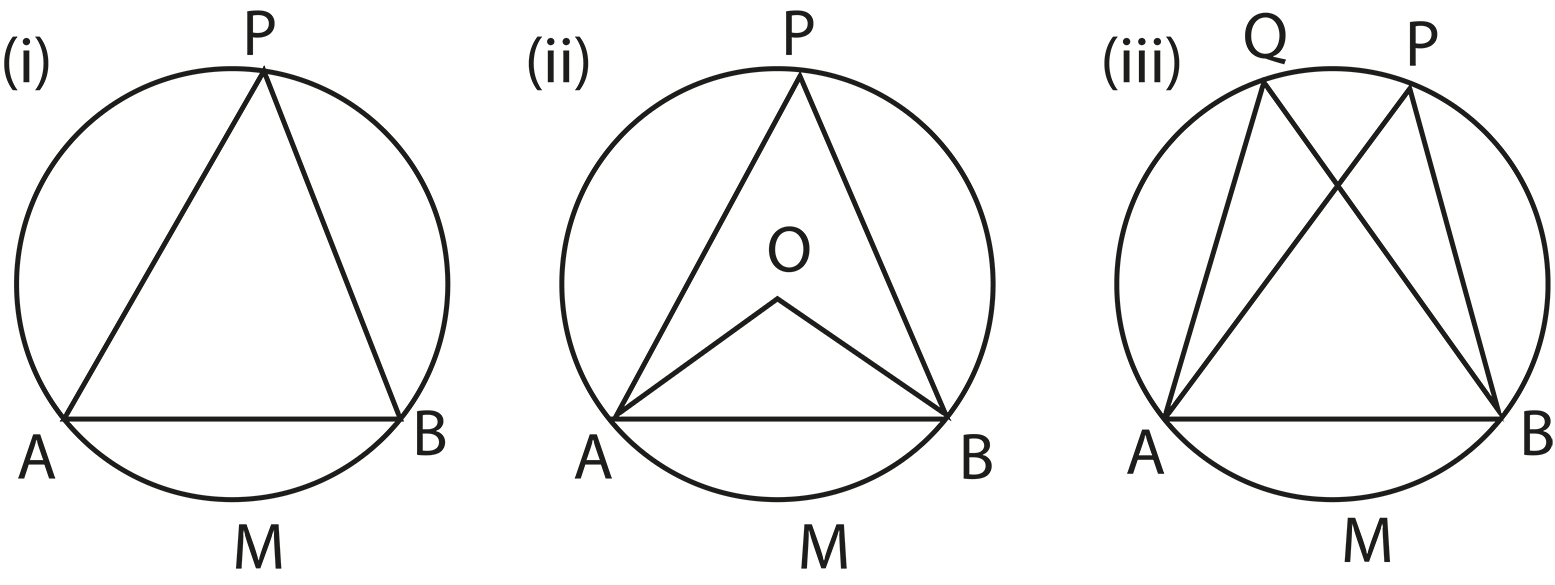
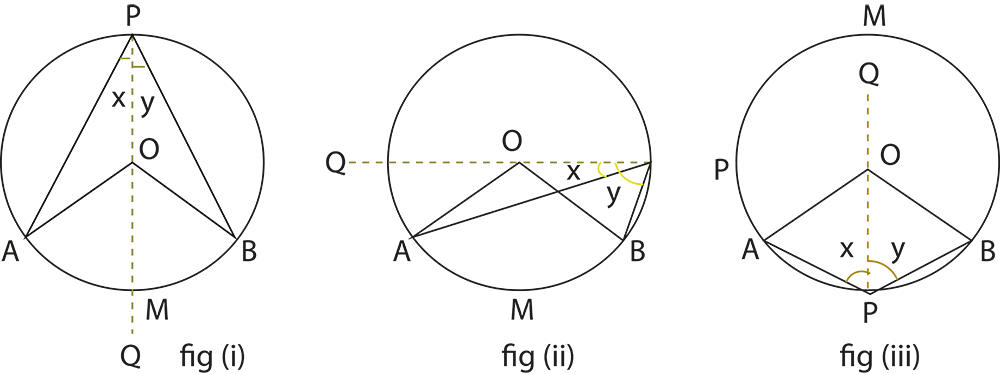
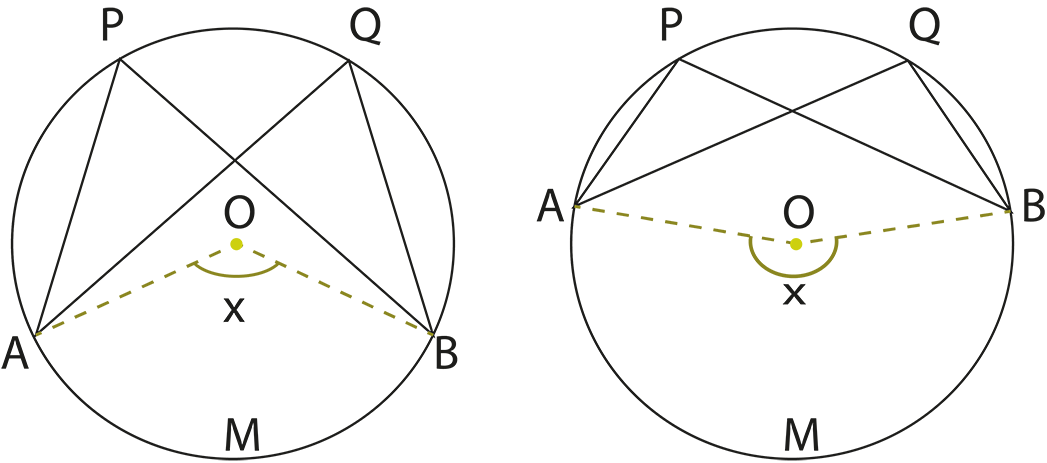
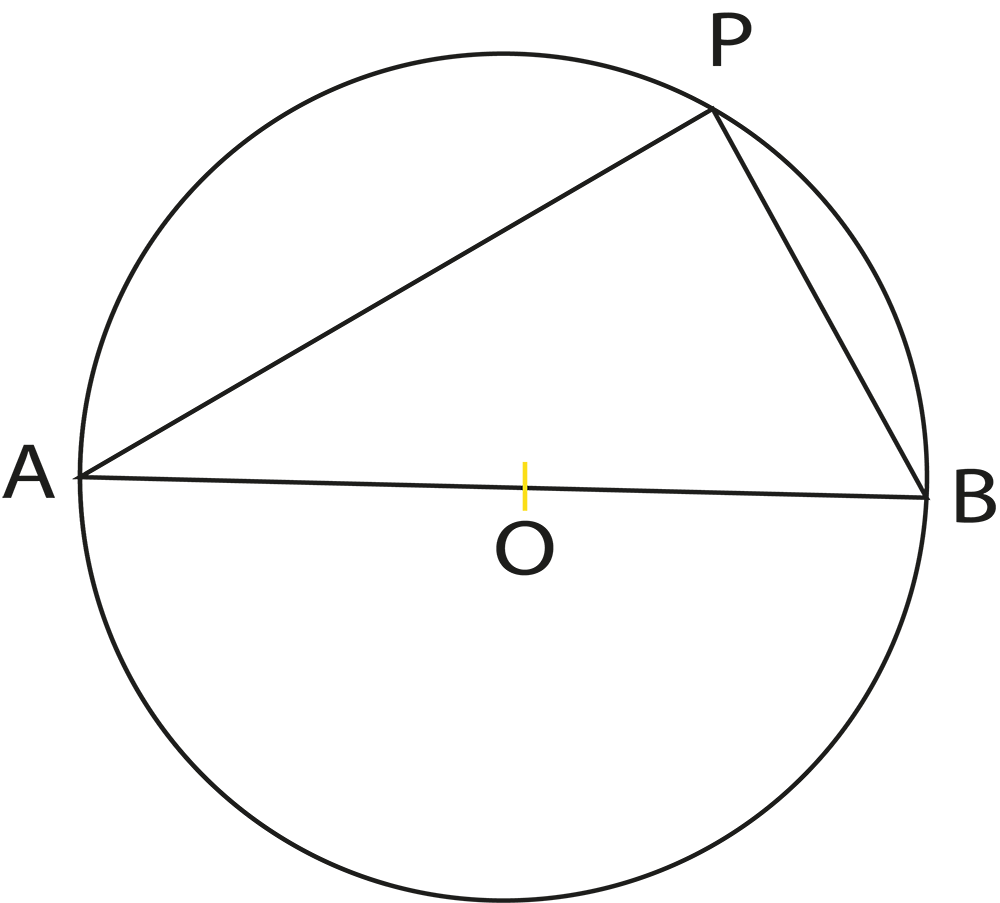
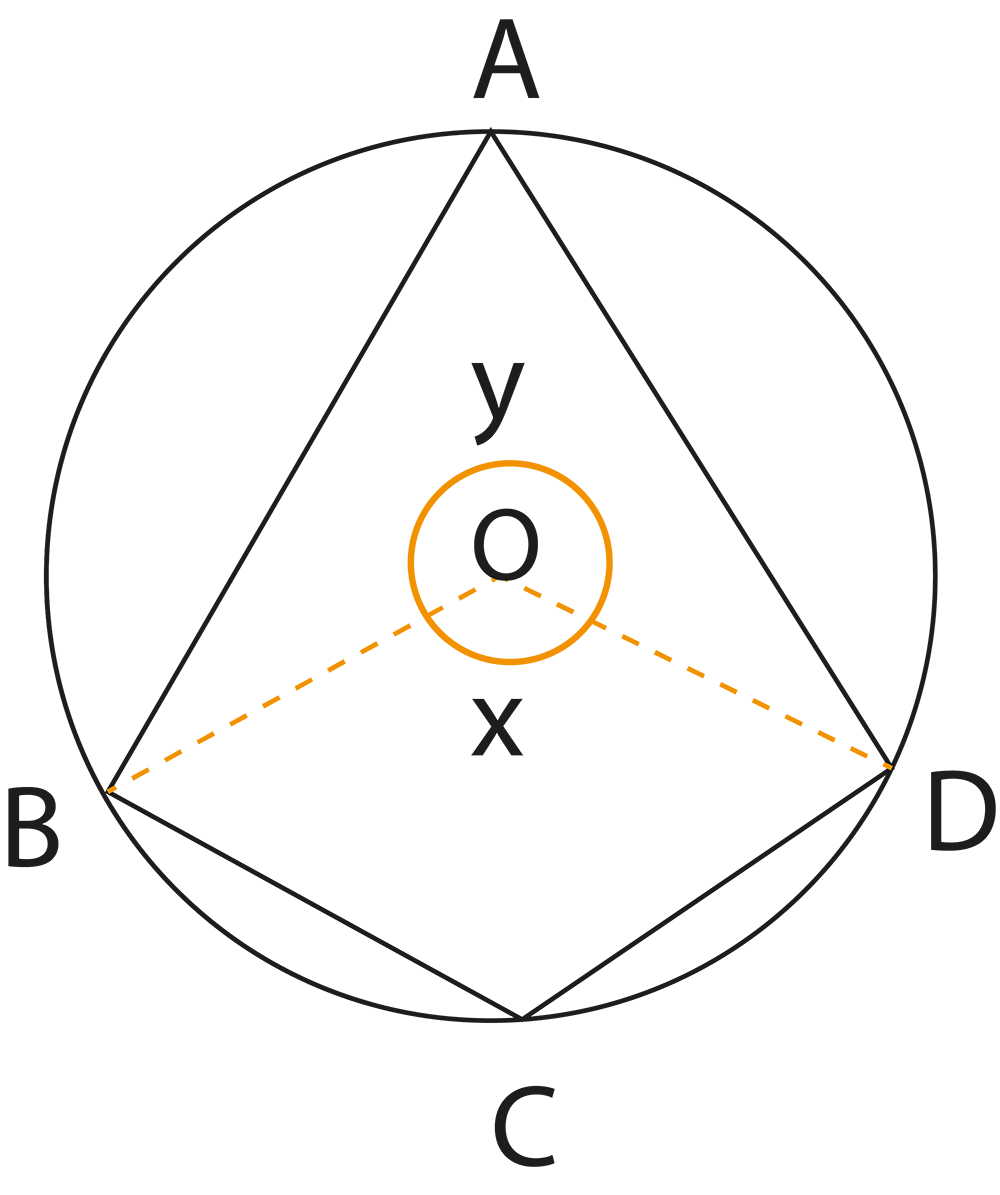
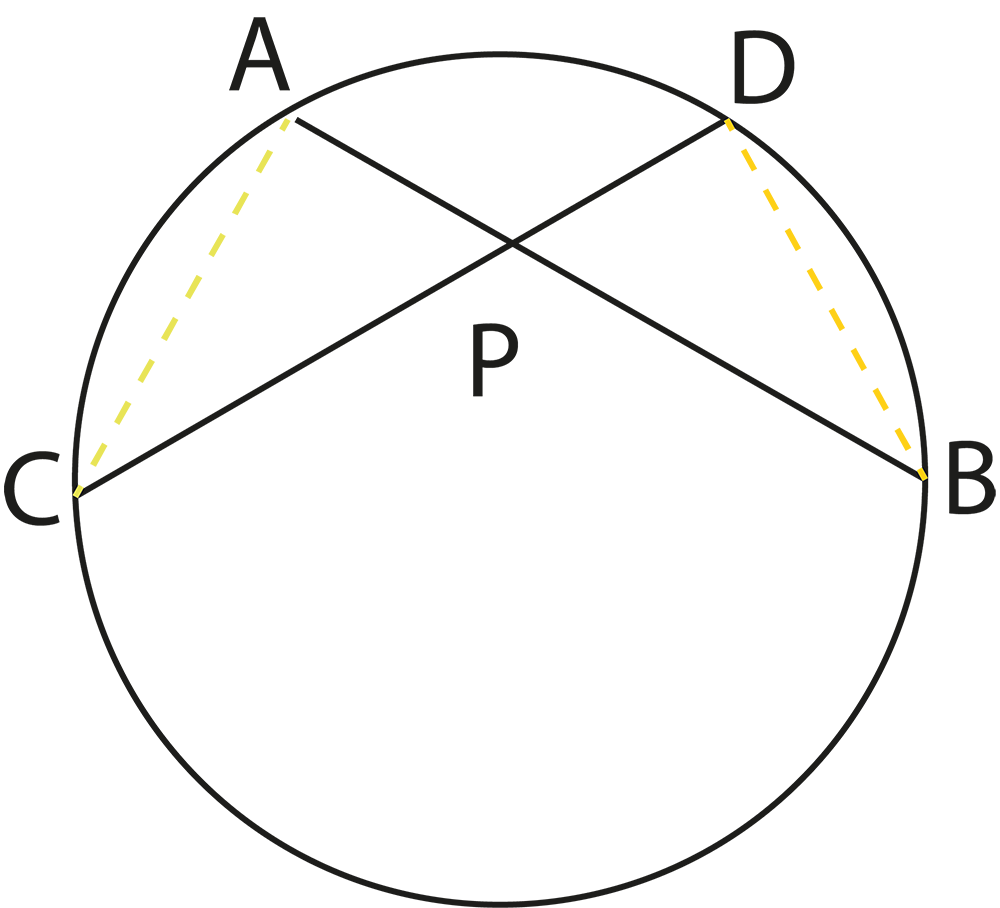
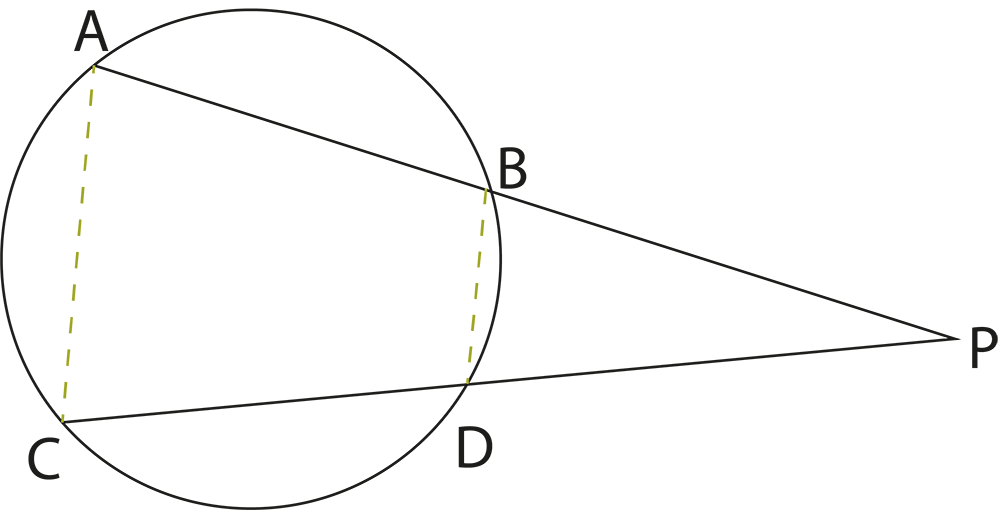
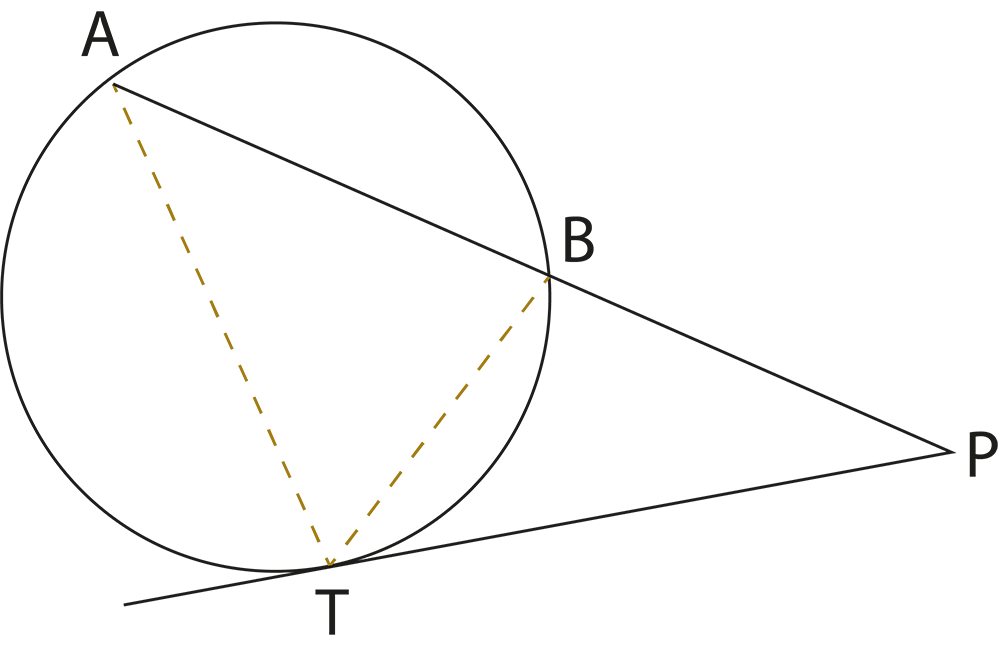
The revision notes summarize theorems like “the angle subtended by an arc at the centre is twice the angle at the circumference” and “angles in the same segment are equal”. These theorems are essential for solving questions involving measurements of angles within different parts of the circle.
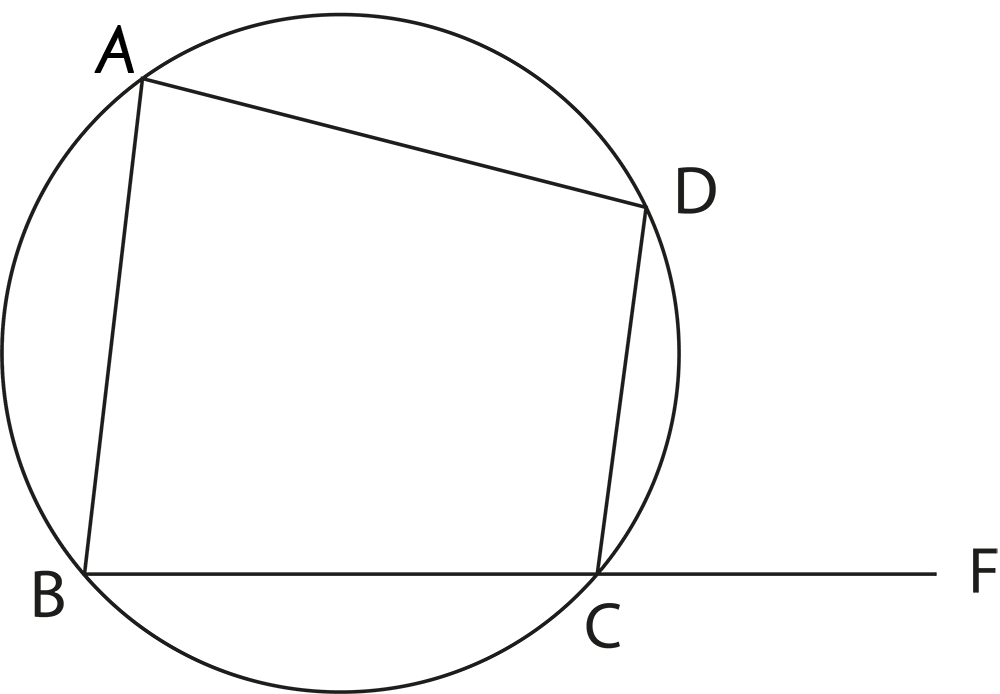
5. Why is it important to understand the concept of cyclic quadrilaterals in Class 9 Circles?
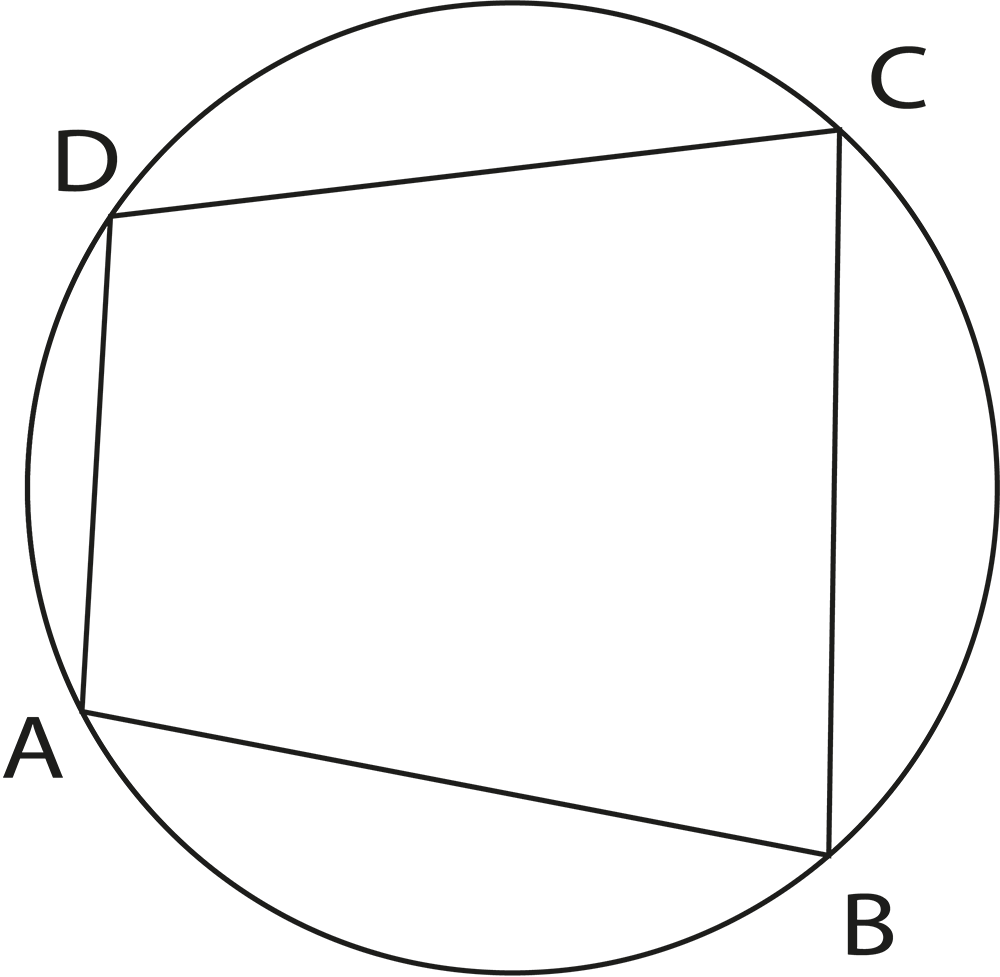
Understanding cyclic quadrilaterals is important because many exam problems involve identifying such quadrilaterals and applying the property that the sum of opposite angles is 180°. This concept connects circles with quadrilaterals and broadens your problem-solving ability in geometry.
6. How should students use revision notes to build connections between different theorems in circles?
Students should review the sequence in which theorems are derived and understand their logical relationships. For example, the converse of a theorem is often tested, so recognizing how one property leads to another strengthens concept retention and application in varied questions.
7. What misconceptions should students avoid when revising the Circles chapter?
Common misconceptions include
- Confusing the difference between radius and diameter
- Assuming every quadrilateral inscribed in a circle is cyclic without checking the angle property
- Misapplying theorems about arcs and chords without noting the required conditions (like ‘not a diameter’ or ‘equal arcs’)
8. How can concept maps or summary tables aid revision for Circles Class 9?
Concept maps or tables in revision notes allow students to visually organize relationships between definitions, theorems, and properties. This helps in quick recall and clarifies how topics such as chords, arcs, and cyclic quadrilaterals are interconnected within the chapter.
9. What is the best order to revise Circles Class 9 to maximize understanding before exams?
Start with the basic definitions (circle, radius, chord, diameter), then move to properties of chords and their theorems, followed by theorems about arcs and angles. Finally, revise cyclic quadrilaterals and their properties. This logical order mirrors how concepts build upon each other in the NCERT syllabus, ensuring you establish a strong foundation for solving complex questions.
10. What types of questions from Circles commonly appear in Class 9 exams, as per revision notes focus?
Exams typically include
- Statements and proofs of key theorems
- Application-based problems involving angles, chords, and cyclic quadrilaterals
- Short concept-based questions on definitions and properties
- Diagram-based problems where students must label or identify properties




















 Watch Video
Watch Video