An Overview of Cbse Class 9 Maths Notes Chapter 5 Introduction To Euclids Geometry
FAQs on CBSE Notes Class 9 Maths Chapter 5 - Introduction to Euclids Geometry - 2025-26
1. What are the key concepts covered in the Class 9 Revision Notes for Introduction to Euclid's Geometry?
The Class 9 Revision Notes for Introduction to Euclid's Geometry focus on the foundational definitions of points, lines, and surfaces, Euclid's five postulates, and key axioms. The notes summarise important terms, present each postulate with examples, and highlight the chapter’s essential theorems. These notes are designed for quick revision before exams and offer a concise summary as per the CBSE syllabus for 2025–26.
2. How should students structure their revision for Introduction to Euclid's Geometry using notes?
To revise effectively, start by reviewing the essential definitions and axioms. Then, move to Euclid’s five postulates, and understand each with examples. Next, summarise key theorems and review concept maps linking definitions, axioms, and postulates. This structured approach helps reinforce logical reasoning and ensures all fundamental concepts are revised quickly.
3. Why is understanding Euclid's postulates crucial for mastering geometry in higher classes?
Euclid's postulates provide the logical framework upon which all later concepts in geometry are built. A clear understanding enables students to apply these ideas in advanced topics, solve proofs, and recognise geometric principles in complex problems, making future chapters much easier to understand and apply.
4. What are the differences between axioms and postulates in Euclid’s Geometry, as highlighted in revision notes?
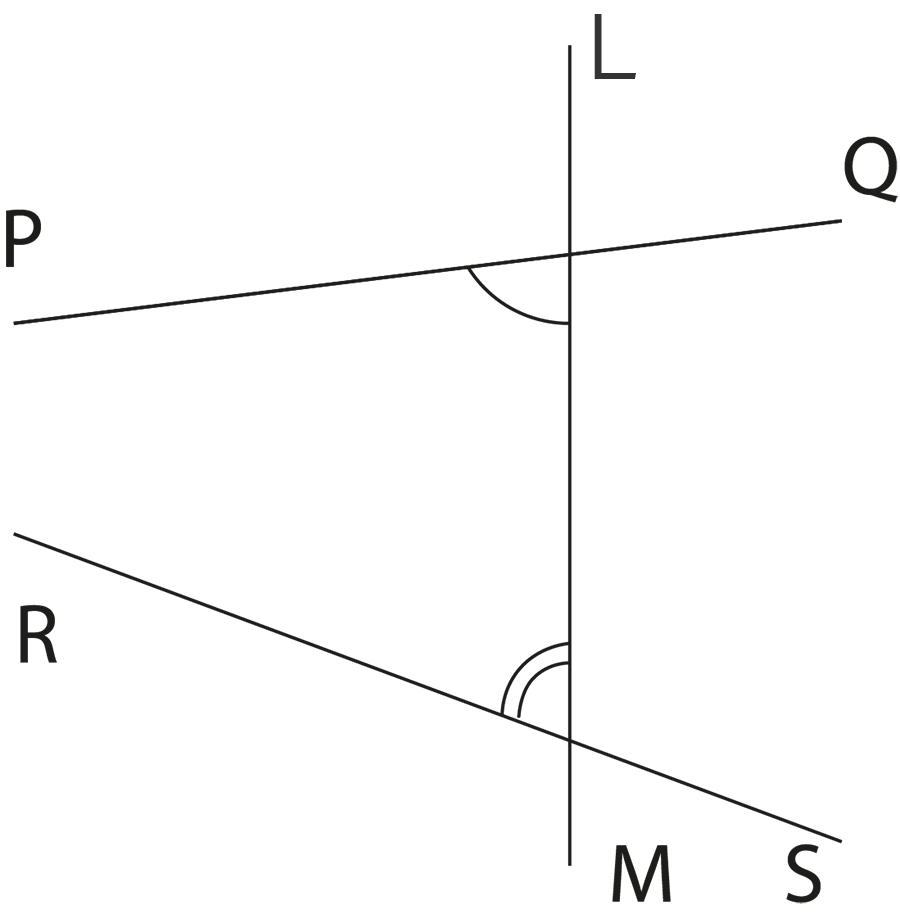
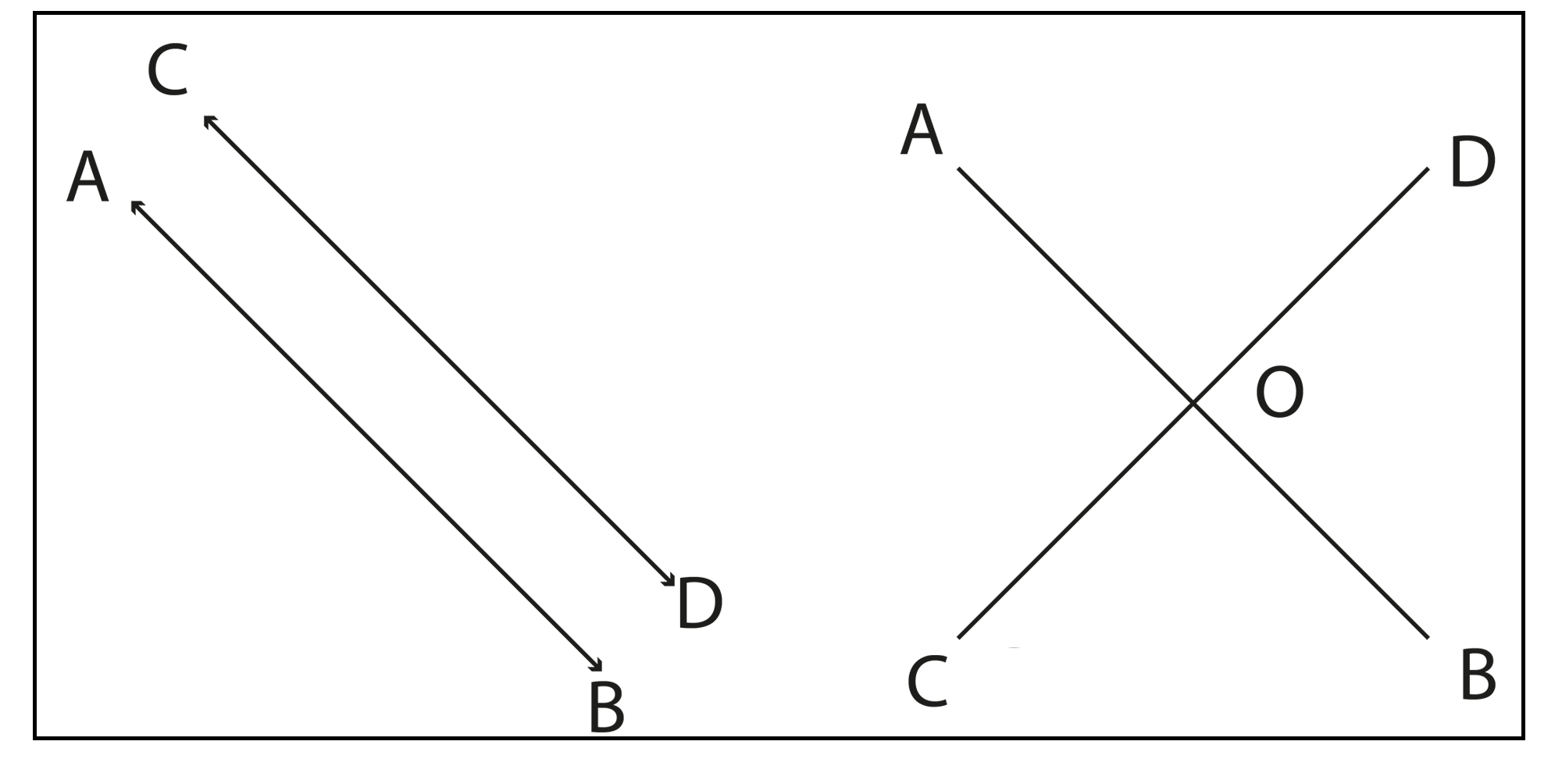
Axioms are general statements accepted as universally true and used across mathematics, while postulates are assumptions specific to geometry. For example, axioms include statements about equality and comparison, whereas postulates specify geometric constructions like drawing a straight line between two points or creating a circle with any centre and radius.
5. How can revision notes help in quickly memorising Euclid’s geometric definitions for exams?
Revision notes present each term—such as point, line, surface, and plane—in a simplified format, often using concept maps or summarised lists. This makes it easier to recall definitions quickly and strengthens conceptual clarity before exams.
6. What is the logical sequence of topics suggested in the revision notes for optimal preparation of Chapter 5?
The revision notes suggest reviewing topics in this sequence for efficient learning:
- Historical background of geometry and Euclid’s contributions
- Definitions of basic geometric terms
- Euclid’s axioms (with simple examples)
- Euclid’s five postulates (with explanations)
- Key theorems and equivalent versions of the fifth postulate
- Interconnections among the above concepts through concept maps
7. How do the revision notes highlight common misconceptions about Euclid’s Geometry?
The notes address common misconceptions such as confusing axioms with postulates, or assuming Euclid’s postulates apply to all types of geometry (including non-Euclidean geometry, which is not the case). Clarifying these distinctions helps prevent errors during exams and deeper mathematical studies.
8. What strategies do the Class 9 revision notes recommend for quick revision before the exam?
The notes recommend creating summary charts, using concept maps, and practicing quick oral recaps of definitions and postulates. Regularly self-assessing through short quizzes or practice questions on axioms and postulates also helps cement understanding just before the exam.
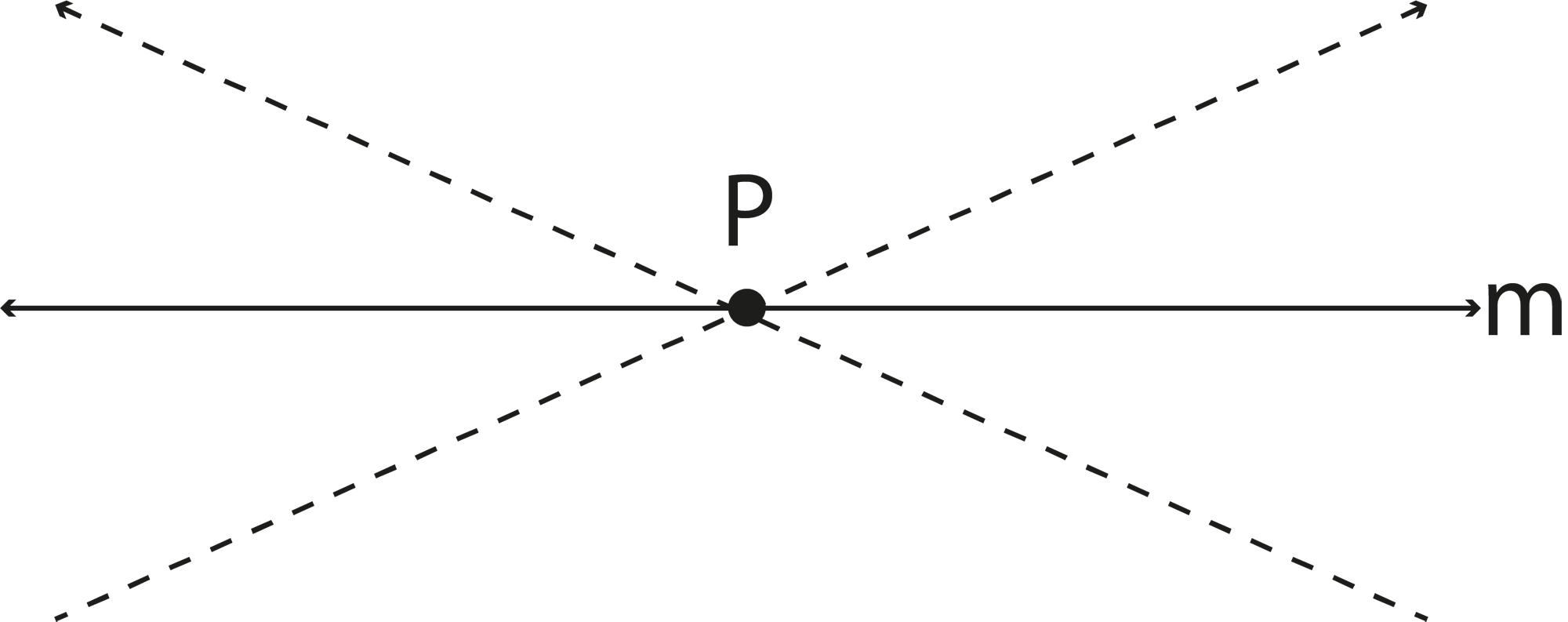
9. In what ways do the revision notes explain the application of Euclid's fifth postulate and its equivalent versions?
The notes use stepwise logic to illustrate the significance of the fifth postulate, including its role in parallel lines and uniqueness principles. By explaining both the original and equivalent versions, students can visualise why only one parallel can exist through a given point, strengthening their grasp of geometric logic.
10. How do the revision notes for Introduction to Euclid's Geometry connect this chapter to real-world applications or later chapters in the CBSE Class 9 Maths syllabus?
Revision notes draw connections between Euclid’s definitions/postulates and practical geometric problems, such as land measurement or architectural design. They also indicate how understanding these foundations will help in subsequent chapters like Lines and Angles, Triangles, and Quadrilaterals, building a strong base for the entire Maths syllabus.