Maths Notes for Chapter 8 Quadrilaterals Class 9 - FREE PDF Download
Quadrilaterals Class 9 Maths Chapter 8 CBSE Notes - 2025-26
FAQs on Quadrilaterals Class 9 Maths Chapter 8 CBSE Notes - 2025-26
1. What are the core concepts students should revise in Quadrilaterals for Class 9?
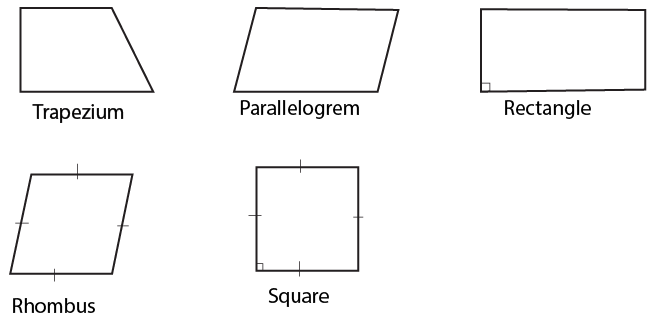
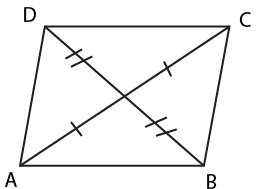
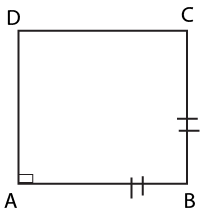
The main concepts to revise in Class 9 Quadrilaterals include the types of quadrilaterals (like parallelogram, rectangle, rhombus, square, trapezium), the angle sum property (sum of angles equals 360°), properties of parallelograms (such as opposite sides/angles being equal, diagonals bisecting each other), and important theorems with their proofs. Ensure you understand the Mid-point Theorem and the relationship among special quadrilaterals.
2. How can students efficiently use revision notes for Class 9 Maths Chapter 8 Quadrilaterals?
Start with the summary of definitions and properties, focus on the key theorems and their proofs, note all important inferred results, and use concept maps to visualize relationships between different types of quadrilaterals. End with a quick recap of key terms and try solving linked exercises for practice.
3. What is the best revision order for Quadrilaterals in Class 9 according to the CBSE 2025-26 syllabus?
Revise Quadrilaterals in this order for optimal coverage:
- Start with the basic definition and properties of quadrilaterals.
- Study types of quadrilaterals (parallelogram, rectangle, rhombus, square, trapezium).
- Move on to theorems proving key properties (opposite sides, diagonals, angle sum).
- Review Mid-point Theorem and its applications.
- Finish with summary, concept maps, and short recaps for each section.
4. Which key terms should be memorized for quick revision before exams in Quadrilaterals?
Important terms to remember include quadrilateral, parallelogram, rhombus, rectangle, square, trapezium, diagonal, opposite sides, opposite angles, consecutive sides, consecutive angles, bisect, perpendicular, congruent, and angle sum property. Understanding these makes recalling properties and solving questions easier.
5. How are special quadrilaterals related to each other in the Class 9 syllabus?
In the context of CBSE Class 9, all rectangles, rhombuses, and squares are specific types of parallelograms. A square is both a rectangle and a rhombus, but not all rectangles or rhombuses are squares. A parallelogram is a quadrilateral with both pairs of opposite sides parallel, whereas a trapezium has only one pair of parallel sides.
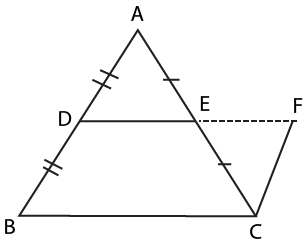
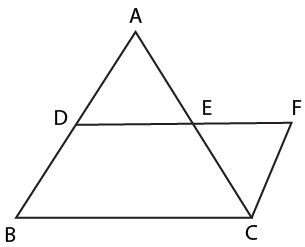
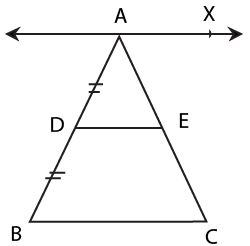
6. What is the importance of the Mid-point Theorem in Quadrilaterals revision notes?
The Mid-point Theorem is essential because it links triangles and quadrilaterals: the line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it. This theorem serves as a foundational tool for proving properties in parallelograms and related questions.
7. How can students connect Quadrilaterals' theorems for a conceptual understanding?
Quadrilaterals' theorems are interconnected. For example, proving that both pairs of opposite sides being equal and parallel leads to parallelogram properties. Theorems about diagonals bisecting, angles' sums, and special cases (like the rectangle‘s equal diagonals and the rhombus’s perpendicular diagonals) reinforce this conceptual network. Creating a concept map is recommended for linking these theorems visually.
8. What common mistakes should students avoid while revising Quadrilaterals?
Students should avoid confusing types of quadrilaterals (e.g., mistaking a rectangle for a square), forgetting to write reasons for each proof statement, and neglecting the properties of diagonals for rectangles, rhombuses, and parallelograms. Always check if a property applies to all quadrilaterals or just special cases.
9. Why is mastering the definitions and properties of quadrilaterals important for Class 9 exams?
Strong grasp on definitions and properties allows students to quickly recognize the type of quadrilateral in a question and apply the correct reasoning or theorem. This leads to accurate answers and is essential for avoiding errors in proofs, MCQs, and application-based questions as per CBSE standards.
10. How do revision notes for Quadrilaterals improve exam preparation and retention?
Revision notes provide a condensed, organized view of the whole chapter, highlight important proofs, and use simple language for definitions and properties. This structure supports fast recall, better conceptual linkage, and more effective last-minute revision—boosting exam performance and retention.




















 Watch Video
Watch Video