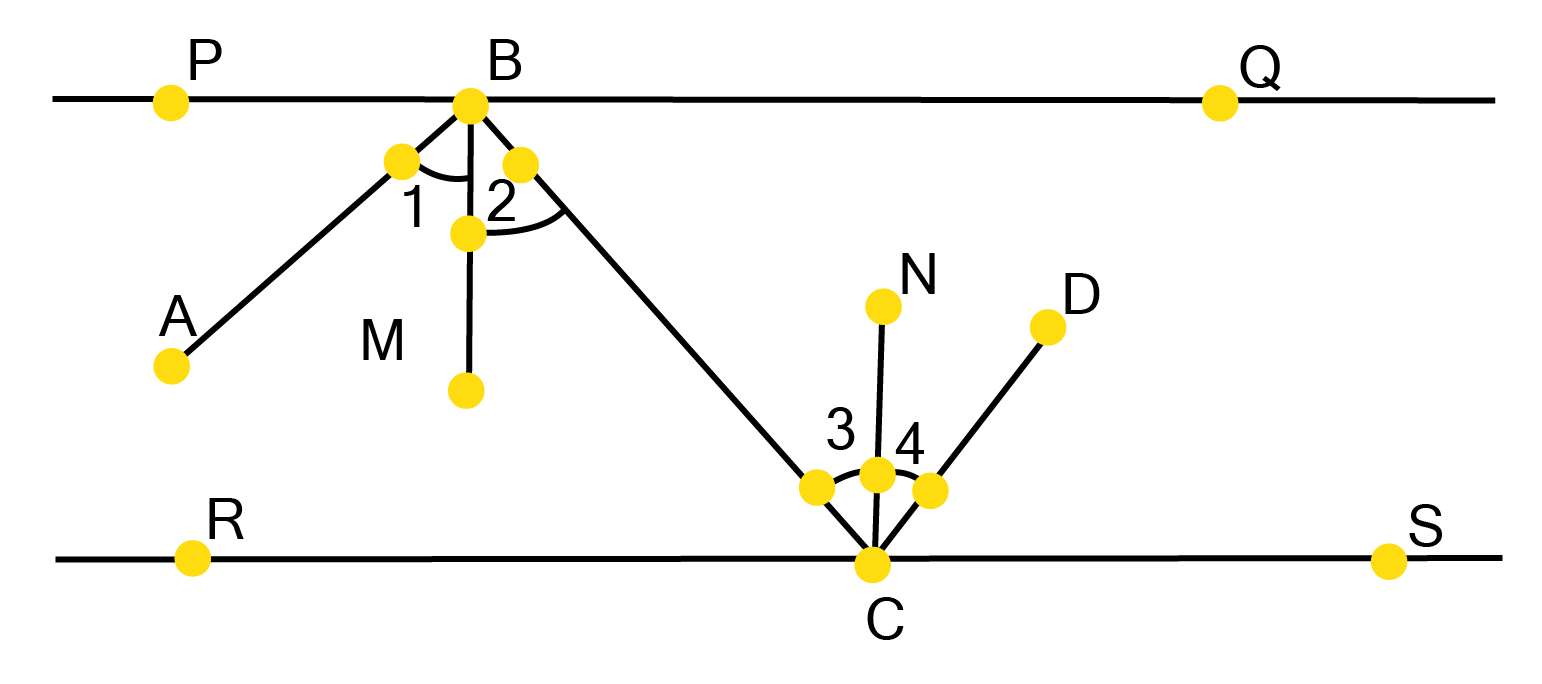
Exam-ready answers for Class 9 Maths Lines and Angles Questions with FREE PDF download
NCERT Solutions For Class 9 Maths Chapter 6 Lines And Angles - 2025-26
FAQs on NCERT Solutions For Class 9 Maths Chapter 6 Lines And Angles - 2025-26
1. Are NCERT solutions available for all exercises in Class 9 Maths Chapter 6?
Yes, NCERT solutions for all exercises in Class 9 Maths Chapter 6 Lines and Angles are available on Vedantu, with every question covered.
2. Do Class 9 Maths Chapter 6 NCERT solutions help in writing proper answers?
Yes, the Class 9 Maths Chapter 6 NCERT solutions on Vedantu help students understand how to write answers in the correct exam format.
3. Can I rely on NCERT solutions for Class 9 Maths Chapter 6 for tests?
Yes, NCERT solutions for Class 9 Maths Chapter 6 Lines and Angles on Vedantu are reliable for school tests as they follow NCERT and CBSE standards.
4. Are Class 9 Maths Chapter 6 solutions written in simple language?
Yes, the Class 9 Maths Chapter 6 solutions provided on Vedantu are written in simple and student-friendly language.
5. Do NCERT solutions for Lines and Angles Class 9 include solved examples?
Yes, the NCERT solutions for Lines and Angles Class 9 on Vedantu include all solved questions as given in the textbook exercises.
6. Is Class 9 Maths Chapter 6 covered completely in NCERT solutions?
Yes, Class 9 Maths Chapter 6 Lines and Angles is covered completely in the NCERT solutions available on Vedantu.
7. Are NCERT solutions for Class 9 Maths Chapter 6 suitable for daily practice?
Yes, students can use NCERT solutions for Class 9 Maths Chapter 6 on Vedantu for daily practice and written work.
8. Do the Lines and Angles Class 9 solutions follow CBSE marking schemes?
Yes, the Lines and Angles Class 9 solutions on Vedantu follow CBSE-recommended answer structure and marking patterns.
9. Can NCERT solutions for Class 9 Maths Chapter 6 be accessed online for free?
Yes, NCERT solutions for Class 9 Maths Chapter 6 Lines and Angles can be accessed online on Vedantu.
10. Is there a single page with all Class 9 Maths Chapter 6 solutions?
Yes, Vedantu provides a single, organised page with all Class 9 Maths Chapter 6 Lines and Angles NCERT solutions.




















 Watch Video
Watch Video





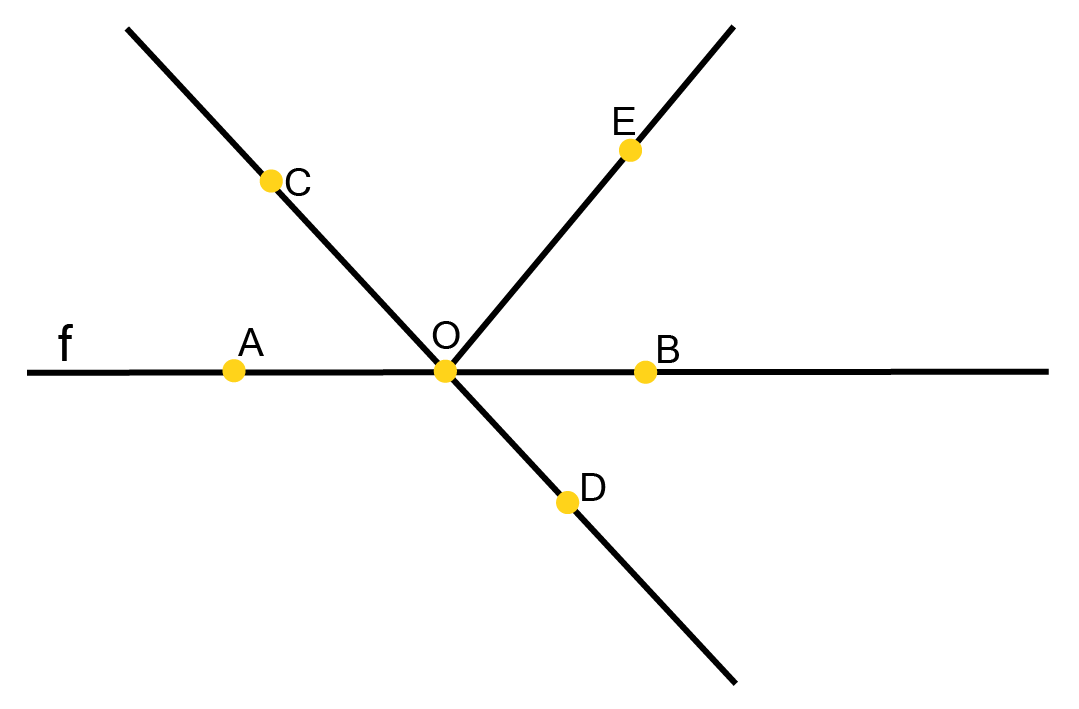

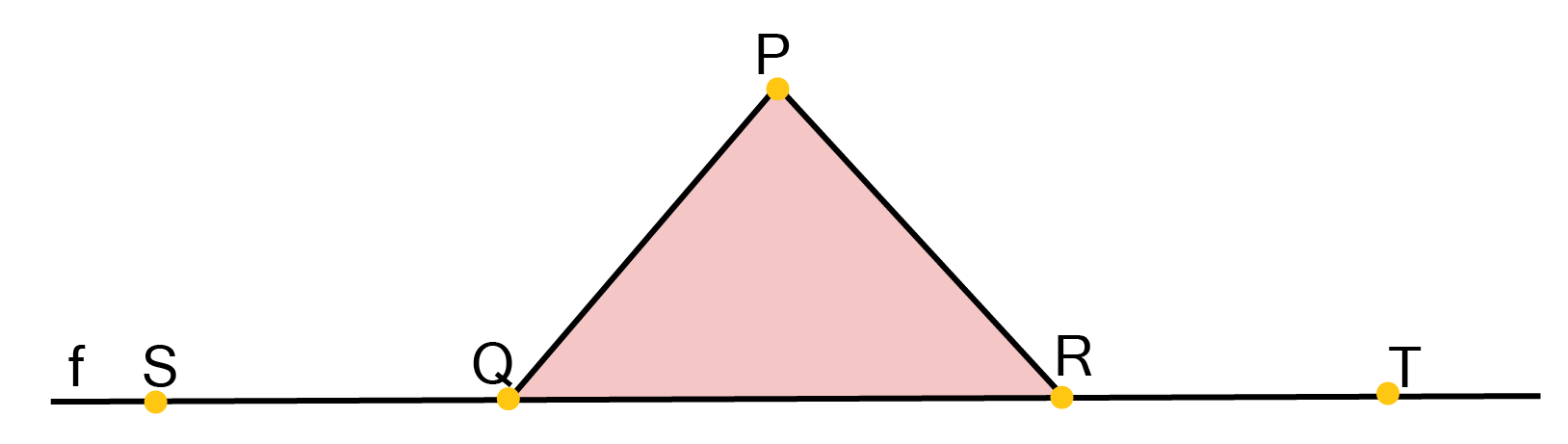
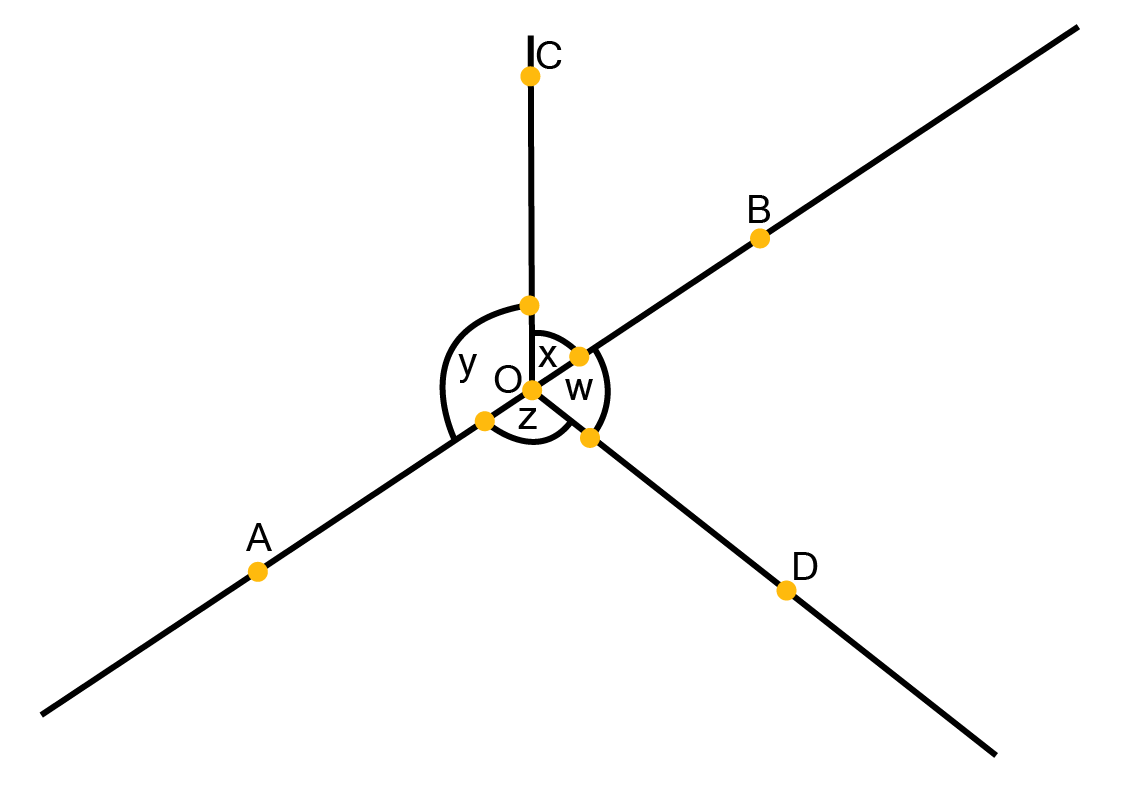
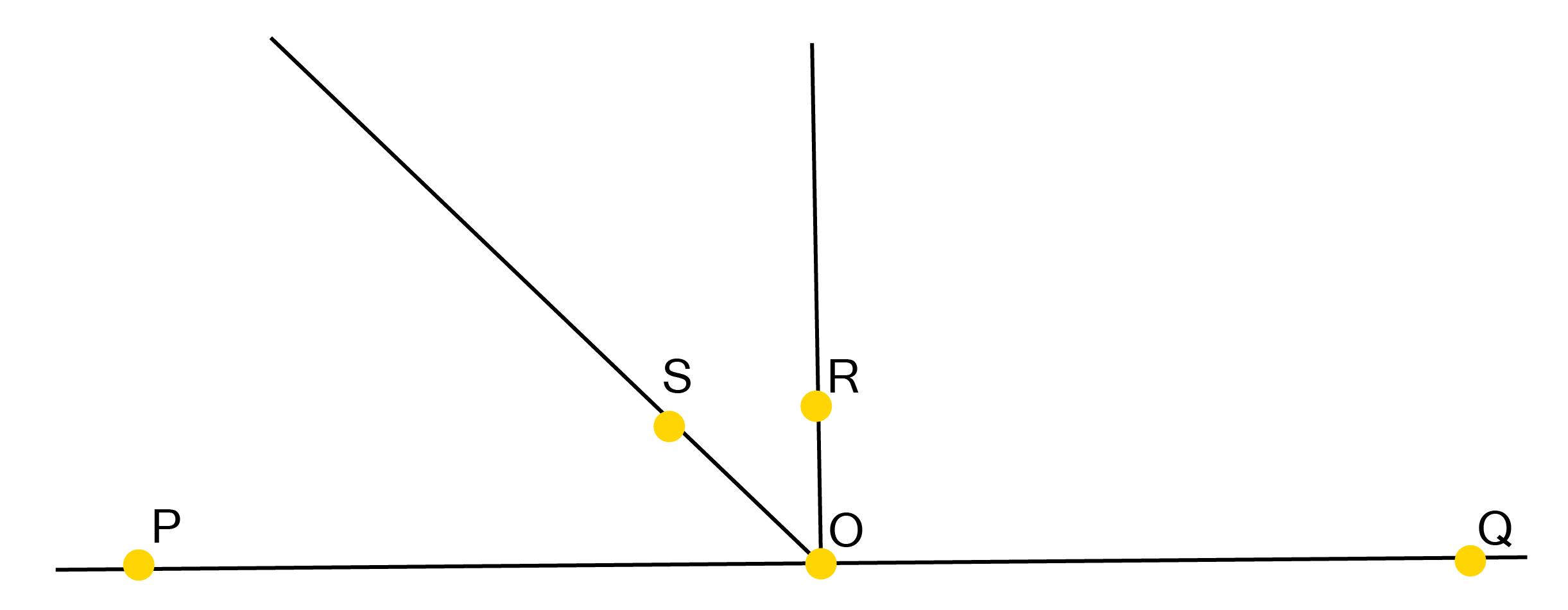

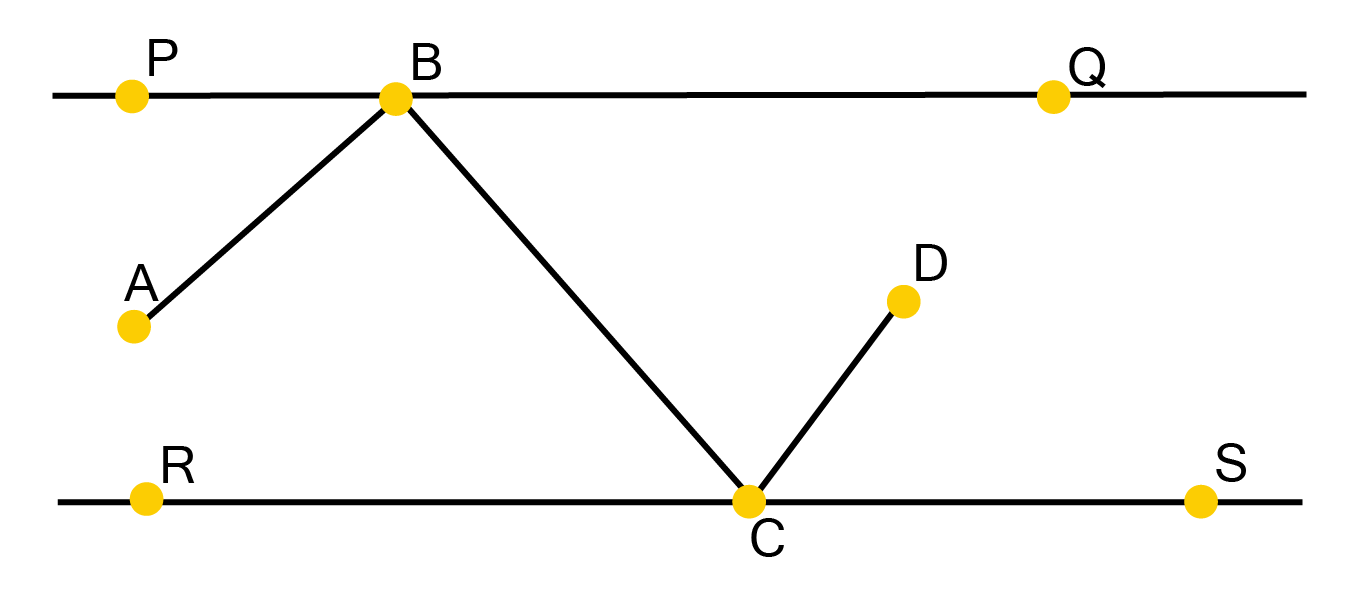
![AB\[\parallel \] CD and CD \[\parallel \] EF](https://www.vedantu.com/seo/content-images/afaa573d-dbd7-4e5d-82bb-36a18cd01a0f.png)