NCERT Exemplar for Class 9 Maths - Lines and Angles
FAQs on NCERT Exemplar for Class 9 Maths Chapter 6 - Lines and Angles (Book Solutions)
1. What topics are covered in NCERT Exemplar Maths Class 9 Chapter 6?
In the chapter of NCERT Exemplar Class 9 Lines and Angles, you will become familiar with the essential terms and definitions which are important to further move alongside the part. You will find out with regards to line section, collinear and non-collinear points, arms and vertex. Students will get information about various kinds of points and their degrees. You will likewise work with equal lines and various sets of angles as well. The idea of parallel lines and transversal lines, as expressed in this chapter are explained. You will find out with regards to corresponding angles and the lines parallel to a similar line.
2. What is the Axioms theorem in NCERT Exemplar Maths Class 9 Chapter 6?
The Axioms theorem in NCERT Exemplar Maths Class 9 Chapter 6 are as follows.
In case a ray remains on a line, then, at that point, the two nearby points that are framed have an amount of 180. This pair of adjacent points is known as a linear pair of points.
If the sum of the two adjacent points is 180, then, at that point, the non-normal arms of these points structure a line.
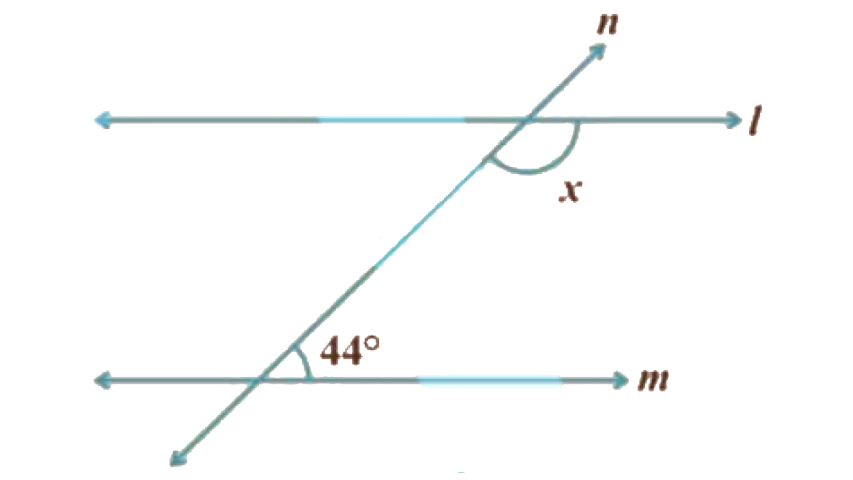
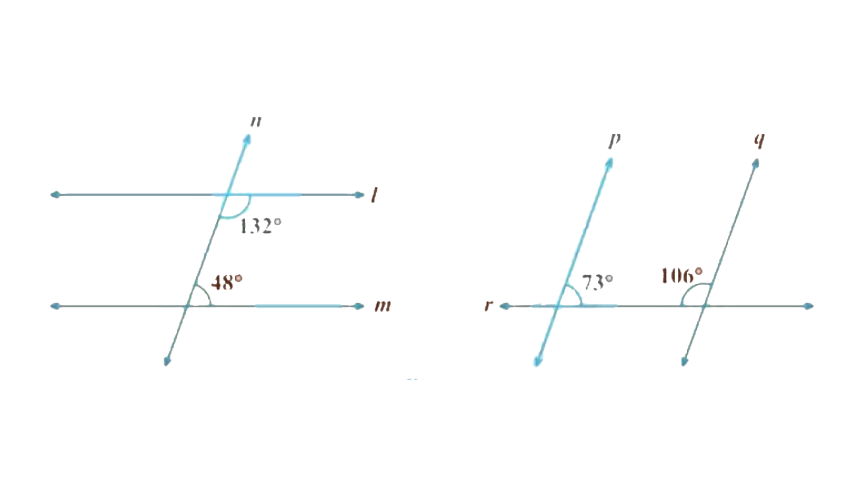
When a transversal converges any two equal lines, each pair of their corresponding angles is equivalent.
Moreover, when a transversal meets any two lines such that the corresponding angles are equivalent, then, at that point, those two lines are equivalent.
3. What theorems are mentioned in NCERT Exemplar Maths Class 9 Chapter 6?
The theorems are mentioned in NCERT Exemplar Maths Class 9 Chapter 6 are as follows.
At the point when the two lines meet one another, the points that are upward opposite are equivalent.
When a transversal converges two equal lines, every one of the pairs of their other interior points is equivalent.
Similarly, when the transversal meets two lines so that each pair of substitute points is equivalent then, at that point, those two lines are equivalent.
When the lines are parallel to a similar line, they are corresponding to one another.
The sum of the multitude of angles of a triangle is 180
At the point when a side of the triangle is made, then, at that point, the exterior angle framed from that side is the sum of two inside inverse angles.
4. What type of questions does Class 9 Maths Chapter 6 consist of?
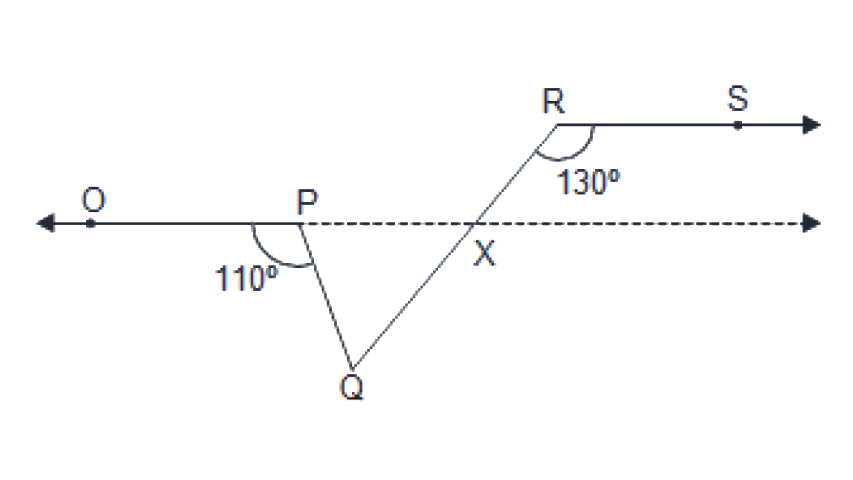
There are a total of 8 questions in the first exercise. In these questions, you will figure out how to discover the angles using the given units. The questions would include given plots for the type of degrees or proportions. You will also be supposed to demonstrate the given statement using the hypotheses learned.
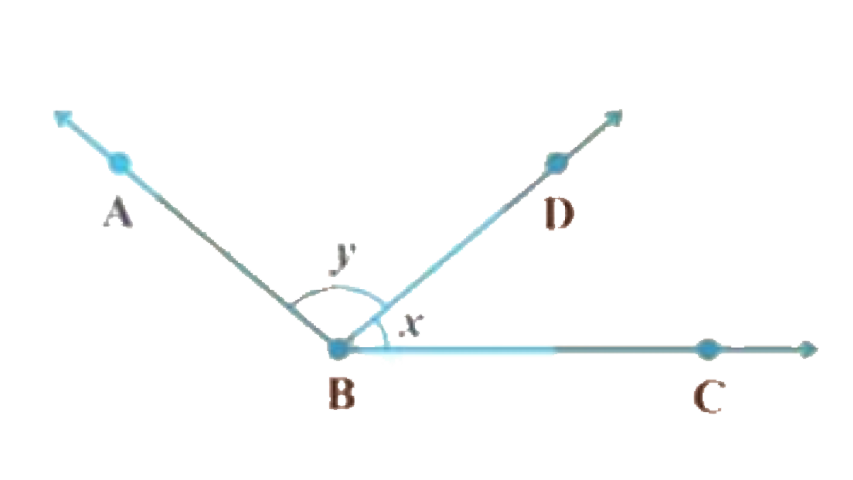
Practice 2 has 10 questions altogether. These questions will assist you with revising the idea of various kinds of angles. You will be given angles as degrees or ratios, and afterwards, you need to find out the degree or ratio of the angle inquired.
In practice 3, there are 10 questions on point bisectors.
In the last exercise, you will acquire information about the points of a triangle and their properties.
5. From where can I download NCERT Exemplar Maths Class 9 Chapter 6?
You can download NCERT Exemplar Maths Class 9 Chapter 6 from the Vedantu app or website in PDF form. Just sign up and click on the download tab and get the solution for free. From the above depiction, you can recognize the commitment of Vedantu in making the review material simple for you. Our experts have the method of successfully directing the students and furnishing them with the best of questions. Alongside these tackled NCERT Exemplar issues for Class 9 Maths Chapter 6, we also offer solved models and review notes for better understanding.