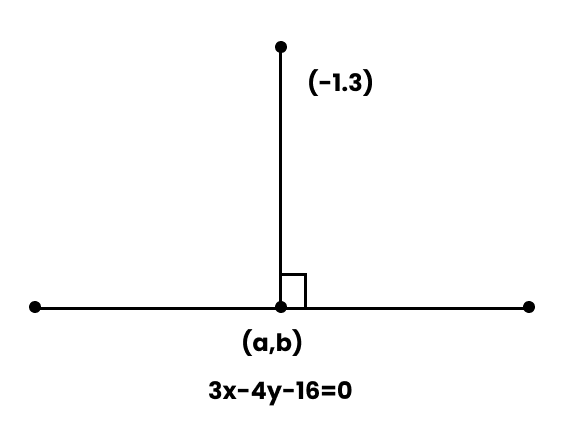
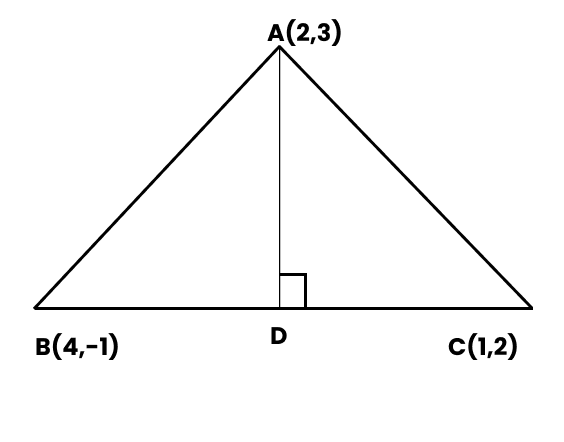
Class 11 Maths Chapter 10 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 11 Maths Chapter 10 Straight Lines Exercise 10.3 - 2025-26
1. What are the 4 examples of conic sections studied in Class 11?
The four main conic sections are circle, ellipse, parabola, and hyperbola. These curves are formed when a plane intersects a double cone at different angles and positions, creating distinct geometric shapes with unique mathematical properties.
2. How many exercises are in conic sections class 11 chapter?
The conic sections chapter in Class 11 contains four exercises: 10.1, 10.2, 10.3, and 10.4, along with a miscellaneous exercise. Each exercise focuses on different aspects like circles, parabolas, ellipses, and hyperbolas respectively.
3. What does Exercise 10.3 class 11 conic sections cover?
Exercise 10.3 deals with ellipses, covering their standard equations, properties, and geometric characteristics. Students learn to identify major and minor axes, foci, vertices, and eccentricity.
4. Is conic section hard for Class 11 students?
Conic sections difficulty varies among students, but with proper understanding of coordinate geometry basics, it becomes manageable. The key is mastering the standard equations and practicing graph plotting regularly.
5. Can students access ex 10.3 Class 11 solutions for free?
Yes, students can access comprehensive solutions through Free PDF downloads available online. These resources include step-by-step explanations for all exercise problems without any cost.
6. What benefits do NCERT Solutions for Exercise 10.3 Class 11 conic sections provide?
NCERT Solutions offer detailed step-by-step explanations for every problem in Exercise 10.3, helping students understand ellipse concepts thoroughly.
These solutions bridge the gap between theory and application, making complex ellipse problems more approachable.
7. Where can students find Class 11 Conic section Solution PDF downloads?
Students can find comprehensive solution PDFs on educational platforms like Vedantu, which offer free downloads covering all exercises including 10.3. These PDFs contain complete solutions with detailed explanations and diagrams.
8. How do ex 10.3 Class 11 maths NCERT solutions help with exam preparation?
These solutions provide systematic problem-solving approaches that align directly with board exam patterns and marking schemes for ellipse-related questions.
Understanding solution methodology helps students tackle similar problems confidently during examinations.
9. What topics are covered in Exercise 10.4 Class 11 Conic Sections?
Exercise 10.4 focuses on hyperbolas, covering their standard equations, properties, asymptotes, and graphical representations. Students learn to identify transverse and conjugate axes, foci, vertices, and calculate eccentricity values greater than 1.
10. How do conic sections class 11 exercise 10.3 worksheets enhance learning?
Conic sections class 11 exercise 10.3 Worksheets provide additional practice problems beyond textbook exercises, reinforcing ellipse concepts through varied question formats and difficulty levels.
Extra practice helps solidify understanding and builds problem-solving confidence for complex ellipse applications.