NCERT Exemplar for Class 11 Maths Chapter 10 - Straight Lines (Book Solutions)

Example 1: Find the equation of a line which passes through the point  $ (2,3) $  and makes an angle of  $ 30{^o} $  with the positive direction of  $ x -  $ axis.

Ans: Given: Line passes through $ (2,3) $ and makes an angle of  $ {30^ \circ } $ with the positive direction of  $ x -  $  axis.

The slope of line  $ m = \tan \theta  = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} $ .

According to the point-slope form, the equation of a line with slope  $ m $ and passing through point  $ ({x_ \circ },{y_ \circ }) $ is  $ y - {y_ \circ } = m(x - {x_ \circ }) $ .

$ \Rightarrow y - 3 = \frac{1}{{\sqrt 3 }}(x - 2) $ 

$ \Rightarrow x - \sqrt 3 y + (3\sqrt 3  - 2) = 0 $ 

Therefore, the equation of the line is  $ x - \sqrt 3 y + (3\sqrt 3  - 2) = 0 $ .

Example 2: Find the equation of a line where length of the perpendicular segment from the origin to the line is  $ 4 $ and the inclination of the perpendicular segment with the positive direction of  $ x -  $ axis is  $ 3{0^o} $ .

Ans: Given: Length of perpendicular segment from origin to line is  $ 4 $ .

normal form of the line is $ x\cos \omega  + y\sin \omega  = p $ .

Using $ p = 4 $ and  $ \omega  = {30^ \circ } $ ,

$ \Rightarrow x\frac{{\sqrt 3 }}{2} + y\frac{1}{2} = 4 $ 

$ \Rightarrow \sqrt 3 x + y = 8 $ 

Therefore, the equation of the line is $ \sqrt 3 x + y = 8 $ .

Example 3: Prove that every straight line has an equation of the form  $ Ax + By + C = 0 $ , where  $ A $ ,  $ B $ and  $ C $ are constants.

Ans: Given: Every straight line has an equation of the form  $ Ax + By + C = 0 $ .

A straight line either cuts the  $ y -  $  axis, or is coincident or parallel to it. The equation of straight line cutting the  $ y -  $  axis can be expressed in the form  $ y = mx + b; $  and if the straight line is parallel or coincident with  $ y -  $ axis, then its equation will be  $ x = {x_1}, $  where  $ x = 0 $ in the case of coincidence. The previous two equations are of the form given in the question.

Hence verified.

Example 4: Find the equation of the straight line passing through  $ (1,2) $ and  perpendicular to the line  $ x + y + 7 = 0 $ .

Ans: Given: The straight line passes through  $ (1,2) $ and is perpendicular to  $ x + y + 7 = 0 $ .

Let the slope of the required line be  $ m $ .

The slope of given line  $ y = ( - 1)x - 7 $ is  $  - 1 $ .

As the two lines are perpendicular, the product of their slopes will be equal to  $  - 1 $ .

$ \Rightarrow m \times ( - 1) =  - 1 $ 

$ \Rightarrow m = 1 $ and the line passes through  $ (1,2) $ .

So, the equation of required line is  $ y - 1 = 1\left( {x - 2} \right) $ .

Therefore, the equation of the line is $ y - 1 = x - 2 $ .

Example 5: Find the distance between the lines $ 3x + 4y = 9 $ and  $ 6x + 8y = 15 $ .

Ans:Given: $ 3x + 4y = 9 $ and  $ 6x + 8y = 15 $ .

The distance between the parallel lines  $ y = mx + {c_1} $  and  $ y = mx + {c_2} $  is  $ d = \frac{{\left| {{c_1} - {c_2}} \right|}}{{\sqrt {1 + {m^2}} }} $ 

The given lines  $ 3x + 4y = 9 $  and  $ 3x + 4y = \frac{{15}}{2} $  are parallel lines.

So, the distance between them is  $ d = \frac{{\left| {{c_1} - {c_2}} \right|}}{{\sqrt {1 + {m^2}} }} $ .

$ \Rightarrow d = \frac{{\left| {9 - \frac{{15}}{2}} \right|}}{{\sqrt {{3^2} + {4^2}} }} $ 

 $ \Rightarrow d = \frac{3}{{10}} $ 

Therefore, the distance between the two lines is  $ \frac{3}{{10}} $ .

Example 6: Show that the locus of the mid-point of the distance between the axes of the variable line  $ xcos\alpha  + ysin\alpha  = p $  is  $ \frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{4}{{{p^2}}} $  where  $ p $ is a constant.

Ans:

Given: $ x\cos \alpha  + y\sin \alpha  = p $ .

The intercept form of the line  $ x\cos \alpha  + y\sin \alpha  = p $ is  $ \frac{x}{{\frac{p}{{\cos \alpha }}}} + \frac{y}{{\frac{p}{{\sin \alpha }}}} = 1 $  which gives us the coordinates  $ \frac{p}{{\cos \alpha }},{\text{ }}0{\text{ and }}0{\text{, }}\frac{p}{{\sin \alpha }} $  where the line intersects  $ x -  $ axis and  $ y -  $ axis.

Let the midpoint of the line segment joining  $ \frac{p}{{\cos \alpha }},{\text{ }}0{\text{ and }}0{\text{, }}\frac{p}{{\sin \alpha }} $ be  $ (h,{\text{ }}k) $ . 

So,  $ h = \frac{p}{{2\cos \alpha }}{\text{ and }}k = \frac{p}{{2\sin \alpha }} $ .

$ \Rightarrow \cos \alpha  = \frac{p}{{2h}}{\text{ and }}\sin \alpha  = \frac{p}{{2k}} $ 

Square both sides of equation and add them.

$ \Rightarrow \frac{{{p^2}}}{{4{h^2}}} + \frac{{{p^2}}}{{4{k^2}}} = 1 $ 

$ \Rightarrow \frac{1}{{{h^2}}} + \frac{1}{{{k^2}}} = \frac{4}{{{p^2}}} $ 

Therefore, the locus is  $ \frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = \frac{4}{{{p^2}}} $ .

Example 7: If the line joining two points  $ A(2,0) $  and  $ B(3,1) $ is rotated about  $ A $  in anticlock wise direction through an angle of  $ 15{^o} $ . Find the equation  of the line in new position.

The slope of the line joining  $ A(2,0) $ and  $ B(3,1) $ is  $ \frac{{1 - 0}}{{3 - 2}} = 1 $  i.e.  $ \tan {45^ \circ } $ .

After rotating the line  $ {15^ \circ } $ , the slope of the line will become  $ \tan {60^ \circ } = \sqrt 3  $ .

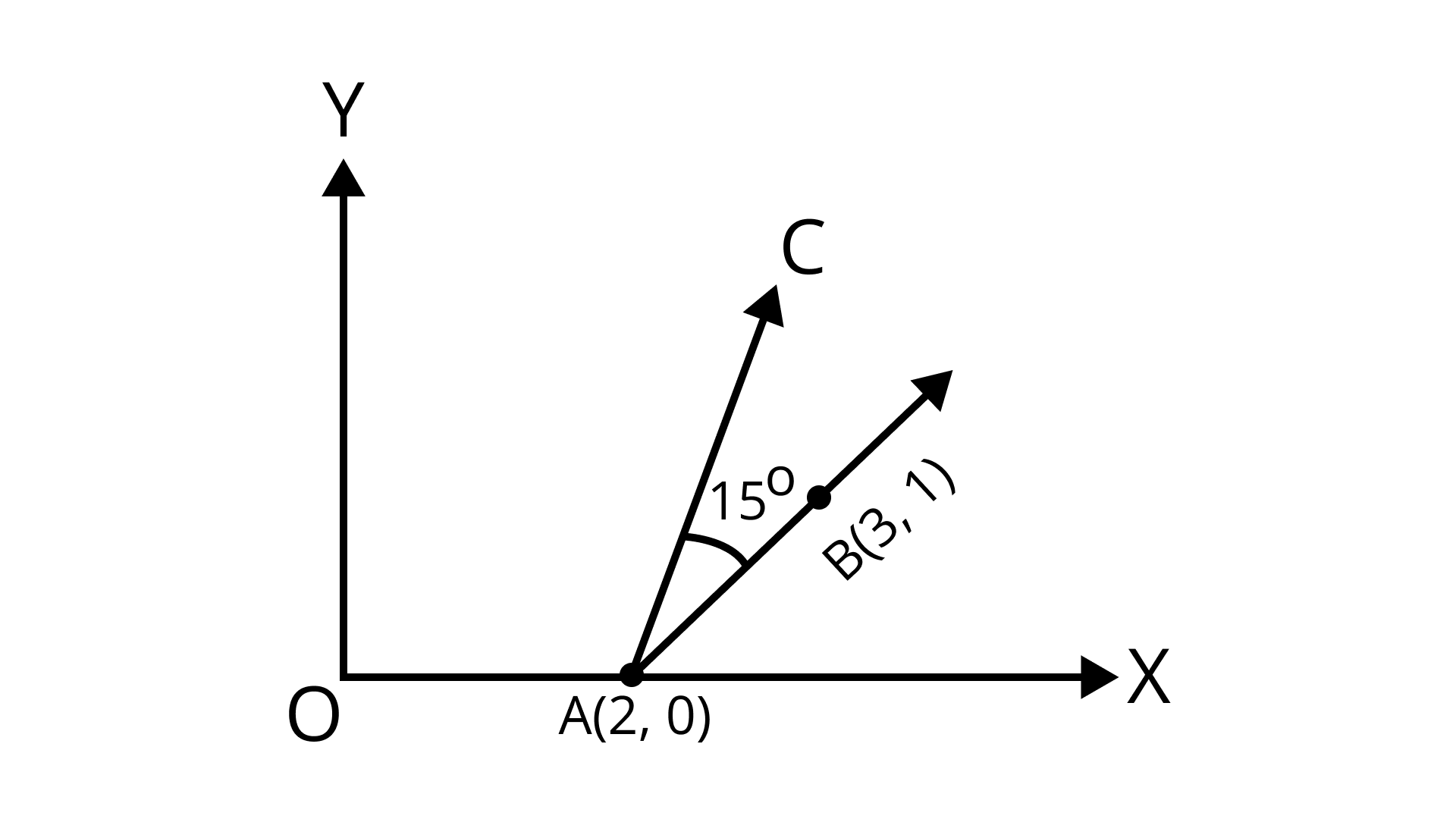
So, the equation of new line will be  $ y - 0 = \sqrt 3 \left( {x - 2} \right) $ .

$ \Rightarrow y - \sqrt 3 x + 2\sqrt 3  = 0 $ 

Therefore, the equation of line is  $ y - \sqrt 3 x + 2\sqrt 3  = 0 $ .

Example 8: If the slope of a line passing through the point  $ A(3,2) $ is  $ \frac{3}{4} $ , then find points on the line which are  $ 5 $  units away from the point  $ A $ .

Ans:  Given:Slope of a line passing through  $ A(3,2) $ is  $ \frac{3}{4} $ .

The equation of line passing through  $ A(3,2) $  with slope  $ \frac{3}{4} $ is  $ y - 2 = \frac{3}{4}\left( {x - 3} \right) $ .

$ \Rightarrow 4y - 3x + 1 = 0 $ 

$ (h,k) $ is a point on line.

So,  $ 4k - 3h + 1 = 0 $ , 

$ k = \frac{{3h - 1}}{4} $ .

$ (h,k) $ is a point on line such that  $ {(h - 3)^2} + {(k - 2)^2} = 25 $ .

Substituting  $ k $ ,

\[{(h - 3)^2} + {\left( {\frac{{3h - 1}}{4} - 2} \right)^2} = 25\]

\[25{h^2} - 150h - 175 = 0\]

\[{h^2} - 6h - 7 = 0\]

\[h =  - 1,7\]

Substitute these values in  $ k = \frac{{3h - 1}}{4} $ .

\[k =  - 1,5\]

Therefore, the points are either  $ ( - 1, - 1) $ or  $ (7,5) $ .

Example 9: Find the equation to the straight line passing through the point of intersection of the lines  $ 5x - 6y - 1 = 0 $ and  $ 3x + 2y + 5 = 0 $  and perpendicular to the line  $ 3x - 5y + 11 = 0 $ .

Ans: Given: Line passes through point of intersection of  $ 5x - 6y - 1 = 0 $ and  $ 3x + 2y + 5 = 0 $ .

The equation of line passing through intersection of  $ 5x - 6y - 1 = 0 $ and  $ 3x + 2y + 5 = 0 $ is:  $ 5x - 6y - 1 + k\left( {3x + 2y + 5} \right) = 0 $ .

Slope of this line is:  $ \frac{{ - (5 + 3k)}}{{ - 6 + 2k}} $ .

Slope of the line  $ 3x - 5y + 11 = 0 $ is  $ \frac{3}{5} $ .

The product of slopes of perpendicular lines will be  $  - 1 $ .

So,  $ \frac{{ - (5 + 3k)}}{{ - 6 + 2k}} \times \frac{3}{5} =  - 1 $ 

 $ k = 45 $ 

So, the equation of required line will be  $ 5x - 6y - 1 + 45\left( {3x + 2y + 5} \right) = 0 $ 

i.e.  $ 5x + 3y + 8 = 0 $ .

Therefore, the equation of line is  $ 5x + 3y + 8 = 0 $ .

Example 10: Aray of light coming from the point  $ (1,2) $ is reflected at a point  $ A $ on the  $ x -  $ axis and then passes through the point  $ (5,3) $ . Find the coordinates of the point  $ A $ .

Ans: Given: Theray of light comes from $ (1,2) $ .

Let the incident ray strike   $ x -  $ axis at  $ A $ having coordinates  $ (x,0) $ .

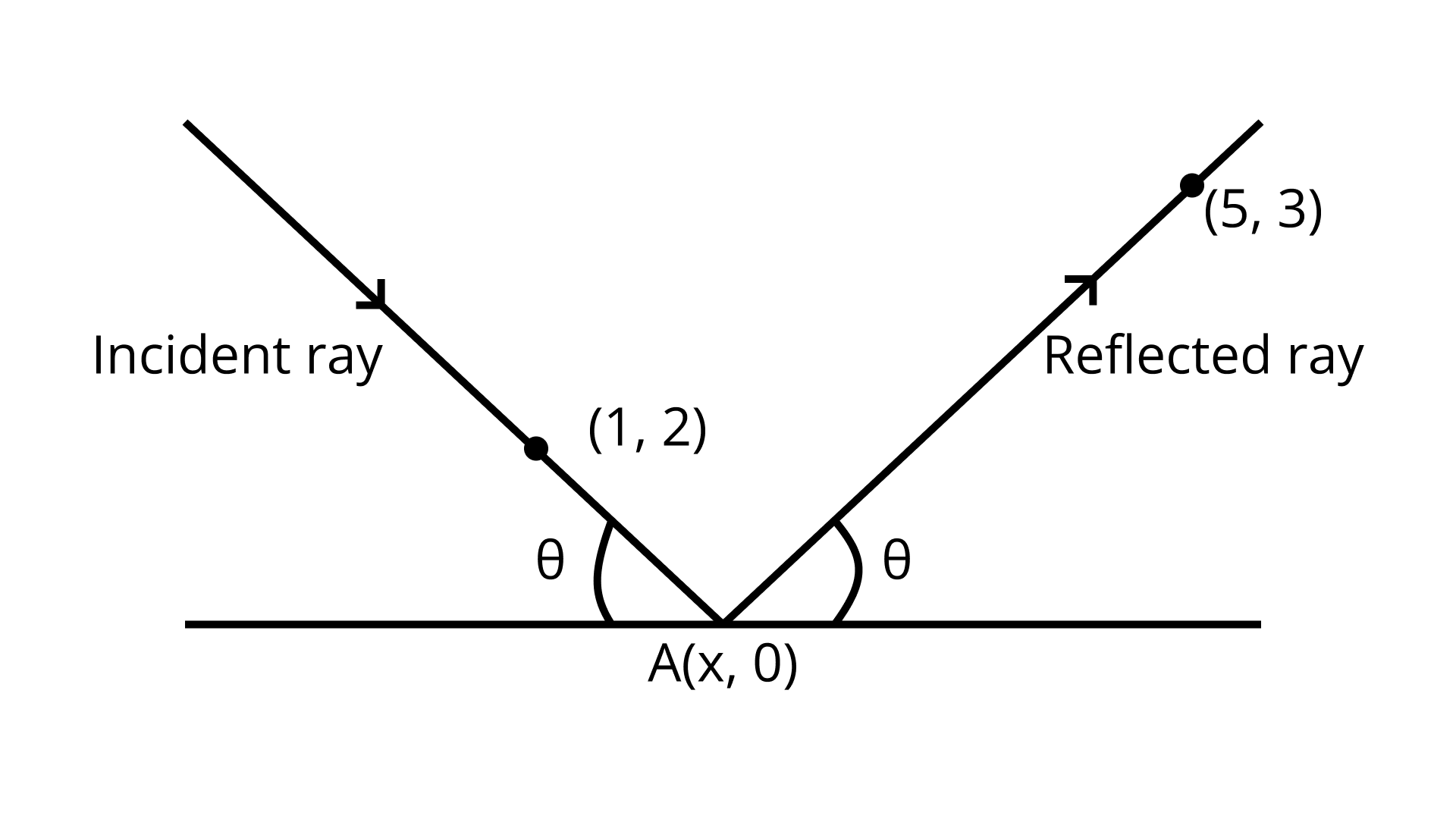
Slope of reflected ray is:  $ \tan \theta  = \frac{3}{{5 - x}}{\text{         }}...{\text{(1)}} $ 

Slope of incident ray is  $ \tan \left( {\pi  - \theta } \right) = \frac{{ - 2}}{{x - 1}} $  i.e. $  - \tan \theta  = \frac{{ - 2}}{{x - 1}}{\text{                }}...{\text{(2)}} $ 

From  $ {\text{(1)}} $ and  $ {\text{(2)}} $ ,

 $ \Rightarrow \frac{3}{{5 - x}} = \frac{2}{{x - 1}} $ 

 $ \Rightarrow x = \frac{{13}}{5} $ 

Therefore, the coordinates of  $ A $ are  $ \left( {\frac{{13}}{5},0} \right) $ .

Example 11: If one diagonal of a square is along the line  $ 8x - 15y = 0 $ and one of its vertex is at  $ (1,2) $ , then find the equation of sides of the square passing through this vertex.

Ans: Given: $ 8x - 15y = 0 $ 

Let the square be  $ ABCD $  and the coordinates of  $ D $  be  $ (1,2) $ .

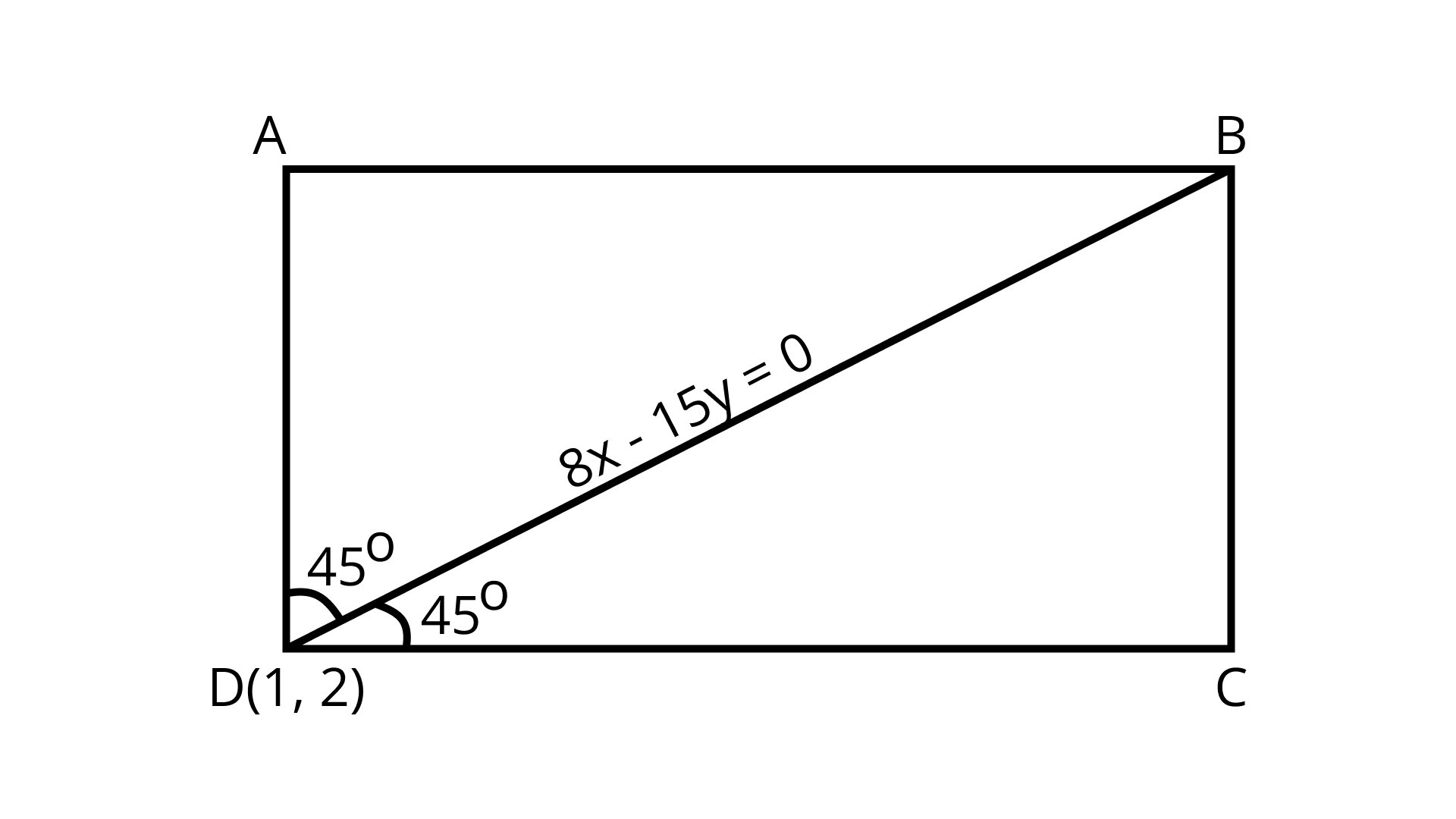
$ BD $ is along  $ 8x - 15y = 0 $  and slope is  $ \frac{8}{{15}} $ .

Let the slope of  $ DC $  be  $ m. $ 

$ \Rightarrow \tan {45^ \circ } = \frac{{m - \frac{8}{{15}}}}{{1 + \frac{{8m}}{{15}}}} $ 

$ \Rightarrow 15 + 8m = 15m - 8 $ 

$ \Rightarrow m = \frac{{23}}{7} $ 

So, equation of  $ DC $ is  $ y - 2 = \frac{{23}}{7}\left( {x - 1} \right) $  i.e.  $ 23x - 7y - 9 = 0 $ .

The equation of  $ AD $ is  $ y - 2 = \frac{{ - 7}}{{23}}\left( {x - 1} \right) $  i.e.  $ 7x + 23y - 53 = 0 $ .

Therefore, the equations are  $ 7x + 23y - 53 = 0 $ and  $ 23x - 7y - 9 = 0 $ .

Example 12: The inclination of the line  $ x - y + 3 = 0 $ with the positive direction of  $ x -  $ axis is

(A)  $ 4{5^o} $ 

(B)  $ 13{5^o} $ 

(C)  $  - 4{5^o} $ 

(D)  $  - 13{5^o} $ 

Ans: Given: $ x - y + 3 = 0 $ 

 $ x - y + 3 = 0 $ can be written as  $ y = x + 3 $ .

 $ \Rightarrow m = \tan \theta  = 1 = \tan {45^ \circ } $  i.e.  $ \theta  = {45^ \circ } $ .

Therefore,  $ \theta  = {45^ \circ } $ .

Correct Option: A

Example 13: The two lines  $ ax + by = c $ and \[a'x + b'y = c'\]are perpendicular if

(A) \[aa' + bb' = 0\]

(B) \[ab' = ba'\]

(C) \[ab + a'b' = 0\]

(D) \[ab' + ba' = 0\]

Ans: Given: $ ax + by = c $ and \[a'x + b'y = c'\].

Slope of  $ ax + by = c $ is  $ \frac{{ - a}}{b} $ .

And slope of \[a'x + b'y = c'\]is  $ \frac{{ - a'}}{{b'}} $ .

The lines will be perpendicular if  $ \left( {\frac{{ - a}}{b}} \right)\left( {\frac{{ - a'}}{{b'}}} \right) =  - 1 $  i.e. \[aa' + bb' = 0\].

Therefore, \[aa' + bb' = 0\].

Correct Option: A

Example 14: The equation of the line passing through  $ (1,2) $ and perpendicular to  $ x + y + 7 = 0 $ is

(A)  $ y - x + 1 = 0 $ 

(B)  $ y - x - 1 = 0 $ 

(C)  $ y - x + 2 = 0 $ 

(D)  $ y - x - 2 = 0 $ 

Ans:

Given: $ x + y + 7 = 0 $ and  $ (1,2) $ .

Let the slope of line be  $ m. $ 

As the line passes through  $ (1,2) $ , the equation of line is  $ y - 2 = m\left( {x - 1} \right) $ .

The lines will be perpendicular if  $ \left( m \right)\left( { - 1} \right) =  - 1 $  i.e.  $ m = 1 $ .

So, the equation of line will be  $ y - 2 = 1\left( {x - 1} \right) $  i.e.  $ y - x - 1 = 0 $ .

Therefore,  $ y - x - 1 = 0 $ .

Correct Options : B

Example 15: The distance of the point  $ P(1, - 3) $  from the line  $ 2y - 3x = 4 $ is

(A)  $ 13 $ 

(B)  $ \frac{7}{{13}}\sqrt {13}  $ 

(C)  $ \sqrt {13}  $ 

(D) None of these

Ans: Given: $ 2y - 3x = 4 $ and  $ P(1, - 3) $ .

The distance of  $ P(1, - 3) $  from  $ 2y - 3x = 4 $ will be equal to the length of perpendicular from the given point to the line.

 $ \Rightarrow \left| {\frac{{2( - 3) - 3 - 4}}{{\sqrt {13} }}} \right| = \sqrt {13}  $ .

Therefore, the distance is $ \sqrt {13}  $ .

Correct Options: C

Example 16: The coordinates of the foot of the perpendicular from the point  $ P(2,3) $  on the line  $ x + y - 11 = 0 $ are

(A)  $ ( - 6,5) $ 

(B)  $ (5,6) $ 

(C)  $ ( - 5,6) $ 

(D)  $ (6,5) $ 

Ans: Given: $ x + y - 11 = 0 $ and  $ P(2,3) $ .

Let  $ (h,k) $  be coordinates of foot of perpendicular from  $ P(2,3) $ on  $ x + y - 11 = 0 $ .

Slope of perpendicular line $  = \frac{{k - 3}}{{h - 2}} $ .

Slope of  $ x + y - 11 = 0 $ is  $  - 1 $ .

The lines will be perpendicular if  $ \left( {\frac{{k - 3}}{{h - 2}}} \right)\left( { - 1} \right) =  - 1 $  i.e.  $ k - h = 1{\text{           }}...{\text{(1)}} $ 

As  $ (h,k) $ lies on  $ x + y - 11 = 0 $ , 

 $ h + k - 11 = 0{\text{            }}...{\text{(2)}} $ 

Solving  $ {\text{(1)}} $ and  $ {\text{(2)}} $ ,

 $ \Rightarrow h = 5,{\text{ }}k = 6 $ 

Therefore,  $ (5,6) $ is the foot of perpendicular.

Correct Option: B

Example 17: The intercept cut off by a line from  $ y -  $ axis is twice than that from  $ x -  $ axis, and the line passes through the point  $ (1,2) $ . The equation of the line is

(A)  $ 2x + y = 4 $ 

(B)  $ 2x + y + 4 = 0 $ 

(C)  $ 2x - y = 4 $                                                                                                                    

(D)  $ 2x - y + 4 = 0 $ 

Ans:                                                                                                                                         

Given: Line passes through the point  $ (1,2) $  . Let the intercept made by the line be  $ a $ on $ x -  $ axis.                

Then intercept on $ y -  $ axis will be  $ 2a $ .

So, equation of line is  $ \frac{x}{a} + \frac{y}{{2a}} = 1 $ .

As the line passes through  $ (1,2) $ ,                             

$ \Rightarrow \frac{1}{a} + \frac{2}{{2a}} = 1 $ 

$ \Rightarrow a = 2 $ 

So, the equation of line will be  $ \frac{x}{2} + \frac{y}{4} = 1 $  i.e.  $ 2x + y = 4 $ .

Therefore,  $ 2x + y = 4 $ .

Correct Option : A

Example 18: A line passes through the point  $ P(1,2) $  such that its intercept between the axes is bisected at  $ P $ . The equation of the line is 

(A)  $ x + 2y = 5 $ 

(B)  $ x - y + 1 = 0 $ 

(C)  $ x + y - 3 = 0 $ 

(D)  $ 2x + y - 4 = 0 $ 

Ans: Given: Line passes through the point  $ (1,2) $ .

Let the intercept made by the line be  $ a $ on $ x -  $ axis and the intercept on $ y -  $ axis be  $ b $ .

So, equation of line is  $ \frac{x}{a} + \frac{y}{b} = 1 $ .

As it is bisected at  $ (1,2) $ , 

 $ \Rightarrow 1 = \frac{{a + 0}}{2} $ and $ \Rightarrow 2 = \frac{{0 + b}}{2} $ 

 $ \Rightarrow a = 2 $ and $ b = 4 $ 

So, the equation of line will be  $ \frac{x}{2} + \frac{y}{4} = 1 $  i.e.  $ 2x + y = 4 $ .

Therefore,  $ 2x + y = 4 $ .

Correct Option: D

Example 19: The reflection of the point  $ (4, - 13) $  about the line  $ 5x + y + 6 = 0 $  is 

(A)  $ ( - 1, - 14) $ 

(B)  $ (3,4) $ 

(C)  $ (0,0) $ 

(D)  $ (1,2) $ 

Ans: Given: $ (4, - 13) $ and  $ 5x + y + 6 = 0 $ .

Let  $ (h,k) $  be point of reflection of  $ (4, - 13) $ about  $ 5x + y + 6 = 0 $ .

The midpoint of line joining  $ (h,k) $  and  $ (4, - 13) $ is  $ \left( {\frac{{h + 4}}{2},\frac{{k - 13}}{2}} \right) $ .

This point is on  $ 5x + y + 6 = 0 $ .

So,  $ 5\left( {\frac{{h + 4}}{2}} \right) + \left( {\frac{{k - 13}}{2}} \right) + 6 = 0 $ 

$ \Rightarrow 5h + k + 19 = 0{\text{        }}...{\text{(1)}} $ 

Slope of line joining  $ (h,k) $ and  $ (4, - 13) $  $  = \frac{{k + 13}}{{h - 4}} $ .This lines will be perpendicular to the given line if  $ \left( { - 5} \right)\left( {\frac{{k + 13}}{{h - 4}}} \right) =  - 1 $ .

$ \Rightarrow h - 5k - 69 = 0{\text{        }}...{\text{(2)}} $ 

Solving  $ {\text{(1)}} $ and  $ {\text{(2)}} $ ,

$ \Rightarrow h =  - 1,{\text{ }}k =  - 14 $ 

Therefore,  $ ( - 1, - 14) $  is the required point.

Correct Option: A

Example 20: A point moves such that its distance from the point  $ (4,0) $  is half that of its distance from the line  $ x = 16 $ . The locus of the point is 

(A)  $ 3{x^2} + 4{y^2} = 192 $ 

(B)  $ 4{x^2} + 3{y^2} = 192 $ 

(C)  $ {x^2} + {y^2} = 192 $ 

(D) None of these

Ans: Given: $ (4,0) $ and  $ x = 16 $ .

Let  $ (h,k) $  be coordinates of the moving point.

Given that the point moves in such a way that its distance from $ (4,0) $  is half that of its distance from $ x = 16 $ .

So,  $ \sqrt {{{\left( {h - 4} \right)}^2} + {k^2}}  = \frac{1}{2}\frac{{h - 16}}{{\sqrt {{1^2} + 0} }} $ 

$ \Rightarrow {\left( {h - 4} \right)^2} + {k^2} = \frac{1}{4}{\left( {h - 16} \right)^2} $ 

$ \Rightarrow 4\left( {{h^2} - 8h + 16 + {k^2}} \right) = {h^2} - 32h + 256 $ 

$ \Rightarrow 3{h^2} + 4{k^2} = 192 $ 

Therefore,  $ 3{x^2} + 4{y^2} = 192 $  is the required locus.

Correct Option: A

Short Answer Type Questions

EXERCISE 10.3:

1. Find the equation of a line which passes through the point  $ (1, - 2) $ and cuts off equal intercepts from axes.

Ans: 

Given: Line passes through the point  $ (1, - 2) $ .

Let the intercept made by the line be  $ a $ on $ x -  $ axis and the intercept on $ y -  $ axis be  $ b $ .

So, equation of line is  $ \frac{x}{a} + \frac{y}{b} = 1 $ .

Given that  $ a = b $ .

 $ \Rightarrow \frac{x}{a} + \frac{y}{a} = 1 $ 

It passes through  $ (1, - 2) $ , so  $ \frac{1}{a} - \frac{2}{a} = 1 $ 

 $ \Rightarrow  - \frac{1}{a} = 1 $ 

 $ \Rightarrow a =  - 1 $ 

So, equation of line will be  $ \frac{x}{{ - 1}} + \frac{y}{{ - 1}} = 1 $ 

 $ x + y =  - 1 $ 

Therefore, the equation is  $ x + y + 1 = 0 $ .

2. Find the equation of a line which passes through the point  $ (5,2) $ and perpendicular to the line joining the points  $ (2,3) $ and  $ (3, - 1) $ .

Ans: 

Given: $ (2,3) $ and  $ (3, - 1) $ .

Slope of line joining  $ (2,3) $ and  $ (3, - 1) $ is   $ \frac{{ - 1 - 3}}{{3 - 2}} =  - 4 $ .

Slope of the line perpendicular to this line is  $ \frac{{ - 1}}{{ - 4}} = \frac{1}{4} $ . 

The equation of line that passes through  $ (5,2) $ is  $ y - 2 = \frac{1}{4}\left( {x - 5} \right) $ .

$ \Rightarrow 4y - 8 = x - 5 $ 

$ \Rightarrow x - 4y + 3 = 0 $ 

Therefore, the equation is  $ x - 4y + 3 = 0 $ .

3.Find the angle between the lines  $ y = \left( {2 - \sqrt 3 } \right)\left( {x + 5} \right) $ and  $ y = \left( {2 + \sqrt 3 } \right)\left( {x - 7} \right) $ .

Ans: 

Given: $ y = \left( {2 - \sqrt 3 } \right)\left( {x + 5} \right) $ and  $ y = \left( {2 + \sqrt 3 } \right)\left( {x - 7} \right) $ .

Slope of line  $ y = \left( {2 - \sqrt 3 } \right)\left( {x + 5} \right) $ is   $ 2 - \sqrt 3  $ .

Slope of the line  $ y = \left( {2 + \sqrt 3 } \right)\left( {x - 7} \right) $ is  $ 2 + \sqrt 3  $ . 

 $ \theta  $ be the angle between two lines.

Using  $ \tan \theta  = \left| {\frac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right| $ ,

 $ \Rightarrow \tan \theta  = \left| {\frac{{2 - \sqrt 3  - 2 - \sqrt 3 }}{{1 + \left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}} \right| $ 

 $ \Rightarrow \tan \theta  = \left| {\frac{{ - 2\sqrt 3 }}{{1 + 4 - 3}}} \right| $ 

 $ \Rightarrow \tan \theta  = \left| { - \sqrt 3 } \right| $ 

 $ \Rightarrow \tan \theta  = \sqrt 3 {\text{ or }} - \sqrt 3  $ 

 $ \Rightarrow \tan \theta  = \tan {60^ \circ }{\text{ or }}\tan {120^ \circ } $ 

Therefore,  $ \theta  = {60^ \circ }{\text{ or }}\theta  = {120^ \circ } $ 

4.Find the equation of lines which passes through the point  $ (3,4) $ and cuts off intercepts from the coordinate axes such that their sum is  $ 14 $ .

Ans: 

Given: Line passes through the point  $ (3,4) $ .

Let the intercept made by the line be  $ a $ on $ x -  $ axis and the intercept on $ y -  $ axis be  $ b $ .

So, equation of line is  $ \frac{x}{a} + \frac{y}{b} = 1 $ .

Given that  $ a + b = 14 $ .

 $ \Rightarrow b = 14 - a $ 

So,  $ \frac{x}{a} + \frac{y}{{14 - a}} = 1 $ 

This equation passes through $ (3,4) $ .

 $ \Rightarrow \frac{3}{a} + \frac{4}{{14 - a}} = 1 $ 

 $ \Rightarrow \frac{{3\left( {14 - a} \right) + 4a}}{{a\left( {14 - a} \right)}} = 1 $ 

 $ \Rightarrow 42 + a = 14a - {a^2} $ 

 $ \Rightarrow {a^2} - 13a + 42 = 0 $ 

 $ \Rightarrow \left( {a - 6} \right)\left( {a - 7} \right) = 0 $ 

 $ \Rightarrow a = 6,7 $ 

\[ \Rightarrow b = 14 - 6,14 - 7\]

\[ \Rightarrow b = 8,7\]

So, the equation of line when \[a = 6\] and \[b = 8\] is  $ \frac{x}{6} + \frac{y}{8} = 1 $  i.e. \[4x + 3y = 24\].

The equation of line when \[a = 7\] and \[b = 7\] is   $ \frac{x}{7} + \frac{y}{7} = 1 $  i.e. \[x + y = 7\].

Therefore, the equations are  $ x + y = 7 $ and \[4x + 3y = 24\].

5. Find the points on the line  $ x + y = 4 $ which lie at a unit distance from the line  $ 4x + 3y = 10 $ .

Ans: 

Given: $ x + y = 4 $ and  $ 4x + 3y = 10 $ .

Let the point  $ ({x_1},{y_1}) $ be the point lying on  $ x + y = 4 $  i.e.  $ {x_1} + {y_1} = 4{\text{        (1)}} $ 

The distance of  $ ({x_1},{y_1}) $ from  $ 4x + 3y = 10 $ : 

 $ \Rightarrow \left| {\frac{{4{x_1} + 3{y_1} - 10}}{{\sqrt {{4^2} + {3^2}} }}} \right| = 1 $ 

 $ \Rightarrow \left| {\frac{{4{x_1} + 3{y_1} - 10}}{5}} \right| = 1 $ 

\[ \Rightarrow 4{x_1} + 3{y_1} - 10 =  \pm 5\]

Take the  $  +  $  sign,

\[ \Rightarrow 4{x_1} + 3{y_1} - 10 = 5\]

\[ \Rightarrow 4{x_1} + 3{y_1} = 15{\text{           }}...{\text{(2)}}\]

From \[{\text{(1)}}\], 

\[ \Rightarrow {y_1} = 4 - {x_1}\]

Put this value in\[{\text{(2)}}\], 

\[ \Rightarrow 4{x_1} + 3\left( {4 - {x_1}} \right) = 15\]

\[ \Rightarrow {x_1} = 3\]and \[{y_1} = 4 - 3 = 1\].

So, the point is  $ (3,1) $ .

Take the  $  -  $  sign,

\[ \Rightarrow 4{x_1} + 3{y_1} - 10 =  - 5\]

\[ \Rightarrow 4{x_1} + 3{y_1} = 5{\text{           }}...{\text{(3)}}\]

From \[{\text{(1)}}\], 

\[ \Rightarrow {y_1} = 4 - {x_1}\]

Put this value in\[{\text{(3)}}\], 

\[ \Rightarrow 4{x_1} + 3\left( {4 - {x_1}} \right) = 5\]

\[ \Rightarrow {x_1} =  - 7\]and \[{y_1} = 4 - ( - 7) = 11\].

So, the point is  $ ( - 7,11) $ .

Therefore, the points are  $ (3,1) $ and  $ ( - 7,11) $ .

6. Show that the tangent of an angle between the lines  $ \frac{x}{a} + \frac{y}{b} = 1 $  and  $ \frac{x}{a} - \frac{y}{b} = 1 $ is  $ \frac{{2ab}}{{{a^2} - {b^2}}} $ .

Ans: 

Given: The tangent of an angle between  $ \frac{x}{a} + \frac{y}{b} = 1 $  and  $ \frac{x}{a} - \frac{y}{b} = 1 $ is  $ \frac{{2ab}}{{{a^2} - {b^2}}} $ .

Given that  $ \frac{x}{a} + \frac{y}{b} = 1{\text{     }}...{\text{(1)}} $ 

 $ \frac{x}{a} - \frac{y}{b} = 1{\text{     }}...{\text{(2)}} $ 

Slope of the line  $ \frac{x}{a} + \frac{y}{b} = 1 $ is  $  - \frac{b}{a} $ .

Slope of the line  $ \frac{x}{a} - \frac{y}{b} = 1 $ is  $ \frac{b}{a} $ .

Using  $ \tan \theta  = \left| {\frac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right| $ ,

 $ \Rightarrow \tan \theta  = \left| {\frac{{ - \frac{b}{a} - \frac{b}{a}}}{{1 + \left( { - \frac{b}{a}} \right)\left( {\frac{b}{a}} \right)}}} \right| $ 

 $ \Rightarrow \tan \theta  = \left| {\frac{{ - \frac{{2b}}{a}}}{{1 - {{\left( {\frac{b}{a}} \right)}^2}}}} \right| $ 

 $ \Rightarrow \tan \theta  = \left| {\frac{{ - 2ab}}{{{a^2} - {b^2}}}} \right| $ 

 $ \Rightarrow \tan \theta  = \frac{{2ab}}{{{a^2} - {b^2}}} $ 

Hence verified.

7. Find the equation of lines passing through  $ (1,2) $ and making angle  $ 3{0^o} $  with  $ y -  $ axis.

Ans: 

Given: lines passing through  $ (1,2) $ .

The line makes  $ {30^ \circ } $  with  $ y -  $ axis.

So, the angle made with  $ x -  $ axis is  $ {60^ \circ } $ .

Slope of line $  = \tan {60^ \circ } = \sqrt 3  $ .

The equation of line that passes through  $ (1,2) $  and slope  $ \sqrt 3  $  is:

 $ \Rightarrow y - {y_1} = m(x - {x_1}) $ 

 $ \Rightarrow y - 2 = \sqrt 3 (x - 1) $ 

 $ \Rightarrow y - \sqrt 3 x + \sqrt 3  - 2 = 0 $ 

Therefore, the equation is  $ y - \sqrt 3 x + \sqrt 3  - 2 = 0 $ .

8. Find the equation of the line passing through the point of intersection of  $ 2x + y = 5 $ and  $ x + 3y + 8 = 0 $  and parallel to the line  $ 3x + 4y = 7 $ .

Ans: 

Given: Line passes through the point of intersection of  $ 2x + y = 5 $ and  $ x + 3y + 8 = 0 $  and parallel to  $ 3x + 4y = 7 $ .

The equation of line that passes through the point of intersection of  $ 2x + y = 5 $ and  $ x + 3y + 8 = 0 $ is  $ \left( {2x + y - 5} \right) + \lambda \left( {x + 3y + 8} \right) = 0 $ .

 $ \Rightarrow \left( {2 + \lambda } \right)x + \left( {1 + 3y} \right)\lambda  - 5 + 8\lambda  = 0 $ 

Slope of this line is  $ \frac{{ - \left( {2 + \lambda } \right)}}{{1 + 3\lambda }} $ .

Slope of  $ 3x + 4y = 7 $ is  $  - \frac{3}{4} $ .

As the two lines are parallel,  $ \frac{{ - \left( {2 + \lambda } \right)}}{{1 + 3\lambda }} =  - \frac{3}{4} $ 

 $ \Rightarrow \frac{{2 + \lambda }}{{1 + 3\lambda }} = \frac{3}{4} $ 

 $ \Rightarrow 8 + 4\lambda  = 3 + 9\lambda  $ 

 $ \Rightarrow 5\lambda  = 5 $ 

 $ \Rightarrow \lambda  = 1 $ 

The equation  $ \left( {2x + y - 5} \right) + \lambda \left( {x + 3y + 8} \right) = 0 $ becomes  $ 3x + 4y + 3 = 0 $ .

Therefore, the equation is  $ 3x + 4y + 3 = 0 $ .

9. For what values of  $ a $  and  $ b $  the intercepts cut off on the coordinate axes by the line \[ax + by + 8 = 0\] are equal in length but opposite in signs to those cut off by the line\[2x--3y + 6 = 0\] on the axes.

Ans: 

Given:\[ax + by + 8 = 0\]and \[2x--3y + 6 = 0\].

We can write \[ax + by + 8 = 0\] as:

\[ \Rightarrow ax + by =  - 8\]

\[ \Rightarrow \frac{a}{{ - 8}}x + \frac{b}{{ - 8}}y = 1\]

\[ \Rightarrow \frac{x}{{\frac{{ - 8}}{a}}} + \frac{y}{{\frac{{ - 8}}{b}}} = 1\]

The intercepts are \[\frac{{ - 8}}{a},{\text{ }}\frac{{ - 8}}{b}\].

We can write \[2x--3y + 6 = 0\] as:

\[ \Rightarrow 2x--3y =  - 6\]

\[ \Rightarrow \frac{{2x}}{{ - 6}} - \frac{{3y}}{{ - 6}} = 1\]

\[ \Rightarrow \frac{x}{{ - 3}} + \frac{y}{2} = 1\]

The intercepts are \[ - 3,{\text{ }}2\].

From the question, \[\frac{{ - 8}}{a} = 3,{\text{ }}\frac{{ - 8}}{b} =  - 2\] i.e. \[a = \frac{{ - 8}}{3},{\text{ }}b = 4\]

Therefore,  $ a =  - \frac{8}{3} $ and  $ b = 4 $ .

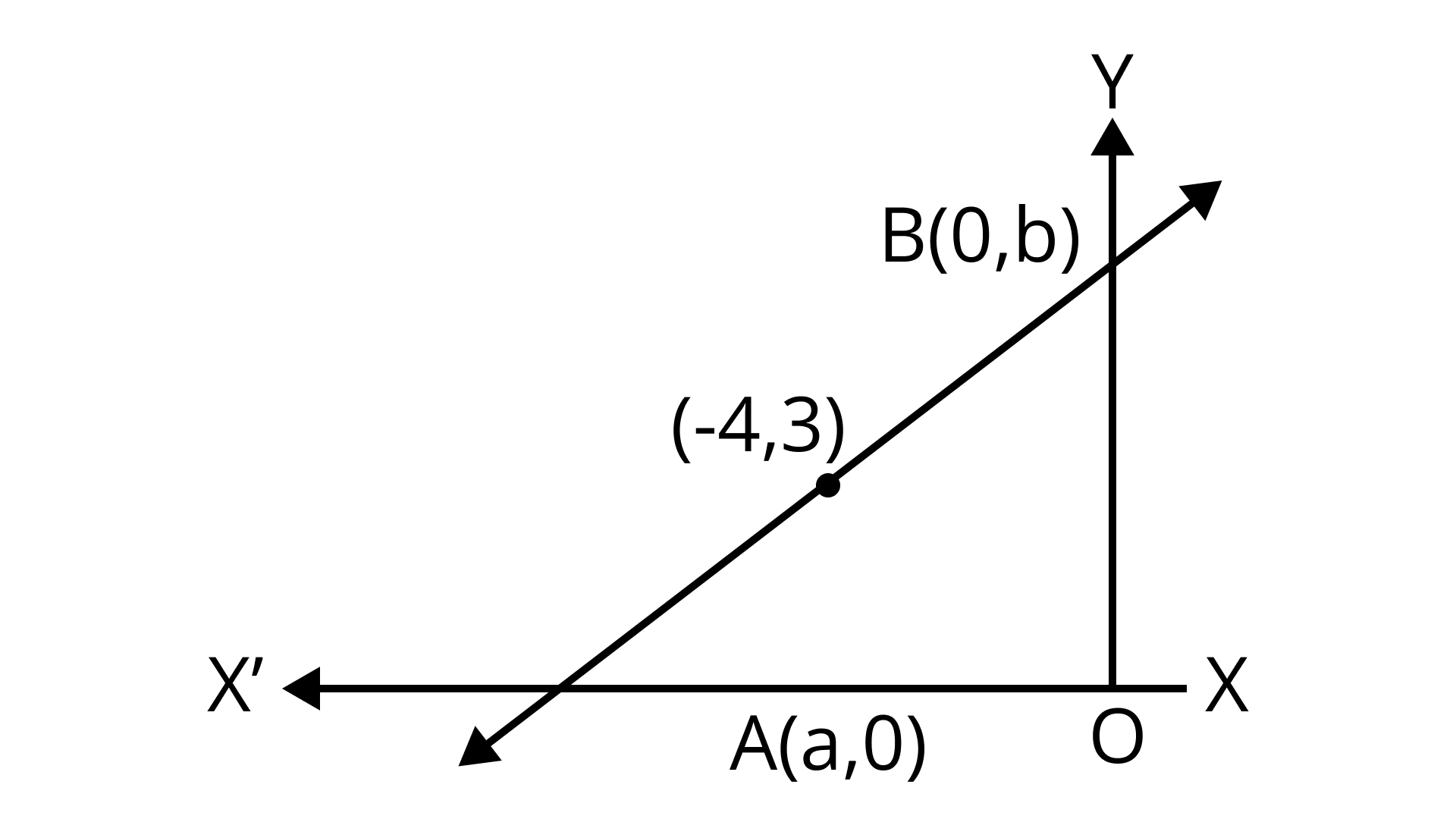
10. If the intercept of a line between the coordinate axes is divided by the point \[\left( {--5, 4} \right)\]in the ratio \[1:2\], then find the equation of the line.

Ans: 

Given:\[\left( {--5,{\text{ }}4} \right)\]

Assume \[a\]and \[b\]are intercepts on given line.

Then, the coordinates are \[A(a,0)\]and \[B(0,b)\].

Using \[x = \frac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}}\]and \[y = \frac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}\],

\[ \Rightarrow  - 5 = \frac{{1 \times 0 + 2 \times a}}{{1 + 2}}\]

\[ \Rightarrow 2a =  - 15\]

\[ \Rightarrow a = \frac{{ - 15}}{2}\]

So, \[A = \left( {\frac{{ - 15}}{2},0} \right)\].

 And \[4 = \frac{{1 \times b + 0 \times 2}}{{1 + 2}}\]

\[ \Rightarrow 4 = \frac{b}{3}\]

\[ \Rightarrow b = 12\]

So, \[B = \left( {0,12} \right)\].

The equation of line \[AB\]is \[y - {y_1} = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)\].

\[ \Rightarrow y - 0 = \left( {\frac{{12 - 0}}{{0 + \frac{{15}}{2}}}} \right)\left( {x + \frac{{15}}{2}} \right)\]

\[ \Rightarrow y = \frac{8}{5}\left( {x + \frac{{15}}{2}} \right)\]

\[ \Rightarrow 5y = 8x + 60\]

Therefore,\[8x - 5y + 60 = 0\].

11. Find the equation of a straight line on which length of perpendicular from the origin is four units and the line makes an angle of  $ 12{0^o} $ with the positive direction of  $ x -  $ axis. 

Ans: 

Given: Line makes  $ {120^ \circ } $ with the positive direction of  $ x -  $ axis. 

The line makes  $ {120^ \circ } $  with the positive direction of  $ x -  $ axis.

So, slope of the line is  $ \tan {120^ \circ } =  - \sqrt 3  $ .

Equation of the required line is: 

 $ y =  - \sqrt 3 x + c $ 

 $ \Rightarrow \sqrt 3 x + y - c = 0 $ . 

This line is 4 units away from  $ (0,0) $ .

 $ \Rightarrow \frac{{\left| {\sqrt 3 (0) + 0 - c} \right|}}{{\sqrt {3 + 1} }} = 4 $ 

 $ \Rightarrow \quad |c| = 8 $ 

 $ \Rightarrow c =  \pm 8 $ 

Therefore, the equation of line is  $ \sqrt 3 x + y \pm 8 = 0 $ .

12. Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by  $ 3x + 4y + 4 = 0 $  and the opposite vertex of the hypotenuse is  $ (2,2) $ .

Ans: 

Given: $ 3x + 4y + 4 = 0 $ 

The hypotenuse is along the line  $ 3x + 4y + 4 = 0 $ 

Slope of the hypotenuse is  $ \frac{{ - 3}}{4} $ .

As the triangle is isosceles right angled triangle, two angles will be equal to  $ {45^\circ } $ .

Let the slope of the line making  $ {45^\circ } $  with the hypotenuse be  $ m $ .

 $ \Rightarrow \tan {45^\circ } = \left| {\frac{{m - \left( { - \frac{3}{4}} \right)}}{{1 + m\left( { - \frac{3}{4}} \right)}}} \right| $ 

 $ \Rightarrow \tan {45^\circ } = \left| {\frac{{4m + 3}}{{4 - 3m}}} \right| $ 

 $ \Rightarrow \frac{{4m + 3}}{{4 - 3m}} =  \pm 1 $ 

 $ \Rightarrow 4m + 3 = 4 - 3m $ or $ 4m + 3 = 3m - 4 $ 

 $ \Rightarrow m = \frac{1}{7} $ or $ m =  - 7 $ 

Slope of this line is  $ \frac{1}{7} $ , so the equation of this line is  $ y - 2 = (1/7)(x - 2) $  i.e.  $ x - 7y + 12 = 0 $ .

The slope of line perpendicular to it is  $  - 7 $ . 

The equation of this line is:  $ y - 2 =  - 7(x - 2) $  i.e.  $ 7x + y - 16 = 0 $ .

Therefore, the equation of required line is  $ 7x + y - 16 = 0 $ .

13. If the equation of the base of an equilateral triangle is  $ x + y - 2 $  and the vertex is  $ (2, - 1) $ , then find the length of the side of the triangle.

Ans: 

Given:  $ x + y - 2 $ and  $ (2, - 1) $ .

The altitude from the vertex  $ (2, - 1) $ on the base  $ x + y - 2 $  meets at the midpoint of base. 

The length of altitude is the distance of  $ (2, - 1) $  from $ x + y - 2 $  $  = \left| {\frac{{2 + ( - 1) - 2}}{{\sqrt {{1^2} + {1^2}} }}} \right| = \frac{1}{{\sqrt 2 }} $ .

The triangle is an equilateral triangle. So,  $ \sin {60^\circ } = \frac{{{\text{Altitude}}}}{{{\text{side of triangle}}}} $ .

$ \Rightarrow {\text{length of side of triangle}} = \frac{{{\text{Altitude}}}}{{\sin {{60}^\circ }}} = \frac{{\frac{1}{{\sqrt 2 }}}}{{\frac{{\sqrt 3 }}{2}}} = \sqrt {\frac{2}{3}}  $ .

Therefore, the length of side of the triangle is  $ \sqrt {\frac{2}{3}}  $ .

14. A variable line passes through a fixed point  $ P $ . The algebraic sum of the perpendiculars drawn from the points  $ (2,0),(0,2) $  and  $ (1,1) $  on the line is zero. Find the coordinates of the point  $ P $ .

Ans: 

Given:  $ (2,0),(0,2) $  and  $ (1,1) $ 

Assume that the variable line passing through the fixed point  $ P $ is  $ ax + by + c = 0 $ .

Perpendicular distance from the point $ A(2,0) = \frac{{2a + 0 + c}}{{\sqrt {{a^2} + {b^2}} }} $ 

Perpendicular distance from the point $ B(0,2) = \frac{{0 + 2b + c}}{{\sqrt {{a^2} + {b^2}} }} $ 

Perpendicular distance from the point $ C(1,1) = \frac{{a + b + c}}{{\sqrt {{a^2} + {b^2}} }} $ 

Given that,  $ \frac{{2a + 0 + c}}{{\sqrt {{a^2} + {b^2}} }} + \frac{{0 + 2b + c}}{{\sqrt {{a^2} + {b^2}} }} + \frac{{a + b + c}}{{\sqrt {{a^2} + {b^2}} }} = 0 $ 

 $ \Rightarrow \quad 3a + 3b + 3c = 0 $ or $ a + b + c = 0 $ 

Therefore, the variable line passes through the fixed point  $ (1,1) $ .

15. In what direction should a line be drawn through the point  $ (1,2) $  so that its point of intersection with the line  $ x + y = 4 $  is at a distance  $ \frac{{\sqrt 6 }}{3} $  from the given point.

Ans: 

Given:  $ x + y = 4 $ and  $ (1,2) $ .

Let the slope of line be  $ m $ . 

It passes through $ A(1,2) $ 

 So, the equation of line is  $ y - 2 = m(x - 1) $  or  $ mx - y + 2 - m = 0{\text{       }}...{\text{(1)}} $ 

The equation of the given line is  $ x + y - 4 = 0\quad ...(2) $ 

Assume that these lines meet at point  $ B $ .

Solving  $ (1) $ and  $ (2) $ , 

$ B \equiv \left( {\frac{{m + 2}}{{m + 1}},\frac{{3m + 2}}{{m + 1}}} \right) $ 

Given that  $ AB = \frac{{\sqrt 6 }}{3} $ 

$ \Rightarrow \quad A{B^2} = \frac{6}{9} $ 

$ \Rightarrow {\left( {\frac{{m + 2}}{{m + 1}} - 1} \right)^2} + {\left( {\frac{{3m + 2}}{{m + 1}} - 2} \right)^2} = \frac{6}{9} $ 

$ \Rightarrow \quad {\left( {\frac{1}{{m + 1}}} \right)^2} + {\left( {\frac{m}{{m + 1}}} \right)^2} = \frac{2}{3} $ 

$ \Rightarrow \frac{{1 + {m^2}}}{{{{(1 + m)}^2}}} = \frac{2}{3} $ 

$ \Rightarrow \quad 3 + 3{m^2} = 2 + 2{m^2} + 4m $ 

$ \Rightarrow {m^2} - 4m + 1 = 0 $ 

$ \Rightarrow m = \frac{{4 \pm \sqrt {16 - 4} }}{2} = 2 \pm \sqrt 3  = 2 + \sqrt 3  $ or $ 2 - \sqrt 3  $ 

$ \Rightarrow \tan \theta  = 2 + \sqrt 3  $ or $ 2 - \sqrt 3  $ 

$ \Rightarrow \theta  = {75^\circ } $ or  $ \theta  = {15^\circ } $ .

Therefore,  $ \theta  = {75^ \circ }{\text{ or }}\theta  = {15^ \circ } $ 

16. A straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point. 

Ans: 

Given:  $ \frac{1}{a} + \frac{1}{b} =  $  constant

The equation of line in intercept form is  $ \frac{x}{a} + \frac{y}{b} = 1 $ .

As  $ \frac{1}{a} + \frac{1}{b} =  $  constant, 

Let  $ \frac{1}{a} + \frac{1}{b} $  $  = \frac{1}{k} $ . 

So,  $ \frac{k}{a} + \frac{k}{b} = 1 $ 

Thus,  $ (k,k) $  lies on  $ \frac{x}{a} + \frac{k}{b} = 1 $ .

Therefore, the line passes through the fixed point  $ (k,k) $ .

17. Find the equation of the line which passes through the fixed point  $( - 4,3)$   and the portion of the line intercepted between the axes id divided internally in the ratio 5:3 by this point.

Ans: Let AB be a line passing through a point (- 4, 3) and meets x-axis at A(a, 0) and y-axis at B(0, b).

$\Rightarrow \therefore  - 4 = \frac{{5 \times 0 + 3a}}{{5 + 3}}$  

$\Rightarrow  - 4 = \frac{{3a}}{8}\left[ {\because X = \frac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},y = \frac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right]$ 

$\Rightarrow 3a =  - 32$                                                                                                              

$\Rightarrow a = \frac{{ - 32}}{3}$   and  $3 = \frac{{5 \times b + 3 \times 0}}{{5 + 3}}$                                                                

$\Rightarrow 3 = \frac{{5 \times b}}{8} \Rightarrow 5b = 24 \Rightarrow b = \frac{{25}}{5}$  

Intercept form of the line is  $\frac{x}{{\frac{{ - 32}}{3}}} + \frac{y}{{\frac{{24}}{5}}} = 1$                      

$\Rightarrow \frac{{ - 3x}}{{32}} + \frac{{5y}}{{24}} = 1$ 

$\Rightarrow  - 9x + 20y = 96 \Rightarrow 9x - 20y + 96 = 0$  

Hence, The required equation is  $9x - 20y + 96 = 0$ 

18. Find the equation of the lines through the point of intersection of the lines  $x - y + 1 = 0 $   and \[2x--3y + 5 = 0\] and whose distance from the point  $(3,2)$   is  $ \frac{7}{5}. $  

Ans: Given equation are

$\mathbf{x}-\mathbf{y}+\mathbf{1}=\mathbf{0} \ldots(\mathbf{i}) $  And  $ \mathbf{2} \mathbf{x}-\mathbf{3} \mathbf{y}+\mathbf{5}=\mathbf{0} \ldots(\mathbf{i i})$  Solving eq. (i) and eq. (ii) 

we get  $2 x-2 y+2=0$   $2 x-3 y+5=0$   

$y-3=0, y=3$ 

From eq. (i) we have 

$\mathbf{x}-\mathbf{3}+\mathbf{1}=\mathbf{0} \Rightarrow \mathbf{x}=\mathbf{2}$ 

So,  $(2,3)$  is the point of intersection of eq.(i) and eq. (ii). 

Let m be the slope of the required line

 $\therefore$  Equation of the line is

 $y-3=m(x-2)$ 

 $\Rightarrow y-3=m x-2 m$ 

 $\Rightarrow m x-y+3-2 m=0$ 

Since, the perpendicular distance from  $(3,2)$ 

to the line is  $\frac{7}{5}$  then,

 $\frac{7}{5}=\left|\frac{m(3)-2+3-2 m}{\sqrt{m^{2}+1}}\right|$ 

 $\Rightarrow \frac{49}{25}=\frac{(3 m-2+3-2 m)^{2}}{m^{2}+1}$ 

 $\Rightarrow \frac{49}{25}=\frac{(m+1)^{2}}{m^{2}+1}$ 

 $\Rightarrow 49 m^{2}+49=25 m^{2}+50 m+25$ 

 $\Rightarrow 49 m^{2}-25 m^{2}-50 m+49-25=0$ 

 $\Rightarrow 24 m^{2}-50 m+24=0$ 

 $\Rightarrow 12 m^{2}-25 m+12=0$ 

 $\Rightarrow 12 m^{2}-16 m-9 m+12=0$ 

 $\Rightarrow 4 m(3 m-4)-3(3 m-4)=0$ 

 $\Rightarrow(3 m-4)(4 m-3)=0$ 

 $\Rightarrow 3 m-4=0 \text { and } 4 m-3=0$ 

 $\Rightarrow 3 m-4=0 \text { and } 4 m-3=0$ 

 $\therefore m=\frac{4}{3}, \frac{3}{4}$ 

Equation of the line taking  $ m=\frac{4}{3}$  is

 $y-3=\frac{4}{3}(x-2)$ 

 $\Rightarrow 3 y-9=4 x-8 \Rightarrow 4 x-3 y+1=0$ 

Equation of the line taking  $m=\frac{3}{4}$  is

 $y-3=\frac{3}{4}(x-2)$ 

 $\Rightarrow 4 y-12=3 x-6 \Rightarrow 3 x-4 y+6=0$ 

Hence, the required equation are

 $4 x-3 y+1=0 \text { and } 3 x-4 y+6=0$ 

19.If the sum of the distance of a moving point in a plane from the axes is 1, then find the locus of the point.

Ans: Let coordinates of a moving point P be  $ (x,y). $  

Given that the sum of the distance from the axes to the point is always 1

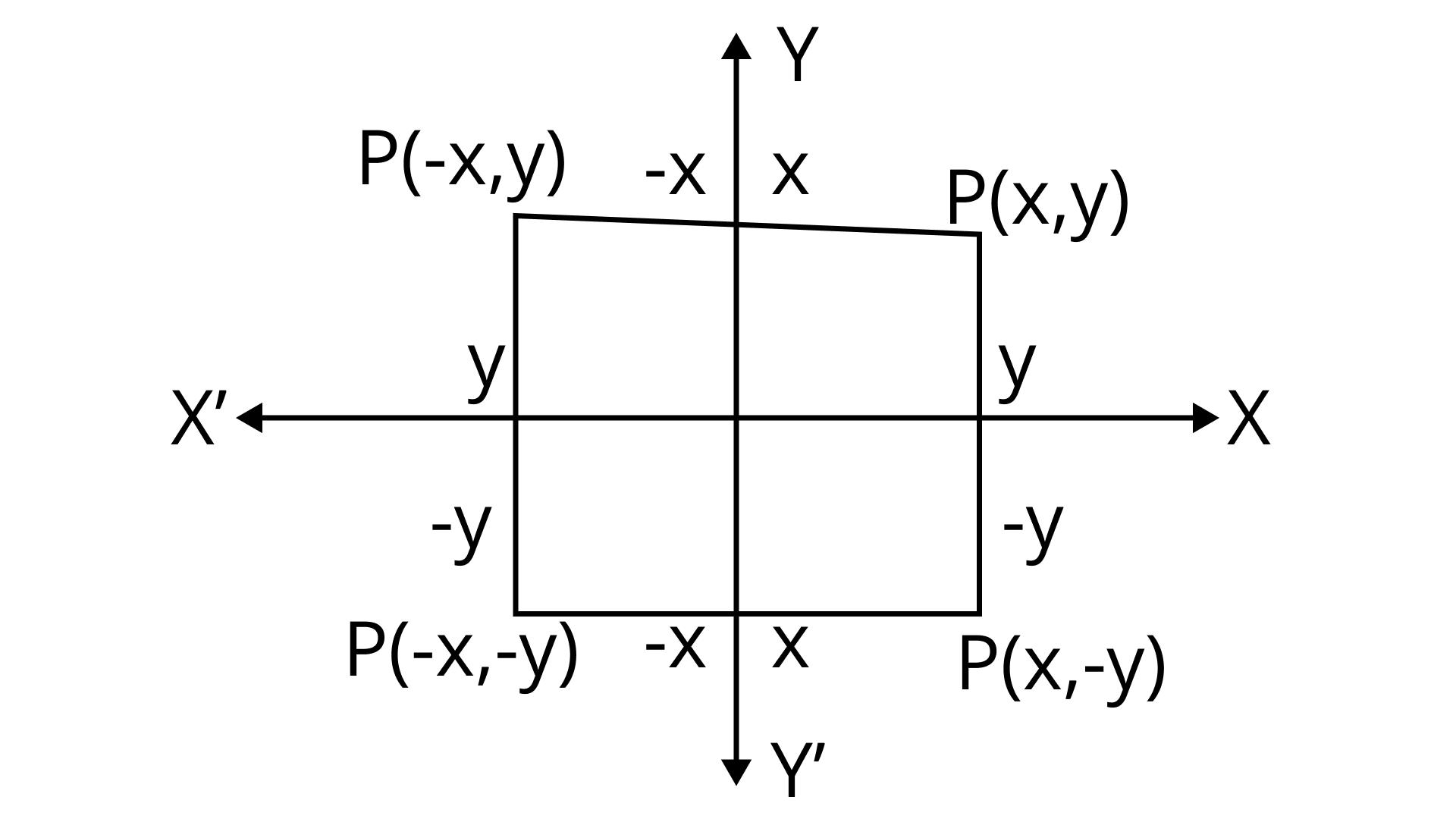
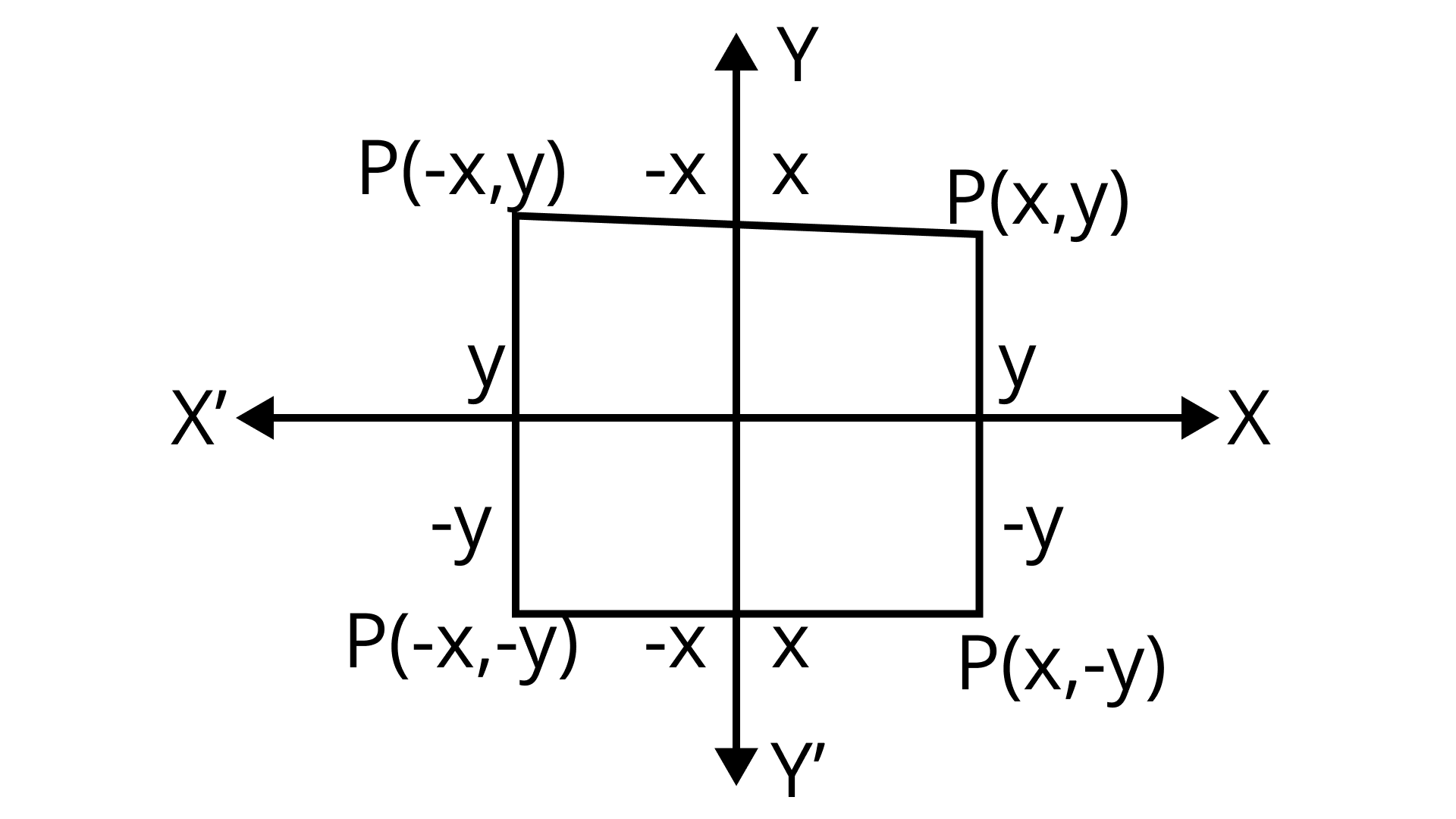
$ {\therefore \left| x \right|{\text{ }} + {\text{ }}\left| y \right|{\text{ }} = {\text{ }}1} $ 

$ { \Rightarrow x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}1} $  

$ { \Rightarrow  - x--y = 1} $  

$ { \Rightarrow  - x + y = 1} $ 

$ { \Rightarrow x--y{\text{ }} = {\text{ }}1} $ 

Hence, these equations gives us the locus of the point P which is a square.

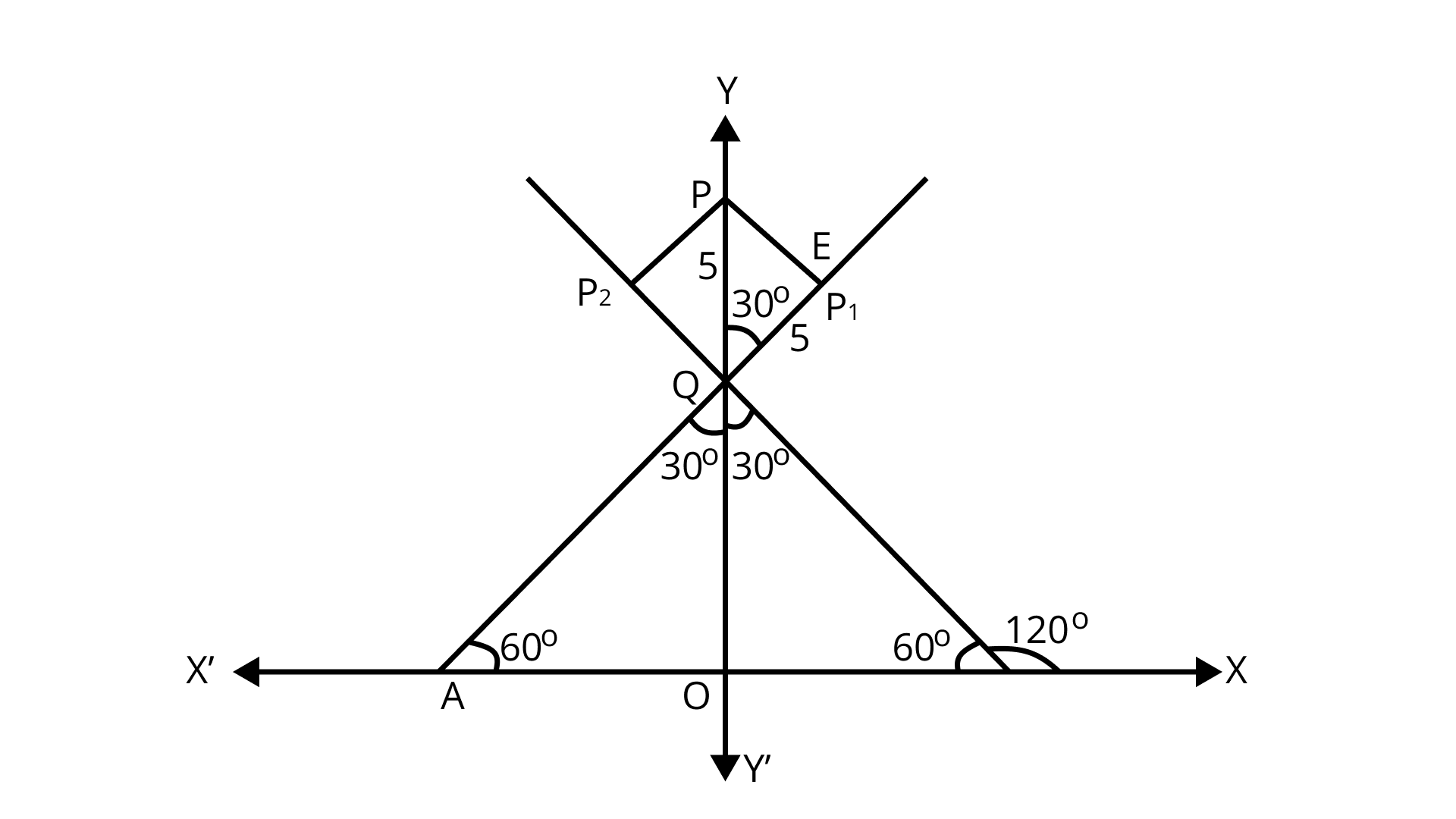
20. P1, P2 are points on either of the two lines  $ y - \sqrt 3 \left| x \right| = 2 $ at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P1, P2 on the bisector of the angle between the given lines.

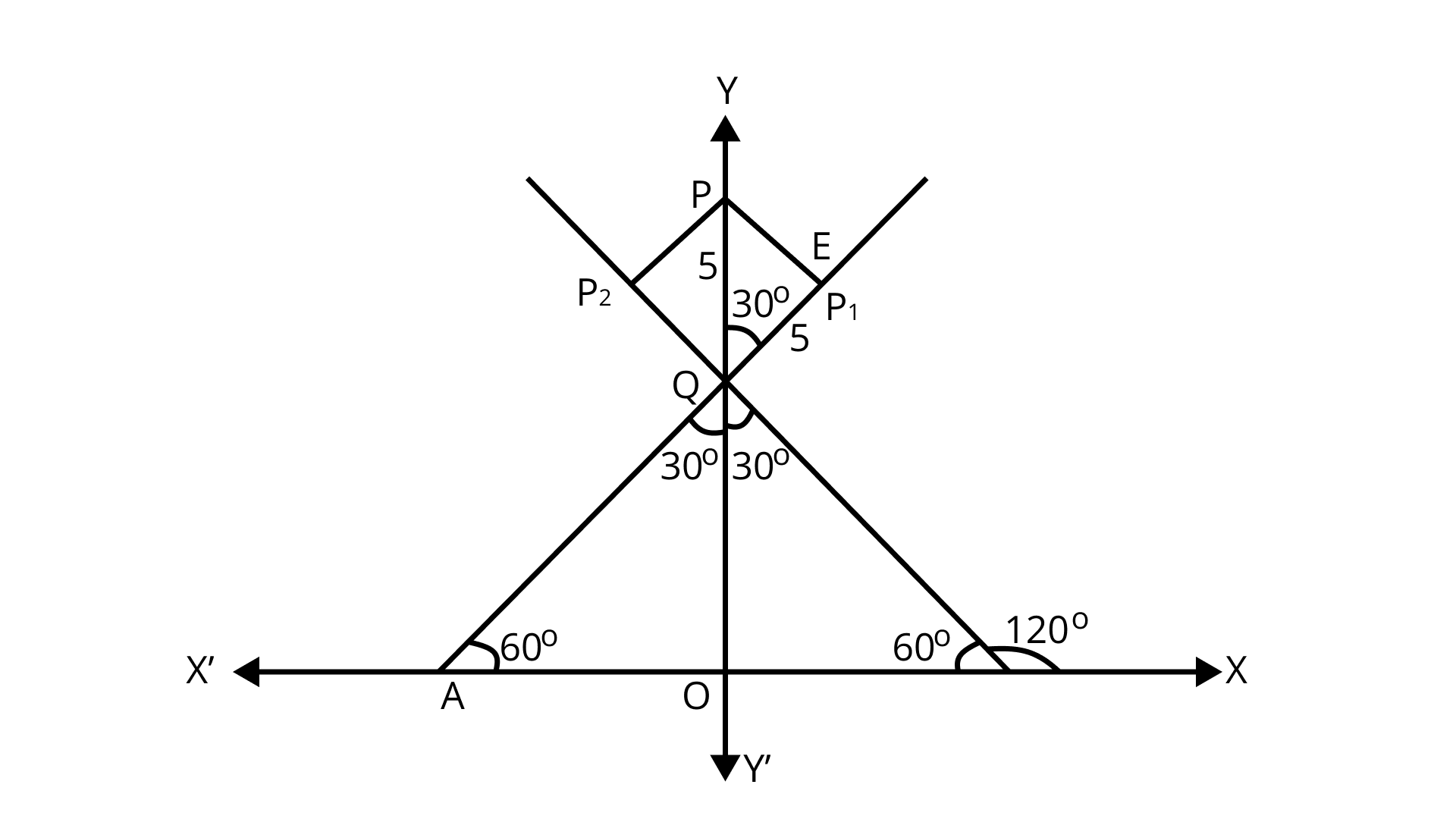
Ans: Given lines are  $ y - \sqrt 3 \left| x \right| = 2 $ 

$ \Rightarrow y - \sqrt 3  x = 2 $   if x ≥ 0 …(i)

And  $ y + \sqrt 3  x = 2 $  if x < 0 …(ii)

Slope of eq. (i) is  $ \tan \theta  = \sqrt 3  $    $ \therefore \theta  = {60^o} $  

Slope of eq. (ii) is  $ \tan \theta  =  - \sqrt 3  $    $ \therefore \theta  = {120^o} $ 

120° Solving eq. (i) and eq. (ii) we get

$ y - \sqrt 3 x = 2 $ 

$ y + \sqrt 3 x = 2 $ 

$ \_\_\_\_\_\_\_\_\_\_ $ 

$ 2y = 4 \Rightarrow y = 2 $  

Putting the value of y is eq. (i) we get

$ x = 0 $  

Point of intersection of line (i) and (ii) is  $ Q(0,2) $  

$ \therefore QO = 2 $  

$  $  In  $ \Delta PEQ, $                                                                                                 

$ \cos {30^o} = \frac{{PQ}}{{QE}} \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{PQ}}{5} $ 

$ \Rightarrow \therefore PQ = \frac{{5\sqrt 3 }}{2} $ 

$ \therefore OP = OQ + PQ $  

$  = 2 + \frac{{5\sqrt 3 }}{2} $  

Hence, the coordinates of the foot of perpendicular  $  = (0,2 + \frac{{5\sqrt 3 }}{2}) $  

21.If p is the length of perpendicular from the origin on the line  $\frac{x}{a} + \frac{y}{b} = 1$  and  ${a^2},{p^2},{b^2}$  are in A.P. then show that  ${a^4} + {b^4} = 0.$  

Ans: Given equation is $\frac{x}{a}+\frac{y}{b}=1$

Since, $\mathrm{p}$ is the length of perpendicular drawn from the origin to the given line

$\therefore p=\left|\frac{\frac{0}{a}+\frac{0}{b}-1}{\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}}}\right|$

Squaring both sides, we have

$p^{2}=\frac{1}{\frac{1}{a^{2}}+\frac{1}{b^{2}}}$ $\Rightarrow \frac{1}{a^{2}}+\frac{1}{b^{2}}=\frac{1}{p^{2}} \ldots \ldots(i)$ Since $a^{2}, p^{2}, b^{2}$ are in A.P. $\therefore 2 p^{2}=a^{2}+b^{2}$ $\Rightarrow p^{2}=\frac{a^{2}+b^{2}}{2} \Rightarrow \frac{1}{p^{2}}=\frac{2}{a^{2}+b^{2}}$

Putting the value of $\frac{1}{p^{2}}$ is eq. (i) we get,

$\frac{1}{a^{2}}+\frac{1}{b^{2}}=\frac{2}{a^{2}+b^{2}}$

$\Rightarrow \frac{a^{2}+b^{2}}{a^{2} b^{2}}=\frac{2}{a^{2}+b^{2}}$

$\Rightarrow\left(a^{2}+b^{2}\right)^{2}=2 a^{2} b^{2}$

$\Rightarrow a^{4}+b^{4}+2 a^{2} b^{2}=2 a^{2} b^{2}$

$\Rightarrow a^{4}+b^{4}=0$

Hence proved.

22. A line cutting off intercept  $  - 3 $  from the  $ y -  $ axis and the tangent at angle to the  $ x -  $ axis is  $ \frac{3}{5} $ ,  its equation is 

(A)  $ 5y - 3x + 15 = 0 $ 

(B)  $ 3y - 5x + 15 = 0 $ 

(C)  $ 5y - 3x - 15 = 0 $ 

(D) None of these

Ans: 

Given: A line cuts off an intercept  $  - 3 $  from the  $ y -  $ axis.

Let the equation of required line be  $ y = mx + c $ .

As  $ c =  - 3 $ and  $ m = \frac{3}{5} $ ,

The equation of line is:  $ y = \frac{3}{5}x - 3 $ 

 $ \Rightarrow 5y - 3x + 15 = 0 $ 

Hence, the equation is  $ 5y - 3x + 15 = 0 $ .

Correct Option : A

23. Slope of a line which cut off intercepts of equal lengths on the axes is 

(A)  $  - 1 $ 

(B)  $ 0 $ 

(C)  $ 2 $ 

(D)  $ \sqrt 3  $ 

Ans: 

Given: A line cuts off intercepts of equal lengths on the axes.

The equation of required line is $ \frac{x}{a} + \frac{y}{a} = 1 $ .

$ \Rightarrow x + y = a $ 

$ \Rightarrow y =  - x + a $ 

Slope $  =  - 1 $ 

Hence, the slope is  $  - 1 $ .

Correct Option: A

24. The equation of the straight line passing through the point  $ (3,2) $  and perpendicular to the line  $ y = x $  is

(A)  $ x - y = 5 $ 

(B)  $ x + y = 5 $ 

(C)  $ x + y = 1 $ 

(D)  $ x - y = 1 $ 

Ans: 

Given: $ (3,2) $ and  $ y = x $ .

Slope of  $ y = x $ is  $ 1 $ .

So, the slope of line perpendicular to it is  $  - 1 $ .

The line passes through  $ (3,2) $ .

So, equation of required line is  $ y - 2 =  - 1(x - 3) $  i.e.  $ x + y = 5 $ .

Hence, equation is  $ x + y = 5 $ .

Correct Option: B

25. The equation of the line passing through the point  $ (1,2) $ and perpendicular to the line  $ x + y + 1 = 0 $  is

(A)  $ y - x + 1 = 0 $ 

(B)  $ y - x - 1 = 0 $ 

(C)  $ y - x + 2 = 0 $ 

(D)  $ y - x - 2 = 0 $ 

Ans: 

Given: $ (1,2) $ and  $ x + y + 1 = 0 $ .

Slope of  $ x + y + 1 = 0 $ is  $  - 1 $ .

So, the slope of line perpendicular to it is  $ 1 $ .

The line passes through  $ (1,2) $ .

So, equation of required line is  $ y - 2 = 1(x - 1) $  i.e.  $ y - x - 1 = 0 $ .

Hence, equation is  $ y - x - 1 = 0 $ .

Correct Option: B

26. The tangent of angle between the lines whose intercepts on the axes are  $ a,  - b $ and  $ b,  - a $ , respectively, is

(A)  $ \frac{{{a^2} - {b^2}}}{{ab}} $ 

(B)  $ \frac{{{b^2} - {a^2}}}{2} $ 

(C)  $ \frac{{{b^2} - {a^2}}}{{2ab}} $ 

(D) None of these

Ans: 

Given: The intercepts on the axes are  $ a,{\text{ }} - b $ and  $ b,{\text{ }} - a $ .

The intercepts of line are  $ a $ and  $  - b $ .

 So, the line passes through the points  $ (a,0) $ and  $ (0, - b) $ .

Thus, the slope of line is  $ {m_1} = \frac{{ - b - 0}}{{0 - a}} = \frac{b}{a} $ .

The intercepts of line are  $ b $ and  $  - a $ .

 So, the line passes through the points  $ (b,0) $ and  $ (0, - a) $ .

Thus, the slope of line is  $ {m_2} = \frac{{ - a - 0}}{{0 - b}} = \frac{a}{b} $ .

Let  $ \theta  $  be the angle between the lines.

 $ \Rightarrow \tan \theta  = \frac{{\frac{b}{a} - \frac{a}{b}}}{{1 + \frac{a}{b} \cdot \frac{b}{a}}} $ 

 $ \Rightarrow \tan \theta  = \frac{{\frac{{{b^2} - {a^2}}}{{ab}}}}{2} $ 

 $ \Rightarrow \tan \theta  = \frac{{{b^2} - {a^2}}}{{2ab}} $ 

Hence,  $ \tan \theta  = \frac{{{b^2} - {a^2}}}{{2ab}} $ .

Correct Option: C

27. If the line  $ \frac{x}{a} + \frac{y}{b} $  passes through the points  $ (2, - 3) $ and  $ (4, - 5) $ , then  $ (a,b) $  is

(A)  $ (1,1) $ 

(B)  $ ( - 1,1) $ 

(C)  $ (1, - 1) $ 

(D)  $ ( - 1, - 1) $ 

Ans: 

Given: $ (2, - 3) $ and  $ (4, - 5) $ .

The points  $ (2, - 3) $  and  $ (4, - 5) $  lie on  $ \frac{x}{a} + \frac{y}{b} = 1 $ .

 $ \Rightarrow \frac{2}{a} - \frac{3}{b} = 1{\text{         }}...{\text{(1)}} $ 

And  $ \frac{4}{a} - \frac{5}{b} = 1{\text{               }}...{\text{(2)}} $ 

Multiply  $ {\text{(1)}} $  by  $ {\text{2}} $  and subtract  $ {\text{(2)}} $ from it.

 $ \Rightarrow  - \frac{6}{b} + \frac{5}{b} = 1 $ 

 $ \Rightarrow \frac{{ - 1}}{b} = 1 $ 

 $ \Rightarrow b =  - 1 $ 

Put  $ b =  - 1 $  in $ {\text{(1)}} $ ,

 $ \Rightarrow \frac{2}{a} + 3 = 1 $ 

 $ \Rightarrow a =  - 1 $ 

So,  $ (a,b) = ( - 1, - 1) $ 

Hence,  $ (a,b) = ( - 1, - 1) $ .

Correct Option: D

28. The distance of the point of intersection of the lines  $ 2x - 3y + 5 = 0 $  and  $ 3x + 4y = 0 $  from the line  $ 5x - 2y = 0 $  is

(A)  $ \frac{{130}}{{17\sqrt {29} }} $ 

(B)  $ \frac{{13}}{{7\sqrt {29} }} $ 

(C)  $ \frac{{130}}{7} $ 

(D) None of these

Ans: 

Given: $ 2x - 3y + 5 = 0 $ and  $ 3x + 4y = 0 $ .

Solve the lines  $ 2x - 3y + 5 = 0 $ and  $ 3x + 4y = 0 $ .

The point of intersection is  $ \left( {\frac{{ - 20}}{{17}},\frac{{15}}{{17}}} \right) $ .

The distance of  $ \left( {\frac{{ - 20}}{{17}},\frac{{15}}{{17}}} \right) $ from  $ 5x - 2y = 0 $  is  $ \frac{{\left| {5 \times \left( { - \frac{{20}}{{17}}} \right) - 2\left( {\frac{{15}}{{17}}} \right)} \right|}}{{\sqrt {25 + 4} }} $ 

The distance of  $ \left( {\frac{{ - 20}}{{17}},\frac{{15}}{{17}}} \right) $ from  $ 5x - 2y = 0 $  is  $ \frac{{\left| {\frac{{ - 100}}{{17}} - \frac{{30}}{{17}}} \right|}}{{\sqrt {29} }} $ 

The distance of  $ \left( {\frac{{ - 20}}{{17}},\frac{{15}}{{17}}} \right) $ from  $ 5x - 2y = 0 $  is  $ \frac{{130}}{{17\sqrt {29} }} $ 

Hence, the distance is  $ \frac{{130}}{{17\sqrt {29} }} $ .

Correct Option: A

29. The equations of the lines which pass through the point  $ (3, - 2) $  and are inclined at  $ 6{0^\circ } $ to the line $ \sqrt 3 x + y = 1 $  is

(A)  $ y + 2 = 0, \sqrt 3 x - y - 2 - 3\sqrt 3  = 0 $ 

(B)  $ x - 2 = 0, \sqrt 3 x - y + 2 + 3\sqrt 3  = 0 $ 

(C)  $ \sqrt 3 x - y - 2 - 3\sqrt 3  = 0 $ 

(D) None of these

Ans: 

Given: $ (3, - 2) $ and  $ \sqrt 3 x + y = 1 $ .

The slope of $ \sqrt 3 x + y = 1 $ is  $ {m_1} =  - \sqrt 3  $ . 

Let the slope of required line which makes  $ {60^\circ } $  with  $ \sqrt 3 x + y = 1 $ be  $ m $ .

Then,  $ \tan {60^\circ } = \left| {\frac{{ - \sqrt 3  - m}}{{1 - \sqrt 3 m}}} \right| $ 

 $ \Rightarrow \left| {\frac{{ - \sqrt 3  - m}}{{1 - \sqrt 3 m}}} \right| = \sqrt 3  $ 

 $ \Rightarrow  - \sqrt 3  - m = \sqrt 3  - 3m $ or\[ - \sqrt 3  - m =  - \sqrt 3  + 3m\]

 $ \Rightarrow m = \sqrt 3  $ or $ m = 0 $ 

Line passes through $ (3, - 2) $ . 

So, the equation of line is:  $ y + 2 = \sqrt 3 (x - 3) $  or  $ y + 2 = 0 $ 

 $ \Rightarrow \sqrt 3 x - y - 2 - 3\sqrt 3  = 0 $ and $ y + 2 = 0 $ 

Hence, the equations are  $ y + 2 = 0,{\text{ }}\sqrt 3 x - y - 2 - 3\sqrt 3  = 0 $ .

Correct Option: A

30. The equations of the lines passing through the point  $ (1,0) $  and at a distance  $ \frac{{\sqrt 3 }}{2} $  from the origin, are

(A)  $ \sqrt 3 x + y - \sqrt 3  = 0, \sqrt 3 x - y - \sqrt 3  = 0 $ 

(B)  $ \sqrt 3 x + y + \sqrt 3  = 0, \sqrt 3 x - y + \sqrt 3  = 0 $ 

(C)  $ x + \sqrt 3 y - 3 = 0, x - \sqrt 3 y - \sqrt 3  = 0 $ 

(D) None of these.

Ans: 

Given: Line passes through  $ (1,0) $ .

Let the slope of the required line be  $ m $ .

The equation of line passing through  $ (1,0) $  is: $ y - 0 = m(x - 1) $  i.e.  $ y - mx + m = 0 $ .

The distance of this line from  $ (0,0) $ is  $ \frac{{\sqrt 3 }}{2} $ .

 $ \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{|0 - 0 + m|}}{{\sqrt {1 + {m^2}} }} $ 

 $ \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{|m|}}{{\sqrt {1 + {m^2}} }} $ 

 $ \Rightarrow 3 + 3{m^2} = 4{m^2} $ 

 $ \Rightarrow {m^2} = 3 $ 

 $ \Rightarrow m =  \pm \sqrt 3  $ 

Hence, equations of lines are:  $ \sqrt 3 x + y - \sqrt 3  = 0 $ , $ \sqrt 3 x - y - \sqrt 3  = 0 $ .

Correct Option: A

31. The distance between the lines  $ y = mx + {c_1} $  and  $ y = mx + {c_2} $  is

(A)  $ \frac{{{c_1} - {c_2}}}{{\sqrt {{m^2} + 1} }} $ 

(B)  $ \frac{{\left| {{c_1} - {c_2}} \right|}}{{\sqrt {1 + {m^2}} }} $ 

(C)  $ \frac{{{c_2} - {c_1}}}{{\sqrt {1 + {m^2}} }} $ 

(D) 0

Ans: 

Given: $ y = mx + {c_1} $ and  $ y = mx + {c_2} $ .

Let  $ P\left( {{x_1},{y_1}} \right) $  be a point on $ y = mx + {c_1} $ .

The other line is:  $ y = mx + {c_2} $  i.e.  $ mx - y + {c_2} = 0 $ .

Distance of  $ P\left( {{x_1},{y_1}} \right) $  from this line is  $ d = \frac{{\left| {m{x_1} - {y_1} + {c_2}} \right|}}{{\sqrt {{m^2} + 1} }} $ .

 $ P\left( {{x_1},{y_1}} \right) $ lies on  $ y = mx + {c_1} $ ,

 $ \Rightarrow {y_1} = m{x_1} + {c_1} $ 

 $ \Rightarrow m{x_1} - {y_1} =  - {c_1} $ 

 $ \Rightarrow d = \frac{{\left| {{c_1} - {c_2}} \right|}}{{\sqrt {{m^2} + 1} }} $ 

Hence, distance is  $ \frac{{\left| {{c_1} - {c_2}} \right|}}{{\sqrt {{m^2} + 1} }} $ .

Correct Option: B

32. The coordinates of the foot of perpendicular from the point  $ (2,3) $  on the line  $ y = 3x + 4 $  is given by

(A)  $ \left( {\frac{{37}}{{10}},\frac{{ - 1}}{{10}}} \right) $ 

(B)  $ \left( { - \frac{1}{{10}},\frac{{37}}{{10}}} \right) $ 

(C)  $ \left( {\frac{{10}}{{37}}, - 10} \right) $ 

(D)  $ \left( {\frac{2}{3}, - \frac{1}{3}} \right) $ 

Ans: 

Given:  $ y = 3x + 4 $ and  $ (2,3) $ .

Let the foot of perpendicular from  $ P(2,3) $  on  $ 3x - y + 4 = 0 $  be $ M(h,k) $ .

 $ M(h,k) $ lies on  $ y = 3x + 4 $ .

 $ \Rightarrow 3h - k + 4 = 0{\text{              }}...(1) $ 

The slope of the given line is  $ 3 $  .

Slope of the line joining  $ P(2,3) $  and  $ M(h,k) $  is  $  - \frac{1}{3} = \frac{{k - 3}}{{h - 2}} $  or  $ h + 3k - 11 = 0{\text{             }}...{\text{(2)}} $ 

Solve  $ {\text{(1)}} $ and  $ {\text{(2)}} $ , 

 $ \Rightarrow (h,k) = \left( { - \frac{1}{{10}},\frac{{37}}{{10}}} \right) $ 

Hence, the coordinates of foot of perpendicular is  $ \left( { - \frac{1}{{10}},\frac{{37}}{{10}}} \right) $ .

Correct Option: B

33. If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is  $ (3,2) $ , then the equation of the line will be

(A)  $ 2x + 3y = 12 $ 

(B)  $ 3x + 2y = 12 $ 

(C)  $ 4x - 3y = 6 $ 

(D)  $ 5x - 2y = 10 $ 

Ans: 

Given: $ (3,2) $ 

As the middle point is  $ P(3,2) $ , the line meets the axes at  $ A(6,0) $  and  $ B(0,4) $ .

So, the equation of the line using intercept form is:  $ \frac{x}{6} + \frac{y}{4} = 1 $  i.e.  $ 2x + 3y = 12 $ .

Hence, the equation is  $ 2x + 3y = 12 $ . 

Correct Option: A

34. Equation of the line passing through  $ (1,2) $  and parallel to the line  $ y = 3x - 1 $  is

(A)  $ y + 2 = x + 1 $ 

(B)  $ y + 2 = 3(x + 1) $ 

(C)  $ y - 2 = 3(x - 1) $ 

(D)  $ y - 2 = x - 1 $ 

Ans: 

Given: $ (1,2) $ and  $ y = 3x - 1 $ .

The required line is parallel to $ y = 3x - 1 $ .

Thus, slope of the line is  $ 3 $ .

The line also passes through  $ (1,2) $ .

So, the equation of line is:  $ y - 2 = 3(x - 1) $ 

Hence, the equation is  $ y - 2 = 3(x - 1) $ . 

Correct Option: C

35.Equations of diagonals of the square formed by the lines  $ x = 0, y = 0, x = 1 $  and  $ y = 1 $  are

(A)  $ y = x, y + x = 1 $ 

(B)  $ y = x, x + y = 2 $ 

(C)  $ 2y = x, y + x = \frac{1}{3} $ 

(D)  $ y = 2x, y + 2x = 1 $ 

Ans: 

Given: $ x = 0,{\text{ }}y = 0,{\text{ }}x = 1 $ and  $ y = 1 $ .

Using the equations  $ x = 0,{\text{ }}y = 0,{\text{ }}x = 1 $ and  $ y = 1 $ , the vertices of square are  $ A(0,0),{\text{ }}B(1,0),{\text{ }}C(1,1),{\text{ }}D(0,1) $ .

The equation of  $ AC $  is:  $ y - 0 = \frac{{1 - 0}}{{1 - 0}}(x - 0) $  i.e.  $ x - y = 0 $ .

The equation of  $ BD $  is:  $ y - 0 = \frac{{1 - 0}}{{0 - 1}}(x - 1) $  i.e.  $ x + y - 1 = 0 $ .

Hence, the diagonals are $ y = x,{\text{ }}y + x = 1 $ .

Correct Option: A

36. For specifying a straight line, many geometrical parameters should be known?

(A)  $ 1 $ 

(B)  $ 2 $ 

(C)  $ 4 $ 

(D)  $ 3 $ 

Ans: 

Given: A straight line is specified.

The general equation of a linear equation in two variables is  $ ax + by + c = 0 $ 

At least one of  $ a $  and  $ b $  should be non-zero. 

Assume $ a \ne 0 $ . 

Then, the equation of the line is:  $ x + \frac{b}{a}y + \frac{c}{a} = 0 $ 

Hence, two parameters should be known.

Correct Option: B

37. The point  $ (4,1) $  undergoes the following two successive transformations:

(i) Reflection about the line  $ y = x $ 

(ii) Translation through a distance  $ 2 $  units along the positive  $ x -  $ axis. Then the final coordinates of the point are

(A)  $ (4,3) $ 

(B)  $ (3,4) $ 

(C)  $ (1,4) $ 

(D)  $ \left( {\frac{7}{2},\frac{7}{2}} \right) $ 

Ans: 

Given: $ (4,1) $  undergoes two successive transformations.

The reflection of  $ A(4,1) $  in  $ {\text{y}} = {\text{x}} $ is  $ B(1,4) $ .

Then, translation of  $ B $ through a distance  $ 2 $  units along the positive  $ x -  $ axis shifts  $ B $  to  $ C(1 + 2,4) $  i.e.  $ C(3,4) $ .

Hence, the final coordinates of point is  $ (3,4) $ .

Correct Option: B 

38. A point equidistant from the lines  $ 4x + 3y + 10 = 0, 5x - 12y + 26 = 0 $  and  $ 7x + 24y - 50 = 0 $  is

(A)  $ (1, - 1) $ 

(B)  $ (1,1) $ 

(C)  $ (0,0) $ 

(D)  $ (0,1) $ 

Ans: Given: $ 4x + 3y + 10 = 0,{\text{ }}5x - 12y + 26 = 0 $ and  $ 7x + 24y - 50 = 0 $ .

The distance of  $ (0,0) $  from  $ 4x + 3y + 10 = 0 $ is  $ \frac{{|0 + 0 + 10|}}{{\sqrt {{4^2} + {3^2}} }} = 2 $ .

The distance of  $ (0,0) $  from  $ 5x - 12y + 26 = 0 $ is  $ \frac{{|0 + 0 + 26|}}{{\sqrt {{5^2} + {{12}^2}} }} = 2 $ .

The distance of  $ (0,0) $  from  $ 7x + 24y - 50 = 0 $ is  $ \frac{{|0 + 0 - 50|}}{{\sqrt {{7^2} + {{24}^2}} }} = 2 $ .

The distance of all the three lines from  $ (0,0) $  is  $ 2 $ units.

Hence,  $ (0,0) $  is the required point.

Correct Option: C

39. A line passes through  $ (2,2) $  and is perpendicular to the line  $ 3x + y = 3 $ . Its  $ y -  $ intercept is

(A)  $ \frac{1}{3} $ 

(B)  $ \frac{2}{3} $ 

(C)  $ 1 $ 

(D)  $ \frac{4}{3} $ 

Ans:

Given: Line passes through  $ (2,2) $ .

The slope of  $ 3x + y = 3 $ is  $  - 3 $ .

So, slope of a line perpendicular to it $  = \frac{1}{3} $ .

The equation of the required line is:  $ y - 2 = \frac{1}{3}(x - 2) $  i.e.  $ x - 3y + 4 = 0 $ .

Put  $ x = 0 $  to find  $ y -  $ intercept.

 $ \Rightarrow 0 - 3y + 4 = 0 $ 

 $ \Rightarrow y = \frac{4}{3} $ which is the $ y -  $ intercept.

Hence, the $ y -  $ intercept is  $ \frac{4}{3} $ .

Correct Option: D

40. The ratio in which the line  $ 3x + 4y + 2 = 0 $  divides the distance between the lines  $ 3x + 4y + 5 = 0 $  and  $ 3x + 4y - 5 = 0 $  is

(A)  $ 1:2 $ 

(B)  $ 3:7 $ 

(C)  $ 2:3 $ 

(D)  $ 2:5 $ 

Ans: Given: $ 3x + 4y + 5 = 0 $ and  $ 3x + 4y - 5 = 0 $ .

Distance between  $ 3x + 4y + 5 = 0 $  and  $ 3x + 4y + 2 = 0 $  is  $ \frac{{|5 - 2|}}{{\sqrt {9 + 16} }} = \frac{3}{5} $ 

Distance between  $ 3x + 4y - 5 = 0 $  and  $ 3x + 4y + 2 = 0 $  is  $ \frac{{| - 5 - 2|}}{{\sqrt {9 + 16} }} = \frac{7}{5} $ 

Hence, the ratio is  $ \frac{3}{5}:\frac{7}{5} $  i.e.  $ 3:7 $ .

Correct Option: B

41. One vertex of the equilateral triangle with centroid at the origin and one side as  $ x + y - 2 = 0 $  is

(A)  $ ( - 1, - 1) $ 

(B)  $ (2,2) $ 

(C)  $ ( - 2, - 2) $ 

(D)  $ (2, - 2) $ 

Ans: Given: $ x + y - 2 = 0 $ 

Let  $ ABC $  be the equilateral triangle with vertex  $ A(h,k) $ .

The centroid is  $ G(0,0) $ .

Slope of line  $ BC $  i.e.  $ x + y - 2 = 0 $ is  $  - 1 $ .

As $ AG \bot BC $ ,

The slope of  $ AG $  is  $ \frac{k}{h} = 1 $ or  $ h = k $ .

The distance of  $ (0,0) $ from  $ BC = \frac{{|0 + 0 - 2|}}{{\sqrt {{1^2} + {1^2}} }} = \sqrt 2  $ .

Distance of  $ A $  from  $ BC = 3\sqrt 2  = \frac{{|h + k - 2|}}{{\sqrt {{1^2} + {1^2}} }} $ 

 $ \Rightarrow |h + k - 2| = 6 $ 

 $ \Rightarrow h + k - 8 = 0 $ or $ h + k + 4 = 0 $ 

 $ \Rightarrow h + h - 8 = 0 $ or $ h + h + 4 = 0 $ 

 $ \Rightarrow h = 4 $ or $ h =  - 2 $ 

Hence, the vertex is  $ ( - 2, - 2) $ 

Correct Option:C

42. If  $ a, b, c $  are in A.P., then the straight line  $ ax + by + c = 0 $  will always pass through.

Ans: Given: $ {\text{a, b, c}} $  are in A.P.

 $ {\text{a, b, c}} $ are in A.P.

So,  $ b = \frac{{a + c}}{2} $  i.e.  $ a - 2b + c = 0 $ 

Compare  $ a - 2b + c = 0 $  and line $ ax + by + c = 0 $ ,

 $ \Rightarrow x = 1,y =  - 2 $ 

Hence, the point  $ (1, - 2) $  lies on the line.

43. The line which cuts off equal intercept from the axes and pass through the point  $ (1, - 2) $  is

Ans: Given: $ (1, - 2) $ 

The line which cuts equal intercepts from the axes is  $ \frac{x}{a} + \frac{y}{a} = 1 $ .

As this line passes through  $ (1, - 2), $ 

 $ \Rightarrow 1 - 2 = a $ or  $ a =  - 1 $ .

Thus, the required equation of line is:  $ x + y =  - 1 $ 

 $ \Rightarrow x + y + 1 = 0 $ 

Hence, the equation is  $ x + y + 1 = 0 $ .

44. Equations of the lines through the point  $ (3,2) $  and making an angle of  $ 4{5^\circ } $  with the line  $ x - 2y = 3 $  are

Ans: Given: Line passes through  $ (3,2) $ .

Slope of  $ x - 2y = 3 $ is  $ \frac{1}{2} $ . 

Let the slope of the required line be  $ m $ .

 $ \Rightarrow \tan {45^\circ } = \left| {\frac{{m - \frac{1}{2}}}{{1 + \frac{1}{2}m}}} \right| $ 

 $ \Rightarrow 1 =  \pm \frac{{2m - 1}}{{2 + m}} $ 

 $ \Rightarrow 2m - 1 = 2 + m{\text{ or }}1 - 2m = 2 + m $ 

 $ \Rightarrow m = 3{\text{ or }}m =  - \frac{1}{3} $ 

The line also passes through $ (3,2) $ .

The equation of the line is:  $ y - 2 = 3(x - 3) $  or  $ y - 2 =  - \frac{1}{3}(x - 3) $ 

Hence, equations of lines are:  $ 3x - y - 7 = 0,{\text{  }}x + 3y - 9 = 0 $ .

45. The points  $ (3,4) $  and  $ (2, - 6) $  are situated on the  $ \_\_\_\_\_\_\_ $  of the line  $ 3x - 4y - 8 = 0 $ .

Ans: Given: $ (3,4) $ and  $ (2, - 6) $ .

Given line is  $ 3x - 4y - 8 = 0 $ .

For the point  $ (3,4): $  $ 3(3) - 4(4) - 8 =  - 15 < 0 $ 

For the point  $ (2, - 6): $  $ 3(2) - 4( - 6) - 8 = 22 > 0 $ 

Hence,  $ (3,4) $  and  $ (2, - 6) $  lie on opposite side of  $ 3x - 4y - 8 = 0 $ .

46. A point moves so that square of its distance from the point  $ (3, - 2) $  is numerically equal to its distance from the line  $ 5x - 12y = 3 $ . The equation of its locus is 

Ans: Given: $ (3, - 2) $ .

Let the moving point be  $ P(h,k) $ . 

Given point is  $ {\text{A}}(3, - 2) $ .

 $ \Rightarrow A{P^2} = {(h - 3)^2} + {(k + 2)^2} = d_1^2 $ 

The distance of  $ (h,k) $  from  $ 5x - 12y - 3 = 0 $  is:

 $ \Rightarrow {d_2} = \left| {\frac{{5h - 12k - 3}}{{\sqrt {25 + 144} }}} \right| $ 

 $ \Rightarrow {d_2} = \left| {\frac{{5h - 12k - 3}}{{13}}} \right| $ 

Given that,  $ d_1^2 = {d_2} $ 

 $ \Rightarrow {(h - 3)^2} + {(k + 2)^2} = \frac{{5h - 12k - 3}}{{13}}\quad  $ 

 $ \Rightarrow {h^2} - 6h + 9 + {k^2} + 4k + 4 = \frac{{5h - 12k - 3}}{{13}} $ 

 $ \Rightarrow 13{h^2} + 13{k^2} - 78h + 52k + 169 = 5h - 12k - 3 $ 

 $ \Rightarrow 13{h^2} + 13{k^2} - 83h + 64k + 172 = 0 $ 

Hence, locus is:  $ 13{x^2} + 13{y^2} - 83x + 64y + 172 = 0 $ 

47. Locus of the mid-points of the portion of the line  $ xsin\theta  + ycos\theta  = p $  intercepted between the axes is

Ans: Given: $ x\sin \theta  + y\cos \theta  = p $ .

 $ x\sin \theta  + y\cos \theta  = p $ meets axes at points $ A\left( {\frac{p}{{\sin \theta }},0} \right) $  and  $ B\left( {0,\frac{p}{{\cos \theta }}} \right) $ .

Let  $ P(h,k) $  be the mid-point of  $ AB. $ 

 $ \Rightarrow h = \frac{p}{{2\sin \theta }} $ and $ k = \frac{p}{{2\cos \theta }} $ 

 $ \Rightarrow \sin \theta  = \frac{p}{{2h}} $ and $ \cos \theta  = \frac{p}{{2k}} $ 

By squaring and adding,

 $ \Rightarrow {\sin ^2}\theta  + {\cos ^2}\theta  = \frac{{{p^2}}}{{4{h^2}}} + \frac{{{p^2}}}{{4{k^2}}} $ 

 $ \Rightarrow 1 = \frac{{{p^2}}}{{4{x^2}}} + \frac{{{p^2}}}{{4{y^2}}} $ 

 $ \Rightarrow 4{x^2}{y^2} = {p^2}\left( {{x^2} + {y^2}} \right) $ 

Hence, the locus is  $ 4{x^2}{y^2} = {p^2}\left( {{x^2} + {y^2}} \right) $ .

State whether the Statements in Exercises  $ 48 $  to  $ 56 $  True or False? Justify.

48. If the vertices of a triangle have integral coordinates, then the triangle cannot be equilateral.

Ans:The given statement is true.

Let us assume an equilateral triangle with vertices  $ A\left( {{x_1},{\text{ }}{y_1}} \right) $ ,  $ B\left( {{x_2},{\text{ }}{y_2}} \right) $  and  $ C\left( {{x_3},{\text{ }}{y_3}} \right) $ . All the angles of an equilateral triangle are  $ {60^ \circ } $ . Assuming the slope of line  $ AB $  as  $ {m_1} $  and the slope of line  $ BC $ as  $ {m_2} $ .

 $ \Rightarrow \tan {60^ \circ } = \left| {\frac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right| $ 

 $ \Rightarrow \sqrt 3  = \left| {\frac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right| $                       ……  $ \left( 1 \right) $ 

Here  $ {m_1} = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ and  $ {m_2} = \frac{{{y_3} - {y_2}}}{{{x_3} - {x_2}}} $ . Since all the coordinates are integers so  $ {m_1} $  and  $ {m_2} $  are rational numbers.

Therefore, in expression  $ \left( 1 \right) $ , the R.H.S is a rational number and the L.H.S is an irrational number. This results in rational number  $  =  $  irrational numbers which are not possible.

49. The points  $ A\left( { - 2, 1} \right) $ ,  $ B\left( {0, 5} \right) $  and  $ C\left( { - 1, 2} \right) $  are collinear.

Ans: The given statement is false.

Using the distance formula, the length  $ AB $ 

$ = \sqrt {{{\left( {0 - \left( { - 2} \right)} \right)}^2} + {{\left( {5 - 1} \right)}^2}}  $ 

$ = \sqrt {4 + 16}  $ 

$ = 2\sqrt 5 {\text{ units}} $  

Similarly, the length  $ BC $ 

$ = \sqrt {{{\left( { - 1 - 0} \right)}^2} + {{\left( {2 - 5} \right)}^2}}  $ 

$ = \sqrt {1 + 9}  $ 

$ = \sqrt {10} {\text{ units}} $  

And, the length  $ AC $ 

$ = \sqrt {{{\left( { - 2 - \left( { - 1} \right)} \right)}^2} + {{\left( {1 - 2} \right)}^2}}  $ 

$ = \sqrt {1 + 1}  $ 

$ = \sqrt 2 {\text{ units}} $  

Clearly the sum of any two line segments is not equal to the third one in any case, so the points are not collinear.

50. Equation of the line passing through the point  $ \left( {aco{s^3}\theta , asi{n^3}\theta } \right) $  and perpendicular to the line  $ xsec\theta  + ycosec\theta  = a $ is  $ xcos\theta  - ysin\theta  = asin2\theta  $ .

Ans:The given statement is false.

The slope of the given line  $ x\sec \theta  + y\cos {\text{ec}}\theta  = a $  is,

$ \Rightarrow {m_1} =  - \frac{{\sec \theta }}{{\cos {\text{ec}}\theta }} $ 

$ \Rightarrow {m_1} =  - \frac{{\left( {\frac{1}{{\cos \theta }}} \right)}}{{\left( {\frac{1}{{\sin \theta }}} \right)}} $ 

$ \Rightarrow {m_1} =  - \left( {\frac{{\sin \theta }}{{\cos \theta }}} \right) $  

Therefore, the slope of the required line which is perpendicular to the given line is,

$ \Rightarrow {m_2} = \frac{{ - 1}}{{{m_1}}} $ 

$ \Rightarrow {m_2} = \frac{{ - 1}}{{ - \left( {\frac{{\sin \theta }}{{\cos \theta }}} \right)}} $  

$ \Rightarrow {m_2} = \frac{{\cos \theta }}{{\sin \theta }} $  

So the equation of the line passing through the point  $ \left( {a{{\cos }^3}\theta ,{\text{ }}a{{\sin }^3}\theta } \right) $  and having slope  $ {m_2} $  is,

$ \Rightarrow \left( {y - a{{\sin }^3}\theta } \right) = {m_2}\left( {x - a{{\cos }^3}\theta } \right) $ 

$ \Rightarrow \left( {y - a{{\sin }^3}\theta } \right) = \frac{{\cos \theta }}{{\sin \theta }}\left( {x - a{{\cos }^3}\theta } \right) $ 

$ \Rightarrow \sin \theta \left( {y - a{{\sin }^3}\theta } \right) = \cos \theta \left( {x - a{{\cos }^3}\theta } \right) $ 

$ \Rightarrow x\cos \theta  - y\sin \theta  = a{\cos ^4}\theta  - a{\sin ^4}\theta  $  

Using the algebraic identity  $ {m^2} - {n^2} = \left( {m + n} \right)\left( {m - n} \right) $  and the trigonometric identity  $ {\sin ^2}\theta  + {\cos ^2}\theta  = 1 $ ,

$ \Rightarrow x\cos \theta  - y\sin \theta  = a\left( {{{\cos }^2}\theta  - {{\sin }^2}\theta } \right)\left( {{{\cos }^2}\theta  + {{\sin }^2}\theta } \right) $ 

$ \Rightarrow x\cos \theta  - y\sin \theta  = a\left( {{{\cos }^2}\theta  - {{\sin }^2}\theta } \right) $  

Using the identity  $ {\cos ^2}\theta  - {\sin ^2}\theta  = \cos 2\theta  $ ,

$ \Rightarrow x\cos \theta  - y\sin \theta  = a\cos 2\theta  $ 

51. The straight line  $ 5x + 4y = 0 $  passes through the point of intersection of the straight lines  $ x + 2y - 10 = 0 $ and  $ 2x + y + 5 = 0 $ .

Ans: The given statement is true.

The intersection of the lines  $ x + 2y - 10 = 0 $  and  $ 2x + y + 5 = 0 $  is their solution coordinates. Solving the two equations algebraically gives,

$ x = \left( { - \frac{{20}}{3}} \right) $ and  $ y = \left( {\frac{{25}}{3}} \right) $ , so the solution coordinate is  $ \left( {\; - \frac{{20}}{3},{\text{ }}\frac{{25}}{3}} \right) $ .

Now, if the line  $ 5x + 4y = 0 $  passes through the above coordinates then it must satisfy the point. On substitution,

$ \Rightarrow 5 \times \left( { - \frac{{20}}{3}} \right) + 4 \times \left( {\frac{{25}}{3}} \right) = 0 $ 

$ \Rightarrow \left( { - \frac{{100}}{3}} \right) + \left( {\frac{{100}}{3}} \right) = 0 $ 

$ \Rightarrow 0 = 0 $  

Hence, the point satisfies the line.

52. The vertex of an equilateral triangle is  $ \left( {2, 3} \right) $  and the equation of the opposite side is  $ x + y = 2 $ . Then the other two sides are  $ y - 3 = \left( {2 \pm \sqrt 3 } \right)\left( {x - 2} \right) $ .

Ans: The given statement is true.

Let us assume the slope of one of the remaining two sides as  $ m $ . The slope of the given line  $ x + y = 2 $ is  $  - 1 $ . If  $ {m_1} $  and  $ {m_2} $  are slopes of two line segments then the angle  $ \left( \theta  \right) $  between them is given as  $ \tan \theta  = \left| {\frac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right| $ .

The angle between any two sides of an equilateral triangle is  $ {60^ \circ } $ ,

$ \Rightarrow \tan {60^ \circ } = \left| {\frac{{ - 1 - m}}{{1 + \left( { - 1} \right) \times m}}} \right| $ 

$ \Rightarrow \sqrt 3  = \left| {\frac{{ - \left( {1 + m} \right)}}{{1 - m}}} \right| $ 

$ \Rightarrow \sqrt 3  = \left| {\frac{{1 + m}}{{1 - m}}} \right| $  

Removing the modulus sign,

 $ \Rightarrow  \pm {\text{ }}\sqrt 3  = \left( {\frac{{1 + m}}{{1 - m}}} \right) $ 

1. Considering the positive sign,

\[ \Rightarrow \sqrt 3  = \left( {\frac{{1 + m}}{{1 - m}}} \right)\]

\[ \Rightarrow m = \left( {\frac{{\sqrt 3  - 1}}{{\sqrt 3  + 1}}} \right)\]

\[ \Rightarrow m = \left( {2 - \sqrt 3 } \right)\] (By rationalization)

2. Considering the negative sign,

$ \Rightarrow  - \left( {\sqrt 3 } \right) = \left( {\frac{{1 + m}}{{1 - m}}} \right) $ 

$ \Rightarrow m = \left( {\frac{{\sqrt 3  + 1}}{{\sqrt 3  - 1}}} \right) $  

\[ \Rightarrow m = \left( {2 + \sqrt 3 } \right)\] (By rationalization)

Hence, there are two values of  $ m $  for the two remaining sides of the triangle. Both the sides will pass through the point  $ \left( {2,{\text{ }}3} \right) $ . So, equation of the other two sides are  $ \left( {y - 3} \right) = \left( {2 \pm \sqrt 3 } \right)\left( {x - 2} \right) $ .

53. The equation of the line joining the point  $ \left( {3, 5} \right) $  to the point of intersection of the lines  $ 4x + y - 1 = 0 $  and  $ 7x - 3y - 35 = 0 $  is equidistant from the points  $ \left( {0, 0} \right) $ and  $ \left( {8, 34} \right) $ .

Ans: The given statement is true.

Solving the equations  $ 4x + y - 1 = 0 $  and  $ 7x - 3y - 35 = 0 $  algebraically gives  $ x = 2 $ and  $ y =  - 7 $ . So the point of intersection is  $ \left( {2,{\text{ }} - 7} \right) $ .

The equation of the line passing through the points \[\left( {3,{\text{ }}5} \right)\] and  $ \left( {2,{\text{ }} - 7} \right) $  is,

$ \Rightarrow \left( {y - 5} \right) = \left( {\frac{{ - 7 - 5}}{{2 - 3}}} \right)\left( {x - 3} \right) $ 

$ \Rightarrow \left( {y - 5} \right) = \left( {12} \right)\left( {x - 3} \right) $ 

$ \Rightarrow 12x - y - 31 = 0 $  

Now, the distance of the point  $ \left( {0,{\text{ }}0} \right) $  from the line  $ 12x - y - 31 = 0 $ ,

$ = \left| {\frac{{\left( {0 \times 12} \right) + \left( {0 \times \left( { - 1} \right)} \right) - 31}}{{\sqrt {{{12}^2} + {{\left( { - 1} \right)}^2}} }}} \right| $ 

$ = \frac{{31}}{{\sqrt {145} }} $  

Similarly, the distance of the point  $ \left( {8,{\text{ }}34} \right) $  from the line  $ 12x - y - 31 = 0 $ ,

$ = \left| {\frac{{\left( {8 \times 12} \right) + \left( {34 \times \left( { - 1} \right)} \right) - 31}}{{\sqrt {{{12}^2} + {{\left( { - 1} \right)}^2}} }}} \right| $ 

$ = \frac{{31}}{{\sqrt {145} }} $  

Hence, the points are equidistant from the required line.

54. The lines  $ \frac{x}{a} + \frac{y}{b} = 1 $  moves in such a ways that  $ \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} = \frac{1}{{{c^2}}} $ , where  $ c $  is a constant. The locus of the foot of the perpendicular from the origin on the given line is  $ {x^2} + {y^2} = {c^2} $ .

Ans: The given statement is true.

Let the coordinates of the foot of perpendicular drawn from the origin $(0,0)$ is $(x, y)$.

The given line is $\frac{x}{a}+\frac{y}{b}=1$ which can be written as $\frac{x}{a}+\frac{y}{b}-1=0$.

The foot of perpendicular is given as,

$\Rightarrow \frac{(x-0)}{\left(\frac{1}{a}\right)}=\frac{(y=0)}{\left(\frac{1}{b}\right)}=\frac{\left(\frac{1}{a} \times 0\right)+\left(\frac{1}{b} \times 0\right)-1}{\left(\frac{1}{a}\right)^{2}+\left(\frac{1}{b}\right)^{2}}$

$\Rightarrow a x=b y=\frac{-1}{\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}\right)}$

Using the given relation $\frac{1}{a^{2}}+\frac{1}{b^{2}}=\frac{1}{c^{2}}$,

$\Rightarrow a x=b y=\frac{-1}{\left(\frac{1}{c^{2}}\right)}$

$\Rightarrow a x=b y=\left(-c^{2}\right)$

Equating the relations $a x=\left(-c^{2}\right)$ and $b y=\left(-c^{2}\right)$ gives

$x=\left(\frac{-c^{2}}{a}\right)$

and $y=\left(\frac{-c^{2}}{b}\right)$, respectively.

On squaring and adding,

$\Rightarrow x^{2}+y^{2}=\left(\frac{c^{4}}{a^{2}}\right)+\left(\frac{c^{4}}{b^{2}}\right)$

$\Rightarrow x^{2}+y^{2}=c^{4}\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}\right)$

$\Rightarrow x^{2}+y^{2}=c^{4}\left(\frac{1}{c^{2}}\right)$

$\Rightarrow x^{2}+y^{2}=c^{2}$

55. The lines ax + 2y + 1 = 0 , bx + 3y + 1 = 0  and cx + 4y + 1 = 0  are concurrent if a, b  and c  are in G.P.

Ans: The given statement is false.

The given lines can be written are $a x+2 y+1=0$, $b x+3 y+1=0$ and $c x+4 y+1=0$. For these to be concurrent it must satisfy the determinant relation,

$\Rightarrow\left|\begin{array}{lll}

a & 2 & 1 \\

b & 3 & 1 \\

c & 4 & 1

\end{array}\right|=0$

Performing the row operations $R_{2} \rightarrow R_{2}-R_{1}$ and $R_{3} \rightarrow R_{3}-R_{1}$,

$\Rightarrow\left|\begin{array}{ccc}

a & 2 & 1 \\

b-a & 1 & 0 \\

c-a & 2 & 0

\end{array}\right|=0$

Expanding the determinant along $C_{3}$,

$\Rightarrow 2(b-a)-(c-a)=0$

$\Rightarrow 2 b-a-c=0$

$\Rightarrow a+c=2 b$

Therefore, for the lines to be concurrent $\mathrm{a}, \mathrm{b}$ and $\mathrm{c}$ must be in A.P.

56. Line joining the points  $ \left( {3,  - 4} \right) $  and  $ \left( { - 2, 6} \right) $  is perpendicular to the line joining the points  $ \left( { - 3, 6} \right) $ and  $ \left( {9,  - 18} \right) $ .

Ans: The given statement is false.

The line joining the points  $ \left( {3,{\text{ }} - 4} \right) $  and  $ \left( { - 2,{\text{ }}6} \right) $  is,

$ \Rightarrow \left( {y - 6} \right) = \left( {\frac{{6 - \left( { - 4} \right)}}{{ - 2 - 3}}} \right)\left( {x - \left( { - 2} \right)} \right) $ 

$ \Rightarrow \left( {y - 6} \right) = \left( { - 2} \right)\left( {x + 2} \right) $ 

$ \Rightarrow y =  - 2x + 2 $   $ \left( {9,{\text{ }} - 18} \right) $ 

The slope of this line is  $  - 2 $ .

Similarly, the line joining the points  $ \left( { - 3,{\text{ }}6} \right) $  and  is,

$ \Rightarrow \left( {y - 6} \right) = \left( {\frac{{6 - \left( { - 18} \right)}}{{ - 3 - 9}}} \right)\left( {x - \left( { - 3} \right)} \right) $ 

$ \Rightarrow \left( {y - 6} \right) = \left( { - 2} \right)\left( {x + 3} \right) $ 

$ \Rightarrow y =  - 2x $  

The slope of this line is also  $  - 2 $ .

For the two lines to be perpendicular the product of their slopes must be  $  - 1 $ , but here the product is  $ \left( { - 2} \right) \times \left( { - 2} \right) = 4 $ .

Match the questions given under Column  $ {C_1} $  with their appropriate answers given under the column  $ {C_2} $  in Exercises  $ 57 $ to  $ 59 $ .

57.

Ans:

(a) Let one of the required point is  $ \left( {a,{\text{ }}b} \right) $ . Since it lies on the line  $ x + 5y = 13 $ , so it will satisfy the line.

 $ \Rightarrow a + 5b = 13 $                       ……  $ \left( 1 \right) $ 

The distance of the point  $ \left( {a,{\text{ }}b} \right) $  from the line  $ 12x - 5y + 26 = 0 $  is  $ 2 $  units,

$ \Rightarrow \left| {\frac{{\left( {12 \times a} \right) + \left( {\left( { - 5} \right) \times b} \right) + 26}}{{\sqrt {{{\left( {12} \right)}^2} + {{\left( { - 5} \right)}^2}} }}} \right| = 2 $ 

$ \Rightarrow \left| {12a - 5b + 26} \right| = 26 $ 

$ \Rightarrow \left( {12a - 5b + 26} \right) =  \pm {\text{ }}26 $  

Considering the positive sign and solving equation  $ \left( 1 \right) $  and  $ \left( {12a - 5b + 26} \right) = 26 $  gives the point  $ \left( {a,{\text{ }}b} \right) = \left( {1,{\text{ }}\frac{{12}}{5}} \right) $ .

Considering the negative sign and solving equation  $ \left( 1 \right) $  and  $ \left( {12a - 5b + 26} \right) =  - 26 $  gives the point  $ \left( {a,{\text{ }}b} \right) = \left( { - 3,{\text{ }}\frac{{16}}{5}} \right) $ .

(b) Let one of the required point is  $ \left( {c,{\text{ }}d} \right) $ . Since it lies on the line  $ x + y = 4 $ , so it will satisfy the line.

 $ \Rightarrow c + d = 4 $                       ……  $ \left( 1 \right) $ 

The distance of the point  $ \left( {c,{\text{ }}d} \right) $  from the line  $ 4x + 3y - 10 = 0 $  is  $ 1 $  unit,

$ \Rightarrow \left| {\frac{{\left( {4 \times c} \right) + \left( {3 \times d} \right) - 10}}{{\sqrt {{{\left( 4 \right)}^2} + {{\left( 3 \right)}^2}} }}} \right| = 1 $ 

$ \Rightarrow \left| {4c + 3d - 10} \right| = 5 $ 

$ \Rightarrow \left( {4c + 3d - 10} \right) =  \pm {\text{ }}5 $  

Considering the positive sign and solving equation  $ \left( 1 \right) $  and  $ \left( {4c + 3d - 10} \right) = 5 $  gives the point  $ \left( {c,{\text{ }}d} \right) = \left( {3,{\text{ }}1} \right) $ .

Considering the negative sign and solving equation  $ \left( 1 \right) $  and  $ \left( {4c + 3d - 10} \right) =  - 5 $  gives the point  $ \left( {c,{\text{ }}d} \right) = \left( { - 7,{\text{ }}11} \right) $ .

(c) Here the points  $ P $  and  $ Q $  trisect the line  $ AB $ . Let the points be  $ P\left( {{x_1},{\text{ }}{y_1}} \right) $ and  $ Q\left( {{x_2},{\text{ }}{y_2}} \right) $ .

For point  $ P $ ,  $ AP:PB = m:n = 1:2 $ . The section formula states that if a point  $ \left( {x,y} \right) $  divides a line segments joining the two points  $ \left( {{x_1},{y_2}} \right) $  and  $ \left( {{x_2},{y_2}} \right) $  in the ratio  $ m:n $  then,

$ \left( {x,{\text{ }}y} \right) = \left( {\frac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\frac{{m{y_2} + n{y_1}}}{{m + n}}} \right) $ 

Using this formula for the points  $ A $ ,  $ P $  and  $ B $ ,

$ \Rightarrow \left( {{x_1},{\text{ }}{y_1}} \right) = \left( {\frac{{\left( {3 \times 1} \right) + \left( {2 \times \left( { - 2} \right)} \right)}}{{1 + 2}},{\text{ }}\frac{{\left( {1 \times 1} \right) + \left( {5 \times 2} \right)}}{{1 + 2}}} \right) $ 

$ \Rightarrow \left( {{x_1},{\text{ }}{y_1}} \right) = \left( { - \frac{1}{3},{\text{ }}\frac{{11}}{3}} \right) $  

Now,  $ P $  is the midpoint of  $ AQ $ . The midpoint formula is a special case of the section formula with  $ m:n = 1:1 $ .

Using the midpoint formula for  $ A $ ,  $ P $  and  $ Q $ , $ \Rightarrow \left( { - \frac{1}{3},{\text{ }}\frac{{11}}{3}} \right) = \left( {\frac{{ - 2 + {x_2}}}{2},{\text{ }}\frac{{5 + {y_2}}}{2}} \right) $ 

Solving for the coordinates of  $ Q $  by comparison gives  $ \left( {{x_2},{\text{ }}{y_2}} \right) = \left( {\frac{4}{3},{\text{ }}\frac{7}{3}} \right) $ .

Hence, the correct match is (a) – (iii), (b) – (i), (c) – (ii).

58. The value of the  $ \lambda  $ , if the lines  $ \left( {2x + 3y + 4} \right) + \lambda \left( {6x - y + 12} \right) = 0 $  are

Ans: Simplifying the line  $ \left( {2x + 3y + 4} \right) + \lambda \left( {6x - y + 12} \right) = 0 $ 

gives  $ \left( {2 + 6\lambda } \right)x + \left( {3 - \lambda } \right)y + \left( {4 + 12\lambda } \right) = 0 $ .

(a) For the line  $ \left( {2 + 6\lambda } \right)x + \left( {3 - \lambda } \right)y + \left( {4 + 12\lambda } \right) = 0 $  to be parallel to the  $ y -  $  axis, the coefficient of  $ y -  $  coordinate must be  $ 0 $ .

$ \Rightarrow \left( {3 - \lambda } \right) = 0 $ 

$ \Rightarrow \lambda  = 3 $  

(b) The slope of the line  $ 7x + y - 4 = 0 $ is  $  - 7 $ , therefore the slope of the line  $ \left( {2 + 6\lambda } \right)x + \left( {3 - \lambda } \right)y + \left( {4 + 12\lambda } \right) = 0 $  must be  $ \frac{1}{7} $  so that the two lines are perpendicular.

$ \Rightarrow  - \frac{{\left( {2 + 6\lambda } \right)}}{{\left( {3 - \lambda } \right)}} = \frac{1}{7} $ 

$ \Rightarrow  - 14 - 42\lambda  = 3 - \lambda  $ 

$ \Rightarrow \lambda  =  - \frac{{17}}{{41}} $  

(c) If the point  $ \left( {1,{\text{ }}2} \right) $  passes through the line  $ \left( {2 + 6\lambda } \right)x + \left( {3 - \lambda } \right)y + \left( {4 + 12\lambda } \right) = 0 $  then it must satisfy the equation. On substitution,

$ \Rightarrow \left( {2 + 6\lambda } \right) + \left( {6 - 2\lambda } \right) + \left( {4 + 12\lambda } \right) = 0 $ 

$ \Rightarrow 16\lambda  =  - 12 $ 

$ \Rightarrow \lambda  =  - \frac{3}{4} $  

(d) For the line  $ \left( {2 + 6\lambda } \right)x + \left( {3 - \lambda } \right)y + \left( {4 + 12\lambda } \right) = 0 $  to be parallel to the  $ x -  $  axis, the coefficient of  $ x -  $  coordinate must be  $ 0 $ .

$ \Rightarrow \left( {2 + 6\lambda } \right) = 0 $ 

$ \Rightarrow \lambda  =  - \frac{1}{3} $  

Hence, the correct match is (a) – (iv), (b) – (iii), (c) – (i), (d) – (ii).

59. The equation of the line through the intersection of the lines  $ 2x - 3y = 0 $  and  $ 4x - 5y = 2 $  and

Ans: The point of intersection of the lines  $ 2x - 3y = 0 $  and  $ 4x - 5y = 2 $  is obtained by solving the equations algebraically. So the intersection point is  $ \left( {3,{\text{ }}2} \right) $ .

(a) The equation of the line passing through the points  $ \left( {2,{\text{ }}1} \right) $  and  $ \left( {3,{\text{ }}2} \right) $  is,

$ \Rightarrow \left( {y - 1} \right) = \left( {\frac{{2 - 1}}{{3 - 2}}} \right)\left( {x - 2} \right) $ 

$ \Rightarrow \left( {y - 1} \right) = \left( {x - 2} \right) $ 

$ \Rightarrow x - y - 1 = 0 $  

(b) The slope of the line  $ x + 2y + 1 = 0 $ is  $ \left( { - \frac{1}{2}} \right) $ , so the slope of the line perpendicular to this line will be  $ 2 $ . Now, the line passes through the point  $ \left( {3,{\text{ }}2} \right) $  so its equation is,

$ \Rightarrow \left( {y - 2} \right) = 2\left( {x - 3} \right) $ 

$ \Rightarrow \left( {y - 2} \right) = \left( {2x - 6} \right) $ 

$ \Rightarrow 2x - y = 4 $  

(c) The slope of the line  $ 3x - 4y + 5 = 0 $ is  $ \left( {\frac{3}{4}} \right) $ , so the slope of the line parallel to this line will also be  $ \left( {\frac{3}{4}} \right) $ . Now, the line passes through the point  $ \left( {3,{\text{ }}2} \right) $  so its equation is,

$ \Rightarrow \left( {y - 2} \right) = \left( {\frac{3}{4}} \right)\left( {x - 3} \right) $ 

$ \Rightarrow \left( {4y - 8} \right) = \left( {3x - 9} \right) $ 

$ \Rightarrow 3x - 4y - 1 = 0 $  

(d) The lines which are equally inclined to the axes have their slope values equal to  $ \tan {45^ \circ } = 1 $ or  $ \tan {135^ \circ } =  - 1 $ . Now, , the line passes through the point  $ \left( {3,{\text{ }}2} \right) $  so its equation is,

Considering the positive slope,

$ \Rightarrow \left( {y - 2} \right) = \left( 1 \right)\left( {x - 3} \right) $ 

$ \Rightarrow x - y - 1 = 0 $  

Considering the negative slope,

$ \Rightarrow \left( {y - 2} \right) = \left( { - 1} \right)\left( {x - 3} \right) $ 

$ \Rightarrow x + y - 5 = 0 $  

Hence, the correct match is (a) – (iii), (b) – (i), (c) – (iv), (d) – (ii) or (iii).

About the Chapter

A straight line is defined as a combination of an infinite number of points joined at both ends of a point. In other words,  it is an endless one-dimensional figure that does not have any curve but the ends can extend up to infinity. A straight line can be horizontal, vertical and slanted and have equations associated with the same. Any straight line, on a plane, will always be measured at 180° for an angle drawn between two points on the same straight line. A straight line can also be called the shortest distance between two points and is represented on the graph as A(x1, y1) and B(x2, y2). There are three kinds of straight lines:

1. A Horizontal Line is parallel to the x-axis and perpendicular to the y axis. The angle formed is 0° or 180° with the x-axis and 90° or 270° with the y axis on the graph.

2. A Vertical Line is parallel to the y axis and perpendicular to the x-axis. The angle formed is 90° or 270° with the x-axis and 0° or 180° with the y axis on the graph.

3. A Slanted Line can form any angle other than 0°, 90°, 180°, 270° and 360° with the horizontal and vertical lines on the graph. 

Other details like equations of the slopes formed by the straight lines, equations of lines parallel to the x-axis or y-axis, various forms of the equation of a line, etc., have also been dealt with.

NCERT Exemplar for Class 11 Maths Chapter 10 - Straight Lines is divided into different sections from 10.1 to 10.1.8. Section 10.2 deals with examples on the different topics of straight lines and Section 10.3 comprises exercises/question bank.