Conic Sections Class 10 Notes CBSE Maths Chapter 10 (Free PDF Download)

Section–A (1 Mark Questions)

1. The equation of circle, which passes through origin and has centre at (–1, 4) is ________.

Ans.  We know that,

Equation of circle with centre (h, k) and passes through the origin is

$(x-h)^{2}+(y-k)^{2}=h^{2}+k^{2}$

Thus, the equation of required circle with centre (-1, 4) is-

$(x+1)^{2}+(y-4)^{2}=(-1)^{2}+4^{2}$

$\Rightarrow x^{2}+2x+1+y^{2}-8y+16=1+16$

$\Rightarrow x^{2}+y^{2}+2x-8y=0$

2. For parabola y2=-16x, find the equation of directrix.

Ans. Given: Equation of parabola: y2=-16x 

Since the given parabola is of the form y2=-4ax 

Thus, on comparison we get,

16=4a

$\Rightarrow$ a=4

Therefore,

Equation of directrix: x = a i.e., x = 4.

3. For the ellipse $\frac{x^{2}}{81}+\frac{y^{2}}{9}=1$, find the coordinates of end points of major axis.

Ans. Equation of ellipse: 

$\frac{x^{2}}{81}+\frac{y^{2}}{9}=1$

Since denominator of x2  > denominator of y2

$\therefore$ major axis: x-axis and minor axis: y-axis.

$\therefore$ On comparing the given equation with $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$  

We get, a = 9 and b = 3

Thus, Coordinates of end points of major axis are $(\pm a,0)$ i.e., $(\pm 9,0)$ 

4. For the hyperbola $\frac{y^{2}}{16}-\frac{x^{2}}{4}=1$, find the length o transverse axis.

Ans. Equation of hyperbola: $\frac{y^{2}}{16}-\frac{x^{2}}{4}=1$ 

Since the given hyperbola is of the form \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 

Thus, on comparison we get, a = 4 and b = 2

Therefore, 

Length of transverse axis $=2a=2\times=8$.

5. Find the equation of parabola with vertex (0, 0) and focus (0, -7)

Ans. Since the vertex is at (0, 0) and focus is at (0, –7), i.e., on y -axis

Thus,  y - axis is the axis of parabola.

Hence, the equation of the parabola is of the form $x^{2}=-4ay$ with a = 7.

Therefore, equation of parabola is given by

$x^{2}=-4ay=-4(7)y$

$\Rightarrow x^{2}=-28y$

Section–B (2 Marks Questions)

6. Find the equation of the circle which touches the y-axis and centre (2, 4).

Ans. Since, the circle is touching y-axis. 

The length CP is equal to the radius of the circle. 

Thus, Radius = CP = 2.

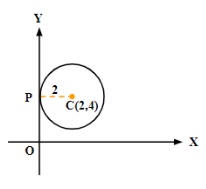
Hence, the equation of the required circle is

$(x-2)^{2}+(y-4)^{2}=2^{2}$

$\Rightarrow x^{2}-4x+4+y^{2}-8y+16=4$

$\Rightarrow x^{2}+y^{2}-4x-8y+16=0$

7. Find the length of latus rectum of the hyperbola $\frac{y^2}{12}-\frac{x^2}{4}=1$.

Ans. Equation of hyperbola: $\frac{y^2}{12}-\frac{x^2}{4}=1$

Since, the given hyperbola is of the form

$$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$$

Thus, on comparison we get,

$$b^2=4, a^2=12 \Rightarrow a=\sqrt{12}$$

Therefore, Length of latus rectum

$$=\frac{2 b^2}{a}=\frac{2 \times 4}{\sqrt{12}}=\frac{4}{\sqrt{3}}$$

8. Find the coordinates of the foci a of the hyperbola $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Ans. Equation of hyperbola: $\frac{x^2}{16}-\frac{y^2}{9}=1$

On comparing with standard equation of hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,

We obtain $a=4$ and $b=3$.

Now, we know that,

$$\begin{aligned}& b^2=c^2-a^2 \\& \Rightarrow c^2=a^2+b^2 \\& \Rightarrow c^2=4^2+3^2=25 \\& \Rightarrow c=5\end{aligned}$$

Thus,Coordinates of foci are $( \pm c, 0)$ i.e., $( \pm 5,0)$

9.Find the equation of the circle which touches the lines x = 0, y = 0 and x = -6.

Ans. Since, the circle is touching the lines $x=0, y=0$ and $x=-6$.

Thus, two such circles are possible

$C_1:(-3,3)$ and $r_1=3$

$C_2:(-3,-3)$ and $r_2=3$

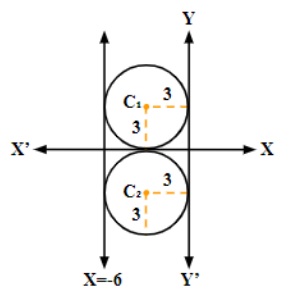
Thus, the equation of circles is-

$$\begin{aligned}& (x+3)^2+(y \pm 3)^2=(3)^2 \\& \Rightarrow x^2+y^2+6 x \pm 6 y+9=0\end{aligned}$$

10.Find the equation of a circle with centre (1, 3) and passes through the point (-1, -3).

Ans. Centre of the circle $(h, k)=(1,3)$.

Since the circle passes through point $(-1,-3)$.

The radius $(r)$ of the circle is the distance between the points $(1,3)$ and $(-1,-3)$.

$\Rightarrow r=\sqrt{(1-(-1))^2+(3-(-3))^2}$

$=\sqrt{(2)^2+(6)^2}=\sqrt{4+36}=\sqrt{40}=2 \sqrt{10}$

Thus, the equation of the circle is given by-

$$\begin{aligned}& (x-1)^2+(y-3)^2=(2 \sqrt{10})^2 \\& \Rightarrow x^2-2 x+1+y^2-6 y+9=40 \\& \Rightarrow x^2+y^2-2 x-6 y-30=0\end{aligned}$$

11. Find the equation of the circle, when the coordinates of end point of diameter is given by (1, 1) and (3, 3).

Ans. We know that equation of the circle with diametric points $\left(x_1, y_1\right)$ and $\left(x_2, y_2\right)$ is given as $\left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0$

Thus, when the coordinates of end points of diameter are $(1,1)$ and $(3,3)$.

Equation of circle:

$$\begin{aligned}& (x-1)(x-3)+(y-1)(y-3)=0 \\& \Rightarrow x^2-4 x+3+y^2-4 y+3=0 \\& \Rightarrow x^2+y^2-4 x-4 y+6=0\end{aligned}$$

12. Find the equation of the ellipse having ends of major axis $( \pm 5,0)$ and ends of minor axis $(0, \pm 3)$.

Ans. Given: ends of major axis $( \pm 5,0)$ and ends of minor axis $(0, \pm 3)$.

Since, the major axis is along $x$ - axis, Therefore, equation of the ellipse will be the form $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, where $a$ is the semimajor axis.

Accordingly, $a=5$ and $b=3$.

Thus, required equation of ellipse is $\frac{x^2}{5^2}+\frac{y^2}{3^2}=1$ or $\frac{x^2}{25}+\frac{y^2}{9}=1$.

13. Find the coordinates of the focus and equation of the directrix for the parabola given by $y^{2}=-2x$.

Ans. Given: Equation of parabola: $y^2=-2 x$ Since, the given parabola is of the form $y^2=-4 a x$,

Thus, on comparison we get.

$$\begin{aligned}& 2=4 a \\& \Rightarrow a=\frac{1}{2}\end{aligned}$$

Therefore,Coordinates of focus:

$$(-a, 0)=\left(-\frac{1}{2}, 0\right)$$

Equation of directrix: $x=a$ i.e., $x=\frac{1}{2}$

PDF Summary - Class 11 Maths Conic Sections (Chapter 10)

1. Conic Sections:

The locus of point which moves in a plane so that its distance from a fixed point is in a constant ratio to its perpendicular distance from a fixed straight line

• The fixed straight line is called the Directrix

• The fixed point is called the Focus. 

• The constant ratio is called the Eccentricity denoted by e. 

• A point of intersection of a conic with its axis is called a Vertex.

• The line passing through the focus & perpendicular to the Directrix is called the Axis. 

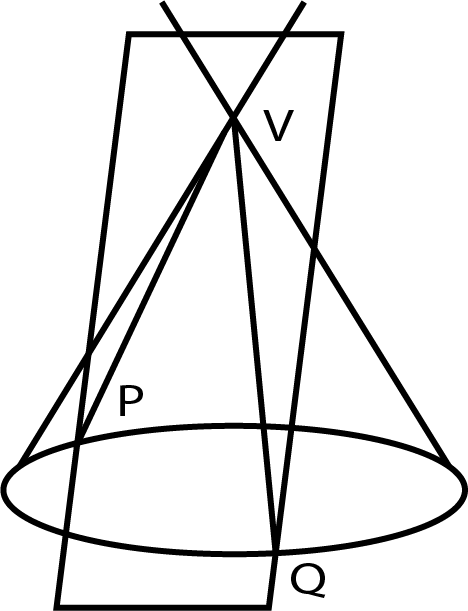
2. Section of Right Circular Cone by Different Planes:

Figure shows right circular cone.

(i) Figure shows the section of a right circular cone by a plane passing through its vertex is a pair of straight lines passing through the vertex.

(ii)  Figure shows section of a right circular cone by a plane parallel to its base is a circle. 

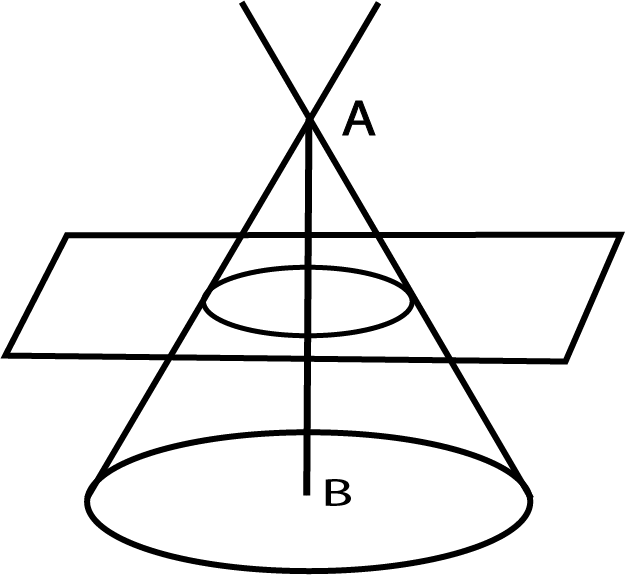
(iii) Figure shows section of a right circular cone by a plane parallel to a generator of the cone is a parabola.

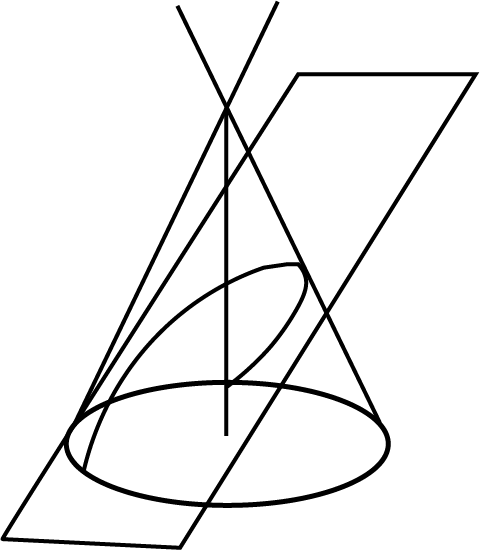
(iv) Below figure shows section of a right circular cone by a plane neither parallel to any generator of the cone nor perpendicular or parallel to the axis of the cone is an ellipse or hyperbola.

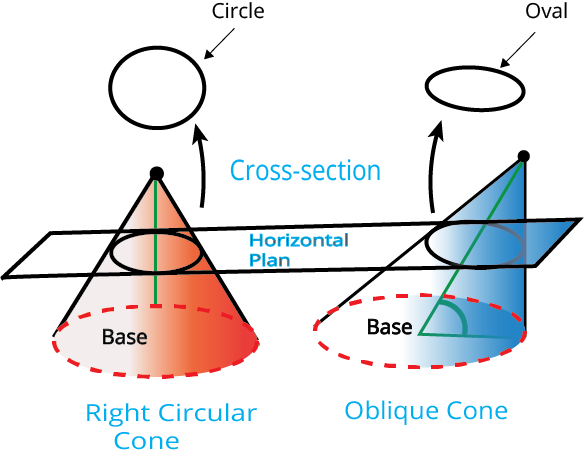
3D view:

3. General Equation of a Conic: Focal Directrix Property.

If focus of conic is \[\left( {p\;,q} \right)\] and equation of directrix is \[lx\; + \;my\; + \;n\; = \;0\],then the general equation of conic is:

$(l^2=m^2)[(x-p)^2+(y-q)^2)]=e^2(lx+my+n)^2\equiv ax^2+2hxy+by^2+2gx+2fy=c=0$

4. Distinguishing Various Conics:

The nature of conic section depends upon value of eccentricity as well as the position of the focus and the directrix. So, there are two different cases:

Case 1: When the Focus Lies on the Directrix.

In this case, \[\Delta  \equiv {\text{ }}abc{\text{ }} + {\text{ }}2fgh{\text{ }}--{\text{ }}a{f^2}{\text{ }}--{\text{ }}b{g^2}{\text{ }}--{\text{ }}c{h^2}{\text{ }} = {\text{ }}0\]

The general equation of a conic represents a pair of straight lines if:

\[e{\text{ }} > {\text{ }}1{\text{ }} \equiv {\text{ }}{h^2}{\text{ }} > {\text{ }}ab\], Real and distinct lines intersecting at focus

\[e{\text{  =  }}1{\text{ }} \equiv {\text{ }}{h^2}{\text{ }} \geqslant {\text{ }}ab\], Coincident lines

\[e{\text{  <  }}1{\text{ }} \equiv {\text{ }}{h^2}{\text{  <  }}ab\], Imaginary lines

Case 2: When the Focus Does not Lies on the Directrix.

A parabola 

An ellipse

A hyperbola

A rectangular hyperbola 

Parabola

Definition and Terminology

The locus of a point, whose distance from a fixed point called focus is equal to perpendicular distance from a fixed straight line called directrix is called Parabola.

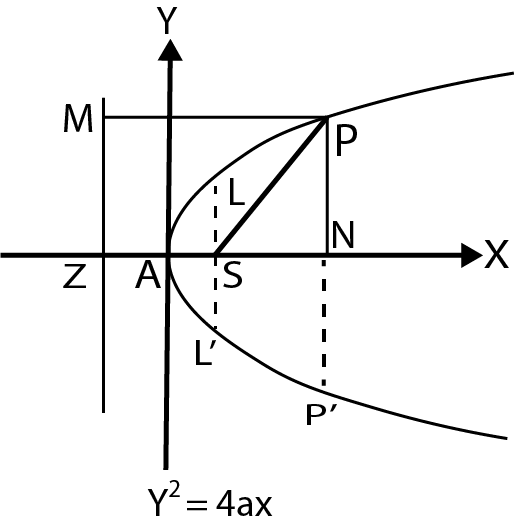
Four standard forms of parabola are:

\[{y^2}\; = \;4ax\;;\;{y^2}\; = \; - 4ax\;;\;{x^2}\; = \;4ay\;;\;{x^2}\; = \; - 4ay\]

For parabola, \[{y^2}\; = \;4ax\]:

(i) Vertex is: \[(0\;,\;0)\]

(ii) Focus is: \[(a\;,\;0)\]

(iii) Axis is: \[y\; = \;0\]

(iv) Directrix is: \[x + a = 0\]

• The distance of a point on the parabola from the focus is called focal distance.

• A chord of the parabola, which passes through the focus is called focal chord.

• A chord of the parabola perpendicular to the axis of the symmetry is called double ordinate.

• A double ordinate passing through the focus or a focal chord perpendicular to the axis of parabola is called the Latus Rectum.

For, \[{y^2}\; = \;4ax\]:

\[ \Rightarrow \]Length of Latus rectum \[ = 4a\]

\[ \Rightarrow \]Ends of Latus rectum are \[(a\;,2a)\;\& \;(a\;, - 2a)\]

Note:

• Perpendicular distance from focus to  directrix = half the latus rectum.

• Vertex is middle point of the focus & the point of intersection of directrix & axis.

• Two parabolas are said to be equal if they have the same latus rectum.

Position of a Point Relative to Parabola:

Point \[({x_1},\;{y_1})\]lies inside, on or outside the parabola \[{y^2}\; = \;4ax\]depends upon the value of \[{y_1}^2\; - \;4a{x_1}\], whether it is positive, negative or zero.

Line and Parabola:

The line \[y = mx + c\] meets parabola \[{y^2}\; = \;4ax\] at:

• Two real points if \[a > mc\]

• Two coincident points if \[a = mc\]

• Two non real points if \[a < mc\]

Condition of Tangency is \[c = \dfrac{a}{m}\]

Length of chord that line \[y = mx + c\]intercepts on parabola \[{y^2}\; = \;4ax\] is:

\[\left( {\dfrac{4}{{{m^2}}}} \right)\sqrt {a\left( {1 + {m^2}} \right)\left( {a - mc} \right)} \]

Note: Length of focal chord making an angle \[\alpha \] with the x-axis is \[4a\;\cos e{c^2}\alpha \]

Parametric Representation:

\[\left( {a{t^2},\;2at} \right)\] represents the co-ordinates of a point on the parabola is \[{y^2}\; = \;4ax\] i.e. the equations \[x = a{t^2},\;y = 2at\] at together represents the parabola with t being the parameter. 

The equation of a chord joining \[{t_1}\;\& \;{t_2}\]is \[2x\;--\;\left( {{t_1} + {\text{ }}{t_2}} \right)y{\text{ }} + {\text{ }}2{\text{ }}a{t_1}{t_2}{\text{ }} = {\text{ }}0.{\text{ }}\]

Note: If \[{t_1}\;\& \;{t_2}\]are ends of the focal chord of the parabola\[{y^2}\; = \;4ax\], then \[{t_1}{t_2}\; = \; - 1\]

Hence, coordinates of extremities of parabola are \[\left( {a{t^2},\;2at} \right)\;or\;\left( {\dfrac{a}{{{t^2}}},\;\dfrac{{ - 2a}}{t}} \right)\]

Tangent to the Parabola \[{y^2}\; = \;4ax\]

\[(i)\;y{y_1}\; = \;2a\left( {x + {x_1}} \right)\] at point \[({x_1},\;{y_1})\]

\[(ii)\;y\; = \;mx\; + \;\dfrac{a}{m}\;\left( {m \ne 0} \right)\] at \[\left( {\dfrac{a}{{{m^2}}},\;\dfrac{{2a}}{m}} \right)\]

\[(iii)\;ty\; = \;x\; + \;a{t^2}\]at point \[\left( {a{t^2},\;2at} \right)\]

Note: Point of intersection of the tangents at the point \[{t_1}\;\& \;{t_2}{\text{ }}is{\text{ }}\left[ {a{t_1}{t_2}{\text{ }},{\text{ }}a\left( {{t_1} + {t_2}} \right)} \right]\]

Normal to the Parabola \[{y^2}\; = \;4ax\]

\[(i)\;y\;-{y_1}\; = \;\dfrac{{ - {y_1}}}{{2a}}\left( {x - {x_1}}\right)\;at\;({x_1},\;{y_1})\]

\[(ii)\;y\; = mx\; - \;2am\; - \;a{m^3}\;at\;(a{m^2},\; - 2am) \]

\[(iii)\;y\; + \;tx\; = \;2at\; + \;a{t^3}\;at\;(a{t^2},\; - 2at)\]

Note: 

 (i) Point of intersection of normals at ${t_1}\;\& \;{t_2}$, are, $\left[ {a\left( {t_1^2 + t_2^2 + {t_1}{t_2} + 2} \right),\; - a{t_1}{t_2}\left( {{t_1} + {t_2}} \right)} \right]$

(ii) If the normals to the parabola ${y^2} = 4ax$ at the point ${t_1}$ meets the parabola again at the point ${t_2}$ then ${t_2} =  - \left( {{t_1} + \dfrac{2}{{{t_1}}}} \right)$

(iii) If the normals to the parabola ${y^2} = 4ax$ at the points ${t_1}\;\& \;{t_2}$ intersect again on the parabola at the point ${{\text{t}}_3}$  then ${{\text{t}}_1}{{\text{t}}_2} = 2,\;{{\text{t}}_3} =  - \left( {{{\text{t}}_1} + {{\text{t}}_2}} \right)$ and the line joining ${t_1}\;\& \;{t_2}$ passes through a fixed point $( - 2a,0)$

Pair of Tangents

The equation to the pair of tangents which can be drawn from any point $\left( {{x_1},\;{y_1}} \right)$ to the parabola ${y^2} = 4ax$ is given by: ${{S}}{{\mathbf{S}}_1} = {{{T}}^2}$ where:

$S \equiv {y^2} - 4ax,\;{S_1} = y_1^2 - 4a{x_1},\;T \equiv y{y_1} - 2a\left( {x + {x_1}} \right)$

Director Circle

Locus of the point of intersection of the perpendicular tangents to a curve is called the director circle. For parabola ${y^2} = 4ax$ it's equation is ${\mathbf{x}} + {\mathbf{a}} = 0$ which is parabola's own directrix.

Chord of Contact

Equation to the chord of contact of tangents drawn from a point $P\left( {{x_1},{y_1}} \right)$ is $y{y_1} = 2a\left( {x + {x_1}} \right);$ (i.e., $\left. {T = 0} \right)$

Note: The area of the triangle formed by the tangents from the point $\left( {{x_1},{y_1}} \right)\;\& \;$the chord of contact is. ${\left( {y_1^2 - 4a{x_1}} \right)^{3/2}} \div \;2a$

Chord With a Given Middle Point

Equation of the chord of the parabola ${{\text{y}}^2} = 4ax$ whose middle point is $\left( {{x_1},\;{y_1}} \right)$ is:

${\mathbf{y}} - {{\mathbf{y}}_1} = \dfrac{{2{\text{a}}}}{{{{\text{y}}_1}}}\left( {{\mathbf{x}} - {{\mathbf{x}}_1}} \right) \equiv {\text{T}} = {{\text{S}}_1}$

Ellipse

Standard Equation and Definitions:

Standard equation of an ellipse referred to its principal axes along the co-ordinate axes is

$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ , where $a > b,\;{b^2} = {a^2}\left( {1 - {e^2}} \right)$

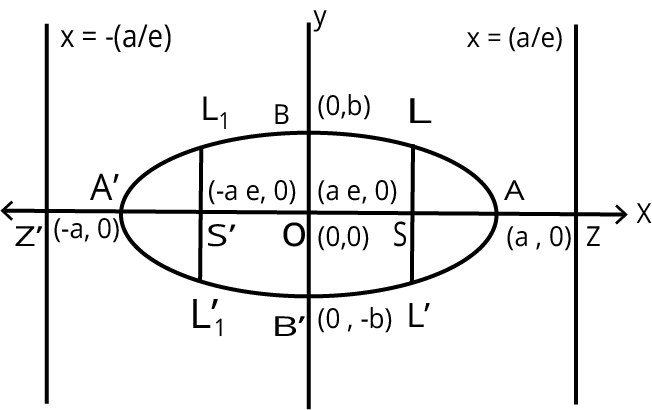
Eccentricity: $e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} ,(0 < e < 1)$

Foci: $S = (ae,0)\;\& \;{S^\prime } = ( - ae,0)$

Equations of Directrices: $x = \dfrac{{\text{a}}}{{\text{e}}}\;\& \;x =  - \dfrac{{\text{a}}}{{\text{e}}}$

Major Axis: The line segment $A'A$ in which the foci $S'\;\& \;S$ lie is of length $2a$ &  is called the major axis $({\text{a}} > {\text{b}})$ of the ellipse. Point of intersection of major axis with directrix is called the foot of the directrix $(Z)$.

Minor Axis: The y-axis intersects the ellipse in the points ${\text{B}}' = (0, - {\text{b}})$ and ${\text{B}} = (0,\;{\text{b}})$. The line segment ${\text{B}}'{\text{B}}$ of length $2{\text{b}}\;(\;{\text{b}} < {\text{a}})$ is called the minor axis of the ellipse.

Principal Axis: The major and minor axis together are called principal axis of the ellipse.

Vertices: $A' \equiv ( - a,0)\;\& \;A \equiv (a,0)$.

Focal Chord : A chord which passes through a focus is called a focal chord.

Double Ordinate: A chord perpendicular to the major axis is called a double ordinate.

Latus Rectum: The focal chord perpendicular to the major axis is called the  latus rectum.

Length of latus rectum (LL’) :

$\dfrac{{2\;{{\text{b}}^2}}}{{\text{a}}} = \dfrac{{{{({\text{ minor axis }})}^2}}}{{{\text{ majer axis }}}} = 2{\text{a}}\left( {1 - {{\text{e}}^2}} \right)$

$ = 2e$ (distance from focus to the corresponding directrix).

Centre: The point which bisects every chord of the conic drawn through it is called the centre of the conic. $C = (0,0)$

The origin is the centre of the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

Note:

(i) If the equation of the ellipse is given as $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ and nothing is mentioned, then the rule is to assume that $a > b$

(ii) If $b > a$ is given then y-axis will become major axis and $x$ axis will become the minor axis and all other points and lines will change accordingly.

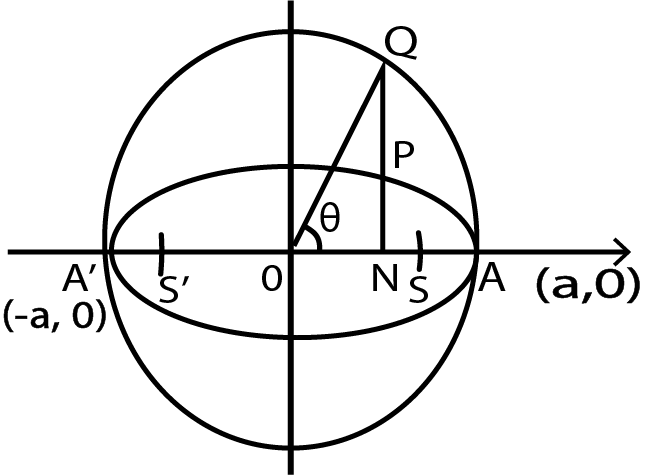
Auxiliary Circle/Eccentric Angle:

A circle described on major axis as diameter is called the auxiliary circle. Let $Q$ be a point on the auxiliary circle ${x^2} + {y^2} = {a^2}$ such that QP  produced is perpendicular to the $x$-axis, then $P$& $Q$ are called as the Corresponding Points on the ellipse and the auxiliary circle respectively. $\theta $ is called the Eccentric angle of the point ${\text{P}}$ on the ellipse $( - \pi  < \theta  \leqslant \pi )$.

Note:

• $\dfrac{{l(PN)}}{{l(QN)}} = \dfrac{b}{a} = \dfrac{{{\text{ Semi major axis }}}}{{{\text{ Semi major axis }}}}$

• If from each point of a circle perpendiculars are drawn upon a fixed diameter then the locus of the points dividing these perpendiculars in a given ratio is an ellipse of which the given circle is the auxiliary circle.

Parametric Representation:

The equations $x = a\cos \theta \;\& \;y = b\sin \theta $ , together represent the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

Where $\theta $ is a parameter. Note that if $P(\theta ) = $ (a cos$\theta ,b\sin \theta )$ is on the ellipse then$Q(\theta ) = (a\cos \theta ,a\sin \theta )$ is on the auxiliary circle.The equation to the chord of the ellipse joining two. points with eccentric angles $\alpha $ and $\beta $ is given by

$\dfrac{x}{a}\cos \dfrac{{a + \beta }}{2} + \dfrac{y}{b}\sin \dfrac{{a + \beta }}{2} = \cos \dfrac{{a - \beta }}{2}$

Position of a Point With Respect to Ellipse:

The point $p\left( {{x_1},{y_1}} \right)$ lies outside, inside or on the ellipse, according as:

$\dfrac{{x_1^2}}{{{a^2}}} + \dfrac{{y_1^2}}{{{b^2}}} - 1 > 0\quad $ (outside)

$\dfrac{{x_1^2}}{{{a^2}}} + \dfrac{{y_1^2}}{{{b^2}}} - 1 < 0\quad $ (inside)

$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 = 0$ (on)

Line and an Ellipse:

The line $y = mx + c$ meets the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ in two points real, coincident or imaginary according as ${{\text{c}}^2}\;{\text{is}} < \;, = \;\& \; > {{\text{a}}^2}\;{{\text{m}}^2} + {{\text{b}}^2}$

Hence $y = mx + c$ is tangent to the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, if ${c^2} = {a^2}{m^2} + {b^2}$.

Tangents:

(a) Slope form $y = mx \pm \sqrt {{a^2}{m^2} + {b^2}} $ is tangent to the ellipse for all values of ${\text{m}}$

(b) Point form $\dfrac{{x{x_1}}}{{{a^2}}} + \dfrac{{y{y_1}}}{{{b^2}}} = 1$ is tangent to the ellipse at $\left( {{x_1},\;{y_1}} \right)$

(c) Parametric for $\dfrac{{xcos\theta }}{a} + \dfrac{{y\sin \theta }}{b} = 1$ is tangent to the ellipse at the point $(a{\text{ }}cos\theta ,{\text{b}}\sin \theta )$.

Note:

(i) There are two tangents to the ellipse having the same m, i.e. there are two tangents parallel to any given direction. These tangents touch the ellipse at extremities of a diameter.

(ii) Point of intersection of the tangents at the point $\alpha \;\& \;\beta $ is:

$\left( {a\;\dfrac{{\cos \dfrac{{\alpha  + \beta }}{2}}}{{\cos \dfrac{{\alpha  - \beta }}{2}}},\;b\;\dfrac{{\sin \dfrac{{\alpha  + \beta }}{2}}}{{\cos \dfrac{{\alpha  - \beta }}{2}}}} \right)$

(iii) The eccentric angles of point of contact of two parallel tangents differ by$\pi $.

Normal:

(i) Equation of the normal at$\left( {{x_1},\;{y_1}} \right)$ is $\dfrac{{{a^2}x}}{{{x_1}}} - \dfrac{{{b^2}y}}{{{y_1}}} = {a^2} - {b^2} = {a^2}{e^2}$

(ii) Equation of the normal at the point (acos$\theta $ , bsin$\theta $ ) is $\operatorname{ax} \sec \theta  - {\text{ by }}\operatorname{cosec} \theta  = \left( {{x^2} - {b^2}} \right)$

(iii) Equation of a normal in terms of its slope m is $y = mx + \dfrac{{\left( {{a^2} - {b^2}} \right)m}}{{\sqrt {{a^2} + {b^2}{m^2}} }}$

Director Circle:

Locus of the point of intersection of the tangents which meet at right angles is called the Director Circle. The equation to this locus is ${{\text{x}}^2} + {{\text{y}}^2} = {{\text{a}}^2} + {{\text{b}}^2}$ i.e. a circle whose centre is the centre of the ellipse & whose radius is the length of the line joining the ends of the major & minor axis.

Note:

Pair of tangents, Chord of contact, Pole & Polar, Chord with a given Middle point are to be interpreted as they, are in Parabola/Circle.

Diameter (Not in Syllabus)

The locus of the middle points of a system of parallel chords with slope 'm' of an ellipse is a straight line passing through the centre of the ellipse, called its diameter and has the equation $y =  - \dfrac{{{{\text{b}}^2}}}{{\;{a^2}m\;}}\;x$

Note:

All diameters of ellipse passes through its centre

Important Highlights:

Referring to the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

(a) If ${\text{P}}$ be any point on the ellipse with S & S’ as to foci then $SP + SP' = 2a$.

(b) The tangent & normal at a point ${\text{P}}$ on the ellipse bisect the external and internal angles between the focal distances of P. This refers to the well known reflection property of the ellipse which states that rays from one focus are reflected through other focus & vice-versa. Hence we can deduce that the straight lines joining each focus to the foot of the perpendicular from the other focus upon the tangent at any point $P$ meet on the normal PC and bisects it where ${\text{G}}$ is the point where normal at $P$ meets the major axis.

(c) The product of the length's of the perpendicular segments from the foci on any tangent to the ellipse is ${{\text{b}}^2}$ and the feet of these perpendiculars lie on its auxiliary circle and the tangents at these feet to the auxiliary circle meet on the ordinate of ${\text{P}}$ and that the locus of their point of intersection is a similar ellipse as that of the original one.

(d) The portion of the tangent to an ellipse between the point of contact & the directrix subtends a right angle at the corresponding focus.

(c) If the normal at any point ${\text{P}}$ on the ellipse with, centre $C$ meet the major and minor axes in $G$ & $g$ respectively &  if CF be perpendicular upon this normal then:

(i) PF. ${\text{PG}} = {{\text{b}}^2}$

(ii) ${\text{PF}}.{\text{Pg}} = {{\text{a}}^2}$

(iii) ${\text{PG}}{\text{.Pg}} = {\text{SP}}{\text{.S'P}}$

(iv) ${\text{CG}}.C\;{\text{T}} = {\text{C}}{{\text{S}}^2}$

(v) locus of the mid point of ${\text{Gg}}$ is another ellipse having the same eccentricity as that of the original ellipse.

(Where $S$ and ${S^\prime }$ are the foci of the ellipse and ${\text{T}}$ is the point where tangent at ${\text{P}}$ meet the major axis)

• The circle on any focal distance as diameter touches the auxiliary circle. Perpendiculars from the centre upon all chords which join the ends of any perpendicular diameters of the ellipse are of constant length.

• If the tangent at the point P of a standard ellipse meets the axis in T and t and CY is the perpendicular on it from the centre then :

     (i) T t.P Y = a2 – b2 and

           (ii) least value of T t is a+b

Hyperbola 

The Hyperbola is a conic whose eccentricity is greater than unity $(e > 1)$

Standard Equation and Definitions:

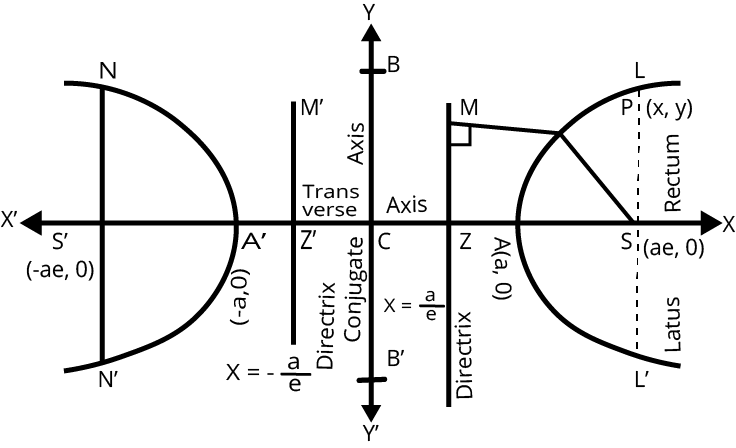
Standard equation of the hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$, where ${b^2} = {a^2}\left( {{e^2} - 1} \right)$

Eccentricity (e):  ${{\text{e}}^2} = 1 + \dfrac{{{{\text{b}}^2}}}{{{{\text{a}}^2}}}\; = \;1 + {\left( {\dfrac{{{\text{C}} \cdot {\text{A}}}}{{{\text{T}}.{\text{A}}}}} \right)^2}$

(C.A $ \to $ Conjugate Axis)

(T.A. $ \to $Transverse Axis)

Foci:  $S = (ae,0)\;\& \;S' = ( - ae,0)$

Equations of Directrix: ${\text{x}} = \dfrac{{\text{a}}}{{\text{e}}}\;\& \;x =  - \dfrac{{\text{a}}}{{\text{e}}}$

Transverse Axis: The line segment $A'A$ of length 2a in which the foci $S'\;\& \;S$ both lie is called the transverse axis of the hyperbola.

Conjugate Axis: The line segment B'B between the two points $B' = (0, - {\text{b}})\;\& \;B = (0,\;{\text{b}})$ is called as the conjugate axis of the hyperbola.

Principal Axes: The transverse & conjugate axis together are called Principal Axes of the hyperbola.

Vertices: ${\text{A}} = ({\text{a}},0)\;\& \;A' = ( - {\text{a}},0)$

Focal Chord: A chord which passes through a focus is called a focal chord.

Double Ordinate: $A$ chord perpendicular to the transverse axis is called a double ordinate.

Latus Rectum (l) L: The focal chord perpendicular to the transverse axis is called the latus rectum.

$\ell  = \dfrac{{2\;{{\text{b}}^2}}}{{\text{a}}} = \dfrac{{{{({\text{C}} \cdot A)}^2}}}{{\;{\text{TA}}}} = 2{\text{a}}\left( {{{\text{e}}^2} - 1} \right)$

Note:

$l(L{\text{R}}) = 2{\text{e}}$ (distance from focus to directrix).

Centre: The point which bisects every chord of the conic drawn through it is called the centre of the conic $C = (0,0)$, the origin is the center of the hyperbola $\dfrac{x}{a} - \dfrac{y}{b} = 1$

Since the fundamental equation to the hyperbola only differs from that to the ellipse in having $ - {{\text{b}}^2}$ instead of ${{\text{b}}^2}$ it will be found that many propositions for the hyperbola are derived from those for the ellipse by simply changing the sign of ${{\text{b}}^2}$.

Rectangular or Equilateral Hyperbola: 

The particular kind of hyperbola in which the lengths of the transverse and conjugate axis are equal is called an Equilateral Hyperbola. Note that the eccentricity of the rectangular hyperbola is $\sqrt 2 $.

Conjugate Hyperbola:

Two hyperbolas such that transverse & conjugate axes of one hyperbola are respectively the conjugate & the transverse axes of the other are called Conjugate Hyperbolas of each other.

e.g. $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\;\& \;\dfrac{{{-x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ are conjugate hyperbolas of each other.

Note:

(a) If ${e_1}$ and ${e_2}$ are the eccentricities of the hyperbola and its conjugate, then $e_1^{ - 2} + {e_2}^{ - 2} = 1$.

(b) The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.

(c) Two hyperbolas are said to be similar if they have the same eccentricity:

(d) Two similar hyperbolas are said to be equal if they have same latus rectum.

(e) If a hyperbola is equilateral, then the conjugate hyperbola is also equilateral.

Auxiliary Circle:

A circle drawn with centre C and T.A. as a diameter is called the Auxiliary Circle of the hyperbola. Equation of the auxiliary circle is ${x^2} + {y^2} = {a^2}$

Note from the figure that P and Q are called the "Corresponding Points" on the hyperbola and the auxiliary circle.

In the hyperbola any ordinate of the curve does not meet the circle on ${\text{AA}}$' as diameter in real points. There is therefore no real eccentric angle as in the case of the ellipse.

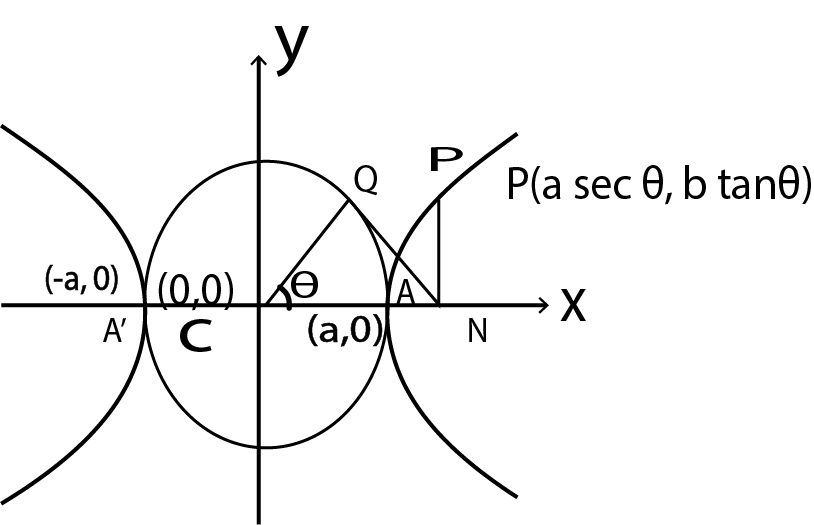
Parametric Representation:

The equation $x = a\sec \theta $ & $y = b\tan \theta $ together represents the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ where $\theta $ is a parameter.

Note that if ${\text{P}}(\theta ) = ({\text{a}}\sec \theta ,{\text{b}}\tan \theta )$ is on the hyperbola then, $Q(\theta ) = ($a$\cos \theta $, a $\tan \theta )$ is on the auxiliary circle.

The equation to the chord of the hyperbola joining two points with eccentric angles $\alpha $ and $\beta $ is given by:

$\dfrac{x}{a}\cos \dfrac{{\alpha  - \beta }}{2} - \dfrac{y}{b}\sin \dfrac{{\alpha  + \beta }}{2} = \cos \dfrac{{\alpha  + \beta }}{2}$

Position of a Point With Respect to Hyperbola:

The quantity ${S_1} = \dfrac{{x_1^2}}{{{a^2}}} - \dfrac{{y_1^2}}{{{b^2}}} - 1$ is positive, zero or negative according as the point $\left( {{x_1},{y_1}} \right)$ lies inside, on or outside the curve.

Line and a Hyperbola:

The straight line $y = mx + c$ is a secant, a tangent or passes outside the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ according as ${c^2} > or = or < {a^2}{m^2} - {b^2}$, respectively.

Tangents:

(i) Slope Form $:y = mx \pm \sqrt {{a^2}{m^2} - {b^2}} $ can be taken as the tangent to the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$

(ii) Point Form: Equation of tangent to the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ at the point $\left( {{x_1}{y_1}} \right)$ is $\dfrac{{x{x_1}}}{{{a^2}}} = \dfrac{{y{y_1}}}{{{b^2}}} = 1$

(iii) Parametric Form: Equation of the tangent to the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ at the point $(a\sec \theta ,b\tan \theta )$  is $\dfrac{{{\text{ x}}\;{\text{sec}}\theta {\text{ }}}}{{\text{a}}} - \dfrac{{{\text{ y}}\;{\text{tan}}\theta {\text{ }}}}{{\text{b}}} = 1$.

Note:
(i) Point of intersection of the tangents at ${\theta _1}\;\& \;{\theta _2}$ is:

$x = \dfrac{{\cos \dfrac{{{\theta _1} - {\theta _2}}}{2}}}{{\cos \dfrac{{{\theta _1} + {\theta _2}}}{2}}}\;,\;y = b\tan \left( {\dfrac{{{\theta _1} + {\theta _2}}}{2}} \right)$

(ii) If\[|{\theta _1}\; + \;{\theta _2}|\; = \;\pi \], then tangents at these points${\theta _1}\;\& \;{\theta _2}$ are parallel

(iii) There are two parallel tangents having the same slope m.These tangents touches the hyperbola at the extremities of a diameter.

Normals:

(i) The equation of the normal to the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ at the point $P({x_1},\;{y_1})$on it is $\dfrac{{{a^2}x}}{{{x_1}}} + \dfrac{{{b^2}y}}{{{y_1}}} = {a^2} + {b^2} = {a^2}{e^2}$

(ii) The equations of the normal at the point ${\text{P}}({\text{a}}\sec \theta ,{\text{b}}\tan \theta )$on the hyperbola

$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1{\text{ is }}\dfrac{{ax}}{{\sec \theta }} + \dfrac{{by}}{{\tan \theta }} = {a^2} + {b^2} = {a^2}{e^2}$

(iii) Equation of a normal in terms of its slope 'm' is$y = mx - \dfrac{{\left( {{a^2} + {b^2}} \right)m}}{{\sqrt {{a^2} - {b^2}{m^2}} }}$

Note:
Equation to the chord of contact, polar, chord with a given middle point, pair of tangents from an external point is to be interpreted as in parabola/circle.

Director Circle:

The locus of the intersection point of tangents which are at right angles is known as the Director Circle of the hyperbola. The equation to the director circle is :${x^2} + {y^2} = {a^2} - {b^2}$

If ${b^2} < {a^2}$ this circle is real

If ${{\text{b}}^2} = {{\text{a}}^2}$ (rectangular hyperbola) ,the radius of the circle is zero and it reduces to a point circle at the origin. In this case the centre is the only point from which the tangents at right angles can be drawn to the curve. 

If ${{\text{b}}^2} > {{\text{a}}^2}$, the radius of the circle is imaginary, so that there is no such circle  & no pair of tangents at right  angle can be drawn to the curve.

Diameter (Not in syllabus):

The locus of the middle points of a system of parallel chords with slope 'm' of an hyperbola is called its diameter. It is a straight line passing through the centre of the hyperbola and has the equation $y =  + \dfrac{{{b^2}}}{{{a^2}m}}x$

Note: All diameters of the hyperbola pass through its centre.

Asymptotes (Not in syllabus):

Definition: If the length of the perpendicular let fall from a point on a hyperbola to a straight line ends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called the Asymptote of the hyperbola.

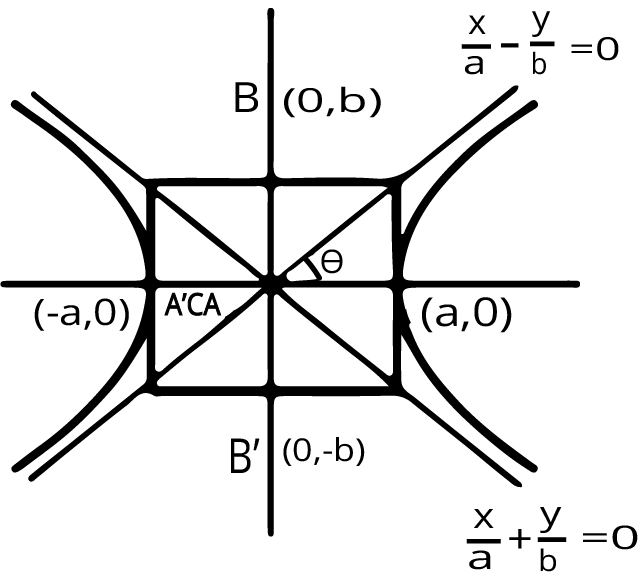
Equation of Assymptote : $\dfrac{x}{a} + \dfrac{y}{b} = 0$ and $\dfrac{x}{a} - \dfrac{y}{b} = 0$

Pairs of Asymptote: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 0$

Note:

(i) A hyperbola and its conjugate have the same asymptote.

(ii) The equation of the pair of asymptotes different form the equation of hyperbola (or conjugate hyperbola) by the constant term only.

(iii) The asymptotes pass through the centre of the hyperbola and are equally inclined to the transverse axis of the hyperbola. Hence the bisectors of the angles between the asymptotes are the principle axes of the hyperbola.

(iv)The asymptotes of a hyperbola are the diagonals of the rectangle formed by the lines drawn through the extremities of each axis parallel to the other axis.

(v) Asymptotes are the tangent to the hyperbola from the centre.

(vi) A simple method to find the co-ordinates of the centre of the hyperbola expressed as a general equation of degree 2 should be remembered as : Let $f(x,y) = 0$ represents a hyperbola.

Find $\dfrac{{\partial {\text{f}}}}{{\partial {\text{x}}}}{\text{ }}$ and $\dfrac{{\partial {\text{f}}}}{{\partial {\text{y}}}}$. Then the point of intersection of $\dfrac{{\partial f}}{{\partial x}} = 0{\text{ }}$ and $\dfrac{{\partial f}}{{\partial y}} = 0$ gives the centre of the hyperbola.

Rectangular Hyperbola $\left( {{\text{xy}} = {{\text{c}}^2}} \right.)$:

It is referred to its asymptotes as axes of co-ordinates.

Vertices: $(c,c)$ and $( - c, - c)$

Foci: $(\sqrt 2 c,\sqrt 2 c)\;\& \;( - \sqrt 2 c, - \sqrt 2 c)$

Directrices:$x + y =  \pm \sqrt 2 c$

Latus Rectum (l):  $l = 2\sqrt 2 c$= T.A. = C.A.

Parametric equation $x = ct,y = \dfrac{c}{t},t \in R - \{ 0\} $

Equation of a chord joining the points $P\left( {{t_1}} \right)$& $Q\left( {{t_2}} \right)$ is ${\text{x + }}{{\text{t}}_{\text{1}}}{{\text{t}}_{\text{2}}}{\text{y = c}}\left( {{{\text{t}}_{\text{t}}}{\text{ + }}{{\text{t}}_{\text{3}}}} \right)$

Equation of the tangent at ${\text{P}}\left( {{{\text{x}}_{\text{l}}},\;{y_1}} \right)$ is $\dfrac{{\text{x}}}{{{{\text{x}}_1}}} + \dfrac{{\text{y}}}{{{{\text{y}}_1}}} = 2$ and at $P(t)$ is $\dfrac{x}{t} + ty = 2c$

Equation of the normal at $P(t)$ is $x{t^3} - yt = c\left( {{t^4} - 1} \right)$ Chordd with a given middle point as $({\text{h}},{\text{k}})$ is ${\text{kx}} + {\text{hy}} = $ $2{\text{hk}}$

Important Highlights:

(i) Locus of the feet of the perpendicular drawn from focus of the hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ upon any tangent is its auxiliary circle i.e. ${{\text{x}}^2} + {y^2} = {{\text{a}}^2}{\text{ }}$ & the product of the feet of these perpendiculars is ${{\text{b}}^2}$.

(ii) The portion of the tangent between the point of contact & the directrix subtends a right angle at the corresponding focus.

(iii) The tangent & normal at any point of a hyperbola bisect the angle between the focal radii. This spell the reflection property of the hyperbola as "An incoming light ray" aimed towards one focus is reflected from the outer surface of the hyperbola towards the other focus. It follows that if an ellipse and a hyperbola have the same foci, they cut at right angles at any of their common point.

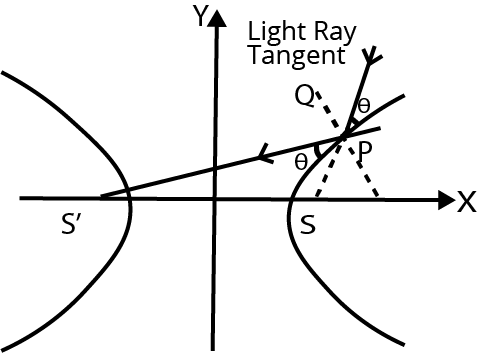
Note that the ellipse $\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} + \dfrac{{{y^2}}}{{\;{{\text{b}}^2}}} = 1\varepsilon $ the hyperbola $\dfrac{{{x^2}}}{{{a^2} - {k^2}}} + \dfrac{{{y^2}}}{{{k^2} - {b^2}}} = 1$ $(a > k > b > 0)$ are confocal and therefore orthogonal

(iv) The foci of the hyperbola and the points ${\text{P}}$ and $Q$ in which any tangent meets the tangents at the vertices are concyclic with PO as diameter of the circle.

(v) If from any point on the asymptote a straight line be drawn perpendicular to the transverse axis, the product of the segments of this line, intercepted between the point and the curve is always equal to the square of the semi conjugate axis.

(vi) Perpendicular from the foci on either asymptote meet it in the same points as the corresponding directrix and the common points of intersection lie on the auxiliary circle.

(vii) The tangent at any point ${\text{P}}$ on a hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ with centre $C$, meets the asymptotes in $Q$ and $R$ and cuts off a $\Delta CQR$ of constant area equal to ab from the asymptotes and the portion of the tangent intercepted between the assymptote is bisected at the point of contact. This implies that locus of the centre of the circle circumscribing the $\Delta CQR$ in case of a rectangular hyperbola is the hyperbola itself and of a standard hyperbola the locus would be the curve, $4\left( {{a^2}{x^2} - {b^2}{y^2}} \right) = {\left( {{a^2} + {b^2}} \right)^2}$

(viii) If the angle between the asymptote of a hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ is $2\theta $ then the eccentricity of the hyperbola is sec$\theta $.

(ix) A rectangular hyperbola circumscribing a triangle also passes through the orthocentre of this triangle,

If $\left( {{\text{c}}{{\text{t}}_i}\dfrac{{\text{c}}}{{{{\text{t}}_i}}}} \right){\text{i}} = 1,2,3$ be the angular points P,

Q , R ,then orthocentre is $\left( {\dfrac{{ - c}}{{{t_1}{t_2}{t_3}}}, - c{t_1}{t_1}{t_3}} \right)$

(x) If a circle and the rectangular hyperbola ${\text{xy}} = $ ${c^2}$ meet in the four points, ${t_1},{t_2},{t_3}$ and ${t_4}$, then

(a) ${t_1}{t_2}{t_3}{t_4} = 1$

(b) the centre of the mean position of the four, points bisects the distance between the centre of the circle through the points ${t_1},{t_2}$ and ${t_3}$ is :

$\left\{ {\dfrac{c}{2}\left( {{t_1} + {t_2} + {t_s} + \dfrac{1}{{{t_1}{t_2}{t_3}}}} \right)\dfrac{c}{2}\left( {\dfrac{1}{{{t_t}}} + \dfrac{1}{{{t_2}}} + \dfrac{1}{{{t_t}}} + {t_1} + {t_2} + {t_3}} \right)} \right\}$

Circle:

A circle is a locus of a point whose distance from a fixed point (called centre) is always constant (called radius).

1. Equation of Circle in Various Forms:

(a) The circle with centre as origin & radius '${\text{r}}\;{\text{'}}$ has the equation ${x^2} + {{\text{y}}^2} = {r^2}$

(b) The Circle with centre $({\text{h}},{\text{k}})$& radius ‘ $r$' has the equation ${(x - h)^2} + {({\text{y}} - k)^2} = {r^2}$

(c) The general equation of a circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$ with centre as $\left( { - g, - f} \right)$ and ${\text{radius }} = \sqrt {{{\text{g}}^2} + {{\text{f}}^2} - {\text{c}}} $.

${\text{If}}\;{{\text{g}}^2} + {{\text{f}}^2} - {\text{c}} > 0 \Rightarrow $ Real circle

${\text{If}}\;{{\text{g}}^2} + {{\text{f}}^2} - {\text{c}} = 0 \Rightarrow $Point circle

${\text{If}}\;{{\text{g}}^2} + {{\text{f}}^2} - {\text{c}} < 0 \Rightarrow $ Imaginary circle with real centre, i.e., $\left( { - g, - f} \right)$

Note that every second degree equation in $x\;\& \;y$, in which coefficient of ${x^2}$ is equal to coefficient of ${y^2}$ and the coefficient of xy is zero, always represents a circle.

(d) The equation of circle with$\left( {{x_1},{y_1}} \right)\;\& \;\left( {{x_2},{y_2}} \right)$ as extremities of its diameter is:

$\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_2}} \right) = 0$

Note that this will be the circle of least radius passing through $\left( {{x_1},{y_1}} \right)\;\& \;\left( {{x_2},{y_2}} \right)$

2. Intercepts Made by Circle on the Axes:

The intercepts made by the circle ${x^2} + {y^2} + 2gx + 2fy + c = 0$ on the co-ordinate axes are $2\sqrt {{g^2} - c} $and  $2\sqrt {{f^2} - c} $ respectively. If:

${g^2} - c\; > \;0\;\; \Rightarrow $ circle cuts the x axis at two distinct points

${g^2} - c\; = \;0\;\; \Rightarrow $ circle touches the x–axis 

${g^2} - c\; < \;0\;\; \Rightarrow $ circle lies completely above or below the x–axis

3. Parametric Equation of the Circle:

The parametric equations of ${(x - h)^2} + {(y - k)^2} = {{\text{r}}^2}$ are :

$x = h + r\cos \theta ,\;y = k + r\sin \theta ,\; - \pi  < \theta  \leqslant \pi $, where$({\text{h}},{\text{k}}$ ) is the centre, ${\text{r}}$ is the radius $\& \;\theta $ is a parameter.

4. Position of a Point with Respect to a Circle:

The point $\left( {{{\text{x}}_1},{{\text{y}}_1}} \right)$ is inside, on or outside the circle $S \equiv {x_1}^2 + y_1^2 + 2gx + 2fy + c = 0$

According as ${{\mathbf{S}}_1} \equiv {{\text{x}}_1}^2 + y_1^2 + 2{\text{x}}{{\text{x}}_1} + 2{\text{y}}{{\text{y}}_1} + {\text{c}}\;{\text{is}}\;\; < \;or\; = \;or\; > \;0$.

Note: The greatest & the least distance of a point A from a circle with centre C $\& $ radius $r$ is \[AC + r\;\& \;AC - r\] respectively.

5. Line and a Circle:

Let $L = 0$ be a line $\& \;S = 0$ be a circle. If $r$ is the radius of the circle & ${\text{p}}$ is the length of the perpendicular from the centre on the line, then:

(i) ${\text{p}} > {\text{r}} \Leftrightarrow $ the line does not meet the circle i.e. passes outside the circle.

(ii) ${\text{p}} = {\text{r}} \Leftrightarrow $ the line touches the circle.

(It is tangent to the circle)

(iii) ${\text{p}} < {\text{r}} \Leftrightarrow $ the line is a secant of the circle.

iv) ${\text{p}} = 0 \Rightarrow $ the line is a diameter of the circle.

Also, if $y = \operatorname{mx}  + c$ is line and ${x^2} + {y^2} = {a^2}$ is circle then

i) ${c^2} < {a^2}\left( {1 + {m^2}} \right) \Leftrightarrow $ the line is a secant of the circle.

(ii) ${c^2} = {a^2}\left( {1 + {m^2}} \right) \Leftrightarrow $ the line touches the circle. (It is tangent to the circle)

(iii) ${c^2} > {a^2}\left( {1 + {m^2}} \right)\quad  \Leftrightarrow \quad $ the line does not meet the circle i.e. passes out side the circle.

6.Tangent:

(a) Slope form: $y = mx + c$ is always a tangent to the circle ${x^3} + {y^2} = {a^2}$ if ${c^2} = {a^2}\left( {1 + {m^2}} \right)$

Hence, equation of tangent is $y = mx \pm a\sqrt {1 + {m^2}} $ and the point of contact is $\left( { - \dfrac{{{{\text{a}}^2}\;{\text{m}}}}{c},\dfrac{{{{\text{a}}^2}}}{c}} \right)$ where ${\text{c}} =  \pm a\sqrt {1 + {{\text{m}}^2}} $

(b) Point form :

(i) The equation of the tangent to the circle ${x^2} + {y^2} = {a^2}$ at its point $\left( {{x_1},\;{y_1}} \right)$ is, $x{x_1} + y{y_1} = {a^2}$ 

(ii) The equation of the tangent to the circle ${x^2} + {y^2} + 2gx + 2fy + c = 0$ at its point $\left( {{x_1},{y_1}} \right)$ is ${\text{x}}{{\text{x}}_1} + y{y_1} + {\text{g}}\left( {{\text{x}} + {{\text{x}}_1}} \right) + {\text{f}}\left( {y + {y_1}} \right) + c = 0$

Where $S \equiv {x^2} + {y^2} + 2gx + 2fy + c$

$\begin{gathered} {{\text{S}}_1} = {{\text{x}}_1}^2 + y_1^2 + 2g{x_1} + 2{\text{f}}{{\text{y}}_1} + {\text{c}} \hfill \\ {\text{T}} = {\text{x}}{{\text{x}}_1} + y{y_1} + g\left( {{\text{x}} + {{\text{x}}_1}} \right) + {\text{f}}\left( {y + {{\text{y}}_1}} \right) \hfill \\ \end{gathered} $

Note:

In general the equation of tangent to any second degree curve at point $\left( {{x_1},{y_1}} \right)$ on it can be obtained by replacing \[{x^2}\] by $x{x_1},\;{y^2}$ by $y{y_1}\;,\;x$ by $\dfrac{{x + {x_1}}}{2},\;y$ by $\dfrac{{y + {y_1}}}{2},xy$ by $\dfrac{{{x_1}y + x{y_1}}}{2}$ and c remains as $c$

(c) Parametric form The equation of a tangent to circle ${x^2} + {y^2} = {a^2}$ at$(a\;\cos \alpha \;,\;a\;\sin \alpha )$ is: $x\cos \alpha  + y\sin \alpha  = a$.

Note: The point of intersection of the tangents at the points $P(\alpha )$ $P(\beta )$ is =

$\left( {\dfrac{{a\;\cos \dfrac{{a + \beta }}{2}}}{{\cos \dfrac{{\alpha  - \beta }}{2}}}\;,\;\dfrac{{a\;\sin \dfrac{{a + \beta }}{2}}}{{\cos \dfrac{{\alpha  - \beta }}{2}}}} \right)$

7. Family of Circles:

(a) The equation of the family of circles passing through the points of intersection of two circles ${S_1} = 0$ and ${S_2} = 0$ is ${S_1} + K{S_2} = 0$

$\left( {K \ne  - 1} \right.$, provided the co-efficient of ${x^2} $ and ${y^2}$ in ${S_1}$ and ${S_2}$ are same)

(b) The equation of the family of circles passing through the point of intersection of a circle $S = 0\;\& $ a line ${\text{L}} = 0$ is given by $S + KL = 0$.

(c) The equation of a family of circles passing through two given points $\left( {{{\text{x}}_1},{y_1}} \right)\;\& \;\left( {{{\text{x}}_2},{{\text{y}}_2}} \right)$ can be written in the form :

$\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_1}} \right) + K\left| {\begin{array}{*{20}{l}} x&y&1 \\ {{x_1}}&{{y_1}}&1 \\ {{x_2}}&{{y_1}}&1 \end{array}} \right| = 0$

where $K$ is a parameter

(d) The equation of a family of circles touching a fixed line $y - {y_1} = m\left( {x - {x_1}} \right)$ at the fixed point $\left( {{x_1},{y_1}} \right)$ is

${\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2} + K\left[ {y - {y_1} - m\left( {x - {x_1}} \right)} \right] = 0$ where ${\text{K}}$ is a parameter.

Note:

• Family of circles circumscribing a triangle whose sides are given by ${{\text{L}}_1} = 0,{L_2} = 0$ and ${L_3} = 0$ is given by $:{{\text{L}}_1}\;{{\text{L}}_2} + \lambda {L_2}\;{{\text{L}}_3} + \mu {{\text{L}}_3}\;{{\text{L}}_1} = 0$ provided co-efficient of ${\text{xy}} = 0$ and co-efficient of ${x^2} = $ co-efficient of${y^2}$.

• Equation of circle circumscribing a quadrilateral whose side in order are represented by the lines ${L_1} = 0,{L_2} = 0,{L_3} = 0$ ${{\text{L}}_4} = 0$ are $\mu {{\text{L}}_1}\;{{\text{L}}_3} + \lambda {L_2}\;{{\text{L}}_4} = 0$ where value of $\mu $ and $\lambda $ can be found out by using condition that co-efficient of ${x^2} = $ co-efficient of ${y^2}$ and co-efficient of $xy = 0$.

8. Normal:

If a line is normal/orthogonal to a circle then it must pass through the centre of the circle. Using this fact normal to the circle ${x^2} + {y^2} + 2gx + 2fy + c = 0$ at $\left( {{x_1},{y_1}} \right)$ is 

$y - {y_1} = \dfrac{{{y_1} + f}}{{{x_1} + g}}\left( {x - {x_1}} \right)$

9. Pair of Tangents From a Point:

The equation of a pair of tangents drawn from the point $A\left( {{x_1},{y_1}} \right)$ to the circle${x^2} + {y^2} + 2gx + 2fy + c = 0\;\;is:S{S_1} = {T^2}$

10. Length of Tangent and Power of a Point:

The length of a tangent from an external point $\left( {{x_1},{y_1}} \right)$ to the circle :

$S = {x^2} + {y^2} + 2gx + 2fy + c = 0$ is given by${\text{ L}}\; = \;\sqrt {{\text{x}}_1^2 + y_1^2 + 2{\text{g}}{{\text{x}}_1} + 2{{\text{f}}_1}y + c}  = \sqrt {{S_1}} $

Square of length of the tangent from the point $P$ is also called the power of point w.r.t. a circle. Power of a point w.r.t a circle remains constant.

Power of a point ${\text{P}}$ is positive, negative or zero according as the point'P’  is outside, inside or on the circle respectively.

11. Director Circle:

The locus of the point of intersection of two perpendicular tangents is called the director circle of the given circle. The director circle of a circle is the concentric circle, having radius equal to $\sqrt 2 $ times the radius of original circle.

12. Chord of Contact:

If two tangents ${\text{P}}{{\text{T}}_1}\;$  and $ {\text{P}}{{\text{T}}_2}$ are drawn from the point $P\left( {{x_1},{y_1}} \right)$ to the circle $S = {x^2} + {y^2} + 2gx + 2fy + c = 0$, then the equation of the chord of contact ${{\text{T}}_1}\;{{\text{T}}_2}$ is :

$x{x_1} + y{y_1} + g\left( {x + {x_1}} \right) + f\left( {y + {y_1}} \right) + c = 0\;,\;\;T = 0$

Here $R\; = \;$ radius, $L\; = \;$ Length of tangent.

Note:

(a) Chord of contact exists only if the point 'P' is not inside.

(b) Length of chord of contact ${{\text{T}}_1}\;{{\text{T}}_2} = \dfrac{{2\;{\text{L}}R}}{{\sqrt {{\text{R}} + L} }}$

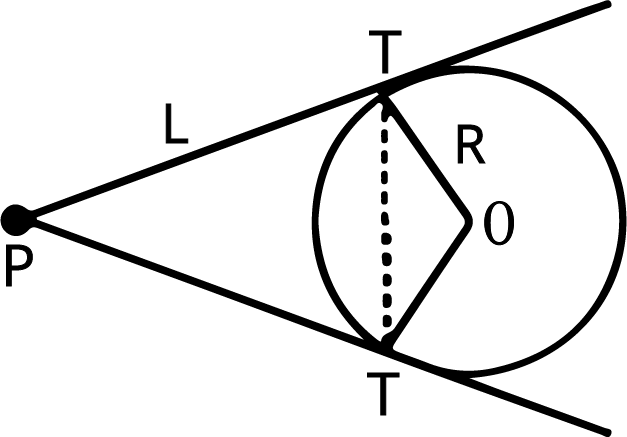
(c) Area of the triangle formed by the pair of the tangents & its chord of contact $ = \dfrac{{{\text{R}}{{\text{L}}^3}}}{{{{\text{R}}^2} + {\text{L}}}}$

(d) Tangent of the angle between the pair of tangents from $\left( {{x_1}{y_1}} \right) = \left( {\dfrac{{2RL}}{{{L^2} - R}}} \right)$

(e) Equation of the circle circumscribing the triangle ${\text{P}}{{\text{T}}_1}\;{{\text{T}}_2}$ is

$\left( {x - {x_1}} \right)(x + g) + \left( {y - {y_1}} \right)(y + f) = 0$

13. Pole and Polar (Not in syllabus):

(i) If through a point${\text{P}}$ in the plane of the circle there be drawn any straight line to meet the circle in $Q$ and $R$, the locus of the point of intersection of the tangents at ${\text{Q}}$ and ${\text{R}}$ is called the Polar of the point ${\text{P}}$, also ${\text{P}}$ is called the Pole of the Polar.

(ii) The equation of the polar of a point $P\left( {{x_1},\;{y_1}} \right)$ w.r.t, the circle ${x^2} + {y^2} = {a^2}$ is given by $x{x_1} + y{y_1} = {a^2}$ and if the circle is general then the equation of the polar becomes $x{x_1} + y{y_1} + g\left( {x + {x_1}} \right) + 8\left( {y + {y_1}} \right) + c = 0$ i.e. ${\text{T}} = 0$. Note that if the point $\left( {{x_1},\;{y_1}} \right)$ be on the circle then the tangent &e polar will be represented by the same equation. Similarly, if the point $\left( {{x_1},\;{y_1}} \right)$ be outside the circle then the chord of contact and polar will be represented by the same equation.

(iii) Pole of a given line ${\text{Ax}} + {\text{By}} + {\text{C}} = 0$ w.r.t. circle

${x^2} + {y^2} = {a^2}{\text{ is }}\left( { - \dfrac{{Aa}}{C}, - \dfrac{{Ba}}{C}} \right)$.

(iv) If the polar of a point P pass through a point $Q$, then the polar of $Q$ passes through $P$.

(v) Two lines ${{\text{L}}_1}\;\& \;{L_2}$ are conjugate of each other if Pole of ${{\text{L}}_1}$ Lies on ${L_2}$ and vice versa. Similarly two points $P$ and $Q$ are said to be conjugate of each other if the polar of P passes through ${\text{Q}}$ and vice-versa.

14. Equation of Chord with a Given Middle Point:

The equation of the chord of the circle $S = {x^2} + {y^2}$ $ + 2gx + 2fy + c = 0$ in terms of its mid-point$M\left( {{x_1},{y_1}} \right)\;is\;x{x_1} + y{y_1} + g\left( {x + {x_1}} \right) + f\left( {y + {y_1}} \right) + c = x_1^2$ $ + y_1^2 + 2g{x_1} + 2f{y_1} + c$ which is designated by $T\; = \;{S_1}$

Note:

(i) The shortest chord of a circle passing through a point $M$  inside the circle is one chord whose middle point is ${\text{M}}$.

(ii) The chord passing through a point  ${\text{M}}$  inside the circle and which is at a maximum distance from the centre is a chord with middle point ${\text{M}}$

15. Equation of the Chord Joining Two Points of the Circle:

The equation of chord ${\text{PQ}}$ of the circle ${{\text{x}}^2} + {{\text{y}}^2} = {{\text{a}}^2}$ joining two points $P(\alpha )$ and $P(\beta )$ on it is given by. The equation of a straight line joining two point $\alpha $ and $\beta $ on the circle ${x^2} + {y^2}$ $ = {a^2}$ is

$xcos\dfrac{{a + \beta }}{2} + y\sin \dfrac{{\alpha  + \beta }}{2} = \cos \dfrac{{a - \beta }}{2}$

16. Common Tangents to the Two Circle:

(i) 

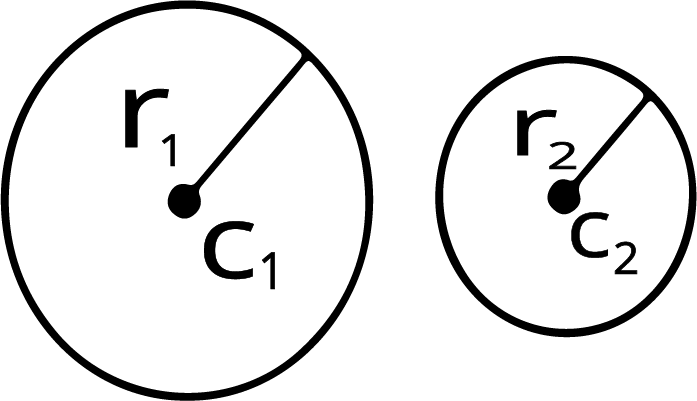
4 common tangents (2 direct and 2 transverse)

${{\text{r}}_1} + {{\text{r}}_2} < {{\text{c}}_1}{{\text{c}}_2}$

(ii) 

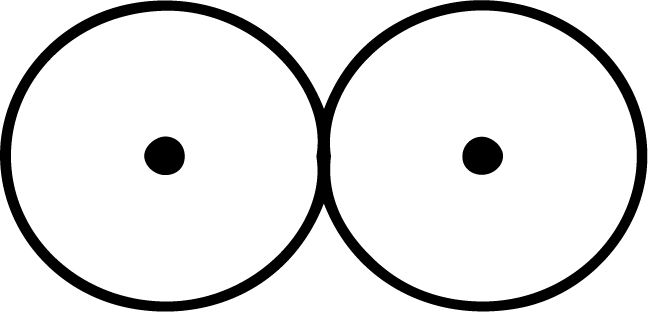
3 common tangents

${r_1} + {r_2} = {c_1}{c_2}$.

(iii) 

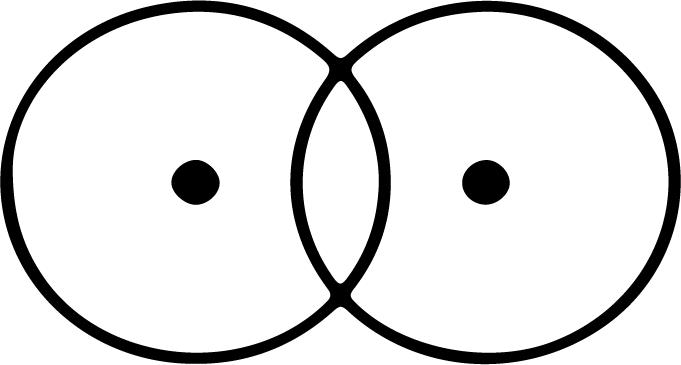
2 common tangents

$\left| {{r_1} - {r_2}} \right| < {c_1}{c_2} < {r_1} + {r_2}$

(iv) 

1 common tangent

$\left| {{r_1} - {r_2}} \right| = {c_1}{c_2}$

(v)

No common tangent

 ${c_1}{c_2} < \left| {{r_1} - {r_2}} \right|$

(Here ,${c_1}{c_2}$ is distance between centers of two circles.)

Note:

(i) The direct common tangents meet at a point which divides the line joining centre of circles externally in the ratio of their radii.

Transverse common tangents meet at a point which divides the line joining centre of circles internally in the ratio of their radii.

(ii) Length of an external (or direct) common tangent & internal (or transverse) common tangent to the two circles are given by : ${L_{{\text{ext }}}} = \sqrt {{d^2} - \left( {{r_1} - {r_2}{)^2}} \right.} $ and ${L_{\operatorname{int} }} = \sqrt {{d^2} - \left( {{r_1} + {r_2}{)^2}} \right.} $, where $d$= between the centers of the two circles and ${r_1},\;{r_2}$ are the radii of the two circles. Note that length of internal common tangent is always less than the length of the external or direct common tangent.

17. Orthogonality of Two Circles:

Two circles ${S_1} = 0\;\& \;{S_2} = 0$ are said to be orthogonal or said to intersect orthogonally if tangents at their point of intersection include a right angle. The condition for two circles to be orthogonal is: $2{g_1}{g_2} + 2{{\text{f}}_1}{{\text{f}}_2} = \;{c_1} + {c_2}$

Note:

(a) The centre of a variable circle orthogonal to two fixed circles lies on the radical axis of two circles.

(b) If two circles are orthogonal, then the polar of a point 'P' on first circle w.r.t. the second circle passes through the point $Q$ which is the other end of the diameter through${\text{P}}$. Hence locus of a point which moves such that its polar wr.t the circles ${S_1} = 0$, ${S_2} = 0$ and  ${S_3} = 0$ are concurrent is a circle which is orthogonal to all the three circles. (Not in syllabus).

(c) The centre of a circle which is orthogonal to three given circles is the radical centre provided the radical centre lies outside all the three circles.

18. Radical Axis and Radical Centre:

The radical axis of two circles is the locus of points whose powers w.r.t. the two circles are equal. The equation of radical axis of the two circles ${S_1} = 0$ and ${S_2} = 0$ is given by: ${S_1} - {S_2} = 0$,i.e., $2\left( {{g_1} - {g_2}} \right)x + 2\left( {{f_1} - {f_2}} \right)y + \left( {{c_1} - {c_2}} \right) = 0$

The common point of intersection of the radical axes of three circles taken two at a time is called the radical centre of three circles. Note that the length of tangents drawn from radical centre to the three circles are equal.

Note:

(a) If two circles intersect, then the radical axis is the common chord of the two circles.

(b) If two circles touch each other then the radical axis is the common tangent of the two circles at the common point of contact.

(c) Radical axis is always perpendicular to the line joining the centers of the two circles.

(d) Radical axis will pass through the mid-point of the line joining the centers of the two circles only if the two circles have equal radii.

(e) Radical axis bisects a common tangent between the two circles.

(f) A system of circles, every two of which have the same radical axis, is called a coaxal system.

(g) Pairs of circles which do not have radical avis are concentric. 

Revision Notes For CBSE Class 11 Maths Chapter 10

Conic Sections: Class 11 Maths Chapter 10 Revision Notes Summary

This chapter is different from that of what you have studied in coordinate geometry. This time, you will study how the syllabus proceeds to a higher level of concepts. You will learn the complex representation of the conic sections. You will also learn the features of those sections and how they are represented on a 2D plane. Let us take a look into Class 11 Maths Revision Notes Chapter 10 and check how you can get help from them.

This chapter begins with the introduction to circles. Students will learn how circles are formed using an equation. There are different kinds of equations described in the chapter that represent a particular set of features of a circle. By learning these equations, you can calculate the radius of a circle, the centre, and other intersection points. This chapter is very crucial for the students as they will need it in the higher classes for equating values of such shapes.

On proceeding further in the Conic Sections Class 11 Notes, you will find the proper explanation of parabolas. In the chapter, you will learn what parabolas are and how they can be represented by an equation. The formula of the parabolas is entirely different from what you have studied. It is quite interesting to learn and remember. This equation will also help you find out the different features of a parabolic curve on a 2D plane. This conic section does not have a centre but a focal point. the behaviour of the X and Y coordinates follow the respective formulas of the curves.

Moving ahead, you will learn what an ellipse is. All elliptical curve has two focal points. The salient feature of that the sum of the distances of any point on this curve is always equal at any instance. Ellipses have their equation that represents the features aptly. Follow the Notes of Class 11 Revision Notes Chapter 10 and find the different features of an ellipse to remember.

Hyperbola is the next concept you will learn in this chapter. This conic section is represented by its equation that perfectly depicts the behaviour of the coordinate points forming the curve. If you follow the Maths Class 11 Conic Sections Notes, you will be able to recall these features along with the equations.

This is how you can use Class 11 Maths Notes of Conic Sections to recapitulate what you have studied in this chapter.

Why Should You Use Class 11 Maths Chapter 10 Revision Notes?

Vedantu has been the primary choice for students of Class 11 for all subjects. The teachers formulate the revision notes in such a way that the students can remember the formulas and concepts easily. The Revision Notes Class 11 Maths Chapter 10 are quite helpful in preparing and revising this chapter before an exam.