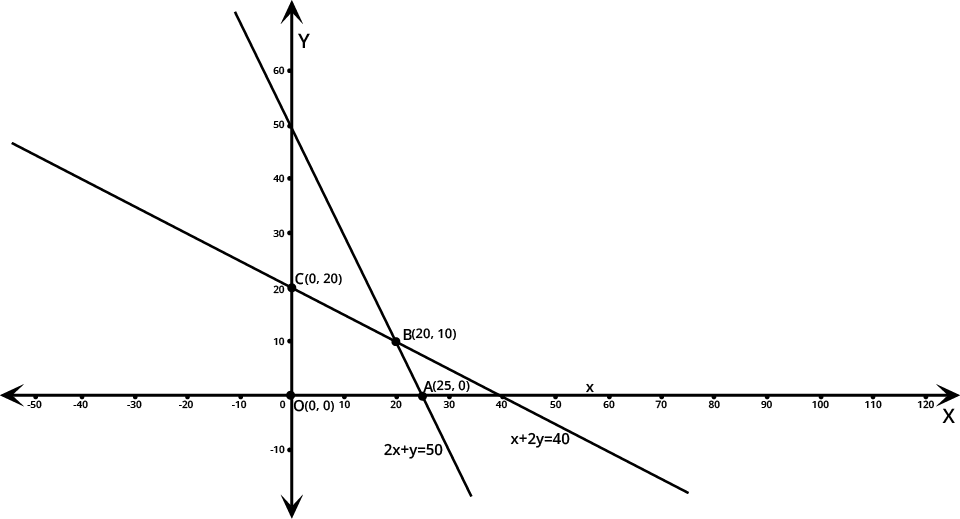
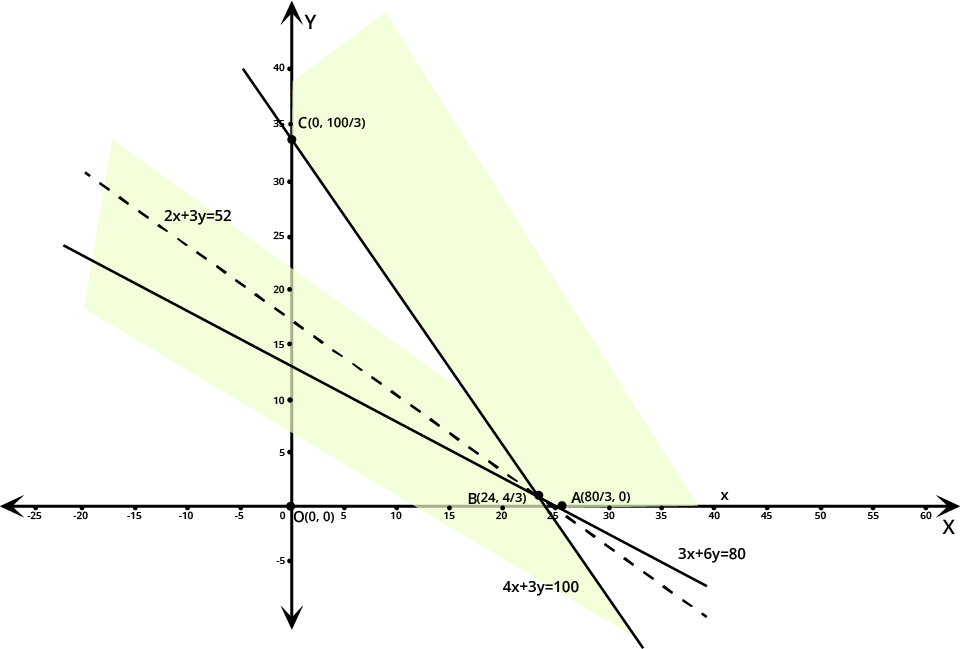
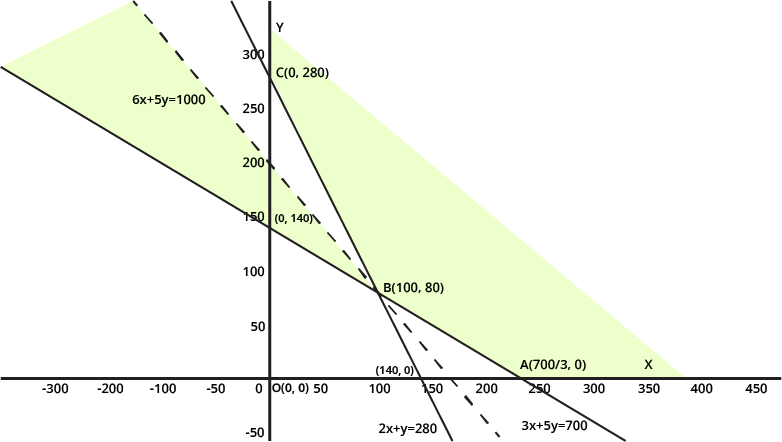
NCERT Solutions for Class 12 Maths Chapter 12: Linear Programming - Exercise 12.2

Exercise 12.2

1. Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs. 60/kg and Food Q costs Rs. 80/kg. Food P contains 3 units /kg of vitamin A and 5 units /kg of vitamin B while food Q contains 4 units /kg of vitamin A and 2 units /kg of vitamin B. Determine the minimum cost of the mixture?

Solution 1:

Let us consider that x kg of food P and y kg of food Q is contained in the mixture.

Then both   \[  x  \] , \[  y \ge 0  \] 

The information given in the question can be put together in a table as follows:

According to the question, the mixture must contain at least 8 units of vitamin A and 11 units of vitamin B.

So, the constraints so formed are

 \[  3x+4y\ge 8  \] 

 \[  5x+2y\ge 11 \]  

For purchasing the food, the total cost Z is given by  \[ Z=60x+80y \] 

 Hence, in mathematical form, the given problem can be written as 

Minimise  \[ Z=60x+80y \]       ….(1)

Subject to the constraints,

 \[ 3x+4y\ge 8 \]             ….(2)

 \[ 5x+2y\ge 11 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ A(8/3,0) \] ,  \[ B(2,1/2) \] and  \[ C(0,11/2) \] are the corner points of the feasible region.

We can clearly see that the feasible region is unbounded

The values of Z at these corner points are calculated as follows.

Clearly, 160 is the smallest value but it may or may not be the minimum value because the feasible region is unbounded

In order to find out if 160 is the minimum value or not, we draw the graph of the inequality  \[ 60x+80y<160 \]  or  \[ 3x+4y<8 \] .

Then we check whether the resulting half-plane has points in common with the feasible region or not.

It can be seen that  \[ 3x+4y<8 \]  and the feasible region has no points in common

Hence, z=160 is the minimum value.

Thus, Rs.160 is the minimum cost of the mixture at the line segment joining the points  \[ A(8/3,0) \]  and  \[ B(2,1/2) \] .

2. One kind of cake requires 200g flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes that can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes? 

Solution 2: 

Let us consider that there are x cakes of one kind and y cakes of another kind.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[  200x+100y\le 5000  \] 

 \[  \Rightarrow 2x+1y\le 50  \] 

 \[  25x+50y\le 1000  \] 

 \[  \Rightarrow x+2y\le 40  \]  

The total number of cakes Z, that can be made is given by  \[ Z=x+y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=x+y \]       ….(1)

Subject to the constraints,

 \[ 2x+y\le 50 \]             ….(2)

 \[ x+2y\le 40 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

 \[ O(0,0) \] ,  \[ A(25,0) \] ,  \[ B(20,10) \] and  \[ C(0,20) \] are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 30 is the maximum value and the feasible region is bounded.

Thus, the maximum number of cakes that can be made is 30 of which 20 are of one kind and 10 are of another kind.

3. A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftsman’s time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftsman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. 

i. What number of rackets and bats must be made if the factory is to work at full capacity? 

Solution 3:

i. Let us consider that x number of rackets and y number of bats must be made.

According to the question, the factory has the availability of not more than 42 hours of machine time.

Therefore,  \[ 1.5x+3y\le 42 \]      ….(1)

It is also given that the factory has the availability of not more than 24 hours of craftsman’s time. 

Therefore,  \[ 3x+y\le 24 \]         .…(2)

Now, if the factory is to work at full capacity, then

 \[ 1.5x+3y=42 \] 

 \[ 3x+y=24 \] 

On solving these two equations, we get  \[ x=4 \]  and  \[ y=12 \] 

Hence, the number of rackets and bats that must be made if the factory is to work at full capacity are 4 and 12 respectively.

ii. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the maximum profit of the factory when it works at full capacity. 

Solution 3:

ii. We already considered that x number of rackets and y number of bats must be made

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[ 1.5x+3y\le 42 \] 

 \[ 3x+y\le 24 \] 

It is given that the profit on a racket is Rs. 20 and on a bat is Rs. 10.

So, we have total profit as   \[ Z=20x+10y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=20x+10y \]       ….(1)

Subject to the constraints,

 \[ 1.5x+3y\le 42 \]             ….(2)

 \[ 3x+y\le 24 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ O(0,0) \] , \[ A(8,0) \] ,  \[ B(4,12) \] and  \[ C(0,14) \] are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 200 is the maximum value 

Thus, Rs.200 is the maximum profit of the factory when it works at full capacity.

4. A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 12 hours a day? 

Solution 4: 

Let us consider that there are x packages of nuts and y packages of bolts that are produced by the manufacturer.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[  x+3y\le 12  \] 

 \[  3x+y\le 12  \] 

It is given that the manufacturer earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts 

So, the total profit is given by  \[ Z=17.5x+7y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=17.5x+7y \]       ….(1)

Subject to the constraints,

 \[ x+3y\le 12 \]             ….(2)

 \[ 3x+y\le 12 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ O(0,0) \] ,  \[ A(4,0) \] ,  \[ B(3,3) \]  and  \[ C(0,4) \]  are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 73.5 is the maximum value and the feasible region is bounded.

Therefore, 3 packages of nuts and 3 packages of bolts should be produced each day to get the maximum profit of Rs. 73.50.

5. A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand-operated one. It takes 4 minutes on the automatic and 6 minutes on hand-operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand-operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs.10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.

Solution 5:

Let us consider that the factory manufacture x screws of type A and y screws of type B each day.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[  4x+6y\le 240  \]  

 \[  6x+3y\le 240  \]  

It is given that; the manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs.10

The total profit is given by,  \[ Z=7x+10y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=7x+10y \]       ….(1)

Subject to the constraints,

 \[ 4x+6y\le 240 \]             ….(2)

 \[ 6x+3y\le 240 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ O(0,0) \] ,  \[ A(40,0) \] ,  \[ B(30,20) \] and  \[ C(0,40) \]  are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 410 is the maximum value and the feasible region is bounded.

Thus, 30 packages of screws A and 20 packages of screws B should be produced in a day in order to maximize his profit. The maximum profit is Rs. 410.

6. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding /cutting machine and a sprayer. It takes 2 hours on the grinding /cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding /cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?

Solution 6:

Let us consider that the cottage industry manufactures x pedestal lamps and y wooden shades.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[  2x+y\le 12  \] 

 \[  3x+2y\le 20  \] 

It is given that; the profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3.

The total profit is given by,  \[ Z=5x+3y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=5x+3y \]       ….(1)

Subject to the constraints,

 \[ 2x+y\le 12 \]             ….(2)

 \[ 3x+2y\le 20 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ O(0,0) \] ,  \[ A(6,0) \] ,  \[ B(4,4) \] and  \[ C(0,10) \] are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 32 is the maximum value and the feasible region is bounded.

Therefore, in order to maximize the profit, the manufacturer should produce 4 pedestal lamps and 4 wooden shades.

7. A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours of assembling. The profit is Rs. 5 each for type A and Rs. 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?

Solution 7:

Let us consider that, x souvenirs of type A and y souvenirs of type B are manufactured by the company.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[ 5x+8y\le 200 \] 

 \[ 10x+8y\le 240 \] 

 \[ \Rightarrow 5x+4y\le 120 \] 

It is given that; the profit is Rs. 5 each for type A and Rs. 6 each for type B souvenirs.

The total profit is given by,  \[ Z=5x+6y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=5x+6y \]       ….(1)

Subject to the constraints,

 \[ 5x+8y\le 200 \]             ….(2)

 \[ 5x+4y\le 120 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ O(0,0) \] ,  \[ A(24,0) \] ,  \[ B(8,20) \] and  \[ C(0,25) \] are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 160 is the maximum value and the feasible region is bounded.

Therefore, in order to maximize the profit of Rs.160, 8 souvenirs of type A and 20 souvenirs of type B should be manufactured by the company.

8. A merchant plans to sell two types of personal computers − a desktop model and a portable model that will cost Rs. 25000 and Rs. 40000 respectively. He estimates that the total monthly demand for computers will not exceed 250 units. Determine the number of units of each type of computer which the merchant should stock to get maximum profit if he does not want to invest more than Rs. 70 lakhs and if h is profit on the desktop model is Rs. 4500 and on portable model is Rs. 5000.

Solution 8:

Let us consider the merchant stock x desktop models and y portable models.

Then both   \[ x \] , \[ y\ge 0 \] 

According to the question, a desktop model and a portable model will cost Rs. 25000 and Rs. 40000 respectively and the merchant can invest a maximum of   Rs. 70 lakhs

Therefore, 

 \[  25000x+40000y\le 7000000  \] 

 \[  \Rightarrow 5x+8y\le 1400  \] 

It is also given that the total monthly demand for computers will not exceed 250 units

 \[ \Rightarrow x+y\le 250 \] 

It is given that; profit on the desktop model is Rs. 4500 and on portable model is Rs. 5000

The total profit is given by,  \[ Z=4500x+5000y \] 

 Hence, in mathematical form, the given problem can be written as 

Maximise  \[ Z=4500x+5000y \]       ….(1)

Subject to the constraints,

 \[ 5x+8y\le 1400 \]             ….(2)

 \[ x+y\le 250 \]           ….(3)

 \[ x \] , \[ y\ge 0 \]          ….(4)

According to these constraints, the feasible region is:

(Image will be uploading soon)

 \[ O(0,0) \] ,  \[ A(250,0) \] ,  \[ B(200,50) \] and  \[ C(0,175) \] are the corner points of the feasible region.

The values of Z at these corner points are calculated as follows.

Clearly, 1150000 is the maximum value and the feasible region is bounded.

Therefore, in order to get the maximum profit of Rs. 1150000, the merchant should stock 200 desktop models and 50 portable models.

9. A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs. 4 per unit of food and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for a diet that consists of a mixture of these two foods and also meets the minimal nutritional requirements?

Solution 9:

Let us consider that x kg of food F1 and y kg of food F2 is contained in the diet.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

So, the constraints so formed are

 \[  3x+6y\ge 80  \] 

 \[  4x+3y\ge 100  \] 

According to the question, Food F1 costs Rs. 4 per unit of food and F2 costs Rs. 6 per unit

The total cost of the diet is given by  \[ Z=4x+6y \] 

 Hence, in mathematical form, the given problem can be written as 

Minimise  \[ Z=4x+6y \]       ….(1)

Subject to the constraints,

 \[ 3x+6y\ge 80 \]             ….(2)

 \[ 4x+3y\ge 100 \]          ….(3)

 \[ x \] , \[ y\ge 0 \]               ….(4)

According to these constraints, the feasible region is:

 \[ A(80/3,0) \] ,  \[ B(24,4/3) \]  and  \[ C(0,100/3) \]  are the corner points of the feasible region.

We can clearly see that the feasible region is unbounded

The values of Z at these corner points are calculated as follows.

Clearly, 104 is the smallest value but it may or may not be the minimum value because the feasible region is unbounded

In order to find out if 104 is the minimum value or not, we draw the graph of the inequality  \[ 4x+6y<104 \]  or  \[ 2x+3y<52 \] .

Then we check whether the resulting half-plane has points in common with the feasible region or not.

It can be seen that  \[ 2x+3y<52 \]  and the feasible region has no points in common

Hence, z=104 is the minimum value.

Thus, Rs.104 is the minimum cost of the mixture.

10. There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds that she needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs Rs. 6/kg and F2 costs Rs. 5/kg, determine how much of each type of fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost? 

Solution 10:

Let us consider that the farmer bought x kg of fertilizer F1 and y kg of fertilizer F2.

Then both   \[ x \] , \[ y\ge 0 \] 

The information given in the question can be put together in a table as follows:

According to the question, F1 consists of 10% nitrogen and F2 consists of 5% nitrogen and the farmer requires at least 14 kg of nitrogen.

Therefore, 10% of x + 5% of y  \[ \ge 14 \] 

 \[  \dfrac{x}{10}+\dfrac{y}{20}\ge 14  \] 

 \[  2x+y\ge 280  \] 

It is also given that, F1 Consists of 6% phosphoric acid and F2 consists of 10% phosphoric acid and the farmer requires at least 14 kg of phosphoric acid.

Therefore, 6% of x+ 10% of y  \[ \ge 14 \] 

 \[  \dfrac{6x}{100}+\dfrac{10y}{100}\ge 14  \] 

 \[  3x+56y\ge 700  \]  

Since F1 cost Rs. 6/kg and F2 costs Rs. 5/kg

So, the total cost of fertilizer is given by  \[ Z=6x+5y \] 

Hence, in mathematical form, the given problem can be written as 

Minimise  \[ Z=6x+5y \]    ….(1)

Subject to the constraints,

 \[ 2x+y\ge 280 \]             ….(2)

 \[ 3x+56y\ge 700 \]        ….(3)

 \[ x \] , \[ y\ge 0 \]           ….(4)

According to these constraints, the feasible region is:

 \[ A(700/3,0) \] ,  \[ B(100,80) \]  and  \[ C(0,280) \]  are the corner points of the feasible region.

We can clearly see that the feasible region is unbounded

The values of Z at these corner points are calculated as follows.

Clearly, 1000 is the smallest value but it may or may not be the minimum value because the feasible region is unbounded

In order to find out if 1000 is the minimum value or not, we draw the graph of the inequality  \[ 6x+5y<1000 \] 

Then we check whether the resulting half-plane has points in common with the feasible region or not.

It can be seen that  \[ 6x+5y<1000 \]  and the feasible region has no points in common

Hence, z=1000 is the minimum value.

Thus, Rs.1000 is the minimum cost, and 100 kg of fertilizer F1 and 80 kg of fertilizer F2 should be used to minimize the cost.

11. The corner points of the feasible region determined by the following system of linear inequalities: \[ \text{2x+y}\le \text{10} \] ,  \[ \text{x+3y}\le \text{15} \] ,  \[ \text{xy}\ge \text{0} \]  are  \[ \text{(0,0),(5,0),(3,4),and(0,5)} \] . Let,  \[ \text{Z=px+qy} \]  where p, q >0. Condition on p and q so that the maximum of Z occurs at both  \[ \text{(3,4)} \] and  \[ \text{(0,5)} \]  is (A) p=q (B) P=2q (C) p=3q (D) q=3p

Solution 11:

Z has a unique maximum value.

According to the question, the maximum value of z occurs at the points  \[ (3,4) \]  and  \[ (0,5) \] 

Therefore, the value of Z will be equal at both the points.

That is, the value of Z at  \[ (3,4) \]  = the value of Z at  \[ (0,5) \] 

\[ \Rightarrow p(3)+q(4)=p(0)+q(5) \] 

\[ \Rightarrow 3p+4q=5q \] 

\[ \Rightarrow q=3p \] 

Therefore (D) is the correct answer.

NCERT Solutions for Class 12 Maths PDF Download

• Chapter 1 - Relations and Functions

• Chapter 2 - Inverse Trigonometric Functions

• Chapter 3 - Matrices

• Chapter 4 - Determinants

• Chapter 5 - Continuity and Differentiability

• Chapter 6 - Application of Derivatives

• Chapter 7 - Integrals

• Chapter 8 - Application of Integrals

• Chapter 9 - Differential Equations

• Chapter 10 - Vector Algebra

• Chapter 11 - Three Dimensional Geometry

• Chapter 12 - Linear Programming

• Chapter 13 - Probability

NCERT Solution Class 12 Maths of Chapter 12 All Exercises

NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming Exercise 12.2

Opting for the NCERT solutions for Ex 12.2 Class 12 Maths is considered as the best option for the CBSE students when it comes to exam preparation. This chapter consists of many exercises. Out of which we have provided the Exercise 12.2 Class 12 Maths NCERT solutions on this page in PDF format. You can download this solution as per your convenience or you can study it directly from our website/ app online.

Vedantu in-house subject matter experts have solved the problems/ questions from the exercise with the utmost care and by following all the guidelines by CBSE. Class 12 students who are thorough with all the concepts from the Maths textbook and quite well-versed with all the problems from the exercises given in it, then any student can easily score the highest possible marks in the final exam. With the help of this Class 12 Maths Chapter 12 Exercise 12.2 solutions, students can easily understand the pattern of questions that can be asked in the exam from this chapter and also learn the marks weightage of the chapter. So that they can prepare themselves accordingly for the final exam.

Besides these NCERT solutions for Class 12 Maths Chapter 12 Exercise 12.2, there are plenty of exercises in this chapter which contain innumerable questions as well. All these questions are solved/answered by our in-house subject experts as mentioned earlier. Hence all of these are bound to be of superior quality and anyone can refer to these during the time of exam preparation. In order to score the best possible marks in the class, it is really important to understand all the concepts of the textbooks and solve the problems from the exercises given next to it. 

Do not delay any more. Download the NCERT solutions for Class 12 Maths Chapter 12 Exercise 12.2 from Vedantu website now for better exam preparation. If you have the Vedantu app in your phone, you can download the same through the app as well. The best part of these solutions is these can be accessed both online and offline as well.