NCERT Exemplar for Class 12 Maths - Linear Programming - Free PDF Download
Free PDF download of NCERT Exemplar for Class 12 Maths Chapter 12 - Linear Programming solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 12 - Linear Programming Exercise questions with solutions to help you to revise complete syllabus and score more marks in your Examinations.
Access NCERT Solutions for Mathematics Chapter 12 – Linear Programming
Short Answer
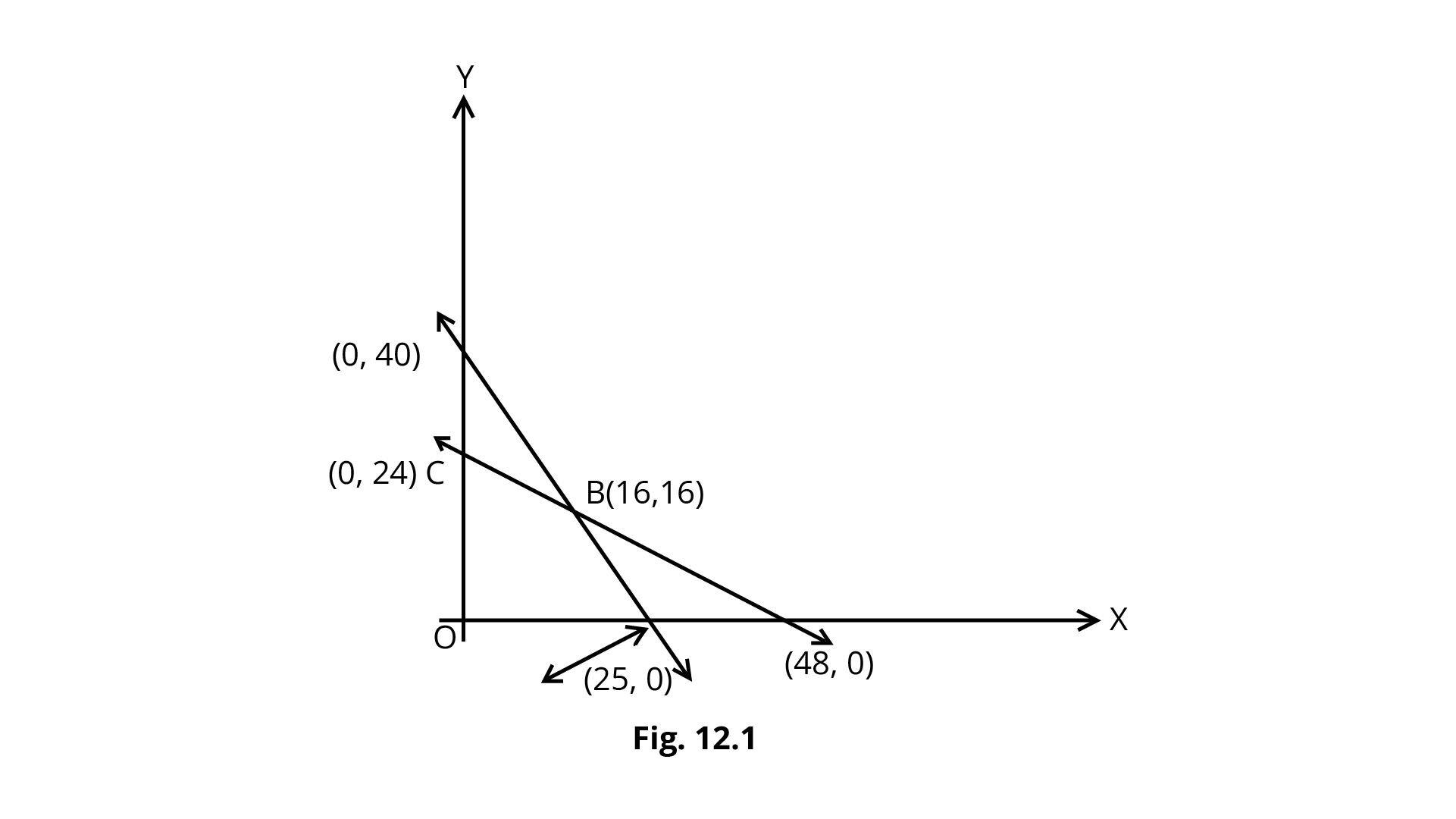
Example 1: Determine the maximum value of $Z=4x+3y$ if the feasible region for an LPP is shown in Fig. 12.1.
Ans: The feasible region is bounded. So, the maximum of $Z$ must occur at the corner point of the feasible region.
Corner Point | Value of $Z$ |
O (0, 0) A (25,0) B (16, 16) C (0,24) | 4 (0) + 3 (0)= 0 4 (25)+3 (0)=100 4 (16)+3 (16)=112(Maximum) 4 (0)+ 3 (24)=72 |
So, the maximum value of $Z$ is 112.
Example 2: Determine the minimum value of $Z=3x + 2y$ (if any), if the feasible region for an LPP is shown in Fig. 12.2.
Ans: The feasible region is unbounded. So the minimum of $Z$ may or may not exist. If it exists, it will be at the corner point(in figure).
Corner Point | Value of $Z$ |
A (12, 0) B (4,2) C (1, 5) D (0,10) | 3 (12)+2 (0)36 3 (4)+ 2 (2)= 16 3 (1)+2 (5) =13 (smallest) 3 (0)+2 (10) =20 |
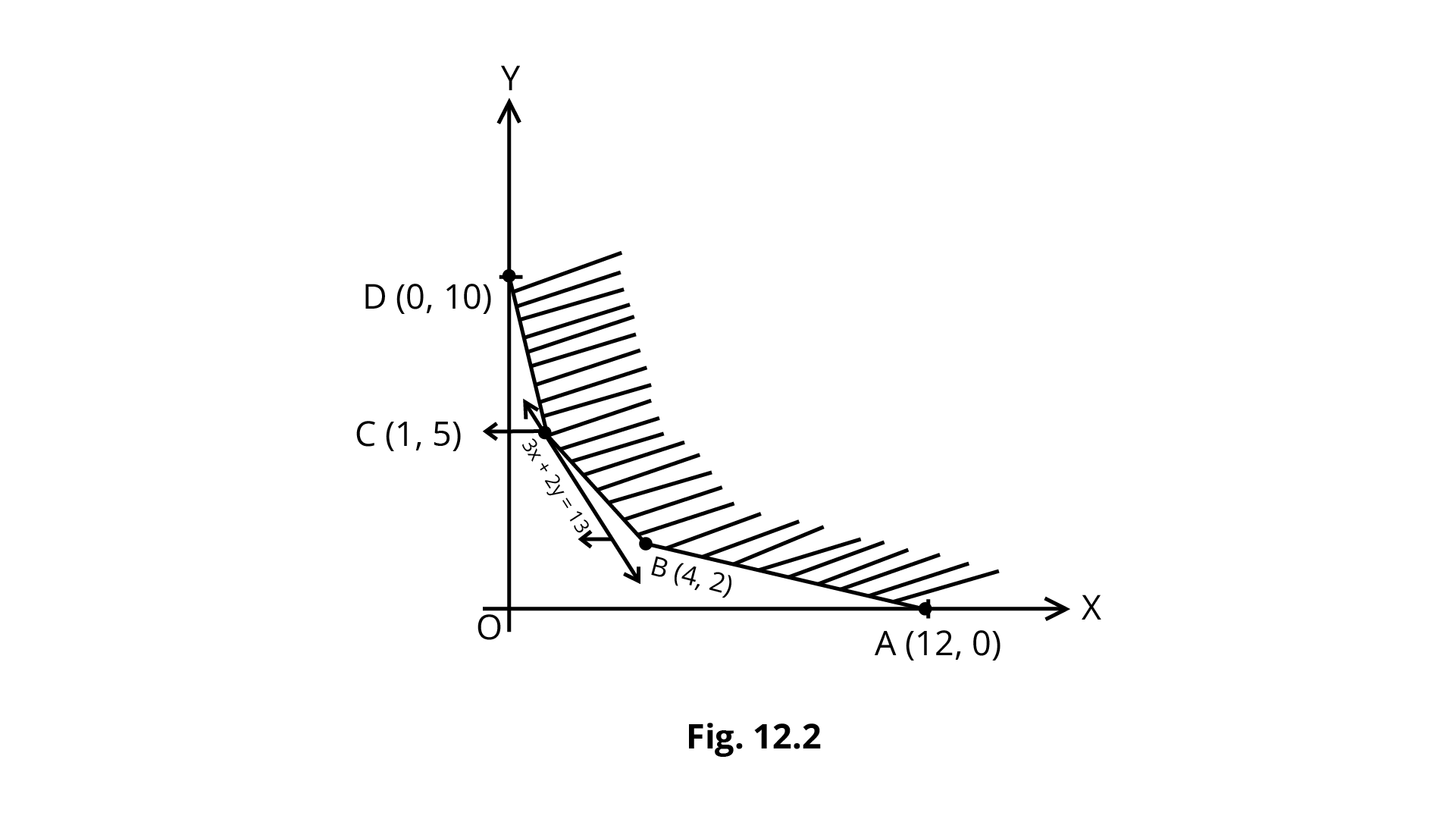
In the graph we see that the open half plane determined by $3x-2y<13$ and R do not have a common point. So, the smallest value = 13 is the minimum value of $Z$.
Example 3: Solve the following LPP graphically:
Maximise $Z=2x+3y$,
subject to $x+y\leq 4$,$x \geq 0$,$y \geq 0$
Ans: The shaded region OAB in Fig. is the feasible region determined by the system of constraints $x\geq0$,$y\geq0$,$x+y\leq 4$.
The feasible region OAB is bounded, so maximum value will occur at a corner point of the feasible region. Corner Points are O(0, 0), A (4,0) and B (0, 4).
Evaluate Z.
Corner Point | Value of $Z$ |
O, (0,0) A (4,0) B (0,4) | 2(0)+3 (0)=0 2 (4)+ 3 (0)=8 2(0)+3 (4)= 12(Maximum) |
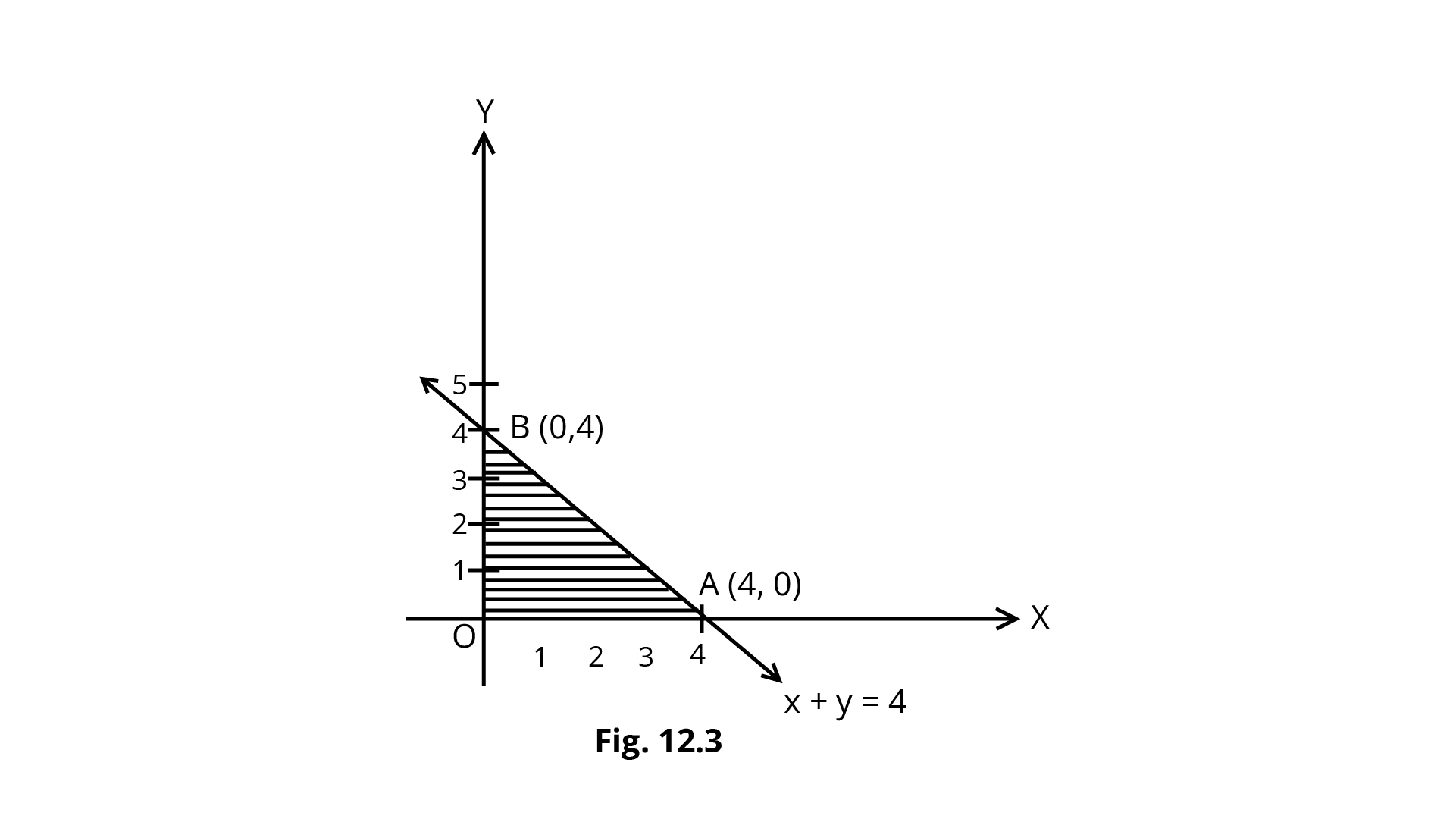
So, the maximum value of $Z$ =12 at the point (0, 4).
Example 4: A manufacturing company makes two types of television sets;one is black and white and the other is colour. The company has resources to make at most 300 sets a week. It takes Rs 1800 to make a black and white set and Rs 2700 to make a coloured set. The company can spend not more than Rs 648000 a week to make. television sets. If it makes a profit of Rs 510 per black and white set and Rs 675 per
coloured set, how many sets of each type should be produced so that the company has maximum profit! Formulate this problem as a LPP given that the objective is to maximise the profit.
Ans: Let's assume the number of black and white sets is $x$ and $y$ is the number of coloured sets made each week. Thus
$x\geq0$,$y\geq0$
Because the company can make at most 300 sets a week, so, $x+y\leq300$
Weekly cost (in Rs) of manufacturing the set is
$1800x+2700y$ and the company can spend upto Rs. 648000. Therefore,
$1800x+2700y\leq648000$, ie., or $2x+3y \leq720$
The total profit on $x$ black and white sets and $y$ colour sets is Rs $(510x-675y)$, Let $Z= 510x+675y$. So,this is the objective function.
So, the mathematical formulation of the problem is
Maximise $Z= 510x+675y$
subject to the constraints: $x+y\leq300$
$2x+3y \leq720$
$x\geq0$,$y\geq0$
Long Answer
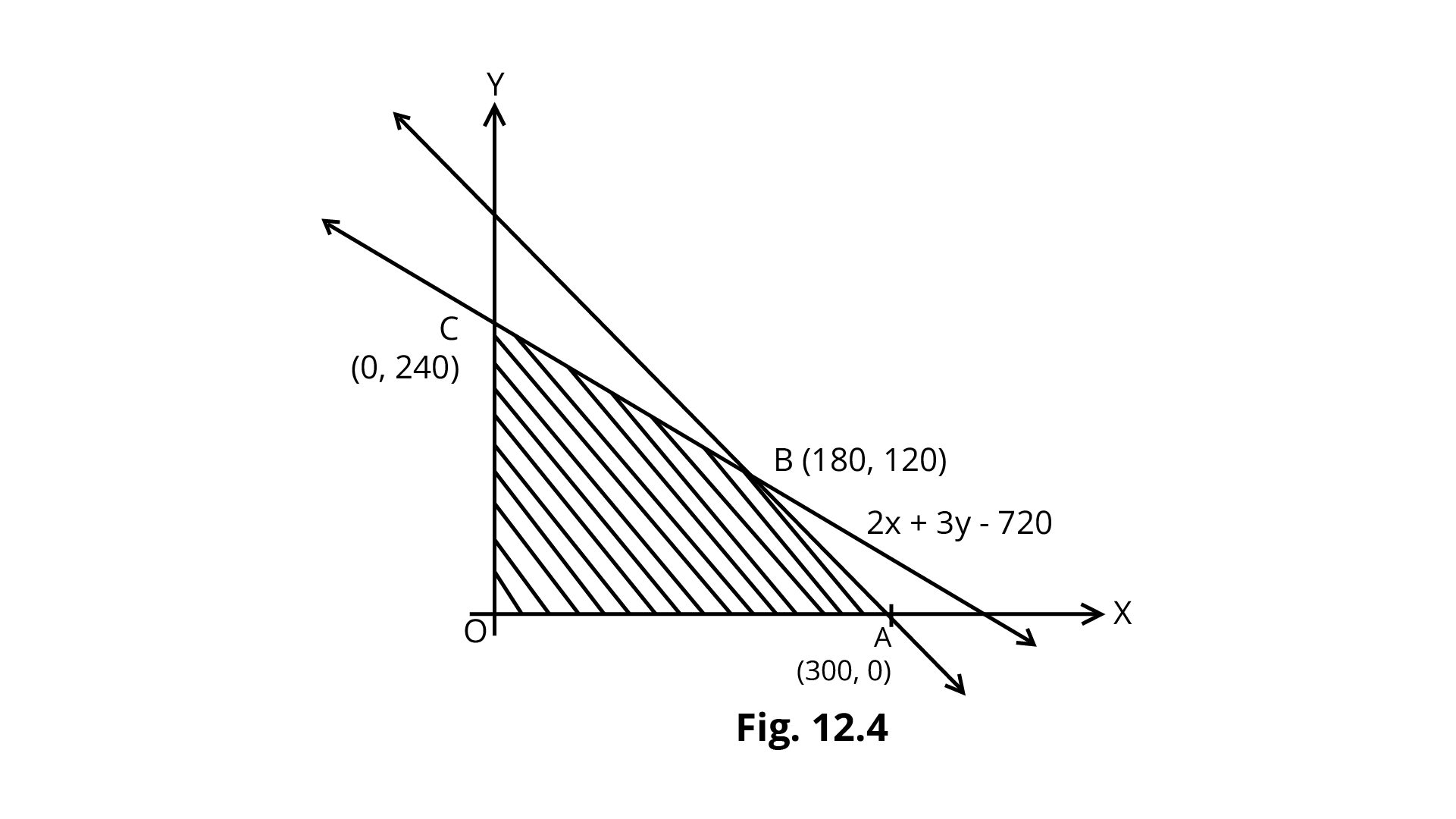
Example 5: Refer to Example 4, Solve the LPP.
Ans: The problem:
Maximise $Z= 510x+675y$
subject to the constraints: $x+y\leq300$
$2x+3y \leq720$
$x\geq0$,$y\geq0$
The feasible region OABC is shown within the Fig.
Because the feasible region is bounded, a maximum of $Z$ must occur at the corner point of OBC.
Corner Point | Value of $Z$ |
O (0,0) A (300, 0) B (180, 120) C (0, 240) | 510 (0)+675 (0)=0 510 (30))+675 (0)= 153000 510 (180) +675 (120)=172800 (maximum) 510 (0)+675 (240)= 162000 |
So, maximum $Z$ = 172800 at the point (180, 120).If the company produces 180 black and white television sets and 120 coloured television sets they will induce maximum profit.
Example 6: Minimise $Z=3x+ 5y$ subject to the constraints:
$x+2y\geq10$
$x+y\geq6$
$3x+y\geq8$
$x,y\geq0$
Ans: We first draw the graphs of x+2y-10, x+y=6,3x+y=8. The shaded region ABCD is the feasible region determined by the above restriction. The feasible region is unbounded. Therefore, a minimum of 7. may or may not occur. If it happens, it will be on the corner point.
Corner Point | Value of $Z$ |
A (0,8) B (1,5) C (2,4) D (10,0) | 40 28 26(smallest) 30 |
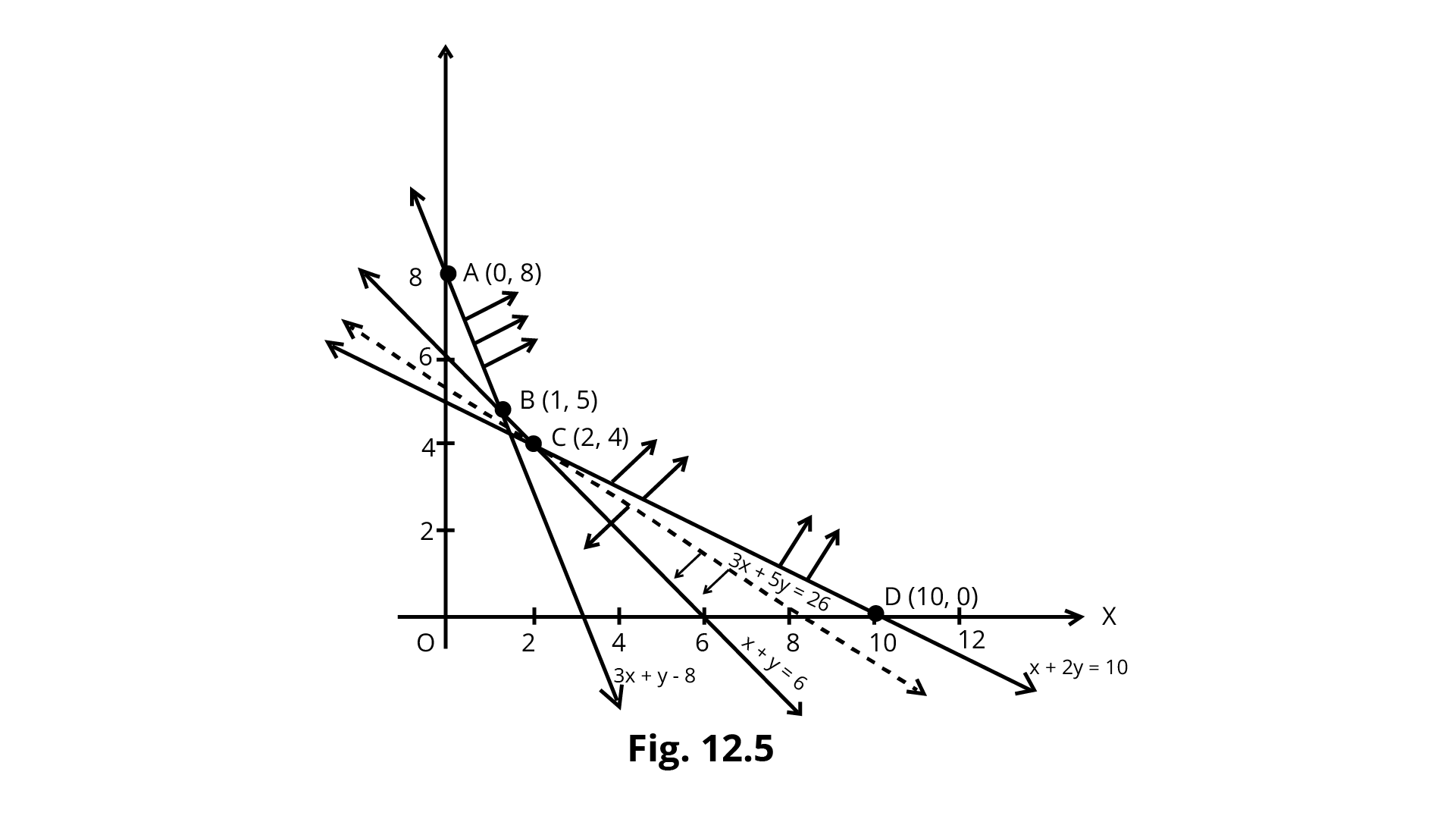
In the graph of $3x+5y\lt26$ as shown in Fig. by dotted line. We see that the open half plane determined by $3x + 5y\lt 26$ and R do not have a point in common. Thus, the minimum value of $Z$ is 26.
Objective Type Questions
Choose the correct answer from the given four options in each of the Examples 7 to 8.
Example 7: The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z-px+qy, where p, q> 0. Condition on p and q so that the maximum of $Z$ occurs at both the points (15, 15) and (0, 20) is
(A) p=q
(B) p=2q
(C) q=2p
(D) q=3p
Ans: Correct option - D
Because $Z$ occurs maximum at (15, 15) and (0, 20)
Therefore,15p+ 15q=0.p+20.q
15p+ 15q=20.q
15p=5q
or, q=3p
Example 8: Feasible region (shaded) for a LPP is shown in the Fig. Minimum of $Z= 4x + 3y$ occurs at the point
(A) (0,8)
(B) (2,5)
(C) (4,3)
(D) (9,0)
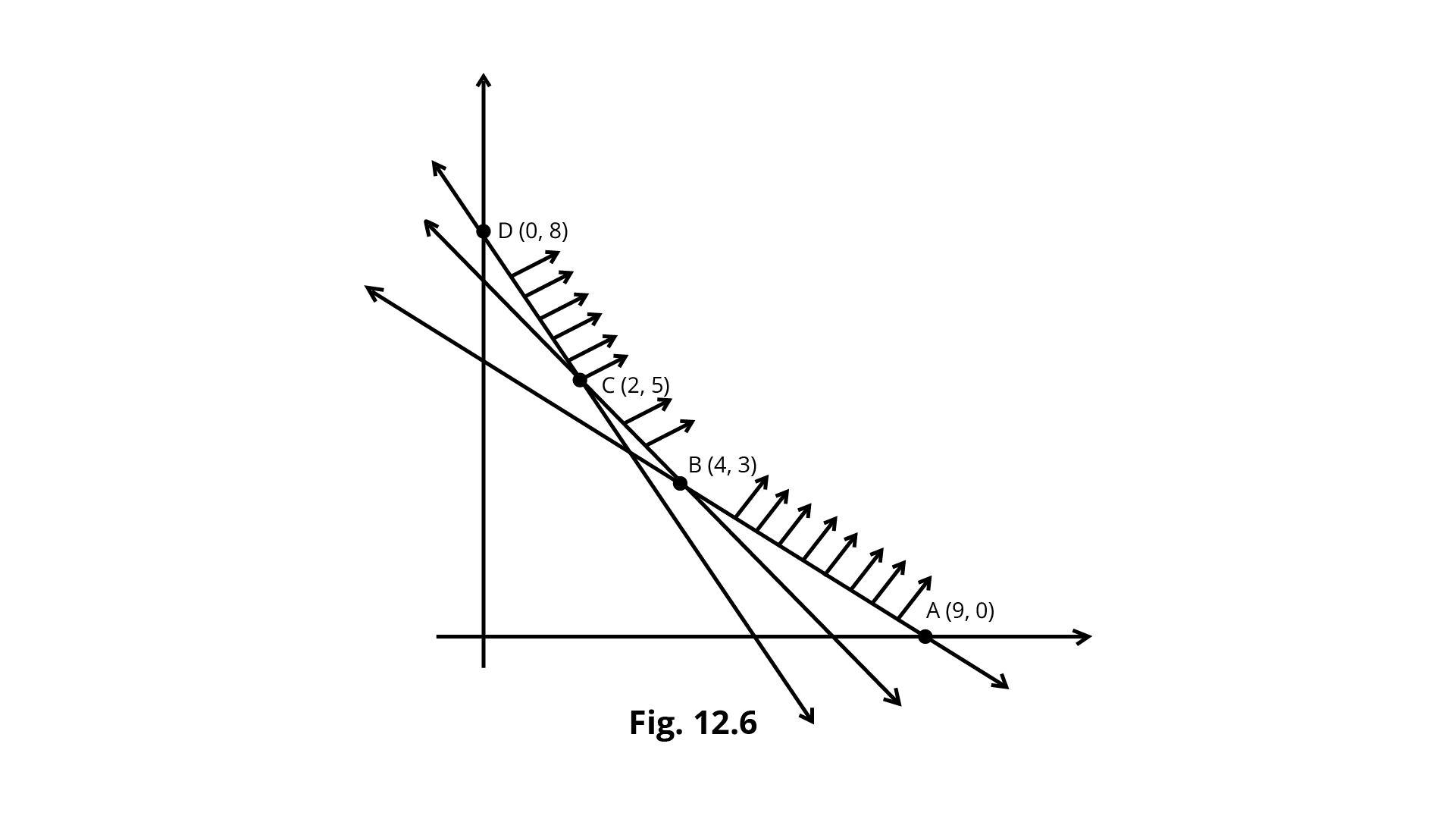
Ans: Correct option - B
Fill in the blanks in each of the Examples 9 and 10.
Example 9: In a LPP, the linear function which has to be maximised or minimised is called a linear……… function.
Ans: In a LPP, the linear function which has to be maximised or minimised is called a linear Objective function.
Example 10: The common region determined by all the linear constraints of a LPP is called the……. region.
Ans: The common region determined by all the linear constraints of a LPP is called the Feasible region.
State whether the statements in Examples 11 and 12 are True or False.
Example 11: If the feasible region for a linear programming problem is bounded, then The objective function $Z=ax+ by$ has both a maximum and a minimum value on R.
Ans: True
Example 12: The minimum value of the objective function $Z= ax + by$ in a linear programming problems always occur at only one corner point of the feasible region.
Ans: False
Because the minimum value can also occur at more than one corner points of the feasible region.
Exercise
Short Answer Questions
1. Determine the maximum value of $Z=11x+7y$ subject to the constraints:
$2x+y\leq 6$,$x\leq 2$,$x\geq 0$,$y\geq 0$.
Ans: We have to maximise $Z=11x+7y$.... (i)
Subject to the constraints
$2x+y\leq 6$...(ii)
$x\leq 2$....(iii)
$x\geq 0$,$y\geq 0$.....(iv)
We plotted these inequalities shown in the figure.
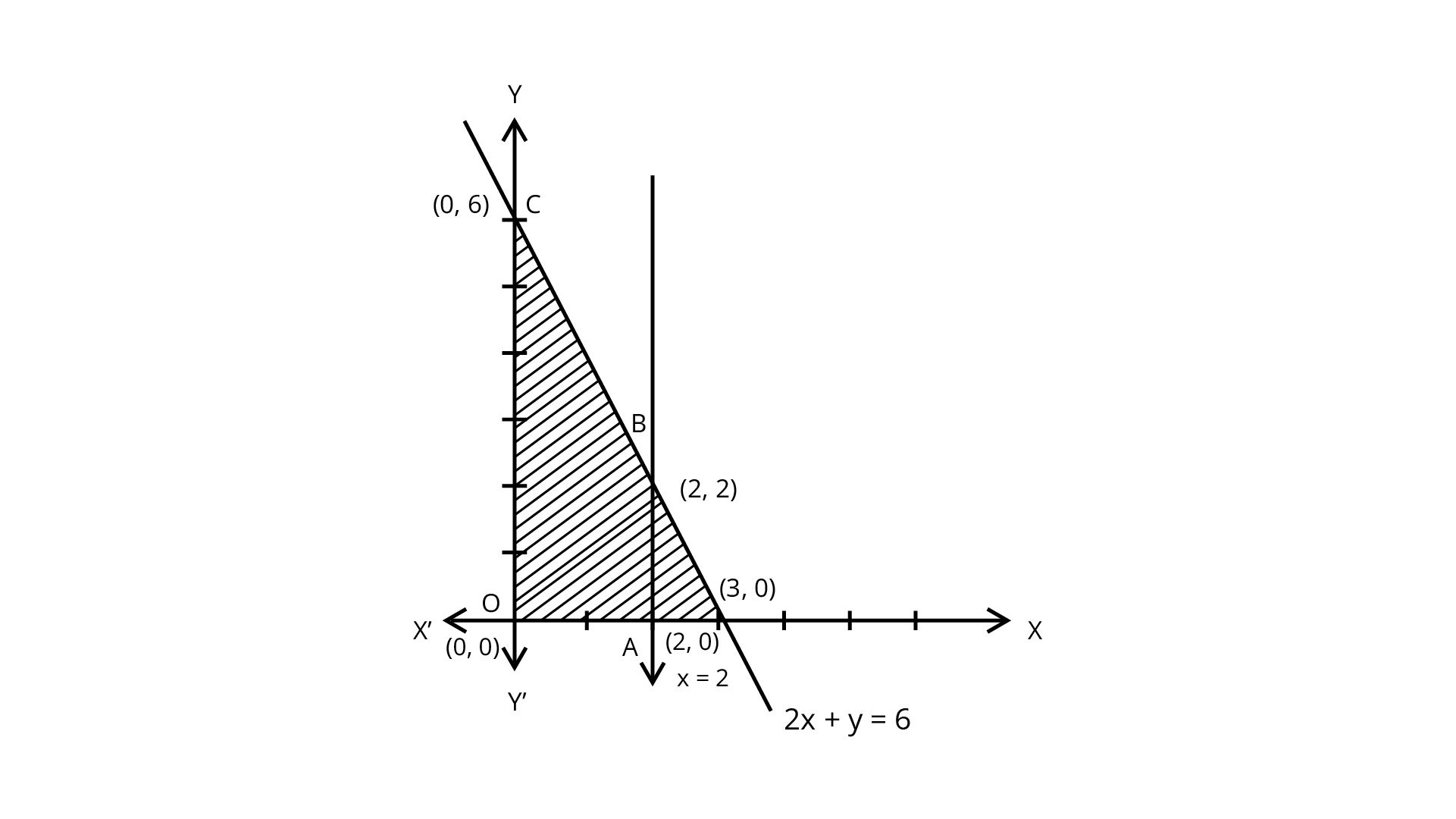
The shaded region is shown as OABC is bounded and the corner points are O(0,0),A(2,0),B(2,2) and C(0,6).
Corner Point | Value of $Z$ |
(0,0) (2,0) (2,2) (0,6) | 0 22 36 42 (maximum) |
So, the maximum value of $Z$ is 42 at (0, 6).
2. Maximise $Z=3x+4y$, subject to the constraints: $x+y\leq1$,$x\geq0$, $y\geq0$.
Ans: Maximise $Z = 3x+4y$
Subject to the constraints
$x+y\leq1$,$x\geq0$, $y\geq0$
We plotted these inequalities shown in the figure.
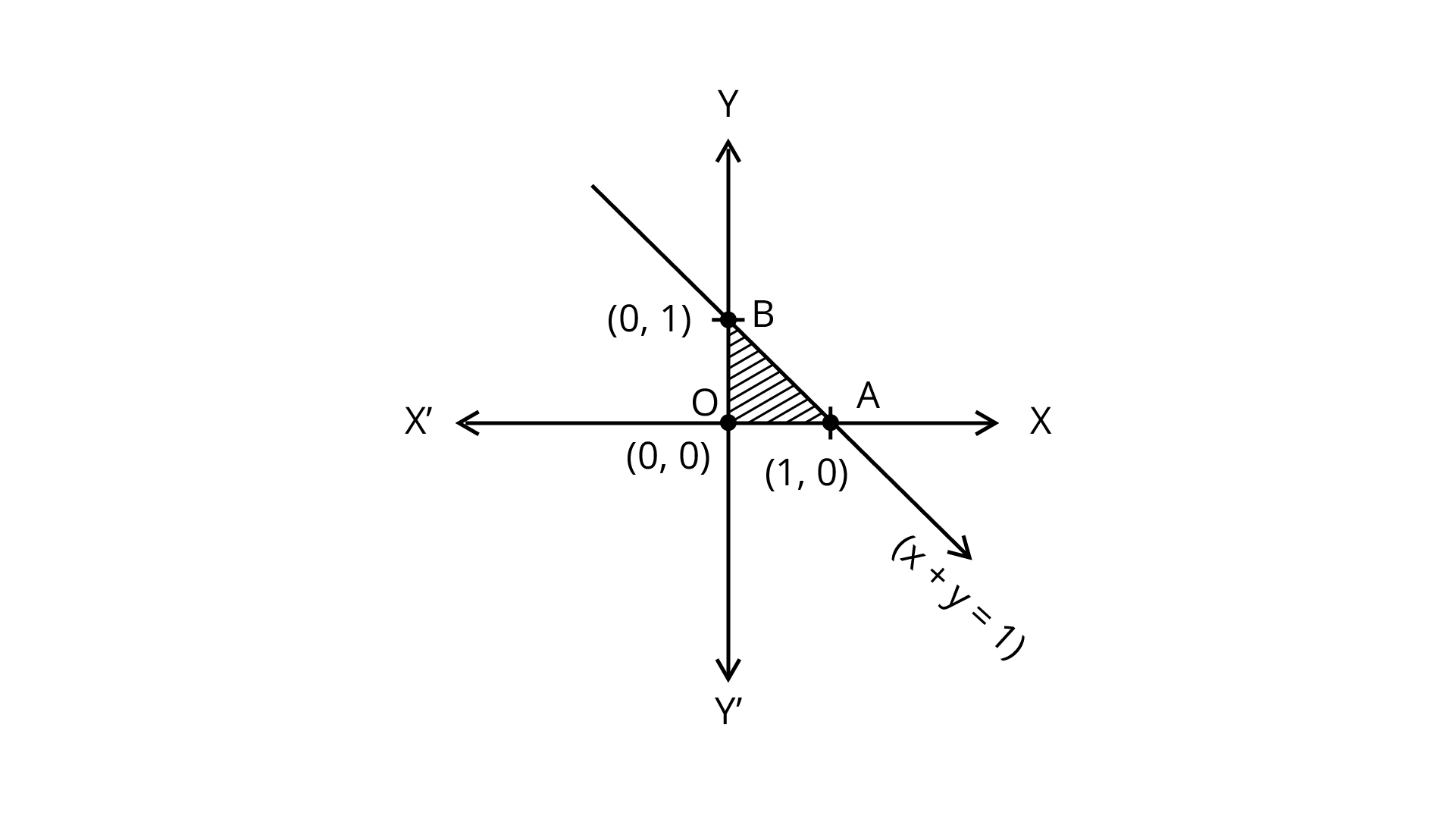
The Shaded region shown in the figure as OAB is bounded and the corner points are O(0,0), A(1,0),B(0,1).
Corner Point | Value of $Z$ |
(0,0) (1,0) (0,1) | 0 3 4 (maximum) |
So, the maximum value of $Z$ is 4 at (0, 1).
3. Maximise the function $Z=11x+7y$, subject to the constraints: $x\leq3$, $y\leq 2$ ,$x\geq0$, $y\geq0$.
Ans: Maximise $Z=11x+7y$
Subject to the constraints
$x\leq3$, $y\leq 2$ ,$x\geq0$, $y\geq0$
We plotted these inequalities shown in the figure
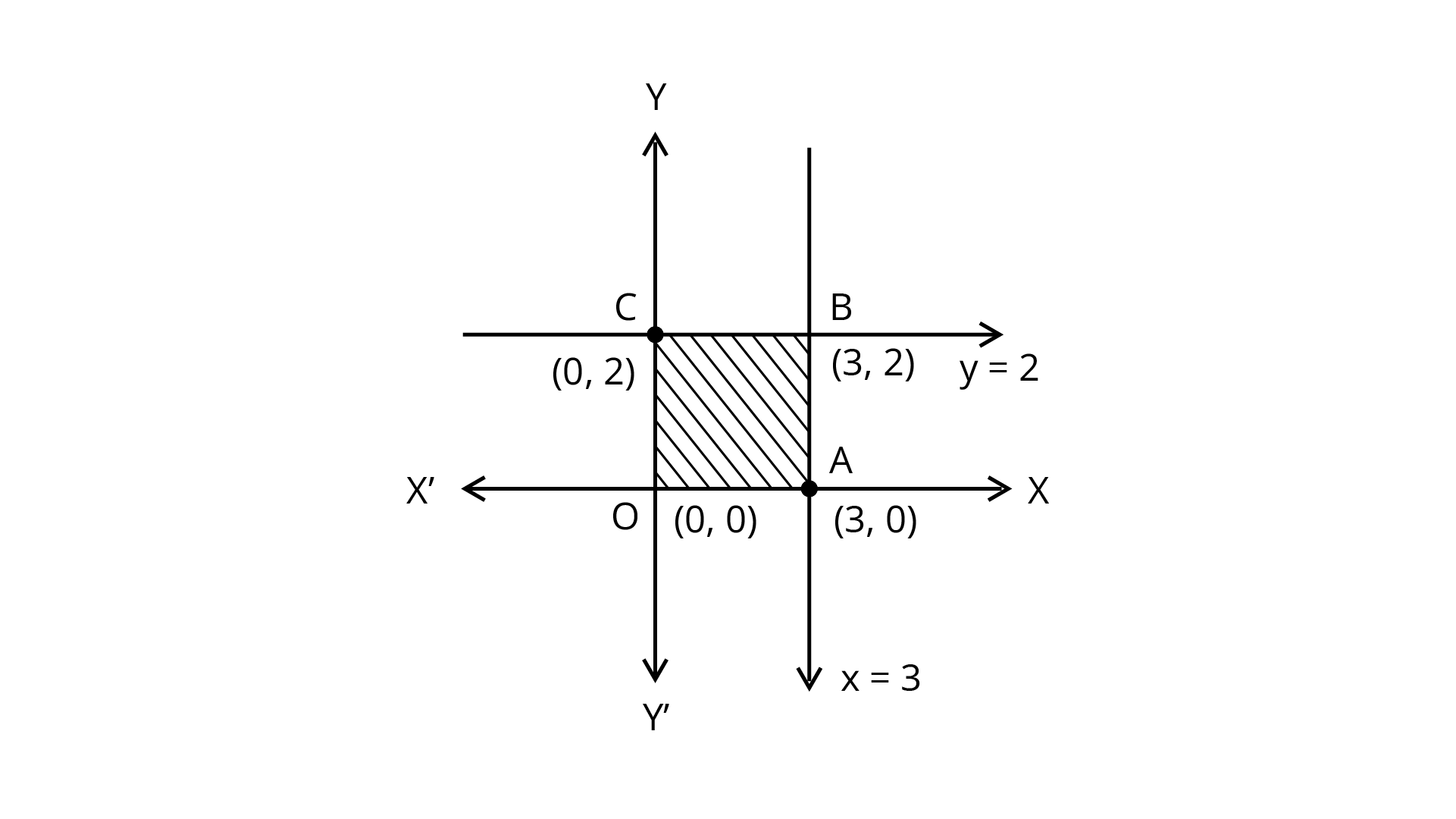
Shaded region shown in the figure as OABC is bounded and the corner points are
O(0,0), A(3,0) ,B(3,2) and C(0,2).
Corner Point | Value of $Z$ |
(0,0) (3,0) (3,2) (0,2) | 0 33 47 (maximum) 14 |
So, the maximum value of $Z$ is 47 at the point (3, 2).
4. Minimise $Z=13x-15y$ subject to the constraints: $x+y\leq7$, $2x-3y+6\geq0$, $x\geq0$,$y\geq0$.
Ans: Minimise $Z=13x-15y$
Subject to the constraints:
$x+y\leq7$, $2x-3y+6\geq0$, $x\geq0$,$y\geq0$.
We plotted these inequalities shown in the figure.
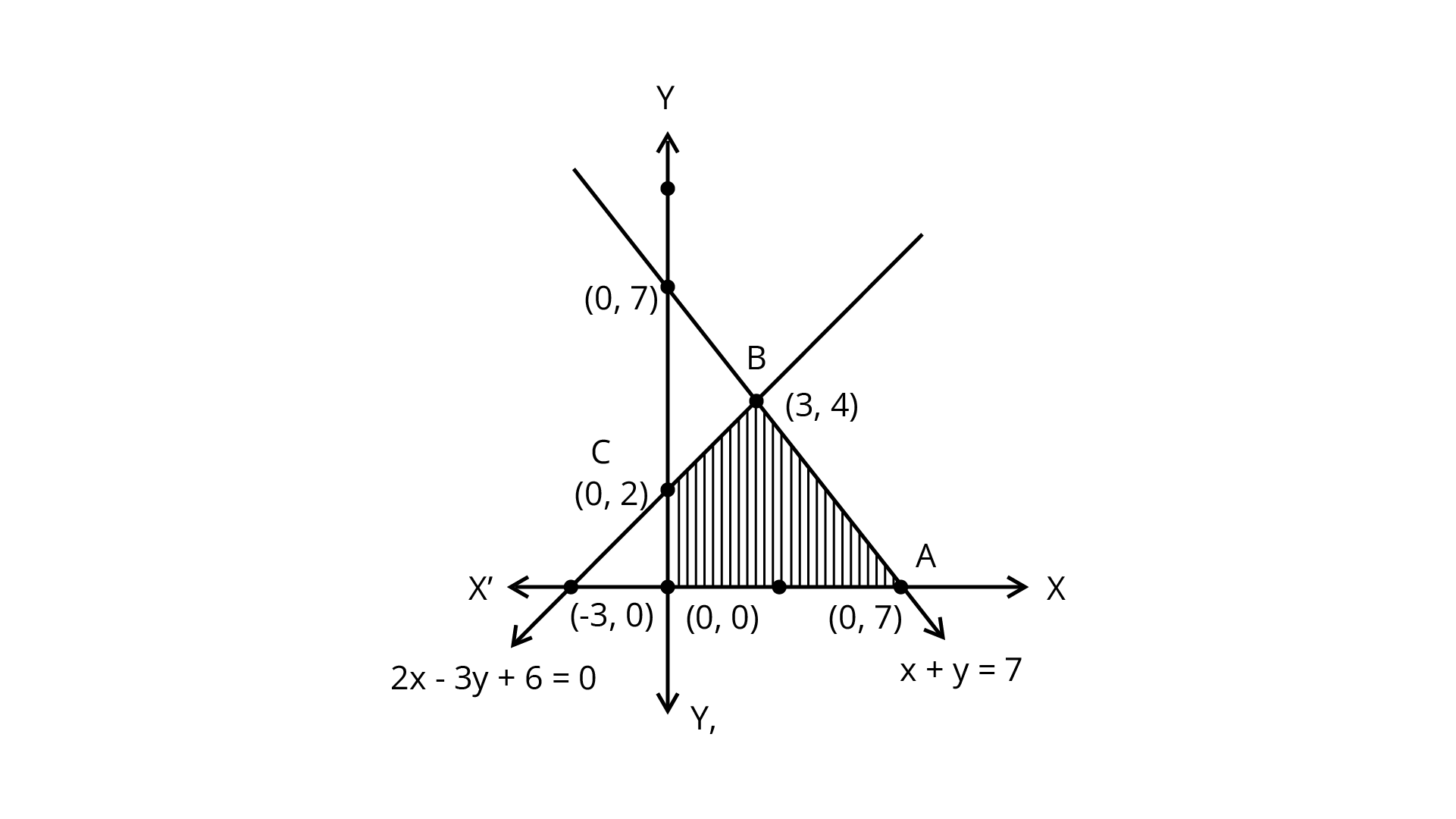
Shaded region shown as OABC is bounded and corner points are O(0,0), A(7,0), B(3,4) and C(0, 2).
Corner Point | Value of $Z$ |
(0,0) (7,0) (3,4) (0,2) | 0 91 -21 -30 (minimum) |
So, the minimum value of $Z$ is -30 at (0,2).
5. Determine the maximum value of $Z=3x+4y$ if the feasible region (shaded) for a LPP is shown in Fig.
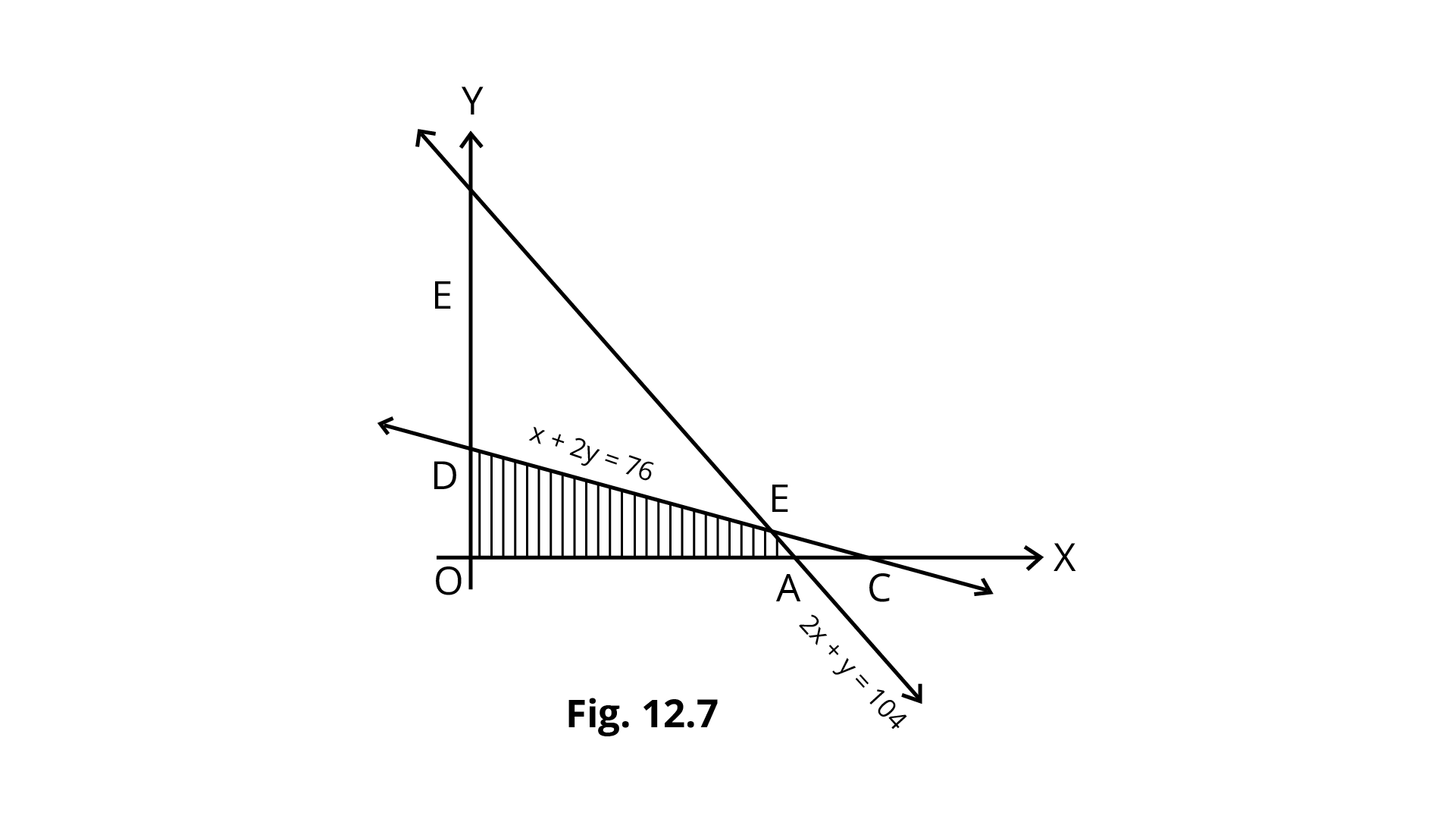
Ans: In given graph lines $x+2y=76$ and $2x+y=104$ intersect at E(44,16)
As clear from the graph, corner points are O. A. E and D with coordinates (0,0), (52,0), (44,16) and (0,38), respectively.
Also , a given region is bounded.
$Z=3x+4y$
Corner Point | Value of $Z$ |
(0,0) (52,0) (44,16) (0,38) | 0 156 196 (maximum) 152 |
So, $Z$ is maximum at (44,16) and its maximum value is 196.
6. Feasible region (shaded) for a LPP is shown in Fig. Maximise $Z= 5x+7y$.
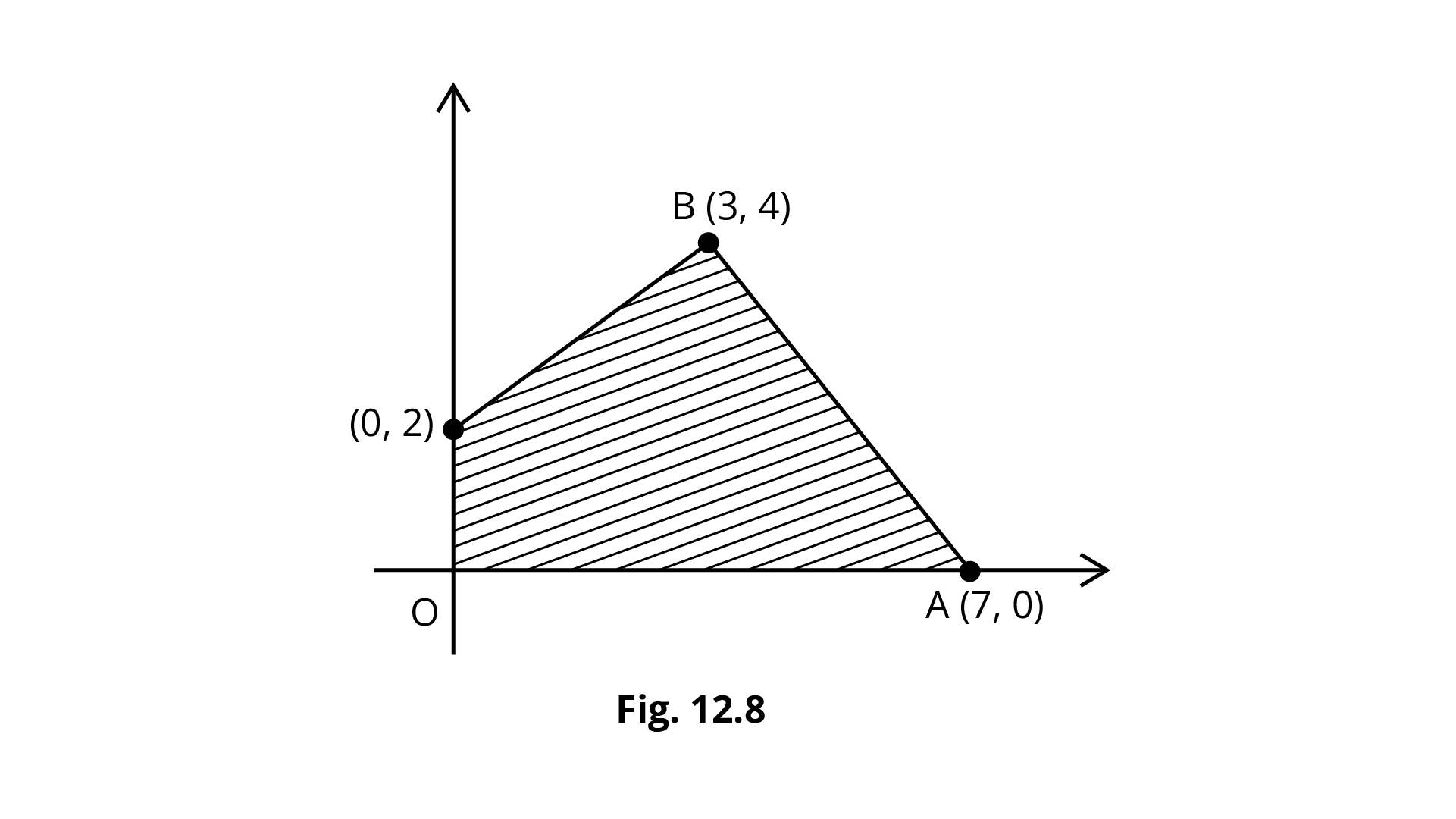
Ans: The Shaded region is bounded and coordinate of corner points O(0,0), A(7,0), B(3,4) and C(0,2).
Also, $Z=5x+7y$.
Corner Point | Value of $Z$ |
(0,0) (7,0) (3,4) (0,2) | 0 35 43 (maximum) 14 |
So, the maximum value of $Z$ is 43 at (3,4).
7. The feasible region for a LPP is shown in Fig. Find the minimum value of $Z=11x+7y$.
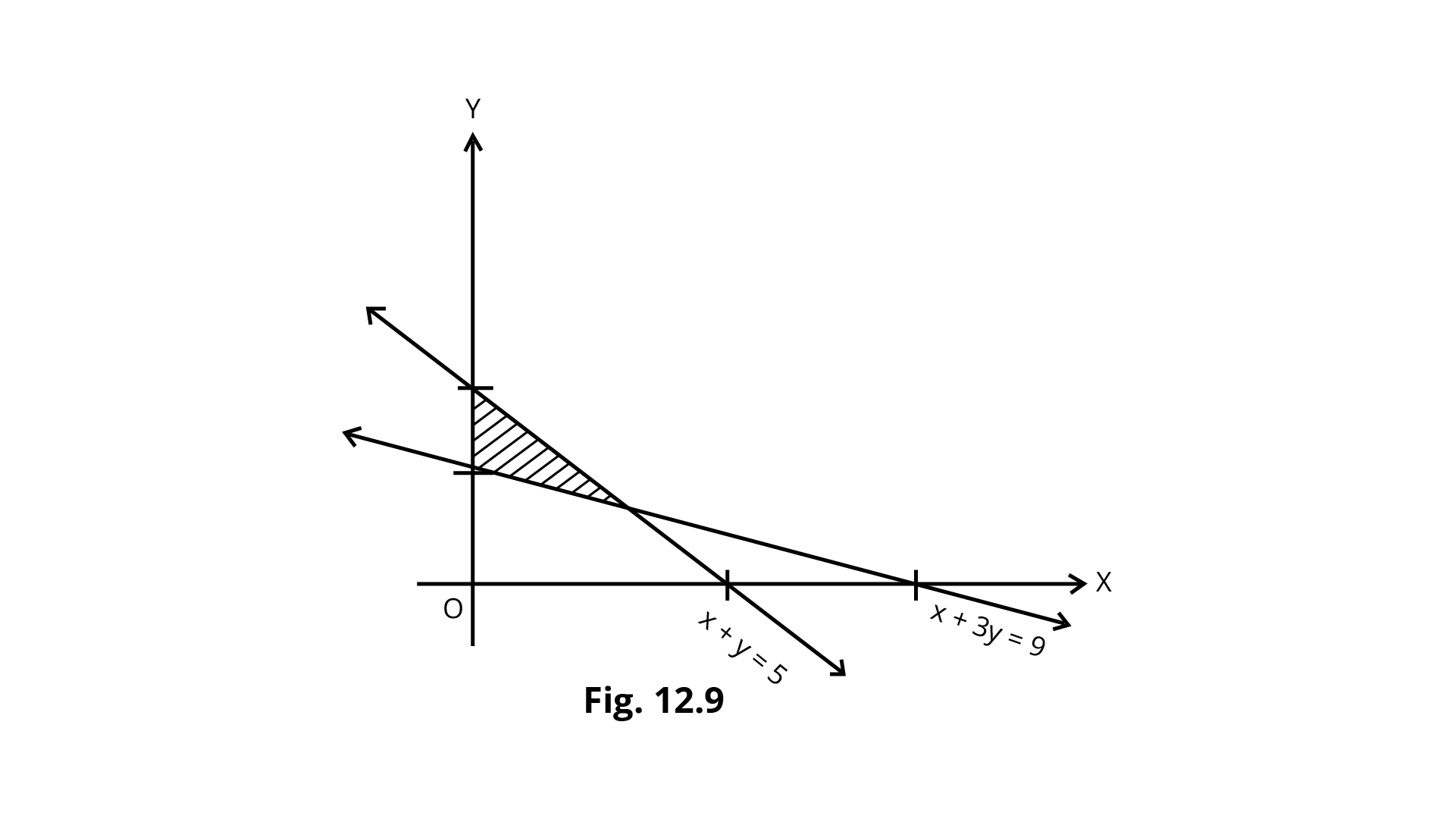
Ans: From the figure ,the feasible region is bounded with coordinates of corner points as C(0,3), A(3,2) and B(0,5).
Also,$Z=11x+7y$.
Corner Point | Value of $Z$ |
(0,3) (3,2) (0,5) | 21 (Minimum) 47 35 |
So, the minimum value of $Z$ is 21 at (0,3).
8. Refer to Exercise 7 above. Find the maximum value of $Z$.
Ans: It is clear that $Z$ is maximum at (3,2) and its maximum value is 47.
9. The feasible region for a LPP is shown in Fig. Evaluate $Z=4x+y$ at each of the corner points of this region. Find the minimum value of $Z$, if it exists.
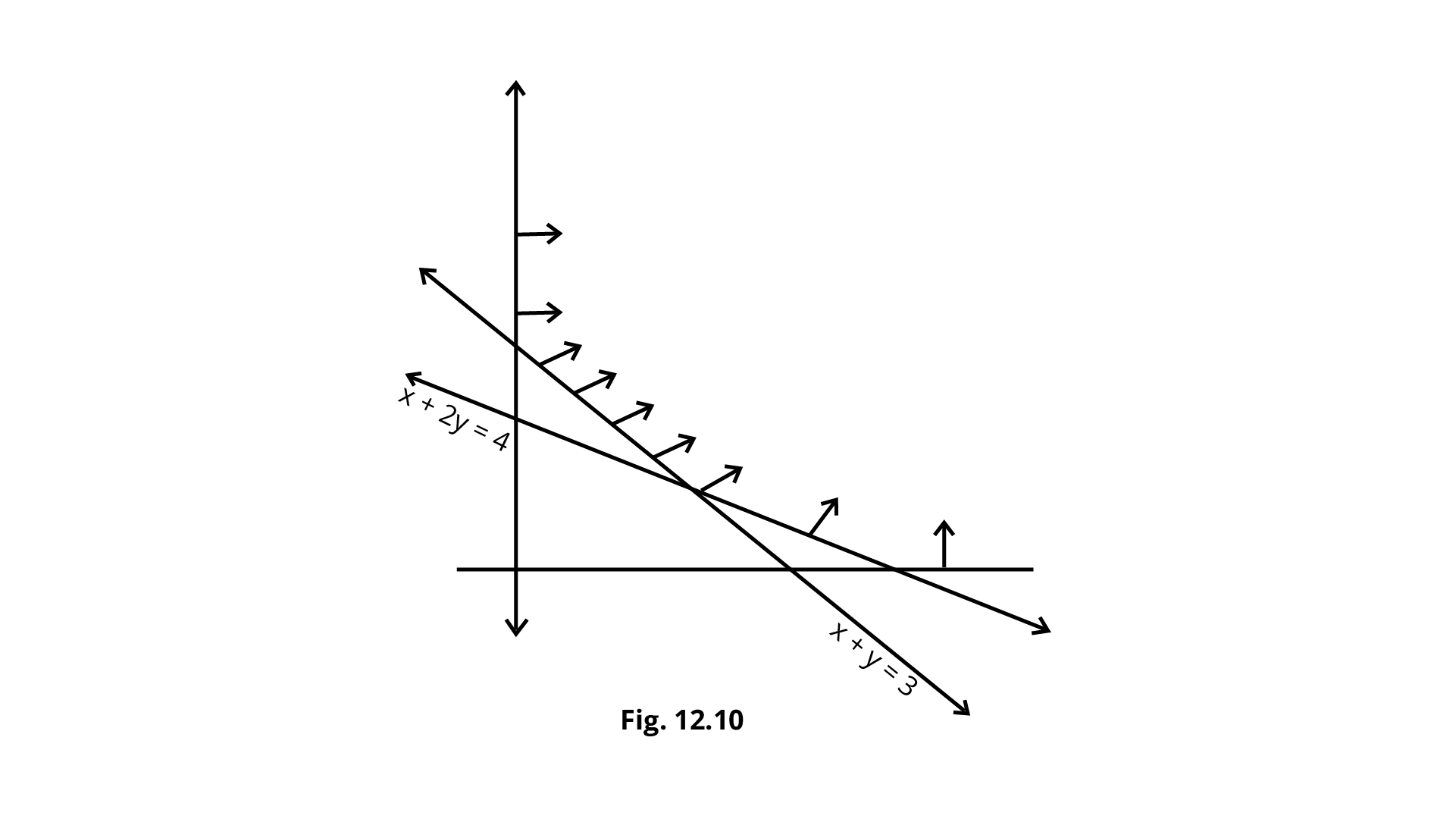
Ans: From the shaded region, the feasible region is unbounded with the corner points A(4,0), B(2,1) and C(0,3).
Also, $Z=4x+y$.
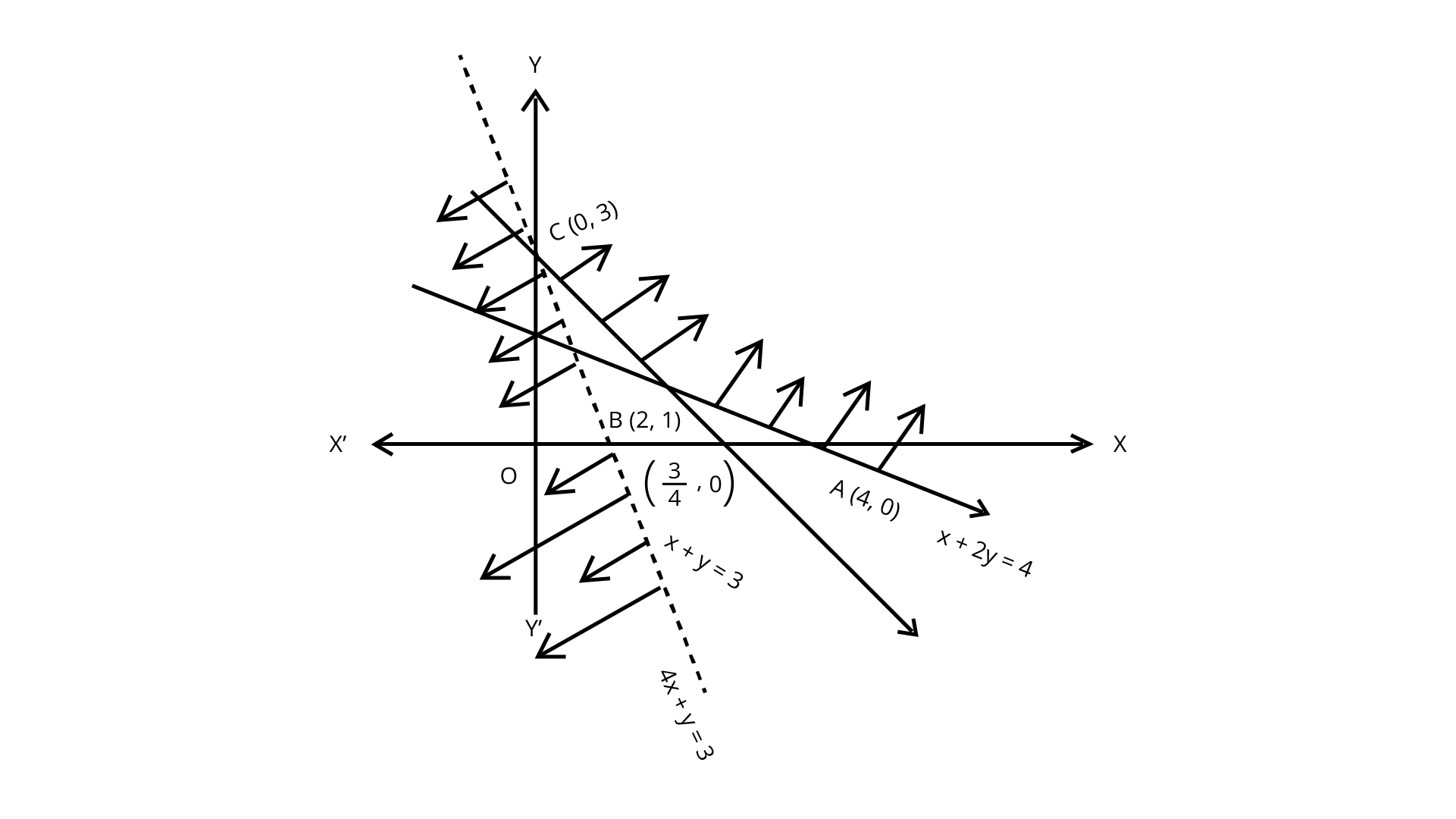
Corner Point | Value of $Z$ |
(4,0) (2,1) (0,3) | 16 9 3 (Maximum) |
And now, we see that 3 is the smallest value of $Z$ at the corner point (0, 3). Here we see that the region is unbounded, so 3 may or may not be the minimum value of $Z$. To decide this issue, we graph the inequality $4x+y\lt3$ and check whether the resulting open half plan has no point in common with the feasible region; otherwise, $Z$ has no minimum common value.
From the graph, it is clear that there is no point in common with the region and hence $Z$ has a minimum value of 3 at (0, 3).
10. In Fig. 12.11, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of $Z=x+2y$.
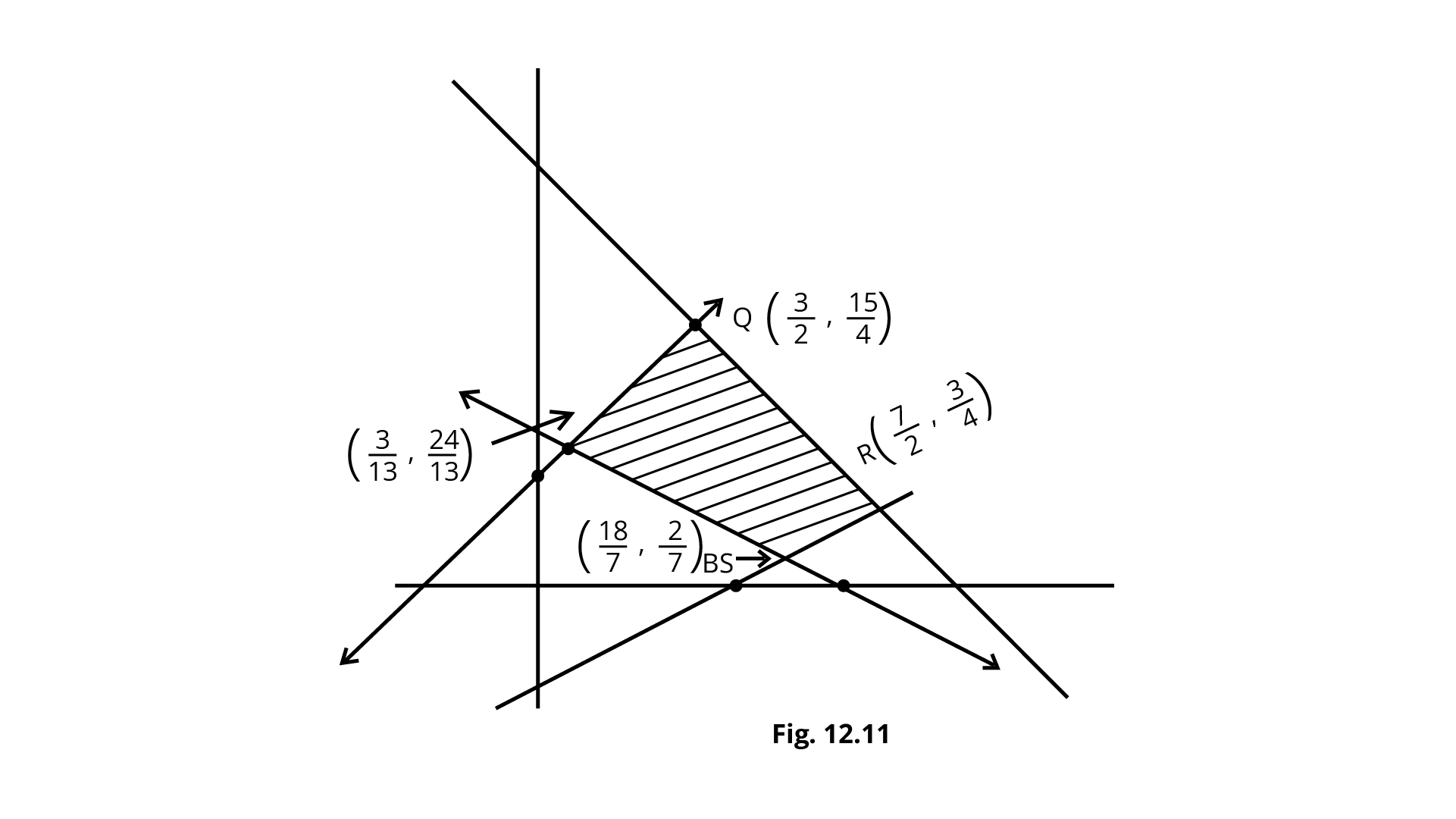
Ans: From the shaded bounded region, the coordinates of corner points are P($\dfrac{3}{13}$,$\dfrac{24}{13}$),Q($\dfrac{3}{2}$,$\dfrac{15}{4}$),R($\dfrac{7}{2}$,$\dfrac{3}{4}$) and S($\dfrac{18}{7}$,$\dfrac{2}{7}$)
Also, $Z=x+2y$.
Corner Point | Value of $Z$ |
($\dfrac{3}{13}$,$\dfrac{24}{13}$) ($\dfrac{18}{7}$,$\dfrac{2}{7}$) ($\dfrac{7}{2}$,$\dfrac{3}{4}$) ($\dfrac{3}{2}$,$\dfrac{15}{4}$) | $\dfrac{51}{13}$=$3\dfrac{12}{13}$ $\dfrac{22}{7}$=$3\dfrac{1}{7}$ (minimum) $\dfrac{20}{4}$=$5$ $\dfrac{36}{4}$=$9$ (maximum) |
So, the maximum and minimum value of $Z$ are 9 and $3\dfrac{1}{7}$ respectively.
11. A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60, formulate this problem as a LPP so that the manufacturer can maximise his profit.
Ans: Let the manufacturer produce $x$ units of type A circuit and $y$ units of type B circuits. From the given information, we have the following corresponding constraint table.
Type A(X) | Type B(y) | Maximum stock | |
Resistors Transistors Capacitors | 20 10 10 | 10 20 30 | 200 120 150 |
Profit | Rs 50 | Rs 60 |
Thus, total profit $Z=50x+60y$ (in Rs).
Now, we have the following mathematical model for the given problem.
Maximise $Z=50x+60y$ …..(i)
Subject to the constraints.
$20x+10y\leq 200$ {resistor constraint}
⇒ $2x+y\leq 20$ ………(ii)
And $10x+20y\leq120$ {transistor constraint}
⇒$x+2y\leq12$..... (iii)
And $10x+30y\leq 150$ {capacitor constraint}
⇒$x+3y\leq15$ ...(iv)
And $x\geq 0$, $y\geq 0$.....(v) {non-negative constraint}
So, Maximise $Z = 50x+60y$, subject to $2x+y\leq20$,$x+2y\leq12$, $x+3y\leq15$, $x\geq 0$, $y\geq 0$.
12. A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
job and the number of large vans cannot exceed the number of small vans. Formulate
this problem as a LPP given that the objective is to minimise cost.
Ans: Let the firm have a $x$ number of large vans and $y$ number of small vans. From the given information, we have the following corresponding constraint table.
Large vans($X$) | small vans($y$) | Maximum/Minimum | |
Package | 200 | 80 | 1200 |
Cost | 400 | 200 | 3000 |
Thus, we see that the objective function for minimum cost is $Z=400x+200y$.
Subject to constraints
$200x+80y\geq1200$ {package constraint}
⇒ $5x+2y\geq30$ ……(i)
And $400x+200y\leq 3000$ {cost constraint}
⇒$2x+y\leq15$ ...(ii)
And $x \leq y$ ...(iii)
And $x\ge0$,$y\geq0$ {non-negative constraints}...(iv)
Thus, required LPP to minimise cot is minimise $Z=400x+200y$, subject to $5x+2y\geq30$,$2x+y\leq15$,$x \leq y$,$x\ge0$,$y\geq0$.
13. A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours.
On selling these screws, the company gets a profit of Rs 100 per box on type A screws
and Rs 170 per box on type B screws.Formulate this problem as a LPP given that the objective is to maximise profit.
Ans: Let the company manufacture $x$ boxes of type $A$ screws and $y$ boxes of type B screws. From the given information, we have following corresponding constraint table
Type A($x$) | Type B($y$) | Maximum time available on each machine in a week | |
Time required for screws on threading machine Time required for screws on slotting machine | 200 | 80 | 60x60 (min) 60x60 (min) |
Profit | Rs 100 | Rs 170 |
Thus, we see that the objective function for maximum profit is $Z=100x+170y$.
Subject to constraints.
$2x+8y\leq60$x60 {time constraint for threading machine}
⇒$x+4y\leq1800$ ……(i)
And $3x+2y\leq 60$x60 {time constraint for slotting machine}
⇒$3x+2y\leq3600$ …..(ii)
Also, $x\geq0$,$y\geq0$ {non-negative constraints}...(iii)
Required LPP is,
Maximise $Z=100x+170y$, Subject to constraints $x+4y\leq1800$,$3x+2y\leq3600$,$x\geq0$,$y\geq0$.
14. A company manufactures two types of sweaters: type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater. The company can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit of the company.
Ans: Let the company manufacture $x$ number of type A sweaters and $y$ number of type B sweaters. The company spent at most Rs 72000 a day.
$360x+120y\leq72000$
⇒$3x+y\leq600$.... (i)
Also, the company can make at most 300 sweaters.
$x+y\leq300$.... (ii)
Further, the number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100.
$y-x\leq100$....(iii)
And $x\geq0$, $y\geq0$...(iv)
Thus, the required LPP to maximise the profit is Maximise $Z=200x+120y$ is subject to
constraints.
$3x+y\leq600$
$x+y\leq300$
$x-y\geq-100$
$x\geq0$, $y\geq0$
15. A man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has at most Rs 120 to spend on petrol and one hour time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
Ans: Let the man ride his motorcycle to a distance $x$ km at the speed of 50 km/h and to a distance $y$ km at the speed of 80 km/h.
Therefore, the cost of petrol is $2x+3y$.
Since, he has to spend Rs 120 at most on petrol.
$2x+3y\leq120$.... (i)
Also, he has at most 1 hour time.
$\dfrac{x}{50}$+$\dfrac{x}{80}$$\leq1$
⇒$8x+5y\leq 400$... (ii)
Also, $x\geq0$, $y\geq0$...(iii) {non-negative constraints}
Thus, required LPP to travel maximum distance by him is
Maximise $Z=x+y$, subject to constraints $2x+3y\leq 120$,$8x+5y\leq 400$,$x\geq0$,$y\geq0$.
Long Answer Questions
16. Refer to Exercise 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximise his profit? Determine the maximum profit.
Ans: Referring to solution 11, we have
Maximise $Z=50x+60y$, subject to
$2x+y\leq20$,$x+2y\leq12$,$x+3y\leq15$,$x\geq0$, $y\geq0$
We plotted these inequalities shown in the figure.
From the shaded region OABCD is bounded with corner points O(0,0), A(10,0),B($\dfrac{28}{3}$,$\dfrac{4}{3}$),C(6,3) and D(0,5).
Corner Point | Value of $Z$ |
(0,0) (10,0) ($\dfrac{28}{3}$,$\dfrac{4}{3}$) (6,3) (0,5) | 0 500 546.66 (Maximum) 480 300 |
So the required maximum profit is 480 where circuits of type A is 6 and circuits of type B is 3.
17. Refer to Exercise 12. What will be the minimum cost?
Ans: Referring to solution 12, we have
Minimise $Z=400x+ 200y$ ,subject to
$5x+2y\geq30$
$2x+y\leq15$
$x\leq y$
$x\geq0$,$y\geq0$
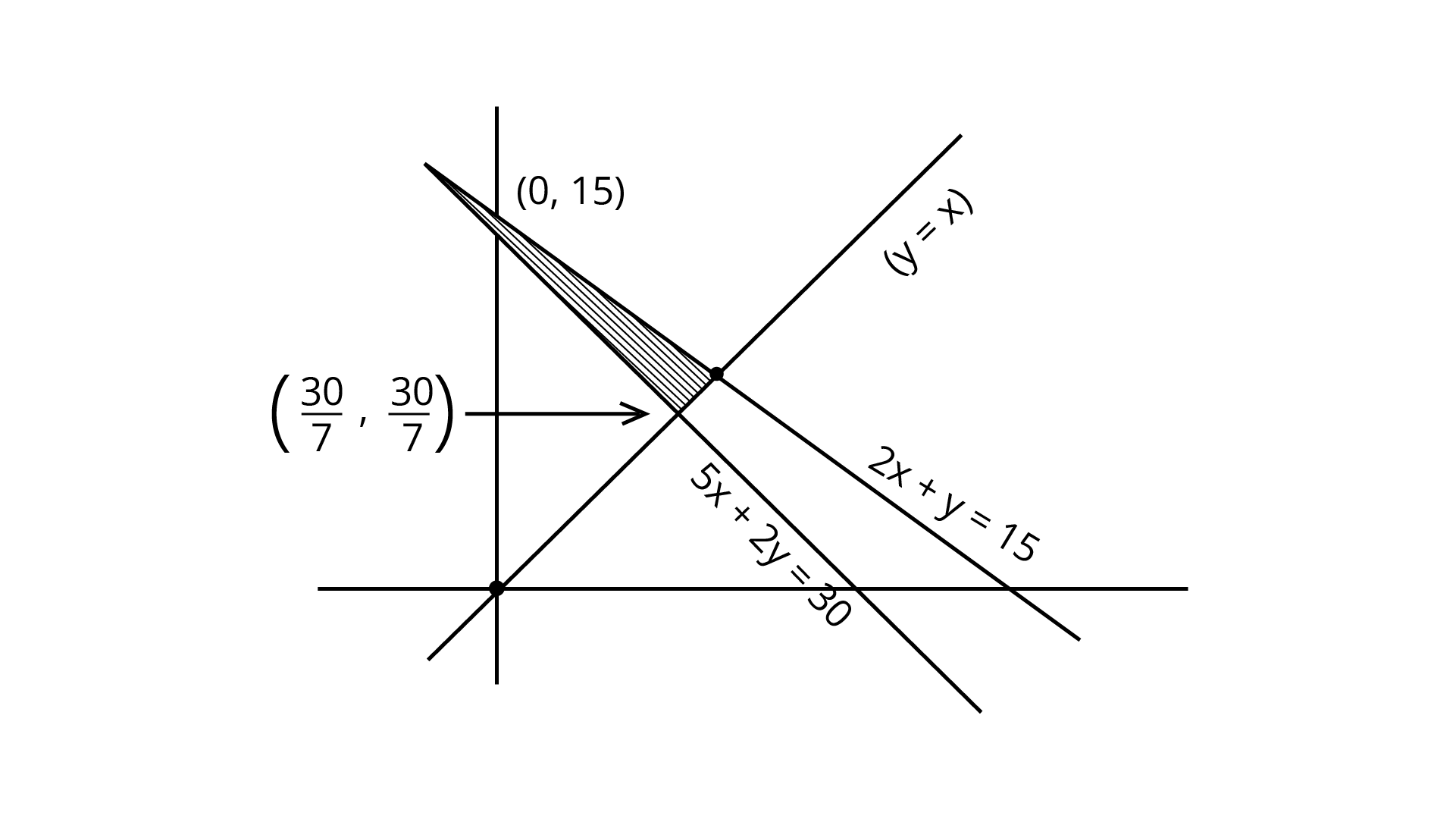
We plotted these inequalities shown in the figure.
The shaded feasible region is bounded and corner points are ($\dfrac{30}{7}$,$\dfrac{30}{7}$),(0,15) and (5,5).
Corner Point | Value of $Z$ |
(0,15) (5,5) ($\dfrac{30}{7}$, $\dfrac{30}{7}$) | 3000 3000 2571.43 (minimum) |
So, the minimum cost is Rs 2571.43.
18. Refer to Exercise 13. Solve the linear programming problem and determine the maximum profit to the manufacturer.
Ans: Referring to solution 13, we have
Maximise $Z=100x+170y$ ,subject to
$3x+2y\leq3600$
$x+4y\leq1800$
$x\geq0$, $y\geq0$
We plotted these inequalities shown in the figure.
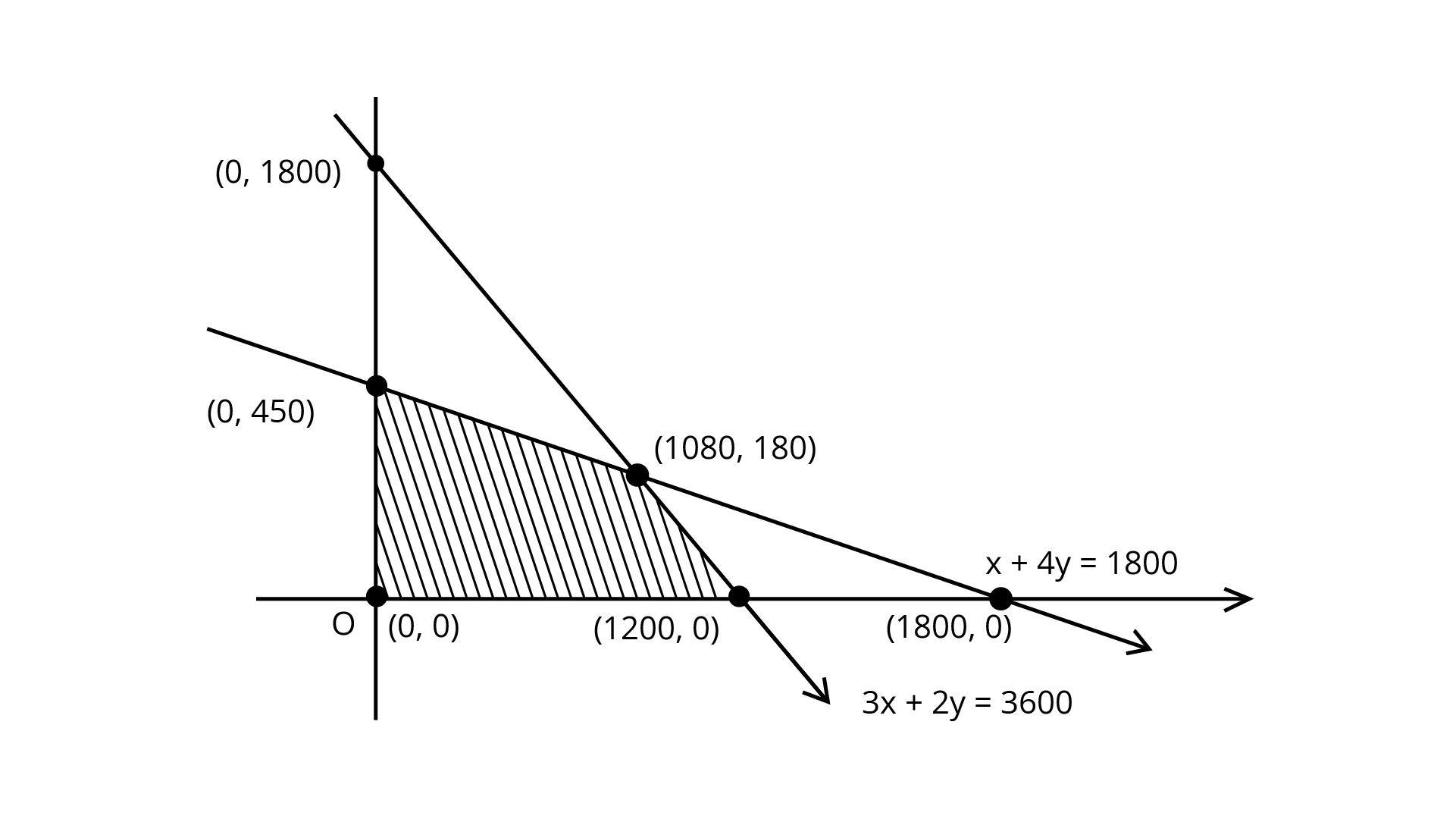
The shaded region is bounded and corner points are (0,0), (1200,0), (1080,180) and (0,450).
Corner Point | Value of $Z$ |
(0,0) (12000,0) (1080,180) (0,450) | 0 120000 138600 (Maximum) 46500 |
So, the maximum profit to the manufacturer is 138600.
19. Refer to Exercise 14. How many sweaters of each type should the company day to get a maximum profit? What is the maximum profit?
Ans: Referring to solution 14, we have
Maximise $Z=200x+120y$, Subject to
$x+y\leq 300$
$3x+y\leqq 600$
$x-y\geq-100$
$x\geq0$, $y\geq0$
We plotted these inequalities shown in the figure.
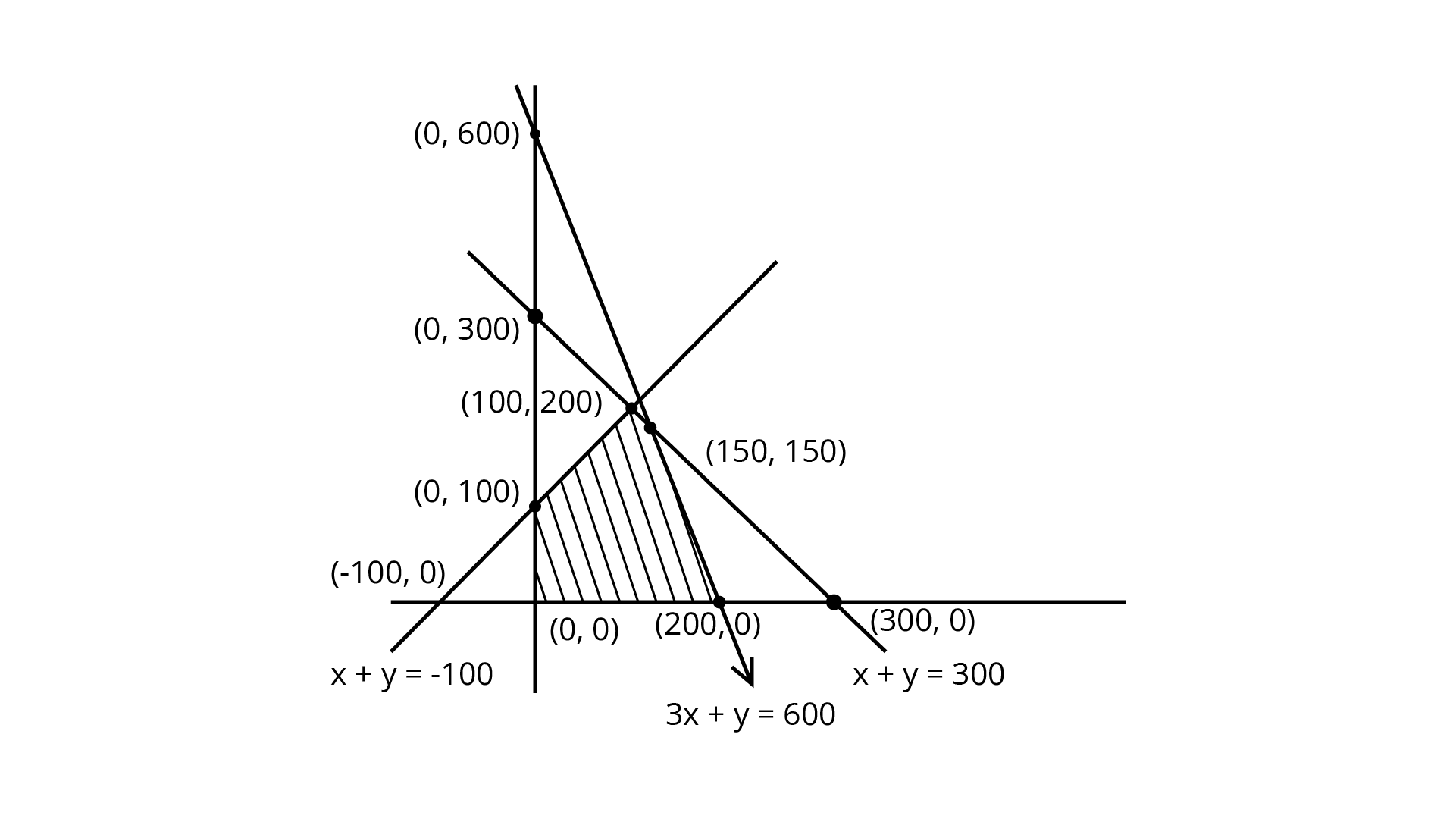
The shaded feasible region is bounded and corner points are (0,0), (200,0), (150,150), (100,200) and (0,100).
Corner Point | Value of $Z$ |
(0,0) (200,0) (150,150) (100,200) (0,100) | 0 40000 48000 (Maximum) 44000 12000 |
So, 150 sweaters of each type are made by the company and maximum profit is Rs 48000.
20. Refer to Exercise 15. Determine the maximum distance that the man can travel.
Ans: Referring to solution 15, we have
Maximise $Z=x+y$, subject to
$2x+3y\leq120$
$8x+5y\leq 400$
$x\geq0$, $y\geq0$
We plotted these inequalities shown in the figure.
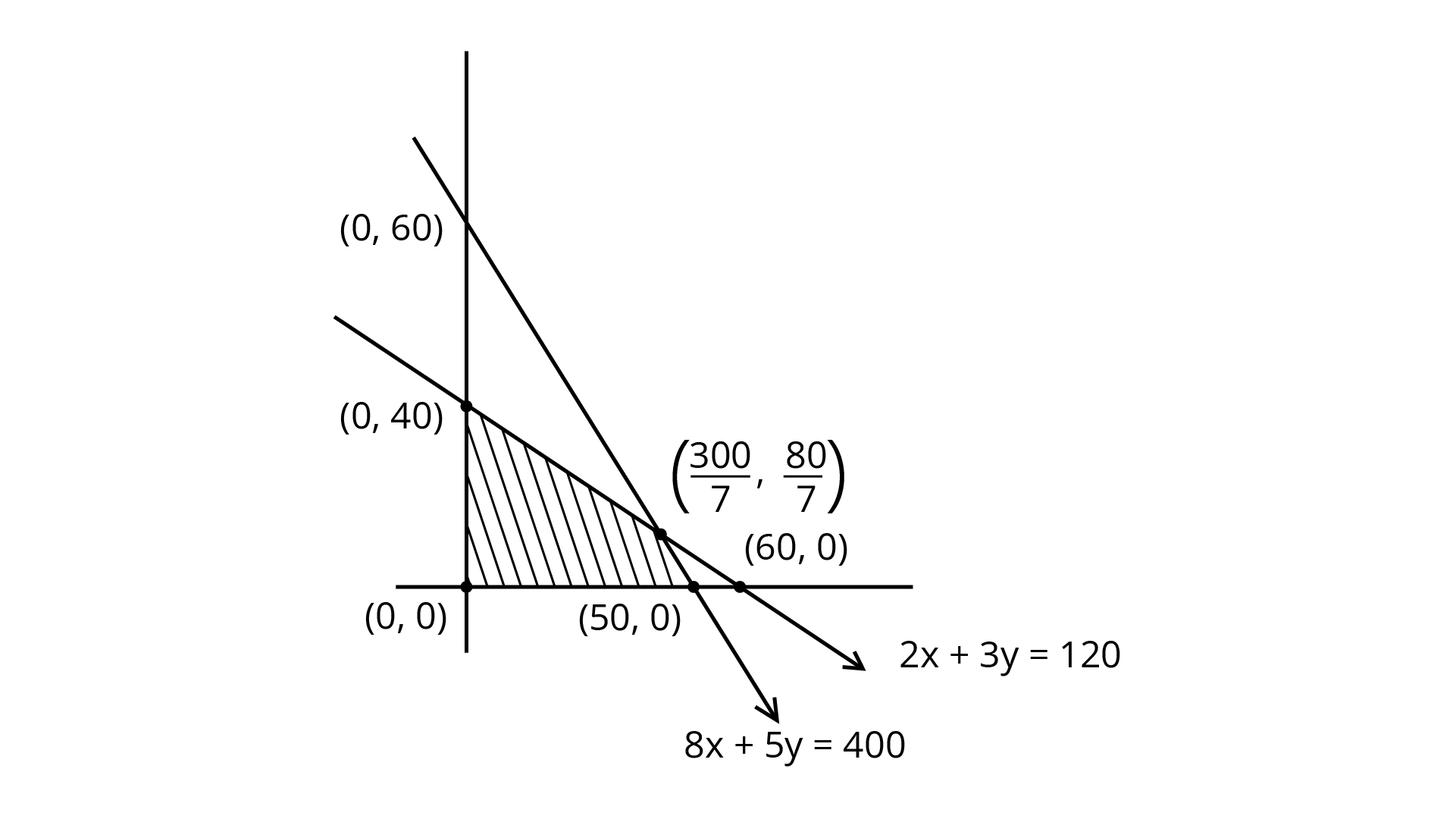
The shaded feasible region is bounded and corner points are (0, 0), (50, 0), ($\dfrac{300}{7}$,$\dfrac{80}{7}$) and (0, 40).
Corner Point | Value of $Z$ |
(0,0) (50,0) ($\dfrac{300}{7}$,$\dfrac{80}{7}$) (0,40) | 0 50 $54\dfrac{2}{7}$(Maximum) 40 |
So, the maximum distance that the man can travel is $54\dfrac{2}{7}$ km.
21. Maximise $Z=x+y$, subject to $x+4y\leq8$, $2x+3y\leq12$, $3x+y\leq9$, $x\geq0$ ,$y\geq0$.
Ans: We have
Maximise $Z=x+y$,subject to,
$x+4y\leq8$
$2x+3y\leq12$
$3x+y\leq9$
$x\geq0$ ,$y\geq0$.
We plotted these inequalities shown in the figure.
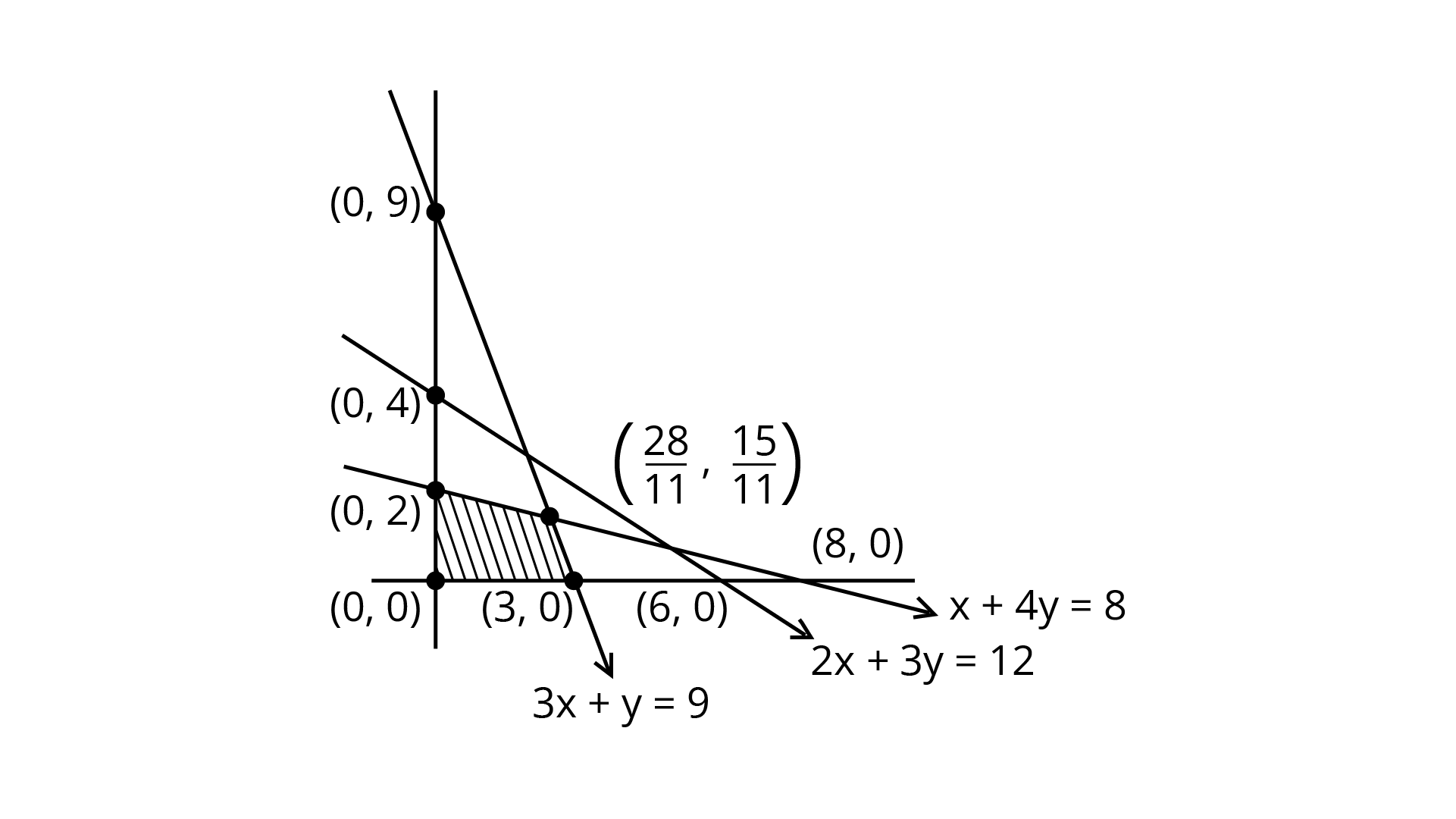
The shaded feasible region is bounded and corner points are (0, 0), (3, 0), ($\dfrac{28}{11}$,$\dfrac{15}{11}$) and (0, 2).
Corner Point | Value of $Z$ |
(0,0) (3,0) ($\dfrac{28}{11}$,$\dfrac{15}{11}$) (0,2) | 0 3 $3\dfrac{10}{11}$(Maximum) 2 |
So,the maximum value is $3\dfrac{10}{11}$.
22. A manufacturer produces two models of bikes - model X and model Y. Model X takes 6 man-hours to make per unit, while model Y takes 10 man-hours per unit. There are a total of 450 man-hours available per week. Handling and marketing costs are Rs 2000 and Rs 1000 per unit for models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
Ans: Let $x$ number of models $X$ and $y$ number of model $Y$ bikes.
Given ,model $X$ takes 6 man-hours to make per unit and model Y takes 10 man-hours to make per unit.
Given,there are a total of 450 man-hours available per week.
So, $6x+10y\leq450$
⇒ $3x+53\leq225$...(i)
Also, for model X and Y handling and marketing costs are Rs 2000 and Rs 1000, respectively and total funds available for these purposes are Rs 80000 per week.
$2000x+1000y\leq 80000$
⇒ $2x+y\leq 80$ …(ii)
Also,$x\geq0$ ,$y\geq0$.
So, the profits per unit for models $X$ and $Y$ are Rs 1000 and Rs 500, respectively,
We have
Maximise $Z=1000x+500y$,Subject to
$3x+5y\leq 225$
$2x+y\leq80$
$x\geq0$ ,$y\geq0$
We plotted these inequalities shown in the figure.
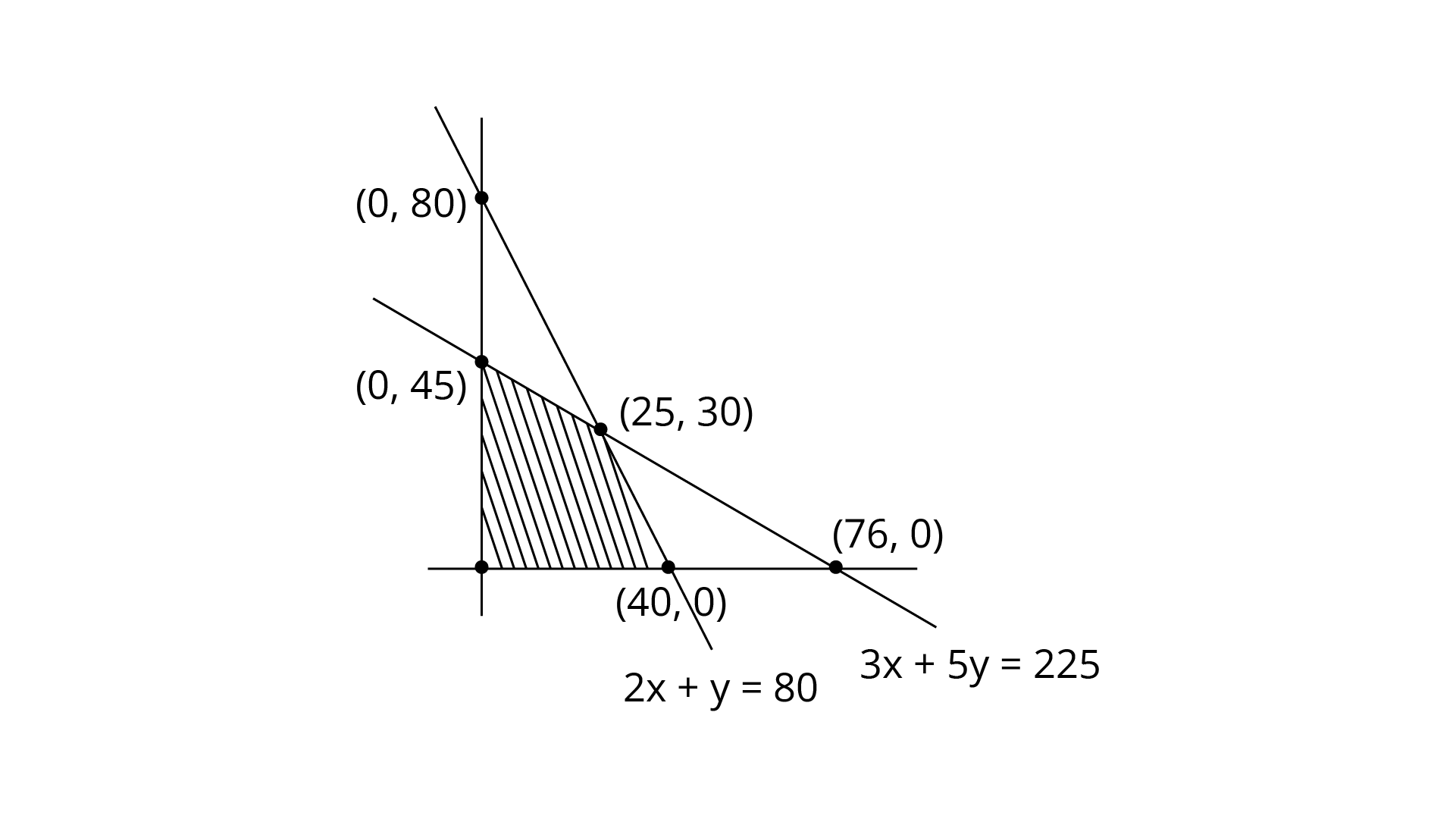
The shaded feasible region is bounded and corner points are (0,0), (40,0), (25,30) and (0,45).
Corner Point | Value of $Z$ |
(0,0) (40,0) (25,30) (0,45) | 0 40000 (maximum) 40000(maximum) 22500 |
So, to get maximum profit the manufacturer should produce 25 bikes of model X and 30 bikes.
23. In order to supplement a daily diet, a person wishes to take some X and some Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligram per tablet) are given as below:
Tablets | Iron | Calcium | Vitamin |
$X$ | 6 | 3 | 2 |
$Y$ | 2 | 3 | 4 |
The person needs at least 18 milligram of iron, 21 milligram of calcium and 16 milligram of vitamins. The price of each tablet of X and Y is Rs 2 and Re 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?
Ans: Let take $x$ units of tablet $X$ and $y$ unit of tablet Y.
We have
$6x+2y\geq18$
⇒$3x+y\geq29$.... (i)
$3x+3y\geq21$
⇒$x+y\geq7$.... (ii)
And $2x+4y\geq16$
⇒$x+2y\geq8$... (iii)
Also, $x\geq0$ ,$y\geq0$ ...... (iv)
Given the price of each tablet of $X$ and $Y$ is Rs 2 and Rs 1 respectively.
So,
Minimise $Z=2x+y$, subject to
$3x+y\geq29$
$x+y\geq7$
$x+2y\geq8$
$x\geq0$ ,$y\geq0$
We plotted these inequalities shown in the figure.
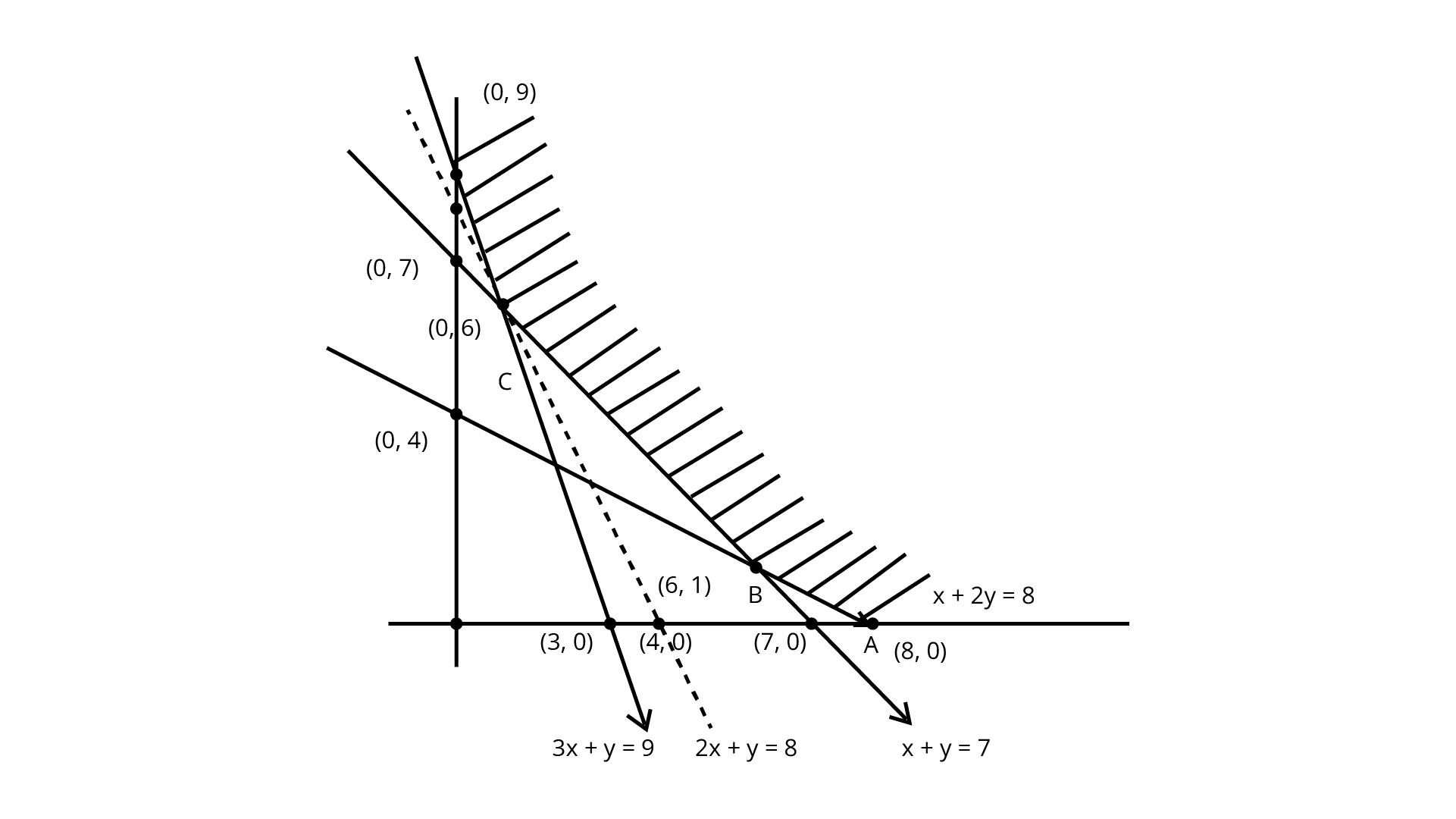
The shaded feasible region is bounded and corner points are (8,0), (6,1), (1,6) and (0,9).
Corner Point | Value of $Z$ |
(8,0) (6,1) (1,6) (0,9) | 16 13 8(minimum) 9 |
Here, we see that 8 is the minimum value of $Z$ at (1,6) but the feasible region is unbounded. So, 8 may or may not be the minimum value of $Z$.
To decide, we graph the inequality $2x+y\lt8$ and check whether it has a common point.
We see from the graph that there is no common point.
So, the person should take 1 unit of$X$ tablet and 6 units of $Y$ tablets to satisfy requirements and at the minimum cost of Rs 8.
24. A company makes 3 models of calculators: A, B and C at factory I and factory II. The company has ordered for at least 6400 calculators of model A, 4000 calculators of model B and 4800 calculators of model C. At factory 1, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A. 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each. day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
Ans: Let factory I be operated for $x$ days and II operate for $y$ days.
At factory I, 50 calculators of model A and at factory II, 40 calculators of model A are made everyday.
Given, the company has ordered at least 6400 calculators of model A.
$50x+40y\geq6400$
⇒$5x+4y\geq640$.... (i)
Also, at factory I, 50 calculators of model B and at factory II, 20 calculators of model B are made everyday.
Since then, the company has ordered at least 4000 calculators of model B.
$50x+20y\geq4000$
⇒$5x+2y\geq400$...(ii)
Similarly, for model C
$30x+40y\geq4800$
⇒ $3x+4y\geq480$...(iii)
Also,$x\geq0$ ,$y\geq0$ .... (iv)
It costs Rs 12000 and Rs 15000 to operate factories I and II, respectively.
Minimise $Z=12000x+15000y$, subject to
$5x+4y\geq640$
$5x+2y\geq400$
$3x+4y\geq480$.
$x\geq0$ ,$y\geq0$
We plotted these inequalities shown in the figure.
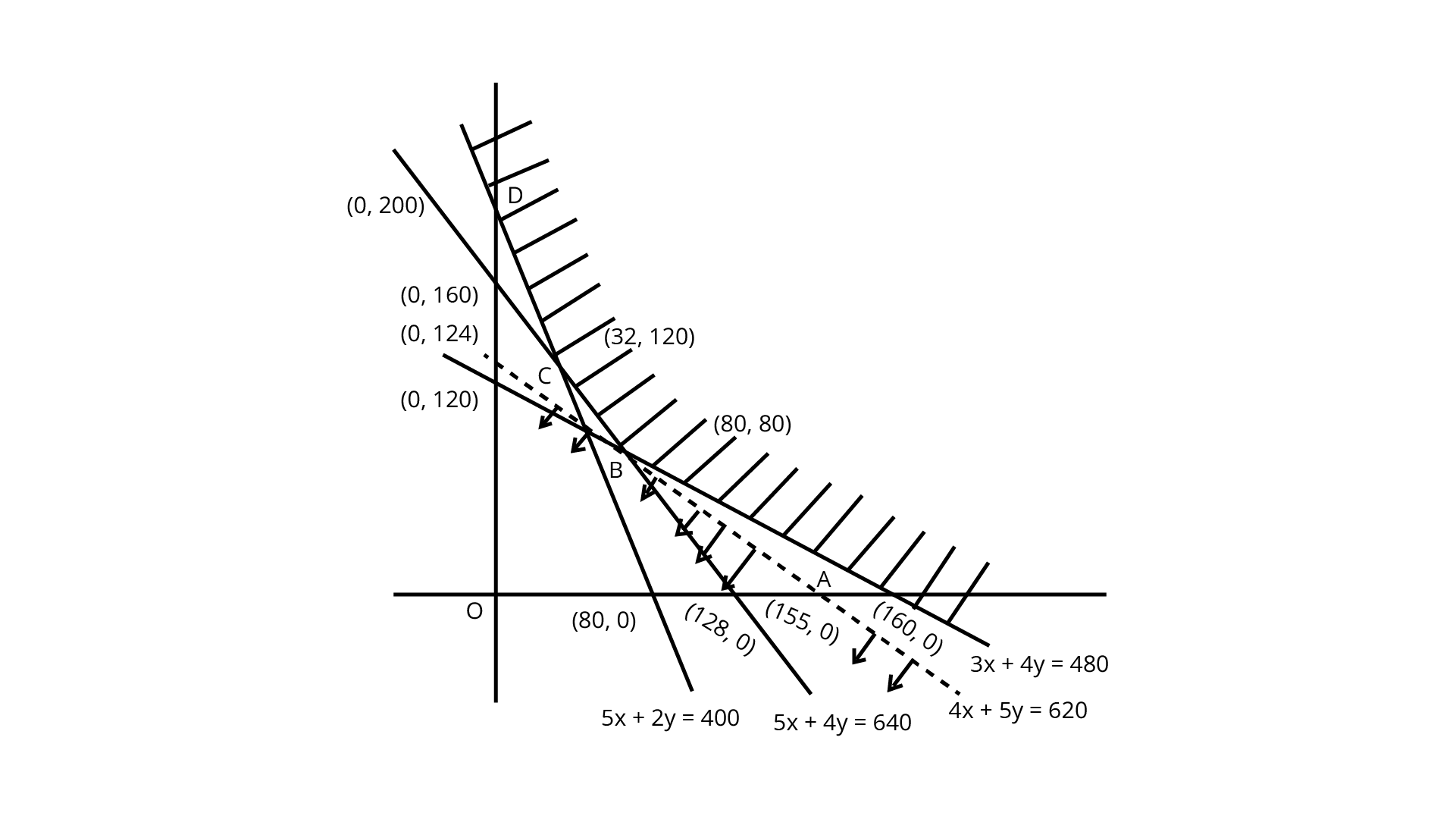
The shaded feasible region is bounded and corner points are (160,0), (80,60), (32,120) and (0,200).
Corner Point | Value of $Z$ |
(160,0) (80,60) (32,120) (0,200) | 1920000 1860000 (minimum) 2184000 3000000 |
We see from the graph that there is no common point.
So, it has no common points ,so, $Z = 12000x+15000y$ has a minimum value of 1860000 at (80,60).
Factory I ; 80 days
Factory II; 60 days.
25. Maximise and Minimise $Z-3x- 4y$, subject to x-2y≤0 -3x+y≤4x-y≤6 $x,y\geq0$
Ans: We have
Maximise and minimise $Z=3x-4y$,subject to
x-2y≤0,-3x+y≤4,x-y≤6,$x,y\geq0$
We plotted these inequalities shown in the figure.
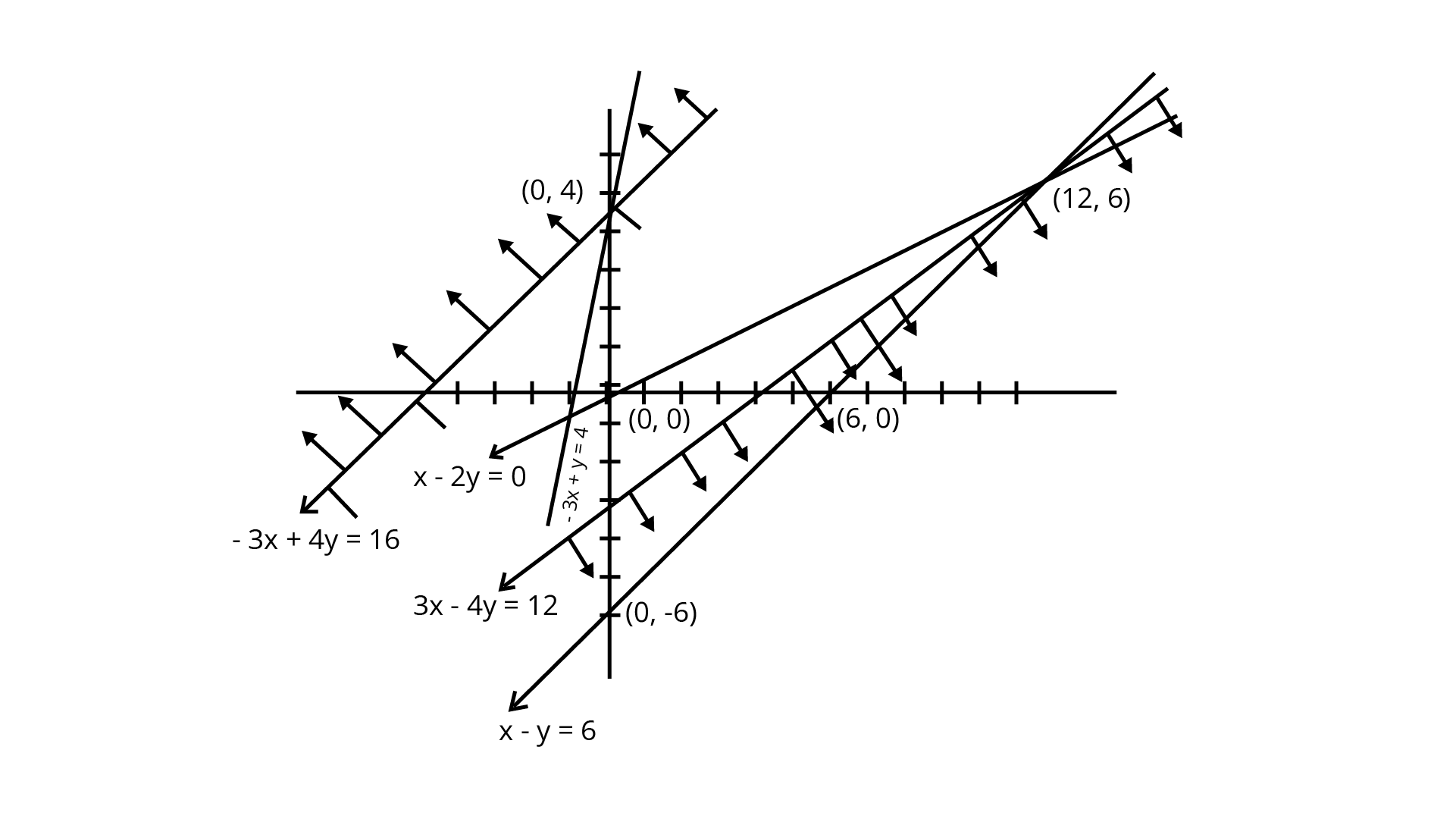
The shaded feasible region is bounded and corner points are (0,0), (12,6) and (0,4).
Corner Point | Value of $Z$ |
(0,0) (0,4) (12,6) | 0 -16 12 |
For this given unbounded region ,the value of $Z$ may or may not be -16.So.
To decide, we graph the inequality $3x-4y\lt-16$ and check whether it has a common point.
We see from the graph that there is a common point. So, it does not have any minimised value.
Also, similarly for maximum value, we graph the inequality $3x-4y\gt12$
We see from the graph that there is no common point.
So, the maximum value of $Z$ is 12.
Objective Type Questions
Choose the correct answer from the given four options in each of the Exercises 26 to 34.
26. The corner points of the feasible region determined by the system of linear constraints are (0.0), (0,40), (20,40), (60,20), (60,0). The objective function is $Z=4x+3y$. Compare the quantity in Column A and Column B
Column A | Column B |
Maximum of Z | 325 |
(A) The quantity in column A is greater
(B) The quantity in column B is greater
(C) The two quantities are equal
(D) The relationship cannot be determined on the basis of the information Supplied
Ans: Correct option - B
Corner points | Value of $Z$ |
(0,0) (0,40) (20,40) (60,20) (60,0) | 0 120 200 300 (maximum) 240 |
So, maximum value of Z=300<325
27. The feasible solution for a LPP is shown in Fig. Let $Z=3x-4y$ be the
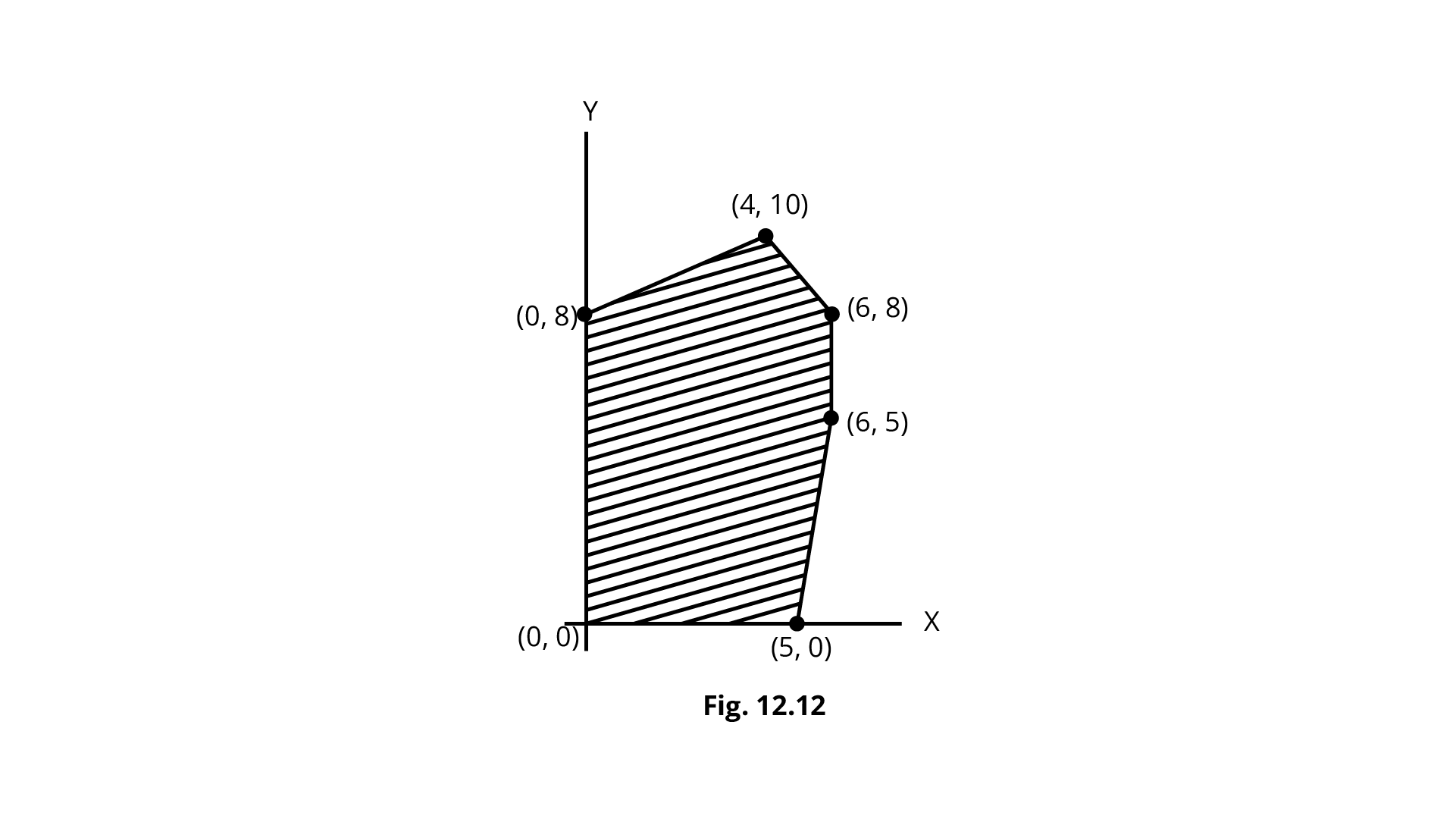
Objective function. Minimum of Z occurs at
(A) (0, 0)
(B) (0,8)
(C) (5,0)
(D) (4, 10)
Ans: Correct option - B
Corner points | Value of $Z$ |
(0,0) (5,0) (6,5) (6,8) (4,10) (0,8) | 0 15 (maximum) -2 -14 -28 -32 (minimum) |
So, the minimum of $Z$ occurs at (0, 8).
28. Refer to Exercise 27. Maximum of $Z$ occurs at
(A) (5,0)
(B) (6,5)
(C) (6,8)
(D) (4, 10)
Ans: Correct option - A
Because,the maximum of $Z$ occurs at (5, 0).
29. Refer to Exercise 27. (Maximum value of Z+ Minimum value of Z) is equal to
(A) 13
(B) 1
(C)-13
(D)-17
Ans: Correct option - D
Because, maximum value of Z+ minimum value of Z =15-32=-17
30. The feasible region for an LPP is shown in the Fig. 12.13. Let $F=3x-4y$ he the objective function. Maximum value of F is.
(A) 0
(B) 8
(C) 12
(D)-18
Ans: Correct option - C.
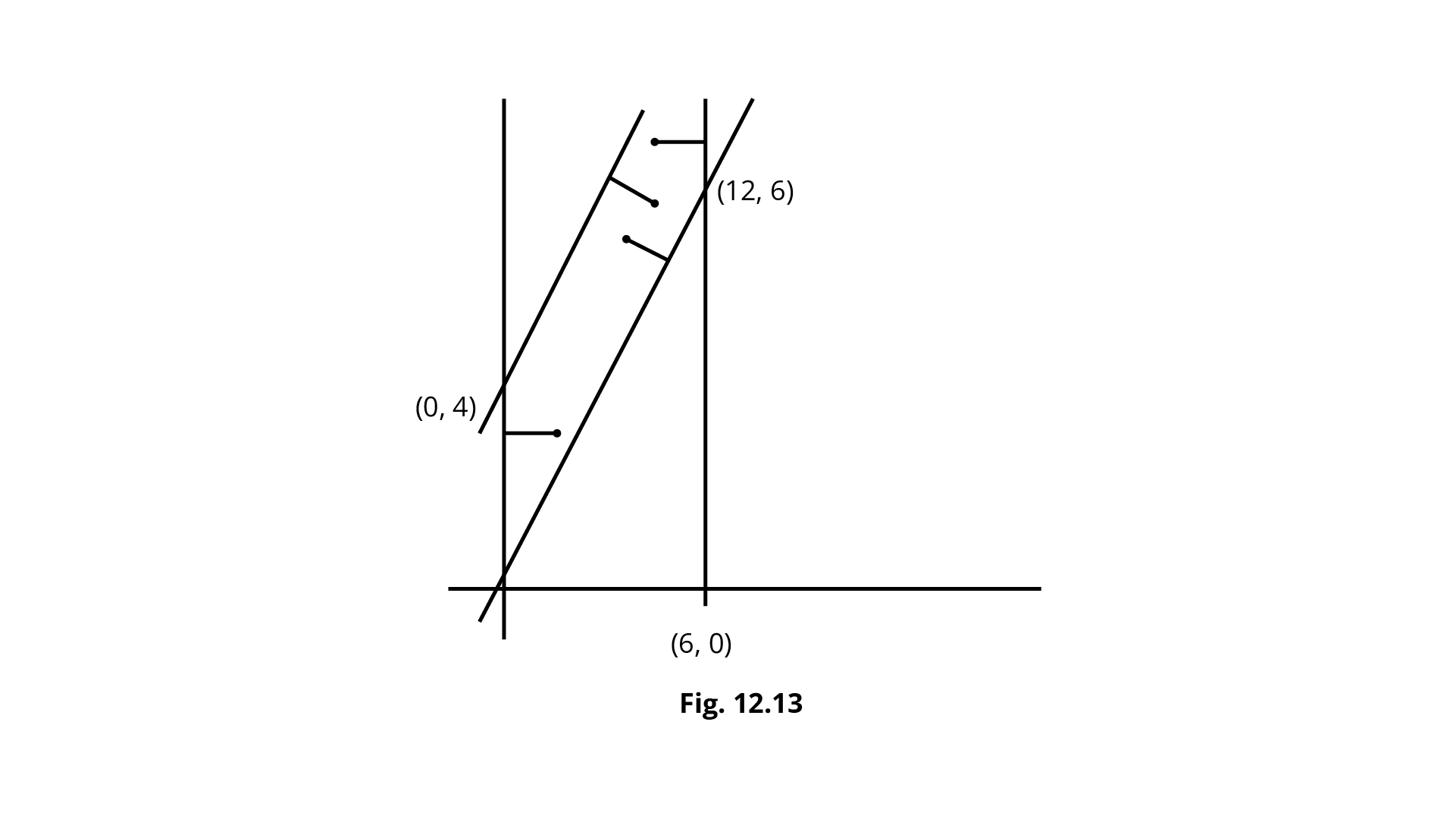
Corner points | Value of $Z$ |
(0,0) (12,6) (0,4) | 0 12 (maximum) -16(minimum) |
So, the maximum value of F is 12.
31. Refer to Exercise 30. Minimum value of F is
(A) 0
(B)-16
(C) 12
(D) does not exist
Ans: Correct option - B
Because, the minimum value of F is -16 at point (0,4).
32. Corner points of the feasible region for an LPP are (0,2), (3,0),(0,5). Let $F= 4x+6y$ be the objective function. The minimum value of F occurs at
(A) (0, 2) only
(B) (3, 0) only
(C) the midpoint of the line segment joining the points (0, 2) and (3, 0) only
(D) any point on the line segment joining the points (0, 2) and (3, 0).
Ans: Correct option - D
Corner points | Value of $Z$ |
(0, 2) (3,0) (6,0) (6,8) (0,5) | 12 (minimum) 12 (maximum) 24 72 (minimum) 30 |
So, the minimum value of F occurs at any points on the line segment joining the points (0, 2) and (3, 0).
33. Refer to Exercise 32, Maximum of F - Minimum of F is equal to
(A) 60
(B) 48
(C) 42
(D) 18
Ans: Correct option - A
Because, maximum of F - minimum of F =72-12=60.
34. Corner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let $Z=px+qy$ ,where p, q>0. Condition on $p$ and $q$ so that the minimum of $Z$ occurs at (3,0) and (1,1) is
(A) $p=2q$
(B) $p$ =$\dfrac{q}{2}$
(C) $p=3q$
(D) $p=q$
Ans: Correct option - B
Corner points | Value of $Z$ |
(0,3) (1,1) (3,0) | $3q$ $p+q$ $3p$ |
So, minimum of $Z$ occurs at (3,0) and (1,1) IS
$p+q=3p$
Or $2p=q$
So, $p$ =$\dfrac{q}{2}$
Fill in the blanks in each of the Exercises 35 to 41.
35. In a LPP, the linear inequalities or restrictions on the variables are called……
Ans: In a LPP, the linear inequalities or restrictions on the variables are called linear constraints.
36. In a LPP, the objective function is always…….
Ans: In a LPP, the objective function is always linear.
37. If the feasible region for a LPP is……. , then the optimal value of the objective function $Z=ax+by$ may or may not exist.
Ans: If the feasible region for a LPP is unbounded, then the optimal value of objective function $Z=ax+by$ may or may not exist.
38. In a LPP if the objective function $Z=ax+by$ has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same……value.
Ans: In a L.PP, if the objective function $Z=ax+by$ has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same maximum value.
39. A feasible region of a system of linear inequalities is said to be ….. if it can be enclosed within a circle.
Ans: A feasible region of a system of linear inequality is said to be bounded, if it can be enclosed within a circle.
40. A corner point of a feasible region is a point in the region which is the …….of two boundary lines.
Ans: A corner point of a feasible region is a point in the region which is the intersection of two boundary lines.
41. The feasible region for an LPP is always a……polygon.
Ans: The feasible region for an LPP is always a convex polygon.
State whether the statements in Exercises 42 to 45 are True or False.
42. If the feasible region for a LPP is unbounded, maximum or minimum of the objective function $Z=ax+by$ may or may not exist.
Ans: True
43. Maximum value of the objective function $Z=ax+by$ in a LPP always occurs at only one corner point of the feasible region.
Ans: False
44. In a LPP, the minimum value of the objective function $Z=ax+by$ is always 0 if origin is one of the corner point of the feasible region.
Ans: False
45. In a LPP, the maximum value of the objective function $Z=ax+by$ is always finite.
Ans: True
The NCERT Exemplars are practice books that contain additional questions of higher difficulty level. It is meant to aid students to gain in-depth knowledge of the concepts. The Exemplar books are also considered important for preparation of competitive Exams such as the JEE mains, JEE advanced Exams, NEET and AIIMS Exam. It is considered highly beneficial for students to go through these books.
FAQs on NCERT Exemplar for Class 12 Maths Chapter-12 (Book Solutions)
1. What will the students gain from solving the NCERT Exemplar Books?
The NCERT Exemplar is designed to provide teachers and students with more problems that are of higher aptitude and greater understanding and application of various concepts learnt in Class. These advanced level questions from the NCERT Exemplar book will help students to develop advanced skills in respective subjects. By solving the questions from the NCERT Exemplar book, students will comprehend the concepts better, rather than memorising them. In addition, the Exemplar book will help students with preparations for competitive Exams like NEET, AIIMS, JEE Main, JEE Advanced.
2. Is NCERT Exemplar enough for boards Class 12?
Although the NCERT Exemplar book contains questions that are of a higher difficulty level, students cannot rely completely on the NCERT Exemplar book for their preparation. It is not sufficient that students only study and solve the NCERT Exemplar book, it is necessary that students solve questions from the NCERT textbook along with the NCERT Exemplar book in order to be thoroughly prepared for the Exam. However, the NCERT Exemplar books are very beneficial for preparation of competitive Exams such as JEE Main and JEE Advanced. CBSE board Exams sometimes contain in-depth sums.
3. How to download NCERT Exemplar for Class 12 Maths Chapter 12 - Linear Programming Solutions from the Vedantu Website?
Free NCERT Exemplar for Class 12 Maths Chapter 12 - Linear Programming Solutions in PDF formation can be accessed through the Vedantu website. Alternatively, you can download the paper by clicking here. The Solution to Questions is written in a simple manner, enabling students to easily understand the concepts. The Solutions will help students to assess their understanding of the Examination while getting an in-depth idea of the difficulty level of the Exam, individual topic weightage and the Exam pattern. In addition to Questions behind the Chapters, students are encouraged to solve multiple Sample papers, Previous Year Question Papers and mock questions during their preparation stage.
4. What is the importance of NCERT Exemplar Class 12 Maths?
Referring to Class 12 Maths NCERT Exemplar will help students to become well acquainted with complex mathematical questions. It will help students in gaining in-depth knowledge and to master the Class 12 Mathematics concepts. In addition, many of the questions that appear in the board Exam, as well as in various competitive entrance Exams such as NEET, JEE (Mains and Advanced), AIIMS Exam etc. are directly asked from the NCERT Exemplar. Solving a variety of difficult questions and numerical problems helps strengthen students' Board Exam preparation.
5. Why Should You Read NCERT Books for Class 12 Maths?
The NCERT Book for Class 12 Maths is useful for students as it provides thorough knowledge and understanding about the subject. Students can follow the book to clear any doubts on Class 12 Maths:
It provides clear and concise information on the subject
It consists of step-by-step solutions for even the most difficult concepts
It enables students to self study from home
Get enough practise at home by solving the Class 12 Math to be prepared for the Exam







































