Motion Class 9 Science Chapter 7 CBSE Notes - 2025-26

Introduction: 

• One of the most common phenomena in the physical world is motion. Mechanics is the branch of Physics that deals with the behavior of moving objects.

• Mechanics is divided further into two sections: Kinematics and Dynamics.

• Kinematics is the study of motion without regard for the cause of motion.

• Dynamics is concerned with the source of motion, which is force. 

Motion and Rest: 

• An object is said to be in motion if its position in relation to its surroundings changes in a given time.

• An object is said to be at rest if its position in relation to its surroundings does not change.

• A frame of reference is another object or scene against which we compare the position of an object.

Figure 1:

Figure 2:

Take a look at the numbers. Figure 1 shows the car to the right of the tree. Figure 2 shows the car to the left of the tree after 2 seconds. The car must have moved from one location to another because the tree does not move. As a result, the tree serves as the frame of reference in this case. 

Types of Motion: 

There are three types of motion: 

• Translatory motion 

• Rotatory motion 

• Vibratory motion 

Translatory Motion: 

• A particle in translatory motion moves from one point in space to another. This movement may be in a straight line or in a curved path.

• Rectilinear motion is defined as motion along a straight line.

• Curvilinear motion is defined as movement along a curved path.

• As an example, consider a car driving down a straight road.

Rectilinear Motion: 

Example: A car negotiating a curve 

Curvilinear Motion: 

Rotatory Motion: 

The particles of the body describe concentric circles around the axis of motion in rotatory motion.

Vibrational Motion:

Particles in vibratory motion move back and forth around a fixed point.

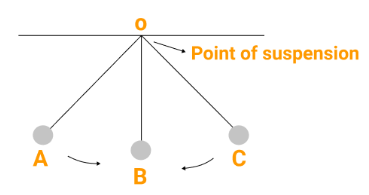
Distance and Displacement: 

The distance between termini A and B is 150 kilometers. A bus connects Terminus A and Terminus B. The bus travels a distance of 150 kilometers. The bus returns from terminus B to terminus A along the same route. As a result, the total distance travelled by the bus from A to B and then from B to A is 150 km + 150 km = 300 km. 

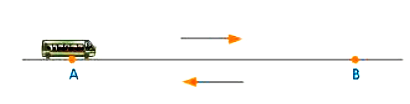
A bus traveling from point A to point B and back again.

• The distance traveled by a moving object is the length of the path the object takes.

• The measure of distance is a scalar quantity. The meter is the SI unit of distance.

• The bus's position changed when it moved from Terminus A to Terminus B. The distance between A and B is 150 kilometres. The distance travelled on the return trip is also 150 kilometres.

• Displacement is the shortest path covered by a moving object in a specified direction from the point of reference (the initial position of the body).

Note: 

• However, the displacement when the bus moves from A B to B B is zero. The meter is the SI unit of displacement.

• Displacement is a vector, which means that it is represented by a number with appropriate units and direction.

• To emphasise the distinction between displacement and distance, consider a few more examples.

Assume a person moves 3 meters from point A to point B and 4 meters from point B to point C, as shown in the figure. He has travelled a total distance of 7 meters. But is he really 7 meters away from his starting point? No, he is only 5 meters away from his initial position, implying that he is displaced by the shortest distance between his initial and final positions.

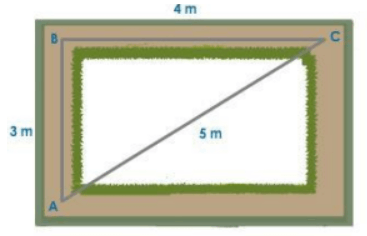
Distance and Displacement 

To determine the displacement in this example, we can use Pythagoras' theorem. Consider an object that is changing its position with respect to a fixed point known as the origin 0. 

${\mathrm{x}}_{\mathrm{i}}$ and ${\mathrm{x}}_{\mathrm{f}}$ are the initial and final positions of the object. Then the displacement of the

object $=x_f-x_i$

Case 1:

Suppose the object is travelling from $+1$ to $+4$, then displacement

$={\mathrm{x}}_{\mathrm{f}}-{\mathrm{x}}_{\mathrm{i}}$

$=+4-(+1)$

$=+3$

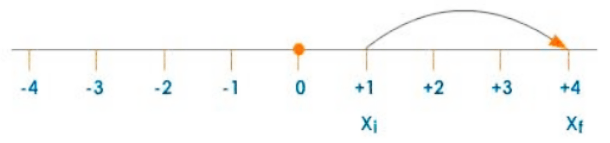
Displacement: Case 1 

Case 2: 

If the object is travelling from -3 to -1, then displacement 

If the object is travelling from $-3$ to $-1$, then displacement

$=x_f-x_i$

$=-1-(-3)$

$=+2$

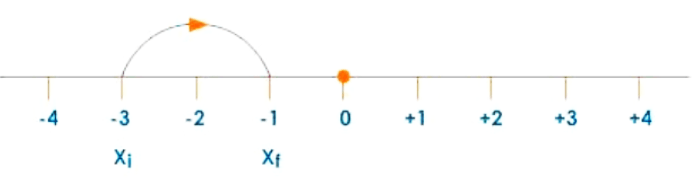
Displacement: Case 2 

Case 3: 

If the object is travelling from +4 to +2, then displacement 

$={\mathrm{x}}_{\mathrm{f}}-{\mathrm{x}}_{\mathrm{i}}$

$=+2-(4)$

$=-2$

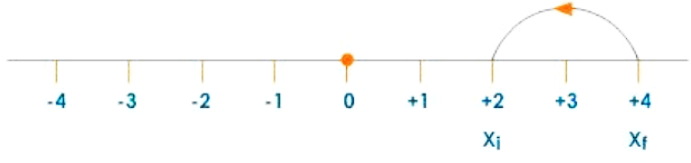
Displacement: Case 3

Case 4: 

If the object follows the path depicted in the figure, the final and initial positions are the same, implying that the displacement is zero.

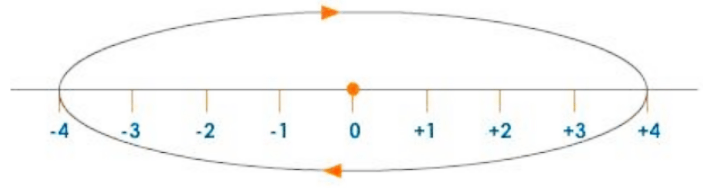
Displacement: Case 4 

We can conclude from the preceding examples that a body's displacement is positive if its final position is on the right side of its initial position and negative if its final position is on the left side of its initial position. The displacement of a moving object is said to be zero when it returns to its original position. Consider an athlete running in a clockwise direction along a circular track with radius r, beginning at A.

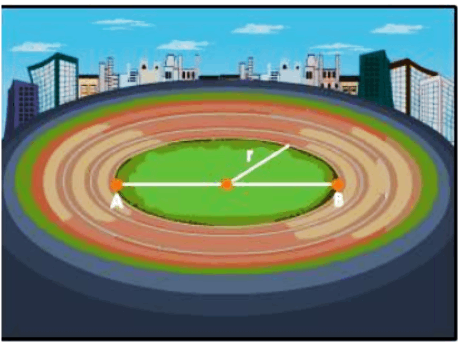
A Circular Track of Radius r 

What is the athlete's total distance traveled when he arrives at point B?

The athlete's total distance traveled when he arrives at point B equals to half of the circumference of the circular track, that is, $\frac{2\pi r}{2}=\pi r$.

Displacement $=AB=2r=$ Diameter of circle (the shortest distance between the initial and final positions).

If the athlete arrives at the starting point $A$, the distance covered is equal to the circumference of the circular track, i.e., $2\pi r.$ However, the displacement is zero because the athlete's initial and final positions are the same.

Difference between Distance and Displacement

Motion: 

Uniform Motion and Non-uniform Motion: 

The distances covered by car A and car B with respect to time is given below:

Car A: 

Car B: 

The car A travels equal distances in equal time intervals, whereas the car B does not travel equal distances in equal time intervals. That is, car A's motion is an example of uniform motion, whereas car B's motion is an example of non-uniform motion.

A body is said to describe uniform motion when it covers equal distances in equal intervals of time.

When a body moves unequal distances in equal time intervals, or vice versa, this is referred to as non-uniform motion.

Speed: 

Ram and Krishna compete in various races over varying distances. Ram covers $1000\mathrm{m}$ in 20 minutes and Krishna covers $700\mathrm{m}$ in 10 minutes. Who is the fastest?

To determine who is faster, we will calculate the distance they cover in one minute.

Distance covered by Ram in one minute $=\frac{1000\mathrm{m}}{20\min }=500\mathrm{m}/\min$

Distance covered by Krishna in one minute $=\frac{700\mathrm{m}}{10\min }=70\mathrm{m}/\min$

Krishna covered more ground in the same amount of time. We conclude that Krishna is the faster of the two. 

Speed is defined as the distance traveled by a moving object in one unit of time.

$\text{ speed }=\frac{\text{ distance }}{\text{ time }}=\frac{\mathrm{S}}{\mathrm{t}}$

Where S denotes the distance traveled and t denotes the time spent.

The SI unit of speed is millimeters per second (m/s). Speed is defined as a scalar quantity.

Uniform Speed:

The graph depicts the distance traveled by a ball every 2 seconds.

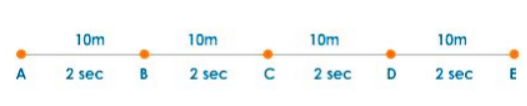
Every 2 seconds, the ball travels 10 meters. At any point between A and E, the ball moves at a speed of 5 m/s. The object is moving at a constant speed.

If an object travels the same distance in the same amount of time, it is said to be moving at a uniform speed.

Surface friction or resistance is ignored in this case.

Variable Speed or Non-Uniform Speed: 

The distance covered varies with time.

Variable Speed: 

For example, when a rubber ball is dropped from a certain height (h1), it bounces up to a height less than the initial one (h2). It keeps bouncing, but the height to which it rises keeps decreasing (h3, h4). The ball's distance travelled per unit of time decreases. The ball's speed varies from point to point. This type of speed is known as variable speed.

Average Speed and Instantaneous Speed:

When we travel by car, the speed varies depending on the road conditions at the time. The speed is calculated in this case by dividing the total distance travelled by the vehicle by the total time required for the journey. This is known as the average speed. 

The average speed of an object travelling S1 in time t1, S2 in time t2, and Sn in time tn is given by,

$\text{ Average speed }=\frac{{\mathrm{S}}_1+{\mathrm{S}}_2+{\mathrm{S}}_3+\dots +{\mathrm{S}}_{\mathrm{n}}}{{\mathrm{t}}_1+{\mathrm{t}}_2+{\mathrm{t}}_3+\dots +{\mathrm{t}}_{\mathrm{n}}}$

When we say that the car travels at an average speed of 60 km/h, we do not mean that it will travel at that speed for the duration of the journey. The actual speed of the car may be less than or greater than the average speed at a given location.

The speed of a moving body at any given point in time is referred to as instantaneous speed.

Velocity:

The diagram below depicts the various routes Shyam can take from his house to school. 

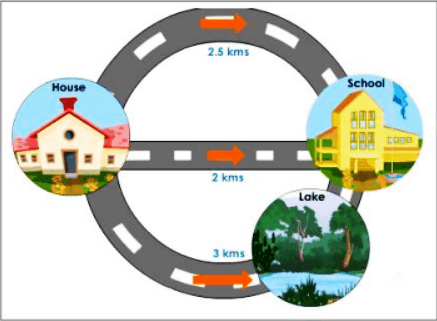
Shyam drives himself to school every day, averaging 60 km/h. Is it possible to find out how long it will take to get to the destination? Yes, you can use the relation to determine the time.

$\text{ speed }=\frac{\text{ distance }}{\text{ time }}$

But you don't know what path he would have taken. As a result, simply providing the speed of a moving object does not allow one to determine the exact position of the object at any given time. As a result, there is a need to define a quantity that has both magnitude and direction.

Starting with A, consider two objects P and Q. Allow them to travel equal distances in equal time intervals, i.e. at the same speed. Can you guess where each of them will be in 20 seconds? P and Q are free to move in any direction. To determine the exact position of P and Q, we must also know their direction of motion.

Pictorial Representation of the Position of the Objects P and Q:

As a result, another physical quantity known as velocity is introduced to provide us with an idea of both speed and direction.

Velocity is defined as the distance travelled in a given direction by a moving object in a given time or speed in a given direction.

$\mathrm{velocity}(v)=\frac{\text{ distance travelled in a specified direction }(s)}{\text{ time taken }(t)}$

Note: 

Velocity is defined as the distance travelled in a given direction in a given amount of time. Displacement is the distance travelled in a specified direction.

As a result, velocity can be defined as the rate at which displacement changes.

Uniform Velocity and Non-Uniform Velocity:

Assume that two athletes, Ram and Shyam, are running at a constant speed of 5 m/s. Ram moves in a straight line, while Shyam follows a circular path. For a layperson, both Ram and Shyam are moving with uniform velocity, but for a physicist, only Ram is running with uniform velocity because his speed and direction of motion do not change.

In the case of Shyam, who is running on a circular track, the direction of motion changes at every instant because a circle is a polygon with infinite sides, and Shyam must change his direction at every instant.

A body is said to be moving with uniform velocity if it travels the same distance in the same amount of time in the same direction.

A body is said to be moving with variable velocity if it covers unequal distances in equal intervals of time and vice versa in a specified direction, or if its direction of motion changes.

Acceleration:

We are all aware that a car moving down the road does not have a uniform velocity. Either the speed or the direction of travel shifts. We say that a vehicle is accelerating when it is speeding up, i.e. when the speed increases.

Let us look at the change in velocity of a train traveling from Bangalore to Mysore to get an idea of acceleration. The train, which was initially at rest, begins to move; its velocity gradually increases until it reaches a constant velocity after a certain time interval. As the train approaches the next station, its speed gradually decreases until it comes to a halt.

When a train starts from a stop, its speed increases from zero, and we say it is accelerating. After a while, the speed becomes uniform, and we say that the train is moving at a uniform speed, which means that it is not accelerating. However, as the train approaches Mysore, it slows down, indicating that the train is accelerating in the opposite direction. When the train comes to a halt in Mysore, it stops accelerating once more.

As a result, it is clear that the term "acceleration" does not always imply that the speed of a moving body increases; it can also decrease, remain constant, or become zero.

In general, acceleration is defined as the rate at which the velocity of a moving body changes over time.

This change could be a change in the object's speed, direction of motion, or both.

Let us now look up a mathematical formula for calculating acceleration.

If an object moves with an initial velocity 'u' and reaches a final velocity 'v' in time 't,' then the acceleration 'a' produced by the object is

Acceleration = Rate at which velocity changes over time.

$a=\frac{v-u}{t}$

Unit of Acceleration:

The SI unit of acceleration is m/s2 and it is a vector quantity.

Different Types of Acceleration: 

It is clear from the preceding example that acceleration takes various forms depending on the change in velocity.

Positive acceleration:

When an object's velocity increases, it is said to be moving with positive acceleration.

Positive Acceleration 

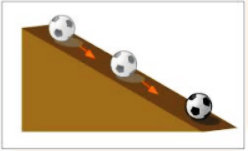
Example: a ball rolling downhill on an inclined plane.

Negative acceleration:

When an object's velocity decreases, it is said to be moving with negative acceleration. Negative acceleration can also be referred to as retardation or deceleration.

Example:

(1) A ball moving up an inclined plane.

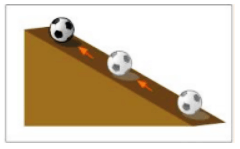
(2) A vertically thrown upward ball has a negative acceleration as its velocity decreases over time.

Zero Acceleration: 

If the change in velocity is zero, indicating that the object is either at rest or moving at uniform velocity, the object is said to have zero acceleration.

A parked car, for example, or a train moving at a constant speed of 90 km/hr.

Uniform Acceleration: 

The object is said to be moving with uniform acceleration if the change in velocity at equal intervals of time is always the same.

As an example, consider a body falling from a great height towards the earth's surface.

Non-uniform or Variable Acceleration: 

If the change in velocity over equal time intervals is not the same, the object is said to be moving with variable acceleration.

Motion: 

Distance-Time Table and Distance-Time Graph: 

Mr. X is taking a bus from New Delhi to Agra and recording his observations.

According to the table above, the bus travels equal distances at equal times. The bus is moving at a constant speed. In such a case, we can compute the distance traveled by the bus at any given point in time.

Consider an object moving from its initial position xi to its final position xf in time t at a uniform speed v. 

$\text{ uniform speed }=\frac{\text{ total distance }}{\text{ time taken }}$

$v=\frac{x_f-x_i}{t}$

$x_f-x_i=vt\cdots \cdots (1)$

The relationship between distance, time, and average speed is given by equation (1). This relationship can be used to generate distance-time tables as well as to determine the position of any moving object at any given time. However, it is a time-consuming and tedious process, especially when we need to determine the position after a long period of time or compare the motion of two objects. In such cases, graphs such as the distance-time graph can be useful. A distance-time graph is a line graph that shows how distance changes over time. A distance-time graph plots time along the x-axis and distance along the y-axis. 

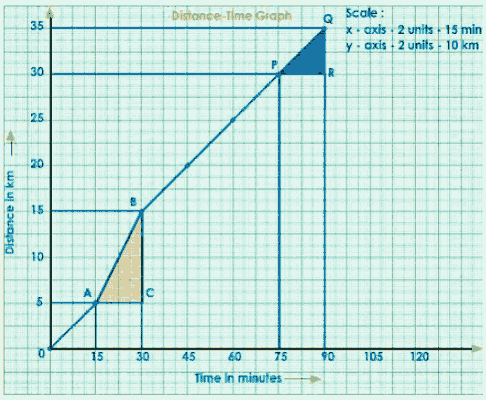
Distance-Time Graph for Non - Uniform Motion 

Let us now look at the nature of a distance-time graph for a non-uniform motion. The distance traveled by a bus every 15 minutes is shown in the table below.

We can deduce from the above table that the motion is non-uniform, i.e. it covers unequal distances in equal time intervals.

• Measure time along the x-axis and distance along the y-axis.

• Analyze the provided data and select the appropriate scale for time and distance.

• Plot the points.

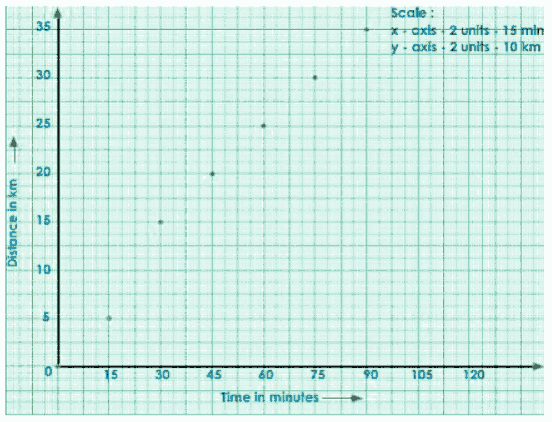
• Join the points.

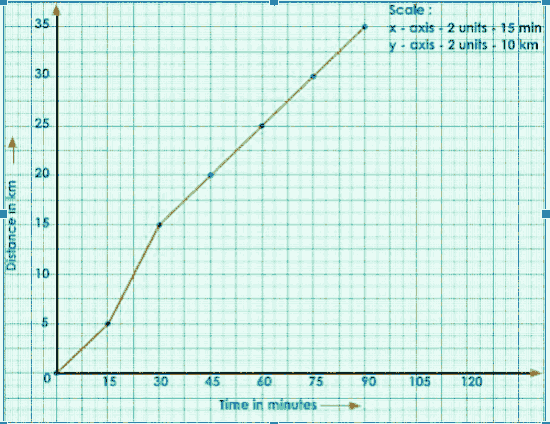
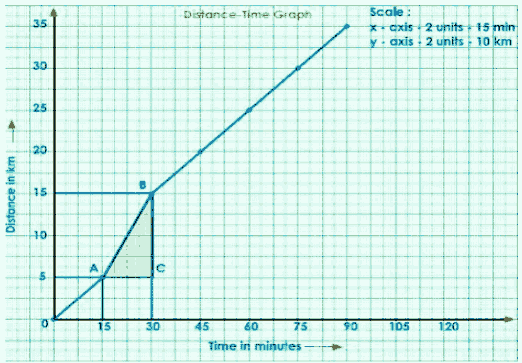
• Consider any two points (A, B) on the graph.

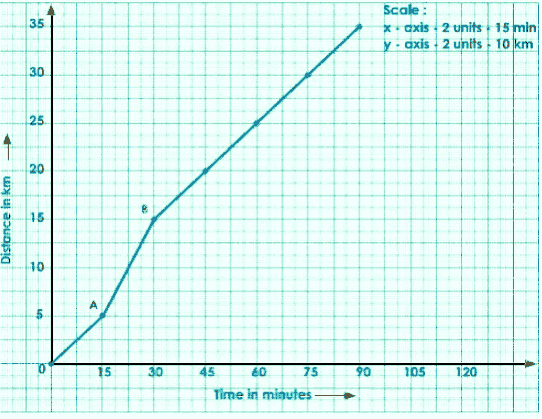
• Draw a perpendicular from A to B to the x and y axes.

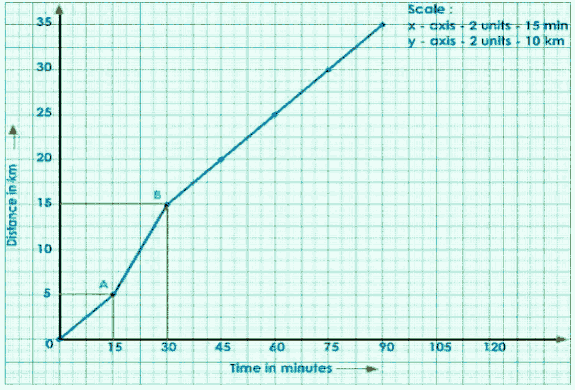
• Join A to C to get a right-angled ACB.

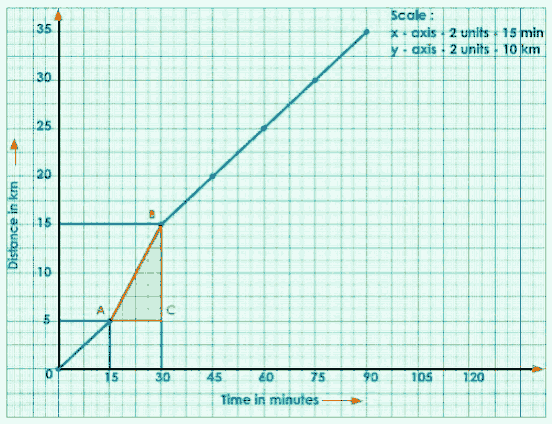
The slope of the graph is shown below.

$\mathrm{AB}=\frac{\mathrm{BC}}{\mathrm{AC}}$

$=\frac{\mathrm{S}}{\mathrm{t}}$

$=\mathrm{speed}$

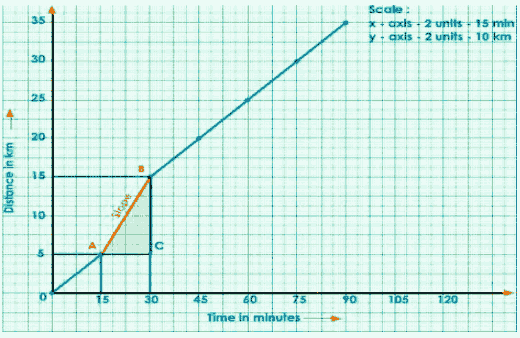
• Write the title and scale chosen for the graph.

$\text{ speed }=\frac{15-5}{30-15}$

$=\frac{10}{15}$

$=\frac{2}{3}$

$=0.666\mathrm{km}/\min$

• Consider another two points on the graph, P and Q, and draw a right-angled triangle PRQ.

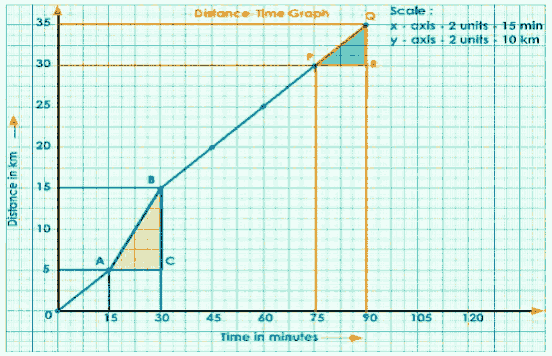
$\text{ slope }=\text{ speed }$

$\mathrm{PQ}=\frac{\mathrm{QR}}{\mathrm{PR}}$

$=\frac{35-30}{90-75}$

$=\frac{5}{15}$

$=0.333\mathrm{Km}/\min$

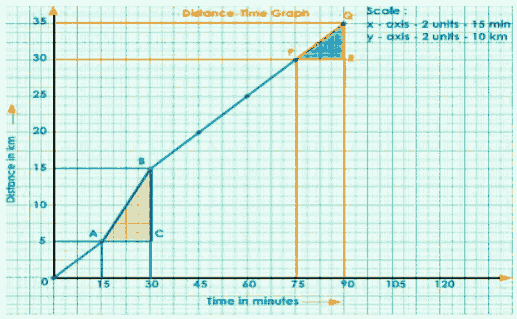
• Complete Graph

Nature of S- t Graph for Non-Uniform Motion and Uses of Graphs

Let us now see the nature of S-t graph for non-uniform motion. 

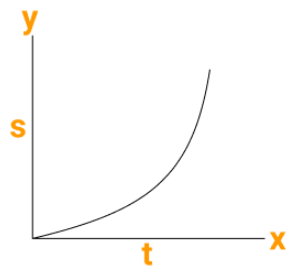
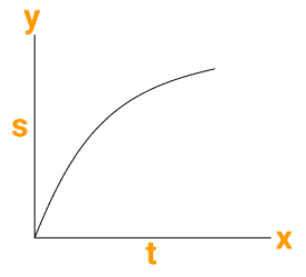
Nature of s-t Graph for Non-Uniform Motion: 

Figure (a) depicts the S-t graph as the speed of a moving object increases, while Figure (b) depicts the S-t graph as the speed of a moving object decreases. The nature of the S-t graph allows us to determine whether the object is moving at a constant or variable speed.

Uses of Graphical Representation: 

• Because it provides a visual representation of two quantities, graphical representation is more informative than tables (e.g., distance vs. time)

• A graph provides more information than a table at a glance. Both of the graphs shown here depict increasing speed.

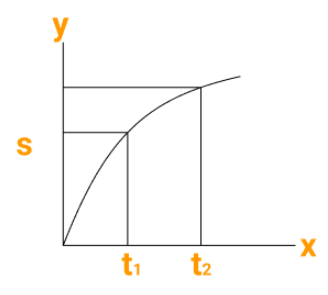
Figure (1) depicts the nature of the variation in speed, indicating that the increase is greater in the beginning up to time t1 and relatively lower after t2.

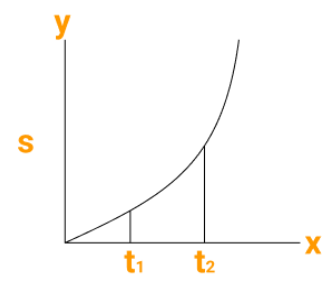
Similarly, fig (2) depicts how the increase in speed becomes greater after t1. A similar explanation applies to the decreasing speed.

• Graphs are simple to read at a glance.

• Graph plotting takes less time and is more convenient.

• Graphs can be used to determine the position of any moving object at any point in time.

• Two moving objects' motions can be easily compared.

• Graphs reveal information about the nature of motion.

Motion: 

Velocity-Time Graph: 

The variation of velocity with time can be graphically represented to calculate acceleration in the same way that we calculated speed from the distance-time graph.

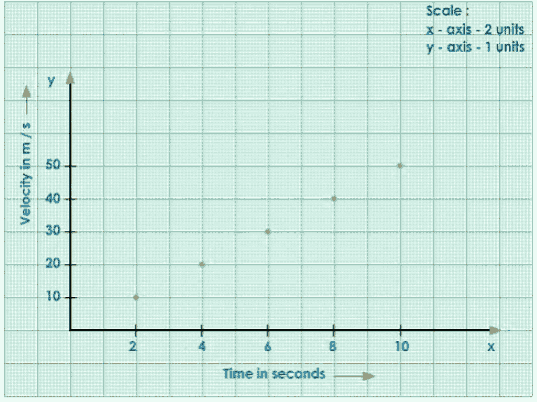
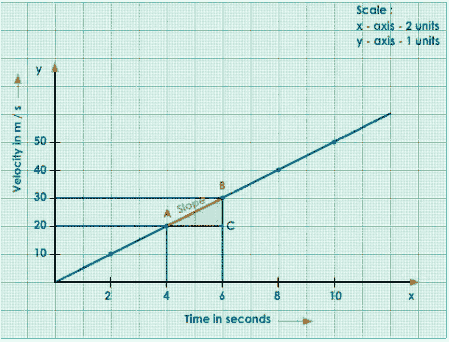
Let us now create a velocity-time(v-t) graph using the data below.

• Draw time on the x-axis and velocity on the y-axis. 

• Analyse the provided data and select the appropriate scale for the x and y axes.

• Plot the Given Points.

• Join the Points

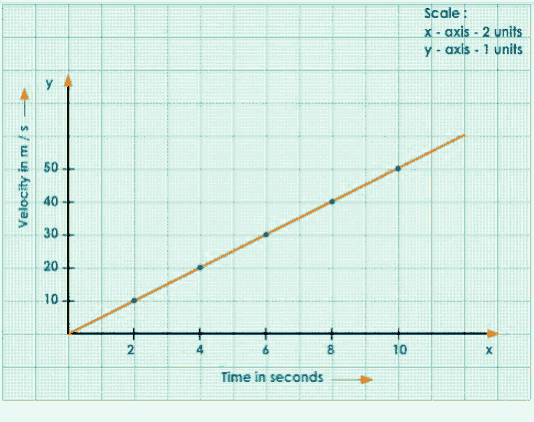
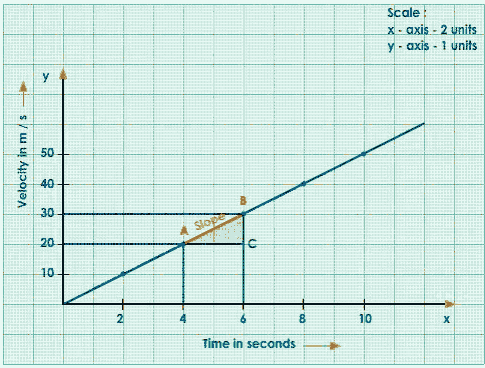
• Consider Any Two Points A and B on the Straight-Line Graph.

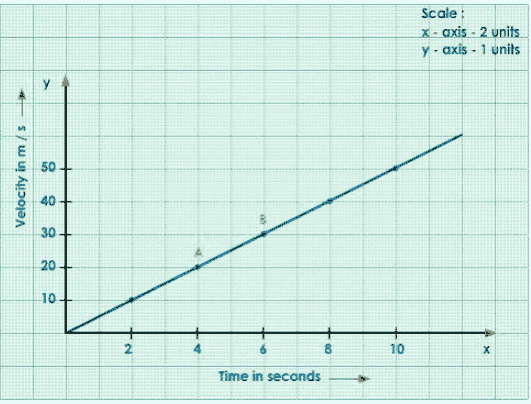
• Draw Perpendiculars from A and B to x and y-axes.

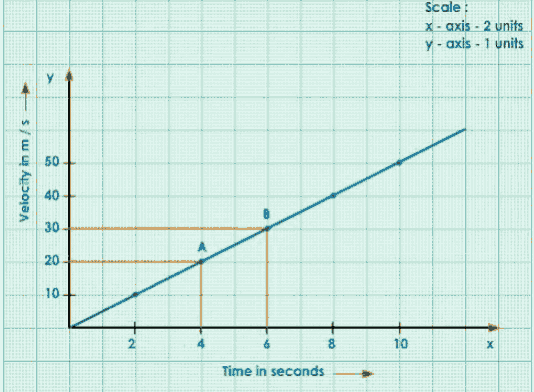
• Join A to C, ACB forms a Right-Angled Triangle.

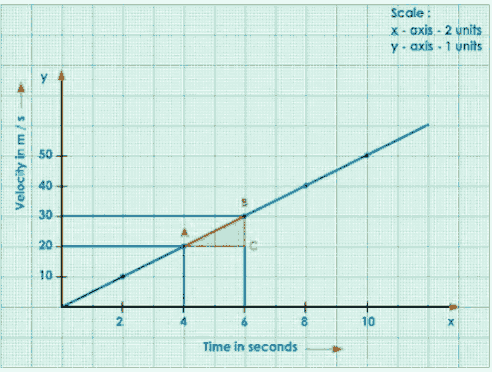
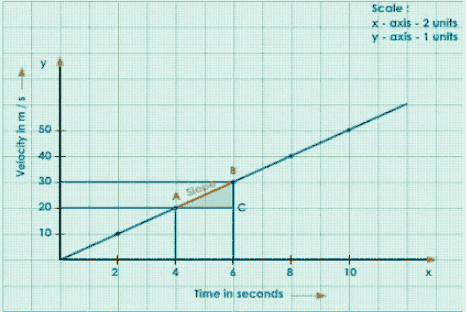
• The Slope of the Graph

$\mathrm{AB}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\text{ Change in velocity }}{\text{ time }}=\text{ acceleration }$

Calculations:

$\text{ Acceleration }=\frac{30-20}{6-4}$

$=\frac{10}{2}$

$=5\mathrm{m}/{\mathrm{s}}^2$

• Write the title for the graph.

• Complete Graph

V - T Graph:

Let us now examine the nature of the v - t graph for various types of motion.

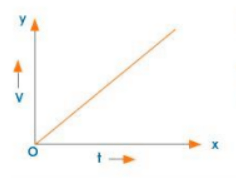
a) Increasing Acceleration:

Uniform Acceleration

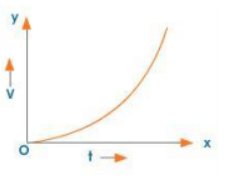
Non-Uniform Acceleration

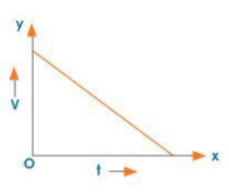
(b) Decreasing Acceleration:

Non-uniform Retardation

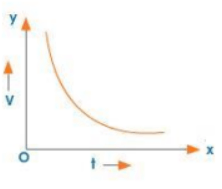
Uniform Retardation

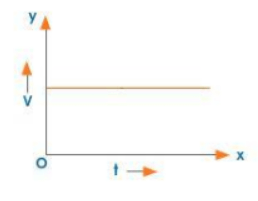
Zero Acceleration

Uses of Velocity-time Graphs 

The velocity-time graph can be used to derive the following results. 

• The acceleration produced in a body. 

• The distance travelled by a moving object. 

• The equations of motion.

Speed - Time Graph

To compute the distance travelled by a moving object using a speed-time graph. 

The graph below depicts the speed-time graph of a car travelling at a constant speed of 60 km/h for 5 hours.

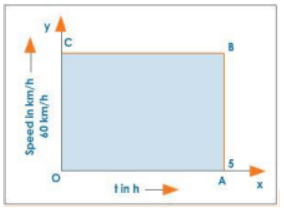
Speed-Time Graph of a Car Moving with Uniform Speed 

Distance travelled by the car,

Distance travelled by the car

$(S)=v\times t$

$=60\times 5$

$=300\mathrm{km}$

But $60\mathrm{km}/\mathrm{h}=\mathrm{OC}=$ breadth of the rectangle $\mathrm{OABC}$

$5h=OA=$ length of the rectangle $OABC$

i.e., the distance covered by the car = length $\times$ breadth $=300\mathrm{km}$.

To calculate the distance travelled by a moving object using a speed-time graph, find the area enclosed by the speed-time graph and the time axis. In the case of non-uniform motion, the distance covered by the object increases in steps as the object's speed increases. During the time intervals $0-t_1,t_1-t_2,t_2-t_3,\dots \dots$, the speed remains constant.

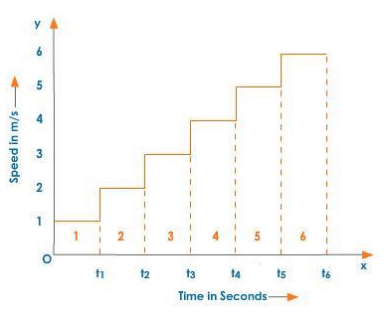
The motion of an object moving at a variable speed is depicted in the figure below.

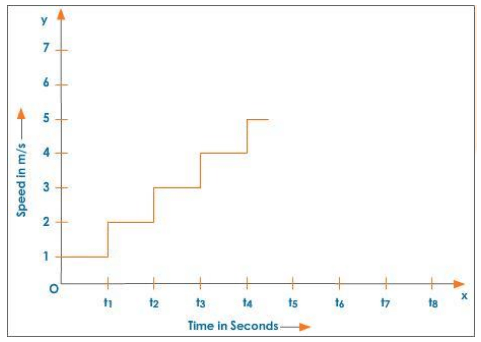
Speed - Time Graph for an Object Moving with Variable Speed

Calculation of Distance:

The object's total distance travelled during the time interval. 

0- t6 = Area of rectangle 1 + area of rectangle 2 + …… + area of rectangle 6. 

Motion 

Equations of Motion 

Time, speed, distance covered, and acceleration are the variables in a uniformly accelerated rectilinear motion. These quantities have simple relationships. These relationships are expressed using equations known as equations of motion. 

The equations of motion are: 

(1) $v=u+at$

(2) $S=ut+{\displaystyle \frac{1}{2}}a{t}^2$

(3) $v^2-u^2=2aS$

Derivation of the First Equation of Motion

Consider a particle moving in a straight line with a constant acceleration ‘a’. Let the particle be at A at t=0, and u be its initial velocity, and v be its final velocity at t=t.

$a={\displaystyle \frac{v-u}{t}}$ 

$v-u=at$ 

$v=u+at$

I Equation of Motion

Second Equation of Motion

$\text{ Average velocity }={\displaystyle \frac{\text{ total distance travelled }}{\text{ total time taken }}}$

$={\displaystyle \frac{S}{t}}\dots \dots (1)$

Average velocity can also be written as

$\frac{u+v}{2}\cdots \cdots (2)$

From equation (1) and (2),

$\frac{S}{t}=\frac{u+v}{2}\cdots \cdots (3)$

The first equation of motion is $v=u+at$. Substituting the value of $v$ in equation (3), we get

$\frac{S}{t}=\frac{u+u+at}{2}=\frac{(u+u+at)t}{2}$

$=\frac{(2u+at)t}{2}$

$S=ut+\frac{1}{2}a{t}^2$

II equation of motion

Third Equation of Motion

The first equation of motion is

$v=u+at$

$v-u=at\dots (1)$

Average velocity $=\frac{S}{t}\cdots \cdots (2)$

Average velocity $=\frac{u+v}{t}\cdots \cdot (3)$

From equation (2) and equation (3) we get,

$\frac{u+v}{t}=\frac{S}{t}\cdots \dots (4)$

Multiplying equation (1) and equation (4) we get,

$(v-u)(v+u)=at\times \frac{2S}{t}$

$(v-u)(v+u)=2aS$

$(v^2-u^2)=2aS$

III equation of motion

Derivations of Equations of Motion (Graphically) 

First Equation of Motion

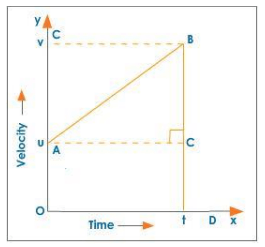
Consider an object moving in a straight line with a uniform velocity u. When its initial velocity is u, give it a uniform acceleration at time t = 0. The object's velocity increases as a result of the acceleration to v (final velocity) in time t, and S is the distance covered by the object in time t.

The graph depicts the velocity-time graph of the object's motion.

The acceleration of a moving object is given by the slope of the v - t graph.

Thus, acceleration = slope

$\mathrm{AB}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{v-u}{t-0}$

$a=\frac{v-u}{t}$

$v-u=at$

$v=u+at$

I equation of motion

Second Equation of Motion 

Let u be an object's initial velocity and 'a' be the acceleration produced in the body. The area enclosed by the velocity-time graph for the time interval 0 to t gives the distance travelled S in time t.

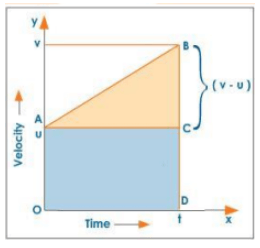
Graphical Derivation of Second Equation

Distance travelled S = area of the trapezium ABDO

Distance travelled $S=$ area of the trapezium ABDO

$=$ area of reactangle $ACDO+$ area of $\mathrm{△}ABC$

$=\mathrm{OD}\times \mathrm{OA}+\frac{1}{2}\mathrm{BC}\times \mathrm{AC}$

$=\mathrm{t}\times \mathrm{u}+\frac{1}{2}(\mathrm{v}-\mathrm{u})\times \mathrm{t}$

$=\mathrm{ut}+\frac{1}{2}(v-u)\times t$

$v=u+$ at $\mid$ equation of motion; $v-u=at$

$S=ut+\frac{1}{2}at\times t$

$=ut+\frac{1}{2}a{t}^2$

II equation of motion

Third Equation of Motion 

Let 'u' be an object's initial velocity and a be the acceleration produced in the body. The area enclosed by the v - t graph gives the distance travelled 'S' in time 't'.

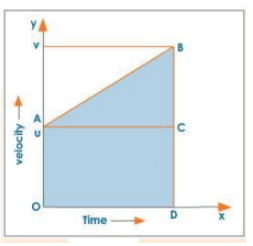
Graphical Derivation of Third Equation

$\mathrm{S}=$ area of trapezium $\mathrm{OABD}$

$=\frac{1}{2}(b_1+b_2)h$

$=\frac{1}{2}(\mathrm{OA}+\mathrm{BD})\mathrm{AC}$

$=\frac{1}{2}(u+v)t\cdots \cdots (1)$

But we know that $a=\frac{v-u}{t}$ or $t=\frac{v-u}{a}$

Substituting the value of $t$ in equation (1) we get,

$S=\frac{1}{2}\frac{(u+v)(v-u)}{a}$

$=\frac{1}{2}\frac{(v+u)(v-u)}{a}$

$2as=(v+u)(v-u)$

$(v+u)(v-u)=2as$

$v^2-u^2=2as$

III Equation of Motion 

Circular Motion 

We classified motion along a circular track as non-uniform motion in the example discussed under the topic of uniform and non-uniform motion. Let's take a look at why circular motion is considered non-uniform motion. The figure depicts an athlete running at a constant speed on a hexagonal track.

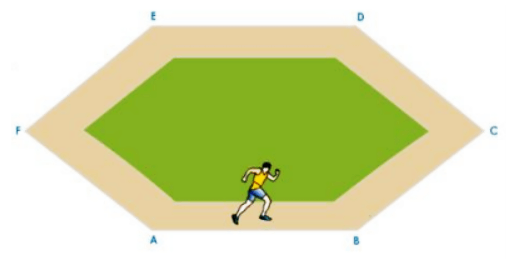
Athlete Running on a Regular Hexagonal Track 

The athlete runs at a constant speed along the track segments AB, BC, CD, DE, EF, and FA, and at the turns, he quickly changes direction to stay on the track without changing his speed. Similarly, if the track had been a regular octagon, the athlete would have had to change directions eight times in order to stay on the track.

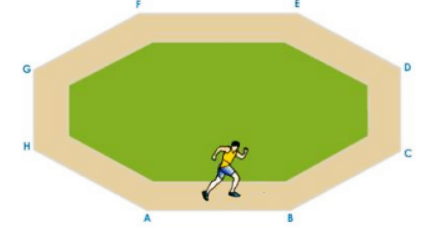
Athlete Running on a Regular Octagonal Track 

The athlete must turn more frequently as the number of sides of the track increases. If we increase the number of sides indefinitely, the track will take on the shape of a circle. As a result, because a circle is a polygon with infinite sides, motion along a circular path is classified as non-uniform motion.

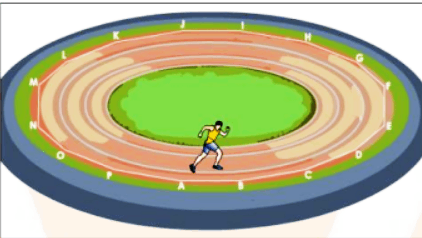
Athlete Running on a Circular Track 

Thus, an object moving at uniform speed along a circular track is an example of non-uniform motion because the object's direction of motion changes at every instant of time. 

Examples of Uniform Circular Motion 

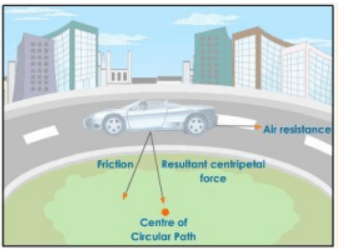
(1) A car negotiating a curve at a constant speed.

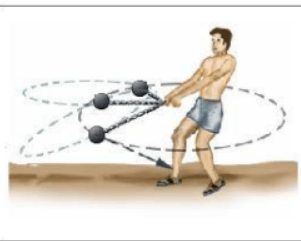
(2) An athlete spinning a hammer in a circle before throwing it.

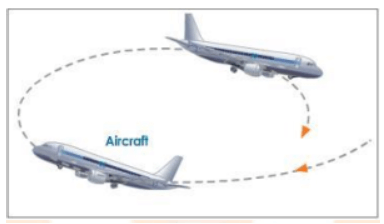
(3) An aircraft looping the loop.

Expression for Linear Velocity

If an athlete takes t seconds to complete one circular path of radius r, then the velocity v is given by the relation,

$\mathrm{v}=\frac{\text{ distance travelled }}{\text{ time }}$

Distance travelled = circumference of the circle

$=2\pi \mathrm{r}$

Linear velocity $=\frac{\text{ 2r }}{\mathrm{t}}$

Important formula in Class 9 Science Chapter 7 Motion

1. Speed:

$\text{Speed}=\frac{\text{Distance}}{\text{Time}}$

2. Velocity:

$\text{Velocity}=\frac{\text{Displacement}}{\text{Time}}$

3. Acceleration:

$\text{Acceleration}=\frac{\text{Change in velocity}}{\text{Time taken}}$

4. Equations of Motion:

These equations describe the relationship between displacement, velocity, acceleration, and time:

• First equation:
  v=u+at
  where v is final velocity, uuu is initial velocity, a is acceleration, and t is time.

• Second equation:
  $s=ut+\frac{1}{2}a{t}^2$
  where s is displacement, u is initial velocity, aaa is acceleration, and ttt is time.

• Third equation:
  $v^2=u^2+2as$
  where v is final velocity, u is initial velocity, a is acceleration, and s is displacement.

5. Average Velocity: 

$\text{Average velocity}=\frac{\text{Initial velocity}+\text{Final velocity}}{2}$

Distance traveled in nnnth second:
$s_n=u+\frac{a}{2}(2n-1)$
where $s_n$​ is the distance covered in the n-th second, u is the initial velocity, and aaa is acceleration.

5 Important Topics of Class 9 Chapter 7 You Shouldn’t Miss!

Importance of Class 9 Science Motion Notes

• The Motion chapter is essential as it forms the foundation for understanding how objects move in the real world.

• These notes simplify concepts like displacement, velocity, speed, and acceleration, which are crucial for solving problems in physics.

• Understanding motion helps in building the base for more advanced topics in higher classes, like kinematics and dynamics.

• The notes provide important formulas and explanations that are frequently asked in exams, ensuring students are well-prepared.

• Learning this chapter is useful for understanding the mechanics behind everyday movements, from vehicles to natural forces like gravity.

• Motion is a fundamental concept that links to other topics in science, helping students gain a clearer picture of the physical world.

Tips for Learning the Class 9 Chapter 7 Science Motion

• Begin by understanding basic terms like distance, displacement, speed, and velocity. These are the building blocks for the rest of the chapter.

• Memorise important formulas, such as the equations of motion, which are crucial for solving numerical problems.

• Practice different types of problems related to uniform and non-uniform motion to gain confidence in applying the concepts.

• Use diagrams to visualise concepts like distance-time graphs and velocity-time graphs. This will help you understand how motion changes over time.

• Revise regularly and summarise key points to ensure you retain the concepts and formulas.

• Relate the concepts to real-life examples, like how cars move on a road or how athletes run, to make the learning process more engaging.

Conclusion

The Motion chapter in Class 9 Science is a key topic that introduces students to the basic principles of how objects move. By learning concepts like speed, velocity, and acceleration, students build a strong foundation for future physics topics. The notes for this chapter help break down these ideas into simple terms and offer important formulas and examples to make studying easier. With regular practice and a clear understanding of the basics, students can perform well in exams and apply these concepts to real-world situations.

Related Study Materials for Class 9 Science Chapter 7 Motion

Chapter-wise Links for Science Notes Class 9 - FREE PDF Download

Important Study Materials for Class 9 - Science