Class 9 Science Chapter 10 Summary Notes PDF Download
Work and Energy Class 9 Science Chapter 10 CBSE Notes - 2025-26
FAQs on Work and Energy Class 9 Science Chapter 10 CBSE Notes - 2025-26
1. How does the concept of 'work' in physics connect to 'energy' for a quick revision?
In physics, work and energy are fundamentally linked through the work-energy principle. Essentially, doing work on an object is the process of transferring energy to it. The amount of work done is exactly equal to the amount of energy transferred. For example, when you lift a book, you do work against gravity and transfer potential energy to the book.
2. What is a quick summary of 'power' as defined in Class 9 Science?
Power is a measure of how quickly work is done or how fast energy is transferred. An engine might be able to do a lot of work, but its power determines how fast it can do it. The key concept to remember for revision is that power is the rate of doing work. Its SI unit is the Watt (W), where 1 Watt equals 1 Joule per second.
3. What is the main difference between kinetic and potential energy?
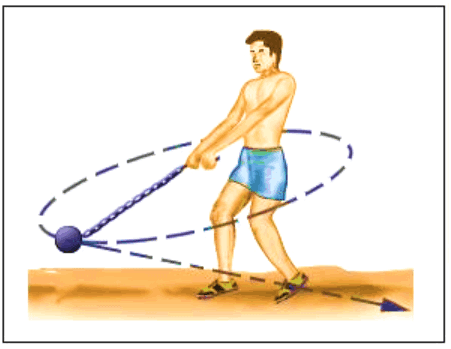
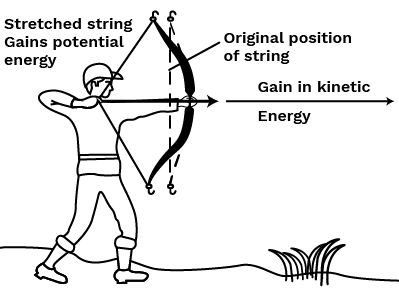
The core difference is that kinetic energy is the energy an object possesses due to its motion, while potential energy is the energy stored in an object due to its position or configuration. A moving car has kinetic energy, whereas a stretched rubber band or a rock at the top of a hill has potential energy.
4. What are the key formulas needed for a quick revision of the Work and Energy chapter?
For a quick summary of Chapter 10, focus on these essential formulas as per the CBSE Class 9 syllabus for 2025-26:
- Work Done (W): W = Force (F) × displacement (s)
- Kinetic Energy (KE): KE = ½ × mass (m) × velocity (v)²
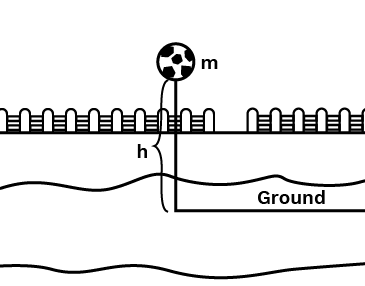
- Potential Energy (PE): PE = mass (m) × acceleration due to gravity (g) × height (h)
- Power (P): P = Work (W) / time (t)
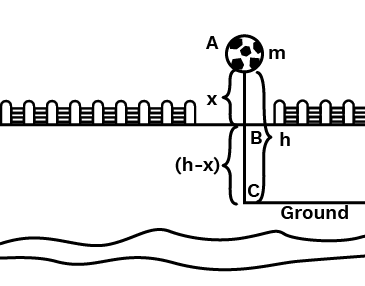
5. What is the law of conservation of energy, and how does it apply to a freely falling body?
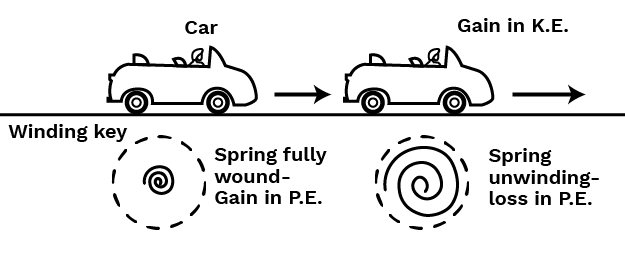
The law of conservation of energy states that energy can neither be created nor destroyed; it only changes from one form to another. For a freely falling body, the total mechanical energy (potential energy + kinetic energy) remains constant. At the highest point, it has maximum potential energy and zero kinetic energy. As it falls, the potential energy converts into kinetic energy, but their sum at any point during the fall is the same.
6. Why do work and energy share the same SI unit, the joule?
Work and energy share the same unit because work is not a substance but a measure of energy being transferred or transformed. When you do 1 joule (J) of work on an object, you have transferred exactly 1 joule of energy to it. This direct equivalence in definition means they must be measured using the same unit, reflecting that work is simply energy in transit.
7. When is the work done on an object considered zero, positive, or negative?
Understanding the conditions for work is crucial for revision. Work done is categorised as follows:
- Positive Work: When the force applied is in the same direction as the object's displacement. Example: Pushing a trolley forward.
- Negative Work: When the force applied is in the opposite direction to the object's displacement. Example: The force of friction acting on a rolling ball.
- Zero Work: When the force is applied perpendicular (at 90°) to the displacement, or if there is no displacement. Example: A man pushing a wall that doesn't move, or carrying a suitcase horizontally at a constant velocity.
8. How is the commercial unit of energy, the kilowatt-hour (kWh), different from the SI unit of energy, the joule?
The joule is the SI unit of energy, but it is too small for measuring large-scale energy consumption, like household electricity. The kilowatt-hour (kWh) is a larger, practical unit used for this purpose. 1 kWh is the energy consumed by a 1000-watt appliance running for one hour. The key relationship for revision is 1 kWh = 3.6 × 10⁶ joules.
9. If an object's velocity is doubled, by what factor does its kinetic energy increase?
The formula for kinetic energy is KE = ½ mv². Since kinetic energy is proportional to the square of the velocity (v²), doubling the velocity has a significant effect. If the velocity becomes 2v, the new kinetic energy will be ½ m(2v)² = ½ m(4v²) = 4 × (½ mv²). Therefore, doubling the velocity increases the kinetic energy by a factor of four.




















 Watch Video
Watch Video