Class 9 Science Chapter 9 Summary Notes PDF Download
Gravitation Class 9 Science Chapter 9 CBSE Notes - 2025-26
FAQs on Gravitation Class 9 Science Chapter 9 CBSE Notes - 2025-26
1. What are the core concepts covered in Class 9 Science Chapter 9 Gravitation revision notes?
The revision notes for Gravitation in Class 9 Science summarise key concepts like the universal law of gravitation, acceleration due to gravity, the difference between mass and weight, formulas for free fall, Archimedes' Principle, and the calculation of density and relative density. The notes help students quickly recap the foundational principles needed for exams as per the CBSE 2025–26 syllabus.
2. How does the universal law of gravitation connect to other topics in the CBSE Class 9 Science syllabus?
The universal law of gravitation forms the basis for understanding topics like orbits of planets, tides, and weightlessness in space. It also provides the foundation for formulas and problems related to motion and force learned in previous chapters, showing the interconnectedness of concepts within the science syllabus.
3. What is the recommended order for revising Gravitation Class 9 notes for effective exam preparation?
Start with understanding the definition and scope of gravitation, then move to the universal law and its formula, followed by derivations and numerical applications. Next, review related concepts such as mass, weight, thrust, and pressure. End with Archimedes’ Principle, density, and real-life examples to connect theory to practice.
4. How can concept maps and summaries in the revision notes help with last-minute preparation for exams?
Concept maps visually link key ideas, making it easier to recall relationships between topics like force, gravity, weight, and mass. Summaries provide quick overviews of main points and formulas, allowing you to revise essential information rapidly before exams without getting overwhelmed by details.
5. What are the main differences between mass and weight as highlighted in the revision notes?
Mass is the amount of matter in a body, remains constant everywhere, and its SI unit is kilogram (kg). Weight is the force with which gravity pulls an object towards the center of the Earth, varies by location, and its SI unit is Newton (N). Mass is a scalar quantity, while weight is a vector quantity.
6. Why does the weight of an object vary on the moon compared to Earth, as per CBSE revision notes?
The weight of an object depends on the acceleration due to gravity (g) of the celestial body. Since the moon’s gravity is weaker than Earth’s, an object’s weight on the moon is about one-sixth of its weight on Earth, while its mass remains unchanged.
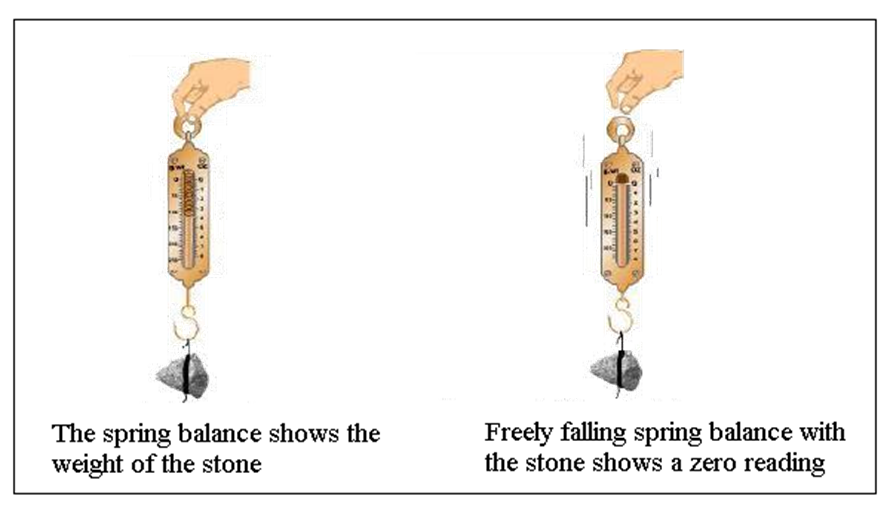
7. How do the revision notes explain the concept of weightlessness and its applications?
According to the notes, weightlessness occurs when an object is in free fall, with no normal force acting upon it—for example, astronauts in orbit. In such cases, both the person and the spacecraft fall towards Earth at the same rate, so the person exerts no force on the floor and experiences a sensation of weightlessness.
8. What quick tips are provided in the notes for revising key formulas in Gravitation for CBSE exams?
The revision notes suggest to:
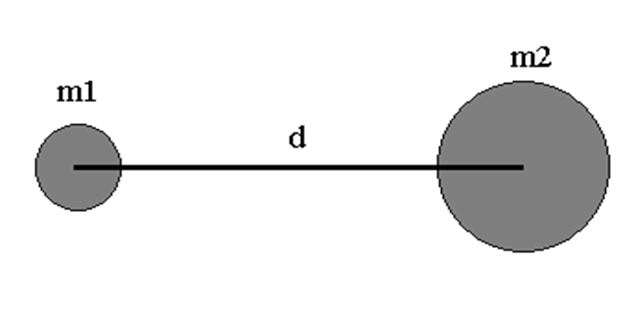
- Regularly write down and practice the important formulas (F = G m₁m₂ / r², g = GM / R², W = mg, etc.).
- Use flashcards or summary sheets for quick recall.
- Solve sample numerical problems to keep formulas fresh in memory.
- Relate formulas to real-world examples for better understanding.
9. How does understanding density and relative density in the revision notes aid in mastering the chapter?
Understanding density and relative density helps students solve practical problems related to floating and sinking, identification of substances, and applications like Archimedes’ Principle. These concepts are frequently tested both in numericals and conceptual questions on CBSE exams.
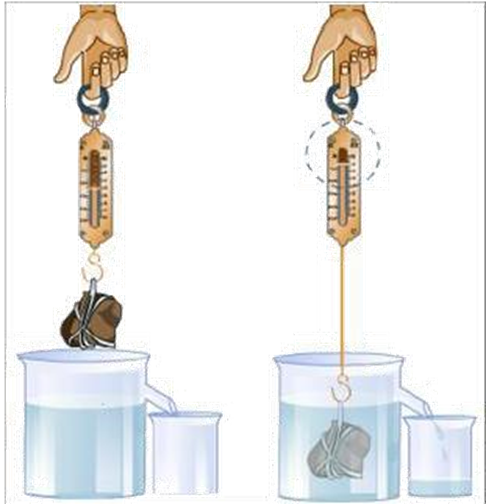
10. Why is Archimedes’ Principle included in Gravitation Class 9 revision notes and how can it be applied?
Archimedes’ Principle explains the upward buoyant force exerted by fluids and is crucial for understanding phenomena such as floating, sinking, and naval engineering (ships, submarines). Its inclusion ensures students can relate gravitation to real-life scenarios and solve related exam questions effectively.
11. How can students avoid common misconceptions in the Gravitation chapter during revision?
Students should remember that mass does not change with location, weight depends on gravity, and density and relative density have distinct definitions. Always refer to definitions and avoid confusing related terms during quick revision. Use the summary tables in revision notes to clarify concepts.
12. What is the best strategy to summarize and revise formulas and definitions for Gravitation right before the exam?
Create a concise formula sheet with all key formulas and definitions; focus on reviewing the sequence of derivations, try diagram-based questions, and practice one or two application-based numericals to ensure a complete recap using the revision notes structure.




















 Watch Video
Watch Video