NCERT Exemplar for Class 12 Physics Chapter-13 (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTION -I

13.1 Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half-life of 1 year. After 1 year,

(a) All the containers will have 5000 atoms of the material.

(b) All the containers will contain the same number of atoms of the material but that number will only be approximately 5000.

(c) The containers will in general have different numbers of the atoms of the material but their average will be close to 5000. 

(d) None of the containers can have more than 5000 atoms.

Ans: Option (c) 

A radioactive material's half-life time is defined as the amount of time that a radioactive atomic substance retains half of its initial value. So one year means one half-life, i.e the average number of atoms of radioactive chemical left in each container after one year is half of 10,000, which is equal to 5000 atoms (average).

13.2 The gravitational force between a H-atom and another particle of mass m will be given by Newton’s law: $F = G\dfrac{{M \cdot m}}{{{r^2}}}$ where r is in km and

(a) ${\text{M}} = {{\text{m}}_{{\text{proton}}}} + {{\text{m}}_{{\text{electron }}}}$

(b) ${\text{M}} = {{\text{m}}_{{\text{proton}}}} + {{\text{m}}_{{\text{electron }}}}$$ - \dfrac{B}{{{c^2}}}(B = 13.6{\text{eV}})$

(c) M is not related to the mass of the hydrogen atom.

(d) ${\text{M}} = {{\text{m}}_{{\text{proton}}}} + {{\text{m}}_{{\text{electron }}}} =  - \dfrac{{|V|}}{{{c^2}}}[|\;{\text{V}}| = $ Magnitude of potential energy electron in the ${\text{H}}$ atom.]

Ans: Option (b) 

During the production of the H-atom, some of the mass of the nucleons is converted into energy, which is then used to bind the nucleons together with the nucleus. As a result, the atom's mass is somewhat less than the total of nucleon and electron masses.

Actual mass of ${\text{H}}$ atom $ = {{\text{M}}_{\text{p}}} + {{\text{M}}_{\text{e}}} - \dfrac{{BE}}{{{c^2}}}$ ($\dfrac{B}{{{c^2}}}$is binding energy)

$B.E.(B)of$ H atoms is $13.6{\text{eV}}$ per atom.

13.3 When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom 

(a) Do not change for any type of radioactivity.

(b) Change for α and β radioactivity but not for γ-radioactivity.

(c) Change for α-radioactivity but not for others.

(d) Change for β-radioactivity but not for others

Ans: Option (b) 

The $\alpha $ particles have two units of positive charge. $\beta $ has one unit of negative charge. $\gamma $ charge has no charge and is electrically neutral. As a result, the electronic energy level of the atom changes in particle emission but not in decay.

13.4 ${M_{\text{x}}}$ and ${M_{\text{y}}}$ denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The ${Q_1}$-value for a ${\beta ^ - }$ decay is ${Q_1}$ and that for a $\beta $ $^ + $ decay is ${Q_2}.$ If ${m_{\text{e}}}$ denotes the mass of an electron, then which of the following statements is correct?

(a) ${{\text{Q}}_1} = \left( {{{\text{M}}_{\text{x}}} - {{\text{M}}_{\text{y}}}} \right){{\text{c}}^2}$ And ${{\text{Q}}_2} = \left( {{{\text{M}}_{\text{x}}} - {{\text{M}}_{\text{y}}} - 2\;{{\text{m}}_{\text{e}}}} \right){{\text{c}}^2}$

(b) ${Q_1} = \left( {{M_x} - {M_y}} \right){c^2}$ And ${Q_2} = \left( {{M_x} - {M_y}} \right){c^2}$

(c) ${Q_1} = \left( {{M_x} - {M_y} - 2{m_e}} \right){c^2}$ And ${Q_2} = \left( {{M_x} - {M_y} + 2{m_e}} \right){c^2}$

(d) ${Q_1} = \left( {{M_x} - {M_y} + 2{m_e}} \right){c^2}$ And ${Q_2} = \left( {{M_x} - {M_y} + 2{m_e}} \right){c^2}$

Ans: Option (a) 

Let the parent nuclei $_z{X^A}$ is a radioactive atom and decay ${\beta ^ - }$ as under, where $Z$ and $A$ have usual meanings.

$_z{X^A}{ \to _{z + 1}}{Y^A}{ + _{ - 1}}{e^0} + \bar v + {Q_1}$

${Q_1} = \left[ {{m_n}\left( {z{X^A}} \right) - {m_n}\left( {_{z + 1}{Y^A}} \right) - {m_e}} \right]{c^2}$

${\text{Q_1= }}\left[ {{m_n}\left( {_z{X^A}} \right) + {m_\varepsilon }Z - {m_n}\left( {_{z + 1}{Y^A}} \right) - (Z + 1){m_\varepsilon }} \right]{c^2} = [m\left( {_z{X^A}} \right) - m{(_{z + 1}}{Y^A}]{C^2}$

Let the nucleus ${ = _Z}{{\text{X}}^A}$ radiate $\beta $ decay $_z{x^A}{ \to _{z- 1}}{Y^A}{ + _1}{e^0} + v + {Q_2}$

${Q_2} = \left[ {{m_n}{(_z}{X^A}) - m\left( {_{z - 1}{Y^A}} \right) - 2{m_e}} \right]{c^2}$

$ \Rightarrow {Q_2} = \left[ {{m_n}{(_z}{X^A}) + {m_e}Z - {m_n}\left( {_{z - 1}{Y^A}} \right) - \left( {Z - 1} \right){m_e} - 2{m_e}} \right]{c^2}$

$ \Rightarrow {Q_2} = \left[ {m{(_z}{X^A}) - {m_e}\left( {_{z - 1}{Y^A}} \right) - 2{m_e}} \right]{c^2}$

${Q_2} = \left( {{M_x} - {M_y} - 2{m_e}} \right){c^2}$

13.5 Tritium is an isotope of hydrogen whose nucleus Triton contains 2 neutrons and 1 proton. Free neutrons decay into${{p}} + \bar e + \bar v$. If one of the neutrons in Triton decays, it would transform into ${}_2{{H}}{{{e}}^3}$ nucleus. This does not happen. This is because

(a) Triton energy is less than that of a ${\text{H}}{{\text{e}}^3}$ nucleus.

(b) The electron created in the beta decay process cannot remain in the nucleus.

(c) Both the neutrons in a triton have to decay simultaneously resulting in a nucleus with 3 protons, which is not a ${\text{H}}{{\text{e}}^3}$ nucleus.

(d) Because free neutrons decay due to external perturbations which is absent in a triton nucleus

Ans: Option (a) 

Triton $\left( {_1{{\text{H}}^3}} \right)$ has 1 proton and 2 neutrons. If a neutron decays as $n \to p + \bar e + \bar v$ then nucleus will have 2 proton and 1 neutron, i.e. triton atom converts in $_2{\text{H}}{{\text{e}}^3}$ (2 proton and 1 neutron). Binding energy of $_1{{\text{H}}^3}$ is much smaller than $_2{\text{H}}{{\text{e}}^3}$ so transformation is not possible energetically.

13.6. Heavy stable nuclei have more neutrons than protons. This is because of the fact that

(a) Neutrons are heavier than protons.

(b) Electrostatic force between protons is repulsive. 

(c) Neutrons decay into protons through beta decay.

(d) Nuclear forces between neutrons are weaker than that between protons.

Ans: Option (b) 

The electrostatic force between proton and proton is repulsive, causing nucleus instability. Neutrons are therefore larger than protons.

13.7 In a nuclear reactor, moderators slow down the neutrons which come out in a fission process. The moderator used has light nuclei. Heavy nuclei will not serve the purpose because

(a) They will break up. 

(b) Elastic collision of neutrons with heavy nuclei will not slow them down. 

(c) The net weight of the reactor would be unbearably high.

(d) Substances with heavy nuclei do not occur in liquid or gaseous state at room temperature.

Ans: Option (b) 

For elastic collisions, both masses must be equivalent so that the velocities can be exchanged. To slow down the speed of neutrons, a substance made up of one proton should be fully elastic, i.e., light nuclei rather than heavy nuclei are required. Only the direction, not the speed, will change in heavy nuclei.

Multiple choice questions - II more than one option

13.8 Fusion processes, like combining two deuterons to form a He nucleus are impossible at ordinary temperatures and pressure. The reasons for this can be traced to the fact: 

(a) Nuclear forces have short range.

(b) Nuclei are positively charged. 

(c) The original nuclei must be completely ionized before fusion can take place.

(d) The original nuclei must first break up before combining with each other

Ans: Options (a) and (b) 

When two deuterons come close to each other in the range where the electrostatic repulsive force between positively charged deuterons does not act, they combine to form a helium atom. 

Now, we know that the electrostatic force increases with the reducing distance between the particles. 

$(\because F\alpha \dfrac{1}{{{r^2}}})$

So, nuclei need very high temperature and pressure to overcome the electrostatic force that repels them apart. Therefore, the nuclei must reach closer to the range of where nuclear force acts and electrostatic repulsive force does not act to combine two nuclei. This verifies that options (a) and (b) are the correct options.

13.9 Samples of two radioactive nuclides A and B are taken. ${\lambda _{\text{A}}}{\text{ and }}{\lambda _{\text{B}}}$ Are the disintegration constants of A and B respectively? In which of the following cases, the two samples can simultaneously have the same decay rate at any time?

(a) Initial rate of decay of A is twice the initial rate of decay of B and. ${\lambda _{\text{A}}} = {\lambda _{\text{B}}}$

(b) Initial rate of decay of A is twice the initial rate of decay of B and ${\lambda _{\text{A}}} = {\lambda _{\text{B}}}$

(c) Initial rate of decay of B is twice the initial rate of decay of A and${\lambda _A} > {\lambda _B}$.

(d) Initial rate of decay of B is same as the rate of decay of A at $t = 2\;{\text{h}}$ and ${\lambda _{\text{B}}} < {\lambda _{\text{A}}}$.

Ans: Options (b) and (d) 

Starting from the initial time, both the radioactive samples can have same decay rate at any time, in the condition that the initial rate of decay of ${\text{A}}$ is equal to the twice the initial decay rate of ${\text{B}}$ and ${\lambda _{\text{A}}} > {\lambda _{\text{B}}}$. The decay rates can be the same if ${\lambda _A} < {\lambda _B}$ and the initial rate of decay of both are equal at $t = 2h$.

13.10 The variation of decay rate of two radioactive samples A and B with time is shown in Fig. 13.1. Which of the following statements are true?

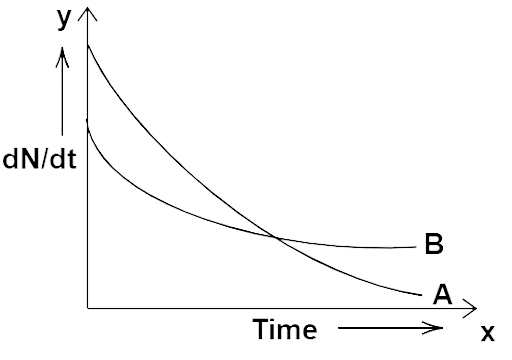
                          Radioactive decay

(a) Decay constant of A is greater than that of B, hence A always decays faster than B.

(b) Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.

(c) Decay constant of A is greater than that of B but it does not always decay faster than B.

(d) Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.

Ans: Options (c) and (d) 

We can observe that the slope of decay A is greater than that of slope of decay B. Now, we know that $\dfrac{{dN}}{{dt}} =  - \lambda t$ at any time instant t. So, we have, $\dfrac{{dN}}{{dt}} \propto \lambda $. Hence, ${\lambda _A} > {\lambda _B}$ point P the intersecting point of two graphs at time t same.

Very short answer type question

13.11  $_1{\text{H}}{e^3}{\text{ and}}{{\text{ }}_2}{\text{H}}{e^{\bar 3}}$ nuclei have the same mass number. Do they have the same binding energy?

Ans: In $_2{\text{H}}{{\text{e}}^3}$ there are two protons which give electrostatic force of repulsion but in $_1{\text{H}}{{\text{e}}^3}$ between nucleons there is only nuclear attractive force. So binding energy of $_1{\text{H}}{{\text{e}}^3}$ is larger than $_2{\text{H}}{{\text{e}}^3}$.

13.12 Draw a graph showing the variation of decay rate with number of active nuclei.

Ans: By law of radioactive decay

$ - \dfrac{{dN}}{{dt}} \propto \lambda N$

${\text{N}}$ is the number of radioactive nuclei in the sample.

So, $\dfrac{{dN}}{{dt}}$ can be negative.

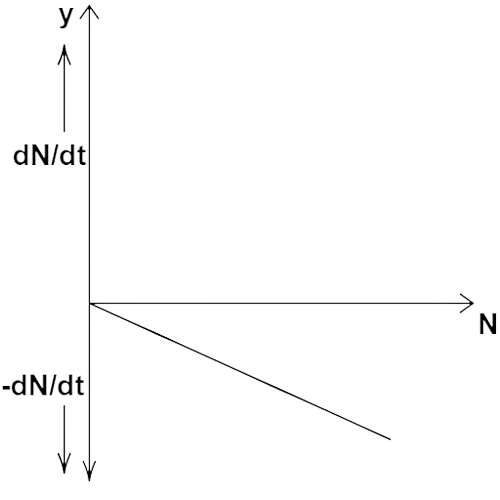
Decay rate with number of active nuclei. The variation of decay rate with the number of active nuclei is shown by the above graph.

13.13 Which sample, A or B shown in Fig. 13.2 have a shorter mean-life?

Ans: Initially at ${\text{t}} = 0$ from figure given

${\left( {\dfrac{{d{N_0}}}{{dt}}} \right)_A} = {\left( {\dfrac{{d{N_0}}}{{dt}}} \right)_B}$

So, ${\left( {{N_0}} \right)_A} = {\left( {{N_0}} \right)_B}$

i.e., initially both samples had an equal number of radioactive atoms. Considering at any instant ${\text{t}} = {\text{t}}$ from figure,

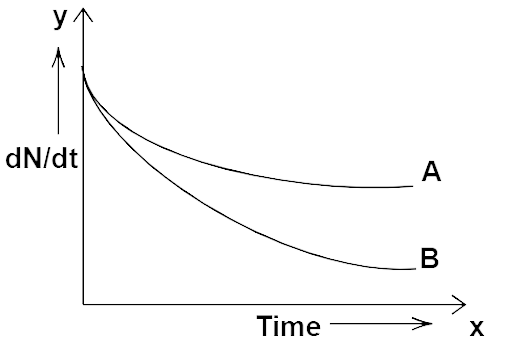
                               Shorter mean-life

${{{\left( {\dfrac{{d{N_0}}}{{dt}}} \right)}_A} > {{\left( {\dfrac{{d{N_0}}}{{dt}}} \right)}_B}} \\ {{\lambda _{\text{A}}}{{\text{N}}_{\text{A}}} > {\lambda _{\text{B}}}{{\text{N}}_{\text{B}}}} \\ {{{\text{N}}_{\text{A}}} > {{\text{N}}_{\text{B}}}} \\ {{\lambda _{\text{A}}} < {\lambda _{\text{B}}}\left( {\dfrac{{ - dN}}{{dt}} = \lambda N} \right)} \\ {\therefore \tau  = \dfrac{1}{\lambda }} $

${\therefore \dfrac{1}{{{\tau _A}}} < \dfrac{1}{{{\tau _B}}}} \\ {{t_A} > {\tau _B}} $

So the mean life time of sample ${\text{A}}$ is greater than of ${\text{B}}$.

13.14 Which one of the following cannot emit radiation and why?

Excited nucleus, excited electron

Ans: Excited electron has energy in eV while excited nucleus in MeV. Energy of gamma- rays have energy of the order of M eV. So, an excited electron cannot emit radiation when the nucleus is excited.

13.15 In pair annihilation, an electron and a positron destroy each other to produce gamma radiation. How is the momentum conserved?

Ans: When an electron and positron combine together coming from opposite directions they destroy each other by the emission of two Υ-rays in opposite direction to conserve linear momentum as below

$_0{e^{ - 1}}{ + _0}{e^{ + 1}} \to 2\gamma  - {\text{ ray photons}}{\text{. }}$

SHORT ANSWER TYPE QUESTIONS

13.16 Why do stable nuclei never have more protons than neutrons?

Ans: If in a stable nucleus the number of protons are larger than neutrons the repulsive electrostatic force between proton-proton becomes larger in place of nuclear force of attraction between nucleons. So for stability, the repulsive force between proton-proton must be smaller than nuclear attractive force between nucleons.

13.17 Consider a radioactive nucleus A which decays to a stable nucleus ${\text{C}}$ through the following sequence:

${\text{A}} \to {\text{B}} \to {\text{C}}$

Here ${\text{B}}$ is an intermediate nuclei which is also radioactive. Considering that there are ${N_0}$ atoms of a initially, plot the graph showing the variation of number of atoms of A and B versus time.

Ans: Let us consider that in sample ${\text{A}}$ initially at${\text{t}} = 0$, there are ${{\text{N}}_0}$ atoms of ${\text{AB}}$ and atoms of ${\text{B}}$ are zero initially.

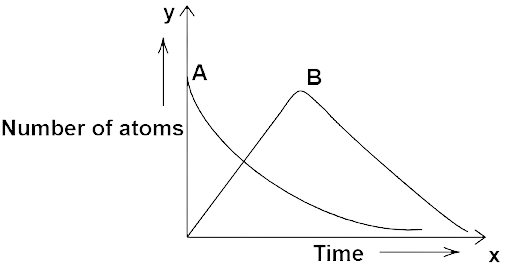
                                 Number of atoms of A and B versus time.

When a decay to B the number of radioactive atoms of A decreases and of B increases. When the rate of decay of A decreases to a lower value, then the number of radioactive atoms of B becomes maximum. After this the radio-active atoms and rate of decay of B decreases. Finally, the number of radioactive atoms of sample A and B becomes very low, near to zero.

13.18 A piece of wood from the ruins of an ancient building was found to have a ${{\text{c}}^{14}}$ activity of 12 disintegration per minute per gram of its carbon content. The ${{\text{c}}^{14}}$ activity of the living wood is 16 disintegration per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given the half-life of ${{\text{c}}^{14}}$ is 5760 years.

Ans: Rate of disintegration in old wood samples of ${\text{C}} - 14$ radioactive atoms is 12 atoms per min gm. Initial rate of disintegration of ${\text{C}} - 14$ when the tree was alive =16 atoms per min per gm.

${{\text{T}}_{1/2}}$ Of ${\text{C}} - 14$ nuclei=5760 years

According to radioactive decay law,

${{\text{N}} = {{\text{N}}_0}{{\text{e}}^{ - \lambda {\text{t}}}}{\text{ or R}} = {{\text{R}}_0}{{\text{e}}^{ - \lambda {\text{t}}}}} \\ {12 = 16{{\text{e}}^{ - \lambda {\text{t}}}}} \\ {{e^{\lambda t}} = \dfrac{{16}}{{12}}} \\ {{{\log }_6}{e^{\lambda t}} = {{\log }_6}\dfrac{4}{3}} \\ {\lambda t = {{\log }_6}\dfrac{4}{3}} \\ {t = \dfrac{{2.303 \times {{\log }_{10}}\left( {\dfrac{4}{3}} \right)}}{\lambda }{\text{ half life }}\left( {\because \lambda  = \dfrac{{0.6931}}{{{T_{1/2}}}}} \right)} $

${ t= \dfrac{{2.303 \times (\log 4 - \log 3) \times 5760}}{{0.6931}}{\text{ year }}} \\ {t = \dfrac{{2.303(0.6020 - 0.4771)5760}}{{0.6931}} = 2391.20{\text{ years }}} $

13.19 Are the nucleons fundamental particles, or do they consist of still smaller parts? One way to find out is to probe a nucleon just as Rutherford probed an atom. What should be the kinetic energy of an electron for it to be able to probe a nucleon? Assume the diameter of a nucleon to be approximately ${10^{ - 15}}\;{\text{m}}$

Ans: To detect the properties of nucleons inside the nucleus the wavelength of particles which may detect nucleons that must be of size of nucleons (${10^{ - 15}}\;{\text{m}}.$). So the wavelength of particles which can detect the nucleons must be equal to or less. 

${\lambda  = {{10}^{ - 15}}\;{\text{m}}} \\ {\lambda  = \dfrac{h}{p}} \\ {\because E = hv = \dfrac{{hc}}{\lambda }[\because c = {\text{v}}\lambda ]} \\ {{\text{ K}}{\text{.E}}{\text{. }} = {\text{ P}}{\text{.E}}{\text{. of }}({\text{electron}}) = \dfrac{{6.6 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{{{10}^{ - 15}}}}} \\ {{\text{ K}}{\text{.E}}{\text{. =  }}\dfrac{{6.6 \times 3 \times {{10}^{ - 34 + 8 + 15}}}}{{1.6 \times {{10}^{ - 19}}}}{\text{eV}} = \dfrac{{99 \times {{10}^{ - 34 + 23 + 19}}}}{8}} \\{{\text{K.E.  = 12}}{{.4 \times 10}}{{\text{ }}^{ - 34 + 42}} = 1.24 \times {{10}^1} \times {{10}^{ + 8}}} $

${\text{ K}}{\text{.E}}{\text{. }} = 1.24 \times {10^9}{\text{eV}}$

So the K.E. of a particle which may detect a nucleon inside the nucleus must be of $1.24 \times {10^9}{\text{eV}}$ per particle.

13.20 A nuclide 1 is said to be the mirror isobar of nuclide 2 if ${Z_1} = {N_2}$ and ${Z_2} = {N_1}$.

(a) What nuclide is a mirror isobar of $2311{\text{Na}}$ ?

Ans: Here ${\text{Z}}$ is atomic number and ${\text{N}}$ is no. of neutron in $_{11}{\text{N}}{{\text{a}}^{23}}$

${{\text{Z}}_1} = 11$

${{\text{N}}_1} = 23 - 11 = 12$

Mirror isobar of $_{11}{\text{N}}{{\text{a}}^{23}}$ is

${{\text{Z}}_2} = {{\text{N}}_1} = 12$

So ${\text{Mg}}$ is an isobar of $_{11}{\text{N}}{{\text{a}}^{23}}$. So $_{12}{\text{M}}{{\text{g}}^{23}}$ is the mirror isobar of $_{11}{\text{N}}{{\text{a}}^{23}}$.

(b) Which nuclei out of the two mirror isobars have greater binding energy and why?

Ans: As the neutrons in $_{12}{\text{M}}{{\text{g}}^{23}}$ are ' 11 ' and in $_{11}{\text{N}}{{\text{a}}^{23}}$ are ' 12 ' so, the number of neutrons in ${\text{Na}}$ is larger than Mg and hence nuclear short range attractive forces in Na will be larger than repulsive electrostatic forces between proton-proton. So, $_{11}{\text{N}}{{\text{a}}^{23}}$ has more binding energy than $_{12}{\text{M}}{{\text{g}}^{23}}$.

Long answer type questions

13.21 Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is:

${}^{38}Sulpher\mathop {\dfrac{{{\text{half life}}}}{{ - 2.48hrs}}}\limits^{}  \to {}^{38}C{l^{}}\dfrac{{H.Life}}{{0.62h}}{}^{38}Ar(stable)$

Assume that we start with $1000\;{{\text{s}}^{38}}$ nuclei at time$t = 0$. The number of ${\text{C}}{{\text{l}}^{38}}$ is of count zero at $t = 0$ and will again be zero at $t = \infty .$ At what value of$t$, would the number of counts be a maximum?

Ans: $Sulpher\mathop {\dfrac{{{\text{half life}}}}{{2.48hrs}}}\limits^{}  \to C{l^{38}}\dfrac{{H.Life}}{{0.62h}} \to A{r^{38}}$

Initially at ${\text{t}} = 0$, number of radioactive atoms of ${{\text{S}}^{38}} = {{\text{N}}_1}$ and of ${\text{C}}{{\text{l}}^{38}}$ are zero.

At any time t, $\dfrac{{d{N_1}}}{{dt}} =  - {\lambda _1}{N_1}$

And ${{\text{N}}_1} = {{\text{N}}_0}{{\text{e}}^{ - {\lambda _1}{\text{t}}}}$

It is the rate of formation of ${\text{C}}{{\text{l}}^{38}}$ from${{\text{S}}^{38}}$. Let ${{\text{N}}_2}$ is the number of ${\text{C}}{{\text{l}}^{38}}$ atoms (radioactive):

${\dfrac{{d{N_2}}}{{dt}} =  - {\lambda _2}{N_2} + {\lambda _1}{N_1}} \\ {\dfrac{{d{N_2}}}{{dt}}  = {\lambda _1}\;{{\text{N}}_0}{{\text{e}}^{ - {\lambda _1}}}\mathop 1\nolimits^t  - {\lambda _2}\;{{\text{N}}_2} \ldots {\text{ (I) }}} $

Multiplying both sides by ${{\text{e}}^{ + {\lambda _2}{{\text{t}}^{\text{t}}}}}{\text{dt}}$

${e^{{\lambda _2}t}}d{N_2} = {\lambda _1}{N_0}{e^{ - {\lambda _1}t + {\lambda _2}t}}dt - {\lambda _2}{N_2}{e^{ + {\lambda _2}t}}dt$

${e^{2t}}d{N_2}dt + {\lambda _2}{N_2}{e^{ + {\lambda _2}t}}dt = {\lambda _1}{N_0}{e^{\left( {{\lambda _2} - \lambda } \right)t}}dt$

Integrating both sides

${N_2}{e^{{\lambda _2}t}} = \dfrac{{{N_0}{\lambda _1}}}{{\left( {{\lambda _2} - {\lambda _1}} \right)}}{e^{\left( {{\lambda _2} - {\lambda _1}} \right)t}} + c\left[ {\because {e^{\lambda t}}d{N_2} \cdot dt = 0} \right]$

$\therefore {\text{C}}{{\text{l}}^{38}}$ Atom is formed after disintegration of ${{\text{S}}^{38}}$, so initially number of ${\text{C}}{{\text{l}}^{38}}$ atoms are ${{\text{N}}_2} = 0$. At ${\text{t}} = 0,\;{{\text{N}}_2} = 0$

$0 \times {e^0} = \dfrac{{{N_0}{\lambda _1}}}{{{\lambda _2} - {\lambda _1}}}{e^0} + c \ldots ({\text{II}})$

$\therefore 0 \times 1 = \dfrac{{{N_0}{\lambda _1}}}{{{\lambda _2} - {\lambda _1}}}(1) + C$

$C = \dfrac{{ - {N_0}{\lambda _1}}}{{{\lambda _2} - {\lambda _1}}}$

Multiplying ${E^{ - \lambda }}_2{t^t}$ to both sides we get

${N_2} = \dfrac{{{N_0}{\lambda _1}}}{{{\lambda _2} - {\lambda _1}}}\left[ {{e^{\left( {{\lambda _2} - {\lambda _1} - {\lambda _2}} \right)t}} - {e^{ - {\lambda _2}t}}} \right]\left[ {\because {{\text{e}}^0} = 1} \right].$

${{N_2} = \dfrac{{{N_0}{\lambda _1}}}{{{\lambda _2} - {\lambda _1}}}\left[ {{e^{ - \lambda ,t}} - {e^{ - {\lambda _2}t}}} \right]} \\ {{N_2}{\lambda _2} - {N_2}{\lambda _1} = {\lambda _1}{N_0}{e^{ - {\lambda _t}t}} - {\lambda _1}{N_0}{e^{ - {\lambda _2}t}}} $

${N_0}$ are the number of ${{\text{S}}^{38}}$ atoms?

No. Are ${\text{C}}{{\text{l}}^{38}}$ atoms after time it will be? ${{\text{N}}_2} = {{\text{N}}_0}{{\text{e}}^{ - \lambda }}_2{\text{t}}$

For ${N_{2\max }} \cdot \dfrac{{d{N_2}}}{{dt}} = 0$

$\therefore {N_2}{\lambda _2} - {N_2}{\lambda _1} = {\lambda _1}{N_0}{e^{ - \lambda lt}} - {\lambda _1}{N_2}$

${{N_2}{\lambda _2} - {\lambda _1}{N_2} + {\lambda _1}{N_2} = {\lambda _1}{e^{ - {\lambda _1}t}}} \\ {{N_2}{\lambda _2} = {\lambda _1}{e^{ - {\lambda _1}t}}} \\ {{N_2}{\lambda _2} = {\lambda _1}{N_0}{e^{ - {\lambda _2}t}}} \\  {{N_2} = \dfrac{{{\lambda _1}}}{{{\lambda _2}}}{N_0}{e^{ - {\lambda _1}t}}} $

Put the value of ${{\text{N}}_2}$ in (III)

${\dfrac{{{\lambda _1}}}{{{\lambda _2}}}{N_0}{e^{ - {\lambda _1}t}}{e^{{\lambda _2}t}} = \dfrac{{{N_0}{\lambda _1}}}{{\left( {{\lambda _2} - {\lambda _1}} \right)}}\left[ {{e^{\left( {{\lambda _2} - {\lambda _1}} \right)t}} - 1} \right]} \\ {{e^{\left( {{\lambda _2} - {\lambda _1}} \right)t}} = \dfrac{{{\lambda _2}}}{{\left( {{\lambda _2} - {\lambda _1}} \right)}}\left[ {{e^{\left( {{\lambda _2} - {\lambda _1}} \right)t}} - 1} \right]} $

By cross multiplication and multiplying both sides by ${e^{ - \left( {{\lambda _2} - {2_1}} \right)t}}$

${\dfrac{{{\lambda _2} - {\lambda _1}}}{{{\lambda _2}}} = 1 - {e^{ - \left( {{\lambda _2} - {\lambda _1}} \right)t}}} \\  {1 - \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = 1 - {e^{\left( {{\lambda _1} - {\lambda _2}} \right)t}}} $

${\dfrac{{{\lambda _1}}}{{{\lambda _2}}} = {e^{\left( {\left( {{\lambda _1} - {\lambda _2}} \right)t} \right.}}} \\ {{{\log }_6}\left( {\dfrac{{{\lambda _1}}}{{{\lambda _2}}}} \right) = {{\log }_6}{e^{\left( {\lambda 1 - \lambda 2} \right)t}}} \\ {{\text{ Or }}{{\log }_6}\left( {\dfrac{{{\lambda _1}}}{{{\lambda _2}}}} \right) = \left( {{\lambda _1} - {{\hat \lambda }_2}} \right)t} $

${t = \dfrac{{{{\log }_e}\left( {\dfrac{{{\lambda _1}}}{{{\lambda _2}}}} \right)}}{{{\lambda _1} - {\lambda _2}}}\left( {\because \lambda  = \dfrac{{0.6931}}{{T/2}}} \right) \ldots ({\text{IV}})} \\ {\therefore \left( {\dfrac{{{\lambda _1}}}{{{\lambda _2}}}} \right) = \dfrac{{\dfrac{{0.6931}}{{2.48}}}}{{\dfrac{{0.6931}}{{0.62}}}} = \dfrac{{0.62}}{{2.48}} = \dfrac{1}{4}} \\ {\left( {{\lambda _1} - {\lambda _2}} \right) = \dfrac{{0.6931}}{{2.48}} - \dfrac{{0.6931}}{{0.62}} = \dfrac{{0.6931( - 1.86)}}{{2.48 \times 0.62}} = \dfrac{{ - 0.6931 \times 1.86}}{{2.48 \times 0.62}}} $

$\therefore \quad t = \dfrac{{{{\log }_e}\left( {\dfrac{1}{4}} \right) \times 2.48 \times 0.62}}{{ - 0.6931 \times 1.86}} = \dfrac{{ - {{\log }_6}4 \times 2.48 \times 0.62}}{{ - 0.6931 \times 1.86}}$

$t = \dfrac{{2.303 \times 0.3010 \times 2.48 \times 0.62}}{{0.6931 \times 1.86}} = \dfrac{{1.06586}}{{1.2892}} = 0.8267{\text{ hrs}}$

Number ${\text{C}}{{\text{l}}^{38}}$ radioactive atoms will be maximum at ${{\text{N}}_2} = 0.8267{\text{ hrs}}$.

13.22 Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A γ-ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident γ-ray. If E = B, show that this cannot happen. Hence calculate how much bigger than B must E be for such a process to happen.

Ans: Binding energy (B) of deuteron =2.2 MeV

Some part of energy of $\gamma $-ray is used up against binding energy ${\text{B}} = 2.2{\text{MeV}}$ and the rest will impart K.E. to neutrons and protons.

$E - B = {K_n} + {K_m}$

$\left( K.E. = \dfrac{1}{2}m{v^2} \times \dfrac{m}{m} \\ K.E. = \dfrac{{{p^2}}}{{2m}} \\\right)$

$ \Rightarrow E - B = \dfrac{{{p_n}^2}}{{2m}} + \dfrac{{{p_p}^2}}{{2m}}$

By law of conservation of momentum,

$\therefore {{\text{P}}_{\text{n}}} + {{\text{p}}_{\text{p}}} = $ Momentum of $\gamma $-ray of Energy ${\text{E}}$

${\left[ {\lambda  = \dfrac{h}{p}{\text{ or }}p = \dfrac{{hv}}{{\lambda v}} = \dfrac{{hv}}{c} = \dfrac{E}{c}} \right]} \\ {\therefore \quad {P_n} + {P_p} = \dfrac{E}{c} \ldots {\text{ (II) }}} $

Case I: If ${\text{E}} = {\text{B}}$ then from

$\therefore \dfrac{{p_n^2}}{{2m}} + \dfrac{{P_p^2}}{{2m}} = 0{\text{ or }}P_n^2 + p_p^2 = 0$

It can be possible if ${p_n} = {p_p} = 0$ because the square of a non-zero number can never be zero.

If ${p_n} = {p_p} = 0$ then equation IInd cannot be satisfied and the process cannot take place.

From II, $0 +  = \dfrac{E}{c}0$ or ${\text{E}} = 0$ but energy E of $\gamma $ ray cannot be zero.

Case II: if ${\text{E}} > {\text{B}}$ or ${\text{E}} = {\text{B}} + \lambda $ where $\lambda $ will be very small than ${\text{B}}$ then from (I),

$(B + \lambda ) - B = \dfrac{{p_n^2}}{{2m}} + \dfrac{{p_p^2}}{{2m}}$

${\lambda  = \dfrac{1}{{2m}}\left( {p_n^2 + p_p^2} \right)} \\ {\lambda  = \dfrac{1}{{2m}}\left[ {{{\left( {\dfrac{E}{c} - {P_p}} \right)}^2} + p_p^2} \right]\left[ {\because {p_n} = \dfrac{E}{c} - {p_p}} \right]} \\ {2m\lambda  = \dfrac{{{E^2}}}{{{c^2}}} + p_p^2 - \dfrac{{2E}}{c}{p_p} + {p^2}} \\ {2p_p^2 - \dfrac{{2E}}{c}{p_p} + \left( {\dfrac{{{E^2}}}{{{c^2}}} - 2m\lambda } \right) = 0} $

It is a quadratic equation so its solution by quadratic formula

$a = 2,b = \dfrac{{ - 2E}}{c},c = \left( {\dfrac{{{E^2}}}{{{c^2}}} - 2m\lambda } \right)  \\ {P_p} = \dfrac{{ + \dfrac{{2E}}{c} \pm \sqrt {\dfrac{{4{E^2}}}{{{c^2}}} - 4 \times 2\left( {\dfrac{{{E^2}}}{{{c^2}}} - 2m\lambda } \right)} }}{4}  \\ $

For a real and equal value of ${{\text{P}}_{\text{p}}}$ discriminant must be zero as the value of ${{\text{p}}_{\text{p}}}$ must be one.

${\therefore \quad \dfrac{{4{E^2}}}{{{c^2}}} - 8\left[ {\dfrac{{{E^2}}}{{{c^2}}} - 2m\lambda } \right] = 0} \\ {\dfrac{4}{{{c^2}}}\left[ {{E^2} - 2{E^2} + 4m{c^2}\lambda } \right] = 0} \\ {\therefore \quad  - {E^2} + 4m{c^2}\lambda  = 0} \\ {\lambda  = \dfrac{{{E^2}}}{{4m{c^2}}}} $

$\because \lambda $ Is very small

So $E = B$

$\lambda  \cong \dfrac{{{B^2}}}{{4m{c^2}}}$

13.23 The deuteron is bound by nuclear forces just as the H-atom is made up of $p$ and $e$ bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge ${e^\prime }F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{e^{\prime 2}}}}{r}$ estimate the value of ( ${e^\prime }/e$ ) given that the binding energy of a deuteron is $2.2{\text{MeV}}$.

Ans: The binding energy of ${\text{H}}$ atom in ground state

$E = \dfrac{{m{e^4}}}{{8\pi \varepsilon _0^2{h^2}}} = 13.6{\text{eV}} \ldots ({\text{I}})$

If proton and neutron had charge e' each and governed by the same electrostatic force, then in the above equation we would need to replace electronic mass $m$ by the reduced mass $m$ ' of proton-neutron (as some mass of proton and neutron is used by binding energy) and electronic charge e is replaced by e'.

$\dfrac{{1}}{{{m^\prime }}} = \dfrac{1}{M} + \dfrac{1}{N} \left( {M = \text{ mass of proton } , N = \text{ mass of neutron }} \right) \\ {{m^\prime } = \dfrac{{M.N}}{{M + N}}({\text{ take M = N }})} $

${m^\prime } = \dfrac{M}{2}$ (if ${\text{m}} = $ mass of electron)

${m^\prime } = \dfrac{{1836m}}{2} = 918m$

$\therefore {\text{ Binding energy }}(E) = \dfrac{{918m{e^{14}}}}{{8\pi \varepsilon _0^2{h^2}}} \ldots {\text{ II }}$

Dividing (II) by (I) we get.

${\dfrac{{{E^\prime }}}{E} = \dfrac{{918{e^\prime }4}}{{{e^4}}} = \dfrac{{2.2{\text{MeV}}}}{{13.6{\text{eV}}}}} \\ {{{\left( {\dfrac{{{e^\prime }}}{e}} \right)}^4} = \dfrac{{2.2 \times {{10}^6}{\text{eV}}}}{{918 \times 13.6{\text{eV}}}}} $

${\dfrac{{{E^\prime }}}{E} = \dfrac{{918{e^\prime }4}}{{{e^4}}} = \dfrac{{2.2{\text{MeV}}}}{{13.6{\text{eV}}}}} \\ {{{\left( {\dfrac{{{e^\prime }}}{e}} \right)}^4} = \dfrac{{2.2 \times {{10}^6}{\text{eV}}}}{{918 \times 13.6{\text{eVV}}}}} \\ {\dfrac{{{e^\prime }}}{e} = \dfrac{{2200000}}{{1248.48}} = {{(176.21)}^{\dfrac{1}{4}}}} $

Required ratio $\dfrac{{{e^\prime }}}{e} = 3.64$

13.24 Before the neutrino hypothesis, the beta decay process was thought to be the transition, $n \to p + \bar e$. If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.

Ans: Neutron was at rest before $\beta $ decay from neutron. Hence energy of neutron $ = {{\text{E}}_{\text{n}}} = {{\text{m}}_{\text{n}}}{{\text{c}}^2}$ and momentum of neutron ${{\text{p}}_{\text{n}}} = 0$ as its velocity is zero.

By the law of conservation of momentum,

${{\text{P}}_{\text{n}}} = {{\text{p}}_{\text{p}}} + {{\text{p}}_{\text{e}}}({\text{ Beta }})$

${\text{O}} = {{\text{p}}_{\text{p}}} + {{\text{p}}_{\text{e}}}$

Let ${{\text{p}}_{\text{e}}} = {{\text{p}}_{\text{p}}}$ then

$ \Rightarrow \left| {{{\text{p}}_{\text{p}}}} \right| = \left| {{{\text{p}}_{\text{e}}}} \right| = {\text{p}}({\text{eV}})$

Energy of proton $ = {{\text{E}}_{\text{p}}} = \sqrt {\left( {m_p^2{c^4} + p_p^2{c^2}} \right)} $

Energy of electron $(\beta ) = {E_e} = \sqrt {\left( {m_p^2{c^4} + p_e^2{c^2}} \right)} \left( {\because \left| {{{\text{p}}_{\text{e}}}} \right| = {{\text{p}}_{\text{p}}}} \right)$

From conservation,

${\therefore \quad {E_p} = \sqrt {m_p^2{c^4} + {p^2}{c^2}} } \\ {{E_e} = \sqrt {{m^2}{c^4} + {p^2}{c^2}} } $

$\therefore $ By the law of conservation of energy,

${{{\left( {m_p^2{c^4} + {p^2}{c^2}} \right)}^{1/2}} + {{\left( {m_6^2{c^4} + {p^2}{c^2}} \right)}^{1/2}} = {m_n}{c^2}} \\ {\because \quad {m_p}{c^2} = 936MeV} $

And ${m_n}{c^2} = 938{\text{MeV}}$

And ${m_e}{c^2} = 0.5{\text{meV}}$

As the energy difference in neutron and proton is very small, pc will be small ${\text{pc}} <  < {{\text{m}}_{\text{p}}}{{\text{c}}^2}$ while pc may be greater than ${{\text{m}}_{\text{e}}}{{\text{c}}^2}$ so by neglecting ${\left( {{{\text{m}}_{\text{e}}}{{\text{c}}^2}} \right)^2} = {(0.5)^2}$ (given)

${ \Rightarrow {m_p}{c^2} + \dfrac{{{p^2}{c^2}}}{{2m_p^2{c^4}}} = {m_n}{c^2} - pc} \\ {{m_p}{c^2} + \dfrac{{{p^2}{c^2}}}{{2m_p^2{c^4}}} + pc = {m_n}{c^2}} $

Again ${\text{pc}} <  < {{\text{m}}_{\text{p}}}{{\text{c}}^2}$ so neglecting $\dfrac{{{p^2}{c^2}}}{{2m_p^2{c^4}}}$ we get

${\text{Pc}} = {{\text{m}}_{\text{n}}}{{\text{c}}^2} - {{\text{m}}_{\text{p}}}{{\text{c}}^2} = 938{\text{MeV}} - 936{\text{MeV}}$

${\text{Pc}} = 2{\text{MeV}}$ Is the momentum

$E = m{c^2}$

$\because {E^2} = {m^2}{c^4}$

$E$ is the energy of either proton or neutron then

${{E_p} = \sqrt {m_p^2{c^4} + {p^2}{c^2}}  = \sqrt {{{(936)}^2} + {2^2}}  = 936{\text{MeV}}} \\ {{E_6} = \sqrt {m_6^2{c^4} + {p^2}{c^2}}  = \sqrt {{{(a)}^2} + {2^2}}  = 2.06{\text{MeV}}} $

13.25 The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:

(i) Plot the graph of $R$ versus $t$ and calculate half-life from the graph.

Ans: Graph between R versus t is an exponential curve. From the graph at slightly more than $t = \dfrac{1}{2}h$ they ${\text{R}}$ should be $50\% $ so at ${\text{R}} = 50\% $ the

$t(h) = 0.7\,h = 0.7 \times 60\;{\text{min}} = 42\;{\text{min}}$

(ii) Plot the graph of log $\dfrac{R}{{{R_0}}}$ versus $t$ and obtain the value of half-life from the graph.

Ans: For Graph between $\log \left( {\dfrac{R}{{{R_0}}}} \right)$ versus t (h)

At ${\text{t}} = 0,{\log _\varepsilon }\dfrac{R}{{{R_0}}}\log \dfrac{{100}}{{100}} = \log 1 = 0$

At t=1 hour, ${\log _\varepsilon }\dfrac{{35.36}}{{100}} = {\log _\varepsilon }0.3536 =  - 1.04$

$ = 2.302{\log _{10}}0.3536 = 1.04$

At ${\text{t}} = 2$ hours, ${\log _\theta }\dfrac{{12.5}}{{100}} = {\log _\theta }0.125$ 

$ = 2.303{\log _{10}}0.125 =  - 2.08$

At t=3 hours, ${\log _e}\dfrac{{4.42}}{{100}} =  - 3.11$

At ${\text{t}} = 4$ hours, ${\log _e}\dfrac{{1.56}}{{100}} =  - 4.16$

The graph showing the variation of ${\log _\theta }\dfrac{R}{{{R_0}}}$ versus t(h) as follows:

We know that disintegration constant

$\lambda  = \dfrac{{{{\log }_e}\dfrac{R}{{{R_0}}}}}{{{t_{1/2}}}} =  - \left( {\dfrac{{4.16 - 3.11}}{1}} \right)$

$\lambda  =  - 1.05$ Per hour

${{t_{1/2}} = \dfrac{{0.6931}}{\lambda } = \dfrac{{0.6931}}{{1.05}}} \\ {{{\text{t}}_{1/2}} = 42\;{\text{min}}} $

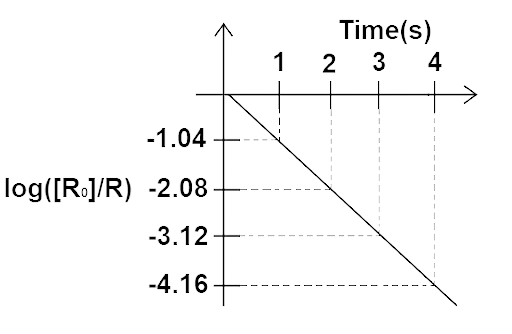
Graph of $\log \left( {\dfrac{R}{{{R_0}}}} \right)$ versus t(h)

13.26 Nuclei with magic no. of proton $Z = 2,8,20,28,50,52$ and magic no. of neutrons 2, 8, 20, 28, 50, 82 and 126 are found to be very stable.

(i) Verify this by calculating the proton separation energy ${s_p}$ for $_{50}{\operatorname{Sn} ^{120}}(Z = 50)$ and $_{51}{\text{S}}{{\text{b}}^{121}} = ({\text{Z}} = 51).$ the proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by

${\text{Sp}} = \left[ {M{Z_{ - 1,N}} + {M_{{H^ - }}}{M_{ZN}}} \right]{c^2}$

Given $^{119}{\text{In}} = 118.9058{\text{u}}{,^{120}}{\text{Sn}} = 119.902199{\text{u}}$

$^{121}{\text{Sb}} = 120.903824{\text{u}}{,^1}{\text{H}} = 1.0078252{\text{u}}$

Ans:${\text{  (i) }}{{\text{S}}_{\text{p}}} = \left[ {{\text{Mz}} - 1,\;{{\text{N}}^ + }{{\text{M}}_{\text{H}}} - {{\text{M}}_{{\text{z}},{\text{N}}}}} \right]{{\text{c}}^2}$

Here in this formula ${{\text{M}}_{{\text{Z}} - 1}}$ is the mass of atom of ${\text{Z}} - 1$ atomic number. 

${{\text{M}}_{\text{Z}}}$ Is the mass of an atom of mass number${\text{Z}}$.

$\therefore {{\text{M}}_{{\text{Z}} - 1}} = $ Mass of atom whose atomic number is $50 - 1 = 49.$

It is $_{49}{\text{I}}{{\text{n}}^{119}}$ in this case ${{\text{M}}_{{\text{Z}} - 1}}{ = _{49}}$ In $^{119} = 118.9058$ and${\text{N}} = 119 - 49 = 70$.

${{\text{S}}_{\text{p}}}$ For $_{50}{\text{S}}{{\text{n}}^{120}} = {{\text{c}}^2}[118.9058 + 1.0078252 - 199.902199]$

${{\text{S}}_{\text{p}}}$ For $_{50}{\text{S}}{{\text{n}}^{120}} = 0.0114362{{\text{c}}^2}$

Now for ${{\text{S}}_{\text{p}}}$ of $_{51}{\text{S}}{{\text{b}}^{121}}$

${{{\text{S}}_{\text{p}}} = \left[ {{{\text{M}}_{{\text{z}} - 1}},\;{{\text{N}}^ + }{{\text{M}}_{\text{H}}} - {{\text{M}}_{{\text{z}},{\text{N}}}}} \right]{{\text{c}}^2}} \\ { \Rightarrow {\text{Z}} = 51,{\text{Z}} - 1 = 50{\text{ for }}{{\text{S}}_{\text{n}}}} \\ {{{\text{M}}_{{\text{Z}} - 1}} = {\text{ mass of}}{{\text{ }}_{50}}{\text{Sn}} = 199.902199{\text{u}}} \\ {\therefore {{\text{S}}_{\text{p}}}{\text{ for}}{{\text{ }}_{51}}{\text{S}}{{\text{b}}^{121}} = [199.902199 + 1.0078252 - 120.903824]{{\text{c}}^2}} $
${ = 0.0059912{c^2}} \\ {\therefore {{\text{S}}_{\text{p}}}\left( {50{\text{S}}{{\text{n}}^{120}}} \right) > {{\text{S}}_{\text{p}}}\left( {_{51}{\text{S}}{{\text{b}}^{121}}} \right)} $

(ii) What does the existence of magic numbers indicate?

Ans: The existence of magic numbers indicates that the shell structure of the nucleus is similar to the shell structure of an atom. This also explains the peaks in binding energy per nucleon curve.

Important Terms Included in NCERT Exemplar for Class 12 Physics Chapter 13 - Nuclei (Book Solutions)

In all Atoms, the positive and negative charge is concentrated in the centre of the Atom that forms its Nucleus. More than 99.9% of the Atomic weight is centred on the Nucleus.

Atomic Mass Unit (AMU) - The Atomic mass is expressed through a unit which is called the Atomic mass unit. The Atomic mass unit is defined as 1/12th carbon Atomic weight (C12).

Nucleus Formation - The Nucleus can be described using the following words and symbols.

1. Atomic Number = Z The Atomic number of an element is the number of Protons present within the Nucleus of an Atomic element.

Atomic number = Number of Protons = number of Electrons

2. Mass Number - The Mass number of an element is the sum of the number of Protons and Neutrons within a Nucleus of an element Atom.

Mass Number = Number of Protons + Number of Neutrons = Number of Electrons + Number of Neutrons i.e. A = Z. + N

Nuclear Density - Nuclear density is a measure of the weight of a Nucleus and its volume.

Radioactivity - It is the occurrence of automatic separation of the Atomic Nucleus and the emission of one or more radiation such as α-particle, β-particle or γ-ray.

Radioactive Decay - The process of nuclear regeneration when radiation emits radiation from the Nucleus of an Atom is called radioactive Decay. This process cannot be accelerated and slowed down by any physical or chemical process.

Radiation Decay Law - According to this law, the rate of Decay of radioactive Atoms at any given time is equal to the number of Atoms present at that time.

Half-life – The Half-life of a radioactive substance is defined as the time at which part of an Atomic number is present at the beginning of decomposition of an element decomposition.

Mean Life / Average Life - The radiation life rate of a radioactive element can be obtained by calculating the total life span of all radioactive Atoms and dividing it by the total number of Atoms present at the beginning as a sample of the element.

Decay Constant - Rigid radiation can be defined as the repetition of time when the number of Atoms in a radioactive substance drops to 36.8% of their original value.

Radioactive Display Law - The radioactive display law is also known as the law of Fagan's and Soddy. This law defines what chemical and isotope elements are formed during a particular type of radioactive Decay.

(i) α- Decay - In α-Decay, the maximum Nucleus of a product is less than a Decaying Nucleus while the number of Atoms decreases by two.

(ii) β-Decay - In β-Decay, the maximum number of the Nucleus of a product remains the same but the number of Atoms increases or decreases separately.

In beta-minus decomposition (β–), Electrons and antineutrino are formed and released from the Nucleus by the reaction.

(iii) γ-Decay - A γ- ray is released when Decay or β-Decay causes the daughter Nucleus to be in a state of happiness. The Atom then returns to the ground with a single Photon change or successive change involving more than one Photon.

The SI Unit of Radioactivity is Becquerel (Bq).

1 Becquerel (Bq) = 1 scatter / second Other units

(i) Curie Radiation sample activity is called One Curie.

1 Curie (Ci) = 3.7 x 1010 Decay / Second

(ii) Rutherford Radiation sample activity is called One Rutherford.

1 r Rutherford (Rd) = 106 Decay / Second