NCERT Exemplar for Class 12 Maths Chapter-2 (Book Solutions)

EXAMPLES:

Solved Examples Short Answer Questions:

1: Find the principal value of $co{s^{ - 1}}x$, for $x = \dfrac{{\sqrt 3 }}{2}$.

Ans:  Given: $x = \dfrac{{\sqrt 3 }}{2}$

The value of the inverse trigonometric function which lies in the range of the principal branch is its principal value.

Assume ${\cos ^{ - 1}}\left( {\dfrac{{\sqrt 3 }}{2}} \right) = \theta$, then $\cos \theta  = \dfrac{{\sqrt 3 }}{2}$.

Considering principal branch, $\theta  \in [0,\pi ]$. 

$\because \dfrac{{\sqrt 3 }}{2} > 0,\theta$ being in the first quadrant

Hence,${\cos ^{ - 1}}\left( {\dfrac{{\sqrt 3 }}{2}} \right) = \dfrac{\pi }{6}$.

Example 2: Evaluate $ta{n^{ - 1}}\left( {sin\left( {\dfrac{{ - \pi }}{2}} \right)} \right).$

Ans:  Given: ${\tan ^{ - 1}}\left( {\sin \left( {\dfrac{{ - \pi }}{2}} \right)} \right).$

Using the property of trigonometric inverse, ${\sin ^{ - 1}}( - x) =  - {\sin ^{ - 1}}x$

$\Rightarrow {\tan ^{ - 1}}\left( {\sin \left( {\dfrac{{ - \pi }}{2}} \right)} \right)$

$\Rightarrow {\tan ^{ - 1}}\left( { - \sin \left( {\dfrac{\pi }{2}} \right)} \right)$

$\Rightarrow {\tan ^{ - 1}}( - 1) =  - \dfrac{\pi }{4}$ 

Example 3: Find the value of $co{s^{ - 1}}\left( {cos\dfrac{{13\pi }}{6}} \right)$.

Ans:  Given: ${\cos ^{ - 1}}\left( {\cos \dfrac{{13\pi }}{6}} \right)$

The value of the inverse trigonometric function which lies in the range of principal branch is its principal value.

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{13\pi }}{6}} \right)$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \left( {2\pi  + \dfrac{\pi }{6}} \right)} \right){\text{(}}\because {\text{cos}}\left( {2\pi  + \theta } \right){\text{ }} = {\text{ cos}}\theta )$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{\pi }{6}} \right) = \dfrac{\pi }{6}\left( {\because {\text{co}}{{\text{s}}^{ - 1}}\left( {{\text{cos }}\theta {\text{ }}} \right) = \theta } \right)$ 

$= \dfrac{\pi }{6}$.

Example 4: Find the value of $ta{n^{ - 1}}\left( {tan\dfrac{{9\pi }}{8}} \right)$.

Ans: Given: ${\tan ^{ - 1}}\left( {\tan \dfrac{{9\pi }}{8}} \right)$

The value of the inverse trigonometric function which lies in the range of principal branch is its principal value.

$\Rightarrow {\tan ^{ - 1}}\left( {\tan \dfrac{{9\pi }}{8}} \right)$

$\Rightarrow {\tan ^{ - 1}}\tan \left( {\pi  + \dfrac{\pi }{8}} \right)\left( {\because \tan \left( {\pi  + \theta } \right) = {\text{tan}}\theta } \right)$

$\Rightarrow {\tan ^{ - 1}}\left( {\tan \left( {\dfrac{\pi }{8}} \right)} \right) = \dfrac{\pi }{8}\left( {\because {{\tan }^{ - 1}}\left( {{\text{tan}}\theta } \right) = \theta } \right)$ 

Example 5: Evaluate $tan\left( {ta{n^{ - 1}}( - 4)} \right)$. 

Ans:  Given: $\tan \left( {{{\tan }^{ - 1}}( - 4)} \right)$

 Using the property of trigonometric inverse, ${\tan ^{ - 1}}( - x) =  - {\tan ^{ - 1}}x$

  $\because \tan \left( {{{\tan }^{ - 1}}x} \right) = x,\forall x \in {\text{R}},$

  $\tan \left( {{{\tan }^{ - 1}}( - 4)} \right) =  - 4$ 

Example 6: Evaluate: $ta{n^{ - 1}}\sqrt 3  - se{c^{ - 1}}( - 2)$.

Ans:  Given: ${\tan ^{ - 1}}\sqrt 3  - {\sec ^{ - 1}}( - 2)$

Using the property of trigonometric inverse, ${\sec ^{ - 1}}( - x) = \pi  - {\sec ^{ - 1}}x$

Example 7: Evaluate: $si{n^{ - 1}}\left[ {cos\left( {si{n^{ - 1}}\dfrac{{\sqrt 3 }}{2}} \right)} \right]$.

Ans:  Given ${\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{{\sqrt 3 }}{2}} \right)} \right]$

The value of the inverse trigonometric function which lies in the range of the principal branch is its principal value.

$\Rightarrow {\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{{\sqrt 3 }}{2}} \right)} \right]$

$\Rightarrow {\sin ^{ - 1}}\left[ {\cos \left( {\dfrac{\pi }{3}} \right)} \right]$

$\Rightarrow {\sin ^{ - 1}}\left[ {\dfrac{1}{2}} \right] = \dfrac{\pi }{6}$ 

Example 8: Prove that $tan\left( {co{t^{ - 1}}x} \right) = cot\left( {ta{n^{ - 1}}x} \right)$. State with reason whether the equality is valid for all values of $x$. 

Ans:  Given $\tan \left( {{{\cot }^{ - 1}}x} \right) = \cot \left( {{{\tan }^{ - 1}}x} \right)$

Using the property of trigonometric inverse,  $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$

Assume ${\cot ^{ - 1}}x = \theta$. $\therefore$$\cot \theta  = x$

$\Rightarrow \tan \left( {\dfrac{\pi }{2} - \theta } \right) = x$

$\Rightarrow {\tan ^{ - 1}}x = \dfrac{\pi }{2} - \theta$ 

So,

  $\tan \left( {{{\cot }^{ - 1}}x} \right) = \tan \theta$

$\Rightarrow \cot \left( {\dfrac{\pi }{2} - \theta } \right)$

$\Rightarrow \cot \left( {\dfrac{\pi }{2} - {{\cot }^{ - 1}}x} \right)$

   $= \cot \left( {{{\tan }^{ - 1}}x} \right)$ 

The equality is valid for all values of $x$ since ${\tan ^{ - 1}}x$ and ${\cot ^{ - 1}}x$ is true for$x \in {\mathbf{R}}$.

Example 9: Find the value of $sec\left( {ta{n^{ - 1}}\dfrac{y}{2}} \right)$. 

Ans:  Given: $\sec \left( {{{\tan }^{ - 1}}\dfrac{y}{2}} \right)$

Assume${\tan ^{ - 1}}\dfrac{y}{2} = \theta$, where$\theta  \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$. 

So, $\tan \theta  = \dfrac{y}{2}$

$\Rightarrow \sec \theta  = \dfrac{{\sqrt {4 + {y^2}} }}{2}$

$\Rightarrow \sec \left( {{{\tan }^{ - 1}}\dfrac{y}{2}} \right) = \sec \theta$

$= \dfrac{{\sqrt {4 + {y^2}} }}{2}$ 

Example 10: Find value of $tan\left( {co{s^{ - 1}}x} \right)$ and hence evaluate $tan\left( {co{s^{ - 1}}\dfrac{8}{{17}}} \right)$.

Ans:  Given: $\tan \left( {{{\cos }^{ - 1}}x} \right)$$,\tan \left( {{{\cos }^{ - 1}}\dfrac{8}{{17}}} \right)$

Using the property of trigonometric inverse,  $\cos \left( {{{\cos }^{ - 1}}x} \right) = x$

:  Assume${\cos ^{ - 1}}x = \theta$, $\therefore$$\cos \theta  = x$, where $\theta  \in [0,\pi ]$

$\Rightarrow \tan \theta  = \dfrac{{\sqrt {1 - {x^2}} }}{x}$

$\therefore \tan \left( {{{\cos }^{ - 1}}\dfrac{8}{{17}}} \right)$ 

$\Rightarrow \tan \left( {{{\cos }^{ - 1}}x} \right)$

$\Rightarrow \tan \theta  = \dfrac{{\sqrt {1 - {{\cos }^2}\theta } }}{{\cos \theta }}$

$= \dfrac{{\sqrt {1 - {{\left( {\dfrac{8}{{17}}} \right)}^2}} }}{{\dfrac{8}{{17}}}} = \dfrac{{15}}{8}$

Example 11: Find the value of $sin\left[ {2co{t^{ - 1}}\left( {\dfrac{{ - 5}}{{12}}} \right)} \right]$

Ans:  Given: $\sin \left[ {2{{\cot }^{ - 1}}\left( {\dfrac{{ - 5}}{{12}}} \right)} \right]$

Using the property of trigonometric inverse.

Assume${\cot ^{ - 1}}\left( {\dfrac{{ - 5}}{{12}}} \right) = y.$ Then $\cot y = \dfrac{{ - 5}}{{12}}$

Now,

$\sin \left[ {2{{\cot }^{ - 1}}\left( {\dfrac{{ - 5}}{{12}}} \right)} \right] = \sin 2y$

Since,$\cot y < 0$, so $\left[ {y \in \left( {\dfrac{\pi }{2},\pi } \right)} \right]$

$\Rightarrow 2\sin y\cos y = 2\left( {\dfrac{{12}}{{13}}} \right)\left( {\dfrac{{ - 5}}{{13}}} \right)$

$= \dfrac{{ - 120}}{{169}}$ 

Example 12: Evaluate $cos\left[ {si{n^{ - 1}}\dfrac{1}{4} + se{c^{ - 1}}\dfrac{4}{3}} \right]$

Ans:  Given: $\cos \left[ {{{\sin }^{ - 1}}\dfrac{1}{4} + {{\sec }^{ - 1}}\dfrac{4}{3}} \right]$

Using the property of trigonometric inverse ${\sin ^{ - 1}}x + {\cos ^{ - 1}}x = \dfrac{\pi }{2}\quad :\quad x \in [ - 1,1]$

$\Rightarrow \cos \left[ {{{\sin }^{ - 1}}\dfrac{1}{4} + {{\sec }^{ - 1}}\dfrac{4}{3}} \right]$

$\Rightarrow \cos \left[ {{{\sin }^{ - 1}}\dfrac{1}{4} + {{\cos }^{ - 1}}\dfrac{3}{4}} \right]$

$\Rightarrow \cos \left( {{{\sin }^{ - 1}}\dfrac{1}{4}} \right)\cos \left( {{{\cos }^{ - 1}}\dfrac{3}{4}} \right) - \sin \left( {{{\sin }^{ - 1}}\dfrac{1}{4}} \right)\sin \left( {{{\cos }^{ - 1}}\dfrac{3}{4}} \right)$

$\Rightarrow \dfrac{3}{4}\sqrt {1 - {{\left( {\dfrac{1}{4}} \right)}^2}}  - \dfrac{1}{4}\sqrt {1 - {{\left( {\dfrac{3}{4}} \right)}^2}}$

$\Rightarrow \dfrac{3}{4}\dfrac{{\sqrt {15} }}{4} - \dfrac{1}{4}\dfrac{{\sqrt 7 }}{4} = \dfrac{{3\sqrt {15}  - \sqrt 7 }}{{16}}$ 

Example 13: Prove that $2si{n^{ - 1}}\dfrac{3}{5} - ta{n^{ - 1}}\dfrac{{17}}{{31}} = \dfrac{\pi }{4}$

Ans:  Given: $2{\sin ^{ - 1}}\dfrac{3}{5} - {\tan ^{ - 1}}\dfrac{{17}}{{31}} = \dfrac{\pi }{4}$

Using the property of trigonometric inverse, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

Assume${\sin ^{ - 1}}\dfrac{3}{5} = \theta$, then $\sin \theta  = \dfrac{3}{5}$, where $\theta  \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

  $\therefore \tan \theta  = \dfrac{3}{4}$

$\Rightarrow \theta  = {\tan ^{ - 1}}\dfrac{3}{4}$ 

Therefore,

$\Rightarrow 2{\sin ^{ - 1}}\dfrac{3}{5} - {\tan ^{ - 1}}\dfrac{{17}}{{31}}$

$\Rightarrow 2\theta  - {\tan ^{ - 1}}\dfrac{{17}}{{31}}$

$\Rightarrow 2{\tan ^{ - 1}}\dfrac{3}{4} - {\tan ^{ - 1}}\dfrac{{17}}{{31}}$

$\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{{2 \cdot \dfrac{3}{4}}}{{1 - \dfrac{9}{{16}}}}} \right) - {\tan ^{ - 1}}\dfrac{{17}}{{31}}$

$\Rightarrow {\tan ^{ - 1}}\dfrac{{24}}{7} - {\tan ^{ - 1}}\dfrac{{17}}{{31}}$

$\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{{\dfrac{{24}}{7} - \dfrac{{17}}{{31}}}}{{1 + \dfrac{{24}}{7} \cdot \dfrac{{17}}{{31}}}}} \right) = \dfrac{\pi }{4}$ 

Example 14: Prove that $co{t^{ - 1}}7 + co{t^{ - 1}}8 + co{t^{ - 1}}18 = co{t^{ - 1}}3$

Ans:  Given: ${\cot ^{ - 1}}7 + {\cot ^{ - 1}}8 + {\cot ^{ - 1}}18 = {\cot ^{ - 1}}3$

Using the property of trigonometric inverse \[{\cot ^{ - 1}}x = {\tan ^{ - 1}}\dfrac{1}{x},{\text{ if }}x > 0\]

\[ \Rightarrow {\cot ^{ - 1}}7 + {\cot ^{ - 1}}8 + {\cot ^{ - 1}}1\]

\[ \Rightarrow {\tan ^{ - 1}}\dfrac{1}{7} + {\tan ^{ - 1}}\dfrac{1}{8} + {\tan ^{ - 1}}\dfrac{1}{{18}}\]

Since, \[x \cdot y = \dfrac{1}{7} \cdot \dfrac{1}{8} < 1\]

$= {\tan ^{ - 1}}\left( {\dfrac{{\dfrac{1}{7} + \dfrac{1}{8}}}{{1 - \dfrac{1}{7} \times \dfrac{1}{8}}}} \right) + {\tan ^{ - 1}}\dfrac{1}{{18}}\quad$

Since $xy < 1$

$\Rightarrow {\tan ^{ - 1}}\dfrac{3}{{11}} + {\tan ^{ - 1}}\dfrac{1}{{18}}$

$\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{{\dfrac{3}{{11}} + \dfrac{1}{{18}}}}{{1 - \dfrac{3}{{11}} \times \dfrac{1}{{18}}}}} \right)$

$\Rightarrow {\tan ^{ - 1}}\dfrac{{65}}{{195}}$

$\Rightarrow {\tan ^{ - 1}}\dfrac{1}{3} = {\cot ^{ - 1}}3$ 

Example 15: Which is greater, tan 1 or $ta{n^{ - 1}}1$ ?

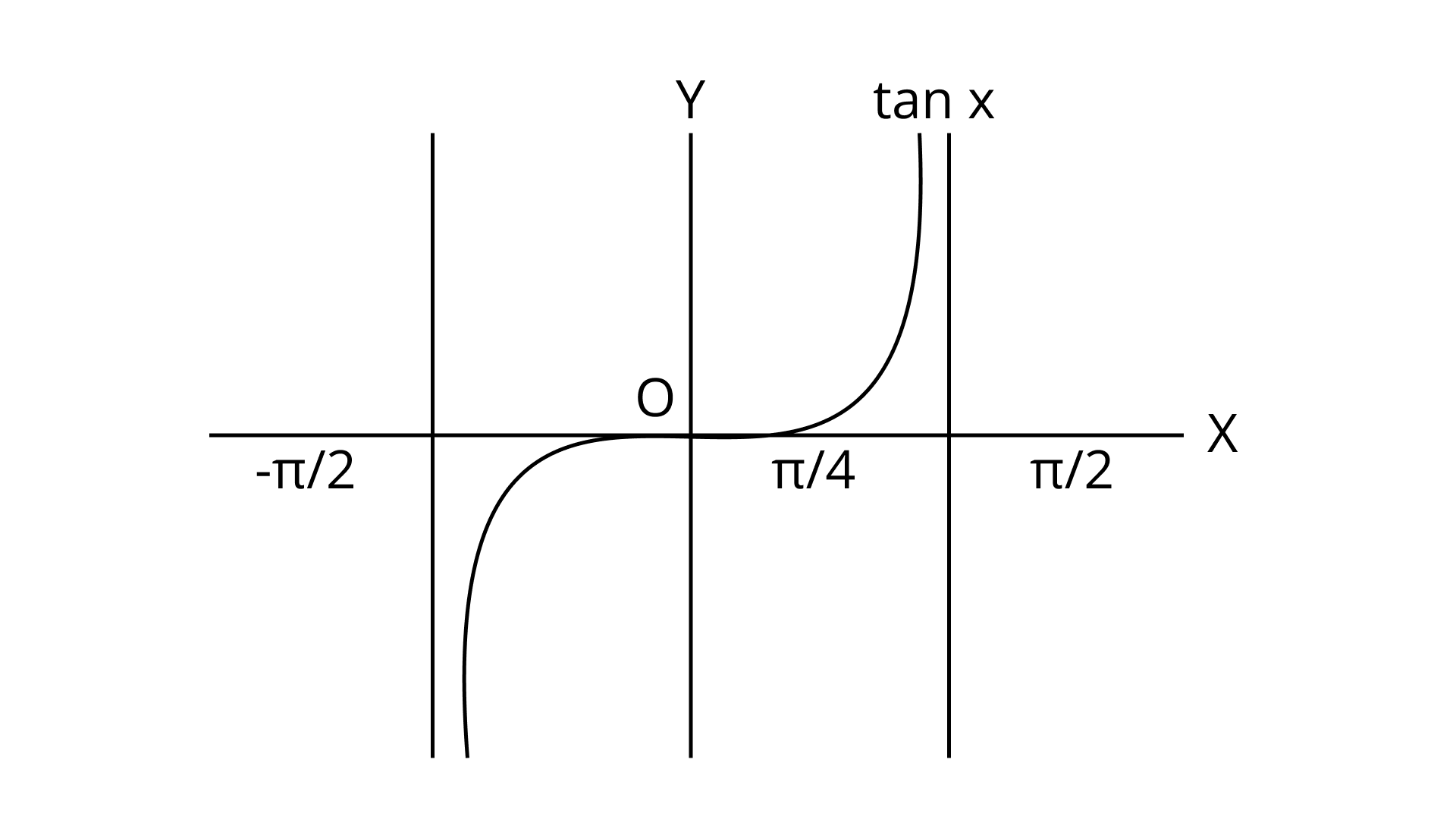
Ans:  Given:  figure

The value of the inverse trigonometric function which lies in the range of the principal branch is its principal value.

From Fig., tan $x$ is an increasing function in the interval$\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right)$,

Since,$1 > \dfrac{\pi }{4} \Rightarrow \tan 1 > \tan \dfrac{\pi }{4}$. 

$\Rightarrow \tan 1 > 1$

$\Rightarrow \quad \tan 1 > 1 > \dfrac{\pi }{4}$

$\Rightarrow \tan 1 > 1 > {\tan ^{ - 1}}(1)$

Example 16: Find the value $sin\left( {2ta{n^{ - 1}}\dfrac{2}{3}} \right) + cos\left( {ta{n^{ - 1}}\sqrt 3 } \right)$

Ans:  Given: $\sin \left( {2{{\tan }^{ - 1}}\dfrac{2}{3}} \right) + \cos \left( {{{\tan }^{ - 1}}\sqrt 3 } \right)$

Using the trigonometric inverse function, $y = {\tan ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

Assume ${\tan ^{ - 1}}\dfrac{2}{3} = x$ and ${\tan ^{ - 1}}\sqrt 3  = y$

$\Rightarrow \tan x = \dfrac{2}{3}$ And $\tan y = \sqrt 3$

Therefore,

$\Rightarrow \sin \left( {2{{\tan }^{ - 1}}\dfrac{2}{3}} \right) + \cos \left( {{{\tan }^{ - 1}}\sqrt 3 } \right)$

$\Rightarrow \sin (2x) + \cos y$

$\Rightarrow \dfrac{{2\tan x}}{{1 + {{\tan }^2}x}} + \dfrac{1}{{\sqrt {1 + {{\tan }^2}y} }}$

$\Rightarrow \dfrac{{2 \cdot \dfrac{2}{3}}}{{1 + \dfrac{4}{9}}} + \dfrac{1}{{1 + \sqrt {{{(\sqrt 3 )}^2}} }}$

$\Rightarrow \dfrac{{12}}{{13}} + \dfrac{1}{2} = \dfrac{{37}}{{26}}$ 

Example 17: Solve for $x$$ta{n^{ - 1}}\left( {\dfrac{{1 - x}}{{1 + x}}} \right) = \dfrac{1}{2}ta{n^{ - 1}}x,x > 0$

Ans:  Given: ${\tan ^{ - 1}}\left( {\dfrac{{1 - x}}{{1 + x}}} \right) = \dfrac{1}{2}{\tan ^{ - 1}}x,x > 0$

Using the trigonometric inverse function, $y = {\tan ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

  ${\tan ^{ - 1}}\left( {\dfrac{{1 - x}}{{1 + x}}} \right) = \dfrac{1}{2}{\tan ^{ - 1}}x$

$\Rightarrow 2{\tan ^{ - 1}}\left( {\dfrac{{1 - x}}{{1 + x}}} \right) = {\tan ^{ - 1}}x$ 

$\Rightarrow 2\left[ {{{\tan }^{ - 1}}1 - {{\tan }^{ - 1}}x} \right] = {\tan ^{ - 1}}x$

$\Rightarrow 2\left( {\dfrac{\pi }{4}} \right) = 3{\tan ^{ - 1}}x$ 

$\Rightarrow \dfrac{\pi }{6} = {\tan ^{ - 1}}x$

$\Rightarrow x = \dfrac{1}{{\sqrt 3 }}$ 

Example 18: Find the values of $x$ which satisfy the equation $si{n^{ - 1}}x + si{n^{ - 1}}(1 - x) = co{s^{ - 1}}x .$

Ans:  Given: ${\sin ^{ - 1}}x + {\sin ^{ - 1}}(1 - x) = {\cos ^{ - 1}}x{\text{ }}{\text{. }}$

Using the trigonometric inverse function, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

Taking the sin on both sides of ${\sin ^{ - 1}}x + {\sin ^{ - 1}}(1 - x) = {\cos ^{ - 1}}x{\text{ }}{\text{. }}$

$\sin \left( {{{\sin }^{ - 1}}x + {{\sin }^{ - 1}}(1 - x)} \right) = \sin \left( {{{\cos }^{ - 1}}x} \right)$

$\Rightarrow \sin \left( {{{\sin }^{ - 1}}x} \right)\cos \left( {{{\sin }^{ - 1}}(1 - x)} \right) + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\sin }^{ - 1}}(1 - x)} \right) = \sin \left( {{{\cos }^{ - 1}}x} \right)$

$\Rightarrow x\sqrt {1 - {{(1 - x)}^2}}  + (1 - x)\sqrt {1 - {x^2}}  = \sqrt {1 - {x^2}}$

$\Rightarrow x\sqrt {2x - {x^2}}  + \sqrt {1 - {x^2}} (1 - x - 1) = 0$

$\Rightarrow x\left( {\sqrt {2x - {x^2}}  - \sqrt {1 - {x^2}} } \right) = 0$

$\Rightarrow x = 0$or$\quad 2x - {x^2} = 1 - {x^2}$

$\therefore x = 0$or$\quad x = \dfrac{1}{2}$.

Example 19: Solve the equation $si{n^{ - 1}}6x + si{n^{ - 1}}6\sqrt 3 x =  - \dfrac{\pi }{2}$

Ans:  Given: ${\sin ^{ - 1}}6x + {\sin ^{ - 1}}6\sqrt 3 x =  - \dfrac{\pi }{2}$

Using the trigonometric inverse function, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

${\text{ }}{\sin ^{ - 1}}6x =  - \dfrac{\pi }{2} - {\sin ^{ - 1}}6\sqrt 3 x$

$\Rightarrow \quad \sin \left( {{{\sin }^{ - 1}}6x} \right) = \sin \left( { - \dfrac{\pi }{2} - {{\sin }^{ - 1}}6\sqrt 3 x} \right)$

$\Rightarrow \quad 6x =  - \cos \left( {{{\sin }^{ - 1}}6\sqrt 3 x} \right)$

$\Rightarrow \quad 6x =  - \sqrt {1 - 108{x^2}}$.

Squaring, 

$\Rightarrow 36{x^2} = 1 - 108{x^2}$

$\Rightarrow 144{x^2} = 1$

$\Rightarrow x =  \pm \dfrac{1}{{12}}$ 

Here, $x =  - \dfrac{1}{{12}}$ is the only root of the equation as $x = \dfrac{1}{{12}}$ does not satisfy it.

Example 20: Show that $2ta{n^{ - 1}}\left\{ {tan\dfrac{\alpha }{2} \times tan\left( {\dfrac{\pi }{4} - \dfrac{\beta }{2}} \right)} \right\} = ta{n^{ - 1}}\dfrac{{sin\alpha cos\beta }}{{cos\alpha  + sin\beta }}$

Ans:  Given: $2{\tan ^{ - 1}}\left\{ {\tan \dfrac{\alpha }{2} \cdot \tan \left( {\dfrac{\pi }{4} - \dfrac{\beta }{2}} \right)} \right\} = {\tan ^{ - 1}}\dfrac{{\sin \alpha \cos \beta }}{{\cos \alpha  + \sin \beta }}$

Using the property of trigonometric inverse $\left( {2{{\tan }^{ - 1}}x = {{\tan }^{ - 1}}\dfrac{{2x}}{{1 - {x^2}}}} \right)$

Taking L.H.S. $= {\tan ^{ - 1}}\dfrac{{2\tan \dfrac{\alpha }{2}\tan \left( {\dfrac{\pi }{4} - \dfrac{\beta }{2}} \right)}}{{1 - {{\tan }^2}\dfrac{\alpha }{2}{{\tan }^2}\left( {\dfrac{\pi }{4} - \dfrac{\beta }{2}} \right)}}$

$= {\tan ^{ - 1}}\dfrac{{2\tan \dfrac{\alpha }{2} \cdot \left( {1 - {{\tan }^2}\dfrac{\beta }{2}} \right)}}{{{{\left( {1 + \tan \dfrac{\beta }{2}} \right)}^2} - {{\tan }^2}\dfrac{\alpha }{2}{{\left( {1 - \tan \dfrac{\beta }{2}} \right)}^2}}}$

$= {\tan ^{ - 1}}\dfrac{{2\tan \dfrac{\alpha }{2}\left( {1 - {{\tan }^2}\dfrac{\beta }{2}} \right)}}{{\left( {1 + {{\tan }^2}\dfrac{\beta }{2}} \right)\left( {1 - {{\tan }^2}\dfrac{\alpha }{2}} \right) + 2\tan \dfrac{\beta }{2}\left( {1 + {{\tan }^2}\dfrac{\alpha }{2}} \right)}}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{{2\tan \dfrac{\alpha }{2}}}{{1 + {{\tan }^2}\dfrac{\alpha }{2}}}\dfrac{{1 - {{\tan }^2}\dfrac{\beta }{2}}}{{1 + {{\tan }^2}\dfrac{\beta }{2}}}}}{{\dfrac{{1 - {{\tan }^2}\dfrac{\alpha }{2}}}{{1 + {{\tan }^2}\dfrac{\alpha }{2}}} + \dfrac{{2\tan \dfrac{\beta }{2}}}{{1 + {{\tan }^2}\dfrac{\beta }{2}}}}}$

$= {\tan ^{ - 1}}\left( {\dfrac{{\sin \alpha \cos \beta }}{{\cos \alpha  + \sin \beta }}} \right)$

$= {\text{R}}.{\text{H}}.{\text{S}}.$ 

L.H.S=R.H.S 

Hence, proved.

Objective Type Questions Choose the Correct Answer from the Given Four Options in Each of the Examples 21 to 41

Example 21: Which of the following corresponds to the principal value branch of ${\tan ^{ - 1}}$?

(A) $\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$

(B) $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right]$

(C) $\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right) - \left\{ 0 \right\}$

(D) $\left( {0,\pi } \right)$

Ans: Correct answer is option A.

Given: ${\tan ^{ - 1}}$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

The principal value branch of ${\tan ^{ - 1}}$ is $\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$.

Hence, $\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$ is the correct answer.

22. The principal value branch of $se{c^{ - 1}}$ is

(A) $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right] - \left\{ 0 \right\}$

(B) $\left[ {0,\pi } \right] - \left\{ {\dfrac{\pi }{2}} \right\}$

(C) $\left( {0,\pi } \right)$

(D) $\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$

Ans:  Correct answer is option B.

Given: ${\sec ^{ - 1}}$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

The principal value branch of ${\sec ^{ - 1}}$ is $\left[ {0,\pi } \right] - \left\{ {\dfrac{\pi }{2}} \right\}$.

Hence, $\left[ {0,\pi } \right] - \left\{ {\dfrac{\pi }{2}} \right\}$ is the correct answer.

23. One branch of $co{s^{ - 1}}$ other than the principal value branch corresponds to

(A) $\left[ {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right]$

(B) $\left[ {\pi ,2\pi } \right] - \left\{ {\dfrac{{3\pi }}{2}} \right\}$

(C) $\left( {0,\pi } \right)$

(D) $\left[ {2\pi ,3\pi } \right]$

Ans: Correct answer is option D.

Given: ${\cos ^{ - 1}}$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

One branch of ${\cos ^{ - 1}}$ other than the principal value branch corresponds to is $\left[ {2\pi ,3\pi } \right]$.

Hence, $\left[ {2\pi ,3\pi } \right]$ is the correct answer.

24. The value of $si{n^{ - 1}}\left( {cos\left( {\dfrac{{43\pi }}{5}} \right)} \right)$ is

(A) $\dfrac{{3\pi }}{5}$

(B) $\dfrac{{ - 7\pi }}{5}$

(C) $\dfrac{\pi }{{10}}$

(D) $- \dfrac{\pi }{{10}}$

Ans:  Correct answer is option D.

Given: ${\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{40\pi  + 3\pi }}{5}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {8\pi  + \dfrac{{3\pi }}{5}} \right)} \right)$

As $\left( {8\pi  + \theta } \right)$ is in the first quadrant, $\cos $will be positive.

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{3\pi }}{5}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \left( {\dfrac{\pi }{2} - \dfrac{{3\pi }}{5}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \left( { - \dfrac{\pi }{{10}}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) =  - \dfrac{\pi }{{10}}$

Hence, ${\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{43\pi }}{5}} \right)} \right) =  - \dfrac{\pi }{{10}}$.

25. The principal value of the expression $co{s^{ - 1}}\left[ {cos\left( { - 68{0^o}} \right)} \right]$ is

(A) $\dfrac{{2\pi }}{9}$

(B) $\dfrac{{ - 2\pi }}{9}$

(C) $\dfrac{{34\pi }}{9}$

(D) $\dfrac{\pi }{9}$

Ans: Correct answer is option A.

Given: ${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right]$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right] = {\cos ^{ - 1}}\left[ {\cos \left( {{{720}^ \circ } - {{40}^ \circ }} \right)} \right]$

${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right] = {\cos ^{ - 1}}\left[ {\cos \left( { - {{40}^ \circ }} \right)} \right]$

As $\cos ( - \theta ) = \cos \theta$,

${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right] = {\cos ^{ - 1}}\left[ {\cos \left( {{{40}^ \circ }} \right)} \right]$

${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right] = {40^ \circ }$

${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right] = \dfrac{{2\pi }}{9}$

Hence, ${\cos ^{ - 1}}\left[ {\cos \left( { - {{680}^ \circ }} \right)} \right] = \dfrac{{2\pi }}{9}$.

26. The value of $cot\left( {si{n^{ - 1}}x} \right)$ is

(A) $\dfrac{{\sqrt {1 + {x^2}} }}{x}$

(B) $\dfrac{x}{{\sqrt {1 + {x^2}} }}$

(C) $\dfrac{1}{x}$

(D) $\dfrac{{\sqrt {1 - {x^2}} }}{x}$

Ans:  Correct answer is option D.

Given: $\cot \left( {{{\sin }^{ - 1}}x} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

Let ${\sin ^{ - 1}}x = \theta$

$\Rightarrow \sin \theta  = x$

$\Rightarrow {\text{cosec}}\theta  = \dfrac{1}{x}$

$\Rightarrow {\text{cose}}{{\text{c}}^2}\theta  = \dfrac{1}{{{x^2}}}$

As \[{\text{cose}}{{\text{c}}^2}\theta  - {\cot ^2}\theta  = 1\],

$\Rightarrow 1 + {\text{co}}{{\text{t}}^2}\theta  = \dfrac{1}{{{x^2}}}$

$\Rightarrow {\text{co}}{{\text{t}}^2}\theta  = \dfrac{1}{{{x^2}}} - 1$

$\Rightarrow {\text{co}}{{\text{t}}^2}\theta  = \dfrac{{1 - {x^2}}}{{{x^2}}}$

$\Rightarrow {\text{cot}}\theta  = \sqrt {\dfrac{{1 - {x^2}}}{{{x^2}}}}$

$\Rightarrow {\text{cot}}\theta  = \dfrac{{\sqrt {1 - {x^2}} }}{x}$

$\Rightarrow \cot \left( {{{\sin }^{ - 1}}x} \right) = \dfrac{{\sqrt {1 - {x^2}} }}{x}$

Hence, $\cot \left( {{{\sin }^{ - 1}}x} \right) = \dfrac{{\sqrt {1 - {x^2}} }}{x}$.

27. If $ta{n^{ - 1}}x = \dfrac{\pi }{{10}}$ for some $x\in R,$ then the value of $co{t^{ - 1}}x$ is

(A) $\dfrac{\pi }{5}$

(B) $\dfrac{{2\pi }}{5}$

(C) $\dfrac{{3\pi }}{5}$

(D) $\dfrac{{4\pi }}{5}$

Ans:  Correct answer is option B.

Given: ${\tan ^{ - 1}}x = \dfrac{\pi }{{10}}$ for some $x \in R.$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

As ${\tan ^{ - 1}}x + {\cot ^{ - 1}}x = \dfrac{\pi }{2}$,

$\Rightarrow {\cot ^{ - 1}}x = \dfrac{\pi }{2} - \dfrac{\pi }{{10}}$

$\Rightarrow {\cot ^{ - 1}}x = \dfrac{{2\pi }}{5}$

Hence, ${\cot ^{ - 1}}x = \dfrac{{2\pi }}{5}$.

28. The domain of$si{n^{ - 1}}2x$ is

(A) $\left[ {0,1} \right]$

(B) $\left[ { - 1,1} \right]$

(C) $\left[ { - \dfrac{1}{2},\dfrac{1}{2}} \right]$

(D) $\left[ { - 2,2} \right]$

Ans: Correct answer is option C.

Given: ${\sin ^{ - 1}}2x$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

Let ${\sin ^{ - 1}}2x = \theta$

$\Rightarrow 2x = \sin \theta$

As $- 1 \leqslant \sin \theta  \leqslant 1$,

$\Rightarrow  - 1 \leqslant 2x \leqslant 1$

$\Rightarrow  - \dfrac{1}{2} \leqslant x \leqslant \dfrac{1}{2}$

Hence, $\left[ { - \dfrac{1}{2},\dfrac{1}{2}} \right]$ is the domain of ${\sin ^{ - 1}}2x$.

29. The principal value of $si{n^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right)$ is

(A) $\dfrac{{ - 2\pi }}{3}$

(B) $\dfrac{{ - \pi }}{3}$

(C) $\dfrac{{4\pi }}{3}$

(D) $\dfrac{{5\pi }}{3}$

Ans: Correct answer is option B.

Given: ${\sin ^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

${\sin ^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) = {\sin ^{ - 1}}\left( { - \sin \dfrac{\pi }{3}} \right)$

${\sin ^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) =  - {\sin ^{ - 1}}\left( {\sin \dfrac{\pi }{3}} \right)$

${\sin ^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) =  - \dfrac{\pi }{3}$

Hence, ${\sin ^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) =  - \dfrac{\pi }{3}$.

30. The greatest and least values of ${\left( {si{n^{ - 1}}x} \right)^2} + {\left( {co{s^{ - 1}}x} \right)^2}$ are respectively

(A) $\dfrac{{5{\pi ^2}}}{4} \text{ and } \dfrac{{{\pi ^2}}}{8}$

(B) $\dfrac{\pi }{2} \text{ and } \dfrac{{ - \pi }}{2}$

(C) $\dfrac{{{\pi ^2}}}{4} \text{ and } \dfrac{{ - {\pi ^2}}}{4}$

(D) $\dfrac{{{\pi ^2}}}{4} \text{ and } 0$

Ans:  Correct answer is option A.

Given: ${\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2}$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

As ${a^2} + {b^2} = {\left( {a + b} \right)^2} - 2ab$,

${\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = {\left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x} \right)^2} - 2{\sin ^{ - 1}}x{\cos ^{ - 1}}x$

$\Rightarrow {\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = {\dfrac{\pi }{4}^2} - 2{\sin ^{ - 1}}x\left( {\dfrac{\pi }{2} - {{\sin }^{ - 1}}x} \right)$

$\Rightarrow {\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = {\dfrac{\pi }{4}^2} - \pi {\sin ^{ - 1}}x + 2{\left( {{{\sin }^{ - 1}}x} \right)^2}$

\[\Rightarrow {\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = 2\left[ {{{\left( {{{\sin }^{ - 1}}x} \right)}^2} - \dfrac{\pi }{2}{{\sin }^{ - 1}}x + \dfrac{{{\pi ^2}}}{8}} \right]\]

\[\Rightarrow {\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = 2\left[ {{{\left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right)}^2} + \dfrac{{{\pi ^2}}}{{16}}} \right]\]

The least value will be \[2\left( {\dfrac{{{\pi ^2}}}{{16}}} \right) = \dfrac{{{\pi ^2}}}{8}\].

The greatest value will be \[2\left[ {{{\left( {\dfrac{{ - \pi }}{2} - \dfrac{\pi }{4}} \right)}^2} + \dfrac{{{\pi ^2}}}{{16}}} \right] = \dfrac{{5{\pi ^2}}}{4}\]

Hence, the greatest and least values of ${\left( {{{\sin }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2}$ are $\dfrac{{5{\pi ^2}}}{4}{\text{ and }}\dfrac{{{\pi ^2}}}{8}$.

31. Let $\theta  = si{n^{ - 1}}\left( {sin\left( { - 60{0^o}} \right)} \right),$ then value of $\theta$ is

(A) $\dfrac{\pi }{3}$

(B) $\dfrac{\pi }{2}$

(C) $\dfrac{{2\pi }}{3}$

(D) $\dfrac{{ - 2\pi }}{3}$

Ans:  Correct answer is option A.

Given: $\theta  = {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

${\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \left( { - 600 \times \dfrac{\pi }{{180}}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \left( {\dfrac{{ - 10\pi }}{3}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = {\sin ^{ - 1}}\left( { - \sin \left( {4\pi  - \dfrac{{2\pi }}{3}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \dfrac{{2\pi }}{3}} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \left( {\pi  - \dfrac{\pi }{3}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \dfrac{\pi }{3}} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = \dfrac{\pi }{3}$

Hence, ${\sin ^{ - 1}}\left( {\sin \left( { - {{600}^ \circ }} \right)} \right) = \dfrac{\pi }{3}$..

32. The domain of the function $y = si{n^{ - 1}}\left( { - {x^2}} \right)$ is

(A) $\left[ {0,1} \right]$

(B) $\left( {0,1} \right)$

(C) $\left[ { - 1,1} \right]$

(D) $f$

Ans: Correct answer is option C.

Given: :$y = {\sin ^{ - 1}}\left( { - {x^2}} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$y = {\sin ^{ - 1}}\left( { - {x^2}} \right)$

$\Rightarrow \sin y =  - {x^2}$

As $- 1 \leqslant \sin y \leqslant 1$,

$\Rightarrow  - 1 \leqslant  - {x^2} \leqslant 1$

$\Rightarrow 1 \geqslant {x^2} \geqslant  - 1$

$\Rightarrow 0 \leqslant {x^2} \leqslant 1$

$\Rightarrow \left| x \right| \leqslant 1$

$\Rightarrow  - 1 \leqslant x \leqslant 1$

Hence, the domain of $y = {\sin ^{ - 1}}\left( { - {x^2}} \right)$ is $\left[ { - 1,1} \right]$.

33. The domain of $y = co{s^{ - 1}}\left( {{x^2} - 4} \right)$ is

(A) $\left[ {3,5} \right]$

(B) $\left[ {0,\pi } \right]$

(C) \[\left[ { - \sqrt 5 , - \sqrt 3 } \right]{C}\left[ { - \sqrt 5 ,\sqrt 3 } \right]\]

(D) \[\left[ { - \sqrt 5 , - \sqrt 3 } \right]\left[ {\sqrt 3 ,\sqrt 5 } \right]\]

Ans:  Correct answer is option D.

Given: $y = {\cos ^{ - 1}}\left( {{x^2} - 4} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$y = {\cos ^{ - 1}}\left( {{x^2} - 4} \right)$

$\Rightarrow \cos y = {x^2} - 4$

As $- 1 \leqslant \cos y \leqslant 1$,

$\Rightarrow  - 1 \leqslant {x^2} - 4 \leqslant 1$

$\Rightarrow 3 \leqslant {x^2} \leqslant 5$

$\Rightarrow \sqrt 3  \leqslant \left| x \right| \leqslant \sqrt 5$

$\Rightarrow x \in \left[ { - \sqrt 5 , - \sqrt 3 } \right] \cup \left[ {\sqrt 3 ,\sqrt 5 } \right]$

Hence, the domain of $y = {\cos ^{ - 1}}\left( {{x^2} - 4} \right)$ is \[\left[ { - \sqrt 5 , - \sqrt 3 } \right] \cup \left[ {\sqrt 3 ,\sqrt 5 } \right]\].

34. The domain of the function defined by $f(x) = si{n^{ - 1}}x + cosx$ is

(A) $\left[ { - 1,1} \right]$

(B) $\left[ { - 1,\pi  + 1} \right]$

(C) $\left( -\infty ,\ \infty  \right)$

(D) \[f\]

Ans: Correct answer is option A.

Given: $f(x) = {\sin ^{ - 1}}x + \cos x$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$f(x) = {\sin ^{ - 1}}x + \cos x$

The domain of $\cos$ is $R$.

The domain of ${\sin ^{ - 1}}$ is $\left[ { - 1,1} \right]$.

So, the domain of ${\sin ^{ - 1}}x + \cos x$ will be $R \cap \left[ { - 1,1} \right]$ i.e. $\left[ { - 1,1} \right]$.

Hence, the domain of $f(x) = {\sin ^{ - 1}}x + \cos x$ is $\left[ { - 1,1} \right]$.

35. The value of $sin\left( {2si{n^{ - 1}}\left( {0.6} \right)} \right)$ is

(A) $0.48$

(B) $0.96$

(C) $1.2$

(D) $sin1.2$

Ans:  Correct answer is option B.

Given: $\sin \left( {2{{\sin }^{ - 1}}\left( {0.6} \right)} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

Let ${\sin ^{ - 1}}\left( {0.6} \right) = \theta$

$\Rightarrow \sin \theta  = 0.6$

As ${\cos ^2}\theta  + {\sin ^2}\theta  = 1$,

$\Rightarrow {\cos ^2}\theta  + {(0.6)^2} = 1$

$\Rightarrow {\cos ^2}\theta  + 0.36 = 1$

$\Rightarrow {\cos ^2}\theta  = 0.64$

$\Rightarrow \cos \theta  = 0.8$

As $\sin 2\theta  = 2\sin \theta \cos \theta$,

$\Rightarrow \sin \left( {2{{\sin }^{ - 1}}\left( {0.6} \right)} \right) = 2(0.6)(0.8)$

$\Rightarrow \sin \left( {2{{\sin }^{ - 1}}\left( {0.6} \right)} \right) = 0.96$

Hence, $\sin \left( {2{{\sin }^{ - 1}}\left( {0.6} \right)} \right) = 0.96$.

36. If $si{n^{ - 1}}x + si{n^{ - 1}}y = \dfrac{\pi }{2},$ then value of $co{s^{ - 1}}x + co{s^{ - 1}}y$ is

(A) $\dfrac{\pi }{2}$

(B) $\pi$

(C) $0$

(D) $\dfrac{{2\pi }}{3}$

Ans:  Correct answer is option A

Given: ${\sin ^{ - 1}}x + {\sin ^{ - 1}}y = \dfrac{\pi }{2}$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

Given that ${\sin ^{ - 1}}x + {\sin ^{ - 1}}y = \dfrac{\pi }{2}$

$\Rightarrow \left( {\dfrac{\pi }{2} - {{\cos }^{ - 1}}x} \right) + \left( {\dfrac{\pi }{2} - {{\cos }^{ - 1}}y} \right) = \dfrac{\pi }{2}$

$\Rightarrow {\cos ^{ - 1}}x + {\cos ^{ - 1}}y = \dfrac{\pi }{2}$

Hence, ${\cos ^{ - 1}}x + {\cos ^{ - 1}}y = \dfrac{\pi }{2}$.

37. The value of $tan\left( {co{s^{ - 1}}\dfrac{3}{5} + ta{n^{ - 1}}\dfrac{1}{4}} \right)$ is

(A) $\dfrac{{19}}{8}$

(B) $\dfrac{8}{{19}}$

(C) $\dfrac{{19}}{{12}}$

(D) $\dfrac{3}{4}$

Ans: Correct answer is option B

Given: $\tan \left( {{{\cos }^{ - 1}}\dfrac{3}{5} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$\tan \left( {{{\cos }^{ - 1}}\dfrac{3}{5} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right) = \tan \left( {{{\tan }^{ - 1}}\dfrac{4}{3} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right)$

As ${\tan ^{ - 1}}x + {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\dfrac{{x + y}}{{1 - xy}}} \right)$,

$\Rightarrow \tan \left( {{{\cos }^{ - 1}}\dfrac{3}{5} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right) = \tan {\tan ^{ - 1}}\left( {\dfrac{{\dfrac{4}{3} + \dfrac{1}{4}}}{{1 - \dfrac{4}{3} \times \dfrac{1}{4}}}} \right)$

$\Rightarrow \tan \left( {{{\cos }^{ - 1}}\dfrac{3}{5} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right) = \tan {\tan ^{ - 1}}\left( {\dfrac{{19}}{8}} \right)$

$\Rightarrow \tan \left( {{{\cos }^{ - 1}}\dfrac{3}{5} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right) = \dfrac{{19}}{8}$

Hence, $\tan \left( {{{\cos }^{ - 1}}\dfrac{3}{5} + {{\tan }^{ - 1}}\dfrac{1}{4}} \right) = \dfrac{{19}}{8}$.

38. The value of the expression $sin\left[ {co{t^{ - 1}}\left( {cos\left( {ta{n^{ - 1}}1} \right)} \right)} \right]$ is

(A) $0$

(B) $1$

(C) $\dfrac{1}{{\sqrt 3 }}$

(D) $\sqrt {\dfrac{2}{3}}$

Ans:  Correct answer is option D

Given: $\sin \left[ {{{\cot }^{ - 1}}\left( {\cos \left( {{{\tan }^{ - 1}}1} \right)} \right)} \right]$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$\sin \left[ {{{\cot }^{ - 1}}\left( {\cos \left( {{{\tan }^{ - 1}}1} \right)} \right)} \right] = \sin \left[ {{{\cot }^{ - 1}}\left( {\cos \dfrac{\pi }{4}} \right)} \right]$

$\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left( {\cos \left( {{{\tan }^{ - 1}}1} \right)} \right)} \right] = \sin \left[ {{{\cot }^{ - 1}}\dfrac{1}{{\sqrt 2 }}} \right]$

$\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left( {\cos \left( {{{\tan }^{ - 1}}1} \right)} \right)} \right] = \sin \left[ {{{\sin }^{ - 1}}\sqrt {\dfrac{2}{3}} } \right]$

$\Rightarrow \sin \left[ {{{\cot }^{ - 1}}\left( {\cos \left( {{{\tan }^{ - 1}}1} \right)} \right)} \right] = \sqrt {\dfrac{2}{3}}$

Hence, $\sin \left[ {{{\cot }^{ - 1}}\left( {\cos \left( {{{\tan }^{ - 1}}1} \right)} \right)} \right] = \sqrt {\dfrac{2}{3}}$.

39. The equation $ta{n^{ - 1}}x - co{t^{ - 1}}x = ta{n^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$ has

(A) no solution

(B) unique solution

(C) infinite number of solutions

(D) two solutions

Ans:  Correct answer is option B

Given: ${\tan ^{ - 1}}x - {\cot ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

\[{\tan ^{ - 1}}x - {\cot ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)\]

$\Rightarrow {\tan ^{ - 1}}x - {\cot ^{ - 1}}x = \dfrac{\pi }{6}{\text{       }}...{\text{(1)}}$

And ${\tan ^{ - 1}}x + {\cot ^{ - 1}}x = \dfrac{\pi }{2}{\text{       }}...{\text{(2)}}$

Add $(1)$ and $(2),$

$\Rightarrow 2{\tan ^{ - 1}}x = \dfrac{{2\pi }}{3}$

$\Rightarrow {\tan ^{ - 1}}x = \dfrac{\pi }{3}$

$\Rightarrow x = \sqrt 3$

Hence, ${\tan ^{ - 1}}x - {\cot ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$ has a unique solution.

40. If $\alpha \le2si{n^{ - 1}}x + co{s^{ - 1}}x\le\beta ,$ then

(A) $\alpha  = \dfrac{{ - \pi }}{2},\beta  = \dfrac{\pi }{2}$

(B) $\alpha  = 0,\beta  = \pi$

(C) $\alpha  = \dfrac{{ - \pi }}{2},\beta  = \dfrac{{3\pi }}{2}$

(D) $\alpha  = 0,\beta  = 2\pi$

Ans:  Correct answer is option B

Given: $\alpha  \leqslant 2{\sin ^{ - 1}}x + {\cos ^{ - 1}}x \leqslant \beta$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

As $\dfrac{{ - \pi }}{2} \leqslant {\sin ^{ - 1}}x \leqslant \dfrac{\pi }{2}$,

$\Rightarrow \dfrac{{ - \pi }}{2} + \dfrac{\pi }{2} \leqslant {\sin ^{ - 1}}x + \dfrac{\pi }{2} \leqslant \dfrac{\pi }{2} + \dfrac{\pi }{2}$

$\Rightarrow 0 \leqslant {\sin ^{ - 1}}x + ({\sin ^{ - 1}}x + {\cos ^{ - 1}}x) \leqslant \pi$

$\Rightarrow 0 \leqslant 2{\sin ^{ - 1}}x + {\cos ^{ - 1}}x \leqslant \pi$

Hence, $\alpha  = 0,\beta  = \pi$.

41. The value of $ta{n^2}(se{c^{ - 1}}2) + co{t^2}(cose{c^{ - 1}}3)$ is

(A) $5$

(B) $11$

(C) $13$

(D) $15$

Ans:  Correct answer is option B

Given: ${\tan ^2}({\sec ^{ - 1}}2) + {\cot ^2}({\text{cose}}{{\text{c}}^{ - 1}}3)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

As ${\text{cose}}{{\text{c}}^2}\theta  - {\cot ^2}\theta  = 1$ and ${\text{se}}{{\text{c}}^2}\theta  - {\tan ^2}\theta  = 1$,

$\Rightarrow {\tan ^2}({\sec ^{ - 1}}2) + {\cot ^2}({\text{cose}}{{\text{c}}^{ - 1}}3) = {\sec ^2}({\sec ^{ - 1}}2) - 1 + {\text{cose}}{{\text{c}}^2}({\text{cose}}{{\text{c}}^{ - 1}}3) - 1$

$\Rightarrow {\tan ^2}({\sec ^{ - 1}}2) + {\cot ^2}({\text{cose}}{{\text{c}}^{ - 1}}3) = {2^2} \times 1 + {3^2} - 2$

$\Rightarrow {\tan ^2}({\sec ^{ - 1}}2) + {\cot ^2}({\text{cose}}{{\text{c}}^{ - 1}}3) = 11$

Hence, ${\tan ^2}({\sec ^{ - 1}}2) + {\cot ^2}({\text{cose}}{{\text{c}}^{ - 1}}3) = 11$.

EXERCISE:

Short Answer Questions:

1. Find the value of $ta{n^{ - 1}}\left( {tan\dfrac{{5\pi }}{6}} \right) + co{s^{ - 1}}\left( {cos\dfrac{{13\pi }}{6}} \right)$.

Ans: Given: ${\tan ^{ - 1}}\left( {\tan \dfrac{{5\pi }}{6}} \right) + {\cos ^{ - 1}}\left( {\cos \dfrac{{13\pi }}{6}} \right)$

Using the property of trigonometric inverse, ${\tan ^{ - 1}}\tan x = x,x \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$

from the relation, ${\tan ^{ - 1}}\tan x = x,x \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$And,

${\tan ^{ - 1}}\left( {\tan \dfrac{{5\pi }}{6}} \right) \ne \dfrac{{5\pi }}{6}$$\Rightarrow \dfrac{{5\pi }}{6} \notin \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$

As, ${\cos ^{ - 1}}\cos x = x;x \in [0,\pi ]$

${\cos ^{ - 1}}\left( {\cos \dfrac{{13\pi }}{6}} \right) \ne \dfrac{{13\pi }}{6}$$\Rightarrow \dfrac{{13\pi }}{6} \notin [0,\pi ]$

Solving the given expression,${\tan ^{ - 1}}\left( {\tan \dfrac{{5\pi }}{6}} \right) + {\cos ^{ - 1}}\left( {\cos \dfrac{{13\pi }}{6}} \right)$

$= {\tan ^{ - 1}}\left[ {\tan \left( {\pi  - \dfrac{\pi }{6}} \right)} \right] + {\cos ^{ - 1}}\left[ {\cos \left( {2\pi  + \dfrac{\pi }{6}} \right)} \right]$

$= {\tan ^{ - 1}}\left( { - \tan \dfrac{\pi }{6}} \right) + {\cos ^{ - 1}}\left( { - \cos \dfrac{{7\pi }}{6}} \right)$

$=  - {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right) + \left[ {{{\cos }^{ - 1}}\cos \left( {\dfrac{\pi }{6}} \right)} \right]$

$=  - \dfrac{\pi }{6} + \dfrac{\pi }{6} = 0$ 

2. Evaluate $cos\left[ {co{s^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) + \dfrac{\pi }{6}} \right].$

Ans:  Given: $\cos \left[ {{{\cos }^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) + \dfrac{\pi }{6}} \right].$

Using the property of trigonometric inverse, ${\cos ^{ - 1}}\cos x = x;x \in [0,\pi ]$

On solving for given expression,

$\cos \left[ {{{\cos }^{ - 1}}\left( {\dfrac{{ - \sqrt 3 }}{2}} \right) + \dfrac{\pi }{6}} \right]$

$= \cos \left[ {{{\cos }^{ - 1}}\left( {\cos \dfrac{{5\pi }}{6}} \right) + \dfrac{\pi }{6}} \right]\quad \left( {\because \cos \dfrac{{5\pi }}{6} = \dfrac{{ - \sqrt 3 }}{2}} \right)$

$= \cos \left( {\dfrac{{5\pi }}{6} + \dfrac{\pi }{6}} \right)\quad \left( {\because {{\cos }^{ - 1}}\cos x = x;x \in [0,\pi ]} \right)$

$= \cos (\pi ) =  - 1$

3. Prove that $cot\left( {\dfrac{\pi }{4} - 2co{t^{ - 1}}3} \right) = 7$.

Ans:  Given: $\cot \left( {\dfrac{\pi }{4} - 2{{\cot }^{ - 1}}3} \right) = 7$

Using the property of trigonometric inverse, $2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)$

Solving the given relation $\cot \left( {\dfrac{\pi }{4} - 2{{\cot }^{ - 1}}3} \right) = 7$

$\Rightarrow \quad \dfrac{\pi }{4} - 2{\cot ^{ - 1}}3 = {\cot ^{ - 1}}7$

$\Rightarrow \quad 2{\tan ^{ - 1}}\dfrac{1}{3} = \dfrac{\pi }{4} - {\tan ^{ - 1}}\dfrac{1}{7}$

$\Rightarrow \quad 2{\tan ^{ - 1}}\dfrac{1}{3} + {\tan ^{ - 1}}\dfrac{1}{7} = \dfrac{\pi }{4}$

Now, solving $2{\tan ^{ - 1}}\dfrac{1}{3} + {\tan ^{ - 1}}\dfrac{1}{7}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{2}{3}}}{{1 - {{\left( {\dfrac{1}{3}} \right)}^2}}} + {\tan ^{ - 1}}\dfrac{1}{7}\left( {\because 2{{\tan }^{ - 1}}x = {{\tan }^{ - 1}}\dfrac{{2x}}{{1 - {x^2}}}} \right)$

$= {\tan ^{ - 1}}\dfrac{3}{4} + {\tan ^{ - 1}}\dfrac{1}{7}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{3}{4} + \dfrac{1}{7}}}{{1 - \dfrac{3}{4} \cdot \dfrac{1}{7}}}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{{(21 + 4)}}{{28}}}}{{\left( {\dfrac{{28 - 3}}{{28}}} \right)}}$

$= {\tan ^{ - 1}}\dfrac{{25}}{{25}}$

$= {\tan ^{ - 1}}1 = \dfrac{\pi }{4}$ 

4. Find the value of $ta{n^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) + co{t^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) + ta{n^{ - 1}}\left( {sin\left( {\dfrac{{ - \pi }}{2}} \right)} \right)$

Ans:  Given: ${\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) + {\cot ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) + {\tan ^{ - 1}}\left( {\sin \left( {\dfrac{{ - \pi }}{2}} \right)} \right)$

Using the property of trigonometric inverse,$\tan \left( {{{\tan }^{ - 1}}x} \right) = x$,${\tan ^{ - 1}}( - x) =  - {\tan ^{ - 1}}x,x \in R$

${\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) + {\cot ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) + {\tan ^{ - 1}}\left( {\sin \left( {\dfrac{{ - \pi }}{2}} \right)} \right)$

$\Rightarrow {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right) + {\cot ^{ - 1}}\left( {\cot \dfrac{\pi }{3}} \right) + {\tan ^{ - 1}}( - 1)$

$\Rightarrow  - \dfrac{\pi }{6} + \dfrac{\pi }{3} + \left( { - \dfrac{\pi }{4}} \right) =  - \dfrac{\pi }{{12}}$ 

5. Find the value of $ta{n^{ - 1}}\left( {tan\dfrac{{2\pi }}{3}} \right)$.

Ans:  Given: ${\tan ^{ - 1}}\left( {\tan \dfrac{{2\pi }}{3}} \right)$

Using the property of trigonometric inverse, ${\tan ^{ - 1}}\tan x = x,x \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$

$= {\tan ^{ - 1}}\left( {\tan \dfrac{{2\pi }}{3}} \right)$

$= {\tan ^{ - 1}}\tan \left( {\pi  - \dfrac{\pi }{3}} \right)$

$= {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{3}} \right)} \right) =  - \dfrac{\pi }{3}$ 

6. Show that $2ta{n^{ - 1}}( - 3) =  - \dfrac{\pi }{2} + ta{n^{ - 1}}\left( {\dfrac{{ - 4}}{3}} \right)$

Ans:  Given:  $2{\tan ^{ - 1}}( - 3) =  - \dfrac{\pi }{2} + {\tan ^{ - 1}}\left( {\dfrac{{ - 4}}{3}} \right)$

Using the property of trigonometric inverse,  $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$,${\tan ^{ - 1}}( - x) =  - {\tan ^{ - 1}}x,x \in R$

Solving for L.H.S,

L.H.S,

$\Rightarrow 2{\tan ^{ - 1}}( - 3) =  - 2{\tan ^{ - 1}}3\left( {\because {{\tan }^{ - 1}}( - x) =  - {{\tan }^{ - 1}}x,x \in R} \right)$

$=  - 2\left[ {\dfrac{\pi }{2} - {{\cot }^{ - 1}}3} \right]\left( {\because {{\tan }^{ - 1}}x + {{\cot }^{ - 1}}x = \dfrac{\pi }{2}} \right)$

$=  - 2\left[ {\dfrac{\pi }{2} - {{\tan }^{ - 1}}\dfrac{1}{3}} \right]\left( {\because {{\tan }^{ - 1}}x = {{\cot }^{ - 1}}\dfrac{1}{x},x > 0} \right)$

$=  - \pi  + 2{\tan ^{ - 1}}\dfrac{1}{3}$ 

Applying $2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\dfrac{{2x}}{{1 - {x^2}}}$

$=  - \pi  + {\tan ^{ - 1}}\dfrac{{2 \cdot \dfrac{1}{3}}}{{1 - {{\left( {\dfrac{1}{3}} \right)}^2}}}$

$=  - \pi  + {\tan ^{ - 1}}\dfrac{{2/3}}{{8/9}} =  - \pi  + {\tan ^{ - 1}}\dfrac{3}{4}$

$=  - \pi  + \dfrac{\pi }{2} - {\cot ^{ - 1}}\dfrac{3}{4}\quad \left( {\because {{\tan }^{ - 1}}x + {{\cot }^{ - 1}}x = \dfrac{\pi }{2}} \right)$

$=  - \dfrac{\pi }{2} - {\tan ^{ - 1}}\dfrac{4}{3}\quad \left( {\because {{\tan }^{ - 1}}x = {{\cot }^{ - 1}}\dfrac{1}{x},x > 0} \right)$

$=  - \dfrac{\pi }{2} + {\tan ^{ - 1}}\left( { - \dfrac{4}{3}} \right)\quad \left( {\because {{\tan }^{ - 1}}( - x) =  - {{\tan }^{ - 1}}x,x \in R} \right)$

7. Find the real solutions of the equation $ta{n^{ - 1}}\sqrt {x(x + 1)}  + si{n^{ - 1}}\sqrt {{x^2} + x + 1}  = \dfrac{\pi }{2}$

Ans: Using the property of trigonometric inverse,  $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$

${\tan ^{ - 1}}\sqrt {x(x + 1)}  + {\sin ^{ - 1}}\sqrt {{x^2} + x + 1}  = \dfrac{\pi }{2}$

Solving 

\[ \Rightarrow {\tan ^{ - 1}}\sqrt {x(x + 1)}  = \dfrac{\pi }{2} - {\sin ^{ - 1}}\sqrt {{x^2} + x + 1} \]

$\Rightarrow {\tan ^{ - 1}}\sqrt {{x^2} + x}  = {\cos ^{ - 1}}\sqrt {{x^2} + x + 1} \left[ {\because {{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x = \dfrac{\pi }{2}} \right]$

$\Rightarrow {\cos ^{ - 1}}\left[ {\dfrac{1}{{\sqrt {1 + {x^2} + x} }}} \right] = {\cos ^{ - 1}}\sqrt {{x^2} + x + 1} \left[ {\because {{\tan }^{ - 1}}x = {{\cos }^{ - 1}}\dfrac{1}{{\sqrt {1 + {x^2}} }}} \right]$

$\Rightarrow \dfrac{1}{{\sqrt {{x^2} + x + 1} }} = \sqrt {{x^2} + x + 1}$

$\Rightarrow {x^2} + x + 1 = 1$

$\Rightarrow {x^2} + x = 0$ 

$\Rightarrow x(x + 1) = 0$

$\Rightarrow x = 0$ 

${\text{Also}},x + 1 = 0$

$\therefore x = 0,x =  - 1$

8. Find the value of the expression $sin\left( {2ta{n^{ - 1}}\dfrac{1}{3}} \right) + cos\left( {ta{n^{ - 1}}2\sqrt 2 } \right)$.

Ans:  Given: $\sin \left( {2{{\tan }^{ - 1}}\dfrac{1}{3}} \right) + \cos \left( {{{\tan }^{ - 1}}2\sqrt 2 } \right)$

Using the property of trigonometric inverse, $\sin \left( {{{\sin }^{ - 1}}x} \right) = x,x \in [ - 1,1]$

Solving for L.H.S and R.H.S separately,

${\text{L}}{\text{.H}}{\text{.S}}{\text{ = }}\sin \left( {2{{\tan }^{ - 1}}\dfrac{1}{3}} \right)$

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{{2 \times \dfrac{1}{3}}}{{1 + {{\left( {\dfrac{1}{3}} \right)}^2}}}} \right)\left( {\because 2{{\tan }^{ - 1}}x = {{\sin }^{ - 1}}\dfrac{{2x}}{{1 + {x^2}}}} \right)$ 

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{{\dfrac{2}{3}}}{{\dfrac{{10}}{9}}}} \right)$

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{3}{5}} \right) = \dfrac{3}{5}\left( {\because \sin \left( {{{\sin }^{ - 1}}x} \right) = x,x \in [ - 1,1]} \right)$ 

${\text{R}}{\text{.HS}}{\text{.}} = \cos \left( {{{\tan }^{ - 1}}2\sqrt 2 } \right)$

$\Rightarrow \cos \left( {{{\cos }^{ - 1}}\dfrac{1}{3}} \right) = \dfrac{1}{3}(\because \left. {\cos \left( {{{\cos }^{ - 1}}x} \right) = x,x \in [ - 1,1]} \right)$

 Adding the values of L.H.S and R.H.S

$\sin \left( {2{{\tan }^{ - 1}}\dfrac{1}{3}} \right) + \cos \left( {{{\tan }^{ - 1}}2\sqrt 2 } \right)$

$= \dfrac{3}{5} + \dfrac{1}{3}$

$= \dfrac{{9 + 5}}{{15}} = \dfrac{{14}}{{15}}$ 

9. If $2ta{n^{ - 1}}(cos\theta ) = ta{n^{ - 1}}(2cosec\theta )$, then show that $\theta  = \dfrac{\pi }{4}$,where n is any integer.

Ans:  Given: $2{\tan ^{ - 1}}(\cos \theta ) = {\tan ^{ - 1}}(2\operatorname{cosec} \theta )$

Using the property of trigonometric inverse, $2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)$

$\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{{2\cos \theta }}{{1 - {{\cos }^2}\theta }}} \right) = {\tan ^{ - 1}}(2\operatorname{cosec} \theta )\quad \left( {\because 2{{\tan }^{ - 1}}x = {{\tan }^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)} \right)$

$\Rightarrow \quad \dfrac{{2\cos \theta }}{{{{\sin }^2}\theta }} = 2\operatorname{cosec} \theta$

$\Rightarrow \quad \dfrac{{2\cos \theta }}{{{{\sin }^2}\theta }} = \dfrac{2}{{\sin \theta }}$

$\Rightarrow \dfrac{{\cos \theta }}{{\sin \theta }} = 1$

$\Rightarrow \cot \theta  = 1$

$\Rightarrow \theta  = \dfrac{\pi }{4}$ 

10. Show that $cos\left( {2ta{n^{ - 1}}\dfrac{1}{7}} \right) = sin\left( {4ta{n^{ - 1}}\dfrac{1}{3}} \right)$.

Ans:  Given: $\cos \left( {2{{\tan }^{ - 1}}\dfrac{1}{7}} \right) = \sin \left( {4{{\tan }^{ - 1}}\dfrac{1}{3}} \right)$

Using the property of trigonometric inverse, $2{\tan ^{ - 1}}x = {\cos ^{ - 1}}\dfrac{{1 - {x^2}}}{{1 + {x^2}}}$, $\cos \left( {{{\cos }^{ - 1}}x} \right) = x,x \in [ - 1,1]$, $\sin \left( {{{\sin }^{ - 1}}x} \right) = x,x \in [ - 1,1]$

Solving for L.H.S and R.H.S separately,

${\text{L}}{\text{.H}}{\text{.S}}{\text{.}} = \cos \left( {2{{\tan }^{ - 1}}\dfrac{1}{7}} \right)$

$= \cos \left( {{{\cos }^{ - 1}}\dfrac{{1 - {{\left( {\dfrac{1}{7}} \right)}^2}}}{{1 + {{\left( {\dfrac{1}{7}} \right)}^2}}}} \right)\left( {\because 2{{\tan }^{ - 1}}x = {{\cos }^{ - 1}}\dfrac{{1 - {x^2}}}{{1 + {x^2}}}} \right)$

$= \cos \left( {{{\cos }^{ - 1}}\dfrac{{\dfrac{{48}}{{49}}}}{{\dfrac{{50}}{{49}}}}} \right)$

$= \cos \left( {{{\cos }^{ - 1}}\dfrac{{24}}{{25}}} \right) = \dfrac{{24}}{{25}}\quad \left( {\because \cos \left( {{{\cos }^{ - 1}}x} \right) = x,x \in [ - 1,1]} \right)$ 

R.H.S

$= \sin \left( {2\left( {2{{\tan }^{ - 1}}\dfrac{1}{3}} \right)} \right)$

$= \sin \left( {2\left( {{{\tan }^{ - 1}}\dfrac{{2 \cdot \dfrac{1}{3}}}{{1 - {{\left( {\dfrac{1}{3}} \right)}^2}}}} \right)} \right)\quad \left( {\because 2{{\tan }^{ - 1}}x{{\tan }^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)} \right)$

$= \sin \left( {2{{\tan }^{ - 1}}\dfrac{{\dfrac{2}{3}}}{{\dfrac{8}{9}}}} \right)$

$= \sin \left( {2{{\tan }^{ - 1}}\dfrac{3}{4}} \right)$ 

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{{2 \times \dfrac{3}{4}}}{{1 + {{\left( {\dfrac{3}{4}} \right)}^2}}}} \right)\quad \left( {\because 2{{\tan }^{ - 1}}x = {{\sin }^{ - 1}}\dfrac{{2x}}{{1 + {x^2}}}} \right)$

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{{\dfrac{3}{2}}}{{\dfrac{{25}}{{16}}}}} \right)$

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{{24}}{{25}}} \right) = \dfrac{{24}}{{25}}\quad \left( {\because \sin \left( {{{\sin }^{ - 1}}x} \right) = x,x \in [ - 1,1]} \right)$ 

\[{\text{L}}{\text{.H}}{\text{.S}}{\text{.  = }}{\text{R}}{\text{.H}}{\text{.S}}{\text{.}}\]

11. Solve the equation $cos\left( {ta{n^{ - 1}}x} \right) = sin\left( {co{t^{ - 1}}\dfrac{3}{4}} \right)$.

Ans:  Given: $\cos \left( {{{\tan }^{ - 1}}x} \right) = \sin \left( {{{\cot }^{ - 1}}\dfrac{3}{4}} \right)$

Using the property of trigonometric inverse, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

Solving for L.H.S and R.H.S separately,

${\text{L}}{\text{.H}}{\text{.S}}{\text{.}} = \cos \left( {{{\tan }^{ - 1}}x} \right)$

$= \cos \left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt {{x^2} + 1} }}} \right)$

$= \dfrac{1}{{\sqrt {{x^2} + 1} }}{\text{ }}$

${\text{R}}{\text{.H}}{\text{.S}}{\text{.}} = \sin \left( {{{\cot }^{ - 1}}\dfrac{3}{4}} \right)$

$= \sin \left( {{{\sin }^{ - 1}}\dfrac{4}{5}} \right) = \dfrac{4}{5}$ 

$\because$$\dfrac{1}{{\sqrt {{x^2} + 1} }} = \dfrac{4}{5}$

$\Rightarrow {16\left( {{x^2} + 1} \right) = 25}$

$\Rightarrow {16{x^2} = 9}$ 

$\Rightarrow {x^2} = \dfrac{9}{{16}}$

$\therefore x =  \pm \dfrac{3}{4}$ 

12. Prove that $ta{n^{ - 1}}\dfrac{{\sqrt {1 + {x^2}}  + \sqrt {1 - {x^2}} }}{{\sqrt {1 + {x^2}}  - \sqrt {1 - {x^2}} }} = \dfrac{\pi }{4} + \dfrac{1}{2}co{s^{ - 1}}{x^2}$.

Ans:  Given: ${\tan ^{ - 1}}\dfrac{{\sqrt {1 + {x^2}}  + \sqrt {1 - {x^2}} }}{{\sqrt {1 + {x^2}}  - \sqrt {1 - {x^2}} }} = \dfrac{\pi }{4} + \dfrac{1}{2}{\cos ^{ - 1}}{x^2}$

Using the property of trigonometric inverse $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$

Assume

${x^2} = \cos 2\theta$

$\Rightarrow \theta  = \dfrac{1}{2}{\cos ^{ - 1}}{x^2}$ 

Now solving for L.H.S

L.H.S. $= {\tan ^{ - 1}}\left[ {\dfrac{{\sqrt {1 + \cos 2\theta }  + \sqrt {1 - \cos 2\theta } }}{{\sqrt {1 + \cos 2\theta }  - \sqrt {1 - \cos 2\theta } }}} \right]$

$\Rightarrow {\tan ^{ - 1}}\left[ {\dfrac{{\sqrt {2{{\cos }^2}\theta }  + \sqrt {2{{\sin }^2}\theta } }}{{\sqrt {2{{\cos }^2}\theta }  - \sqrt {2{{\sin }^2}\theta } }}} \right]$

$\Rightarrow {\tan ^{ - 1}}\left[ {\dfrac{{\sqrt 2 \cos \theta  + \sqrt 2 \sin \theta }}{{\sqrt 2 \cos \theta  - \sqrt 2 \sin \theta }}} \right]$

$\Rightarrow {\tan ^{ - 1}}\left[ {\dfrac{{1 + \tan \theta }}{{1 - \tan \theta }}} \right]$

$\Rightarrow {\tan ^{ - 1}}\left[ {\dfrac{{\tan \dfrac{\pi }{4} + \tan \theta }}{{1 - \tan \dfrac{\pi }{4}\tan \theta }}} \right]$

$\Rightarrow {\tan ^{ - 1}}\left( {\tan \left( {\dfrac{\pi }{4} + \theta } \right)} \right) = \dfrac{\pi }{4} + \theta$ 

Substituting the value of \[\theta  = \dfrac{1}{2}{\cos ^{ - 1}}{x^2}\]

$= \dfrac{\pi }{4} + \dfrac{1}{2}{\cos ^{ - 1}}{x^2}$

Hence, proved.

13. Find the simplified form of $co{s^{ - 1}}\left[ {\dfrac{3}{5}cosx + \dfrac{4}{5}sinx} \right],x \in \left[ {\dfrac{{ - 3\pi }}{4},\dfrac{\pi }{4}} \right]$

Ans:  Given: ${\cos ^{ - 1}}\left[ {\dfrac{3}{5}\cos x + \dfrac{4}{5}\sin x} \right],x \in \left[ {\dfrac{{ - 3\pi }}{4},\dfrac{\pi }{4}} \right]$

Using the property of trigonometric inverse, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

${\cos ^{ - 1}}\left[ {\dfrac{3}{5}\cos x + \dfrac{4}{5}\sin x} \right],x \in \left[ {\dfrac{{ - 3\pi }}{4},\dfrac{\pi }{4}} \right]$

Assume $\cos \alpha  = \dfrac{3}{5} \Rightarrow \sin \alpha  = \dfrac{4}{5} \Rightarrow \tan \alpha  = \dfrac{4}{3}$

$\Rightarrow {\cos ^{ - 1}}\left[ {\dfrac{3}{5}\cos x + \dfrac{4}{5}\sin x} \right] = {\cos ^{ - 1}}(\cos \alpha  \cdot \cos x + \sin \alpha  \cdot \sin x]$

$\Rightarrow {\cos ^{ - 1}}[\cos (\alpha  - x)] = \alpha  - x = {\tan ^{ - 1}}\dfrac{4}{3} - x$ 

14.  Prove that $si{n^{ - 1}}\dfrac{8}{{17}} + si{n^{ - 1}}\dfrac{3}{5} = si{n^{ - 1}}\dfrac{{77}}{{85}}$.

Ans:  Given: ${\sin ^{ - 1}}\dfrac{8}{{17}} + {\sin ^{ - 1}}\dfrac{3}{5} = {\sin ^{ - 1}}\dfrac{{77}}{{85}}$

Using the property of trigonometric inverse, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

${\sin ^{ - 1}}\dfrac{8}{{17}} + {\sin ^{ - 1}}\dfrac{3}{5} = {\sin ^{ - 1}}\dfrac{{77}}{{85}}$

Solving for L.H.S

${\text{L}} \cdot {\text{H}} \cdot {\text{S}} = {\sin ^{ - 1}}\dfrac{8}{{17}} + {\sin ^{ - 1}}\dfrac{3}{5}\left[ {\because {{\tan }^{ - 1}}x - {{\tan }^{ - 1}}y = {{\tan }^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)} \right]$

$= {\tan ^{ - 1}}\dfrac{8}{{15}} + {\tan ^{ - 1}}\dfrac{3}{4}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{8}{{15}} + \dfrac{3}{4}}}{{1 - \dfrac{8}{{15}} \times \dfrac{3}{4}}}$ 

$= {\tan ^{ - 1}}\dfrac{{\dfrac{{32 + 45}}{{60}}}}{{\dfrac{{60 - 24}}{{60}}}}$

$= {\tan ^{ - 1}}\dfrac{{77}}{{36}}$

$= {\sin ^{ - 1}}\dfrac{{77}}{{\sqrt {5929 + 1296} }}$

$= {\sin ^{ - 1}}\dfrac{{77}}{{85}}$

$= {\text{ R}}{\text{.H}}{\text{.S}}{\text{.}}$ 

15. Show that $si{n^{ - 1}}\dfrac{5}{{13}} + co{s^{ - 1}}\dfrac{3}{5} = ta{n^{ - 1}}\dfrac{{63}}{{16}}$

Ans:  Given: ${\sin ^{ - 1}}\dfrac{5}{{13}} + {\cos ^{ - 1}}\dfrac{3}{5} = {\tan ^{ - 1}}\dfrac{{63}}{{16}}$

Using the property of trigonometric inverse $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$

Here,

${\sin ^{ - 1}}\dfrac{5}{{13}} = {\tan ^{ - 1}}\dfrac{5}{{12}}$

${\cos ^{ - 1}}\dfrac{3}{5} = {\tan ^{ - 1}}\dfrac{4}{3}$

Now, solving for L.H.S

${\text{L}}{\text{.H}}{\text{.S}}. = {\sin ^{ - 1}}\dfrac{5}{{13}} + {\cos ^{ - 1}}\dfrac{3}{5}$

$= {\tan ^{ - 1}}\dfrac{5}{{12}} + {\tan ^{ - 1}}\dfrac{4}{3}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{5}{{12}} + \dfrac{4}{3}}}{{1 - \dfrac{5}{{12}} \cdot \dfrac{4}{3}}}\left[ {\because {{\tan }^{ - 1}}x + {{\tan }^{ - 1}}y = {{\tan }^{ - 1}}\left( {\dfrac{{x + y}}{{1 - xy}}} \right)} \right]$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{{15 + 48}}{{36}}}}{{\dfrac{{36 - 20}}{{36}}}} = {\tan ^{ - 1}}\dfrac{{63}}{{16}}$

$= {\text{R}}{\text{.H}}{\text{.S}}$ 

16. Prove that $ta{n^{ - 1}}\dfrac{1}{4} + ta{n^{ - 1}}\dfrac{2}{9} = si{n^{ - 1}}\dfrac{1}{{\sqrt 5 }}$.

Ans:  Given: ${\tan ^{ - 1}}\dfrac{1}{4} + {\tan ^{ - 1}}\dfrac{2}{9} = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 5 }}$

Using the property of trigonometric inverse $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$

Solving for L.H.S

${\text{LH}}{\text{.S}}. = {\tan ^{ - 1}}\dfrac{1}{4} + {\tan ^{ - 1}}\dfrac{2}{9}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{1}{4} + \dfrac{2}{9}}}{{1 - \dfrac{1}{4} \cdot \dfrac{2}{9}}}\left[ {\because {{\tan }^{ - 1}}x + {{\tan }^{ - 1}}y = {{\tan }^{ - 1}}\left( {\dfrac{{x + y}}{{1 - xy}}} \right)} \right]$

$= {\tan ^{ - 1}}\dfrac{{9 + 8}}{{36 - 2}}$

$= {\tan ^{ - 1}}\dfrac{1}{2} = {\sin ^{ - 1}}\dfrac{1}{{\sqrt 5 }} = {\text{R}}{\text{.H}}{\text{.S}}$ 

Hence, proved.

17. Find the value of $4ta{n^{ - 1}}\dfrac{1}{5} - ta{n^{ - 1}}\dfrac{1}{{239}}$.

Ans:  Given: $4{\tan ^{ - 1}}\dfrac{1}{5} - {\tan ^{ - 1}}\dfrac{1}{{239}}$

Using the property of trigonometric inverse $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$ and ${\tan ^{ - 1}}x - {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)$, $\because 2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\dfrac{{2x}}{{1 - {x^2}}}$

$4{\tan ^{ - 1}}\dfrac{1}{5} - {\tan ^{ - 1}}\dfrac{1}{{239}}$

$=2\left( {2{{\tan }^{ - 1}}\dfrac{1}{5}} \right) - {\tan ^{ - 1}}\dfrac{1}{{239}}$

$= 2{\tan ^{ - 1}}\dfrac{{\dfrac{2}{5}}}{{1 - {{\left( {\dfrac{1}{5}} \right)}^2}}} - {\tan ^{ - 1}}\dfrac{1}{{239}}\quad \left( {\because 2{{\tan }^{ - 1}}x = {{\tan }^{ - 1}}\dfrac{{2x}}{{1 - {x^2}}}} \right)$ 

$= 2{\tan ^{ - 1}}\dfrac{{\dfrac{2}{5}}}{{\dfrac{{24}}{{25}}}} - {\tan ^{ - 1}}\dfrac{1}{{239}}$

$= {\tan ^{ - 1}}\dfrac{{2 \cdot \dfrac{5}{{12}}}}{{1 - {{\left( {\dfrac{5}{{12}}} \right)}^2}}} - {\tan ^{ - 1}}\dfrac{1}{{239}}$

$= {\tan ^{ - 1}}\dfrac{{144 \times 5}}{{119 \times 6}} - {\tan ^{ - 1}}\dfrac{1}{{239}}$

$= {\tan ^{ - 1}}\dfrac{{120}}{{119}} - {\tan ^{ - 1}}\dfrac{1}{{239}}$

$= {\tan ^{ - 1}}\dfrac{{\dfrac{{120}}{{119}} - \dfrac{1}{{239}}}}{{1 + \dfrac{{120}}{{119}} \cdot \dfrac{1}{{239}}}}\quad \left( {\because {{\tan }^{ - 1}}x - {{\tan }^{ - 1}}y = {{\tan }^{ - 1}}\dfrac{{x - y}}{{1 + xy}}} \right)$

$= {\tan ^{ - 1}}\dfrac{{120 \times 239 - 119}}{{119 \times 239 + 120}} = {\tan ^{ - 1}}\dfrac{{28680 - 119}}{{28441 + 120}}$

$= {\tan ^{ - 1}}\dfrac{{28561}}{{28561}} = {\tan ^{ - 1}}1 = \dfrac{\pi }{4}$ 

18. Show that $tan\left( {\dfrac{1}{2}si{n^{ - 1}}\dfrac{3}{4}} \right) = \dfrac{{4 - \sqrt 7 }}{3}$ and justify why the other value $\dfrac{{4 + \sqrt 7 }}{3}$ is ignored.

Ans:  Given: $\tan \left( {\dfrac{1}{2}{{\sin }^{ - 1}}\dfrac{3}{4}} \right) = \dfrac{{4 - \sqrt 7 }}{3}$

Using the trigonometric inverse function, $y = {\sin ^{ - 1}}x$,$x \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

Assume,

$\dfrac{1}{2}{\sin ^{ - 1}}\dfrac{3}{4} = \theta$

$\Rightarrow {\sin ^{ - 1}}\dfrac{3}{4} = 2\theta$ 

$\Rightarrow \sin 2\theta  = \dfrac{3}{4}$

Now, solving for L.H.S

$\Rightarrow \quad \dfrac{{2\tan \theta }}{{1 + {{\tan }^2}\theta }} = \dfrac{3}{4}$

$\Rightarrow \quad 3{\tan ^2}\theta  - 8$ and $\theta  + 3 = 0$

$\Rightarrow \quad \tan \theta  = \dfrac{{8 \pm \sqrt {64 - 36} }}{6}$

$\Rightarrow \quad \tan \theta  = \dfrac{{8 \pm \sqrt {28} }}{6} = \dfrac{{8 \pm 2\sqrt 7 }}{6} = \dfrac{{4 \pm \sqrt 7 }}{3}$

Now $- \dfrac{\pi }{2} \leqslant {\sin ^{ - 1}}\dfrac{3}{4} \leqslant \dfrac{\pi }{2}$

$\Rightarrow \quad \dfrac{{ - \pi }}{4} \leqslant \dfrac{1}{2}{\sin ^{ - 1}}\dfrac{3}{4} \leqslant \dfrac{\pi }{2}$

$\therefore \tan \left( {\dfrac{{ - \pi }}{4}} \right) \leqslant \tan \left( {\dfrac{1}{2}\left( {{{\sin }^{ - 1}}\dfrac{3}{4}} \right)} \right) \leqslant \tan \dfrac{\pi }{4}$

$\Rightarrow \quad  - 1 \leqslant \tan \left( {\dfrac{1}{2}{{\sin }^{ - 1}}\dfrac{3}{4}} \right) \leqslant 1$

$\Rightarrow \tan \theta  = \dfrac{{4 - \sqrt 7 }}{3}$

L.H.S = R.H.S

$\tan \theta  = \dfrac{{4 + \sqrt 7 }}{3} > 1$which is not possible 

19. If ${a_1},{a_2},{a_3}, \ldots ,{a_n}$ is an arithmetic progression with common difference$d$, then evaluate the following expression.

$\tan \left[ {{{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_1}{a_2}}}} \right) + {{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_2}{a_3}}}} \right)} \right.\left. {\quad  + {{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_3}{a_4}}}} \right) +  \cdots  + {{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_{n - 1}}{a_n}}}} \right)} \right]$

Ans:  Given: ${a_1},{a_2},{a_3}, \ldots ,{a_n}$ is an arithmetic progression with common difference$d$

Using the property of trigonometric inverse $\tan \left( {{{\tan }^{ - 1}}x} \right) = x$ and ${\tan ^{ - 1}}x - {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)$

Common difference $d$ is, $d = {a_2} - {a_1} = {a_3} - {a_2} = {a_4} - {a_3} =  \ldots  \ldots  = {a_n} - {a_{n - 1}}$

$\therefore {\tan ^{ - 1}}\dfrac{d}{{1 + {a_1}{a_2}}} = {\tan ^{ - 1}}\dfrac{{{a_2} - {a_1}}}{{1 + {a_1}{a_2}}} = {\tan ^{ - 1}}{a_2} - {\tan ^{ - 1}}{a_1}$

Similarly ${\tan ^{ - 1}}\dfrac{d}{{1 + {a_2}{a_3}}} = {\tan ^{ - 1}}\dfrac{{{a_3} - {a_2}}}{{1 + {a_2}{a_3}}} = {\tan ^{ - 1}}{a_3} - {\tan ^{ - 1}}{a_2}.....{\tan ^{ - 1}}\dfrac{d}{{1 + {a_{n - 1}}{a_n}}} = {\tan ^{ - 1}}\dfrac{{{a_n} - {a_{n - 1}}}}{{1 + {a_{n - 1}}{a_n}}} = {\tan ^{ - 1}}{a_n} - {\tan ^{ - 1}}{a_{n - 1}}$

$\therefore \quad \tan \left[ {{{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_1}{a_2}}}} \right) + {{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_2}{a_3}}}} \right)} \right. + \left. {..... + {{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_3}{a_4}}}} \right) +  \cdots  + {{\tan }^{ - 1}}\left( {\dfrac{d}{{1 + {a_{n - 1}}{a_n}}}} \right)} \right]$

$= \tan \left[ {\left( {{{\tan }^{ - 1}}{a_2} - {{\tan }^{ - 1}}{a_1}} \right) + \left( {{{\tan }^{ - 1}}{a_3} - {{\tan }^{ - 1}}{a_2}} \right)} \right.\left. { +  \ldots  + \left( {{{\tan }^{ - 1}}{a_n} - {{\tan }^{ - 1}}{a_{n - 1}}} \right)} \right]$

$= \tan \left[ {{{\tan }^{ - 1}}{a_n} - {{\tan }^{ - 1}}{a_1}} \right]$

$\because {\tan ^{ - 1}}x - {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)$

$\Rightarrow \tan \left[ {{{\tan }^{ - 1}}\dfrac{{{a_n} - {a_1}}}{{1 + {a_n}{a_1}}}} \right]$

$\Rightarrow \dfrac{{{a_n} - {a_1}}}{{1 + {a_n}{a_1}}}$ 

Choose the correct answers from the given four options in each of the exercises from 20 to 37 (M.C.Q):

20. Which of the following is the principal value branch of $co{s^{ - 1}}x$?

(A) $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right]$

(B) $\left( {0,\pi } \right)$

(C) $\left[ {0,\pi } \right]$

(D) $\left( {0,\pi } \right) - \left\{ {\dfrac{\pi }{2}} \right\}$

Ans: Correct answer is option C.

Given: ${\cos ^{ - 1}}x$

Use the properties of inverse trigonometric functions.

The principal value branch of ${\cos ^{ - 1}}x$ is $\left[ {0,\pi } \right]$.

Therefore, $\left[ {0,\pi } \right]$ is the correct answer.

21. Which of the following is the principal value branch of $cose{c^{ - 1}}x$?

 (A) $\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)$

(B) $\left[ {0,\pi } \right] - \left\{ {\dfrac{\pi }{2}} \right\}$

(C) $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right]$

(D) $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right] - \left\{ 0 \right\}$

Ans: Correct answer is option D 

Given: ${\text{cose}}{{\text{c}}^{ - 1}}x$

Use the properties of inverse trigonometric functions.

The principal value branch of ${\text{cose}}{{\text{c}}^{ - 1}}x$ is $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right] - \left\{ 0 \right\}$ as ${\text{cose}}{{\text{c}}^{ - 1}}(0) = \infty$ which is not defined.

Hence, $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right] - \left\{ 0 \right\}$ is the correct answer.

22. If $3ta{n^{ - 1}}x + co{t^{ - 1}}x = \pi$, then $x$ equals

(A) $0$

(B) $1$

(C) $- 1$

(D) $\dfrac{1}{2}$

Ans: Correct answer is option B.

Given: $3{\tan ^{ - 1}}x + {\cot ^{ - 1}}x = \pi$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

$3{\tan ^{ - 1}}x + {\cot ^{ - 1}}x = \pi$

$\Rightarrow 2{\tan ^{ - 1}}x + {\tan ^{ - 1}}x + {\cot ^{ - 1}}x = \pi$

$\Rightarrow 2{\tan ^{ - 1}}x + \dfrac{\pi }{2} = \pi$

$\Rightarrow 2{\tan ^{ - 1}}x = \dfrac{\pi }{2}$

$\Rightarrow {\tan ^{ - 1}}x = \dfrac{\pi }{4}$

$\Rightarrow x = 1$

Hence, $x = 1$.

23. The value of $si{n^{ - 1}}\left( {cos\left( {\dfrac{{33\pi }}{5}} \right)} \right)$ is

(A) $\dfrac{{3\pi }}{5}$

(B) $\dfrac{{ - 7\pi }}{5}$

(C) $\dfrac{\pi }{{10}}$

(D) $- \dfrac{\pi }{{10}}$

Ans: Correct answer is option D.

Given: ${\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right)$

Use the properties of inverse trigonometric functions.

${\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{30\pi  + 3\pi }}{5}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {6\pi  + \dfrac{{3\pi }}{5}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{3\pi }}{5}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{\pi }{2} + \dfrac{\pi }{{10}}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( { - \sin \left( {\dfrac{\pi }{{10}}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = {\sin ^{ - 1}}\left( {\sin \left( {\dfrac{{ - \pi }}{{10}}} \right)} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = \dfrac{{ - \pi }}{{10}}$

Hence, ${\sin ^{ - 1}}\left( {\cos \left( {\dfrac{{33\pi }}{5}} \right)} \right) = \dfrac{{ - \pi }}{{10}}$.

24. The domain of the function $co{s^{ - 1}}\left( {2x - 1} \right)$ is

(A) $\left[ {0,1} \right]$

(B) $\left[ { - 1,1} \right]$

(C) $\left( { - 1,1} \right)$

(D) $\left[ {0,\pi } \right]$

Ans: Correct answer is option A.

Given: ${\cos ^{ - 1}}\left( {2x - 1} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

Let $f(x) = {\cos ^{ - 1}}\left( {2x - 1} \right)$

$- 1 \leqslant 2x - 1 \leqslant 1$

$\Rightarrow  - 1 + 1 \leqslant 2x \leqslant 1 + 1$

$\Rightarrow 0 \leqslant 2x \leqslant 2$

$\Rightarrow 0 \leqslant x \leqslant 1$

Hence, the domain of ${\cos ^{ - 1}}\left( {2x - 1} \right)$ is $\left[ {0,1} \right]$.

25. The domain of the function defined by $f(x) = si{n^{ - 1}}\sqrt {x - 1}$ is

(A) $\left[ {1,2} \right]$

(B) $\left[ { - 1,1} \right]$

(C) $\left[ {0,1} \right]$

(D) none of these

Ans: Correct answer is option A.

Given: $f(x) = {\sin ^{ - 1}}\sqrt {x - 1}$

Use the properties of inverse trigonometric functions.

Let $f(x) = {\sin ^{ - 1}}\sqrt {x - 1}$

As $\sqrt {x - 1}  \geqslant 0$ and $- 1 \leqslant \sqrt {x - 1}  \leqslant 1$,

$\Rightarrow 0 \leqslant x - 1 \leqslant 1$

$\Rightarrow 1 \leqslant x \leqslant 2$

Hence, the domain of $f(x) = {\sin ^{ - 1}}\sqrt {x - 1}$ is $\left[ {1,2} \right]$.

26. If $cos\left( {si{n^{ - 1}}\dfrac{2}{5} + co{s^{ - 1}}x} \right) = 0,$ then $x$ is equal to

(A) $\dfrac{1}{5}$

(B) $\dfrac{2}{5}$

(C) $0$

(D) $1$

Ans: Correct answer is option B.

Given: $\cos \left( {{{\sin }^{ - 1}}\dfrac{2}{5} + {{\cos }^{ - 1}}x} \right) = 0$

Use the properties of inverse trigonometric functions.

$\cos \left( {{{\sin }^{ - 1}}\dfrac{2}{5} + {{\cos }^{ - 1}}x} \right) = 0$

$\Rightarrow {\sin ^{ - 1}}\dfrac{2}{5} + {\cos ^{ - 1}}x = {\cos ^{ - 1}}(0)$

$\Rightarrow {\sin ^{ - 1}}\dfrac{2}{5} + {\cos ^{ - 1}}x = \dfrac{\pi }{2}$

$\Rightarrow {\sin ^{ - 1}}\dfrac{2}{5} = \dfrac{\pi }{2} - {\cos ^{ - 1}}x$

$\Rightarrow {\sin ^{ - 1}}\dfrac{2}{5} = {\sin ^{ - 1}}x$

$x = \dfrac{2}{5}$

Hence, $x = \dfrac{2}{5}$.

27. The value of $sin\left( {2ta{n^{ - 1}}\left( {.75} \right)} \right)$ is equal to

(A) $.75$

(B) $1.5$

(C) $.96$

(D) $\sin 1.5$

Ans:  Correct answer is option C.

Given: $\sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right)$

Use the properties of inverse trigonometric functions.

$\sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = \sin \left( {2{{\tan }^{ - 1}}\dfrac{3}{4}} \right)$

As $2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\dfrac{{2x}}{{1 + {x^2}}}$,

$\Rightarrow \sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = \sin \left( {{{\sin }^{ - 1}}\dfrac{{2 \times \dfrac{3}{4}}}{{1 + \dfrac{9}{{16}}}}} \right)$

$\Rightarrow \sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = \sin \left( {{{\sin }^{ - 1}}\dfrac{{\dfrac{3}{2}}}{{\dfrac{{25}}{{16}}}}} \right)$

$\Rightarrow \sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = \sin \left( {{{\sin }^{ - 1}}\dfrac{{24}}{{25}}} \right)$

$\Rightarrow \sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = \sin \left[ {{{\sin }^{ - 1}}\left( {0.96} \right)} \right]$

$\Rightarrow \sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = 0.96$

Hence, $\sin \left( {2{{\tan }^{ - 1}}\left( {.75} \right)} \right) = 0.96$.

28. The value of $co{s^{ - 1}}\left( {cos\dfrac{{3\pi }}{2}} \right)$ is equal to

(A) $\dfrac{\pi }{2}$

(B) $\dfrac{{3\pi }}{2}$

(C) $\dfrac{{5\pi }}{2}$

(D) $\dfrac{{7\pi }}{2}$

Ans:  Correct answer is option A.

Given: ${\cos ^{ - 1}}\left( {\cos \dfrac{{3\pi }}{2}} \right)$

Use the properties of inverse trigonometric functions.

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{3\pi }}{2}} \right) = {\cos ^{ - 1}}\left[ {\cos \left( {\pi  + \dfrac{\pi }{2}} \right)} \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{3\pi }}{2}} \right) = {\cos ^{ - 1}}\left[ { - \cos \dfrac{\pi }{2}} \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{3\pi }}{2}} \right) = {\cos ^{ - 1}}\left[ 0 \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{3\pi }}{2}} \right) = \dfrac{\pi }{2}$

Hence, ${\cos ^{ - 1}}\left( {\cos \dfrac{{3\pi }}{2}} \right) = \dfrac{\pi }{2}$.

29. The value of the expression $2se{c^{ - 1}}2 + si{n^{ - 1}}\left( {\dfrac{1}{2}} \right)$ is

(A) $\dfrac{\pi }{6}$

(B) $\dfrac{{5\pi }}{6}$

(C) $\dfrac{{7\pi }}{6}$

(D) $1$

Ans:  Correct answer is option A.

Given: $2{\sec ^{ - 1}}2 + {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right)$

Use the properties of inverse trigonometric functions.

$\Rightarrow 2{\sec ^{ - 1}}2 + {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) = 2{\sec ^{ - 1}}\left( {\sec \dfrac{\pi }{3}} \right) + {\sin ^{ - 1}}\left( {\sin \dfrac{\pi }{6}} \right)$

$\Rightarrow 2{\sec ^{ - 1}}2 + {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) = 2.\dfrac{\pi }{3} + \dfrac{\pi }{6}$

$\Rightarrow 2{\sec ^{ - 1}}2 + {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) = \dfrac{{5\pi }}{6}$

Hence, $2{\sec ^{ - 1}}2 + {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) = \dfrac{{5\pi }}{6}$.

30. If $ta{n^{ - 1}}x + ta{n^{ - 1}}y = \dfrac{{4\pi }}{5},$ then $co{t^{ - 1}}x + co{t^{ - 1}}y$ equals

(A) $\dfrac{\pi }{5}$

(B) $\dfrac{{2\pi }}{5}$

(C) $\dfrac{{3\pi }}{5}$

(D) $\pi$

Ans:  Correct answer is option A.

Given: ${\tan ^{ - 1}}x + {\tan ^{ - 1}}y = \dfrac{{4\pi }}{5}$

Use the properties of inverse trigonometric functions.

${\tan ^{ - 1}}x + {\tan ^{ - 1}}y = \dfrac{{4\pi }}{5}$

$\Rightarrow \dfrac{\pi }{2} - {\cot ^{ - 1}}x + \dfrac{\pi }{2} - {\cot ^{ - 1}}y = \dfrac{{4\pi }}{5}$

$\Rightarrow \pi  - \left( {{{\cot }^{ - 1}}x + {{\cot }^{ - 1}}y} \right) = \dfrac{{4\pi }}{5}$

$\Rightarrow {\cot ^{ - 1}}x + {\cot ^{ - 1}}y = \dfrac{\pi }{5}$

Hence, ${\cot ^{ - 1}}x + {\cot ^{ - 1}}y = \dfrac{\pi }{5}$.

31. If ${\sin^{ - 1}}\left( {\dfrac{{2a}}{{1 + {a^2}}}} \right) + co{s^{ - 1}}\left( {\dfrac{{1 - {a^2}}}{{1 + {a^2}}}} \right) = ta{n^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right),$ where $a,x \in \left[0,1\right]$. then the value of $x$ is

(A) $0$

(B) $\dfrac{a}{2}$

(C) $a$

(D) $\dfrac{{2a}}{{1 - {a^2}}}$

Ans: Correct answer is option D.

Given: ${\sin ^{ - 1}}\left( {\dfrac{{2a}}{{1 + {a^2}}}} \right) + {\cos ^{ - 1}}\left( {\dfrac{{1 - {a^2}}}{{1 + {a^2}}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)$

Use the properties of inverse trigonometric functions.

Given that ${\sin ^{ - 1}}\left( {\dfrac{{2a}}{{1 + {a^2}}}} \right) + {\cos ^{ - 1}}\left( {\dfrac{{1 - {a^2}}}{{1 + {a^2}}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)$

As $2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right) = {\cos ^{ - 1}}\left( {\dfrac{{1 - {x^2}}}{{1 + {x^2}}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)$,

\[ \Rightarrow 2{\tan ^{ - 1}}a + 2{\tan ^{ - 1}}a = 2{\tan ^{ - 1}}x\]

\[ \Rightarrow 4{\tan ^{ - 1}}a = 2{\tan ^{ - 1}}x\]

\[ \Rightarrow 2{\tan ^{ - 1}}a = {\tan ^{ - 1}}x\]

\[ \Rightarrow {\tan ^{ - 1}}\dfrac{{2a}}{{1 - {a^2}}} = {\tan ^{ - 1}}x\]

\[\Rightarrow x = \dfrac{{2a}}{{1 - {a^2}}}\]

Hence, \[x = \dfrac{{2a}}{{1 - {a^2}}}\].

32. The value of $cot\left[ {co{s^{ - 1}}\left( {\dfrac{7}{{25}}} \right)} \right]$ is

(A) $\dfrac{{25}}{{24}}$

(B) $\dfrac{{25}}{7}$

(C) $\dfrac{{24}}{{25}}$

(D) $\dfrac{7}{{24}}$

Ans: Correct answer is option D.

Given: $\cot \left[ {{{\cos }^{ - 1}}\left( {\dfrac{7}{{25}}} \right)} \right]$

Use the properties of inverse trigonometric functions.

Let ${\cos ^{ - 1}}\left( {\dfrac{7}{{25}}} \right) = \theta$

$\Rightarrow \cos \theta  = \dfrac{7}{{25}}$

$\Rightarrow \cot \theta  = \dfrac{7}{{24}}$

$\Rightarrow \cot \left[ {{{\cos }^{ - 1}}\left( {\dfrac{7}{{25}}} \right)} \right] = \cot \theta$

\[\Rightarrow \cot \left[ {{{\cos }^{ - 1}}\left( {\dfrac{7}{{25}}} \right)} \right] = \dfrac{7}{{24}}\]

Hence, \[\cot \left[ {{{\cos }^{ - 1}}\left( {\dfrac{7}{{25}}} \right)} \right] = \dfrac{7}{{24}}\].

33. The value of the expression $\tan\left( {\dfrac{1}{2}co{s^{ - 1}}\dfrac{2}{{\sqrt 5 }}} \right)$ is

(A) $2 + \sqrt 5$

(B) $\sqrt 5  - 2$

(C) $\dfrac{{\sqrt 5  + 2}}{2}$

(D) $5 + \sqrt 2$

$\left[ {Hint: tan\dfrac{\theta }{2} = \sqrt {\dfrac{{1 - cos\theta }}{{1 + cos\theta }}} } \right]$

Ans: Correct answer is option B.

Given: $\tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\dfrac{2}{{\sqrt 5 }}} \right)$

Use the properties of inverse trigonometric functions.

Let $\theta  = \dfrac{1}{2}{\cos ^{ - 1}}\dfrac{2}{{\sqrt 5 }}$

$\Rightarrow 2\theta  = {\cos ^{ - 1}}\dfrac{2}{{\sqrt 5 }}$

$\Rightarrow \cos 2\theta  = \dfrac{2}{{\sqrt 5 }}$

As $\cos 2\theta  = \dfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}$,

$\Rightarrow \dfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }} = \dfrac{2}{{\sqrt 5 }}$

$\Rightarrow 2 + 2{\tan ^2}\theta  = \sqrt 5  - \sqrt 5 {\tan ^2}\theta$

$\Rightarrow \left( {\sqrt 5  + 2} \right){\tan ^2}\theta  = \sqrt 5  - 2$

$\Rightarrow {\tan ^2}\theta  = \dfrac{{\sqrt 5  - 2}}{{\sqrt 5  + 2}}$

$\Rightarrow {\tan ^2}\theta  = \dfrac{{\left( {\sqrt 5  - 2} \right)\left( {\sqrt 5  - 2} \right)}}{{\left( {\sqrt 5  + 2} \right)\left( {\sqrt 5  - 2} \right)}}$

$\Rightarrow {\tan ^2}\theta  = \dfrac{{{{\left( {\sqrt 5  - 2} \right)}^2}}}{{5 - 4}}$

$\Rightarrow \tan \theta  =  \pm \left( {\sqrt 5  - 2} \right)$

$\Rightarrow \tan \theta  = \sqrt 5  - 2$

$\Rightarrow \tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\dfrac{2}{{\sqrt 5 }}} \right) = \sqrt 5  - 2$

Hence, $\tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\dfrac{2}{{\sqrt 5 }}} \right) = \sqrt 5  - 2$.

34. If $\left| x \right|\le1,$then $2ta{n^{ - 1}}x + si{n^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)$ is equal to

(A) $4ta{n^{ - 1}}x$

(B) $0$

(C) $\dfrac{\pi }{2}$

(D) $\pi$

Ans:  Correct answer is option A.

Given: $\left| x \right| \leqslant 1,$

Use the properties of inverse trigonometric functions.

As $2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)$,

$\Rightarrow 2{\tan ^{ - 1}}x + {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right) = 2{\tan ^{ - 1}}x + 2{\tan ^{ - 1}}x$

$\Rightarrow 2{\tan ^{ - 1}}x + {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right) = 4{\tan ^{ - 1}}x$

Hence, $2{\tan ^{ - 1}}x + {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right) = 4{\tan ^{ - 1}}x$..

35. If $co{s^{ - 1}}\alpha  + co{s^{ - 1}}\beta  + co{s^{ - 1}}\gamma  = 3\pi ,$ then $\alpha \left( {\beta  + \gamma } \right) + \beta \left( {\gamma  + \alpha } \right) + \gamma (\alpha  + \beta )$ equals

(A) $0$

(B) $1$

(C) $6$

(D) $12$

Ans:  Correct answer is option C.

Given: ${\cos ^{ - 1}}\alpha  + {\cos ^{ - 1}}\beta  + {\cos ^{ - 1}}\gamma  = 3\pi$

Use the properties of inverse trigonometric functions.

Given that ${\cos ^{ - 1}}\alpha  + {\cos ^{ - 1}}\beta  + {\cos ^{ - 1}}\gamma  = 3\pi$

${\cos ^{ - 1}}\alpha  + {\cos ^{ - 1}}\beta  + {\cos ^{ - 1}}\gamma  = \pi  + \pi  + \pi$

\[ \Rightarrow {\cos ^{ - 1}}\alpha  = \pi ,{\text{ }}{\cos ^{ - 1}}\beta  = \pi ,{\text{ }}{\cos ^{ - 1}}\gamma  = \pi \]

\[ \Rightarrow \alpha  = \cos \pi ,{\text{ }}\beta  = \cos \pi ,{\text{ }}\gamma  = \cos \pi \]

\[ \Rightarrow \alpha  =  - 1,{\text{ }}\beta  =  - 1,{\text{ }}\gamma  =  - 1\]

$\Rightarrow \alpha \left( {\beta  + \gamma } \right) + \beta \left( {\gamma  + \alpha } \right) + \gamma (\alpha  + \beta ) = \left( { - 1} \right)\left( { - 1 - 1} \right) + \left( { - 1} \right)\left( { - 1 - 1} \right) + \left( { - 1} \right)\left( { - 1 - 1} \right)$

$\Rightarrow \alpha \left( {\beta  + \gamma } \right) + \beta \left( {\gamma  + \alpha } \right) + \gamma (\alpha  + \beta ) = 6$

Hence, $\alpha \left( {\beta  + \gamma } \right) + \beta \left( {\gamma  + \alpha } \right) + \gamma (\alpha  + \beta ) = 6$.

36. The number of real solutions of the equation $\sqrt {1 + cos2x}  = \sqrt 2 co{s^{ - 1}}\left( {cosx} \right)$ in $\left[ {\dfrac{\pi }{2},\pi } \right]$ is

(A) $0$

(B) $1$

(C) $2$

(D) Infinite

Ans:  Correct answer is option A.

Given: $\sqrt {1 + \cos 2x}  = \sqrt 2 {\cos ^{ - 1}}\left( {\cos x} \right)$

Use the properties of inverse trigonometric functions.

$\sqrt {1 + \cos 2x}  = \sqrt 2 {\cos ^{ - 1}}\left( {\cos x} \right)$

$\Rightarrow \sqrt {2{{\cos }^2}x}  = \sqrt 2 x$

$\Rightarrow \sqrt 2 \cos x = \sqrt 2 x$

$\Rightarrow \cos x = x$ which is not possible for any value of $x$.

Hence, the number of real solutions of $\sqrt {1 + \cos 2x}  = \sqrt 2 {\cos ^{ - 1}}\left( {\cos x} \right)$ in $\left[ {\dfrac{\pi }{2},\pi } \right]$ is $0.$.

37. If $co{s^{ - 1}}x > si{n^{ - 1}}x,$ then

(A) $\dfrac{1}{{\sqrt 2 }} < x\le1$

(B) $0 \le x < \dfrac{1}{{\sqrt 2 }}$      

(C) $- 1 \le x < \dfrac{1}{{\sqrt 2 }}$

(D) $x > 0$

Ans:  Correct answer is option C.

Given: ${\cos ^{ - 1}}x > {\sin ^{ - 1}}x$

: The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

${\cos ^{ - 1}}x > {\sin ^{ - 1}}x$

$\Rightarrow \sin \left[ {{{\cos }^{ - 1}}x} \right] > x$

$\Rightarrow \sin \left[ {{{\sin }^{ - 1}}\sqrt {1 - {x^2}} } \right] > x$

$\Rightarrow \sqrt {1 - {x^2}}  > x$

$\Rightarrow x < \sqrt {1 - {x^2}}$

$\Rightarrow {x^2} < 1 - {x^2}$

$\Rightarrow 2{x^2} < 1$

$\Rightarrow {x^2} < \dfrac{1}{2}$

\[ \Rightarrow x <  \pm \dfrac{1}{{\sqrt 2 }}\]

As $- 1 \leqslant x \leqslant 1$, $- 1 \leqslant x < \dfrac{1}{{\sqrt 2 }}$.

Hence, $- 1 \leqslant x < \dfrac{1}{{\sqrt 2 }}$.

38. The principal value of ${\cos^{ - 1}}\left( { - \dfrac{1}{2}} \right)$ is

Ans:  Given: ${\cos ^{ - 1}}\left( { - \dfrac{1}{2}} \right)$

Use the properties of inverse trigonometric functions.

Let ${\cos ^{ - 1}}\left( { - \dfrac{1}{2}} \right) = x$

$\Rightarrow \cos x =  - \dfrac{1}{2}$

$\Rightarrow \cos x = \cos \left( { - \dfrac{\pi }{3}} \right)$

$\Rightarrow \cos x = \cos \left( {\pi  - \dfrac{\pi }{3}} \right)$

$\Rightarrow \cos x = \cos \left( {\dfrac{{2\pi }}{3}} \right)$

$\Rightarrow x = \dfrac{{2\pi }}{3} \in \left[ {0,\pi } \right]$

Therefore, the principal value of ${\cos ^{ - 1}}\left( { - \dfrac{1}{2}} \right)$ is $\dfrac{{2\pi }}{3}$.

39. The value of $\sin^{ - 1}\left( {sin\dfrac{{3\pi }}{5}} \right)$ is

Ans:  Given: ${\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right)$

Use the properties of inverse trigonometric functions.

${\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right) \ne \dfrac{{3\pi }}{5}$ as $\dfrac{{3\pi }}{5} \notin \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

So, ${\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right) = {\sin ^{ - 1}}\sin \left( {\pi  - \dfrac{{2\pi }}{5}} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right) = {\sin ^{ - 1}}\sin \left( {\dfrac{{2\pi }}{5}} \right)$

$\Rightarrow {\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right) = \dfrac{{2\pi }}{5} \in \left[ {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right]$

Therefore, the value of ${\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right)$ is $\dfrac{{2\pi }}{5}$.

40. If \[cos\left( {ta{n^{ - 1}}x + co{t^{ - 1}}\sqrt 3 } \right) = 0,\] then value of \[x\] is

Ans:  Given: \[\cos \left( {{{\tan }^{ - 1}}x + {{\cot }^{ - 1}}\sqrt 3 } \right) = 0\]

Use the properties of inverse trigonometric functions.

\[\cos \left( {{{\tan }^{ - 1}}x + {{\cot }^{ - 1}}\sqrt 3 } \right) = 0\]

\[\Rightarrow {\tan ^{ - 1}}x + {\cot ^{ - 1}}\sqrt 3  = {\cos ^{ - 1}}\left( 0 \right)\]

\[\Rightarrow {\tan ^{ - 1}}x + {\cot ^{ - 1}}\sqrt 3  = \dfrac{\pi }{2}\]

\[\Rightarrow {\tan ^{ - 1}}x = \dfrac{\pi }{2} - {\cot ^{ - 1}}\sqrt 3 \]

\[\Rightarrow {\tan ^{ - 1}}x = {\tan ^{ - 1}}\sqrt 3 \]

\[\Rightarrow x = \sqrt 3 \]

Therefore, \[x = \sqrt 3 \].

41. The set of values of \[{\sec ^{ - 1}}\left( {\dfrac{1}{2}} \right)\] is

Ans:  Given: \[{\sec ^{ - 1}}\left( {\dfrac{1}{2}} \right)\]

Use the properties of inverse trigonometric functions.

Let \[{\sec ^{ - 1}}\left( {\dfrac{1}{2}} \right) = x\]

\[ \Rightarrow \sec x = \dfrac{1}{2}\]

The domain of \[{\sec ^{ - 1}}x\] is \[R - \left\{ { - 1,1} \right\}\] and \[\dfrac{1}{2} \notin R - \left\{ { - 1,1} \right\}\]. 

Therefore, \[{\sec ^{ - 1}}\left( {\dfrac{1}{2}} \right)\] has no set of values.

42. The principal value of $ta{n^{ - 1}}\sqrt 3$ is

Ans:  Given: ${\tan ^{ - 1}}\sqrt 3$

Use the properties of inverse trigonometric functions.

$\Rightarrow {\tan ^{ - 1}}\sqrt 3  = {\tan ^{ - 1}}\left( {\tan \dfrac{\pi }{3}} \right)$

\[\Rightarrow {\tan ^{ - 1}}\sqrt 3  = \dfrac{\pi }{3} \in \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right)\]

Therefore, the principal value of ${\tan ^{ - 1}}\sqrt 3$ is $\dfrac{\pi }{3}$.

43. The value of $co{s^{ - 1}}\left( {cos\dfrac{{14\pi }}{3}} \right)$ is

Ans:  Given: ${\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right)$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

${\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right) = {\cos ^{ - 1}}\left[ {\cos \left( {5\pi  - \dfrac{\pi }{3}} \right)} \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right) = {\cos ^{ - 1}}\left[ {\cos \left( { - \dfrac{\pi }{3}} \right)} \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right) = {\cos ^{ - 1}}\left[ {\cos \left( {\pi  - \dfrac{\pi }{3}} \right)} \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right) = {\cos ^{ - 1}}\left[ {\cos \left( {\dfrac{{2\pi }}{3}} \right)} \right]$

$\Rightarrow {\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right) = \dfrac{{2\pi }}{3} \in \left[ {0,\pi } \right]$

Therefore, the value of ${\cos ^{ - 1}}\left( {\cos \dfrac{{14\pi }}{3}} \right)$ is $\dfrac{{2\pi }}{3}$.

44. The value of $cos\left(si{{n}^{-1}}x+co{{s}^{-1}}x \right),\left| x \right|\le 1$ is

Ans:  Given: $\left| x \right| \leqslant 1$

Use the properties of inverse trigonometric functions.

$\Rightarrow \cos \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x} \right) = \cos \dfrac{\pi }{2}$

$\Rightarrow \cos \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x} \right) = 0$

Therefore, $\cos \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x} \right) = 0$.

45. The value of expression \[tan\left( {\dfrac{{si{n^{ - 1}}x + co{s^{ - 1}}x}}{2}} \right),\] when $x = \dfrac{{\sqrt 3 }}{2}$ is

Ans:  Given: $x = \dfrac{{\sqrt 3 }}{2}$

Use the properties of inverse trigonometric functions.

\[\tan \left( {\dfrac{{{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x}}{2}} \right) = \tan \left( {\dfrac{\pi }{4}} \right)\]

\[\Rightarrow \tan \left( {\dfrac{{{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x}}{2}} \right) = 1\]

Therefore, \[\tan \left( {\dfrac{{{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}x}}{2}} \right) = 1\].

46. If \[y = 2ta{n^{ - 1}}x + si{n^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)\] for all $x,$ then $..... < y < .....$

Ans:  Given: \[y = 2{\tan ^{ - 1}}x + {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)\]

Use the properties of inverse trigonometric functions.

\[y = 2{\tan ^{ - 1}}x + {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)\]

As \[2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)\],

\[ \Rightarrow y = 2{\tan ^{ - 1}}x + 2{\tan ^{ - 1}}x\]

\[ \Rightarrow y = 4{\tan ^{ - 1}}x\]

As $\dfrac{{ - \pi }}{2} < {\tan ^{ - 1}}x < \dfrac{\pi }{2}$,

$\Rightarrow - 4 \times \dfrac{\pi }{2} < 4{\tan ^{ - 1}}x < 4 \times \dfrac{\pi }{2}$

$\Rightarrow - 2\pi  < y < 2\pi$

Therefore, $- 2\pi  < y < 2\pi$

47. The result \[ta{n^{ - 1}}x - ta{n^{ - 1}}y = ta{n^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)\] is true when value of \[xy\] is

Ans:  Given: \[{\tan ^{ - 1}}x - {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)\]

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

\[{\tan ^{ - 1}}x - {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\dfrac{{x - y}}{{1 + xy}}} \right)\] is true when $xy >  - 1$.

Therefore, $xy >  - 1$.

48. The value of \[co{t^{ - 1}}( - x)\] for all \[x \in R\] in terms of \[co{t^{ - 1}}x\] is

Ans:  Given: \[{\cot ^{ - 1}}( - x)\]

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

\[{\cot ^{ - 1}}( - x) = \pi  - {\cot ^{ - 1}}x,{\text{ }}x \in R\]

Therefore, \[{\cot ^{ - 1}}( - x) = \pi  - {\cot ^{ - 1}}x,{\text{ }}x \in R\].

State True or False for the statement in each of the Exercises 49 to 55:

49. All trigonometric functions have inverse over their respective domains.

Ans:  Given: All trigonometric functions have inverse over their respective domains.

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

All the inverse trigonometric functions are restricted over their respective domains.

Therefore, the statement is false.

50. The value of the expression ${\left( {co{s^{ - 1}}x} \right)^2}$ is equal to $se{c^2}x$.

Ans:  Given: The value of the expression ${\left( {{{\cos }^{ - 1}}x} \right)^2}$ is equal to ${\sec ^2}x$.

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

As ${\cos ^{ - 1}}x = {\sec ^{ - 1}}\left( {\dfrac{1}{x}} \right) \ne \sec x$,

${\left( {{{\cos }^{ - 1}}x} \right)^2} \ne {\sec ^2}x$

Therefore, the statement is false.

51. The domain of trigonometric functions can be restricted to any one of their branches (not necessarily principal value) in order to obtain their reverse functions.

Ans:  Given: The domain of trigonometric functions can be restricted to any one of their branch (not necessarily principal value) in order to obtain their reverse functions.

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

All the trigonometric functions are restricted over their respective domains to get their inverse functions.

Therefore, the statement is true.

52. The least numerical value, either positive or negative, of angle $\theta$ is called the principal value of the inverse trigonometric function.

Ans:  Given: The least numerical value, either positive or negative of angle $\theta$ is called the principal value of the inverse trigonometric function.

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

Principal value of any inverse trigonometric function is the least numerical value, either positive or negative of $\theta$. 

Therefore, the statement is true.

53. The graph of inverse trigonometric functions can be obtained from the graph of their corresponding trigonometric function by interchanging $x$ and $y$ axes.

Ans:  Given: The graph of inverse trigonometric function can be obtained from the graph of their corresponding trigonometric function by interchanging $x$and $y$axes.

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

The domain and the range are interchanged in the graph of inverse trigonometric functions to that of their corresponding trigonometric functions.

Therefore, the statement is true.

54. The minimum value of $n$ for which $ta{n^{ - 1}}\dfrac{n}{\pi } > \dfrac{\pi }{4}, n \in N$ is valid is 5.

Ans:  Given: The minimum value of $n$ for which ${\tan ^{ - 1}}\dfrac{n}{\pi } > \dfrac{\pi }{4},{\text{ }}n \in N$ is valid is $5.$

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, secant, tangent, and cosecant are called inverse trigonometric functions.

${\tan ^{ - 1}}\dfrac{n}{\pi } > \dfrac{\pi }{4}$

$\Rightarrow \dfrac{n}{\pi } > \tan \dfrac{\pi }{4}$

$\Rightarrow \dfrac{n}{\pi } > 1$

$\Rightarrow n > \pi$

$\Rightarrow n > 3.14$

So, the value of $n$ is $4.$

Therefore, the statement is false.

55. The principal value of ${\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right]$ is $\dfrac{\pi }{3}$.

Ans:  Given: The principal value of ${\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right]$ is $\dfrac{\pi }{3}$.

The inverse functions of the basic trigonometric functions sine, cotangent, cosine, 

${\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right] = {\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\sin \dfrac{\pi }{6}} \right)} \right]$

$\Rightarrow {\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right] = {\sin ^{ - 1}}\left[ {\cos \dfrac{\pi }{6}} \right]$

$\Rightarrow {\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right] = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt 3 }}{2}} \right)$

$\Rightarrow {\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right] = {\sin ^{ - 1}}\left( {\sin \dfrac{\pi }{3}} \right)$

$\Rightarrow {\sin ^{ - 1}}\left[ {\cos \left( {{{\sin }^{ - 1}}\dfrac{1}{2}} \right)} \right] = \dfrac{\pi }{3}$

Therefore, the statement is true.

In the  NCERT Exemplar for Class 12 Maths Chapter 2 - Inverse Trigonometric Functions (Book Solutions), the following sub-topics are covered:

2.1 An Overview

2.2 Fundamental ideas

2.3 Inverse Trigonometric function properties

Students will obtain the complete solution to the questions in the NCERT  Exemplar book after each topic thoroughly with our comprehensive NCERT Exemplar for Class 12 Maths Chapter 2 - Inverse Trigonometric Functions (Book Solutions)

NCERT Exemplar for Class 12 Maths Chapter 2 - Inverse Trigonometric Functions (Book Solutions) covers a variety of topics that will assist you in preparing for higher learning and Examinations. Class 12 Maths Solutions from NCERT Inverse Trigonometric Functions, their principles, range, domain, and Functions are all covered in Chapter 2.