NCERT Exemplar for Class 10 Maths - Pair of Linear Equations in Two Variables - Free PDF Download
Free PDF download of NCERT Exemplar for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 3 - Pair of Linear Equations in Two Variables exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations.
You can also Download Maths NCERT Solutions Class 10 to help you to revise the complete Syllabus and score more marks in your examinations. Vedantu is a platform that provides free CBSE Solutions and other study materials for students. Subjects like Science, Maths, English will become easy to study if you have access to NCERT Solution Class 10 Science, Maths solutions, and solutions of other subjects.
Access NCERT Exemplar Solutions for Class 10 Maths Chapter 3 – Pair of Linear Equations in Two Variables
Sample Questions
1. The pair of equations $5x - 15y = 8$ and $3x - 9y = \frac{{24}}{5}$ has
(A) one solution
(B) two solutions
(C) infinitely many solutions
(D) no solution
Ans: D
Given equations are $5x - 15y = 8$and $3x - 9y = \frac{{24}}{5}$
The equation $3x - 9y = \frac{{24}}{5}$ can be written as
$ \Rightarrow 15x - 45y = 24$
The equations $5x - 15y = 8$ and $15x - 45y = 24$
Comparing with ${a_1}x + {b_1}y = {c_1}$and${a_2}x + {b_2}y = {c_2}$, we get:
$\frac{{{{\text{a}}_1}}}{{{{\text{a}}_2}}} = \frac{5}{{15}} = \frac{1}{3}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{15}}{{45}} = \frac{1}{3}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{8}{{24}} = \frac{1}{3}$
$ \Rightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{\;{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$
Therefore, the pair of equations $5x - 15y = 8$ and $3x - 9y = \frac{{24}}{5}$ has infinitely many solutions.
2. The sum of the digits of a two-digit number is$9$. If $27$ is added to it, the digits of the number get reversed. The number is
(A) 25
(B) 72
(C) 63
(D) 36
Ans: D
Consider one digit number be $x$ and tens digit number be $y$.
And, to find the number be $x + 10y$
We have:
The sum of the digits of a two-digit number is $9$
i.e., $x + y = 9$ …………..(i)
And if $27$ is added to it, the digits of the number get reversed then,
$(x + 10y) = (10x + y) + 27$
$x + 10y = 10x + y + 27$
$9y - 9x = 27$
$9(y - x) = 27$
$y - x = \frac{{27}}{9}$
$y = 3 + x$…………(ii)
Substitute the value of $y$ in equation (i), we get:
$3 + x + x = 9$
$2x = 9 - 3$
$x = \frac{6}{2}$
$x = 3$
Substitute the value of $x$ in equation (ii) , we get:
$y = 3 + 3$
$y = 6$
Then ,
Number $ = (10x + y)$
Number $ = 10 \times 3 + 6$
Number $ = 30 + 6$
Number $ = 36$
EXERCISE 3.1
Choose the correct answer from the given four options:
1. Graphically, the pair of equations
$6x - 3y + 10 = 0$
$2x - y + 9 = 0$
represents two lines which are
(A) intersecting at exactly one point.
(B) intersecting at exactly two points.
(C) coincident.
(D) parallel.
Ans: D
Given, the linear equations are $6x - 3y + 10 = 0$and $2x - y + 9 = 0$
On comparing with ${a_1}x + {b_1}y = {c_1}$and${a_2}x + {b_2}y = {c_2}$, we get:
So, ${a_1} = 6,{b_1} = - 3,{c_1} = 10$
${a_2} = 2,{b_2} = - 1,{c_2} = 9$
$\frac{{{a_1}}}{{{a_2}}} = \frac{6}{2} = 3$
And
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 3}}{{ - 1}} = 3$
And
$\frac{{{c_1}}}{{{c_2}}} = \frac{{10}}{9}$
$\Rightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
Therefore, the lines representing the given equations are parallel.
2. The pair of equations $x + 2y + 5 = 0$ and $ - 3x - 6y + 1 = 0$ have
(A) a unique solution
(B) exactly two solutions
(C) infinitely many solutions
(D) no solution
Ans: D
From the equations \[x + 2y + 5 = 0\] and \[ - 3x - 6y + 1 = 0\].
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$.
$\frac{{{a_1}}}{{{a_2}}} = - \frac{1}{3}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{2}{{ - 6}} = - \frac{1}{3}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{5}{1}$
$ \Rightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{\;{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
Therefore, the pair of equations $x + 2y + 5 = 0$ and \[ - 3x - 6y + 1 = 0\] have no solution.
3. If a pair of linear equations is consistent, then the lines will be
(A) parallel
(B) always coincident
(C) intersecting or coincident
(D) always intersecting
Ans: C
If a pair of linear equations is consistent, then it has unique solutions and infinite solutions.
If $\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$, then the graph will be a pair of lines intersecting at a unique point, which is the solution of the pair of equations.
If $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$, then the graph will be a pair of coincident lines. Each point on the lines will be a solution, and so the pair of equations will have infinitely many solutions
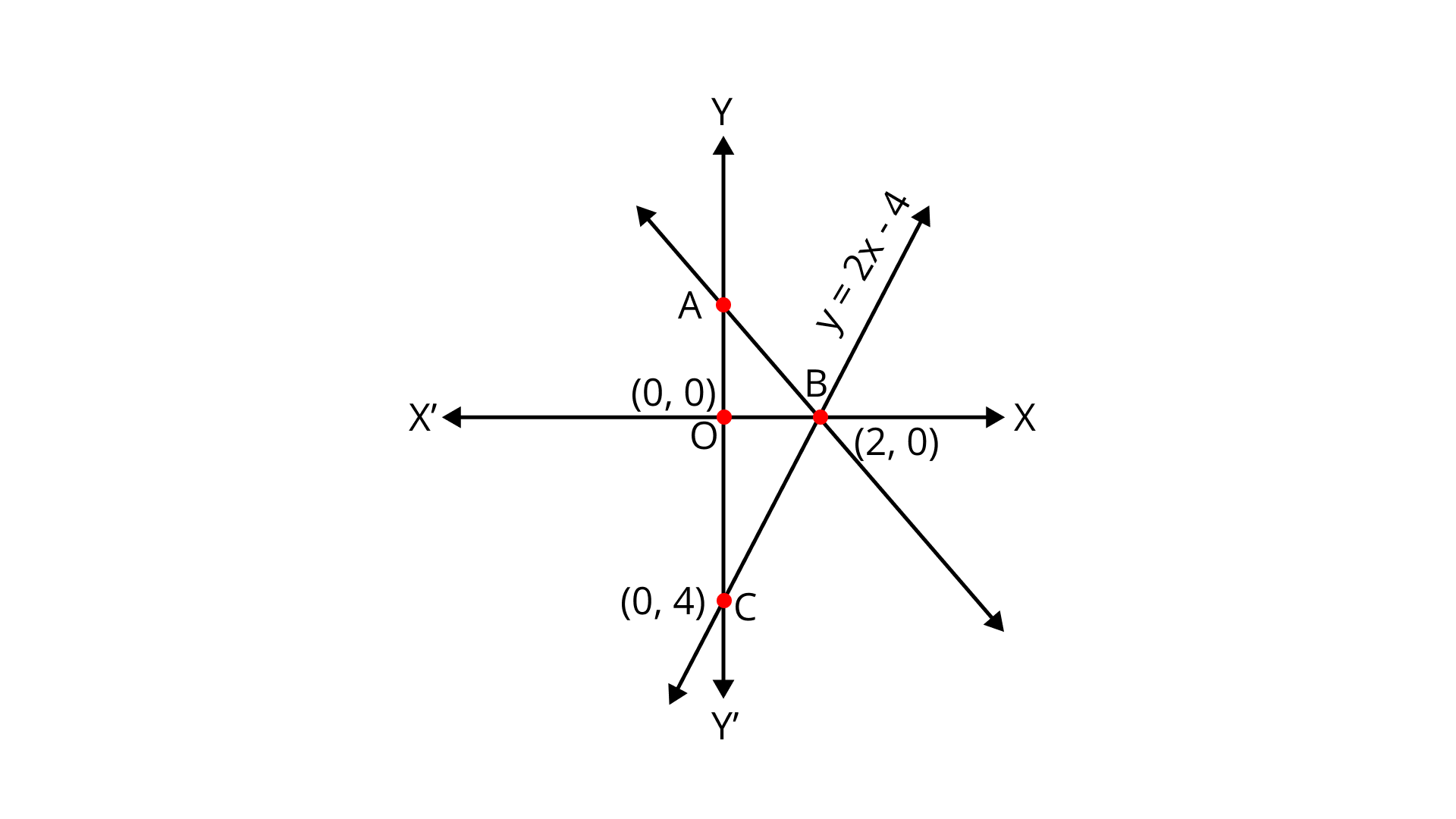
4. The pair of equations $y = 0$ and $y = - 7$ has
(A) one solution
(B) two solutions
(C) infinitely many solutions
(D) no solution
Ans: D
Given the pair of equations are $y = 0$ and $y = - 7$
Graph the pair of equations $y = 0$and $y = - 7$
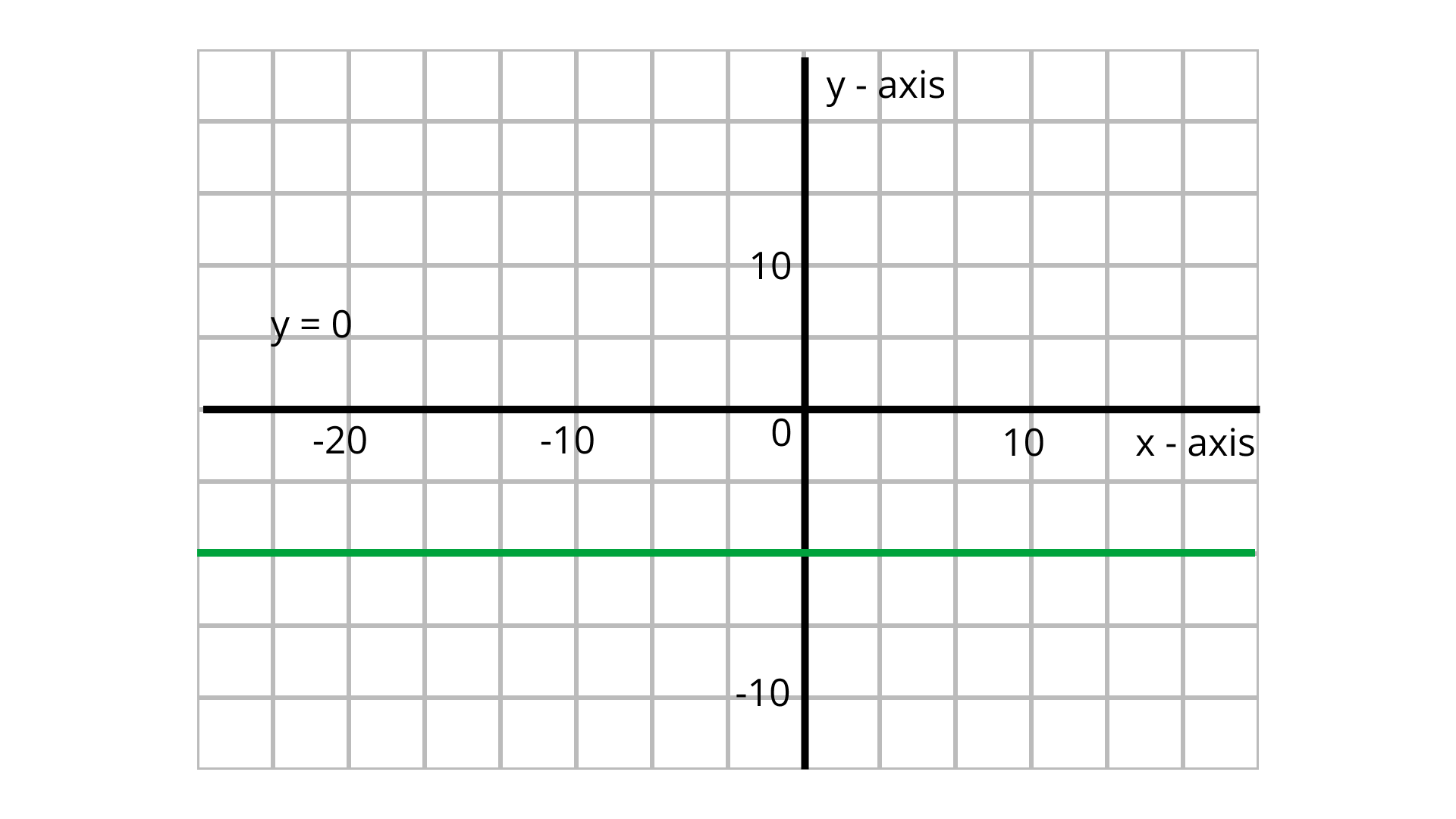
From the above graph $y = 0$ and $y = - 7$ are parallel, so the pair of equations $y = 0$ and $y = - 7$ have no solutions.
5. The pair of equations $x = a$ and $y = b$ graphically represents lines which are
(A) parallel
(B) intersecting at $(b,a)$
(C) coincident
(D) intersecting at $(a,b)$
Ans: D
Given pair of equations $x = a$ and $y = b$
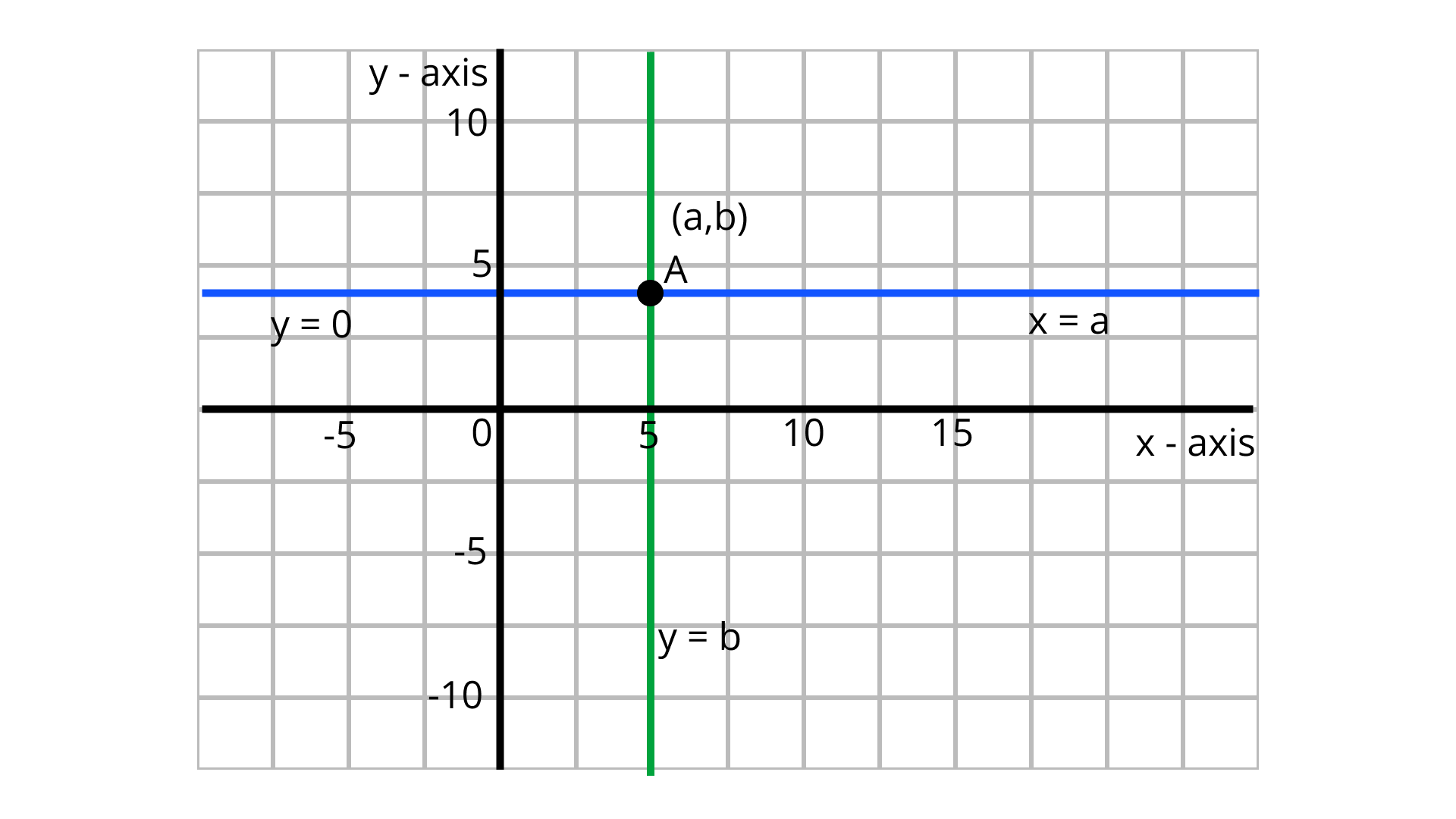
From the graph, the lines are $x = a$ and $y = b$ intersecting lines and they intersect at the point $(a,\;b)$
6. For what value of $k$, do the equations $3x - y + 8 = 0$ and $6x - ky = - 16$ represent coincident lines?
(A) $\frac{1}{2}$
(B) $- \frac{1}{2}$
(C) $2$
(D) $--2$
Ans: C
Given equations $3x - y + 8 = 0$ and $6x - ky = - 16$
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = 3,\;{b_1} = - \;1,\;{c_1} = 8$ and ${a_2} = 6,\;{b_2} = - k,\;{c_2} = 16$
since, lines are coincident
therefore, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$
$\frac{3}{6} = \frac{{ - \;1}}{{ - \;k}} = \frac{8}{{16}}$
$\frac{1}{k} = \frac{1}{2}$
$k = 2$
7. If the lines given by $3x + 2ky = 2$ and $2x + 5y + 1 = 0$ are parallel, then the value of $k$ is
(A) $\frac{{ - \;5}}{4}$
(B) $\frac{2}{5}$
(C) $\frac{{15}}{4}$
(D) $\frac{3}{2}$
Ans: C
Given lines $3x + 2ky - 2 = 0$ and $2x + 5y - 1 = 0$are parallel.
On comparing the linear equations with ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$, we get:
${a_1} = 3,{b_1} = 2k,{c_1} = - 2$ and ${a_2} = 2,{b_2} = 5,{c_2} = - 1$
Since, the lines are parallel.
$\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
$\frac{3}{2} = \frac{{2k}}{5}$
$k = \frac{{15}}{4}$
8. The value of $c$ for which the pair of equations $cx - y = 2$ and $6x - 2y = 3$ will have infinitely many solutions is
(A) \[3\]
(B) $ - \;3$
(C) $ - \;12$
(D) no value
Ans: D
Given a pair of equations $cx - y = 2$ and $6x - 2y = 3$ will have infinitely many solutions.
On comparing the linear equations with ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$, we get:
${a_1} = c,{b_1} = - 1,{c_1} = - 2$ and ${a_2} = 6,{b_2} = - 2,{c_2} = - 3$.
since,
\[\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\]
Then,
$\frac{c}{6} = \frac{{ - 1}}{{ - 2}} = \frac{{ - 2}}{{ - 3}}$
$\frac{c}{6} = \frac{1}{2}$ and $\frac{c}{6} = \frac{2}{3}$
$c = 3$ and $c = 4$
Here, the value of $c$has no value because $c$value has different values.
9. One equation of a pair of dependent linear equations is $ - \;5x + 7y = 2$. The second equation can be
(A) $10x + 14y + 4 = 0$
(B) $ - 10x - 14y + 4 = 0$
(C) $ - 10x + 14y + 4 = 0$
(D) \[10x - 14y = - \;4\]
Ans: D
Given pair of dependent linear equation is $ - \;5x + 7y - 2$
From the equation $ - \;5x + 7y - 2$
${a_1} = - \;5,{b_1} = 7,{c_1} = - \;2$
Then, from the dependent linear condition $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}} = \frac{1}{k}$
$ - \frac{5}{{{a_2}}} = \frac{7}{{{b_2}}} = - \frac{2}{{{c_2}}} = \frac{1}{k}$
\[\Rightarrow a_{2} = -5k, b_{2} = 7k, c_{2} = -2k\]
where, $k$ is an arbitrary constant.
Substituting$k = 2$, then
${a_2} = - 10,{b_2} = 14$and ${c_2} = - \;4$
The required second line becomes ${a_2}x + {b_2}y + {c_2} = 0$
\[\Rightarrow { - 10x + 14y - 4 = 0}\]
\[\Rightarrow {10x - 14y + 4 = 0}\]
10. A pair of linear equations which has a unique solution $x = 2,y = - 3$ is
(A) $x + y = - 1$
$2x - 3y = - 5$
(B) $2x + 5y = - 11$
$4x + 10y = - 22$
(C) $2x - y = 1$
$3x + 2y = 0$
(D) $x - 4y - 14 = 0$
$5x - y - 13 = 0$
Ans: (B, D)
The pair of linear equations which have a unique solution $x = 2,y = - \;3$ .
If $x = 2$ and $y = - \;3$ substitute in all equations it must satisfy the \[\;{\text{L}}{\text{.H}}{\text{.S}}{\text{ = }}{\text{R}}{\text{.H}}{\text{.S}}\]
Substitute $x = 2,y = - \;3$ in option (A)
$x + y = - 1;2x - 3y = - \;5$
$2 - 3 = - 1;2(2) - 3( - \;3) = - \;5$
$- \;1 = - \;1;13 = - \;5$
${\text{True}}{\text{;}}{\text{False}}$
Substitute $x = 2,y = - \;3$ in option (B)
$2x + 5y = - \;11;\quad 4x + 10y = - \;22$
$2(2) + 5( - \;3) = - \;11;\quad 4(2) + 10( - \;3) = - \;22$
$4 - 15 = - 11;\quad 8 - 30 = - 22$
$ - 11 = - 11$ True ;$\quad - 22 = - 22$ True
Substitute $x = 2,y = - 3$ in option (C)
$2x - y = 1\quad ;\quad 3x + 2y = 0$
$2(2) - ( - 3) = 1;\quad 3(2) + 3( - 3) = 0$
$4 + 3 = 1\quad ;\quad 6 - 6 = 0$
$7 = 1\left( {{\text{False}}} \right){\text{ }};\;0 = 0\left( {{\text{True}}} \right)$
Substitute $x = 2,y = - 3$ in option (D)
$x - 4y - 14 = 0\quad ;\quad 5x - y - 13 = 0$
$2 - 4( - 3) - 14 = 0\quad ;\quad 5(2) - ( - 3) - 13 = 0$
$2 + 12 - 14 = 0\quad ;10 + 3 - 13 = 0$
$0 = 0{\text{ (True) }}\quad {\text{ }};\quad 13 - 13 = 0$
$0 = 0{\text{ (True)}};0 = 0{\text{ (True) }}\quad {\text{ }}$
By substituting the values in $x = 2,y = - 3$ in options(A),(B),(C) and (D) , two options (B),(D) satisfy the \[\;{\text{L}}{\text{.H}}{\text{.S}}{\text{ = }}{\text{R}}{\text{.H}}{\text{.S}}\].
11. If $x = a,y = b$ is the solution of the equations $x - y = 2$ and $x + y = 4$, then the values of $a$ and $b$ are, respectively
(A) $3$ and $5$
(B) $5$ and $3$
(C) $3$ and $1$
(D) $ - 1$ and $ - 3$
Ans: C
Given $x = a$ and $y = b$
Substitute the values of $x = a,y = b$ in given equations $x - y = 2$ and $x + y = 4$, then
$ \Rightarrow a - b = 2 \ldots \ldots \ldots ..(1)$
$ \Rightarrow a + b = 4 \ldots \ldots \ldots \ldots (2)$
Add equations (1) and (2)
$a + b = 4$
$\underline {a - b = 2}$
$2a = 6$
$\Rightarrow a = \frac{6}{2}$
$\Rightarrow a = 3$
Substitute the value of $a$ in equation (1)
$\Rightarrow 3 - b = 2$
$\Rightarrow - b = 2 - 3$
$\Rightarrow b = 1$
Therefore, the value of $a = 3$ and $b = 1$
12. Aruna has only Rs $1$ and Rs $2$ coins with her. If the total number of coins that she has is $50$ and the amount of money with her is $Rs75$, then the number of $Re1$ and Rs $2$ coins are, respectively
(A)$35$ and $15$
(B) $35$ and $20$
(C) $15$ and $35$
(D) $25$and $25$
Ans: D
Consider,
$x$: Aruna has only Rs $1$ coins with her.
$y$: Aruna has only Rs $1$ coins with her.
From the question,
The total number of coins that she has is $50$
Total number of coins \[ = x + y = 50\] …………. (i)
Also, Amount of money with her
=(Number of Rs$1 \times {\text{coin}}1$)$ + $ ( Number of $\operatorname{Rs} 2 \times \operatorname{coin} 2$)
$ = x + 2y = 75$
Subtract Eq. (i) from Eq. (ii), then
$(x + 2y) - (x + y) = (75 - 50)$
So, $y = 25$
Substituting $y = 25$ in eq(i)
$\Rightarrow x + 25 = 50$
$\Rightarrow x = 50 - 25$
$\Rightarrow x = 25$
Therefore, Aruna has $25$ Re $1$ coins and $25$ Rs $2$ coins.
13. The father's age is six times his son's age. Four years hence, the age of the father will be four times his son's age. The present ages, in years, of the son and the father are, respectively
(A) $4$ and $24$
(B) $5$ and $30$
(C) $6$ and $36$
(D) $3$ and $24$
Ans: C
Consider the present age of father be ' $x$ ' year and the present age of son be '$y$' year .
From the given question, Four years hence, the age of the father will be four times his son's age then
$(x + 4) = 4(y + 4)$
$x + 4 = 4y + 16$
$x - 4y - 12 = 0$ ……..(i)
And the father's age is six times his son's age,
$x = 6y$ ………(ii)
Substituting the value of Eq. (ii) in Eq. (i) then
$6y - 4y - 12 = 0$
$2y = 12$
Therefore, $y = 6$
Substituting$y = 6$ in eq (ii),
$x = 6\left( 6 \right)$
$x = 36$
Therefore, the present age of the father is \[36\] years and the age of the son is $6$ years.
Sample Question
Short Answer Questions with Reasoning
1. Is it true to say that the pair of equations$ - x + 2y + 2 = 0 and \frac{1}{2}x - \frac{1}{4}y - 1 = 0$has a unique solution? Justify your answer.
Ans: The given equations are in the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = - 1,{b_1} = 2,{c_1} = 2$ and ${a_2} = \frac{1}{2},{b_2} = - \frac{1}{4},{c_2} = - 1$
Consider,
$\Rightarrow \frac{a_{1}}{a_{2}}=\frac{-1}{\frac{1}{2}}=-2$
$\Rightarrow \frac{b_{1}}{b_{2}}=\frac{2}{-\frac{1}{4}}=-8$
Since,$\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$
Therefore, the pair of equations $ - x + 2y + 2 = 0{\text{ and }}\frac{1}{2}x - \frac{1}{4}y - 1 = 0$has a unique solution.
Hence, the given statement “Is it true to say that the pair of equations$ - x + 2y + 2 = 0{\text{ and }}\frac{1}{2}x - \frac{1}{4}y - 1 = 0$has a unique solution?” is true.
2. Do the equations $4x + 3y - 1 = 5$ and $12x + 9y = 15$ represent a pair of coincident lines? Justify your answer.
Ans: The equations $4x + 3y - 1 = 5$ and $12x + 9y = 15$ represent a pair of coincident lines.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = 4,{b_1} = 3,{c_1} = - 6$ and ${a_2} = 12,{b_2} = 9,{c_2} = - 15$
So that
$\frac{{{a_1}}}{{{a_2}}} = \frac{4}{{12}} = \frac{1}{3}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{3}{9} = \frac{1}{3}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 6}}{{ - 15}} = \frac{2}{5}$
Here, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$,
Thus, The given equations $4x + 3y - 1 = 5$ and $12x + 9y = 15$does not represent a pair of coincident lines.
Hence, the given statement “The statement is “the equations $4x + 3y - 1 = 5$ and $12x + 9y = 15$ represent a pair of coincident lines?” is true.
3. Is the pair of equations $x + 2y - 3 = 0$ and $6y + 3x - 9 = 0$consistent? Justify your answer.
Ans: Equations $x + 2y - 3 = 0$ and $3x + 6y - 9 = 0$are consistent.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = 1,{b_1} = 2,{c_1} = - 3$ and ${a_2} = 3,{b_2} = 6,{c_2} = - 9$
Then,
$\frac{{{a_1}}}{{{a_2}}} = \frac{1}{3},$
$\frac{{{b_1}}}{{{b_2}}} = \frac{2}{6} = \frac{1}{3},$
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 3}}{{ - 9}} = \frac{1}{3}$
Therefore, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$then, the pair of equations is consistent.
EXERCISE 3.2
1. Do the following pair of linear equations have no solution? Justify your answer.
(i) $2x + 4y = 3$
$12y + 6x = 6$
(ii) $x = 2y$
$y = 2x$
(iii) $3x + y - 3 = 0$
$2x + \frac{2}{3}y = 2$
Ans:
(i) Given Linear equations $2x + 4y = 3$and $12y + 6x = 6$
The above equations are of the form ${a_1}x + {b_1}y = {c_1}$and ${a_2}x + {b_2}y = {c_2}$
So, ${a_1} = 2,{b_1} = 4,{c_1} = - 3$ and ${a_2} = 12,{b_2} = 6,{c_2} = - 6$
$\frac{{{a_1}}}{{{a_2}}}\; = {\text{ }}\frac{2}{6} = {\text{ }}\frac{1}{3}$
$\frac{{{b_1}}}{{{b_2}}}\; = {\text{ }}\frac{4}{6} = {\text{ }}\frac{1}{3}$
And
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 3}}{{ - 6}} = \frac{1}{2}$
From the above $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$ i.e., parallel lines
Therefore, the given pair of linear equations $2x + 4y = 3$and $12y + 6x = 6$has no solutions.
(ii) Given, pair of Linear equations $x = 2y$and $y = 2x$.
Rewrite the equations as $x - 2y = 0$and $y - 2x = 0$.
The above equations are of the form ${a_1}x + {b_1}y = {c_1}$and ${a_2}x + {b_2}y = {c_2}$
So, ${a_1} = 1,{b_1} = - 2,{c_1} = 0$ and ${a_2} = - 2,{b_2} = 1,{c_2} = 0$
$\frac{{{a_1}}}{{{a_2}}} = - \frac{1}{2}$
And
${\text{ }}\frac{{{b_1}}}{{{b_2}}}\; = \frac{{ - 2}}{1} = - 2$
Here, $\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$
Therefore, the given pair of linear equations$x = 2y$ and $y = 2x$has not unique solutions.
(iii) Given, the pair of Linear equations $3x + y - 3 = 0$and $2x + \frac{2}{3}y = 2$
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y = {c_2}$
So, ${a_1} = 3,{b_1} = 1,{c_1} = - 3$ and ${a_2} = 2,{b_2} = \frac{2}{3},{c_2} = - 2$
$\frac{{{a_1}}}{{{a_2}}}\; = \frac{3}{2}{\text{ }}$
$\frac{{{b_1}}}{{{b_2}}}\; = \frac{1}{{\frac{2}{3}}} = \frac{3}{2} $
And
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 3}}{{ - 2}} = \frac{3}{2} $
From the above $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}} $i.e., coincident lines
Therefore, the given pair of linear equations $3x + y - 3 = 0$ and $2x + \frac{2}{3}y = 2$has many solutions.
2. Do the following equations represent a pair of coincident lines? Justify your answer.
(i)$3x + \frac{1}{7}y = 3$
$7x + 3y = 7$
(ii)$ - 2x - 3y = 1$
$6y + 4x = - 2$
(iii) $\frac{x}{2} + y + \frac{2}{5} = 0$
$4x + 8y + \frac{5}{{16}} = 0$
Ans:
(i)Given, the pair of linear equations are$3x + \frac{1}{7}y = 3$and $7x + 3y = 7$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So,${a_1} = 3,{b_1} = \frac{1}{7},{c_1} = - 3;$
And ${a_2} = 7,{b_2} = 3,{c_2} = - 7$
$\frac{{{a_1}}}{{{a_2}}} = \frac{3}{7}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{\frac{1}{7}}}{3}\; = \frac{1}{{21}}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 3}}{{ - 7}} = \frac{3}{7}$
From the above $\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$
Therefore, the given pair of linear equations has a unique solution.
A pair of equations $3x + \frac{1}{7}y = 3$and $7x + 3y = 7$does not represent a pair of coincident lines.
(ii) Given, the pair of linear equations are $ - 2x - 3y - 1 = 0$ and $4x + 6y + 2 = 0$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$.
So, ${a_1} = - 2,{b_1} = - 3,{c_1} = - 1$, and ${a_2} = 4,{b_2} = 6,{c_2} = 2$
Then,
$\frac{{{a_1}}}{{{a_2}}} = \frac{{ - 2}}{4} = \frac{{ - 1}}{2}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 3}}{6} = \frac{{ - 1}}{2}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 1}}{2}$
Hence,$\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}},$ i.e. system has infinitely many solutions.
Therefore, the given pair of linear equations $ - 2x - 3y - 1 = 0$ and $4x + 6y + 2 = 0$ represent a pair of coincident lines.
(iii) Given, the pair of linear equations are $\frac{x}{2} + y + \frac{2}{5} = 0$and $4x + 8y + \frac{5}{{16}} = 0$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = \frac{1}{2},{b_1} = 1,{c_1} = \frac{2}{5}$; and ${a_2} = 4,\;{b_2} = 8,{c_2} = \frac{5}{{16}}$;
Then
$\frac{{{a_1}}}{{{a_2}}} = \frac{1}{8}$
$\frac{{{b_1}}}{{{{\text{b}}_2}}} = \frac{1}{8}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{{32}}{{25}}$
Hence, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}},$ i.e. system has no solution.
Therefore, the given pair of linear equations $\frac{x}{2} + y + \frac{2}{5} = 0$and $4x + 8y + \frac{5}{{16}} = 0$ does not represent a pair of coincident lines
3. Are the following pair of linear equations consistent? Justify your answer.
(i)$ - 3x - 4y = 12$
$4y + 3x = 12$
(ii)$\frac{3}{5}x - y = \frac{1}{2}$
$\frac{1}{5}x - 3y = \frac{1}{6}$
(iii) $2ax + by = a$
(iv) $x + 3y = 11$
$2(2x + 6y) = 22$
Ans:
(i) Given, Pair of linear equations are $ - 3x - 4y - 12 = 0$ and $4y + 3x - 12 = 0$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$.
Then
${a_1} = - 3,{b_1} = - 4,{c_1} = - 12$, ${a_2} = 3,{b_2} = 4,{c_2} = - 12$
So,
$\frac{{{a_1}}}{{{a_2}}} = \frac{{ - 3}}{3} = - 1$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 4}}{4} = - 1$
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 12}}{{ - 12}} = 1$
Hence, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}},$ system has no solution.
Therefore, the pair of linear equations $ - 3x - 4y - 12 = 0$ and $4y + 3x - 12 = 0$ is not consistent.
(ii) Given, the pair of linear equations are $\frac{3}{5}x - y = \frac{1}{2}$ and$\frac{1}{5}x - 3y = \frac{1}{6}$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and${a_2}x + {b_2}y + {c_2} = 0$.
So, ${a_1} = \frac{3}{5},{b_1} = - 1,{c_1} = \frac{{ - 1}}{2}$ and ${a_2} = \frac{1}{5},{b_2} = - 3,{c_2} = \frac{{ - 1}}{6}$
Then,
$\frac{{{a_1}}}{{{a_2}}} = 3$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 1}}{{ - 3}} = \frac{1}{3}$
And $\frac{{{c_1}}}{{{c_2}}} = 3$
Hence, $\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$, system has unique solution.
Therefore, the pair of linear equations are $\frac{3}{5}x - y = \frac{1}{2}$ and$\frac{1}{5}x - 3y = \frac{1}{6}$is consistent.
(iii) Given , Pair of linear equations are $2ax + by - a = 0$ and $4ax + 2by - 2a = 0$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = 2a,{b_1} = b,{c_1} = - a;$
${a_2} = 4a,{b_2} = 2b,{c_2} = - 2a;$
Then,
$\frac{{{a_1}}}{{{a_2}}} = \frac{{2a}}{{4a}} = \frac{1}{2}$
\[\frac{{{b_1}}}{{{b_2}}} = \frac{b}{{2b}} = \frac{1}{2}\]
$\frac{{{c_1}}}{{{c_2}}} = \frac{{ - a}}{{ - 2a}} = \frac{1}{2}$
Hence, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$, system has infinitely many solution.
Therefore, the pairs of linear equations $2ax + by - a = 0$ and $4ax + 2by - 2a = 0$ are consistent.
(iv) Given , pairs of linear equations are $x + 3y = 11$ and $2x + 6y = 11$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y + {c_2} = 0$
So, ${a_1} = 1,{b_1} = 3,{c_1} = 11$and ${a_2} = 2,{b_2} = 6,{c_2} = 11$
Then,
$\frac{{{a_1}}}{{{a_2}}} = \frac{1}{2}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{1}{2}$
$\frac{{{c_1}}}{{{c_2}}} = 1$ $$
Hence, $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$, system has no solution.
Therefore, Pair of linear equations $x + 3y = 11$ and $2x + 6y = 11$ is not consistent.
4. For the pair of equations
$\lambda x + 3y = - 7$
$2x + 6y = 14$to have infinitely many solutions, the value of $\lambda $ should be 1 . Is the statement true? Give reasons.
Ans: Pair of linear equations are $\lambda x + 3y + 7 = 0$ and $2x + 6y - 14 = 0$.
The above equations are of the form ${a_1}x + {b_1}y + {c_1} = 0$and ${a_2}x + {b_2}y = {c_2}$.
So, ${a_1} = \lambda ,{b_1} = 3,{c_1} = 7;{a_2} = 2,{b_2} = 6,{c_2} = - 14$.
If $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$, then system has infinitely many solutions.
$ \Rightarrow $$\frac{\lambda }{2} = \frac{3}{6} = - \frac{7}{{14}}$
Since,
$\frac{\lambda }{2} = \frac{3}{6}$
$\Rightarrow \lambda = 1$
And
$\frac{\lambda }{2} = - \frac{7}{{14}}$
$\Rightarrow \lambda = - 1$
Therefore, $\lambda $ have different values.
So, the value of $\lambda $ should not be $1$ .
Therefore, the given statement “For the pair of equations
$\lambda x + 3y = - 7$
$2x + 6y = 14$to have infinitely many solutions, the value of $\lambda $ should be 1” is not true.
5. For all real values of$c$, the pair of equations $x - 2y = 8$and $5x - 10y = c$have a unique solution. Justify whether it is true or false.
Ans: The statement for all real values of $c$, the pair of equations $x - 2y = 8$and $5x - 10y = c$have a unique solution is true .
Given the pair of equations $x - 2y = 8$and $5x - 10y = c$
The above equations are of the form ${a_1}x + {b_1}y = {c_1} = 0$and ${a_2}x + {b_2}y = {c_2}$
So, ${a_1} = 1,{b_1} = - 2,{c_1} = 8$ and ${a_2} = 5,{b_2} = - 10,{c_2} = c$
$\frac{{{a_1}}}{{{a_2}}} = \frac{1}{5}\quad$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 2}}{{10}}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 1}}{5}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{8}{c}$
From the above $\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$, system has unique solution.
The statement that for all real values of$c$, the pair of equations $x - 2y = 8$and $5x - 10y = c$ have a unique solution is true .
6. The line represented by $x = 7$ is parallel to the $x$ -axis. Justify whether the statement is true or not.
Ans: The line represented by $x = 7$ is parallel to the $x$ -axis.
In the given statement the line represented by $x = 7$ is parallel to the $x$ -axis is not true.
SAMPLE QUESTIONS
1. For which values of $p$ and $q$, will the following pair of linear equations have infinitely many solutions?
$4x + 5y = 2$
$\left( {2p + 7q} \right)x + \left( {p + 8q} \right)y = 2q - p + 1$
Ans:
Given: A pair of linear equation
$4x + 5y = 2$
$\left( {2p + 7q} \right)x + \left( {p + 8q} \right)y = 2q - p + 1$
If $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$ , the system has finitely many solutions.
From the given Equations we can derive the below as,
$\frac{{{a_1}}}{{{a_2}}} = \frac{4}{{2p + 7q}}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{5}{{p + 8q}}$
$\frac{{{c_1}}}{{{c_2}}} = \frac{2}{{2q - p + 1}}$
If $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$ , system has finitely many solutions.
Therefore,
$\frac{4}{{2p + 7q}} = \frac{5}{{p + 8q}} = \frac{2}{{2q - p + 1}}$
So we can write that,
$\frac{4}{{2p + 7q}} = \frac{5}{{p + 8q}}$ and $\frac{4}{{2p + 7q}} = \frac{2}{{2q - p + 1}}$
$4p{\text{ }} + {\text{ }}32q{\text{ }} = {\text{ }}10p{\text{ }} + {\text{ }}35q{\text{ and }}8q{\text{ }}--{\text{ }}4p{\text{ }} + {\text{ }}4{\text{ }} = {\text{ }}4p{\text{ }} + {\text{ }}14q$
$6p{\text{ }} + {\text{ }}3q{\text{ }} = {\text{ }}0{\text{ and }}8p{\text{ }} + {\text{ }}6q{\text{ }} = 4$
$q{\text{ }} = {\text{ }}--2p{\text{ }}.....{\text{eq}}\left( {\text{1}} \right){\text{ and }}$
$4p{\text{ }} + {\text{ }}3q{\text{ }} = {\text{ }}2{\text{ }}.....{\text{eq}}\left( {\text{2}} \right)$
By substituting the value of q in eq (2) we get:
$4p{\text{ }}--{\text{ }}6p{\text{ }} = {\text{ }}2$ or $p{\text{ }} = {\text{ }}--1$
${\text{Substituting the value of p in eq}}\left( 1 \right),{\text{ we get}}$
$q{\text{ }} = {\text{ }}2$
Hence, For$p = - 1$ and $q = 2$ the pair of linear equations have infinitely many solutions.
2. Solve the following pair of linear equations:
$21x + 47y = 110.....\left( 1 \right)$
$47x + 21y = 162.....\left( 2 \right)$
Ans: A pair of linear equations
$21x{\text{ }} + {\text{ }}47y{\text{ }} = {\text{ }}110.....\left( 1 \right)$
$47x{\text{ }} + {\text{ }}21y{\text{ }} = {\text{ }}162.....\left( 2 \right)$
Multiplying Equation (1) by 21 and Equation (2) by 47 then,
$441x + 987y = 2310{\text{ }}.....{\text{ (3)}}$
$2209x + 987y = 7849{\text{ }}.....{\text{ (4)}}$
Subtracting Equation (3) from Equation (4), we get
$1768x = 5548$
Therefore, $x = 3$
Substituting value of $x$in Equation (1) we get,
$63 + 47y = 110$
$47y = 110 - 63$
$47y = 47$
$y = 1$
3. Draw the graphs of the pair of linear equations $x - y + 2 = 0$ and $4x - y - 4 = 0$. Calculate the area of the triangle formed by the lines so drawn and the $x - $ axis.
Ans:
(1) Considering the equation$x - y + 2 = 0$.
The line will cut the $x$ axis at$y = 0$, so at $y = 0$ the value of$x = - 2$. The coordinate is $\left( { - 2,0} \right)$.
It will cut the $y$ axis at$x = 0$, so at $x = 0$ the value of $y = 2$. The coordinate is $\left( {0,2} \right)$.
(2) Considering the equation$4x - y - 4 = 0$.
The line will cut the $x$ axis at$y = 0$, so at $y = 0$ the value of$x = 1$. The coordinate is $\left( {1,0} \right)$.
It will cut the $y$ axis at$x = 0$, so at $x = 0$ the value of $y = - 4$. The coordinate is $\left( {0, - 4} \right)$.
Therefore, the graph of the two lines is shown below by taking $1{\text{ cm}} = 1{\text{ unit}}$ on the $x$ axis and $1{\text{ cm}} = 1{\text{ unit}}$ on the $y$ axis: -

The two lines intersect at the point $\left( {2,4} \right)$, which can be obtained algebraically by solving the two equations. The shaded region is the area subtended by the two lines and the $x - $ axis.
The distance of the point $\left( {1,0} \right)$ from the point $\left( { - 2,0} \right)$ is $3$ units, which is the base of the triangle.
Now, the distance of the point $\left( {2,4} \right)$ from the $x$ axis is $4$ units, which is the height of the triangle.
Hence, the area of the triangle
$= \frac{1}{2} \times 3 \times 4{\text{ square units}}$
$ = 6{\text{ square units}}$
EXERCISE 3.3
1. For which value(s) of λ, do the pair of linear equations
$\lambda x + y = {\lambda ^2} and x + \lambda y = 1 have$
(i) No Solution?
(ii) Infinitely many solutions?
(iii) a unique solution
Ans: The given equations are as follows:
$\lambda x{\text{ }} + {\text{ }}y - {\lambda ^2} = 0$
$x{\text{ }} + {\text{ }}\lambda y - 1 = 0$
Comparing the above equations with \[ax + by + c = 0\] we get:
${a_1}\; = \lambda ,{\text{ }}{b_1} = {\text{ }}1,{\text{ }}{c_1}\; = {\text{ }}--{\text{ }}{\lambda ^2}{\text{ }}$
${a_2}\; = 1,{\text{ }}{b_2} = \lambda ,{\text{ }}{c_2} = - 1$
(i) For no solution
$\frac{{{a_1}\;}}{{{a_2}\;}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
$\lambda \; = \frac{1}{\lambda }{\text{ }} \ne {\text{ }}{\lambda ^2}$
${\text{ so}},\;\lambda {\;^2}\; = {\text{ }}1;$
${\text{ and}}\;\lambda {\;^2}\; \ne \;\lambda {\text{ }}$
${\text{Here, we take only}}\;\lambda \; = --{\text{ }}1,{\text{ }}$
${\text{Hence, the system of linear equations has no solution at}}\;\lambda \; = - {\text{ }}1.$
(ii) For infinitely many solutions
$\frac{{{a_1}\;}}{{{a_2}\;}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$
$\lambda \; = \frac{1}{\lambda }{\text{ = }}{\lambda ^2}$
${\text{so}},\;\lambda \; = \frac{1}{\lambda }{\text{ gives }}\lambda = \pm 1;$
${\text{and}}\;\lambda \;\; = \;{\lambda ^2}{\text{ gives }}\lambda = 1,0$
Hence, the system of linear equations has infinitely many solutions at \[\lambda = 1\].
(iii) For a unique solution
$\frac{{{a_1}\;}}{{{a_2}\;}} \ne \frac{{{b_1}}}{{{b_2}}}$
${\text{so}}\;\lambda \; \ne \frac{1}{\lambda }$
${\text{hence}},\;{\lambda ^2}\; \ne \;1;{\text{ }}$
$\lambda {\text{ }} \ne \; \pm \;1;{\text{ }}$
${\text{Hence, the system of linear equation has infinitely many solution at all real values of }}\lambda \;{\text{except }} \pm 1.$
2. For which value(s) of \[k\]will the pair of equations
$kx + 3y = k - 3$
$12x + ky = k$
Have no solution?
Ans: Comparing the above equations with \[ax + by + c = 0\] we get:
${a_1}\; = k,{\text{ }}{b_1} = {\text{ 3}},{\text{ }}{c_1}\; = {\text{ }}--(k - 3){\text{ }}$
${a_2}\; = 12,{\text{ }}{b_2} = k,{\text{ }}{c_2} = - k$
${\text{For no solution of the pair of linear equations, }}$
$\frac{{{a_1}\;}}{{{a_2}\;}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}\;}}{{{c_2}\;}}{\text{ }}$
$\frac{k}{{12}}\; = \frac{3}{k}{\text{ }} \ne \frac{{\left( {k - 3} \right)}}{k}{\text{ }}$
${\text{Taking first two parts, we get }}$
$\frac{k}{{12}} = \frac{3}{k}{\text{ }}$
${\text{Then}},{\text{ }}{a_1}\;/{a_2}\; = \;k/12{\text{ }}$
${b_1}\;/{b_2}\; = {\text{ }}3/k{\text{ }}$
${c_1}\;/{c_2}\; = {\text{ }}\left( {k - 3} \right)/k{\text{ }}$
${\text{For no solution of the pair of linear equations, }}$
${a_1}/{a_2}\; = {\text{ }}{b_1}/{b_2} \ne \;{c_1}/{c_2}{\text{ }}$
$k/12\; = {\text{ }}3/k{\text{ }} \ne {\text{ }}\left( {k - 3} \right)/k{\text{ }}$
${\text{Taking first two parts, we get }}$
$k/12{\text{ }} = {\text{ }}3/k{\text{ }}$
${k^2}\; = {\text{ }}36{\text{ }}$
$k{\text{ }} = {\text{ }} + \;6{\text{ }}$
${\text{Taking last two parts, we get }}$
$3/k{\text{ }} \ne {\text{ }}\left( {k - 3} \right)/k{\text{ }}$
$3k\; \ne \;k\left( {k{\text{ }}--{\text{ }}3} \right){\text{ }}$
${k^2}\;--{\text{ }}6k\; \ne {\text{ }}0{\text{ }}$
${\text{so}},{\text{ }}k\; \ne \;0,6{\text{ }}$
$k = - 6$
${k^2}\; = {\text{ }}36{\text{ }}$
$k{\text{ }} = {\text{ }} \pm \;6{\text{ }}$
${\text{Taking last two parts, we get }}$
$\frac{3}{k}{\text{ }} \ne \frac{{\left( {k - 3} \right)}}{k}$
$3k\; \ne \;k\left( {k{\text{ }}--{\text{ }}3} \right){\text{ }}$
${k^2}\;--{\text{ }}6k\; \ne {\text{ }}0{\text{ }}$
${\text{so}},{\text{ }}k\; \ne \;0,6{\text{ }}$
Hence for $k = - 6$ the given pair of linear equations has no solution.
3. For which values of a and b will the following pair of linear equations have infinitely many solutions?$x + 2y = 1$
$(a - b)x + (a + b)y = a + b - 2$
Ans: Given pair of linear equations are
$x + 2y = 1$
$(a - b)x + (a + b)y = a + b - 2$
Rewrite the above equation, we get:
$ \Rightarrow x + 2y - 1 = 0$ .....(i)
$\Rightarrow (a - b)x + (a + b)y - (a + b - 2) = 0 \ldots (ii)$
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${a_1} = 1,\;{b_1} = 2$ and ${c_1} = - 1$ [from (i) ]
${a_2} = (a - b),{b_2} = (a + b)$ and ${c_2} = - (a + b - 2)$ [from (ii) ]
The system has infinitely many solutions if \[\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = $\frac{{{c_1}}}{{{c_2}}}\]$
$\Rightarrow \frac{1}{{a - b}} = \frac{2}{{a + b}} = \frac{{ - 1}}{{ - (a + b - 2)}}$
Choose the first two parts, we get:
$\frac{1}{{a - b}} = \frac{2}{{a + b}}$
$\Rightarrow a + b = 2a - 2b$
$\Rightarrow 2a - a = 2b + b$
$\Rightarrow a = 3b$….(iii)
Taking last two parts,
$\frac{2}{{a + b}} = \frac{1}{{(a + b - 2)}}$
$\Rightarrow {\text{ }}2a + 2b - 4 = a + b$
$\Rightarrow a + b = 4\quad \ldots $ (iv)
Now, solve the equation (iii) and (iv), we get
$\Rightarrow $$3b + b = 4$
$\Rightarrow 4\;{\text{b}} = 4$
$\Rightarrow {\text{b}} = 1$
Put the value of $b$ in eq. (iii), we get
$a = 3 \times 1$
$\Rightarrow a = 3$
So, the value $(a,b) = (3,1)$ satisfies all the parts.
Hence, required values of ${\text{a}}$ and ${\text{b}}$ are 3 and 1 respectively for which the given pair of linear equations has infinitely many solutions.
4. Find the value(s) of p in (i) to (iv) and p and q in (v) for the following pair of equations:
(i) $3x - y - 5 = 0$and $6x - 2y - p = 0$, if the lines represented by these equations are parallel.
(ii) $ - x + py = 1 and px -- y = 1$ , if the pair of equations has no solution.
(iii)\[ - 3x + 5y = 7 and 2px -- 3y = 1\] , if the lines represented by these equations are intersecting at a unique point.
(iv) \[2x + 3y -- 5 = 0 and px -- 6y -- 8 = 0\] , if the pair of equations has a unique solution.
(v)\[2x + 3y = 7 and 2px + py = 28 -- qy\] , if the pair of equations have infinitely many solutions.
Ans: (i) Given pair of linear equations are
$3x - y - 5 = 0$.... (i)
and $6{\text{x}} - 2{\text{y}} - {\text{p}} = 0$.... (ii)
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${a_1} = 3,{b_1} = - 1$ and ${c_1} = - 5$ [from (i)]
${a_2} = 6,{b_2} = - 2,{c_2} = - p$ [from (ii) ]
Since, the lines represented by these equations are parallel, then
$\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
$\frac{3}{6} = \frac{{ - 1}}{{ - 2}} \ne \frac{{ - 5}}{{ - p}}$
Taking last two parts, we get
$\frac{{ - 1}}{{ - 2}} \ne \frac{{ - 5}}{{ - p}}$
$\Rightarrow \frac{1}{2} \ne \frac{5}{p}$
$\Rightarrow p \ne 10$.
Hence, the given pair of linear equations are parallel for all real values of $p$ except 10
(ii) Given pair of linear equation are
$ - x{\text{ }} + {\text{ }}py{\text{ }}--{\text{ }}1{\text{ }} = {\text{ }}0{\text{ }} \ldots \left( i \right)$
$ px{\text{ }}--{\text{ }}y{\text{ }}--{\text{ }}1{\text{ }} = {\text{ }}0{\text{ }} \ldots \left( {ii} \right) $
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${a_1} = - 1,\;{b_1} = p$ and ${c_1} = - 1$ [from (i) ]
${a_2} = p,{b_2} = - 1$ and ${c_2} = - 1$ [from (ii) ]
Since, the pair of linear equations has no solution.
i.e., both lines are parallel to each other
$\therefore \quad \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
$ \Rightarrow \frac{{ - 1}}{p} = \frac{p}{{ - 1}} \ne \frac{{ - 1}}{{ - 1}}$
Taking first two parts, we get
$\frac{{ - 1}}{p} = \frac{p}{{ - 1}}$
$\Rightarrow {p^2} = 1$
$\Rightarrow p = \pm 1$
Taking last two parts, we get
$\frac{p}{{ - 1}} \ne \frac{{ - 1}}{{ - 1}}$
$\Rightarrow p \ne - 1$
Hence, the given pair of linear equations has no solution for ${\text{p}} = 1$.
(iii) Given, pair of linear equations are
$ - 3x + 5y - 7 = 0$ ....(i)
$2px - 3y - 1 = 0$ ....(ii)
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${a_1} = - 3,{b_1} = 5$ and ${c_1} = - 7$ [from (i) ]
${{\text{a}}_2} = 2{\text{p}},{{\text{b}}_2} = - 3$ and ${{\text{c}}_2} = - 1$ [from (ii) ]
Since, the lines are intersecting at a unique point,
i.e. it has a unique solution.
$\therefore \frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$
$\Rightarrow \frac{{ - 3}}{{2p}} \ne \frac{5}{{ - 3}}$
$\Rightarrow 9 \ne 10p$
$\Rightarrow p \ne \frac{9}{{10}}$
Hence, the lines represented by these equations are intersecting at a unique point for all real values of p except $\frac{9}{{10}}$
(iv) Given pair of linear equations are
$2x + 3y - 5 = 0 \ldots $ (i)
$px - by - 8 = 0 \ldots $ (ii)
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${{\text{a}}_1} = 2,\;{{\text{b}}_1} = 3$ and ${{\text{c}}_1} = - 5$ from (i)]
${{\text{a}}_2} = {\text{p}},{{\text{b}}_2} = - 6$ and ${{\text{c}}_2} = - 8$ [from (ii)]
Since, the pair of linear equations has a unique solution,
$\therefore \frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$
$\Rightarrow \frac{2}{p} \ne \frac{3}{{ - 6}}$
$\Rightarrow p \ne - 4$
Hence, the pair of linear equations has a unique solution for all values of $p$ except $ - 4.$
(v) Given pair of linear equation are
$2{\text{x}} + 3{\text{y}} = 7$
$2{\text{px}} + {\text{py}} = 28 - q{\text{y}}$
Rewrite the equations, we get:
$\Rightarrow 2{\text{x}} + 3{\text{y}} - 7 = 0$ ....(i)
$\Rightarrow 2{\text{px}} + ({\text{p}} + {\text{q}}){\text{y}} - 28 = 0$ ...(ii)
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${{\text{a}}_1} = 2,\;{{\text{b}}_1} = 3$ and ${{\text{c}}_1} = - 7$ [from (i)]
${{\text{a}}_{\text{2}}}{\text{ = 2p,}}{{\text{b}}_{\text{2}}}{\text{ = (p + q)}}$ and ${c_2} = - 28$ [from (ii)]
Since, the pair of equations has infinitely many solutions
i.e., both lines are coincident.
$\therefore \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$
$\Rightarrow \frac{2}{{2p}} = \frac{3}{{(p + q)}} = \frac{{ - 7}}{{ - 28}}$
Taking first and third parts, we get
$\frac{2}{{2p}} = \frac{{ - 7}}{{ - 28}}$
$\Rightarrow \frac{1}{p} = \frac{1}{4}$
$\Rightarrow p = 4$
Again, taking last two parts, we get
$\frac{3}{{p + q}} = \frac{{ - 7}}{{ - 28}}$
$\Rightarrow \frac{3}{{p + q}} = \frac{1}{4}$
$\Rightarrow p + q = 12$
$\Rightarrow \quad 4 + q = 12\quad [\because p = 4]$
$\therefore \quad q = 8$
Hence, the pair of equations has infinitely many solutions for the values of $p = 4$ and $q = 8$.
5. Two straight paths are represented by the equations $x{\text{ }}--{\text{ }}3y{\text{ }} = {\text{ }}2{\text{ and }} - 2x{\text{ }} + {\text{ }}6y{\text{ }} = {\text{ }}5$ . Check whether the paths cross each other or not.
Ans:
Given linear equations are
$x - 3y - 2 = 0 \ldots $ (i)
and $ - 2{\text{x}} + 6{\text{y}} - 5 = 0 \ldots $ (ii)
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${a_1} = 1,{b_1} = - 3$ and ${c_1} = - 2$ [from (i) ]
${a_2} = - 2,\;{b_2} = 6$ and ${c_2} = - 5$ [from (ii) ]
Here, $\frac{{{a_1}}}{{{a_2}}} = \frac{1}{{ - 2}}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{{ - 3}}{6} = - \frac{1}{2}$
and $\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 2}}{{ - 5}} = \frac{2}{5}$
i.e., $\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$ system has no solution.
Thus, lines are parallel.
Hence, two straight paths represented by the given equations never cross each other, because they are parallel to each other.
6. Write a pair of linear equations which has the unique solution\[x = - 1,{\text{ }}y = 3\] . How many such pairs can you write?
Ans: Let the equations are ${a_1}x + {b_1}y + {c_1} = 0$ and ${a_2}x + {b_2}y + {c_2} = 0$
If${{\text{a}}_1}{{\text{a}}_2} \ne {{\text{b}}_1}\;{{\text{b}}_2}$, then pair of system have unique solution.
Given, $x = - 1$ and $y = 3$ is the unique solution of these two equations.
Then it must satisfy the given equation.
${a_1}( - 1) + {b_1}(3) + {c_1} = 0$
$\Rightarrow - {{\text{a}}_1} + 3\;{{\text{b}}_1} + {{\text{c}}_1} = 0 \ldots \ldots $ (i)
and ${{\text{a}}_2}( - 1) + {{\text{b}}_2}(3) + {{\text{c}}_2} = 0$
$\Rightarrow - {{\text{a}}_2} + 3\;{{\text{b}}_2} + {{\text{c}}_2} = 0 \ldots \ldots $ (ii)
So, many values of ${{\text{a}}_1},{{\text{a}}_2},\;{{\text{b}}_1},\;{{\text{b}}_2},{{\text{c}}_1}$ and ${{\text{c}}_2}$ satisfy the eq. (i) and eq. (ii).
Hence, infinitely many pairs of linear equations are possible.
7. If $2x + y = 23 and 4x -- y = 19$ , find the values of $5y -- 2x and\;\frac{y}{x}\;-- 2$ .
Ans: Given equation are
$2{\text{x}} + {\text{y}} = 23 \ldots $ (i)
and $4{\text{x}} - {\text{y}} = 19 \ldots $ (ii)
On adding both equations, we get
$6x = 42$
$\Rightarrow x = 7$
Put the value of ${\text{x}}$ in eq. (i), we get
$2(7) + y = 23$
$\Rightarrow 14 + y = 23$
$\Rightarrow {\text{y}} = 23 - 14$
$\Rightarrow {\text{y}} = 9$
We have, $5y - 2x = 5 \times 9 - 2 \times 7 = 45 - 14 = 31$
and $\frac{y}{x} - 2 = \frac{9}{7} - 2 = \frac{{9 - 14}}{7} = - \frac{5}{7}$
Hence, the values of $(5y - 2x)$ and $\left( {\frac{y}{x} - 2} \right)$ are 31 and $ - \frac{5}{7}$ respectively.
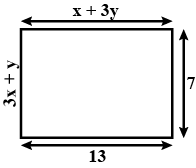
8. Find the values of x and y in the following rectangle (see figure).
Ans:

By property of rectangle,
Lengths are equal i.e., ${\text{CD}} = {\text{AB}}$
$\Rightarrow x + 3y = 13 \ldots $ (i)
Breadth are equal i.e., ${\text{AD}} = {\text{BC}}$
$\Rightarrow 3{\text{x}} + {\text{y}} = 7 \ldots $ (ii)
On multiplying eq. (ii) by 3 and then subtracting eq. (i), we get
$8x = 8$
$\Rightarrow {\text{x}} = 1$
On putting ${\text{x}} = 1$ in eq.(i), we get
$3y = 12$
$\Rightarrow y = 4$
Hence, the required values of $x$ and $y$ are 1 and 4 , respectively.
9. Solve the following pairs of equations:
(i) $x+y=3.3, \dfrac{0.6}{3 x-2 y}=-1, \quad 3 x-2 y^{\prime} 0$
(ii) $\dfrac{x}{3}+\frac{y}{4}=4, \dfrac{5 x}{6}-\dfrac{y}{8}=4$
(iii) $4 x+\dfrac{6}{y}=15,6 x-\dfrac{8}{y}=14, y^{1} 0$
(iv) $\dfrac{1}{2 x}-\frac{1}{y}=-1, \dfrac{1}{x}+\dfrac{1}{2 y}=8, x, y^{1} 0$
(v) $43 x+67 y=-24,67 x+43 y=24$
(vi) $\dfrac{x}{a}+\dfrac{y}{b}=a+b, \quad \dfrac{x}{a^{2}}+\dfrac{y}{b^{2}}=2, a, b^{1} 0$
(vii) $\dfrac{2 x y}{x+y}=\dfrac{3}{2}, \dfrac{x y}{2 x-y}=\dfrac{-3}{10}, x+y^{1} 0,2 x-y^{1} 0$
Ans: Given pair of linear equations are
${\text{x}} + {\text{y}} = 3.3 \ldots $ (i)
$\frac{{0.6}}{{3x - 2y}} = - 1$
$\Rightarrow 0.6 = - 3x + 2y$
$3x - 2y = - 0.6 \ldots $ (ii)
Now, multiplying eq. (i) by 2 and then adding with eq. (ii), we get
$5{\text{x}} = 6$
$\Rightarrow {\text{x}} = \frac{6}{5} = 1.2$
Now, put the value of $x$ in eq. (i), we get
$1.2 + y = 3.3$
$\Rightarrow {\text{y}} = 3.3 - 1.2$
$\Rightarrow {\text{y}} = 2.1$
Hence, the required values of ${\text{x}}$ and ${\text{y}}$ are 1.2 and 2.1 respectively.
(ii) Given, pair of linear equations are
$\Rightarrow \frac{x}{3} + \frac{y}{4} = 4$
$\Rightarrow 4x + 3y = 48$ ...(i)
and $\frac{{5x}}{6} - \frac{y}{8} = 4$
$\Rightarrow \quad 20x - 3y = 96$ ...(ii)
Now, adding eq. (i) and eq. (ii), we get
$24{\text{x}} = 144$
$\Rightarrow {\text{x}} = 6$
Now, put the value of ${\text{x}}$ in eq. (i), we get
$4 \times 6 + 3y = 48$
$\Rightarrow 3{\text{y}} = 48 - 24$
$\Rightarrow 3{\text{y}} = 24$
$\Rightarrow {\text{y}} = 8$
Hence, the required values of $x$ and $y$ are 6 and 8 , respectively.
(iii) Given pair of linear equations are
$4x + \frac{6}{y} = 15$....(i)
and $6x - \frac{8}{y} = 14$....(ii)
Let $u = \frac{1}{{{y^\prime }}}$, then above equations become
$4x + 6u = 15$ ...(iii)
and $6x - 8u = 14$...(iv)
On multiplying eq. (iii) by 8 and eq. (iv) by 6 and then adding both of them, we get
$68{\text{x}} = 204$
$\Rightarrow {\text{x}} = 3$
Now, put the value of $x$ in eq. (iii), we get
$4 \times 3 + 6u = 15$
$\Rightarrow 6u = 15 - 12$
$\Rightarrow 6{\text{u}} = 3$
$\Rightarrow u = \frac{1}{2}$
$\Rightarrow \frac{1}{y} = \frac{1}{2}$ $\left[ {\because u = \frac{1}{y}} \right]$
$\Rightarrow y = 2$
Hence, the required values of $x$ and $y$ are 3 and 2 , respectively.
(iv) Given pair of linear equations are
$\frac{1}{{2x}} - \frac{1}{y} = - 1$$ \ldots ({\text{i}})$
and $\frac{1}{x} + \frac{1}{{2y}} = 8$...(ii)
Put $u = \frac{1}{x}$ and $v = \frac{1}{y}$, then the above equations become
$\frac{u}{2} - v = - 1$
$\Rightarrow u - 2v = - 2$$ \ldots $ (iii)
and $u + \frac{v}{2} = 8$
$\Rightarrow 2u + v = 16$ $ \ldots ({\text{iv}})$
On multiplying eq. (iv) by 2 and then adding with eq. (iii), we get
$5{\text{u}} = 30$
$\Rightarrow {\text{u}} = 6$
Now, put the value of u in eq. (iv), we get
$2\times 6 + v = 16$
$\Rightarrow v = 16 - 12 = 4$
$\Rightarrow v = 4$
$\therefore {\text{x}} = \frac{1}{u} = \frac{1}{6}$ and ${\text{y}} = \frac{1}{v} = \frac{1}{4}$
Hence, the required values of ${\text{x}}$ and ${\text{y}}$ are $\frac{1}{6}$ and $\frac{1}{4}$ respectively.
(v) Given pair of linear equations are
$43x + 67y = - 24$...(i)
and $67x + 43y = 24$ ...(ii)
On multiplying eq. (i) by 43 and eq. (ii) by 67 and then subtracting eq (i) from eq (ii), we get
$\left\{ {{{(67)}^2} - {{(43)}^2}} \right\}x = 24(67 + 43)$
$\Rightarrow (67 + 43)(67 - 43)x = 24 \times 110\left[ {\because \left( {{a^2} - {b^2}} \right) = (a - b)(a + b)} \right]$
$\Rightarrow 110 \times 24x = 24 \times 110$
$\Rightarrow x = 1$
Now, put the value of $x$ in eq. (i), we get
$43 \times 1 + 67y = - 24$
$\Rightarrow 67y = - 24 - 43$
$\Rightarrow 67y = - 67$
$\Rightarrow y = - 1$
Hence, the required values of $x$ and $y$ are 1 and $ - 1$, respectively.
(vi) Given pair of linear equations are
$\frac{x}{a} + \frac{y}{b} = a + b \ldots (i)$
and $\frac{x}{{{a^2}}} + \frac{y}{{{b^2}}} = 2$...(ii)
On multiplying eq. (i) by $\frac{1}{a}$ and then subtracting from eq. (ii), we get
$y\left( {\frac{1}{{{b^2}}} - \frac{1}{{ab}}} \right) = 2 - 1 - \frac{b}{a}$
$\Rightarrow \quad y\left( {\frac{{a - b}}{{a{b^2}}}} \right) = 1 - \frac{b}{a} = \left( {\frac{{a - b}}{a}} \right)$
$\Rightarrow \quad y = \frac{{a{b^2}}}{a} \Rightarrow y = {b^2}$
Now, put the value of $y$ in eq. (ii), we get
$\frac{x}{{{a^2}}} + \frac{{{b^2}}}{{{b^2}}} = 2$
$\Rightarrow \frac{x}{{{a^2}}} = 2 - 1 = 1$
$\Rightarrow \quad x = {a^2}$
Hence, the required values of $x$ and z$y$ are ${a^2}$ and ${b^2}$, respectively.
(vii) Given pair of equations are
$\frac{{2xy}}{{x + y}} = \frac{3}{2}$
$\Rightarrow \quad \frac{{x + y}}{{2xy}} = \frac{2}{3}$
$\Rightarrow \frac{x}{{xy}} + \frac{y}{{xy}} = \frac{4}{3}$
$\Rightarrow \frac{1}{y} + \frac{1}{x} = \frac{4}{3}$
and $\frac{{xy}}{{2x - y}} = \frac{{ - 3}}{{10}}$,
$\Rightarrow \quad \frac{{2x - y}}{{xy}} = \frac{{ - 10}}{3}$
$\Rightarrow \frac{{2x}}{{xy}} - \frac{y}{{xy}} = \frac{{ - 10}}{3}$
$\Rightarrow \frac{2}{y} - \frac{1}{x} = \frac{{ - 10}}{3}$
Now, put $\frac{1}{x} = u$ and $\frac{1}{y} = v$,
then the above equations become
$v + u = \frac{4}{3}$....(iii)
and $2v - u = \frac{{ - 10}}{3}$...(iv)
On adding both equations, we get
$3v = \frac{4}{3} - \frac{{10}}{3} = \frac{{ - 6}}{3}$
$\Rightarrow 3v = - 2$
$\Rightarrow \quad v = \frac{{ - 2}}{3}$
Now, put the value of $v$ in eq. (iii). we get
$\frac{{ - 2}}{3} + u = \frac{4}{3}$
$\Rightarrow u = \frac{4}{3} + \frac{2}{3} = \frac{6}{3} = 2$
$\therefore \quad x = \frac{1}{u} = \frac{1}{2}$
and
$y = \frac{1}{v}$
$\Rightarrow \frac{1}{{\left( {\frac{{ - 2}}{3}} \right)}} = \frac{{ - 3}}{2}$
Hence, the required values of $x$ and $y$ are $\frac{1}{2}$ and \[\frac{{ - 3}}{2}\] respectively.
10. Find the solution of the pair of equations
$\frac{x}{{10}} + \frac{y}{5} - 1 = 0\;and\;\frac{x}{8} + \frac{y}{6} = 15$. Hence, $find \lambda , if y = \lambda x + 5$ .
Ans: Given pair of equations are $\frac{x}{{10}} + \frac{y}{5} - 1 = 0$
$\Rightarrow x + 2y - 10 = 0 \ldots (i)$
$\Rightarrow x + 2y = 10$
and $\frac{x}{8} + \frac{y}{6} = 15$
$\Rightarrow 3x + 4y = 360$...(ii)
On multiplying eq. (i) by 2 and then subtracting from eq. (ii), we get
$(3x + 4y) - (2x + 4y) = 360 - 20$
$\Rightarrow x = 340$
Put the value of $x$ in eq. (i), we get
$340 + 2y = 10$
$\Rightarrow 2y = 10 - 340 = - 330$
$\Rightarrow y = - 165$
Now, $y = \lambda x + 5$
Put the values of $x$ and $y$ in above relation, we get
$ - 165 = \lambda (340) + 5$
$\Rightarrow 340\lambda = - 170$
$\Rightarrow \lambda = - \frac{1}{2}$
Hence, the solution of the pair of equations are $x = 340,y = - 165$ and the required value of $\lambda $ is $ - \frac{1}{2}$.
11. By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them.
(i) $ 3x + y + 4 = 0,6x -- 2y + 4 = 0 $
(ii) $ x -- 2y = 6, 3x -- 6y = 0 $
(iii) $ x + y = 3, 3x + 3y = 9 $
Ans: (i) Given pair of equations are
$3x + y + 4 = 0$... (i)
$6x - 2y + 4 = 0 \ldots $ (ii)
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${{\text{a}}_1} = 3,\;{{\text{b}}_1} = 1$ and ${{\text{c}}_1} = 4$ [from, (i)]
${{\text{a}}_2} = 6,\;{{\text{b}}_2} = - 2$ and ${{\text{c}}_2} = 4$ [from (ii)]
Here, $\frac{{{a_1}}}{{{a_2}}} = \frac{3}{6} = \frac{1}{2}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{1}{{ - 2}}$
and, $\frac{{{c_1}}}{{{c_2}}} = \frac{4}{4} = \frac{1}{1}$
$\because \quad \frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$
So, the given pair of linear equations are intersecting at one point, therefore these lines have a unique solution.
Hence, given pairs of linear equations are consistent.
We have, $3x + y + 4 = 0$
$\Rightarrow y = - 4 - 3x$We have ,$3x + y + 4 = 0$
$\Rightarrow \;\;\;\;y = - \;{\text{4}}\; - 3x$
x | 0 | -1 | -2 |
Y | -4 | -1 | 2 |
And $6x + y + 4 = 0$
$\Rightarrow \;2y = 6x + 4\;\; \Rightarrow \;y = 3x + 2$
x | -1 | 0 | 1 |
Y | -1 | 2 | 5 |
Plot the points ${\text{B}}(0, - 4)$ and ${\text{A}}( - 2,2)$, and join it. We get the straight line${\text{AB}}$.
Plot the point ${\text{Q}}(0,2)$ and ${\text{P}}(1,5)$ and join it. We get the straight line ${\text{PQ}}$. The lines ${\text{AB}}$ and PQ intersect at ${\text{C}}( - 1, - 1)$.
(ii) Given pair of equation is
$x - 2y = 6 \ldots (i)$
and $3x - 6y = 0 \ldots (ii)$
On comparing with ${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${{\text{a}}_1} = 1,\;{{\text{b}}_1} = - 2$ and ${{\text{c}}_1} = - 6$ [from (i)]
${{\text{a}}_2} = 3,\;{{\text{b}}_2} = - 6$ and ${{\text{c}}_2} = 0$ [from (ii)]
Here, $\frac{{{a_1}}}{{{a_2}}} = \frac{1}{3}$
$\frac{{{b_1}}}{{{b_2}}}\frac{{ - 2}}{{ - 6}} = \frac{1}{3}$
and $\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 6}}{0}$
$\therefore \quad \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}$
Hence, the lines represented by the given equations are parallel.
Therefore, it has no solution. So, the given pair of lines is inconsistent.
(iii) Given pair of equation are
$x + y = 3$
$\Rightarrow {\text{x}} + {\text{y}} - 3 = 0 \ldots ({\text{i}})$
and $3x + 3y = 9$
$\Rightarrow 3{\text{x}} + 3{\text{y}} - 9 = 0$... (ii)
On comparing with${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${{\text{a}}_1} = 1,\;{{\text{b}}_1} = 1$ and ${{\text{c}}_1} = - 3$ [from (i) ]
${{\text{a}}_2} = 3,\;{{\text{b}}_2} = 3$ and ${{\text{c}}_2} = - 9$ [from (ii)]
Here, $\frac{{{a_1}}}{{{a_2}}} = \frac{1}{3}$
$\frac{{{b_1}}}{{{b_2}}} = \frac{1}{3}$
and $\frac{{{c_1}}}{{{c_2}}} = \frac{{ - 3}}{{ - 9}} = \frac{1}{3}$
$\Rightarrow \quad \frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}$
So, the given pair of lines is coincident.
Therefore, these lines have infinitely many solutions.
Hence, the given pair of linear equations are consistent.
Now, $x + y = 3$
$ \Rightarrow y = 3 - x$
x | 0 | 3 | 3 |
Y | 3 | 0 | 1 |
and
$3x + 3y = 9$
$\Rightarrow 3y = 9 - 3x$
$\Rightarrow y = \frac{{9 - 3x}}{3}$
x | 0 | 1 | 3 |
Y | 3 | 2 | 0 |
Plotting the points we get the graph of lines.
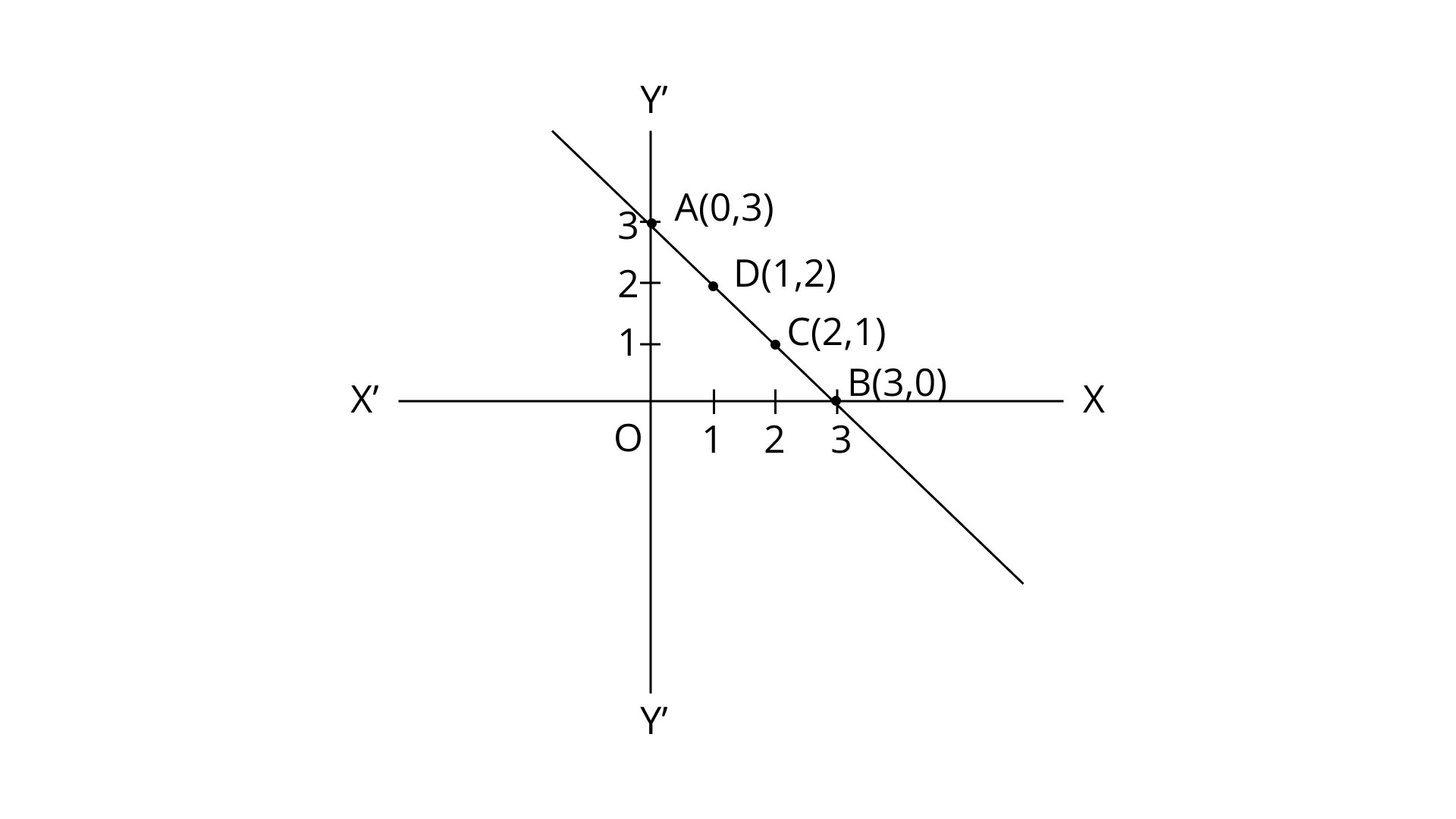
We observe that the lines represented by (i) and (ii) are coincident.
12. Draw the graph of the pair of equations $2x + y = 4$and \[2x{\text{ }}--{\text{ }}y{\text{ }} = {\text{ }}4\]. Write the vertices of the triangle formed by these lines and the y-axis. Also, find the area of this triangle?
Ans:
Consider the line $2x + y = 4$
$\Rightarrow y = 4 - 2x$
x | 0 | 2 |
y | 4 | 0 |
Now, consider the line
$ 2x{\text{ }}--{\text{ }}y{\text{ }} = {\text{ }}4 $
$ \Rightarrow y{\text{ }} = {\text{ }}2x{\text{ }}--{\text{ }}4 $
x | 0 | 2 |
y | -4 | 0 |
Graphical representation of both lines are as follows:
Here, both lines and ${\text{y}}$ -axis form $\Delta {\text{ABC}}$
Hence, the vertices of a $\Delta {\text{ABC}}$ are ${\text{A}}(0,4),{\text{B}}(2,0)$ and ${\text{C}}(0, - 4)$
$\therefore $ Required area of $\Delta {\text{ABC}}$$ = 2 \times $ Area of $\Delta {\text{AOB}} = 2 \times \frac{1}{2} \times 4 \times 2 = 8{\text{ sq}}$ units
Hence, the required area of the triangle is 8 sq units.
13. Write an equation of a line passing through the point representing the solution of the pair of linear equations $x + y = 2$and $2x - y = 1$. How many such lines can we find?
Ans: Given pair of linear equation are
$x + y - 2 = 0 \ldots $ (i)
and $2{\text{x}} - {\text{y}} - 1 = 0 \ldots $ (ii)
On comparing with${{\text{a}}_1}x + {{\text{b}}_1}y + {{\text{c}}_1} = 0,{\text{ and }}{{\text{a}}_2}x + {{\text{b}}_2}y + {{\text{c}}_2} = 0$, we get
${{\text{a}}_1} = 1,{{\text{b}}_1} = 1$ and ${{\text{c}}_1} = - 2$ [from (i) ]
${{\text{a}}_2} = 2,{{\text{b}}_2} = - 1$ and ${{\text{c}}_2} = - 1$ [from (ii)]
$\Rightarrow \frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}$, System is unique solution i.e. consistent.
Hence, both lines intersect at a point.
Consider the line $x + y = 2$
$ \Rightarrow y = 2 - x$
x | 0 | 2 | 1 |
Y | 2 | 0 | 1 |
The line $2x - y - 1 = 0$
$y = 2x - 1$
x | 0 | 1/2 | 1 |
Y | -1 | 0 | 1 |
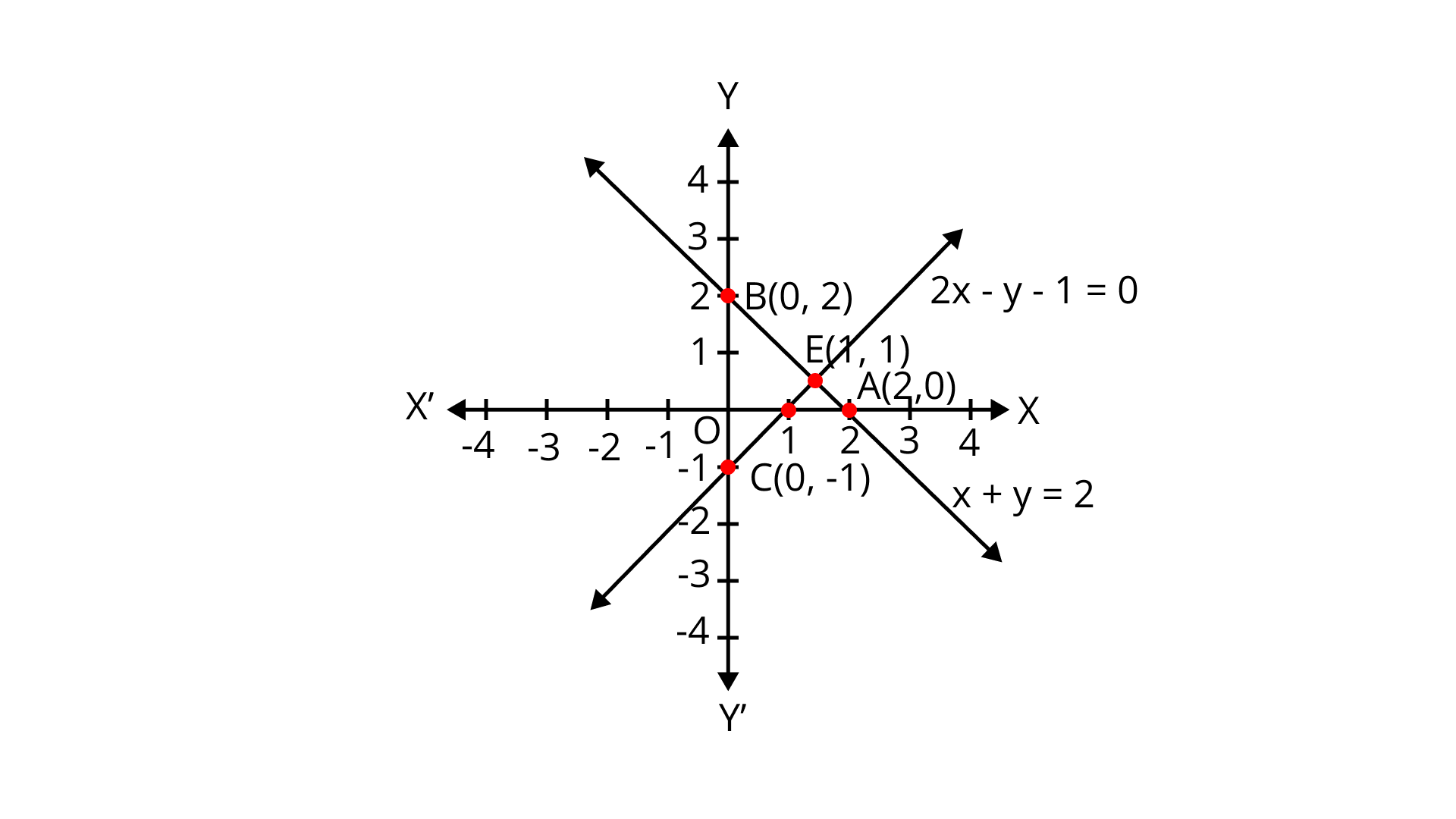
The given lines intersect at ${\text{E}}(1,1)$ .
Hence, infinite lines can pass through the intersection point of linear equations ${\text{x}} + {\text{y}} = 2$ and $2{\text{x}} - {\text{y}} = 1$ .
14. If $ x + 1 $ is a factor of $ 2{x^3} + a{x^2} + 2bx + 1 $, then find the values of $ a and b $ given that $ 2a--3b = 4. $
Ans: Let $ f\left( x \right) = 2{x^3} + a{x^2} + 2bx + 1 $, and
$x + 1 = 0$
$\therefore x = - 1$
Putting $ x = - 1 in f\left( x \right) $
$ f\left( x \right) = 2{x^3} + a{x^2} + bx + 1 $
$ f\left( { - 1} \right) = 2{x^3} + a{x^2} + 2bx + 1 $
$ \Rightarrow 2{\left( { - 1} \right)^3} + a{\left( { - 1} \right)^2} + 2b\left( { - 1} \right) + 1 = 0 $
$ \Rightarrow - 2 + a - 2b + 1 = 0 $
$ \Rightarrow a - 2b - 1 = 0{\text{ }}...\left( i \right) $
Now, $ 2a--3b = 4 $ (given)
$ \Rightarrow 2a--3b = 4$
$ \Rightarrow b = \left( {\frac{{2a - 4}}{3}} \right) $
Putting the value of\[b\], in equation \[\left( i \right)\]
$ a - 2\left( {\frac{{2a - 4}}{3}} \right) - 1 = 0 $
$ \Rightarrow 32 - a\left( {2a - 4} \right) - 3 = 0 $
$ \Rightarrow 3a - 4 + 8 - 3 = 0 $
$ \Rightarrow - a + 5 = 0 $
$ \Rightarrow a = 5 $
Putting the value of \[a\], in equation \[\left( i \right)\]
$ 5 - 2b - 1 = 0 $
$ \Rightarrow 2b = 4 $
$ \Rightarrow b = 2 $
Hence, the values of $ a{\text{ and }}b\] are \[5{\text{ and }}2 $
15. The angles of a triangle are $ x, y and 40^\circ $. The difference between the two angles $ x and y is 30^\circ $ . Find $ x and y $.
Ans: According to the given question
$ x - y = 30^\circ $
$ \Rightarrow x = y + 30^\circ ...\left( i \right) $
Since, sum of all sides of a triangle is $ 180^\circ $
$ \Rightarrow x + y + 40^\circ = 180^\circ $
$ \Rightarrow y + 30^\circ + y + 40^\circ = 180^\circ (from equation \left( i \right))$
$ \Rightarrow 2y + 70^\circ = 180^\circ $
$ \Rightarrow 2y = 110^\circ $
$ \Rightarrow y = 55^\circ $
Putting the value of \[y\] in equation $ \left( i \right) $
$ x = y + 30^\circ $
$ \Rightarrow x = 55^\circ + 30^\circ $
$ {\text{ }} = 85^\circ $
The value of $ x{\text{ and }}y is 85^\circ {\text{ and }}55^\circ $, respectively.
16. Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now?
Ans: Let Salim and his daughter’s age be $ x{\text{ and }}y $ year respectively.
Now, according to question
Two years ago, Salim was thrice as old as his daughter
$\therefore x - 2 = 3\left( {y - 2} \right)$
$\Rightarrow x - 2 = 3y - 6$
$\Rightarrow x - 3y = - 4$
$\Rightarrow x = 3y - 4$
Again according to the given question
six years later, Salim will be four years older than her daughter’s age.
$x + 6 = 2\left( {y + 6} \right) + 4$
$\Rightarrow x + 6 = 2y + 12 + 4$
$\Rightarrow x + 6 = 2y + 16$
$\Rightarrow x = 2y + 10...\left( i \right)$
Now, putting the value of $\[x\]$ in equation $ \left( i \right) $
$\Rightarrow x - 2y = 10$
$\Rightarrow \left( {3y - 4} \right) - 2y = 10$
$\Rightarrow 3y - 4 - 2y = 10$
$\Rightarrow y = 14$
Now, putting the value of $\[y\]$ in equation $ \left( i \right) $
$x = 3y - 4$
${\text{ }} = 3 \times 14 - 4$
${\text{ }} = 38$
Thus, Salim and his daughter’s age are $ 38 $ year and $ 14 $ year, respectively.
17. The age of the father is twice the sum of the ages of his two children. After $ 20 $ years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Ans: Let the present age (in year) of father and his two children be $ x,{\text{ }}y{\text{ and }}z $ year, respectively.
According to the question
$ x = 2\left( {y + z} \right) \ldots \left( i \right) $
And after $\[20\]$ year
$ \left( {x + 20} \right) = \left( {y + 20} \right) + \left( {z + 20} \right) $
$ \Rightarrow y + z + 40 = x + 20 $
$ \Rightarrow y + z = x--20 $
On putting the value of $ \left( {y + z} \right) $ in the equation $ \left( i \right) $ and get the present age of the father.
$x = 2\left( {x{\text{ }} - 20} \right)$
$\Rightarrow x = 2x--40$
$\Rightarrow - x = - 40$
$\Rightarrow x = 40$
Thus, the father’s age is $ 40 $ year.
18. Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes $ 4:5 $. Find the numbers.
Ans: Let the two numbers be $ x{\text{ and }}y $.
Two numbers are in the ratio 5 : 6 (given)
$ \frac{x}{y} = \frac{5}{6} $
$ \Rightarrow x = \frac{{5y}}{6} $
If $ 8 $ is subtracted from each of the numbers, the ratio becomes $ 4:5 $ (given)
$ \frac{{x - 8}}{{y - 8}} = \frac{4}{5} $
$ \Rightarrow 5\left( {x - 8} \right) = 4\left( {y - 8} \right) $
$ \Rightarrow 5x - 40 = 4y - 32 $
$ \Rightarrow 5x - 4y = 8 $
$ \Rightarrow 5\left( {\frac{{5y}}{6}} \right) - 4y = 8 $(from equation \[\left( i \right)\])
$ \Rightarrow \frac{{25y - 24y}}{6} = 8 $
$ \Rightarrow y = 48 $
Putting the value of $ y $ in equation $ \left( i \right) $
$ x = \frac{{5y}}{6} $
$ \Rightarrow x = \frac{{5 \times 48}}{6} $
$ {\text{ }} = 5 \times 8 $
$ {\text{ }} = 40 $
The value of $ x{\text{ and }}y\]is \[40{\text{ and }}48 $, respectively.
19. There are some students in the two examination halls $ A and B $. To make the number of students equal in each hall, $ 10 $ students are sent from $ A to B $. But if $ 20 $ students are sent from $ B to A $ , the number of students in A becomes double the number of students in $ B $. Find the number of students in the two halls.
Ans: Let the number of students in halls $ A{\text{ and }}B\] are\[x{\text{ and }}y $, respectively.
Now, by according to the question,
$x - 10 = y + 10$
$\Rightarrow \;{\text{ }}x{\text{ }}--{\text{ }}y{\text{ }} = 20 \ldots {\text{ }}\left( i \right)$
${\text{and}}\;\left( {x{\text{ }} + {\text{ }}20} \right){\text{ }} = {\text{ }}2{\text{ }}\left( {y - 20} \right)$
$\Rightarrow \;x - 2y = - 60\; \ldots \left( {ii} \right)$
On subtracting equation $ \left( {ii} \right) $ from equation $ \left( i \right) $, we get
$\Rightarrow \left( {x - y} \right) - \left( {x - {\text{ }}2{\text{ }}y} \right) = 20 + 60\;$
$\Rightarrow x - y - x + 2y = 80{\text{ }}$
$\Rightarrow y = 8$
On putting $ y = 80 $ in equation $ \left( i \right) $, we get:
$x--80 = 20{\text{ }}$
$\Rightarrow x = 100{\text{ }}$
${\text{and\; }}y = 80$
Hence, $ 100 $ students are in hall $ A $ and $ 80 $ students are in hall $ B $.
20. A shopkeeper gives books on rent for reading. She takes a fixed charge for the
first two days, and an additional charge for each day thereafter. Latika paid $ {\text{Rs }}22 $ for a book kept for six days, while Anand paid $ {\text{Rs }}164 $ for the book kept for four days. Find the fixed charges and the charge for each extra day.
Ans: Let Latika take a fixed charge for the first two day is $ {\text{Rs }}x $ and additional charge for each day thereafter is $ {\text{Rs }}y $.
Latika paid $ {\text{Rs }}22 $ for a book kept for six days i.e.,
For Latika, Number of days = 6 = 2 (fixed days) + 4 (additional days).
$ x + 4y = 22\;...\left( i \right) $
Anand paid $ {\text{Rs }}16 $ for a book kept for four days i.e.,
For Anand, Number of days = 4 = 2 (fixed days) + 2 (additional days).
$ x + 2y = 16\;...\left( {ii} \right) $
Now, subtracting equation $ \left( {ii} \right) $ from equation $ \left( i \right) $, we get
$2y = 6$
$\Rightarrow y = 3$
On putting the value of y in equation $\[\left( {ii} \right)\]$, we get
$\Rightarrow x + 2 \times 3{\text{ }} = 16$
$\Rightarrow x = 16 - 6$
${\text{ }} = 10$
Hence, the fixed charge $ = {\text{Rs }}10 $
and the charge for each extra day $ = {\text{Rs 3}} $
21. In a competitive examination, one mark is awarded for each correct answer while $ \frac{1}{2} $ mark is deducted for every wrong answer. Jayanti answered $ 120 $ questions and got $ 90 $ marks. How many questions did she answer correctly?
Ans: Total number of questions $ = 120 $.
Let x be the number of correct answers.
The number of wrong answers $ = \left( {120 - x} \right) $.
The marks scored by Jayanti is $ 90 $.
Now, according to the given question
$ x \times 1 - \left( {120 - x} \right) \times \frac{1}{2} = 90 $
$ \Rightarrow 2x - 120 + x = 180 $
$ \Rightarrow 3x = 180 + 120 $
$ \Rightarrow 3x = 300 $
$ \Rightarrow x = 100 $
Thus, Jayanti answered correctly $ 100 $ questions.
22. The angles of a cyclic quadrilateral $ ABCD $ are
$ \angle A = \left( {6x + 10} \right)^\circ ,\angle B = \left( {5x} \right)^\circ $
$ \angle C = \left( {x + y} \right)^\circ ,\angleD = \left( {3y--10} \right)^\circ $
Find $ x and y $, and hence the values of the four angles.
Ans: Since, the sum of two opposite angles in a cyclic quadrilateral is $ 180^\circ $
$ \therefore \angle A + \angle C = 180^\circ {\text{and }}\angle B + \angle D = 180^\circ $
$ \angle A + \angle C = 180^\circ $
$ \Rightarrow \left( {6x + 10} \right)^\circ + \left( {x + y} \right)^\circ = 180^\circ $
$ \Rightarrow \left( {7x} \right)^\circ + y^\circ = 170^\circ $
$ \Rightarrow y^\circ = 170^\circ - \left( {7x} \right)^\circ ...\left( i \right) $
$ \angle B + \angle D = 180^\circ $
$ \Rightarrow \left( {5x} \right)^\circ + \left( {3y--10} \right)^\circ = 180^\circ $
$ \Rightarrow \left( {5x} \right)^\circ + \left( {3y} \right)^\circ = 190^\circ ...\left( {ii} \right) $
Now, equating equation $ \left( i \right){\text{ and }}\left( {ii} \right) $
$ \Rightarrow \left( {5x} \right)^\circ + 3\left( {170^\circ - \left( {7x} \right)^\circ } \right) = 190^\circ $
$ \Rightarrow \left( {5x} \right)^\circ + 510 - \left( {21x} \right)^\circ = 190^\circ $
$ \Rightarrow - \left( {16x} \right)^\circ = - 320^\circ $
Negative sign will get eliminated
$ \Rightarrow x^\circ = 20^\circ $
Now, putting value of $ x $ in equation $ \left( i \right) $
$ y^\circ = 170^\circ - \left( {7x} \right)^\circ $
$ {\text{ = 170}}^\circ - \left( {7 \times 20} \right)^\circ $
$ {\text{ }} = {\text{170}}^\circ - 140^\circ $
$ {\text{ }} = 30^\circ $
Thus, four angle of a cyclic quadrilateral are:
$\angle A = \left( {6x + 10} \right)^\circ$
${\text{ }} = \left( {6 \times 20 + 10} \right)^\circ$
${\text{ }} = \left( {130} \right)^\circ$
$\angle B{\text{ }} = \left( {5x} \right)^\circ$
${\text{ }} = \left( {5 \times 20} \right)^\circ$
${\text{ }} = \left( {100} \right)^\circ$
$\angle C = \left( {x + y} \right)^\circ$
${\text{ }} = \left( {20 + 30} \right)^\circ$
${\text{ }} = \left( {50} \right)^\circ$
$\angle D = \left( {3y--10} \right)^\circ$
${\text{ }} = \left( {3 \times 30 - 10} \right)^\circ$
${\text{ }} = \left( {90 - 10} \right)^\circ$
${\text{ }} = 80^\circ$
SAMPLE QUESTIONS
1. Draw the graphs of the lines $x = - 2$ and $y = 3.$ Write the vertices of the figure formed by these lines, the $x - $axis and the $y - $axis. Also, find the area of the figure.
Ans: The graph of $x = - 2$ is a line parallel to $y - $axis present at $2$ units distance to the left of it.
Thus, the line $l$ is the graph of $x = - 2$.
The graph of $y = 3$ is a line parallel to the $x - $axis at $3$ units distance above it.
Thus, the line $m$ is the graph of $y = 3$.
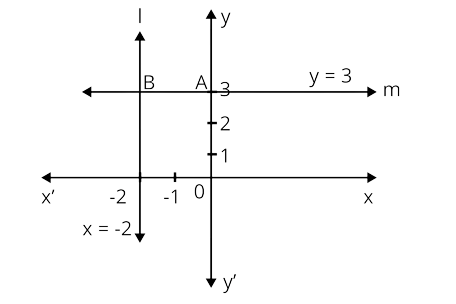
The figure enclosed by $x = - 2,y = 3$, $x - $axis and $y - $axis is $OABC$.
The vertices of ${\text{OABC}}$ are ${\text{O}}(0,0),{\text{ A}}(0,3),{\text{ B}}( - 2,3),{\text{ C}}( - 2,0)$.
The length of ${\text{OABC}}$is ${\text{2}}$ units.
The breadth of ${\text{OABC}}$is ${\text{3}}$units.
Area of a rectangle $ = l \times b$
Therefore, area of rectangle $OABC = 2 \times 3 = 6$ sq. units.
2. Determine, algebraically, the vertices of the triangle formed by the lines
$5x - y = 5,{\text{ }}x + 2y = 1$ and$6x + y = 17$.
Ans: The common solution of the two equations forming its two sides is the vertex of the triangle. So, solving the given equations pairwise gives us the required vertices of the triangle.
The three pairs of equations are:
$5x - y = 5$ and $x + 2y = 1$
$x + 2y = 1\quad $ and $\quad 6x + y = 17$
$5x - y = 5$ and $6x + y = 17$
Solving the first pair of equations $5x - y = 5$ and$x + 2y = 1$:
$\Rightarrow x = 1,{\text{ }}y = 0$.
Thus, one vertex of the triangle is $(1,0)$
Solving the second pair of equations$x + 2y = 1$ and $6x + y = 17$:
$\Rightarrow x = 3,{\text{ }}y = - 1$.
Thus, other vertex of the triangle is $(3, - 1)$
Solving the third pair of equations $5x - y = 5$ and $6x + y = 17$:
$\Rightarrow x = 2,{\text{ }}y = 5$.
Thus, the third vertex of triangle is $(2,5).$
Therefore, the three vertices of the triangle are $(1,0),{\text{ }}(3, - 1)$ and $(2,5)$.
3. Jamila sold a table and a chair for $Rs 1050$, thereby making a profit of $10\% $ on the table and $25\% $ on the chair. If she had taken a profit of $25\% $ on the table and $10\% $ on the chair she would have got $Rs 1065$. Find the cost price of each.
Ans: Assume that the cost price of the table is$\operatorname{Rs} x$ and the cost price of the chair is ${\text{Rs }}y$.
The selling price of table when sold at a profit of $10\% $$ = \operatorname{Rs} {\text{ }}x + \frac{{10}}{{100}}x = \operatorname{Rs} {\text{ }}\frac{{110}}{{100}}x$.
The selling price of chair when sold at a profit of $25\% $$ = \operatorname{Rs} {\text{ }}y + \frac{{25}}{{100}}y = \operatorname{Rs} {\text{ }}\frac{{125}}{{100}}y$.
$ \Rightarrow \frac{{110}}{{100}}x + \frac{{125}}{{100}}y = 1050{\text{ }}...\left( 1 \right)$
When the table is sold at a profit of $25\% $, then selling price $= \operatorname{Rs} {\text{ }}\left( {x + \frac{{25}}{{100}}x} \right) = \operatorname{Rs} {\text{ }}\frac{{125}}{{100}}x$.
When the chair is sold at a profit of $10\% $, then selling price $ = \operatorname{Rs} {\text{ }}\left( {y + \frac{{10}}{{100}}y} \right) = \operatorname{Rs} {\text{ }}\frac{{110}}{{100}}y$.
$\Rightarrow \frac{{125}}{{100}}x + \frac{{110}}{{100}}y = 1065{\text{ }}...{\text{(2)}}$
From${\text{(1) and (2)}}$,
$\Rightarrow 110x + 125y = 105000$ and $125x + 110y = 106500$
By adding and subtracting these equations,
$\Rightarrow 235x + 235y = 211500$ and $15x - 15y = 1500$
i.e. $x + y = 900{\text{ }}...\left( 3 \right)$
and $x - y = 100{\text{ }}...\left( 4 \right)$
From${\text{(3) and (4)}}$,
$\Rightarrow x = 500,{\text{ }}y = 400$.
Therefore, the cost price of a table is ${\text{Rs }}500$and the cost price of chair is ${\text{Rs 400}}$.
4. It can take $12$ hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for $4$hours and the pipe of smaller diameter for $9$ hours, only half the pool can be filled. How long would it take for each pipe to fill the pool separately?
Ans: Assume the time taken by the pipe of larger diameter to fill the pool as $x$ hours and that taken by the pipe of smaller diameter pipe as$y$ hours.
In $x$ hours, the pipe having a larger diameter fills the pool.
Thus, in $1$ hour the pipe of larger diameter fills the $\frac{1}{x}$ part of the pool.
In $4$ hours, the pipe of larger diameter fills the $\frac{4}{x}$ part of the pool.
In $9$ hours, the pipe of smaller diameter fills the $\frac{9}{y}$ part of the pool.
$\Rightarrow \frac{4}{x} + \frac{9}{y} = \frac{1}{2}{\text{ }}...{\text{(1)}}$
Using both pipes, the pool can be filled in ${\text{12}}$ hours.
$\Rightarrow \frac{{12}}{x} + \frac{{12}}{y} = 1{\text{ }}...{\text{(2)}}$
Let $\frac{1}{x} = u$ and $\frac{1}{y} = v$.
Then $(1)$ and $(2)$will become:
$\Rightarrow 4u + 9v = \frac{1}{2}{\text{ }}...{\text{(3)}}$
And $12u + 12v = 1{\text{ }}...{\text{(4)}}$
Multiply equation$(3)$ by $3$ and subtract equation$(4)$from it.
$\Rightarrow 15v = \frac{1}{2}$
$\Rightarrow v = \frac{1}{{30}}$
Substituting the value of $v$ in equation$(4)$,
$\Rightarrow u = \frac{1}{{20}},{\text{ }}v = \frac{1}{{30}}$
$\Rightarrow \frac{1}{x} = \frac{1}{{20}},{\text{ }}\frac{1}{y} = \frac{1}{{30}}$
$\Rightarrow x = 20,y = 30$
Therefore, the pipe of larger diameter alone can fill the pool in$20$ hours and the pipe of smaller diameter alone can fill the pool in $30$ hours.
EXERCISE 3.4:
1. Graphically, solve the following pair of equations:
$2x + y = 6$ and $2x - y + 2 = 0$
Find the ratio of the areas of the two triangles formed by the lines representing these equations with the $x - $axis and the lines with the $y - $axis.
Ans: Table for the line $2x + y = 6$is as follows:
$x$ | $0$ | $3$ |
$y$ | $6$ | $0$ |
Table for the line $2x - y + 2 = 0$is as follows:
$x$ | $0$ | $ - 1$ |
$y$ | $2$ | $0$ |
Graph of the lines is as follows:
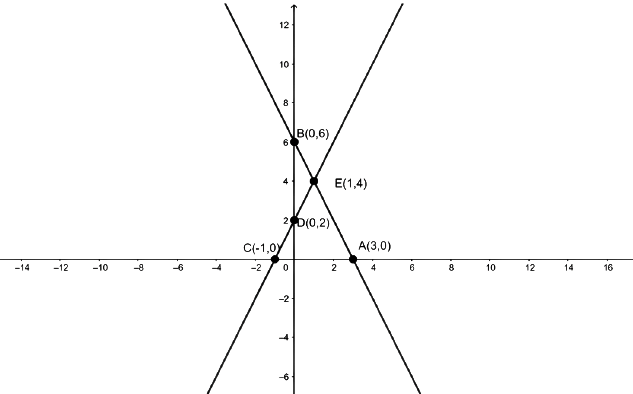
So, the pair of equations intersect graphically at ${\text{E}}(1,4)$ i.e. $x = 1$ and$y = 4$.
Let ${A_1}$ and ${A_2}$ represent the areas of $\Delta ACE$ and$\Delta BDE$.
${A_1} = $ Area of $\Delta ACE = \frac{1}{2} \times AC \times PE$$ = \frac{1}{2} \times 4 \times 4 = 82$.
And ${A_2} = $ Area of $\Delta BDE = \frac{1}{2} \times BD \times QE$$ = \frac{1}{2} \times 4 \times 1 = 2$.
Therefore, the required ratio $ = {{\text{A}}_1}:{{\text{A}}_2} = 8:2 = 4:1$.
2. Determine, graphically, the vertices of the triangle formed by the lines $y = x, 3y = x$ and $x + y = 8$.
Ans: Table for the line $y = x$ is as follows:
$x$ | $0$ | $1$ | $2$ |
$y$ | $0$ | $1$ | $2$ |
Table for the line $3y = x$ is as follows:
$x$ | $0$ | $3$ | $6$ |
$y$ | $0$ | $1$ | $2$ |
Table for the line $x + y = 8$ is as follows:
$x$ | $0$ | $4$ | $8$ |
$y$ | $8$ | $4$ | $0$ |
Graph of the lines is as follows:
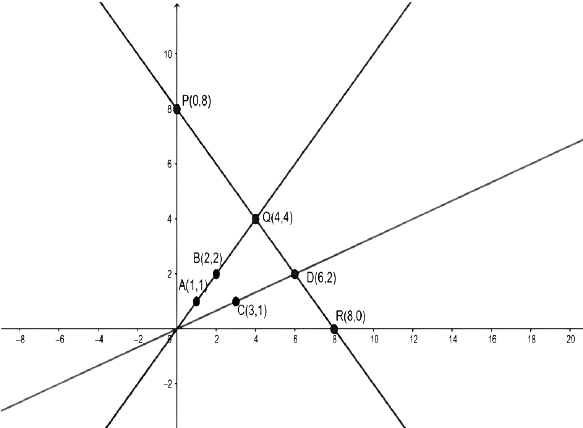
The lines $y = x$ and $3y = x$ intersect the line $x + y = 8$ at $Q$ and D.
Thus, \[\Delta OQD\] is formed by these lines.
Therefore, the vertices of $\vartriangle OQD$ are $ O(0,0),Q(4,4)and(6,2). $
3. Draw the graphs of the equations $x = 3,x = 5$ and $2x - y - 4 = 0$. Also find the area of the quadrilateral formed by the lines and the x-axis.
Ans: The given equation of lines are $2x - y - 4 = 0,x = 3and x = 5$.
Table for the line$2x - y - 4 = 0$ is as follows:
X | 0 | 2 |
Y | -4 | 0 |
Plot (0, -4) and (2, 0) and join these points to get the graph of $2x - y - 4 = 0$. Draw x = 3 and x = 5.
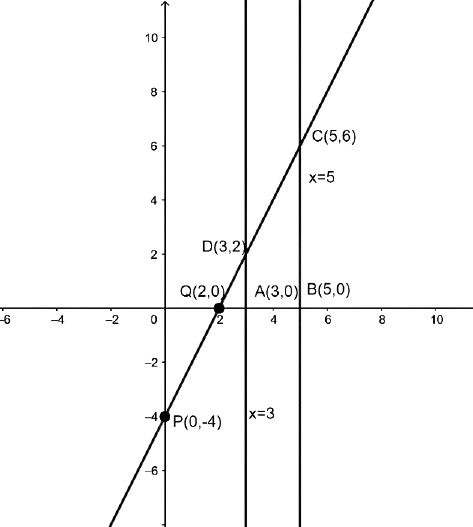
From the graph, ABCD is the quadrilateral formed by the given lines and x-axis.
AB = OB - OA = 5 - 3 = 2,AD = 2 and BC = 6
Area of quadrilateral \[\ABCD=\frac{1}{2}x\] distance between parallel lines x sum of parallel sides $ \frac{1}{2} \times AB \times (AD + BC) = \frac{1}{2} \times 2 \times (2 + 6) = 8sq.units $=8 sq. units.
Therefore, the area of the quadrilateral is 8 sq units.
4. The cost of $4$ pens and $4$ pencils boxes is $100$. Three times the cost of a pen is ₹$15$more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and a pencil box.
Ans: Let the cost of one pen be x and the cost of one pencil box be y .
$\Rightarrow 4x + 4y = 100$
$\Rightarrow x + y = 25.....(1)$
and $3x = y + 15$
$\Rightarrow 3x - y = 15......(2)$
Add equation (1) and equation (2),
$\Rightarrow 4x = 40$
$\Rightarrow x = 10$
Substitute x=10 in equation (1),
$\Rightarrow y = 25 - 10 = 15$
Therefore, the cost of one pen and one pencil box are ₹10 and ₹15, respectively.
5. Determine, algebraically, the vertices of the triangle formed by the lines $3x - y = 3,2x - 3y = 2$ and $x + 2y = 8$.
Ans: The common solution of the two equations forming its two sides is the vertex of the triangle.
Consider, the two lines $AB:3x - y = 3,BC:2x - 3y = 2$
Multiply $3x - y = 3$ by 3 and subtract $2x - 3y = 2$ from it.
$\Rightarrow \left( {9x - 3y} \right) - \left( {2x - 3y} \right) = 9 - 2$
$\Rightarrow 7x = 7$
$\Rightarrow x = 1$
Put $x$ in $3x - y = 3:$
$\Rightarrow 3 \times 1 - y = 3$
$\Rightarrow y = 0$
Thus, vertex $B$is $(1,0)$.
Now, consider the two lines $A C: x+2 y=8$ and $\mathrm{BC}: 2 x-3 y=2$.
Multiply $x+2 y=8$ by 2 and subtract $2 x-3 y=2$ from it.
$\Rightarrow(2 x+4 y)-(2 x-3 y)=16-2$
$\Rightarrow 7 y=14$
$\Rightarrow \mathrm{y}=2$
Put $y$ in $x+2 y=8$ :
$\Rightarrow x+2 \times 2=8$
$\Rightarrow x=8-4$
$\Rightarrow x=4$
Thus, vertex $\mathrm{C}$ is $(4,2)$.
Now, consider the lines $A B: 3 x-y=3$ and $A C: x+2 y=8$
Multiply $3 x-y=3$ by 2 and add $x+2 y=8$
$\Rightarrow(6 x-2 y)+(x+2 y)=6+8$
$\Rightarrow 7 x=14$
$\Rightarrow x=2$
Put $x$ in $3 x-y=3:$
$\Rightarrow 3 \times 2-y=3$
$\Rightarrow y=6-3$
$\Rightarrow y=3$
Thus, vertex A is $(2,3)$.
Therefore, the vertices of the $\triangle \mathrm{ABC}$ are $\mathrm{A}(2,3), \mathrm{B}(1,0)$ and $\mathrm{C}(4,2)$
6. Ankita travels 14km to her home partly by rickshaw and partly by bus. She takes half an hour, if she travels 2km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
Ans: Let the speed of rickshaw and bus be $x \mathrm{~km} / \mathrm{h}$ and $y \mathrm{~km} / \mathrm{h}$, respectively.
The time taken to travel $2 \mathrm{~km}$ by rickshaw:
As speed $=\frac{\text { distance }}{\text { time }}$
$\Rightarrow t_{1}=\frac{2}{x}hours
And the time taken to travel the remaining distance i.e. $(14-2)=12 \mathrm{~km}$ by bus, $t_{2}=\frac{12}{y}$ hours.
Given that $t_{1}+t_{2}=\frac{1}{2}$
$\Rightarrow \frac{2}{x}+\frac{12}{y}=\frac{1}{2} \quad \ldots$ (i) The time taken to travel $4 \mathrm{~km}$ by rickshaw is $\mathrm{t}_{3}=\frac{4}{x}$ hours.
And the time taken to travel the remaining distance i.e. $(14-4)=10 \mathrm{~km}$ by bus is $\mathrm{t}_{4}=\frac{10}{y}$ hours.
Given that $t_{3}+t_{4}=\frac{1}{2}+\frac{9}{60}=\frac{1}{2}+\frac{3}{20}$
$\Rightarrow \frac{4}{x}+\frac{10}{y}=\frac{13}{20}$
(ii)Let $\frac{1}{x}=u$ and $\frac{1}{y}=v$, then equation (i) and equation(ii) will become:
$2 u+12 v=\frac{1}{2}$...(iii)
And $4 \mathrm{u}+10 \mathrm{v}=\frac{13}{20} \quad \ldots \ldots$ (iv)
Multiply equation(iii) by 2 and subtract equation(iv) from it.
$\Rightarrow(4 u+24 v)-(4 u+10 v)=1-\frac{13}{20}$
$\Rightarrow 14 v=\frac{7}{20}$
$\Rightarrow 2 v=\frac{1}{20}$
$\Rightarrow v=\frac{1}{40}$
Put $v$ in equation(iii), we get:
$\Rightarrow 2 u+12\left(\frac{1}{40}\right)=\frac{1}{2}$
$\Rightarrow 2 u=\frac{1}{2}-\frac{3}{10}=\frac{5-3}{10}$
$\Rightarrow 2 u=\frac{2}{10}$
$\Rightarrow u=\frac{1}{10}$
As, $\Rightarrow \frac{1}{x}=\frac{1}{10}$
$\Rightarrow x=10$
$\Rightarrow \frac{1}{y}=\frac{1}{40}$
$\Rightarrow y=40$
Therefore, the speeds of rickshaw and bus are $10 \mathrm{~km} / \mathrm{h}$ and $40 \mathrm{~km} / \mathrm{h}$, respectively.
7. A person, rowing at the rate of $5 \mathrm{~km} / \mathrm{h}$ in still water, takes thrice as much time in going $40 \mathrm{~km}$ upstream as in going $40 \mathrm{~km}$ downstream. Find the speed of the stream.
Ans: Let the speed of the stream be $v \mathrm{~km} / \mathrm{h}$.
Speed of a person rowing in still water $=5 \mathrm{~km} / \mathrm{h}$.
Speed of a person rowing downstream $=(5+v) \mathrm{km} / \mathrm{h}$
Speed of person rowing upstream $=(5-v) \mathrm{km} / \mathrm{h}$.
The time taken by the person to cover $40 \mathrm{~km}$ downstream is:
$t_{1}=\frac{40}{5+v}$ hours ........ speed $=\frac{\text { distance }}{\text { time }}$
The time taken by the person to cover $40 \mathrm{~km}$ upstream is:
$t_{2}=\frac{40}{5-v}$ hours
As $t_{2}=t_{1} \times 3$
$\Rightarrow \frac{40}{5-v}=\frac{40}{5+v} \times 3$ $\Rightarrow \frac{1}{5-v}=\frac{3}{5+v}$ $\Rightarrow 5+v=15-3 v$ $\Rightarrow 4 v=10$ $\Rightarrow v=\frac{10}{4}=2.5 \mathrm{~km} / \mathrm{h}$
Therefore, the speed of the stream is $2.5 \mathrm{~km} / \mathrm{h}$.
8. A motorboat can travel $30km$upstream and $28km$downstream in $7$ hours. It can travel $21km$upstream and return in $5$ hours. Find the speed of the boat in still water and the speed of the stream.
Ans: Let the speed of the motorboat in still water and speed of stream be $u \mathrm{~km} / \mathrm{h}$ and $v \mathrm{~km} / \mathrm{h}$, respectively.
The downstream speed of the motorboat $=(u+v) \mathrm{km} / \mathrm{h}$.
And the upstream speed of the motorboat $=(u-v) \mathrm{km} / \mathrm{h}$.
The time taken to travel $30 \mathrm{~km}$ upstream is:
$\Rightarrow t_{1}=\frac{30}{u-v}$ hours
And time taken to travel $28 \mathrm{~km}$ downstream is: $\Rightarrow t_{2}=\frac{28}{u+v}$ hours
Given that $t_{1}+t_{2}=7$ hours.
$\Rightarrow \frac{30}{u-v}+\frac{28}{u+v}=7$
Time taken to travel $21 \mathrm{~km}$ upstream is:
$\Rightarrow \mathrm{t}_{3}=\frac{21}{u-v} \text { hours }$
And time taken to travel $21 \mathrm{~km}$ downstream is:
$\Rightarrow t_{4}=\frac{21}{u+v} \text { hours }$
Given that $t_{4}+t_{3}=5$ hours.
$\Rightarrow \frac{21}{u+v}+\frac{21}{u-v}=5$
$\text { Let } x=\frac{1}{u+v} \text { and } y=\frac{1}{u-v}$
Then (1) and (2) will become:
$30 x+28 y=7 \quad \ldots \text { (3) }$
And $21 x+21 y=5$
$\Rightarrow x+y=\frac{5}{21}$
Multiply (4) by 28 and subtract from (3), we get:
$\Rightarrow(30 x-28 y)-(28 x+28 y)=7-\frac{140}{21}$
$\Rightarrow 2 x=7-\frac{20}{3}$
$\Rightarrow 2 x=\frac{1}{3}$
$\Rightarrow x=\frac{1}{6}$
Put $x$ in equation (4):
$\Rightarrow \frac{1}{6}+y=\frac{5}{21}$
$\Rightarrow y=\frac{5}{21}-\frac{1}{6}=\frac{10-7}{42}=\frac{3}{42}$
$\Rightarrow y=\frac{1}{14}$
Now, $x=\frac{1}{u+v}=\frac{1}{6}$
$\Rightarrow u+v=6$
And $y=\frac{1}{u-v}=\frac{1}{14}$
$\Rightarrow u-v=14$
Add (5) and (6) :
$\Rightarrow 2 \mathrm{u}=20$
$\Rightarrow \mathrm{u}=10$
Put $u$ in equation (5):
$\Rightarrow 10+v=6$
$\Rightarrow v=-4$
Therefore, the speed of the boat in still water is $10 \mathrm{~km} / \mathrm{h}$ and speed of the stream is $4 \mathrm{~km} / \mathrm{h}$.
9. A two-digit number is obtained by either multiplying the sum of the digits by $8$ and then subtracting $5$ or by multiplying the difference of the digits by $16$ and then adding $3$. Find the number.
Ans: Let the two-digit number be $10 x+y$.
Case I: Multiplying the sum of digits by 8 and then subtracting $5=$ two-digit number $\Rightarrow 8(x+y)-5=10 x+y$ $\Rightarrow 8 x+8 y-5=10 x+y$ $\Rightarrow 2 x-7 y=-5 \quad \ldots$ (i)
Case II: Multiplying the difference of digits by 16 and then adding $3=$ two-digit number $\Rightarrow 16 x(x-y)+3=10 x+y$ $\Rightarrow 16 x-16 y+3=10 x+y$ $\Rightarrow 6 x-17 y=-3 \quad \ldots$ (ii)
Multiply (i) by 3 and subtract from (ii):
$\Rightarrow(6 x-17 y)-(6 x-21 y)=-3-(-15)$
$\Rightarrow 4 y=12$
$\Rightarrow y=3$
Put $y$ in equation (i):
$\Rightarrow 2 x-7 \times 3=-5$
$\Rightarrow 2 x=21-5=16$
$\Rightarrow x=8$
Therefore, the required two-digit number $=10 x+y=10 \times 8+3=80+3=83$
10. A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the stations A to B costs ₹2530. Also, one reserved first class ticket and one reserved first class half ticket from $A$ to $8$ costs ₹$3810$. Find the full first class fare from station $A$ to $B$ and also the reservation charges for a ticket.
Ans: Let the cost of full and half first class fare be $x$ and $\frac{x}{2}$ respectively.
Let the reservation charges be ₹ $y$ per ticket.
Case I: The cost of one reserved first class ticket from the stations $A$ to $B=₹ 2530$ $\Rightarrow x+y=2530$...(1)
Case II: The cost of one reserved first class ticket and one reserved first class half ticket from stations $A$ to $B=₹ 3810$
$\Rightarrow x+y+\frac{x}{2}+y=3810$
$\Rightarrow \frac{3 x}{2}+2 y=3810$
$\Rightarrow 3 x+4 y=7620$
Multiply (1) by 4 and subtract from $(2)$,
$\Rightarrow(3 x+4 y)-(4 x+4 y)=7620-10120$
$\Rightarrow-x=-2500$
$\Rightarrow x=2500$
Put $x$ in equation (1),
$\Rightarrow 2500+y=2530$
$\Rightarrow y=2530-2500$
$\Rightarrow y=30$
Therefore, full first class fare from stations $A$ to $B$ is $₹ 2500$ and the reservation charge for the ticket is $₹ 30$.
11. A shopkeeper sells a saree at $8\% $ profit and a sweater at $10\% $discount, thereby, getting a sum ₹$1008$. If she had sold the saree at $10\% $ profit and the sweater at 8% discount, she would have got ₹$1028$ . Find the cost price of the saree and the list price (price before discount) of the sweater.
Ans: Let the cost price of saree and list price of sweater be $₹ x$ and $₹ y$, respectively. Case I: He sells a saree at $8 \%$ profit $+$ He sells a sweater at $10 \%$ discount $=₹ 1008$ $\Rightarrow(100+8) \%$ of $x+(100-10) \%$ of $y=1008$
$\Rightarrow 108 \% \text { of } x+90 \% \text { of } y=1008$
$\Rightarrow 1.08 x+0.9 y=1008 \quad \text {... (i) }$
Case II: He sells the saree at $10 \%$ profit + He sells the sweater at $8 \%$ discount $=₹ 1028$ $\Rightarrow(100+10) \%$ of $x+(100-8) \%$ of $y=1028$ $\Rightarrow 110 \%$ of $x+92 \%$ of $y=1028$
$\Rightarrow 1.1 x+0.92 y=1028 \quad \ldots \text { (ii) }$
Put $y$ from equation (i) into equation (ii),
$\Rightarrow 1.1 \times 0.92\left(\frac{1008-1.08 x}{0.9}\right)=1028$
$\Rightarrow 1.1 \times 0.9 x+927.36-0.9936 x=1028 \times 0.9$
$\Rightarrow 0.99 x-0.9936 x=925.2-927.36$
$\Rightarrow-0.0036 x=-2.16$
$\Rightarrow x=\frac{2.16}{0.0036}=600$
Put $x$ in equation (i),
$\Rightarrow 1.08 \times 600+0.9 y=1008$
$\Rightarrow 648+0.9 y=1008$
$\Rightarrow 0.9 y=1008-648$
$\Rightarrow 0.9 y=360$
$\Rightarrow y=\frac{360}{0.9}=400$
Therefore, the cost price of a saree and the list price of a sweater are $₹ 600$ and $₹ 400$, respectively.
12. Susan invested a certain amount of money in two schemes $A$ and$B$, which offer interest at the rate of $8\% $ per annum and $9\% $ per annum, respectively. She received ₹$1860$ as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received ₹$20$ more as annual interest. How much money did she invest in each scheme?
Ans: Let the amount of investments in schemes $\mathrm{A}$ and $\mathrm{B}$ be $₹ x$ and $₹ y$, respectively.
Case I: Interest at the rate of $8 \%$ per annum on scheme $\mathrm{A}+$ Interest at the rate of $9 \%$ per annum on scheme B = ₹1860.
$\Rightarrow \frac{x \times 8 \times 1}{100}+\frac{y \times 9 \times 1}{100}=1860 \ldots \ldots \ldots \ldots \ldots . . \text { simple interest }=\frac{\text { principal } \times \text { rate } \times \text { time }}{100}$
$\Rightarrow 8 x+9 y=186000 \quad \ldots(\text { i })$
Case II: Interest at the rate of $9 \%$ per annum on scheme $\mathrm{A}+$ Interest at the rate of $8 \%$ per annum on scheme $\mathrm{B}=₹ 1860+₹ 20$
$\Rightarrow \frac{x \times 9 \times 1}{100}+\frac{y \times 8 \times 1}{100}=20+1860$
$\Rightarrow \frac{9 x}{100}+\frac{8 y}{100}=1880$
$\Rightarrow 9 x+8 y=188000 \quad \text {...(ii) }$
Multiply (i) by 9 and (ii) by 8 and subtract them.
$\Rightarrow(72 x+81 y)-(72 x+64 y)=9 \times 186000-8 \times 188000$ $\Rightarrow 17 y=1000[(9 \times 186)-(8 \times 188)]$ $\Rightarrow 17 y=1000(1674-1504)=1000 \times 170$ $\Rightarrow 17 y=1000 \times 170$ $\Rightarrow 17 y=170000$ $\Rightarrow y=10000$ Put $y$ in equation (i), $\Rightarrow 8 x+9 \times 10000=186000$ $\Rightarrow 8 x=186000-90000$
$\Rightarrow 8 \mathrm{x}=96000$
$\Rightarrow x=12000$
Therefore, she invested ₹ 12000 and ₹ 10000 in schemes $\mathrm{A}$ and $\mathrm{B}$ respectively.
13. Vijay had some bananas, and he divided them into two lots $A$ and $B$. He sold the first lot at the rate of ₹$2$ for $3$ bananas and the second lot at the rate of ₹1 per banana, and got a total of ₹400. If he had sold the first lot at the rate of ₹1 per banana and the second lot at the rate of ₹4 for 5 bananas, his total collection would have been ₹460. Find the total number of bananas he had.
Ans: Let the number of bananas in lots $A$ and $B$ be $x$ and $y$ respectively
Case I: Cost of first lot at the rate of $₹ 2$ for 3 bananas $+$ Cost of second lot at the rate of $₹ 1$ per banana $=₹ 400$
$\Rightarrow \frac{2}{3} x+y=400$
$\Rightarrow 2 x+3 y=1200$
Case II: Cost of first lot at the rate ₹ 1 per banana + Cost of second lot at the rate of ₹ 4 for 5 bananas = amount received
$\Rightarrow x+\frac{4}{5} y=460$
$\Rightarrow 5 x+4 y=2300$
Multiply (1) by 4 and (2) by 3 and subtract them.
$\Rightarrow(8 x+12 y)-(15 x+12 y)=4800-6900$
$\Rightarrow-7 x=-2100$
$\Rightarrow x=300$
Put $x$ in equation (1),
$\Rightarrow 2 \times 300+3 y=1200$
$\Rightarrow 600+3 y=1200$
$\Rightarrow 3 y=1200-600$
$\Rightarrow 3 y=600$
$\Rightarrow y=200$
The total number of bananas = Number of bananas in lot $\mathrm{A}+$ Number of bananas in $\operatorname{lot} \mathrm{B}=x+y=300+200=500$
Therefore, he had 500 bananas.
Why NCERT Exemplar for Class 10 Maths - Pair of Linear Equations in Two Variables
The NCERT Maths Exemplar for Class 10 is useful for students who want to do well in their Class 10 board exams. Aside from that, you can use reference books to help you answer the questions, however, these reference books can occasionally lead you astray and confuse you. To achieve well in the Class 10 board exams, it is best to stick to the NCERT books for Class 10 and practice various tasks.
Refer to the NCERT Exemplar Solutions for Class 10 for the answers to the NCERT Maths exemplar questions. For a better comprehension of the subject's subjects, these solutions are offered in a concise, quick, and correct manner. These solutions can be used to effectively prepare for the Maths topic of the Class 10th board exams.
Concepts Included in Class 10 Maths - Pair of Linear Equations in Two Variables
Equations
Linear Equations
General Form of Linear Equation in two Variables
Geometrical Representation of a linear equation
Comparing the ratios of coefficients of a linear equation
Algebraic Solution
Substitution Method
Elimination Method
Cross-Multiplication Method
Number of Exercises in NCERT Exemplar for Class 10 Maths - Pair of Linear Equations in Two variables
Exercise 3.1 (13 Questions)
Exercise 3.2 (5 Questions)
Exercise 3.3 (22 Questions)
Exercise 3.4 (13 Questions)
Benefits of solving Problems from NCERT Exemplar for Class 10 Maths
Mathematics is a subject that demands not only a thorough comprehension of the material but also many practice sessions to master it and get high grades. As a result, just finishing NCERT isn't enough to learn this subject; you'll also need the necessary study tools. As a result, to grasp the material quickly, you need to use NCERT Exemplar for Class 10 Maths. Take a look at the advantages of using these NCERT Maths examples to help you prepare for your board test. Some of these advantages are as follows:
NCERT exemplars adhere to the CBSE curriculum and cover the entire syllabus for the Class 10 board exam. This study material will also assist you in forming a foundation for studying for board examinations, as the questions in this textbook are based on the subject's prescribed syllabus.
Aids in board preparation- The NCERT Maths example contains advanced-level questions that appear in board exams. Solving NCERT example problems can assist you in honing your math skills. This will undoubtedly assist you in completing difficult questions and MCQs.
Clears topic fundamentals- The NCERT books not only cover the whole test syllabus but also offer all of the fundamentals on all topics in plain language. To avoid rehashing the same themes, make sure your concepts are crystal clear. To create a clear concept, you must refer to the NCERT Maths Exemplar for a complete and extensive study. As a result, you will be required to update the formulas, terms, and execution during the revision.
NCERT Exemplars are essentially practice books that contain additional key questions at a higher level and allow you to learn in greater depth. Conceptual sums are included in these examples, which are important for CBSE and competitive exams. These NCERT Exemplar Class 10 Maths Solutions will provide you with MCQs, skill-development questions, and new topics. All of the themes under each subject are covered in NCERT Exemplars.
FAQs on NCERT Exemplar for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables (Book Solutions)
1. Will solving Exemplar exercises for Class 10 Maths benefit me?
These NCERT exemplars are written by subject experts following extensive research into the difficulties surrounding the subject. They offer in-depth information. You'll be able to get accurate and trustworthy information on the topics. Each topic in the exemplar is described in detail. By answering questions from the NCERT Exemplar, you will check your basic grasp and thoroughly understand the in-depth features of the material. Students can solve the Exemplar questions to practice for the final board exams and score high marks in the exams.









































