Circles Class 9 Important Questions: CBSE Maths Chapter 9

Very Short Answer Type Questions: (1 Marks)

1. An angle in the semicircle is

(a) Right angle

(b) \[{180^\circ }\]

(c) \[{360^\circ }\]

(d) None of these

Ans: (a) Right angle

If an angle is inscribed in a semicircle, it will be half the measure of a semicircle (\[{\mathbf{180^\circ}}\]), therefore measuring \[{\mathbf{90^\circ}}\] .

2. If the angles subtended by two chords of a circle at the centre are equal then the chords are

(a) Not Equal

(b) Equal

(c) Angle Equal

(d) Line Equals

Ans: (b) Equal

3. How many circle passing through three non-collinear points

(a) One

(b) Two

(c) Three

(d) Four

Ans: (a) One

4. The constant distance is called

(a) Diameter

(b) Radius

(c) Centre

(d) Circle

Ans: b) Radius

5. Given \[{\text{PS}}\] and \[{\text{RS}}\] are two chord's of a circle such that \[{\text{PQ}} = 10\;{\text{cm}}\] and \[{\text{RS}} = 24\;{\text{cm}}\] and \[{\text{PQ}}||{\text{RS}}.\] The distance between \[PQ\] and \[RS\] is \[17\;{\text{cm}}.\] Find the radius of circle

(a) \[10\;{\text{cm}}\]

(b) \[13\;{\text{cm}}\]

(c) \[15\;{\text{cm}}\]

(d) none of these

Ans: (b) \[13\;{\text{cm}}\]

6. A circle is drawn. It divides the plane into

(a) \[{\mathbf{3}}\]Parts

(b) \[{\mathbf{4}}\]Parts

(c) \[{\mathbf{5}}\]Parts

(d) No Parts

Ans:  (a) \[{\mathbf{3}}\] Parts

7. The relation between diameter and radius of a circle is

(a) \[{\mathbf{r}} = {\mathbf{2d}}\]

(b) \[{\mathbf{d}} = {\mathbf{r}}\]

(c) \[{\text{d}} = 2{\text{r}}\]

(d) \[{\text{d}} = 2\pi {\mathbf{r}}\]

Ans: (c) \[d = 2r\]

8. If \[P\] and \[Q\] are any two Points on a circle then \[PQ\] is called a

(a) diameter

(b) secant

(c) chord

(d) radius

Ans: c) Chord

9. What is a diameter

(a) \[r = 2d\]

(b) \[d = 2\pi r\]

(c) \[d = r\]

(d) \[d = 2r\]

Ans: (d) \[d = 2r\]

10. The whole arc of a circle is called

(a) Circumference

(b) Semi-circle

(c) Sector

(d) Segment

Ans: (a) circumference

11. One half of the whole arc of a circle

(a) Semi-circle

(b) Circumference

(c) Segment

(d) Sctor

Ans: (a) semi-circle

12. Circle having same centre are said to be

(a) Concentric

(b) Circle

(c) Chord

(d) Secant

Ans: (a) Concentric

13. The line which meet a circle in two points is called a

(a) Chord of Circle

(b) Diameter

(c) Radius

(d) Secant of Circle

Ans: (d) Secant of Circle

14. The sum of either pair of opposite angle of cyclic quadrilateral is

(a) \[{360^\circ }\]

(b) \[{90^\circ }\]

(c) \[{180^\circ }\]

(d) \[{270^\circ }\]

Ans: c) \[{180^\circ }\]

15. Two circle are congruent if they have equal.

(a) Diameter

(b) Radius

(c) Chord

(d) Secant

Ans: (b) Radius

16. The \[\dfrac{1}{2}\]of the whole circle shows

(a) Semi-Circle

(b) Circumference

(c) Sector

(d) Segments

Ans. (a) Semi-Circle

Short Answer Type Questions : (2 Marks)

1. Fill in the Blanks:

(i) The centre of a circle lies in__________ of the circle.

Ans: Interior

(ii) A point, whose distance from the centre of a circle is greater than its radius lies in_______________ of the circle.

Ans: Exterior

(iii) The longest chord of a circle is a _______________ of the circle.

Ans: Diameter

(iv) An arc is a _______________ when its ends are the ends of a diameter

Ans: Semi-circle

(v) Segment of a circle is the region between an arc and _______________ of the circle.

Ans: Chord

2. Write True or False:

(i) Line segment joining the centre to any point on the circle is a radius of the circle.

Ans: True

(ii) A circle has only finite number of equal chords.

Ans: False

(iii) If a circle is divided into three equal arcs each is a major arc.

Ans: False

(iv) A chord, which is twice as long as its radius is a diameter of the circle.

Ans: True

(v) Sector is the region between the chord and its corresponding arc.

Ans: False

(vi) A circle is a plane figure.

Ans: True

3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.

Ans: Given:\[{\text{AB}}\] and \[{\text{CD}}\] be two equal chords of a circle with centre \[{\text{O}}\] intersecting each other with in the circle at point \[{\text{X}}\].

\[{\text{OX}}\] is joined.

To prove: \[\angle {\text{OXM}} = \angle {\text{OXN}}\]

Construction: Draw \[{\text{OM}} \bot {\text{AB}}\] and \[{\text{ON}} \bot {\text{CD}}\]

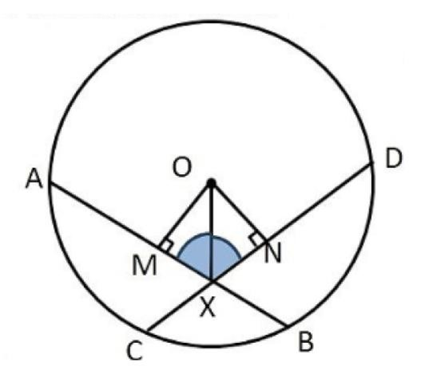
Proof: In right angled triangles \[{\text{OMX}}\] and \[{\text{ONX,}}\]

\[\angle {\text{OMX}} = \angle {\text{ONX}}\]\[\left[ {{\text{Each}}{\kern 1pt} \,{\kern 1pt} \left. {{{90}^\circ }} \right]} \right.\]

\[{\text{OM}} = {\text{ON}}\] (Equal chords are equidistant from the centre)

\[{\text{OX}} = {\text{OX}}\] (Common)

\[\Delta {\text{OMX}} \cong \Delta {\text{ONX}}\] (RHS rule of congruence)

\[\angle {\text{OXM}} = \angle {\text{OXN}}\] (By CPCT)

4. In figure, \[{\text{A,B,C}}\] are three points on a circle with centre \[{\text{O}}\] such that \[\angle {\text{BOC}} = {30^\circ },{\kern 1pt} {\kern 1pt} {\kern 1pt} \,{\kern 1pt} \angle {\text{AOB}} = {60^\circ }.\]

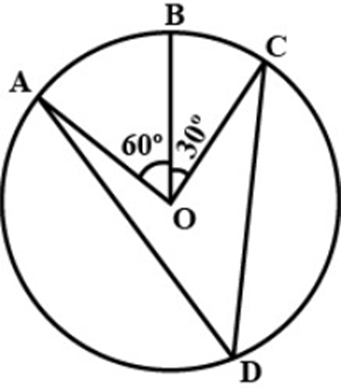
If \[{\text{D}}\]is a point on the circle other than the arc \[{\text{ABC}},\]find \[\angle {\text{ADC}}{\text{.}}\]

Ans: \[\angle {\text{AOC}} = \angle {\text{AOB}} + \angle {\text{BOC}}\]

\[ \Rightarrow \angle {\text{AOC}} = {60^\circ } + {30^\circ }\]

\[ = {90^\circ }\]

Now \[\angle {\text{AOC}} = 2\angle {\text{ADC}}\]

Angled subtended by an arc, at the centre of the circle is double the angle subtended by the same arc at any point in the remaining part of the circle

\[ \Rightarrow \angle {\text{ADC}} = \dfrac{1}{2}\angle {\text{AOC}}\]

\[ \Rightarrow \angle {\text{ADC}} = \dfrac{1}{2} \times {90^\circ } = {45^\circ }\]

5. In figure, $\angle {\text{PQR}} = {100^\circ }$, where P, Q, R are points on a circle with centre 0 . Find $\angle OPR.$

Ans: In the figure, $Q$ is a point in the minor arc $\widehat {PQR}$.

$\therefore m\widehat {{\text{RP}}} = 2\angle {\text{PQR}}$

$ \Rightarrow \angle {\text{ROP}} = 2\angle {\text{PQR}}$

$ \Rightarrow \angle {\text{ROP}} = 2 \times {100^\circ } = {200^\circ }$

Now $m\widehat {{\text{PR}}} + m\widehat {{\text{RP}}} = {360^\circ }$

$ \Rightarrow \angle {\text{POR}} + \angle {\text{ROP}} = {360^\circ }$

$ \Rightarrow \angle {\text{POR}} + {200^\circ } = {360^\circ }$

$ \Rightarrow \angle {\text{POR}} = {360^\circ } - {200^\circ } = {160^\circ }{\kern 1pt} \,\,\,\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \,\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \, \ldots ..({\text{i}})$

Now $\Delta {\text{OPR}}$ is an isosceles triangle.

$\therefore $ \[OP = OR\] (radii of the circle)

$ \Rightarrow \angle {\text{OPR}} = \angle {\text{ORP}}$ (angles opposite to equal sides are equal) \[.....\left( {ii} \right)\]

Now in isosceles triangle OPR,

$\angle {\text{OPR}} + \angle {\text{ORP}} + \angle {\text{POR}} = {180^\circ }$

$ \Rightarrow \angle {\text{OPR}} + \angle {\text{ORP}} + {160^\circ } = {180^\circ }$

$ \Rightarrow 2\angle {\text{OPR}} = {180^\circ } - {160^\circ }$         $[{\text{Using}}({\text{i}}){\text{ & }}({\text{ii}})]$

$ \Rightarrow 2\angle {\text{OPR}} = {20^\circ }$

$ \Rightarrow \angle {\text{OPR}} = {10^\circ }$

6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. $\angle {\text{DBC}} = {70^\circ }$,

$\angle {\mathbf{BAC}}$ is ${30^\circ }$ find $\angle {\mathbf{BCD}}$. Further if ${\mathbf{AB}} = {\mathbf{BC}}$, find $\angle {\mathbf{ECD}}$.

Ans:  Here, $\angle {\text{DBC}} = {70^\circ }$ and $\angle {\text{BAC}} = {30^\circ }$

And $\angle {\text{DAC}} = \angle {\text{DBC}} = {70^\circ }$ (Angles in same circle)

Now ABCD is a cyclic quadrilateral.

$\therefore \angle {\text{DAB}} + \angle {\text{BCD}} = {180^\circ }$

(Sum of opposite angles of a cyclic quadrilateral is supplementary)

$ \Rightarrow {100^\circ } + \angle {\text{BCD}} = {180^\circ }$

$ \Rightarrow \angle {\text{BCD}} = {80^\circ }$

7. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Ans. Given: A trapezium ${\text{ABCD}}$ in which and ${\text{AD}} = {\text{BC}}$.

To prove: The points A, B, C, D are concyclic.

Construction: Draw DE .

Proof: Since DE||CB  and EB||DC.

$\therefore {\text{EBCD}}$ is a parallelogram.

$\therefore {\text{DE}} = {\text{CB}}$ and $\angle {\text{DEB}} = \angle {\text{DCB}}$

Now ${\text{AD}} = {\text{BC}}$ and ${\text{DA}} = {\text{DE}}$

$ \Rightarrow \angle {\text{DAE}} = \angle {\text{DEB}}$

But $\angle {\text{DEA}} + \angle {\text{DEB}} = {180^\circ }$

$ \Rightarrow \angle {\text{DAE}} + \angle {\text{DCB}} = {180^\circ }[\because \angle {\text{DEA}} = \angle {\text{DAE}}$ and $\angle {\text{DEB}} = \angle {\text{DCB}}]$

$ \Rightarrow \angle {\text{DAB}} + \angle {\text{DCB}} = {180^\circ }$

$ \Rightarrow \angle {\text{A}} + \angle {\text{C}} = {180^\circ }$

Hence, ${\text{ABCD}}$ is a cyclic trapezium.

8. Two circles intersect at two points ${\text{B}}$ and ${\text{C}}$. Through B, two line segments ${\text{ABD}}$ and PBQ are drawn to intersect the circles at A, D, P, Q respectively (see figure). Prove that $\angle {\text{ACP}} = \angle {\text{QCD}}$

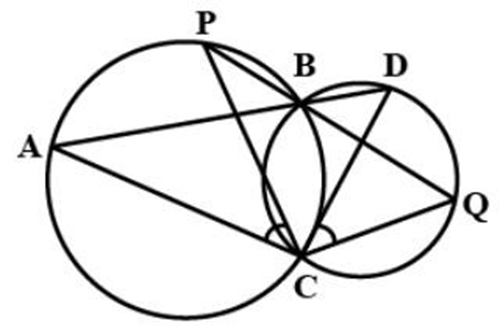
Ans: In triangles ${\text{ACD}}$ and ${\text{QCP}}$,

$\angle {\text{A}} = \angle {\text{P}}$ and $\angle {\text{Q}} = \angle {\text{D}}$ (Angles in same segment)

$\therefore \angle {\text{ACD}} = \angle {\text{QCP}}$ (Third angles) ..........(i)

Subtracting $\angle {\text{PCD}}$ from both the sides of eq. (i), we get,

$\angle {\text{ACD}} - \angle {\text{PCD}} = \angle {\text{QCP}} - \angle {\text{PCD}}$

$ \Rightarrow \angle {\text{ACPO}} = \angle {\text{QCD}}$

Hence proved.

9. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.

Ans: Let two circles with respective centers ${\text{A}}$ and ${\text{B}}$ intersect each other at points ${\text{C}}$ and ${\text{D}}$.

We have to prove $\angle {\text{ACB}} = \angle {\text{ADB}}$

Proof: In triangles ${\text{ABC}}$ and ${\text{ABD}}$,

${\text{AC}} = {\text{AD}} = r$

${\text{BC}} = {\text{BD}} = r$

${\text{AB}} = {\text{AB}}$ (Common)

$\therefore \vartriangle {\text{ABC}} \cong \Delta {\text{ABD}}$ (SSS rule of congruency)

$ \Rightarrow \angle {\text{ACB}} = \angle {\text{ADB}}$ ${\text{[ByCPCT]}}$

10. Prove that the circle drawn with any drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.

Ans: Let ${\text{ABCD}}$ be a rhombus in which diagonals AC and BD intersect each other at point ${\text{O}}$.

As we know that diagonals of a rhombus bisect and perpendicular to each other.

$\therefore \angle {\text{AOB}} = {90^\circ }$

And if we draw a circle with side ${\text{AB}}$ as diameter, it will definitely pass through point ${\text{O}}$ (the point intersection of diagonals) because then $\angle {\text{AOB}} = {90^\circ }$ will be the angle in a semi-circle.

11. ${\text{AB}} = {\text{DC}}$ and diagonal AC and BD intersect at P in cyclic quadrilateral Prove that $\Delta PAB \cong \Delta PDC$

Ans: In $\Delta {\text{PAB}}$ and $\Delta {\text{PDC}}$

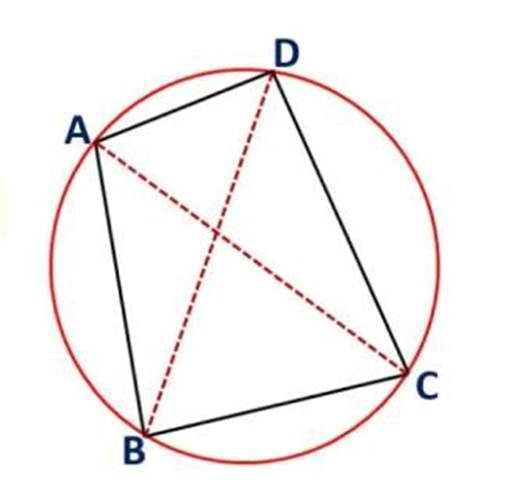
${\text{AB}} = {\text{DC}}$

$\angle ABP = \angle DCP$ (Angle in the same segment)

$\angle PAB = \angle PDC$ (Angle in the same segment)

$\Delta PAB \cong \Delta PDC$ (ASA criterion)

12. Prove that $\angle CAD = \angle CBD$, if ${\text{ABC}}$ and ADC are two right triangle with common hypotenuse AC.

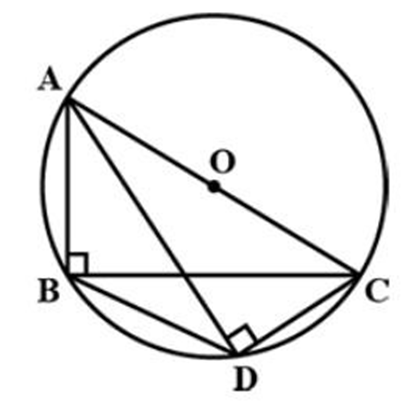
Ans: $\angle ADC = \angle ABC = {90^\circ }[{\text{AC}}$ is the common hypotenuse of it $\Delta sADC$ and $A B C$ ]

$\angle ADC + \angle ABC = {180^\circ }$

$ \Rightarrow $ Quadrilateral ABCD is cyclic

Now, chord CD subtends $\angle CAD$ and $\angle CBD$

$\angle CAD = \angle CBD$ (Angle in the same segment)

13.  In isosceles triangle ${\text{ABC}},{\text{AB}} = {\text{AC}}$ and B,C intersects the sides ${\text{AB}}$ and ${\text{AC}}$ at ${\mathbf{D}}$ and ${\text{E}}$ respectively. Prove that DE || BC.

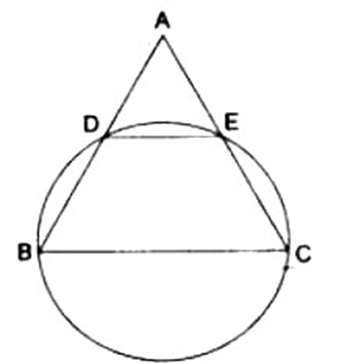
Ans: In triangle ABC, given AB=AC

So $\angle B = \angle C$ (i)

Now ,BCED forms a cyclic quadrilateral

$\angle ADC = \angle C \ldots  \ldots ...(ii)$

From (i) and (ii) we get

$\angle ADE = \angle B$

Hence DE || BC

14. Prove that cyclic parallelogram is a rectangle.

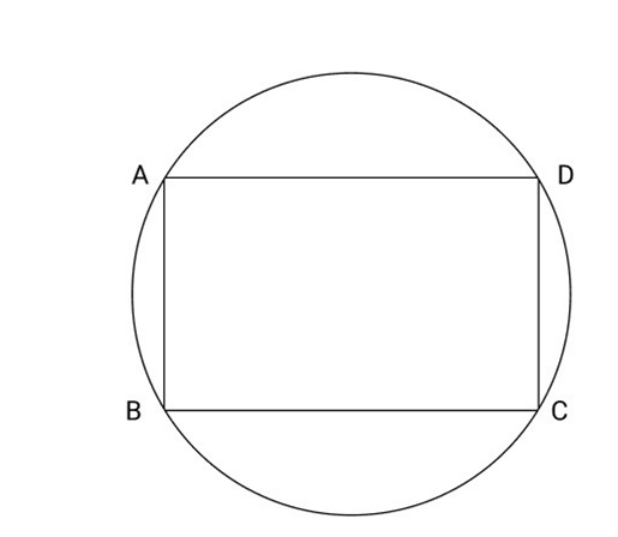
Ans: Let ABCD be the given cyclic parallelogram

$\angle A + \angle C = {180^\circ }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}  \ldots  \ldots  \ldots ..(i)$

$\angle A = \angle C$

(Opposite angle of a parallelogram are equal)  ........(ii)

From (i) and (ii)

$2\angle A =  {180^\circ }$

$\angle A= 90^\circ$

So, ABCD is a parallelogram having one angle $90^\circ$ .

Hence, $\angle ABCD$ is a rectangle.

15. A line is Passing through the centre of a circle. If it bisects chord AB and CD of the circle. Prove that ${\text{AB}}||{\text{CD}}$.

Ans: Line EF passes through the centre $O$ and bisects chord \[{\text{AB}}\] at $P$ and chord \[{\text{CD}}\]at $Q$

$\therefore {\text{P}}$, is the mid-Point of ${\text{AB}}$ and ${\text{Q}}$ is the mid-point of ${\text{CD}}$

But the line joining the mid-point of a chord to the centre of the circle is perpendicular to the

chord.

$OP \bot AB$ and $OQ \bot CD$

$\angle OPB = \angle OQD = {90^\circ }$

$\angle OPB + \angle OQD = {180^\circ }$

Hence,  ${\text{AB}}||{\text{CD}}$.

16. ${\text{AB}}$ and ${\text{CB}}$ are two chords of circle. Prove that BO bisects $\angle ABC$.

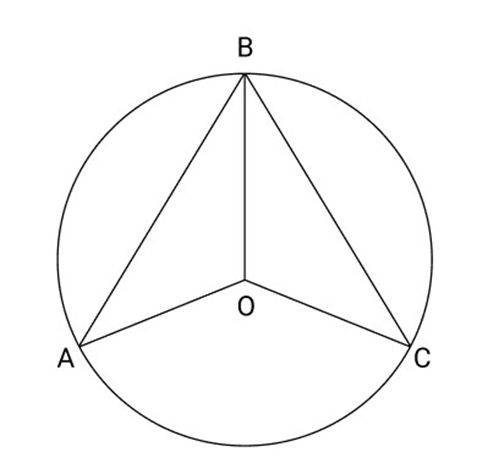
Ans: Join OA and OC

In $\vartriangle OAB$ And $\Delta OCB$

${\text{OA}} = {\text{OC}}$ (radii of circle)

${\text{OB}} = {\text{OB}}$ (common)

${\text{AB}} = {\text{CB}}$ (given)

$\Delta OAB = \Delta OCB$ (by SSS )

$\angle ABO = \angle CBO$

Hence, BO bisects $\angle ABC$

17. If ${\text{BC}}$ is diameter of circle with centre ${\text{O}}$ and ${\text{OD}}$ is $ \bot $ to chord AB so prove ${\text{CA}} = 2{\text{OD}}$

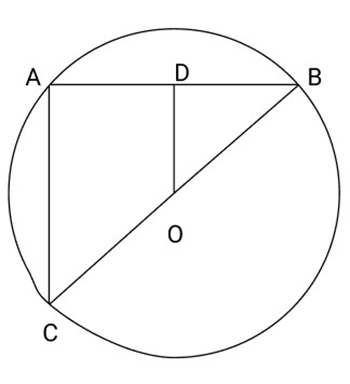
Ans:  Join AC Given that \[{\text{OD}} \bot {\text{AB}}\]

\[{\text{D}}\]is the mid-point of \[{\text{AB}}\]

O is the mid-Point of BC

Now in \[\Delta {\text{ABC}},\]

OD is the line joining the mid points of sides \[{\text{BC}}\]and \[{\text{AB}}\]

\[OD = \dfrac{1}{2}AC\]

$AC = 2OD$

$CA = 2OD$

Hence proved.

18. Given a method to find the centre of a circle

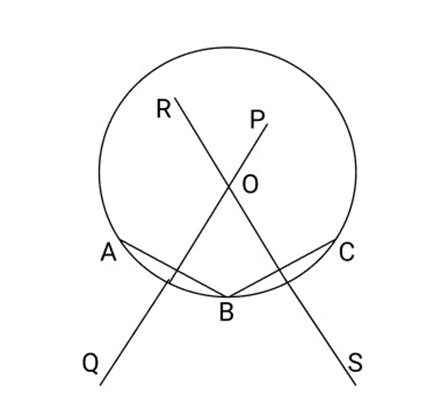
Ans:  Take three distinct points (non-collinear) \[{\text{A, B}}\]and \[{\text{C}}\]on the circle. Join \[{\text{AB}}\]and \[{\text{BC}}\]Draw bisectors \[{\text{PQ}}\]and \[{\text{RS}}\]of \[{\text{AB}}\]and \[{\text{BC}}\]respectively, to intersect at \[{\text{O}}\]

Now, \[{\text{P,}}\]is the centre of the circle.

19. ${\text{C}}$ point is taken so that $m\angle CAB = {\mathbf{3}}{{\mathbf{0}}^{\mathbf{0}}}$ from a semi-circle with AB as diameter. So find $m\angle ACB$ and $m\angle ABC$.

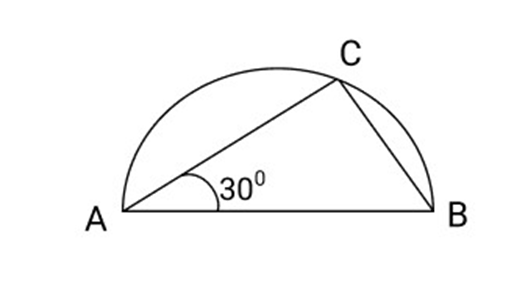
Ans: ${\text{AB}}$ is a diameter and ${\text{C}}$ is a point on the semi-circle

$m\angle ACB = {90^\circ }$

$m\angle CAB = {30^\circ }$

In $\vartriangle ACB$,

$m\angle ABC + {30^\circ } + {90^\circ } = {180^\circ }$

$m\angle ABC + {120^\circ } = {180^\circ }$

$m\angle ABC = {180^\circ } - {120^\circ } = {60^\circ }$

$m\angle ACB = {90^\circ }$ and $m\angle ABC = {60^\circ }$

20. Two different circle can't interact each other at more than two points so, prove it.

Ans: Let the two different circles intersect in three points ${\text{A}},{\text{B}},{\text{C}}$. Then these points ${\text{AB}}$ and ${\text{C}}$ one non-collinear.

We know that through three non-collinear Points, one and only one circle can pass so, it contradicts the hypothesis.

21. In the given figure, $\mathrm{O}$ is the centre of the circle $\mathrm{OB}=5 \mathrm{~cm}$. Distance from $\mathrm{O}$ to chord $\mathrm{OP}$ is $3 \mathrm{~cm}$. Find the length of $\mathrm{AB}$.

Ans: Perpendicular drawn from the centre to the chord bisects the chord.

$AP = PB = \dfrac{1}{2}AB$

In right angled triangle BPO,

$O{B^2} = O{P^2} + B{P^2}$

${(5)^2} = {(3)^2} + {(BP)^2}$

$(BP = \sqrt {16}  = 4\;{\text{cm}})$

$AB = 2BP = 2 \times 4 = 8\;{\text{cm}}$

Hence, the length of chord is equal to 8 cm.

22. If OA is perpendicular to ${\text{CB}}$ and OB is equal to 5cm and OA is equal to 3cm, find the length of ${\text{AB}}$?

Ans: $OA \bot CB$

In right angles triangle ${\text{OAB}}$,

$O{B^2} = O{A^2} + A{B^2}$

$O{B^2} - O{A^2} = A{B^2}$

$25 - 9 = A{B^2}$

$A{B^2} = 16$

${\text{AB}} = 4$

23. Prove that ADE is an isosceles triangle if $OD \bot AB$ and $OE \bot AC$

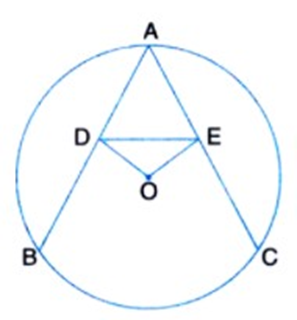
Ans: Given that ${\text{AB}}$ and ${\text{AC}}$ is two equal chords of the circle with centre ${\text{O}}$,

$OD \bot AB$ And $OE \bot AC$

$OD = OE$ (Equal chords are equidistant)

$\angle ODE = \angle OED \ldots  \ldots  \ldots .(i)$

$\angle ODA = \angle OEA \ldots  \ldots  \ldots (ii)$

Subtracting (i) from (ii)

$\angle ODA - \angle OD = \angle OEA - \angle OED$

$\angle ADE = \angle AED$

${\text{AD}} = {\text{AE}}$

$ \Rightarrow ADE$ is an isosceles $\Delta $

24. Prove that the exterior angle formed by producing a side of a cyclic quadrilateral is equal to the interior opposite angle.

Ans: $\angle ABC + \angle ADC = {180^\circ }$ (Opposite angles of a cyclic quadrilateral)

$\angle ABC + \angle CBE = {180^\circ }$

$\angle ABC + \angle ADC = \angle ABC + \angle CBE$

$\angle ADC = \angle CBE$

$\angle CBE = \angle ADC$

25. Show that $\angle OMN = \angle ONM$ if ${\text{AB}}$ and ${\text{CD}}$ are two equal chord.

Ans: We know that equal chords of a circle are equidistant from the centre

$AB = CD \Rightarrow OM = ON$

In $\Delta OMN$,

$OM = ON$

$\angle OMN = \angle ONM$

26. From the above question. Show that $\angle BMN = \angle DNM$

Ans: $OM \bot AB$ And $ON \bot CD$

$\angle OMD = \angle OND = {90^\circ }$

Adding equal to equals we get

$\angle OMN + \angle OMB = \angle ONM + \angle OND$

$\angle BMN = \angle DNM$

27. Show that $\angle AOB = \angle COD$ if OA and OC are radii of same circle. \[{\text{OB}}\]and \[{\text{OD}}\]are also radii of same circle.

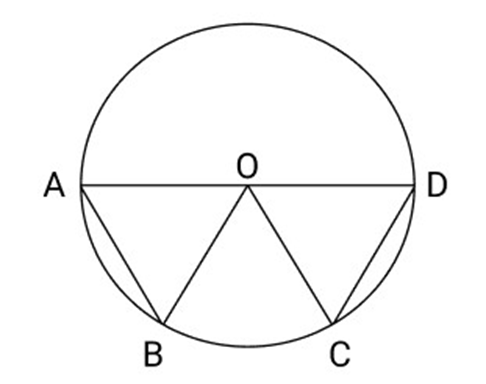
Ans: In $\Delta {\text{AOB}}$ and $\Delta {\text{COD}}$

${\text{OA}} = {\text{OC}}$ (radii of same circle)

${\text{OB}} = {\text{OD}}$ (radii of same circle)

$\Delta {\text{AOB}} \cong \Delta {\text{COD}}$ (by SSS)

$\angle AOB = \angle COD[{\text{CPCT}}]$

28. Prove that OM Bisect AB. If $OM \bot $ AB.

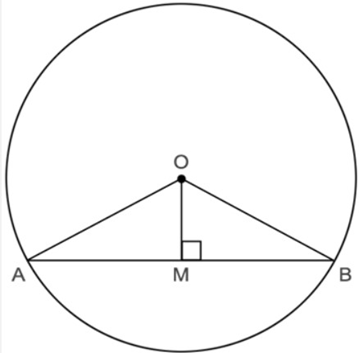
Ans: ${\text{AB}}$ is a chord of the circle with centre ${\text{O}}$.

${\text{OM}} \bot {\text{AB}}$

${\text{OA}} = {\text{OB}}$ (radii of same circle)

${\text{OM}} = {\text{OM}}$ (common)

$\Delta {\text{AOB}} \cong \Delta {\text{COD}}$ (by SSS)

$\angle {\text{OMA}} = \angle {\text{OMB}}$\[[{\text{each }}{\kern 1pt} {90^0}]\] 

$\Delta {\text{OAM}} \cong \Delta {\text{OBM}}$ (by SAS)

${\text{AB}} = {\text{BM}}$

Hence OM bisects AB

29. Prove that ${\text{OM}} \bot {\text{AB}}$ if ${\text{AB}}$ is chord of the circle with centre O. ${\text{O}}$ is joined to the mi point ${\mathbf{M}}$ and ${\text{AB}}$.

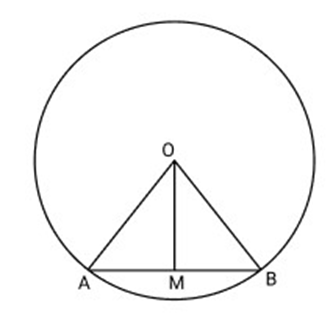
Ans: ${\text{O}}$ is joined to the mid-point ${\text{M}}$ to ${\text{AB}}$

${\text{OM}} = {\text{OM}}$ (common)

${\text{AM}} = {\text{MB}}$ (M is midpoint of AM)

${\text{OA}} = {\text{OB}}$ (radii of same circle)

$\Delta {\text{AOB}} \cong \Delta {\text{COD}}$ (by SSS)

$\angle {\text{OMA}} = \angle {\text{OMB}}({\text{CPCT}})$

But $\angle {\text{OMA}} + \angle {\text{OMB}} = {180^\circ }$ (linear pair)

$\because \angle OMA = \angle OMB)$

$\therefore \angle OMA = \dfrac{{{{180}^\circ }}}{2} = {90^\circ }$

Thus, $\angle {\text{OMA}} = \angle {\text{OMB}} = {90^\circ }$

Hence, \[{\text{OM}} \bot {\text{AB}}\] 

30. ABCD is a cyclic quadrilateral in a circle with centre \[{\text{O}}.\]Prove that $\angle A + \angle C = {180^\circ }$

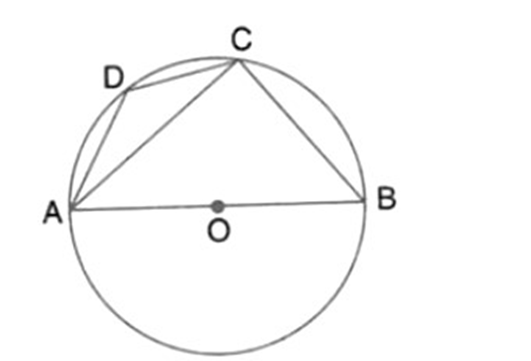
Ans: If we join ${\text{OD}}$ and ${\text{OB}}$, we can get $\angle {\text{DOB}} = 2\angle {\text{C}},\angle {\text{DOB}} = 2\angle {\text{A}}$

$2(\angle {\text{A}} + \angle {\text{C}}) = \angle {\text{DOB}} + $ reflex $\angle {\text{DOB}} = {360^\circ }$

$\angle {\text{A}} + \angle {\text{C}} = {180^\circ }$

Short Answer Type Questions: (3 Marks)

1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.

Ans: I Part: Two circles are said to be congruent if and only if one of them can be superposed on the other so as to cover it exactly

Let ${\text{C}}({\text{O}},r)$ and ${\text{C}}\left( {{{\text{O}}^\prime },{\text{s}}} \right)$ be two circles. Let us imagine that the circle ${\text{C}}\left( {{{\text{O}}^\prime },{\text{s}}} \right)$ is superposed on ${\text{C}}({\text{O}},r)$ so that ${\text{O}}$ ' coincide with ${\text{O}}$. Then it can easily be seen that ${\text{C}}\left( {{{\text{O}}^\prime },{\text{s}}} \right)$will cover ${\text{C}}({\text{O}},r)$ completely if and only if

Hence, we can say that two circles are congruent, if and only if they have equal radii.

II Part: Given: In a circle $(0,r),AB$ and $C D$ are two equal chords, subtend $\angle AOB$ and $\angle $COB at the centre.

To Prove: $\angle {\text{AOB}} = \angle {\text{COD}}$

Proof: In $\Delta {\text{AOB}}$ and $\Delta {\text{COD}}$,

${\text{AB}} = {\text{CD}}$ (Given)

${\text{AO}} = {\text{CO}}$ (Radii of the same circle)

${\text{BO}} = {\text{DO}}$ (Radii of the same circle)

$\therefore \Delta {\text{AOB}} \cong \Delta {\text{COD}}[{\text{By}}$ (SSS axiom)

$ \Rightarrow \angle {\text{AOB}} = \angle {\text{COD}}[{\text{ByCPCT}}]$

Hence Proved.

2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal

Ans: Given: In a circle $({\text{O}},r),{\text{AB}}$ and ${\text{CD}}$ subtend two angles at the centre such that $\angle {\text{AOB}} = $$\angle {\text{COD}}$

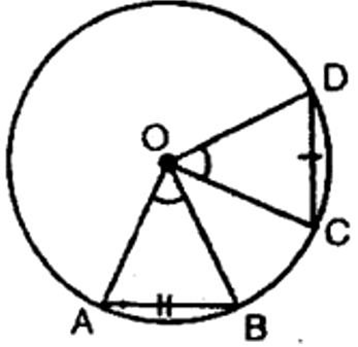
To Prove: $AB = CD$

Proof: In $\Delta {\text{AOB}}$ and $\Delta {\text{COD}}$,

${\text{AO}} = {\text{CO}}$ (Radii of the same circle)

${\text{BO}} = {\text{DO}}$ (Radii of the same circle)

$\angle {\text{AOB}} = \angle {\text{COD}}$ (Given)

$\therefore \Delta {\text{AOB}} \cong \Delta {\text{COD}}$ (By SAS axiom)

$ \Rightarrow {\text{AB}} = {\text{CD}}{\kern 1pt} {\kern 1pt} \,{\text{ }}[{\text{ByCPCT}}]$

Hence proved.

3. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?

Ans: From the figure, we observe that when different pairs of circles are drawn, each pair have two points (say A and B) in common.

Maximum number of common points are two in number.

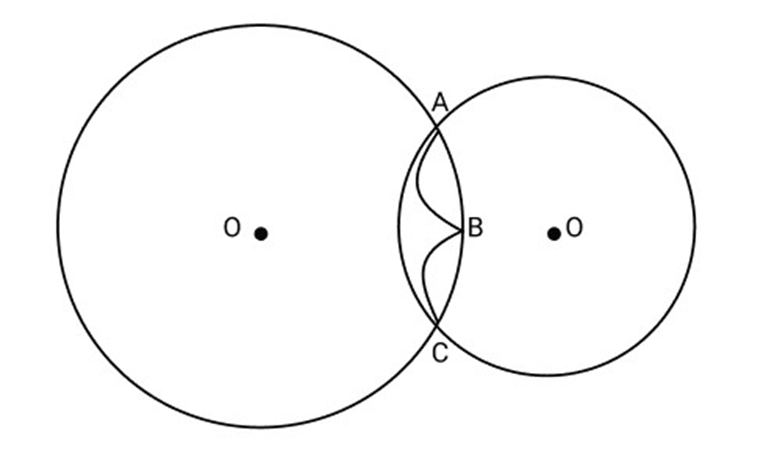
Suppose two circles $C(0,r)$ and $C\left( {{0^\prime },s} \right)$ intersect each other in three points, say A, B and C.

Then \[A,B\]and $C$ are non-collinear points.

We know that:

There is one and only one circle passing through three non-collinear points.

Therefore, a unique circle passes through ${\text{A}},{\text{B}}$ and ${\text{C}}$.

$ \Rightarrow {\text{O}}$' coincides with ${\text{O}}$ and $s = r$.

A contradiction to the fact that $C\left( {{O^\prime },s} \right) \ne C(O,r)$

$\therefore $ Our supposition is wrong.

Hence two different circles cannot intersect each other at more than two points.

4. Suppose you are given a circle. Give a construction to find its centre.

Ans. Steps of construction:

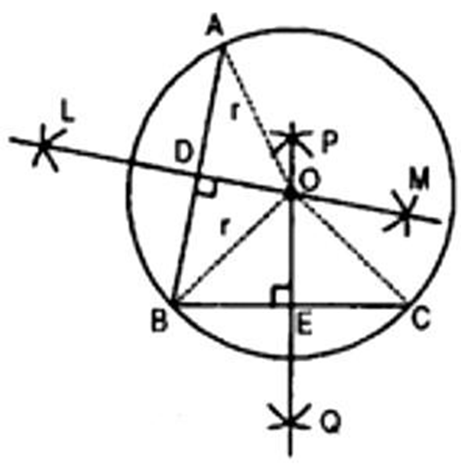
(a) Take any three points ${\text{A}},{\text{B}}$ and ${\text{C}}$ on the circle.

(b) Join ${\text{AB}}$ and ${\text{BC}}$.

(c) Draw perpendicular bisector say LM of ${\text{AB}}$.

(d) Draw perpendicular bisector PQ of BC.

(e) Let LM and PQ intersect at the point ${\text{O}}$.

Then ${\text{O}}$ is the centre of the circle.

Verification:

O lies on the perpendicular bisector of ${\text{AB}}$.

$\therefore {\text{OA}} = {\text{OB}} \ldots  \ldots  \ldots .$ (i)

O lies on the perpendicular bisector of \[{\text{BC}}{\text{.}}\]

$\therefore {\text{OB}} = {\text{OC}} \ldots  \ldots  \ldots ..$ (ii)

From eq. (i) and (ii), we observe that

${\text{OA}} = {\text{OB}} = {\text{OC}} = r$ (say)

Three non-collinear points A, B and $C$ are at equal distance $(r)$ from the point $O$ inside the circle.

Hence ${\text{O}}$ is the centre of the circle.

5. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.

Ans: Given: Let $C(0,r)$ and $C\left( {{O^\prime },{r^\prime }} \right)$ be two circles intersecting at $A$ and \[{\text{B}}.\]\[{\text{AB}}\]is the common chord.

To prove: OO' is the perpendicular bisector of the chord AB.

Construction: Join OA, OB, O'A, O'B.

Proof: In triangles OAO' and OBO',

${\text{OA}} = {\text{OB}}$ (Each radius)

${{\text{O}}^\prime }{\text{A}} = {{\text{O}}^\prime }{\text{B}}$ (Each radius)

${\text{O}}{{\text{O}}^\prime } = {\text{O}}{{\text{O}}^\prime }$ (Common)

$\therefore \Delta {\text{OA}}{{\text{O}}^\prime } \cong \Delta {\text{OB}}{{\text{O}}^\prime }$ (By SSS congruency)

$ \Rightarrow \angle {\text{AO}}{{\text{O}}^\prime } = \angle {\text{BO}}{{\text{O}}^\prime }{\kern 1pt} {\kern 1pt} \,[{\text{ByCPCT}}]$

$ \Rightarrow \angle {\text{AOM}} = \angle {\text{BOM}}$

Now in $\Delta {\text{AOB}},{\text{OA}} = {\text{OB}}$

And $\angle {\text{AOB}} = \angle {\text{OBA}}$ (Proved earlier)

Also $\angle {\text{AOM}} = \angle {\text{BOM}}$

$\therefore $ Remaining $\angle {\text{AMO}} = \angle {\text{BMO}}$

$ \Rightarrow \angle {\text{AMO}} = \angle {\text{BMO}} = {90^\circ }$ (Linear pair)

$ \Rightarrow {\text{OM}} \bot {\text{AB}}$

$ \Rightarrow {00^\prime } \bot {\text{AB}}$

Since ${\text{OM}} \bot {\text{AB}}$

$\therefore {\text{M}}$ is the mid-point of ${\text{AB}}$.

Hence ${\text{OO}}$ ' is the perpendicular bisector of ${\text{AB}}$.

6. Two circles of radii $5\;{\text{cm}}$ and $3\;{\text{cm}}$ intersect at two points and the distance between their centers is $4\;{\text{cm}}$. Find the length of the common chord.

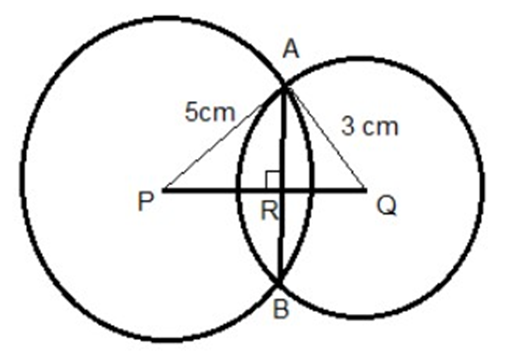
Ans: Let two circles with centres 0 and O' intersect each other at points ${\text{A}}$ and ${\text{B}}$. On joining ${\text{A}}$ and B, AB is a common chord.

Radius ${\text{OA}} = 5\;{\text{cm}}$, Radius ${{\text{O}}^\prime }{\text{A}} = 3\;{\text{cm}}$,

Distance between their centers ${\text{O}}{{\text{O}}^\prime } = 4\;{\text{cm}}$

In triangle ${\text{AOO}}$,

${5^2} = {4^2} + {3^2}$

$ \Rightarrow 25 = 16 + 9$

$ \Rightarrow 25 = 25$

Hence ${\text{AOO}}$ ' is a right triangle, right angled at ${\text{O}}$ '.

Since, perpendicular drawn from the center of the circle bisects the chord.

Hence ${\text{O}}$ ' is the mid-point of the chord ${\text{AB}}$. Also ${\text{O}}$ ' is the centre of the circle II.

Therefore, length of chord ${\text{AB}} = $ Diameter of circle II

$\therefore $ Length of chord $AB = 2 \times 3 = 6\;{\text{cm}}$

7. If a line intersects two concentric circles (circles with the same centre) with centre 0

at A, B, C and D, prove that ${\text{AB}} = {\text{CD}}$. (See figure)

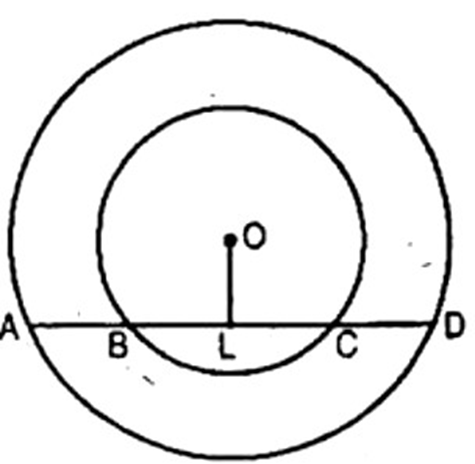
Ans: Given: Line $l$ intersects two concentric circles with centre ${\text{O}}$ at points ${\text{A}},{\text{B}},{\text{C}}$ and ${\text{D}}$.

To prove: ${\text{AB}} = {\text{CD}}$

Construction: Draw OL $ \bot l$

Proof: ${\text{AD}}$ is a chord of outer circle and ${\text{OL}} \bot {\text{AD}}$.

- AL = LD .........(i) [Perpendicular drawn from the centre bisects the chord]

Now, ${\text{BC}}$ is a chord of inner circle and ${\text{OL}} \bot {\text{BC}}$

$\therefore {\text{BL}} = {\text{LC}} \ldots  \ldots $

(ii) (Perpendicular drawn from the centre bisects the chord)

Subtracting (ii) from (i), we get,

${\text{AL}} - {\text{BL}} = {\text{LD}} - {\text{LC}}$

$ \Rightarrow {\text{AB}} = {\text{CD}}$

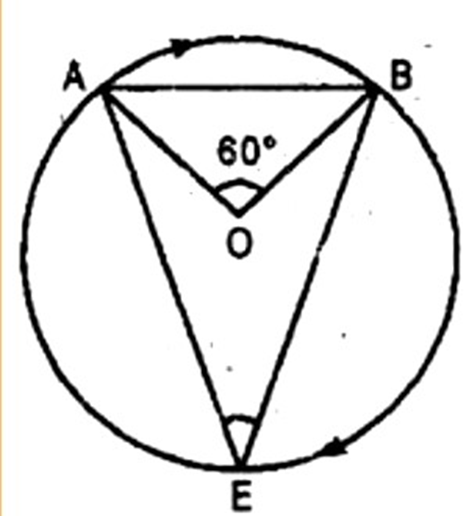
8. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.

Ans: Let ${\text{AB}}$ be the minor arc of circle.

$\therefore $ Chord ${\text{AB}} = $ Radius ${\text{OA}} = $ Radius ${\text{OB}}$

$\therefore \Delta {\text{AOB}}$ is an equilateral triangle.

$ \Rightarrow \angle {\text{AOB}} = {60^\circ }$

Now $m\widehat {{\text{AB}}} + m\widehat {{\text{BA}}} = {360^\circ }$

$ \Rightarrow \angle {\text{AOB}} + \angle {\text{BOA}} = {360^\circ }$

$ \Rightarrow {60^\circ } + \angle {\text{BOA}} = {360^\circ }$

$ \Rightarrow \angle {\text{BOA}} = {360^\circ } - {60^\circ } = {300^\circ }$

${\text{D}}$ is a point in the minor arc.

$\therefore m\widehat {{\text{BA}}} = 2\angle {\text{BDA}}$

$ \Rightarrow \angle {\text{BOA}} = 2\angle {\text{BDA}}$

$ \Rightarrow \angle {\text{BDA}} = \dfrac{1}{2}\angle {\text{BOA}} = \dfrac{1}{2} \times {300^\circ }$

$ \Rightarrow \angle {\text{BDA}} = {150^\circ }$

Thus, angle subtended by major arc, $\widehat {BA}$ at any point $D$ in the minor arc is ${150^\circ }$.

Let $E$ be a point in the major arc $\widehat {BA}$

$\therefore m\widehat {{\text{AB}}} = 2\angle {\text{AEB}}$

$ \Rightarrow \angle {\text{AOB}} = 2\angle {\text{AEB}}$

$ \Rightarrow \angle {\text{AEB}} = \dfrac{1}{2}\angle {\text{AOB}}$

$ \Rightarrow \angle {\text{AEB}} = \dfrac{1}{2} \times {60^\circ } = {30^\circ }$

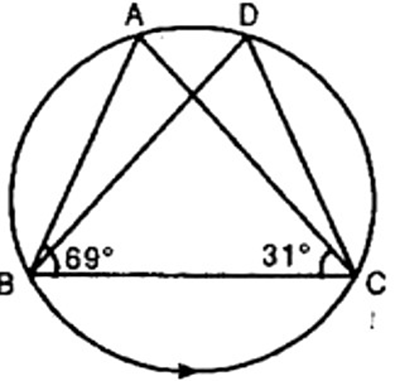
9. In figure, $\angle {\text{ABC}} = {69^\circ },\angle {\text{ACB}} = {31^\circ }$, find $\angle {\text{BDC}}$.

Ans: In triangle ${\text{ABC}}$,

$\angle {\text{BAC}} + \angle {\text{ABC}} + \angle {\text{ACB}} = {180^\circ }$

$ \Rightarrow \angle {\text{BAC}} + {69^\circ } + {31^\circ } = {180^\circ }$

$ \Rightarrow \angle {\text{BAC}} = {180^\circ } - {69^\circ } - {31^\circ }$

$ \Rightarrow \angle {\text{BAC}} = {80^\circ } \ldots  \ldots  \ldots ..({\text{i}})$

Since, ${\text{A}}$ and ${\text{D}}$ are the points in the same segment of the circle.

$\angle {\text{BDC}} = \angle {\text{BAC}}$

(Angles subtended by the same arc at any points in the alternate segment of a circle are equal)

$ \Rightarrow \angle {\text{BDC}} = {80^\circ }$

10. In figure, A, B, C, D are four points on a circle. AC and BD intersect at a point E such that $\angle {\text{BEC}} = {130^\circ }$ and $\angle {\text{ECD}} = {20^\circ }$. Find $\angle {\text{BAC}}$.

Ans: Given: $\angle {\text{BEC}} = {130^\circ }$ and $\angle {\text{ECD}} = {20^\circ }$

$\angle {\text{DEC}} = {180^\circ } - \angle {\text{BEC}} = {180^\circ } - {130^\circ } = {50^\circ }$ (Linear pair)

Now in $\Delta $ DEC,

$\angle {\text{DEC}} + \angle {\text{DCE}} + \angle {\text{EDC}} = {180^\circ }$ (Angle sum property)

$ \Rightarrow {50^\circ } + {20^\circ } + \angle {\text{EDC}} = {180^\circ } \Rightarrow \angle {\text{EDC}} = {110^\circ }$

$ \Rightarrow \angle {\text{BAC}} = \angle {\text{EDC}} = {110^\circ }$ (Angles in same segment)

11. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Ans: Since ${\text{AC}}$ is a diameter.

$\therefore \angle {\text{B}} = \angle {\text{D}} = {90^\circ } \ldots  \ldots  \ldots .$ (i) (Angle in semicircle is right angle)

Similarly, $\angle {\text{A}} = \angle {\text{C}} = {90^\circ } \ldots  \ldots  \ldots $.(ii)

Now AC = BD (Diameters of same circle)

$ \Rightarrow \widehat {{\text{AC}}} \cong \widehat {{\text{BD}}}$ [Arcs opposite to equal chords]

$ \Rightarrow \widehat {{\text{AC}}} - \widehat {{\text{DC}}} \cong \widehat {{\text{BD}}} - \widehat {{\text{DC}}}$

$ \Rightarrow \widehat {{\text{AD}}} \cong \overrightarrow {{\text{BC}}} $

$ \Rightarrow {\text{AD}} = {\text{BC}}[$ Chords opposite to equal arcs] ..........(iii)

Similarly, ${\text{AB}} = {\text{DC}}$..........(iv)

From eq. (i), (ii), (iii) and (iv), we observe that each angles of the quadrilateral is ${90^\circ }$ and opposite sides are equal.

Hence ${\text{ABCD}}$ is a rectangle.

12. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Ans: Given: Two circles intersect each other at points A and B. AP and AQ be their respective diameters.

To prove: Point B lies on the third side PQ.

Construction: Join ${\text{A}}$ and ${\text{B}}$.

Proof: AP is a diameter.

$\therefore \angle 1 = {90^\circ }$

(Angle in semicircle)

Also, AQ is a diameter.

$\therefore \angle 2 = {90^\circ }$

(Angle in semicircle)

$\angle 1 + \angle 2 = {90^\circ } + {90^\circ }$

$ \Rightarrow \angle {\text{PBQ}} = {180^\circ }$

$ \Rightarrow {\text{PBQ}}$ is a line.

Thus point B. i.e. point of intersection of these circles lies on the third side i.e., on PQ.

13. ${\text{ABC}}$ and ADC are two right triangles with common hypotenuse AC. Prove that $\angle {\text{CAD}} = \angle {\text{ABD}}$

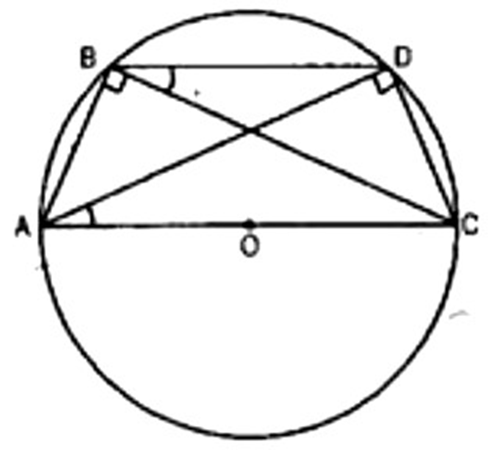
Ans: We have ${\text{ABC}}$ and ADC two right triangles, right angled at ${\text{B}}$ and ${\text{D}}$ respectively.

\[ \Rightarrow \angle {\text{ABC}} = \operatorname{ADC} {\kern 1pt} {\kern 1pt} {\kern 1pt} \] [$\operatorname{Each} {90^0}$]

If we draw a circle with AC (the common hypotenuse) as diameter, this circle will definitely passes through of an arc AC, Because ${\text{B}}$ and ${\text{D}}$ are the points in the alternate segment of an$\operatorname{arc} {\text{AC}}$.

Now we have $\widehat {{\text{CD}}}$ subtending $\angle {\text{CBD}}$ and $\angle {\text{CAD}}$ in the same segment.

$\therefore \angle {\text{CAD}} = \angle {\text{CBD}}$

Hence proved.

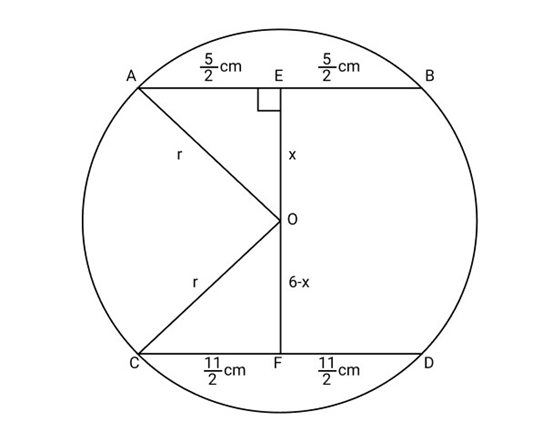
14. Two chords ${\text{AB}}$ and CD of lengths $5\;{\text{cm}}$ and $11\;{\text{cm}}$ respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between ${\text{AB}}$ and ${\text{CD}}$ is $6\;{\text{cm}}$, find the radius of the circle.

Ans: Let $O$ be the centre of the circle.

Join ${\text{OA}}$ and ${\text{OC}}$.

Since perpendicular from the centre of the circle to the chord bisects the chord.

$\therefore {\text{AE}} = {\text{EB}} = \dfrac{1}{2}{\text{AB}} = \dfrac{1}{2} \times {\mathbf{5}} = \dfrac{5}{2}\;{\text{cm}}$

And ${\text{CF}} = {\text{FD}} = \dfrac{1}{2}{\text{CD}} = \dfrac{1}{2} \times 11 = \dfrac{{11}}{2}\;{\text{cm}}$

Let ${\text{OE}} = x$

$\therefore {\text{OF}} = 6 - x$

Let radius of the circle be $r$.

In right angled triangle AEO,

${\text{A}}{{\text{O}}^{\text{2}}}{\text{ = A}}{{\text{E}}^{\text{2}}}{\text{ + O}}{{\text{E}}^{\text{2}}}$

(Using Pythagoras theorem)

$ \Rightarrow {r^2} = {\left( {\dfrac{5}{2}} \right)^2} + {x^2}{\kern 1pt} {\kern 1pt} {\kern 1pt}  \ldots  \ldots  \ldots ..({\text{i}})$

Again, In right angled triangle ${\text{CFO}}$,

$O{C^2} = C{F^2} + O{F^2}$

(Using Pythagoras theorem)

$ \Rightarrow {r^2} = {\left( {\dfrac{{11}}{2}} \right)^2} + {(6 - x)^2}{\kern 1pt} {\kern 1pt} \, \ldots  \ldots  \ldots ..\left( {ii} \right)$

Equating eq. (i) and (ii),

${\left( {\dfrac{5}{2}} \right)^2} + {x^2} = {\left( {\dfrac{{11}}{2}} \right)^2} + {(6 - x)^2}$

$ \Rightarrow \dfrac{{25}}{4} + {x^2} = \dfrac{{121}}{4} + 36 + {x^2} - 12x$

$ \Rightarrow 12x = \dfrac{{121}}{4} - \dfrac{{25}}{4} + 36$

$ \Rightarrow 12x = \dfrac{{96}}{4} + 36$

$ \Rightarrow 12x = 24 + 36$

$ \Rightarrow 12x = 60$

$ \Rightarrow x = 5$

Now from eq. (i),

${r^2} = \dfrac{{25}}{4} + {x^2}$

$ \Rightarrow {r^2} = \dfrac{{25}}{4} + {5^2}$

$ \Rightarrow {r^2} = \dfrac{{125}}{4}$

$ \Rightarrow r = \dfrac{{5\sqrt 5 }}{2}\;{\text{cm}}$

Hence radius of the circle is $\dfrac{{5\sqrt 5 }}{2}\;{\text{cm}}$.

15. The lengths of two parallel chords of a circle are $6\;{\text{cm}}$ and $8\;{\text{cm}}$. If the smaller chord is at a distance of $4\;{\text{cm}}$ from the centre, what is the distance of the other chord form the centre?

Ans: Let ${\text{AB}} = 6\;{\text{cm}}$ and ${\text{CD}} = 8\;{\text{cm}}$ are the chords of circle with centre ${\text{O}}$.

Join ${\text{OA}}$ and ${\text{OC}}$.

Since perpendicular from the centre of the circle to the chord bisects the chord.

$\therefore {\text{AE}} = {\text{EB}} = \dfrac{1}{2}{\text{AB}} = \dfrac{1}{2} \times 6 = 3\;{\text{cm}}$

And ${\text{CF}} = {\text{FD}} = \dfrac{1}{2}{\text{CD}} = \dfrac{1}{2} \times 8 = 4\;{\text{cm}}$

Perpendicular distance of chord ${\text{AB}}$ from the centre ${\text{O}}$ is ${\text{OE}}$.

$\therefore O{\text{OE}} = 4\;{\text{cm}}$

Now in right angled triangle AOE,

$O{A^2} = A{E^2} + O{E^2}$ (Using Pythagoras theorem)

$ \Rightarrow {r^2} = {3^2} + {4^2}$

$ \Rightarrow {r^2} = 9 + 16 = 25$

$ \Rightarrow r = 5\;{\text{cm}}$

Perpendicular distance of chord CD from the center ${\text{O}}$ is ${\text{OF}}$.

Now in right angled triangle OFC,

$O{C^2} = C{F^2} + O{F^2}$ (Using Pythagoras theorem)

$ \Rightarrow {r^2} = {4^2} + O{F^2}$

$ \Rightarrow {5^2} = 16 + O{F^2}$

$ \Rightarrow O{F^2} = 9$

$ \Rightarrow {\text{OF}} = 3\;{\text{cm}}$

Hence distance of other chord from the centre is $3\;{\text{cm}}$.

16. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced it necessary) at ${\text{E}}$. Prove that ${\text{AE}} = {\text{AD}}$.

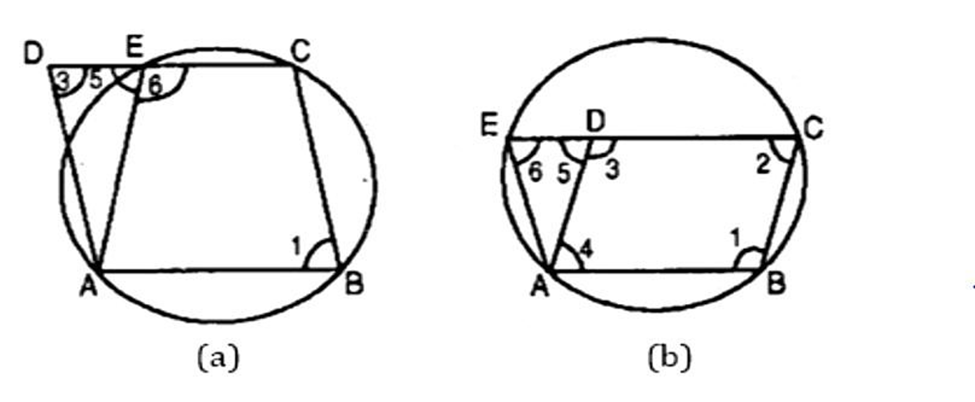
Ans: In figure (a),

ABCD is a parallelogram.

$ \Rightarrow \angle 1 = \angle 3 \ldots  \ldots  \ldots .$ (i)

${\text{ABCE}}$ is a cyclic quadrilateral.

(ii) $\therefore \angle 1 + \angle 6 = {180^\circ } \ldots  \ldots  \ldots .$.

And $\angle 5 + \angle 6 = {180^\circ } \ldots  \ldots  \ldots $.(iii) (Linear pair)

From eq. (ii) and (iii), $\angle 1 = \angle 5 \ldots  \ldots  \ldots $ (iv)

Now, from eq. (i) and (iv),

$\angle 3 = \angle 5 \Rightarrow {\text{AE}} = {\text{AD}}$ (Sides opposite to equal angles are equal)

In figure (b),

${\text{ABCD}}$ is a parallelogram.

$\therefore \angle 1 = \angle 3$ and $\angle 2 = \angle 4$

Also  and $B C$ meets them.

$\therefore \angle 1 + \angle 2 = {180^\circ } \ldots  \ldots  \ldots .$ (i)

And  and EC meets them.

$\therefore \angle 5 = \angle 2 \ldots  \ldots  \ldots .$ (ii) (Corresponding angles)

Since ${\text{ABCE}}$ is a cyclic quadrilateral.

$\therefore \angle 1 + \angle 6 = {180^\circ } \ldots  \ldots  \ldots .$ (iii)

From eq. (i) and (iii),

$\angle 1 + \angle 2 = \angle 1 + \angle 6$

$ \Rightarrow \angle 2 = \angle 6$

But from eq. (ii), $\angle 2 = \angle 5$

$\therefore \angle 5 = \angle 6$

Now in triangle AED,

$\angle 5 = \angle 6$

$ \Rightarrow {\text{AE}} = {\text{AD}}$ (Sides opposite to equal angles)

Hence in both the cases, ${\text{AE}} = {\text{AD}}$

17. Two congruent circles intersect each other at points ${\text{A}}$ and B. Through A any line segment PAQ is drawn so that ${\mathbf{P}}$, Q lie on the two circles. Prove that ${\mathbf{BP}} = {\mathbf{BQ}}$.

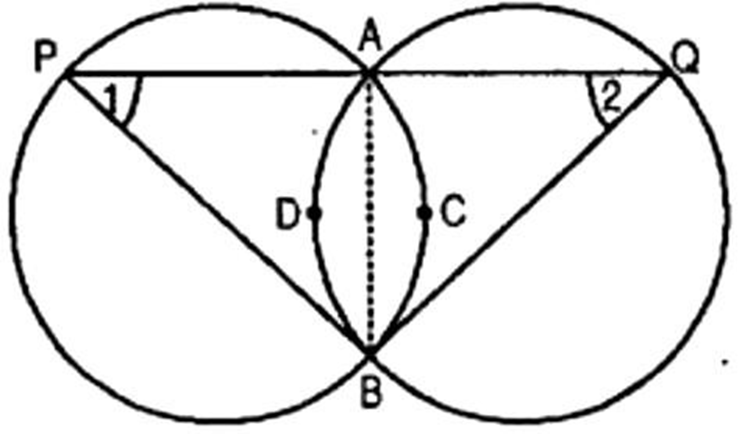
Ans: Given: Two equal circles intersect in ${\text{A}}$ and ${\text{B}}$.

A straight line through A meets the circles in P and Q.

To prove: ${\text{BP}} = {\text{BQ}}$

Construction: Join ${\text{A}}$ and ${\text{B}}$.

Proof: ${\text{AB}}$ is a common chord and the circles are equal.

$\therefore $ Arc about the common chord are equal, i.e.,

$\widehat {{\text{ACB}}} = \widehat {{\text{ADB}}}$

Since equal arcs of two equal circles subtend equal angles at any point on the remaining part

of the circle, then we have,

$\angle 1 = \angle 2$

In triangle PBQ,

$\angle 1 = \angle 2$ (proved)

- Sides opposite to equal angles of a triangle are equal.

Then we have, ${\text{BP}} = {\text{BQ}}$

18. Pair of opposite sides of a cyclic quadrilateral are equal, Prove that the other two sides are parallel.

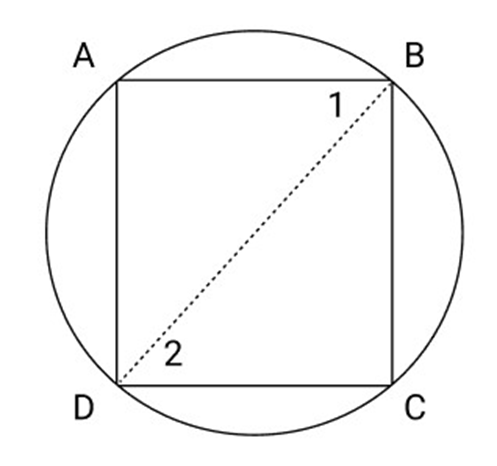
Ans: Given: A cyclic quadrilateral ${\text{ABCD}}$ in which ${\text{AD}} = {\text{BC}}$

To Prove: ${\text{AB}}||{\text{CD}}$

Construction: Join B and D

Proof: ${\text{AD}} = {\text{BC}}$

$A\hat D = \widehat {BC}$

$\angle 1 = \angle 2$

But these are alternate angles

${\text{AB}}||{\text{CD}}$

19. Prove that the centre of the circle through A, B, C, D is the Point intersection of its diagonals.

Ans: Given: A cyclic rectangle ABCD in which diagonals AC and BD intersect at Point 0

To Prove: ${\text{O}}$ is the centre of the circle

Proof: ${\text{ABCD}}$ is a rectangle

$AC = BD$

Now as the diagonals ${\text{AC}}$ and ${\text{BD}}$ are intersecting at ${\text{O}}$

${\text{AO}} = {\text{OC}},{\text{OB}} = {\text{OD}}$

${\text{AO}} = {\text{OC}} = {\text{OB}} = {\text{OD}}$

A, B, C, D lie on the same circle.

20. In isosceles triangle ABC, AD = AE and D and ${\mathbf{E}}$ are equal on side ${\text{AB}}$ and AC so prove that B,C,E and $\Delta $ are cyclic.

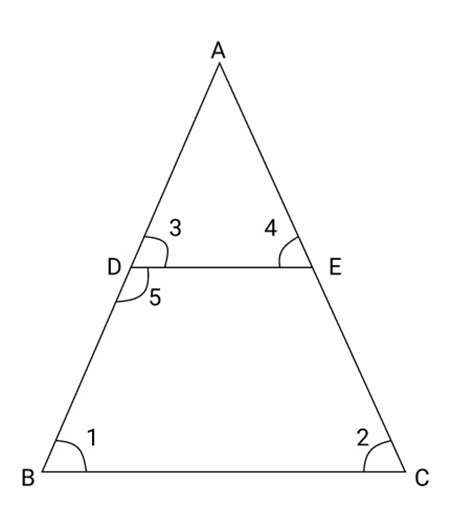
Ans: Given - In $\triangle A B C, A B=A C$ and $D$ and $E$ are points on $A B$ and $A C$

Such that $A D=A E$. DE is joined.

To prove $B, C, E, D$ are concyclic.

Proof $-\ln \triangle \mathrm{ABC}, \mathrm{AB}=\mathrm{AC}$

$\therefore \angle B=\angle C \quad$ (Angles opposite to equal sides)

Similarly, In $\triangle \mathrm{ADE}, \mathrm{AD}=\mathrm{AE} \quad$ (Given)

$\therefore \angle \mathrm{ADE}=\angle \mathrm{AED} \quad$ (Angles opposite to equal sides)

In $\triangle \mathrm{ABC}_{1}$

$\therefore \frac{A D}{A B}=\frac{A E}{A C}$

$\mathrm{DE} \| \mathrm{BC}$

$\therefore \angle A D E=\angle B \quad$ (corresponding angles)

But $\angle B=\angle C \quad$ (proved)

$\therefore$ Ext $\angle \mathrm{ADE}=$ its interior opposite $\angle \mathrm{C}$

$\therefore B C E D$ is a cyclic quadrilateral

Hence $B, C, E$ and $D$ are concyclic.

21. If two non - parallel sides of a trapezium are equal, prove that it is cyclic.

Ans: Given: $A B C D$ is a trapezium where AB || DC $\&$ non parallel sides are equal, i.e., $A D=B C$

To prove: $\mathrm{ABCD}$ is cyclic quadrilateral

Construction: We draw $D E \perp A B \& C F \perp A B$

Proof: To prove $\mathrm{ABCD}$ is a cyclic quadrilateral,we prove that sum of one pair of opposite angles is $180^{\circ}$

In $\triangle \mathrm{ADE} \& \triangle \mathrm{BCF}$

$\begin{array}{ll}

\angle A E D & \left.=\angle B F C \quad \text { (Both } 90^{\circ} \text { as } A E \perp D C \& B F \perp D C\right) \\

A D & =B C \quad \text { (Given) }

\end{array}$

$\mathrm{DE}=\mathrm{CF}$ (Distance between parallel sides is equal,)

$\therefore \triangle \mathrm{ADE} \cong \triangle \mathrm{BCF}$ (RHS congruence rule)

So, $\angle \mathrm{DAE}=\angle \mathrm{CBF}$

i.e., $\angle \mathrm{A}=\angle \mathrm{B}$

Now, for parallel lines $A B$ and DC , \& AD is the transversal line.

$\angle A+\angle D=180^{\circ}$(Interior angles on the same side

of transversal are supplementary)

$\angle B+\angle D=180^{\circ}$ (From (1))

So, in $\mathrm{ABCD}$, sum of one pair of opposite angles is $180^{\circ}$ Therefore, $\mathrm{ABCD}$ is a cyclic quadrilateral

Hence proved

22. In circle bisector AD of $\angle BAC$ of $\Delta ABC$ Passes through the center ${\mathbf{O}}$ of the circum

circle of $\Delta ABC$ Prove ${\text{AB}} = {\mathbf{AC}}$

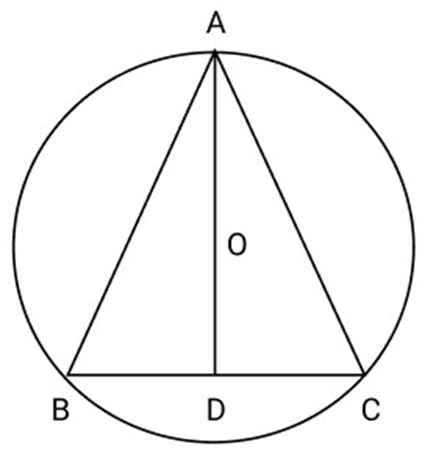
Ans: Draw $OP \bot AB$ and $OQ \bot AC$

In $\vartriangle OPA$ and $\Delta OQA$

$\angle PAO = \angle QAO$

$\angle APO = \angle AQO$

${\text{AO}} = {\text{AO}}$

$\Delta {\text{OPA}} \cong \Delta {\text{OQA}}$

${\text{OP}} = {\text{OQ}}$

Chords ${\text{AB}}$ and ${\text{AC}}$ are equidistant from centre O

${\text{AB}} = {\text{AC}}$

23. Prove that the circle drawn with the equal sides as a diameter passes through the Point D. if ${\text{D}}$ is the mid Point of BC of an isosceles triangle ABC with AB=AC

Ans: Given $-\ln \triangle A B C, A B=A C$ and a circle with $A B$ as diameter is drawn

Which intersects the side $\mathrm{BC}$ and $\mathrm{D}$.

To prove $-\mathrm{D}$ is the mid point of $\mathrm{BC}$

Construction - Join AD.

Proof $-\angle 1=90^{\circ} \quad$ [Angle in a semi circle]

But $\angle 1+\angle 2=180^{\circ} \quad[$ Linear pair]

$\therefore \angle 2=90^{\circ}$

Now in right $\triangle A B D$ and $\triangle A C D$, Hyp. AB = Hyp. AC (Given)

Side AD = AD [ Common]

$\therefore$ By the right Angle - Hypotenuse - side criterion of congruence, we have

$\triangle \mathrm{ABD} \cong \triangle \mathrm{ACD} \quad$ (RHS criterion of congruence)

The corresponding parts of the congruent triangle are congruent.

$\therefore \mathrm{BD}=\mathrm{DC} \quad[\text { c.p.c.t] }$

Hence $D$ is the mid point of $B C$.

24. If a Pair of opposite sides of a cyclic quadrilateral are equal, then the diagonals are also equal.

Ans: Given: A cyclic quadrilateral ${\text{ABCD}}$ in which ${\text{AB}} = {\text{DC}}$

To Prove: diagonal ${\text{AC}} = $ diagonal BD

Proof: $\angle 1 = \angle 2$ (Angle in same segment of circle)

$\angle 3 = \angle 4$

$\angle 1 + \angle 3 = \angle 2 + \angle 4$

$\angle ADC = \angle BAD$

But these are the angles subtended by the diagonals AC and BD in the same circle

$AC = BD$

25. $\angle DBC = {70^\circ }$ and $\angle CAB = {30^\circ }$ find $\angle BCD$

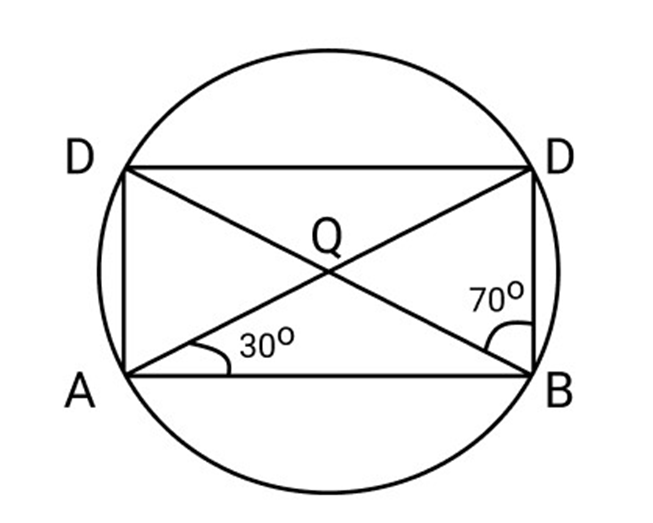
Ans: $\angle DBC = \angle DAC = {70^\circ }$ (Angle in same segment)

$\angle DAB = \angle DAC + \angle CAB$

$ = {70^\circ } + {30^\circ } = {100^\circ }$

$\angle DAB + \angle BCD = \angle {180^\circ }$

${100^\circ } + \angle BCD = {180^\circ }$

$\angle BCD = {180^\circ } - {100^\circ } = {80^\circ }$

26. AB is chord of a circle and AB Produced to ${\text{C}}$ such that \[{\mathbf{BC}} = {\mathbf{OB}}\]and CO joined and produce the circle and meet to ${\text{D}}$ if $\angle ACD = {y^\circ }$ and $\angle AOD = {x^\circ }$, prove that $x = 3y$

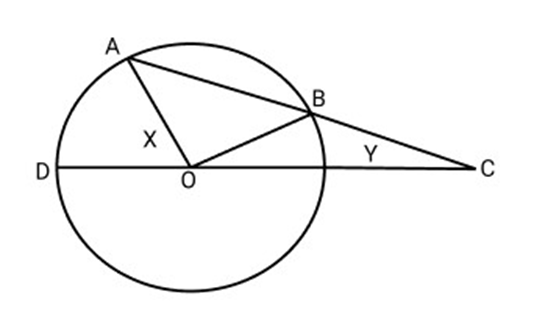
Ans: Proof: In $\vartriangle BOC$,

${\text{BO}} = {\text{BC}}$

$\angle BOC = \angle BCO = y$

In $\vartriangle BOC,CB$ is produced to ${\text{A}}$, forming exterior $\angle OBA$

$\angle OBA = \angle BOC + \angle BCO = y + y = 2y$

${\text{OB}} = {\text{OA}}$ [Radii of the same circle

$\angle OBA = \angle OAB = 2y$

Again in $\vartriangle ACO,$ $CO$ is produced to D, forming exterior $\angle AOD$

$\angle AOD = \angle OAC + \angle ACO$

$x = 2y + y$

$x = 3y$

Hence proved.

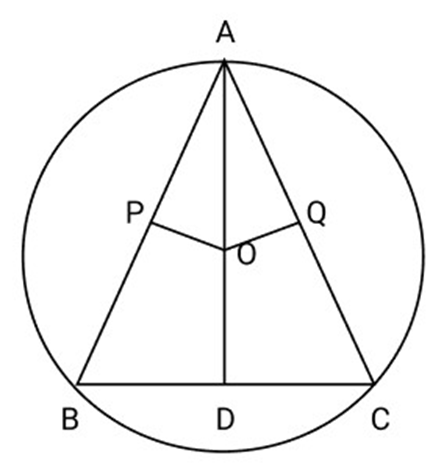
27. Prove that $\angle XPZ = 2(\angle xzy + \angle yxz)$ if ${\mathbf{P}}$ is the centre of circle

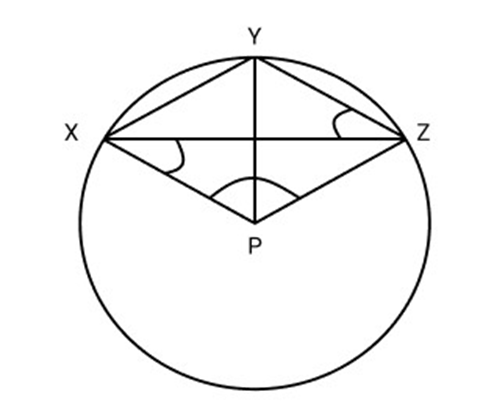
Ans: Given: A circle with centre P, XY and YZ are two chords

To Prove: $\angle XPZ = 2(\angle XZY + \angle YXZ)$

Proof: $\angle XPY = 2\angle XZY \ldots  \ldots  \ldots ..(i)$ (An arc of a circle subtends twice the angle it subtends at any point on the remaining half of the circle.)

Similarly arc YZ subtends $\angle YPZ$ at centre and $\angle YXZ$ at remaining Part of the circle

$\angle YPZ = 2\angle YXZ \ldots  \ldots  \ldots .(ii)$ (An arc of a circle subtends twice the angle it subtends at any point on the remaining half of the circle.)

Adding (i) and (ii) $\angle XPY + \angle YPZ = 2\angle XZY + 2\angle YXZ$

$\angle XPZ = 2(\angle XZY + \angle YXZ)$

28. Prove that OA is the perpendicular bisector of ${\text{BC}}$ if $\overrightarrow {AB}  \cong \widehat {AC}$

Ans: Let OA intersect BC in P produce AO to meet the circle at ${\text{K}}$

Now, AOK is the diameter

$\overline {ABK}  \cong \overline {ACK} $

$A\widehat {BK} - A\hat B = A\vec CK - A\vec C$

$B\hat K \cong \widehat {CK}$

$\angle 1 = \angle 2$

In $\Delta {\text{ABP}}$ and $\Delta {\text{ACP}}$

${\text{AB}} = {\text{AC}}$

\[{\text{AP = AP}}\] (Common)

$\angle 1 = \angle 2$

$\Delta ABP \cong \Delta ACP({\text{SAS}})$

${\text{BP}} = {\text{CP}}$

$\angle APB = \angle APC$

$\angle APB + \angle APC = {180^\circ }$

Each $ = {90^\circ }$

29. Prove that the line joining the midpoint of the two parallel chords of a circle passes through the centre of the circle.

Ans: Let ${\text{AB}}$ and ${\text{CD}}$ be the two parallel chords of the circle with centre ${\text{OP}}$ and ${\text{Q}}$ are the mid-points of ${\text{AB}}$ and ${\text{CD}}$ join OP and ${\text{OQ}}$.

$OP \bot AB$ And $OQ \bot CD$

$\angle POX = {90^\circ }$ And also $\angle QOX = {90^\circ }$

$\angle POX + \angle QOX = {180^\circ }$

POQ is a straight line.

30. ${\text{ABCD}}$ is a quadrilateral in which ${\text{AD}} = {\text{BC}}$ and $\angle ADC = \angle BCD$ show A, B, C, D lie on a circle

Ans: Join ${\text{AC}}$ and ${\text{BD}}$

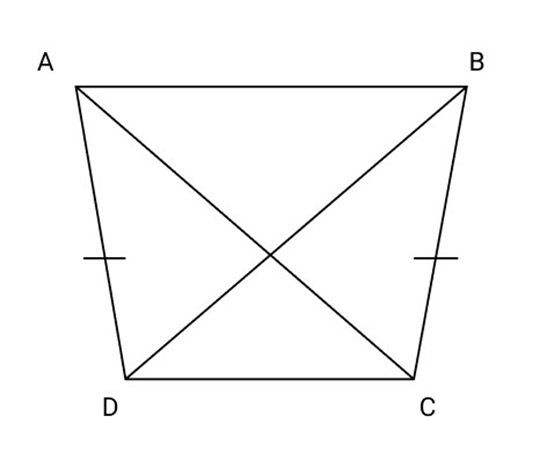
In $\Delta ACD$ and $\Delta BDC$

$AD = BC$

$\angle ADC = \angle BCD$

$DC = DC$ (Common)

$\vartriangle ACD \cong \Delta BDC$ (By S.A.S]\)

$\angle DAC = \angle DBC$

As these are two equal angles on the same side of a line segment ${\text{CD}}$.

The four points ${\text{A}},{\text{B}},{\text{C}}$ and ${\text{D}}$ are concyclic.

31. Prove that diagonal is also equal when pair of opposite sides of a cyclic quadrilateral are equal.

Ans: Given: A cyclic quadrilateral ${\text{ABCD}}$ in which ${\text{AB}} = {\text{DC}}$

To Prove: diagonal AC= Diagonal BD

Proof: $\angle 1 = \angle 2$ (Angle in the same segment)

$\angle 3 = \angle 4$

$\angle 1 + \angle 3 = \angle 2 + \angle 4$

$\angle ADC = \angle BAC$

But these are the angle subtended by the diagonal AC and BD in the same circle.

$AC = BD$

32. In ABCD cyclic quadrilateral diagonal Intersect at $Q.\angle DBC = {70^\circ }$ and

$\angle CAB = {30^\circ }$ so find $\angle BCD$

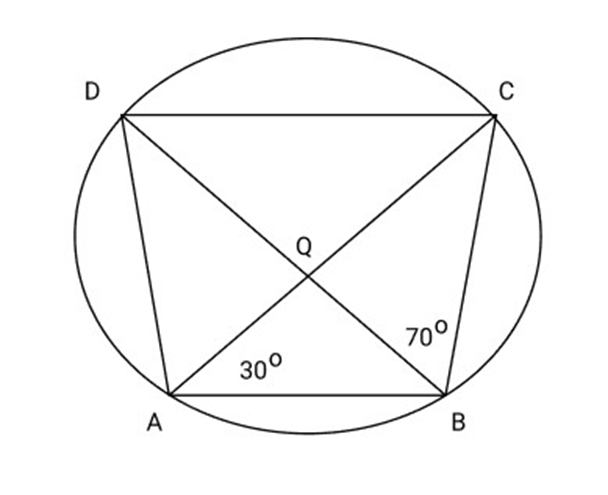
Ans: $\angle DBC = \angle DAC = {70^\circ }$ (Angle in the same segment)

$\angle DAB = \angle DAC + \angle CAB$

${70^\circ } + {30^\circ } = {100^\circ }$

$\angle DAB + \angle BCD = {180^\circ }$

${100^\circ } + \angle BCD = {180^\circ }$

$\angle BCD = {180^\circ } - {100^\circ } = 80$

33. Find the value of $x$ if A, B, C, D are concyclic points.

Ans: $\angle ABC = {180^\circ } - {130^\circ }$ (Linear pair)

$ = {50^\circ }$

$\angle x = \angle ABC$ (Exterior angle of a cyclic quadrilateral = interior Opp. angle)

$\angle x = {50^\circ }$

34. Calculate the measure of $\angle PQB$, where ${\mathbf{O}}$ is the centre of the circle.

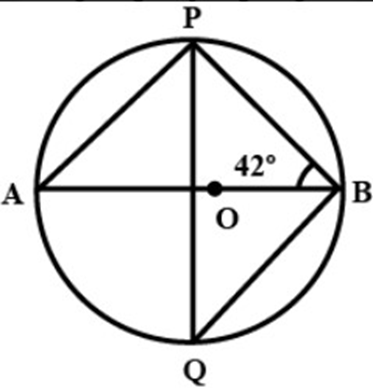
Ans: $\angle {\text{ABP}} = {42^\circ }$

$\angle {\text{APB}} = {90^\circ }$

$\angle {\text{APB}} + \angle {\text{ABP}} + \angle {\text{PAB}} = {180^\circ }$

${90^\circ } + {42^\circ } + \angle {\text{PAB}} = {180^\circ }$

$\angle {\text{PAB}} = {180^\circ } - {90^\circ } - {42^\circ } = {48^\circ }$

$\widehat {PB}$ Subtends $\angle {\text{PAB}}$ and $\angle {\text{PQB}}$ in the same segment of the circle

$\angle {\text{PAB}} = \angle {\text{PQB}} = {48^\circ }$

35. In the given Fig $\angle PQR = {40^\circ }\angle SPR = {65^\circ }$ find $\angle SRP$.

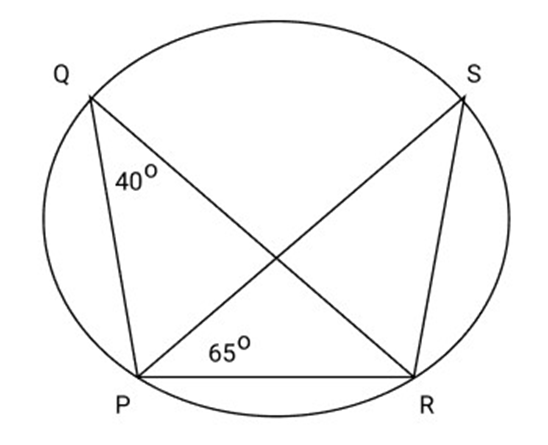
Ans: $PR$ Subtends $\angle {\text{PQR}}$ and $\angle {\text{PSR}}$ in the same segment of the circle

$\angle {\text{PQR}} = \angle {\text{PSR}} = {40^\circ }$

$\angle {\text{SPR}} + \angle {\text{PSR}} + \angle {\text{SRP}} = {180^\circ }$ (angle sum property of a triangle)

${65^\circ } + {40^\circ } + \angle SRP = {180^\circ }$

$\angle {\text{SRP}} = {180^\circ } - {40^\circ } - {65^\circ }$

$ = {75^\circ }$

36. Find the length of AB, CD,AC and BD if two concentric circles with centre 0 have

A,B,C,D as the Point of intersection with line $l$.  If AD=12cm and BC=8 cm, the length of AB,CD,AC and BD are respectively.

Ans: $OM \bot BC$

$BM = MC \ldots  \ldots ..(i)$

$OM \bot AD$

${\text{AM}} = {\text{MD}} \ldots  \ldots $ (ii)

From (i) and (ii)

${\text{AM}} - {\text{BM}} = {\text{MD}} - {\text{MC}} = 6 - 4$

${\text{AB}} = {\text{CD}} = 2\;{\text{cm}}$

${\text{AC}} = {\text{AB}} + {\text{BC}}$

$ = 2 + 8 = 10\;{\text{cm}}$

${\text{BD}} = {\text{BC}} + {\text{CD}}$

$ = 8 + 2 = 10\;{\text{cm}}$

Long Answer Type Questions: (4 Marks)

1. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

Ans: Given: Let ${\text{AB}}$ and ${\text{CD}}$ are two equal chords of a circle of centers

O intersecting each other at point $E$ within the circle.

To prove: (a) ${\text{AE}} = {\text{CE}}$ (b) ${\text{BE}} = {\text{DE}}$

Construction: Draw ${\text{OM}} \bot {\text{AB}},{\text{ON}} \bot {\text{CD}}$. Also join OE.

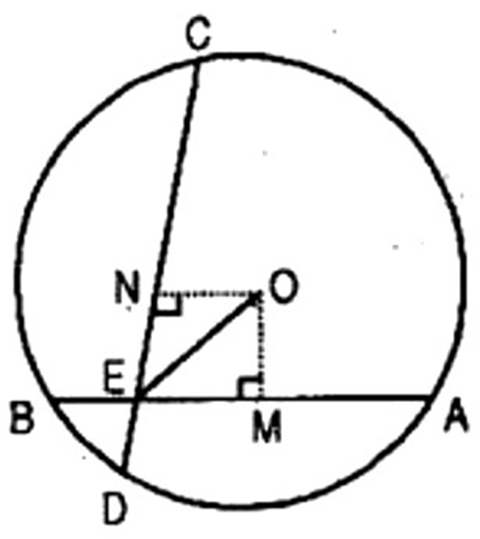
Proof: In right triangles OME and ONE,

$\angle {\text{OME}} = \angle {\text{ONE}} = {90^\circ }$

${\text{OM}} = {\text{ON}}$

(Equal chords are equidistance from the centre)

${\text{OE}} = {\text{OE}}$ (Common)

$\therefore \Delta {\text{OME}} \cong \Delta $ ONE (RHS rule of congruency)

$\therefore {\text{ME}} = {\text{NE}}[{\text{ByCPCT}}] \ldots  \ldots  \ldots ..$ (i)

Now, ${\text{O}}$ is the centre of circle and ${\text{OM}} \bot {\text{AB}}$

$\therefore {\text{AM}} = \dfrac{1}{2}{\text{AB}}$ [Perpendicular from the centre bisects the chord] .....(ii)

Similarly, ${\text{NC}} = \dfrac{1}{2}{\text{CD}} \ldots  \ldots  \ldots $ (iii)

But $AB = CD$ (Given)

From eq. (ii) and (iii), ${\text{AM}} = {\text{NC}}$..........(iv)

Also ${\text{MB}} = {\text{DN}}$..........(v)

Adding (i) and (iv), we get,

${\text{AM}} + {\text{ME}} = {\text{NC}} + {\text{NE}}$

$ \Rightarrow {\text{AE}} = {\text{CE}}$ (Proved part (a))

Now ${\text{AB}} = {\text{CD}}$

${\text{AE}} = {\text{CE}}$

$ \Rightarrow {\text{AB}} - {\text{AE}} = {\text{CD}} - {\text{CE}}$

$ \Rightarrow {\text{BE}} = {\text{DE}}$ (Proved part (b))

2. Three girls Reshma, Salma and Mandip are standing on a circle of radius $5{\mathbf{m}}$ drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is $6\;{\text{m}}$ each, what is the distance between Reshma and Mandip?

Ans: Let Reshma, Salma and Mandip takes the position C, A and B on the circle.

Since ${\text{AB}} = {\text{AC}}$

The centre lies on the bisector of $\angle {\text{BAC}}$.

Let ${\text{M}}$ be the point of intersection of ${\text{BC}}$ and ${\text{OA}}$.

Again, since ${\text{AB}} = {\text{AC}}$ and ${\text{AM}}$ bisects $\angle {\text{CAB}}$.

$\therefore {\text{AM}} \bot {\text{CB}}$ and ${\text{M}}$ is the mid-point of ${\text{CB}}$.

Let ${\text{OM}} = x$, then ${\text{MA}} = 5 - x$

From right angled triangle OMB, $O{B^2} = O{M^2} + M{B^2}$

$ \Rightarrow {5^2} = {x^2} + {\text{M}}{{\text{B}}^2} \ldots  \ldots  \ldots ..({\text{i}})$

Again, in right angled triangle AMB, $A{B^2} = A{M^2} + M{B^2}$

$ \Rightarrow {6^2} = {(5 - x)^2} + {\text{M}}{{\text{B}}^2} \ldots  \ldots  \ldots $.(ii)

Equating the value of ${\text{M}}{{\text{B}}^2}$ from eq. (i) and (ii),

${5^2} - {x^2} = {6^2} - {(5 - x)^2}$

$ \Rightarrow {(5 - x)^2} - {x^2} = {6^2} - {5^2}$

$ \Rightarrow 25 - 10x + {x^2} - {x^2} = 36 - 25$

$ \Rightarrow 10x = 25 - 11$

$ \Rightarrow 10x = 14$

$ \Rightarrow x = \dfrac{{14}}{{10}}$

Hence, from eq. (i),

$M{B^2} = {5^2} - {x^2} = {5^2} - {\left( {\dfrac{{14}}{{10}}} \right)^2}$

$ = \left( {5 + \dfrac{4}{{10}}} \right)\left( {5 - \dfrac{{14}}{{10}}} \right) = \dfrac{{64}}{{10}} \times \dfrac{{36}}{{10}}$

$ \Rightarrow {\text{MB}} = \dfrac{{8 \times 6}}{{10}} = 4.8\;{\text{cm}}$

$\therefore {\text{BC}} = 2{\text{MB}} = 2 \times 4.8 = 9.6\;{\text{cm}}$

3. A circular park of radius $20\;{\text{m}}$ is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.

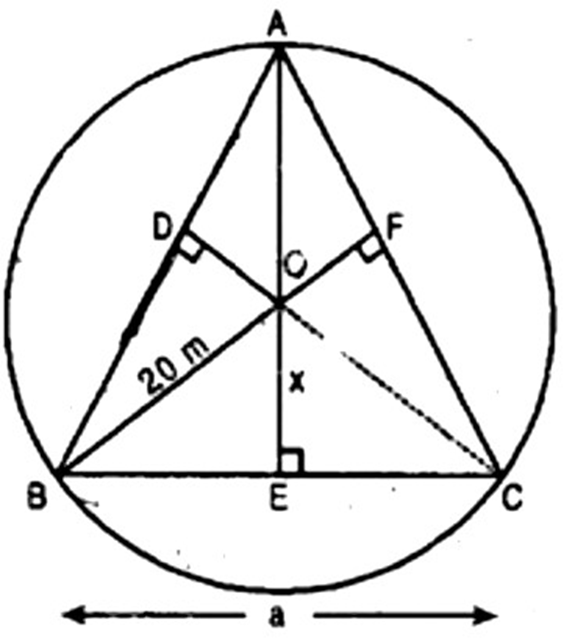
Ans: Let position of three boys Ankur, Syed and David are denoted by the points ${\text{A}},{\text{B}}$ and ${\text{C}}$

respectively.

${\text{A}} = {\text{B}} = {\text{C}} = \alpha [{\text{sa}}y]$

Since equal sides of equilateral triangle are as equal chords and perpendicular distances of equal chords of a circle are equidistant from the centre.

$\therefore {\text{OD}} = {\text{OE}} = {\text{OF}} = x\;{\text{cm}}[{\text{say}}]$

Join ${\text{OA}},{\text{OB}}$ and ${\text{OC}}$.

$ \Rightarrow $ Area of $\Delta {\text{AOB}} = $ Area of $\Delta {\text{BOC}} = $ Area of $\Delta {\text{AOC}}$

And 

Area of $\Delta {\text{ABC}}$\[ = \]Area of $\Delta {\text{AOB}} + $ Area of $\Delta {\text{BOC}} + $ Area of $\Delta {\text{AOC}}$

$ \Rightarrow $ And Area of $\Delta {\text{ABC}} = 3 \times $ Area of \[BOC\]

$ \Rightarrow \dfrac{{\sqrt 3 }}{4}{a^2} = 3\left( {\dfrac{1}{2}BC \times OE} \right)$

$ \Rightarrow \dfrac{{\sqrt 3 }}{4}{a^2} = 3\left( {\dfrac{1}{2} \times a \times x} \right)$

$ \Rightarrow \dfrac{{{a^2}}}{a} = 3 \times \dfrac{1}{2} \times \dfrac{4}{{\sqrt 3 }} \times x$

$ \Rightarrow a = 2\sqrt 3 x \cdots  \cdots  \ldots ..({\text{i}})$

Now, ${\text{CE}} \bot {\text{BC}}$

$\therefore {\text{BE}} = {\text{EC}} = \dfrac{1}{2}{\text{BC}}[\because $ (Perpendicular drawn from the centre bisects the chord)

$ \Rightarrow {\text{BE}} = {\text{EC}} = \dfrac{1}{2}a$

$ \Rightarrow {\text{BE}} = {\text{EC}} = \dfrac{1}{2}(2\sqrt 3 x)$ )Using eq. (i))

$ \Rightarrow {\text{BE}} = {\text{EC}} = \sqrt 3 x$

Now in right angled triangle BEO,

${\text{O}}{{\text{E}}^2} + {\text{B}}{{\text{E}}^2} = {\text{O}}{{\text{B}}^2}$ [Using Pythagoras theorem]

$ \Rightarrow {x^2} + {(\sqrt 3 x)^2} = {(20)^2}$

$ \Rightarrow {x^2} + 3{x^2} = 400$

$ \Rightarrow 4{x^2} = 400$

$ \Rightarrow {x^2} = 100$

$ \Rightarrow x = 10\;{\text{m}}$

And $a = 2\sqrt 3 x = 2\sqrt 3  \times 10 = 20\sqrt 3 \;{\text{m}}$

Thus, distance between any two boys is $20\sqrt 3 \;{\text{m}}$.

4. Let vertex of an angle ABC be located outside a circle and let the sides of the angle intersect chords AD and CE with the circle. Prove that $\angle {\text{ABC}}$ is equal to half the difference of the angles subtended by the chords AC and DE at the centre.

Ans: Vertex B of $\angle {\text{ABC}}$ is located outside the circle with centre ${\text{O}}$.

Side AB intersects chord CE at point $E$ and side BC intersects chord AD at point D with the

circle.

We have to prove that

$\angle {\text{ABC}} = \dfrac{1}{2}[\Delta {\text{AOC}} - \Delta {\text{DOE}}]$

Join ${\text{OA}},{\text{OC}},{\text{OE}}$ and ${\text{OD}}$.

Now $\angle {\text{AOC}} = 2\angle {\text{AEC}}$

[Angle subtended by an arc at the centre of the circle is twice the angle subtended by the same arc at any point in the alternate segment of the circle]

$ \Rightarrow \dfrac{1}{2}\angle {\text{AOC}} = \angle {\text{AEC}} \ldots  \ldots  \ldots .$ (i)

Similarly $\dfrac{1}{2}\angle {\text{DOE}} = \angle {\text{DCE}} \ldots  \ldots  \ldots $ (ii)

Subtracting eq. (ii) from eq. (i),

$\dfrac{1}{2}[\Delta {\text{AOC}} - \Delta {\text{DOE}}] = \angle {\text{AEC}} - \angle {\text{DCE}} \ldots  \ldots  \ldots $ (iii)

Now $\angle {\text{AEC}} = \angle {\text{ADC}}$ (Angles in same segment in circle) ..........(iv)

Also $\angle {\text{DCE}} = \angle {\text{DAE}}$ (Angles in same segment in circle) ..........(v)

Using eq. (iv) and (v) in eq. (iii),

$\dfrac{1}{2}[\Delta {\text{AOC}} - \Delta {\text{DOE}}] = \angle {\text{DAE}} + \angle {\text{ABD}} - \angle {\text{DAE}}$

$ \Rightarrow \dfrac{1}{2}[\Delta {\text{AOC}} - \Delta {\text{DOE}}] = \angle {\text{ABD}}$

Or $\dfrac{1}{2}[\Delta {\text{AOC}} - \Delta {\text{DOE}}] = \angle {\text{ABC}}$ 

Hence proved.

5. AC and BD are chords of a circle which bisect each other.

Prove that:

(i) AC and BD are diameters.

Ans: Given: AC and BD of a circle bisect each other at $O$.

Then ${\text{OA}} = {\text{OC}}$ and ${\text{OB}} = {\text{OD}}$

To prove:

(i) AC and BD are the diameters. In other words, $O$ is the centre of the circle.

Proof: (i) In triangles AOD and BOC,

${\text{AO}} = {\text{OC}}$ [given]

$\angle {\text{AOD}} = \angle {\text{BOC}}$ [Vertically opp.]

${\text{OD}} = {\text{OB}}$ [given]

$\therefore \Delta {\text{AOD}} \cong \Delta $ COB [SAS congruency]

$ \Rightarrow {\text{AD}} = {\text{CB}}[{\text{ByCPCT}}]$

Similarly, $\Delta {\text{AOB}} \cong \Delta $ COD

$ \Rightarrow {\text{AB}} = {\text{CD}}$

$ \Rightarrow \widehat {{\text{AB}}} \cong \widehat {{\text{CD}}}$ [Arcs opposite to equal chords]

$ \Rightarrow \widehat {{\text{AB}}} + \widehat {{\text{BC}}} \cong {\text{CD}} + \widehat {{\text{BC}}}$

$ \Rightarrow \widehat {{\text{ABC}}} \cong \widehat {{\text{BCD}}}$

$ \Rightarrow AC = BD$ [Chords opposites to equal arcs]

$\therefore $ AC and BD are the diameters as only diameters can bisect each other as the chords of the

circle.

AC is the diameter. [Proved in (i)]

$\therefore \angle {\text{B}} = \angle {\text{D}} = {90^\circ } \ldots  \ldots  \ldots $..(i) [Angle in semi-circle]

Similarly, BD is the diameter.

(ii) ABCD is a reactangle

Ans: [Angle in semi-circle]

$\therefore \angle {\text{A}} = \angle {\text{C}} = {90^\circ } \ldots  \ldots  \ldots ..$

Now diameters ${\text{AC}} = {\text{BD}}$

$ \Rightarrow \widehat {{\text{AC}}} \cong \widehat {{\text{BD}}}$ [Arcs opposite to equal chords]

$ \Rightarrow \widehat {{\text{AC}}} - \widehat {{\text{DC}}} \cong \widehat {{\text{BD}}} - \widehat {{\text{DC}}}$

$ \Rightarrow \widehat {{\text{AD}}} \cong \widehat {{\text{BC}}}$

$ \Rightarrow {\text{AD}} = {\text{BC}}$ [Chords corresponding to the equal arcs] ..........(iii)

Similarly, ${\text{AB}} = {\text{DC}}$.........(iv)

From eq. (i), (ii), (iii) and (iv), we observe that each angle of the quadrilateral is ${90^\circ }$ and

opposite sides are equal.

Hence ${\text{ABCD}}$ is a rectangle.

6. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and respectively. Prove that angles of the triangle are $\left( {{{90}^\circ } - \dfrac{{\text{A}}}{2}} \right),\left( {{{90}^\circ } - \dfrac{{\text{B}}}{2}} \right)$ and $\left( {{{90}^\circ } - \dfrac{{\text{C}}}{2}} \right)$ respectively.

Ans: According to question, ${\text{AD}}$ is bisector of $\angle {\text{A}}$.

$\therefore \angle 1 = \angle 2 = \dfrac{{\text{A}}}{2}$

And BE is the bisector of $\angle B$.

$\therefore \angle 3 = \angle 4 = \dfrac{{\text{B}}}{2}$

Also ${\text{CF}}$ is the bisector of $\angle {\text{C}}$.

$\therefore \angle 5 = \angle 6 = \dfrac{{\text{C}}}{2}$

Since the angles in the same segment of a circle are equal.

$\therefore \angle 9 = \angle 3$ [angles subtended by $\widehat {{\text{AE}}}] \ldots  \ldots  \ldots ..$ (i)

And $\angle 8 = \angle 5$ [angles subtended by $\widehat {{\text{FA}}}$ ] ...........(ii)

Adding both equations,

$\angle 9 + \angle 8 = \angle 3 + \angle 5$

$ \Rightarrow \angle {\text{D}} = \dfrac{{\text{B}}}{2} + \dfrac{{\text{C}}}{2}$

Similarly, $\angle E = \dfrac{A}{2} + \dfrac{C}{2}$ and $\angle F = \dfrac{A}{2} + \dfrac{B}{2}$

In triangle DEF,

$\angle {\text{D}} + \angle {\text{E}} + \angle {\text{F}} = {180^\circ }$

$ \Rightarrow \angle {\text{D}} = {180^\circ } - (\angle {\text{E}} + \angle {\text{F}})$

$ \Rightarrow \angle {\text{D}} = {180^\circ } - \left( {\dfrac{{\text{A}}}{2} + \dfrac{{\text{C}}}{2} + \dfrac{{\text{A}}}{2} + \dfrac{{\text{B}}}{2}} \right)$

$ \Rightarrow \angle {\text{D}} = {180^\circ } - \left( {\dfrac{{\text{A}}}{2} + \dfrac{{\text{B}}}{2} + \dfrac{{\text{C}}}{2}} \right) - \dfrac{{\text{A}}}{2}$

$ \Rightarrow \angle {\text{D}} = {180^\circ } - {90^\circ } - \dfrac{{\text{A}}}{2}\left[ {\because \angle {\text{A}} + \angle {\text{B}} + \angle {\text{C}} = {{180}^\circ }{\text{J}}} \right.$

$ \Rightarrow \angle D = {90^\circ } - \dfrac{A}{2}$

Similarly, we can prove that

$\angle {\text{E}} = {90^\circ } - \dfrac{{\text{B}}}{2}$ and $\angle {\text{F}} = {90^\circ } - \dfrac{{\text{C}}}{2}$

7. The bisector of $\angle B$ of an isosceles triangle ${\text{ABC}}$ with ${\text{AB}} = {\text{AC}}$ meets the circum circle of $\vartriangle ABC$ at ${\mathbf{P}}$ if AP and BC produced meet at ${\mathbf{Q}}$, prove that ${\text{CQ}} = {\text{CA}}$

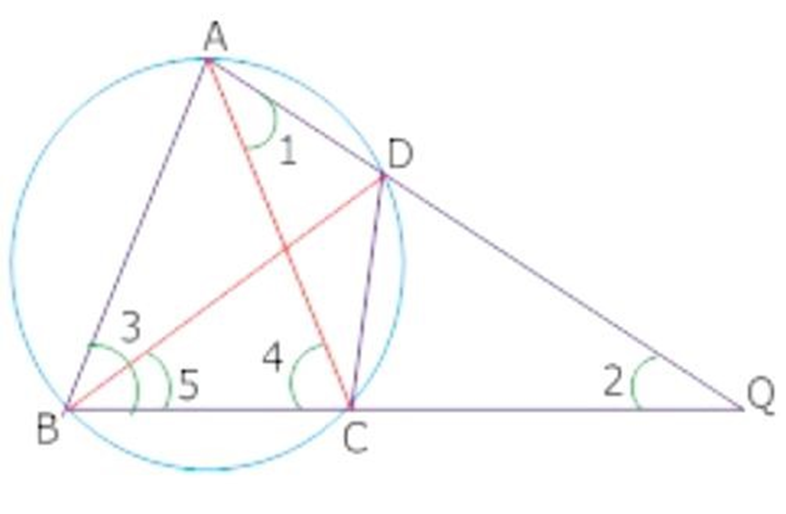
Ans: Join P and C

Considered $\vartriangle ACQ$

$\angle 4 = \angle 1 + \angle 2 \ldots  \ldots  \ldots $(i)

(Exterior angle is equal to the sum of two interior opposite angles)

$\angle 4 = \angle 3 \ldots  \ldots  \ldots ..$(ii)

From (i) and (ii)

$\angle 1 + \angle 2 = \angle 3$

$\angle 3 = 2\angle 5$ (BP is bisector of $\angle 3$)

$\angle 1 + \angle 2 = 2\angle 5$

$\angle 1 + \angle 2 = \angle 5 + \angle 5$

$\angle 5 = \angle 1$ [Angle in the same segments]

$\angle 1 + \angle 2 = \angle 1 + \angle 1$

$\angle 2 = \angle 1$

In $\vartriangle ACQ,CQ = CA$ (sides opposite to equal angles)

8. OC radius equal to chord ${\text{CD}}$ and ${\text{AB}}$ is diameter and AC and BD produced meet at P so prove that $\angle CPD = {60^\circ }$

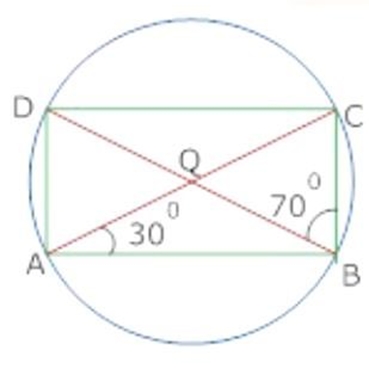
Ans. Join BC

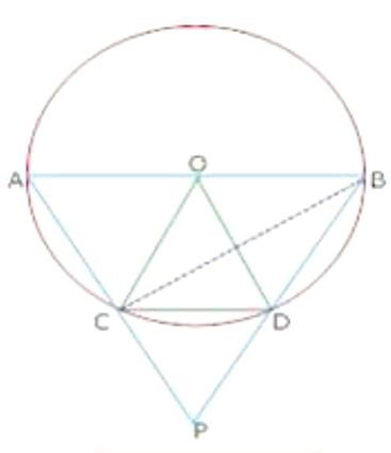
In $\Delta OCD,OC = OD$ (Radii of same circle)

${\text{OC}} = {\text{CD}}$ (Given)

${\text{OC}} = {\text{OD}} = {\text{CD}}$

$\Delta OCD$ is equilateral

Hence, $\angle COD = {60^\circ }$

$\angle CBD = {30^\circ }$

(Angle subtended by arc ${\text{CD}}$ at centre is double the angle at any Pont of the remaining part)

$\angle ACB = {90^\circ }$

Exterior $\angle ACB = \angle CBP + \angle CPB$

${90^\circ } = {30^\circ } + \angle CPB$

$\angle CPB = {60^\circ }$

$\angle CPD = {60^\circ }$

9. The two chords bisect each other AD and BC show that

(i) ${\text{AD}}$ and ${\text{BC}}$ are diameter

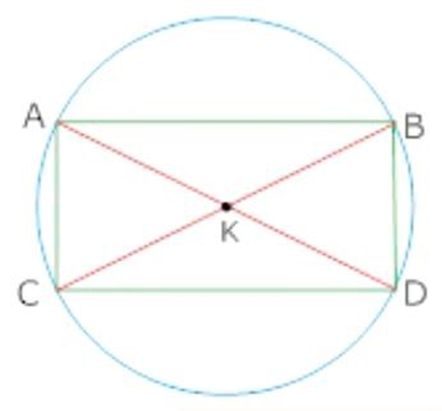
Ans: Given that the two chords ${\text{AD}},{\text{BC}}$ of the circle bisect each other.

Let these cords bisect at ${\text{K}}$

In $\Delta {\text{AKB}}$ and $\vartriangle {\text{DKC}}$

${\text{AK}} = {\text{DK}}[{\text{AB}},{\text{CD}}$ bisect each other at ${\text{K}}]$

${\text{BK}} = {\text{CK}}$

$\angle AKB = \angle DKC[$ Vertically opposite $\Delta ]$

$\Delta AKB \cong \Delta DKC$ (by SAS)

$AB = CD({\text{CPCT}})$

$\overrightarrow {AB}  = \overrightarrow {CD} $

$\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {CD}  + \widehat {BC}$

$A\vec C = B\hat D$

$AC = BD$

Also, in quadrilateral ${\text{ABCD}}$

${\text{AB}} = {\text{CD}}$

$\angle A = \angle B = \angle C = \angle D = {90^\circ }[{\text{AC}},{\text{BD}}$ is diameter so angle is semicircle)

(ii) ${\text{ABCD}}$ is a rectangle

Ans: Since, from the first answer, we can see that we have AC and BD as a diameter and both are equal to each other. 

Now we can say that,

$\mathrm{ABCD}$ is a parallelogram with one angle $90^{\circ}$

$\therefore \mathrm{ABCD}$ is a rectangle

10. Show that $\angle AHE$ and $\angle EGC$ are supplementary. Given that ABC AEG and HEC are straight lines.

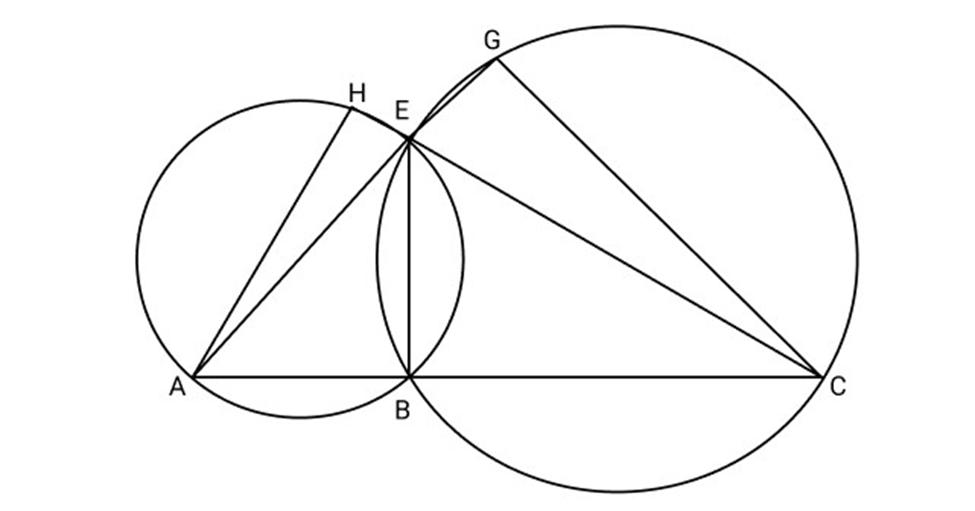
Ans: $\angle H + \angle 1 = {180^\circ }$ [Opposite $\angle s$ of cyclic quadrilateral $\left. {{\text{ABEH}}} \right] \ldots  \ldots  \ldots .(i)$

$\angle G + \angle 2 = {180^\circ }$ [Opposite $\angle s$ of cyclic quadrilateral BCGE]......... (ii)

Adding (i) and (ii) we get

$\angle H + \angle G + \angle 1 + \angle 2 = {360^\circ }$

$\angle H + \angle G = {360^\circ } - (\angle 1 + \angle 2)$

$ = {360^\circ } - {180^\circ }\left[ {\angle 1 + \angle 2 = {{180}^\circ }} \right.$ (Linear pair)

$ = {180^\circ }$

11. OP $ \bot {\text{AB}},{\mathbf{OQ}} \bot {\text{CD}},{\text{AB}}||{\text{CD}}.{\text{AB}} = 6\;{\text{cm}}$ and ${\text{CD}} = 8\;{\text{cm}}$, Determine length of ${\text{PQ}}$.

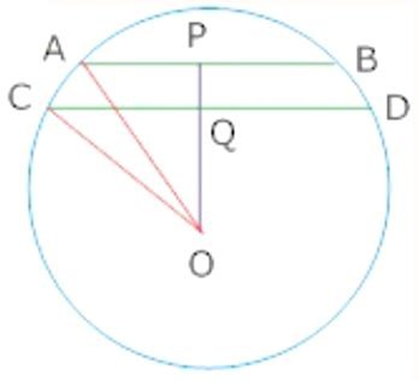
Ans: Join ${\text{OA}}$ and ${\text{O}}$

$AB = 6\;{\text{cm}}$

$AP = \dfrac{1}{2}AB$

${\text{AP}} = 3\;{\text{cm}}$

${\text{CD}} = 8\;{\text{cm}}$

$CQ = \dfrac{1}{2}CD$

${\text{CQ}} = 4\;{\text{cm}}$

In right angled triangle $\vartriangle APQ$

$A{O^2} = P{O^2} + A{P^2}$

${(5)^2} = P{O^2} + {(3)^2}$

$P{O^2} = 16$

$PO = \sqrt {16} $

$ = 4\;{\text{cm}}$

In rt. $\Delta OQC$

$C{O^2} = C{Q^2} + O{Q^2}$

${(5)^2} = {(4)^2} + O{Q^2}$

$OQ = \sqrt 9 $

$ = 3\;{\text{cm}}$

$\angle APO = \angle CQO$

${\text{PO}}$ and ${\text{QO}}$ are in the same line

$PQ = PO - OQ = 4 - 3 = 1$

Hence, length of PQ= 1 cm

CBSE Class 9 Maths Chapter 9 Important Questions - Free PDF Download

Definition of Circle

A circle is defined as a set of all points in a plane which are equally spaced from a fixed point. The fixed point is called the centre of the circle and the distance between any point on the circle and its centre is called the radius of the circle.

Parts of Circle

Based on the positions and their properties a circle has different parts. The important parts of a circle are explained below in detail.

• Arc - It is basically the connected curve of a circle.

• Sector - A region bounded by two radii and an arc.

• Segment - It is the region bounded by a chord and an arc lying between the chord’s endpoints. Points to remember that segments do not contain the centre.

• Centre - Midpoint of a circle is known as the centre.

• Chord - It is a line segment that joins two points on the circle. Endpoints of the chord lie on the circle.

• Diameter - It is a line segment having both the endpoints on the circle and is the largest chord of the circle.

• Radius - It is the line segment connecting the centre of a circle to any point on the circle itself.

• Secant - It is a straight line which cuts the circle at two points. It is also known as an extended chord.

• Tangent - It is a straight line touching the circle at a single point.

Radius of Circle

A line segment connecting the centre of a circle to any point on the circle itself is known as the radius of the circle. The radius is denoted by R or r.

Diameter  of Circle

Diameter is defined as the longest chord of the circle. It is twice the length of radius i.e. d = 2r. The radius of the circle can be derived from the diameter of the circle. Formula for radius of circle is given by  r= d/2.

All the important point related to the circle are shown below in the diagram

 Properties of Circles

The important basic properties of the circle are as follows:

• The outer line of a circle ( which is circumference ) is at equidistant from the centre.

• The diameter of the circle divides the circle into two equal parts.

• Two circles are said to be congruent to each other if they have equal radii.

• Circles which are different in size or have different radii are known as similar circles.

• The diameter is the largest chord of the circle and is double the radius.

A tangent to a circle is a line which touches the circle exactly at one point. For every point on the circle, There is a unique tangent for every point on the circle passing through it.

The tangent to the circle at any point is the perpendicular to the radius of the circle that passes through the point of contact.

Here, O is the centre and OP⊥XY.

Length of a Tangent

The length of the tangent to the circle is defined as the segment of the tangent from the external point A to the point of tangency (B) with the circle. In the given diagram below, AB is the length of a tangent.

Lengths of Tangents Drawn from an External Point

Two tangents of equal length can be drawn from an external point of a circle. 

PT = QT

Area of Circle:

The space occupied by the shape circle is known as an area of the circle. The area of a circle  is given by the formula below

Area of Circle, A = πr² Square units

Circumference of Circle 

The circumference of a circle is the length of the line around the edges of the circle. Circumference of a circle is calculated by multiplying pi with 2 times radius. Mathematically can be expressed as 

C = 2πr

Important Theorem Related to Circle

• Equal chord of a circle subtends an equal angle at the centre.

• The perpendicular to a chord bisects the chord if the line drawn from the centre of the circle.

• Equal chords of a circle are equidistant (i.e equal distance) from the centre of the circle.

• The measure of angles subtended to any point on the circumference of the circle from the same arc is equal to half of the angle subtended at the centre by the same arc.

• In a cyclic quadrilateral, the opposite angles are supplementary.

5 Important Formulas from Class 9 Maths Chapter 9 Circles

Tips to learn Class 9 Maths Chapter 9 Circles

• Get comfortable with key terms like radius, diameter, chord, arc, tangent, and secant. These are the building blocks for everything else in the chapter.

• Draw diagrams for every concept, like tangents, cyclic quadrilaterals, and angles subtended by arcs. Visual learning helps you remember better.

• Focus on understanding and applying the main theorems, like “The radius perpendicular to a chord bisects it” and “Equal chords subtend equal angles at the centre.” Practice problems based on these.

• Work through important questions related to circles. Start with simpler problems and gradually move to complex ones involving multiple concepts.

• Go over your notes and solve examples frequently. Regular revision will help you retain concepts and apply them faster during exams.

Key Takeaways of Important Questions by Vedantu Class 9 Maths Chapter 9 - Circles Free PDF

The circles class 9 questions with solutions allow the students to take several benefits. They are:

• Students can score better marks and gain good knowledge.

• These PDFs are available for free.

• Students can take either a soft copy or hard copy.

Conclusion 

CBSE Class 9 Maths Chapter 9 Circles, is a key part that explores geometric concepts. Understanding the properties of tangents, chords, and cyclic quadrilaterals not only builds a strong foundation for higher studies but also sharpens your problem-solving skills. Practising important questions from this chapter helps you focus on critical topics, familiarizes you with common exam patterns, and improves your confidence. By learning these questions, you can ensure better performance in exams and develop a solid understanding of geometry.

Related Study Materials for CBSE Class 9 Maths Chapter 9

CBSE Class 9 Maths Chapter-wise Important Questions

Related Important Links for Maths Class 9

Along with this, students can also download additional study materials provided by Vedantu for Maths Class 9–