CBSE Important Questions for Class 6 Maths Playing with Constructions - 2025-26
FAQs on Important Questions For Class 6 Maths Chapter 8 Playing with Constructions - 2025-26
1. What are the most important types of questions to practice from Chapter 8, Playing with Constructions, for the 2025-26 exam?
For the 2025-26 exams, students should focus on questions that require practical skills. The most frequently asked types include:
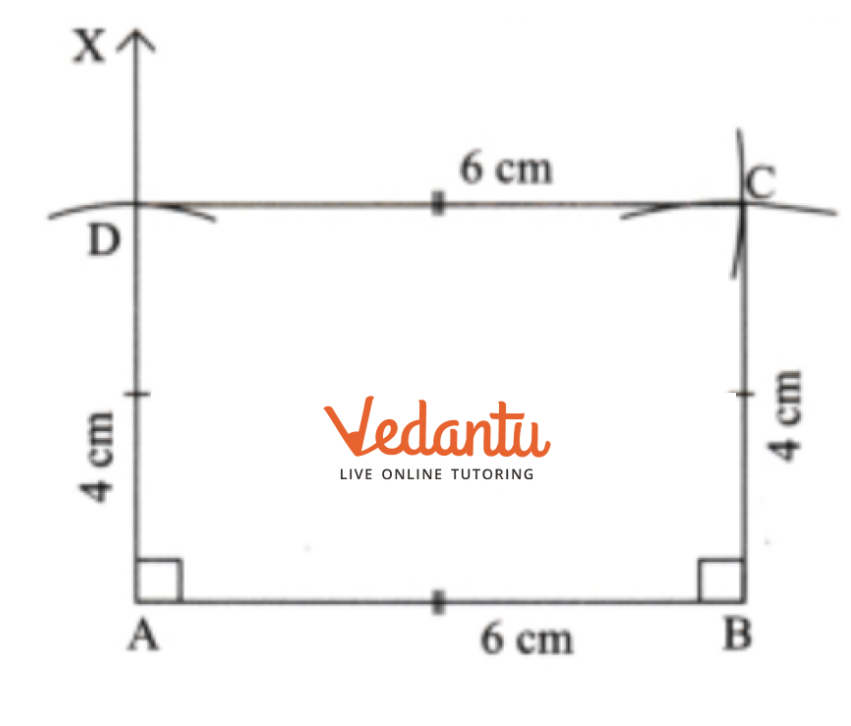
- Constructing a perpendicular bisector of a given line segment.
- Constructing an angle of a specific measure (like 60°, 90°, 45°, 120°) using only a ruler and compass.
- Constructing the bisector of a given angle.
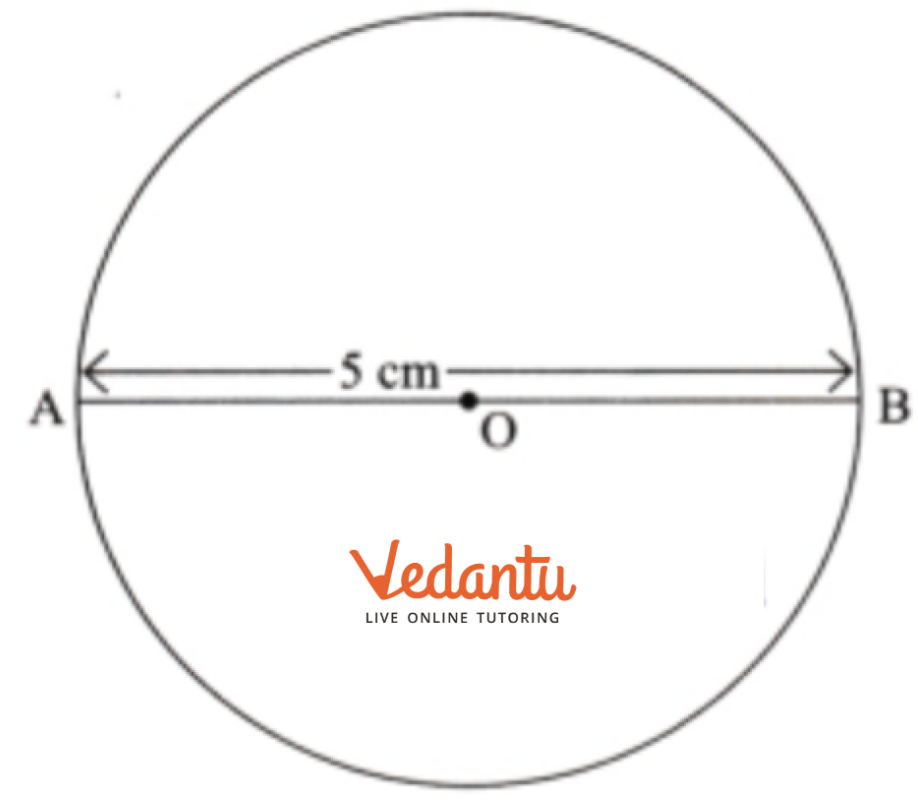
- Drawing a circle of a given radius and marking its parts (centre, radius, diameter).
2. How are marks awarded for construction questions in the Class 6 Maths exam?
Marks for construction questions are typically divided to assess different skills. To score full marks, you must ensure:
- Accuracy: The final drawing must be precise, with correct lengths and angles.
- Construction Arcs: Faint arcs must be visible to show that you have used the correct method and not just a protractor.
- Neatness: The drawing should be clean, with sharp pencil lines and clear labelling of points.
- Steps of Construction: Writing the steps is often required and carries specific marks.
3. What kind of short-answer or 1-mark questions can be expected from this chapter?
While this is a practical chapter, some theoretical short-answer questions are often asked. For the 2025-26 session, expect questions like:
- What are the essential instruments in a geometry box for constructions?
- What is the first step to construct a 90° angle?
- What does it mean to bisect a line segment?
- If you bisect a 90° angle, what is the measure of the two resulting angles?
4. Why is using only a ruler and compass important for constructions, even when a protractor seems easier?
This is a key conceptual point. Using only a ruler and compass forces you to rely on pure geometric principles and logic, not just measurement. These classical constructions are based on the foundational axioms of geometry. A protractor is a measuring device, while a compass helps create circles and arcs of specific radii, which are the building blocks of logical geometric proofs. Excelling at this demonstrates a deeper understanding of geometric relationships rather than just an ability to measure.
5. What are the most common mistakes students make in construction questions that lead to a loss of marks?
To avoid losing marks, be careful of these common errors:
- Using a thick or blunt pencil, which leads to inaccurate lines.
- Erasing the construction arcs, which are necessary proof of your method.
- A loose compass screw, which can cause the radius to change midway through an arc.
- Incorrectly labelling the points, lines, and angles in the final diagram.
- Forgetting to write the steps of construction when they are asked for.
6. How does understanding angle bisection help in constructing more complex angles like 45° or 22.5°?
Angle bisection is a fundamental technique that allows you to build other angles. The logic works in steps:
- First, you construct a standard angle, like 90° (by bisecting a straight line and constructing a perpendicular).
- Then, you bisect the 90° angle to get a perfect 45° angle.
- If you need an even smaller angle like 22.5°, you can simply bisect the 45° angle again.
7. Besides drawing them, what is the practical importance of a perpendicular bisector?
A perpendicular bisector is a very powerful tool in geometry. Every point on the perpendicular bisector of a line segment is equidistant from the two endpoints of that segment. This property is crucial for more advanced constructions, such as:
- Finding the centre of a circle that passes through three given points (the circumcenter of a triangle).
- Solving problems related to symmetry and reflection.
- Dividing a shape into two identical, mirror-image halves.