NCERT Solutions for Class 5 Maths Chapter 4 Parts and Wholes

1. Draw a rectangle of length 9 cm and width 6 cm. Divide it into three equal parts and complete the flag.

The top one-third of our flag is saffron (or orange).

(i) What is the colour of the middle one-third of the flag? 

Ans: The colour of the middle one-third of the flag is white.

(ii) Where will you draw the Ashoka chakra?

Ans: For Ashoka Chakra I will draw it in the middle of the white portion of the flag.

(iii) How much of the flag will you colour green? 

Ans: $(⅓)^{rd}$ portion of the flag will be coloured green.

(iv) Is the white colour now less than of the flag? Why?

Ans: Yes, the white colour is less than the ⅓ of the flag because the Ashoka Chakra is present in the white portion.

2. Now look at this flag. How much of it is black? _________ 

Ans: From the picture, we can see that there are 3 portions, so the $(⅓)^{rd}$ portion of the flag contains black colour.

(i) The green part of the flag can be written as __________

Ans: The green part of the flag can be written as one-third.

(ii) Is red less than one-third of the flag? Why? _________ 

Ans: Yes, the red colour is less than ⅓ of the flag because the white emblem is present in the red portion of the flag.

3. This is the flag of Myanmar, our neighbour. 

(i) Is blue more than one-fourth of the flag or less ?

Ans: No, the blue colour is less than one-fourth of the flag.

(ii) Guess how much of the flag is red. Is it more than ? Is it more than three-fourths?

Ans: Yes, the red portion in the flag is more than half and also it is more than three-fourths.

Practice Time

A) Chocolate bar

Manju had a chocolate. She gave onefourth of it to Raji, one-third to Sugatha and one-sixth to Sheela. She ate the remaining part. How many pieces of chocolate did each get? Write here.

Ans: Manju had a chocolate

From above picture we know that the number of bites in the chocolate is 12

She gave one-fourth of the chocolate to Raji = ¼ $\times$ 12 = 3 bites

Sugatha got one-third of the chocolate = ⅓ $\times$ 12 = 4 bites

Sheela got one-sixth of the chocolate = ⅙ $\times$ 12 = 2 bites

(i) What part of the chocolate did Manju eat?

Ans: The part of the chocolate that remains with Manju is 

= 12-(3+4+2)

= 12-(9)

= 3 bites

Therefore, Manju ate 3 bites of chocolate.

B) Colour the hats

(i) Colour ⅓ of the hats red.

(ii) Colour three-fifth hats blue.

(iii) How many hats did you colour red?

(iv) How many hats did you colour blue?

(v) What part of the hats are not coloured?

Ans: The total number of hats that are given in the picture = 15

(i) Out of 15 hats, ⅓ of the hats are in red

= ⅓ $\times$ 15

= 5 hats

(ii) Out of 15 hats, three-fifth of the hats are in blue colour

= ⅗ $\times$ 15

= 3 $\times$ 3

= 9 hats

(iii) I coloured red to 5 hats.

(iv) I coloured blue to 9 hats

(v) Total number of hats that are coloured are 14

Total number of hats = 15

So, the number of not coloured hat = 15 - 14 = 1 hat

Therefore, $(1/15)^{th}$ part of the hats are not coloured.

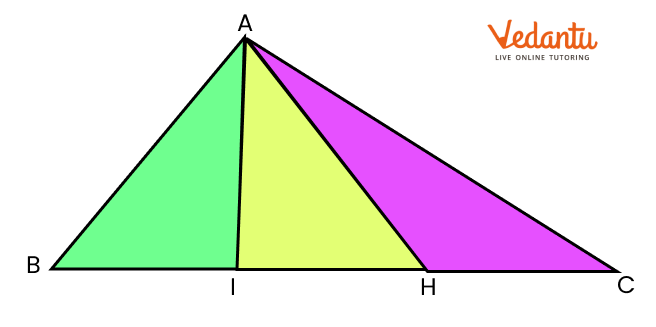
C) Equal parts of a triangle

(i) The white triangle is divided into three equal parts. Fill each one-third part with a different colour. Can you show that these parts are equal? Think how.

Ans: Yes, that can be done by making a cut of the parts of the triangle by using tracing paper.

If 1 part is placed over another part, it is seen that the first part fully covers the second part. Along with that the second part also fully covers the first or third part. This shows that all parts are equal.

(ii)  Now try to make three equal parts of this triangle in a different way. Colour each one third with a different colour.

Ans:

The triangle is coloured with different colors

D) Six parts of a rectangle

Rani has divided a green rectangle into six equal parts like this.

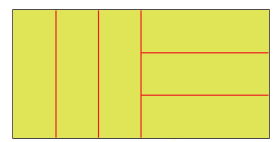
Now you divide each of these rectangles into six equal parts. Use a different way for each of the three rectangles.

Ans: 

Discuss 

1. How will you check that each part is really one-sixth of that rectangle?

Ans: You can do this by making shapes on tracing paper. Place one shape on top of another. If one shape completely covers the other, and the reverse is also true, then both shapes are equal. Repeat this for all shapes to check if they are each 1/6th of the rectangle.

2. The green rectangle is bigger than the blue one. Can we say that of the green rectangle is bigger than ⅙ of the blue rectangle?

Ans: Yes, if the whole is bigger, then a part of it is also bigger. So, 1/6 of the green rectangle is bigger than 1/6 of the blue rectangle.

Greedy Gatekeepers

Remember Birbal, the clever minister of King Akbar? (MathMagic Class IV, page 14) Do you know how he became a minister?

What happened after that? Complete the story. What part of the prize did the poet get?

Ans: The poet got 100 slaps and was happy. But when he got to the first gate, he had to give half of the slaps to the gatekeeper, which was 50 slaps. When he got to the second gate, he had to give 40 slaps. Finally, when he reached the last gate, he had to give 10 slaps. So, Birbal gave 50 + 40 + 10 = 100 slaps to the three gatekeepers. Because he was smart, Birbal did not get any slaps and taught the gatekeepers a lesson.

Patterns in Parts

1) Make different patterns by colouring some squares in the grids B, C, D. What part of the grid did you colour? What part of the grid remained white? Write

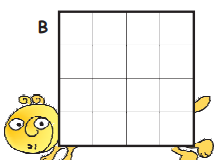
Ans:

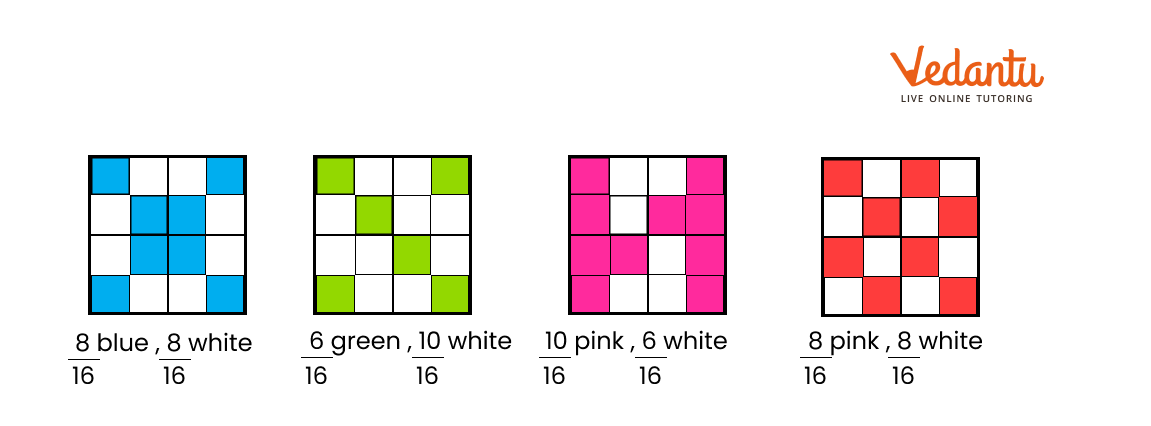
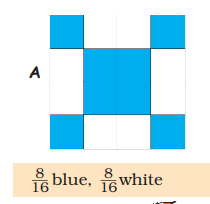
2) Look at grid A again. Is the grid coloured — 

a) $\dfrac{1}{2}$ blue, $\dfrac{1}{2}$ white?

b) $\dfrac{2}{4}$ blue , $\dfrac{2}{4}$ white? 

c) $\dfrac{3}{8}$ blue, $\dfrac{5}{8}$ white? 

d) $\dfrac{4}{8}$ blue, $\dfrac{4}{8}$ white?

Mark ($\times$ ) on the wrong answer.

Ans: 

a) $\dfrac{1}{2}$ blue, $\dfrac{1}{2}$ white

b) $\dfrac{2}{4}$ blue , $\dfrac{2}{4}$ white 

c) $\dfrac{3}{8}$ blue, $\dfrac{5}{8}$ white($\times$) 

d) $\dfrac{4}{8}$ blue, $\dfrac{4}{8}$ white

Because,

a) $\dfrac{1}{2}$ blue, $\dfrac{1}{2}$ white = $\dfrac{8}{16}$=$\dfrac{1}{2}$ (divide both denominator and numerator by 8)

b) $\dfrac{2}{4} blue, \dfrac{2}{4} white =\dfrac{8}{16}= \dfrac{2}{8}$ ....(divide both denominator and numerator by 2)

d) $\dfrac{4}{8} blue, \dfrac{4}{8} white =\dfrac{4}{8}= \dfrac{4}{8}$ ....(divide both denominator and numerator by 2)

3) Draw grids of 16 squares and make patterns with

a) $\dfrac{2}{8}$ red, $\dfrac{1}{2}$ yellow, $\dfrac{1}{4}$ green

b) $\dfrac{3}{16}$ blue, $\dfrac{5}{16}$ red, $\dfrac{1}{2}$ yellow

Ans: 

a) $\dfrac{2}{8}$ red, $\dfrac{1}{2}$ yellow, $\dfrac{1}{4}$ green 

Out of 16 squares $\dfrac{2}{8}$ red = $\dfrac{2}{8} \times 16$ = 2 $\times$ 2 = 4 red squares

Out of 16 squares $\dfrac{1}{2}$ yellow = $\dfrac{1}{2} \times 16$ = 1 $\times$ 8 = 8 yellow squares

Out of 16 squares $\dfrac{1}{4}$ green = $\dfrac{1}{4} \times 16$ = 1 $\times$ 4 = 4 green squares

b) $\dfrac{3}{16}$ blue, $\dfrac{5}{16}$ red, $\dfrac{1}{2}$ yellow

Out of 16 squares $\dfrac{3}{16}$ red = $\dfrac{3}{16} \times 16$ = 3 $\times$ 1 = 3 blue squares

Out of 16 squares $\dfrac{5}{16}$ red = $\dfrac{5}{16} \times 16$ = 5 $\times$ 1 = 5 red squares

Out of 16 squares $\dfrac{1}{2}$ red = $\dfrac{1}{2} \times 16$ = 1 $\times$ 8 = 8 green squares

Ramu’s Vegetable Field

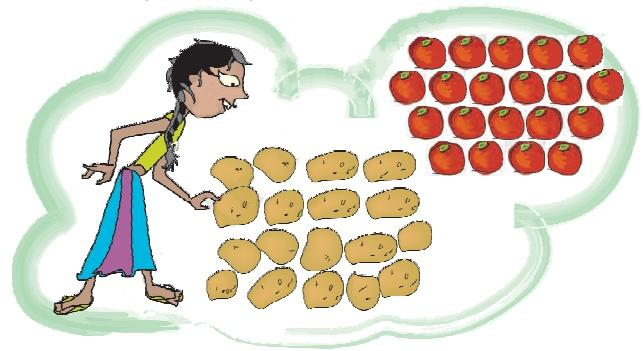
Ramu’s vegetable field has 9 equal parts. What vegetables does he grow?

1) Which vegetable grows in the biggest part of his field? What part?

Ans: He grows tomatoes in the biggest part of the field. 

Out of 9 equal parts, 3 of them contain tomatoes, i,e., $(3/9)^{th}$ part of his field contains tomatoes.

2) On what part of the field does he grow potatoes?

Ans: Out of 9 equal parts, 2 of them contain potatoes.

So, $(2/9)^{th}$ part of his field contains potatoes.

3) What part of the field is used to grow spinach? What part is used for brinjals?

Ans: Out of 9 equal parts, only one part of them contain spinach.

So, $(1/9)^{th}$ part of his field contains spinach.

Out of 9 equal parts, 2 parts of them contain brinjals.

So, $(2/9)^{th}$ part of his field contains brinjals.

4) Now you write some questions by looking at this picture.

Ans: 

• Which part of the field is used for growing chillies?

• Which two vegetables are grown on equal part of the field?

Ramu wanted to give these vegetables to his friends. He gave Aboobacker one-fifth of these tomatoes and of the potatoes. Srija got of the tomatoes and of the potatoes. Nancy got the rest of these vegetables. Circle Aboobacker’s share in blue. Circle Srija’s share in yellow.

Ans: From the figure given,

Total number of potatoes = 18

Total number of tomatoes = 20

From the given question,

Ramu wanted to give these vegetables to his friends

Aboobacker got one-fifth of these tomatoes = $\dfrac{1}{5} \times 20 $ = 1 $\times$ 4 = 4

Aboobacker got one-fifth of the potatoes = $\dfrac{1}{3} \times 18 $ = 1 $\times$ 6 = 6

Srija got $\dfrac{2}{5}$ of the tomatoes = $\dfrac{2}{5} \times 20 $ = 2 $\times$ 4 = 8

Srija got $\dfrac{3}{6}$ of the potatoes = $\dfrac{3}{6} \times 18 $ = 3 $\times$ 3 = 9

Then, Nancy got the rest of these vegetables

Total number of vegetables, including potatoes and tomatoes = 20 +18 = 38

Number of vegetables Abokobacker and Srija got = 4+6+8+9 = 27

So, Nancy got = 38 - 27 = 11 vegetables

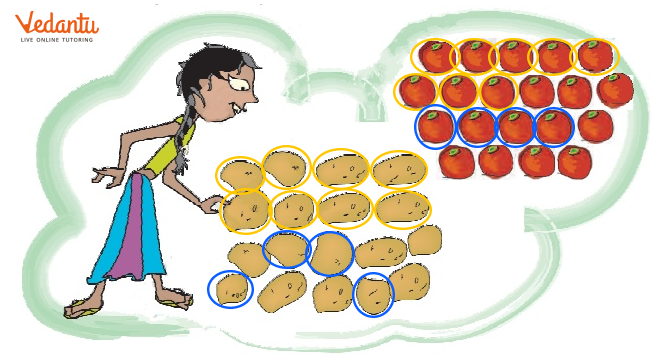
(i) How many potatoes and tomatoes did Nancy get? 

Ans: From the above answer,

Total number of tomatoes = 20

Total number of potatoes = 18

Then,

Number of tomatoes Aboobacker and Srija got = 4+8 = 12

Number of potatoes Aboobacker and Srija got = 6+9 =15

Now,
Number of tomatoes Nancy got = 20 -12 = 8 tomatoes

Number of potatoes Nancy got = 18 -15 = 3

Therefore, Nancy got 3 potatoes and 8 tomatoes.

Game: Who Colours the Circle First?

This game is tp be played in groups of 4. Each player has to make a circle as shown. Each one has to make 15 tokens on slips of paper. Write $\dfrac{1}{2}$, $\dfrac{1}{3}$, $\dfrac{1}{4}$, $\dfrac{1}{6}$, $\dfrac{1}{12}$, $\dfrac{2}{12}$, $\dfrac{3}{12}$, $\dfrac{4}{12}$.......$\dfrac{11}{12}$ to make your tokens.

Shuffle the tokens and make a pile in the middle of the group. Now you are ready to start the game.

The first player takes a token from the pile, colours that part of the picture, and puts the token under the pile. The next player does the same, and so on. The winner is the one who first colours the circle completely.

(i) Who won the game?

Ans: The player who got the most number of the tokens.

(ii) What are the winner’s tokens?

Ans: The winner’s tokens are $\dfrac{1}{12}$, $\dfrac{2}{12}$, $\dfrac{3}{12}$, etc.

(iii) Write the tokens you got.

Ans: Assuming that I am the winner, then I got the tokens $\dfrac{1}{12}$, $\dfrac{2}{12}$, $\dfrac{3}{12}$, etc.

(iv) What part of the circle did you colour?

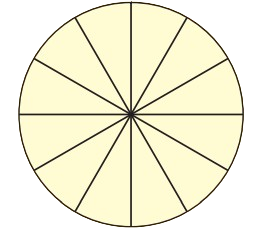
Ans: I coloured 1+2+3 = 6 segments initially

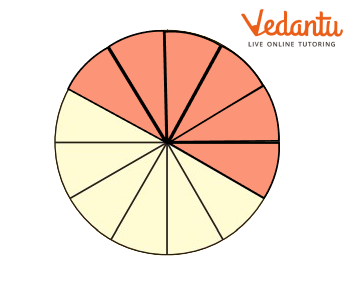
Guess and Check

A) What part of each shape is coloured?

First guess the answer, then check.

Ans: 

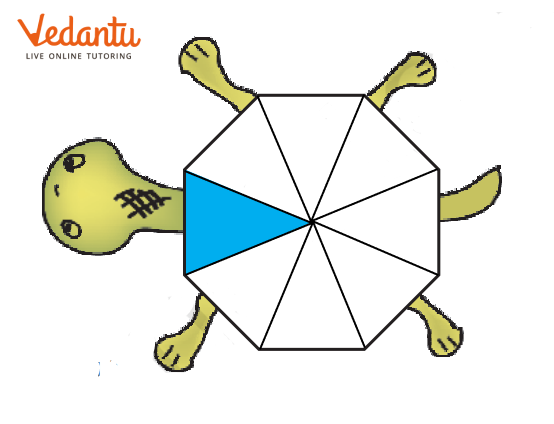
From the image, we can say that $\dfrac{1}{8}$ of the shape is coloured.

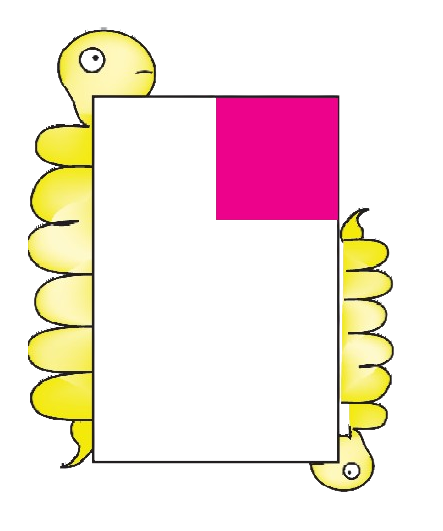
Ans: 

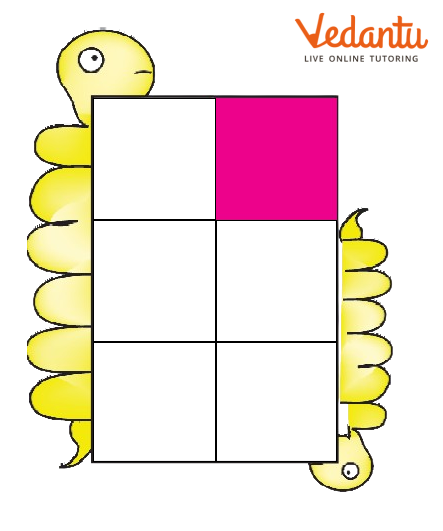
From the above image, we can say that $\dfrac{1}{6}$ of the shape is coloured.

Ans:

From the above image, we can say that $\dfrac{2}{9} of the shape is coloured. 

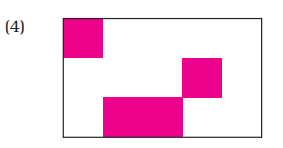
Ans: 

From the above image, we can say that $\dfrac{33}{12}$ of the shape is coloured.

Coloured Parts 

Complete these

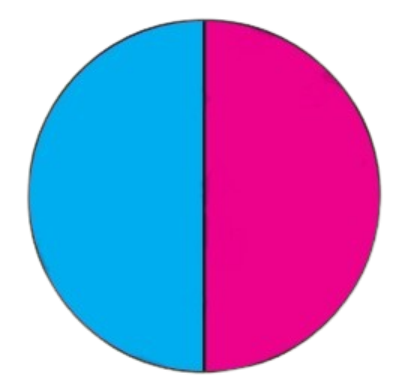
This _____ circle is divided into two equal parts. Out of equal parts one part is coloured blue.

Ans: The circle is divided into two equal parts. Out of two equal parts, one part is coloured blue.

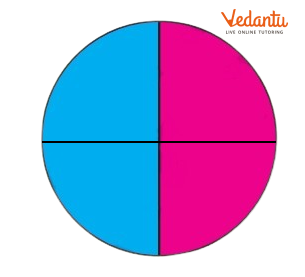
Here the circle is divided into_______ equal parts. Out of ______ equal parts, ________ parts are coloured blue.

Ans: Here the circle is divided into four equal parts. Out of four equal parts, two parts are coloured blue.

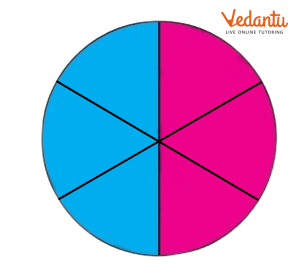
Here the circle is ........... ..................................... 

Ans: Here the circle is divided into 6 equal parts. Out of six equal parts, three parts are coloured blue.

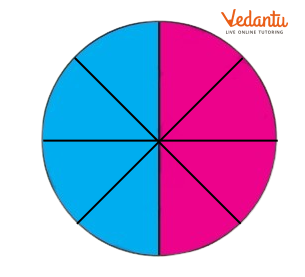
Here the circle is ........... ..................................... 

Ans: Here, the circle is divided into eiht equal parts. Out of eight equal parts, four parts are coloured blue.

So, we can say that ½ = $\dfrac{2}{4}$ = $\dfrac{3}{6}$ = $\dfrac{4}{8}$

Cutting the Halwa

Ramesh bought a piece of halwa for his children Ammu and Anu.

He divided it equally for them.

(i) Each will get ________ part of halwa.

Ans: Each will get ½ part of the halwa.

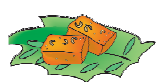
“This piece is too big. We can't eat it”, they said.

(ii) So he divided the pieces into half again. Now how many pieces will Ammu get? ________ 

Ans: Ammu gets two pieces.

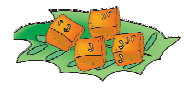
(iii) What part of the halwa is it? ________ 

Ans: $\dfrac{2}{4}$ part of halwa, or $\dfrac{1}{2}$ part of halwa.

“Make it even smaller, Dad” they asked

So he again cut the halwa into smaller pieces.

“Ok, thank you, Dad.”

(i) Now how many pieces will each get? 

Ans: Now, Ammu and Anu gets four pieces each.

(ii) What part of the halwa is each piece now?

Ans: Each piece is now $\dfrac{1}{8}$ of halwa.

(iii) If Ramesh had cut the halwa into 6 equal parts how many pieces each have got? Look at your answers for questions 1 to 4 and write — 

Ans: If Ramesh had cut the halwa into 6 equal parts, each got 3 pieces of halwa.

Then, $\dfrac{1}{2}=\dfrac{2}{4}=\dfrac{4}{8}=\dfrac{5}{10}=\dfrac{6}{12}$

Parts of the Strip 

(i) Look at the picture. Write what part of the strip is each green piece. Write the part for a piece of each colour.

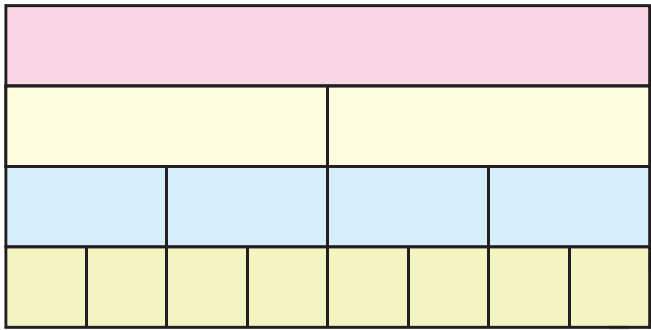
Ans: 

(ii) How many one-fourths will make a half?

Ans: We know that, 2 one-fourth will make a half = ¼ +¼ 

= $\dfrac{2}{4}$ (divide both numerator and denominator by 2)

= $\dfrac{1}{2}$ = half

(iii) How many $\dfrac{1}{8}$ will make $\dfrac{1}{4}$?

Ans: We know that, 2 $\dfrac{1}{8}$ will make $\dfrac{1}{4}$ 

= $\dfrac{1}{8}$ + $\dfrac{1}{8}$

= $\dfrac{2}{8}$ (divide both numerator and denominator by 2)

= $\dfrac{1}{4}$

(iv) How many $\dfrac{1}{8}$ are in $\dfrac{1}{2}$?

Ans: We know that, 4 $\dfrac{1}{8}$ will make $\dfrac{1}{2}$

= $\dfrac{1}{8}$+$\dfrac{1}{8}$+$\dfrac{1}{8}$+$\dfrac{1}{8}$

= $\dfrac{4}{8}$

= $\dfrac{1}{2}$ (divide both numerator and denominator by 4)

Patterns

Look at this square.

(i) What part is coloured blue?

Ans: 

From the above image, we can say that out of 16 squares, only 2 squares are coloured blue.

I.e. $\dfrac{2}{16}$ or $\dfrac{1}{8}$ part is coloured blue.

(ii) What part is green?

Ans: From the above image, we can say that out of 16 squares, only one square is coloured green.

I.e. $\dfrac{1}{16}$ part is coloured green.

Puzzle: Is it Equal?

Ammini says half of half and one-third of three-quarters are equal. Do you agree? How will you show this?

Ans: Yes, she is right. This can be shown in below images.

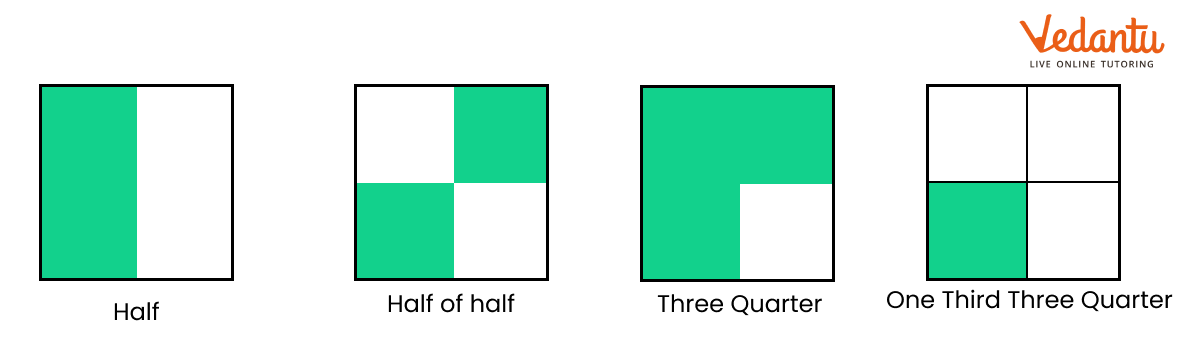
From a Part to the Whole

1) The picture show petals of a flower. Complete the flower by drawing the other petals.

Ans: 

2) The picture shows one-third of the blades of a fan. Complete the picture by drawing the other blades.

Ans: 

3) Half of the blades of another fan are shown here. Complete the picture by drawing the other half. How many blades have you drawn? 

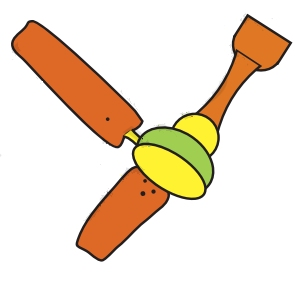
Ans: 

Rupees and Paise

(i)

How many will make one rupee?

Ans: Two 50 paise coins make one rupee.

(ii) Is 50 paise half of one rupee?

Ans: Yes, 50 paise is half of one rupee.

(iii)

How many will make one rupee?

Ans: Four 25 paise coins will make one rupee.

(iv) 25 paise is _________ part of one rupee

Ans: 25 paise is $\dfrac{1}{4}$ part of one rupee.

(v) 20 paise is _________ part of one rupee

Ans: 20 paise is $\dfrac{1}{5}$ part of one rupee.

Therefore, five 20 paise coins will make one rupee.

(vi) How many 10 paise will make one rupee?

Ans: Ten 10 paise coins will make one rupee.

(vii) So 10 paise is _____ part of one rupee.

Ans: So 10 paise is $\dfrac{1}{10}$ part of one rupee.

An Old Woman's Will

Once there lived an old woman. She lived with her three daughters. She was quite rich and had 19 camels. One day she fell ill. The daughters called the doctor. The doctor tried his best but could not save the woman. After her death, the daughters read what she had written in her will

My eldest daughter will get $\dfrac{1}{2}$ of my camels

My second daughter will get $\dfrac{1}{4}$ of my camels

My third daughter will get $\dfrac{1}{5}$ of my camels

The daughters were really puzzled. “How can I get $\dfrac{1}{2}$ of the 19 camels?”asked the eldest daughter. “Half of 19 is nine and a half. But we can’t cut the camel!” The second daughter said. “That is right. But what will we do now?” asked the third daughter”. Just then they saw their aunt coming. The daughters told her their problem. “Show me the will. I have an idea. You take my camel. So you have 20 camels. Now can you divide them as your mother wanted?” the aunt said. “You want half of the camels, don’t you? Take 10 camels” she said to the eldest daughter. “Take your share”, the aunt told the second daughter. She took one-fourth of the camels and got _____ camels. “You can take one-fifth of the camels”, the aunt told the third daughter. She got _____ camels. The daughters were very happy and counted their camels 10+ _____ + _____ =19.

“The one remaining is mine”, said the aunt and took her camel away!

How did this happen? Discuss.

Ans: By adding the aunt’s camel, the number of camel became 20.

First daughter’s share = $\dfrac{1}{2} of 20$ 

= $\dfrac{1}{2} \times 20$ = 10

Second daughter’s share = $\dfrac{1}{4} of 20$

= $\dfrac{1}{4} \times 20$ = 5

Third daughter’s share = $\dfrac{1}{5} of 20$

= $\dfrac{1}{5} \times 20$ = 4

So finally, 10+5+4 = 19 which is equal to the given number of camels. But this calculation is not correct mathematically, but it solved the problem of the three sisters.

Arun’s Time Table

Sleeping: One third of a day

Use different colours to show

Playing: One eighth of a day 

Studying: $\dfrac{1}{4}$ of a day

Ans:  We know that, a day has 24 hours and the given figure contains 25 boxes.

So, Arun spent one eighth of a day for playing 

= $\dfrac{1}{8} \times 24$

= 1 $\times$ 3

= 3 hours = 3 boxes

He spent $\dfrac{1}{4}$ of a day for studying

= $\dfrac{1}{4} \times 24 $

= 1 $\times$ 6

= 6 hours = 6 boxes

Sleeping, Playing, Studying and other activities

(i) How many hours does Arun take for Sleeping, Studying and Playing?

Ans: 8 hours for sleeping, 6 hours for studying and 3 hours for playing

(ii) What part of the day does he use for other activities?

Ans: He uses $\dfrac{7}{24}$ part of the day for other activities.

School Magazine

A school has decided to bring out a magazine every quarter of the year. How many magazines will they have in a year? If they want to print it at the end of each quarter of a year, which are the months for printing? Mark the number for those months.

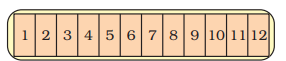
Ans: It is given that the school has decided to bring out a magazine every quarter of the year.

We know that there are 12 months in a year

Quarter of the year = $\dfrac{1}{4} \times 12$

=1 $\times$ 3 = 3 months

So, every three months, the school has to bring out a new magazine

Sleeping Beauty! 

Have you heard of Kumbhakarna, the brother of Ravana? He is famous for sleeping for half a year.

(i) Most people sleep about 8 hours a day. Then what part of a day is it? ________ 

Ans: We know that a day has 24 hours

Given, most of the people sleep about 8 hours a day 

= $\dfrac{8}{24}$

= $\dfrac{1}{3}$ part for a day

(ii) So what part of a year do they sleep? A person 60 years old must have slept _______ years!!!

Ans: A person 60 years old must have slept for = $\dfrac{1}{3} \times 60$

= 1 $\times$ 20

= 20 years

Keerti’s Shopping List

Look at the yellow price list.

a) How much does 2 kg of tomato cost?

Ans: From the price list, we can say that 1 kg tomato = Rs 12

Then, the cost of 2 kg of tomatoes = 12 $\times$ 2 = Rs 24

b)  How much does $\dfrac{1}{2}$  kg of tomato cost?

Ans: From the price list, we can say that 1 kg of tomatoes = Rs 12

Then, the cost of $\dfrac{1}{2}$ of tomatoes = $\dfrac{1}{2} \times 12$

= Rs 6 

c) Kiran wants 2$\dfrac{1}{2}$ kg of tomato. How much will it cost?

Ans: From the price list, we know that 1 kg of tomatoes = Rs 12

For $\dfrac{1}{2}$ kg of tomatoes = $\dfrac{1}{2} \times 12$ = Rs 6

Then, the cost of 2 kg of tomatoes = 12 $\times$ 2 = Rs 24

So, the cost of 2 $\dfrac{1}{2}$ kg = 24 +6 = Rs 30

d) How much does 3$\dfrac{1}{2}$ kg potato cost?

Ans: from price list, we know that 1 kg of potatoes = Rs 10

For $\dfrac{1}{2}$ kg of potatoes = $\dfrac{1}{2} \times 10$ = Rs 5

Then, 3 kg of potatoes = 3 $\times$ 10 = Rs 30

So, the cost of 3 $\dfrac{1}{2}$ kg of potatoes = 30 + 5 = Rs 35

e) What is the price of 1$\dfrac{1}{4}$ kg of carrot?

Ans: From price list, we know that the cost of 1 kg of carrot = Rs 18

For $\dfrac{1}{2}$ kg of carrots = $\dfrac{1}{2} \times 18 $ = $\dfrac{9}{2}$ = Rs 4.5

Then, 1 $\dfrac{1}{4}$ kg of carrots = 18 +4.5 = 22.5

f) He bought a gourd of weight 4$\dfrac{3}{4}$ kg and it costs _________ 

Ans: From the price list we know that 1 kg of gourd = Rs 8

For 4 kg = 4 $\times$ 8 = Rs 32

For $\dfrac{3}{4}$ kg = $\dfrac{3}{4} \times 8$ = 3 $\times$ 2 = Rs 6

Then, the cost of  4$\dfrac{3}{4}$ kg of gourd = 32 + 6 =  Rs 38

g) Look at the shopping list in Keerti’s hand. How much will she have to pay to buy all of these? 

Ans: 

Practice time

1) Raheem’s journey Raheem has to travel 1 $\dfrac{1}{4}$ km to reach school. What distance does he travel to go to school and come back home?

Ans: It is given that to reach the school Raheem has to travel = 1 $\dfrac{1}{4}$ = $\dfrac{5}{4}$ km

Total distance travelled by Raheem = $\dfrac{5}{4}$+$\dfrac{5}{4}$

=$\dfrac{10}{4}$

=$\dfrac{5}{2}$

= 2 $\dfrac{1}{2}$km

Therefore, he travels to go to school and comes back home = 2 $\dfrac{1}{2} km

2) What coins? 

Latha bought a pencil and a pen for seven and a half rupees. She gave ` 10/–. The shopkeeper gave back the money in half and quarter rupees. What are the coins she got? 

Ans: it is given that Latha bought a pencil and a pen for = 7 $\dfrac{1}{2}$

Money given by Latha to the shopkeeper = Rs 10

Shopkeeper gave back the money = 10 - 7.5 = Rs 2.5

So, the shopkeeper can return Rs 2.5 in the following ways

1. 1 half rupee coins and 8 quarter rupee coins 

2. 2 half rupee coins and 6 quarter rupee coins 

3. 3 half rupee coins and 4 quarter rupee coins

4. 4 half rupee coins and 2 quarter rupee coins

3) At the railway station

Your attention please. Mangalore Express coming from Mangalore and going to Thiruvananthapuram is now running late by half an hour.

Oh, the train is late today. The right time is a quarter to 7.

a) What time is the train expected to come today?

Ans: The right time is a quarter to 7 that is 6:45

But, the train is delayed by half an hour, that is 30 minutes 

So, the exact time the train will arrive at 6:45 + 0:30 = 7:15

b) Nazia gets off at a station after 2$\dfrac{1}{2}$ hours from this station. What time will she get off?

Ans: It is given that, Nazia gets off at station after 2:30 hours

Then, total time taken by Nazia to reach = 2:30 + 7: 15 = 9:45

c) Shaji will take 5 hours to reach Ernakulam by this train. At what time will he reach there?

Ans: It is given that Shaji will take 5 hours to reach Ernakulam.

Then, the total time taken by Shaji to reach Ernakulam = 7:15 + 5 = 12:15

Conclusion

Throughout Class 5 Maths Chapter 4 solutions, you have learned how to represent parts using fractions, visualized them with drawings and activities, and even discovered their applications in everyday life. Remember, fractions are just a fancy way of talking about parts and wholes. This knowledge serves as a crucial stepping stone for your future adventures in the world of mathematics. As you move forward, fractions will become an essential tool for solving problems involving parts, portions, and ratios.

From previous years' exams, typically 3-5 questions have been asked from this chapter. These questions often include identifying and representing fractions, comparing and ordering fractions, finding equivalent fractions, and performing simple addition and subtraction of fractions. 

Other Study Material for CBSE Class 5 Maths Chapter 4

Chapter-Specific NCERT Solutions for Class 5 Maths

Given below are the chapter-wise NCERT Solutions for Class 5 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for CBSE Class 5 Maths