NCERT Solutions for Class 12 Maths Chapter 6 - In Hindi

प्रश्नावली 6.1

1. वृत के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या ${\text{r}}$ के सापेक्ष ज्ञात कीजिए जबकि

1: ${\text{r  =  3cm}}$ है।

2: ${\text{r  =  4cm}}$ है।

उत्तर:   हमें ज्ञात है कि त्रिज्या $\mathrm{r}$ वाले वृत का क्षेत्रफल $\mathrm{A}=π x^{2}$ के सापेक्ष $\mathrm{A}$ की परिवर्तन दर,

$\dfrac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=2 π \mathrm{r}$

$\text { 1: } \mathrm{r}=3 \mathrm{~cm}$

$\therefore \dfrac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=2 π(3)=6 π \mathrm{cm}$

$\text { 2: } \mathrm{r}=4 \mathrm{~cm}$

$\therefore \dfrac{\mathrm{d} \mathrm{A}}{\mathrm{dr}}=2 π(4)=8 π \mathrm{cm}$

2. एक घन की आयतन ${\text{8c}}{{\text{m}}^{\text{2}}}{\text{/s}}$की दर से बढ रहा है। पृष्ठ का क्षेत्रफल किस दर से बढ रहा है जबकि इसके किनारे की लंबाई ${\text{12cm}}$ है।

उत्तर:  मान लेते हैं घन के किनारे कि लंबाई $=x$

$\Rightarrow$ घन का आयतन, $\mathrm{V}=\mathrm{x}^{3}$

$\Rightarrow t$, के सापेक्ष $V$ का परिवर्तन दर $\dfrac{d V}{d t}=3 x^{2} \dfrac{d x}{d t}$

$\Rightarrow 8=3 \mathrm{x}^{2} \dfrac{\mathrm{dx}}{\mathrm{dt}} \Rightarrow 8=3(12)^{2} \dfrac{\mathrm{dx}}{\mathrm{dt}} \Rightarrow \dfrac{8}{3 \times 144}=\dfrac{\mathrm{dx}}{\mathrm{dt}}$

$\Rightarrow$ घन का क्षेत्रफल, $A=6 x^{2}$

$\Rightarrow \mathrm{A}$ की परिवर्तन दर, $\dfrac{\mathrm{d} \mathrm{A}}{\mathrm{dt}}=12 \mathrm{x} \dfrac{\mathrm{dx}}{\mathrm{dt}}=12 \times 12 \times \dfrac{8}{3 \times 144}=\dfrac{8}{3}$

3. एक वृत की त्रिज्या समान रूप से ${\text{8cm/s}}$की दर से बढ रही है । ज्ञात कीजिए कि वृत की वृत का क्षेत्रफल किस दर से बढ रहा है जब त्रिज्या ${\text{10}}$ है।

उत्तर: मान लेते है वृत कि त्रिज्या $=\mathrm{r}$

दिया गया है $\dfrac{\mathrm{dr}}{\mathrm{dt}}=8 \mathrm{~cm} / \mathrm{s}$

$\mathrm{t}$, सापेक्ष $\mathrm{A}$ कि परिवर्तन दर, $\dfrac{\mathrm{d} \mathrm{A}}{\mathrm{di}}=2 π \mathrm{r} \dfrac{\mathrm{dr}}{\mathrm{dt}}=2 π \mathrm{r}(3)=6 π \mathrm{r}$ $\mathrm{r}=10 \mathrm{~cm}$

$\dfrac{\mathrm{d} \mathrm{A}}{\mathrm{dt}}=6 π(10)=60 π \mathrm{cm}^{2} / \mathrm{s}$

$\Rightarrow$ वृत का क्षेत्रफल $60 π \mathrm{cm}^{2} / \mathrm{s}$ की दर से बदलेगा

4. एक परिवर्तनशील घन का किनारा ${\text{3cm/s}}$ की दर से बढ रहा है । घन का आयतन किस दर से बढ रहा है जबकि घन का किनारा ${\text{10}}$ लंबा है।

उत्तर: मान लेते हैं कि घन की लंबाई $\mathrm{x} \mathrm{cm}$

$\Rightarrow$ घन का आयतन $\mathrm{V}=\mathrm{x}^{3}$

दिया गया है $\dfrac{\mathrm{dx}}{\mathrm{dt}}=3 \mathrm{~cm} / \mathrm{s}$

$\Rightarrow \mathrm{t}$ के सापेक्ष $\mathrm{V}$ का परिवर्तन दर $\dfrac{\mathrm{dV}}{\mathrm{dt}}=3 \mathrm{x}^{2} \dfrac{\mathrm{dx}}{\mathrm{dt}}$

$\Rightarrow \dfrac{\mathrm{dV}}{\mathrm{dt}}=3 \mathrm{x}^{2}(3)$

$\Rightarrow \dfrac{\mathrm{dV}}{\mathrm{dt}}=9 \mathrm{x}^{2}=9 \times(10)^{2}=900 \mathrm{~cm}^{3} / \mathrm{s}$

$\Rightarrow$ घन का आयतन $900 \mathrm{~cm}^{3} / \mathrm{s}$ की दर से बढेगा

5. एक स्थिर झील में एक पत्थर डाला जाता है और तरंगें वृतों में ${\text{5 cm / s}}$ की गति से चलती हैं। जब वृताकार तरंगों की त्रिज्या ${\text{8cm}}$ है तो उस क्षण घिरा हुआ क्षेत्रफल किस दर से बढ रहा है 

उत्तर:  मान लेते हैं कि वृत की त्रिज्या = $\mathrm{r}$

दिया गया है $\dfrac{\mathrm{dr}}{\mathrm{dt}}=5 \mathrm{~cm} / \mathrm{s}$

वृत का क्षेत्रफल $A=π r^{2}$

$\mathrm{t}$ के सापेक्ष $\mathrm{A}$ की परिवर्तन दर, $\dfrac{\mathrm{d} \mathrm{A}}{\mathrm{d} \mathrm{i}}=2 π \mathrm{r} \dfrac{\mathrm{dr}}{\mathrm{dt}}=2 π \mathrm{r}(5)=10 π \mathrm{r}$

$\mathrm{r}=8 \mathrm{~cm}$

$\therefore \dfrac{\mathrm{d} \mathrm{A}}{\mathrm{d} \mathrm{t}}=10 π(8)=80 π \mathrm{cm}^{2} / \mathrm{s}$

$\Rightarrow$ वृत का क्षेत्रफल $80 π \mathrm{cm}^{2} / \mathrm{s}$ की दर से बदलेगा

6. एक वृत की त्रिज्या $0.7{\text{cm}}/{\text{s}}$की दर से बढ रही है। इसकी परिधि कि वृद्धि की दर क्या है जब ${\text{r  =  4}}{\text{.9 cm}}$ है।

उत्तर: मान लेते हैं कि वृत की त्रिज्या = $\mathrm{r}$

दिया गया है $\dfrac{\mathrm{dr}}{\mathrm{dt}}=0.7 \mathrm{~cm} / \mathrm{s}$

वृत की परिधि $\mathrm{C}=2 π \mathrm{r}$

$\mathrm{t}$ के सापेक्ष $\mathrm{C}$ की परिवर्तन दर, $\dfrac{\mathrm{dC}}{\mathrm{di}}=2 π \dfrac{\mathrm{dr}}{\mathrm{dt}}=2 π(0.7)=1.4 π$

जब $\mathrm{r}=4.9 \mathrm{~cm}$ हो तो $\dfrac{\mathrm{dC}}{\mathrm{di}}=1.4 π=1.4 \times \dfrac{22}{7}=4.4 \mathrm{~cm} / \mathrm{s}$

$\Rightarrow$ वृत की परिधि $4.4 \mathrm{~cm} / \mathrm{s}$ की दर से बढेगी।

7. एक आयत की लंबाई ${\text{x}},5{\text{cm}}/{\text{min}}$की दर से घट रही है और चौडाई ${\text{y, 4cm / min}}$की दर से घट रही है। जब ${\text{x = 8cm,  y =  6cm}}$

हैं तब आयत के $\left( {\text{a}} \right)$ परिमाप $\left( {\text{b}} \right)$ क्षेत्रफल के परिवर्तन की दर ज्ञात कीजिए।

उत्तर: दिया गया है, आयत की लंबाई $=x$ और चौडाई $=y$,

$\dfrac{d x}{d t}=-5 \mathrm{~cm} / \mathrm{min}, \dfrac{d y}{d t}=4 \mathrm{~cm} / \mathrm{min}$

$\text { (a) } \mathrm{P}=2(x+y)$

$\Rightarrow \dfrac{\mathrm{dP}}{\mathrm{dt}}=2\left(\dfrac{d x}{\mathrm{dt}}+\dfrac{d y}{d t}\right)=2(-5+4)=-2 \mathrm{~cm} / \mathrm{min}$

आयत का परिमाप $-2 \mathrm{~cm} / \mathrm{min}$ से घट रहा है।

(b) $\mathrm{A}=\mathrm{xy}$

$\Rightarrow \dfrac{\mathrm{d} A}{\mathrm{dt}}=\left(\mathrm{y} \dfrac{\mathrm{dx}}{\mathrm{dt}}+\mathrm{x} \dfrac{\mathrm{dy}}{\mathrm{dt}}\right)=6 \times(-5)+4 \times 8=2 \mathrm{~cm}^{2} / \mathrm{min}$

आयत का क्षेत्रफल $2 \mathrm{~cm}^{2} / \mathrm{min}$ की दर से बढेगा।

8. एक गुब्बारा जो सदेव गोलाकार रहता है, एक पम्प द्वारा ${\text{900}}$ गैस प्रति सेकंड भर कर फुलाया जाता है गुब्बारे की त्रिज्या के परिवर्तन दर ज्ञात कीजिए, जब त्रिज्या $15{\text{cm}}$

उत्तर: मान लेते हैं, गुब्बारे की त्रिज्या $=\mathrm{r}$

गुब्बारे का आयतन $\mathrm{V}=\dfrac{4}{3} π \mathrm{r}^{3}$

$\Rightarrow \mathrm{t}$ के सापेक्ष $\mathrm{V}$ का परिवर्तन दर $\dfrac{\mathrm{dV}}{\mathrm{dr}}=4 π \mathrm{r}^{2}$

दिया गया है, $\dfrac{\mathrm{dV}}{\mathrm{dt}}=900, \mathrm{r}=15 \mathrm{~cm}$

$\therefore 900=4 π(15)^{2} \dfrac{\mathrm{dr}}{\mathrm{dt}} \Rightarrow \dfrac{\mathrm{dr}}{\mathrm{dt}}=\dfrac{900}{4 \times 225 π}=\dfrac{1}{π} \mathrm{cm} / \mathrm{s}$

गुब्बारे की त्रिज्या में वृद्धि $=\dfrac{1}{π} \mathrm{cm} / \mathrm{s}$

9. एक गुब्बारा जो सदैव गोलाकार रहता है की त्रिज्या परिवर्तनशील है। त्रिज्या की सापेक्ष आयतन का परिवर्तन दर ज्ञात कीजिए, जब त्रिज्या $10{\text{cm}}$ है।

उत्तर: मान लेते हैं, गुब्बारे की त्रिज्या = $\mathrm{r}$

गुब्तारे का आयतन $\mathrm{V}=\dfrac{4}{3} π \mathrm{r}^{3}$

$\Rightarrow \mathrm{t}$ के सापेक्ष $\mathrm{V}$ का परिवर्तन दर $\dfrac{\mathrm{dV}}{\mathrm{dr}}=4 π \mathrm{r}^{2}$

दिया गया है, $\mathrm{r}=10 \mathrm{~cm}$

$\Rightarrow \dfrac{\mathrm{dV}}{\mathrm{dr}}=4 π(10)^{2}=400 π \mathrm{cm}^{2} / \mathrm{s}$

गुब्बारे का आयतन $400 π \mathrm{cm}^{2} / \mathrm{s}$ की दर से बढेगा।

10. एक $5$ लंबी सीढी दीवार के सहारे झुकी है। सीढी के नीचे का सिरा, ज़मीन के अनुदिश, दीवार से दूर $2{\text{cm}}/{\text{s}}$ कि दर से खींचा जाता है। दीवार पर उसकी ऊँचाई किस दर से घट रही है जबकि सीढी के नीचे का सिरा दीवार से ${\text{4m}}$दूर है ।

उत्तर: मान लेते हैं $\mathrm{BC}=\mathrm{x}, \mathrm{AB}=\mathrm{y}$

दिया गया है $\dfrac{\mathrm{dx}}{\mathrm{dt}}=2 \mathrm{~cm}^{2} / \mathrm{s}, \mathrm{AC}=5 \mathrm{~cm}$

त्रिभुज $\mathrm{ABC}$ मे

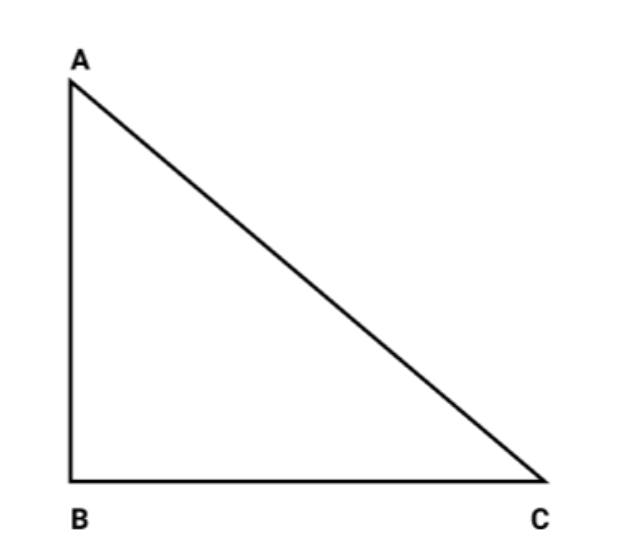
$A C^{2}=A B^{2}+B C^{2} \Rightarrow 25=x^{2}+y^{2}$

$\Rightarrow y^{2}=25-16=9 \Rightarrow y=3$

$\Rightarrow \mathrm{t}$, के सापेक्ष परिवर्तन दर,

$0=2 \mathrm{x} \dfrac{\mathrm{dx}}{\mathrm{dt}}+2 \mathrm{y} \dfrac{\mathrm{dy}}{\mathrm{dt}}$

$\Rightarrow \dfrac{\mathrm{dy}}{\mathrm{dt}}=(-2) \times(4) \times \dfrac{2}{6}=-\dfrac{8}{3} \mathrm{~cm} / \mathrm{s}$

$\mathrm{y}= \dfrac{8}{3} \mathrm{~cm} / \mathrm{s}$ की दर से घट रही है।

11. एक कण वक्र ${\text{6y  =  }}{{\text{x}}^{\text{3}}}{\text{  +  2}}$के अनुगत गति कर रहा है । वक्र पर उन बिंदुओं को ज्ञात कीजिए जबकि ${\text{x}}$निर्देशांक की तुलना ${\text{y}}$निर्देशांक ${\text{8}}$ गुना तीव्रता से बदल रहा है।

उत्तर: दिया गया है $\dfrac{d y}{d t}=8 \dfrac{d x}{d t}$,

$6 y=x^{3}+2 \Rightarrow 6 \dfrac{d y}{d t}=3 x^{2} \dfrac{d x}{d t}$

$\Rightarrow 6(8) \dfrac{d x}{d t}=3 x^{2} \dfrac{d x}{d t} \Rightarrow x^{2}=16 \Rightarrow x=\pm 4$

(i) $x=4 \Rightarrow y=\dfrac{4^{3}+2}{6}=11$

(ii) $x=-4 \Rightarrow y=\dfrac{(-4)^{3}+2}{6}=-\dfrac{31}{3}$

वक्र पर उन बिन्दुओ के निर्देशांक होंगे $(4,11)$ या $(-4,-31 / 3)$

12. हवा के बुलबुले की त्रिज्या $1/2{\text{cm}}/{\text{s}}$की दर से बढ रही है। बुलबुले का आयतन किस दर से बढ रहा है जबकि त्रिज्या $1{\text{cm}}$ है 

उत्तर: मान लेते है, बुलबुले की त्रिज्या = $\mathrm{r}$

बुलबुले का आयतन $\mathrm{V}=\dfrac{4}{3} π \mathrm{r}^{3}$

$\Rightarrow \mathrm{t}$, के सापेक्ष $\mathrm{V}$ का परिवर्तन दर $\dfrac{\mathrm{dV}}{\mathrm{dt}}=4 π \mathrm{r}^{\mathrm{2}} \dfrac{\mathrm{dr}}{\mathrm{dt}}$

दिया गया है, $\mathrm{r}=1 \mathrm{~cm}$

$\Rightarrow \dfrac{\mathrm{dV}}{\mathrm{dr}}=4 π(1)^{2}\left(\dfrac{1}{2}\right)=2 π \mathrm{cm}^{3} / \mathrm{s}$

13. एक गुब्बारा जो सदैव गोलाकार रहता है, क परिवर्तनशील व्यास $\dfrac{{\text{3}}}{{\text{2}}}{\text{(2x  +  1)}}$है ${\text{x}}$ के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए।

उत्तर: मान लेते हैं, गुब्बारे की त्रिज्या $=\dfrac{3}{4}(2 \mathrm{x}+1)$

गुब्तारे का आयतन $\mathrm{V}=\dfrac{4}{3} π\left(\dfrac{3}{4}(2 \mathrm{x}+1)\right)^{3}$

$\Rightarrow x$ के सापेक्ष $V$ का परिवर्तन दर $\dfrac{d V}{d x}=4 π\left(\dfrac{3}{4}(2 x+1)\right)^{2}\left(\dfrac{3}{4}(2 x)\right)=\dfrac{27}{8} π((2 x+1))^{2}$

गुब्बारे का आयतन का परिवर्तन $=\dfrac{27}{8} π((2 \mathrm{x}+1))^{2}$

14. एक पाइप से रेत $12{\text{c}}{{\text{m}}^3}/{\text{s}}$की दर से गिर रही है । गिरती रेत ज़मीन पर ऐसा शंकु बनाती है जिसकी ऊँचाई सदैव आथार की त्रिज्या का छटा भाग है । रे से बने शंकु की ऊँचाई किस दर से बढ रही है जबकि उसकी ऊँचाई ${\text{4cm}}$ है 

उत्तर: मान लेते है शंकु कि ऊंचाई $=h$

$t$, के सापेक्ष $V$ का परिवर्तन दर $\dfrac{d V}{d t}=12 \mathrm{~cm}^{3} / \mathrm{s}$

$\mathrm{h}=\dfrac{1}{6} \mathrm{r}$

$\mathrm{V}=\dfrac{1}{3} π \mathrm{r}^{2} \mathrm{~h}=\dfrac{1}{3} π(6 \mathrm{~h})^{2} \mathrm{~h} \Rightarrow \dfrac{\mathrm{dV}}{\mathrm{dt}}=12 π \mathrm{h}^{3}$

$\mathrm{t}$, के सापेक्ष $\mathrm{V}$ का परिवर्तन दर $\dfrac{\mathrm{dV}}{\mathrm{dt}}=36 π \mathrm{h}^{2} \dfrac{\mathrm{dh}}{\mathrm{dt}}$

$\Rightarrow \dfrac{d h}{d t}=\dfrac{12}{36 π h^{2}}=\dfrac{1}{3 π(4)^{2}}=\dfrac{1}{48 π} \mathrm{cm} / \mathrm{s}$

15. एक वस्तु की इकाइयों के उत्पादन से संबंध कुल लागत ${\text{C(x)}}$(रुपये में)

${\text{C(x)  =  0}}{\text{.007}}{{\text{x}}^{\text{3}}}{\text{  -  0}}{\text{.003}}{{\text{x}}^{\text{2}}}{\text{  +  15x  +  4000}}$

से प्रदत्त है। सीमांत लागत ज्ञात कीजिए जबकि $17$ इकाइयों का उत्पादन किया गया है ।

उत्तर: $\mathrm{C}(\mathrm{x})=0.007 \mathrm{x}^{3}-0.003 \mathrm{x}^{2}+15 \mathrm{x}+4000$

$\Rightarrow \dfrac{\mathrm{dC}}{\mathrm{dx}}=0.021 \mathrm{x}^{2}-0.006 \mathrm{x}+15$

$\mathrm{x}=17 \Rightarrow \dfrac{\mathrm{dC}}{\mathrm{dx}}=0.021(17)^{2}-0.006(17)+15$

$=6.069-0.102+15=20.967$

17 इकाइयों का उत्पादन में सीमांत लागत $20.967$

16. किसी उत्पाद की इकाइयों के विक्रय से प्राप्त कुल आय ${\text{R(x)}}$ रुपये में

${\text{R(x)  =  13}}{{\text{x}}^{\text{2}}}{\text{  +  26x  +  15}}$

से प्रदत्त है । सीमांत आय ज्ञात कीजिए जब ${\text{x  =  7}}$ है।

उत्तर: $R(x)=13 x^{2}+26 x+15$

$\Rightarrow \dfrac{\mathrm{dR}}{\mathrm{dx}}=26 \mathrm{x}+26$

$\mathrm{x}=17 \Rightarrow \dfrac{\mathrm{dR}}{\mathrm{dx}}=26(7)+26=208$

अतः $\mathrm{x}=7$ में सीमांत आय होगा 208 रुपये

17. एक वृत की त्रिज्या ${\text{r  =  6cm}}$पर ${\text{r}}$ के सापेक्ष क्षेत्रफल में परिवर्तन की दर है

(A) ${\text{10π }}$

(B) ${\text{12π }}$

(C) ${\text{8π }}$

(D) ${\text{11π }}$

उत्तर: दिया गया है वृत की त्रिज्या ${\text{r  =  6cm}}$

हमें ज्ञात है कि ${\text{A  =  π }}{{\text{r}}^{\text{2}}} \Rightarrow \dfrac{{{\text{dA}}}}{{{\text{dr}}}}{\text{  =  2π r  =  12π }}$

अतः (B) सही विकल्प है ।

18. एक उत्पाद की ${\text{x}}$ इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में

${\text{R(x)  =  3}}{{\text{x}}^{\text{2}}}{\text{  +  36x  +  5}}$है। जब ${\text{x  =  15}}$है तो सीमांत आय है :

(A) ${\text{116}}$

(B) ${\text{96}}$

(C) $90$

(D) ${\text{126}}$

उत्तर: (D) सही विकल्प है ।

${\text{R(x)  =  3}}{{\text{x}}^{\text{2}}}{\text{  +  36x  +  5}} $

$\Rightarrow \dfrac{{{\text{dR}}}}{{{\text{dx}}}}{\text{  =  6x  +  36}}$

${\text{x  =  15}} \Rightarrow \dfrac{{{\text{dR}}}}{{{\text{dx}}}}{\text{  =  6(15)  +  36  =  126}}$

प्रश्नावली 6.2

1. सिद्ध कीजिए कि ${\text{R}}$पर ${\text{f}}({\text{x}}) = 3{\text{x}} + 17$से प्रदत्त फलन वर्धमान है। 

उत्तर: ${\text{f}}({\text{x}}) = 3{\text{x}} + 17$

${\text{f '(x)  =  3  >  0, x}} \in {\text{R}}$

इसलिए फलन ${\text{R}}$ पर निरंतर वर्धमान है 

2. सिद्ध कीजिए कि ${\text{R}}$ पर ${\text{f(x)  =  }}{{\text{e}}^{{\text{2x}}}}$से प्रदत्त फलन वर्धमान है। 

उत्तर: ${\text{f(x)  =  }}{{\text{e}}^{{\text{2x}}}}$

${\text{f '(x)  =  2}}{{\text{e}}^{{\text{2x}}}}{\text{ >  0, x}} \in {\text{R}}$

इसलिए फलन ${\text{R}}$ पर निरंतर वर्धमान है 

3. सिद्ध कीजिए ${\text{f(x)  =  sin x}}$से प्रदत्त फलन

(a) $\left( {0,\dfrac{π }{2}} \right)$ में वर्धमान है

उत्तर:  ${\text{f(x)  =  sin x}}$

${\text{f '(x)  =  cos x  >  0, x}} \in \left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right)$

इसलिए फलन $\left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right)$ पर निरंतर वर्धमान है 

(b) $\left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$ में हासमान है

उत्तर: ${\text{f(x)  =  sin x}}$

${\text{f '(x)  =  cos x  <  0, x}} \in \left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$

इसलिए फलन $\left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$ पर निरंतर हासमान है 

(c) ${\text{(0,π )}}$ में न तो वर्धमान है न ही हासमान है

उत्तर: ${\text{f(x)  =  sin x}}$

${\text{f '(x)  =  cos x}}$

${\text{f '(x)  =  cos x  <  0, x}} \in \left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$${\text{f '(x)  =  cos x  >  0, x}} \in \left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right){\text{   ;   f '(x)  =  cos x  <  0, x}} \in \left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$

इसलिए फलन ${\text{(0,π )}}$ में न तो वर्धमान है न हासमान है

4. अंतराल ज्ञात ज्ञात किजीए जिनमें ${\text{f (x)  =  2}}{{\text{x}}^{\text{2}}}{\text{  -  3x}}$से प्रदत्त फलन ${\text{f}}$

(a) वर्धमान

उत्तर: ${\text{f (x)  =  2}}{{\text{x}}^{\text{2}}}{\text{  -  3x}}$

${\text{f '(x)  =  4x  -  3n}} $

$\forall {\text{ f '(x)  =  0}} $

${\text{4x  -  3  =  0}}$

${\text{x  =  }}\dfrac{{\text{3}}}{{\text{4}}}$

${\text{f '(x)  =  4x  -  3  >  0, x}} \in \left( {\dfrac{{\text{3}}}{{\text{4}}}{\text{,}}\infty } \right)$

इसलिए फलन  $\left( {\dfrac{{\text{3}}}{{\text{4}}}{\text{,}}\infty } \right)$ पर निरंतर वर्धमान है

(b) हासमान उत्तर:

उत्तर: ${\text{f (x)  =  2}}{{\text{x}}^{\text{2}}}{\text{  -  3x}}$

${\text{f '(x)  =  4x  -  3n}} $

$\forall {\text{ f '(x)  =  0}} $

${\text{4x  -  3  =  0}} $

${\text{x  =  }}\dfrac{{\text{3}}}{{\text{4}}} $

${\text{f '(x)  =  cos x  <  0, x}} \in \left( {{\text{ -  }}\infty {\text{,}}\dfrac{{\text{3}}}{{\text{4}}}} \right) $ 

इसलिए फलन $\left( {{\text{ -  }}\infty {\text{,}}\dfrac{{\text{3}}}{{\text{4}}}} \right)$ पर निरंतर हसमान है 

5. अंतराल ज्ञात ज्ञात किजीए जिनमें ${\text{f(x)  =  2}}{{\text{x}}^{\text{3}}}{\text{  -  3}}{{\text{x}}^{\text{2}}}{\text{  -  36x  +  7}}$से प्रदत्त फलन ${\text{f}}$

(a) वर्धमान

उत्तर: ${\text{f(x)  =  2}}{{\text{x}}^{\text{3}}}{\text{  -  3}}{{\text{x}}^{\text{2}}}{\text{  -  36x  +  7}}$

${\text{f '(x)  =  6}}{{\text{x}}^{\text{2}}}{\text{ -  6x  -  36}} $

${\text{ =  6}}\left( {{{\text{x}}^{\text{2}}}{\text{ -  x  -  6}}} \right) $

${\text{ =  6(x  -  3)(x  +  2)}} $

$\forall {\text{ f '(x)  =  0}} $

${\text{6 (x  -  3)(x  +  2)  =  0}}$

$x =  - 2,3$ वास्तविक रेखा के तीन अंतरालों $\left( { - \infty , - 2} \right),\left( { - 2,3} \right)$ और $\left( {3,\infty } \right)$ में विबक्त करता है 

इसलिए फलन ${\text{f}}$अंतरालों $\left( { - \infty , - 2} \right)$ और $\left( {3,\infty } \right)$  पर निरंतर वर्धमान है

(b) हासमान

उत्तर: ${\text{f(x)  =  2}}{{\text{x}}^{\text{3}}}{\text{  -  3}}{{\text{x}}^{\text{2}}}{\text{  -  36x  +  7}}$

${\text{f '(x)  =  6}}{{\text{x}}^{\text{2}}}{\text{ -  6x  -  36}} $

${\text{ =  6}}\left( {{{\text{x}}^{\text{2}}}{\text{ -  x  -  6}}} \right) $

${\text{ =  6(x  -  3)(x  +  2)}} $

$\forall {\text{ f '(x)  =  0}} $

${\text{6 (x  -  3)(x  +  2)  =  0}} $ 

$x =  - 2,3$ वास्तविक रेखा के तीन अंतरालों $\left( { - \infty , - 2} \right),\left( { - 2,3} \right)$ और $\left( {3,\infty } \right)$ में विबक्त करता है 

इसलिए फलन ${\text{f}}$ अंतरालों $\left( { - \infty , - 2} \right)$ और $\left( {3,\infty } \right)$ पर निरंतर हसमान है

इसलिए फलन ${\text{f}}$ अंतरालों $\left( { - 2,3} \right)$ पर निरंतर हसमान है

6. अंतराल ज्ञात ज्ञात किजीए जिनमें निम्नलिखित फलन ${\text{f}}$ वर्धमान या हासमान है 

(a) ${\text{f (x)  =  }}{{\text{x}}^{\text{2}}}{\text{  +  2x  +  5}}$

उत्तर: ${\text{f '(x)  =  2x  +  2}}$

$\forall {\text{ f '(x)  =  0}}$

${\text{2x  +  2  =  0}}$

${\text{x  =   -  1}} $ 

${\text{f '(x)  =  2x  +  2  <  0, x}} \in {\text{( -  }}\infty {\text{,  -  1)}}$ में निरंतर हसमान है 

${\text{f '(x)  =  2x  +  2  >  0, x}} \in {\text{(  -  1,}}\infty {\text{)}}$ में निरंतर वर्धमान है 

(b) ${\text{f(x)  =  10  -  6x  -  2}}{{\text{x}}^{\text{2}}}$

उत्तर: ${\text{f '(x)  =   -  6  -  4x}}$

$\forall {\text{ f '(x)  =  0}} $

${\text{ -  6  -  4x  =  0}} $

${\text{x  =  }}\dfrac{{{\text{ - 3}}}}{{\text{2}}} $ 

${\text{f '(x)  =   -  6  -  4x  >  0, x}} \in \left( {{\text{ - }}\infty {\text{,}}\dfrac{{{\text{ - 3}}}}{{\text{2}}}} \right)$ में निरंतर हसमान है 

${\text{f '(x)  =   -  6  -  4x  >  0, x}} \in \left( {\dfrac{{{\text{ - 3}}}}{{\text{2}}},{\text{ - }}\infty } \right)$ में निरंतर वर्धमान है 

(c) ${\text{f(x)  =   -  2}}{{\text{x}}^{\text{3}}}{\text{  -  9}}{{\text{x}}^{\text{2}}}{\text{  -  12x  +  1}}$

उत्तर: ${\text{f '(x)  =   -  6}}{{\text{x}}^{\text{2}}}{\text{ -  18x  -  12 }}$

${\text{ =  6}}\left( {{{\text{x}}^{\text{2}}}{\text{ +  3x  +  2}}} \right) $

${\text{ =   -  6(x  +  2)(x  +  1)}} $

$\forall {\text{ f '(x)  =  0}} $

${\text{ -  6(x  +  2)(x  +  1)  =  0}} $ 

$x =  - 2, - 1$ वास्तविक रेखा के तीन अंतरालों $\left( { - \infty , - 2} \right),\left( { - 2, - 1} \right)$ और $\left( { - 1,\infty } \right)$ में विबक्त करता है 

इसलिए फलन ${\text{f}}$ अंतरालों $\left( { - \infty , - 2} \right)$ और $\left( { - 1,\infty } \right)$ पर निरंतर वर्धमान है

इसलिए फलन ${\text{f}}$ अंतरालों $\left( { - 2, - 1} \right)$ पर निरंतर हसमान है

(d) ${\text{f (x)  =  6  -  9x  -  }}{{\text{x}}^{\text{2}}}$

उत्तर: ${\text{f '(x)  =   -  9  -  2x}}$

$\forall {\text{ f '(x)  =  0}} $

${\text{ -  9  -  2x  =  0}} $

${\text{x  =  }}\dfrac{{{\text{ - 9}}}}{{\text{2}}} $ 

${\text{f '(x)  =    -  9  -  2x  >  0, x}} \in \left( {{\text{ - }}\infty {\text{,}}\dfrac{{{\text{ - 9}}}}{{\text{2}}}} \right)$ में निरंतर हसमान है 

${\text{f '(x)  =    -  9  -  2x  >  0, x}} \in \left( {\dfrac{{{\text{ - 9}}}}{{\text{2}}},{\text{ - }}\infty } \right)$ में निरंतर वर्धमान है 

(e) ${\text{f (x)  =  (x  +  1}}{{\text{)}}^{\text{3}}}{{\text{(x  -  3)}}^{\text{3}}}$

उत्तर: ${\text{f '(x)  =  3(x  +  1}}{{\text{)}}^{\text{2}}}{{\text{(x  -  3)}}^{\text{3}}}{\text{  +  (x  +  1}}{{\text{)}}^{\text{3}}}\left( {{\text{3(x  -  3}}{{\text{)}}^{\text{2}}}} \right)$

${\text{ =  6(x  +  1}}{{\text{)}}^{\text{2}}}{{\text{(x  -  3)}}^{\text{2}}}{\text{(x  -  1)}} $

${\text{f '(x)  =  6(x  +  1}}{{\text{)}}^{\text{2}}}{{\text{(x  -  3)}}^{\text{2}}}{\text{(x  -  1)}} $

$\forall {\text{ f '(x)  =  0}} $

${\text{6(x  +  1}}{{\text{)}}^{\text{2}}}{{\text{(x  -  3)}}^{\text{2}}}{\text{(x  -  1)  =  0}} $

${\text{x  =   -  1, 1, 3}} $ 

${\text{x  =   -  1,x  =  1, x  =  3}}$ वास्तविक रेखा के अंतरालों ${\text{( - }}\infty {\text{, - 1), ( - 1,1), (1,3)}}$ और ${\text{(3,}}\infty {\text{)}}$ में विभक्त करता है 

इसलिए फलन ${\text{f}}$ अंतरालों ${\text{( - }}\infty {\text{, - 1)}}$ पर निरंतर हसमान है .

7. सिद्ध कीजिए कि ${\text{y  =  log(1  +  x)  -  }}\dfrac{{{\text{2x}}}}{{{\text{2  +  x'}}}}{\text{ x  >   -  1,}}$अपने संपूर्ण प्रांत में एक वर्धमान फलन है।

उत्तर: ${\text{y  =  log(1  +  x)  -  }}\dfrac{{{\text{2x}}}}{{{\text{2  +  x'}}}}$

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{1  +  x}}}}{\text{  -  }}\dfrac{{{\text{(2  +  x)(2  -  2x)}}}}{{{{{\text{(2  +  x)}}}^{\text{2}}}}}{\text{ }} $

${\text{ =  }}\dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{(1  +  x)(2  +  x}}{{\text{)}}^{\text{2}}}}} $

${{\text{x}}^{\text{2}}}{\text{,(1  +  x), (2  +  x}}{{\text{)}}^{\text{2}}}{\text{  >  0}}$

अतः फलन सम्पूर्ण प्रांत में वर्धमान है 

8. ${\text{x}}$ के उन मानों को ज्ञात कीजिए जिनके लिए ${\text{y  =  [x ( x  -  2)}}{{\text{]}}^{\text{2}}}$एक वर्धमान फलन है।

उत्तर: ${\text{y  =  [x ( x  -  2)}}{{\text{]}}^{\text{2}}}$

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2[x(x  -  2)]}}\dfrac{{\text{d}}}{{{\text{dx}}}}{\text{[x(x  -  2)]}} $

${\text{ =  4[x(x  -  2)(x  -  1)]}} $

${\text{f '(x)  =  0}} $

${\text{4[x(x  -  2)(x  -  1)]  =  0}}$

${\text{x  =  0, 1, 2}}$

${\text{x  =  0 , x  = 1 , x  =  2 }}$ वास्तविक रेखा के अंतरालों ${\text{( - }}\infty {\text{, 0), (0 ,1), (1,2)}}$ और $\left( {2,\infty } \right)$ में विभक्त करता है 

इसलिए फलन ${\text{y}}$ अंतरालों ${\text{(0,1)  }}$ और $\left( {2,\infty } \right)$ पर वर्धमान है

9. सिद्ध कीजिए कि $\left[ {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right]$ में ${\text{y  =  }}\dfrac{{{\text{4 sin θ }}}}{{{\text{(2  +  cos θ )}}}}{\text{  -  θ , θ }}$ का एक वर्धमान फलन है।

उत्तर: ${\text{y  =  }}\dfrac{{{\text{4 sin θ }}}}{{{\text{(2  +  cos θ )}}}}{\text{  -  θ }}$

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{(2  +  cos θ )(4cos θ )  -  4sin θ (0  -  sin θ )}}}}{{{{{\text{(2  +  cosθ )}}}^{\text{2}}}}}{\text{  -  1}} $

${\text{ =  }}\dfrac{{{\text{cos θ (4  -  cos θ )}}}}{{{{{\text{(2  +  cos θ )}}}^{\text{2}}}}} $

${{\text{(2  +  cos θ )}}^{\text{2}}}{\text{  >  0, cos θ   >  0, θ }} \in \left[ {{\text{0, }}\dfrac{{\text{π }}}{{\text{2}}}} \right]$

${\text{(4  -  cos θ )  >  0, θ }} \in \left[ {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right]$

अतः ${\text{θ }}$ का वर्धमान फलन है 

10. सिद्ध कीजिए कि लघुगणकीय फलन $(0,\infty )$में वर्धमान फलन है।

उत्तर: ${\text{f(x)  =  log x }}$

${\text{f '(x)  =  }}\dfrac{{\text{1}}}{{\text{x}}}{\text{  >  0}}$

${\text{x}} \in {\text{(0,}}\infty {\text{)}}$

अतः ${\text{(0,}}\infty {\text{)}}$ का वर्धमान फलन है 

11. सिद्ध कीजिए कि $( - 1,1)$ में ${\text{f (x)  =  }}{{\text{x}}^{\text{2}}}{\text{  -  x  +  1}}$से प्रदत्त फलन न तो वर्धमान है और न ही हासमान है।

उत्तर: ${\text{f (x)  =  }}{{\text{x}}^{\text{2}}}{\text{  -  x  +  1}}$

${\text{f '(x)  =  2x  -  1}}$

${\text{f '(x)  =  0}}$

${\text{2x  -  1  =  0}}$

${\text{x  =  }}\dfrac{{\text{1}}}{{\text{2}}}$

${\text{x  =  }}\dfrac{{\text{1}}}{{\text{2}}}$ अंतराल ${\text{(  -  1,1),}}\left( {{\text{ -  1, }}\dfrac{{\text{1}}}{{\text{2}}}} \right){\text{, }}\left( {\dfrac{{\text{1}}}{{\text{2}}}{\text{,1}}} \right)$ में विभक्ति है

अतः ${\text{(  -  1,1)}}$ में न तो  वर्धमान और न ही हसमान है 

12. निम्नलिखित में कौन से फलन $\left( {0,\dfrac{π }{2}} \right)$ में हासमन है

(A) ${\text{cos x}}$

(B) ${\text{cos 2x}}$

(C) ${\text{cos 3x}}$

(D) ${\text{tan x}}$

उत्तर: (A) ${\text{f (x)  =  cos x}}$

${\text{f '(x)  =   -  sin x  <  0}}$अतः निरंतर हासमान है।

(B) ${\text{f}}({\text{x}}) = \cos 2x$

${\text{f '(x)  =   -  2sin x  <  0}}$अतः निरंतर हासमान है।

(C) ${\text{f (x)  =  cos3x}}$

${\text{f '(x)  =   - 3sin x  <  0}}$अतः निरंतर हासमान है।

(D)${\text{f (x)  =  tan x}}$

${\text{f '(x)  =  se}}{{\text{c}}^{\text{2}}}{\text{x  >  0}}$ अतः निरंतर वर्धमान है। 

इसलिए विकल्प (A) और (B) सहीं है।

13. निम्नलिखित अंतरालों में से किस अंतराल में ${\text{f (x)  =  }}{{\text{x}}^{{\text{100}}}}{\text{  +  sin x  -  1}}$ द्वारा प्रदत्त फलन ${\text{f}}$ हासमान है

(A) $(0,1)$

(B) $\left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$

(C) $\left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right)$

(D) इनमें से कोई नहीं

उत्तर: (D) सही विकल्प है 

14. ${\text{a}}$ का वह न्यूनतम मान कीजिए जिसके लिए अंतराल $[1,2]$ में ${\text{f (x)  =  }}{{\text{x}}^{\text{2}}}{\text{  +  ax  +  1}}$से प्रदत्त फलन वर्धमान है।

उत्तर: ${\text{f (x)  =  }}{{\text{x}}^{\text{2}}}{\text{  +  ax  +  1}}$

${\text{f '(x)  =  2x  +  a}}$

पर ${\text{f (1,2)}}$ निरंतर वर्धमान है।

${\text{f '(x)  >  0}}$

${\text{2x  +  a  >  0}}$

${\text{x  >   -  }}\dfrac{{\text{a}}}{{\text{2}}}{\text{, x}} \in {\text{(1,2)}}$

अतः ${\text{(1,2)}}$ का फलन निरंतर वर्धमान है। 

$ - \dfrac{a}{2} = 1$

${\text{a  =   -  2}}$

15. मान लीजिए $[ - 1,1]$ से असंयुक्त एक अंतराल। हो तो सिद्ध कीजिए कि । में ${\text{f(x)  =  x  +  }}\dfrac{{\text{1}}}{{\text{x}}}$ से प्रदत्त फलन 

${\text{f}}$, वर्धमान है।

उत्तर: ${\text{f(x)  =  x  +  }}\dfrac{{\text{1}}}{{\text{x}}}$

${\text{f '(x)  =  }}\dfrac{{{\text{(x  -  1)(x  +  1)}}}}{{{{\text{x}}^{\text{2}}}}}$

$\forall {\text{ f '(x)  =  0}}$

${\text{(x  -  1)(x  +  1)  =  0}}$

${\text{x  =  1,  -  1}}$

${\text{x  =  1}}$ और ${\text{x  =   -  1}}$ वास्तविक रेखा को अंतरालों $( - \infty , - 1),( - 1,1)$और $(1,\infty )$  में विभक्त करता है। अत: 

$( - \infty , - 1)$ और $(1,\infty )$अंतराल को दर्शता है। फलन ${\text{f}}$ अंतरालों $( - \infty , - 1)\,$ और $(1,\infty )$ निरंतर वर्धमान है।

16. सिद्ध कीजिए कि फलन ${\text{f (x)  =  log sin x,  }}\left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right)$में वर्धमान और $\left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{,π }}} \right)$में हासमान है।

उत्तर: ${\text{f (x)  =  log sin x}}$

${\text{f '(x)  =  }}\dfrac{{{\text{cos x}}}}{{{\text{sin x}}}}{\text{  =  tan x}}$

${\text{f '(x)  =  tan x  >  0, x}} \in \left( {{\text{0, }}\dfrac{{\text{π }}}{{\text{2}}}} \right)$ इसलिए फलन वर्धमान है। 

${\text{f '(x)  =  tan x  <  0, x}} \in \left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{, π }}} \right)$ इसलिए फलन हासमान है।

17. सिद्ध कीजिए कि फलन ${\text{f (x)  =  log | cos x |  }}\left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right)$में वर्धमान और $\left( {\dfrac{{{\text{3π }}}}{{\text{2}}}{\text{,2π }}} \right)$ में हासमान है।

उत्तर: ${\text{f (x)  =  log | cos x |  }}$

${\text{f '(x)  =  }}\dfrac{{{\text{cos x}}}}{{{\text{sin x}}}}{\text{  =   -  cot x}}$

${\text{f '(x)  =   -  cotx  >  0, x}} \in \left( {{\text{0,}}\dfrac{{\text{π }}}{{\text{2}}}} \right)$इसलिए फलन हासामान है  

${\text{f '(x)  =   -  cot x  <  0, x}} \in \left( {\dfrac{{\text{π }}}{{\text{2}}}{\text{, π }}} \right)$ इसलिए फलन वर्धमान है।

18. सिद्ध कीजिए कि ${\text{R}}$ में दिया गया फलन ${\text{f (x)  =  }}{{\text{x}}^{\text{3}}}{\text{  -  3}}{{\text{x}}^{\text{2}}}{\text{  +  3x  -  100}}$वर्धमान है।

उत्तर: ${\text{f (x)  =  }}{{\text{x}}^{\text{3}}}{\text{  -  3}}{{\text{x}}^{\text{2}}}{\text{  +  3x  -  100}}$

${\text{f '(x)  =  3(x  -  1}}{{\text{)}}^{\text{2}}}$

${\text{3(x  -  1}}{{\text{)}}^{\text{2}}} \geqslant {\text{ 0}}$क्यूंकि ये पूर्ण वर्ग है। इसलिए ${\text{f (x)  =  }}{{\text{x}}^{\text{3}}}{\text{  -  3}}{{\text{x}}^{\text{2}}}{\text{  +  3x  -  100}}$ वर्धमान है।

19. निम्नलिखित में से किस अंतराल में ${\text{y  =  }}{{\text{x}}^{\text{2}}}{\text{  -  }}{{\text{e}}^{{\text{ -  x}}}}$वर्धमान है

(A) $( - \infty ,\infty )$

(B) $( - 2,0)$

(C) $(2,\infty )$

(D) $(0,2)$

उत्तर: ${\text{y  =  }}{{\text{x}}^{\text{2}}}{\text{  -  }}{{\text{e}}^{{\text{ -  x}}}}$

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2x}}{{\text{e}}^{{\text{ -  x}}}}{\text{ -  }}{{\text{x}}^{\text{2}}}{{\text{e}}^{{\text{ -  x}}}}{\text{  =  x}}{{\text{e}}^{{\text{ -  x}}}}{\text{(2  -  x)}}$

यदि ${\text{f '(x)  =  0}}$

${\text{x }}{{\text{e}}^{{\text{ -  x}}}}{\text{(2  -  x)  =  0}}$ 

${\text{x  =  0, 2}}$

${\text{x  =  0}}$ और ${\text{x  =  0}}$ वास्तविक रेखा को अंतरालों $( - \infty ,0),(0,2)$ और $(2,\infty )$ में विभक्त करता है। 

अतः$( - \infty , - 1)$ और $(1,\infty )$ अंतराल को दर्शता है। फलन ${\text{y}}$ अंतरालों $(0,2)$ निरंतर वर्धमान है। 

इसलिए (D) सही विकल्प है।

प्रश्नावली 6.3

1: वक्र ${\text{y  =  3}}{{\text{x}}^{\text{4}}}{\text{  -  4x,  x  =  4}}$ पर स्पर्श रेखा की प्रवणता ज्ञात कीजिये।

उत्तर: दिए वक्र की ${\text{x  =  4}}$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{x  =  4}}}}{\text{ =  12}}{{\text{x}}^{\text{3}}}{\text{  -  4}}} \right]_{{\text{x  =  4}}}}{\text{ =  12(4}}{{\text{)}}^{\text{3}}}{\text{  -  4  =  764}}$

2. वक्र ${\text{y  =  }}\dfrac{{{\text{x  -  1}}}}{{{\text{x  -  2'}}}}{\text{ , x}} \ne {\text{2 ,x  =  10}}$पर स्पर्श रेखा क प्रवणता ज्ञात कीजिये।

उत्तर: दिए वक्र की ${\text{x  =  10}}$पर स्पर्श रेखा की प्रवणता 

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{x  =  10}}}}{\text{ =  }}\dfrac{{{\text{ -  1}}}}{{{{{\text{(x  -  2)}}}^{\text{2}}}}}} \right]_{x = 10}}{\text{  =  }}\dfrac{{{\text{ -  1}}}}{{{\text{64}}}}$

3. वक्र ${\text{y  =  }}{{\text{x}}^{\text{3}}}{\text{  -  x  +  1}}$की स्पर्श रेखा की प्रवणता उस बिंदु पर ज्ञात कीजिये जिसका ${\text{x}}$ - निर्देशांक ${\mathbf{2}}$ हैं।

उत्तर: दिए वक्र की ${\text{x  =  2}}$ पर स्पर्श रेखा की प्रवणता 

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{x  =  2}}}}{\text{ =  3}}{{\text{x}}^{\text{2}}}{\text{  -  1}}} \right]_{{\text{x  =  2}}}}{\text{ =  11}}$ है।

4. वक्र ${\text{y}} = {{\text{x}}^3} - 3{\text{x}} + 2$की स्पर्श रेखा की प्रणवता उस बिंदु पर ज्ञात कीजिये जिसका ${\text{x}}$ निर्देशक ${\mathbf{3}}$ हैं।

उत्तर:  दिए वक्र की ${\text{x  =  3}}$पर स्पर्श रेखा की प्रवणता 

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{x  =  3}}}}{\text{ =  3}}{{\text{x}}^{\text{2}}}{\text{  -  3}}} \right]_{{\text{x  =  3}}}}{\text{ =  24}}$ है 

5. वक्र ${\text{x}} = {\text{aco}}{{\text{s}}^3}θ ,{\text{y}} = {\operatorname{asin} ^3}θ $के ${\text{θ   =  }}\dfrac{{\text{π }}}{{\text{4}}}$पर अभिलंभ की प्रवणता ज्ञात कीजिये।

उत्तर: ${\text{x}} = {\text{aco}}{{\text{s}}^3}θ $

$\dfrac{{{\text{dx}}}}{{{\text{dθ }}}}{\text{  =   -  3a co}}{{\text{s}}^{\text{2}}}{\text{θ  sin θ }}$ 

${\text{y  =  a si}}{{\text{n}}^{\text{3}}}{\text{θ }}$

$\dfrac{{{\text{dy}}}}{{{\text{dθ }}}}{\text{  =  3a si}}{{\text{n}}^{\text{2}}}{\text{θ  cos θ }}$

दिए वक्र की ${\text{θ   =  }}\dfrac{{\text{π }}}{{\text{4}}}$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{θ   =  }}\dfrac{{\text{π }}}{{\text{4}}}}}{\text{ =   -  tan θ }}} \right]_{{\text{θ   =  }}\dfrac{{\text{π }}}{{\text{4}}}}}{\text{  =   -  1}}$ है 

इसलिए इसके अभिलंब की प्रवणता ${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  1}}$ है

6. वक्र ${\text{x  =  1  -  a sin θ , y  =  b co}}{{\text{s}}^{\text{2}}}{\text{θ }}$ के ${\text{θ   =  }}\dfrac{{\text{π }}}{{\text{2}}}$पर अभिलंभ की प्रवणता ज्ञात कीजिये।

उत्तर: ${\text{x  =  1  -  a sin θ }}$

$\dfrac{{{\text{dx}}}}{{{\text{dθ }}}}{\text{  =   -  a cos θ }}$ 

${\text{y  =  b co}}{{\text{s}}^{\text{2}}}{\text{θ }}$

$\dfrac{{{\text{dy}}}}{{{\text{dθ }}}}{\text{  =   -  2b cos θ  sin θ }}$

दिए वक्र की ${\text{θ   =  }}\dfrac{{\text{π }}}{{\text{2}}}$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{θ  = }}\dfrac{{\text{π }}}{{\text{2}}}}}{\text{ =  }}\dfrac{{{\text{2b}}}}{{\text{a}}}{\text{sin θ }}} \right]_{{\text{θ   =  }}\dfrac{{\text{π }}}{{\text{2}}}}}{\text{ =  }}\dfrac{{{\text{2b}}}}{{\text{a}}}$

इसलिए इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  }}\dfrac{{{\text{ -  a}}}}{{{\text{2b}}}}$

7. वक्र ${\text{y}} = {{\text{x}}^3} - 3{{\text{x}}^2} - 9{\text{x}} + 7$पर उन बिंदुओं को ज्ञात कीजिये जिन पर स्पर्श रेखाएँ ${\mathbf{x}}{\text{ }} - $अक्ष के समांतर हैं।

उत्तर: $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  3}}{{\text{x}}^{\text{2}}}{\text{  -  6x  -  9}}$

अब, स्पर्श रेखा ${\text{x  - }}$अक्ष के समांतर है यदि उसकी प्रवणता शुन्य है, जिससे $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$

${\text{3}}{{\text{x}}^{\text{2}}}{\text{  -  6x  -  9  =  0}}$

${{\text{x}}^{\text{2}}}{\text{  -  2x  -  3  =  0}}$ 

${\text{x  =  3 ;  x  =   -  1}}$

जब ${\text{x  =  3}}$

तब ${\text{y  =  }}{{\text{3}}^{\text{3}}}{\text{  -  3}}\left( {{{\text{3}}^{\text{2}}}} \right){\text{  -  9(3)  +  7  =   -  20}}$

जब ${\text{x  =   -  1}}$

तब ${\text{y}} = {( - 1)^3} - 3{( - 1)^2} - 9( - 1) + 7 = 12$

बिंदुओं $(3, - 20)$ और $( - 1,12)$ पर स्पर्श रेखा ${\text{x  - }}$ अक्ष के समांतर हैं।

8. वक्र ${\text{y}} = {({\text{x}} - 2)^2}$पर एक बिंदु ज्ञात कीजिये जिस पर स्पर्श रेखा, बिंदुओं $(2,0)$और $(4,4)$को मिलने वाली रेखा के समांतर हैं।

उत्तर: $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\left( {{\text{x  -  2}}} \right){\text{  =  2x  -  4}}$

अब, स्पर्श रेखा बिंदुओं $(2,0)$और $(4,4)$ को मिलने वाली रेखा के समांतर हैं।

इसलिए $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{4  -  0}}}}{{{\text{4  -  2}}}}{\text{  =  2}}$

${\text{2x  -  4  =  2}}$

${\text{x  =  3}}$

जब ${\text{x  =  3}}$

तब ${\text{y  =  (3  -  2}}{{\text{)}}^{\text{2}}}{\text{  =  1}}$

बिंदुओं $(3,1)$ निम्लिखित शर्तो पर परिमाणित है

9. वक्र ${\text{y}} = {{\text{x}}^3} - 11{\text{x}} + 5$पर उस बिंदु को ज्ञात कीजिये जिस पर स्पर्श रेखा ${\text{y  =  x  -  11}}$ हैं।

उत्तर: $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  3}}{{\text{x}}^{\text{2}}}{\text{  -  11}}$

अब, स्पर्श रेखा ${\text{y  =  x  -  11}}$ हैं। 

इसलिए

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  1}}$

${\text{3}}{{\text{x}}^{\text{2}}}{\text{  -  11  =  1}}$

${{\text{x}}^{\text{2}}}{\text{  =  4}}$ 

${\text{x  =  2,  -  2}}$

जब ${\text{x  =  2}}$

तब ${\text{y  =  }}{{\text{2}}^{\text{3}}}{\text{  -  11(2)  +  5  =   -  9}}$

जब ${\text{x  =   -  2}}$

तब ${\text{y  =  (  -  2}}{{\text{)}}^{\text{3}}}{\text{  -  11(  -  2)  +  5  =  19}}$

बिंदुओं ${\text{(2,  -  9)}}$ और  ${\text{( -  2, 19)}}$निम्लिखित शर्तो पर परिमाणित है,

10. प्रवणता $ - 1$ वाली सभी रेखाओं का समीकरण ज्ञात कीजिये जो वक्र ${\text{y  =  }}\dfrac{{\text{1}}}{{{\text{x  -  1'}}}}{\text{, x}} \ne  - 1$को स्पर्श करती हैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$पर स्पर्श रेखा की प्रवणता $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{ -  1}}}}{{{{{\text{(x  -  1)}}}^{\text{2}}}}}$है क्योंकि प्रवणता ${\text{ -  1}}$ दिया गया है इसलिए,

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   -  1}}$ 

$\dfrac{{{\text{ -  1}}}}{{{{{\text{(x  -  1)}}}^{\text{2}}}}}{\text{  =   -  1}}$

${\text{1  =  (x  -  1}}{{\text{)}}^{\text{2}}}$

${{\text{x}}^{\text{2}}}{\text{  -  2x  =  0}}$

${\text{x (x  -  2)  =  0}}$ 

${\text{x  =  0, x  =  2}}$

जब ${\text{x  =  0}}$

तब ${\text{y  =  }}\dfrac{{\text{1}}}{{{\text{0  -  1}}}}{\text{  =   -  1}}$

जब $x = 2$

तब ${\text{y  =  }}\dfrac{{\text{1}}}{{{\text{2  -  1}}}}{\text{  =  1}}$

बिंदु $(0, - 1)$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  +  1  =   -  1(x)}}$ 

${\text{y  +  x  +  1  =  0}}$

बिंदु $(2,1)$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  1  =   -  1(x  -  2)}}$ 

${\text{y  +  x  -  3  =  0}}$

11. प्रवणता ${\mathbf{2}}$ वाली सभी रेखाओं का समीकरण ज्ञात कीजिये जो वक्र ${\text{y}} = \dfrac{1}{{{\text{x}} - {3^\prime }}}{\text{x}} \ne 3$ को स्पर्श करतीहैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x,y)}}$पर स्पर्श रेखा की प्रवणता $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{ -  1}}}}{{{{{\text{(x  -  3)}}}^{\text{2}}}}}$है क्योंकि प्रवणता $2$ दिया गया है इसलिए,

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2}}$

$\dfrac{{{\text{ -  1}}}}{{{{{\text{(x  -  3)}}}^{\text{2}}}}}{\text{  =  2}}$ 

${\text{ -  1  =  2(x  -  3}}{{\text{)}}^{\text{2}}}$

${\text{2}}{{\text{x}}^{\text{2}}}{\text{  -  12x  +  19  =  0}}$

${\text{D  =  }}{{\text{b}}^{\text{2}}}{\text{  -  4ac  =  144  -  152  =   -  8}}$

इसलिए इस समीकरण का कोई भी असली हल नहीं हैं

इसलिए इस वक्र को ${\text{2}}$ प्रवणता वाली कोई भी रेखा स्पर्श नहीं करती

12. प्रवणता ${\text{0}}$ वाली सभी रेखाओं का समीकरण ज्ञात कीजिये जो वक्र ${\text{y  =  }}\dfrac{{\text{1}}}{{{{\text{x}}^{\text{2}}}{\text{  -  2x  +  3}}}}$ को स्पर्श करती हैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$पर स्पर्श रेखा की प्रवणता $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{ -  (2x  -  2)}}}}{{{{\left( {{{\text{x}}^{\text{2}}}{\text{  -  2x  +  3}}} \right)}^{\text{2}}}}}$ है वयोंकि प्रवणता $0$ दिया गया है

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$ 

$\dfrac{{{\text{ -  (2x  -  2)}}}}{{{{\left( {{{\text{x}}^{\text{2}}}{\text{  -  2x  +  3}}} \right)}^{\text{2}}}}}{\text{  =  0}}$ 

${\text{2x  -  2  =  0}}$ 

${\text{x  =  1}}$

जब ${\text{x  =  1}}$

तब ${\text{y}} = \dfrac{1}{{{1^2} - 2(1) + 3}} = \dfrac{1}{2}$

बिंदु $\left( {{\text{1,}}\dfrac{{\text{1}}}{{\text{2}}}} \right)$ से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{  =  0 (x  -  1)}}$ 

${\text{y  -  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{  =  0}}$

13. वक्र $\dfrac{{{{\text{x}}^{\text{2}}}}}{{\text{9}}}{\text{  +  }}\dfrac{{{{\text{y}}^{\text{2}}}}}{{{\text{16}}}}{\text{  =  1}}$ पर उन बिन्दुओं को ज्ञात कीजिये जिन पर स्पर्श रेखाएँ

I) ${\text{x  - }}$अक्ष के समांतर हैं

उत्तर: $\dfrac{{{{\text{x}}^{\text{2}}}}}{{\text{9}}}{\text{  +  }}\dfrac{{{{\text{y}}^{\text{2}}}}}{{{\text{16}}}}{\text{  =  1}}$ का ${\text{x}}$ के सापेक्ष अवकलन करने पर हम प्राप्त करते हैं :

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{ -  16x}}}}{{{\text{9y}}}}$

अब, स्पर्श रेखा ${\text{x   - }}$अक्ष के समांतर है यदि उसकी प्रवणता शुन्य है, जिससे $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$

$\dfrac{{{\text{ -  16x}}}}{{{\text{9y}}}}{\text{  =  0}}$

${\text{x  =  0}}$

जब ${\text{x  =  0}}$

तब ${\text{y  =  }}\sqrt {{\text{16}}} { =   \pm 4}$

बिंदुओं $(0,4)$और $(0, - 4)$पर स्पर्श रेखाएँ ${\text{x   - }}$अक्ष के समांतर हैं।

ii) ${\text{y  - }}$ अक्ष के समांतर हैं

उत्तर: $\dfrac{{{{\text{x}}^{\text{2}}}}}{{\text{9}}}{\text{  +  }}\dfrac{{{{\text{y}}^{\text{2}}}}}{{{\text{16}}}}{\text{  =  1}}$का ${\text{x}}$के सापेक्ष अवकलन करने पर हम प्राप्त करते हैं :

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{ -  16x}}}}{{{\text{9y}}}}$

अब, स्पर्श रेखा ${\text{y  - }}$अक्ष के समांतर है यदि इसके अभिलंभ की प्रवणता शुन्य है

जिससे $\dfrac{{{\text{9y}}}}{{{\text{16x}}}}{\text{  =  0}}$

$\dfrac{{{\text{9y}}}}{{{\text{16x}}}}{\text{  =  0}}$ 

${\text{y  =  0}}$

जब ${\text{y  =  0}}$

तब ${\text{x  =  }}\sqrt {\text{9}} { = \pm  3}$

बिंदुओं $(3,0)$और $( - 3,0)$ पर स्पर्श रेखाएँ ${\text{y  - }}$ अक्ष के समांतर हैं।

14: दिए वक्रों पर निर्दिष्ट बिंदुओं पर स्पर्श रेखा और अभिलंभ के समीकरण ज्ञात कीजिए

i) ${\text{y  =  }}{{\text{x}}^{\text{4}}}{\text{  -  6}}{{\text{x}}^{\text{3}}}{\text{  +  13}}{{\text{x}}^{\text{2}}}{\text{  -  10x  +  5,}}$ के ${\text{(0,5)}}$पर

उत्तर: दिए वक्र कि ${\text{(0,5)}}$पर स्पर्श रेखा कि प्रवणता 

${\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]_{\left( {{\text{0,5}}} \right)}}{\text{  =  4}}{{\text{x}}^{\text{3}}}{\text{  -  18}}{{\text{x}}^{\text{2}}}{\text{  +  26x  - }}{\left. {{\text{ 10}}} \right]_{\left( {{\text{0,5}}} \right)}}{\text{  =   -  10}}$

बिन्दु $\left( {0,5} \right)$से जाने वाली स्पर्श रेखा का समीकरण 

${\text{y  -  5  =   -  10}}\left( {{\text{x  -  0}}} \right)$

${\text{y  +  10x  =  5}}$

इसलिए इसके अभिलंब की प्रवणता 

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{10}}}}$

बिंदु $(0,5)$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  5  =  }}\dfrac{{\text{1}}}{{{\text{10}}}}{\text{(x  -  0)}}$ 

${\text{10y  -  x  =  5}}$

ii) ${\text{y  =  }}{{\text{x}}^{\text{4}}}{\text{  -  6}}{{\text{x}}^{\text{3}}}{\text{  +  13}}{{\text{x}}^{\text{2}}}{\text{  -  10x  +  5}}$ के $(1,3)$पर

उत्तर: दिए वक्र कि $(1,3)$ पर स्पर्श रेखा कि प्रवणता 

${\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]_{(1,3)}}{\text{  =  4}}{{\text{x}}^{\text{3}}}{\text{  -  18}}{{\text{x}}^{\text{2}}}{\text{  +  26x  - }}{\left. {{\text{ 10}}} \right]_{(1,3)}}{\text{  =   -  10}}$

बिन्दु $(1,3)$ से जाने वाली स्पर्श रेखा का समीकरण 

${\text{y  -  3  =  2}}\left( {{\text{x  -  1}}} \right)$

${\text{y  -  2x  =  1 }}$

इसलिए इसके अभिलंब की प्रवणता 

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =   -  }}\dfrac{{\text{1}}}{{\text{2}}}$

बिंदु $(1,3)$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  3  =   -  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{(x  -  1)}}$ 

${\text{2y  +  x  =  7}}$

iii) ${\text{y  =  }}{{\text{x}}^{\text{3}}}$ के ${\text{(1,1)}}$पर

उत्तर: दिए वक्र की $(1,1)$पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{(1,1)}}}}{\text{ =  3}}{{\text{x}}^{\text{2}}}} \right]_{{\text{(1,1)}}}}{\text{  =  3 }}$

बिंदु $(1,1)$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  1  =  3(x  -  1)}}$ 

${\text{y  -  3x  +  2  =  0}}$

इसलिए इसके अभिलंब की प्रवणता 

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =   -  }}\dfrac{{\text{1}}}{3}$

बिंदु $(1,1)$ से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  1  =   -  }}\dfrac{{\text{1}}}{{\text{3}}}{\text{(x  -  1)}}$ 

${\text{3y  +  x  =  4}}$

iv) ${\text{y  =  }}{{\text{x}}^{\text{2}}}$ के ${\text{(0,0)}}$पर

उत्तर: दिए वक्र की ${\text{(0,0)}}$पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{(0,0)}}}}{\text{ =  2x}}} \right]_{{\text{(0,0)}}}}{\text{ =  0}}$

बिंदु ${\text{(0,0)}}$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  0  =  0(x  -  0)}}$ 

${\text{y  =  0}}$

इसलिए इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  0}}$

बिंदु ${\text{(0,0)}}$ से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  0  =  0(x  -  0)}}$ 

${\text{x  =  0}}$

v) ${\text{x  =  cos }}{{\text{t}}_{\text{,}}}{\text{ y  =  sin t}}$के ${\text{t  =  }}\dfrac{{\text{π }}}{{\text{4}}}$ पर

उत्तर: ${\text{x  =  cos t}}$

$\dfrac{{{\text{dx}}}}{{{\text{dθ }}}}{\text{  =   -  sin t}}$ 

${\text{y  =  sin t}}$

$\dfrac{{{\text{dy}}}}{{{\text{dθ }}}}{\text{  =  cos t}}$

दिए वक्र की ${\text{t  =  }}\dfrac{{\text{π }}}{{\text{4}}}$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{t  =  }}\dfrac{{\text{π }}}{{\text{4}}}}}{\text{  =   -  cot t}}} \right]_{{\text{t  =  }}\dfrac{{\text{π }}}{{\text{4}}}}}{\text{ =   -  1}}$

बिंदु $\left( {\dfrac{1}{{\sqrt 2 }},\dfrac{1}{{\sqrt 2 }}} \right)$ से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  }}\dfrac{{\text{1}}}{{\sqrt {\text{2}} }}{\text{  =  3}}\left({{\text{x -  }}\dfrac{{\text{1}}}{{\sqrt {\text{2}} }}} \right)$ 

${\text{y  +  x  =  }}\sqrt {\text{2}}$

इसलिए इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  1}}$

बिंदु $\left( {\dfrac{1}{{\sqrt 2 }},\dfrac{1}{{\sqrt 2 }}} \right)$ से जाने वाली स्पर्श रेखा का समीकरण

$y-\dfrac{1}{2}= x - \dfrac{1}{2}$

${\text{y  =  x}}$

15: वक्र ${\text{y  =  }}{{\text{x}}^{\text{2}}}{\text{  -  2x  +  7}}$की स्पर्श रेखा का समीकरण ज्ञात कीजिये जो

A) रेखा ${\text{2x  -  y  +  9  =  0}}$के समांतर हैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$ पर स्पर्श रेखा की प्रवणता $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2x  -  2}}$

अब, स्पर्श रेखा ${\text{2x  -  y  +  9  =  0}}$के समांतर हैं।

${\text{y  =  2x  +  9}}$

इसलिए $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2}}$

${\text{2x  -  2  =  2}}$ 

${\text{x  =  2}}$

जब ${\text{x  =  2}}$

तब ${\text{y  =  13}}$

बिंदु $(2,13)$से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  13  =  2(x  -  2)}}$ 

${\text{y  -  2x  =  3}}$

B) रेखा ${\text{5y  -  15x  =  13}}$ पर लंब हैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$ पर स्पर्श रेखा की प्रवणता $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2x  -  2}}$

इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  }}\dfrac{{{\text{ -  1}}}}{{{\text{2x  -  2}}}}$

अब, स्पर्श रेखा ${\text{5y  -  15x  =  13}}$पर लंब है। 

${\text{y  =  3x  +  13 / 5}}$

इसलिए $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  3}}$

$\dfrac{{{\text{ -  1}}}}{{{\text{2x  -  2}}}}{\text{  =  3}}$

${\text{x  =  }}\dfrac{{\text{5}}}{{\text{6}}}$

जब ${\text{x  =  }}\dfrac{{\text{5}}}{{\text{6}}}$

तब ${\text{y  =  }}\dfrac{{{\text{51}}}}{{{\text{10}}}}$

बिंदु $\left( {\dfrac{5}{6},\dfrac{{51}}{{10}}} \right)$ से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  }}\dfrac{{{\text{51}}}}{{{\text{10}}}}{\text{  =  2}}\left( {{\text{x  -  }}\dfrac{{\text{5}}}{{\text{6}}}} \right)$ 

${\text{36y  +  12x  =  227}}$

16: सिद्ध कीजिये की वक्र के${\text{y  =  7}}{{\text{x}}^{\text{3}}}{\text{  +  11}}$ उन बिंदुओं पर स्पर्श रेखाएँ समांतर हैं जहाँ ${\text{x  =  2}}$तथा ${\text{x  =   - 2}}$ हैं।

उत्तर: दिए वक्र की ${\text{x  =  2}}$पर स्पर्श रेखा की प्रवणता 

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{x  =  2}}}}{\text{ =  21}}{{\text{x}}^{\text{2}}}} \right]_{{\text{x  =  2}}}}{\text{  =  84}}$

दिए वक्र की ${\text{x}} =  - 2$पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{{\text{x  =   -  2}}}}{\text{ =  21}}{{\text{x}}^{\text{2}}}} \right]_{{\text{x  =   -  2}}}}{\text{ =  84}}$

इसलिए दिए गए वक्र के उन बिंदुओं पर स्पर्श रेखाएँ समांतर हैं जहाँ ${\text{x  =  2}}$तथा ${\text{x  =   -  2}}$

17: वक्र ${\text{y  =  }}{{\text{x}}^{\text{3}}}$पर उन बिंदुओं को ज्ञात कीजिये जिन पर स्पर्श रेखा को प्रवणता बिंदु के ${\text{y - }}$ निर्देशांक के बराबर हैं

उत्तर: दिए वक्र के बिंदु ${\text{(x,y)}}$पर स्पर्श रेखा की प्रवणता 

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  3}}{{\text{x}}^{\text{2}}}$

अब , स्पर्श रेखा प्रवणता बिंदु के ${\text{y  - }}$निर्देशांक के बराबर हैं

इसलिए ${\text{3}}{{\text{x}}^{\text{2}}}{\text{  =  y}}$

और ${\text{y  =  }}{{\text{x}}^{\text{3}}}$

इसलिए ${\text{3}}{{\text{x}}^{\text{2}}}{\text{  =  }}{{\text{x}}^{\text{3}}}$

${{\text{x}}^{\text{2}}}{\text{(3  -  x)  =  0}}$

${\text{x  =  0, x  =  3}}$

जब ${\text{x  =  0}}$

तब ${\text{y  =  0}}$

जब ${\text{x  =  3}}$

तब ${\text{y  =  }}{{\text{3}}^{\text{3}}}{\text{  =  27}}$

बिंदुओं $(0,0)$और ${\text{(3,27)}}$पर स्पर्श रेखा प्रवणता बिंदु के ${\text{y}}$ निर्देशांक के बराबर हैं

18. वक्र ${\text{y  =  4}}{{\text{x}}^{\text{3}}}{\text{  -  2}}{{\text{x}}^{\text{5}}}$पर उन बिंदुओं को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ मूल बिंदु से होकर जाती हैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$पर स्पर्श रेखा की प्रवणता 

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  12}}{{\text{x}}^{\text{2}}}{\text{  -  10}}{{\text{x}}^{\text{4}}}$

यह स्पर्श रेखा $(0,0)$ से गुज़रती है इसलिए इस स्पर्श रेखा का समीकरण होगा

${\text{(y  -  0)  =  12}}{{\text{x}}^{\text{2}}}{\text{  -  10}}{{\text{x}}^{\text{4}}}{\text{(x  -  0)}}$ 

${\text{y  =  12}}{{\text{x}}^{\text{3}}}{\text{  -  10}}{{\text{x}}^{\text{5}}}$

और ${\text{y  =  4}}{{\text{x}}^{\text{3}}}{\text{  -  2}}{{\text{x}}^{\text{5}}}$

इसलिए ${\text{4}}{{\text{x}}^{\text{3}}}{\text{  -  2}}{{\text{x}}^{\text{5}}}{\text{  =  12}}{{\text{x}}^{\text{3}}}{\text{  -  10}}{{\text{x}}^{\text{5}}}$

${\text{8}}{{\text{x}}^{\text{3}}}\left( {{\text{1  -  }}{{\text{x}}^{\text{2}}}} \right){\text{  =  0}}$ 

${\text{x  =  0, x  =  1, x  =   -  1}}$

जब ${\text{x  =  0}}$

तब ${\text{y  =  0}}$

जब ${\text{x  = 1 }}$

तब ${\text{y  =  4  -  2  =  2}}$

जब ${\text{x   =   -  1 }}$

तब ${\text{y  =   -  4  +  2  =   -  2}}$

बिंदुओं $(0,0),(1,2)$ और $( - 1, - 2)$

पर स्पर्श रेखाएँ मूल बिंदु से होकर जाती हैं।

19: वक्र ${{\text{x}}^{\text{2}}}{\text{  +  }}{{\text{y}}^{\text{2}}}{\text{  -  2x  -  3}}$ के उन बिंदुओं पर स्पर्श रेखाओं के समीकरण ज्ञात कीजिये जहाँ पर वे ${\text{x  -  }}$ अक्ष के समांतर हैं।

उत्तर: ${{\text{x}}^{\text{2}}}{\text{  +  }}{{\text{y}}^{\text{2}}}{\text{  -  2x  -  3  =  0}}$

का ${\text{x}}$ के सापेक्ष अवकलन करने पर हम प्राप्त करते हैं

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1  -  x}}}}{{\text{y}}}$

अब, स्पर्श रेखा ${\text{x  - }}$अक्ष के समांतर है यदि उसकी प्रवणता शुन्य है,

जिससे $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$

$\dfrac{{{\text{1  -  x}}}}{{\text{y}}}{\text{  =  0}}$

जब ${\text{x  =  1}}$

तब ${y  =  \pm  2}$

बिंदुओं $(1,2)$ और  ${\text{(1,  -  2)}}$पर स्पर्श रेखाएँ ${\text{x  - }}$ अक्ष के समांतर हैं।

20. वक्र ${\text{a}}{{\text{y}}^{\text{2}}}{\text{  =  }}{{\text{x}}^{\text{3}}}$ के बिंदु $\left( {{\text{a}}{{\text{m}}^{\text{2}}}{\text{,a}}{{\text{m}}^{\text{3}}}} \right)$ पर अभिलंब का समीकरण ज्ञात कीजिये।

उत्तर: दिए वक्र की $\left( {{\text{a}}{{\text{m}}^{\text{2}}}{\text{,a}}{{\text{m}}^{\text{3}}}} \right)$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{\left( {{\text{a}}{{\text{m}}^{\text{2}}}{\text{, a}}{{\text{m}}^{\text{3}}}} \right)}}{\text{ =  }}\dfrac{{{\text{3}}{{\text{x}}^{\text{2}}}}}{{{\text{2ay}}}}} \right]_{\left( {{\text{a}}{{\text{m}}^{\text{2}}}{\text{, a}}{{\text{m}}^{\text{3}}}} \right)}}{\text{ =  }}\dfrac{{{\text{3m}}}}{{\text{2}}}$

इसलिए इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  }}\dfrac{{{\text{ -  2}}}}{{{\text{3m}}}}$

बिंदु $\left( {{\text{a}}{{\text{m}}^{\text{2}}}{\text{, a}}{{\text{m}}^{\text{3}}}} \right)$से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  a}}{{\text{m}}^{\text{3}}}{\text{  =  }}\dfrac{{{\text{ -  2}}}}{{{\text{3m}}}}\left( {{\text{x  -  a}}{{\text{m}}^{\text{2}}}} \right)$

${\text{3my  +  2x  =  a}}{{\text{m}}^{\text{2}}}\left( {{\text{2  +  3}}{{\text{m}}^{\text{2}}}} \right)$

21. वक्र ${\text{y}} = {{\text{x}}^3} + 2{\text{x}} + 6$के उन अभिलम्बो के समीकरण ज्ञात कीजिये जो रेखा ${\text{x  +  14y  +  4  =  0}}$ के समांतर हैं

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$पर स्पर्श रेखा की प्रवणता 

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  3}}{{\text{x}}^{\text{2}}}{\text{  +  2}}$

इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{\text{ -  1}}}}{{{\text{dx}}}}$

अब, स्पर्श रेखा ${\text{x  +  14y  +  4  =  0}}$ के समांतर हैं। 

${\text{y  =   -  }}\dfrac{{\text{x}}}{{{\text{14}}}}{\text{  -  }}\dfrac{{\text{1}}}{{\text{6}}}$

 इसलिए $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   -  }}\dfrac{{\text{1}}}{{{\text{14}}}}$

$\dfrac{{{\text{ -  1}}}}{{{\text{3}}{{\text{x}}^{\text{2}}}{\text{  +  2}}}}{\text{  =   -  }}\dfrac{{\text{1}}}{{{\text{14}}}}$ 

${\text{14  =  3}}{{\text{x}}^{\text{2}}}{\text{  +  2}}$ 

${\text{x  =  }} \pm {\text{2}}$

जब ${\text{x  =   2}}$

तब ${\text{y  =  18}}$

बिंदु ${\text{(2, 18)}}$से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  8  =  }}\dfrac{{{\text{ -  1}}}}{{{\text{14}}}}{\text{(x  -  2)}}$ ${\text{14y  +  x  =  254}}$

जब ${\text{x  =   -  2}}$

तब ${\text{y  =   -  6 }}$

बिंदु $( - 2, - 6)$से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  +  6  =  }}\dfrac{{{\text{ -  1}}}}{{{\text{14}}}}{\text{(x  +  2)}}$

${\text{14y  +  x  =   -  86}}$

22. परवलय ${{\text{y}}^{\text{2}}}{\text{  =  4ax}}$के बिंदु $\left( {{\text{a}}{{\text{t}}^{\text{2}}}{\text{,2at}}} \right)$पर स्पर्श रेखा और अभिलंब के समीकरण ज्ञात कीजिये।

उत्तर: दिए वक्र के बिंदु $\left( {{\text{a}}{{\text{t}}^{\text{2}}}{\text{,2at}}} \right)$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{\left( {{\text{a}}{{\text{t}}^{\text{2}}}{\text{, 2at}}} \right)}}{\text{ =  }}\dfrac{{{\text{2a}}}}{{\text{y}}}} \right]_{\left( {{\text{a}}{{\text{t}}^{\text{2}}}{\text{, 2at}}} \right)}}{\text{ =  }}\dfrac{{\text{1}}}{{\text{t}}}$

बिंदु ${\text{(a}}{{\text{t}}^2}{\text{, 2at)}}$से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  2at  =  }}\dfrac{{\text{1}}}{{\text{t}}}\left( {{\text{x  -  a}}{{\text{t}}^{\text{2}}}} \right)$ 

${\text{ty  =  x  +  a}}{{\text{t}}^{\text{2}}}$

इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =   -  t}}$

बिंदु $\left( {{\text{a}}{{\text{t}}^{\text{2}}}{\text{, 2at}}} \right)$से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  2at  =   -  t}}\left( {{\text{x  -  a}}{{\text{t}}^{\text{2}}}} \right)$

${\text{y  +  tx  =  a}}{{\text{t}}^{\text{2}}}{\text{+ 2at}}$

23. सिद्ध कीजिये की वक्र ${\text{x  =  }}{{\text{y}}^{\text{2}}}$ और ${\text{xy  =  k}}$ एक दूसरे को समकोण पर काटती हैं, यदि ${\text{8}}{{\text{k}}^2}{\text{  =  1}}$ हैं।

उत्तर: ${\text{xy  =  k}}$

${{\text{x}}^{\text{2}}}{{\text{y}}^{\text{2}}}{\text{  =  }}{{\text{k}}^{\text{2}}}$ 

${{\text{y}}^{\text{2}}}{\text{  =  }}\dfrac{{{{\text{k}}^{\text{2}}}}}{{{{\text{x}}^{\text{2}}}}}$ 

${\text{x  =  }}{{\text{y}}^{\text{2}}}$

$\therefore {\text{x  =  }}\dfrac{{{{\text{k}}^{\text{2}}}}}{{{{\text{x}}^{\text{2}}}}}$ 

${\text{x  =  }}{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}$

${\text{y   =  k / x}}$ 

${\text{y  =  }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}$

${\text{x}} = {{\text{y}}^2}$और ${\text{xy}} = {\text{k}}$ एक दूसरे को बिंदु $\left( {{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)$ पर कटती है

दिए वक्र ${\text{x  =  }}{{\text{y}}^{\text{2}}}$ की $\left( {{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)$ पर स्पर्श रेखा की प्रवणता

${\left. {{{\left. {{{\text{m}}_{\text{1}}}{\text{  =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{\left( {{{\text{k}}^{\dfrac{2}{3}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{2y}}}}} \right]_{\left( {{{\text{k}}^{\dfrac{2}{3}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{2}}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}}}$

दिए वक्र ${\text{xy  =  k}}$ की $\left( {{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)$ पर स्पर्श रेखा की प्रवणता 

${\left. {{{\left. {{{\text{m}}_{\text{2}}}{\text{  =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{\left( {{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)}}{\text{ =  }}\dfrac{{{\text{ -  y}}}}{{\text{x}}}} \right]_{\left( {{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{, }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}} \right)}}{\text{ =  }}\dfrac{{{\text{ -  }}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}}}{{{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}}}$

अब , ${{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{2}}{{\text{k}}^{\dfrac{{\text{1}}}{{\text{3}}}}}}}\dfrac{{{\text{ -  }}\dfrac{{\text{1}}}{{\text{3}}}}}{{{{\text{k}}^{\dfrac{{\text{2}}}{{\text{3}}}}}}}{\text{  =   -  1}}$

$\therefore \,$ वक्र ${\text{x  = }}$ ${{\text{y}}^{\text{2}}}$ और ${\text{xy  =  k}}$ एक दूसरे को समकोण पर काटती हैं

24. अतिपरवलय $\dfrac{{{{\text{x}}^{\text{2}}}}}{{{{\text{a}}^{\text{2}}}}}{\text{  -  }}\dfrac{{{{\text{y}}^{\text{2}}}}}{{{{\text{b}}^{\text{2}}}}}{\text{  =  1}}$ के बिंदु $\left( {{{\text{x}}_{\text{0}}}{\text{,}}{{\text{y}}_{\text{0}}}} \right)$पर स्पर्श रेखा तथा अभिलंब के समीकरण ज्ञात कीजिये

उत्तर: दिए वक्र की $\left( {{{\text{x}}_{\text{0}}}{\text{, }}{{\text{y}}_{\text{0}}}} \right)$पर स्पर्श रेखा की प्रवणता 

${\left. {{{\left. {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right]}_{\left( {{{\text{x}}_{\text{0}}}{\text{, }}{{\text{y}}_{\text{0}}}} \right)}}{\text{ =  }}\dfrac{{{\text{x}}{{\text{b}}^{\text{2}}}}}{{{\text{y}}{{\text{a}}^{\text{2}}}}}} \right]_{\left( {{{\text{x}}_{\text{0}}}{\text{, }}{{\text{y}}_{\text{0}}}} \right)}}{\text{  =  }}\dfrac{{{{\text{x}}_{\text{0}}}{{\text{b}}^{\text{2}}}}}{{{{\text{y}}_{\text{0}}}{{\text{a}}^{\text{2}}}}}$

बिंदु $\left( {{{\text{x}}_{\text{0}}}{\text{, }}{{\text{y}}_{\text{0}}}} \right)$ से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  }}{{\text{y}}_{\text{0}}}{\text{  =  }}\dfrac{{{{\text{x}}_{\text{0}}}{{\text{b}}^{\text{2}}}}}{{{{\text{y}}_{\text{0}}}{{\text{a}}^{\text{2}}}}}\left( {{\text{x  -  }}{{\text{x}}_{\text{0}}}} \right)$

$\dfrac{{{\text{x}}{{\text{x}}_{\text{0}}}}}{{{{\text{a}}^{\text{2}}}}}{\text{  - }}\dfrac{{{\text{y}}{{\text{y}}_{\text{0}}}}}{{{{\text{b}}^{\text{2}}}}}{\text{  =  1}}$

इसलिए इसके अभिलंब की प्रवणता

${\text{ -  }}\dfrac{{\text{1}}}{{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  }}\dfrac{{{\text{ -  }}{{\text{y}}_{\text{0}}}{{\text{a}}^{\text{2}}}}}{{{{\text{x}}_{\text{0}}}{{\text{b}}^{\text{2}}}}}$

बिंदु $\left( {{{\text{x}}_{\text{0}}}{\text{, }}{{\text{y}}_{\text{0}}}} \right)$से जाने वाली स्पर्श रेखा का समीकरण

${\text{y  -  }}{{\text{y}}_{\text{0}}}{\text{  =  }}\dfrac{{{\text{ -  }}{{\text{y}}_{\text{0}}}{{\text{a}}^{\text{2}}}}}{{{{\text{x}}_{\text{0}}}{{\text{b}}^{\text{2}}}}}\left( {{\text{x  -  }}{{\text{x}}_{\text{0}}}} \right)$

$\dfrac{{{\text{y  -  }}{{\text{y}}_{\text{0}}}}}{{{{\text{y}}_{\text{0}}}{{\text{a}}^{\text{2}}}}}{\text{  +  }}\dfrac{{{\text{x  -  }}{{\text{x}}_{\text{0}}}}}{{{{\text{x}}_{\text{0}}}{{\text{b}}^{\text{2}}}}}{\text{  =  0}}$

25. वक्र ${\text{y  =  }}\sqrt {{\text{3x  -  2}}} $की उन स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जो रेखा ${\text{4x  -  2y  +  5  =  0}}$के समांतर हैं।

उत्तर: दिए वक्र के बिंदु ${\text{(x, y)}}$पर स्पर्श रेखा की प्रवणता

$\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{3}}}{{{\text{2}}\sqrt {{\text{3x  -  2}}} }}$

अब, स्पर्श रेखा ${\text{4x  -  2y  +  5  =  0}}$के समांतर हैं।

${\text{y  =  2x  +  5 / 2}}$

इसलिए $\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2}}$

$\dfrac{{\text{3}}}{{{\text{2}}\sqrt {{\text{3x  -  2}}} }}{\text{  =  2}}$

${\text{x  =  }}\dfrac{{{\text{41}}}}{{{\text{48}}}}$

जब ${\text{x  =  }}\dfrac{{{\text{41}}}}{{{\text{48}}}}$

तब ${\text{y  =  }}\dfrac{{\text{3}}}{{\text{4}}}$

बिंदु $\left( {\dfrac{{41}}{{48}},\dfrac{3}{4}} \right)$से जाने वाली स्पर्श रेखा का समीकरण :

${\text{y  -  }}\dfrac{{\text{3}}}{{\text{4}}}{\text{  =  2}}\left( {{\text{x  -  }}\dfrac{{{\text{41}}}}{{{\text{48}}}}} \right)$ 

${\text{48x  -  24y  =  23}}$

26. वक्र ${\text{y}} = 2{{\text{x}}^2} + 3\sin {\text{x}}$ के ${\text{x}} = 0$पर अभिलंब की प्रवणता हैं

A) $3$

B) ${\text{1 / 3}}$

(C) $ - 3$

(D) $ - 1/3$

उत्तर: D) $\dfrac{{{\text{ -  1}}}}{{{\text{ 3}}}}$ सही उत्तर है 

27. किस बिंदु पर ${\text{y  =  x  +  1,}}$ वक्र ${{\text{y}}^{\text{2}}}{\text{  =  4x}}$की स्पर्श रेखा है

A) $(1,2)$

B) $(2,1)$

C) $(1, - 2)$

D) $( - 1,2)$

उत्तर: A) $(1,2)$ सही उत्तर है

प्रश्नावली 6.4

1. अवकल का प्रयोग करके निम्नलिखित में से प्रत्येक का सिन्कट मान दशमलव के तीन स्थानों तक ज्ञात कीजिये:

(I) $\sqrt {25.3} $

उत्तर: यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${{f (x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =  0}}{\text{.3}}$ और ${\text{x  =  25}}$:

$\sqrt {{\text{25  +  0}}{\text{.3}}}  \,\,\approx \sqrt {{\text{25}}} {\text{  +  0}}{\text{.3}}\dfrac{{{\text{d}}\sqrt {{\text{25}}} }}{{{\text{dx}}}}$

$\Rightarrow \sqrt {{\text{25  +  0}}{\text{.3}}}  \,\, \approx \sqrt {{\text{25}}} {\text{  +  0}}{\text{.3}}\left({\dfrac{{\text{1}}}{{\text{2}}}{{{\text{(25)}}}^{\dfrac{{ - 1}}{2}}}} \right)$ 

$\Rightarrow \sqrt {{\text{25  +  0}}{\text{.3}}}   \,\,\approx {\text{5  +  0}}{\text{.3}}\left( {\dfrac{{\text{1}}}{{{\text{10}}}}} \right)$

$\Rightarrow \sqrt {{\text{25}}{\text{.3}}}  \,\, \approx {\text{5}}{\text{.030}}$

(ii) $\sqrt {49.5} $

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =  0}}{\text{.5}}$और ${\text{x  =  49}}$

$\sqrt {{\text{49  +  0}}{\text{.5}}}  \approx \sqrt {{\text{49}}} {\text{  +  0}}{\text{.5}}\dfrac{{{\text{d}}\sqrt {{\text{49}}} }}{{{\text{dx}}}}$ $\Rightarrow \sqrt {{\text{49  +  0}}{\text{.5}}}  \approx \sqrt {{\text{49}}} {\text{  +  0}}{\text{.5}}\left({\dfrac{{\text{1}}}{{\text{2}}}{{{\text{(49)}}}^{\dfrac{{ - 1}}{2}}}} \right)$ 

$\Rightarrow \sqrt {{\text{49  +  0}}{\text{.5}}}  \approx {\text{7  +  0}}{\text{.5}}\left( {\dfrac{{\text{1}}}{{{\text{14}}}}} \right)$

$\Rightarrow \sqrt {{\text{49}}{\text{.5}}}  \approx {\text{7}}{\text{.036}}$

(iii) $\sqrt {0.6} $

उत्तर: यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${\text{f}}({{x + \Delta x}}) \approx {\text{f}}({\text{x)}} + \Delta x\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  0}}{\text{.4 }}$ और ${\text{x  =  1}}$

$\sqrt {{\text{1 - 0}}{\text{.4}}}  \approx \sqrt {\text{1}} {\text{  -  0}}{\text{.4}}\dfrac{{{\text{d}}\sqrt {\text{1}} }}{{{\text{dx}}}}$

$\Rightarrow \sqrt {{\text{1  -  0}}{\text{.4}}}  \approx \sqrt {\text{1}} {\text{  -  0}}{\text{.4}}\left( {\dfrac{{\text{1}}}{{\text{2}}}{{{\text{(1)}}}^{{\text{ - }}\dfrac{{ - 1}}{2}}}} \right)$ 

$\Rightarrow \sqrt {{\text{1  -  0}}{\text{.4}}}  \approx {\text{1  -  0}}{\text{.4}}\left( {\dfrac{{\text{1}}}{{\text{2}}}} \right)$ 

$\Rightarrow \sqrt {{\text{0}}{\text{.6}}}  \approx {\text{0}}{\text{.800}}$

(iv) ${(0.009)^{\dfrac{1}{3}}}$

उत्तर: यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की: ${{f (x + \Delta x}}) \approx {\text{f}}({\text{x)}} + \Delta x\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =  0}}{\text{.001}}$और${\text{x  =  0}}{\text{.008}}$:

${(0.008 + 0.001)^{\dfrac{1}{3}}} \approx {(0.008)^{\dfrac{1}{3}}} + 0.001\dfrac{{{\text{d(0}}{\text{.008}}{{\text{)}}^{\dfrac{{\text{1}}}{{\text{3}}}}}}}{{{\text{dx}}}}$

$\Rightarrow {{\text{(0}}{\text{.008  +  0}}{\text{.001)}}^{\dfrac{1}{3}}} \approx {{\text{(0}}{\text{.008)}}^{\dfrac{1}{3}}}{\text{ +  0}}{\text{.001}}\left({\dfrac{{\text{1}}}{{\text{3}}}{{{\text{(0}}{\text{.008)}}}^{\dfrac{{{\text{ -  2}}}}{{\text{3}}}}}} \right)$  

$\Rightarrow {{\text{(0}}{\text{.008  +  0}}{\text{.001)}}^{\dfrac{1}{3}}} \approx {\text{0}}{\text{.2  +  0}}{\text{.001}}\left( {\dfrac{{\text{1}}}{{{\text{0}}{\text{.12}}}}} \right)$  

$\Rightarrow {{\text{(0}}{\text{.009)}}^{\dfrac{{\text{1}}}{{\text{3}}}}} \approx {\text{0}}{\text{.208}}$

(v) ${(0.999)^{\dfrac{1}{{10}}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  0}}{\text{.001 }}$ और ${\text{x}} = 1$

${{\text{(1  -  0}}{\text{.001)}}^{\text{1}}}{\text{10}} \approx {{\text{(1)}}^{{\text{10  -  0}}{\text{.001}}}}\dfrac{{{\text{d(1}}{{\text{)}}^{\dfrac{{\text{1}}}{{{\text{10}}}}}}}}{{{\text{dx}}}}$  

$\Rightarrow {{\text{(1  -  0}}{\text{.001)}}^{\dfrac{1}{{10}}}} \approx {{\text{(1)}}^{{\text{10}}}}{\text{  -  0}}{\text{.001}}\left( {\dfrac{{\text{1}}}{{{\text{10}}}}{{{\text{(1)}}}^{\dfrac{{{\text{ -  9}}}}{{{\text{10}}}}}}} \right)$  

$\Rightarrow {{\text{(1  -  0}}{\text{.001)}}^{\dfrac{1}{{10}}}} \approx {\text{1  -  0}}{\text{.001}}\left( {\dfrac{{\text{1}}}{{{\text{10}}}}} \right)$

$\Rightarrow {{\text{(0}}{\text{.999)}}^{\dfrac{1}{{10}}}} \approx {\text{0}}{\text{.9999}}$

(vi) ${(15)^{\dfrac{1}{4}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  1 }}$और ${\text{x  =  16 }}$

${(16 - 1)^{\dfrac{1}{4}}} \approx {(16)^{\dfrac{1}{4}}}4 - 1\dfrac{{{\text{d(16}}{{\text{)}}^{\dfrac{{\text{1}}}{{\text{4}}}}}}}{{{\text{dx}}}}$

$\Rightarrow {(16 - 1)^1} \approx {(16)^{\dfrac{1}{4}}} - 1\left( {\dfrac{1}{4}{{(16)}^{\dfrac{{ - 3}}{4}}}} \right)$

$\Rightarrow {(16 - 1)^{\dfrac{1}{4}}} \approx 2 - 1\left( {\dfrac{1}{{32}}} \right)$

$\Rightarrow {(15)^{\dfrac{1}{4}}} \approx 1.968$

(vii) ${(26)^{\dfrac{1}{3}}}$

उत्तर: यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  1}}$और ${\text{x  =  27}}$

${(27 - 1)^{\dfrac{1}{3}}} \approx {(27)^{\dfrac{1}{3}}} - 1\dfrac{{d{{(27)}^{\dfrac{1}{3}}}}}{{dx}}$

$\Rightarrow {(27 - 1)^{\dfrac{1}{3}}} \approx {(27)^{\dfrac{1}{3}}} - 1\left( {\dfrac{1}{3}{{(27)}^{\dfrac{{ - 2}}{3}}}} \right)$

$\Rightarrow {(27 - 1)^{\dfrac{1}{3}}} \approx 3 - 1\left( {\dfrac{1}{{27}}} \right)$

$\Rightarrow {(26)^{\dfrac{1}{3}}} \approx 2.963$

(viii) ${(255)^{\dfrac{1}{4}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  1}}$और ${\text{x  =  256}}$

${(256 - 1)^{\dfrac{1}{4}}} \approx {(256)^{\dfrac{1}{4}}} - 1\dfrac{{d{{(256)}^{\dfrac{1}{4}}}}}{{dx}}$

$\Rightarrow {(256 - 1)^{\dfrac{1}{4}}} \approx {(256)^{\dfrac{1}{4}}} - 1\left( {\dfrac{1}{4}{{(256)}^{\dfrac{{ - 3}}{4}}}} \right)$

$\Rightarrow {(256 - 1)^{\dfrac{1}{4}}} \approx 4 - 1\left( {\dfrac{1}{{256}}} \right)$

$\Rightarrow {(255)^{\dfrac{1}{4}}} \approx 3.996$

(ix) ${(82)^{\dfrac{1}{4}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  1}}$और ${\text{x  =  81}}$

${(81 + 1)^{^{\dfrac{1}{4}}}} \approx {(81)^{^{\dfrac{1}{4}}}} + 1\dfrac{{d{{(81)}^{\dfrac{1}{4}}}}}{{dx}}$

$\Rightarrow {(81 + 1)^{\dfrac{1}{4}}} \approx {(81)^{\dfrac{1}{4}}} + 1\left( {\dfrac{1}{4}{{(81)}^{\dfrac{{ - 3}}{4}}}} \right)$

$\Rightarrow {(81 + 1)^{\dfrac{1}{4}}} \approx 3 + 1\left( {\dfrac{1}{{108}}} \right)$

$\Rightarrow {(82)^{\dfrac{1}{4}}} \approx 3.009$

(x) ${(401)^{\dfrac{1}{4}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  1}}$और ${\text{x  =  400}}$

${(400 + 1)^{\dfrac{1}{2}}} \approx {(400)^{\dfrac{1}{2}}} + 1\dfrac{{d{{(400)}^{\dfrac{1}{2}}}}}{{dx}}$

$\Rightarrow {(400 + 1)^{\dfrac{1}{2}}} \approx {(400)^{\dfrac{1}{2}}} + 1\left( {\dfrac{1}{2}{{(400)}^{\dfrac{{ - 1}}{2}}}} \right)$

$\Rightarrow {(400 + 1)^{\dfrac{1}{2}}} \approx 20 + 1\left( {\dfrac{1}{{40}}} \right){\text{ }}$

$\Rightarrow {(401)^{\dfrac{1}{2}}} \approx 20.025$

(xi) ${(0.0037)^{\dfrac{1}{2}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =  0}}{\text{.0001}}$और ${\text{x  =  0}}{\text{.0036}}$

${(0.0036 + 0.0001)^{\dfrac{1}{2}}} \approx {(0.0036)^{\dfrac{1}{2}}} + 0.0001\dfrac{{d{{(0.0036)}^{\dfrac{1}{2}}}}}{{dx}}$

$\Rightarrow {(0.0036 + 0.0001)^{\dfrac{1}{3}}} \approx {(0.0036)^{\dfrac{1}{3}}} + 0.0001\left( {\dfrac{1}{2}{{(0.0036)}^{\dfrac{{ - 1}}{2}}}} \right)$

$\Rightarrow {(0.0036 + 0.0001)^{\dfrac{1}{2}}} \approx 0.06 + 0.0001\left( {\dfrac{1}{{0.12}}} \right)$

$\Rightarrow {(0.0037)^{\dfrac{1}{2}}} \approx 0.060$

(xii) ${(26.57)^{\dfrac{1}{3}}}$

उत्तर: यदि $\Delta x$सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  0}}{\text{.43}}$और ${\text{x  =  27}}$

${(27 - 0.43)^{\dfrac{1}{3}}} \approx {(27)^{\dfrac{1}{3}}} - 0.43\dfrac{{d{{(27)}^{\dfrac{1}{3}}}}}{{dx}}$

$\Rightarrow {(27 - 0.43)^{\dfrac{1}{3}}} \approx {(27)^{\dfrac{1}{3}}} - 0.43\left( {\dfrac{1}{3}{{(27)}^{\dfrac{{ - 2}}{3}}}} \right)$

$\Rightarrow {(27 - 0.43)^{\dfrac{1}{3}}} \approx 3 - 0.43\left( {\dfrac{1}{{27}}} \right)$

$\Rightarrow {(26.57)^{\dfrac{1}{3}}} \approx 2.984$

(xiii) ${(81.5)^{\dfrac{1}{4}}}$

उत्तर: यदि  $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =  0}}{\text{.5}}$और ${\text{x  =  81}}$

${(81 + 0.5)^{\dfrac{1}{4}}} \approx {(81)^{\dfrac{1}{4}}} + 0.5\dfrac{{d{{(81)}^{\dfrac{1}{4}}}}}{{dx}}$

$\Rightarrow {(81 + 0.5)^{\dfrac{1}{4}}} \approx {(81)^{\dfrac{1}{4}}} + 0.5\left( {\dfrac{1}{4}{{(81)}^{\dfrac{{ - 3}}{4}}}} \right)$

$\Rightarrow {(81 + 0.5)^{\dfrac{1}{4}}} \approx 3 + 0.5\left( {\dfrac{1}{{108}}} \right)$

$\Rightarrow {(81.5)^{\dfrac{1}{4}}} \approx 3.004$

(xiv) ${(3.968)^{\dfrac{3}{2}}}$

उत्तर: यदि $\Delta x$  सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =   -  0}}{\text{.032}}$और ${\text{x  =  4}}$

${(4 - 0.032)^{\dfrac{3}{2}}} \approx {(4)^{\dfrac{3}{2}}} - 0.032\dfrac{{d{{(4)}^{\dfrac{3}{2}}}}}{{dx}}$

$\Rightarrow {(4 - 0.032)^{\dfrac{3}{2}}} \approx {(4)^{\dfrac{3}{2}}} - 0.032\left( {\dfrac{3}{2}{{(4)}^{\dfrac{1}{2}}}} \right)$

$\Rightarrow {(4 - 0.032)^{\dfrac{3}{2}}} \approx 8 - 0.032(3)$

$\Rightarrow {(3.968)^{\dfrac{3}{2}}} \approx 7.904$

(xv) ${(32.15)^{\dfrac{1}{5}}}$

उत्तर: यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${{f(x  +  \Delta x)}} \approx {{f(x)  +  \Delta x}}\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

इसका तात्पर्य है की यदि मानलिया जाए की ${{\Delta x  =  0}}{\text{.15}}$और ${\text{x  =  32}}$

${(32 + 0.15)^{^{\dfrac{1}{5}}}} \approx {(32)^1} + 0.15\dfrac{{d{{(32)}^{\dfrac{1}{5}}}}}{{dx}}$

$\Rightarrow {(32 + 0.15)^{\dfrac{1}{5}}} \approx {(32)^{\dfrac{1}{5}}} + 0.15\left( {\dfrac{1}{5}{{(32)}^{ - \dfrac{4}{5}}}} \right)$

$\Rightarrow {(32 + 0.15)^{\dfrac{1}{5}}} \approx 2 + 0.15\left( {\dfrac{1}{{80}}} \right)$

$\Rightarrow {(32.15)^{\dfrac{1}{5}}} \approx 2.001$

2. ${\text{f (2}}{\text{.01)}}$का सन्रिकट मान ज्ञात कीजिये जहां ${\text{f (x)  =  4}}{{\text{x}}^{\text{2}}}{\text{  +  5x  +  2}}$है।

उत्तर: ${\text{f (x)  =  4}}{{\text{x}}^{\text{2}}}{\text{  +  5x  +  2}}$

${\text{f (2}}{\text{.0}}1) = 4{(2 + 0.01)^2} + 5(2.01) + 2$

यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${{f (x  +  \Delta x)}} \approx {\text{f (x) }} +  \Delta x\dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

तात्पर्य:

$\Rightarrow {\text{f (2}}.01) \approx 4\left( {{2^2} + 0.01\dfrac{{d{2^2}}}{{dx}}} \right) + 5(2.01) + 2$

$\Rightarrow {\text{f (2}}{\text{.01)}} \approx 4(4 + 0.04) + 5(2.01) + 2$  $\Rightarrow {\text{f (2}}{\text{.01)}} \approx 28.21$

3. ${\text{f (5}}{\text{.001)}}$का सत्रिकट मान ज्ञात कीजिये जहां ${\text{f (x)  =  }}{{\text{x}}^{\text{3}}}{\text{  -  7}}{{\text{x}}^{\text{2}}}{\text{  +  15}}$ है।

उत्तर: ${\text{f (x)  =  }}{{\text{x}}^{\text{3}}}{\text{  -  7}}{{\text{x}}^{\text{2}}}{\text{  +  15}}$ यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की

${\text{f (5}}.001) = {(5 + 0.001)^3} - 7{(5 + 0.001)^2} + 15$

$f (x  +  \Delta x) \approx {\text{f (x)  + }} \Delta x \dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

तात्पर्य-

$\Rightarrow {\text{f (5}}.001) \approx \left( {{5^3} + 0.001\dfrac{{d{5^3}}}{{dx}}} \right) - 7\left( {{5^2} + 0.001\dfrac{{d{5^2}}}{{dx}}} \right) + 15$

$\Rightarrow {\text{f (}}5.001) \approx 125 + 0.001(75) - 7(25 + 0.001(10)) + 15$

$\Rightarrow {\text{f (}}5.001) \approx  - 34.995$
4. ${\text{x m}}$भुजा वाले घन की भुजा में $1\% $वृद्धि के कारण घन के आयतन में होने वाले सन्निकट परिवर्तन ज्ञात कीजिये।

उत्तर: ${\text{x m}}$भुजा वाले घन का आयतन होता है: 

$\Rightarrow {{\text{x}}^3}$

$1\% $ वृद्धि होने पश्चात आयतन है: 

$\Rightarrow {({\text{x}} + 0.01{\text{x}})^3}$

$\Rightarrow {{\text{x}}^3}{(1 + 0.01)^3}$

आयतन में आया बदलाव है:

${(1 + 0.01)^3}$ गुना 

यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${\text{f (x  + }} (\Delta x) \approx {\text{f(x)}}  +  \Delta x \dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

$\Rightarrow {1^3} + 0.01\left( {3{{(1)}^2}} \right)$

$\Rightarrow 1.03$

अर्थर्थ आयतन पहेले के मुकाबले $0.3$ गुनना और बड़ेगा।

5. ${\text{x m}}$भुजा वाले घन की भुजा में $1\% $ ह्यास के कारण घन के आयतन में होने वाले सन्रिकट परिवर्तन ज्ञात कीजिये।

उत्तर: ${\text{x m}}$ भुजा वाले घन का आयतन होता है: 

$\Rightarrow 6{{\text{x}}^2}$

$1\% $ह्यास होने पश्चात आयतन है:

$\Rightarrow 6{({\text{x  -  0}}{\text{.01x}})^2}$

$\Rightarrow 6{{\text{x}}^2}{(1 - 0.01)^2}$

आयतन में आया बदलाव है${(1 - 0.01)^2}$गुना

यदि $\Delta x$ सूक्ष्म है तो यह स्थापित है की:

${\text{f (x  + }} (\Delta x) \approx {\text{f (x)  + }} \Delta x \dfrac{{{\text{d(f (x))}}}}{{{\text{dx}}}}$

$\Rightarrow {1^2} - 0.01(2(1))$

$\Rightarrow 0.98$

अर्थर्थ आयतन पहेले के मुकाबले ${0.02^ \star }6 = 0.12{{\text{m}}^2}$ गुना और घटेगा।

6. एक गोले की त्रिज्या $7{\text{m}}$ मापी जाती है जिसमे $0.02{\text{m}}$की त्रुटी है। इसके आयतन के परिकलन में सत्रिकट त्रुटी ज्ञात किजिये।

उत्तर:गोले का आयतन होता है:

$\Rightarrow {\text{V}} = \dfrac{4}{3}{\text{π }}{{\text{r}}^{\text{3}}}$

$\Rightarrow \dfrac{{{\text{dV}}}}{{{\text{dr}}}} = 4{\text{π }}{{\text{r}}^{\text{2}}}$

जहा ${\text{r}}$ गोले का त्रिज्या है।

अगर त्रिज्या $7{\text{m}}$है और इसमें $0.02{\text{m}}$की त्रुटी है तो

$\Rightarrow {\text{dV  =  4π }}{{\text{r}}^{\text{2}}}{\text{dr}}$  

$\Rightarrow {\text{dV =  4π }}{{\text{7}}^{\text{2}}}( \pm  0{\text{.02)}}$  $\Rightarrow {\text{dV}}  =   \pm  3{\text{.92π }}{{\text{m}}^{\text{3}}}$

7. एक गोले की त्रिज्या $7{\text{m}}$मापी जाती है जिसमे ${\text{0}}{\text{.03m}}$की त्रुटी है। इसके पृष्ट क्षेत्रफल के परिकलन में सत्रिकट त्रुटी ज्ञात किजिये।

उत्तर: गोले का क्षेत्रफल होता है

$\Rightarrow {\text{A  =  4π }}{{\text{r}}^{\text{2}}}$

$\Rightarrow \dfrac{{{\text{dA}}}}{{{\text{dr}}}}{\text{  =  8π r}}$

जहा ${\text{r}}$ गोले का त्रिज्या है।

अगर त्रिज्या $9{\text{m}}$है और इसमें $0.03$ की त्रुटी है तो

$\Rightarrow {\text{dA  =  8π rdr }}$  

$\Rightarrow {\text{dA  =  8π (9) }}(  \pm  0{\text{.03)}}$  

$\Rightarrow {\text{dA  = }}  \pm  2{\text{.16π }}{{\text{m}}^{\text{2}}}$  

8. यदि ${\text{f}}({\text{x}}) = 3{{\text{x}}^2} + 15{\text{x}} + 5$हो, तो ${\text{f}}(3.02)$ का सत्रिकट मान है:

(A) $47.66$

(B) $57.66$

(C) $67.66$

(D) $77.6$

उत्तर: ${\text{f (x)  =  3}}{{\text{x}}^{\text{2}}}{\text{  +  15x  +  5}}$

$\Rightarrow {\text{f (3}}{\text{.02)  =  3(3}}{\text{.02}}{{\text{)}}^{\text{2}}}{\text{  +  15(3}}{\text{.02)  +  5}}$  $\Rightarrow {\text{f (3}}{\text{.02)  =  3(3  +  0}}{\text{.02}}{{\text{)}}^{\text{2}}}{\text{  +  15(3  +  0}}{\text{.02)  +  5}}$

$\Rightarrow {\text{f }}(3.02) \approx 3\left( {{3^2} + 2(0.02)} \right) + 15(3 + 0.02) + 5$

$\Rightarrow {\text{f }}(3.02) \approx 27.12 + 45.3 + 5$

$\Rightarrow {\text{f (3}}.02) \approx 77.66$

अतः (D) $77.66$ सही उत्तर है

9. भुजा में $3\% $ वृद्धि के कारन भुजा ${\text{x}}$ के घन के आयतन में सत्रिकट परिवर्तन है:

(A)${\text{0}}{\text{.06}}{{\text{x}}^{\text{3}}}{\text{}}{{\text{m}}^{\text{3}}}$

(B)${\text{0}}{\text{.6}}{{\text{x}}^{\text{3}}}{\text{}}{{\text{m}}^{\text{3}}}$

(C)${\text{0}}{\text{.09}}{{\text{x}}^{\text{3}}}{\text{m}}$

(D)${\text{0}}{\text{.9}}{{\text{x}}^{\text{3}}}{\text{}}{{\text{m}}^{\text{3}}}$

उत्तर:घन का आयतन होता है:

$\Rightarrow {\text{V  =  }}{{\text{x}}^{\text{3}}}$

$\Rightarrow \dfrac{{{\text{dV}}}}{{{\text{dx}}}}{\text{  =  3}}{{\text{x}}^{\text{2}}}$

जहा ${\text{x}}$घन की भुजा की लम्बाई है। ${\text{x}}$ में वृद्धि है $3\% $ की अर्थाथि

$\Rightarrow {\text{dV  =  3}}{{\text{x}}^{\text{2}}}{\text{dx}}$

$\Rightarrow {\text{dV}} \approx 3{{\text{x}}^{\text{2}}}(0.03{\text{x}})$

$\Rightarrow {\text{dV}} \approx 0.09{{\text{x}}^3}{{\text{m}}^3}$

$\therefore $(C) $0.09{{\text{x}}^{\text{3}}}{{\text{m}}^3}$ सही उत्तर है

प्रश्नावली 6.5

1. निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई तो, ज्ञात कीजिए:

(i) ${{f (x)  =  (2x  -  1}}{{{)}}^{{2}}}{{  +  3}}$

उत्तर: ${{f (x)  =  (2x  -  1}}{{{)}}^{{2}}}{{  +  3}}$

यहाँ, ${{{(2x  -  1)}}^2} \geqslant 0$ है

$\Rightarrow {{f (x)}} \geqslant 0$

इसलिए, फलन ${{f}}$ का मान निम्नतम होगा, यदि ${{2x  -  1  =  0}}$ अर्थात ${{x  =  }}\dfrac{{{1}}}{{{2}}}$ हो

अतः, इस फलन का निम्नतम मान बिंदु ${{x  =  }}\dfrac{{{1}}}{{{2}}}$ पर ${{3}}$ होगा परन्तु कोई उच्चतम मान नहीं है।

(ii) ${{f (x)  =  9}}{{{x}}^{{2}}}{{  +  12x  +  2}}$

उत्तर:  $\left. {{{f (x)  =  9}}{{{x}}^{{2}}}{{  +  12x  +  2  =  99}}{{{x}}^{{2}}}{{  +  12x  +  4}}} \right){{  -  2}}$

इसलिए, फलन ${{f}}$ का मान निम्नतम होगा, यदि ${{3x  +  2  =  0}}$ अर्थात ${{x  =-  }}\dfrac{{{2}}}{{{3}}}$ हो।

अंतः, इस फलन का निम्नतम मान बिंदु ${{x  =-  }}\dfrac{{{2}}}{{{3}}}$पर $ - 2$ होगा परन्तु कोई निम्नतम मान नहीं है

(iii) ${{f (x)  =-  (x  -  1}}{{{)}}^{{2}}}{{  +  10}}$

उत्तर: ${{f (x)  =-  (x  -  1}}{{{)}}^{{2}}}{{  +  10}}$

${{{(x  -  1}})^2} \geqslant 0$

$\Rightarrow {{{(x  -  1)}}^{{2}}} \leqslant {{ 0}}$

$\Rightarrow {{f (x) }} \leqslant {{ 10}}$

इसलिए, फलन ${{f}}$ का मान उच्चतम होगा, यदि ${{x  -  1  =  0}}$ अर्थात ${{x  =  1}}$ हो।

अतः, इस फलन का उच्चतम मान बिंदु ${{x  =  1}}$ पर ${{10}}$ होगा परन्तु कोई निम्नतम मान नहीं है।

(iv) ${{g (x)  =  }}{{{x}}^{{3}}}{{  +  1}}$

उत्तर: ${{g (x)  =  }}{{{x}}^{{3}}}{{  +  1}}$

यहाँ, ${{{x}}^{{3}}}{{  >  0}}$ यदि ${{x  >  0}}$ और ${{{x}}^{{3}}}{{  <  0}}$ यदि ${{x  <  0}}$ है।

अतः, इस फलन का न तो उच्चतम मान होगा और न ही कोई निम्नतम मान होगा। 

2. निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हों, तो ज्ञात कीजिए:

(i) ${{f (x)  =  | x  +  2|  -  1}}$

उत्तर: ${{f (x)  =  | x  +  2|  -  1}}$

${{|x  +  2|}} \geqslant {{ 0}}$  

$\Rightarrow {{f (x)}} \geqslant {{ -  1}}$

इसलिए, फलन ${{f}}$ का मान निम्नतम होगा, यदि ${{x  +  2  =  0}}$अर्थात ${{x  =-  2}}$ हो।

अतः, बिंदु ${{x  =-  2}}$ पर, इस फलन का निम्नतम मान ${{ -  1}}$ होगा, परन्तु कोई उच्चतम मान नहीं है।

(ii) ${{g (x)  =-  | x  +  1|  +  3}}$

उत्तर: ${{g (x)  =-  | x  +  1|  +  3}}$

यहाँ, $|{{x  +  1 }}|\, \geqslant 0$ अर्थात $ - |{{x}} + 1|\, \leqslant 0$ है,

इसलिए, ${{g}}\,{{(x)}} \leqslant {{3}}$है।

इसलिए, फलन ${{g}}$ का मान उच्चतम होगा, यदि ${{x  +  1  =  0}}$अर्थात ${{x  =-  1}}$ हो।

अतः, बिंदु ${{x  =-  1}}$ पर, इस फलन का उच्चतम मान ${{3}}$ होगा, परन्तु कोई निम्नतम मान नहीं है।

(iii) ${{h (x)  =  sin (2x)  +  5}}$

उत्तर: ${{h (x)  =  sin (2x)  +  5}}$

${{ -  1}} \leqslant {{sin 2x}} \leqslant {{1}}$  

$\Rightarrow {{ 4}} \leqslant {{sin 2x  +  5}} \leqslant {{6}}$

इसलिए, फलन ${{h}}$ का उच्चतम मान ${{6}}$ होगा तथा निम्नतम मान ${{ 4}}$  होगा।

(iv) ${{f (x)  =  | sin 4x  +  3|}}$

उत्तर: ${{f (x)  =  | sin 4x  +  3|}}$

${{ -  1}} \leqslant {{sin 4x}} \leqslant {{1}}$  

$\Rightarrow {{2}} \leqslant {{sin 4x  +  3}} \leqslant {{4}}$  

$\Rightarrow {{2}} \leqslant {{| sin 4x  +  3 | }} \leqslant {{ 4}}$

इसलिए, फलन का उच्चतम मान ${{ 4}}$ होगा तथा निम्नतम मान ${{ 2}}$ होगा।

(v) ${{h (x)  =  x  +  1, x}} \in {{( -  1, 1)}}$

उत्तर: ${{h (x)  =  x  +  1, x}} \in {{( -  1, 1)}}$

${{ -  1  <  x  <  1}}$  

$\Rightarrow {{0  <  x  +  1  <  2}}$

इसलिए, फलन ${{h}}$ का न उच्चतम मान होगा और नही निम्नतम मान होगा।

3. निम्नलिखित फलनों के स्थानीय उच्चतम या निम्नतम, यदि कोई हों तो, ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम मान, जैसी स्थिति हो, भी ज्ञात कीजिए।

(I) ${{f (x)  =  }}{{{x}}^{{2}}}$

उत्तर: ${{f (x)  =  }}{{{x}}^{{2}}}$

$\Rightarrow {{f '(x)  =  2x}}$

अब, ${{f '(x)  =  0}} \Rightarrow {{2x  =  0}} \Rightarrow {{x  =  0}}$

इस प्रकार, केवल ${{x  =  0}}$ ही एक ऐसा बिंदु (क्रांतिक बिंदु) है जो ${{f}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकता है।

अब, ${{f ''(0)  =  2  >  0}}$

यहाँ, ${{f ''(0)  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  0}}$ स्थानीय निम्नतम बिंदु है और का स्थानीय निम्नतम मान ${{f}}(0) = 0$ है।

(ii) ${{g (x)  =  }}{{{x}}^{{3}}}{{  -  3x}}$

उत्तर: ${{g (x)  =  }}{{{x}}^{{3}}}{{  -  3x}}$

$\Rightarrow {{g '(x)  =  3}}{{{x}}^{{2}}}{{  -  3}}$

अब, ${{g '(x)  =  0}} \Rightarrow {{3}}{{{x}}^{{2}}}{{  -  3}} \Rightarrow {{x  =\pm 1}}$

इस प्रकार, केवल ${{x  =\pm 1}}$ ही ऐसे बिंदु (क्रांतिक बिंदु) हैं जो ${{g}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकतेहैं।

अब, ${{g ''(x)  =  6x}}$

${{x  =  1}}$ के लिए, ${{g ''(1)  =  6  >  0}}$

यहाँ, ${{g ''(1)  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  1}}$ स्थानीय निम्नतम बिंदु है और ${{g}}$ का स्थानीय निम्नतम मान ${{g (1)  =  }}{{{1}}^{{3}}}{{  -  3(1)  =-  2}}$ है।

${{x  =-  1}}$ के लिए, ${{g'' }}\left( {{{ -  1}}} \right){{  =-  6  <  0}}$

यहाँ, ${{g'' }}\left( {{{ -  1}}} \right){{  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =-  1}}$ स्थानीय उच्चतम बिंदु हैऔर ${{g}}$ का स्थानीय

उच्चतम मान ${{g( - 1)  =  (  -  1}}{{{)}}^{{3}}}{{  -  3(  -  1)  =  2}}$ है।

 (iii) ${{h (x)  =  sin x  +  cos x, 0  <  x  <  }}\dfrac{{{π }}}{{{2}}}$

उत्तर: ${{h (x)  =  sin x  +  cos x}}$

$\Rightarrow {{h '(x)  =  cos x  -  sin x}}$

अब, ${{h '(x)  =  0}} \Rightarrow {{cos x  -  sin x  =  0}} \Rightarrow {{tan x  =  1}} \Rightarrow {{x  =  }}\dfrac{{{π }}}{{{4}}} \in \left( {{{0, }}\dfrac{{{π }}}{{{4}}}} \right)$

इस प्रकार, केवल ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ ही एक ऐसा बिंदु (क्रांतिक बिंदु ) है जो ${{h}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकता है।

अब, ${{h ''(x)  =-  sin x  -  cos x}}$

${{x  =  }}\dfrac{{{π }}}{{{4}}}$ के लिए, ${{h ''}}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  =-  sin}}\dfrac{{{π }}}{{{4}}}{{  -  cos}}\dfrac{{{π }}}{{{4}}}{{  =-  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  -  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =-  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =-  }}\sqrt {{2}} {{  <  0}}$

यहाँ, ${{h ''}}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ स्थानीय उच्चतम बिंदु है और ${{h}}$ का स्थानीय उच्चतम मान ${{h}}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  =  sin }}\dfrac{{{π }}}{{{4}}}{{  +  cos }}\dfrac{{{π }}}{{{4}}}{{  =  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  +  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =  }}\sqrt {{2}} {{  >  0}}$ है।

(iv) ${{f (x)  =  sin x  -  cos x, 0  <  x  <  23π }}$

उत्तर: ${{f (x)  =  sin x  -  cos x}}$

$\Rightarrow {{f '(x)  =  cos x  +  sin x}}$

अब, ${{f '(x)  =  0}} \Rightarrow {{cos x  +  sin x  =  }}0 \Rightarrow {{tan x  =-  1}} \Rightarrow {{x  =  }}\dfrac{{{{3π }}}}{{{4}}}{{ , }}\dfrac{{{{7π }}}}{{{4}}} \in \left( {{{0,}}\dfrac{{{π }}}{{{4}}}} \right)$

इस प्रकार, केवल ${{x  =  }}\dfrac{{{{3π }}}}{{{4}}}$ और ${{x  =  }}\dfrac{{{{7π }}}}{{{4}}}$ ही एक ऐसा बिंदु क्रांतिक बिंदु ) है जो ${{f}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकते हैं।

अब, ${{f '(x ) =-  sin x  +  cos x}}$

${{x  =  }}\dfrac{{{{3π }}}}{{{4}}}$ के लिए, ${{f ''}}\left( {\dfrac{{{{3π }}}}{{{4}}}} \right){{  =-  sin}}\dfrac{{{{3π }}}}{{{4}}}{{  +  cos}}\dfrac{{{{3π }}}}{{{4}}}{{  ==--  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =- }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =- }}\sqrt {{2}} {{  >  0}}$ है, 

इसलिए, द्वितीय अवकलज परिक्षण द्वारा ${{x  =  }}\dfrac{{{{3π }}}}{{{4}}}$ स्थानीय उच्चतम बिंदु है और ${{f}}$ का स्थानीय

उच्चतम मान ${{f }}\left( {\dfrac{{{{3π }}}}{{{4}}}} \right){{  =  sin}}\dfrac{{{{3π }}}}{{{4}}}{{  -  cos}}\dfrac{{{{3π }}}}{{{4}}}{{  =  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  -  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =  }}\sqrt {{2}} {{  >  0}}$है।

${{x  =  }}\dfrac{{{{7π }}}}{{{4}}}$के लिए, ${{f ''}}\left( {\dfrac{{{{7π }}}}{{{4}}}} \right){{  =-  sin}}\dfrac{{{{7π }}}}{{{4}}}{{  +  cos}}\dfrac{{{{7π }}}}{{{4}}}{{  =-  }}\left( {{{  -  }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right){{  +  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =  }}\sqrt {{2}} {{  >  0}}$

यहाँ, ${{f ''}}\left( {\dfrac{{{{7π }}}}{{{4}}}} \right){{  >  0}}$है, 

इसलिए, द्वितीय अवकलज परिक्षण द्वारा ${{x  =  }}\dfrac{{{{7π }}}}{{{4}}}$ स्थानीय उच्चतम बिंदु है और ${{f}}$ का स्थानीय

उच्चतम मान ${{f}}\left( {\dfrac{{{{7π }}}}{{{4}}}} \right){{  =  sin}}\dfrac{{{{7π }}}}{{{4}}}{{  -  cos}}\dfrac{{{{7π }}}}{{{4}}}{{  =-  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  -  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =-  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =-  }}\sqrt {{2}} {{  <  0}}$ है।

(v) ${{f (x)  =  }}{{{x}}^{{3}}}{{  -  6}}{{{x}}^{{2}}}{{  +  9x  +  15}}$

उत्तर: ${{f (x)  =  }}{{{x}}^{{3}}}{{  -  6}}{{{x}}^{{2}}}{{  +  9x  +  15}}$

$\Rightarrow {{f '(x)  =  3}}{{{x}}^{{2}}}{{  -  12x  +  9}}$

अब, ${{ f '(x)  =  0}} \Rightarrow {{3}}{{{x}}^{{2}}}{{  -  12x  +  9  =  0}} \Rightarrow {{(x  -  1) (x  -  3)  =  0}} \Rightarrow {{ x  =  1, 3}}$

इसप्रकार, केवल ${{x  =  1}}$ और ${{x}} = 3$ ही ऐसे बिंदु (क्रांतिक बिंदु) हैं जो ${{f}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकते हैं।

अब, ${{f ''(x)  =  6x  -  12}}$

${{x  =  1}}$ के लिए, ${{f ''(1)  =  6(1)  -  12  =-  6  <  0}}$

यहाँ, ${{f ''(1)  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  1}}$ स्थानीय उच्चतम बिंदु है और ${{f}}$ का स्थानीय उच्चतम मान ${{f (1)  =  (1}}{{{)}}^{{3}}}{{  -  6(1}}{{{)}}^{{2}}}{{  +  9(1)  +  15  =  19}}$

${{x}} = 3$ केलिए, ${{f ''(3)  =  6(3)  -  12  =  6  >  0}}$

यहाँ, ${{f ''(3)  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x}} = 3$ स्थानीय निम्नतम बिंदु है और ${{f}}$ का स्थानीय निम्नतम मान ${{f (1)  =  (3}}{{{)}}^{{3}}}{{  -  6(3}}{{{)}}^{{2}}}{{  +  9(3)  +  15  =  15}}$

vi) ${{g (x)  =  }}\dfrac{{{x}}}{{{2}}}{{  +  }}\dfrac{{{2}}}{{{x}}}{{,  x  >  0}}$

उत्तर: ${{g (x)  =  }}\dfrac{{{x}}}{{{2}}}{{  +  }}\dfrac{{{2}}}{{{x}}}$

$\Rightarrow {{g'(x)  =  }}\dfrac{{{1}}}{{{2}}}{{  -  }}\dfrac{{{2}}}{{{{{x}}^{{2}}}}}$

अब, ${{g'(x)  =  0}} =  > {{{x}}^{{2}}}{{  -  4  =  0 }} \Rightarrow {{x  \pm  2}} \Rightarrow {{x  =  2}}$ क्यांकि ${{x  >  0}}$ है।

इस प्रकार, केवल ${{x  =  2}}$ ही एक ऐसा बिंदु (क्रांतिक बिंदु) है जो ${{g}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकता है।

अब, ${{g''(x)  =  }}\dfrac{{{4}}}{{{{{x}}^{{3}}}}}$

${{x  =  2}}$ के लिए. ${{g''(2)  =  }}\dfrac{{{4}}}{{{{{2}}^{{3}}}}}{{  =  }}\dfrac{{{1}}}{{{2}}}{{  >  0}}$

यहाँ, ${{g''(2)  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  2}}$ स्थानीय निम्नतम बिंदु है और ${{g}}$ का स्थानीय निम्नतम मान ${{g (2)  =  }}\dfrac{{{2}}}{{{2}}}{{  +  }}\dfrac{{{2}}}{{{2}}}{{  =  2}}$ है।

vii) ${{g (x)  =  }}\dfrac{{{1}}}{{{{{x}}^{{2}}}{{  +  2}}}}$

उत्तर: $\Rightarrow {{g'(x)  =-  }}\dfrac{{{{2x}}}}{{{{\left( {{{{x}}^{{2}}}{{  +  2}}} \right)}^{{2}}}}}$

अब, ${{g '(x)  =  0 }} \Rightarrow {{  -  }}\dfrac{{{{2x}}}}{{{{\left( {{{{x}}^{{2}}}{{  +  2}}} \right)}^{{2}}}}}{{  =  0}} \Rightarrow {{x=  0}}$है।

इस प्रकार, केवल ${{x=  0}}$ ही एक ऐसा बिंदु (क्रांतिक बिंदु) है जो ${{g}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकता है।

अब, ${{g ''(x)  =-  }}\dfrac{{{{\left( {{{{x}}^{{2}}}{{  +  2}}} \right)}^{{2}}}{{(2)  -  2x}}\left[ {{{2}}\left( {{{{x}}^{{2}}}{{  +  2}}} \right){{2x}}} \right)}}{{{{\left( {{{{x}}^{{2}}}{{ +  2}}} \right)}^{{3}}}}}{{  =-  }}\dfrac{{{{2}}\left( {{{2  -  }}{{{x}}^{{2}}}} \right)}}{{{{\left( {{{{x}}^{{2}}}{{ +  2}}} \right)}^{{2}}}}}$

${{x  =  0}}$ के लिए, ${{g ''(0)  =-  }}\dfrac{{{4}}}{{{4}}}{{  =-  1  <  0}}$

यहाँ, ${{g''(0)  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x=  0}}$ स्थानीय उच्चतम बिंदु है और ${{g}}$ का स्थानीय उच्चतम मान ${{g(0)  =  }}\dfrac{{{1}}}{{{{0  +  2}}}}{{  =  }}\dfrac{{{1}}}{{{2}}}$ है।

(viii) ${{f (x)  =  x}}\sqrt {{{1  -  x}}} {{ ,  0  <  x  < 1}}$

उत्तर: ${{f (x)  =  x}}\sqrt {{{1  -  x}}} $

$\Rightarrow {{f '(x)  =  x }}{{. }}\dfrac{{{{ -  1}}}}{{{{2}}\sqrt {{{1  -  x}}} }}{{  +  }}\sqrt {{{1  -  x}}} {{  =  }}\dfrac{{{{ -  x  +  2  -  2x}}}}{{{{2}}\sqrt {{{1  -  x}}} }}{{  =  }}\dfrac{{{{2  -  3x}}}}{{{{2}}\sqrt {{{1  -  x}}} }}$

अब, ${{f '(x)  =  0}} \Rightarrow {{2  -  3x  =  0}} \Rightarrow {{x  =  }}\dfrac{{{2}}}{{{3}}}$

इसप्रकार, केवल ${{x  =  }}\dfrac{{{2}}}{{{3}}}$ ही एक ऐसा बिंदु (क्रांतिक बिंदु) है जो ${{f}}$ का स्थानीय उच्चतम या स्थानीय निम्नतम संभावित बिंदु हो सकता है।

अब,

${{f ''(x)  =  }}\dfrac{{\sqrt {{{1  -  x}}} {{(  -  3)  -  (2  -  3x) }}{{. }}\dfrac{{{{ -  1}}}}{{{{2}}\sqrt {{{1  -  x}}} }}}}{{{{2(1  -  x)}}}}$  

${{ =  }}\dfrac{{{{ -  6(1  -  x)  +  (2  -  3x)}}}}{{{{4(1  -  x)}}\sqrt {{{1  -  x}}} }}{{  =  }}\dfrac{{{{ -  4  +  3x}}}}{{{{4(1  -  x)}}\sqrt {{{1  -  x }}} }}$

${{x  =  }}\dfrac{{{2}}}{{{3}}}$ के लिए,

${{f ''}}\left( {\dfrac{{{2}}}{{{3}}}} \right){{  =  }}\dfrac{{{{ -  4  +  3}}\left( {\dfrac{{{2}}}{{{3}}}} \right)}}{{{{4}}\left( {{{1  -  }}\dfrac{{{2}}}{{{3}}}} \right)\sqrt {{{1  -  }}\dfrac{{{2}}}{{{3}}}} }}{{  =  }}\dfrac{{{{ -  4  +  2}}}}{{{{4}}\left( {\dfrac{{{1}}}{{{3}}}} \right)\sqrt {\dfrac{{{1}}}{{{3}}}} }}{{  =-  }}\dfrac{{{{3}}\sqrt {{3}} }}{{{{2}}\sqrt {{2}} }}{{  <  0}}$

यहाँ, ${{f ''}}\left( {\dfrac{{{2}}}{{{3}}}} \right){{  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  }}\dfrac{{{2}}}{{{3}}}$ स्थानीय उच्चतम बिंदु है और ${{f}}$ का स्थानीय उच्चतम मान ${{f (1)=  }}\dfrac{{{2}}}{{{3}}}\sqrt {{{1  -  }}\dfrac{{{2}}}{{{3}}}} {{  =  }}\dfrac{{{2}}}{{{{3}}\sqrt {{3}} }}{{  =  }}\dfrac{{{{2}}\sqrt {{3}} }}{{{9}}}$ है।

4. सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम या निम्नतम मान नहीं है 

(i) ${{f (x)  =  }}{{{e}}^{{x}}}$

उत्तर: ${{f (x)  =  }}{{{e}}^{{x}}}$

$\Rightarrow {{f '(x)  =  }}{{{e}}^{{x}}} = 0$

अब, यदि ${{f ''(x)  =  0}}$ है तो ${{{e}}^{{x}}} = 0$ होगा।

परन्तु, हम जानते हैं कि ${{x}}$ का कोई भी मान, ${{c }} \in {{R}}$ ऐसा नहीं है ताकि 

${{f '(c)  =  }}{{{e}}^{{c}}}{{  =  0}}$ हो।

अतः, इस फलन का न तो उच्चतम मान है और नही निम्नतम मान है।

(ii) ${{g (x)  =  log x}}$

उत्तर: ${{g (x)  =  log x}}$

$\Rightarrow {{g '(x)  =  }}\dfrac{{{1}}}{{{x}}}$

अब, यदि ${{g '(x)  =  0}}$ है तो $\dfrac{{{1}}}{{{x}}}{{  =  0}}$ होगा।

परन्तु, हम जानते हैं कि ${{x}}$ का कोई भी मान, ${{c }} \in {{R}}$ ऐसा नहीं है ताकि 

${{g '(c)  =  }}\dfrac{{{1}}}{{{c}}}{{  =  0}}$ हो।

अतः, इस फलन का न तो उच्चतम मान है और न ही निम्नतम मान है।

(iii) ${{h (x)  =  }}{{{x}}^{{3}}}{{  +  }}{{{x}}^{{2}}}{{  +  x  +  1}}$

उत्तर: ${{h (x)  =  }}{{{x}}^{{3}}}{{  +  }}{{{x}}^{{2}}}{{  +  x  +  1}}$

$\Rightarrow {{h '(x)  =  3}}{{{x}}^{{2}}}{{  +  2x  +  1}}$

अब, यदि ${{h '}}({{x}}) = 0$ है तो ${{3}}{{{x}}^{{2}}}{{  +  2x  +  1  =  0 }}$ होगा।

यहाँ, समीकरण ${{3}}{{{x}}^{{2}}}{{  +  2x  +  1  =  0 }}$ के मूल वास्तविक नहीं हैं।

अतः, ${{x}}$ का कोई भी मान, $c \in R$ ऐसा नहीं है ताकि ${{h '(x)  =  3}}{{{x}}^{{2}}}{{  +  2x  +  1}}$ हो। 

अतः, इस फलन का न तो उच्चतम मान है और न ही निम्नतम मान है।

5. प्रदत्त अंतरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।

(i) ${{f (x)  =  }}{{{x}}^{{3}}}{{, x}} \in [ - 2,2]$

उत्तर: ${{f (x)  =  }}{{{x}}^{{3}}}$

$ f’(x) = 3x^2$
अब, ${{f '(x)  =  0}} \Rightarrow {{3}}{{{x}}^{{2}}}{{  =  0 }} \Rightarrow {{ x  =  0}}$

यहाँ, केवल ${{x  =  0}}$ ही क्रांतिक बिंदु है।

फलन ${{f}}$ के मान ${{x  =  2}}$ और ${{x  =-  2}}$ पर

${{f (0)  =  (0}}{{{)}}^{{3}}}{{  =  0}}$  

${{f (  -  2)  =  ( -  2}}{{{)}}^{{3}}}{{  =-  8}}$  

${{f( 2)  =  (2}}{{{)}}^{{3}}}{{ =  8}}$

इस प्रकार, ${{x  =  2}}$ पर फलन का निरपेक्ष उच्चतम मान $8$ है और ${{x  =-  2}}$, पर फलन का निरपेक्ष निम्नतम मान ${{ -  8}}$ है।

(ii) ${{f (x)  =  sin x  +  cos x,  x}} \in [0,π ]$

उत्तर: ${{f (x)  =  sin x  +  cos x}}$

$\Rightarrow {{f '(x)  =  cos x  -  sin x}}$

अब, ${{f '(x)  =  0}}$

$\Rightarrow {{cos x  -  sin x  =  0}} \Rightarrow {{tan x  =  1}} \Rightarrow {{x  =  }}\dfrac{{{π }}}{{{4}}}$

${{x  =-  2}}$ और ${{x  =  2}}$ पर 

यहाँ, केवल ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ ही क्रांतिक बिंदु है।क्रांतिक बिंदु ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ तथा अन्तराल केअंत्य बिन्दुओं ${{x  =  0}}$और${{x  =  π }}$ पर, फलन ${{f}}$ के मान का परिकलन करने पर

${{f }}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  =  sin}}\dfrac{{{π }}}{{{4}}}{{  +  cos}}\dfrac{{{π }}}{{{4}}}{{  =  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  +  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =  }}\sqrt {{2}} $  

${{f (0)  =  sin 0  +  cos 0  =  0  +  1  =  1}}$  

${{f (π )  =  sin π+  cos π=  0  -  1  =-  1}}$

इस प्रकार, ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ पर फलन ${{f}}$ का निरपेक्ष उच्चतम मान $\sqrt {{2}} $ है और ${{x  =  π }}$ पर फलन ${{f}}$ का निरपेक्ष निम्नतम मान ${{ -  1}}$ है।

(iii) ${{f (x)  =  4x  -  }}\dfrac{{{1}}}{{{2}}}{{{x}}^{{2}}}{{,  x}} \in \left[ { - \,\,2,\,\,\dfrac{9}{2}} \right]$

उत्तर: ${{f (x)  =  4x  -  }}\dfrac{{{1}}}{{{2}}}{{{x}}^{{2}}}$

$\Rightarrow {{f '(x)  =  4  -  x}}$

अब, ${{f '(x)  =  0}} \Rightarrow {{4  -  x  =  0}} \Rightarrow {{x  =  4}}$

यहाँ, केवल ${{x  =  4}}$  ही क्रांतिक बिंदु है।क्रांतिक बिंदु ${{x  =  4}}$ तथा अन्तराल के अंत्य बिन्दुओं ${{x  =-  2}}$ और $\dfrac{{{9}}}{{{2}}}$ पर,

फलन ${{f}}$ के मान का परिकलन करने पर

${{f (4)  =  4(4)  -  }}\dfrac{{{1}}}{{{2}}}{{{(4)}}^{{2}}}{{  =  16  -  8  =  8}}$  

${{f (  -  2)  =  4(  -  2)  -  }}\dfrac{{{1}}}{{{2}}}{{{(  -  2)}}^{{2}}}{{  =-  8  -  2  =-  10}}$  

${{f }}\left( {\dfrac{{{9}}}{{{2}}}} \right){{  =  4}}\left( {\dfrac{{{9}}}{{{2}}}} \right){{  -  }}\dfrac{{{1}}}{{{2}}}{\left( {\dfrac{{{9}}}{{{2}}}} \right)^{{2}}}{{  =  18  -  }}\dfrac{{{{81}}}}{{{8}}}{{  =  18  -  10}}{{.125  =  7}}{{.875}}$ 

इस प्रकार, ${{x  =  4}}$ पर फलन ${{f}}$ का निरपेक्ष उच्चतम मान 8 है और ${{x  =-  2}}$ पर फलन ${{f}}$ का निरपेक्ष निम्नतम मान $ - 10$

(iv) ${{f (x)  =  (x  -  1}}{{{)}}^{{2}}}{{  +  3,  x}} \in [ - \,3,\,1]$

उत्तर: ${{f (x)  =  (x  -  1}}{{{)}}^{{2}}}{{  +  3}}$

$\Rightarrow {{f '(x)  =  2(x  -  1)}}$

अब, ${{f (x)  =  0}} \Rightarrow {{2(x  -  1)  =  0}} \Rightarrow {{x  =  1}}$

यहाँ, केवल ${{x  =  1}}$ ही क्रांतिक बिंदु है।क्रांतिक बिंदु ${{x  =  1}}$ तथा अन्तराल के अंत्य बिन्दुओं ${{x  =-  3}}$ और ${{x  =  1}}$ पर, फलन ${{f}}$ के मान का परिकलन करने पर

${{f (1)  =  (1  -  1}}{{{)}}^{{2}}}{{  +  3  =  3}}$  

${{f ( -  3)  =  ( -  3  -  1}}{{{)}}^{{2}}}{{  +  3  =  16  +  3  =  19}}$ 

इस प्रकार, ${{x  =-  3}}$ पर फलन ${{f}}$ का निरपेक्ष उच्चतम मान ${{19}}$ है और ${{x  =  1}}$ पर फलन का निरपेक्ष निम्नतम मान ${{3}}$ है।

6. यदि लाभ फलन ${{p (x)  =  41  -  72x  -  18}}{{{x}}^{{2}}}$ से प्रदत्त है तो किसी कंपनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।

उत्तर: ${{p (x)  =  41  -  72x  -  18}}{{{x}}^{{2}}}$

$\Rightarrow {{p'(x)  =-  72  -  36x}}$

अब, ${{p'(x)  =  0}} \Rightarrow {{ -  72  -  36x  =  0}} \Rightarrow {{x  =-  2}}$

अब, ${{p''(x)  =-  36}}$

${{x}} =  - 2$केलिए, ${{p''( -  2)  =-  36  <  0}}$

यहाँ, ${{p''(  -  2)  <  0}}$है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x}} =  - 2$ स्थानीय उच्चतम बिंदु है और ${{p}}$ का स्थानीय

उच्चतम मान ${{p (  -  2)  =  41  -  72  \times  (  -  2)  -  18( -  2}}{{{)}}^{{2}}}{{  =  31}}$है। अतः, कंपनी द्वारा अर्जित उच्चतम लाभ ${{31}}$ है।

7. अंतराल $[0,3]$ पर ${{3}}{{{x}}^{{4}}}{{  -  8}}{{{x}}^{{3}}}{{  +  12}}{{{x}}^{{2}}}{{  -  48x  +  25}}$ के उच्चतम मान ओर निम्नतम मान ज्ञात कीजिए।

उत्तर: ${{3}}{{{x}}^{{4}}}{{  -  8}}{{{x}}^{{3}}}{{  +  12}}{{{x}}^{{2}}}{{  -  48x  +  25}}$

$\Rightarrow {{f '(x)  =  12}}{{{x}}^{{3}}}{{  -  24}}{{{x}}^{{2}}}{{  +  24x  -  48}}$

अब, ${{f '(x)  =  0}}$

$\Rightarrow {{12}}{{{x}}^{{3}}}{{  -  24}}{{{x}}^{{2}}}{{  +  24x  -  48  =  0}} \Rightarrow {{12}}\left( {{{{x}}^{{2}}}{{  +  2}}} \right){{ (x  -  2)  =  0}} \Rightarrow {{x  =  2}}$

यहाँ, केवल ${{x  =  2}}$ ही क्रांतिक बिंदु है। क्रांतिक बिंदु ${{x  =  2}}$ तथा अन्तराल के अंत्य बिन्दुओं ${{x  =  0}}$ और ${{x  =  3}}$ पर, फलन ${{f}}$ के मान का परिकलन करने पर

${{f (2 ) =  3(2}}{{{)}}^{{4}}}{{  -  8(2}}{{{)}}^{{3}}}{{  +  12(2}}{{{)}}^{{2}}}{{  -  48(2)  +  25  =-  39}}$  

${{f (0)  =  3(0}}{{{)}}^{{4}}}{{  -  8(0}}{{{)}}^{{3}}}{{  +  12(0}}{{{)}}^{{2}}}{{  -  48(0)  +  25  =  25}}$  

${{f (3)  =  3(3}}{{{)}}^{{4}}}{{  -  8(3}}{{{)}}^{{3}}}{{  +  12(3}}{{{)}}^{{2}}}{{  -  48(3)  +  25  =  16}}$

इस प्रकार, ${{x  =  0}}$पर फलन ${{f}}$ का उच्चतम मान ${{25}}$ है और ${{x  =  2}}$ पर फलन ${{f}}$ का निम्नतम मान ${{  -  39}}$ है।

8. अंतराल ${{[0, 2π ]}}$ के किन बिंदुओं पर फलन ${{sin 2x}}$ अपना उच्चतम मान प्राप्त करता है?

उत्तर: ${{f}}\left( {{x}} \right){{  =  sin 2x}}$

$\Rightarrow {{f '}}\left( {{x}} \right){{  =2cos 2x}}$

अब ${{f ''}}\left( {{x}} \right){{  =  0 }}$

$\Rightarrow {{2 cos 2x  =  0}} \Rightarrow {{2x  =  }}\dfrac{{{π }}}{{{2}}}{{, }}\dfrac{{{{3π }}}}{{{2}}}{{, }}\dfrac{{{{5π }}}}{{{2}}}{{, }}\dfrac{{{{7π }}}}{{{2}}} \Rightarrow {{x  =  }}\dfrac{{{π }}}{{{4}}}{{, }}\dfrac{{{{3π }}}}{{{4}}}{{, }}\dfrac{{{{5π }}}}{{{4}}}{{, }}\dfrac{{{{7π }}}}{{{4}}}$

यहाँ, ${{x  =  }}\dfrac{{{π }}}{{{4}}}{{, }}\dfrac{{{{3π }}}}{{{4}}}{{, }}\dfrac{{{{5π }}}}{{{4}}}{{, }}\dfrac{{{{7π }}}}{{{4}}}$ क्रांतिक बिंदु हैं।क्रांतिक बिन्दुओं तथा अन्तराल के अंत्य बिन्दुओं ${{x  =  0}}$और ${{x  =  2π }}$ पर, फलन ${{f}}$के मान का परिकलन करने पर

${{f (0)  =  sin 2  \times  0  =  sin 0  =  0}}$  

${{f }}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  =  sin 2}}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  =  sin }}\dfrac{{{π }}}{{{2}}}{{  =  1}}$  

${{f }}\left( {\dfrac{{{{3π }}}}{{{4}}}} \right){{  =  sin 2}}\left( {\dfrac{{{{3π }}}}{{{4}}}} \right){{  =  sin }}\dfrac{{{{3π }}}}{{{2}}}{{  =-  1}}$  

${{f }}\left( {\dfrac{{{{5π }}}}{{{4}}}} \right){{  =  sin 2}}\left( {\dfrac{{{{5π }}}}{{{4}}}} \right){{  =  sin }}\dfrac{{{{5π }}}}{{{2}}}{{  =  1}}$  

${{f }}\left( {\dfrac{{{{7π }}}}{{{4}}}} \right){{  =  sin 2}}\left( {\dfrac{{{{7π }}}}{{{4}}}} \right){{  =  sin }}\dfrac{{{{7π }}}}{{{2}}}{{  =-  1}}$  

${{f (2π )  =  sin 2(2π )  =  sin 4π=  0}}$

इस प्रकार, ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ और ${{x  =  }}\dfrac{{{{5π }}}}{{{4}}}$ पर फलन ${{f}}$ का उच्चतम ${{1}}$ मान है 

9. फलन ${{sin x  +  cos x}}$ का उच्चतम मान क्या है?

उत्तर: ${{f }}\left( {{x}} \right){{  =  sin x  +  cos x}}$

$\Rightarrow {{f '(x)  =  cos x  -  sin x}}$

अब, ${{f '(x)  =  0}}$

$\Rightarrow {{cos x  -  sin x  =  0}} \Rightarrow {{tan x  =  1}} \Rightarrow {{x  =  }}\dfrac{{{π }}}{{{4}}}{{, }}\dfrac{{{{5π }}}}{{{4}}}{{, \ldots  \ldots }}$

यहा, ${{x  =  }}\dfrac{{{π }}}{{{4}}}{{, }}\dfrac{{{{5π }}}}{{{4}}}{{, \ldots  \ldots }}$ क्रांतिक बिंदु हैं।क्रांतिक बिन्दुओं तथा अन्तराल के अंत्य बिन्दुओं ${{x  =  0}}$  और ${{x  =  2π }}$ पर, फलन ${{f}}$ के मान का परिकलन करने पर

${{f (0)  =  sin 0  +  cos 0  =  0  +  1  =  1}}$  

${{f }}\left( {\dfrac{{{π }}}{{{4}}}} \right){{  =  sin }}\dfrac{{{π }}}{{{4}}}{{  +  cos }}\dfrac{{{π }}}{{{4}}}{{  =  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  +  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =  }}\sqrt {{2}} $  

${{f }}\left( {\dfrac{{{{5π }}}}{{{4}}}} \right){{  =  sin }}\dfrac{{{{5π }}}}{{{4}}}{{  +  cos }}\dfrac{{{{5π }}}}{{{4}}}{{  =-  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  -  }}\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =-  }}\dfrac{{{2}}}{{\sqrt {{2}} }}{{  =-  }}\sqrt {{2}} $  

${{f (2π )  =  sin 2π+  cos 2π=  0  +  1  =  1}}$

इस प्रकार, ${{x  =  }}\dfrac{{{π }}}{{{4}}}$ पर फलन ${{f}}$ का उच्चतम मान $\sqrt {{2}} $ है।

10. अंतराल ${{[1, 3]}}$ में ${{2}}{{{x}}^{{3}}}{{  -  24x  +  107}}$  का महत्तम मान ज्ञात कीजिए ।इसी फलन का अंतराल ${{[  -  3,  -  1]}}$ में भी महत्तम मान ज्ञात कीजिए।

उत्तर: ${{f}}\left( {{x}} \right){{  =  2}}{{{x}}^{{3}}}{{  -  24x  +  107}}$

$\Rightarrow {{f '(x)  =  6}}{{{x}}^{{2}}}{{  -  24}}$

अब ${{f '(x)  =  0}}$

$\Rightarrow {{6}}{{{x}}^{{2}}}{{  -  24  =  0}} \Rightarrow {{x  =\pm  2}}$

यहाँ, ${{x  =  2}}$क्रांतिक बिंदु (क्योंकि ${{ -  2}} \notin {{[1, 3]}}$  हैं।क्रांतिक बिन्दुओं तथा अन्तराल के अंत्य बिन्दुओं ${{x  =  1}}$ और 

${{x  =  3}}$ पर, फलन ${{f}}$ के मान का परिकलन करने पर

${{f (1)  =  2(1}}{{{)}}^{{3}}}{{  -  24(1)  +  107  =  2  -  24  +  107  =  85}}$  

${{f (2)  =  2(2}}{{{)}}^{{3}}}{{  -  24(2)  +  107  =  16  -  48  +  107  =  75}}$  

${{f (3)  =  2(3}}{{{)}}^{{3}}}{{  -  24(3)  +  107  =  54  -  72  +  107  =  89}}$

इस प्रकार, ${{x  =  3}}$ पर फलन ${{f}}$ का उच्चतम मान ${{89}}$ है।

अब, अंतराल ${{[1, 3]}}$ के लिए,

यहाँ, ${{x  =-  2}}$ क्रांतिक बिंदु (क्योंकि ${{ -  2}} \notin {{[1, 3]}}$  हैं।क्रांतिक बिन्दुओं तथा अन्तराल के अंत्य बिन्दुओं ${x = - 1}$ और

${x = -  3}$ पर, फलन ${f}$ के मान का परिकलन करने पर

${{f ( -  1)  =  2( -  1}}{{{)}}^{{3}}}{{ -  24( -  1)  +  107  =-  2  +  24  +  107  =  129}}$  

${{f ( -  2)  =  2( -  2}}{{{)}}^{{3}}}{{ -  24( -  2)  +  107  =  16  -  48  +  107  =  139}}$  

${{f ( -  3)  =  2( -  3}}{{{)}}^{{3}}}{{  -  24(  -  3)  +  107  =  54  -  72  +  107  =  125}}$

इस प्रकार, ${x = - 2}$ पर फलन ${f}$ का उच्चतम मान ${139}$ है।

11. यदि दिया है कि अंतराल $[0,2]$ में ${{x  =  1}}$ पर फलन ${{{x}}^{{4}}}{{  -  62}}{{{x}}^{{2}}}{{  +  ax  +  9}}$

 उच्चतममानप्राप्त करता है, तो ${{a}}$ का मान ज्ञात कीजिए।

उत्तर: ${{f (x)  =  }}{{{x}}^{{4}}}{{  -  62}}{{{x}}^{{2}}}{{  +  ax  +  9}}$

$\Rightarrow {{f '(x)  =  4}}{{{x}}^{{3}}}{{  -  124x  +  a}}$

दिया है कि अंतराल $[0,2]$ में ${{x  =  1}}$ पर फलन उच्चतम मान प्राप्त करता है।

$\Rightarrow {{f '(1)  =  4(1}}{{{)}}^{{3}}}{{  -  124(1)  +  a}} \Rightarrow {{a  =  120}}$

अतः, ${{a}}$ का मान ${{120}}$ है।

12. ${{[0,2π ]}}$ पर ${{x  +  sin 2x}}$का उच्चतम और निम्नतम मान ज्ञात कीजिए।

उत्तर: ${{f (x)  =  x  +  sin 2x}}$

$\Rightarrow {{f '(x)  =  x  +  2 cos 2x}}$

 अब, ${{f '(x)  =  0}}$

${{1  +  2 cos 2x  =  0}} \Rightarrow {{cos 2x  =-  }}\dfrac{{{1}}}{{{2}}}{{  =  cos}}\dfrac{{{{2π }}}}{{{3}}}$

$\Rightarrow {{2x  =  2nπ\pm  }}\dfrac{{{{2π }}}}{{{3}}}{{, n}} \in {{Z}}$  

${{x  =  nπ\pm  }}\dfrac{{{π }}}{{{3}}} \Rightarrow {{x  =  }}\dfrac{{{π }}}{{{3}}}{{, }}\dfrac{{{{2π }}}}{{{3}}}{{, }}\dfrac{{{{4π }}}}{{{3}}}{{,}}\dfrac{{{{5π }}}}{{{3}}} \in {{[0,2π ]}}$

यहाँ ${{x  =  }}\dfrac{{{π }}}{{{3}}}{{, }}\dfrac{{{{2π }}}}{{{3}}}{{, }}\dfrac{{{{4π }}}}{{{3}}}{{,}}\dfrac{{{{5π }}}}{{{3}}}$ क्रांतिक बिंदु है 

क्रांतिक बिंदु तथा अन्तराल के अंत्य बिन्दुओं ${{x  =  0}}$ और ${{x  =  2π }}$ पर, फलन ${{f}}$ के मान का परिकलन करने पर

${{f (0)  =  0  +  sin 2(0)  =  0  +  0  =  0}}$  

${{f }}\left( {\dfrac{{{π }}}{{{3}}}} \right){{  =  }}\dfrac{{{π }}}{{{3}}}{{  +  sin 2}}\left( {\dfrac{{{π }}}{{{3}}}} \right){{  =  }}\dfrac{{{π }}}{{{3}}}{{  +  }}\dfrac{{\sqrt {{3}} }}{{{2}}}$  

${{f }}\left( {\dfrac{{{{2π }}}}{{{3}}}} \right){{  =  }}\dfrac{{{{2π }}}}{{{3}}}{{  +  sin 2}}\left( {\dfrac{{{{2π }}}}{{{3}}}} \right){{  =  }}\dfrac{{{{2π }}}}{{{3}}}{{  -  }}\dfrac{{\sqrt {{3}} }}{{{2}}}$  

${{f }}\left( {\dfrac{{{{4π }}}}{{{3}}}} \right){{  =  }}\dfrac{{{{4π }}}}{{{3}}}{{  +  sin 2}}\left( {\dfrac{{{{4π }}}}{{{3}}}} \right){{  =  }}\dfrac{{{{4π }}}}{{{3}}}{{  +  }}\dfrac{{\sqrt {{3}} }}{{{2}}}$  

${{f}}\left( {\dfrac{{{{5π }}}}{{{3}}}} \right){{  =  }}\dfrac{{{{5π }}}}{{{3}}}{{  +  sin 2}}\left( {\dfrac{{{{5π }}}}{{{3}}}} \right){{  =  }}\dfrac{{{{5π }}}}{{{3}}}{{  -  }}\dfrac{{\sqrt {{3}} }}{{{2}}}$  

${{f (2π )  =  2π+  sin 2π=  2π+  0  =  2π }}$

इस प्रकार ${{x  =  2π }}$ पर फलन ${{f}}$ का उच्चतम मान ${{2π }}$ है और ${{x  =  0}}$ पर ${{f}}$ का निम्नतम मान ${{0}}$ है 

13. ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग ${\mathbf{24}}$ है और जिनका गुणन फल उच्चतम हो।

उत्तर: माना, दो संख्याएँ ${{x}}$ और ${{y}}$ हैं।

${{x  +  y  =  24}} \Rightarrow {{y  =  24 x}}.............{{(1)}}$

गुणनफल ${{p  =  xy}}$

$\Rightarrow {{P  =  x (24  -  x)  =  24x  -  }}{{{x}}^{{2}}}$ [समीकरण (1) से मान रखने पर] 

$\Rightarrow {{P '(x)  =  24  -  2x}}$

अब, ${{P '(x)  =  0}} \Rightarrow {{24  -  2x  =  }}0\, \Rightarrow {{x  =  12}}$

${{P ''(x)  =-  2}}$

${{x  =  12}}$के लिए, ${{P''(12)  =-  2  <  0}}$

यहाँ, ${{P''(12)  <  0}}$है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  12}}$ स्थानीय उच्चतम बिंदु है।

समीकरण (1) से, ${{y  =  24  -  12  =  12}}$

अतः, संख्याओं ${{x}}$ और ${{y}}$ के मान क्रमशः ${{12}}$ और ${{12}}$ हैं।

14. ऐसी दो धन संख्याएँ ${{x}}$ और ${{y}}$ ज्ञात कीजिए ताकि ${{x  +  y  =  60}}$ और ${{x}}{{{y}}^{{3}}}$ उच्चतम हो।

उत्तर: ${{x  +  y  =  60}} \Rightarrow {{y  =  60  -  x \ldots  \ldots }}{{.(1)}}$

माना ${{P  =  x}}{{{y}}^{{3}}}$

$\Rightarrow {{P  =  x (60  -  x}}{{{)}}^{{3}}}$[समीकरण (1) से मान रखने पर]

$\Rightarrow {{P'(x)  =  0  -  3x (60  -  x}}{{{)}}^{{2}}}{{  +  (60  -  x}}{{{)}}^{{3}}}$  

${{ =  (60  -  x}}{{{)}}^{{2}}}{{(  -  3x  +  60  -  x)  =  (60  -  x}}{{{)}}^{{2}}}{{(60  -  4x)}}$

अब, ${{P'(x)  =  0}}$

$\Rightarrow {{{(60  -  x)}}^{{2}}}{{(60  -  4x)  =  0}} \Rightarrow {{x  =  15}}$या ${{60}}$

[${{x}} \ne 60$, क्योंकि यदि ${{x  =  60}}$ तो ${{y  =  60  -  60  =  0}}$ होगा।परन्तु दिया गया है कि ${{y}}$ एक धन संख्या है।

अब, ${{P''(x)  -  4(60  -  x}}{{{)}}^{{2}}}{{  -  2(60  -  4x) (60  -  x)  =-  2(60  -  x) (180  -  6x)}}$

${{x  =  15}}$ के लिए, $\Rightarrow {{ -  2(60  -  15)(180  -  90)  =-  8100  <  0}}$

यहाँ, ${{{P}}^{\prime \prime }}(15) < 0$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  15}}$ स्थानीय उच्चतम बिंदु है।

समीकरण (1) से, ${{y  =  60  -  15  =  45}}$

अतः, संख्याओं ${{x}}$ और ${{y}}$ के मान क्रमशः ${{15}}$ और $45$ हैं।

15. ऐसी दो धन संख्याएँ ${{x}}$ और ${{y}}$ ज्ञात कीजिए जिनका योग ${{35}}$ हो और गुणन फल ${{{x}}^{{2}}}{{{y}}^{{5}}}$ उच्चतम हो।

उत्तर: ${{x  +  y  =  35}}...............{{(1)}}$

माना ${{P  =  }}{{{x}}^{{2}}}{{{y}}^{{5}}} \Rightarrow {{P  =  }}{{{x}}^{{2}}}{{{(35  -  x)}}^{{5}}}$ [समीकरण (1) से मान रखने पर ].

$\Rightarrow {{P'(x)  =  2x (35  -  x}}{{{)}}^{{5}}}{{  -  5}}{{{x}}^{{2}}}{{{(35  -  x)}}^{{4}}}$  

${{ =  x (35  -  x}}{{{)}}^{{4}}}{{(70  -  2x  -  5x)}}$  

${{ =  x (35  -  x}}{{{)}}^{{4}}}{{(70  -  7x)}}$

अब, ${{P'(x)  =  0}}$

$\Rightarrow {{x(35  -  x}}{{{)}}^{{4}}}{{(70  -  7x)  =  }}0 \Rightarrow {{x  =  0, 10, 35}}$

${{x}} \ne {{ }}0$,${{x}} \ne {{ 35}}$, क्योंकि यदि ${{x  =  35}}$ तो ${{y  =  35  -  35  =  0}}$ होगा।परन्तु दिया गया है कि ${{y}}$ एक धन संख्या है।

अब, ${{P''(x)  =  (35  -  x}}{{{)}}^{{4}}}{{(70  -  7x)  -  4x (35  -  x}}{{{)}}^{{3}}}{{(70  -  7x)  -  7x(35  -  x}}{{{)}}^{{4}}}$

${{x  =  10}}$के लिए,

$\Rightarrow {{{(35  -  10)}}^{{4}}}{{(70  -  70)  -  40 (35  -  10}}{{{)}}^{{3}}}{{(70  -  70)  -  70(35  -  10}}{{{)}}^{{4}}}{{  =-  70 (25}}{{{)}}^{{4}}}{{  <  0}}$

यहाँ, ${{{P}}^{\prime \prime }}(10) < 0$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  10}}$ स्थानीय उच्चतम बिंदु है।

समीकरण (1) से, ${{y  =  35  -  10  =  25}}$

अतः संख्याओं ${{x}}$ और ${{y}}$ के मान क्रमशः ${{10}}$ और ${{ 25}}$ हैं।

16. ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग ${{16}}$ हो और जिनके घनों का योग निम्नतम हो।

उत्तर: माना, दो संख्याएँ ${{x}}$ और ${{y}}$ हैं।

${{x  +  y  =  16}} \Rightarrow {{y  =  16  -  x}}.......................{{(1)}}$

घनों का योग ${{P  =  }}{{{x}}^{{3}}}{{  +  }}{{{y}}^{{3}}}$

$\Rightarrow {{P  =  }}{{{x}}^{{3}}}{{  +  (16  -  x}}{{{)}}^{{3}}}$[समीकरण (1) से मान रखने पर]

$\Rightarrow {{P '(x)  =  3}}{{{x}}^{{2}}}{{  -  3(16  -  x}}{{{)}}^{{2}}}{{  =  3}}{{{x}}^{{2}}}{{  -  3}}\left( {{{256  +  }}{{{x}}^{{2}}}{{  -  32x}}} \right)$  

${{ =  96x  -  768}}$

अब, ${{P '(x)  =  0}} \Rightarrow {{96x  -  768  =  0}} \Rightarrow {{x  =  8}}$

$\Rightarrow {{{P}}^{\prime \prime }}({{x}}) = 96 > 0$

${{x  =  8}}$के लिए

$\Rightarrow {{{P}}^{\prime \prime }}({{x}}) = 96 > 0$

यहाँ, ${{P ''(8)  >  0}}$है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  8}}$स्थानीय निम्नतम बिंदु है।

समीकरण (1) से, ${{y  =  16  -  8  =  8}}$

अतः, संख्याओं ${{x}}$ और ${{y}}$ के मान क्रमशः ${{8}}$ और ${{8}}$ हैं।

17. ${{18cm}}$ भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बनेंटिन के फलकों को मोड़कर

ढक्कन रहित एक संदूक बनाना है।काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम हो?

उत्तर: माना, कोने पर कटे गए वर्ग की भुजा ${{ =  xcm}}$

इसलिए, संदूक की लम्बाई${{ =  18  -  2x cm}}$, संदूक की चौड़ाई ${{ =  18  -  2x cm}}$ तथा 

ऊँचाई ${{ =  xcm}}$

आयतन ${{V  =  x(18  -  2  \times  x)(18  -  2x)  =  x(18  -  2x}}{{{)}}^{{2}}}$

$\Rightarrow {{V '(x)  =  (18  -  2x}}{{{)}}^{{2}}}{{  -  4x (18  -  2x)  =  (18  -  2x)(18  -  6x)}}$है।

अब, ${{V '(x)  =  0}} \Rightarrow {{(18  -  2x)(18  -  6x)  =  0}} \Rightarrow {{x  =  9, 3}}$

[${{x}} \ne 9$, क्योंकि यदि ${{x  =  9}}$ तो लम्बाई $ = 18 - 18 = 0$ होगी, जो संभव नहीं है।]

${{V ''(x)  =-  2(18  -  6x)  -  6(18  -  2x)}}$

${{x  =  3}}$ के लिए, ${{V ''(3)  =-  2(18  -  6  \times  3)  -  6(18  -  6)  =-  72  <  0}}$

यहाँ, ${{V ''(3)  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  3}}$ स्थानीय उच्चतम बिंदु है 

अतः, काटे जाने वाले वर्ग की भुजा ${{3cm}}$ होगी।

18. ${{45cm  \times  24cm}}$की टिन की आयताकार चादर के कोनों पर वर्ग काटकर तथा इस प्रकार बनेंटिन के फलकों को मोड़कर ढक्कन रहित एक संदूक बनाना है काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम हो।

उत्तर: माना, कोने पर कटे गए वर्ग की भुजा ${{ =  xcm}}$

इसलिए, संदूक की लम्बाई ${{ =  45  -  2x cm,}}$ संदूक की चौड़ाई ${{ =  24  -  2x cm}}$ तथा ऊँचाई ${{ =  xcm}}$

आयतन ${{V  =  x(45  -  2x) (24  -  2x)  =  }}\left( {{{45x  -  2}}{{{x}}^{{2}}}} \right){{(24  -  2x)}}$है।

$\Rightarrow {{V '(x)  =  (45  -  4x) (24  -  2x)  -  2}}\left( {{{45x  -  2}}{{{x}}^{{2}}}} \right)$

अब, ${{V '(x)  =  0}} \Rightarrow {{(45  -  4x)(24  -  2x)  -  2}}\left( {{{45x  -  2}}{{{x}}^{{2}}}} \right){{  =  0}}$

$\Rightarrow {{1080  -  186x  +  8}}{{{x}}^{{2}}}{{  -  90x  +  4}}{{{x}}^{{2}}}{{  =  0}}$  

$\Rightarrow {{12}}\left( {{{{x}}^{{2}}}{{  -  23x  +  90}}} \right){{  =  0}}$  

$\Rightarrow {{12(x  -  18) (x  -  5)  =  0}}$  

$\Rightarrow {{x  =  18, 5}}$

[${{x}} \ne 18\,,$क्योंकि यदि ${{x  =  18}}$ तो चौड़ाई ${{ =  24  -  36  =-  12}}$होगी, जो संभव नहीं है।]

अब, ${{V ''(x)  =  12(x  -  5)  +  12(x  -  18)}}$

${{x  =  5}}$ के लिए, ${{V ''(5)  =  12(5  -  5)  +  12(5  -  18)  =-  156  <  0}}$

यहाँ, ${{V ''(5)  <  0}}$है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  5}}$ स्थानीय उच्चतम बिंदुहै।

अतः, काटे जाने वाले वर्ग की भुजा $5{{cm}}$ होगी।

19. सिद्ध किजिए कि एक दिए वृत्त के अंतर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।

उत्तर: माना ${{ABCD}}$एक आयत है, वृत्त ${{C(0,r)}}$के अंतर्गत स्थित है। माना, आयत की लंबाई ${{ =  x}}$ तथा चौड़ाई ${{ =  y}}$ है।

त्रिभुज ${{BCD}}$ में,

${{{x}}^{{2}}}{{  +  }}{{{y}}^{{2}}}{{  =  (2r}}{{{)}}^{{2}}} \Rightarrow {{{y}}^{{2}}}{{  =  4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}} \Rightarrow {{y  =  }}\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} $

आयत का क्षेत्रिफल 

${{ =  A  =  xy  =  x }}\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} $  

${{A'(x)  =  }}\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} {{  +  xX}}\dfrac{{{1}}}{{\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} }}{{X(  -  2x)  =  }}\dfrac{{{{4}}{{{r}}^{{2}}}{{  -  2}}{{{x}}^{{2}}}}}{{\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} }}$

अब, ${{A'(x)  =  0}}$

$\Rightarrow \dfrac{{{{4}}{{{r}}^{{2}}}{{  -  2}}{{{x}}^{{2}}}}}{{\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} }}{{  =  0}} \Rightarrow {{4}}{{{r}}^{{2}}}{{  -  2}}{{{x}}^{{2}}}{{  =  0}} \Rightarrow {{{x}}^{{2}}}{{  =  2}}{{{r}}^{{2}}} \Rightarrow {{x  =  }}\sqrt {{2}} {{r}}$

${{A''(x)  =  }}\dfrac{{\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} {{( -  4x)  -  }}\left( {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} \right){{X}}\dfrac{{{1}}}{{\sqrt {{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}} }}{{X(  -  2x)}}}}{{{{4}}{{{r}}^{{2}}}{{  -  }}{{{x}}^{{2}}}}}$

${{x  =  5}}$ के लिए  ${{A''(}}\sqrt {{2}} {{r)}}$

$\Rightarrow {{ -  }}\dfrac{{{{4}}\sqrt {{2}} \sqrt {{{2}}{{{r}}^{{2}}}} }}{{{{2}}{{{r}}^{{2}}}}}{{  =-  4  <  0}}$

यहाँ ${{A''(}}\sqrt {{2}} {{r)  <  0 }}$ है इसलिए द्वितीय अवकल परीक्षण द्वारा, ${{x  =  }}\sqrt {{2}} {{r}}$ स्थानीय उच्चतम बिन्दु है 

यदि  ${{x  =  }}\sqrt {{2}} {{r}}$ तो ${{ y  =  }}\sqrt {{{4}}{{{r}}^{{2}}}{{  -  (}}\sqrt {{2}} {{r}}{{{)}}^{{2}}}} {{  =  }}\sqrt {{{4}}{{{r}}^{{2}}}{{  -  2}}{{{r}}^{{2}}}} {{  =  }}\sqrt {{{2}}{{{r}}^{{2}}}} {{  =  }}\sqrt {{{2r}}} $

यहाँ ${{x  =  y}}$ है, इसलिए ${{ABCD}}$ वर्ग है 

20. सिद्ध किजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई, आधार के व्यास के बराबर होती है।

उत्तर: माना बेलन के ऊँचाई तथा त्रिज्या क्रमशः ${{h}}$ और ${{r}}$ हैं। 

इसलिए, बेलन का पृष्ठ क्षेत्रफल ${{S  =  2π }}{{{r}}^{{2}}}{{  +  2π rh }}$

$\Rightarrow {{h  =  }}\dfrac{{{{S  -  2π }}{{{r}}^{{2}}}}}{{{{2π r}}}}$

अतः, बेलन का आयतन

${{V  =  π }}{{{r}}^{{2}}}{{h  =  π }}{{{r}}^{{2}}}\left( {\dfrac{{{{S  -  2π }}{{{r}}^{{2}}}}}{{{{2π r}}}}} \right){{  =  }}\dfrac{{{1}}}{{{2}}}\left( {{{Sr  -  2π }}{{{r}}^{{3}}}} \right)$  

$\Rightarrow {{V '(r)  =  }}\dfrac{{{1}}}{{{2}}}\left( {{{S  -  6π }}{{{r}}^{{2}}}} \right)$

अब, ${{V '(r)  =  0}}$

${{  =  }}\dfrac{{{1}}}{{{2}}}\left( {{{S  -  6π }}{{{r}}^{{2}}}} \right){{  =  0}} \Rightarrow {{S  -  6π }}{{{r}}^{{2}}}{{  =  0}}$  

$\Rightarrow {{{r}}^{{2}}}{{  =  }}\dfrac{{{S}}}{{{{6π }}}} \Rightarrow {{r  =  }}\sqrt {\dfrac{{{S}}}{{{{6π }}}}} $  

$\Rightarrow {{V ''(r)  =  }}\dfrac{{{1}}}{{{2}}}{{(0  -  12π r)}}$

${{r  =  }}\sqrt {\dfrac{{{s}}}{{{{6π }}}}} {{ }}$के लिए 

${{V ''}}\left( {\sqrt {\dfrac{{{s}}}{{{{6π }}}}} } \right){{  =-  6π }}\sqrt {\dfrac{{{s}}}{{{{6π }}}}} {{  =-  }}\sqrt {{{6π S}}} {{  <  0}}$

यहाँ, ${{V ''}}\left( {\sqrt {\dfrac{{{s}}}{{{{6π }}}}} } \right){{  <  0}}$इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{r  =  }}\sqrt {\dfrac{{{s}}}{{{{6π }}}}} {{ }}$स्थानीय उच्चतम बिंदु है।

यदि, ${{r  =  }}\sqrt {\dfrac{{{s}}}{{{{6π }}}}} {{ }}$

${{h  =  }}\dfrac{{{{S  -  2π }}{{{r}}^{{2}}}}}{{{{2π r}}}}{{  =  }}\dfrac{{{{S  -  2π  }} \times {{ }}\dfrac{{{S}}}{{{{6π }}}}}}{{{{2π }}\sqrt {\dfrac{{{S}}}{{{{6π }}}}} }}{{  =  }}\dfrac{{\dfrac{{{{2S}}}}{{{3}}}}}{{\sqrt {\dfrac{{{{2Sπ }}}}{{{3}}}} }}{{  =  }}\sqrt {\dfrac{{{{2S}}}}{{{{3π }}}}} {{  =  2}}\sqrt {\dfrac{{{S}}}{{{{6π }}}}} $  

$\Rightarrow {{h  =  2r}}$

21. ${{100c}}{{{m}}^{{3}}}$आयतन वाले डिब्बे सभी बंद बेलना कार (लंब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात किजिए।

उत्तर: माना बेलन के ऊँचाई तथा त्रिज्या क्रमशः ${{h }}$और ${{r}}$ हैं। 

अतः, बेलन का आयतन ${{V  =  π }}{{{r}}^{{2}}}{{h=  100c}}{{{m}}^{{3}}}$

$\Rightarrow {{h  =  }}\dfrac{{{{100}}}}{{{{π }}{{{r}}^{{2}}}}}$

बेलन का पृष्ठ क्षेत्रफल ${{S  =  2π }}{{{r}}^{{2}}}{{  +  2π rh}}$

$\Rightarrow {{S  =  2π }}{{{r}}^{{2}}}{{  +  2π r}}\left( {\dfrac{{{{100}}}}{{{{π }}{{{r}}^{{2}}}}}} \right){{  =  2π }}{{{r}}^{{2}}}{{  +  }}\dfrac{{{{200}}}}{{{r}}}$

$\Rightarrow {{S'(r)  =  π r  -  }}\dfrac{{{{200}}}}{{{{{r}}^{{2}}}}}$

अब, ${{S'(r)  =  0}}$

$\Rightarrow {{4π r  -  }}\dfrac{{{{200}}}}{{{{{r}}^{{2}}}}}{{  =  0}} \Rightarrow {{4π }}{{{r}}^{{3}}}{{  -  200  =  0}} \Rightarrow {{{r}}^{{3}}}{{  =  }}\dfrac{{{{50}}}}{{{π }}} \Rightarrow {{r  =  }}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$  

$\Rightarrow {{S''(r)  =  4π-  }}\dfrac{{{{400}}}}{{{{{r}}^{{3}}}}}$

${{r  =  }}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$के लिए, 

${{S''}}\left( {{{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)}^{\dfrac{{{1}}}{{{3}}}}}} \right){{  =  4π-  }}\dfrac{{{{400}}}}{{{{50}}}}{{  =  12π>  0}}$

यहाँ ${{S''}}\left( {{{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)}^{\dfrac{{{1}}}{{{3}}}}}} \right){{  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{r  =  }}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$ स्थानीय निम्नतम बिंदु है।

यदि ${{r  =  }}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$

$\Rightarrow {{h  =  }}\dfrac{{{{100}}}}{{{{π }}{{\left( {\left( {{{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)}^{\dfrac{{{1}}}{{{3}}}}}} \right)} \right)}^{{2}}}}}{{  =  }}{\left[ {\dfrac{{{{100  \times  100  \times  100  \times  }}{{{π }}^{{2}}}}}{{{{{π }}^{{3}}} \times {{ 50 }} \times {{ 50}}}}} \right]^{\dfrac{{{1}}}{{{3}}}}}$  

${{ =  }}{\left[ {\dfrac{{{{4000}}}}{{{π }}}} \right]^{\dfrac{{{1}}}{{{3}}}}}{{  =  2}}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$

अतः, न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ${{r  =  }}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$

और ${{h  =  2}}{\left( {\dfrac{{{{50}}}}{{{π }}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$ हैं।

22. एक ${{28cm}}$ लंबे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे वृत्त बनाया जाना है। दोनों टुकड़ों की लंबायीं

कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?

उत्तर: माना, बनाए गए वर्ग की भुजा ${{x}}$ है तथा वृत्त की त्रिज्या है।

${{4x  +  2π r  =  28}} \Rightarrow {{2x  +  π r  =  14}} \Rightarrow {{x  =  }}\dfrac{{{{14  -  π r}}}}{{{2}}}$

वर्ग और वृत्त का सम्मिलित क्षेत्रफल

${{ =  A  =  }}{{{x}}^{{2}}}{{  +  π }}{{{r}}^{{2}}}$  

$\Rightarrow {{A  =  }}{\left( {\dfrac{{{{14  -  π r}}}}{{{2}}}} \right)^{{2}}}{{  +  π }}{{{r}}^{{2}}}$

$\Rightarrow {{A'(r)  =  2}}\left( {\dfrac{{{{14  -  π }}{{{r}}^{{2}}}}}{{{2}}}} \right)\,\, \times \,\,\left( {{{ -  }}\dfrac{{{π }}}{{{2}}}} \right){{  +  2π r}}$

अब, ${{A'(r)  =  0}}$

$\Rightarrow {{2}}\left( {\dfrac{{{{14  -  π }}{{{r}}^{{2}}}}}{{{2}}}} \right)\,\, \times \,\,\left( {{{ -  }}\dfrac{{{π }}}{{{2}}}} \right){{  +  2π r  =  0}}$  

$\Rightarrow {{ -  }}\dfrac{{{π }}}{{{2}}}{{(14  -  π r)  +  2π r  =  0}} \Rightarrow \dfrac{{{π }}}{{{2}}}{{[  -  14  +  π r  +  4r]  =  0}}$  

$\Rightarrow {{(π+  4)r  =  14}} \Rightarrow {{r  =  }}\dfrac{{{{14}}}}{{{{π+  4}}}}$  

${{A''(r)  =  }}\dfrac{{{π }}}{{{2}}}{{[π+  4]}}$

${{r  =  }}\dfrac{{{{14}}}}{{{{π+  4}}}}$
यहाँ, ${{A''}}\left( {\dfrac{{{{14}}}}{{{{π+  4}}}}} \right){{  >  0}}$ है, इसलिए द्वितीय अवकलज परिक्षण द्वारा, ${{r  =  }}\dfrac{{{{14}}}}{{{{π+  4}}}}$ स्थानीय निम्नतम बिंदु है।

इसलिए, वृत्ताकार टुकड़े की लंबाई ${{ =  2π r  =  }}\dfrac{{{{28π }}}}{{{{π+  4}}}}$

$\Rightarrow {{x  =  }}\dfrac{{{{14  -  π }}\left( {\dfrac{{{{14}}}}{{{{π+  4}}}}} \right)}}{{{2}}}{{  =  }}\dfrac{{{{14π+  56  -  14π }}}}{{{{2(π+  4)}}}}{{  =  }}\dfrac{{{{56}}}}{{{{2(π+  4)}}}}{{  =  }}\dfrac{{{{28}}}}{{{{(π+  4)}}}}$

तथा आयताकार टुकड़े की लंबाई ${{ =  4x  =  4}} \times \dfrac{{{{28}}}}{{{{(π+  4)}}}}{{  =  }}\dfrac{{{{112}}}}{{{{π+  4}}}}$

23. सिद्ध कीजिए कि ${{R}}$ त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन, गोले के आयतन का $\dfrac{{{8}}}{{{{27}}}}$ होता है।

उत्तर: माना, बनाए गए शंकु की ऊँचाई ${{h}}$ तथा त्रिज्या $r$ है। 

इसलिए, त्रिभुज ${{OAM}}$ में,

शंकु का आयतन

${{O}}{{{A}}^{{2}}}{{ =  O}}{{{M}}^{{2}}}{{  +  A}}{{{M}}^{{2}}} \Rightarrow {{{R}}^{{2}}}{{{(h  -  R)}}^{{2}}}{{  +  }}{{{r}}^{{2}}}$  

$\Rightarrow {{{R}}^{{2}}}{{{h}}^{{2}}}{{  +  }}{{{R}}^{{2}}}{{  -  2hR  +  }}{{{r}}^{{2}}}$  

$\Rightarrow {{{r}}^{{2}}}{{  =  2hR  -  }}{{{h}}^{{2}}}$  

${{V  =  }}\dfrac{{{1}}}{{{3}}}{{π }}{{{r}}^{{2}}}{{h}}$  

$\Rightarrow \dfrac{{{1}}}{{{3}}}{{π }}\left( {{{2hR  -  }}{{{h}}^{{2}}}} \right){{h  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{2}}{{{h}}^{{2}}}{{R  -  }}{{{h}}^{{3}}}} \right){{ \ldots  \ldots  \ldots }}..{{ (1)}}$  

$\Rightarrow {{V '(x)  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{4hR  -  3}}{{{h}}^{{2}}}} \right)$

अब, ${{V '}}\left( {{h}} \right){{  =  0}}$

$\Rightarrow \dfrac{{{1}}}{{{3}}}{{π }}\left( {{{4hR  -  3}}{{{h}}^{{2}}}} \right){{  =  0}} \Rightarrow \dfrac{{{1}}}{{{3}}}{{π h(4R  -  3h)  =  0}}$  

$\Rightarrow {{h  =  0, }}\dfrac{{{{4R}}}}{{{3}}}$

 $[{{h}} \ne 0$, क्योंकि ${{h}}$ शंकु की ऊँचाई है, अतः ${{h  =  0}}$ संभव नहीं है।]

अब,

${{V ''(h) =  }}\dfrac{{{1}}}{{{3}}}{{π (4R  -  6h)}}$

${{h  =  }}\dfrac{{{{4R}}}}{{{3}}}$ के लिए

$\Rightarrow {{V ''(h)  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{4R  -  6}}\left( {\dfrac{{{{4R}}}}{{{3}}}} \right)} \right){{  =-  }}\dfrac{{{4}}}{{{3}}}{{π R  <  0}}$

यहाँ, ${{V ''(h)  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{h  =  }}\dfrac{{{{4R}}}}{{{3}}}$  स्थानीय उच्चतम बिंदु है।

समीकरण (1) से

इस उच्चतम बिंदु पर शंकु का आयतन ${{ =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{2}}{{{h}}^{{2}}}{{R  -  }}{{{h}}^{{3}}}} \right)$

${{ =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left[ {{{2}}{{\left( {\dfrac{{{{4R}}}}{{{3}}}} \right)}^{{2}}}{{R  -  }}{{\left( {\dfrac{{{{4R}}}}{{{3}}}} \right)}^{{3}}}} \right]{{  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left[ {\dfrac{{{{32}}{{{R}}^{{3}}}}}{{{9}}}{{  -  }}\dfrac{{{{64}}{{{R}}^{{3}}}}}{{{{27}}}}} \right]$  

${{ =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left[ {\dfrac{{{{32}}{{{R}}^{{3}}}}}{{{{27}}}}} \right]{{  =  }}\dfrac{{{8}}}{{{{27}}}}\left( {\dfrac{{{4}}}{{{3}}}} \right){{π }}{{{R}}^{{3}}}{{  =  }}\dfrac{{{8}}}{{{{27}}}}$

24. सिद्ध कीजिए कि न्यूनतम पृष्ठ का दिए आयतन के लंबवृत्तीय शंकु की ऊँचाई, आधार की

त्रिज्या की $\sqrt {{2}} $ गुनी होती है।

उत्तर: 

माना, दिए गए शंकु की ऊँचाई  ${{h}}$, त्रिज्या ${{r}}$ तथा आयतन ${{V}}$ है। 

शंकु का आयतन

${{V  =  }}\dfrac{{{1}}}{{{3}}}{{π }}{{{r}}^{{2}}}{{h}}$  

$\Rightarrow {{h  =  }}\dfrac{{{{3V}}}}{{{{π }}{{{r}}^{{2}}}}}.....{{ \ldots }}.......{{(1)}}$

शंकु का पृष्ठ क्षेत्रफल

${{S  =  π rl  =  π r}}\sqrt {{{{r}}^{{2}}}{{  +  }}{{{h}}^{{2}}}} {{  =  π r}}\sqrt {{{{r}}^{{2}}}{{  +  }}{{\left( {\dfrac{{{{3V}}}}{{{{π }}{{{r}}^{{2}}}}}} \right)}^{{2}}}} {{  =  }}\dfrac{{{1}}}{{{r}}}\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} $  

${{S '(r)  =   -  }}\dfrac{{{1}}}{{{r}}}\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} {{  +  }}\dfrac{{{1}}}{{{r}}}\dfrac{{{1}}}{{{{2}}\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }} \times \left[ {{{{π }}^{{2}}}{{6}}{{{r}}^{{5}}}} \right]$  

$\Rightarrow \dfrac{{{1}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{{ -  }}{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}{{  +  3}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }}} \right]$

अब, ${{S '(r)  =  0}}$

$\Rightarrow \dfrac{{{1}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{{ -  }}{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}{{  +  3}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }}} \right]{{  =  0}}$  

$\Rightarrow {{9}}{{{V}}^{{2}}}{{  +  3}}{{{π }}^{{2}}}{{{r}}^{{6}}}{{  =  0}} \Rightarrow {{{r}}^{{6}}}{{  =  }}\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}$  

$\Rightarrow {{r  =  }}{\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)^{\dfrac{{{1}}}{{{6}}}}}$

अब, ${{S ''(r)  =  0}}$

$\Rightarrow {{  -  }}\dfrac{{{2}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }}} \right]$

$\Rightarrow \dfrac{{{1}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{1}}}{{\dfrac{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }}}}{{ \times }}\dfrac{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} \left( {{{12}}{{{π }}^{{2}}}{{{r}}^{{5}}}} \right){{  +  }}\left( {{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}} \right)\dfrac{{{6}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}} }}}}{{{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}}}} \right.$

$\Rightarrow {{ -  }}\dfrac{{{2}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }}} \right]{{  +  }}\dfrac{{{1}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{1}}}{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}\,\, \times \,\,\dfrac{{{{6}}{{{π }}^{{2}}}{{{r}}^{{5}}}\left\{ {\left( {{{2}}{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  18}}{{{V}}^{{2}}}} \right){{  +  }}\left( {{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}} \right)} \right\}}}{{{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}}}} \right]$  

$\Rightarrow {{ -  }}\dfrac{{{2}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{\sqrt {{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}} }}} \right]{{  +  }}\dfrac{{{1}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{1}}}{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}{{{r}}^{{6}}}}} \times \dfrac{{{{54}}{{{V}}^{{2}}}{{{π }}^{{2}}}{{{r}}^{{6}}}}}{{{{{π }}^{{2}}}{{{r}}^{{6}}}{{  +  9}}{{{V}}^{{2}}}}}} \right]$ 

${{r  =  }}{\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)^{\dfrac{{{1}}}{{{6}}}}}$ के लिए ${{S ''}}\left( {{{\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)}^{\dfrac{{{1}}}{{{6}}}}}} \right)$

$\Rightarrow {{ -  }}\dfrac{{{2}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)}}{{\sqrt {{{{π }}^{{2}}}\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right){{  +  9}}{{{V}}^{{2}}}} }}} \right]{{  +  }}\dfrac{{{1}}}{{{{{r}}^{{2}}}}}\left[ {\dfrac{{{1}}}{{{{9}}{{{V}}^{{2}}}{{  +  2}}{{{π }}^{{2}}}\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)}}\,\, \times \,\,\dfrac{{{{54}}{{{V}}^{{2}}}{{{π }}^{{2}}}\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)}}{{{{{π }}^{{2}}}\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right){{  +  9}}{{{V}}^{{2}}}}}} \right]$  

$\Rightarrow {\left( {\dfrac{{{{2}}{{{π }}^{{2}}}}}{{{{9}}{{{V}}^{{2}}}}}} \right)^{\dfrac{{{1}}}{{{2}}}}}{{[  -  4}}\sqrt {{6}} {{V  +  1]  <  0}}$

यहाँ, ${{S ''}}\left( {{{\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)}^{\dfrac{{{1}}}{{{6}}}}}} \right){{  <  0}}$है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{r  =  }}{\left( {\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}} \right)^{\dfrac{{{1}}}{{{6}}}}}$ स्थानीय उच्चतम बिंदु है।

यहाँ, ${{{r}}^{{6}}}{{  =  }}\dfrac{{{{9}}{{{V}}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}} \Rightarrow {{{r}}^{{6}}}{{  =  }}\dfrac{{{{9}}{{\left( {\dfrac{{{1}}}{{{3}}}{{π }}{{{r}}^{{2}}}{{h}}} \right)}^{{2}}}}}{{{{2}}{{{π }}^{{2}}}}}{{  =  }}\dfrac{{{{{r}}^{{4}}}{{{h}}^{{2}}}}}{{{2}}} \Rightarrow {{2}}{{{r}}^{{2}}}{{  =  }}{{{h}}^{{2}}} \Rightarrow \sqrt {{2}} {{r}}$

25. सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्ध शीर्ष कोण ${{ta}}{{{n}}^{{{ - 1}}}}\sqrt {{2}} $ होता है।

उत्तर: माना, दिए गए शंकु की ऊँचाई ${{h}}$, त्रिज्या ${{r}}$ तथा तिर्यक ऊँचाई। है, जिसका अर्धशीर्ष कोण ${{a}}$ है।

इसलिए ${{{l}}^{{2}}}{{  =  }}{{{r}}^{{2}}}{{  +  }}{{{h}}^{{2}}}{{ \ldots }}.............{{(1)}}$

$\Rightarrow {{{r}}^{{2}}}{{  =  }}{{{l}}^{{2}}}{{  -  }}{{{h}}^{{2}}}$  

${{V  =  }}\dfrac{{{1}}}{{{3}}}{{π }}{{{r}}^{{2}}}{{h}}$

$\Rightarrow {{V  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{{l}}^{{2}}}{{  -  }}{{{h}}^{{2}}}} \right){{h  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{h}}{{{l}}^{{2}}}{{  -  }}{{{h}}^{{3}}}} \right)$  

$\Rightarrow {{V '(h)  =  }}\dfrac{{{1}}}{{{3}}}{{π }}\left( {{{{l}}^{{2}}}{{  -  3}}{{{h}}^{{2}}}} \right)$

अब, ${{V '(h)  =  0}}$

$\Rightarrow \dfrac{{{1}}}{{{3}}}{{π }}\left( {{{{l}}^{{2}}}{{  -  3}}{{{h}}^{{2}}}} \right){{  =  0}} \Rightarrow {{{h}}^{{2}}}{{  =  }}\dfrac{{{{{l}}^{{2}}}}}{{{2}}} \Rightarrow {{h  =  }}\dfrac{{{l}}}{{\sqrt {{3}} }}$

अब, ${{V ''(h)  =  }}\dfrac{{{1}}}{{{3}}}{{π (  -  6h)  =   -  2π h}}$

${{h  =  }}\dfrac{{{l}}}{{\sqrt {{3}} }}$के लिए, ${{V ''}}\left( {\dfrac{{{l}}}{{\sqrt {{3}} }}} \right){{  =   -  2π }}\left[ {\dfrac{{{1}}}{{\sqrt {{3}} }}} \right]{{  <  0}}$

यहाँ, ${{V ''}}\left( {\dfrac{{{l}}}{{\sqrt {{3}} }}} \right){{  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{h  =  }}\dfrac{{{l}}}{{\sqrt {{3}} }}$ स्थानीय उच्चतम बिंदु है।

इस उच्चतम बिंदु पर शंकु की त्रिज्या ${{r  =  }}\sqrt {{{{l}}^{{2}}}{{  -  }}\dfrac{{{{{l}}^{{2}}}}}{{{3}}}} {{  =  }}\sqrt {\dfrac{{{{2}}{{{l}}^{{2}}}}}{{{3}}}} {{  =  }}\dfrac{{\sqrt {{2}} {{l}}}}{{\sqrt {{3}} }}$  [समीकरण (1) से]

$\Rightarrow {{tan a  =  }}\dfrac{{{r}}}{{{h}}}{{  =  }}\dfrac{{\dfrac{{\sqrt {{2}} {{l}}}}{{\sqrt {{3}} }}}}{{\dfrac{{{l}}}{{\sqrt {{3}} }}}}{{  =  }}\sqrt {{2}}  \Rightarrow {{ta}}{{{n}}^{{{ - 1}}}}\sqrt {{2}} $

26. सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लंबवृत्तीय शंकु का अर्धशीर्ष कोण ${{si}}{{{n}}^{{{ - 1}}}}\left( {\dfrac{{{1}}}{{{3}}}} \right)$ होता है।

उत्तर: माना, दिए गए शंकु की ऊँचाई ${{h}}$, त्रिज्या ${{r}}$ तथा तिर्यक ऊँचाई। है, जिसका अर्धशीर्ष कोण ${{a}}$ है।

इसलिए शंकु का पृष्ठ क्षेत्रफल

${{S  =  π rl  +  π }}{{{r}}^{{2}}}{{  =  π r}}\sqrt {{{{r}}^{{2}}}{{  +  }}{{{h}}^{{2}}}} {{  +  π }}{{{r}}^{{2}}}$

$\Rightarrow \sqrt {{{{r}}^{{2}}}{{  +  }}{{{h}}^{{2}}}} {{  =  }}\dfrac{{{{S  -  π }}{{{r}}^{{2}}}}}{{{{π r}}}}$

$\Rightarrow {{{r}}^{{2}}}{{  +  }}{{{h}}^{{2}}}{{  =  }}{\left( {\dfrac{{{{S  -  π }}{{{r}}^{{2}}}}}{{{{π r}}}}} \right)^{{2}}}$

$\Rightarrow {{{h}}^{{2}}}{{  =  }}{\left( {\dfrac{{{{S  -  π }}{{{r}}^{{2}}}}}{{{{π r}}}}} \right)^{{2}}}{{  -  }}{{{r}}^{{2}}}$  

$\Rightarrow {{{h}}^{{2}}}{{  =  }}\dfrac{{{{{S}}^{{2}}}{{  +  }}{{{π }}^{{2}}}{{{r}}^{{2}}}{{  -  2Sπ }}{{{r}}^{{2}}}{{  -  }}{{{π }}^{{2}}}{{{r}}^{{2}}}}}{{{{{π }}^{{2}}}{{{r}}^{{2}}}}}$  

$\Rightarrow {{{h}}^{{2}}}{{  =  }}\dfrac{{{{{S}}^{{2}}}{{  -  2Sπ }}{{{r}}^{{2}}}}}{{{{{π }}^{{2}}}{{{r}}^{{2}}}}}{{ \ldots  \ldots }}.....{{ (1) }}$

शंकु का आयतन 

${{V  =  }}\dfrac{{{1}}}{{{3}}}{{π }}{{{r}}^{{2}}}{{h}} \Rightarrow {{{V}}^{{2}}}{{  =  }}\dfrac{{{1}}}{{{9}}}{{{π }}^{{2}}}{{{r}}^{{4}}}{{{h}}^{{2}}}$

$\Rightarrow {{{V}}^{{2}}}{{  =  }}\dfrac{{{1}}}{{{9}}}{{{π }}^{{2}}}{{{r}}^{{4}}}\left( {\dfrac{{{{{S}}^{{2}}}{{  -  2Sπ }}{{{r}}^{{2}}}}}{{{{{π }}^{{2}}}{{{r}}^{{2}}}}}} \right){{  =  }}\dfrac{{{1}}}{{{9}}}{{S}}\left( {{{S}}{{{r}}^{{2}}}{{  +  2π }}{{{r}}^{{4}}}} \right)$ 

माना,

${{{V}}^{{2}}}{{  =  M  =  }}\dfrac{{{1}}}{{{9}}}{{S}}\left( {{{S}}{{{r}}^{{2}}}{{  +  2π }}{{{r}}^{{4}}}} \right)$  

$\Rightarrow {{M '(r)  =  }}\dfrac{{{1}}}{{{9}}}{{S}}\left( {{{2Sr  +  8π }}{{{r}}^{{3}}}} \right)$

अब, ${{M '(r)  =  0}}$

$\Rightarrow \dfrac{{{1}}}{{{9}}}{{S}}\left( {{{2Sr  +  8π }}{{{r}}^{{3}}}} \right){{  =  0}} \Rightarrow \dfrac{{{1}}}{{{9}}}{{2Sr}}\left( {{{S  -  4π }}{{{r}}^{{2}}}} \right){{  =  0}}$

$\Rightarrow {{r  =  0}}$ या ${{{r}}^{{2}}}{{  =  }}\dfrac{{{S}}}{{{{4π }}}}$

$\Rightarrow {{r  =  0}}$ या ${{r  =  }}\sqrt {\dfrac{{{S}}}{{{{4π }}}}} $

[${{r}} \ne 0,$क्योंकि ${{r}}$ शंकु की त्रिज्या है, अतः ${{r  =  0}}$संभव नहीं है।]

अब, ${{M ''(r)  =  }}\dfrac{{{1}}}{{{9}}}{{S}}\left( {{{2S  +  24π }}{{{r}}^{{2}}}} \right)$

${{r  =  }}\sqrt {\dfrac{{{S}}}{{{{4π }}}}} $के लिए, ${{M ''}}\left( {\sqrt {\dfrac{{{s}}}{{{{4π }}}}} } \right){{  =  }}\dfrac{{{1}}}{{{9}}}{{S}}\left[ {{{2S  +  24π }}\left( {\sqrt {\dfrac{{{s}}}{{{{4π }}}}} } \right)} \right]{{  =   -  }}\dfrac{{{{22}}}}{{{9}}}{{{S}}^{{2}}}{{  <  0}}$

${{M ''}}\left( {\sqrt {\dfrac{{{s}}}{{{{4π }}}}} } \right){{  <  0}}$इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{r  =  }}\sqrt {\dfrac{{{S}}}{{{{4π }}}}} $स्थानीय उच्चतम बिंदु है।

इस उच्चतम बिंदु पर शंकु कि त्रिज्या ${{r  =  }}\sqrt {\dfrac{{{S}}}{{{{4π }}}}} $

$\Rightarrow {{{r}}^{{2}}}{{  =  }}\dfrac{{{S}}}{{{{4π }}}} \Rightarrow {{4π }}{{{r}}^{{2}}}{{  =  S}} \Rightarrow {{4π }}{{{r}}^{{2}}}{{  =  π rl  +  π }}{{{r}}^{{2}}}$  

$\Rightarrow {{3r  =  l }} \Rightarrow \dfrac{{{r}}}{{{l}}}{{  =  }}\dfrac{{{1}}}{{{3}}}$  

यहाँ, ${{sin a  =  }}\dfrac{{{r}}}{{{l}}}{{  =  }}\dfrac{{{1}}}{{{3}}} \Rightarrow {{a  =  si}}{{{n}}^{{{ - 1}}}}\left( {\dfrac{{{1}}}{{{3}}}} \right)$

प्रश्न संख्या 27 से 29 में सही उत्तर का चुनाव कीजिए।

उत्तर:

27. वक्र ${{{x}}^{{2}}}{{  =  2y}}$पर ${{(0,5)}}$ से न्यूनतम दूरी पर स्थित बिंदु है:

A. ${{(2}}\sqrt {{2}} {{, 4)}}$

B. ${{(2}}\sqrt {{2}} {{,0)}}$

C. $(0,0)$

D. $(2,2)$

उत्तर: ${{x}}$ के प्रत्येक मान के लिए किसी बिंदु की स्थिति $\left( {{{x,}}\dfrac{{{{{x}}^{{2}}}}}{{{2}}}} \right)$ होगी 

इसलिए बिंदु $\left( {{{x,}}\dfrac{{{{{x}}^{{2}}}}}{{{2}}}} \right)$ और ${{(0,5)}}$ के बीच की दूरी

${{D  =  }}\sqrt {{{{{(x  -  0)}}}^{{2}}}{{  +  }}{{\left( {\dfrac{{{{{x}}^{{2}}}}}{{{2}}}{{  -  5}}} \right)}^{{2}}}} $

माना ${{{D}}^{{2}}}{{  =  A}}$

$\Rightarrow {{{(x  -  0)}}^{{2}}}{{  +  }}{\left( {\dfrac{{{{{x}}^{{2}}}}}{{{2}}}{{  -  5}}} \right)^{{2}}} \Rightarrow {{{x}}^{{2}}}{{  +  }}\dfrac{{{{{x}}^{{4}}}}}{{{4}}}{{  +  25  -  5}}{{{x}}^{{2}}} \Rightarrow \dfrac{{{{{x}}^{{4}}}}}{{{4}}}{{  +  25  -  4}}{{{x}}^{{2}}}$  

${{A'(x)  =  }}{{{x}}^{{3}}}{{ -  8x}}$

अब, ${{A'(x)  =  0}}$

$\Rightarrow {{{x}}^{{3}}}{{  -  8x  =  }}0 \Rightarrow {{x }}\left( {{{{x}}^{{2}}}{{  -  8}}} \right){{  =  }}0 \Rightarrow {{x  =  0}}$ या ${{x  =   \pm  2}}\sqrt {{2}} $

अब, ${{A''(x)  =  3}}{{{x}}^{{2}}}{{  -  8}}$

${{x  =  0}}$ के लिए,

$\Rightarrow {{A''(0)  =  3(0}}{{{)}}^{{2}}}{{  -  8  =   -  8  <  0}}$

यहाँ, ${{A''(0)  <  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =  0}}$ स्थानीय उच्चतम बिंदु है। 

${{x  =   \pm  2}}\sqrt {{2}} $ के लिए

${{A''(  \pm  2}}\sqrt {{2}} {{)  =  24  -  8  =  16  >  0}}$

यहाँ, ${{A''(  \pm  2}}\sqrt {{2}} {{)  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा, ${{x  =   \pm  2}}\sqrt {{2}} $ स्थानीय निम्नतम बिंदु है।

यदि ${{x  =   \pm  2}}\sqrt {{2}} $  तो ${{y  =  }}\dfrac{{{{{x}}^{{2}}}}}{{{2}}}{{  =  }}\dfrac{{{8}}}{{{2}}}{{  =  4}}$

इसलिए, वक्र ${{{x}}^{{2}}}{{  =  2y}}$पर ${{(0,5)}}$ से न्यूनतम दूरी पर स्थित बिंदु ${{( \pm  2}}\sqrt {{2}} {{, 4)}}$है।

अतः, विकल्प (A) सही है।

28. ${{x}}$, के सभी वास्तविक मानों के लिए $\dfrac{{{{1  -  x  +  }}{{{x}}^{{2}}}}}{{{{1  +  x  +  }}{{{x}}^{{2}}}}}$ का न्यूनतम मान है,

A. ${{0 }}$

B. ${{1}}$

C. ${{3}}$

D. $\dfrac{1}{3}$

उत्तर: माना ${{A  =  }}\dfrac{{{{1  -  x  +  }}{{{x}}^{{2}}}}}{{{{1  +  x  +  }}{{{x}}^{{2}}}}}$

${{A'(x)  =  }}\dfrac{{\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right){{(  -  1  +  2x)  -  }}\left( {{{1  -  x  +  }}{{{x}}^{{2}}}} \right){{(1  +  2x)}}}}{{{{\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right)}^{{2}}}}}$

अब, ${{A'(x)  =  0}}$

$\Rightarrow \dfrac{{\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right){{(  -  1  +  2x)  -  }}\left( {{{1  -  x  +  }}{{{x}}^{{2}}}} \right){{(1  +  2x)}}}}{{{{\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right)}^{{2}}}}}{{  =  0}} \Rightarrow {{2}}{{{x}}^{{2}}}{{  -  2  =  0 }}$  

$\Rightarrow {{x  =  }} \pm {{ 1}}$

अब,

${{A''(x)  =  }}\dfrac{{{{\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right)}^{{2}}}{{4x  -  }}\left( {{{2}}{{{x}}^{{2}}}{{  -  2}}} \right){{2}}\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right){{(1  +  2x)}}}}{{{{\left( {{{1  +  x  +  }}{{{x}}^{{2}}}} \right)}^{{4}}}}}$

${{x  =   -  1}}$ के लिए,

${{A''(  -  1)  =  }}\dfrac{{{{4(1  -  3  +  1)}}}}{{{{{{(1  -  1  +  1)}}}^{{3}}}}}{{  =   -  4  <  0}}$

यहाँ, ${{A''(  -  1)  <  0}}$ है, इसलिए, द्वितीयअ वकलज परिक्षण द्वारा, ${{x  =   -  1}}$, स्थानीय उच्चतम बिंदु है।

${{x}} = 1$ के लिए,

${{A''(1)  =  }}\dfrac{{{{4(1  +  3  -  1)}}}}{{{{{{(1  +  1  +  1)}}}^{{3}}}}}{{  =  }}\dfrac{{{4}}}{{{9}}}{{  >  0 }}$
यहाँ, ${{A''(1)  >  0}}$ है, इसलिए, द्वितीय अवकलज परिक्षण द्वारा ${{x}} = 1$स्थानीय निम्नतम बिंदु है।

इसलिए, ${{A}}$ का न्यूनतम मान

${{A (1)  =  }}\dfrac{{{{1  -  1  +  1}}}}{{{{1  +  1  +  1}}}}$है।

अतः, विकल्प (D) सही है।

29. ${{{[x(x  -  1)  +  1]}}^{\dfrac{{{1}}}{{{3}}}}}{{,   0 }} \leqslant {{ x }} \leqslant {{ 1}}$का उच्चतम मान है:

A. ${\left( {\dfrac{{{1}}}{{{3}}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$

B. $\dfrac{{{1}}}{{{2}}}$

C. $1$ 

D. ${{0}}$

उत्तर: माना ${{A  =  [x (x  -  1)  +  1}}{{{]}}^{\dfrac{{{1}}}{{{3}}}}}{{  =  }}{\left[ {{{{x}}^{{2}}}{{  -  x  +  1}}} \right]^{\dfrac{{{1}}}{{{3}}}}}$

${{A'(x)  =  }}\dfrac{{{1}}}{{{3}}}\dfrac{{{{(2x  - 1)}}}}{{{{\left[ {{{{x}}^{{2}}}{{  -  x  +  1}}} \right]}^{\dfrac{{{2}}}{{{3}}}}}}}$

अब, ${{A'(x)  =  0}}$

$\Rightarrow \dfrac{{{1}}}{{{3}}}\dfrac{{{{(2x  -  1)}}}}{{{{\left[ {{{{x}}^{{2}}}{{  -  x  +  1}}} \right]}^{\dfrac{{{2}}}{{{3}}}}}}}{{  =  0}} \Rightarrow {{2x  -  1  =  0}} \Rightarrow {{x  =  }}\dfrac{{{1}}}{{{2}}}$

${{x  =  0, x  =  }}\dfrac{{{1}}}{{{2}}}{{, x  =  1}}$ पर का ${{A}}$मान ज्ञात करने पर 

${{A(0)  =  [0(0  -  1)  +  1}}{{{]}}^{\dfrac{{{1}}}{{{3}}}}}{{ =  1}}$  

${{A}}\left( {\dfrac{{{1}}}{{{2}}}} \right){{  =  }}{\left[ {\dfrac{{{1}}}{{{2}}}\left( {\dfrac{{{1}}}{{{2}}}{{  -  1}}} \right){{  +  1}}} \right]^{\dfrac{{{1}}}{{{3}}}}}{{  =  }}{\left( {\dfrac{{{3}}}{{{4}}}} \right)^{\dfrac{{{1}}}{{{3}}}}}$  

${{A(1)  =  [1(1  -  1)  +  1}}{{{]}}^{\dfrac{{{1}}}{{{3}}}}}{{  =  1}}$

${{x  =   - 1}}$ के लिए

${{A''(  -  1)  =  }}\dfrac{{{{4(1  -  3  +  1)}}}}{{{{{{(1  -  1  +  1)}}}^{{3}}}}}{{  =   -  4  <  0}}$

यहाँ, ${{{[x(x  -  1)  +  1]}}^{\dfrac{{{1}}}{{{3}}}}}{{,   0 }} \leqslant {{ x }} \leqslant {{ 1}}$ उच्चतम मान 1 है।

अतः, विकल्प (C) सही है।

प्रश्नावली A6

1. अवकलज का प्रयोग करके निम्नलिखित में से प्रत्येक का सन्रिकट मान ज्ञात कीजिए:

(a) ${(17/81)^{1/4}}$ 

उत्तर: मान लीजिए ${{y  =  }}{{{x}}^{{{1/4}}}}$जहां ${{x  =  16 / 81}}$ तथा

${{\Delta x  =  1/81}}$

तब,

${{\Delta y  =  (x  +  \Delta x}}{{{)}}^{{{1/4}}}}{{  -  }}{{{x}}^{{{1/4}}}}$  

${{ =  (17/81}}{{{)}}^{{{1/4}}}}{{  -  (16/81}}{{{)}}^{{{1/4}}}}$  

${{ =  (17/81}}{{{)}}^{{{1/4}}}}{{ - 2/3}}$  

${{{(17 / 81)}}^{{{1/4}}}}{{  =  2 / 3  +  \Delta y}}$

अब ${{\Delta y}}$ सन्रिकटतः ${{dy}}$ के बराबर है और

${{ =  (dy / dx) \Delta x}}$  

${{ =  \Delta x / 4(x}}{{{)}}^{{{3/4}}}}$

${{ =  (1/81)/4(16/81)3/4}}$  

${{ =  27/81  \times  4  \times  8}}$  

${{ =  1/96}}$  

${{ =  0 }}{{. 010}}$

इस प्रकार, ${(17/81)^{1/4}}$ का सत्रिकट मान है:

${{ =  2 / 3  +  0}}{{.010  =  0}}{{.677}}$

(b) $(33) - 1/5$

उत्तर: मान लीजिए ${{y  =  }}\left( {{x}} \right){{ 1 / 5}}$ जहां ${{x  =  32}}$ तथा

${{\Delta x  =  1}}$

तब,

${{\Delta y  =  (x  +  \Delta x) 1/5  -  x1/5}}$  

${{ =  (33) 1/5  -  (32) 1/5}}$  

${{ =  (33)1/5  -  1/2}}$  

${{(33)1/5  =  1/2  -  \Delta y}}$

अब ${{\Delta y}}$ सन्रिकटतः ${{dy}}$ के बराबर है और

${{dy  =  (dy / dx)\Delta x}}$  

${{ =   -  \Delta x / 5(x) 6 / 5}}$  

${{ =   -  1/5(2) 6 / 5}}$  

${{ =   - 1/320}}$  

${{ =   -  0}}{{.003}}$

इस प्रकार, $\left( {33} \right) - 1/5$ का सन्रिकट मान है:

$ = 1/2 + ( - \,0.003) = 0.497$

2. सिद्ध कीजिए कि ${{f (x)  =  log x / x}}$द्वारा प्रदत्त फलन ${{x  =  e}}$पर उच्चतम है।

उत्तर: ${{f (x)  =  log x / x}}$

$f’(x) = 1 - logx$
${{{x}}^{{2}}}$ से भाग करने पर 

${{ =  (1  -  log x) /}}{{{x}}^{{2}}}$

अब ${{f '(x)  =  0}}$

${{(1  -  log x) /}}{{{x}}^{{2}}}{{  =  0}}$  

${{1  -  log x  =  0}}$  

${{log x  =  1}}$  

${{log x  =  log e}}$  

${{x  =  e}}$

अब, ${{f ''(x)  =  }}{{{x}}^{{2}}}{{(  -  1/x)  -  (1  -  log x)  \times  2x}}$

${\left( {{{{x}}^{{2}}}} \right)^{{2}}}$से भाग करने पर 

${{ =  ( -  x  -  2x  +  2x log x) /}}{{{x}}^{{4}}}$  

${{ =  x (2 log x  -  3) /}}{{{x}}^{{4}}}$  

${{ =  (2 log x  -  3)/ }}{{{x}}^{{3}}}$

${{x  =  e}}$ पर,

${{f}}''{{(x)}}$  

${{ =  (2 log e  -  3) /}}{{{e}}^{{3}}}$  

${{ =  (2  \times  1  -  3) /}}{{{e}}^{{3}}}$  

${{ =   -  1 / }}{{{e}}^{{3}}}{{  <  0}}$

अतः ${{f}}$, द्वारा प्रदत्त फलन ${{x  =  e}}$ पर उच्चतम है। 

3. किसी निश्चित आधार ${{b}}$ के एक समद्विबाहु त्रिभुज की सामान भुजाएं ${{3cm/s}}$की दर से घट रहीं है। उस समय जब त्रिभुज की समान भुजाएं आधार के बराबर हैं, उसका क्षेत्रफल कितनी तेजी से घट रहा है।

उत्तर: मान लीजिए ${{ABC}}$ एक समद्विबाहु त्रिभुज है जहां ${{BC  =  b }}$ एक निश्चित आधार है।

मान लीजिए समद्विबाहु त्रिभुज की समान भुजाएं ${{x}}$ है।

${{BC  =  b }}$ पर ${{AD}}$ लंब खीचिए।

पाइथागोरस प्रमेय से,

${{AD  =  }}{\sqrt {{x}} ^{{2}}}{{  -  (b / 2}}{{{)}}^{{2}}}{{ = }}{\sqrt {{x}} ^{{2}}}{{ -  }}{{{b}}^{{2}}}{{/4}}$

त्रिभुज का क्षेत्रफल $\left( {{A}} \right){{  = }}$$1/2 \times $ आधार $ \times $ ऊंचाई

${{ =  b /2}}\sqrt {{{{x}}^2}} {{  -  }}{{{b}}^{{2}}}{{/4}}$

क्षेत्रफल $\left( {{A}} \right)$ के घटने का दर ${{ =  dA / dt}}$

${{ =  b / 2  \times  2x / 2}}\sqrt {{{{x}}^2}} {{ -  }}{{{b}}^{{2}}}{{/ 4  \times  dx / dt}}$  

${{ =  xb /}}\sqrt {{4}} {{{x}}^{{2}}}{{  -  }}{{{b}}^{{2}}}{{  \times  dx / dt }}$

दो समान भुजाएं ${{3cm / s}}$ की दर से घट रही है।

${{dx / dt  =   -  3cm / s}}$  

${{dA / dt  =   -  3xb /}}\sqrt {{{4}}{{{x}}^{{2}}}} {{ -  }}{{{b}}^{{2}}}{{c}}{{{m}}^{{2}}}{{/ s}}$

जब ${{x  =  b,}}$

${{dA / dt  =   -  3}}{{{b}}^{{2}}}{{/}}\sqrt {{3}} {{}}{{{b}}^{{2}}}$

${{ =   -  }}\sqrt {{{3b}}} {{ c}}{{{m}}^{{2}}}{{/s}}$

अतः, जब त्रिभुज की सामान भुजाएं आधार के बराबर है तब उसका क्षेत्रफल $\sqrt {{{3b}}} {{ c}}{{{m}}^{{2}}}{{/s}}$तेजी से घटेगा।

4. वक्र ${{{x}}^{{2}}}{{  =  4y}}$ के बिंदु $(1,2)$ पर अभिलंब का समीकरण ज्ञात कीजिए।

उत्तर: ${{{y}}^{{2}}}{{  =  4x}}$का, ${{x}}$ के सापेक्ष अवकलन करने पर,

$\begin{array}{*{20}{l}} {{{2y d y / dx  =  4}}} \\  {{{d y / dx  =  4 / 2y  =  2 /y}}}  \end{array}$

$(1,2)$ पर स्पर्श रेखा की प्रवणता ${{ =  dy / dx] (1, 2)  =  2 / 2  =  1}}$

$(1,2)$ पर अभिलंब की प्रवणता ${{ =   -  1 / 1  =   -  1}}$

अभिलंब का समीकरण ${{ =  y  -  2  =   -  1(x  -  1)}}$

${{y  -  2  =   -  x  +  1}}$

  ${{x  +  y  -  3  =  0}}$

5. सिद्ध कीजिए की वक्र ${{x  =  a cos }}\emptyset {{  +  a}}\emptyset \,{{sin }}\emptyset {{, y  =  a sin }}\emptyset {{  -  a }}\emptyset \,{{cos }}\emptyset $के लिए बिंदु $\emptyset $ पर अभिलंब मूल बिंदु से अचर दूरी पर है।

उत्तर: ${{x  =  a cos }}\emptyset {{  +  a}}\emptyset \,{{sin }}\emptyset $

${{dx / d}}\emptyset {{  =   -  a sin }}\emptyset {{  +  a [}}\emptyset \,{{cos }}\emptyset {{  +  sin }}\emptyset {{]}}$  

${{ =   -  a sin }}\emptyset \,{{ +  a}}\emptyset \,{{cos }}\emptyset {{  +  a sin }}\emptyset $  

${{ =  a}}\emptyset \,{{cos }}\emptyset $  

${{y  =  a sin }}\emptyset {{  -  a}}\emptyset \,{{cos }}\emptyset $  

${{dy / d}}\emptyset {{  =  a cos}}\,\emptyset {{  -  a[}}\emptyset \,{{(  -  sin }}\emptyset {{)  +  cos }}\emptyset {{]}}$  

${{ =  a cos }}\emptyset {{  +  a}}\emptyset \,{{sin }}\emptyset {{  -  a cos}}\emptyset $  

${{ = a}}\emptyset \,{{sin }}\emptyset $

$\emptyset $ पर स्पर्श रेखा की प्रवणता ${{dy / dx}}$

${{ =  dy / d}}\emptyset {{  \times  d}}\emptyset {{/ dx}}$  

${{ =  a}}\emptyset \,{{sin }}\emptyset {{ / a}}\emptyset \,{{cos }}\emptyset $  

${{ =  tan }}\emptyset $  

$\emptyset $ पर अभिलंब की प्रवणता ${{ =   -  1 / (dy / dx)}}$

${{ =   -  1 / tan }}\emptyset $  

${{ =   -  cot }}\emptyset $

अभिलंब का समीकरण 

${{y  -  [a sin  -  a cos }}\emptyset {{]  =   -  cot }}\emptyset {{[x  -  (a cos }}\emptyset {{  +  a sin }}\emptyset {{)]}}$

$\Rightarrow {{y}} - [{{asin}}\emptyset {{ -  a}}\emptyset \cos \emptyset ] =  - \cos \emptyset /\sin \emptyset [x - ({{ac}}os\emptyset  + a\emptyset \sin \emptyset )]$

${{ =   -  x cos }}\emptyset {{  +  a co}}{{{s}}^{{2}}}\emptyset {{  +  a}}\emptyset \,{{sin }}\emptyset {{ cos }}\emptyset $  

$\Rightarrow {{x cos }}\emptyset {{  +  y sin }}\emptyset {{  =  a}}\left( {{{si}}{{{n}}^{{2}}}\emptyset {{  +  co}}{{{s}}^{{2}}}\emptyset } \right)$  

$\Rightarrow {{x cos }}\emptyset {{  +  y sin }}\emptyset {{  =  a}}$  

$\Rightarrow {{x cos }}\emptyset {{  +  y sin }}\emptyset {{  -  a  =  0}}$

अब लंब कि दूरी ${{ =  |  -  a | /}}\sqrt {{{co}}{{{s}}^{{2}}}\emptyset {{  +  si}}{{{n}}^{{2}}}\emptyset } $

${{ =  |  -  a | /}}\sqrt {{1}} $  

${{ =  |  -  a |}}$

अतः $\emptyset $ पर अभिलम्ब मूल बिन्दु से अचर दूरी पर है  

6. अंतराल ज्ञात कीजिए जिन पर

${{f (x)  =  (4 sin x  -  2x  -  x cos x) / 2  +  cos x}}$ से प्रदत्त फलन ${{f}}$

उत्तर: ${{f (x)  =  (4 sin x  -  2x  -  x cos x) / 2  +  cos x}}\quad $

अब ${{f '(x)  =  (2  +  cos x)( 4 cos x  -  2  -  cos x  +  x sin x)  -  (4 sin x  -  2x  -  x cos x)(  -  sin x)}}$

${{{(2  +  cos x)}}^{{2}}}$ से भाग करने पर 

${{  =  (2  +  cos x)(3 cos x  -  2  +  x sin x)  +  sin x(4 sin x  -  2x  -  x cos x)}}$

${{{(2  +  cos x)}}^{{2}}}$ से भाग करने पर 

${{ =  6 cos x  -  4  +  2x sin x  +  3 co}}{{{s}}^{{2}}}{{x  -  2 cos x  +  x sin x cos x  +  4 si}}{{{n}}^{{2}}}{{x  -  2x sin x  -  x sin x cos x}}$

${{{(2  +  cos x)}}^{{2}}}$ से भाग करने पर 

${{ =  }}\left( {{{4 cos x  -  4  +  3 co}}{{{s}}^{{2}}}{{x  +  4 si}}{{{n}}^{{2}}}{{x}}} \right){{ / (2  +  cos x}}{{{)}}^{{2}}}$  

${{ = }}\left( {{{4 cos x  -  4  +  3 co}}{{{s}}^{{2}}}{{x  +  4  -  4 co}}{{{s}}^{{2}}}{{x}}} \right){{ / (2  +  cos x}}{{{)}}^{{2}}}$  

${{ =  4 cos x  -  co}}{{{s}}^{{2}}}{{x / (2  +  cos x}}{{{)}}^{{2}}}$  

${{ =  cos x(4  -  cos x) / (2  +  cos x}}{{{)}}^{{2}}}$  

${{ -  1}} \leqslant {{cos x}} \leqslant {{1}}$

(i) निरंतर वर्धमान 

उत्तर: ${{f '(x)  >  0}}$ जब ${{cos x  >  0}}$

${{(0,π /2)}}$ तथा ${{(3π /2, 2π )}}$

(ii) निरंतर ह्रासमान है।

उत्तर: ${{f '(x)  <  0}}$जब ${{cos x  <  0}}$

${{(π /2, 3π /2)}}$

7. अंतराल ज्ञात कीजिए जिन पर

${{f (x)  =  }}{{{x}}^{{3}}}{{  +  1 / }}{{{x}}^{{3}}}{{,x}} \ne 0$

से प्रदत्त फलन 

(i) वर्धमान 

उत्तर: ${{f '(x)  >  0}}$

$\Rightarrow {{ 3}}{{{x}}^{{2}}}{{  -  3 / }}{{{x}}^{{4}}}{{  >  0}}$  

$\Rightarrow {{(3  \times  6  -  3) / }}{{{x}}^{{4}}}{{  >  0}}$  

$\Rightarrow {{3  \times  6  -  3  >  0}}$  

$\Rightarrow {{x6  >  1}}$  

$\Rightarrow {\left( {{{{x}}^{{2}}}} \right)^{{3}}}{{ > 1}}$  

$\Rightarrow {{{x}}^{{2}}}{{ > 1}}$

${{x}} \in ( - \infty , - 1);(1,\infty )$

${{x  <   -  1 }}$तथा ${{x  > 1}}$

(ii) ह्रासमान है।

उत्तर: ${{f '(x)  <  0}}$

$\Rightarrow {{3}}{{{x}}^{{2}}}{{  -  3 / }}{{{x}}^{{4}}}{{  <  0}}$  

$\Rightarrow {{{x}}^{{2}}}{{  <  1}}$  

$\Rightarrow {{ -  1  <  x  <  1}}$

8. दीर्घवृत्त ${{{x}}^{{2}}}{{ / }}{{{a}}^{{2}}}{{  +  }}{{{y}}^{{2}}}{{/ }}{{{b}}^{{2}}}{{  =  1}}$ के अंतर्गत उस समद्विबाहु त्रिभुज का महत्तम क्षेत्रफल ज्ञात कीजिए जिसका शीर्ष दीर्घ अक्ष का एक सिरा है। 

उत्तर: ${{{x}}^{{2}}}{{ / }}{{{a}}^{{2}}}{{  +  }}{{{y}}^{{2}}}{{/ }}{{{b}}^{{2}}}{{  =  1}}$

मान लीजिए $\vartriangle {{ABC}}$ दीर्घवृत्त के अंतर्गत का समद्विबाहु त्रिभुज है जहां शीर्ष ${{A, (a,0)}}$पर है।

${{A  =  (a cos }}\emptyset {{, b sin }}\emptyset \,\,{{)}}$  

${{B  =  (a cos }}\emptyset {{,  -  b sin }}\emptyset {{)}}$  

$\vartriangle {{ABC}}$ का क्षेत्रफल ${{ =  S}}$

${{S  =  2  \times  1 / 2  \times  AM  \times  BM}}$  

${{ =  (OA  -  OM)  \times  MB}}$  

${{ =  (a  -  a cos }}\emptyset {{)  \times  b sin }}\emptyset $  

${{ =  ab (sin }}\emptyset {{  -  sin }}\emptyset \,{{cos }}\emptyset {{)}}$  

${{ =  ab (sin }}\emptyset {{  -  1 / 2 sin 2}}\emptyset {{)}}$  

${{dS / d}}\emptyset {{  =  ab (cos }}\emptyset {{  -  cos 2}}\emptyset {{)}}$

फिर से,

${{{d}}^{{2}}}{{S / d}}{\emptyset ^{{2}}}{{  =  ab ( -  sin }}\emptyset {{  +  2 sin 2}}\emptyset {{)}}$

अब,

${{dS / d}}\emptyset {{  =  0}}$  

$\Rightarrow {{cos }}\emptyset {{  =  cos 2}}\emptyset $  

$\Rightarrow {{2}}\emptyset {{  =  2π   -  }}\emptyset $  

$\Rightarrow \emptyset {{  =  2π  / 3}}$

$\emptyset {{  =  2π  / 3}}$ पर,

$\left( {{{{d}}^{{2}}}{{S / d}}{\emptyset ^{{2}}}} \right){{  =  ab [  -  sin 2π  / 3  +  2 sin (2  \times  2π  / 3)]}}$  

${{ =  ab [  -  sin (π   -  π  / 3)  +  2 sin (π   +  π  / 3)]}}$  

${{ =  ab(  -  sin π  / 3  -  2 sin π  / 3)}}$  

${{ =  ab (  -  }}\sqrt {{3}} {{/ 2  -  2}}\sqrt {{3}} {{/ 2)}}$  

${{ =  ab (  -  3}}\sqrt {{3}} {{ /2 )}}$  

${{ =   -  3}}\sqrt {{3}} {{ab / 2  <  0}}$

महत्तम है जब $\emptyset {{  =  2π  / 3}}$ है।

महातम क्षेत्रफल ${{ =  ab (sin 2π  / 3  -  1 / 2 }}{{. 2 sin 2π  / 3 cos 2π  / 3)}}$

${{ =  ab [sin ( π   -  π  / 3)  -  sin (π   -  π  / 3) cos (π   -  π  / 3)]}}$  

${{ =  ab [sin π  / 3  -  sin π  / 3  \times  (  -  cos π  / 3)]}}$  

${{ =  ab (sin π  / 3  +  sin π  / 3 cos π  / 3)}}$  

${{ =  ab(}}\sqrt {{3}} {{ / 2  +  }}\sqrt {{3}} {{ / 2  \times  1 / 2)}}$

${{ =  ab [(2}}\sqrt {{3}} {{  +  }}\sqrt {{3}} {{) / 4]}}$

${{ =  3}}\sqrt {{3}} {{ / 4 ab \, sq unit}}$

9. आयताकार आधार व आयताकार दीवारों की ${{2m}}$ गहरी और ${{8}}{{{m}}^{{3}}}$आयतन की एक बिना ढक्कन की टंकी का निर्माण करना है। यदि टंकी के निर्माण में आधार के लिए ${{Rs 70/}}{{{m}}^{{2}}}$और दीवारों पर ${{Rs }}45/{{{m}}^2}$ व्यय आता है तो निम्नतम खर्च से बनी टंकी की लागत क्या है?

उत्तर: मान लीजिए ${{l , b}}$और ${{ h}}$ टंकी कि लंबाई, चौड़ाई तथा गहराई है।

${{h  =  2m}}$

टंकी की आयतन ${{ =  8}}{{{m}}^3}$

टंकी की आयतन ${{ =  l  \times  b  \times  h}}$

$\Rightarrow {{8  =  lb  \times  2}}$  

$\Rightarrow \,{{l b  =  4}}$

आधार का क्षेत्रफल $ = {{l b  =  4}}$

${{4}}$ दीवारों का क्षेत्रफल $\left( {{A}} \right){{  =  2h}}\left( {{{l  +  b}}} \right)$ 

$\mathrm{A}=4(1+4 / \mathrm{I}) $

अब,

$ \mathrm{d} \mathrm{A} / \mathrm{dl}=0 $

$ \Rightarrow 1-4 / \mathrm{l}^{2}=0 $

$ \Rightarrow \left(\mathrm{I}^{2}-4\right) / \mathrm{l}^{2}=0 $

$ \Rightarrow \mathrm{I}^{2}=4 $

$ \Rightarrow \mathrm{I}=\pm 2 $

$ \Rightarrow 1=2 $

$ \Rightarrow \mathrm{b}=4 / 1=4 / 2=2 $

आधार को बनाने का खर्च $=\operatorname{Rs} 70(\mathrm{lb})$ $=\operatorname{Rs} 70 \times 4$ $=\operatorname{Rs} 280$ दीवारों को बनाने का खर्च $=\operatorname{Rs} 45 \times 2 \mathrm{~h}(1+\mathrm{b})$ $=\operatorname{Rs} 45 \times 4(4)$ $=\operatorname{Rs} 45 \times 16$ $=\operatorname{Rs} 720$

निम्रतम खर्च $=\operatorname{Rs}(280+720)$

$=$ Rs 1000

10. एक वृत्त और एक वर्ग के परिमापों का योग $k$ है, जहां $k$ एक अचर है। सिद्ध कीजिए कि उनके

क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।

उत्तर: मान लीजिए वृत्त की त्रिज्या $r$ है तथा वर्ग की भुजा $x$ है

वृत्त का परिमाप $=2 π \mathrm{r}$

वर्ग का परिमाप $=4 \mathrm{x}$

$2 π \mathrm{r}+4 x=\mathrm{k}$

$\Rightarrow \mathrm{x}=(\mathrm{k}-2 π \mathrm{r}) / 4$

वर्ग का क्षेत्रफल $+$ वृत्त का क्षेत्रफल $=\mathrm{A}$

$\mathrm{A}=\mathrm{x}^{2}+π \mathrm{r}^{2}$

$=[(\mathrm{k}-2 π \mathrm{r}) / 4]^{2}+π \mathrm{r}^{2}$

$=(1 / 16)\left(\mathrm{k}^{2}-4 \mathrm{k} π \mathrm{r}+4 π^{2} \mathrm{r}^{2}\right)+π \mathrm{r}^{2}$

$\mathrm{~d} \mathrm{~A} / \mathrm{dr}=(1 / 16)\left(-4 \mathrm{k} π+8 π^{2} \mathrm{r}\right)+2 π \mathrm{r}$

फिर से,

$\mathrm{d}^{2} \mathrm{~A} / \mathrm{dr}^{2}=1 / 16\left(0+8 π^{2}\right)+2 π$

$=2 π+π^{2} / 2>0$

अब,

$\mathrm{d} \mathrm{A} / \mathrm{dr}=0$

$\Rightarrow 2 π \mathrm{r}-4 \mathrm{k} π / 16+8 π^{2} \mathrm{r} / 16=0$

$\Rightarrow \mathrm{r}\left(2 π+π^{2} / 2\right)=\mathrm{k} π / 4$

$\Rightarrow \mathrm{r}=(\mathrm{k} π / 4) /\left(2 π+π^{2} / 2\right)$

$\Rightarrow \mathrm{r}=\mathrm{k} / 8+2 π$

हम जानते है $: \mathrm{x}=(\mathrm{k}-2 π \mathrm{r}) / 4$

अब $=1 / 4(\mathrm{k}-2 π \times \mathrm{k} / 8+2 π)$

$=1 / 4[(8 \mathrm{k}+2 π \mathrm{k}-2 π \mathrm{k}) / 8+2 π]$

$=2 \mathrm{k} / 8+2 π$

$=2(\mathrm{k} / 8+2 π)$

$=2 \mathrm{r}$ $\Rightarrow \mathrm{r}\left(2 π+π^{2} / 2\right)=\mathrm{k} π / 4$

$\Rightarrow \mathrm{r}=(\mathrm{k} π / 4) /\left(2 π+π^{2} / 2\right)$

हम जानते है : $\mathrm{x}=(\mathrm{k}-2 π \mathrm{r}) / 4$

$=2 \mathrm{k} / 8+2 π$

$=2(\mathrm{k} / 8+2 π)$

$=2 \mathrm{r}$

अतः वृत और वर्ग के क्षेत्रफल का योग निम्रतम है

11. किसी आयत के ऊपर बने अर्धवृत्त के आकार वाली खिड़की है। खिड़की का संपूर्ण परिमाप $10 \mathrm{~m}$ है। पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लिए खिड़की की विमाए॰ ज्ञात कीजिए।

उत्तर: मान लीजिए अर्धवृत कि त्रिज्या $\mathrm{r}$ है

आयत की एक भुजा $2 \mathrm{r}$ है तो मान लीजिए दूसरी भुजा $\mathrm{x}$ है

परिमाप $(\mathrm{P})=10 \mathrm{~m}$  

$\begin{aligned} \mathrm{x}+2 \mathrm{r}+1 / 2(2 π \mathrm{r})=10 \\ \Rightarrow 2 \mathrm{x}=10-\mathrm{r}(π+2) \end{aligned} $

अर्धवृत्त का क्षेत्रफल $+$ आयत का क्षेत्रफल $=\mathrm{A}$

$\begin{array}{l} \mathrm{A}=1 / 2 π \mathrm{r}^{2}+2 \mathrm{rx} \\ =1 / 2 π \mathrm{r}^{2}+\mathrm{r}[10-\mathrm{r}(π+2)] \\ =1 / 2 π \mathrm{r}^{2}+10 \mathrm{r}-\mathrm{r}^{2} π-2 \mathrm{r}^{2} \\ =10 \mathrm{r}-π \mathrm{r}^{2} / 2-2 \mathrm{r}^{2} \\ \mathrm{~d} \mathrm{~A} / \mathrm{dr}=10-π \mathrm{r}-4 \mathrm{r} \\ \mathrm{d}^{2} \mathrm{~A} / \mathrm{dr}^{2}=-π-4 \end{array}$

अब $ \mathrm{d} \mathrm{A} / \mathrm{dr}=0 $

$ \Rightarrow 10-π \mathrm{r}-4 \mathrm{r}=0 $

$ \Rightarrow 10=(4+π) \mathrm{r} $

$ \Rightarrow \mathrm{r}=10 / 4+π $

अर्धवृत्त की त्रिज्या $=10 / 4+r$,

आयत की एक भुजा $=2 \mathrm{r}=20 / 4+π$

आयत की दूसरी भुजा $=2 \mathrm{x}=10-\mathrm{r}(π+2)$

$2 \mathrm{x}=10-[10 / π+4)(π+2)]$

$2 \mathrm{x}=(10 π+40-10 π-20) /(π+4)$

$\mathrm{x}=20 / 2(π+4)$

$\mathrm{x}=10 / π+4$

खिड़की की विमाएं :

लंबाई $=20 / π+4$

चौड़ाई $=10 / π+4$

12. त्रिभुज कि भुजाओं से $a$ और $b$ की दूरी पर त्रिभुज के कर्ण पर स्थित एक बिंदु है। सिद्ध कीजिए की कर्ण की न्यूनतम लंबाई $\left(a^{2} / 3+b^{2} / 3\right)^{3} / 2$ है।

उत्तर: मान लीजिए $\triangle \mathrm{ABC}$ एक समकोण त्रिभुज है

मान लीजिए त्रिभुज के $\mathrm{AC}$ कर्ण पर स्थित बिन्दु $\mathrm{P}$ है

13. उन बिंदुओं को ज्ञात कीजिए जिन पर $f(x)=(x-2)^{4}(x+1)^{3}$ द्वारा प्रदत्त फलन $f$ का उत्तर: $f(x)=(x-2)^{4}(x+1)^{3}$

$\begin{array}{l} \mathrm{f}^{\prime}(\mathrm{x})=4(\mathrm{x}-2)^{3}(\mathrm{x}+1)^{3}+3(\mathrm{x}+1)^{2}(\mathrm{x}-2)^{4} \\ =(\mathrm{x}-2)^{3}(\mathrm{x}+1)^{2}[3(\mathrm{x}-2)+4(\mathrm{x}+1)] \\ =(\mathrm{x}-2)^{3}(\mathrm{x}+1)^{2}(7 \mathrm{x}-2) \\ \mathrm{f}^{\prime}(\mathrm{x})=0 \\ (\mathrm{x}-2)^{3}(\mathrm{x}+1)^{2}(7 \mathrm{x}-2)=0 \\ \Rightarrow \mathrm{x}=2,-1,2 / 7 \end{array}$

(i) स्थानीय उच्चतम बिंदु है

उत्तर: = $2 / 7$

(ii) स्थानीय निम्नतम बिंदु है,

उत्तर: = 2

(iii) नत परिवर्तन बिंदु है।

उत्तर: $=-1$

14. $\mathrm{f}(\mathrm{x})=\cos ^{2} \mathrm{x}+\sin \mathrm{x}, \mathrm{x} \in[0, π]$ द्वारा प्रदत्त फलन $\mathrm{f}$ का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।

उत्तर:

$\mathrm{f}^{\prime}(\mathrm{x})$

$=-2$

अब,

$f^{\prime}(x)=0$

$\Rightarrow-2 \sin x \cos x+\cos x=0$

$\Rightarrow \cos x(-2 \sin x+1)=0$

$\Rightarrow \cos x=0 ; \sin x=1 / 2$

$\Rightarrow x=π / 6, π / 2$

$x=π / 6$ पर,

$f(π / 6)=\cos ^{2}(π / 6)+\sin π / 6$

$=(\sqrt{3 / 2})^{2}+1 / 2$

$=5 / 4$

$x=π / 2$ पर,

$f(π / 2)=\cos ^{2}(π / 2)+\sin π / 2$

$=0^{2}+1$

$=1$

15. सिद्ध कीजिए की एक $\mathrm{r}$ त्रिज्या के गोले के अंतर्गत उच्चतम आयतन के लंब वृत्तीय शंकु की ऊंचाई $4 \mathrm{r} / 3$ है।

उत्तर: मान लीजिए शंकु कि त्रिज्या $\mathrm{r}$ है तथा शंकु कि ऊंचाई है $\Delta OAB$ में,

$\begin{array}{l} \mathrm{r}^{2}=\mathrm{R}^{2}+(\mathrm{h}-\mathrm{r})^{2} \\ \Rightarrow \mathrm{r}^{2}=\mathrm{R}^{2}+\mathrm{h}^{2}+\mathrm{r}^{2}-2 \mathrm{hr} \\ \Rightarrow \mathrm{R}^{2}=2 \mathrm{hr}-\mathrm{h}^{2} \end{array}$

शंकु का आयतन $(\mathrm{V})=1 / 3 π \mathrm{R}^{2} \mathrm{~h}$

$\begin{array}{l} =1 / 3 π \mathrm{h}\left(2 \mathrm{hr}-\mathrm{h}^{2}\right) \\ =1 / 3 π\left(2 \mathrm{~h}^{2} \mathrm{r}-\mathrm{h}^{3}\right) \\ \mathrm{dV} / \mathrm{dh}=1 / 3 π\left(4 \mathrm{th}-3 \mathrm{~h}^{2}\right) \end{array}$

अब,

$\begin{array}{l} \mathrm{dV} / \mathrm{dh}=0 \\ 4 \mathrm{rh}=3 \mathrm{~h}^{2} \\ \Rightarrow 4 \mathrm{r}=3 \mathrm{~h} \\ \Rightarrow \mathrm{h}=4 \mathrm{r} / 3 \\ \mathrm{~d}^{2} \mathrm{~V} / \mathrm{dh}^{2}=1 / 3 π(4 \mathrm{r}-6 \mathrm{~h}) \\ \mathrm{h}=4 \mathrm{r} / 3 \\ \mathrm{~d}^{2} \mathrm{~V} / \mathrm{dh}^{2}=1 / 3 π(4 \mathrm{r}-6 \times 4 \mathrm{r} / 3) \\ =π / 3(4 \mathrm{r}-8 \mathrm{r}) \\ =-4 \mathrm{r} π / 3<0 \end{array}$

$\mathrm{V}$ उच्चतम है जब $\mathrm{h}=4 \mathrm{r} / 3$ है

16. मान लीजिए $[a, b]$ पर परिभाषित एक फलन $f$ है द्स प्रकार की सभी $x \in(a, b)$ के लिए $f^{\prime}(x)>0$ है तो सिद्ध कीजिए कि $(a, b)$ पर $f$ एक वर्धमान फलन है।

उत्तर: [a,b] पर, $f^{\prime}(x)>0$

मान लीजिए $\mathrm{x} 1, \mathrm{x} 2 \in[\mathrm{a}, \mathrm{b}]$ तथा $\mathrm{x} 2>\mathrm{x} 1$

अब $c \in[a, b]$,

$f^{\prime}(c)=f(x 2)-f(x 1)$

$\mathrm{x} 2-\mathrm{x} 1$ भाग करने पर

$\Rightarrow f(x 2)-f(x 1)=(x 2-x 1) f^{\prime}(c)$

$\Rightarrow f(x 2)-f(x 1)>0$ जैसे $x 2>x 1$ तथा

$f^{\prime}(x)>0 \Rightarrow f(x 2)>f(x 1)$

$\mathrm{x} 1<\mathrm{x} 2$ के लिए

$f(x 1)<f(x 2)$

अतः $(a, b)$ पर $f$ एक वर्धमान फलन है।

17. सिद्ध कीजिए कि एक $R$ त्रिज्या के गोले के अंतर्गत अध्धिकतम आयतन के बेलन की ऊंचाई $2 R / \sqrt{3}$

है। अध्धिकतम आयतन भी ज्ञात कीजिए।

उत्तर: गोले का त्रिज्या $R$

मान लीजिए बेलन की ऊचाई $\mathrm{h}$ है तथा उसके आधार का व्यास $\mathrm{x}$ है।

तब, $\mathrm{h}^{2}+\mathrm{x}^{2}=(2 \mathrm{R})^{2}$ $\Rightarrow \mathrm{h}^{2}+\mathrm{x}^{2}=4 \mathrm{R}^{2}$ बेलन का आयतन $(\mathrm{V})=π(\mathrm{r})^{2} \times \mathrm{h}$

बेलन का आयतन $(\mathrm{V})=π(\mathrm{r})^{2} \times \mathrm{h}$

$ \Rightarrow \mathrm{V}=π(\mathrm{x} / 2)^{2} \cdot \mathrm{h} $

$ \Rightarrow \mathrm{V}=1 / 4 π \mathrm{x}^{2} \mathrm{~h} $

$ \Rightarrow \mathrm{V}=1 / 4 π$

$\mathrm{h}\left(4\mathrm{R}^{2}-\mathrm{h}^{2}\right) $

$ \Rightarrow \mathrm{V}=π \mathrm{R}^{2} \mathrm{~h}-1 / 4 π \mathrm{h}^{3}$

$\mathrm{dV} / \mathrm{dh}=π \mathrm{R}^{2}-3 / 4 π \mathrm{h}^{2} $

=$π\left(\mathrm{R}^{2}-3 / 4 \mathrm{~h}^{2}\right) $

$ \mathrm{dV} / \mathrm{dh}=0 $

$ \Rightarrow \mathrm{R}^{2}=3 / 4 \mathrm{~h}^{2}$

$\Rightarrow \mathrm{h}=2 \mathrm{R} / \sqrt{3} $

$ \mathrm{~d}^{2} \mathrm{~V} / \mathrm{dh}^{2}=-3 / 4 \times 2 π \mathrm{h} $ $\mathrm{h}=2 \mathrm{R} / \sqrt{3} $ पर, 

$ \mathrm{d}^{2} \mathrm{~V} / \mathrm{dh}^{2}=-3 / 4 \times 2 π(2 \mathrm{R} / \sqrt{3}) \\ =-\sqrt{3} π \mathrm{R} $

$ \mathrm{V} $ अधिकतम है  $\mathrm{h}=2 \mathrm{R} / \sqrt{3}  $ पर 

$ \mathrm{V}=1 / 4 π \mathrm{h}\left(4 \mathrm{R}^{2}-\mathrm{h}^{2}\right) $

=$1 / 4 π(2 \mathrm{R} / \sqrt{3})\left(4 \mathrm{R}^{2}-4 \mathrm{R}^{2} / 3\right) $ =$π \mathrm{R} / 2 \sqrt{3}\left(8 \mathrm{R}^{2} / 3\right) $

=$4 π \mathrm{R}^{3} / 3 \sqrt{3}  $sq. unit

18. सिद्ध कीजिए कि अर्द्धशीर्ष कोण $\varnothing$ और ऊंचाई $h$ के लंब वृत्तीय शंकु के अंतर्गत अधिकतम आयतन के बेलन की ऊंचाई, शंकु के ऊंचाई की एक तिहाई है और बेलन का अधिकतम आयतन $4 / 27 π \mathrm{h}^{3} \tan ^{2} \varnothing$ है।

उत्तर: मान लीजिए $\mathrm{VAB}$ एक शंकु है जिसके ऊंचाई $\mathrm{h}$ है, अर्द्धशीर्ष कोम $\varnothing$ है। मान लीजिए बेलन के आधार का त्रिज्या $x$ है। बेलन की ऊचाई $O O^{\prime}$ है।

$\begin{array}{l} \mathrm{OO}^{\prime}=\mathrm{VO}-\mathrm{VO}^{\prime} \\ =\mathrm{h}-\mathrm{x} \cot \varnothing \end{array}$

बेलन का आयतन $(\mathrm{V})=π \mathrm{x}^{2}(\mathrm{~h}-\mathrm{x} \cot \varnothing)$,

$\begin{array}{l} \mathrm{dV} / \mathrm{dx}=2 π \mathrm{xh}-3 π \mathrm{x}^{2} \cot \varnothing \\ \mathrm{dV} / \mathrm{dx}=0 \\ \Rightarrow 2 π \mathrm{xh}-3 π \mathrm{x}^{2} \cot \varnothing=0 \\ \Rightarrow \mathrm{x}=2 \mathrm{~h} \tan \varnothing / 3 \end{array}$

अब,

$ \mathrm{d}^{2} \mathrm{~V} / \mathrm{d} \mathrm{x}^{2}=2 π \mathrm{h}-6 π \mathrm{x} \cot \varnothing $

$ \mathrm{x}=2 \mathrm{~h} / 3 \tan \varnothing  $ पर

$ \mathrm{d}^{2} \mathrm{~V} / \mathrm{dx}^{2}=π(2 \mathrm{~h}-4 \mathrm{~h}) $ $=-2 π \mathrm{h}<0 $

$\mathrm{V}$ अधिकतम है जब $\mathrm{x}=2 \mathrm{~h} / 3 \tan \varnothing$ है $O O^{\prime}=h-x \cot \varnothing=h-2 h / 3=h / 3$

बेलन का अधिकतम आयतन :

$\begin{array}{l} \mathrm{V}=π(2 \mathrm{~h} \tan \varnothing / 3)^{2}(\mathrm{~h}-2 \mathrm{~h} / 3) \\ =4 / 27 π \mathrm{h}^{3} \tan ^{2} \varnothing \end{array}$

19 से 24 तक के प्रश्रों के सही उत्तर चुनिए:

19. एक $10 \mathrm{~m}$ त्रिज्या के बेलनाकार टंकी में $314 \mathrm{~m}^{3} / \mathrm{h}$ की दर मैं गेहूं भरा जाता है। भरे गए गेहूं की गहराई की वृद्धि दर है:

(A) $1 \mathrm{~m} / \mathrm{h}$

(B) $0.1 \mathrm{~m} / \mathrm{h}$

(C) $1.1 \mathrm{~m} / \mathrm{h}$

(D) $0.5 \mathrm{~m} / \mathrm{h}$

उत्तर: मान लीजिए बेलन का आयतन $\mathrm{V}$ है

बेलन का त्रिज्या $(\mathrm{r})=10 \mathrm{~cm}$

$\mathrm{V}=π \mathrm{r}^{2} \mathrm{~h}$

$=π(10)^{2} \mathrm{~h}=100 π \mathrm{h}$

$\mathrm{dV} / \mathrm{dt}=100 π \mathrm{dh} / \mathrm{dt}$

प्रश्न के अनुसार,

$\mathrm{dV} / \mathrm{dt}=314$

अब

$314=100 π \mathrm{dh} / \mathrm{dt}$

$\Rightarrow \mathrm{dh} / \mathrm{dt}=314 / 100(3.14)=1 \mathrm{cubic} \mathrm{m} / \mathrm{h}$

1 cubic $\mathrm{m} / \mathrm{h}$

अतः (A) सही उत्तर है

20. वक्र $\mathrm{x}=\mathrm{t}^{2}+3 \mathrm{t}-8, \mathrm{y}=2 \mathrm{t}^{2}-2 \mathrm{t}-5$ के बिंदु $(2,-1)$ पर स्पर्श रेखा की प्रवणता है:

(A) $22 / 7$

(B) $6 / 7$

(C) $7 / 6$

(D) $-6 / 7$

$-0^{-}-0 / 7$

उत्तर: $x=t^{2}+3 t-8, y=2 t^{2}-2 t-5$

$d x / \mathrm{dt}=2 t+3$

$d y / d t=4 t-2$

$d y / d x=d y / d t \times d t / d x$

$=(4 t-2) /(2 t+3)$

बिन्दु $(2,-1)$

$\mathrm{t}$ का सामात्य मान स्पर्श रे।

बिंदु $(2,-1)$ पर स्पर्श रेखा की प्रवणता: $4 \mathrm{v} / \mathrm{dx}=(4 \times 2-2) /(2 \times 2+3)=6 / 7$

$\mathrm{dy} / \mathrm{dx}$

$6 / 7$ अत: (B) सही उत्तर है

21. रेखा $y=m x+1$, वक्र $y^{2}=4 x$ की एक स्पर्श रेखा है यदि $m$ का मान है:

(A) 1

(B) 2

(C) 3

(D) $1 / 2$

उत्तर: वक्र की स्पर्श रेखा: $y=m x+1$

वक्र: $y^{2}=4 x$.

$2 \mathrm{y} \mathrm{dy} / \mathrm{dx}=4$

$\Rightarrow d y / d x=2 / y$

$\mathrm{y}=\mathrm{mx}+1$ वक्र $\mathrm{y}^{2}=4 \mathrm{x}$

$2 / \mathrm{y}=\mathrm{m}$

$\Rightarrow \mathrm{y}=2 / \mathrm{m}$

अब,

$\Rightarrow \mathrm{y}=\mathrm{c}_{2}$ अब, $\mathrm{y}^{2}=4 \mathrm{x}$ $\Rightarrow \mathrm{x}=\mathrm{y}^{2} / 4$ $\Rightarrow \mathrm{x}=1 / 4(2 / \mathrm{m})^{2}$ $\Rightarrow \mathrm{x}=1 / \mathrm{m}^{2}$ $\mathrm{y}=\mathrm{mx}+1$ $2 / \mathrm{m}=\mathrm{m}\left(1 / \mathrm{m}^{2}\right)+1$ $1 / \mathrm{m}=1$ $\mathrm{~m}=1$

(A) सही उत्तर है

22. वक्र $2 \mathrm{y}+\mathrm{x}^{2}=3$ के बिंदु $(1,1)$ पर अभिलंब का समीकरण है

(A) $x+y=0$

(B) $x-y=0$

(C) $x+y+1=0$

(D) $x-y=1$

उत्तर: $2 \mathrm{y}+\mathrm{x}^{2}=3$.

$2 \mathrm{dy} / \mathrm{dx}+2 \mathrm{x}=0$

$\mathrm{dy} / \mathrm{dx}=-\mathrm{x}$

अभिलम्ब कि प्रवणता

$=-1 /(\mathrm{dy} / \mathrm{dx})$

$=-1 /-1$

$=1$

अभिलंब का समीकरण :

$\begin{array}{l} y-1=1(x-1) \\ y-1=x-1 \\ x-y=0\end{array}$

अतः (B) सही उत्तर है

23. वक्र $\mathrm{x}^{2}=4 \mathrm{y}$ का बिंदु $(1,2)$ से हो कर जाने वाला अभिलंब है:

(A) $x+y=3$

(B) $x-y=3$

(C) $x+y=1$

(D) $x-y=1$

उत्तर: $\mathrm{x}^{2}=4 \mathrm{y}$

मान लीजिए $(a, b)$ एक बिंदु है वक्र पर जिससे होकर अभिलंब जाएगा।

$a^{2}=4 b $

$ 2 x=4 \mathrm{dy} / d x $

$ \Rightarrow \mathrm{dy} / \mathrm{dx}=\mathrm{x} / 2 $

$ \Rightarrow \mathrm{dy} / \mathrm{dx}=\mathrm{a} / 2 $

$(a,b)$ पर अभिलम्ब 

$\mathrm{y}-\mathrm{b}=(\mathrm{x}-\mathrm{a}) /(\mathrm{dy} / \mathrm{dx})$

$ \Rightarrow \mathrm{y}-\mathrm{b}=-2(\mathrm{x}-\mathrm{a}) / \mathrm{a} $

$(1,2)$  पर 

$ 2-\mathrm{b}=-2(1-\mathrm{a}) / \mathrm{a} $

$ 2-\mathrm{b}=2 / \mathrm{a}+2 $

$ \Rightarrow \mathrm{b}=2 / \mathrm{a} $  अब 

$ \mathrm{a}^{2}=4 \mathrm{~b} $

$ \Rightarrow \mathrm{a}^{2}=4 \times 2 / \mathrm{a} $

$ \Rightarrow \mathrm{a}^{3}=8 $

$ \Rightarrow \mathrm{a}=2 $

$ \mathrm{~b}=\mathrm{a}^{2} / 4 $

$ \Rightarrow \mathrm{b}=4 / 4=1 $ $\mathrm{y}-\mathrm{b}=-2(\mathrm{x}-\mathrm{a}) / \mathrm{a} $

$ \Rightarrow \mathrm{y}-1=-2(\mathrm{x}-2) / 2 $

$\Rightarrow \mathrm{y}-1=-\mathrm{x}+2 $

$ \Rightarrow \mathrm{x}+\mathrm{y}=3 $

अतः (A) सही उत्तर है

24. वक्र $9 y^{2}=x^{3}$ पर वे बिंदु जहां पर चक्र का अभिलंब अक्षों से समान अंतः खंड बनाता है:

(A) $(4, \pm 8 / 3)$

(B) $(4,-8 / 3)$

(C) $(4, \pm 3 / 8)$

(D) $(\pm 4,3 / 8)$

उत्तर: $9 \mathrm{y}^{2}=\mathrm{x}^{3}$

$18 \mathrm{y} \mathrm{dy} / \mathrm{dx}=3 \mathrm{x}^{2}$

$\Rightarrow \mathrm{dy} / \mathrm{dx}=\mathrm{x}^{2} / 6 \mathrm{y}$

मान लीजिए $(a, b)$ एक बिंदु है वक्र पर जहां पर चक्र का अभिलंब भक्षों के सामान अंतः खंड बनाता है।

$ 9 b^{2}=a^{2} $ 

$(a, b)$  पर  

$ -1 /(d y / d x)=-1 / a^{2} / 6 b=-6 b / a^{2} $

अभिलंब अक्षों से समान अंतः खंड बनाता है इसलिए अभिलंब के प्रवणता = $\tan 45$ या =$\tan 135^{\circ} =\pm 1$

$-6 b / a^{2}=\pm 1$

$\Rightarrow b=\pm a^{2} / 6$

अब,

$ 9 b^{2}=a^{3}$

$ \Rightarrow 9\left(\pm-a^{2}6\right)^{2}=a^{3}$

$ \Rightarrow a^{4}=4 a^{3} $

$\Rightarrow a^{3}(a-4)=0 $

$\Rightarrow a=0 $ या $a=4 $

$ a=4, b=\pm 4^{2} / 6=\pm 8 / 3 $

$ (4, \pm 8 / 3) $

अतः (A) सही उत्तर है

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives In Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 12 Maths Chapter 6 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 12 Maths Chapter 6 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 12 Maths Chapter 6 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 12 Maths Application of Derivatives solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that.

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 12 Maths Application of Derivatives in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 12 can download these solutions at any time as per their convenience for self-study purpose.

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 12 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.