Statistics Class 9 Important Questions with Answers PDF Download
Class 9 Maths Chapter 12 Important Questions from Statistics chapter includes the content developed by experts on various topics of collection and representation of data, graphical representation of data using a bar graph, Histogram, and Pie Chart, Measures of central tendency, i.e., mean, median, and mode and exercise problems.
 Table of Content
Table of ContentVedantu provides FREE PDF solutions on Important Questions for Class 9 Maths Chapter 12 Statistics according to CBSE Class 9 Maths Syllabus which is useful for students to prepare for their exams. Also one can refer to Class 9 Maths Important Questions to learn all the maths concepts and to solve problems effectively.
Access Class 9 Maths Chapter 12: Statistics Important Questions
Section A
1. If the mean of $2,4,6,8,{\text{x}},{\text{y}}$ is 5 then find the value of x+y.
Ans: 10
2. Write the class mark of $90 - 110$ group.
Ans: 100
3. If the ratio of mean and median of a certain data is 2: 3, then find the ratio of its mode and mean.
Ans: 5:2
4. Tally marks are used to find ...............
Ans: Frequency
5. The following marks were obtained by the students in a test. 81,72,90,90,86,85,92,70,71,83,89,95,85,79,62. What is the range?
Ans: 33
6. In a histogram, each class rectangle is constructed with base as
1. frequency
2. class interval
3. range
4. size of the class
Ans: class interval
Section B
7. The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?
Ans: Let ${{\text{x}}_1},{{\text{x}}_2}, \ldots {x_{10}}$ be 10 numbers with their mean equal to 20 .
Then,
$\bar X = \dfrac{1}{n}\left( {\sum{{x_i}} } \right)$
$20 = \dfrac{{{x_1} + {x_2} + \ldots .. + {x_{20}}}}{{10}}$
$\Rightarrow 200 = {{\text{x}}_1} + {x_2} + \ldots . + {x_{10}}$
New numbers are ${{x}_{1}}-5,\ {{x}_{2}}-5,\ \ldots \text{}\!\!~\!\!\text{ }\ldots ,\ {{x}_{10}}-5$
Let $\bar X$ be the mean of new number.
$\bar{X}\text{ }\!\!~\!\!\text{}=\dfrac{\left( {{x}_{1}}-5 \right)+\left( {{x}_{2}}-5 \right)+\text{}\!\!~\!\!\text{ }\ldots .+\left( {{x}_{10}}-5 \right)}{10}$
$X=\dfrac{\left({{x}_{1}}+{{x}_{2}}+\text{ }\!\!~\!\!\text{ }\ldots \text{ }\!\!~\!\!\text{}\ldots \text{ }\!\!~\!\!\text{ }+{{x}_{10}} \right)-5\times 10}{10}$
$=\dfrac{200-50}{10}=15$
8. Find the mean of the first 10 even natural no.
Ans: \[\bar{x}\ =\ \dfrac{2+4+6+8+10+12+14+16+18+20}{10}\ =\ \dfrac{10\ \times \ 11}{10}\ =\ 11\]
9. Calculate the mean for the following distribution.
$\begin{array}{*{20}{c}}{\mathbf{x}}&5&6&7&8&9 \\ {\mathbf{f}}&4&8&{14}&{11}&3 \\ \end{array}$
Ans: 7.025
10. Find the median of 37, 31, 42, 43, 46, 25, 39, 45, 32.
Ans: 39
11. Find the mode of the following series. 25, 23, 22, 22, 24, 27, 27, 25, 23, 22, 26, 32.
Ans: 22
12. If the median of a series of data is 3 and mean is 2 then, find the mode.
Ans: 5
Section C
13. Find the median of the following data 19, 25, 59, 48, 35, 31, 30, 32, 51. If 25 is replaced by 52, what will be the new median.
Ans: 32, 35
14. If the mean of the following distribution is 6, then find the value of p.
$\begin{array}{*{20}{c}} {\mathbf{x}}&2&4&6&{10}&{p + {\mathbf{5}}} \\ {\mathbf{f}}&3&2&3&1&2 \\ \end{array}$
Ans: 7
15. If the mean of five observations ${\text{x}},{\text{x}} + 2,{\text{x}} + 4,{\text{x}} + 6,{\text{x}} + 8$ is 11, find the mean of first three observation.
Ans: 9
16. The mean of 5 numbers is 18. If one number is excluded, their mean is 16, find the excluded number.
Ans: 26
17. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
$29,32,48,50,x,x + 2,72,78,84,95$
Ans: 62
Section D
18. Find the value of x and y in the following distribution if it is known that the mean of the distribution is 1.46.
Ans: $x = 76,y = 38$
19. The mean monthly salary of 10 members of a group is Rs 1445 , one more member whose monthly salary is Rs 1500 has joined the group. Find the mean monthly salary of 11 members of the group.
Ans: Rs 1450
20. Given below is a cumulative frequency distribution table showing the age of people living in a locality.
Age in years | Number of persons |
Above 108 | 0 |
Above 96 | 1 |
Above 84 | 3 |
Above 72 | 5 |
Above 60 | 20 |
Above 48 | 158 |
Above 36 | 427 |
Above 24 | 809 |
Above 12 | 1026 |
Above 0 | 1124 |
Prepare a frequency distribution table.
Ans: $\begin{array}{*{20}{c}} {{\text{ Marks }}}&{0 - 12}&{12 - 24}&{24 - 36}&{36 - 48}&{48 - 60}&{60 - 72}&{72 - 84}&{84 - 96}&{96 - 108} \\ {{\text{ Person }}}&{98}&{217}&{382}&{269}&{138}&{15}&2&2&1 \\ \end{array}$
21. If ${\mathbf{x}},{{\mathbf{x}}_2} \ldots ..{{\text{x}}_{\text{n}}}$ are ${\mathbf{n}}$ values of a variable x such that $\sum\limits_{i = 1}^n {\left( {{x_1} - 2} \right)} = 110$ and $\sum\limits_{i = 1}^n {\left( {{x_1} - 5}\right)} = 20$ find the value of n and mean.
Ans: $\sum\limits_{i = 1}^n {\left( {{x_1} - 2} \right)} = 110$
\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}-\ \ 2n}\text{ }\!\!~\!\!\text{ }=110\]
\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}=\ \ 2n}\text{ }\!\!~\!\!\text{ +}110\]
$\sum\limits_{i = 1}^n {\left( {{x_1} - 5} \right)} = 20$
\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}-\ \ 5n}\text{ }\!\!~\!\!\text{ }=20\]
\[\Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{1}}=\ \ 5n}\text{ }\!\!~\!\!\text{ +20}\]
\[\Rightarrow \ 5n~+20\ =\ 2n\ +\ 110\]
\[ \Rightarrow 3n = 90 \]
\[ \Rightarrow n=30 \]
\[\Rightarrow \ \bar{x}=\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{1}}}}{n}\text{ }\!\!~\!\!\text{ =}\ \dfrac{2n+110}{n}\ =\ \dfrac{2(30)\,\ +110}{30}\ =\ \dfrac{170}{30}\ =\ \dfrac{17}{3}\]
n $= 30$, mean $= \;\dfrac{{17}}{3}$
22. The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Ans:
\[ \bar{x}\ =\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n}\ \]
\[ \Rightarrow \ 50\ =\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{200} \]
\[ \Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{i}}}\ =\ 200\ \times \ 50\ =\ 10000 \]
For new mean,
\[ \Rightarrow \ \sum\limits_{i=1}^{n}{{{x}_{i}}}\ =\ 10000-\ (92\ +\ 8)\ +\ (192\ +\ 88)\ \ =\ 10180 \]
\[ \Rightarrow \ \bar{x}\ =\ \dfrac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n}\ =\ \dfrac{10180}{200}\ =\ 50.9 \]
23. Find the value of p, if the mean of the following distribution is 20 .
$\begin{array}{*{20}{c}} {\text{x}}&{15}&{17}&{19}&{20 + {\text{p}}}&{23} \\ {{\text{ frequency }}}&2&3&4&{5{\text{p}}}&6 \\ \end{array}$
Ans: 1
Important Questions
1 Marks Questions
1. If the mean of $2,4,6,8,{\text{x}},{\text{y}}$ is 5 then find the value of x+y.
Ans: 10
2. Write the class mark of $90 - 110$ group.
Ans: 100
3. If the ratio of mean and median of a certain data is 2: 3, then find the ratio of its
mode and mean.
Ans: 5:2
4. Tally marks are used to find ...............
Ans: Frequency
5. The following marks were obtained by the students in a test. 81,72,90,90,86,85,92,70,71,83,89,95,85,79,62. What is the range?
Ans: 33
6. In a histogram, each class rectangle is constructed with base as
1. frequency
2. class interval
3. range
4. size of the class
Ans: class interval
7. Find the range of the following data: 25, 20, 30, 18, 16, 15.
(a) 15
(b) 10
(c) 5
(d) 20
Ans: (a) 15
8. Find the median of the given data: 7, 8, 7, 7, 9, 10, 13.
(a) 7
(b) 9
(c) 8
(d) 10
Ans: (c) 8
9. Find the mode of the given data: 7, 9, 11, 13, 9, 13, 9, 9, 7, 8.
(a) 10
(b) 9
(c) 11
(d) 8
Ans: (b) 9
10. Find the mean of the first five multiples of 3?
(a) 9
(b) 12
(c) 14
(d) None of these
Ans: (a) 9
11. The mean of 7 observations is 20. If the mean of the first 4 observations is 12 & that of last 4 observations is 28, find the ${4^{{\text{th }}}}$observation ?
Ans: Since mean of 7 observations $ = 20$
$\therefore $ Total of 7 observations $ = 20 \times 7 = 140$
$\therefore $ Mean of first 4 observations $ = \;12$ $ \Rightarrow $ Total of first 4 observations $ = 12 \times 4 = 48$
$\therefore $ Mean of last 4 observations $ = \;28$ $ \Rightarrow $ Total of first 4 observations $ = 4 \times 28 = 92$
$\therefore $ Total of 7 observations $ + {4^{{\text{th }}}}$ observation $ = 48 + 92$
$140 + {4^{{\text{th }}}}$ observation $ = 140$
$ \Rightarrow {4^{{\text{th }}}}$observation $ = 140 - 140 = 0$
12. What is the upper limit of the interval: $20 - 23?$
(a) 20
(b) 23
(c) 22
(d) None of these
Ans: (b) 23
13. What is class size of interval 10, 12, 14, 16, 18 ?
(a) 2
(b) 1
(c) 10
(d) 18
Ans: (a) 2
14. Find the class mark of the interval $15.7 - 25.7?$
(a) 15.3
(b) 16.3
(c) 17.3
(d) 20.7
Ans: (a) 20.7
15. what is the mid-point of class interval $12.3 - 22.3\;?$
(a) 17.3
(b) 15.3
(c) 18.3
(d) 16.7
Ans: (a) 17.3
16. The median of the following observations arranged in ascending order is 40. find x $15,\;12,\;11,\;14,\;x + 2,\;x + 4,\;32,\;30,\;41,\;35$
Ans: No. of observation $ = 10$ which is even
$\therefore $ Median is the average of ${\left( {\dfrac{n}{2}} \right)^{th}}\;\& \;{\left( {\dfrac{n}{2} + 1} \right)^{th}}$ abservations
So, ${5^{{\text{th }}}}$ observation $ = x + 2$and ${6^{{\text{th }}}}$observation $ = x + 4$
Median $ = \dfrac{{(x + 2) + (x + 4)}}{2}$
$40 = \dfrac{{2x + 6}}{2}$
$40 = x + 3$
$\therefore x = 37$
17. What is the class Mark of the interval 15-20 ?
(A) 15
(B) 20
(C) 17.5
(D) none of these
Ans: (C) 17.5
18. What is the range of interval 15-20?
(A) 5
(B) 10
(C) 15
(D) none of these
Ans: (A) 5
19. What is the class - size of the interval 15-20?
(A) 5
(B) 10
(C) 15
(D) none of these
Ans: (A) 5
20. Find out the mean of following data. 5,10,15,20,25,30.
(A) 16.5
(B) 17.5
(C) 18.5
(D) none of these
Ans: (B) 17.5
21. Find the arithmetic mean of first 6 natural numbers?
(a) 3.5
(b) 4.5
(c) 2.5
(d) none of these
Ans: (a) 3.5
22. What is the mid-point of interval 3-6 ?
(a) 3.5
(b) 4.5
(c) 5.5
(d) none of these
Ans: (b) 4.5
23. Find out the range of the following: 5, 10, 15, 20, 25, 30.
(a) 25
(b) 20
(c) 30
(d) none of these
Ans: (a) 25
24. Find out the mode of the following: 5, 4, 3, 5, 6, 6, 6, 5, 4, 5, 5, 3, 2, 1.
(a) 6
(b) 4
(c) 5
(d) none of these
Ans: (c) 5
25. What is the class size of the intervals 10-20 ?
(a) 10
(b) 5
(c) 15
(d) 20
Ans: (a) 10
26. What is the upper class limit of the class 37-43 ?
(a) 37
(b) 40
(c) 43
(d) none of these
Ans: (c) 43
27. What is the lower class limit of the class 37-43 ?
(a) 37
(b) 40
(c) 43
(d) none of these
Ans: (a) 37
28. Find the median of the following data: 15, 35, 18, 26, 19, 25, 29, 20, 27, 30.
(a) 25.5
(b) 24.5
(c) 26.5
(d) none of these
Ans: (a) 25.5
2 Marks Questions
1. The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?
Ans: 15
2. Find the mean of first 10 even natural no.
Ans: 11
3. Calculate the mean for the following distribution.
$\begin{array}{*{20}{c}} {\mathbf{x}}&{\mathbf{5}}&{\mathbf{6}}&7&{\mathbf{8}}&{\mathbf{9}} \\ {\mathbf{f}}&{\mathbf{4}}&{\mathbf{8}}&{{\mathbf{14}}}&{{\mathbf{11}}}&{\mathbf{3}} \\ \end{array}$
Ans: 7.025
4. Find the median of 37, 31, 42, 43, 46, 25, 39, 45, 32.
Ans: 39
5. Find the mode of following series. 25, 23, 22, 22, 24, 27, 27, 25, 23, 22, 26, 32.
Ans: 22
6. If the median of a series of data is 3 and mean is 2 then, find the mode.
Ans: 5
7. If the mean of 5 observation ${\text{x}},{\text{x}} + 4,{\text{x}} + 8,{\text{x}} + 12,{\text{x}} + 16$ is 13, find the mean of the observations?
Ans: $\bar x = \dfrac{{{{\sum x }_i}}}{n}$
$ \Rightarrow 13 = \dfrac{{x + (x + 4) + (x + 8) + (x + 12) + (x + 16)}}{5}$
$ \Rightarrow 5 \times 13 = 5x + 40$
$ \Rightarrow 13 = x + 8$
$\therefore x = 5$
$\therefore $ The five given observations are 5, 9, 13, 17, 21
$\bar x = \dfrac{{5 + 9 + + 13 + 17 + 21}}{5} = 12.8$
8. The class marks of the observations are 17, 21, 25, 29, 33, 37, 41, 45. Find the class intervals.
Ans: Class marks are 17, 21, 25, 29, 33, 37, 41 and 45
Class size $ = \;21 - 17\; = \;25 - 21\; = \;4$
Half of class size $ = \dfrac{4}{2} = 2$
Thus, Class intervals are:
17-2=15 | & | 17+2=19 | i.e | 15-19 |
21-2=19 | & | 21+2=23 | i.e | 19-23 |
25-2=23 | & | 25+2=27 | i.e | 23-27 |
29-2=27 | & | 29+2=31 | i.e | 27-31 |
33-2=31 | & | 33+2=35 | i.e | 31-35 |
37-2=35 | & | 37+2=39 | i.e | 35-39 |
41-2=39 | & | 41+2=43 | i.e | 39-43 |
45-2=43 | & | 45+2=47 | i.e | 43-47 |
9. The value of $\pi $ up to 15 decimal places is: $3.419078023195679$
(i) List the digits from 0 to 9 & make frequency distributions of the digit after the decimal points.
(ii) What are the most and the least frequently occurring digits?
Ans: (i) Frequency distribution table
Digits | Tally Marks | Frequency |
0 | || | 2 |
1 | || | 2 |
2 | | | 1 |
3 | | | 1 |
4 | | | 1 |
5 | | | 1 |
6 | | | 1 |
7 | || | 2 |
8 | | | 1 |
9 | ||| | 3 |
(ii) Most frequency occurring digits $ = \;9$
Least frequently occurring digits $ = \;2,\;3,\;4,\;5,\;6,\;8$
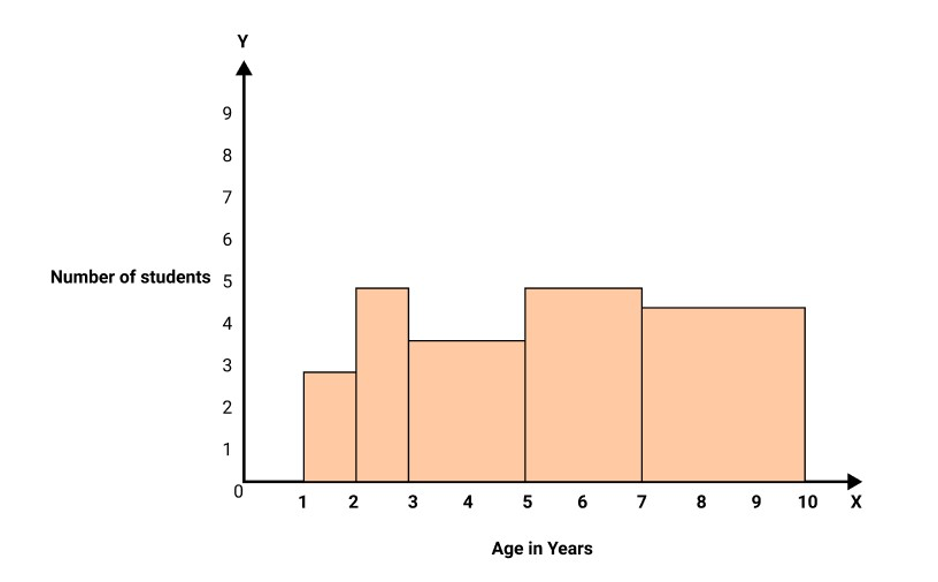
10. A random survey of the number of children of various age group playing in the park was found:
$\begin{array}{*{20}{c}} {{\text{Age}}[{\text{in years}}]}&{1 - 2}&{2 - 3}&{3.5}&{5 - 7}&{7 \cdot 10} \\ {{\text{ No}}{\text{. of children }}}&3&5&7&{10}&{13} \\ \end{array}$
Draw a histogram to represent the data above?
Ans: we will calculate the adjusted frequencies [AF] for histogram because the class intervals are not of equal width.
Minimum class size [CS] = 1
Age (In Years) | Frequency | Class Size(CS) | ${\text{AF = }}\dfrac{{{\text{Minimum CS}}}}{{{\text{CS of this class}}}}{\text{ \times Its frequency}}$ |
1-2 | 3 | 1 | $\dfrac{1}{1} \times 3 = 3$ |
2-3 | 5 | 1 | $\dfrac{1}{1} \times 5 = 5$ |
3-5 | 7 | 2 | $\dfrac{1}{2} \times 7 = 3.5$ |
5-7 | 10 | 2 | $\dfrac{1}{2} \times 10 = 5$ |
7-10 | 13 | 3 | $\dfrac{1}{3} \times 13 = 4.3$ |
To get the required histogram, draw rectangles with base equal to class interval and heights equal to the corresponding adjusted frequencies.
11. The mean of $20,\;8,\;12,\;13,\;15\;{\text{\& }}\;P$ is 30 . Find the value of $P$ ?
Ans. Mean $ = \bar x = \dfrac{{20 + 8 + 12 + 13 + 15 + P}}{6}$
$30 = \dfrac{{68 + P}}{6}$
$ \Rightarrow 180 = 68 + P$
$\therefore P = 180 - 68 = 112$
12. Find the mode of the following data: 14, 25, 14, 14, 25, 24, 20, 28, 18, 20.
Ans: Arrange the given data in ascending order:
14, 14, 14, 18, 20, 20, 24, 25, 25, 28
The value 14 occurs most frequently i.e. 3 times as observed.
So, Mode is 14
13. Find the median of 5, 7, 10, 9, 5, 12, 15, 12, 18, 20. If 9 is replaced by 14, what will be the new median?
Ans: Arrange the given data in ascending order:
5, 5, 7, 9, 10, 12, 15, 18, 20
Here, ${\text{n}} = 10$ [even number]
So, Median $ = \dfrac{{{5^{{\text{th }}}}{\text{ observation }} + {6^{{\text{th }}}}{\text{ observaiton }}}}{2} = \dfrac{{10 + 12}}{2} = 11$
After replacing 9 by 14:
5, 5, 7, 10, 12, 12, 14, 15, 18, 20
Now, ${5^{{\text{th }}}}$observation $ = {6^{{\text{th }}}}$observation $ = 12$
So, New Median $ = \dfrac{{12 + 12}}{2} = 12$
14. The average mark of boys in an examination is 68 & that of girls in 89. If the average mark of all candidates in that examination is 80 , find the ratio of the no. of boys to the number of girls that appeared in the examinations.
Ans: Let number of boys be $x$ & girls be y .
$\therefore $ Total marks of boys $ = 68 \times x = 68{\text{x}}$
$\therefore $ Total marks of girls $ = 89 \times y = 89y$
Hence, total marks for boys & girls $ = \;68x + 89y$
Also, total of boys & girls $ = x + y$ & average for all the candidates $ = 80$
$ \Rightarrow \;\;80\; = \;\dfrac{{68x + 89y}}{{x\; + \,y}}$
$80x + 80y = 68x + 89y$
$80x - 68x = 89y - 80y$
$12x = 9y$
$ \Rightarrow \;\dfrac{x}{y} = \dfrac{9}{{12}} = \dfrac{3}{4}$
$\therefore $ Ratio of boys & girls $ = 3:4$
15. The mean of 6 numbers is 30. If one number is excluded, their mean is 24. Find the excluded number.
Ans: Here, ${\text{n}} = 6\;,\;\;\bar x = 30$
$\therefore \;\;\overline x = \dfrac{1}{n}\left( {\sum {{x_i}} } \right)\; \Rightarrow \;\sum {{x_i}} = n\overline x $
$\sum {{x_i}} = 6 \times 30 = 180$
So, total of 6 numbers $ = 180$
Let the excluded number be a.
Now, total of 5 number is 180 -a
Mean of 5 number $ = \dfrac{{180 - a}}{5}$
$ \Rightarrow 24 = \dfrac{{180 - a}}{5}$
$ \Rightarrow 24 \times 5 = 180 - a$
$ \Rightarrow a = 180 - 120$
$ \Rightarrow a = 60$
Thus, excluded number is 60.
16. The median of the observation $11,\;12,\;14,\;18,\;x + 2,\;x + 4,\;30,\;32,\;35,\;41$, arranged in ascending order is 24 . find the value of x.
Ans: Number of observation, ${\text{n}}\;{\text{ = }}\;10$
Since ${\text{n}}$ is even,
$\therefore $ median $ = \dfrac{{{{\left[ {\dfrac{n}{2}} \right]}^{th}}{\text{observation }} + {{\left[ {\dfrac{n}{2} + 1} \right]}^{th}}{\text{ observation }}}}{2}$
$ \Rightarrow 24 = \dfrac{{{5^{th}}{\text{observation }} + {6^{th}}{\text{ observation }}}}{2}$
$ \Rightarrow 24 = \dfrac{{(x + 2) + (x + 4)}}{2}$
$ \Rightarrow 24 = \dfrac{{2x + 6}}{2} \Rightarrow 24 = x + 3$
$ \Rightarrow x = 21$
So, ${\text{x}} = 21$
17. Find the median of the following data: 25, 34, 31, 23, 22, 26, 35, 28, 20, 32.
Ans: Arrange the data in ascending order:
20, 22, 23, 25, 26, 28, 31, 32, 34, 35.
Hence, the no. of observation $n\; = \;10$ (even)
$ \Rightarrow \;{\text{median}}\; = \dfrac{{{5^{th}}{\text{observation }} + {6^{th}}{\text{ observation }}}}{2}$
$ = \dfrac{{26 + 28}}{2} = 27$
So, median of the data is 27 .
18. In x standard, these are three sections A, B, C with 25, 40 and 30 students respectively. The average mark of section A is $70\% $, of section B is $65\% $ and of section B is $50\% $. Find the average marks of the entire X standard.
Ans: ${n_1} = 25,{n_2} = 40,{n_3} = 35$
${\bar x_1} = 70,{\bar x_2} = 65$, and ${\overline x _3} = 50$
Let $\overline X $, denote the average mark of the entire X standard.
Then, $\bar X = \dfrac{{{n_1}{{\bar X}_1} + {{\text{n}}_2}{{\bar X}_2} + {{\text{n}}_3}{{\bar X}_3}}}{{{n_2} + {{\text{n}}_2} + {{\text{n}}_3}}}$
$ = \dfrac{{25 \times 70 + 40 \times 65 + 35 \times 50}}{{25 + 40 + 35}}$
$ = \dfrac{{1750 + 2600 + 1750}}{{100}}$
$ = \dfrac{{6100}}{{100}} = 61$
So, the average marks of the entire X standard is $61\% $.
19. If $\bar x$ is a mean of ${x_1}{\text{,}}\;{{\text{x}}_2},\;{{\text{x}}_3} - - - - - - {{\text{x}}_n}$ then the mean of $a{x_1},\;a{x_2},\; - - - - ,\;a{x_n}$ is $a\bar x$ where ‘a’ is any number different from 2 era i.e. if each observation is multiplied by a non 2 era number a, then the mean is also multiplied by a.
Ans: We have: $\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{X_i}} } \right]$
Let $X$ be the mean of $a{x_1},a{x_2} \ldots .a{x_n}$. Then,
$X = \dfrac{{a{x_1} + a{x_2} + \ldots + a{x_n}}}{n}$
$ = \dfrac{{a\left( {{{\text{x}}_1} + {{\text{x}}_7} + \ldots \ldots + {{\text{x}}_n}} \right)}}{n}$
$ = {\text{a}}\left[ {\dfrac{1}{n}\sum\limits_{i = 1}^n {{X_i}} } \right]$
$ = a\overline X $
Thus, mean gets multiplied by a.
20. The class marks of a distribution are 26, 31, 41, 36, 46, 51, 56, 61, 66, 71. Find the true class limits.
Ans: Class size is the difference between any two consecutive class marks because class marks are uniformly spaced.
$\therefore $ Class size $ = 31 - 26 = 5$
If a is the class mark of a class interval of size $h$, then the lower and upper limits of the class intervals are $a - \dfrac{h}{2}$ and $a + \dfrac{n}{2}$ respectively .
Here ${\text{h}} = 5$
$\therefore $ Lower limit of first class interval $ = 26 - \dfrac{5}{2} = 23.5$ and upper limit of first class interval $ = 26 + \dfrac{5}{2} = 28.5$
$\therefore $ First class interval is 23.5-28.5
So, true class limits:
$23.5 - 28.5,\;\;28.5 - 33.5,\;\;33.5 - 38.5,\;\;38.5 - 43.5,\;\;43.5 - 48.5,\;\;48.5 - 53.5$
21. The marks obtained by 15 students in an examination are given below;
125, 130, 130, 120, 141, 146, 162, 163, 169, 173, 179, 188, 192, 195, 199.
Form a cumulative frequency table with class interval of length 20.
Ans:
Class Interval | Tally Marks | Frequency | Cumulative frequency |
120-140 | $||||$ | 4 | 4 |
140-160 | \[||\] | 2 | 6 |
160-180 | \[{{||||}}\] | 5 | 11 |
180-200 | $||||$ | 4 | 15 |
Total |
| 15 | 15 |
|
|
|
|
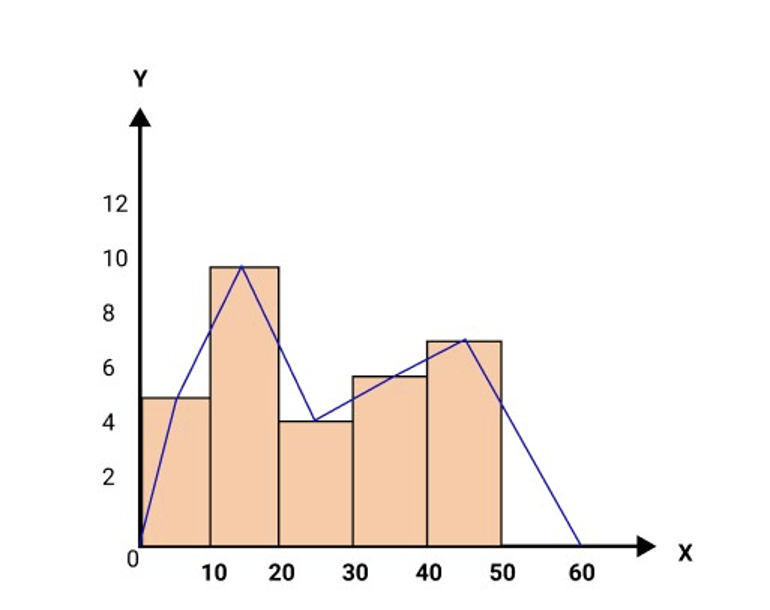
22. For the following data, draw a histogram and a frequency polygon.
Mark | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
No. of Students | 5 | 10 | 4 | 6 | 7 |
Ans:
23. If $X$ is the mean of $n$ observation ${x_1},{{\text{x}}_2} \ldots \ldots ,{x_n}$, then prove that the mean of ${x_1} - a,\;{x_2} - a \ldots ..,\;{x_n} - a$, is $X - a$, where a is any real number.
Ans: We have $\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{X_t}} } \right]$
Let $X$ be the mean of ${x_1} - {a_2},\;{x_2} - a,... \ldots ,\;{x_3} - a$.
Then, $X = \dfrac{{\left( {{x_1} - a} \right) + \left( {{x_2} - a} \right) + \ldots . + \left( {{x_n} - a} \right)}}{n}$
$ = \dfrac{{\left( {{x_1} + {x_1} + \ldots .{x_n}} \right) - na}}{n}$
$ = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{X_t}} } \right] - \dfrac{{na}}{a}$
$ = \bar X - a\quad $
Hence, proved.
24. The mean of 16 numbers is 8. If 2 is added to every number, what will be new mean?
Ans: Let ${{\text{x}}_1},{{\text{x}}_2}{{\text{x}}_3} \ldots \ldots ,{x_{16}}$ be 16 numbers with their mean equal to 8 .
Then, $\bar X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right)$
$ \Rightarrow 8 = \dfrac{{{x_1} + {x_2} + \ldots .. + {x_{15}}}}{{16}}$
$ \Rightarrow 16 \times 8 = {x_1} + {x_2} + \ldots \ldots + {x_{16}}$
New numbers are : ${x_1} + 2,\;{{\text{x}}_2} + 2,\;{{\text{x}}_3} + 2,\; \ldots \ldots ,\;{x_{16}} + 2$
Let $X$ Be the mean of new numbers. Then,
$X = \dfrac{{\left( {{x_1} + 2} \right) + \left( {{x_2} + 2} \right) + \ldots .. + \left( {{x_{16}} + 2} \right)}}{{16}}$
$ = \dfrac{{\left( {{x_1} + {x_2} + \ldots \ldots + {x_{16}}} \right) + 2 \times 16}}{{16}}$
$ = \dfrac{{128 + 32}}{{16}}$
$ = \dfrac{{160}}{{16}} = 10$
25. Calculate the mean from the given data.
Mark | 15 | 20 | 25 | 30 | 35 | 40 |
No. of students | 6 | 7 | 12 | 14 | 15 | 6 |
Ans:
${x_i}$ | ${f_i}$ | ${f_1} \times {x_i}$ |
15 | 6 | 90 |
20 | 7 | 140 |
25 | 12 | 300 |
30 | 14 | 420 |
35 | 15 | 525 |
40 | 6 | 240 |
${\sum f _i} = n = 60$ and ${\sum f _i}{x_i} = 1715$
$\therefore $ mean $ = \dfrac{{{{\sum f }_i}{x_i}}}{n} = \dfrac{{1715}}{{60}} = 28.5$
26. The following table gives the mark scored by 50 students in an entrance examination:
Mark | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
No. of students | 7 | 6 | 13 | 16 | 8 |
From this table find:
(i) the less than series and
(ii) the more than series.
Ans: (i) Less than cumulative frequency table.
Mark Obtained | Number of Students (Cumulative Frequency) |
Less than 20 | 7 |
Less than 40 | 13 |
Less than 60 | 26 |
Less than 80 | 42 |
Less than 100 | 50 |
(ii) More than cumulative frequency table.
Mark Obtained | Number of Students (Cumulative Frequency) |
More than 0 | 50 |
More than 20 | 43 |
More than 40 | 37 |
More than 60 | 24 |
More than 80 | 8 |
More than 100 | 0 |
27. Find the sum of the deviations of the various values 3, 4, 6, 8, 14 from their mean.
Ans: Recall that the deviations of the values ${{\text{x}}_1},{{\text{x}}_2},{{\text{x}}_3} \ldots \ldots .{{\text{x}}_{\text{n}}}$ about ${\text{A}}$ are
${{\text{X}}_1} - {\text{A}},\;\;{{\text{x}}_2} - {\text{A}},\;\;{{\text{x}}_3} - {\text{A,}}\;\; \ldots \ldots \ldots .,\;{{\text{x}}_{\text{n}}} - {\text{A}}$
Let $X$ be the deviations of the values 3, 4, 6, 8, 14. Then,
$X = \dfrac{{3 + 4 + 6 + 8 + 14}}{5} = \dfrac{{35}}{5} = 7$
Now, sum of the deviations of the values 3, 4, 6, 8 and 14 , From their mean $\overline X = 7$ is given by
$(3 - 7) + (4 - 7) + (6 - 7) + (8 - 7) + (14 - 4) = - 4 - 3 - 1 + 1 + 7 = 0$
28. The mean of 40 observations was 200 . It was detected on rechecking that the value of 65 was wrongly copied as 25 for computation of mean. Find the correct mean.
Ans: ${\text{n}} = 40,\;\;\overline X = 200$
So, $X = \dfrac{1}{n}\left( {\sum x } \right) \Rightarrow 200 = \dfrac{1}{{40}}\left( {\sum {{x_i}} } \right)$
$\sum {{x_1}} = 200 \times 40 = 8000$
$\therefore $ Incorrect value of $\sum x = 8000$
correct value of $\sum {{x_i}} = $ incorrect value of $\sum {{x_1}} $- incorrect item + correct item $ = 8000 - 25 + 65\;\; = \;\;8040$
$\therefore $ correct mean $ = \dfrac{{8040}}{{40}} = 201$
29. It $\overline X $ is the mean of n observation ${x_1},\;{x_2}, \ldots \ldots .,\;{x_2}$, then prove that $\sum\limits_{i = 1}^n {\left( {{X_t} - \overline X } \right)} = 0$
i.e., the algebraic sum of deviations from mean is zero.
Ans: We have $\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$
$ \Rightarrow {\text{n}}\bar X = \sum\limits_{{\text{l}} = 1}^n {{x_i}} $
Now, $\sum\limits_{{\text{i}} = 1}^n {\left( {{x_{\text{i}}} - \bar X} \right)} = \left( {{x_i} - \bar X} \right) + \left( {{x_2} - \bar X} \right) + \ldots . + \left( {{{\text{x}}_n} - \bar X} \right)$
$ = \left( {{x_1} + {x_2} + \ldots . + {x_n}} \right) - n\overline X $
$ = \sum\limits_{{\text{i}} - 1}^n {{x_{\text{i}}}} - n\bar X$
$ = \;n\overline X \; - \;n\overline X $
= 0
So, $\sum\limits_{i = 1}^n {\left( {{x_i} - \bar X} \right)} = 0$
3 Marks Questions
1. Find the median of the following data 19, 25, 59, 48, 35, 31, 30, 32, 51. If 25 is replaced by 52, what will be the new median.
Ans: 32, 35
2. If the mean of the following distribution is 6, then find the value of p.
x | 2 | 4 | 6 | 10 | p+5 |
f | 3 | 2 | 3 | 1 | 2 |
Ans: 7
3. If the mean of five observations ${\text{x}},{\text{x}} + 2,{\text{x}} + 4,{\text{x}} + 6,{\text{x}} + 8$ is 11, find the mean of first three observation.
Ans: 9
4. The mean of 5 numbers is 18. If one number is excluded, their mean is 16, find the excluded number.
Ans: 26
5. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
$29,32,48,50,x,x + 2,72,78,84,95$
Ans: 62
6. (i) Find the mean of the following data: 25, 27, 19, 29, 21, 23, 25, 30, 28, 20.
Show that the sum of deviation of all the observations from the mean is zero.
(ii) Find the median of the data given above.
Ans: (i) Mean$ = \;\bar x = \dfrac{{25 + 27 + 19 + 29 + 21 + 23 + 25 + 30 + 28 + 20}}{{10}} = \dfrac{{247}}{{10}} = 24.7$
Sum of the deviations of all the observations from the mean $ = \sum\limits_{i = 1}^{10} {(x - \bar x)} $
$ = (25 - 24.7) + (27 - 24.7) + (19 - 24.7) + (27 - 24.7) + $
$(23 - 24.7) + (25 - 24.7) + (30 - 24.7) + (28 - 24.7) + (20 - 24.7)$
$ = 0.3 + 2.3 - 5.7 + 4.3 - 2.7 - 1.7 + 03 + 5.3 + 3.3 - 4.7 = 0$
(ii) Arranging the data in ascending order: $19,20,21,23,25,25,27,28,29,30$
Here, ${\text{n}} = 10$ [even number]
$\therefore $ Median $ = \;\;\dfrac{{{{\left[ {\dfrac{n}{2}} \right]}^{[th}}{\text{observation }} + {{\left[ {\dfrac{n}{2} + 1} \right]}^{th}}{\text{observation }}}}{2}$
$ = \dfrac{{{5^{{\text{th }}}}{\text{observation }} + {6^{{\text{th }}}}{\text{observation }}}}{2} = \dfrac{{25 + 25}}{2} = 25$
7. If the mean of the following data is 21 . Find the value of ${\text{P}}$.
X 7 15 28 5 1
Y 8 20 P 3 2
Ans:
${x_i}$ | ${f_i}$ | ${f_1} \times {x_i}$ |
7 | 8 | 56 |
15 | 20 | 300 |
28 | p | 28p |
5 | 3 | 15 |
1 | 2 | 2 |
Total | 33+p | 373+28p |
$\sum {{f_i}} = 33 + P\quad \sum {{x_i}} {f_i} = 373 + 28P$
$\bar x = \dfrac{{\sum {{x_1}} {f_f}}}{{\sum {{f_i}} }}$
$21 = \dfrac{{373 + 28P}}{{33 + P}}$
$21 \times 33 + 21P = 373 + 28P$
$693 + 21P = 373 + 28P$
$693 - 373 = 28P - 21P$
$320 = 7P$
$P = \dfrac{{320}}{7}$
$\therefore P = 45.7$
8. In a mathematics test given to 10 students, the following marks [out of 100] are recorded as: 82, 41, 39, 52, 53, 45, 96, 47, 50, 60.
Find out the mean & median of the above marks.
Ans: The given observation are: 82, 41, 39, 52, 53, 45, 96, 47, 50, 60
Sum of 10 observations $ = 82 + 41 + 39 + 52 + 53 + 45 + 96 + 47 + 50 + 60\; = \;565$
$\bar X = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$
$\therefore \;\;\overline X \; = \dfrac{{565}}{{10}} = 56.5$
Arrange given observation in ascending order:
39, 41, 45, 47, 50, 52, 53, 60, 82, 96.
Here, n = 10 [even no.]
$\therefore $ Median $ = \dfrac{{{{\left( {\dfrac{n}{2}} \right)}^{{\text{th }}}}{\text{observation }} + {{\left( {\dfrac{n}{2} + 1} \right)}^{th}}{\text{observation }}}}{2}$
$ = \dfrac{{{5^{{\text{th }}}}{\text{observation }} + {6^{{\text{th }}}}{\text{observation }}}}{2}$
$ = \dfrac{{50 + 52}}{2} = \dfrac{{102}}{2} = 51$
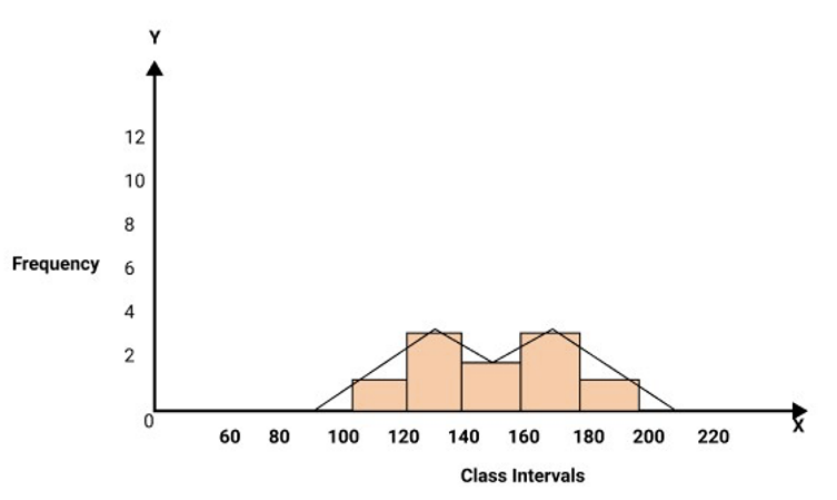
9. The following is the monthly expenditure (Rs.) of ten families of the particular area:
145, 115, 129, 135, 139, 158, 170, 175, 188, 163
(a) Make a frequency distribution table by using the following class interval:
100-120, 120-140, 140-160, 160-180, 180-200.
(b) Construct a frequency polygon for the above frequency distribution.
Ans:
Frequency distribution | ||
Class Intervals | Tally Marks | Frequency |
100-120 | I | 1 |
120-140 | III | 3 |
140-160 | II | 2 |
160-180 | III | 3 |
180-120 | I | 1 |
Total | 10 | |
10. The mean of 5 numbers is 39. If one number is excluded, their mean is 35 , find the excluded number.
Ans: The mean of 5 numbers $ = 39$
So, sum of five numbers $ = 39 \times 5 = 195$
The mean of 4 numbers $ = 35$
So, sum of four numbers $ = 35 \times 4 = 140$
Thus, Excluded numbers = Sum of five numbers - Sum of four numbers
$ = 195 - 140 = 55$
11. If the mean of 8 observation $x,\;x + 1,\;x + 3,\;x + 4,\;x + 5,\;x + 6,\;x + 7$ is 50, find the mean of first 5 observation.
Ans: Mean $ = \dfrac{{\sum {{x_i}} }}{n}$
$\bar x = \dfrac{{x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) + (x + 6) + (x + 7)}}{8}$
$50 = \dfrac{{8x + 28}}{8}$
$400 - 28 = 8x$
$\therefore x = \dfrac{{372}}{8} = 46.5$
The given set of 8 observations is 46.5, 47.5, 48.5, 50.5, 49.5, 51.5, 52.5, 53.5.
So, mean of first 5 observations is:
$\bar x = \dfrac{{46.5 + 47.5 + 48.5 + 49.5 + 50.5}}{5} = \dfrac{{242.5}}{5} = 48.5$
12. Represent the following data by means of histogram.
Weekly wages (in Rs) | 10-15 | 15-20 | 20-25 | 25-30 | 30-40 | 40-60 | 60-80 |
Number of workers(frequency) | 7 | 9 | 8 | 5 | 12 | 12 | 8 |
Ans:
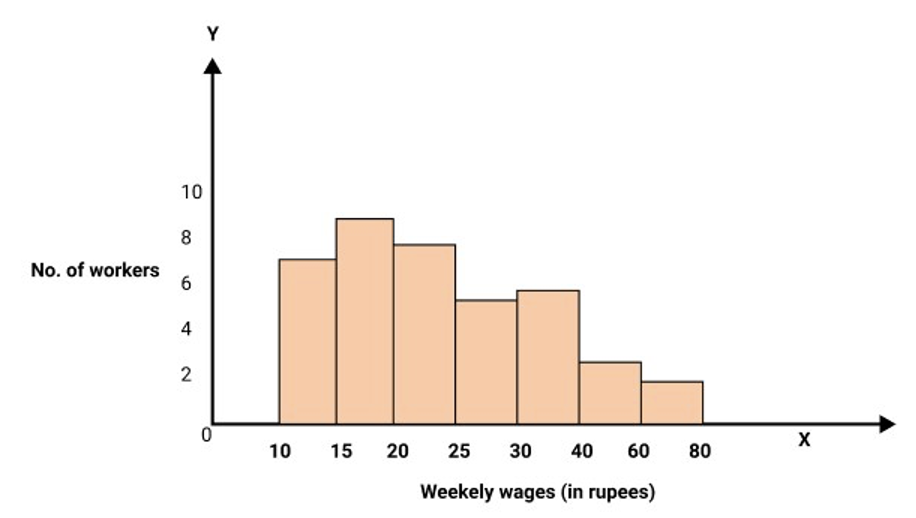
Following will be the adjusted Frequencies:
Weekly wages (in rupees) | Frequency | Adjusted frequencies |
10-15 | 7 | $\dfrac{5}{5} \times 7 = 7$ |
15-20 | 9 | $\dfrac{5}{5} \times 9 = 9$ |
20-25 | 8 | $\dfrac{5}{5} \times 8 = 8$ |
25-30 | 5 | $\dfrac{5}{5} \times 5 = 5$ |
30-40 | 12 | $\dfrac{5}{{10}} \times 12 = 6$ |
40-60 | 12 | $\dfrac{5}{{20}} \times 12 = 3$ |
60-80 | 8 | $\dfrac{5}{{20}} \times 8 = 2$ |
13. The Mean of monthly salary of 10 members of a group is Rs 1445, one more member whose monthly salary is Rs 1500 has joined the group. Find mean monthly salary of 11 member of the group.
Ans: Here $n = 10,\;\;\bar X = 1445$
So, $\bar X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right) \Rightarrow {\text{n}}\bar X = \sum {{x_i}} \Rightarrow 10 \times 1445 = \sum {{x_i}} $
$ \Rightarrow \sum {{x_i}} = 14450$
So, total monthly wages of 10 person ${\text{Rs}} = 14450$
Monthly salary wages of one more person who joined the group is 1500 .
$\therefore $ Total monthly wages of 11 persons = Rs $14450 + 1500 = $ Rs 15950
So, average monthly salary to 11 person
$ = \dfrac{{{\text{ total monthly wages }}}}{{11}} = \dfrac{{15950}}{{11}} = \operatorname{Rs} 1450$
14. The sum of the deviations of a set of n values ${{\text{x}}_1},\;{{\text{x}}_2},\;..........\;{{\text{x}}_n}$ measured from 50 is -10 and the sum of deviation of the values from 46 is 70. Find the values of ${\text{n}}$ and the mean.
Ans: We have,
$\sum\limits_{i = 1}^n {\left( {{x_i} - 50} \right)} = - 10$ and $\sum\limits_{i = 1}^n {\left( {{x_i} - 46} \right)} = 70$
$ \Rightarrow \sum\limits_{i = 1}^n {{x_i}} - 50n = 10 \to $ (i)
$ \Rightarrow \sum\limits_{i = 1}^n {{x_i}} - 46n = 70 \to $ (ii)
Subtracting (ii) from (i), we get $ - \;4{\text{n}} = - \;80$
${\text{n}} = 20$
Putting ${\text{n}} = 20$ in (i), we get
$\sum\limits_{i = 1}^n {{x_i} - 50 \times 20 = \;\; - 10} $
$ \Rightarrow \sum\limits_{{\text{l}} = 1}^n {{X_i}} = 990$
$\therefore $ mean $ = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right] = \dfrac{{990}}{{20}}$ $ = \,\;49.5$
So, ${\text{n}} = 20$ and mean $ = 49.5$
15. There are 50 students in a class out of which 40 are boys and rest girls. The average weight of the class is 44 kg and the average weight of the girls is40 kg. Find the average weight of the boys.
Ans: We have, n = No. of students in a class $ = 50$
${{\text{n}}_1} = $ No. of boys in a class $ = 40$
${{\text{n}}_2} = $ No. of girls in a class $ = 10$
${\bar X_1} = $ Average weight of boys $ = ?$
${X_2} = $ Average weight of girls $ = 40\;{\text{kg}}$
$\therefore \bar X = \dfrac{{{n_1}{{\bar X}_1} + {n_2}{{\bar X}_2}}}{{{n_1} + {n_2}}}$
$ \Rightarrow 44 = \dfrac{{40{{\overline X }_1} + 10 \times 40}}{{40 + 10}}$
$ \Rightarrow 50 \times 44 = 40{\overline X _1} + 400$
$ \Rightarrow 2200 = 40{\bar X_1} + 400$
$ \Rightarrow {\bar X_1} = 45$
Hence, the average weight of boys is $45{\text{Kg}}$
16. The mean of 100 items was found to be 300. If at the time of calculation two items were wrongly taken as 32 and 12 instead of 23 and 11 , find the correct mean.
Ans: Here, ${\text{n}} = 100,\quad X = 30$
So, $\overline X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right) \Rightarrow \sum {{x_i}} = n\bar X$
$ \Rightarrow \sum {{x_i}} = 100 \times 30$ $ = 3000$
$\therefore $ Incorrect value of $\sum {{x_i}} = 3000$
Now, correct value of $\sum {{x_i}} = $ incorrect value of $\sum {{x_i}} - ($ sum of incorrect value $) + ($ sum of correct value)
$ = 3000 - (32 + 12) + (23 + 11)\;\; = \;2990$
Correct mean $ = \dfrac{{{\text{ Correct value of }}\sum {{x_i}} }}{n} = \dfrac{{2990}}{{100}}$ $ = \;\;29.9$
17. The mean of 10 numbers is 20 . If 8 is subtracted from every number, what will be the new mean?
Ans: Let ${{\text{x}}_1},{{\text{x}}_2}, \ldots {x_{10}}$ be 10 numbers with their mean equal to 20 .
Then,
$\bar X = \dfrac{1}{n}\left( {\sum {{x_i}} } \right)$
$20 = \dfrac{{{x_1} + {x_2} + \ldots .. + {x_{20}}}}{{10}}$
$ \Rightarrow 200 = {{\text{x}}_1} + {x_2} + \ldots . + {x_{10}}$
New numbers are ${x_1} - 8,\;{x_2} - 8,\; \ldots \ldots ,\;{x_{10}} - 8$
Let $\bar X$ be the mean of new number.
$\overline X = \dfrac{{\left( {{x_1} - 8} \right) + \left( {{x_2} - 8} \right) + \ldots . + \left( {{x_{10}} - 8} \right)}}{{10}}$
$X = \dfrac{{\left( {{x_1} + {x_2} + \ldots \ldots + {x_{10}}} \right) - 8 \times 10}}{{10}}$
$ = \dfrac{{200 - 80}}{{10}} = 12$
18. The mean of n observation ${x_1},\;{x_2},\;.......,\;{x_n}$, is $\overline X $. If $(a - b)$ is added to each of the observation, show that the mean of the new set of observation is $\overline X + (a - b)$.
Ans: We have, $\bar X = \dfrac{{{x_1} + {x_1} + \ldots + {x_n}}}{n} \to $ (i)
Let $X$ be the mean of ${x_1} + (a - b),\;{x_2} + (a - b), \ldots \ldots ,\;{x_n} + (a - b)$. Then, $X = \dfrac{{\left[ {{x_1} + (a - b)} \right] + \left[ {{x_2} + (a - b)} \right] + \ldots \ldots + \left[ {{x_n} + (a - b)} \right]}}{n}$
$ = \dfrac{{{x_1} + {x_2} + \ldots + {x_n} + n(a - b)}}{n}$
$ = \dfrac{{{x_1} + {x_2} + \ldots + {x_n}}}{n} + \dfrac{{n(a - b)}}{n}$
$ = X + (a - b)$ [using (i)]
19. If ${{\text{x}}_1},{{\text{x}}_2} \ldots \ldots {{\text{x}}_{\text{n}}}$ are n values of a variable X such that $\sum\limits_{i = 1}^n {\left( {{x_{\text{i}}} - 2} \right)} = 110$ and $\sum\limits_{i = 1}^n {\left( {{x_1} - 5} \right)} .$ Find the value of n and the mean.
Ans: We have: $\sum\limits_{i = 1}^n {({x_i}} - 2) = 110$ and $\sum\limits_{i = 1}^n {({x_i}} - 5) = 20$
$ \Rightarrow \left( {{x_1} - 2} \right) + \left( {{x_2} - 2} \right) + \ldots .. + \left( {{x_n} - 2} \right) = 110$
$ \Rightarrow \left( {{x_1} - 5} \right) + \left( {{x_2} - 5} \right) + \ldots .. + \left( {{x_n} - 5} \right) = 20$
$ \Rightarrow \left( {{x_1} + {x_2} + \ldots + {x_n}} \right) - 2n = 110$ and $\left( {{x_1} + {x_2} + \ldots + {x_1}} \right) - 5n = 20$
$ \Rightarrow \sum\limits_{i = 1}^n {{x_i}} - 2n = 110$ and $\sum\limits_{i = 1}^e {{x_1}} - 5n = 20$
Thus, we have $S - 2n = 110$....(i)
and $S - 5n = 20$....(ii)
Subtracting (ii) from (i), we get:
$3n = 90$
$n = 30$
Putting ${\text{n}} = 30$ in (i), we get:
${\text{S}} - 60 = 110\;\; \Rightarrow \;{\text{S}} = 170 \Rightarrow \sum\limits_{{\text{i}} = 1}^n {{x_i}} = 170$
$\therefore $ mean $ = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$
$ = \dfrac{{170}}{{30}} = \dfrac{{17}}{3}$
20. Find the missing frequencies in the following frequency distribution shown that the mean of the distribution is 1.46.
No. of accidents(x) | 0 | 1 | 2 | 3 | 4 | 5 | Total |
Frequency(f) | 45 | ? | ? | 25 | 10 | 5 | 200 |
Ans: Let the missing frequencies be f1 and f2.
${x_i}$ | ${f_i}$ | ${f_i}{x_i}$ |
0 | 46 | 0 |
1 | ${f_1}$ | ${f_1}$ |
2 | ${f_2}$ | $2{f_2}$ |
3 | 25 | 75 |
4 | 10 | 40 |
5 | 5 | 25 |
| \[\sum {{f_i}} = 86 + {f_1} + {f_2}\] | \[\sum {{f_i}} {x_i} = 140 + {f_1} + 2{f_2}\] |
We have: ${\text{N}} = 200$
$\therefore 200 = 86 + {f_1} + {f_2}$
$114 = {f_1} + {f_2}.............({\text{i}})$
Also, Mean $ = 1.46$
$ \Rightarrow 1.46 = \dfrac{{\sum {{f_i}} {x_i}}}{N}$
$ \Rightarrow 1.46 = \dfrac{{140 + {f_1} + 2{f_2}}}{{200}}$
$ \Rightarrow 292 = 140 + {{\text{f}}_1} + 2{{\text{f}}_2}$
$ \Rightarrow 152 = {{\text{f}}_1} + 2{{\text{f}}_2}..........(ii)$
Solving (i) and (ii), we get
${{\text{f}}_1} = 76$ and ${{\text{f}}_2} = 38$
21. Give some examples of data that you can collect from your day to day life.
Ans: Some examples of data that we can gather from our day to day life are:
Number of students in our college.
Number of fans in our school library.
Electricity bills of our shop for last three years.
Election results obtained from television or newspapers.
Literacy rate figures obtained from National Survey.
Heights of 30 students of our class.
Maximum temperatures of the days of a particular week from weather forcast.
Number of members in the families of your locality from a record.
Distances from the college of the homes of five students.
22. Classify the data in Q21 above as primary or secondary data.
Ans: Primary Data: When investigator himself collects the information with some specific objective in mind, data obtained is called Primary data. Such types of data are collected for first time for their own use. Above mentioned (i), (ii), (iii), (iv) and (ix) are the examples of primary data.
Secondary Data: It includes the collection of information from sources which already had the information stored such as newspaper, television, etc. Above mentioned (iv), (v), (vii) and (viii) are the examples of secondary data.
23. The blood groups of 30 students of a class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O .
Represent this data in the form of a frequency distribution table. Which is the most common and which is the rarest blood group among these students?
Ans: The frequency distribution table for the given data is as follows:
Blood Group | Tally Marks | Frequency (Number of students) |
A | \[{{||||}}||||\] | 9 |
B | \[{{||||}}|\] | 6 |
O | \[{{||||}}{{||||}}||\] | 12 |
AB | \[|||\] | 3 |
Total |
| 30 |
From the table, It can be observed that the most common blood group is O and the rarest group is AB.
24. Distance (in km) of 40 engineers from their place of residence to their place of work were found as follows:
5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Construct a grouped frequency distribution table with class size 5 for the data given 40 above taking the first interval as 0 – 5 (5 not included). What main features do you observe from this tabular representation?
Ans. The grouped frequency distribution table for the given data is as follows:
Blood group | Tally Marks | Frequency (Number of female engineer’s) |
0-5 | \[{{||||}}\] | 5 |
5-10 | \[{{||||}}|{{||||}}\] | 11 |
10-15 | \[{{||||}}|{{||||}}\] | 11 |
15-20 | \[{{||||}}||||\] | 9 |
20-25 | $|$ | 1 |
25-30 | $|$ | 1 |
30-35 | $||$ | 2 |
Total |
| 40 |
From the table we observe that out of 40 female engineers $36(5 + 11 + 11 + 9)$ engineers i.e. $90\% $ of the total female engineers reside less than $20\;{\text{km}}$ from their place of work.
25. The relative humidity (in %) of a certain city for a month of 30 days was as follows:
98.1 | 98.6 | 98.2 | 98.3 | 86.5 | 95.3 | 92.9 | 96.3 | 94.2 | 95.1 |
89.2 | 92.3 | 97.1 | 93.5 | 92.7 | 95.1 | 97.2 | 93.3 | 95.2 | 97.3 |
96.2 | 92.1 | 84.9 | 90.2 | 95.7 | 98.3 | 97.3 | 96.1 | 92.1 | 89 |
(i) Construct a grouped frequency distribution table with classes $84 - 86,86 - 88$ etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
Ans: (i) The grouped frequency distribution table for the given data is as follows:
Relative humidity (in %) | Tally Marks | No. of days |
84-86 | $|$ | 1 |
86-88 | $|$ | 1 |
88-90 | $|$$|$ | 2 |
90-92 | $|$$|$ | 2 |
92-94 | $|$$|$${{||||}}$ | 7 |
94-96 | $|$ | 6 |
96-98 | $|$$|$${{||||}}$ | 7 |
98-100 | $|$$|$$|$$|$ | 4 |
(ii) Data appears to be taken in the rainy season because we observe that relative humidity is high.
(iii) From the data, we observe
Highest relative humidity $ = 99.2\% $
Lowest relative humidity $ = 84.9\% $
Range $ = \;\;(99.2 - 84.9)\% = 14.3\% $
26. The heights of 50 students, measured to the nearest centimeters have been found to be as follows:
$\begin{array}{llllllllll} \mathbf{1 6 1} & \mathbf{1 5 0} & \mathbf{1 5 4} & \mathbf{1 6 5} & \mathbf{1 6 8} & \mathbf{1 6 1} & \mathbf{1 5 4} & \mathbf{1 6 2} & \mathbf{1 5 0} & \mathbf{1 5 1} \\ \mathbf{1 6 2} & \mathbf{1 6 4} & \mathbf{1 7 1} & \mathbf{1 6 5} & \mathbf{1 5 8} & \mathbf{1 5 4} & \mathbf{1 5 6} & \mathbf{1 7 2} & \mathbf{1 6 0} & \mathbf{1 7 0} \\ \mathbf{1 5 3} & \mathbf{1 5 9} & \mathbf{1 6 1} & \mathbf{1 7 0} & \mathbf{1 6 2} & \mathbf{1 6 5} & \mathbf{1 6 6} & \mathbf{1 6 8} & \mathbf{1 6 5} & \mathbf{1 6 4} \\ \mathbf{1 5 4} & \mathbf{1 5 2} & \mathbf{1 5 3} & \mathbf{1 5 6} & \mathbf{1 5 8} & \mathbf{1 6 2} & \mathbf{1 6 0} & \mathbf{1 6 1} & \mathbf{1 7 3} & \mathbf{1 6 6} \\ \mathbf{1 6 1} & \mathbf{1 5 9} & \mathbf{1 6 2} & \mathbf{1 6 7} & \mathbf{1 6 8} & \mathbf{1 5 9} & \mathbf{1 5 8} & \mathbf{1 5 3} & \mathbf{1 5 4} & \mathbf{1 5 9} \end{array}$
(i) Represent the data given above by a grouped frequency distribution table, taking the class - intervals as $160 - 165,165 - 170$ etc.
(ii) What can you conclude about their heights from the table?
Ans: (i) The grouped frequency distribution table for the given data is as follows:
Distance | Tally Marks | No. of students Frequency |
150-155 | \[{{||||}}\]\[{{||||}}\]$|$$|$ | 12 |
155-160 | \[{{||||}}\]$|$$|$$|$$|$ | 9 |
160-165 | \[{{||||}}\]\[{{||||}}\]$|$$|$$|$$|$ | 14 |
165-170 | \[{{||||}}\]\[{{||||}}\] | 10 |
170-175 | \[{{||||}}\] | 5 |
Total |
| 50 |
(ii) From the frequency distribution table drawn above, we conclude that more than $50\% $ of the students are shorter than $165\;{\text{cm}}$.
27. A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:
$\begin{array}{llllll} 0.03 & 0.08 & 0.08 & 0.09 & 0.04 & 0.17 \\ 0.16 & 0.05 & 0.02 & 0.06 & 0.18 & 0.20 \\ 0.11 & 0.08 & 0.12 & 0.13 & 0.22 & 0.07 \\ 0.08 & 0.01 & 0.10 & 0.06 & 0.09 & 0.18 \\ 0.11 & 0.07 & 0.05 & 0.07 & 0.01 & 0.04 \end{array}$
(i) Make a grouped frequency distribution table for this data with class intervals as
0.01 - 0.04, 0.04-0.08 and so on.
(ii) For how many days, was the concentration of sulphur dioxide more than 0.11 parts per million.
Ans: (i) The minimum and maximum concentration of Sulphur dioxide in the air in parts per million is 0.01 and 0.22 respectively.
It is given that 0.00-0.04 is one of the class intervals and the class size is the same.
So, the classes of equal size are
0.00-0.04, 0.04-0.08 , .. , 0.20-0.24
Thus, the frequency distribution table is as under.
$\begin{array}{|c|c|} \hline \begin{array}{c} \text { Concentration of } \\ \text { Sulphur dioxide (in ppm) } \end{array} & \text { Frequency } \\ \hline 0.00-0.04 & 4 \\ 0.04-0.08 & 9 \\ 0.08-0.12 & 9 \\ 0.12-0.16 & 2 \\ 0.16-0.20 & 4 \\ 0.20-0.24 & 2 \\ \hline \text { Total } & 30 \\ \hline \end{array}$
(ii) The concentration of sulphur dioxide was more than 0.11 ppm for 8 days.
28. Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows:
$\begin{array}{*{20}{l}} 0&1&2&2&1&2&3&1&3&0 \\ 1&3&1&1&2&2&0&1&2&1 \\ 3&0&0&1&1&2&3&2&2&0 \end{array}$
Prepare a frequency distribution for the data given above.
Ans:
$\begin{array}{|c|c|} \hline \text { Number of heads } & \text { Number of times (frequency) } \\ \hline 0 & 6 \\ \hline 1 & 10 \\ \hline 2 & 9 \\ \hline 3 & 5 \\ \hline \text { Total } & 30 \\ \hline \end{array}$
29. The value of $\pi $ up to 50 decimal places is given below:
3.1415926535 8979323846 2643383279 5028841971 6939937510
(a) Make a frequency distribution of the digits after the decimal point and list the digits from 0 to 9 in your first column.
(b) What are the most and the least frequency occurring digits?
Ans: (i) The frequency distribution table is as under:
$\begin{array}{|c|c|} \hline \text { Digits } & \text { Frequency } \\ \hline 0 & 2 \\ 1 & 5 \\ 2 & 5 \\ 3 & 8 \\ 4 & 4 \\ 5 & 5 \\ 6 & 4 \\ 7 & 4 \\ 8 & 5 \\ 9 & 8 \\ \hline \text { Total } & 50 \\ \hline \hline \end{array}$
(ii) The most frequently occurring digits are 3 and 9.
The least occurring is 0.
30. Thirty children were asked about the number of hours they watched TV programmers in the previous week. The results were found as follows:
$\begin{array}{llllllllll} 1 & 6 & 2 & 3 & 5 & 12 & 5 & 8 & 4 & 8 \\ 10 & 3 & 4 & 12 & 2 & 8 & 15 & 1 & 17 & 6 \\ 3 & 2 & 8 & 5 & 9 & 6 & 8 & 7 & 14 & 12 \end{array}$
(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class interval 5 – 10.
(ii) How many children watched television for 15 or more hours a week?
Ans: (i) The minimum and maximum number of hours children watched TV programmers in the previous week are 1 hour and 17 hours, respectively. It is given that 5 – 10 is one of the class intervals and the class size is same. So, the classes of equal size are 0 – 5, 5 – 10, 10 – 15, 15 – 20.
Thus, the frequency distribution table is as under.
$\begin{array}{|c|c|} \hline \text { Number of heads } & \text { Frequency } \\ \hline 0-5 & 10 \\ 5-10 & 13 \\ 10-15 & 5 \\ 15-20 & 2 \\ \hline \text { Total } & 30 \\ \hline \end{array}$
(ii) 2 children watched television for 15 or more hours a week
31. A company manufactures car-batteries of particular type. The live (in years) of 40 such batteries were recorded as follows:
$\begin{array}{llllllll} 2.6 & 3.0 & 3.7 & 3.2 & 2.2 & 4.1 & 3.5 & 4.5 \\ 3.5 & 2.3 & 3.2 & 3.4 & 3.8 & 3.2 & 4.6 & 3.7 \\ 2.5 & 4.4 & 3.4 & 3.3 & 2.9 & 3.0 & 4.3 & 2.8 \\ 3.5 & 3.2 & 3.9 & 3.2 & 3.2 & 3.1 & 3.7 & 3.4 \\ 4.6 & 3.8 & 3.2 & 2.6 & 3.5 & 4.2 & 2.9 & 3.6 \end{array}$
Construct a grouped frequency distribution table for this data, using class intervals of 45 size 0.5 starting from the interval 2 – 2.5.
Ans: The minimum and maximum life (in number of years) of car batteries are 2.2 years and 4.6 years. It is given that 2 – 2.5 is one of the class interval with uniform size of 0.5. So, the classes of equal size are 2.0 – 2.5, 2.5 – 3.0, 3.0 – 3.5,……, 4.5 – 5.0.
Thus, the frequency distribution table is as under:
$\begin{array}{|c|c|} \hline \begin{array}{c} \text { Life of batteries } \\ \text { (in years) } \end{array} & \text { Frequency } \\ \hline 2.0-2.5 & 2 \\ 2.5-3.0 & 6 \\ 3.0-3.5 & 14 \\ 3.5-4.0 & 11 \\ 4.0-4.5 & 4 \\ 4.5-5.0 & 3 \\ \hline \text { Total } & 30 \\ \hline \end{array}$
4 Marks Questions
1. Find the value of x and y in the following distribution if it is known that the mean of the distribution is 1.46.
Ans: $x = 76,y = 38$
2. The mean monthly salary of 10 members of a group is Rs 1445 , one more member whose monthly salary is Rs 1500 has joined the group. Find the mean monthly salary of 11 members of the group.
Ans: Rs 1450
3. Given below is a cumulative frequency distribution table showing the age of people living in a locality.
$\begin{array}{l|l} \text { Age in years } & \text { No. of persons } \\ \hline \text { Above 108 } & 0 \\ \hline \text { Above 96 } & 1 \\ \hline \text { Above 84 } & 3 \\ \hline \text { Above 72 } & 5 \\ \hline \text { Above 60 } & 20 \\ \hline \text { Above 48 } & 158 \\ \hline \text { Above } 36 & 427 \\ \hline \text { Above 24 } & 809 \\ \hline \text { Above 12 } & 1026 \\ \hline \text { Above 0 } & 1124 \\ \hline \end{array}$
Prepare a frequency distribution table.
Ans:
$\begin{array}{|l|l|l|l|l|l|l|l|l|l|} \hline \text { Marks } & 0-12 & 12-24 & 24-36 & 36-48 & 48-60 & 60-72 & 72-84 & 84-96 & 96-108 \\ \hline \text { Person } & 98 & 217 & 382 & 269 & 138 & 15 & 2 & 2 & 1 \\ \hline \hline \end{array}$
4. If ${\mathbf{x}},{{\mathbf{x}}_2} \ldots ..{{\text{x}}_{\text{n}}}$ are ${\mathbf{n}}$ values of a variable x such that $\sum\limits_{i = 1}^n {\left( {{x_1} - 2} \right)} = 110$ and $\sum\limits_{i = 1}^n {\left( {{x_1} - 5} \right)} = 20$ find the value of n and mean.
Ans: n $ = 30$, mean $ = \;\dfrac{{17}}{3}$
5. The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Ans: 50.9
6. Find the value of p, if the mean of the following distribution is 20 .
$\begin{array}{|l|l|l|l|l|l|} \hline \mathrm{x} & 15 & 17 & 19 & 20+p & 23 \\ \hline \text { frequency } & 2 & 3 & 4 & 5 p & 6 \\ \hline \end{array}$
Ans: 1
7. Prove that the sum of the deviations of an individual's observations from the mean is zero.
Ans: Let ${{\text{x}}_1},{{\text{x}}_2},{{\text{x}}_3}, \cdots ,{{\text{x}}_{\text{n}}}$ be n individual observations whose mean is $\bar x$. The sum of the deviations of these n observations from $\overline x $ is given by:
$\sum\limits_{{\text{i}} = 1}^n {\left( {{x_{\text{i}}} - \overline x } \right)} = \left( {{x_i} - \overline x } \right) + \left( {{x_2} - \overline x } \right) + \ldots . + \left( {{{\text{x}}_n} - \overline x } \right)$
Also, we have $\overline x = \dfrac{1}{n}\left[ {\sum\limits_{i = 1}^n {{x_i}} } \right]$
$ \Rightarrow {\text{n}}\overline x = \sum\limits_{{\text{l}} = 1}^n {{x_i}} $
Now, $\sum\limits_{{\text{i}} = 1}^n {\left( {{x_{\text{i}}} - \overline x } \right)} = \left( {{x_i} - \overline x } \right) + \left( {{x_2} - \overline x } \right) + \ldots . + \left( {{{\text{x}}_n} - \overline x } \right)$
$ = \left( {{x_1} + {x_2} + \ldots . + {x_n}} \right) - n\overline x $
$ = \sum\limits_{{\text{i}} - 1}^n {{x_{\text{i}}}} - n\overline x $
$ = \;n\overline x \; - \;n\overline x $
= 0
So, $\sum\limits_{i = 1}^n {\left( {{x_i} - \overline x } \right)} = 0$
8. From the data given below find:
(a) Lower limit of the third class
(b) Upper limit of the seventh class.
(c) Class boundaries of the sixth class.
(d) The class mark of the fifth class.
(e) The size of the second class
(f) Draw histogram of the data.
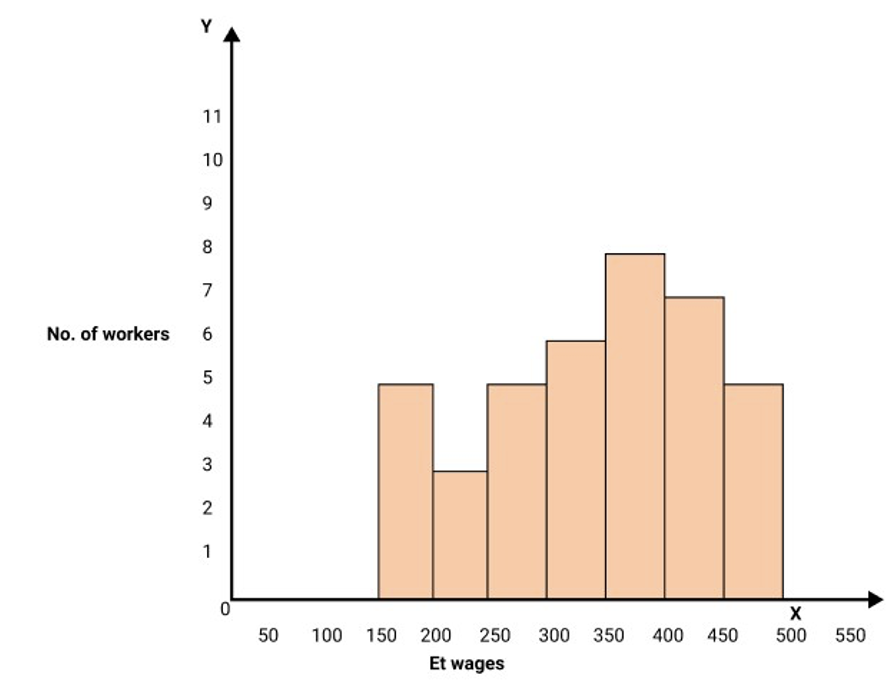
$\begin{array}{|l|l|l|l|l|l|l|l|} \hline \text { No. of Wage[Rs.] } & 150-200 & 200-250 & 250-300 & 300-350 & 350-400 & 400-450 & 450-500 \\ \hline \text { Employees } & 5 & 3 & 5 & 6 & 8 & 7 & 5 \\ \hline \end{array}$
Ans:
(a) Lower limit of the third class = 250
(b) Upper limit of the seventh class = 500
(c) Class boundaries of the sixth class = 400 – 450
(d) The class mark of the fifth class = 375
(e) The size of the second class = 50
(f) Histogram
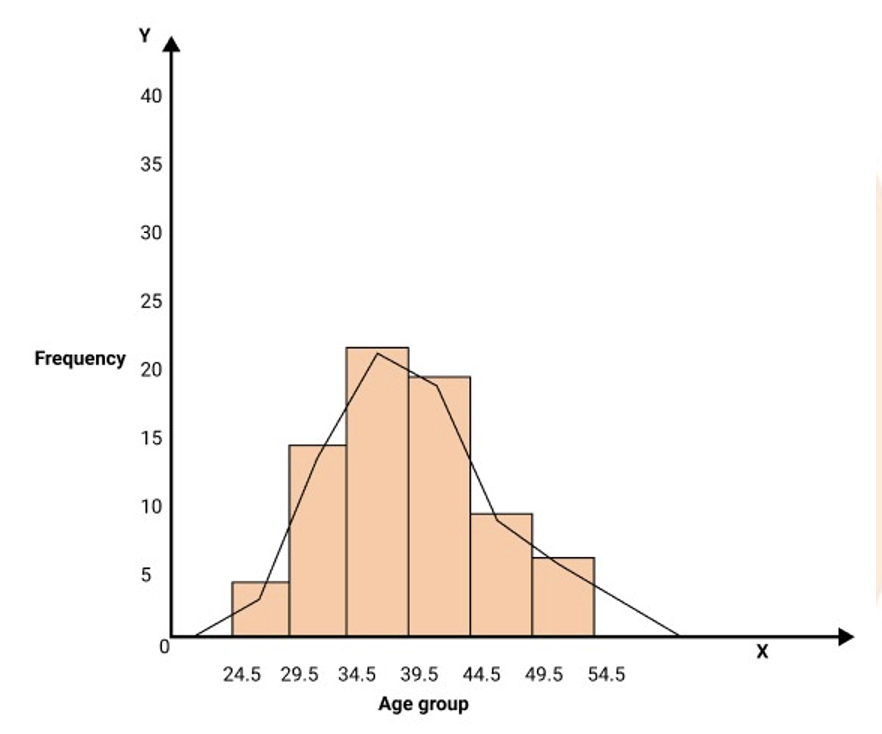
9. Draw a histogram with frequency polygon for the following data.
$\begin{array}{|c|c|c|c|c|c|c||} \hline \text { class interval } & 25-29 & 30-34 & 35-39 & 40-44 & 45-49 & 50-54 \\ \hline \text { frequency } & 5 & 15 & 23 & 20 & 10 & 7 \\ \hline \end{array}$
Ans: Ascertainment of lower and upper class limits: since the difference between the second and first mid-points is 25-29
Let ${\text{h}} = 1$
Then for continuous frequency distribution, we subtract $\dfrac{h}{2}$ from the lower limit and Add $\dfrac{h}{2}$ to the upper limit.
$\therefore \dfrac{h}{2} = 0.5$
$\begin{array}{||l|c|c|c|c|c|c|} \hline \text { class interval } & 24.5-29.5 & 29.5-34.5 & 34.5-39.5 & 39.5-44.5 & 44.5-49.5 & 49.5-54.5 \\ \hline \text { frequency } & 5 & 15 & 23 & 20 & 10 & 7 \\ \hline \end{array}$
10. The average score of girls in class examinations in a school is 67 and that of boys is 63. The average score for the whole class is 64.5. Find the percentage of girls and boys in the class.
Ans: Let the number of girls and boys be n1 and n2 respectively.
We have:
$\overline {{X_1}} $: Average score of girls $ = 67$
$\overline {{X_2}} $ : Average score of boys $ = 63$
$X$: Average score of the whole class $ = 64.5$
$X = \dfrac{{{n_1}\overline {{X_1}} + {n_2}\overline {{X_2}} }}{{{n_2} + {n_2}}}$
$ \Rightarrow 64.5 = \dfrac{{67{n_1} + 63{n_2}}}{{{n_1} + {n_2}}}$
$ \Rightarrow 64.5{{\text{n}}_{\text{1}}} + 64.5{{\text{n}}_2} = 67{{\text{n}}_1} + 63{{\text{n}}_2}$
$ \Rightarrow 2.5{{\text{n}}_1} = 1.5{{\text{n}}_2}$
$ \Rightarrow 25{{\text{n}}_1} = 15{{\text{a}}_2}$
$ \Rightarrow 5{{\text{n}}_1} = 3{{\text{n}}_2}$
Total number of students in the class $ = {n_1} + {n_2}$
$\therefore $ percentage of girls $ = \dfrac{{{n_1}}}{{{n_1} + {n_2}}} \times 100$
$ = \dfrac{{{n_1}}}{{{n_1} + \dfrac{{5{n_1}}}{3}}} \times 100$
$ = \dfrac{{3{n_1}}}{{3{n_1} + 5{n_1}}} \times 100$
$ = \dfrac{3}{8} \times 100 = 37.5$
Percentage of boys $ = \dfrac{{{n_2}}}{{{n_1} + {n_2}}} \times 100$
$ = \dfrac{{{n_2}}}{{\dfrac{{3{n_2}}}{5} + {n_2}}} \times 100$
$ = \dfrac{{5{n_2}}}{{3{n_2} + 5{n_2}}} \times 100$
$ = 62.5$
11. Find the unknown entries (a, b, c, d, e, f) from the following frequency distribution of heights of 50 students in a class.
Class Intervals (height in cm) | Frequency | Cumulative Frequency |
150-155 | 12 | a |
155-160 | b | 25 |
160-165 | 10 | c |
165-170 | d | 43 |
170-175 | e | 48 |
175-180 | 2 | f |
Ans: Since the given frequency distribution is the frequency distribution of 50 students.
Therefore, $g = 50$
From the table, we have
$a = 12,\;\;b + 12 = 25,\;\;12 + b + 10 = c,\;\;12 + b + 10 + d = 43$
$12 + b + 10 + d + e = 48$ and $12 + b + 10 + d + e + g = f$
Now,
${\text{b}} + 12 = 25 \Rightarrow {\text{b}} = 13$
$12 + b + 10 = c$
$ \Rightarrow 12 + 13 + 10 = {\text{c}}$
$ \Rightarrow c = 35$
$12 + b + 10 + d - 43$
$ \Rightarrow 12 + 13 + 10 + d = 43$
$ \Rightarrow d = 8$
$12 + b + 10 + d + e = 48$
$ \Rightarrow 12 + 13 + 10 + 8 + e = 48$
$ \Rightarrow e = 5$
$12 + b + 10 + d + e + 2 = f$
$ \Rightarrow 12 + 13 + 10 + 8 + 5 + 2 = f$
$ \Rightarrow \;f = 50$
5 Important Formulas from CBSE Class 9 Maths Chapter 12 Statistics
S. No | Formula | Description |
1. | Mean (Arithmetic Mean): | Mean=$ \frac{\sum f x}{\sum f} $where ff is frequency and xx is the value of data. |
2. | Median: | For ungrouped data, arrange in order and find the middle value. For grouped data, use the median formula. |
3. | Mode: | The value that appears most frequently in a data set. |
4. | Range: | Range = $\text{Highest Value} - \text{Lowest Value}$ |
5. | Standard Deviation (SD): | SD = $\sqrt{\frac{\sum f(x - \mu)^2}{N}} $where μ is mean and f is frequency. |
Important Topics Covered in Important Questions for Class 9 Maths Chapter 12
The collection, arrangement, examination, interpretation, and presentation of data are defined by Statistics.
Steps in assessing the data:
Collection of data
Presentation of data (Tabular/ Graphical)
The measure of central tendency
We will address all these aspects of data briefly in this chapter.
Collection of Data
Data collection is the method by which information on targeted variables is collected and measured in a defined framework, which then helps one to answer relevant questions and analyze results.
For statistical analysis, there are several methods used to gather or collect data. Three of the methods that are most commonly used are:
Direct observation
Experimentation
Surveys
Ex: In a class of 50 students a teacher has to collect the data of blood groups of all students. So this task is regarding data collection.
How this is achieved is the method of data collection.
So here the teacher can look into the documents of students to collect the blood group data or the teacher can organize a doctor to check all 50 students and collect the data.
Presentation of Data
Data presentation refers to the arrangement of data into tables, graphs or charts so that the collected measurements can draw logical and statistical conclusions.
Ex: Teacher has collected the blood groups of all 50 students and he has prepared a report to show it to the School management as follows:
Student 1- A+
Student 2- AB+
Student 3- O+
Student 4- B+
Student 5- O+
Student 6- A+
Student 7- AB+
Student 8- B-
Student 9- O+
.
.
.
.
Student 50- B-
So data represented in this way doesn’t look good and it won’t give a proper knowledge for the person who is seeing it for the first time. So the representation of data plays an important role. We can represent data using tables and graphs.
Data Representation Using Tables:
So the data represented in the table look more presentable than giving raw data.
Number of Students | Blood Group |
10 | A+ |
2 | A- |
7 | B+ |
2 | B- |
15 | O+ |
0 | O- |
12 | AB+ |
2 | AB- |
Data Representation Using Graphs:
Graphical representation of data has three different types:
Bar graph
Histograms
Pie charts
Bar Graphs
A bar chart or bar graph is a chart or graph that provides rectangular bars with categorical data with heights or lengths proportional to the values they represent. It is possible to plot the bars vertically or horizontally.
Histograms
A histogram is a graphical data display using bars of various heights. Each bar groups numbers into ranges in a histogram. Taller bars indicate that in that range, more data drop. The form and distribution of continuous sample data are shown in a histogram.
Pie Chart
A pie chart is a circular statistical graph which, to illustrate numerical proportions, is divided into slices. In a pie map, each slice's arc length is equal to the sum that it represents.

The Measure of Central Tendency
By using frequency distribution tables, bar graphs, histograms and frequency polygons, we depicted the data in different types. Now, whether we still need to analyze all the data in order to make sense of it, or whether we can define some essential features of it by considering only some data members, the question arises. By using a measure of central tendency, this is possible.
The measure of central tendency includes a summary measure seeking to characterize a whole set of single-value data reflecting the middle or centre of its distribution.
The measure of central tendency helps us to locate the centre of a data set, or the average. The Mean, Median, and Mode are the 3 most common measures of central tendency.
Mean:
The sum of all values divided by the total number of values is the arithmetical mean of a data set. It is the most widely used central tendency metric since the equation uses all values for calculation.
Formula to calculate the Mean is
Mean (x̄) = Sum of the given data/ total number of data
Ex: There are 5 students whose marks are as follows. Calculate the Mean marks.
Students | 1 | 2 | 3 | 4 | 5 |
Marks | 80 | 60 | 75 | 95 | 40 |
To calculate the mean first we have to find the sum of the marks of 5 students.
Sum of marks = 80+60+75+95+35= 350
Number of students = 5
Mean = Sum of marks / Number of students
Mean = 350/5 = 70.
The Mean of the marks is 70. That is, the average marks obtained is 70.
Median:
When the data is sorted ascending or descending, the median of a data set is the value that is exactly in the centre.
Ex: Calculate the median for the given set of data.
Students | 1 | 2 | 3 | 4 | 5 |
Marks | 80 | 60 | 75 | 95 | 40 |
So here there is an odd number of students i.e 5. So the median will be the marks obtained by the 3rd student who is the centre of the data.
Therefore the median value is 75.
Mode:
The most frequently occurring value in the data set is the mode. There can be no mode, one mode, or more than one mode.
To find mode sort the data set numerically or categorically to find the mode, and choose the answer that occurs most often.
Ex: Find the mode for the following data set.
Students | 1 | 2 | 3 | 4 | 5 |
Marks | 80 | 40 | 75 | 95 | 40 |
Here 40 marks have been scored by 2nd and 5th students. So this mark is repetitive in the data. Therefore the mode of the following data set is 40 as it occurs more often.
When to Use Mean, Median and Mode?
In conjunction with each other, the 3 main measures of central tendency are best used because they have complementary strengths and weaknesses. But sometimes only 1 or 2 of them are applicable to our data set, depending on the level of measurement of the variable.
The mean can only be used on measurement interval and ratio levels since it needs equal spacing in the scale between adjacent values or ratings.
The median can only be used on data that can be ordered, that is, from measurement levels of ordinal, interval and ratio.
The mode can be used for any measurement level, but for nominal and ordinal levels, it is most appropriate.
For more information on Class 9 Maths Chapter 12 Important Questions of Statistics students can go through the free NCERT notes and Solutions provided by Vedantu to get deep knowledge on the topic and to score good marks in their exams.
Practice Questions from CBSE Class 9 Maths Chapter 12 - Statistics
1. The mean of 20 observations is 17. If in the observations, observation 40 is replaced by 12, then find the new mean.
2. If the mean of five observations x, x + 2, x + 4, x + 6, and x + 8 is 11, then write the value of x.
3. Write the class mark of an interval 90 – 120.
4. The mean of 8 observations is 40. If 5 is added to each observation, then what will be the new mean?
5. Find the median of the values 37, 31, 42, 43, 46, 25, 39, 45, and 32.
6. The median of the data 26, 56, 32, 33, 60, 17, 34, 29, and 45 is 33. If 26 is replaced by 62, then find the new median.
7. The class marks of a frequency distribution are 104, 114, 124, 134, 144, 154, and 164. Find the class size and class intervals.
8. The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them in kg are 52, 54, 55, 53, 56, and 54. Find the weight of the seventh student.
9. The questions solved by a student during a week are as follows: Find the mean.
Monday | Tuesday | Wednesday | Thursday | Friday | Saturday |
35 | 30 | 27 | 32 | 23 | 28 |
Tips to learn Class 9 Maths Chapter 12 Statistics
Start by learning the basics like mean, median, mode, and how they represent data.
Work on drawing bar graphs, histograms, and frequency polygons to visualize data better.
Memorize and practice applying formulas for mean, median, mode, and range to strengthen your calculations.
Break problems into smaller steps to avoid confusion and double-check your answers.
Practice examples from your textbook and important questions to build confidence.
Key Features of Important Questions CBSE Class 9 Maths Chapter 12 - Statistics
Exam-Oriented Content: Class 9 Maths Chapter 12 - Statistics includes crucial questions tailored for exams to ensure comprehensive preparation.
Detailed Solutions: Thorough and step-by-step explanations for all questions, aiding in a deeper understanding of the concepts.
Expert-Crafted Solutions: Solutions crafted by experienced Maths subject experts, aligning with the curriculum for easy comprehension.
Foundation Building: Important questions contribute to building a strong foundation crucial for success in board and competitive exams.
Free and Accessible: Solutions are freely available, downloadable in a convenient PDF format for easy access and offline studying.
Conclusion
Learning CBSE Class 9 Maths Chapter 12 Statistics becomes easier with consistent practice of important questions. These questions are designed to cover all key topics like mean, median, mode, and data representation. By solving them, students can strengthen their understanding of core concepts and improve their problem-solving skills. Practising regularly not only improves confidence but also ensures better performance in exams. Statistics is all about understanding and analysing data, and these questions help build a strong foundation. Focus on understanding the formulas and applying them step-by-step for accurate results.
Related Study Materials for Class 9 Maths Chapter 12 Statistics
S. No | Study Materials for Class 9 Maths Chapter 12 |
1. | |
2. | |
3. | |
4. | |
5. | |
6. |
CBSE Class 9 Maths Chapter-wise Important Questions
S. No | Chapter-wise Important Questions for Class 9 Maths |
1. | |
2. | |
3. | |
4. | |
5. | |
6. | |
7. | |
8. | |
9. | |
10. | |
11. |
Related Important Links for Maths Class 9
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 9–
S. No | Study Materials for Class 9 Maths |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | |
8 | |
9. |
FAQs on CBSE Important Questions for Class 9 Maths Statistics - 2025-26
1. What are the most important topics covered in the CBSE Class 9 Maths Chapter 12 Statistics for 2025–26 board exams?
- Data collection methods (primary and secondary data)
- Presentation of data using tables and graphical tools (bar graphs, histograms, frequency polygons, pie charts)
- Measures of central tendency—mean, median, and mode
- Calculation of range in a data set
- Construction and use of frequency distribution tables
2. How is the mean of a frequency distribution calculated for Class 9 Statistics?
The mean (arithmetic mean) is calculated using the formula:
Mean = \( \frac{\sum{f x}}{\sum{f}} \),
where f is the frequency and x is the data value for each class interval. Sum up all products of f and x, then divide by the total frequency.
3. What is the difference between primary and secondary data in statistics?
- Primary data is collected firsthand by the investigator for a specific purpose (e.g., measuring students’ heights directly).
- Secondary data is collected by someone else and used by the investigator (e.g., using published survey results).
4. Why is the median considered a robust measure of central tendency in statistics?
The median is the middle value of an ordered data set. It is robust because:
- It is not affected by extremely high or low values (outliers).
- It accurately reflects the center for skewed distributions, while the mean can be misleading.
5. How do you construct a histogram, and what types of data require adjustment of frequencies?
- To draw a histogram, divide data into class intervals and use bars to represent the frequency of each.
- If class intervals are of unequal width, calculate adjusted frequencies using:
Adjusted Frequency = (Minimum class width / Class width) × Actual frequency. - This ensures all bars are comparable visually.
6. What is the modal value in a data set, and how can there be more than one mode?
The mode is the value that appears most frequently in a data set. A data set can have no mode (if all values are unique), one mode (unimodal), or more than one mode (bimodal or multimodal) if multiple values have the same highest frequency.
7. Explain how to find the range and why it is not a strong indicator of data distribution in statistics.
- The range = highest value − lowest value in a data set.
- Although easy to calculate, the range only considers two data points and ignores the rest, making it sensitive to outliers and not reflective of data spread or variation.
8. A question in the exam asks: 'If 5 is subtracted from all observations of a data set with mean 20, what is the new mean?' What is the solution logic?
- Subtracting a constant from each value decreases the mean by that constant.
- New mean = 20 − 5 = 15.
9. Why do frequency polygons accompany histograms in Class 9 Statistics, and how are they constructed?
- Frequency polygons provide a clearer view of distribution shape and trends, especially when comparing datasets.
- They are constructed by plotting the frequency at the midpoint of each class interval and joining these points with straight lines.
10. In CBSE board exams, how are HOTS (Higher Order Thinking Skills) questions structured in Statistics Chapter 12?
HOTS questions typically require:
- Interpreting data tables or graphs beyond simple calculation
- Explaining the impact of outliers on mean and median
- Justifying the choice of a measure of central tendency for a specific scenario
11. How can students avoid common mistakes when finding class marks and class intervals in statistics problems?
- Class mark = (Upper limit + Lower limit)/2.
- Always check if intervals are continuous (adjacent classes share limits).
- Accurate calculation prevents errors in constructing histograms or frequency polygons.
12. How is the sum of deviations from the mean always zero, and why does this matter?
The algebraic sum of all deviations from the mean is always zero because the mean precisely balances the data values. This property validates the mean as a true measure of central tendency and is a common theoretical 2-mark question.
13. What steps should students follow to efficiently prepare for CBSE Class 9 Maths Chapter 12 Statistics important questions?
- Practice solving a variety of questions on mean, median, and mode—conceptual and numerical.
- Rehearse drawing and interpreting bar graphs, histograms, and frequency polygons.
- Memorize key formulas and understand when to use each measure of central tendency.
- Attempt previous years’ board questions for familiarity with exam patterns.
14. How do you classify data as discrete or continuous in the context of Class 9 Statistics, and why is this important?
- Discrete data: Countable and exact values (e.g., number of students).
- Continuous data: Measurable and can take any value within a range (e.g., heights).
15. If the mean of a data set is incorrect due to a wrongly entered value, how is the correct mean calculated?
- Subtract the incorrect value and add the correct value to the total sum.
- Divide the updated sum by the total number of observations for the correct mean.































