CBSE Class 9 Maths Important Questions - Chapter 8 Quadrilaterals

1 Mark Questions

1. A quadrilateral ${\text{ABCD}}$ is a parallelogram if

(a) ${\text{AB}} = {\text{CD}}$

(b) $\mathbf{A B} \| \mathbf{B C}$

(c) $\angle A = {60^\circ },\angle C = {60^\circ },\angle B = {120^\circ }$

(d) $AB = AD$

Ans: (c) $\angle A = {60^\circ },\angle C = {60^\circ },\angle B = {120^\circ }$

2. In figure, ABCD and AEFG are both parallelogram if $\angle C = {80^\circ }$, then $\angle DGF$ is

(a) ${100^\circ }$

(b) ${60^\circ }$

(c) ${80^\circ }$

(d) ${120^\circ }$

Ans: (c) ${80^\circ }$

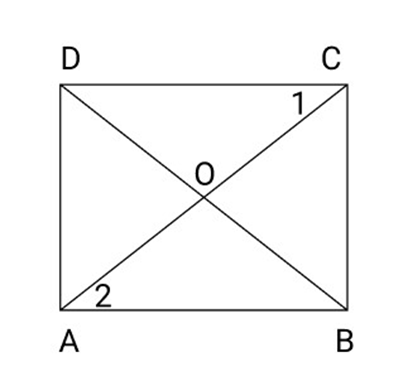
3. In a square ABCD, the diagonals AC and BD bisects at O . Then $\vartriangle AOB$ is

(a) Acute angled

(b) Obtuse angled

(c) Equilateral

(d) Right-angled

Ans: (d) Right-angled

4. ${\text{ABCD}}$ is a rhombus. If $\angle ACB = {30^\circ }$, then $\angle ADB$ is

(a) ${30^\circ }$

(b) ${120^\circ }$

(c) ${60^\circ }$

(d) ${45^\circ }$

Ans: (c) ${60^\circ }$

5. In fig ${\text{ABCD}}$ is a parallelogram. If $\angle DAB = {60^\circ }$ and $\angle DBC = {80^\circ }$ then $\angle CDB$ is

(A) ${80^\circ }$

(B) ${60^\circ }$

(C) ${20^\circ }$

(D) ${40^\circ }$

Ans: (D) ${40^\circ }$

6. If the diagonals of a quadrilateral bisect each other, then the quadrilateral must be.

(a) Square

(b) Parallelogram

(c) Rhombus

(d) Rectangle

Ans: (b) Parallelogram

7. The diagonal AC and BD of quadrilateral ABCD are equal and are perpendicular bisector of each other then quadrilateral ABCD is a

(a) Kite

(b) Square

(c) Trapezium

(d) Rectangle

Ans: (b) Square

8. The quadrilateral formed by joining the mid points of the sides of a quadrilateral ABCD taken in order, is a rectangle if

(a) ${\text{ABCD}}$ is a parallelogram

(b) ${\text{ABCD}}$ is a rut angle

(c) Diagonals ${\text{AC}}$ and ${\text{BD}}$ are perpendicular

(d) ${\text{AC}} = {\text{BD}}$

Ans: (a) ${\text{ABCD}}$ is a parallelogram

9. In the fig ${\text{ABCD}}$ is a Parallelogram. The values of $x$ and $y$ are

(a) 30,35

(b) 45,30

(c) 45,45

(d) 55,35

Ans: (b) 45,30

10. In fig if ${\text{DE}} = 8\;{\text{cm}}$ and ${\text{D}}$ is the mid-Point of ${\text{AB}}$, then the true statement is

(a) ${\text{AB}} = {\text{AC}}$

(b) ${\text{DE||BC}}$

(c) ${\text{E}}$ is not mid-Point of AC

(d) \[\text{DE} \ne \text{BC}\]

Ans: (c) ${\text{E}}$ is not mid-Point of AC

11. The sides of a quadrilateral extended in order to form an exterior angler. The sum of these exterior angles is

(a) ${180^\circ }$

(b) ${270^\circ }$

(c) ${90^\circ }$

(d) ${360^\circ }$

Ans: (d) ${360^\circ }$

12. ${\text{ABCD}}$ is rhombus with $\angle ABC = {40^\circ }$. The measure of $\angle ACD$ is

(a) ${90^\circ }$

(b) ${20^\circ }$

(c) ${40^\circ }$

(d) ${70^\circ }$

Ans: (b) ${20^\circ }$

13. In fig ${\text{D}}$ is mid-point of ${\text{AB}}$ and  BC then AE is equal to

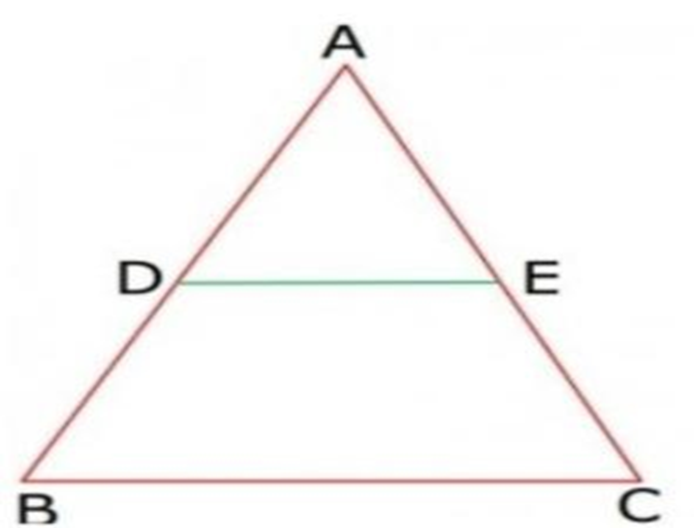
(a) AD

(b) ${\text{EC}}$

(c) ${\text{DB}}$

(d) ${\text{BC}}$

Ans: (b) EC

14. In fig ${\text{D}}$ and ${\text{E}}$ are mid-points of ${\text{AB}}$ and AC respectively. The length of DE is

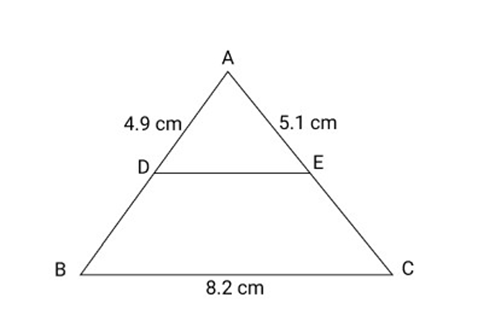
(a) $8.2\;{\text{cm}}$

(b) $5.1\;{\text{cm}}$

(c) $4.9\;{\text{cm}}$

(d) $4.1\;{\text{cm}}$

Ans: (d) $4.1\;{\text{cm}}$

15. A diagonal of a parallelogram divides it into

(a) Two congruent triangles

(b) Two similes triangles

(c) Two equilateral triangles

(d) None of these

Ans: (a) Two congruent triangles

16. A quadrilateral is a, if it’s opposite sides are equal:

(a) Kite

(b) Trapezium

(c) Cyclic quadrilateral

(d) Parallelogram

Ans: (d) Parallelogram

17. In the adjoining Fig. ${\text{AB}} = {\text{AC}}\,\,.\,\,{\text{CD}}||{\text{BA}}$ and ${\text{AD}}$ is the bisector of $\angle PAC$ prove that

(a) $\angle DAC = \angle BCA$

Ans: In $\Delta ABC\quad AB = AC$ is given.

$\therefore\:\angle B=\angle C$ 

$\left [ angle\:opposite\:to\:equal\:sides\:of\:the\:\Delta \right ]$ 

$ \Rightarrow \angle BCA = \angle ABC$ (Opposite angle of equal sides are equal)

$\angle PAC = \angle BCA + \angle ABC$ (Exterior angle)

$2\angle CAD = 2\:\angle BCA$

$ \Rightarrow \angle DAC = \angle BCA$

Hence proved.

(b) ABCD is a parallelogram

Ans:  Now, $\angle PAC = \angle BCA$

Also $CD\parallel BA$ (According to the question)

$\therefore ABCD$ is a parallelogram.

18. Which of the following is not a parallelogram?

(a) Rhombus

(b) Square

(c) Trapezium

(d) Rectangle

Ans: (c) Trapezium

19. The sum of all the four angles of a quadrilateral is

(a) ${180^0}$

(b) ${360^0}$

(c) ${270^0}$

(d) ${90^0}$

Ans: (b) ${360^\circ }$

20. In Fig ABCD is a rectangle P and ${\mathbf{Q}}$ are mid-points of AD and DC respectively. Then length of ${\text{PQ}}$ is

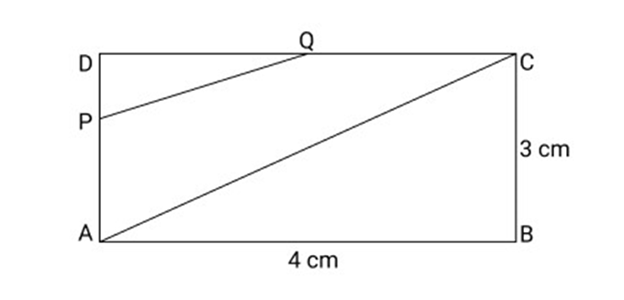
(a) 5 ${\text{cm}}$

(b) $4\;{\text{cm}}$

(c) $2.5\;{\text{cm}}$

(d) $2\;{\text{cm}}$

Ans: (c) $2.5\;{\text{cm}}$

21. In Fig ABCD is a rhombus. Diagonals AC and BD intersect at $0.{\text{E}}$ and ${\text{F}}$ are mid points of AO and BO respectively. If $AC = 16\;{\text{cm}}$ and $BD = 12\;{\text{cm}}$ then EF is

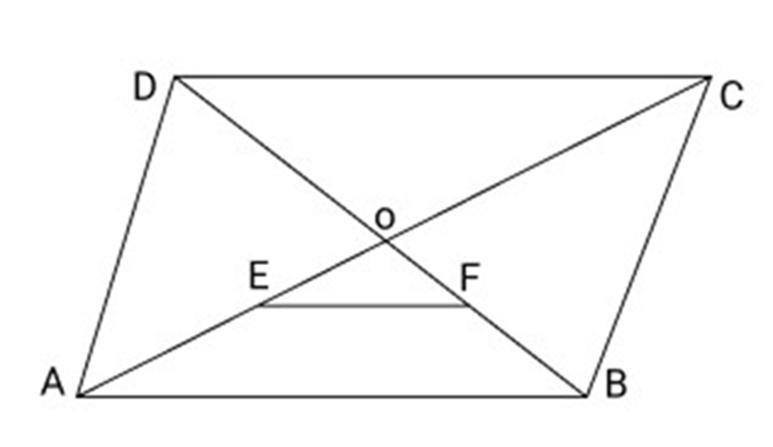
(a) $10\;{\text{cm}}$

(b) $5\;{\text{cm}}$

(c) $8\;{\text{cm}}$

(d) $6\;{\text{cm}}$

Ans: (b) $5\;{\text{cm}}$

2 Marks Questions

1. The angles of a quadrilateral are in the ratio 3: 5: 9: 13. Find all angles of the quadrilateral

Ans: Assume that in quadrilateral ${\text{ABCD}},\angle {\text{A}} = 3x,\angle {\text{B}} = 5x,\angle {\text{C}} = 9x$ and $\angle {\text{D}} = 13x$.

We know that the sum of all the angles of a quadrilateral $ = {360^\circ }$

So, $\angle {\text{A}} + \angle {\text{B}} + \angle {\text{C}} + \angle {\text{D}} = {360^\circ } \Rightarrow 3x + 5x + 9x + 13x = {360^\circ }$

$ \Rightarrow 30x = {360^\circ } \Rightarrow x = {12^\circ }$

Now, $\angle {\text{A}} = 3x = 3 \times 12 = {36^\circ }$

$\angle {\text{B}} = 5x = 5 \times 12 = {60^\circ }$

$\angle {\text{C}} = 9x = 9 \times 12 = {108^\circ }$

And $\angle {\text{D}} = 13x = 13 \times 12 = {156^\circ }$

Therefore, angles of a given quadrilateral are ${36^\circ },{60^\circ },{108^\circ }$ and ${156^\circ }$.

2. If the diagonals of a parallelogram are equal, show that it is a rectangle.

Ans: According to the question: ${\text{ABCD}}$ is a parallelogram with diagonal ${\text{AC}} = $ diagonal BD

To prove: ${\text{ABCD}}$ is a rectangle.

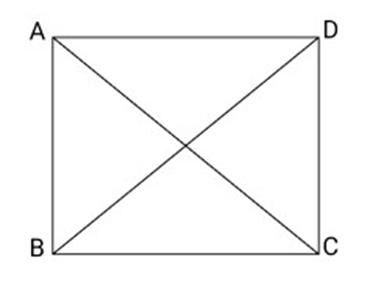
Proof: In triangles ${\text{ABC}}$ and ${\text{ABD}}$,

${\text{AB}} = {\text{AB}}$ (Common)

${\text{AC}} = {\text{BD}}$ (According to the question)

${\text{AD}} = {\text{BC}}$ (Opposite Sides of a 

So, $\Delta {\text{ABC}} \cong \Delta {\text{BAD}}$ (By SSS congruence)

$ \Rightarrow \angle {\text{DAB}} = \angle {\text{CBA}}\,\,\,\,\,\,({\text{By}}\,\,{\text{C}}.{\text{P}}.{\text{C}}.{\text{T}}.) \ldots  \ldots  \ldots ..({\text{i}})$

But $\angle {\text{DAB}} + \angle {\text{CBA}} = {180^\circ } \ldots  \ldots  \ldots $ (ii)

and ${\text{AB}}$ cuts them, the sum of the interior angles of the same side of transversal is ${180^\circ }$ )

According to the equations (i) and (ii),

$\angle {\text{DAB}} = \angle {\text{CBA}} = {90^\circ }$

Therefore, ${\text{ABCD}}$ is a rectangle.

3. Diagonal AC of a parallelogram ABCD bisects $\angle $ A (See figure). Show that:

(i) It bisects $\angle {\text{C}}$ also.

(ii) ${\text{ABCD}}$ is a rhombus.

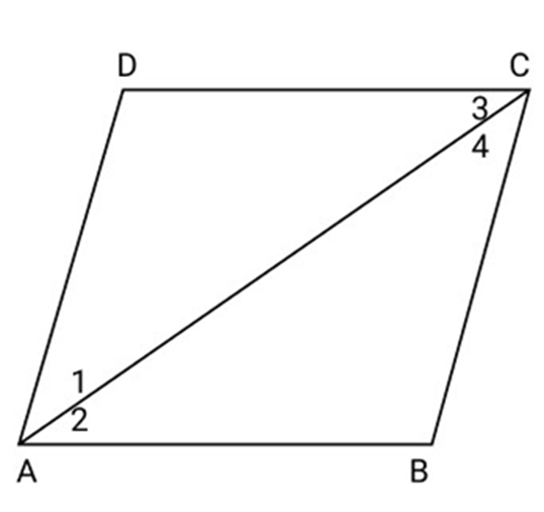
Ans: Diagonal AC bisects $\angle {\text{A}}$ of the parallelogram ${\text{ABCD}}$.

(i) Since  and AC intersects them.

So, $\angle 1 = \angle 3$ (Alternate angles) ..........(i)

Similarly $\angle 2 = \angle 4 \ldots  \ldots  \ldots ..$ (ii)

But $\angle 1 = \angle 2$ (Given) ..........(iii) 

So, $\angle 3 = \angle 4$ (Using eq. (i), (ii) and (iii)) 

Hence ${\text{AC}}$ bisects $\angle {\text{C}}$.

(ii) $\angle 2 = \angle 3 = \angle 4 = \angle 1$

$ \Rightarrow {\text{AD}} = {\text{CD}}$ (Sides opposite to equal angles)

So, ${\text{AB}} = {\text{CD}} = {\text{AD}} = {\text{BC}}$

Therefore ABCD is a rhombus.

4. ABCD is a parallelogram and AP and Care the perpendiculars from vertices $A$ and $C$ on its diagonal BD (See figure). Show that:

(i) $\Delta {\text{APB}} \cong \Delta {\text{CQD}}$

(ii) ${\text{AP}} = {\text{CQ}}$

Ans: According to the question,

ABCD is a parallelogram.

$AP \bot BD$ and $CQ \bot $ BD

To prove: 

(i) $\Delta {\text{APB}} \cong \Delta {\text{CQD}}$ 

(ii) ${\text{AP}} = {\text{CQ}}$

Proof: 

(i) In $\Delta {\text{APB}}$ and $\Delta {\text{CQD}}$,

$\angle 1 = \angle 2$ (Alternate interior angles)

$AB = CD$ (Opposite sides of a parallelogram are equal)

$\angle {\text{APB}} = \angle {\text{CQD}} = {90^\circ }$

So, $\Delta {\text{APB}} \cong \Delta {\text{CQD}}$ (By ASA Congruency)

(ii) Since $\Delta {\text{APB}} \cong \Delta {\text{CQD}}$

${\text{AP}} = {\text{CQ}}$ (By C.P.C.T.)

Hence proved.

5. ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See figure). AC is a diagonal. Show that:

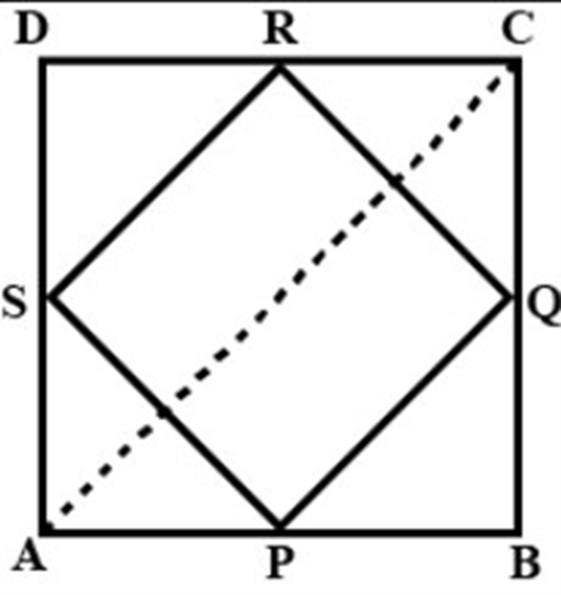
(i)  and ${\text{SR}} = \dfrac{1}{2}{\text{AC}}$

(ii) ${\text{PQ}} = {\text{SR}}$

(iii) PQRS is a parallelogram.

Ans: (i) In $\triangle \mathrm{DAC}, \mathrm{S}$ is the mid point of $\mathrm{DA}$ and $\mathrm{R}$ is the mid point of $\mathrm{DC}$. Therefore, $\mathrm{SR} \| \mathrm{AC}$ and $\mathrm{SR}=\frac{1}{2} \mathrm{AC}$.By mid-point theorem.

(ii) In $\triangle \mathrm{BAC}, \mathrm{P}$ is the mid point of $\mathrm{AB}$ and $\mathrm{Q}$ is the mid point of $\mathrm{BC}$. Therefore, $\mathrm{PQ} \| \mathrm{AC}$ and $\mathrm{P} \mathrm{Q}=\frac{1}{2} \mathrm{AC}$.By mid-point theorem. But from (i) $\mathrm{SR}=\frac{1}{2} \mathrm{AC}$ therefore $\mathrm{P} \mathrm{Q}=\mathrm{SR}$

(iii) $\mathrm{PQ} \| \mathrm{AC}$ \& SR $\| \mathrm{AC}$ therefore $\mathrm{PQ} \| \mathrm{SR}$ and $\mathrm{P} \mathrm{Q}=\mathrm{SR}$. Hence, a quadrilateral with opposite sides equal and parallel is a parallelogram. Therefore PQRS is a parallelogram.

6. The angles of a quadrilateral are in the ratio 3:5:9:13. Find all the angles of the quadrilateral.

Ans: Assume that angles of quadrilateral ${\text{ABCD}}$ are $3{\text{x}},5{\text{x}},9{\text{x}}$, and $13{\text{x}}$

$\angle A + \angle B + \angle C + \angle D = {360^\circ }$ (We know that the sum of angles of a quadrilateral is $\left. {{{360}^\circ }} \right)$

$30x = {360^\circ }$

$x = {12^\circ }$

So, $\angle A = 3x = 3 \times 12 = {36^\circ }$

$\angle B = 5x = 5 \times 12 = {60^\circ }$

$\angle C = 9x = 9 \times 12 = {108^\circ }$

$\angle D = 13x = 13 \times 12 = {156^\circ }$

Hence, the value of all angles are ${36^ \circ },{60^ \circ },{108^ \circ },{156^ \circ }.$

7. Show that each angle of a rectangle is a right angle.

Ans: As we also know that a rectangle is a parallelogram whose one angle is right angle.

Assume that ${\text{ABCD}}$ be a rectangle.

$\angle A = {90^\circ }$

To prove $\angle B = \angle C = \angle D = {90^\circ }$

Proof: 

 and ${\text{AB}}$ is transversal

So, $\angle A + \angle B = {180^\circ }$

${90^\circ } + \angle B = {180^\circ }$

$\angle B = {180^\circ } - {90^\circ } = {90^\circ }$

$\angle C = \angle A$

So, $\angle C = {90^\circ }$

$\angle D = \angle B$

So, $\angle D = {90^\circ }$

Hence proved.

8. A transversal cuts two parallel lines prove that the bisectors of the interior angles

enclose a rectangle.

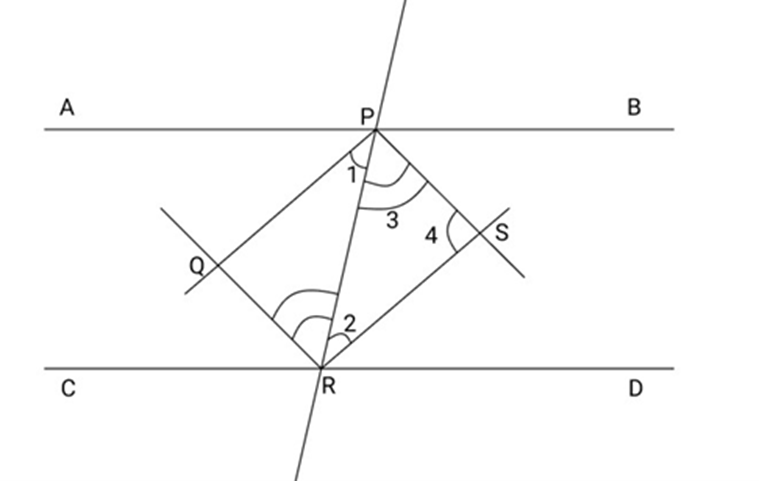
Ans: According to the question,

 and EF cuts them at ${\text{P}}$ and ${\text{R}}$.

$\angle APR = \angle PRD$ (Alternate interior angles)

So, $\dfrac{1}{2}\angle APR = \dfrac{1}{2}\angle PRD$

i.e. $\angle 1 = \angle 2$

 (Alternate)

Hence, proved.

9. Prove that diagonals of a rectangle are equal in length.

Ans: ${\text{ABCD}}$ is a rectangle and AC and BD are diagonals.

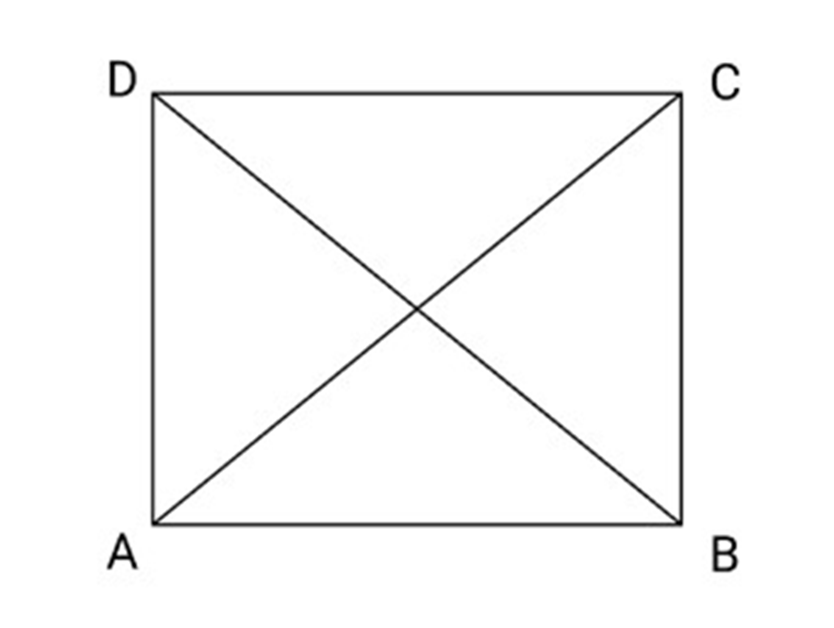
To prove $AC = BD$

Proof: 

In $\Delta DAB$ and CBA

${\text{AD}} = {\text{BC}}$ (In a rectangle opposite sides are equal)

$\angle A = \angle B\quad \left( {{{90}^\circ }{\text{each}}} \right)$

${\text{AB}} = {\text{AB}}$ (common)

So, $\Delta DAB \cong \Delta CAB$ (By SAS)

So, $AC = BD$ (By C.P.C.T)

10. If each pair of opposite sides of a quadrilateral is equal, then prove that it is a parallelogram.

Ans: According to the question,

A quadrilateral ${\text{ABCD}}$ in which ${\text{AB}} = {\text{DC}}$ and ${\text{AD}} = {\text{BC}}$

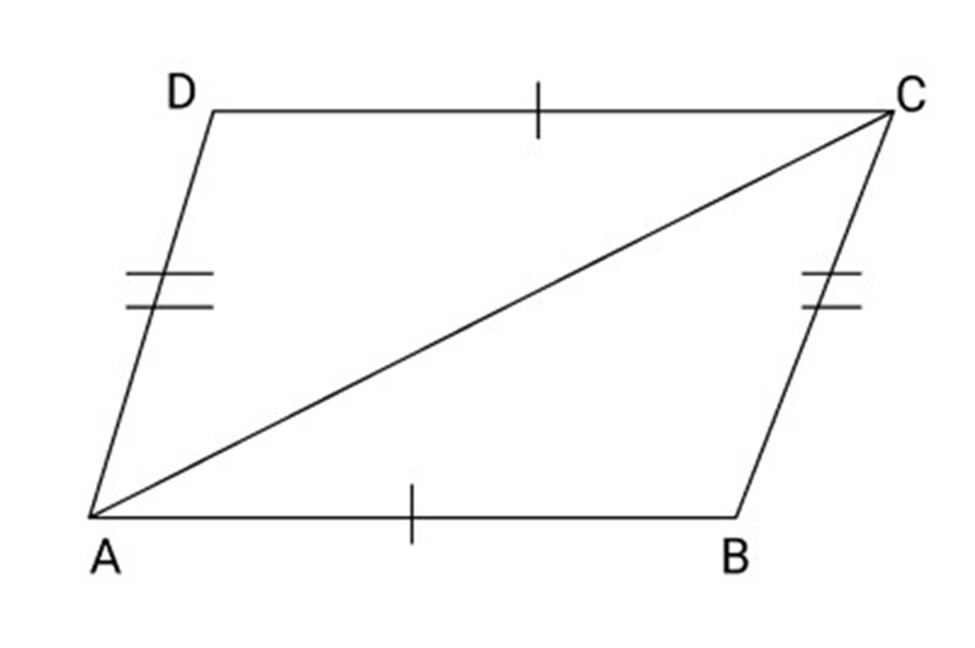
To prove: 

${\text{ABCD}}$ is a parallelogram

We construct a line AC to with join point A with point C.

Proof: In $\vartriangle ABC$ and $\vartriangle ADC$

${\text{AD}} = {\text{BC}}$ (According to the question)

${\text{AB}} = {\text{DC}}$

${\text{AC}} = {\text{AC}}$ (common)

So, $\Delta ABC \cong \Delta ADC$ (By SSS )

So, $\angle BAC = \angle DAC$ (By CPCT)

So, $ABCD$ is a parallelogram.

12. Show that the line segments joining the mid points of opposite sides of a quadrilateral bisect each other.

Ans: According to the question,

${\text{ABCD}}$ is quadrilateral ${\text{E}},{\text{F}},{\text{G}},{\text{H}}$ are mid points of the side ${\text{AB}},{\text{BC}},{\text{CD}}$ and ${\text{DA}}$ respectively

To prove:

EG and HF bisect each other.

In $\vartriangle ABC,\,\,{\text{E}}$ is mid-point of ${\text{AB}}$ and ${\text{F}}$ is mid-point of ${\text{BC}}$

So,  and $EF = \dfrac{1}{2}AC \ldots  \ldots .(i)$

Similarly,  and $HG = \dfrac{1}{2}AC \ldots  \ldots .(ii)$

According to equations (i) and (ii), 

 and $EF = GH$

So, $EFGH$ is a parallelogram and EG and HF are its diagonals

The diagonals of a parallelogram bisect each other

Hence, EG and HF bisect each other.

13. ABCD is a rhombus show that diagonal AC bisects $\angle A$ as well as $\angle C$ and diagonal BD bisects $\angle B$ as well as $\angle D$

Ans: According to the question,

${\text{ABCD}}$ is a rhombus

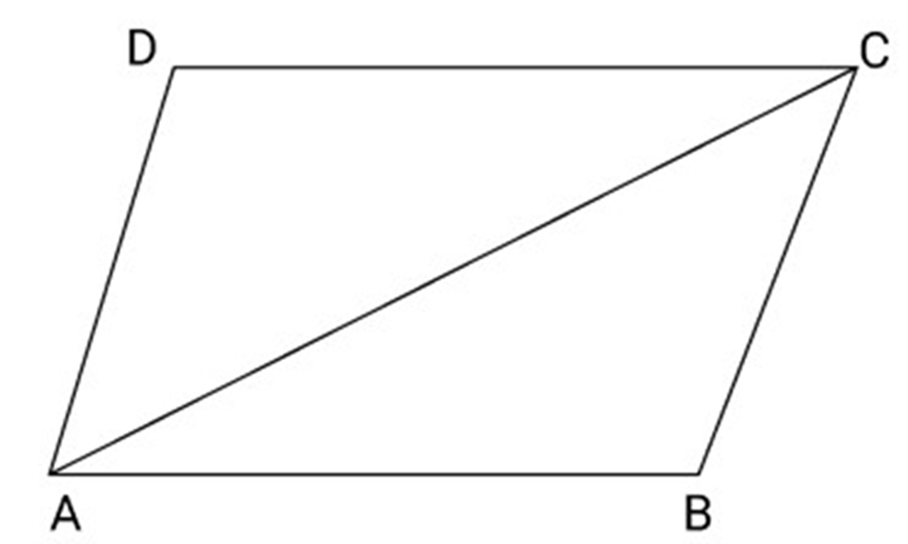
In $\Delta ABC$ and $\Delta ADC$

$AB = AD$ (Sides of a rhombus)

$BC = DC$ (Sides of a rhombus)

$AC = AC$ (Common)

So, $\Delta ABC \cong \Delta ADC$ (By SSS Congruency)

So, $\angle CAB = \angle CAD$ and $\angle ACB = \angle ACD$

Therefore, AC bisects $\angle A$ as well as $\angle C$

Similarly, by joining B to D, we can prove that $\vartriangle ABD \cong \Delta CBD$

Therefore, BD bisects $\angle B$ as well as $\angle D$

14. In fig AD is a median of $\vartriangle ABC,E$ is mid-Point of AD. BE produced meet AC at ${\text{F}}$. Show that $AF = \dfrac{1}{3}AC$

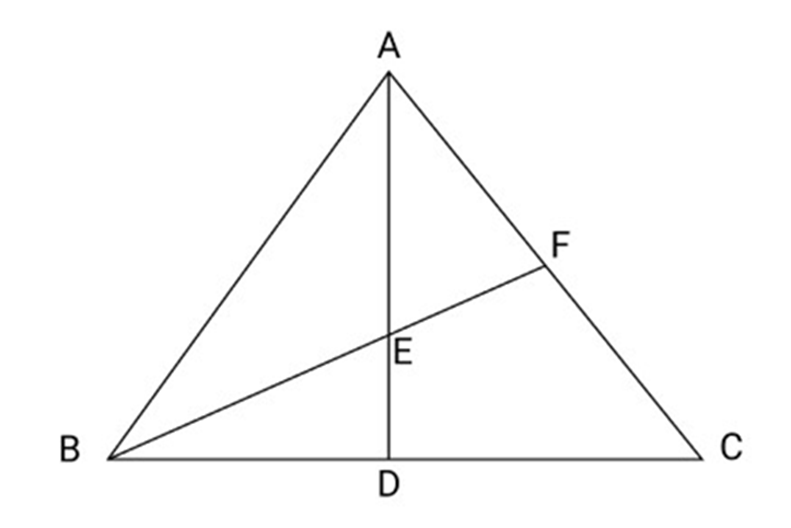
Ans: Suppose ${\text{M}}$ is mid-Point of CF Join DM

So, 

In \(\vartriangle ADM,\,E\) is mid- Point of AD and

 is mid-point of AM

So, $AF = FM$

${\text{FM}} = {\text{MC}}$

So, $AF = FM = MC$

So, $AC = AF + FM + MC$

$ = AF + AF + AF$

$ \Rightarrow AC = 3AF$

$ \Rightarrow AF = \dfrac{1}{3}AC$

Hence Proved.

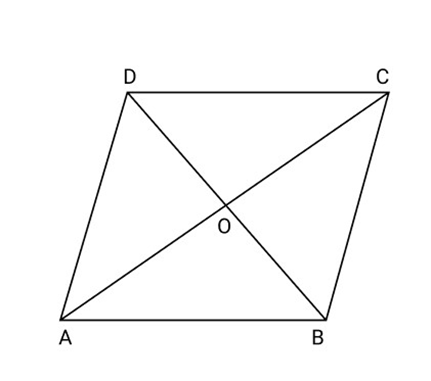
15. Prove that a quadrilateral is a parallelogram if the diagonals bisect each other.

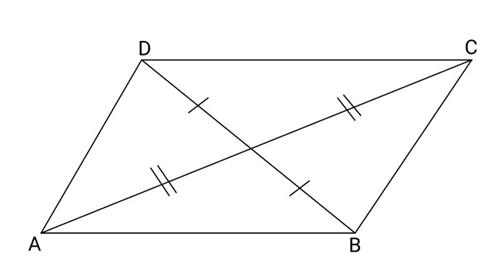
Ans: According to the given figure,

${\text{ABCD}}$ is a quadrilateral in which diagonals AC and BD intersect each other at O

In $\vartriangle AOB$ and $\vartriangle DOC$

$OA = OC$ (Given)

$OB = OD$ (Given)

And $\angle AOB = \angle COD$ (Vertically apposite angle)

So, $\vartriangle AOB \cong \Delta COD$ (By SAS)

So, $\angle OAB = \angle OCD$ (By C.P.C.T)

But this is Pair of alternate interior angles

So, $AD\parallel BC$

So, Quadrilateral ${\text{ABCD}}$ is a Parallelogram.

16. In fig ABCD is a Parallelogram. AP and Care Perpendiculars from the Vertices ${\text{A}}$ and C on diagonal BD.

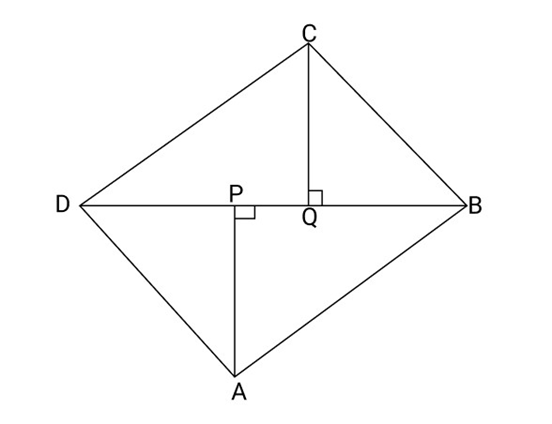
Show that

(i) $\vartriangle APB \cong \Delta CQD$

(ii) $AP = CQ$

Ans:  (I) in $\Delta APB$ and $\Delta CQD$

${\text{AB}} = {\text{DC}}$ (Opposite sides of a Parallelogram)

$\angle P = \angle Q$ (each ${90^\circ }$)

And $\angle ABP = \angle CDQ$

So, $\vartriangle APB \cong \Delta CQD$ (By ASA)

(II) So, $AP = CQ$ (By C.P.C.T)

17. ABCD is a Parallelogram ${\text{E}}$ and ${\text{F}}$ are the mid-Points of ${\text{BC}}$ and AD respectively. Show that the segments BF and DE trisect the diagonal AC.

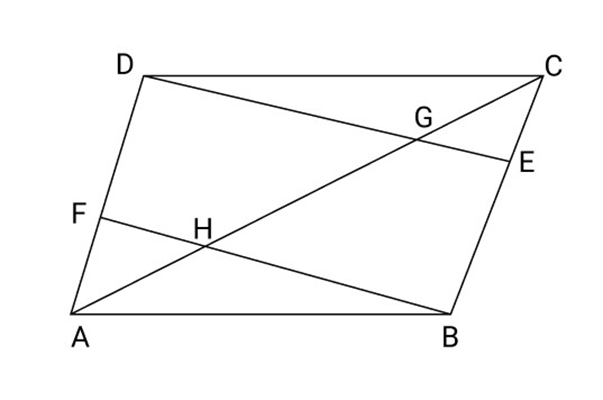
Ans: $FD\parallel BE$ and $FD = BE$

So, BEDF Is a Parallelogram

${\text{EG}}\parallel {\text{BH}}$ and ${\text{E}}$ is the mid-Point of BC

So, ${\text{G}}$ is the mid-point of ${\text{HC}}$

Or ${\text{HG}} = {\text{GC}} \ldots  \ldots  \ldots  \ldots ..$ (i)

Similarly ${\text{AH}} = {\text{HG}} \ldots  \ldots  \ldots  \ldots ..$ (ii)

According to equations (i) and (ii) we get

${\text{AH}} = {\text{HG}} = {\text{GC}}$

Hence, the segments BF and DE bisects the diagonal AC.

18. Prove that if each pair of apposite angles of a quadrilateral is equal, then it is a parallelogram.

Ans: According to the figure and question,

${\text{ABCD}}$ is a quadrilateral in which $\angle A = \angle C$ and $\angle B = \angle D$

To Prove: 

${\text{ABCD}}$ is a parallelogram

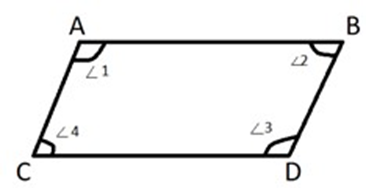
Proof: 

$\angle A = \angle C$ (According to the question)

$\angle B = \angle D$ (According to the question)

$\angle A + \angle B = \angle C + \angle D \ldots  \ldots (i)$

In quadrilateral. ABCD

$\angle A + \angle B + \angle C + \angle D = {360^\circ }$

$(\angle A + \angle B) + (\angle A + \angle B) = {360^\circ }({\text{By}} \ldots .({\text{i}}))$

$\angle A + \angle B = {180^\circ }$

$\angle A + \angle B = \angle C + \angle D = {180^\circ }$

These are sum of interior angles on the same side of transversal

So, $AD\|BC$ and $A B \| D C$ 

So, ABCD is a parallelogram.

19. In Fig. ABCD is a trapezium in which ${\text{AB}}||{\text{DCE}}$ is the mid-point of AD. A line through ${\text{E}}$ is parallel to AB show that $l$ bisects the side BC

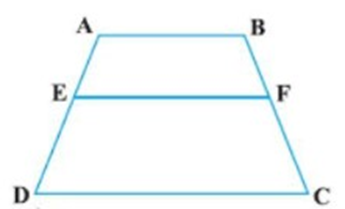
Ans: We draw a line AC with join point A to Point C.

In $\Delta ADC$

E is mid-point of ${\text{AD}}$ and ${\text{EO}}||{\text{DC}}$

So, $O$ is mid point of ${\text{AC}}$ (A line segment joining the midpoint of one side of a triangle parallel to second side and bisect the third side)

In $\vartriangle ACB$

${\text{O}}$ is mid point of ${\text{AC}}$

OF ||$AB$ 

So, F is mid point of BC

So, EF Bisect BC.

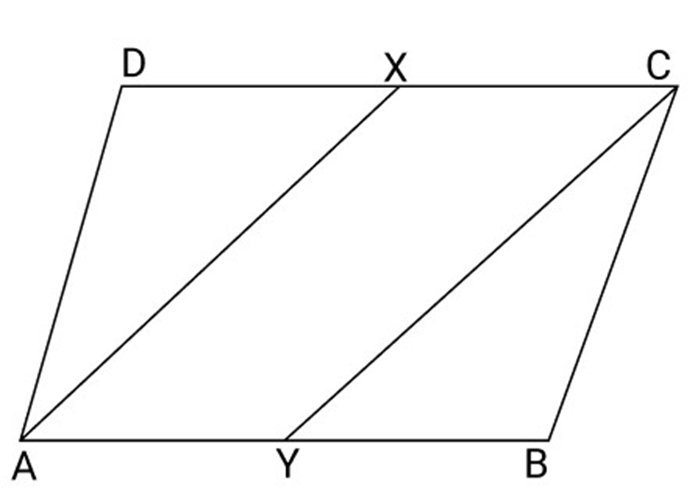
20. In Fig. ABCD is a parallelogram in which ${\text{X}}$ and ${\text{Y}}$ are the mid-points of the sides DC and AB respectively. Prove that AXCY is a parallelogram

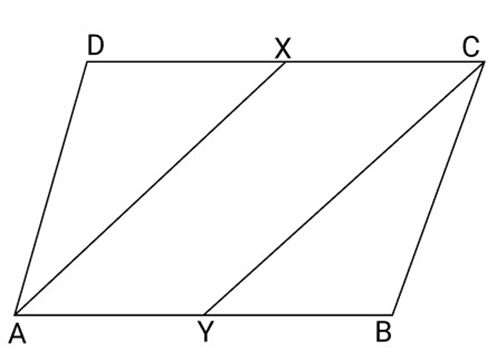
Ans: According to the given figure,

${\text{ABCD}}$ is a parallelogram

So,  and ${\text{AB}} = {\text{CD}}$

 And $\dfrac{1}{2}AB = \dfrac{1}{2}CD$

 And $XC = AY$

(X and Y are mid-point of DC and AB respectively)

$ \Rightarrow AXCY$ is a parallelogram

21. The angles of quadrilateral are in the ratio 3:5:10:12. Find all the angles of the quadrilateral.

Ans: Assume that angles of quadrilaterals are

3x, 5x, 10x, and 12x

$\angle A = 3x,\angle B = 5x,\angle C = 10x,\angle D = 12x$

In a quadrilateral

$\angle A + \angle B + \angle C + \angle D = {360^\circ }$

$3x + 5x + 10x + 12x = {360^\circ }$

$30{\text{x}} = 360$

$x = \dfrac{{360}}{{30}} = 12$

$\angle A = 3 \times 12 = {36^\circ },\angle B = 5 \times 12 = {60^\circ }$

$\angle C = 10 \times 12 = {120^\circ },\angle D = 12 \times 12 = {144^\circ }$

Hence, the values of all angles are ${36^ \circ },{60^ \circ },{120^ \circ },{144^ \circ }.$

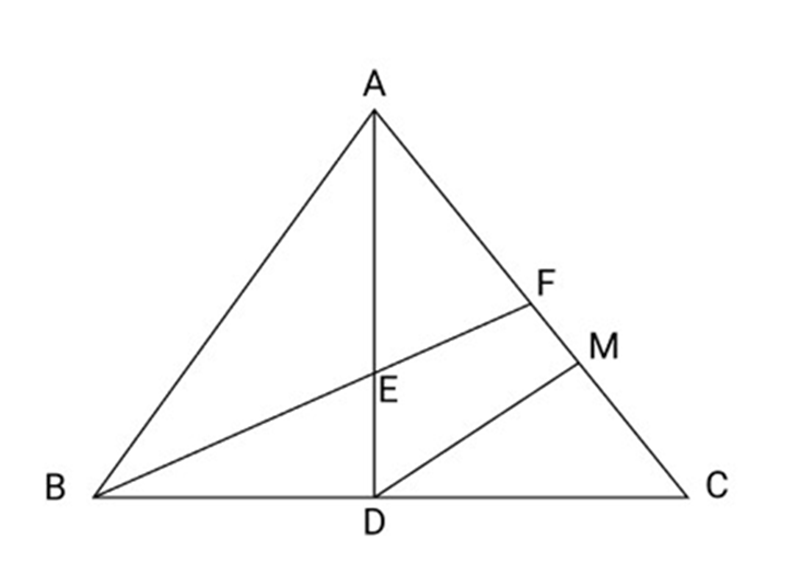
22. In fig ${\text{D}}$ is mid-points of AB. $P$ is on AC such that $PC = \dfrac{1}{2}AP$ and $DE\parallel BP$ show that $AE = \dfrac{1}{3}AC$

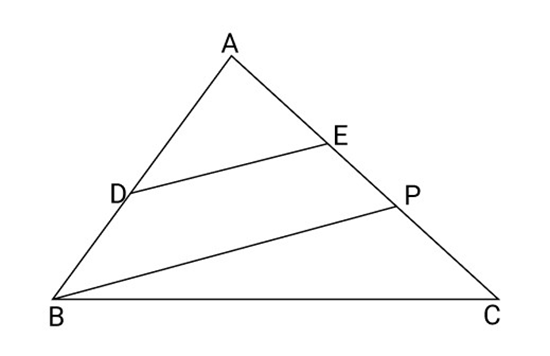
Ans: According to $\Delta $ ABP

${\text{D}}$ is mid points of ${\text{AB}}$ and ${\text{DE}}\mid {\text{BP}}$

${\text{E}}$ is midpoint of ${\text{AP}}$ 

So, $AE = EP$ also $PC = \dfrac{1}{2}AP$

$2{\text{PC}} = {\text{AP}}$

$2{\text{PC}} = 2{\text{AE}}$

$ \Rightarrow {\text{PC}} = {\text{AE}}$

So, $AE = PE = PC$

So, $AC = AE + EP + PC$

${\text{AC}} = {\text{AE}} + {\text{AE}} + {\text{AE}}$

$ \Rightarrow {\text{AE}} = \dfrac{1}{3}{\text{AC}}$

Hence Proved.

23. Prove that the bisectors of the angles of a Parallelogram enclose a rectangle. It is given that adjacent sides of the parallelogram are unequal.

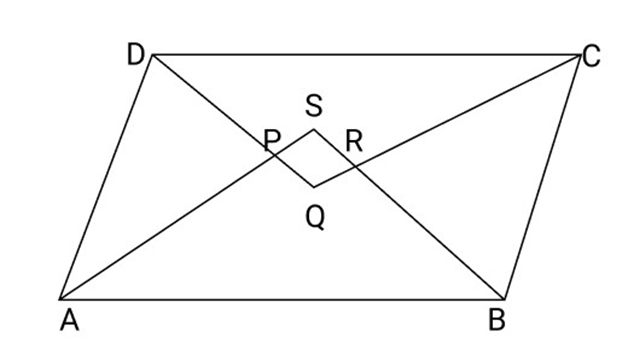
Ans: According to the given figure,

$ABCD$ is a parallelogram 

So, $\angle A + \angle D = {180^\circ }$

or $\dfrac{1}{2}(\angle A + \angle D) = {90^\circ }$

Or $\angle APD = {90^\circ }$ (We know that the sum of all angles of a triangle is ${180^\circ }$ )

So, $\angle SPQ = \angle APD = {90^\circ }$

Similarly, $\angle QRS = {90^\circ }$ and $\angle PQR = {90^\circ }$

$\angle P + \angle Q + \angle R + \angle S = {360^\circ }$

So, $\angle PSR = {90^\circ }$. 

Hence, each angle of quadrilateral PQRS is ${90^\circ }$ .

Therefore, PQRS is a rectangle.

24. Prove that a quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.

Ans: According to the question and figure,

${\text{ABCD}}$ is a quadrilateral in which ${\text{AB}}||{\text{DC}}$ and ${\text{BC}}||{\text{AD}}$.

To Prove: 

${\text{ABCD}}$ is a parallelogram

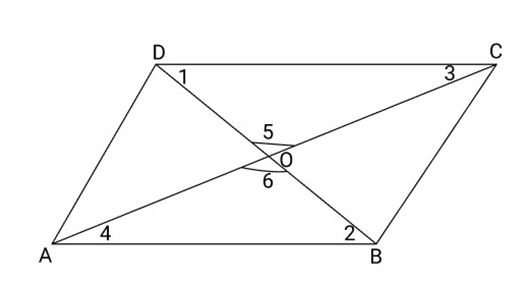
Construction: Join AC and BD intersect each other at $O$.

Proof: 

$\vartriangle AOB \cong \Delta DOC$ (By AAA)

 Because $\angle 1 = \angle 2$

$\angle 3 = \angle 4$ and $\angle 5 = \angle 6$

So, ${\text{AO}} = {\text{OC}}$

And ${\text{BO}} = {\text{OD}}$

So, ${\text{ABCD}}$ is a parallelogram

Because, diagonals of a parallelogram bisect each other.

3 Marks Questions

1. Show that is diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Ans: According to the question and figure,

Suppose ${\text{ABCD}}$ is a quadrilateral.

Suppose its diagonal AC and BD bisect each other at right angle at point $O$.

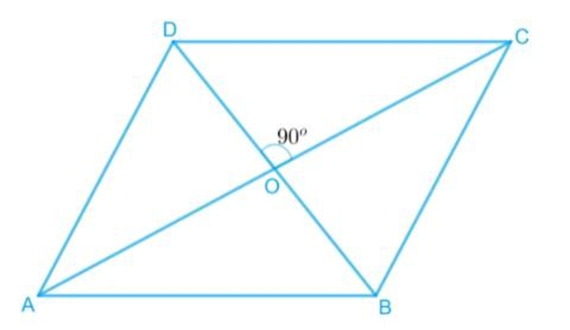
So, $OA = OC,OB = OD$

And $\angle {\text{AOB}} = \angle {\text{BOC}} = \angle {\text{COD}} = \angle {\text{AOD}} = {90^\circ }$

To prove: 

${\text{ABCD}}$ is a rhombus.

Proof: 

In $\Delta {\text{AOD}}$ and $\Delta {\text{BOC}}$,

${\text{OA}} = {\text{OC}}$ (According to the figure)

$\angle {\text{AOD}} = \angle {\text{BOC}}$ (According to the figure)

${\text{OB}} = {\text{OD}}$ ?(According to the figure)

So, $\Delta {\text{AOD}} \cong \Delta {\text{COB}}$  (By SAS congruency)

$ \Rightarrow {\text{AD}} = {\text{CB}}$ (By C.P.C.)..........(i)

Again, In $\Delta {\text{AOB}}$ and $\Delta {\text{COD}}$,

${\text{OA}} = {\text{OC}}$ (According to the figure)

$\angle {\text{AOB}} = \angle {\text{COD}}$ (According to the figure)

${\text{OB}} = {\text{OD}}$ (According to the figure)

So, $\Delta {\text{AOB}} \cong \Delta {\text{COD}}$ (By SAS congruency)

$ \Rightarrow {\text{AD}} = {\text{CB}}$ (By C.P.C.T.) ..........(ii)

Now In $\Delta {\text{AOD}}$ and $\Delta {\text{BOC}}$,

${\text{OA}} = {\text{OC}}$ (According to the figure)

$\angle {\text{AOB}} = \angle {\text{BOC}}$ (According to the figure)

${\text{OB}} = {\text{OB}}\,\,$(Common)

So, $\Delta {\text{AOB}} \cong \Delta {\text{COB}}$ (By SAS congruency)

$ \Rightarrow {\text{AB}} = {\text{BC}}$ (By C.P.C.T)..........(iii)

According to the equations (i), (ii) and (iii),

${\text{AD}} = {\text{BC}} = {\text{CD}} = {\text{AB}}$

And the diagonals of quadrilateral ABCD bisect each other at right angle.

Hence, ${\text{ABCD}}$ is a rhombus.

2. Show that the diagonals of a square are equal and bisect each other at right angles.

Ans: According to the question and figure,

ABCD is a square. 

AC and BD are its diagonals bisect each other at point O.

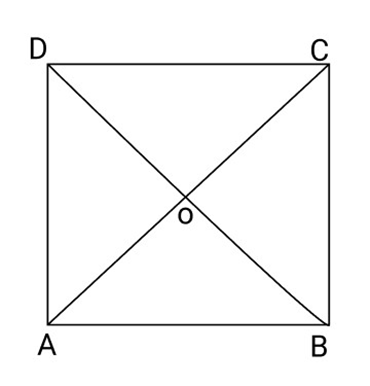
To prove: 

${\text{AC}} = {\text{BD}}$ and ${\text{AC}} \bot {\text{BD}}$ at point ${\text{O}}$.

Proof: 

In triangles ${\text{ABC}}$ and BAD,

${\text{AB}} = {\text{AB}}$ (Common)

$\angle {\text{ABC}} = \angle {\text{BAD}} = {90^\circ }$

${\text{BC}} = {\text{AD}}$ (Sides of a square)

So, $\Delta {\text{ABC}} \cong \Delta {\text{BAD}}$ (By SAS congruency)

$ \Rightarrow {\text{AC}} = {\text{BD}}$ (By C.P.C.T.)

Hence proved.

Now in triangles ${\text{AOB}}$ and AOD,

${\text{AO}} = {\text{AO}}$ (Common)

${\text{AB}} = {\text{AD}}$ (Sides of a square)

OB = OD (Diagonals of a square bisect each other)

So, $\Delta {\text{AOB}} \cong \Delta {\text{AOD}}$  (By SSS congruency)

$\angle {\text{AOB}} = \angle {\text{AOD}}$ (By C.P.C.T.)

But $\angle {\text{AOB}} + \angle {\text{AOD}} = {180^\circ }$ (Linear pair)

So, $\angle {\text{AOB}} = \angle {\text{AOD}} = {90^\circ }$

$ \Rightarrow OA \bot BD$ or $AC \bot BD$

Hence proved.

3. ABCD is a rhombus. Show that the diagonal AC bisects $\angle A$ as well as $\angle C$ and diagonal BD bisects $\angle {\text{B}}$ as well as $\angle {\text{D}}$.

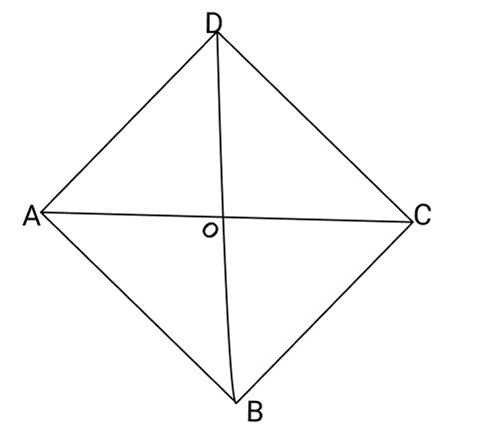
Ans: ABCD is a rhombus. 

Hence, $AB = BC = CD = AD$

Suppose ${\text{O}}$ be the point of bisection of diagonals.

So, ${\text{OA}} = {\text{OC}}$ and ${\text{OB}} = {\text{OD}}$

In $\Delta {\text{AOB}}$ and $\Delta {\text{AOD}}$,

${\text{OA}} = {\text{OA}}$ (Common)

${\text{AB}} = {\text{AD}}$ (Equal sides of rhombus)

${\text{OB}} = {\text{OD}}$ (Diagonals of rhombus bisect each other)

So, $\Delta {\text{AOB}} \cong \Delta {\text{AOD}}$ (By SSS congruency)

$ \Rightarrow \angle {\text{OAD}} = \angle {\text{OAB}}$ (By C.P.C.T.)

$ \Rightarrow $ OA bisects $\angle {\text{A}}$ ..........(i)

Similarly $\Delta {\text{BOC}} \cong \Delta {\text{DOC}}$ (By SSS congruency)

$ \Rightarrow \angle {\text{OCB}} = \angle {\text{OCD}}$ (By C.P.C.T.)

$ \Rightarrow {\text{OC}}$ bisects $\angle {\text{C}} \ldots  \ldots  \ldots $.

(ii)

According to the equations (i) and (ii), we can say that diagonal AC bisects $\angle {\text{A}}$ and $\angle {\text{C}}$.

Now in $\Delta {\text{AOB}}$ and $\Delta {\text{BOC}}$,

${\text{OB}} = {\text{OB}}$ (Common)

${\text{AB}} = {\text{BC}}$ (Equal sides of rhombus)

${\text{OA}} = $ OC (Diagonals of rhombus bisect each other)

So, $\Delta {\text{AOB}} \cong \Delta {\text{COB}}$ (By SSS congruency)

$ \Rightarrow \angle {\text{OBA}} = \angle {\text{OBC}}$ (By C.P.C.T.)

$ \Rightarrow {\text{OB}}$ bisects $\angle {\text{B}} \ldots  \ldots  \ldots $

(iii)

Similarly $\Delta {\text{AOD}} \cong \Delta {\text{COD}}$ (By SSS congruency)

$ \Rightarrow \angle {\text{ODA}} = \angle {\text{ODC}}$ (By C.P.C.T.)

$ \Rightarrow $ BD bisects $\angle D \ldots  \ldots  \ldots $..(iv)

According to the equations (iii) and (iv), we can say that diagonal BD bisects $\angle {\text{B}}$ and $\angle {\text{D}}$.

4. In parallelogram ABCD, two points ${\text{P}}$ and ${\text{Q}}$ are taken on diagonal BD such that DP = B(See figure). Show that:

(i) $\Delta {\text{APD}} \cong \Delta {\text{CQB}}$

(ii) ${\text{AP}} = {\text{CQ}}$

(iii) $\Delta {\text{AQB}} \cong \vartriangle {\text{CPD}}$

(iv) ${\text{AQ}} = {\text{CP}}$

(v) APCis a parallelogram.

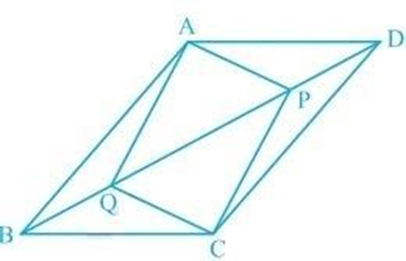
Ans: (i) In $\Delta $ APD and $\Delta $ CQB,

${\text{DP}} = {\text{BQ}}$ (According to the figure)

$\angle {\text{ADP}} = \angle {\text{QBC}}$ (Alternate angles  and ${\text{BD}}$ is transversal))

${\text{AD}} = {\text{CB}}$ (Opposite sides of parallelogram)

So, $\Delta {\text{APD}} \cong \Delta {\text{CQB}}$ (By SAS congruency)

(ii) Since $\Delta {\text{APD}} \cong \Delta {\text{CQB}}$

$ \Rightarrow {\text{AP}} = {\text{CQ}}$ (By C.P.C.T.)

(iii) In $\Delta {\text{AQB}}$ and $\Delta {\text{CPD}}$,

${\text{BQ}} = {\text{DP}}$ (According to the figure)

$\angle {\text{ABQ}} = \angle {\text{PDC}}$ (Alternate angles  and ${\text{BD}}$ is transversal))

${\text{AB}} = {\text{CD}}$ (Opposite sides of parallelogram)

$\Delta {\text{AQB}} \cong \Delta {\text{CPD}}$ (By SAS congruency )

(iv) Since $\Delta {\text{AQB}} \cong \Delta {\text{CPD}}$

$ \Rightarrow {\text{AQ}} = {\text{CP}}$ (By C.P.C.T.)

(v) In quadrilateral APCQ,

${\text{AP}} = $ C(Proved in part (i))

${\text{AQ}} = {\text{CP}}$ (Provedin part (iv))

Since opposite sides of quadrilateral APCare equal.

Therefore, APCis a parallelogram.

5. ABCD is a rhombus and P, Q, R, S are mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.

Ans: According to the question and figure,

P, Q, R and S are the mid-points of respective sides AB, BC, CD and DA of rhombus. PQ, QR, RS and SP are joined.

To prove: 

PQRS is a rectangle.

We draw a line AC with join point A to Point C.

Proof: 

In $\Delta {\text{ABC}},{\text{P}}$ is the mid-point of ${\text{AB}}$ and ${\text{Q}}$ is the mid-point of ${\text{BC}}$.

So,  and $PQ = \dfrac{1}{2}AC \ldots  \ldots  \ldots .$ (i)

In $\Delta {\text{ADC}},{\text{R}}$ is the mid-point of ${\text{CD}}$ and ${\text{S}}$ is the mid-point of ${\text{AD}}$.

So,  and ${\text{SR}} = \dfrac{1}{2}$ AC..........(ii)

According to the equations (i) and (ii),

$PQ\parallel SR$ and $PQ = SR$

So, PQRS is a parallelogram.

Now ABCD is a rhombus. (According to the question)

So, $AB = BC$

$ \Rightarrow \dfrac{1}{2}{\text{AB}} = \dfrac{1}{2}{\text{BC}} \Rightarrow {\text{PB}} = {\text{BQ}}$

So, $\angle 1 = \angle 2$ (Angles opposite to equal sides are equal)

Now in triangles APS and CQR, we have,

${\text{AP}} = {\text{CQ}}\,\,({\text{P}}$ and ${\text{Q}}$ are the mid-points of ${\text{AB}}$ and ${\text{BC}}$ and ${\text{AB}} = {\text{BC}}$ )

Similarly AS = CR and PS = QR (Opposite sides of a parallelogram)

$\Delta {\text{APS}} \cong \Delta {\text{CQR}}$(By SSS congreuancy)

$ \Rightarrow \angle 3 = \angle 4$ (By C.P.C.T.)

Now we have $\angle 1 + \angle {\text{SPQ}} + \angle 3 = {180^\circ }$

And $\angle 2 + \angle {\text{PQR}} + \angle 4 = {180^\circ }$ (Linear pairs)

So, $\angle 1 + \angle {\text{SPQ}} + \angle 3 = \angle 2 + \angle {\text{PQR}} + \angle 4$

Since $\angle 1 = \angle 2$ and $\angle 3 = \angle 4$ (Proved above)

So, $\angle {\text{SPQ}} = \angle {\text{PQR}} \ldots  \ldots  \ldots .$ (iii)

Now PQRS is a parallelogram (Proved above)

So, $\angle {\text{SPQ}} + \angle {\text{PQR}} = {180^\circ } \ldots  \ldots  \ldots $.(iv)    (Interior angles)

Using equations (iii) and (iv),

$\angle {\text{SPQ}} + \angle {\text{SPQ}} = {180^\circ } \Rightarrow 2\angle {\text{SPQ}} = {180^\circ }$

$ \Rightarrow \angle {\text{SPQ}} = {90^\circ }$

Hence, PQRS is a rectangle.

6. ${\text{ABCD}}$ is a rectangle and P, Q, R and S are the mid-points of the sides ${\text{AB}},{\text{BC}},{\text{CD}}$ and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Ans: According to the question,

 A rectangle ${\text{ABCD}}$ in which ${\text{P}},{\text{Q}},{\text{R}}$ and ${\text{S}}$ are the mid-points of the sides ${\text{AB}},{\text{BC}}$, CD and DA respectively. PQ, QR, RS and SP are joined.

To prove: 

PQRS is a rhombus.

We draw a line AC with join point A to Point C.

Proof: 

In $\Delta {\text{ABC}},{\text{P}}$ and ${\text{Q}}$ are the mid-points of sides ${\text{AB}},{\text{BC}}$ respectively.

So,  and ${\text{PQ}} = \dfrac{1}{2}{\text{AC}} \ldots  \ldots  \ldots .$ (i)

In $\Delta {\text{ADC}},{\text{R}}$ and ${\text{S}}$ are the mid-points of sides ${\text{CD}},{\text{AD}}$ respectively.

So,  and ${\text{SR}} = \dfrac{1}{2}{\text{AC}} \ldots  \ldots  \ldots $ (ii)

According to the equations (i) and (ii), 

${\text{PQ}}\parallel {\text{SR}}$and ${\text{PQ}} = {\text{SR}}$ ..........(iii)

So, PQRS is a parallelogram.

Now ${\text{ABCD}}$ is a rectangle. (According to the question)

So, $AD = BC$

$ \Rightarrow \dfrac{1}{2}{\text{AD}} = \dfrac{1}{2}{\text{BC}} \Rightarrow {\text{AS}} = {\text{BQ}} \ldots  \ldots  \ldots .$ (iv)

In triangles APS and BPQ,

${\text{AP}} = {\text{BP}}$ (P is the mid-point of ${\text{AB}}$ )

$\angle {\text{PAS}} = \angle {\text{PBQ}}\left( {\operatorname{Each} {{90}^\circ }} \right)$

And $AS = BQ$ (From equation (iv))

So, $\Delta {\text{APS}} \cong \Delta {\text{BPQ}}$(By SAS congruency)

$ \Rightarrow {\text{PS}} = {\text{PQ}}$ (By C.P.C.T.).........(v)

According to the equation (iii) and (v), 

We get that PQRS is a parallelogram.

$ \Rightarrow {\text{PS}} = {\text{PQ}}$

$ \Rightarrow $ Two adjacent sides are equal.

Therefore, PQRS is a rhombus.

7. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (See figure). Show that the line segments AF and EC trisect the diagonal BD.

Ans: According to the question, 

$E$ and $F$ are the mid-points of AB and CD respectively.

So, ${\text{AE}} = \dfrac{1}{2}{\text{AB}}$ and ${\text{CF}} = \dfrac{1}{2}{\text{CD}} \ldots  \ldots  \ldots .$ (i)

But ${\text{ABCD}}$ is a parallelogram.

So, ${\text{AB}} = {\text{CD}}$ and 

$ \Rightarrow \dfrac{1}{2}{\text{AB}} = \dfrac{1}{2}{\text{CD}}$ and 

$ \Rightarrow {\text{AE}} = {\text{FC}}$ and  (From equation (i))

AECF is a parallelogram.

 (FP is a part of ${\text{FA}}$ and ${\text{CQ}}$ is a part of ${\text{CE}}$ ) .........(ii)

Because a segment traced at the midpoint of one of a triangle's sides and parallel to the other side bisects the third.

In $\Delta {\text{DCQ}},{\text{F}}$ is the mid-point of ${\text{CD}}$ and 

So, $P$ is the mid-point of DQ.

$ \Rightarrow {\text{DP}} = {\text{PQ}} \ldots  \ldots  \ldots $..(iii)

Similarly, In $\Delta {\text{ABP}},{\text{E}}$ is the mid-point of ${\text{AB}}$ and  AP

So, $Q$ is the mid-point of BP.

$ \Rightarrow {\text{BQ}} = {\text{PQ}} \ldots  \ldots  \ldots $.(iv)

Acccording to the equations (iii) and (iv),

${\text{DP}} = {\text{PQ}} = {\text{BQ}} \ldots  \ldots  \ldots $.(v)

Now ${\text{BD}} = {\text{BQ}} + {\text{PQ}} + {\text{DP}} = {\text{BQ}} + {\text{BQ}} + {\text{BQ}} = 3{\text{BQ}}$

$ \Rightarrow {\text{BQ}} = \dfrac{1}{3}{\text{BD}} \ldots  \ldots  \ldots $ (vi)

According to the equations (v) and (vi),

${\text{DP}} = {\text{PQ}} = {\text{BQ}} = \dfrac{1}{3}{\text{BD}}$

$ \Rightarrow $ Points P and trisects BD.

So AF and CE trisects BD.

8. ${\text{ABC}}$ is a triangle right angled at ${\text{C}}$. A line through the mid-point M of hypotenuse ${\text{AB}}$ and parallel to BC intersects AC at D.

Ans: (i) In $\Delta {\text{ABC}},{\text{M}}$ is the mid-point of ${\text{AB}}$ (According to the question)

So, $AD = DC$ (Converse of mid-point theorem)

Hence ${\text{D}}$ is the mid-point of ${\text{AC}}$.

(ii)  (given) consider AC as a transversal.

So, $\angle 1 = \angle {\text{C}}$ (Corresponding angles)

$ \Rightarrow \angle 1 = {90^\circ }\left( {\angle {\text{C}} = {{90}^\circ }} \right)$

Hence, ${\text{MD}} \bot {\text{AC}}$.

(iii) In $\vartriangle AMD$ and $\vartriangle CMD$,

${\text{AD}} = {\text{DC}}$ (Proved above)

$\angle 1 = \angle 2 = {90^\circ }$ (Proved above)

${\text{MD}} = {\text{MD}}$ (Common)

So, $\Delta {\text{AMD}} \cong \Delta {\text{CMD}}$ (By SAS congruency)

$ \Rightarrow {\text{AM}} = {\text{CM}}$ (By C.P.C.T.)..........(i)

According to the question ${\text{M}}$ is the mid-point of ${\text{AB}}$.

So, ${\text{AM}} = \dfrac{1}{2}{\text{AB}} \ldots  \ldots  \ldots $.(ii)

According to the equations (i) and (ii),

${\text{CM}} = {\text{AM}} = \dfrac{1}{2}{\text{AB}}$

9. In a parallelogram ABCD, bisectors of adjacent angles ${\text{A}}$ and ${\text{B}}$ intersect each other at P. prove that $\angle APB = {90^\circ }$

Ans: According to the question,

${\text{ABCD}}$ is a parallelogram is and bisectors of $\angle A$ and $\angle B$ intersect each other at P.

To prove:

$\angle APB = {90^\circ }$

Proof:

$\angle 1 + \angle 2 = \dfrac{1}{2}\angle A + \dfrac{1}{2}\angle B$

$ = \dfrac{1}{2}(\angle A + \angle B)\quad  \to (i)$

But ${\text{ABCD}}$ is a parallelogram and 

So, $\angle A + \angle B = {180^\circ }$

So, $\angle 1 + \angle 2 = \dfrac{1}{2} \times {180^\circ } = {90^\circ }$

In $\vartriangle APB$

$\angle 1 + \angle 2 + \angle APB = {180^\circ }$

${90^\circ } + \angle APB = {180^\circ }$

$\angle APB = {90^\circ }$

Hence Proved.

10. In figure diagonal AC of parallelogram ABCD bisects $\angle A$ show that

(i) if bisects $\angle C$

ABCD is a rhombus

Ans: (i)$AB\parallel DC$ and ${\text{AC}}$ is transversal

So, $\angle 1 = \angle 2$ (Alternate angles)

And $\angle 3 = \angle 4$ (Alternate angles)

But, $\angle 1 = \angle 3$

So, $\angle 2 = \angle 4$

So, $AC$ bisecsts $\angle C$

(ii) In $\vartriangle ABC$ and $\vartriangle ADC$

${\text{AC}} = {\text{AC}}$ (Common)

$\angle 1 = \angle 3$ (Given)

$\angle 2 = \angle 4$ (Proved)

So, $\vartriangle ABC \cong \vartriangle ADC$

So, $AB = AD$ (By CPCT)

So, $ABCD$ is a rhombus.

11. In figure ABCD is a parallelogram. AX and CY bisects angles ${\text{A}}$ and ${\text{C}}$. Prove that AYCX is a parallelogram.

Ans: According to the question,

In a parallelogram AX and CY bisects $\angle A$ and $\angle C$ respectively and we have to

show that AYCX in a parallelogram.

In $\Delta ADX$ and $\Delta CBY$

$\angle D = \angle B \ldots $..(i) (Opposite angles of parallelogram)

$\angle DAX = \dfrac{1}{2}\angle A$ (Given) ...(ii)

And $\angle {\text{BCY}} = \dfrac{1}{2}\angle {\text{C}}$ (Given) .....(iii)

But $\angle {\text{A}} = \angle {\text{C}}$

By equations (2) and (3), we get

$\angle DAX = \angle BCY \to (iv)$

Also, $AD = BC$ (opposite sides of parallelogram) ....(v)

According to the equations (i), (iv) and (v), we get

$\Delta ADX \cong \Delta CBY\quad $(By ASA)

So, $DX = BY\quad $(By CPCT)

But,$AB\, = \,CD$(opposite sides of parallelogram)

${\text{AB}} - {\text{BY}} = {\text{CD}} - {\text{DX}}$

Or

${\text{AY}} = {\text{CX}}$

But  is 

So, $AYCX$ is a parallelogram.

12. Prove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.

Ans: According to the question,

$\Delta {\text{ABC}}$ in which ${\text{E}}$ and ${\text{F}}$ are mid points of side ${\text{AB}}$ and ${\text{AC}}$ respectively.

To prove: 

${\text{EF}}\parallel {\text{BC}}$

Construction: 

Produce EF to D such that ${\text{EF}} = $ FD. Join CD

Proof: In $\vartriangle AEF$ and $\Delta CDF$

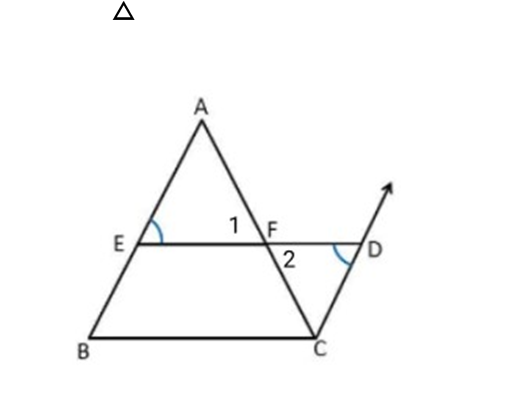
${\text{AF}} = {\text{FC}}\,\,\,\,(Because,\,F$ is mid-point of AC)

$\angle 1 = \angle 2$ (Vertically opposite angles) 

EF=FD (By construction)

So, $\Delta AEF \cong \Delta CDF$ (By SAS)

And So, $AE = CD$ (By CPCT)

${\text{AE}} = {\text{BE}}\,\,\,(Because,\,\,E$ is the mid-point)

And So, $BE = CD$

So, $BCDE$ is a parallelogram.

Hence proved.

13. Prove that a quadrilateral is a rhombus if its diagonals bisect each other at right angles.

Ans: Let $\mathrm{ABCD}$ be a quadrilateral, where diagonals bisect each other

$\therefore \mathrm{OA}=\mathrm{OC}$

-.- ( 1$)$

And $\mathrm{OB}=\mathrm{OD} \quad$-.-- $(2)$

And they bisect at right angles

$\therefore \angle \mathrm{AOB}=\angle \mathrm{BOC}=\angle \mathrm{COD}=\angle \mathrm{AOD}=90^{\circ}$

In $\triangle \mathrm{AOD}$ and $\triangle \mathrm{COD}$,

$\mathrm{OA}=\mathrm{OC} \quad($ From $(1))$

$\angle \mathrm{AOD}=\angle \mathrm{COD} \quad($ From $(3))$

$\mathrm{OD}=\mathrm{OD} \quad($ Common side $)$

$\therefore \triangle \mathrm{AOD} \cong \triangle \mathrm{COD} \quad($ SAS congruence rule $)$

$\Rightarrow \mathrm{AD}=\mathrm{CD} \quad \cdots-(4) \quad(\mathrm{CPCT})$

Similarly, we can prove that

$\mathrm{AD}=\mathrm{AB}$ and $\mathrm{AB}=\mathrm{BC} \quad \ldots$

From (4) and ( 5$)$

$\Rightarrow \mathrm{AD}=\mathrm{CD}=\mathrm{AB}=\mathrm{BC}$

In quadrilateral $\mathrm{ABCD}$,

$\mathrm{AB}=\mathrm{CD}$ and $\mathrm{AD}=\mathrm{BC}$

Both pairs of opposite sides are equal $\therefore \mathrm{ABCD}$ is a parallelogram.

Also, $\mathrm{AB}=\mathrm{CD}=\mathrm{AD}=\mathrm{BC}$

All sides of parallelogram $\mathrm{ABCD}$ are equal $\therefore \mathrm{ABCD}$ is a rhombus.

14. Prove that the straight line joining the mid points of the diagonals of a trapezium is parallel to the parallel sides.

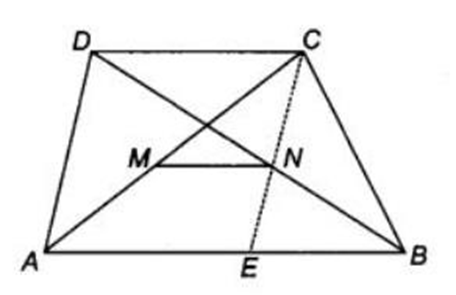
Ans: To prove $M N\|A B\| C D$

Construction Join $C N$ and produce it to meet $A B$ at $E$.

In $\triangle C D N$ and $\triangle E B N$, we have

$\begin{array}{lrr} & D N & =B N & {(\text { since, } N \text { is the mid-point of } B D)} \\ & \angle D C N & =\angle B E N & \text { (alternate interior angles) } \\ \text { and } & \angle C D N & =\angle E B N & \text { (alternate interior angles) } \\ \therefore & \Delta C D N & \cong \Delta E B N & \text { (by AAS congruence rule) } \\ \therefore & D C & =E B \text { and } C N=N E & \text { (by CPCT rule) }\end{array}$

Thus, in $\Delta C A E$, the points $M$ and $N$ are the mid-points of $A C$ and $C E$, respectively.

$\therefore$ $\Rightarrow$$M N \| A E$

$M N\|A B\| C D$(by mid-point theorem) Hence proved

15. In fig $\angle B$ is a right angle in $\vartriangle ABCD$ is the mid-point of  intersects ${\text{BC}}$  at ${\text{E}}$. show that

(i) ${\text{E}}$ is the mid-point of ${\text{BC}}$

(ii) ${\text{DE}} \bot {\text{BC}}$

(iii) ${\text{BD}} = {\text{AD}}$

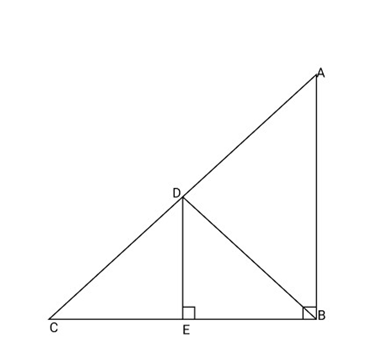
Ans:

Proof: 

So,  and ${\text{D}}$ is mid points of ${\text{AC}}$

In $\Delta DCE$ and $\Delta DBE$

${\text{CE}} = {\text{BE}}$

${\text{DE}} = {\text{DE}}$

And $\angle DEC = \angle DEB = {90^\circ }$

So, $\Delta DCE = \Delta DBE$

So, $\Delta DCE \cong \Delta DBE$

So, $CD = BD$

16. ABC is a triangle and through vertices A, B and C lines are drawn parallel to BC, AC and ${\text{AB}}$ respectively intersecting at D, E and ${\mathbf{F}}$. Prove that perimeter of $\Delta DEF$ is double the perimeter of $\vartriangle ABC$.

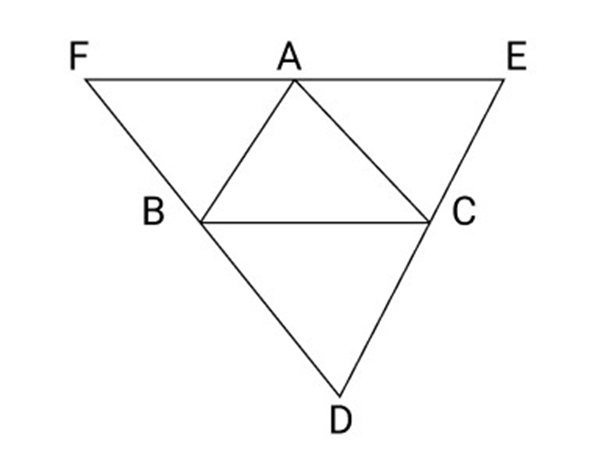
Ans: According to the figure,

$BCAF$ is a parallelogram

So, $BC = AF$

According to the figure,

$ABCE$ is a parallelogram

So, $BC = AE$

$AF + AE = 2BC$

Or $EF = 2BC$

Similarly, 

${\text{ED}} = 2{\text{AB}}$ and ${\text{FD}} = 2{\text{AC}}$

Because, Perimeter of $\Delta ABC = AB + BC + AC$

Perimeter of $\Delta DEF = DE + EF + DF$

$ = 2{\text{AB}} + 2{\text{BC}} + 2{\text{AC}}$

$ = 2({\text{AB}} + {\text{BC}} + {\text{AC}})$

$ = 2$ Perimeter of $\Delta ABC$

Hence Proved.

17. In fig ABCD is a quadrilateral P, Q, R and S are the mid Points of the sides ${\text{AB}},{\text{BC}},{\text{CD}}$ and ${\text{DA,}}\,{\text{AC}}$ is diagonal. Show that

(i) ${\text{SR}}||{\text{AC}}$

(ii) ${\text{PQ}} = {\text{SR}}$

(iii) PQRS is a parallelogram

(iv) PR and Sbisect each other

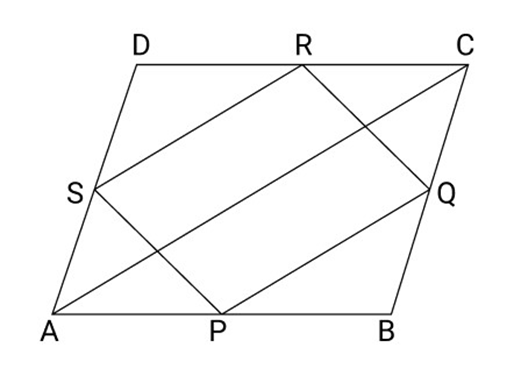
Ans: In $\Delta {\text{ABC}},{\text{P}}$ and ${\text{Q}}$ are the mid-points of the sides ${\text{AB}}$ and ${\text{BC}}$ respectively

(i) So, ${\text{PQ}}||{\text{AC}}$ and ${\text{PQ}} = \dfrac{1}{2}{\text{AC}}$

(ii) Similarly ${\text{SR}}||{\text{AC}}$ and ${\text{SR}} = \dfrac{1}{2}{\text{AC}}$

So, $PQ||SR$ and $PQ = SR$

(iii) Therefore, PQRS is a Parallelogram.

Because, $PQ\parallel SR$.

(iv) PR and Sbisect each other.

Because, $PQ\parallel SR$.

If we meet point P to R and point S to they bisect each other.

18. In $\Delta ABC,D,E,F$ are respectively the mid-Points of sides ${\text{AB}},{\text{DC}}$ and ${\text{CA}}$. show that $\vartriangle ABC$ is divided into four congruent triangles by Joining D,E,F.

Ans: According to the question,

D and $E$ are mid-Points of sides ${\text{AB}}$ and BC of $\Delta {\text{ABC}}$

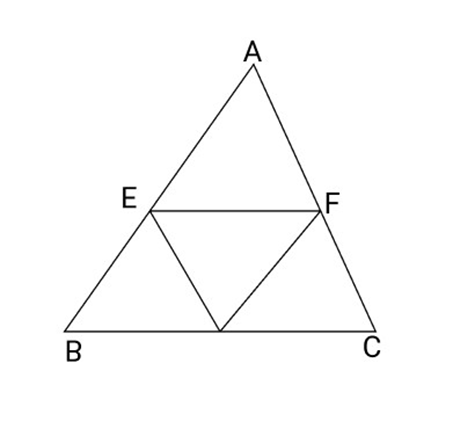
So, ${\text{DE}}||{\text{AC}}\,\,\,$ {Because a line segment joining the mid-Point of any two sides of a triangle parallel to third side $\} $

Similarly, ${\text{DF}}\parallel {\text{BC}}$ and ${\text{EF}}||{\text{AB}}$

ADEF, BDEF and DFCE are all Parallelograms.

DE is diagonal of Parallelogram BDFE

$\Delta BDE \cong \Delta FED$

Similarly, $\Delta {\text{DAF}} \cong \Delta {\text{FED}}$

And $\Delta {\text{EFC}} \cong \Delta {\text{FED}}$

So all triangles are congruent

19. ABCD is a Parallelogram is which P and are mid-points of opposite sides AB and CD. If Aintersect DP at S, Bintersects ${\text{CP}}$ at ${\text{R}}$, show that

(i) APCis a Parallelogram

(ii) DPBis a parallelogram

(iii) PSQR is a parallelogram

Ans: (i) In quadrilateral APCQ

${\text{AP}}||{\text{QC}}\,\,(Because,\,{\text{AB}}||{\text{CD}}) \ldots  \ldots  \ldots $ (i)

${\text{AP}} = \dfrac{1}{2}{\text{AB}},{\text{CQ}} = \dfrac{1}{2}{\text{CD}}$ (Given)

Also ${\text{AB}} = {\text{CD}}$

So ${\text{AP}} = {\text{QC}} \ldots  \ldots  \ldots $...(ii)

Therefore, APCis a parallelogram

(If any two sides of a quadrilateral equal and parallel then quad is a parallelogram)

(ii) Similarly, quadrilateral DPBis a Parallelogram because ${\text{DQ}}\parallel {\text{PB}}$ and ${\text{DQ}} = {\text{PB}}$

(iii) In quadrilateral PSQR,

${\text{SP}}\parallel {\text{QR}}$ (SP is a part of DP and QR is a Part of QB)

Similarly, ${\text{SQ}}\parallel {\text{PR}}$

So, PSQR is also parallelogram.

20. l, m, n are three parallel lines intersected by transversals P and such that l, m and $n$ cut off equal intercepts ${\text{AB}}$ and ${\text{BC}}$ on ${\text{P}}$ .In fig Show that l, m, n cut off equal intercepts DE and EF on also.

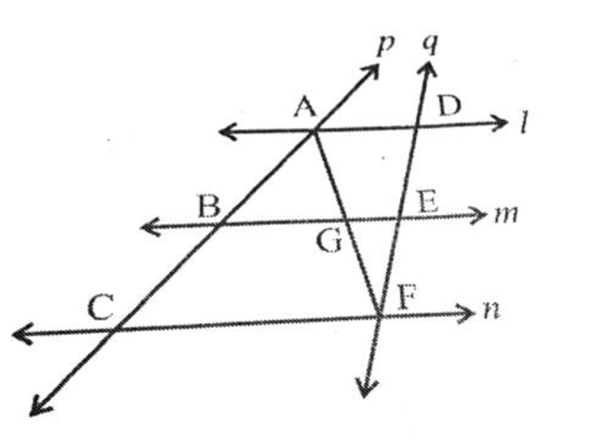
Ans: In fig l, m, n are 3 parallel lines intersected by two transversal ${\text{P}}$ and ${\text{Q}}$.

To Prove:

${\text{DE}} = {\text{EF}}$

Proof: 

In $\Delta ACF$

${\text{B}}$ is mid-point of ${\text{AC}}$

And ${\text{BG}}\parallel {\text{CF}}$

So, ${\text{G}}$ is mid-point of AF (By mid-point theorem)

Now In $\Delta AFD$

${\text{G}}$ is mid-point of ${\text{AF}}$ and ${\text{GE}}\parallel {\text{AD}}$.

So, ${\text{E}}$ is mid-point of FD (By mid-point theorem)

So, ${\text{DE}} = {\text{EF}}$

Hence Proved.

21. ABCD is a parallelogram in which $E$ is mid-point of AD. ${\text{DF}}\parallel {\text{EB}}$ meeting AB produced at ${\text{F}}$ and ${\text{BC}}$ at ${\text{L}}$ prove that ${\text{DF}} = 2{\text{DL}}$

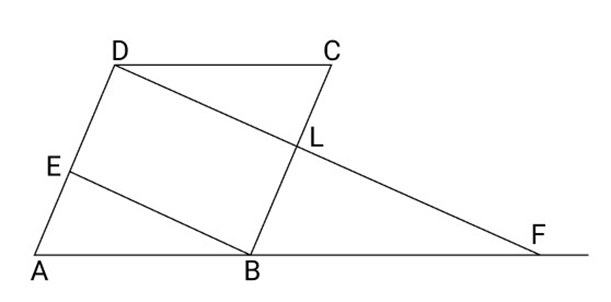
Ans: In $\vartriangle AFD$

Because, $E$ is mid-point of AD (According to the question)

${\text{BE}}||{\text{DF}}$ (According to the question)

So, by converse of mid-point theorem B is mid-point of AF

So, $AB = BF \ldots .(i)$

${\text{ABCD}}$ is parallelogram

So, $AB = CD \ldots  \ldots (ii)$

According to the equation (i) and (ii)

${\text{CD}} = {\text{BF}}$

Consider $\Delta DLC$ and $\Delta FLB$

${\text{DC}} = {\text{FB}}$ (Proved above)

$\angle DCL = \angle FBL$ (Alternate angles)

$\angle DLC = \angle FLB$ (Vertically opposite angles)

$\Delta DLC = \Delta FLB$  (By ASA)

So, ${\text{DL}} = {\text{LF}}$

So, ${\text{DF}} = 2{\text{DL}}$

Hence proved.

22. PQRS is a rhombus if $\angle P = {65^\circ }$ find $\angle RSQ$.

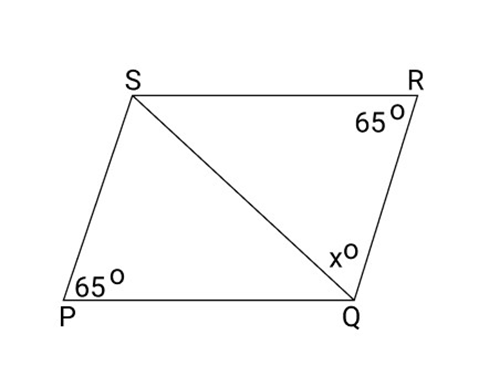
Ans: According to the question and figure,

$\angle R = \angle P = {65^\circ }$ (Opposite angles of a parallelogram are equal)

Suppose, $\angle RSQ = {x^\circ }$

In $\vartriangle RSQ$ 

We have ${\text{RS}} = {\text{RQ}}$

$\angle RQS = \angle RSQ = {x^\circ }$ (Opposite Sides of equal angles are equal)

In $\vartriangle RSQ$

$\angle S + \angle Q + \angle R = {180^\circ }$ (By angle sum property)

${x^\circ } + {x^\circ } + {65^\circ } = {180^\circ }$

$2{x^\circ } = {180^\circ } - {65^\circ }$

$2{x^\circ } = {115^\circ }$

$x = \dfrac{{115}}{2} = {57.5^\circ }$

Hence, the value of$\angle RSQ = {57.5^\circ }$.

23. ${\text{ABCD}}$ is a trapezium in which ${\text{AB}}||{\text{CD}}$ and ${\text{AD}} = {\text{BC}}$ show that

(i) $\angle A = \angle B$

(ii) $\angle C = \angle D$

(iii) $\vartriangle ABC \cong \Delta BAD$

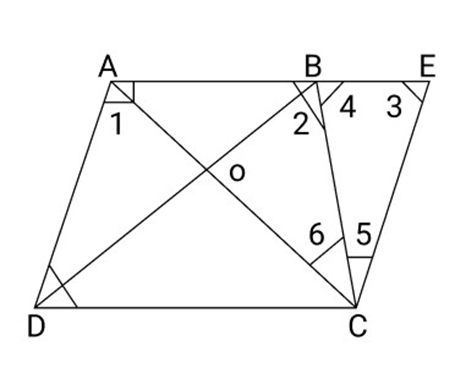
Ans: (i) Produce ${\text{AB}}$ and Draw a line Parallel to DA meeting at ${\text{E}}$

Because,$AD||EC$

$\angle 1 + \angle 3 = {180^\circ } \ldots .$ (1) (We know that the sum of interior angles on the some side of transversal is ${180^\circ }$ )

In $\Delta BEC$

BC=CE (given)

So, $\angle 3 = \angle 4$.....(2) (In a triangle equal side to opposite angles are equal)

$\angle 2 + \angle 4 = {180^\circ } \ldots  \ldots .(3)$

By equation (1) and (3)

$\angle 1 + \angle 3 = \angle 2 + \angle 4$

$\angle 3 = \angle 4$

So, $\angle 1 = \angle 2$

So, $\angle A = \angle B$

(ii) Because,

$\angle D + \angle 6 + \angle 5 = {180^\circ } \ldots  \ldots (i)$

$\angle 6 + \angle 5 + \angle 3 = {180^\circ } \ldots  \ldots .(ii)$

$\angle D + \angle 6 + \angle 5 = \angle 6 + \angle 5 + \angle 3$

$\angle D = \angle 3 = \angle 4$

So, $\angle C = \angle D$.

(iii) In $\Delta {\text{ABC}}$ and $\Delta {\text{BAD}}$

${\text{AB}} = {\text{AB}}$ (common)

$\angle 1 = \angle 2$ (Proved above)

${\text{AD}} = {\text{BC}}$ (According to the question)

So, $\Delta ABC \cong \Delta BAD$ (By SAS)

24. Show that diagonals of a rhombus are perpendicular to each other.

Ans:

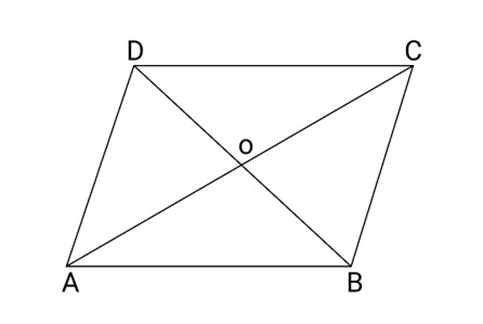
According to the figure,

A rhombus ABCD whose diagonals AC and BD intersect at a Point O.

To Prove: 

$\angle BOC = \angle DOC = \angle AOD = \angle AOB = {90^\circ }$

Proof: 

Clearly ABCD is a Parallelogram in which

${\text{AB}} = {\text{BC}} = {\text{CD}} = {\text{DA}}$

As we know that diagonals of a Parallelogram bisect each other

So, ${\text{OA}} = {\text{OC}}$ and ${\text{OB}} = {\text{OD}}$

Now in $\Delta {\text{BOC}}$ and $\Delta {\text{DOC}}$, we have

${\text{OB}} = {\text{OD}}$

${\text{BC}} = {\text{DC}}$

${\text{OC}} = {\text{OC}}$

So, $\Delta {\text{BOC}} \cong \Delta {\text{DOC}}$   (By SSS)

So,$\angle BOC = \angle DOC$ (By C.P.C.T)

But $\angle BOC + \angle DOC = {180^\circ }$

So, $\angle BOC = \angle DOC = {90^\circ }$

Similarly, $\angle AOB = \angle AOD = {90^\circ }$

Therefore, diagonals of a rhombus bisect each other at ${90^\circ }$.

25. Prove that the diagonals of a rhombus bisect each other at right angles.

Ans: According to the question and figure given a rhombus ABCD whose diagonals AC and BD intersect each other at $O$.

As we need to prove that ${\text{OA}} = {\text{OC}},{\text{OB}} = {\text{OD}}$ and $\angle AOB = {90^\circ }$

In $\vartriangle AOB$ and $\Delta COD$

${\text{AB}} = {\text{CD}}$ (Sides of rhombus)

$\angle AOB = \angle COD$ (Vertically opposite angles)

And $\angle ABO = \angle CDO$ (Alternate angles)

So, $\Delta {\text{AOB}} \cong \Delta {\text{COD}}$(By ASA)

So, ${\text{OA}} = {\text{OC}}$

And ${\text{OB}} = {\text{OD}}$ (By C.P.C.T)

Also in $\Delta {\text{AOB}}$ and $\Delta {\text{COB}}$

OA=OC (Proved)

${\text{AB}} = {\text{CB}}$ (Sides of rhombus)

And ${\text{OB}} = {\text{OB}}$ (Common)

$\Delta {\text{AOB}} \cong \Delta {\text{COB}}$ (By SSS)

So, $\angle AOB = \angle COB$ (By C.P.C.T)

But $\angle AOB + \angle COB = {180^\circ }$ (linear pair)

So, $\angle AOB = \angle COB = {90^\circ }$

Hence proved.

26. In fig ${\text{ABCD}}$ is a trapezium in which ${\text{AB}}||{\text{DC}}$ and ${\text{AD}} = {\text{BC}}.$ Show that $\angle A = \angle B$

Ans: To show that $\angle A = \angle B$,

Draw ${\text{CP}}\parallel {\text{DA}}$ meeting ${\text{AB}}$ at ${\text{P}}$

Because, ${\text{AP}}||{\text{DC}}$ and ${\text{CP}}||{\text{DA}}$

So, ${\text{APCD}}$ is a parallelogram

Again in  ∆ CPB

${\text{CP}} = {\text{CB}}\,\,(Because,\,{\text{BC}} = {\text{AD)}}$ (Given)

$\angle CPB = \angle CBP \ldots (i)$ (Angles opposite to equal sides)

But $\angle CPA + \angle CPB = {180^\circ }($ By linear pair)

Also $\angle A + \angle CPA = {180^\circ }\,\,(Because,\,{\text{APCD}}$ is a parallelogram)

So, $\angle A + \angle CPA = \angle CPA + \angle CPB$ Or $\angle A = \angle CPB$

$ = \angle {\text{CB}}$

Hence proved.

27. In fig ABCD and ABEF are Parallelograms, prove that CDFE is also a parallelogram.

Ans: According to the question,

 $ABCD$ is a parallelogram

So, ${\text{AB}} = {\text{DC also AB}}||{\text{DC}} \ldots  \ldots  \ldots  \ldots ..{\text{ (i) }}$

Also ABEF is a parallelogram

Because, ${\text{AB}} = {\text{FE}}$ and ${\text{AB}}||{\text{FE}} \ldots  \ldots  \ldots $..(ii)

By equations (i) and (ii)

${\text{AB}} = {\text{DC}} = {\text{FE}}$

So, ${\text{AB}} = {\text{FE}}$

And ${\text{AB}}||{\text{DC}}||{\text{FE}}$

So, ${\text{AB}}||{\text{FE}}$

So, CDEF is a parallelogram.

Hence Proved.

4 Marks Questions

1. ABCD is a rectangle in which diagonal AC bisects $\angle {\text{A}}$ as well as $\angle {\text{C}}$. Show that:

(i) ABCD is a square.

(ii) Diagonal BD bisects both $\angle {\text{B}}$ as well as $\angle {\text{D}}$.

Ans: According to the question,

${\text{ABCD}}$ is a rectangle. 

Hence ${\text{AB}} = {\text{DC}}$.........(i)

And ${\text{BC}} = {\text{AD}}$

Also $\angle {\text{A}} = \angle {\text{B}} = \angle {\text{C}} = \angle {\text{D}} = {90^\circ }$

(i) In $\Delta {\text{ABC}}$ and $\Delta {\text{ADC}}$

$\angle 1 = \angle 2$ and $\angle 3 = \angle 4$

(AC bisects $\angle {\text{A}}$ and $\angle {\text{C}}$ (According to the question))

${\text{AC}} = {\text{AC}}$ (Common)

So, $\Delta {\text{ABC}} \cong \Delta {\text{ADC}}$ (By ASA congruency)

$ \Rightarrow {\text{AB}} = {\text{AD}} \ldots  \ldots  \ldots ..$ (ii)

According to the equations (i) and (ii), 

${\text{AB}} = {\text{BC}} = {\text{CD}} = {\text{AD}}$

Therefore, ${\text{ABCD}}$ is a square.

(ii) In $\Delta {\text{ABC}}$ and $\Delta {\text{ADC}}$

${\text{AB}} = {\text{BA}}$ (Since ${\text{ABCD}}$ is a square)

${\text{AD}} = {\text{DC}}$ (Since ${\text{ABCD}}$ is a square)

${\text{BD}} = {\text{BD}}$ (Common)

So, $\Delta {\text{ABD}} \cong \Delta {\text{CBD}}$ (By SSS congruency)

$ \Rightarrow \angle {\text{ABD}} = \angle {\text{CBD}}$ (By C.P.C.T.) ..........(iii)

And $\angle {\text{ADB}} = \angle {\text{CDB}}$ (By C.P.C.T.) ...........(iv)

According to the equations (iii) and (iv), 

It is clear that diagonal BD bisects both $\angle {\text{B}}$ and $\angle {\text{D}}$.

2. An $\Delta {\text{ABC}}$ and  and . Vertices ${\text{A}},{\text{B}}$ and ${\text{C}}$ are joined to vertices D, E and F respectively (See figure). Show that:

(i) Quadrilateral ABED is a parallelogram.

(ii) Quadrilateral BEFC is a parallelogram.

(iii)  and ${\text{AD}} = {\text{CF}}$

(iv) Quadrilateral ACFD is a parallelogram.

(v) ${\text{AC}} = {\text{DF}}$

(vi) $\Delta {\text{ABC}} \cong \Delta {\text{DEF}}$

Ans: (i) In $\Delta {\text{ABC}}$ and $\Delta {\text{DEF}}$

${\text{AB}} = {\text{DE}}$ (According to the question)

And ${\text{AB}}\parallel {\text{DE}}$ (According to the question)

So, ABED is a parallelogram.

(ii) In $\Delta {\text{ABC}}$ and $\Delta {\text{DEF}}$

${\text{BC}} = $ EF (According to the question)

And ${\text{BC}}\parallel {\text{EF}}$(According to the question)

So, BEFC is a parallelogram.

(iii) As ABED is a parallelogram.

So,  and ${\text{AD}} = {\text{BE}}$..........(i)

Also BEFC is a parallelogram.

So,  and ${\text{CF}} = {\text{BE}} \ldots  \ldots  \ldots .$ (ii)

According to the equations (i) and (ii), we get

So,  and ${\text{AD}} = {\text{CF}}$

(iv) As  and ${\text{AD}} = {\text{CF}}$

$ \Rightarrow $ ACFD is a parallelogram.

(v) As ACFD is a parallelogram.

So, ${\text{AC}} = {\text{DF}}$

(vi) In $\Delta {\text{ABC}}$ and $\Delta {\text{DEF}}$,

${\text{AB}} = {\text{DE}}$ (According to the question)

${\text{BC}} = {\text{EF}}$ (According to the question)

${\text{AC}} = {\text{DF}}$ (Proved)

So, $\Delta {\text{ABC}} \cong \Delta {\text{DEF}}$ (By SSS congruency)

3. ABCD is a trapezium, in which  is a diagonal and ${\text{E}}$ is the mid-point of AD. A line is drawn through E, parallel to AB intersecting BC at F (See figure). Show that ${\text{F}}$ is the mid-point of BC.

Ans: Suppose diagonal BD intersect line EF at point P.

In $\Delta {\text{DAB}}$,

E is the mid-point of AD and  (According to the question) $P$ is the part of EF)

So, ${\text{P}}$ is the mid-point of other side, ${\text{BD}}$ of $\Delta {\text{DAB}}$.

(A line drawn parallel to one side of a triangle and through the mid-point of the other intersects the third side at the mid-point.)

Now in $\Delta {\text{BCD}}$,

P is the mid-point of BD and  (according to the question) and $AB\parallel DC$ (according to the question))

So,  and PF is a part of ${\text{EF}}$.

So, ${\text{F}}$ is the mid-point of other side, BC of $\Delta {\text{BCD}}$. (Converse of mid-point of theorem)

4. Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.

Ans: According to the question and figure,

A quadrilateral ABCD in which EG and FH are the line-segments joining the midpoints of opposite sides of a quadrilateral.

To prove: 

EG and FH bisect each other.

Construction: 

Join AC, EF, FG, GH and HE.

Proof: 

In $\Delta {\text{ABC}},{\text{E}}$ and ${\text{F}}$ are the mid-points of respective sides ${\text{AB}}$ and ${\text{BC}}$.

So,  and ${\text{EF}}\,{\text{ = }}\,\dfrac{1}{2}{\text{AC}} \ldots  \ldots  \ldots $.. (i)

Similarly, in $\Delta $ ADC,

G and ${\text{H}}$ are the mid-points of respective sides ${\text{CD}}$ and ${\text{AD}}$.

So,  and ${\text{HG}}\,{\text{ = }}\dfrac{1}{2}{\text{AC}} \ldots  \ldots  \ldots .$ (ii)

According to the equations (i) and (ii),

 and ${\text{EF}} = {\text{HG}}$

So, EFGH is a parallelogram.

Line segments (i.e. diagonals) EG and FH (of parallelogram EFGH) bisect each other because the diagonals of a parallelogram bisect each other.

5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Ans: Suppose${\text{ABCD}}$ be a quadrilateral in which equal diagonals AC and BD bisect each other at right angle at point $O$.

We have ${\text{AC}} = {\text{BD}}$ and ${\text{OA}} = {\text{OC}}$

And ${\text{OB}} = {\text{OD}} \ldots  \ldots  \ldots $..(ii)

Now ${\text{OA}} + {\text{OC}} = {\text{OB}} + {\text{OD}}$

$ \Rightarrow {\text{OC}} + {\text{OC}} = {\text{OB}} + {\text{OB}}$(Using equation (i) and (ii))

$ \Rightarrow 2{\text{OC}} = 2{\text{OB}}$

$ \Rightarrow {\text{OC}} = {\text{OB}} \ldots  \ldots  \ldots ..$ (iii)

According to the equations (i), (ii) and (iii), 

we get, 

$OA = OB = OC = OD$..........(iv)

Now in $\Delta {\text{AOB}}$ and $\Delta {\text{COD}}$,

${\text{OA}} = $ OD (Proved)

$\angle {\text{AOB}} = \angle {\text{COD}}$ (Vertically opposite angles)

${\text{OB}} = {\text{OC}}$ (Proved)

So, $\Delta {\text{AOB}} \cong \Delta {\text{DOC}}$ (By SAS congruency)

$ \Rightarrow {\text{AB}} = {\text{DC}}$ (By C.P.C.T.) ..........(v)

Similarly, 

$\Delta {\text{BOC}} \cong \Delta {\text{AOD}}$ (By SAS congruency)

$ \Rightarrow {\text{BC}} = {\text{AD}}$ (By C.P.C.T.) ..........(vi)

According to the equation (v) and (vi), it is determined that ${\text{ABCD}}$ is a parallelogram because opposite sides of a quadrilateral are equal.

Now in $\Delta {\text{ABC}}$ and $\Delta {\text{BAD}}$,

${\text{AB}} = {\text{BA}}$ (Common)

${\text{BC}} = {\text{AD}}$ (Proved above)

${\text{AC}} = {\text{BD}}$ (According to the figure)

So, $\Delta {\text{ABC}} \cong \Delta {\text{BAD}}$ (By SSS congruency)

$ \Rightarrow \angle {\text{ABC}} = \angle {\text{BAD}}$ (By C.P.C.T.) $ \ldots  \ldots  \ldots ..$ (vii)

But $\angle {\text{ABC}} + \angle {\text{BAD}} = {180^\circ }\,\,({\text{ABCD}}$ is a parallelogram) ..........(viii)

So,  and ${\text{AB}}$ is a transversal.

$ \Rightarrow \angle {\text{ABC}} + \angle {\text{ABC}} = {180^\circ }$ (Using equations (vii) and (viii))

$ \Rightarrow 2\angle {\text{ABC}} = {180^\circ } \Rightarrow \angle {\text{ABC}} = {90^\circ }$

So, $\angle {\text{ABC}} = \angle {\text{BAD}} = {90^\circ } \ldots  \ldots  \ldots $ (ix)

Opposite angles of a parallelogram are equal.

But $\angle {\text{ABC}} = \angle {\text{BAD}} = $

So, $\angle {\text{ABC}} = \angle {\text{ADC}} = {90^\circ } \ldots  \ldots  \ldots .({\text{x}})$

So, $\angle {\text{BAD}} = \angle {\text{BDC}} = {90^\circ } \ldots  \ldots  \ldots .({\text{xi}})$

According to the equations (x) and (xi), we get

$\angle {\text{ABC}} = \angle {\text{ADC}} = \angle {\text{BAD}} = \angle {\text{BDC}} = {90^\circ } \ldots  \ldots  \ldots ..({\text{xii}})$

Now in $\Delta {\text{AOB}}$ and $\Delta {\text{BOC}}$,

${\text{OA}} = {\text{OC}}$ (Given)

$\angle {\text{AOB}} = \angle {\text{BOC}} = {90^\circ }$ (Given)

${\text{OB}} = {\text{OB}}$ (Common)

So, $\Delta {\text{AOB}} \cong \Delta {\text{COB}}$ (By SAS congruency)

$ \Rightarrow {\text{AB}} = {\text{BC}} \ldots  \ldots  \ldots $.(xiii)

According to the equations (v), (vi) and (xiii), we get,

${\text{AB}} = {\text{BC}} = {\text{CD}} = {\text{AD}} \ldots  \ldots  \ldots ..({\text{xiv}})$

Now, according to the equations (xii) and (xiv), we have a quadrilateral whose equal diagonals bisect each other at right angle.

Also sides are equal make an angle of ${90^\circ }$ with each other.

So, ABCD is a square.

6. ${\text{ABCD}}$ is a trapezium in which  and ${\text{AD}} = {\text{BC}}$ (See figure). Show that:

(i) $\angle {\text{A}} = \angle {\text{B}}$

(ii) $\angle {\text{C}} = \angle {\text{D}}$

(iii) $\Delta {\text{ABC}} \cong \Delta {\text{BAD}}$

(iv) Diagonal AC = Diagonal BD

Ans: According to the question,

${\text{ABCD}}$ is a trapezium.

and ${\text{AD}} = {\text{BC}}$

To prove: 

(i) $\angle {\text{A}} = \angle {\text{B}}$

(ii) $\angle {\text{C}} = \angle {\text{D}}$

(iii) $\Delta {\text{ABC}} \cong \Delta {\text{BAD}}$

(iv) Diagonal AC = Diagonal BD

Construction: 

Draw CE  AD and extend AB to intersect CE at $E$.

Proof: 

(i) As AECD is a parallelogram. (By construction)

So, ${\text{AD}} = {\text{EC}}$

But ${\text{AD}} = {\text{BC}}$ (According to the question)

So, ${\text{BC}} = {\text{EC}}$

$ \Rightarrow \angle 3 = \angle 4$ (Angles opposite to equal sides are equal)

Now $\angle 1 + \angle 4 = {180^\circ }$ (Interior angles)

And $\angle 2 + \angle 3 = {180^\circ }$ (Linear pair)

$ \Rightarrow \angle 1 + \angle 4 = \angle 2 + \angle 3$

$ \Rightarrow \angle 1 = \angle 2\,\,(Because,\angle 3 = \angle 4)$

$ \Rightarrow \angle {\text{A}} = \angle {\text{B}}$

(ii) $\angle 3 = \angle {\text{C}}$ (Alternate interior angles)

And $\angle {\text{D}} = \angle 4$ (Opposite angles of a parallelogram)

But $\angle 3 = \angle 4$ ( $\Delta {\text{BCE}}$ is an isosceles triangle)

So, $\angle {\text{C}} = \angle {\text{D}}$

(iii) In $\Delta {\text{ABC}}$ and $\Delta {\text{BAD}}$,

${\text{AB}} = {\text{AB}}$ (Common)

$\angle 1 = \angle 2$ (Proved)

${\text{AD}} = {\text{BC}}$ (According to the question)

So, $\Delta {\text{ABC}} \cong \Delta {\text{BAD}}$ (By SAS congruency)

$(iv)\,\,{\text{AC}} = {\text{BD}}$ (By C.P.C.T.)

7. Prove that if the diagonals of a quadrilateral are equal and bisect each other at right angles then it is a square.

Ans: According to the question and figure,

In a quadrilateral ${\text{ABCD}},{\text{AC}} = {\text{BD}},{\text{AO}} = {\text{OC}}$ and ${\text{BO}} = {\text{OD}}$ and $\angle AOB = {90^\circ }$

To prove: 

${\text{ABCD}}$ is a square.

Proof: 

In $\vartriangle AOB$ and $\Delta COD$

${\text{OA}} = {\text{OC}}$

${\text{OB}} = {\text{OD}}$ (According to the question and figure)

And

$\angle AOB = \angle COD$ (Vertically opposite angles)

So, $\Delta AOB \cong \Delta COD$ (By SAS)

So, $AB = CD$ (By C.P.C.T.)

$\angle 1 = \angle 2$ (By C.P.C.T) But these are alternate angles So, 

ABCD is a parallelogram whose diagonals bisects each other at right angles.

So, $ABCD$ is a rhombus

Again in $\vartriangle ABD$ and $\Delta BCA$

${\text{AB}} = {\text{BC}}$ (Sides of a rhombus)

${\text{AD}} = {\text{AB}}$ (Sides of a rhombus)

And ${\text{BD}} = {\text{CA}}$ (Given)

So, $\vartriangle ABD \cong \Delta BCA$

So, $\angle BAD = \angle CBA$ (By CPCT)

These are alternate angles of these same side of transversal

So, $\angle BAD + \angle CBA = {180^\circ }$ or $\angle BAD = \angle CBA = {90^\circ }$

Therefore, ${\text{ABCD}}$ is a square.

8. Prove that in a triangle, the line segment joining the mid points of any two sides is parallel to the third side.

Ans: According to the question and figure,

A $\Delta ABC$ in which D and E are mid-points of the side ${\text{AB}}$ and ${\text{AC}}$ respectively

To Prove:  and $DE = \dfrac{1}{2}BC$

Construction: Draw 

Proof: In $\vartriangle ADE$ and $\Delta CFE$

$\angle 1 = \angle 2$ (Vertically opposite angles)

${\text{AE}} = {\text{CE}}$ (Given)

And $\angle 3 = \angle 4$ (Alternate interior angles)

So, $\Delta ADE \cong \Delta CFE$ (By ASA)

So, ${\text{DE}} = {\text{FE}}$ (By C.P.C.T)

But DA = DB

So, ${\text{DB}} = {\text{FC}}$

So, DBCF is a parallelogram

Also ${\text{DE}} = {\text{EF}} = \dfrac{1}{2}{\text{BC}}$

Hence,  and $DE = \dfrac{1}{2}BC$.

9. ${\text{ABCD}}$ is a rhombus and P, Q, R, and ${\text{S}}$ are the mid-Points of the sides ${\text{AB}},{\text{BC}},{\text{CD}}$ and DA respectively. Show that quadrilateral PQRS is a rectangle.

Ans: Join AC and BD which intersect at O let BD intersect RS at E and AC intersect Rat F

In $\Delta {\text{ABD,}}\,\,\,{\text{P}}$ and ${\text{S}}$ are mid-points of sides ${\text{AB}}$ and ${\text{AD}}$.

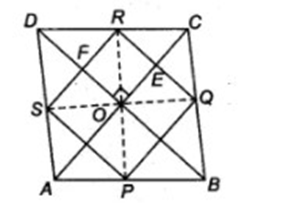
So, ${\text{PS}}||{\text{BD}}$ and ${\text{PS}} = \dfrac{1}{2}BD$

Similarly, ${\text{RQ}}||{\text{DB}}$ and ${\text{RQ}} = \dfrac{1}{2}{\text{BD}}$

So, ${\text{RS}}||{\text{BD}}||{\text{RQ}}$ and ${\text{PS}} = \dfrac{1}{2}BD = RQ$

${\text{PS}} = {\text{RQ}}$ and ${\text{PS}}||{\text{RQ}}$

So, PQRS is a parallelogram

Now, ${\text{RF}}\parallel {\text{EO}}$and ${\text{RE}}\parallel {\text{FO}}$

So, OFRE is also a parallelogram.

Again, we also know that diagonals of a rhombus bisect each other at right angles.

Because, $\angle EOF = {90^\circ }$

Because, $\angle EOF = \angle ERF$ (Opposite angles of a parallelogram)

So, $\angle ERF = {90^\circ }$

So, each angle of the parallelogram PQRS is ${90^\circ }$

Therefore, PQRS is a rectangle.

10. In the given Fig. ABCD is a parallelogram ${\mathbf{E}}$ is mid-point of AB and CE bisects $\angle BCD$ Prove that:

(i) ${\text{AE}} = {\text{AD}}$

(ii) ${\text{DE}}$ bisects $\angle ADC$

(iii) $\angle DEC = {90^\circ }$

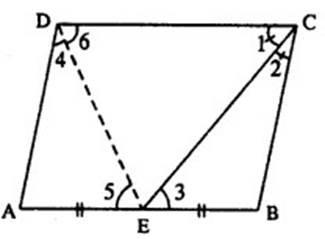
Ans: According to the question,

${\text{ABCD}}$ is a parallelogram

So,  and EC cuts them

$ \Rightarrow \angle BEC = \angle ECD$ (Alternate interior angle)

$ \Rightarrow \angle BEC = \angle ECB\quad (\angle ECD = \angle ECB)$

$ \Rightarrow EB = BC$

$ \Rightarrow AE = AD$

(i) Now ${\text{AE}} = {\text{AD}}$

$ \Rightarrow \angle ADE = \angle AED$

$ \Rightarrow \angle ADE = \angle EAC\,\,(So,\angle AED = \angle EDC$ Alternate interior angles)

(ii) So, DE bisects $\angle ADC$

(iii) Now $\angle ADC + \angle BCD = {180^\circ }$

$ \Rightarrow \dfrac{1}{2}\angle ADC + \dfrac{1}{2}\angle BCD = {90^\circ }$

$ \Rightarrow \angle EDC + \angle DCE = {90^\circ }$

But, the sum of all the angles of the triangle is ${180^\circ }$

$ \Rightarrow {90^\circ } + \angle DEC = {180^\circ }$

$ \Rightarrow \angle DEC = {90^\circ }$

Hence proved.

11. ABC is a triangle right angled at ${\mathbf{C}}$. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. show that

(i) ${\text{D}}$ is mid-point of ${\text{AC}}$

(ii) ${\text{MD}} \bot {\text{AC}}$

(iii) ${\text{CM}} = {\text{MA}} = \dfrac{1}{2}{\text{AB}}$

Ans: According to the question,

${\text{ABC}}$ is a triangle right angle at ${\text{C}}$

(i) ${\text{M}}$ is mid-point of ${\text{AB}}$

And ${\text{MD}}\parallel {\text{BC}}$

So, ${\text{D}}$ is mid-Point of ${\text{AC}}$ (a line through midpoint of one side of a triangle parallel to another side bisect the third side)

(ii) Because, ${\text{MD}}||{\text{BC}}$

$\angle ADM = \angle DCB$ (Corresponding angles)

$\angle ADM = {90^\circ }$

(iii) In $\Delta ADM$ and $\Delta CDM$

${\text{AD}} = {\text{DC}}\,\,$ (Because D is mid-point of ${\text{AC}})$

${\text{DM}} = {\text{DM}}$ (Common)

So, $\Delta {\text{ADM}} \cong \Delta {\text{CDM}}$ (By SAS)

${\text{AM}} = {\text{CM}}$ (By C.P.C.T)

${\text{AM}} = {\text{CM}} = {\text{MB}}$ (Because M is mid-point of ${\text{AB}})$

So, ${\text{CM}} = {\text{MA}} = \dfrac{1}{2}{\text{AB}}$

Hence proved.

Download Important Questions Of Chapter 8 Maths Class 9 PDF

Let’s Learn About Quadrilateral and Its Type

Definition of Quadrilateral 

Quadrilateral derived from two words, i.e quad means four and lateral means sides. Any closed figures which are having four sides are called quadrilaterals. The sides of the quadrilateral may be equal, unequal, parallel, or irregular shapes.

Types of Quadrilaterals

Based on angles and side lengths, there are various types of quadrilaterals:

• Parallelogram

• Rectangle

• Square

• Rhombus

• Trapezium

• Kite

Parallelogram - A parallelogram is a quadrilateral which has opposite sides parallel. In a parallelogram, all the opposite sides are equal and the angles made by each opposite side are also equal. In the figure shown below, PQRS is a quadrilateral and since PQ || RS and PS || QR we call it a parallelogram.

Rectangle - Rectangle is also a type of parallelogram with a little difference in the angles of the sides. All the sides of the rectangle are at the right angle or to say perpendicular to each other. The figure below shows a quadrilateral ABCD. Since all its sides are parallel to each other, we may also call it a type of parallelogram with line segments placed at the right angle to each other. Mathematically represented as AB || CD and AC || BD. ∠A =∠B =∠C=∠D= 90°.

Square - A square is a quadrilateral with all four sides equal. All the vertex of a square makes a right angle with its sides.  Suppose WXYZ is a square which shows the following characteristic:

WX || YZ and WY || XZ. ∠W =∠X =∠Y=∠Z= 90°

Rhombus - A rhombus is also a parallelogram which has all sides equal. In other words, a parallelogram that shows resemblance to a square with respect to its length of sides is called a rhombus. These are sometimes referred to as Diamonds also. Rhombus shows a very important feature regarding their diagonals. The diagonals of a rhombus meet exactly in the middle at a right angle and are also bisect with each other.

In the figure above, we can see that STUV is a quadrilateral with sides ST || UV and SV || TU. All the sides of a rhombus are equal, thus ST=TU=UV=VS which also happen to form equal angles.

Trapezium - Among all the other types of quadrilaterals, a trapezium shows different characteristics. In a trapezium, all the sides may not be equal but one of the pairs of sides has to be parallel to each other.

In the above figure, ABCD is a trapezium with sides AB || DC. A trapezium is also known as an irregular quadrilateral because it does not show similarity in lengths and angles of sides.

Kite - A kite is a quadrilateral which has two pairs of equal-length sides and these sides are adjacent to each other. The pair of adjacent sides of a kite are of equal length.

Important Formulas and Properties for Class 9 Maths Chapter 8 Quadrilaterals

Benefits of Class 9 Maths Chapter 8 Quadrilaterals Important Questions

• Comprehensive Revision: These important questions cover all the key topics in Chapter 8, ensuring that students thoroughly revise essential concepts like the angle sum property, properties of parallelograms, and various quadrilateral types.

• Exam-Focused Preparation: The questions are designed to reflect the CBSE exam pattern, helping students understand the kind of problems they might encounter during exams.

• Concept Clarity: Solving these questions enhances understanding of theorems and their applications, strengthening conceptual clarity for better problem-solving.

• Improved Time Management: Practising these important questions aids students in improving their speed and accuracy, essential for managing time effectively during exams.

• Free Access to Quality Material: The PDF of these important questions is available for free, making it easy for students to access reliable study material anytime and anywhere.

Conclusion

After going through the above Class 9 Maths Chapter 8 important questions, now it will be easier for you to differentiate between them and learn all the important concepts. So, every quadrilateral is a four-sided figure but still, there is a lot of difference between them, depending on the length of sides and the equality of angle. The difference between them is mentioned in their properties, so go through the above properties carefully which will help you to differentiate between every type of quadrilateral. Also, practise Class 9 Maths Chapter 8 extra questions so that you can through the concept and get good marks in the exam.

Related Study Materials for Class 9 Maths Chapter 8 Quadrilaterals

CBSE Class 9 Maths Chapter-wise Important Questions

Related Important Links for Maths Class 9

Along with this, students can also download additional study materials provided by Vedantu for Maths Class 9–