Important Questions for CBSE Class 9 Maths Chapter 5 - Introduction to Euclids Geometry

Extra Question For Practice: Do It Yourself

Short Answer Questions (3 Marks)

1. Which of the following statements are true and which are false? Give reasons for your answers.

(i) Only one line can pass through a single point.

Ans: False

Correct statement: Infinite many lines can pass through a single point.

This is self-evident and can be seen visually by the student given below:

(Image will be uploaded soon)

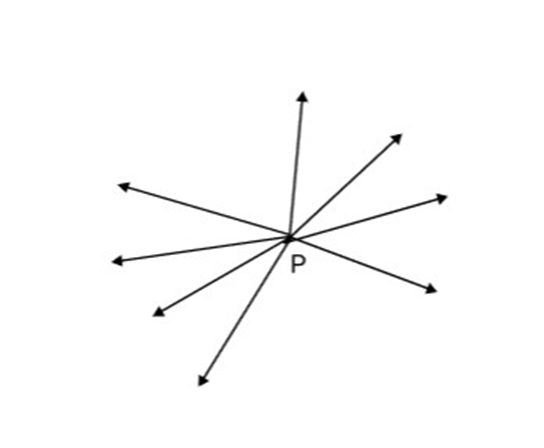
(ii) There are infinite number of lines which pass through two distinct points.

Ans:False 

The given statement contradicts the postulate ${\text{I}}$ of the Euclid that assures that there is a unique line that passes through two distinct points.

(Image will be uploaded soon)

Through two points ${\text{P}}$ and ${\text{Q}}$ a unique line can be drawn.

(iii) A terminated line can be produced indefinitely on both the sides.

Ans: True

(Image will be uploaded soon)

We need to consider Euclid's Postulate 2: "A terminated line can be produced indefinitely.

(iv) If two circles are equal, then their radii are equal.

Ans: True

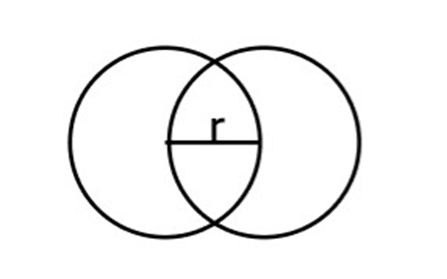
Let us consider two circles with same radii.

We can conclude that, when we make the two circles overlap with each other, we will get a superimposed figure of the two circles.

Therefore, we can conclude that the radii of both the circles will also coincide and still be same.

(Image will be uploaded soon)

(v) In Fig.  if $A{\mathbf{B}} = PQ$ and $PQ = XY$, then $A{\mathbf{B}} = XY$

(Image will be uploaded soon)

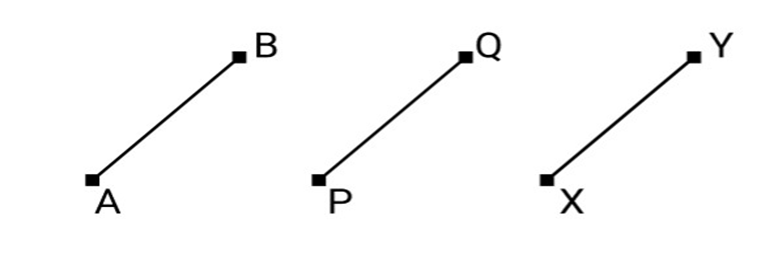
Ans: True

We are given that $AB = PQ$ and $PQ = XY$.

We need to consider the axiom: "Given two distinct points, there is a unique line that passes through them."

Therefore, we can conclude that ${\text{AB}},{\text{PQ}}$ and ${\text{XY}}$ are the lines with same dimensions, and hence if ${\text{AB}} = {\text{PQ}}$ and ${\text{PQ}} = {\text{XY}}$, then ${\text{AB}} = {\text{XY}}$.

2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?

(i) Parallel lines

Ans: Two lines are said to be parallel, when the perpendicular distance between these lines is always constant or we can say that the lines that never intersect each other are called as parallel lines.

(Image will be uploaded soon)

We need to define line first, in order to define parallel lines.

(ii) Perpendicular lines

Ans: Two lines are said to be perpendicular lines, when angle between these two lines is ${90^\circ }$.

(Image will be uploaded soon)

We need to define line and angle, in order to define perpendicular lines.

(iii) Line segment

Ans: A line of a fixed dimension between two given points is called as a line segment.

(Image will be uploaded soon)

We need to define line and point, in order to define a line segment.

(iv) Radius of a circle

Ans: The distance of any point lying on the boundary of a circle from the center of the circle is called as radius of a circle.

(Image will be uploaded soon)

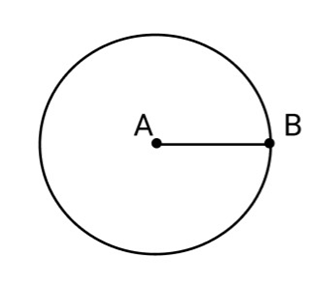
We need to define circle and center of a circle, in order to define radius of a circle.

(v) Square

Ans: A quadrilateral with all four sides equal and all four angles of ${90^\circ}$ is called as a square.

(Image will be uploaded soon)

We need to define quadrilateral and angle, in order to define a square.

3. If a point $C$ lies between two points $A$ and $B$ such that $AC = BC$, then prove that $AC = \dfrac{1}{2}AB \cdot $ Explain by drawing the figure.

Ans: We are given that a point $C$ lies between two points $B$ and $C$, such that $AC = BC$.

We need to prove that $AC = \dfrac{1}{2}AB \cdot $

Let us consider the given below figure.

(Image will be uploaded soon)

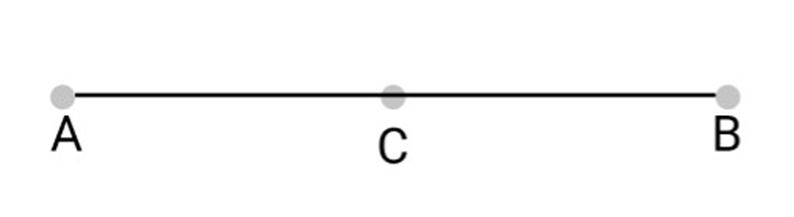
We are given that $AC = B{C_ - } \ldots (i)$

An axiom of the Euclid says that "If equals are added to equals, the wholes are equal."

Let us add $A C$ to both sides of equation $(i)$.

$AC + AC = BC + AC.$

An axiom of the Euclid says that "Things which coincide with one another are equal to one another." "

We can conclude that $BC + AC$ coincide with AB, or

$AB = BC + AC. \ldots (ii)$

An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another."

From equations (i) and (ii), we can conclude that

$AC + AC = AB$, or $2AC = AB$

An axiom of the Euclid says that "Things which are halves of the same things are equal to one another."

Therefore, we can conclude that $AC = \dfrac{1}{2}AB$

4. In the following figure, if ${\text{AC}} = {\text{BD}}$, then prove that ${\text{AB}} = {\text{CD}}$.

(Image will be uploaded soon)

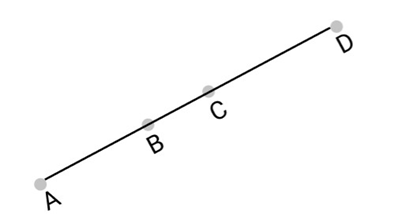
Ans: We are given that $AC = BD$

We need to prove that $AB = CD$ in the figure given below.

(Image will be uploaded soon)

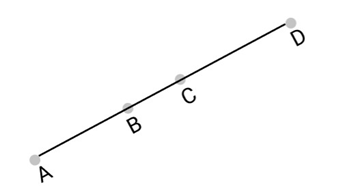
From the figure, we can conclude that

$AC = AB + BC$, and

$BD = CD + BC.$

An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another."

$AB + BC = CD + BC$

An axiom of the Euclid says that "when equals are subtracted from equals, the remainders are also equal."

We need to subtract BC from equation(i) to get \[A{\text{ }}B + B{\text{ }}C - B{\text{ }}C = C{\text{ }}D + B{\text{ }}C - B{\text{ }}C\]

$AB = CD$

Therefore, we can conclude that the desired result is proved.

5. Why is axiom 5, in the list of Euclid's axioms, considered as a 'universal truth'? (Note that the question if not about fifth postulate) 

Ans: We need to prove that Euclid's fifth axiom is considered as a universal truth.

Euclid's fifth axiom states that "the whole is greater than the part."

The above given axiom is a universal truth. We can apply the fifth axiom not only mathematically but also universally in daily life.

Mathematical proof:

Let us consider a quantity $z$, which has different parts as $a,b,x$ and $y$ 

So, $z = a + b + x + y$.

Therefore, we can conclude that $z$ will always be greater than its corresponding parts $a,b,x$ and $y$.

Universal proof:

We know that Mumbai is located in Maharashtra and Maharashtra is located in India.

In other words, we can conclude that Mumbai is a part of Maharashtra and Maharashtra is a part of India.

Therefore, we can conclude that whole India will be greater than Mumbai or Maharashtra or both.

Therefore, we can conclude that Euclid's fifth axiom is considered as a 'Universal truth'.

6. How would you rewrite Euclid's fifth postulate so that it would be easier to understand?

Ans: We need to rewrite Euclid's fifth postulate so that it is easier to understand.

We know that Euclid's fifth postulate states that "No intersection of lines will take place when the sum of the measures of the interior angles on the same side of the falling line is exactly ${180^\circ }.$

We know that Playfair's axiom states that "For every line $l$ and for every point $P$ not lying on

1, there exists a unique line m passing through $P$ and parallel to $\Gamma $.

The above mentioned Playfair's axiom is easier to understand in comparison to the Euclid's fifth postulate.

Let us consider a line $l$ that passes through a point $p$ and another line $m$. Let these lines be at a same plane.

Let us consider the perpendicular $C$$D$ on $l$ and $F$$E$ on $m$.

(Image will be uploaded soon)

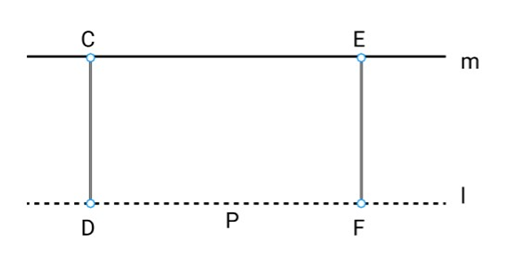
From the above figure, we can conclude that $CD = EF$.

Therefore, we can conclude that the perpendicular distance between lines $m$ and $l$ will b. constant throughout, and the lines $m$ and $l$ will never meet each other or in other words, $w$ can say that the lines $m$ and $I$ are equidistant from each other.

7. Does Euclid's fifth postulate imply the existence of parallel lines? Explain.

Ans: We need to verify whether Euclid's fifth postulate imply the existence of parallel lines

or not.

The answer to the above statement is Yes.

Let us consider two lines $m$ and ${l }$

In the figure given below, we can conclude that the lines $m$ and $l$ will intersect further.

(Image will be uploaded soon)

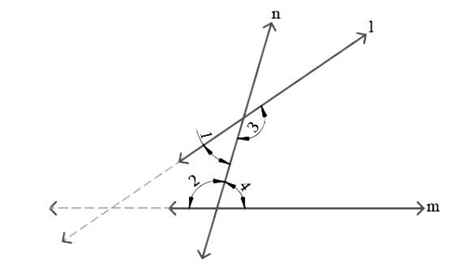
From the figure, we can conclude that

$\angle 1 + \angle 2 < {180^\circ }$ and $\angle 3 + \angle 4 > {180^\circ }$

We know that Euclid's fifth postulate states that "No intersection of lines will take place when the sum of the measures of the interior angles on the same side of the falling line is exactly ${180^\circ }.$

Let us consider lines $l$ and $m$.

(Image will be uploaded soon)

From the above figure, we can conclude that lines $I$ and $m$ will never intersect from either side. Therefore, we can conclude that the lines $l$ and $m$ are parallel.

8. Consider the two 'postulates' given below:

(i) Given any two distinct points $A$ and $B$, there exists a third point $C$, which is between ${\text{A}}$ and ${\text{B}}$.

(ii) There exists at least three points that are not on the same line. Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates? Explain.

Ans: Given any two distinct points $A$ and $B$, there exists a third point $C$, which is between $A$ and $B$.

There exists at least three points that are not on the same line. The undefined terms in the given postulates are point and line. The two given postulates are consistent, as they do not refer to similar situations and they refer to two different situations. We can also conclude that, it is impossible to derive at any conclusion or any statement that contradicts any well-known axiom and postulate.

The two given postulates do not follow from the postulates given by Euclid. The two given postulates can be observed following from the axiom, "Given two distinct points, there is a unique line that passes through them".

4 Marks Questions

1. In the above question, point $C$ is called a mid-point of line segment $A$$B$, prove that every line segment has one and only one mid-point.

Ans: We need to prove that every line segment has one and only one mid-point.

Let us consider the given below line segment $A$$B$ and assume that $C$ and $D$ are the mid-points of the line segment $A$$B$.

(Image will be uploaded soon)

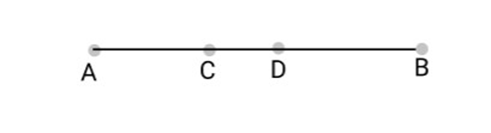
If $C$ is the mid-point of line segment $A$$B$, then

$AC = CB$

An axiom of the Euclid says that "If equals are added to equals, the wholes are equal."

$AC + AC = CB + AC.(i)$

From the figure, we can conclude that $CB + AC$ will coincide with $A$$B$.

An axiom of the Euclid says that "Things which coincide with one another are equal to one another." "

$AC + AC = A{B_.}(ii)$

An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another." "

Let us compare equations (i) and (ii), to get

$AC + AC = AB$, or $2AC = AB.(iii)$

If $D$ is the mid-point of line segment $A$$B$, then

$AD = DB$

An axiom of the Euclid says that "If equals are added to equals, the wholes are equal."

$AD + AD = DB + AD.$ (iv)

From the figure, we can conclude that $DB + AD$ will coincide with $A$$B$.

An axiom of the Euclid says that "Things which coincide with one another are equal to one another."

$AD + AD = A{B_.}(v)$

An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another:"

Let us compare equations (iv) and (v), to get

$AD + AD = AB$, or

$2AD = AB.({\text{vi}})$

An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another."

Let us compare equations (iii) and (vi), to get

$2AC = 2AD$

An axiom of the Euclid says that "Things which are halves of the same things are equal to one another."

$AC = AD$

Therefore, we can conclude that the assumption that we made previously is false and a line segment has one and only one mid-point.

• If a point C lies between two points A and B such that AB = BC, then prove that AC = ½ AB

• Find the number of dimensions a solid, surface, and point have.

• Let x  + y = 10, and x = z. Show that y + z = 10

• There are two sales employees who received equal incentives during the month of July. In August, each sales employee received double incentives in comparison to the month of July. Compare the employees' incentives for the month of August.

• Prove that an equilateral triangle can be formed on any of the given line segments.

Important Related Links for CBSE Class 9