CBSE Class 9 Maths Important Questions - Chapter 1 Number Systems

1 Marks Questions

1. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is irrational number.

Ans: We know that the square root of every positive integer will not yield an integer.

We know that \[\sqrt{4}\] is $2$, which is an integer. But, $\sqrt{7}$ or $\sqrt{10}$ will give an irrational number.

Therefore, we conclude that the square root of every positive integer is not an irrational number.

2. Write three numbers whose decimal expansions are non-terminating non-recurring.

Ans: The three numbers that have their expansions as non-terminating on recurring decimals are given below.

0.04004000400004.... 

0.07007000700007....

0.13001300013000013.... 

3. Find three different irrational numbers between the rational numbers $\frac{\text{5}}{\text{11}}$ and $\frac{\text{9}}{\text{11}}$.

Ans: Let us convert $\frac{5}{11}$ and $\frac{9}{11}$ into decimal form, to get

$\frac{5}{7}=0.714285....and\frac{9}{11}=0.818181....$

Three irrational numbers that lie between $0.714285....$ and $0.818181....$ are:

0.73073007300073...

0.74074007400074.... 

0.76076007600076.... 

4. Which of the following rational numbers have terminating decimal representation?

 $(i)\frac{3}{5}$             

$(ii)\frac{2}{13} $

$(iii)\frac{40}{27}   $    

$(iv)\frac{23}{7}$

Ans: $(i)\frac{3}{5}$

5. How many rational numbers can be found between two distinct rational numbers?

(i) Two

(ii) Ten

(iii) Zero

(iv) Infinite

Ans: (iv) Infinite

6. The value of $\left( \text{2+}\sqrt{\text{3}} \right)\left( \text{2-}\sqrt{\text{3}} \right)$ in

(i) $\text{1}$

(ii) $\text{-1}$

(iii) $\text{2}$

(iv) none of these

Ans: (i) $1$

7. ${{\left( \text{27} \right)}^{\text{-2/3}}}$ is equal to

(i) $\text{9}$

(ii) $\text{1/9}$

(iii) $\text{3}$

(iv) none of these

Ans: (ii) $1/9$

8. Every natural number is

(i) not an integer

(ii) always a whole number

(iii) an irrational number

(iv) not a fraction

Ans: (ii) always a whole number

9. Select the correct statement from the following

(i) $\frac{\text{7}}{\text{9}}\text{}\frac{\text{4}}{\text{5}}$

(ii) $\frac{\text{2}}{\text{6}}\text{}\frac{\text{3}}{\text{9}}$

(iii) $\frac{\text{-2}}{\text{3}}\text{}\frac{\text{-4}}{\text{5}}$

(iv)$\frac{\text{-5}}{\text{7}}\text{}\frac{\text{-3}}{\text{4}}$

Ans: (iii) $\frac{-2}{3}>\frac{-4}{5}$

10. $\text{7}\text{.}\overline{\text{2}}$ is equal to

(i) $\frac{\text{68}}{\text{9}}$

(ii) $\frac{\text{64}}{\text{9}}$

(iii) $\frac{\text{65}}{\text{9}}$

(iv) $\frac{\text{63}}{\text{9}}$

Ans: (iii) $\frac{65}{9}$

11. $\text{0}\text{.83458456}......$ is

(i) an irrational number

(ii) rational number

(iii) a natural number

(iv) a whole number

Ans: (i) an irrational number

12. A terminating decimal is

(i) a natural number

(ii) a rational number

(iii) a whole number

(iv) an integer.

Ans: (ii) a rational number

13. The $\frac{\text{p}}{\text{q}}$ form of the number $\text{0}\text{.8}$ is

(i) $\frac{\text{8}}{\text{10}}$

(ii) $\frac{\text{8}}{\text{100}}$

(iii) $\frac{\text{1}}{\text{8}}$

(iv) $\text{1}$

Ans: (i) $\frac{8}{10}$

14. The value of $\sqrt[\text{3}]{\text{1000}}$ is

(i) $1$

(ii) $10$

(iii) $3$

(iv) $0$

Ans: (ii) $10$

15. The sum of rational and an irrational number

(i) may be natural

(ii) may be irrational

(iii) is always irrational

(iv) is always rational

Ans: (iii) is always rational

16. The rational number not lying between $\frac{\text{3}}{\text{5}}$ and $\frac{\text{2}}{\text{3}}$ is

(i) $\frac{\text{49}}{\text{75}}$

(ii) $\frac{\text{50}}{\text{75}}$

(iii) \[\frac{\text{47}}{\text{75}}\]

(iv) $\frac{\text{46}}{\text{75}}$

Ans: (B) $\frac{50}{75}$

17. $\text{0}\text{.12}\overline{\text{3}}$ is equal to

(i) $\frac{\text{122}}{\text{90}}$

(ii) $\frac{\text{122}}{\text{100}}$

(iii) $\frac{\text{122}}{\text{99}}$

(iv) None of these

Ans: (a) $\frac{122}{990}$

18. The number ${{\left( \text{1+}\sqrt{\text{3}} \right)}^{\text{2}}}$ is

(a) natural number

(b) irrational number

(c) rational number

(d) integer

Ans: (b) irrational number

19. The simplest form of $\sqrt{\text{600}}$ is

(i) $\text{10}\sqrt{\text{60}}$

(ii) $\text{100}\sqrt{\text{6}}$

(iii) $\text{20}\sqrt{\text{3}}$

(iv) $\text{10}\sqrt{\text{6}}$

Ans: (D) $10\sqrt{6}$

20. The value of $\text{0}\text{.}\overline{\text{23}}\text{+0}\text{.}\overline{\text{22}}$ is

(i) $\text{0}\text{.4}\overline{\text{5}}$

(ii) $\text{0}\text{.4}\overline{\text{4}}$

(iii) $\text{0}\text{.}\overline{\text{45}}$

(iv) $\text{0}\text{.}\overline{\text{44}}$

Ans: (A) $0.\overline{23}=0.232323....$

$0.\overline{22}=0.222222....$

$0.\overline{23}+0.\overline{22}=0.454545....$

$=0.\overline{45}$

21. The value of ${{\text{2}}^{\frac{\text{1}}{\text{3}}}}\text{ }\!\!\times\!\!\text{ }{{\text{2}}^{\text{-}\frac{\text{4}}{\text{3}}}}$ is

(i) $\text{2}$

(ii) $\frac{\text{1}}{\text{2}}$

(iii) $\text{3}$

(iv) None of these

Ans: (B) ${{2}^{\frac{1}{3}}}\times {{2}^{-\frac{4}{3}}}={{2}^{\frac{1}{3}-\frac{4}{3}}}={{2}^{\frac{1-4}{3}}}={{2}^{-\frac{3}{3}}}$

22. \[\text{16}\sqrt{\text{13}}\text{ }\!\!\div\!\!\text{ 9}\sqrt{\text{52}}\] is equal to

(i) $\frac{\text{3}}{\text{9}}$

(ii) $\frac{\text{9}}{\text{8}}$

(iii) $\frac{\text{8}}{\text{9}}$

(iv) None of these

Ans: $16\sqrt{13}\div 9\sqrt{52}$

$\frac{16\sqrt{13}}{9\sqrt{52}}=\frac{16}{9}\sqrt{\frac{13}{52}}=\frac{8}{9}$

23. $\sqrt{\text{8}}$ is an

(i) natural number

(ii) rational number

(iii) integer

(iv) irrational number

Ans: (D) $\sqrt{8}$ is an irrational number

$\therefore \sqrt{4\times 2}=2\sqrt{2}$

2 Marks Questions

1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$?

Ans: Consider the definition of a rational number. A rational number is the one that can be written in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$.

Zero can be written as $\frac{0}{1},\frac{0}{2},\frac{0}{3},\frac{0}{4},\frac{0}{5}......$

So, we arrive at the conclusion that $0$ can be written in the form $\frac{p}{q}$, where $q$is any integer.

Therefore, zero is a rational number.

2. Find six rational numbers between $3$ and $4$.

Ans: We know that there are infinite rational numbers between any two numbers.

A rational number is the one that can be written in the form of $\frac{p}{q}$, where p and q are integers and $q\ne 0$.

We know that the numbers 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6 all lie between 3 and 4.

We need to rewrite the numbers 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6 in $\dfrac{p}{q}$ form to get the rational numbers between 3 and 4.

So, after converting we get $\frac{32}{10},\frac{32}{10},\frac{33}{10},\frac{34}{10},\frac{35}{10},$ and $\frac{36}{10},$ into lowest fractions.

On converting the fractions into lowest fractions, we get $\frac{16}{5},\frac{17}{5},\frac{7}{2}$ and $\frac{18}{5}$.

Therefore, six rational numbers between $3$ and $4$are \[\frac{31}{10},\frac{16}{5},\frac{33}{10},\frac{17}{5},\frac{7}{2}\] and $\frac{18}{5}$.

3. Find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$.

Ans: We know that there are infinite rational numbers between any two numbers.

A rational number is the one that can be written in the form of $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$.

We know that the numbers $\frac{3}{5}$ and $\frac{4}{5}$ can also be written as $0.6\text{ and }0.8$.

We can conclude that the numbers$0.61,0.62,0.63,0.64$ and $0.65$ in \[\frac{p}{q}\] form to get the rational numbers between $3\text{ and }4$.

So, after converting, we get $\frac{61}{100},\frac{62}{100},\frac{63}{100},\frac{64}{100}\text{ and }\frac{65}{100}$.

We can further convert the rational numbers $\frac{62}{100},\frac{64}{100}\text{ and }\frac{65}{100}$ into lowest fractions.

On converting the fractions, we get $\frac{31}{50},\frac{16}{25}\text{ and }\frac{13}{20}$.

Therefore, six rational numbers between $3\text{ and }4$ are $\frac{61}{100},\frac{31}{50},\frac{63}{100},\frac{16}{50}\text{ and }\frac{13}{50}$.

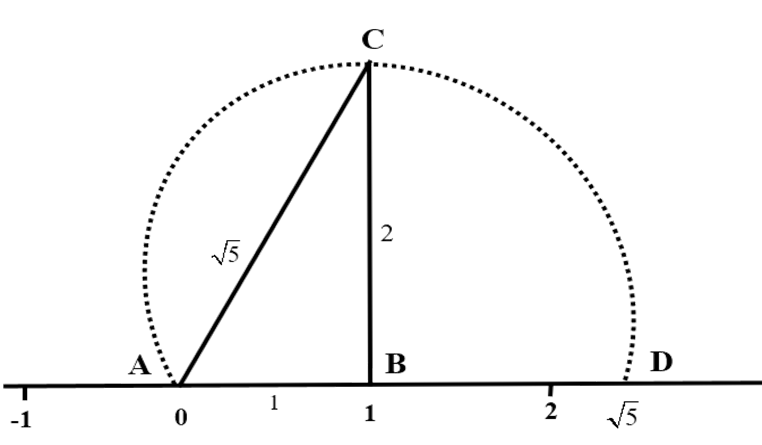
4. Show how $\sqrt{5}$ can be represented on the number line.

Ans: According to Pythagoras theorem, we can conclude that

${{\left( \sqrt{5} \right)}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}$.

We need to draw a line segment $AB\text{ of }1$unit on the number line. Then draw a straight line segment $BC\text{ of }2$ units. Then join the points $C$ and $A$, to form a line segment $BC$.

Then draw the arc $ACD$, to get the number $\sqrt{5}$ on the number line.

5. You know that $\frac{1}{7}=0.142857....$. Can you predict what the decimal expansion of $\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7}$ are, without actually doing the long division? If so, how?

(Hint: Study the remainder while finding the value of $\frac{1}{7}$ carefully.)

Ans: We are given that $\frac{1}{7}=0.\overline{142857}$ or $\frac{1}{7}=0.142857....$

We need to find the value of \[\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\text{ and }\frac{6}{7}\], without performing long division.

We know that \[\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\text{ and }\frac{6}{7}\] can be rewritten as

$2\times \frac{1}{7},3\times \frac{1}{7},4\times \frac{1}{7},5\times \frac{1}{7}\text{ and }6\times \frac{1}{7}$.

On substituting value of $\frac{1}{7}$ as $0.142857....$, we get 

$2\times \frac{1}{7}=2\times 0.142857....=0.285714.... $

$3\times \frac{1}{7}=3\times 0.142857....=0.428571.... $ 

$4\times \frac{1}{7}=4\times 0.142857....=0.571428....$ 

$5\times \frac{1}{7}=5\times 0.142857....=0.714285.... $ 

 $6\times \frac{1}{7}=6\times 0.142857....=0.857142.... $ 

Therefore, we conclude that, we can predict the values of \[\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\text{ and }\frac{6}{7}\], without performing long division, to get 

\[\frac{2}{7}=0.\overline{285714},\frac{3}{7}=0.\overline{428571},\frac{4}{7}=0.\overline{571428},\frac{5}{7}=0.\overline{714285},\frac{6}{7}=0.\overline{857142}\]

6. Express $0.99999....$in the form $\frac{p}{q}$. Are you surprised by your answer? Discuss why the answer makes sense with your teacher and classmates.

Ans: Let $x=0.99999....\text{ }......(a)$

We need to multiply both sides by $10$ to get 

$10x=9.9999....\text{ }......(b)$

We need to subtract $(a)\text{ from }(b)$, to get

10x=9.99999.... 

x=0.99999.... 

_____________

$9x=9$

We can also write $9x=9\text{ as }x=\frac{9}{9}\text{ or }x=1$.

Therefore, on converting $0.99999....$ in the $\frac{p}{q}$ form, we get the answer as $1$.

Yes, at a glance we are surprised at our answer. But the answer makes sense when we observe that $0.99999....$ goes on forever. So there is no gap between $1$  and $0.9999....$ and hence they are equal.

7. Visualize $3.765$ on the number line using successive magnification.

Ans: We know that the number $3.765$ will lie between $3.764\text{ and }3.766$.

We know that the number $3.764$and $3.766$ will lie between $3.76\text{ and }3.77$.

We know that the number $3.76\text{ and }3.77$. will lie between $3.7\text{ and }3.8$.

We know that the number  $3.7\text{ and }3.8$ will lie between $3\text{ and }~4$.

Therefore, we can conclude that we need to use the successive magnification, after locating numbers $3\text{ and }~4$ on the number line

(Image will be uploaded soon)

(Image will be uploaded soon)

(Image will be uploaded soon)

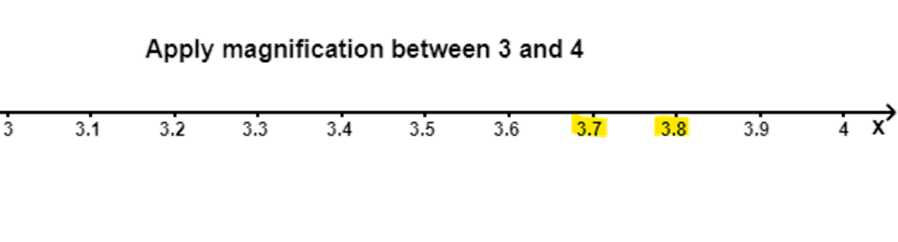
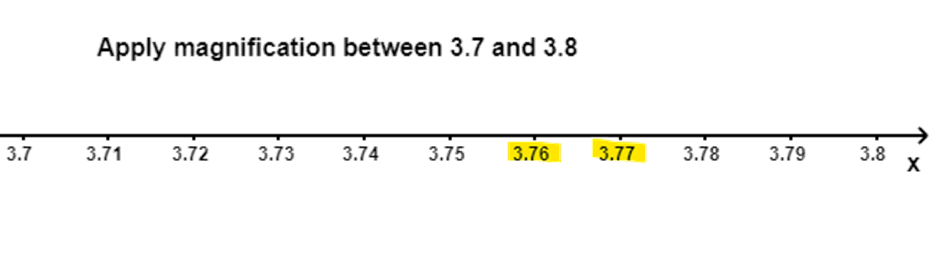
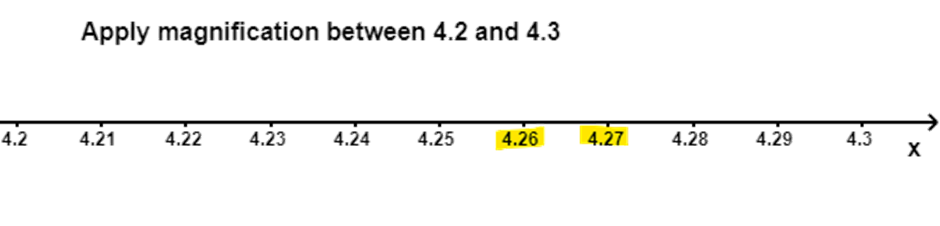
8. Visualize $4.\overline{26}$ on the number line, upto $4$decimal places.

Ans: We know that the number $4.\overline{26}$ can also be written as$4.262....$.

We know that the number $4.262....$ will lie between $4.261\text{ and }4.263$.

We know that the number  $4.261\text{ and }4.263$ will lie between $4.26\text{ and }4.27$.

We know that the number $4.26\text{ and }4.27$ will lie between $4.2\text{ and }4.3$.

We know that the number $4.2\text{ and }4.3$ will lie between $4\text{ and }5$.

Therefore, we can conclude that we need to use the successive magnification, after locating numbers $4\text{ and }5$ on the number line.

(Image will be uploaded soon)

(Image will be uploaded soon)

(Image will be uploaded soon)

(Image will be uploaded soon)

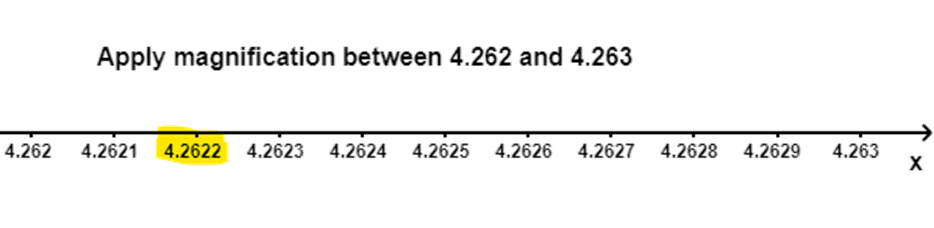
9. Recall, $\pi $is defined as the ratio of the circumference (say $c$) of a circle of its diameter (say $d$). That is, $\pi =\frac{c}{d}$. This seems to contradict the fact that $\pi $ is irrational. How you resolve this contradiction?

Ans: We know that when we measure the length of the line or a figure by using a scaleneory device, we do not get an exact measurement. In fact, we get an approximate rational value. So, we are not able to realize that either the circumference ($c$) or diameter ($d$) of a circle is irrational.

Therefore, we can conclude that as such there is not any contradiction regarding the value of $\pi $ and we realize that the value of $\pi $ is irrational.

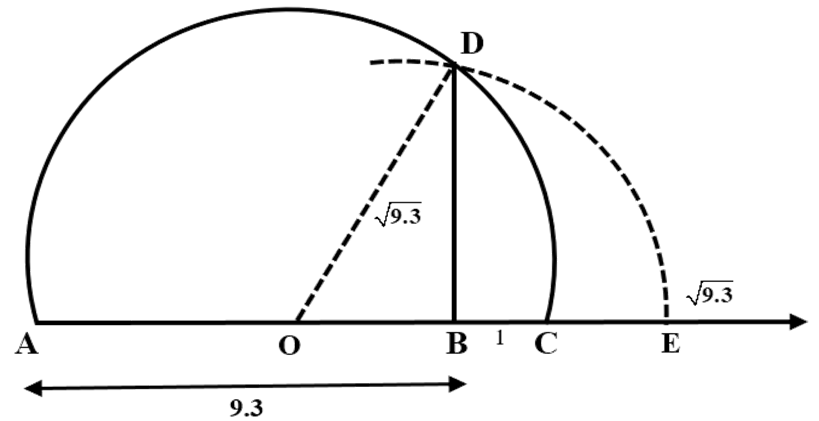
10. Represent $9.3$ on the number line.

Ans: Mark the distance $9.3$ units from a fixed point $A$ on a given line to obtain a point $B$ such that $AB=9.3$ units. From $B$ mark a distance of $1$ unit and call the new point as $C$. Find themid-point of $AC$ and call that point as $O$. Draw a semi-circle with centre $O$ and radius $OC=5.15$units. Draw a line perpendicular to $AC$ passing through $B$ cutting the semi-circle at $D$.

Then $BD=\sqrt{9.3}$.

(Image will be uploaded soon)

11. Find (i) ${{64}^{\frac{1}{5}}}$ (ii) ${{32}^{\frac{1}{5}}}$ (iii) ${{125}^{\frac{1}{3}}}$

Ans:

(i) ${{64}^{\frac{1}{2~}}}$

We know that${{a}^{\frac{1}{n}}}=\sqrt[n]{a},\text{ where }a>0$

We conclude that  ${{64}^{\frac{1}{2~}}}$can also be written as $\sqrt[2]{64}=\sqrt[2]{8\times 8}$

$\sqrt[2]{64}=\sqrt[2]{8\times 8}$$=8$

Therefore, the value of  ${{64}^{\frac{1}{2~}}}$will be $8$.

(ii) ${{32}^{\frac{1}{5}}}$

We know that${{a}^{\frac{1}{n}}}=\sqrt[n]{a},\text{ where }a>0$

We conclude that  ${{32}^{\frac{1}{5}}}$can also be written as $\sqrt[5]{32}=\sqrt[5]{2\times 2\times 2\times 2\times 2}$

$\sqrt[5]{32}=\sqrt[5]{2\times 2\times 2\times 2\times 2}=2$

Therefore, the value of  ${{32}^{\frac{1}{5}}}$will be $2$.

(iii) ${{125}^{\frac{1}{3}}}$

We know that${{a}^{\frac{1}{n}}}=\sqrt[n]{a},\text{ where }a>0$

We conclude that ${{125}^{\frac{1}{3}}}$can also be written as $\sqrt[3]{125}=\sqrt[3]{5\times 5\times 5}$

$\sqrt[3]{125}=\sqrt[3]{5\times 5\times 5}=5$

Therefore, the value of ${{125}^{\frac{1}{3}}}$will be $5$.

12. Simplify $\sqrt[3]{2}\times \sqrt[4]{3}$

Ans: $\sqrt[3]{2}\times \sqrt[4]{3}$

${{2}^{\frac{1}{3}}}\times {{3}^{\frac{1}{4}}}$

The LCM of $3\text{ and }4\text{ is }12$

$\therefore {{2}^{\frac{1}{3}}}={{2}^{\frac{4}{12}}}={{\left( {{2}^{4}} \right)}^{\frac{1}{12}}}={{16}^{\frac{1}{12}}} $

${{3}^{\frac{1}{4}}}={{3}^{\frac{3}{12}}}={{\left( {{3}^{3}} \right)}^{\frac{1}{12}}}={{27}^{\frac{1}{12}}} $

${{2}^{\frac{1}{3}}}\times {{3}^{\frac{1}{4}}}={{16}^{\frac{1}{12}}}\times {{27}^{\frac{1}{12}}}={{\left( 16\times 27 \right)}^{\frac{1}{12}}} $

$={{\left( 432 \right)}^{\frac{1}{12}}} $

13. Find the two rational numbers between$\frac{1}{2}$ and $\frac{1}{3}$.

Ans: First rational number between $\frac{1}{2}$ and $\frac{1}{3}$

$=\frac{1}{2}\left[ \frac{1}{2}+\frac{1}{3} \right]\Rightarrow \frac{1}{2}\left[ \frac{3+2}{6} \right]\Rightarrow \frac{5}{12} $

$ =\frac{1}{2},\frac{5}{12}\text{ and }\frac{1}{3} $

Second rational number between $\frac{1}{2}$ and $\frac{1}{3}$

$=\frac{1}{2}\left[ \frac{1}{2}+\frac{5}{12} \right]\Rightarrow \frac{1}{2}\left[ \frac{6+5}{12} \right]\Rightarrow \frac{11}{24}$

$=\frac{5}{12}\text{ and }\frac{11}{24}$ are two rational numbers between $\frac{1}{2}$ and $\frac{1}{3}$.

14. Find two rational numbers between $2$ and $3$.

Ans: Irrational numbers between $2$ and $3$ is $\sqrt{2\times 3}=\sqrt{6}$

Irrational number between $2$ and $3$ is $\sqrt{6}$.

$\sqrt{2\times \sqrt{6}}={{2}^{\frac{1}{2}}}\times {{6}^{\frac{1}{4}}}={{2}^{2\times \frac{1}{4}}}\times {{6}^{\frac{1}{4}}} $

$ ={{\left( {{2}^{2}} \right)}^{\frac{1}{4}}}\times {{6}^{\frac{1}{4}}}={{4}^{\frac{1}{4}}}\times {{6}^{\frac{1}{4}}}={{\left( 24 \right)}^{\frac{1}{4}}}=\sqrt[4]{24} $

$\sqrt{6}\text{ and }\sqrt{24}$ are two rational numbers between $2$ and $3$.

15. Multiply $\left( 3-\sqrt{5} \right)$ by $\left( 6+\sqrt{2} \right)$.

Ans: $\left( 3-\sqrt{5} \right)$$\left( 6+\sqrt{2} \right)$

$  =3\left( 6-\sqrt{2} \right)-\sqrt{5}\left( 6+\sqrt{2} \right) $

$=18+3\sqrt{2}-6\sqrt{5}-\sqrt{5}\times \sqrt{2} $

$  =18+3\sqrt{2}-6\sqrt{5}-\sqrt{10} $

16. Evaluate (i) $\sqrt[3]{125}$ (ii) $\sqrt[4]{1250}$

Ans:

(i) $\sqrt[3]{125}$$={{\left( 5\times 5\times 5 \right)}^{\frac{1}{3}}}={{\left( {{5}^{3}} \right)}^{\frac{1}{3}}}=5$

(ii) $\sqrt[4]{1250}$$\begin{align}

$={{\left( 2\times 5\times 5\times 5\times 5 \right)}^{\frac{1}{4}}}={{\left( 2\times {{5}^{4}} \right)}^{\frac{1}{4}}} $ 

$={{2}^{\frac{1}{4}}}\times {{\left( {{5}^{4}} \right)}^{\frac{1}{4}}}=5\times \sqrt[4]{2} $

17. Find rationalizing factor of $\sqrt{300}$.

Ans: $\sqrt{300}=\sqrt{2\times 2\times 3\times 5\times 5}$

$  =\sqrt{{{2}^{2}}\times 3\times {{5}^{2}}} $

$ =2\times 5\sqrt{3}=10\sqrt{3} $

Rationalizing factor is $\sqrt{3}$

18. Rationalizing the denominator $\frac{1}{\sqrt{5}+\sqrt{2}}$ and subtract it from $\sqrt{5}-\sqrt{2}$.

Ans: $\frac{1}{\sqrt{5}+\sqrt{2}}\times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}$

$=\frac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}=\frac{\sqrt{5}-\sqrt{2}}{5-2}=\frac{\sqrt{5}-\sqrt{2}}{3}$

Difference between $\left( \sqrt{5}-\sqrt{2} \right)\text{ and }\left( \sqrt{5}-\frac{\sqrt{2}}{3} \right)$

$=\sqrt{5}-\sqrt{2}-\left( \frac{\sqrt{5}-\sqrt{2}}{3} \right) $

$ =\sqrt{5}-\sqrt{2}-\frac{\sqrt{5}}{3}+\frac{\sqrt{2}}{3} $

$=\left( \sqrt{5}-\frac{\sqrt{5}}{3} \right)-\left( \sqrt{2}-\frac{\sqrt{2}}{3} \right) $

$=\frac{2\sqrt{5}}{3}-\frac{2\sqrt{2}}{3}=\frac{2}{3}\left( \sqrt{5}-\sqrt{2} \right) $

19. Show that $\sqrt{7}-3$ is irrational.

Ans: Suppose $\sqrt{7}-3$ is rational

Let $\sqrt{7}-3=x$ ($x$ is a rational number)

$\sqrt{7}=x+3$

$x$ is a rational number $3$ is also a rational number

$\therefore x+3$ is a rational number

But is $\sqrt{7}$ irrational number which is contradiction

$\therefore \sqrt{7}-3$ is an irrational number.

20. Find two rational numbers between $7$ and $5$.

Ans: First rational number $=\frac{1}{2}\left[ 7+5 \right]=\frac{12}{2}=6$

Second rational number $=\frac{1}{2}\left[ 7+6 \right]=\frac{1}{2}\times 13=\frac{13}{2}$

Two rational numbers between $7\text{ and }5\text{ are }6\text{ and }\frac{13}{2}$.

21. Show that $5+\sqrt{2}$ is not a rational number.

Ans: Let $5+\sqrt{2}$ is a rational number.

Say $5+\sqrt{2=x}$ i.e., $\sqrt{2}=x-5$

$x$ is a rational number $5$ is also rational number

$\therefore x-5$ is also a rational number.

But $\sqrt{2}$ is irrational number which is a contradiction

$\therefore 5+\sqrt{2}$ is an irrational number.

22. Simplify ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$.

Ans: ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}+2\sqrt{5}\times \sqrt{2}=5+2+2\sqrt{10}=7+2\sqrt{2}$

23. Evaluate $\frac{{{11}^{\frac{5}{2}}}}{{{11}^{\frac{3}{2}}}}$.

Ans: $\frac{{{11}^{\frac{5}{2}}}}{{{11}^{\frac{3}{2}}}}={{11}^{\frac{5}{2}-\frac{3}{2}}}\left[ \because \frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}} \right]$

$ ={{11}^{\frac{5-3}{2}}}={{11}^{\frac{2}{2}}} $

$=11 $ 

24. Find four rational numbers between $\frac{3}{7}$ and $\frac{4}{7}$.

Ans:

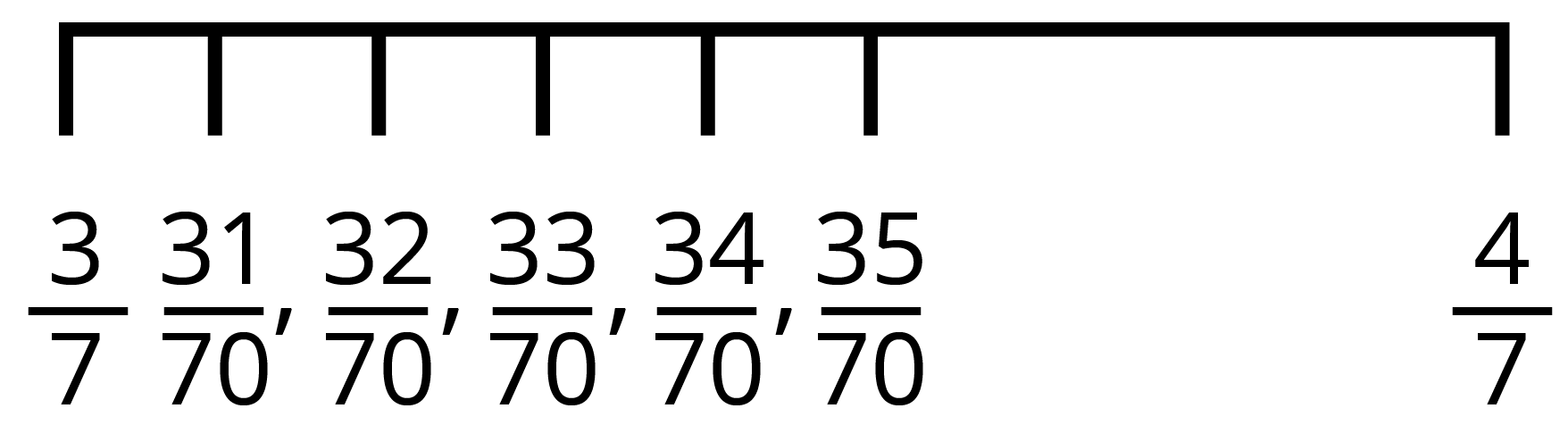
$\frac{3}{7}\times \frac{10}{10}=\frac{30}{70}\text{ and }\frac{4}{7}\times \frac{10}{10}=\frac{40}{70}$

Take any four rational numbers between $\frac{30}{70}\text{ and }\frac{40}{70}$ i.e., rational numbers between  $\frac{3}{7}$ and $\frac{4}{7}$ are $\frac{31}{70},\frac{32}{70},\frac{33}{70},\frac{34}{70},\frac{35}{70}$

25. Write the following in decimal form (i) $\frac{36}{100}$ (ii) $\frac{2}{11}$

Ans: 

(i) $\frac{36}{100}=0.36$

(ii) $\frac{2}{11}=0.\overline{18}$

26. Express $2.417\overline{8}$ in the form $\frac{a}{b}$

Ans: $x=2.4\overline{178}$

$10x=24.\overline{178}$$......(1)$$[\text{Multiplying both sides by }10]$

$10x=24.178178178.... $

$1000\times 10x=1000\times 24.178178178....$Multiplying both sides by 1000

$10,000x=24178.178178.... $

$ 10000x=24178.\overline{178}\text{ }......(2) $

Subtracting $(1)\text{ from }(2)$

$10,000x-x=24178.\overline{178}-24.\overline{178} $

$9990x=24154 $

$x=\frac{24154}{9990} $

$ 2.4\overline{178}=\frac{24154}{9990}+\frac{12077}{4995} $

27. Multiply $\sqrt{3}$ by $\sqrt[3]{5}$.

Ans: $\sqrt{3}\text{ and }\sqrt[3]{5}$

Or ${{3}^{\frac{1}{2}}}\text{ and }{{5}^{\frac{1}{3}}}$

$LCM\text{ of }2\text{ and }3\text{ is }6 $

${{3}^{\frac{1}{2}}}={{3}^{\frac{1}{2}\times \frac{3}{3}}}={{\left( {{3}^{3}} \right)}^{\frac{1}{6}}}={{\left( 27 \right)}^{\frac{1}{6}}} $

 ${{5}^{\frac{1}{3}}}={{5}^{\frac{1}{3}\times \frac{2}{2}}}={{\left( {{5}^{2}} \right)}^{\frac{1}{6}}}={{\left( 25 \right)}^{\frac{1}{6}}} $

 $\sqrt{3}\times \sqrt[3]{5}={{\left( 27 \right)}^{\frac{1}{6}}}\times {{\left( 25 \right)}^{\frac{1}{6}}}={{\left( 27\times 25 \right)}^{\frac{1}{6}}} $

$ ={{675}^{\frac{1}{6}}}=\sqrt[6]{675} $

28. Find the value of $\frac{\sqrt{2}+\sqrt{5}}{\sqrt{5}}$ if $\sqrt{5}=2.236$ and $\sqrt{10}=3.162$.

Ans: $\frac{\sqrt{2}+\sqrt{5}}{\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}}=\frac{\sqrt{10}+5}{5}=\frac{8.162}{5}=1.6324$

29. Convert $0.\overline{25}$ into rational number.

Ans: Let \[x=0.\overline{25}\]                            ......(i)

$x=0.252525....$

Multiply both sides by 100

$100x=25.252525....$

$100x=25.\overline{25}$                                                  ......(ii)

Subtract (i) from (ii)

$100x-x=25.\overline{25}-0.\overline{25} $

$99x=25 $

 $x=\frac{25}{99} $

30. Simplify $\left( 3\sqrt{3}+2\sqrt{2} \right)\left( 2\sqrt{3}+3\sqrt{2} \right)$.

Ans: By multiplying each terms in the given product we have,

 $ \left( 3\sqrt{3}+2\sqrt{2} \right)\left( 2\sqrt{3}+3\sqrt{2} \right) $

 $=3\sqrt{3}\left( 2\sqrt{3}+3\sqrt{2} \right)+2\sqrt{2}\left( 2\sqrt{3}+3\sqrt{2} \right) $

 $=18+9\sqrt{6}+4\sqrt{6}+12 $

 $ =30+\left( 9+4 \right)\sqrt{6} $

 $=30+13\sqrt{6} $

31. Simplify $\frac{{{9}^{\frac{3}{2}}}\times {{9}^{-\frac{4}{2}}}}{{{9}^{\frac{1}{2}}}}$.

Ans: By using the formulas of exponents with same base we get,

$\frac{{{9}^{\frac{3}{2}}}\times {{9}^{-\frac{4}{2}}}}{{{9}^{\frac{1}{2}}}}=\frac{{{9}^{\frac{3}{2}-\frac{4}{2}}}}{{{9}^{\frac{1}{2}}}}\left[ {{a}^{m}}.{{a}^{n}}={{a}^{m-n}} \right]$

$\frac{{{9}^{-\frac{1}{2}}}}{{{9}^{\frac{1}{2}}}}=\frac{1}{{{9}^{\frac{1}{2}+\frac{1}{2}}}}\left[ {{a}^{-m}}=\frac{1}{{{a}^{m}}} \right] $

$ =\frac{1}{{{9}^{\frac{2}{2}}}}=\frac{1}{9} $

3 Marks Questions

1. State whether the following statements are true or false. Give

reasons for your answers.

i. Every natural number is a whole number.

Ans:

Separately, consider whole numbers and natural numbers.

We know that the whole number series is 0,1,2,3,4,5....

We know that the natural number series is 0,1,2,3,4,5....

As a result, every number in the natural number series may be found in the whole number series.

Therefore, we can safely conclude that any natural number is a whole number.

ii. Every integer is a whole number.

Ans: Separately, consider whole numbers and integers.

We know that integers are those numbers that can be written in the form of $\frac{p}{q}$ where q=1.

In the case of an integer series, we now have.... 4,3,2,1,0,1,2,3,4....

We know that the whole number series is 0,1,2,3,4,5....

We can conclude that all whole number series numbers belong to the integer series.

However, the whole number series does not contain every number of integer series.

As a result, we can conclude that no integer is a whole number.

iii. Every rational number is a whole number.

Ans: Separately, consider whole numbers and rational numbers.

We know that integers are those numbers that can be written in the form of $\frac{p}{q}$ where $q\ne 0$.

We know that the whole number series is 0,1,2,3,4,5....

We know that every number of whole number series can be written in the form of $\frac{p}{q}$ as $\frac{0}{1},\frac{1}{1},\frac{2}{1},\frac{3}{1},\frac{4}{1},\frac{5}{1}...$

We conclude that every number of the whole number series is a rational number. 

But, every rational number does not appear in the whole number series.

2. State whether the following statements are true or false. Justify your answers.

i. Every irrational number is a real number.

Ans: Separately, consider irrational numbers and real numbers.

We know that irrational numbers are the numbers that cannot be converted in the form $\frac{p}{q}$, where p and q are integers and $q\ne 0$.

A real number is made up of both rational and irrational numbers, as we all know.

As a result, we might conclude that any irrational number is, in fact, a real number.

ii. Every point on the number line is of the form $\sqrt{m}$, where m is a natural number.

Ans: Consider a number line. We know that we can express both negative and positive numbers on a number line.

We know that when we take the square root of any number, we cannot receive a negative value.

Therefore, we conclude that not every number point on the number line is of the form $\sqrt{m}$, where m is a natural number.

iii. Every real number is an irrational number.

Ans: Separately, consider irrational numbers and real numbers.

We know that irrational numbers are the numbers that cannot be converted in the form $\frac{p}{q}$, where p and q are integers and $q\ne 0$.

A real number is made up of both rational and irrational numbers, as we all know.

As a result, we can deduce that any irrational number is actually a real number. However, not every real number is irrational.

Therefore, we conclude that every real number is not a rational number.

3. Express the following in the form $\frac{p}{q}$ where $p$ and $q$ are integers and $q\ne 0$.

i. $0.\overline{6}$

Ans: 

Let $x=0.\overline{6}$

$\Rightarrow x=0.6666$            ......(a)

Multiplying both sides by 10 we get

$10x=6.6666$             ......(b)

We need to subtract (a) from (b), to get

$9x=6$

We can also write $9x=6$ as $x=\frac{6}{9}$ or $x=\frac{2}{3}$.

Therefore, on converting $0.\overline{6}$ in the $\frac{p}{q}$ form, we get the answer as $\frac{2}{3}$.

ii. $0.4\overline{7}$

Ans: Let $x=0.4\overline{7}\Rightarrow x=0.47777$                     ......(a)

Multiplying both sides by 10 we get 

$10x=4.7777$                                            ......(b)

We need to subtract (a) from (b), to get

$9x=4.3$

We can also write $9x=4.3$ as $x=\frac{4.3}{9}$ or $x=\frac{43}{90}$

Therefore, on converting $0.4\overline{7}$ in the $\frac{p}{q}$ form, we get the answer as $\frac{43}{90}$.

iii. $0.\overline{001}$

Ans: Let $x=0.\overline{001}\Rightarrow x=0.001001$                     ......(a)

Multiplying both sides by 1000 we get 

$1000x=1.001001$                                         ......(b)

We need to subtract (a) from (b), to get

$999x=1$

We can also write $999x=1$ as $x=\frac{1}{999}$

Therefore, on converting $0.\overline{001}$ in the $\frac{p}{q}$ form, we get the answer as $\frac{1}{999}$.

4. What can the maximum number of digits be in the recurring block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.

Ans: The number of digits in the recurring block of $\frac{1}{17}$ must be determined.

To acquire the repeating block of $\frac{1}{17}$ we'll use long division.

We need to divide 1 by 17, to get 0.0588235294117647.... and we got the remainder as 1, which will continue to be 1 after carrying out 16 continuous divisions.

Therefore, we conclude that

\[\frac{1}{17}=0.0588235294117647\] or \[\frac{1}{17}=0.\overline{0588235294117647}\] which is a non-terminating decimal and recurring decimal.

5. Look at several examples of rational numbers in the form $\frac{p}{q}\left( q\ne 0 \right)$ where $p$ and $q$ are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property $q$ must satisfy?

Ans: Let us consider the examples of the form $\frac{p}{q}$ that are terminating decimals.

$ \frac{5}{2}=2.5 $ 

$ \frac{5}{4}=1.25 $ 

$ \frac{2}{5}=0.4 $

$  \frac{5}{16}=0.3125 $ 

It can be observed that the denominators of the above rational numbers have powers of 2,5 or both.

Therefore, we can conclude that property, which $q$ must satisfy in $\frac{p}{q}$ , so that the rational number $\frac{p}{q}$ is a terminating decimal is that q must have powers of 2,5 or both.

6. Classify the following numbers as rational or irrational:

i. $2-\sqrt{5}$

Ans: $2-\sqrt{5}$

We know that $\sqrt{5}=2.236....$, which is an irrational number.

$2-\sqrt{5}=2-2.236....$

$=-0.236...$, which is also an irrational number.

As a result, we can deduce that $2-\sqrt{5}$ is an irrational number.

ii. $\left( 3+\sqrt{23} \right)-\sqrt{23}$

Ans: $\left( 3+\sqrt{23} \right)-\sqrt{23}$

$\left( 3+\sqrt{23} \right)-\sqrt{23}=3+\sqrt{23}-\sqrt{23}=3$

As a result, we can deduce that $\left( 3+\sqrt{23} \right)-\sqrt{23}$ is a rational number.

iii. $\frac{2\sqrt{7}}{7\sqrt{7}}$

Ans: $\frac{2\sqrt{7}}{7\sqrt{7}}$

We can cancel $\sqrt{7}$ in the numerator and denominator to get $\frac{2\sqrt{7}}{7\sqrt{7}}=\frac{2}{7}$, because $\sqrt{7}$ is a common number in both the numerator and denominator.

iv. $\frac{1}{\sqrt{2}}$

Ans: $\frac{1}{\sqrt{2}}$

We know that $\sqrt{2}=1.4142...$, which is an irrational number.

$\frac{1}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}$

$=\frac{1.4142...}{2}=0.707...$ which is also an irrational number.

As a result, we can deduce that $\frac{1}{\sqrt{2}}$ is an irrational number.

v. $2\pi $

Ans: $2\pi $

We know that $\pi =3.1415....,$ which is an irrational number.

We can conclude that $2\pi $ will also be an irrational number.

As a result, we can deduce that $2\pi $ is an irrational number.

7. Simplify each of the following expression:

i. $\left( 3+3\sqrt{3} \right)\left( 2+\sqrt{2} \right)$

Ans: 

$(3+3\sqrt{3})(2+\sqrt{2})$

Applying distributive law,

\[(3+3\sqrt{3})(2+\sqrt{2})=3(2+\sqrt{2})\sqrt{3}(2+\sqrt{2})\]

\[=6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}\]

ii. \[\left( 3+3\sqrt{3} \right)3-\sqrt{3}\]

Ans: $(3+3\sqrt{3})(3-\sqrt{3})$

Applying distributive law,

$  (3+3\sqrt{3})(3-\sqrt{3})=(3-\sqrt{3})+\sqrt{3}(3-\sqrt{3}) $ 

$ =9-3\sqrt{3}+3\sqrt{3}-3 $

$=6$

iii. ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$

Ans: ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$

Applying the formula ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$

${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+2\times \sqrt{5}\times \sqrt{2}+{{\left( \sqrt{2} \right)}^{2}} $

$ =5+2\sqrt{10}+2 $

$=7+2\sqrt{10}$

iv. $\left( 5+\sqrt{2} \right)\left( 5+\sqrt{2} \right)$

Ans: $\left( 5+\sqrt{2} \right)\left( 5+\sqrt{2} \right)$

Applying the formula $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$

$ \left( 5+\sqrt{2} \right)\left( 5+\sqrt{2} \right)={{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}} $

$ =5-2 $

$=3$

8. Find 

i. ${{9}^{\frac{3}{2}}}$

Ans: We know that ${{a}^{\frac{1}{n}}}=\sqrt[n]{a},a>0$

As a result, we can deduce that ${{9}^{\frac{3}{2}}}$ can also be written as

$\sqrt[2]{{{\left( 9 \right)}^{3}}}=\sqrt[2]{9\times 9\times 9}=\sqrt[2]{3\times 3\times 3\times 3\times 3\times 3}$

$=3\times 3\times 3 $

$ =27 $

Therefore, the value of ${{9}^{\frac{3}{2}}}$ will be $27$.

ii. ${{32}^{\frac{2}{5}}}$

Ans: We know that ${{a}^{\frac{1}{n}}}=\sqrt[n]{a},a>0$

As a result, we can deduce that ${{32}^{\frac{2}{5}}}$ can also be written as

$ \sqrt[5]{{{\left( 32 \right)}^{2}}}=\sqrt[5]{\left( 2\times 2\times 2\times 2\times 2 \right)\left( 2\times 2\times 2\times 2\times 2 \right)} $

$=2\times 2 $ 

$=4$

Therefore, the value of ${{32}^{\frac{2}{5}}}$ will be $4$.

iii. ${{16}^{\frac{3}{4}}}$

Ans: We know that ${{a}^{\frac{1}{n}}}=\sqrt[n]{a},a>0$

As a result, we can deduce that ${{16}^{\frac{3}{4}}}$ can also be written as 

$\sqrt[4]{{{\left( 16 \right)}^{3}}}=\sqrt[4]{\left( 2\times 2\times 2\times 2 \right)\left( 2\times 2\times 2\times 2 \right)\left( 2\times 2\times 2\times 2 \right)} $

$ =2\times 2\times 2 $

 & =8 $

Therefore, the value of ${{16}^{\frac{3}{4}}}$ will be $8$.

iv. ${{125}^{-\frac{1}{3}}}$

Ans: We know that ${{a}^{-n}}=\frac{1}{{{a}^{n}}}$

As a result, we can deduce that ${{125}^{-\frac{1}{3}}}$ can also be written as $\frac{1}{{{125}^{\frac{1}{3}}}},or{{\left( \frac{1}{125} \right)}^{\frac{1}{3}}}$

We know that ${{a}^{\frac{1}{n}}}=\sqrt[n]{a},a>0$

$ \sqrt[3]{\frac{1}{125}}=\sqrt[3]{\left( \frac{1}{5}\times \frac{1}{5}\times \frac{1}{5} \right)} $

$=\frac{1}{5} $

Therefore, the value of ${{125}^{-\frac{1}{3}}}$ will be $\frac{1}{5}$.

9. Simplify

i. ${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}$

Ans: We know that ${{a}^{m}}.{{a}^{n}}={{a}^{\left( m+n \right)}}$

As a result, we can deduce that ${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}={{\left( 2 \right)}^{\frac{2}{3}+\frac{1}{5}}}$

${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}=\left( 2 \right)\frac{10+3}{15}={{\left( 2 \right)}^{\frac{13}{15}}}$

Therefore, the value of ${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}$ will be ${{\left( 2 \right)}^{\frac{13}{15}}}$.

ii. ${{\left( {{3}^{\frac{1}{3}}} \right)}^{7}}$

Ans: We know that ${{a}^{m}}.{{a}^{n}}={{a}^{\left( m+n \right)}}$

As a result, we can deduce that ${{\left( {{3}^{\frac{1}{3}}} \right)}^{7}}$ can also be written as ${{3}^{\frac{7}{3}}}$

iii. $\frac{{{11}^{\frac{1}{2}}}}{{{11}^{\frac{1}{4}}}}$

Ans: We know that $\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{\left( m-n \right)}}$

As a result, we can deduce that  $\begin{align}

$ \frac{{{11}^{\frac{1}{2}}}}{{{11}^{\frac{1}{4}}}}={{11}^{\frac{1}{2}}}-{{11}^{\frac{1}{4}}} $

$={{11}^{\frac{2-1}{4}}}={{11}^{\frac{1}{4}}} $

Therefore, the value of  $\frac{{{11}^{\frac{1}{2}}}}{{{11}^{\frac{1}{4}}}}$ will be ${{11}^{\frac{1}{4}}}$.

iv. ${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}$

Ans: We know that ${{a}^{m}}.{{b}^{m}}={{\left( a\times b \right)}^{m}}$

As a result, we can deduce that ${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}={{\left( 7\times 8 \right)}^{\frac{1}{2}}}.$

${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}={{\left( 7\times 8 \right)}^{\frac{1}{2}}}={{\left( 56 \right)}^{\frac{1}{2}}}.$

Therefore, the value of ${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}$ will be ${{\left( 56 \right)}^{\frac{1}{2}}}$.

10. Express $0.8888....$ in the form $\frac{p}{q}$.

Ans: Let us assume that the given decimal as,

$x=0.8888$

$x=0.\overline{8}......\left( 1 \right)$

$10x=10\times 0.8888$ (Multiply both sides by 10)

$ 10x=8.8888 $

$10x=8.\overline{8}.....\left( 2 \right) $

$10x-x=8.\overline{8}-0.\overline{8}$ (Subtracting (1) from (2))

9x=8 

$x=\frac{8}{9} $

11.  Simplify by rationalizing denominator $\frac{7+3\sqrt{5}}{7-3\sqrt{5}}$.

Ans: We are given the fraction to rationalize. By rationalizing the denominator we get,

$\frac{7+3\sqrt{5}}{7-3\sqrt{5}}=\frac{7+3\sqrt{5}}{7-3\sqrt{5}}\times \frac{7+3\sqrt{5}}{7+3\sqrt{5}}$ 

$=\frac{{{\left( 7+3\sqrt{5} \right)}^{2}}}{{{7}^{2}}-{{\left( 3\sqrt{5} \right)}^{2}}} $

$ =\frac{{{7}^{2}}+{{\left( 3\sqrt{5} \right)}^{2}}+2\times 7\times 3\sqrt{5}}{49-{{3}^{2}}\times 5} $

$=\frac{49+9\times 5+42\sqrt{5}}{49-45} $

$=\frac{49+45+42\sqrt{5}}{4} $

$ =\frac{94+42\sqrt{5}}{4} $ 

$ =\frac{94}{4}+\frac{42}{4}\sqrt{5} $

$ =\frac{47}{2}+\frac{21}{2}\sqrt{5} $

12. Simplify ${{\left\{ {{\left[ {{625}^{-}}^{\frac{1}{2}} \right]}^{-\frac{1}{4}}} \right\}}^{2}}$.

Ans:  Let us take the given expression to simplify and using the exponents formulas we get,

  \[{{\left\{ {{\left[ {{625}^{-}}^{\frac{1}{2}} \right]}^{-\frac{1}{4}}} \right\}}^{2}}\]

$ ={{\left\{ {{\left( \frac{1}{{{625}^{\frac{1}{2}}}} \right)}^{-\frac{1}{4}}} \right\}}^{2}} $

$={{\left\{ {{\left( \frac{1}{{{\left( {{25}^{2}} \right)}^{\frac{1}{2}}}} \right)}^{-\frac{1}{4}}} \right\}}^{2}}\left( {{a}^{-m}}=\frac{1}{{{a}^{m}}} \right) $

 $ =\left\{ {{\left( \frac{1}{25} \right)}^{-\frac{1}{4}\times 2}} \right\} $

$=\left( \frac{1}{{{25}^{-\frac{1}{2}}}} \right)=\frac{1}{{{\left( {{5}^{2}} \right)}^{-\frac{1}{2}}}}=\frac{1}{{{5}^{-1}}}=5 $

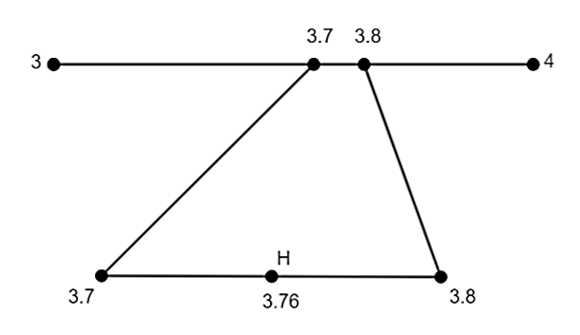
13. Visualize 3.76 on the number line using successive magnification.

Ans: 

(Image will be uploaded soon)

14. Prove that $\frac{1}{1+{{x}^{b-a}}+{{x}^{c-a}}}+\frac{1}{1+{{x}^{a-b}}+{{x}^{c-b}}}+\frac{1}{1+{{x}^{a-c}}+{{x}^{b-c}}}=1$

Ans: We are asked to prove the expression,

$\frac{1}{1+{{x}^{b-a}}+{{x}^{c-a}}}+\frac{1}{1+{{x}^{a-b}}+{{x}^{c-b}}}+\frac{1}{1+{{x}^{a-c}}+{{x}^{b-c}}}=1$

Let us take the LHS of the given expression that is,

$LHS=\frac{1}{1+{{x}^{b}}.{{x}^{-a}}+{{x}^{c}}.{{x}^{-a}}}+\frac{1}{1+{{x}^{a}}.{{x}^{-b}}+{{x}^{c}}.{{x}^{-b}}}+\frac{1}{1+{{x}^{a}}.{{x}^{-c}}+{{x}^{b}}.{{x}^{-c}}} $

$=\frac{1}{{{x}^{-a}}.{{x}^{a}}+{{x}^{b}}.{{x}^{-a}}+{{x}^{c}}.{{x}^{-a}}}+\frac{1}{{{x}^{b}}.{{x}^{-b}}+{{x}^{a}}.{{x}^{-b}}+{{x}^{c}}.{{x}^{-b}}}+\frac{1}{{{x}^{c}}.{{x}^{-c}}+{{x}^{a}}.{{x}^{-c}}+{{x}^{b}}.{{x}^{-c}}} $

$ =\frac{1}{{{x}^{-a}}\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{1}{{{x}^{-b}}\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{1}{{{x}^{-c}}\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)} $

$=\frac{{{x}^{a}}}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{{{x}^{b}}}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{{{x}^{c}}}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)} $ $ =\frac{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}=1 $

15. Represent $\sqrt{3}$ on number line.

Ans: Consider a number line $\text{OD}$ such that the construction to form two triangles is done as shown below.

(Image will be uploaded soon)

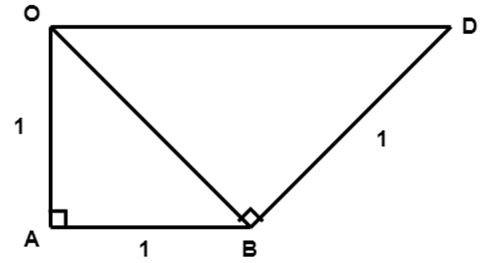
Take $OA=AB=1$ unit.

And $\angle A=90{}^\circ $

In $\Delta OAB$, by using the Pythagorean theorem we get,

$O{{B}^{2}}={{1}^{2}}+{{1}^{2}}$

$O{{B}^{2}}=2 $

$ OB=\sqrt{2}$ 

Now from triangle $\text{ }\!\!\Delta\!\!\text{ OBD}$, using the Pythagorean theorem we get,

$O{{D}^{2}}=O{{B}^{2}}+B{{D}^{2}} $

$ O{{D}^{2}}={{\left( \sqrt{2} \right)}^{2}}+{{\left( 1 \right)}^{1}} $

$O{{D}^{2}}=2+1=3 $

$OD=\sqrt{3} $

Now, if the point $\text{O}$ is $0$ units then the point $\text{D}$ represents $\sqrt{3}$units.

16. Simplify ${{\left( 3\sqrt{2}+2\sqrt{3} \right)}^{2}}{{\left( 3\sqrt{2}-2\sqrt{3} \right)}^{2}}$.

Ans: We are given the expression as,

${{\left( 3\sqrt{2}+2\sqrt{3} \right)}^{2}}{{\left( 3\sqrt{2}-2\sqrt{3} \right)}^{2}}$

Now, by regrouping the terms in the above expression we have,

$ =\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right) $

$ =\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right)\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right) $

$=\left[ {{\left( 3\sqrt{2} \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}} \right]\left[ {{\left( 3\sqrt{2} \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}} \right] $

$ =\left[ 9\times 2-4\times 3 \right]\left[ 9\times 2-4\times 3 \right] $

$ =\left[ 18-12 \right]\left[ 18-12 \right] $ 

$=6\times 6=36 $

17. Express $2.\overline{4178}$ in the form $\frac{p}{q}$.

Ans: Let $\frac{p}{q}=2.\overline{4178}$

$\frac{p}{q}=2.4178178178$

Multiply by 10

$10\frac{p}{q}=24.178178$

Multiply by 1000

$10000\frac{p}{q}=1000\times 24.178178 $ 

$1000\frac{p}{q}-\frac{p}{q}=24178.178178-14.178178 $

$9999\frac{p}{q}=24154 $

$\frac{p}{q}=\frac{24154}{9999} $

18. Simplify ${{\left( 27 \right)}^{-\frac{2}{3}}}\div {{9}^{\frac{1}{2}}}{{.3}^{-\frac{3}{2}}}$.

Ans: ${{\left( 27 \right)}^{-\frac{2}{3}}}\div {{9}^{\frac{1}{2}}}{{.3}^{-\frac{3}{2}}}$

$ =\frac{{{\left( 3\times 3\times 3 \right)}^{-\frac{2}{3}}}\times {{3}^{\frac{3}{2}}}}{{{\left( 3\times 3 \right)}^{\frac{1}{2}}}}\left[ {{a}^{-m}}=\frac{1}{{{a}^{m}}} \right] $

$ =\frac{{{\left( {{3}^{3}} \right)}^{-\frac{2}{3}}}\times {{3}^{\frac{3}{2}}}}{{{\left( {{3}^{2}} \right)}^{\frac{1}{2}}}} $

$=\frac{{{3}^{\frac{3}{2}-2}}}{3}=\frac{{{3}^{-\frac{1}{3}}}}{3} $

$=\frac{1}{{{3}^{\frac{4}{3}}}}=\frac{1}{\sqrt[3]{81}} $

19. Find three rational numbers between $2.\overline{2}$ and $2.\overline{3}.$

Ans: The irrational numbers are the numbers that do not end after the decimal point nor repeat its numbers in a sequence. 

Representing the given numbers in decimal form we have,

$ 2.\overline{2}=2.222222222...... $

$ 2.\overline{3}=2.333333333....... $ 

So any numbers between these two numbers that do not end nor repeat in any sequence gives the required irrational numbers.

Three rational numbers between $2.\overline{2}$ and $2.\overline{3}$ are $2.222341365....$, $2.28945187364....$ and $2.2321453269....$

20. Give an example of two irrational numbers whose

i. Sum is a rational number

Ans: The required two irrational numbers are $2+\sqrt{2}$ and $2-\sqrt{2}$

Sum $2+\sqrt{2}+2-\sqrt{2}=4$ which is a rational number.

ii. Product is a rational number

Ans: The required two irrational numbers are $3\sqrt{2}$ and $6\sqrt{2}$

Product $3\sqrt{2}\times 6\sqrt{2}=18\times 2=36$ which is rational.

iii. Quotient is a rational number

Ans: The required two irrational numbers are $2\sqrt{125}$ and $3\sqrt{5}$

Quotient $\frac{2\sqrt{125}}{3\sqrt{5}}=\frac{2}{3}\sqrt{\frac{125}{5}}=\frac{2}{3}\times 5=\frac{10}{3}$

21. If $\sqrt{2}=1.414$ and $\sqrt{3}=1.732$, find the value of $\frac{5}{\sqrt{2}+\sqrt{3}}$.

Ans: First let us take the given expression and by rationalizing the denominator we get,

$\frac{5}{\sqrt{2}+\sqrt{3}}\times \frac{\sqrt{2}-\sqrt{3}}{\sqrt{2}-\sqrt{3}}$ 

$\frac{5\left( \sqrt{2}-\sqrt{3} \right)}{{{\left( \sqrt{2} \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}} $

$=\frac{5\left( \sqrt{2}-\sqrt{3} \right)}{2-3} $

Now, substituting the required values of irrational numbers we get,

$=-5\left[ 1.414-1.732 \right] $

$  =-5\times -0.318 $

$  =1.59 $ 

22. Visualize 2.4646 on the number line using successive magnification.

Ans: 

(Image will be uploaded soon)

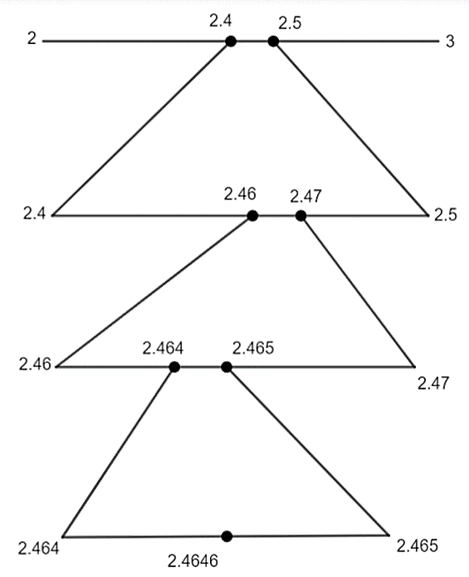
23. Rationalizing the denominator of $\frac{1}{4+2\sqrt{3}}$.

Ans: First let us take the given expression and rationalizing the denominator by multiplying the numerator and denominator with its conjugate we get,

$\frac{1}{4+2\sqrt{3}}=\frac{1}{4+2\sqrt{3}}\times \frac{4-2\sqrt{3}}{4+2\sqrt{3}} $

$ =\frac{4-2\sqrt{3}}{{{\left( 4 \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}}} $

$=\frac{4-2\sqrt{3}}{16-{{\left( 2\sqrt{3} \right)}^{2}}} $ 

$=\frac{4-2\sqrt{3}}{16-12} $ 

$  =\frac{4-2\sqrt{3}}{4} $

$ =\frac{2\left( 2-\sqrt{3} \right)}{4} $

$ =\frac{2-\sqrt{3}}{2} $

24. Visualize the representation of $5.3\overline{7}$ on the number line up to 3 decimal places.

Ans: The representation of $5.3\overline{7}$ on the number line is given below:

(Image will be uploaded soon)

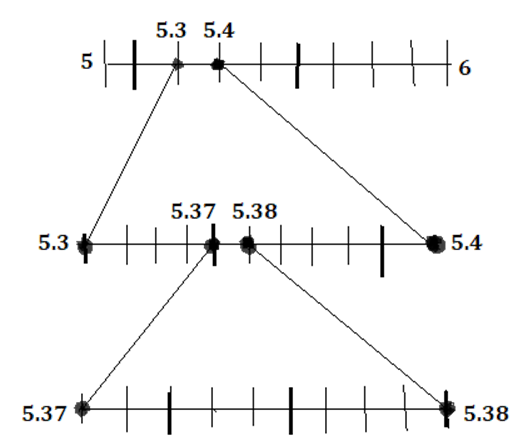
25. Show that \[5\sqrt{2}\] is not a rational number.

Ans: Let us assume that \[5\sqrt{2}\] is a rational number.

Take \[x=5\sqrt{2}\] , with \[x\]being rational as well.

Now, 

\[x=5\sqrt{2}\]

\[\Rightarrow \frac{x}{5}=\sqrt{2}\]

Let us compare the terms in LHS and RHS.

In LHS, we have\[\frac{x}{5}\] , with \[x\] and $5$ being rational numbers (Here \[x\] is rational, based on our assumption). So \[\frac{x}{5}\] is a rational number.

In RHS, we have$\sqrt{2}$, which is not a rational number, but an irrational number.

This is a contradiction, i.e. $LHS\ne RHS$.

So, we can conclude that  \[5\sqrt{2}\] is not a rational number.

26. Simplify \[3\sqrt[3]{250}+7\sqrt[3]{16}-4\sqrt[3]{54}\].

Ans: Let us first find the cube roots of given numbers to their simplest forms by using the prime factorization then we get,

\[3\sqrt[3]{250}+7\sqrt[3]{16}-4\sqrt[3]{54}=3\sqrt[3]{5\times 5\times 5\times 2}+7\sqrt[3]{2\times 2\times 2\times 2}-4\sqrt[3]{3\times 3\times 3\times 2}\]

\[=\left( 3\times 5\sqrt[3]{2} \right)+\left( 7\times 2\sqrt[3]{2} \right)-\left( 4\times 3\sqrt[3]{2} \right)\]

\[=\left( 15\sqrt[3]{2} \right)+\left( 14\sqrt[3]{2} \right)-\left( 12\sqrt[3]{2} \right)\]

\[=\left( 15+14-12 \right)\sqrt[3]{2}\]

\[=17\sqrt[3]{2}\]

Thus, we get \[3\sqrt[3]{250}+7\sqrt[3]{16}-4\sqrt[3]{54}=17\sqrt[3]{2}\]

27. Simplify \[3\sqrt{48}-\frac{5}{2}\sqrt{\frac{1}{3}}+4\sqrt{3}\].

Ans: Let us first find the square roots of given numbers to their simplest forms by using the prime factorization then we get,

\[3\sqrt{48}-\frac{5}{2}\sqrt{\frac{1}{3}}+4\sqrt{3}=\left( 3\sqrt{2\times 2\times 2\times 2\times 3} \right)-\left[ \frac{5}{2}\left( \sqrt{\frac{1}{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \right) \right]+\left( 4\sqrt{3} \right)\]

\[=\left( 3\times 2\times 2\sqrt{3} \right)-\left[ \frac{5}{2}\left( \frac{\sqrt{3}}{3} \right) \right]+\left( 4\sqrt{3} \right)\]

\[=\left( 12\sqrt{3} \right)-\left( \frac{5\sqrt{3}}{6} \right)+\left( 4\sqrt{3} \right)\]

\[=\left( 12-\frac{5}{6}+4 \right)\sqrt{3}\]

\[=\left( \frac{72-5+24}{6} \right)\sqrt{3}\]

\[=\frac{91}{6}\sqrt{3}\]

Thus, we get \[3\sqrt{48}-\frac{5}{2}\sqrt{\frac{1}{3}}+4\sqrt{3}=\frac{91}{6}\sqrt{3}\]

28. If $\frac{1}{7}=0.\overline{142857}$. Find the value of $\frac{2}{7},\frac{3}{7},\frac{4}{7}$

Ans: It is given that – $\frac{1}{7}=0.\overline{142857}$

Now,

(i) $\frac{2}{7}=2\times \frac{1}{7}$

$=2\times 0.\overline{142857}$

$=0.\overline{285714}$

$\Rightarrow \frac{2}{7}=0.\overline{285714}$

(ii) $\frac{3}{7}=3\times \frac{1}{7}$

$=3\times 0.\overline{142857}$

$=0.\overline{428571}$

$\Rightarrow \frac{3}{7}=0.\overline{428571}$

(iii) $\frac{4}{7}=4\times \frac{1}{7}$

$=4\times 0.\overline{142857}$

$=0.\overline{571428}$

$\Rightarrow \frac{4}{7}=0.\overline{571428}$

29. Find $6$ rational numbers between $\frac{6}{5}$ and $\frac{7}{5}$

Ans: It is possible to divide the interval between $\frac{6}{5}$ and $\frac{7}{5}$ into $10$ equal parts.

Then we will have – $\frac{6}{5},\frac{6.1}{5},\frac{6.2}{5},\frac{6.3}{5},\frac{6.4}{5},\frac{6.5}{5},\frac{6.6}{5},\frac{6.7}{5},\frac{6.8}{5},\frac{6.9}{5},\frac{7}{5}$

i.e. $\frac{60}{50},\frac{61}{50},\frac{62}{50},\frac{63}{50},\frac{64}{50},\frac{65}{50},\frac{66}{50},\frac{67}{50},\frac{68}{50},\frac{69}{50},\frac{70}{50}$

From these fractions, it is possible to choose $6$ rational numbers between $\frac{6}{5}$ and $\frac{7}{5}$

Thus, $6$ rational numbers between $\frac{6}{5}$ and $\frac{7}{5}$ are $\frac{61}{50},\frac{62}{50},\frac{63}{50},\frac{64}{50},\frac{65}{50},\frac{66}{50}$

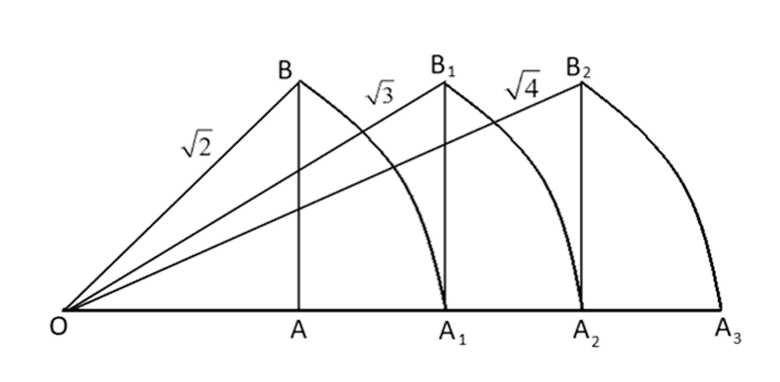
30. Show how $\sqrt{4}$ can be represented on the number line.

Ans: Take $AB=OA=1\text{ }unit$ on a number line.

Also, $\angle A={{90}^{\circ }}$

In $\vartriangle OAB$, apply Pythagoras Theorem,

$\therefore O{{A}^{2}}+A{{B}^{2}}=O{{B}^{2}}$

$\Rightarrow O{{B}^{2}}={{1}^{2}}+{{1}^{2}}$

$\Rightarrow O{{B}^{2}}=1+1$

$\Rightarrow O{{B}^{2}}=2$

$\Rightarrow OB=\sqrt{2}$

Now, draw $OB=O{{A}_{1}}=\sqrt{2}$

And, ${{A}_{1}}{{B}_{1}}=1\text{ unit}$ with$\angle {{A}_{1}}={{90}^{\circ }}$

In \[\vartriangle O{{A}_{1}}{{B}_{1}}\], apply Pythagoras Theorem,

$\therefore O{{A}_{1}}^{2}+{{A}_{1}}{{B}_{1}}^{2}=O{{B}_{1}}^{2}$

$\Rightarrow O{{B}_{1}}^{2}={{\left( \sqrt{2} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow O{{B}_{1}}^{2}=2+1$

$\Rightarrow O{{B}_{1}}^{2}=3$

$\Rightarrow O{{B}_{1}}=\sqrt{3}$

Now, draw $O{{B}_{1}}=O{{A}_{2}}=\sqrt{3}$

And, \[{{A}_{2}}{{B}_{2}}=1\text{ unit}\] with$\angle {{A}_{2}}={{90}^{\circ }}$

In \[\vartriangle O{{A}_{2}}{{B}_{2}}\], apply Pythagoras Theorem,

$\therefore O{{A}_{2}}^{2}+{{A}_{2}}{{B}_{2}}^{2}=O{{B}_{2}}^{2}$

$\Rightarrow O{{B}_{2}}^{2}={{\left( \sqrt{3} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow O{{B}_{2}}^{2}=3+1$

$\Rightarrow O{{B}_{2}}^{2}=4$

$\Rightarrow O{{B}_{2}}=\sqrt{4}$

Now, draw $O{{B}_{2}}=O{{A}_{3}}=\sqrt{4}$

Thus line segment $O{{A}_{3}}=\sqrt{4}$

(Image will be uploaded soon)

Short Answer Questions (4 Marks)

1. Write the following in decimal form and say what kind of decimal expansion each has:

i. $\frac{36}{100}$

Ans: Performing long division of $36$ by $100$

$\begin{matrix} &{0.36}\\ 100&{\overline{)\;36\quad}}\\ &\underline{-0\quad}\\ &360\\ &\underline{-300\quad}\\ &\;\;600\\ &\underline{-600}\\ &\underline{\quad 0 \;\;} \end{matrix}$

Thus, $\frac{36}{100}=0.36$ - this is a terminating decimal.

ii. $\frac{1}{11}$

Ans: Performing long division of $1$ by $11$

$\begin{matrix} {} & 0.0909.. \\ 11 & \overline{)\text{ }1\text{ }} \\ {} & \underline{-0} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-99} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-99} \\ {} & 1 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $1$ continuously.

Thus, $\frac{1}{11}=0.09090...$ i.e. $\frac{1}{11}=0.\overline{09}$, this is a non-terminating, but recurring decimal.

iii. $4\frac{1}{8}$

Ans: First convert the mixed fraction into an improper fraction –

$4\frac{1}{8}=\frac{(4\times 8)+1}{8}=\frac{33}{8}$

Performing long division of $33$ by $8$

$\begin{matrix} {} & 4.125 \\ 8 & \overline{\left){\text{ }33\text{ }}\right.} \\ {} & \underline{-32} \\ {} & 10 \\ {} & \underline{-8} \\ {} & 20 \\ {} & \underline{-16} \\ {} & 40 \\ {} & \underline{-40} \\ {} & 0 \\ \end{matrix}$

Thus, $4\frac{1}{8}=4.125$ - this is a terminating decimal.

iv. $\frac{3}{13}$

Ans: Performing long division of $3$ by $13$

$\begin{matrix} {} & 0.230769.. \\ 13 & \overline{\left){\text{ }3\text{ }}\right.} \\ {} & \underline{-0} \\ {} & 30 \\ {} & \underline{-26} \\ {} & 40 \\ {} & \underline{-39} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-91} \\ {} & 90 \\ {} & \underline{-78} \\ {} & 120 \\ {} & \underline{-117} \\ {} & 3 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $3$ periodically, after every six divisions.

Thus, $\frac{3}{13}=0.230769...$ i.e. \[\frac{3}{13}=0.\overline{230769}\], this is a non-terminating, but recurring decimal.

v. $\frac{2}{11}$

Ans: Performing long division of $2$ by $11$

$\begin{matrix} {} & 0.1818.. \\ 11 & \overline{)\text{ 2 }} \\ {} & \underline{-0} \\ {} & 20 \\ {} & \underline{-11} \\ {} & 90 \\ {} & \underline{-88} \\ {} & 20 \\ {} & \underline{-11} \\ {} & 90 \\ {} & \underline{-88} \\ {} & 2 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $2$followed by $9$ alternatively.

Thus, $\frac{2}{11}=0.181818...$ i.e. $\frac{2}{11}=0.\overline{18}$this is a non-terminating, but recurring decimal.

vi. $\frac{329}{400}$

Ans: Performing long division of $33$ by $8$

$\begin{matrix} {} & 0.8225 \\ 400 & \overline{)\text{ 329 }} \\ {} & \underline{-0} \\ {} & 3290 \\ {} & \underline{-3200} \\ {} & 900 \\ {} & \underline{-800} \\ {} & 1000 \\ {} & \underline{-800} \\ {} & 2000 \\ {} & \underline{-2000} \\ {} & 0 \\ \end{matrix}$

Thus, $\frac{329}{400}=0.8225$ - this is a terminating decimal.

2. Classify the following as rational or irrational:

i. $\sqrt{23}$

Ans: It is known that the root of $23$ will produce a non-terminating and non-recurring decimal number (it is not a perfect square value), also it cannot be represented as a fraction. Thus we can say that $\sqrt{23}$ is an irrational number.

ii. $\sqrt{225}$

Ans: It is known that $\sqrt{225}=15$, which is an integer.

Thus $\sqrt{225}$ is a rational number.

iii. $0.3796$

Ans: Here, $0.3796$ is a terminating decimal number, and also it can be expressed as a fraction.

i.e. $0.3796=\frac{3796}{10000}=\frac{949}{2500}$

Thus $0.3796$ is a rational number.

iv. $7.478478...$

Ans: Here, $7.478478...$ is a non-terminating, but recurring decimal number, and also it can be expressed as a fraction.

i.e. $7.478478...=7.\overline{487}$

Converting it into fraction 

If $x=7.478478...\text{          (1)}$

Then $1000x=7478.478478...\text{          (2)}$

Subtract equations $(2)-(1)$

$ 1000x=7478.478478... $

$  \underline{-\text{      }x=\text{      }7.478478...} $

$ \text{  }999x=7471 $

Now, $999x=7471$

$\Rightarrow x=\frac{7471}{999}$

i.e. $7.\overline{478}=\frac{7471}{999}$

Thus $7.478478...$ is a rational number.

v. $1.101001000100001...$

Ans: Here,  $1.101001000100001...$ is a non-terminating and non-recurring decimal number and also it cannot be represented as a fraction. Thus we can say that $1.101001000100001...$ is an irrational number.

3. Rationalize the denominator of the following:

(i) $\frac{1}{\sqrt{7}}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{7}}$ by $\sqrt{7}$

$\frac{1}{\sqrt{7}}\times \frac{\sqrt{7}}{\sqrt{7}}=\frac{\sqrt{7}}{7}$

Rationalizing the denominator of  $\frac{1}{\sqrt{7}}$ produces $\frac{\sqrt{7}}{7}$.

ii. $\frac{1}{\sqrt{7}-\sqrt{6}}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{7}-\sqrt{6}}$ by $\sqrt{7}+\sqrt{6}$

$\frac{1}{\sqrt{7}-\sqrt{6}}\times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}=\frac{\sqrt{7}+\sqrt{6}}{\left( \sqrt{7}-\sqrt{6} \right)\left( \sqrt{7}+\sqrt{6} \right)}$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\frac{\sqrt{7}+\sqrt{6}}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( \sqrt{6} \right)}^{2}}}$

$=\frac{\sqrt{7}+\sqrt{6}}{7-6}$

$=\frac{\sqrt{7}+\sqrt{6}}{1}$

$\Rightarrow \frac{1}{\sqrt{7}-\sqrt{6}}=\sqrt{7}+\sqrt{6}$

Rationalizing the denominator of  $\frac{1}{\sqrt{7}-\sqrt{6}}$ produces $\sqrt{7}+\sqrt{6}$.

iii. $\frac{1}{\sqrt{5}+\sqrt{2}}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{5}+\sqrt{2}}$ by $\sqrt{5}-\sqrt{2}$

$\frac{1}{\sqrt{5}+\sqrt{2}}\times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}=\frac{\sqrt{5}-\sqrt{2}}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)}$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\frac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}$

$=\frac{\sqrt{5}-\sqrt{2}}{5-2}$

$=\frac{\sqrt{5}-\sqrt{2}}{3}$

$\Rightarrow \frac{1}{\sqrt{5}+\sqrt{2}}=\frac{\sqrt{5}-\sqrt{2}}{3}$

Rationalizing the denominator of  $\frac{1}{\sqrt{5}+\sqrt{2}}$ produces $\frac{\sqrt{5}-\sqrt{2}}{3}$.

iv. $\frac{1}{\sqrt{7}-2}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{7}-2}$ by $\sqrt{7}+2$

$\frac{1}{\sqrt{7}-2}\times \frac{\sqrt{7}+2}{\sqrt{7}+2}=\frac{\sqrt{7}+2}{\left( \sqrt{7}-2 \right)\left( \sqrt{7}+2 \right)}$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\frac{\sqrt{7}+2}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( 2 \right)}^{2}}}$

$=\frac{\sqrt{7}+2}{7-4}$

$=\frac{\sqrt{7}+2}{3}$

$\Rightarrow \frac{1}{\sqrt{7}+2}=\frac{\sqrt{7}+2}{3}$

Rationalizing the denominator of  $\frac{1}{\sqrt{7}-2}$ produces $\frac{\sqrt{7}+2}{3}$.

Long Answer Questions (5 Marks)

1. Write the following in decimal form and say what kind of decimal expansion each has:

i. $\frac{36}{100}$

Ans: Performing long division of $36$ by $100$

$\begin{matrix} &{0.36}\\ 100&{\overline{)\;36\quad}}\\ &\underline{-0\quad}\\ &360\\ &\underline{-300\quad}\\ &\;\;600\\ &\underline{-600}\\ &\underline{\quad 0 \;\;} \end{matrix}$

Thus, $\frac{36}{100}=0.36$ - this is a terminating decimal.

ii. $\frac{1}{11}$

Ans: Performing long division of $1$ by $11$

$\begin{matrix} {} & 0.0909.. \\ 11 & \overline{)\text{ }1\text{ }} \\ {} & \underline{-0} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-99} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-99} \\ {} & 1 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $1$ continuously.

Thus, $\frac{1}{11}=0.09090...$ i.e. $\frac{1}{11}=0.\overline{09}$, this is a non-terminating, but recurring decimal.

iii. $4\frac{1}{8}$

Ans: First convert the mixed fraction into an improper fraction –

$4\frac{1}{8}=\frac{(4\times 8)+1}{8}=\frac{33}{8}$

Performing long division of $33$ by $8$

$\begin{matrix} {} & 4.125 \\ 8 & \overline{\left){\text{ }33\text{ }}\right.} \\ {} & \underline{-32} \\ {} & 10 \\ {} & \underline{-8} \\ {} & 20 \\ {} & \underline{-16} \\ {} & 40 \\ {} & \underline{-40} \\ {} & 0 \\ \end{matrix}$

Thus, $4\frac{1}{8}=4.125$ - this is a terminating decimal.

iv. $\frac{3}{13}$

Ans: Performing long division of $3$ by $13$

$\begin{matrix} {} & 0.230769.. \\ 13 & \overline{\left){\text{ }3\text{ }}\right.} \\ {} & \underline{-0} \\ {} & 30 \\ {} & \underline{-26} \\ {} & 40 \\ {} & \underline{-39} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-91} \\ {} & 90 \\ {} & \underline{-78} \\ {} & 120 \\ {} & \underline{-117} \\ {} & 3 \\ \end{matrix}$

It can be seen that performing further divisions will produce a reminder of $3$ periodically, after every six divisions.

Thus, $\frac{3}{13}=0.230769...$ i.e. \[\frac{3}{13}=0.\overline{230769}\], this is a non-terminating, but recurring decimal.

v. $\frac{2}{11}$

Ans: Performing long division of $2$ by $11$

$\begin{matrix} {} & 0.1818.. \\ 11 & \overline{)\text{ 2 }} \\ {} & \underline{-0} \\ {} & 20 \\ {} & \underline{-11} \\ {} & 90 \\ {} & \underline{-88} \\ {} & 20 \\ {} & \underline{-11} \\ {} & 90 \\ {} & \underline{-88} \\ {} & 2 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $2$followed by $9$ alternatively.

Thus, $\frac{2}{11}=0.181818...$ i.e. $\frac{2}{11}=0.\overline{18}$this is a non-terminating, but recurring decimal.

vi. $\frac{329}{400}$

Ans: Performing long division of $33$ by $8$

$\begin{matrix} {} & 0.8225 \\ 400 & \overline{)\text{ 329 }} \\ {} & \underline{-0} \\ {} & 3290 \\ {} & \underline{-3200} \\ {} & 900 \\ {} & \underline{-800} \\ {} & 1000 \\ {} & \underline{-800} \\ {} & 2000 \\ {} & \underline{-2000} \\ {} & 0 \\ \end{matrix}$

Thus, $\frac{329}{400}=s0.8225$ - this is a terminating decimal.

4. If $\sqrt{5}=2.236$ and $\sqrt{3}=1.732$. Find the value of $\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}$.

Ans: It is given that – 

$\sqrt{5}=2.236$

$\sqrt{3}=1.732$

Now, $\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}$

Taking LCM

$\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}=\left[ \frac{2}{\left( \sqrt{5}+\sqrt{3} \right)}\times \frac{\left( \sqrt{5}-\sqrt{3} \right)}{\left( \sqrt{5}-\sqrt{3} \right)} \right]+\left[ \frac{7}{\left( \sqrt{5}-\sqrt{3} \right)}\times \frac{\left( \sqrt{5}+\sqrt{3} \right)}{\left( \sqrt{5}+\sqrt{3} \right)} \right]$

$=\left[ \frac{2\left( \sqrt{5}-\sqrt{3} \right)}{\left( \sqrt{5}+\sqrt{3} \right)\left( \sqrt{5}-\sqrt{3} \right)} \right]+\left[ \frac{7\left( \sqrt{5}+\sqrt{3} \right)}{\left( \sqrt{5}-\sqrt{3} \right)\left( \sqrt{5}+\sqrt{3} \right)} \right]$

$=\left[ \frac{\left( 2\sqrt{5}-2\sqrt{3} \right)+\left( 7\sqrt{5}+7\sqrt{3} \right)}{\left( \sqrt{5}+\sqrt{3} \right)\left( \sqrt{5}-\sqrt{3} \right)} \right]$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\left[ \frac{2\sqrt{5}-2\sqrt{3}+7\sqrt{5}+7\sqrt{3}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}} \right]$

$=\left[ \frac{(2+7)\sqrt{5}+(7-2)\sqrt{3}}{5-3} \right]$

$=\left[ \frac{9\sqrt{5}+5\sqrt{3}}{2} \right]$

Since, $\sqrt{5}=2.236$ and $\sqrt{3}=1.732$

$=\left[ \frac{(9\times 2.236)+(5\times 1.732)}{2} \right]$

$=\left[ \frac{20.124+8.66}{2} \right]$

$=\left[ \frac{28.784}{2} \right]$

$=14.392$

Thus, $\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}=14.392$

5. Find the value of $\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}$, if $\sqrt{5}=2.236$ and $\sqrt{2}=1.414$.

Ans: It is given that – 

• $\sqrt{5}=2.236$

• $\sqrt{2}=1.414$

Now, $\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}$

Taking LCM

$\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}=\left[ \frac{3}{\left( \sqrt{5}+\sqrt{2} \right)}\times \frac{\left( \sqrt{5}-\sqrt{2} \right)}{\left( \sqrt{5}-\sqrt{2} \right)} \right]+\left[ \frac{7}{\left( \sqrt{5}-\sqrt{2} \right)}\times \frac{\left( \sqrt{5}+\sqrt{2} \right)}{\left( \sqrt{5}+\sqrt{2} \right)} \right]$

$=\left[ \frac{3\left( \sqrt{5}-\sqrt{2} \right)}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)} \right]+\left[ \frac{7\left( \sqrt{5}+\sqrt{2} \right)}{\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)} \right]$

$=\left[ \frac{\left( 3\sqrt{5}-3\sqrt{2} \right)+\left( 7\sqrt{5}+7\sqrt{2} \right)}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)} \right]$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\left[ \frac{3\sqrt{5}-3\sqrt{2}+7\sqrt{5}+7\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}} \right]$

$=\left[ \frac{(3+7)\sqrt{5}+(7-3)\sqrt{2}}{5-2} \right]$

$=\left[ \frac{10\sqrt{5}+4\sqrt{2}}{3} \right]$

Since, $\sqrt{5}=2.236$ and $\sqrt{2}=1.414$

$=\left[ \frac{(10\times 2.236)+(4\times 1.414)}{3} \right]$

$=\left[ \frac{22.36+5.656}{3} \right]$

$=\left[ \frac{28.016}{3} \right]$

Thus, $\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}=\frac{28.016}{3}$

6. Simplify $\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}$

Ans: $\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}$

Taking LCM

\[\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}=\left[ \frac{2+\sqrt{5}}{2-\sqrt{5}}\times \frac{\left( 2+\sqrt{5} \right)}{\left( 2+\sqrt{5} \right)} \right]+\left[ \frac{2-\sqrt{5}}{2+\sqrt{5}}\times \frac{\left( 2-\sqrt{5} \right)}{\left( 2-\sqrt{5} \right)} \right]\]

\[=\left[ \frac{\left( 2+\sqrt{5} \right)\left( 2+\sqrt{5} \right)}{\left( 2-\sqrt{5} \right)\left( 2+\sqrt{5} \right)} \right]+\left[ \frac{\left( 2-\sqrt{5} \right)\left( 2-\sqrt{5} \right)}{\left( 2+\sqrt{5} \right)\left( 2-\sqrt{5} \right)} \right]\]

\[=\left[ \frac{{{\left( 2+\sqrt{5} \right)}^{2}}+{{\left( 2-\sqrt{5} \right)}^{2}}}{\left( 2-\sqrt{5} \right)\left( 2+\sqrt{5} \right)} \right]\]

Using the identities –

• \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

• \[{{(a+b)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]

• \[{{(a-b)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\]

\[=\left[ \frac{\left( {{\left( 2 \right)}^{2}}+{{\left( \sqrt{5} \right)}^{2}}+\left( 2\times 2\times \sqrt{5} \right) \right)+\left( {{\left( 2 \right)}^{2}}+{{\left( \sqrt{5} \right)}^{2}}-\left( 2\times 2\times \sqrt{5} \right) \right)}{{{\left( 2 \right)}^{2}}-{{\left( \sqrt{5} \right)}^{2}}} \right]\]

\[=\left[ \frac{\left( 4+5+\left( 4\sqrt{5} \right) \right)+\left( 4+5-\left( 4\sqrt{5} \right) \right)}{4-5} \right]\]

$=\left[ \frac{9+9}{-1} \right]$

$=\left[ \frac{18}{-1} \right]$

$=-18$

Thus, $\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}=\left( -18 \right)$

7. Find a and b, if $\frac{3-\sqrt{6}}{3+2\sqrt{6}}=a\sqrt{6}-b$

Ans: $\frac{3-\sqrt{6}}{3+2\sqrt{6}}=a\sqrt{6}-b$

Here, 

$LHS=\frac{3-\sqrt{6}}{3+2\sqrt{6}}$

$RHS=a\sqrt{6}-b$

Start by rationalizing the denominator in LHS

In order to rationalize the denominator, we multiply and divide $\frac{3-\sqrt{6}}{3+2\sqrt{6}}$ by $3+2\sqrt{6}$

$\frac{3-\sqrt{6}}{3+2\sqrt{6}}\times \frac{3-2\sqrt{6}}{3-2\sqrt{6}}=\frac{\left( 3-\sqrt{6} \right)\left( 3-2\sqrt{6} \right)}{\left( 3+2\sqrt{6} \right)\left( 3-2\sqrt{6} \right)}$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\frac{\left( 3\times 3 \right)-\left( 3\times 2\sqrt{6} \right)-\left( \sqrt{6}\times 3 \right)+\left( \sqrt{6}\times 2\sqrt{6} \right)}{{{\left( 3 \right)}^{2}}-{{\left( 2\sqrt{6} \right)}^{2}}}$

$=\frac{\left( 9 \right)-\left( 6\sqrt{6} \right)-\left( 3\sqrt{6} \right)+\left( 12 \right)}{9-24}$

$=\frac{\left( 21 \right)-\left( 9\sqrt{6} \right)}{-15}$

$=\frac{\left( 21 \right)}{-15}-\frac{\left( 9\sqrt{6} \right)}{-15}$

They are all divisible by $3$

$=-\frac{7}{5}+\frac{\left( 3\sqrt{6} \right)}{5}$

Thus, $LHS=\frac{3}{5}\sqrt{6}-\frac{7}{5}$

Comparing with RHS, we get – 

$RHS=a\sqrt{6}-b$

Thus, 

$a=\frac{3}{5}$

$b=\frac{7}{5}$

Important Topics Covered in Class 9 Maths Chapter 1 Number System

• Introduction to number system

• Irrational Number

• Real Number and Their Decimal Expansion

• Representation of Real Number on Number Line

• Operations on Real Number

• Laws of Exponents for Real Number

Important Questions for Class 9 Maths Chapter 1 - Free PDF Download

Class 9 is like beginning to your academics career, which is right before board 10th. Thus students need to be very serious regarding their studies during preparation. No matter what we learn in class 9, it is important to clarify your concepts better. Hence, clearing Number System concepts will help students further apply in electronics physics and higher maths. Thus it is better to build a good base in mathematics with these Important Questions Maths Class 9 Chapter 1.

Vedantu provides a free PDF to download for Class 9 Chapter 1 Important Questions such that students can prepare well according to the CBSE syllabus. CBSE is strict to its pattern and follows the same throughout the question paper set. Students need to understand these guidelines and find solutions with a proper explanation. This free PDF online will surely help students master their concepts and build a Number System base. This PDF covers all the important concepts in the form of question example to learn how to implement them during exams. Thus PDF proves to be magical for those who are weak in mathematics as they also get solutions to the concepts covered in the back exercise.

Number System Class 9 Important Questions

Before you begin practising Class 9 Chapter 1 Maths Important Questions, you need to know the different topics and subtopics to cover in the chapter. Chapter 1 of Mathematics Class 9 covers a total of 6 exercises with a small introduction of the number system, number lines, defining real numbers, natural numbers, whole numbers, rational, and irrational numbers. Also, students become familiar with the concepts of addition, subtraction, division, and multiplication of the real numbers. The last topic in the chapter will be covering the law of exponents in the real numbers.

Below are the mentioned section-wise topics and concepts that a student to prepare through important questions.

Exercise 1.1

Under exercise 1.1, students will become familiar with the basic understanding of rational and irrational numbers. There is also a revision on whole numbers, real number, integers, and natural numbers and definition. They will even know how to represent a number in the form of p/q, where q is not equal to 0.

Exercise 1.2

Further moving to in-depth study about rational and irrational numbers, there are questions on justification with true and false. Also, students become familiar with the concept of representing rational and irrational numbers on the number line. A new concept of constructing a square root spiral comes in exercise 1.2.

Exercise 1.3

Here the student will know how to represent fractions into decimal form and find if it is terminating or non-terminating. Thus the concepts of terminating and non-terminating fractions will further help to identify it is a rational or irrational number.

Exercise 1.4

Now comes the basic calculations of different rational and irrational numbers. It includes addition, multiplication, subtraction, and division of the rational and irrational numbers. Questions will be based on such concepts, and thus you have to simplify the statement accordingly. Also, students become familiar with the concept of rationalising.

Exercise 1.5

Here students will learn to solve questions based with a number having power in fractional form. Also, it might cover the basic addition and subtraction of powers for in-depth conceptual and extra knowledge.

These are the six exercises which will be covered under Chapter 1 Maths Class 9 Important Questions. Hence, students can prepare questions according to the concepts discussed above.

Chapter 1 Maths Class 9 Important Questions

According to the syllabus mentioned above exercise-wise, below are some important questions covered to let students prepare well for important questions for class 9 maths number system. These exercise-wise solutions will let students master each concept in detail. Below are some of the questions that are usually picked to set question paper as prepared by CBSE.

Exercise 1.1

• State if zero is a rational number. Justify your statement by representing it in p/q where q is not equal to 0 and p and q are both integers.

• Find 5 different rational numbers between 5 and 6. Mention each step in detail.

• Find out 5 different rational numbers between 12/11 and 10/11.

Exercise 1.2

• Justify your statement for the following terms stating true or false.

1. Rational numbers are real.

2. A number line having representation in the form of √m has m as a natural number.

3. A real number is always an irrational number.

• Check if true or false. Square roots of all positive numbers will be irrational. Explain your answer statement with the help of an example.

• Try to represent √5 on the number line.

Exercise 1.3

• Represent the following in the form of decimal expansion:

(i) 36/100  (ii) 1/11  (iii) 4⅛  (iv) 3/13  (v) 2/11  (vi) 329/400

• Turn 2/7, 13/7, 4/7, 5/7, 6/7

into decimal expansions without actually doing any long division calculations. Here 1/7= 0.142857.

• Express the following as fractional form p/q where q is not 0.

(i) \[0.\overline{6}\]

(ii) \[0.4 \overline{7}\]

(iii) \[0. \overline{001}\]

Exercise 1.4

• State if the numbers are rational or irrational.

(i) \[2 - \sqrt{5}\]  (ii)  \[(3 + \sqrt{23}) - \sqrt{23}\]  (iii) \[\frac{2\sqrt{7}}{7\sqrt{7}}\]  (iv) \[\frac{1}{\sqrt{2}}\]  (v) \[2 \pi\]

• Simplify the following terms:

(i) \[(3 + \sqrt{3}) ( 2 + \sqrt{2})\] (ii) \[(3 + \sqrt{3}) (3 + \sqrt{3})\]

(iii) \[(\sqrt{5} + \sqrt{2})^{2}\] (iv)\[(\sqrt{5} - \sqrt{2})(\sqrt{5} + \sqrt{2})\]

• Rationalise the following terms with their denominators:

(i) \[\frac{1}{7}\] (ii) \[\frac{1}{\sqrt{7} - \sqrt{6}}\] (iii) \[\frac{1}{\sqrt{5} + \sqrt{2}}\] (iv) \[\frac{1}{\sqrt{7} - 2}\]

Exercise 1.5

• Simplify:

(i) \[64^{1}{2}\] (ii) \[32^{1}{5}\] (iii) \[125^{1}{3}\]

Class 9 Maths Chapter 1 Extra Questions

1. Find three rational numbers between $\frac{1}{3}$ and $\frac{1}{2}$. 

2. Express 0.4323232 in the form of  $\frac{a}{b}$ where a and b are integers and b 0.

3. Simplify and find the value of $(729)^{1/6}$.

4. Rationalise the denominator 19 + 5 + 6.

5. Find 6 rational numbers between 4 and 6.

6. Simplify $\sqrt[3]{2}$+$\sqrt[4]{3}$ and $\sqrt{5}+\sqrt{2}$.

7. Locate $\sqrt{5}$ on the number line.

8. Visualise the representation of 4.26 on the number line upto 3 decimal places.

9. Is 2 - 5  a rational number or irrational number?

10. Convert 0.45 into rational numbers.

Benefits of Important Questions for Class 9 Maths Number Systems

Number System Class 9 Important Questions PDF is prepared by Vedantu experts and is free of cost. Students can also schedule additional problems to prepare in-depth to clarify their concepts. These questions turn to be magical for those weak in mathematics or do not show interest in it. The questions are prepared precisely accordingly to CBSE guidelines for their question paper pattern such that students need not search them anywhere else.

Below are the mentioned reasons why students should refer to the Important Question of Maths Class 9 Chapter 1:

• Students are free to access these important questions PDF. They need not pay for any study material on Vedantu website.

• These Number System Class 9 Important Questions are helpful during exams and help students clarify their concepts of homework questions.

• These crucial questions are available in PDF format, which can be easily downloaded through the website. Thus students need not unnecessarily waste their precious time in finding solutions to problems.

• Students can print these PDF questions and solutions, which reduces the stress of preparing through soft copies.

• All the questions and solutions to the questions are prepared according to CBSE guidelines. Thus it will help students to know question paper pattern.

There is a total of 100 marks for the Class 9 Mathematics paper where 20 marks are for internal assessment, and rest 80 is for the written exam. The marks weightage for Chapter 1 Maths Class 9 is 8 out of 80. Rest 72 marks are for rest of the syllabus of Class 9 Mathematics.

Conclusion

There are a total of 26 sums to be solved according to NCERT book for Chapter 1 Of Class 9 Maths in its six exercises. However, there are other Class 9 Maths Chapter 1 Important Questions prepared by the experts and solutions to each of them provided. Thus, students can build a good base in mathematics through this PDF of important questions available with Vedantu for free. According to exercise-wise, some questions describe different questions and situations that students generally encounter while sitting in the exam. Thus, students need to struggle to find essential concepts in the chapter and solutions to each of them.

Important Study Materials for Class 9 Maths Chapter 1 Number Systems

CBSE Class 9 Maths Chapter-wise Important Questions

CBSE Class 9 Maths Chapter-wise Important Questions and Answers include topics from all chapters. They help students prepare well by focusing on important areas, making revision easier.

Other Important Related Links for CBSE Class 9 Maths